Opettajan sähköposti: Algebra ja geometria 5 op
|
|
|
- Ilmari Haapasalo
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Opettjn sähköposti: Algebr j geometri 5 op
2 Os: Sisältö Algebrn lskulit (luvut j lusekkeet) Tärkeimmät yhtälötyypit Suorn yhtälöt, linerinen mlli Toisen steen polynomimlli Muit yhtälötyyppejä, linerinen yhtälöpri Os: Suorkulmisen kolmion geometri Yleinen kolmion rtkiseminen Kurssitvoitteet. Käytännön lskutidon j lskurutiinin kehittäminen käänteisen opetuksen metodi noudtten (trkoitt, että nnetn lskutehtävät, teorin käytetään vähemmän ik, sitä löytyy mm. Moodlest). Lskentn suunniteltujen työvälineohjelmien käytön omksuminen. (Käytetään Online- lskint, jok löytyy osoitteest
3 Trvittvt välineet Tulukkokirj (Mol ti Tekniikn tulukot) Lskin, esim. Lskuvihko Huom! Tunneill käytetään useimmiten Online- lskint, jok löytyy osoitteest Knnettv tietokone mukn tunneille.
4 Arviointi Arvosn-steikko: hyl,,,,4,5 Arvosn määräytyy seurvien suoritusten perusteell: Tehtävien teko koett A. Tehtävien lskeminen (rvosnt,, m ). Kurssin luss jetn lskumoniste, jok sisältää lskutehtäviä koko kurssin lueelt.. Tunneill edetään lskumonisteen mukn ihe-lue (A-M) kerrlln. Lskumonisteen lskujen lskemisell pääsee rvosnoihin. Pisterjt: 0 8 p hyl 9 p 4 7p 8 - p 5 p p B. Kokeet (kikki rvosnt). Kokeill voi päästä prhimpiin rvosnoihin 4 j 5.. Koe ei voi lske tehtävillä nsittu rvosn.. Bonuspisteitä s läsnäolost (m p) sekä lsketuist lskuist (p), jotk lisätään koekeskirvoon. 4. Kokeist yleensä järjestetään uusintkert prin viikon kuluess C. Itseopiskelumetodi: Opiskelij, joll on hyvät mtemttiset vlmiudet j kyky itsenäiseen työskentelyyn
5 . Hylätyn kurssin suorittminen Yleisiä uusinttenttipäiviä järjestetään kerrn kuuss Vihtoehtoinen tp prnt rvosn hyväksytyksi on pyytää opettjlt lisätehtäviä. Itseopiskeluvihtoehto Syitä: Työssä käynti opiskelun ohell, perhesit, hyvin suoritetut mtemtiikn pohj-opinnot esim. lukioss, kyky j motivtio itsenäiseen opiskeluun Kurssin voin suoritt lopputentillä kerrn kuukudess järjestettävänä yleisenä tenttipäivänä, johon ilmoittudutn SOLE sovelluksess. Lskukokoelmn lskut pluttmll voi esittää näytön osmisest (m /5) Itseopiskeluun sopivi kirjoj löytyy muutm kpple kirjstost nimellä AMK mtemtiikk (ti vstv). Lukion oppikirjt käyvät myös oppimterilien
6 Os Potenssien lskusäännöt Murtolukujen lskusäännöt Juurilusekkeet
7 Ennkkotesti: Potenssien lskusäännöt ) ( ) ( ) ( 9 ) ( ) ( ) ( u u u c c c c c ) ( ) (4 ) ( b b b b b b b b b ) ( 0 b Säännöt: m n m n m n m n m n m n ) ( m n m y y ) ( 0 n n n n b b ) ( ) ( n n n y y ) ( rtkisut
8 Testi Sievennä lusekkeet käyttäen potenssien lskusääntöjä ) ( ) ( b b b ) 5 ( ) 5 ( ) ) (( t t t 5 5 y y y y Säännöt: m n m n m n m n m n m n ) ( m m m y y ) ( 0 n n n n b b ) ( ) ( n n n y y ) ( ) 5 ( ) ( ) (4 c b c b bc bc rtkisut
9 Murtolusekkeiden sievennys lgebrlskimell (esim. Wolfrmlph) Kikki edellä esitetyt esimerkit voidn rtkist lgebrlskimen simplify komennoll, jok trkoitt suomeksi sievennä
10 Aihe A Potenssien lskusäännöt
11 Smnkntisten potenssien kertolsku Esimerkki smnkntisten potenssien kertolskust kpl kpl 5 ( )( ) Kertominen voidn suoritt lskemll eksponentit yhteen 5 Yleisesti: n m = m+n
12 Smnkntisten potenssien jkolsku Esimerkki smnkntisten potenssien supistmisest 7 4 Hvinto: Supistus voidn tehdä vähentämällä eksponentit toisistn 7 = 7 = 4 Yleisesti: n m = n m
13 Miten määritellään 0:s potenssi 0? Esimerkki smnkntisten potenssien supistmisest, joss osoittjn eksponentti on sm kuin nimittäjän = = 0 Sm esimerkki käyttämällä potenssien osmäärän sääntöä Tuloksen perusteell on määriteltävä, että 0:s potenssi 0 = Yleisesti: 0 =
14 Negtiivinen potenssi -n Esimerkki smnkntisten potenssien supistmisest, joss osoittjn eksponentti on suurempi kuin nimittäjän 5 5 = 5 = Sm esimerkki käyttämällä potenssien osmäärän sääntöä Esimerkin perusteell - trkoitt sm kuin Yleisesti: Luvun negtiivinen potenssi määritellään luvun positiivisen potenssin käänteisluvuksi n = n
15 Perättäiset potenssiin korotukset Esimerkki smnkntisten potenssien kertolskust ( ) ( )( )( ) 6 Lsku voidn suoritt kertomll eksponentit keskenään ( ) 6 Yleisesti: ( n ) m = mn
16 Tulon korottminen potenssiin Esimerkki : (b) ( b)( b)( b) bbb b Siis: tulo korotetn potenssiin siten, että kukin tulon tekijä korotetn erikseen ko. potenssiin Yleisesti: (b) n = n b n
17 Osmäärän korottminen potenssiin Esimerkki : ( b ) b b b bbb b Osmäärä korotetn potenssiin siten, että osoittj j nimittäjä korotetn erikseen ko. potenssiin Yleisesti: ( b )n = n b n
18 Murtoluvun negtiivinen potenssi Esimerkki : ( b ) b b b b ( b ) Murtoluvun negtiivinen potenssi on sm kuin sen käänteisluvun vstv positiivinen potenssi Yleisesti: ( b ) n = ( b )n Esim. ( ) = ( ) = 9 4
19 Yhteenveto perussäännöistä m n m n m n m n m n m n ) ( m n m y y ) ( 0 n n n n y y ) ( ) ( n n n y y ) (
20 Murtopotenssit Esimerkki : Mitä trkoitt potenssimerkintä Jos vditn, että perättäisten potenssiinkorotusten sääntö on voimss, niin ( ) =. = = Toislt tiedetään, että ( ) = Johtopäätös on se, että potenssi puoli vst neliöjuuren otto Esim. Luku 0 voidn lske lskimell myös 0^(/)
21 Muit murto- potenssimerkintöjä j.n.e Yleisesti: n n 4 4 j.n.e Yleisesti: n m m n Esim. Luku voidn lske lskimell ^(/)
22 Aihe B Murtolukujen supistettu muoto Murtolukujen summ, erotus, tulo, osmäärä
23 Murtolusekkeen supistminen Jos osoittjll j nimittäjällä on jokin yhteinen tekijä, se voidn supist pois Sievennä: b( b ) Yhteinen tekijä b voidn supist b ( ) ( ) b
24 . Murtolukujen supistminen y y Murtoluku supistetn perusmuotoon siten, että osoittj j nimittäjä jetn tekijöihin (=esitetään tulon). Jos osoittjss j nimittäjässä on yhteisiä tekijöitä, ne voidn supist pois Esim. Supist perusmuotoon Supistminen voidn tehdä viheittin kuten yllä ti yhdellä kerrll etsimällä osoittj j nimittäjän suurin yhteinen tekijä
25 . Murtolukujen yhteenlsku. Murtoluvut lvennetn siten, että niille sdn sm nimittäjä (=lkuperäisten nimittäjien pienin yhteinen jettv). Lopuksi osoittjt lsketn yhteen. Esim. Lske ( (4 9 4 Sekmurtoluvut muunnetn ennen lvennust perusmuotoisiksi murtoluvuiksi. Kokonisluvut lvennetn Esim. Lske ( 7 4 ( 0 (
26 . Murtolukujen vähennyslsku. Murtoluvut lvennetn siten, että niille sdn sm nimittäjä (=lkuperäisten nimittäjien pienin yhteinen jettv). Lopuksi osoittjt yhdistetään etumerkit huomioiden Esim. Lske - ( ( Sekmurtoluvut muunnetn ennen lvennust perusmuotoisiksi murtoluvuiksi. Kokonisluvut lvennetn Esim. Lske ( 5 (4 4 (
27 . Murtolukujen kertolsku b c d c bd * Murtoluvut kerrotn siten, että osoittjt kerrotn keskenään j nimittäjät kerrotn keskenään. * Supistminen voidn tehdä lopuss ti väliviheess Esim. Lske 4 * Sekmurtoluvut muunnetn ennenkertolsku perusmuotoisiksi Esim. Lske 4 * * * 4 70 ) 5 6
28 . Murtolukujen jkolsku * Murtoluvut jetn siten, että osoittj kerrotn jkjn käänteisluvull : 4 Esim. Lske 4 : 4 7 Esim. Lske 5 4 bc d c d b d c b :
29 4. Murtoluvun potenssi ( b ) n b n n Murtoluku korotetn potenssiin niin, että osoittj j nimittäjä kumpikin korotetn ko. potenssiin Esim. ) 4 4 ( 7 64 Esim. Jos potenssi on miinusmerkkinen, kntluvun käänteisluku korotetn vstvn posit. potenssiin ) ( ) ( 9 4
30 Virheellinen supistus! VÄÄRIN! SUMMASTA EI VOI SUPISTAA, supistminen edellyttää, että osoittj j nimittäjä ovt tulomuodoss Sen sijn seurv supistus on oikein, kosk siinä osoittj on viety ensin tulomuotoon ( ) ( )
31 Aihe C Murtolusekkeiden supistminen Murtolusekkeiden summ, erotus, tulo, osmäärä
32 Murtolusekkeen supistminen Jos osoittjll j nimittäjällä on jokin yhteinen tekijä, se voidn supist pois Sievennä: ( )( ) ( ) Yhteinen tekijä + voidn supist ( )( ) ( ) ( )
33 Onko oikein? Summst ei voi supist, Tämä on VÄÄRIN supistettu! Osoittjn j nimittäjän on oltv tulomuodoss supistettess Seurv sievennys on tehty oikein! ( ) Osoittj. steen polynomi on viety ensin tulomuotoon (+), sitten supistminen :ll on mhdollist
34 Miten summmuotoinen osoittj ti nimittäjä sdn tulomuotoon? (supistust vrten) Algebrlskimen fctor komennoll: esim. fctor ^+5*b Tpus: Yhteisen tekijän ottminen sulkumerkkien eteen 5b ( 5b) Tpus: Jos osoittj ti nimittäjä on khden neliön erotus (esim. ti 4 ti 9 b ), se voidn kirjoitt tulon, jonk tekijöinä ovt kntlukujen summ j erotus (*) 4 ( )( (*) Kvkirjn kv ( b ) = (+b)(-b) ) Myös kv + b + b = (+b) voidn käyttää
35 Sievennä supistmll 5 7 h k k h h h 4 4 ) ( b b 4 4 ) ( y y h 7 k k ) 5 ( 5) ( ) ( 4 ) ( 4 h h h h ) ( ) )( ( ) ( b b b b ) (4 4 ) ( ) ( ) )( ( ) ( y y y y y
36 . Murtolusekkeiden summ. Murtolusekkeet voi lske yhteen vst kun niillä on sm nimittäjä (vtii lvennuksen). Lopuksi osoittjt lsketn yhteen. Esim. Ilmoit yhtenä murtolusekkeen ( 4 h h h h h (h h h h( h ) h( h ) h h( h )
37 . Murtolusekkeiden vähennyslsku Myös vähennyslsku loitetn lventmll murtolusekkeille sm nimittäjä Esim. - + ( ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) Tehtävässä käytettiin ns. ristiin lvennust, yksinkertisimmilln y b b b y b b y b
38 4. Murtoluskkeiden kertolsku b c d c bd * Osoittjt kerrotn keskenään j nimittäjät kerrotn keskenään. Lopuss supistetn, jos on trpeen Esim. * b 4y 7 b 4y 7 b 8y yksi supistuu pois
39 5. Murtolusekkeiden jkolsku * Murtolusekkeell jetn siten, että kerrotn jkjn käänteisluvull Sievennä : y 4 b 4 b y b 8 y b 8y Sievennä ( )
40 Aihe D Juuret: neliöjuuri, kuutiojuuri,... Juurten sieventäminen Juurten potenssimuoto
41 Neliöjuuri trkoitt sitä positiivist luku, jonk neliö on ( ) Esim. 4 = kosk = 4 49 = 7 kosk 7 = kosk.44*.44 =.00 4 ei ole olemss (minkään luvun neliö ei negt.) Määritelmä voidn ilmist myös siten, että on yhtälön = positiivinen juuri.
42 Kuutiojuuri trkoitt sitä luku, jonk kuutio on ( ) Kuutiojuuren voi ott myös negtiivisest luvust. Juuri on tällöin negtiivinen Esim. 8 = kosk =** = 8 5 = -5 kosk (-5) =(-5)*(-5)*(-5)= kosk.54 = 0.0 Määritelmä voidn ilmist myös siten, että on yhtälön = juuri.
43 Muut juuret n trkoitt sitä luku, jonk n:s potenssi on ( n ) n Määritelmä voidn ilmist myös siten, että n on yhtälön n = juuri. Kun n on prillinen, n voidn ott vin positiivisest luvust Kun n on priton, n, juurrettv voi oll myös negtiivinen, jolloin juurikin on negtiivinen
44 Juurten potenssiesitys voidn esittää potenssimuodoss ( ) j ( ) Ts. Sekä neliöjuuri että potenssiin puoli korotettun toiseen ntvt luvun => neliöjuuri j potenssi puoli ovt smt. Vstvsti =, 4 = 4, j.n.e Lske käyttäen muoto 0.5
45 Juuret lskimiss kokeile lskimellsi * Uudemmt lskimet eivät lske likirvo linkn, jos juurrettvksi nnetn kokonisluku. Likirvon voi sd esim. lisäämällä juurettvn desimlipisteen. Yleisimmät juurinäppäimet lskimiss y Esim. Windowsin lskimess ei ole kuin neliöjuuri: siinä esim. 5. juuri luvust 7 lsketn: 7 ^ ( / 5 ) Ecelissä = 7 ^ (/5)
46 Juurten sieventäminen, tulo j osmäärä Melkein kikki uudemmt lskimet osvt sieventää juurilusekkeit. Kun syötät lskimeen esim. se vst Sievennys perustuu khteen sääntöön:
47 Esimerkkejä sievennyksistä Tpus: Juurrettvss on tekijöitä, jotk ovt kokonisluvun neliöitä. Juuren voi ott kustkin tekijästä erikseen Tpus: Kun kerrotn kksi juurt, voidn juurrettvt yhdistää ennen juuren otto, jolloin juurrettvn stt muodostu neliötekijäitä 6 4 Tpus: Kun jetn kksi juurt, voidn juurrettvt supist ennen juuren otto => tulos yksinkertistuu
48 Pohdi seurv? Miten kirjoitettisiin juurimerkintää käyttäen seurv potenssi? -/ Vihje: Eksponentin edessä olev miinus merkki trkoitt, että kyseessä on kntluvun vstvn positiivisen potenssin käänteisluku. Vstus seurvll klvoll.
49 Potenssi -/ juurimuodoss? Vstus :
50 Polynomien peruslskutoimitukset Summ j erotus Vkioll kertominen Kertolsku Potenssilsku Jkolsku
51 Polynomit ste, steluku = muuttuj n n + n- n termejä vkiotermi Esim. + 5 on :nnen steen polynomi, joss on 4 termiä. Vkiotermi on -. Polynomin kertoimet ovt, -, 5 j -
52 Polynomien yhteenlsku Yhteenlskuss sulkumerkit voi poist suorn. Tämän jälkeen yhdistetään smnsteiset termit lskemll niiden kertoimet yhteen Esim. Lske summ ( ) + ( ) Sulkuj ei trvit. Yhdistetään smnsteiset termit: = ( + 4) 5 + (7 + ) =
53 Polynomien vähennyslsku Vähennyslskuss vähennettävään lisätään vähentäjän vstpolynomi, joss kikkien termien etumerkit on käännetty. Ts. Vähentäjän edessä olev miinusmerkki kääntää vähentäjän kikkien termien etumerkki Vähennettävä Vähentäjä Esim. Lske erotus ( ) - ( ) Sulut poistetn kääntämällä vähentäjän termien etumerkit: =
54 Vkio * polynomi ( b c) b c Polynomi kerrotn vkioll siten, että sen kukin termi kerrotn ko. vkioll Esim. ( + 5) = * + *5 = Esim. - ( 5 - ) = -*5 + (- )*(-) = Polynomi vkio b c c b c Esim. 5 = 5 - = 5 -
55 Polynomien kertolsku ( b)( c d) c d bc bd Kertolskuss tulon. jäsenen kikill termeillä kerrotn. jäsenen kikki termit (ns. ristiin kertominen). Ts. jos. jäsenessä on termiä j toisess termiä, Kertolsku tuott = 6 tulo, jotk lsketn yhteen Esim. Lske ( + 5) * ( - + ) ( + 5) * ( - + ) = * + *(-)+ * + 5* + 5*(-) + 5 = =
56 Polynomien potenssi Polynomien potenssi voidn lske ) Muuttmll se kertolskuksi b) Kvston kvoill muodoill (+b) n Esim. Lske ( + ) Tp: ( + ) = (+)(+) = *+*+*+* = + + Tp: Kvkirjn kv ( + b) = + b + b nt kun = j b = ( + ) = +* + = + + Esim. Lske ( - ) Tp: ( - ) = (-)(-) = *+*(-)+ (-)*+(-)*(-) = Tp: Kvkirjn kv ( - b) = - b + b nt kun = j b = ( - ) = () - * + =
57 Polynomien jkolsku Vikehko, ei kokeiss Polynomien jkolsku voidn suoritt jkokulmll, jok muistutt lsteell opittu kokonislukujen jkolskun jkokulm Esim. Suorit jkolsku ( 4 - ) : ( + ) jkj osmäärä jettv Tulos: jkojäännös
58 Luku : Yhtälöt Os: Ensimmäisen steen yhtälöt
59 Esimerkki mtemttisest ongelmst, jok rtkistn ensimmäisen steen yhtälön vull: Eräällä kokonisluvull on sellinen ominisuus, että kun lukuun lisätään 0, niin luku kolminkertistuu. Mikä luku on kyseessä? Ongelm muunnettun yhtälöksi Rtkisu: + 0 = 0 = = => = 5
60 Käytännön tehtävä. steen yhtälön vull Kukolämmön kuukusilsku muodostuu 55 perusmksust + kulutukseen perustuvst energimksust, jonk yksikköhint on 50 /MWh. Erään perheen mliskuun lsku oli 85 Euro. Kuink mont MWh:t energi he kuluttivt mliskuuss? Ongelm muunnettun yhtälöksi Rtkisu: * = 85 ( = kulutettu energi) 50 = = 0 = 0/50 =.6 Energin kulutus oli.6 MWh
61 Ensimmäisen steen yhtälön perustyypit Perustyypit: ) 5 = ) + = 5 Yhtälöt joiss esiintyy sulkuj: ) ( + ) - = 5 ( + ) Yhtälöt joiss esiintyy kokonislukunimittäjiä: 4) Kertoimet voivt oll myös desimlilukuj ti juuri: 5) 5 Kertoimet voivt oll myös symbolej: 6) + = Ensimmäisen steen yhtälöjä esiintyy usein fysiikss: 7) v = v 0 + t rtkise t
62 Perustyypit ) 5 = = / 5 Tyypin = b rtkisu sdn jkmll :n kertoimell. = b / ) + = 5-5 = - - = - = - /- = / Muuttujien j vkioiden erottminen: Viedään muuttuj sisältävät termit yhdelle puolen yhtälöä j vkiot toiselle puolen. (Termejä siirrettäessä etumerkki vihdetn) Tämän jälkeen kertoimet yhdistetään, jollon tuloksen on perusmuoto = b
63 Yhtälöt joiss on sulkulusekkeit ( + ) - = 5 ( + ) = Rtkiseminen lk sulkujen poistoll 6 + = = 0 - = 9
64 Yhtälöt joiss esiintyy kokonislukunimittäjiä ) 6) ) Lvennetn kikkiin nimittäjä 6 ( ) 6 ( ) Kerrotn kikki 6:ll (+) + 6 = (-) = = -- 7 = -5 X = -5/7
65 ( Kertoimet voivt esim. juuri ti symbolej 5 5 ) + = v = v 0 + t 4 - = - ( ) = - => = - v - v 0 = t v v 0 t 4, rtkise t Jetn tuntemttomn t kertoimell
66 Toisen steen yhtälöt + b + c = 0
67 Esimerkki mtemttisest ongelmst, jok rtkistn. steen yhtälön vull: Erästä suorkiteen muotoist tontti ympäröi it, jonk pituus on 00 m. Tontin pint-l on 600 m. Määritä tontin sivujen pituudet? Yhtälö : (50 ) = 600 Sievennetään : 50 - = 600 Viedään kikki termit oikelle puolen yhtälöä: 0 = eli = 0 Rtkisu koneell: Vstus: Suorkulmion sivut = 0 m j y = 50 0 = 0 m (toinen vihtoehto = 0 m j y=0 m on sm)
68 Toisen steen yhtälön rtkisumenetelmiä HUOM!. Toisen steen yhtälöitä joudutn rtkisemn usein eri oppiineiss. Knntt hnkki lskin, jok os rtkist utomttisesti. steen yhtälöt, kun lskimeen syötetään sen kertoimet, b j c Tp: Rtkisukvn käyttö (toimii in). Viedään yhtälö perusmuotoon + b + c = 0. Sijoitetn kertoimet, b j c kvn b b 4 c Esim. Rtkise yhtälöstä = 0 kertoimet (.).7 Sievennetään juurilusekett = ti =.46
69 Toisen steen yhtälön rtkisumenetelmiä Tp: Grfinen rtkisu: Piirretään lusekkeen + b + c kuvj j luetn juurten likirvot kuvjst Juuret likimin j.4
70 Villininen. steen yhtälö ( tpus c = 0) Ei trvit lrtkisukvn käyttöä. Yhtälö on muoto + b = 0 Fktoroidn vsen puoli: ( + b ) = 0 joko = 0 ti + b = 0 Juuret: = 0 ti = - b/ Näissä toinen juuri on in = 0 Toinen juuri sdn tulomuodon toisen tekijän + b nollkohdst. Esim. Rtkise 5 = 0 ( 5 ) = 0 = 0 ti 5 = 0 = 0 ti = 5/ plot 5
71 Villininen. steen yhtälö ( tpus b = 0) Ei trvit rtkisukvn käyttöä. Yhtälö on muoto + c = 0 Rtkistn luksi yhtälöstä smn tpn kuin. steen yhtälöä rtkistess = - c = -c/ Otetn neliöjuuri: Jos oike puoli < 0, rtkisu ei ole Jos oike puoli > 0, rtkisun c Näissä toinen juuri on in = 0 Toinen juuri sdn tulomuodon toisen tekijän + b nollkohdst. Esim. Rtkise 5 = 0 = 5 = 5/ = 5.6 Plot - 5
72 A. Perusmuoto j rtkisukvn käyttö Muut muotoon + b + c = 0 j merkitse tulukkoon kertoimet, b j c ) 5 = ) + = 5 ) - = 7 4) ( ) ( + ) = 0 Rtkise edellä olleist tehtävistä ) j ) ilmn rtkisukv Villinnisen. steen yhtälönä b) 5 = b) - = 7 5 =0-5 +=0 ) =0 + -0=0 + =0 b c b c -5 b c b c - Mitkä ovt, b j c seurvss yhtälössä, joss rtkistv muuttuj on t 5) = v 0 t + ½ t b c
73 Yhtälön + b + c = 0 juurten lukumäärä Rtkisukvss b b 4 c b 4 c on nimeltään diskriminntti Juurten lukumäärä riippuu neliöjuuren sisällä olevn ns. diskriminntin rvost Kun b 4 c > 0, yhtälöllä on erisuurt juurt kuvj leikk kseli khdesti Kun b 4 c < 0, yhtälöllä ei ole relijuuri kuvj ei leikk -kseli Kun b 4 c = 0, yhtälöllä on yksi juuri kuvj sivu -kseli
74 Funktion y = + b + c kuvj Kuvj on prbeli > 0 => prbeli uke ylös < 0 => prbeli uke ls Kolme tärkeää pistettä: Nollkohdt: b b 4 c Huipun koordintti b nollkohtien keskirvo:
75 Aihe H Suorn yhtälö
76 Suorn yhtälön perusmuoto y = k + b Esim. Piirrä suor y = + k = kulmkerroin b = vkiotermi Esimerkissä kulmkerroin k = - Se kertoo y:n muutoksen, kun ksv yhdellä Vkio b = - Vkio kertoo kohdn, missä suor leikk y kseli.
77 Suorn yhtälö kun kulmkerroin k j yksi suorn piste ( 0,y 0 ) tunnetn y y k( 0 0 ) Esim. Määritä sen suorn yhtälö, jonk kulmkerroin on j jok kulkee pisteen (, ) kutt y ( ) Poistetn sulut y 6 y 8
78 Suorn yhtälö kun kksi sen pistettä (,y ) j (,y ) tunnetn. Kulmkerroin määritetään kvll. Suorn yhtälö on y y k( ) Esim. Määritä sen suorn yhtälö, jok kulkee pisteiden (, ) j (-, 7) kutt kulmkerroin Suorn yhtälö k y ( ) y 7 k 6 4 y 9 y y
79 Aihe I Linerinen mlli = jokin käytännön probleem ti tilnne, jot voidn kuvt yhtälöllä y = k + b
80 Esimerkkinä mikä thns plvelu, joss hint muodostuu kiinteästä perusmksust+ kulutuksest riippuvst osst Esim. Rovniemellä omkotitlon kukolämmön kuukusimksu koostuu 55 perusmksust + energimksust, joss yksikköhint on 50 /MWh Esitä kuukusilskun loppusumm Y energin kulutuksen X (MWh) funktion y 50 55
81 Esim. Vuosittinen vesimksu koostuu liittymämksust + veden kulutukseen perustuvst osst. Esim. Eräs siks mksoi vuodess 85 Euro vesimksu. Hän kulutti vettä 5 m. Mikä oli vuotuinen liittymämksu, jos vesikuution hint on 5.0 Euro y 5. 0 b Sijoitettn pri = 5 j y = 85 yhtälöön j rtkistn vkio b, jok on kysyttty liittymämksu b b
82 Määritä kupungin kukolämmön kk- mksu j perusmksu sikkn lskujen perusteell Mttisen perheen lsku oli 46,40 kun kulutus oli,70 MWh, Sipoln lsku oli 8,0 kun kulutus oli,5 MWh. Määritä perusmksu j energin yksikköhint ( /MWh) TAPA: Muodostetn suorn yhtälö, kun suor kulkee pisteiden (.5, 8.) j (.70, 46.4) kutt k y y y (.7) y y kulmkerroin Perusmksu = 58 J energimksu 5
83 TAPA: Sijoitetn (, y ) prit ( = kulutus, y = lsku) Yhtälöön y = k + b j rtkistn yhtälöprist k j b Mttinen,7 MWh 46,40 Eur Sipol,5 MWh 8,0 Eur = k *.7 + b 8. = k*.5 + b Kerrotn lempi yhtälö :llä, Lsketn yhtälöt yhteen, jolloin b eliminoituu = k *.7 + b -8. = -k*.5 b ================== 8. =.7k.5k = 0.5 k Jetn 0.5 : llä k = 8. / 0.5 = 5 Sijoitetn k = 5 ensimmäiseen yhtälöön 46.4 = 5*.7 + b => b = *.7 = 58.0
84 Suorien leikkuspiste sdn grfiikst ti yhtälöprist Esim. Kuink mont km vuodess pitää vähintään j, jott diesel uto tulisi edullisemmksi kuin bens-uto. kulutus litrhint Vero Km- kustnnus Bens-uto 5.8 L/00 km.8 /L 5 5.8*.8/00 = 0,080 Dieseluto 4.8 L /00 km.5 /L *.5/00 = 0,060 Tp: Merkitään vuotuisi jokilometrejä X: llä. Kokoniskustnnukset ovt tällöin Bens- utolle: Y = X + 5 Diesel-utolle : Y = X Etsitään sellinen km- määrä X, joss suort risteävät: Y = X Y = X ==================== 0 = 0.00 X - 5 => X = 5/0.00 = 650 km
85 Tp: Grfinen rtkisu Grfiikss lempi suor kuv bens-uto j ylempi dieseliä Dieselin kokoniskustnnukset menevät bensuton kustnnuksen lle n 6 tkm:n kohdll
86 Tp: Päättely. Kilometrikustnnusten ero on = 0.0 Eur/km. Veroiss on ero = 5 Euro. On jettv niin mont kilometri, että tästä kertyy 5 Euro. Jos kilometrimäärää merkitään X:llä niin bens- j dieselutojen kustnnukset ovt smt kun 0.0 * X = 5 Jost X = 5/0.0 = 650 km
87 Aihe J Verrnnot j verrnnollisuus
88 Verrnnoll rtkevi lskuj. 45 m sunto eräässä kerrostloss mks Pljonko mks 68 m sunto smss rpuss jos neliöhint on sm? l hint Eur 68m 45m Eur 967Eur. Uim-ltn täyttö pumppusnopeudell 0 ltr/min kestää 4.0 h. Kunko täyttö kestää pumpull, jonk nopeus on 0 ltr/min nopeus ik 0 L/min 4 h 0 L/min L 0 4h L 0 4h. h 0 0 min min Hintojen suhde = lojen suhde ti myös Hint / l = vkio Täyttönopeus kert täyttöik = vkio
89 RISTIIN KERTOMINEN b c Nimitykset: Lukuj j snotn verrnnon äärijäseniksi Lukuj b, c snotn verrnnon keskijäseniksi Kun hlutn rtkist verrnnon jokin jäsen, yleensä loitetn ns. ristiin kertomisell: Ääriäsenten tulo = keskijäsenten tulo. bc sdn jkmll toinen puoli sen kertoimell = bc/
90 Tvllisimmt verrnnollisuustyypit Verrnnollisuustyyppi Ominisuus Kvn X j Y suorn verrnnolliset Y/X = vkio y = k X j Y kääntäen verrnnolliset X*Y = vkio y = k Y verrnnollinen X:n neliöön Y/X = vkio Y = k Y kääntäen verrnnollinen X:n neliöön Y*X = vkio Y = k Fysiikn kvoj, joiss esiintuu verrnnollisuutt: s = v t P = R I F = G Mm r
91 Esim. Oletetn, että uton polttoineen kulutus (L/00 km) suurimmll vihteell jettess on verrnnollinen uton nopeuden neliöön. Jos nopeudell 90 km/h kulutus on 5.8 L/00km, mikä se on nopeudell 0 km/h jettess? Polttoineen kulutus y k v Kumpi seurvist on oikein? k = jokin vkio Kulutus hint km/h Y 0 km/h A y y L 00km B y L y km
92 d m h Sylinterin tiheyden kv 4 m d h m = mss d = pohjn hlkisij h = korkeus Millinen verrnnollisuus on tiheyden j korkeuden h välillä? Kääntäen verrnnollisi: tulo ρ h = vkio Millinen verrnnollisuus on tiheyden j hlkisijn d välillä? Tiheys on kääntäen verrnnollinen hlkisijn neliöön: tulo ρ d = vkio Millinen verrnnollisuus on tiheyden j mssn m välillä? Suorn verrnnollisi: ρ/m = vkio
93 Verrntojen käyttöesimerkkejä Metllilngn Resistnssi Ohmein R k d s k = metllist riippuv vkio s = johdon pituus d = johdon pksuus Eräästä metllilngst leiktun 5 m johdon resitnssi on mω. Mikä on smst lngs leiktun 60 m johdon resitnssi? Resistnssin kvst hvitn, että R on suorn verrnnollinen pituuteen. R S mω 5 m X 60 m 60m 5m m
94 Metllilngn Resistnssi Ohmein R k Eräs metllilnk, jonk pksuus on.00 mm j resistnssi 50 moh, korvtn yhtä pitkällä lngll, jonk pksuus on 0.60 mm. Mikä on resistnssi nyt? d Mikä seurvist on oike rtkisu? s k = metllist riippuv vkio s = johdon pituus d = johdon pksuus R d 50 mohm.00 mm X 0.60 mm m 0.6mm 50m.0mm m (0.6mm) 50m(.0mm) m m R d vkio
95 Hrjoituksi : Rtkise ristiin kertomll Rtkise T yhtälöstä Rtkise T yhtälöstä p GMT T G M r pv T 4r T 4 r r 4 r 4 r r T GM GM 4 V T pvt T pvt p V pv T
96 Aihe J Mittkv
97 Mittkvn liittyviä kysymyksiä (Vnhoj monimuotokoulutuksen pääsykoetehtäviä) 5 cm 50 cm Kuink monikertinen on isommn huen tilvuus (j mss) pienempään verrttun? ) Kksinkertinen b) 4- kertinen c) 6 - kertinen d) 8 - kertinen Kuink monikertinen on vrjostimen kuvn pintl verrttun lkuperäiseen kun projektori siirretään kksinkertiselle etäisyydelle? ) Al on kksinkertinen b) Al on 4- kertinen c) Al on 6- kertinen d) Al on 8 - kertinen
98 Yhdenmuotoiset kuviot j kppleet Yhdenmuotoisiss kuvioiss j kppleiss vstinjnojen suhteet ovt smt
99 Mittkv k Yhdenmuotoisien kuvioiden vstinjnojen suhde on vkio, jot kutsutn mittkvksi j merkitään k:ll Alkuperäinen kuvio Yhdenmuotoinen kuvio Kuvss olevn oikenpuolimmisen kolmion mittkv lkuperäiseen nähden on 6cm k cm Kolmion lojen suhde A /A = k = 4
100 Alojen j tilvuuksien suhde Oikenpuolimmisen kuution mittkv lkuperäiseen nähden on : eli k = Kuutioiden yhden thkon pint-lojen suhde on 9 : = = k Kuutioiden tilvuuksien suhde on 7 : = = k YLEISSÄÄNTÖ: Olkoon kpple B yhdenmuotoinen kppleen A knss mittkvss k. Tällöin kppleiden B j A vstinpint-lojen suhde on k j kppleiden tilvuuksien suhde on k.
101 Krtn mittkv. Kuink pitkä on mstoss jn, jok krtll on.5 cm? 5000*.5 cm = 500 cm =5 m. Arvioi krtll olevn stdionin pint-l, kun sen pint-l krtll on.5 cm. cm =.0 cm 5000 * cm = cm = 7500 m = 0.75 h :5000 trkoitt, että cm krtll = 5000 cm eli 50 m mstoss
102 Yksikkömuunnokset m 0 dm 00 cm 000 mm m 00 dm 0000 cm mm m 000 dm (ltr) cm 0 9 mm
103 Tlon pienoismlli Todellinen tlo pienoismllin mittkv :60 5 cm. Mikä on pienoismllin mittkv? ) Muodoss : X b) Desimlilukun 5/ 900= : m. Todellisen tlon pohjn l on 56 m ) Mikä on pienoismllin pohjn l? b) Mikä on pienoismllin leveys? (/60) * cm = 56 cm 56 cm / 5 cm = 0.4 cm. Tlon olohuoneen tilvuus on 70 m Mikä on pienoismllin olohuoneen tilvuus? cm*(/60) = 4 cm
104 Suorkulmisen kolmion geometri Nimitykset: α,β = terävät kulmt c = hypotenuus,b = kteetit
105 Suorkulmisen kolmion kvt 90 c b Pythgorn luse jost rtkistun c b b c Jo kreikkliset huomsivt, että suorkulmisen kolmion terävä kulm määrää sivujen suhteet. He mittsivt, lskivt j tulukoivt sivujen suhteet kikille kulmille 0 90 o. Nykyisin ne löytyvät lskimest näppäimillä sin, cos j tn. sin cos c b c Kulmn α sini = kulmn vstisen kteetin suhde hypotenuusn Kulmn α kosini = kulmn viereisen kteetin suhde hypotenuusn tn b Kulmn α tngentti = kulmn vstisen kteetin suhde viereiseen kteettiin
106 Suorkulmisen kolmion rtkiseminen Kun suorkulmisest kolmiost tunnetn kksi os, joist vähintään toinen on sivu, voidn kikki muut sivut j kulmt rtkist käyttäen esitettyjä kvoj. Tätä kutsutn kolmion rtkisemiseksi.
107 sin, cos vi tn? Oikein vi väärin? Väite Oikein Väärin sin(β) = 5 / 5.8 X tn(α) = 5 / 5 X cos(β) = 5 / 5.8 X sin(α) = 5.8 / 5 X tn(β) = 5 / 5 X cos(α) = 5 / 5.8 X 5 = = 5 + 5
108 Perustidot Sivun rtkiseminen, kun terävä kulm j jokin muu sivu tunnetn. sin( 70) sin(70) 85. Kulmn rtkiseminen kun kksi sivu tunnetn tn( ) tn (0.49). Lskin DEG moodiin
109 Esim. Rtkise kuvn kolmioss, sekä kulmt α j β Kun tunnetn sivu, on helpoint rtkst. sivu Pythgorn luseell. Sen jälkeen voidn käyttää mitä thns sivujen suhdett sin, cos ti tn kulmn lskemiseksi. Rtkistn Pythgorn luseest ( + 4 = 0 ) Kulm α voidn rtkist esim. yhtälöstä cos(α) = 4/0 = 0.7 Sen rtkisu on α = cos - (0.7) = o Toinen terävä kulm β = 90 o o = 44.4 o
110 Esim. Rtkise tuntemttomt sivut j kulmt Toinen terävä kulm α = 90 o - 6 o = 7 o Kun tunnetn sivu, j jokin kulmist, lsketn ensin toinen terävä kulm. Sen jälkeen käytetään sellist sivujen suhdett, joss tunnettu sivu esiintyy toisen sivun lskemiseen. Viimeinen sivu voidn lske Pythgorn luseell Kun tunnetn kulm α j sen viereinen kteetti (b), voidn käyttää kvoj tn(α) = /b j/ti cos(α) = b/c muiden sivujen rtkisemiseen tn( 7) / 5 5tn(7).548 c
111 Vihjeitä tehtäviin: Suorkulmisi kolmioit löytyy monist pikoist 6 h 0 Tskylkisestä kolmiost Toisin sivuvien ympyröiden väliltä Pyrmidin sisältä Tehtävät 6-69 rtkistn suorkulmisi kolmioit käyttäen.
112 Yleinen kolmion rtkiseminen Siniluse j Kosiniluse
113 Kosiniluse, siniluse, l. Kosiniluse c b bcos myös = b + c b c cosα j b = + c c cosβ. Siniluse: ( kolmion kulmn sinin suhde vstiseen sivuun on vkio ) sin b sin c sin ti sin sin b sin c. Al voidn lske khdell tvll A sin b csin bcsin ½ khden sivun tulo niiden välisen kulmn sini Heronin kv: (sopii silloin kun tunnetn kolmion kikki sivut) A p( p )( p b)( p c) p = kolmion sivujen summn puoliks
114 Etäisyyksien mittus kolmiomittuksell, esim. Mnmittrin perustyöklut ovt historiss olleet mittnuh j kulmmittri Mnmittrin tehtävänä oli määrittää pisteiden A j B välimtk. Pisteiden välissä on vr, jok kierretään pisteen C kutt, jost on näköyhteys pisteisiin A j B. Määritä jnn AB pituus kuvn mittustuloksien vull. Sovelletn kosinilusett c b bcos AB cos AB m
115 Etäisyyksien mittus kolmiomittuksell, esim. Mtti hlusi tietää kuink kukn rnnst on merellä näkyvä sri. (kuvn h) Hän vlitsi rnnlt kksi kiintopistettä A j B, mittsi näiden välimtkksi AB = 780 m. Lisäksi hän mittsi molemmist pisteistä kulmt, joss sri näkyi jnn AB nähden. Kulm kärjessä A : α = 78 o Kulm kärjessä B : β = 5 o 50 o Kolms kulm γ = = 50 o Väli AC sdn siniluseell AC sin5 780 sin50 AC 780sin5 sin m Etäisyys h on kulmn α =78 o vstinen kteetti kolmioss, jonk hypotenuus AC = 80.4 sin78 h AC h AC sin 80.4sin78 785m
116 Kosinilusett käytetään tvllisesti seurviss tpuksiss: TAPAUS: TUNNETAAN KOLMION KAKSI SIVUA JA VÄLINEN KULMA Rtkise kolmion tuntemttomt sivut, kulmt j l Sivu b rtkistn kosiniluseell: b cos b Seurv tuntemton kulm rtkistn siniluseell: sin sin40 0sin40 sin 0.6 sin (0.6) Viimeinen kulm sdn vähentämällä muut kulmt 80 o :st γ = 80 o 40 o 7.7 o = 0. o 7.7 Al: A = ½ 0*6*sin40 o = 5.4
117 Kosiniluseen käyttö: TAPAUS: TUNNETAAN KOLMION SIVUT MUTTA EI KULMIA Rtkise kolmion kulmt j l A p( p )( p b)( p c) 4(48)(49)(4) 5.5 = 8 b = 9 c = p =(8+9+)/=4 Rtkistn kosiniluseell ensin cosγ, jost sdn kulm γ cos cos 89cos cos cos (0.67) Seurv tuntemton kulm rtkistn siniluseell: sin sin80.4 8sin80.4 sin 0.77 sin (0.77) γ = 80 o 80.4 o 45.8 o = 5.8 o
118 ESIM. SINILAUSEESTA Rtkise kolmion tuntemttom sivut j kulmt Todetn ensin että α = 80 o 8 o 5 o = 47 o Puuttuvt sivut lsketn siniluseett käyttäen. 9 c sin 47 sin5 sin8 9sin 47 sin c 9sin8 sin5.47
119 Muit yhtälötyyppejä Murtoyhtälöt Juuriyhtälöt Potenssiyhtälöt
120 Perusmenetelmä : ristiinkertominen (ti nimittäjien pois kertominen)... 5 GMT M G r r 4 r T r kerrotn :llä rtkise r kerrotn -:llä 5 0. _ ti _ 0.8 GMT 4 r kerro ristiin GMT 4 4. pv T p V T rtkise T kerro ristiin p V T p V T T pvt p V
121 .. ( ) ( )( ) korot toiseen korot toiseen 0 ( ) 0 Perusmenetelmä : Juurist päästään eroon potenssiin korotuksell (toiseen korotus). Tuloksen on yleensä. ti. steen yhtälö.. Juuriehdokkt =0 j = testtn sijoittmll T 0 0 T m k m k T, rtkise k m k Epätosi: 0 ei käy Tosi: = on juuri 4 m T k 4 m k 4 T korot kolmnteen potenssiin 8 9 4b, rtkise b 4b 4b
122 Potenssiyhtälöt n =b Prillinen potenssi ei ole koskn < 0 =>ei rtkisu
123 Aihe I Toisen steen polynomimlli
124 Funktio y = + b + c. Funktion kuvj on prbeli. Aukemissuunt ylöspäin, kun > 0 lspäin kun < 0. Juuret (= kohdt, joiss prbeli leikk -kselin) b b 4c Juuri ei ole, jos juuren sisällä olev b 4c < 0. Tällöin prbeli on kokonn kselin ylä- ti lpuolell. 4. Huippu on juurten puolivälissä b Huipun y sdn sijoittmll tämä prbelin yhtälöön y = + b + c
125 Esim. Ei juuri: (b -4c) = (-7) Juuret -.5 j Juuret j
126 Esim. Piirrä prbeli y = Rtkisu: Kuvn riittää kolme pistettä: juurt + huippu.. Juuret rtkisukvll ti koneell = ti = - 7/ = -.5. Huippu = - 5 /(*) = - 5/4 = -.5 (toinen tp: juurten keskirvo.5+ = -.5) y = *(-.5) + 5*(-.5) 7 = -0.5
127 Esimerkki funktion suurimmn rvon määrittämisestä. Olkoon erään älypuhelimen myyntihint X j sen vlmistuskulut 50 Euro. Tällöin tuotto puhelint kohden on X Myyntimäärä riippuu hinnst kvll X ) Määritä puhelimen myynnistä stv kokonisvoitto X:n funktion b) Lske, millä hinnll X voitto on mksimissn., Hint = myyntimäärä M=( ) Rtk. ) Kokonisvoitto = myyntimäärä * tuotto per puhelin Y = ( X) (X 50) b) Sievennetään funktion luseke polynomiksi Y = X X X Y = - 00 X X Kuivj on lspäin ukev prrbeli: Huippu on kohdss X = -b/ = /(*-00) = 75 Euro => Tuottoisin hint on 75 Euro
128
601 Olkoon tuntematon kateetti a ja tuntemattomat kulmat α ja β Ratkaistaan kulmat. 8,4 = 12. Ratkaistaan varjon pituus x. 14 x = 44,
 Pyrmidi 3 Geometri tehtävien rtkisut sivu 08 60 Olkoon tuntemton kteetti j tuntemttomt kulmt j β Rtkistn kulmt. 8,4 cos 8,4 cos 45,579... 46 β 90 60 4 Rtkistn vrjon pituus 3 44,470... 44 Rtkistn kteetti.
Pyrmidi 3 Geometri tehtävien rtkisut sivu 08 60 Olkoon tuntemton kteetti j tuntemttomt kulmt j β Rtkistn kulmt. 8,4 cos 8,4 cos 45,579... 46 β 90 60 4 Rtkistn vrjon pituus 3 44,470... 44 Rtkistn kteetti.
Ristitulo ja skalaarikolmitulo
 Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
Sinilause ja kosinilause
 Siniluse j kosiniluse GEOMETRI M3 Mikäli kolmion korkeus j knt tiedetään, voidn pint-l lske. Esimerkki: Lske kolmion l, kun 38 kulmn viereiset sivut ovt 8, j 6,8. Nyt knt tiedetään, korkeutt ei! 38 8,
Siniluse j kosiniluse GEOMETRI M3 Mikäli kolmion korkeus j knt tiedetään, voidn pint-l lske. Esimerkki: Lske kolmion l, kun 38 kulmn viereiset sivut ovt 8, j 6,8. Nyt knt tiedetään, korkeutt ei! 38 8,
Syksyn 2015 Pitkän matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
 Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
Reaalinen lukualue. Millainen on luku, jossa on päättymätön ja jaksoton desimaalikehitelmä?
 Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
( ) Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 321 Päivitetty 19.2.2006. Saadaan yhtälö. 801 Paraabeli on niiden pisteiden ( x,
 Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Tee B-osion konseptiin etusivulle pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Välivaiheet perustelevat vastauksesi!
 MAA8 Koe 4.4.016 Jussi Tyni Tee B-osion konseptiin etusivulle pisteytysruudukko! Muist kirjt nimesi j ryhmäsi. Väliviheet perustelevt vstuksesi! A-osio. Ilmn lskint. MAOLi s käyttää. Mksimissn 1h ik. Lske
MAA8 Koe 4.4.016 Jussi Tyni Tee B-osion konseptiin etusivulle pisteytysruudukko! Muist kirjt nimesi j ryhmäsi. Väliviheet perustelevt vstuksesi! A-osio. Ilmn lskint. MAOLi s käyttää. Mksimissn 1h ik. Lske
4 Pinta-alasovelluksia
 Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
R4 Harjoitustehtävien ratkaisut
 . Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
. Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
 OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
MATEMATIIKKA. Matematiikkaa pintakäsittelijöille. Peruslaskutoimitukset. Isto Jokinen 2015
 MATEMATIIKKA Mtemtiikk pintkäsittelijöille Peruslskutoimitukset Isto Jokinen 01 SISÄLTÖ 1. Lskujärjestys 1. Murtoluvuill lskeminen. Suureet j mittyksiköt. Potenssi. Juuri 6. Tekijäyhtälöiden rtkiseminen
MATEMATIIKKA Mtemtiikk pintkäsittelijöille Peruslskutoimitukset Isto Jokinen 01 SISÄLTÖ 1. Lskujärjestys 1. Murtoluvuill lskeminen. Suureet j mittyksiköt. Potenssi. Juuri 6. Tekijäyhtälöiden rtkiseminen
6 Kertausosa. 6 Kertausosa
 Kertusos Kertusos. ) b). ) b). ) ( ( ) : ) ( : ) b) { : [ ( ) ]} { :[ - ]} { : } -{ - } -{} c) ( ) : - ( ) ( ) ( ) ( 9) 9 9 Kertusos. ) ( ) b) ( ). ) ) ) b) / / c) : 7 7. ) ) ) b) Kertusos c) : 7 ( 9)
Kertusos Kertusos. ) b). ) b). ) ( ( ) : ) ( : ) b) { : [ ( ) ]} { :[ - ]} { : } -{ - } -{} c) ( ) : - ( ) ( ) ( ) ( 9) 9 9 Kertusos. ) ( ) b) ( ). ) ) ) b) / / c) : 7 7. ) ) ) b) Kertusos c) : 7 ( 9)
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ PISTEYTYSKOKOUS
 0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
MATEMATIIKAN HARJOITTELUMATERIAALI
 SAVONIA-AMMATTIKORKEAKOULU Tekniikk Infrrkentmisen j kivnnisln työnjohdon koulutus (ESR) MATEMATIIKAN HARJOITTELUMATERIAALI Hrjoitustehtävien rtkisut Ari Tuomenlehto - 0 - Hrjoitustehtävien rtkisut 1.
SAVONIA-AMMATTIKORKEAKOULU Tekniikk Infrrkentmisen j kivnnisln työnjohdon koulutus (ESR) MATEMATIIKAN HARJOITTELUMATERIAALI Hrjoitustehtävien rtkisut Ari Tuomenlehto - 0 - Hrjoitustehtävien rtkisut 1.
MATEMATIIKAN HARJOITTELUMATERIAALI
 SAVONIA-AMMATTIKORKEAKOULU Tekniikk Infrrkentmisen j kivnnisln työnjohdon koulutus (ESR) MATEMATIIKAN HARJOITTELUMATERIAALI Ari Tuomenlehto - 0 - Lusekkeen käsittelyä Luseke j lusekkeen rvo Näkyviin merkittyä
SAVONIA-AMMATTIKORKEAKOULU Tekniikk Infrrkentmisen j kivnnisln työnjohdon koulutus (ESR) MATEMATIIKAN HARJOITTELUMATERIAALI Ari Tuomenlehto - 0 - Lusekkeen käsittelyä Luseke j lusekkeen rvo Näkyviin merkittyä
2.4 Pienimmän neliösumman menetelmä
 2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
Tasogeometriassa käsiteltiin kuvioita vain yhdessä tasossa. Avaruusgeometriassa tasoon tulee kolmas ulottuvuus, jolloin saadaan kappaleen tilavuus.
 KOLMIULOTTEISI KPPLEIT Tsogeometriss käsiteltiin kuvioit vin ydessä tsoss. vruusgeometriss tsoon tulee kolms ulottuvuus, jolloin sdn kppleen tilvuus. SUORKULMINEN SÄRMIÖ Suorkulmisess särmiössä kikki kulmt
KOLMIULOTTEISI KPPLEIT Tsogeometriss käsiteltiin kuvioit vin ydessä tsoss. vruusgeometriss tsoon tulee kolms ulottuvuus, jolloin sdn kppleen tilvuus. SUORKULMINEN SÄRMIÖ Suorkulmisess särmiössä kikki kulmt
Tehtävä 1. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi
 Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
Preliminäärikoe Pitkä Matematiikka 5.2.2013
 Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
2.1 Vaillinaiset yhtälöt
 .1 Villiniset yhtälöt Yhtälö, jok sievenee muotoon x + bx + c = 0 (*) on yleistä normlimuoto olev toisen steen yhtälö. Tämän rtkiseminen ei olekn enää yhtä meknist kuin normlimuotoisen ensisteen yhtälön
.1 Villiniset yhtälöt Yhtälö, jok sievenee muotoon x + bx + c = 0 (*) on yleistä normlimuoto olev toisen steen yhtälö. Tämän rtkiseminen ei olekn enää yhtä meknist kuin normlimuotoisen ensisteen yhtälön
VEKTOREILLA LASKEMINEN
 ..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [
![1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [ 1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [](/thumbs/58/42571602.jpg) 1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
1.1. Laske taskulaskimella seuraavan lausekkeen arvo ja anna tulos kolmen numeron tarkkuudella: tan 60,0 = 2,950... 2,95
 9..008 (9). Lskime käyttö.. Lske tskulskimell seurv lusekkee rvo j tulos kolme umero trkkuudell: 4 + 7 t 60,0 + Rtkisu: 4 + 7 =,950...,95 t 60,0 + Huom: Lskimiss o yleesä kolme eri kulmyksikköjärjestelmää:
9..008 (9). Lskime käyttö.. Lske tskulskimell seurv lusekkee rvo j tulos kolme umero trkkuudell: 4 + 7 t 60,0 + Rtkisu: 4 + 7 =,950...,95 t 60,0 + Huom: Lskimiss o yleesä kolme eri kulmyksikköjärjestelmää:
MITEN MÄÄRITÄN ASYMPTOOTIT?
 MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
3.5 Kosinilause. h a c. D m C b A
 3.5 Kosiniluse Jos kolmiost tunnetn kksi sivu j näien välinen kulm, sinilusett on sngen vike sovelt kolmion rtkisemiseen. Luse on työklun vuton myös kolmion kulmien rtkisemiseen tpuksess, jolloin kolmion
3.5 Kosiniluse Jos kolmiost tunnetn kksi sivu j näien välinen kulm, sinilusett on sngen vike sovelt kolmion rtkisemiseen. Luse on työklun vuton myös kolmion kulmien rtkisemiseen tpuksess, jolloin kolmion
LYHYEN MATEMATIIKAN SIMULOITU YO-KOE 2 RATKAISUT
 Lyhyt mtemtiikk YO-vlmennus 8. mliskuut 00 LYHYEN MATEMATIIKAN SIMULOITU YO-KOE RATKAISUT. Trkstelln yhtälöpri, polynomin sievennöstä j lusekkeeseen sijoittmist. ) Rtkistn jälkimmäisestä yhtälöstä x, jolle
Lyhyt mtemtiikk YO-vlmennus 8. mliskuut 00 LYHYEN MATEMATIIKAN SIMULOITU YO-KOE RATKAISUT. Trkstelln yhtälöpri, polynomin sievennöstä j lusekkeeseen sijoittmist. ) Rtkistn jälkimmäisestä yhtälöstä x, jolle
Pythagoraan lause. Pythagoras Samoslainen. Pythagoraan lause
 Pythgorn luse Pythgors Smoslinen Pythgors on legendrinen kreikklinen mtemtiikko j filosofi. Tiedot hänen elämästään ovt epävrmoj j ristiriitisi. Tärkein Pythgorst j pythgorlisi koskev lähde on Lmlihosin
Pythgorn luse Pythgors Smoslinen Pythgors on legendrinen kreikklinen mtemtiikko j filosofi. Tiedot hänen elämästään ovt epävrmoj j ristiriitisi. Tärkein Pythgorst j pythgorlisi koskev lähde on Lmlihosin
10. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA
 MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
VEKTOREILLA LASKEMINEN
 3..07 VEKTOREILLA LASKEMINEN YHTEENLASKU VEKTORIT, MAA Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on
3..07 VEKTOREILLA LASKEMINEN YHTEENLASKU VEKTORIT, MAA Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on
Luku 1 = = = + = + 3 ( 7) = 2 + = + = = = = = + 1+ = + 1+ = + 1= = + 1 = = b) ( ) + = + = + c)
 Luku ) 8 8 + = + 6 6 ) ) + = + = = b) ) 7 := 7 := 7 : ) ) 9 6 7 7 = 7 := = = ( 7) ( 7) b) 5 5 5 5 + : = + 6 6 ) + + + = + + + 9 ) 5 5 6) 5+ 5 = + = = = 6 6 6 6 = + + + = + + = + + = + = 9 9 9 ( c) ) 9
Luku ) 8 8 + = + 6 6 ) ) + = + = = b) ) 7 := 7 := 7 : ) ) 9 6 7 7 = 7 := = = ( 7) ( 7) b) 5 5 5 5 + : = + 6 6 ) + + + = + + + 9 ) 5 5 6) 5+ 5 = + = = = 6 6 6 6 = + + + = + + = + + = + = 9 9 9 ( c) ) 9
Integraalilaskentaa. 1. Mihin integraalilaskentaa tarvitaan? MÄNTÄN LUKIO
 Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Numeeriset menetelmät TIEA381. Luento 9. Kirsi Valjus. Jyväskylän yliopisto. Luento 9 () Numeeriset menetelmät / 29
 Numeeriset menetelmät TIEA381 Luento 9 Kirsi Vljus Jyväskylän yliopisto Luento 9 () Numeeriset menetelmät 17.4.2013 1 / 29 Luennon 9 sisältö Numeerisest integroinnist Newtonin j Cotesin kvt Luento 9 ()
Numeeriset menetelmät TIEA381 Luento 9 Kirsi Vljus Jyväskylän yliopisto Luento 9 () Numeeriset menetelmät 17.4.2013 1 / 29 Luennon 9 sisältö Numeerisest integroinnist Newtonin j Cotesin kvt Luento 9 ()
6 Integraalilaskentaa
 6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
A-Osio. Valitse seuraavista kolmesta tehtävästä kaksi, joihin vastaat. A-osiossa ei saa käyttää laskinta.
 MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
Painopiste. josta edelleen. x i m i. (1) m L A TEX 1 ( ) x 1... x k µ x k+1... x n. m 1 g... m n g. Kuva 1. i=1. i=k+1. i=1
 Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
Algebran ja Geometrian laskukokoelma
 Algebran ja Geometrian laskukokoelma A. Potenssien laskusäännöt Sievennä 1. (r 3 ) 4 2. (2a 3 ) 3 3. x 3 x 5 4. k11 k 5 5. 2a2 a 7 5a 3 6. (-3x 2 y 3 ) 3 7. ( 1 4 ) 3 8. (2 a2 Lisätehtäviä b 3)3 9. (a
Algebran ja Geometrian laskukokoelma A. Potenssien laskusäännöt Sievennä 1. (r 3 ) 4 2. (2a 3 ) 3 3. x 3 x 5 4. k11 k 5 5. 2a2 a 7 5a 3 6. (-3x 2 y 3 ) 3 7. ( 1 4 ) 3 8. (2 a2 Lisätehtäviä b 3)3 9. (a
.) (b) Vertaa p :tä vastaavaa kineettistä energiaa perustilan kokonaisenergiaan. ( ) ( ) = = Ek
 S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
7.lk matematiikka. Geometria 1
 7.lk mtemtiikk 1 Htnpään koulu 7B j 7C Kevät 2017 2 Sisällys 1. Koordintisto... 4 2. Kulmien nimeäminen j luokittelu... 8 3. Kulmien mittminen j piirtäminen... 10 4. Ristikulmt j vieruskulmt... 14 5. Suort,
7.lk mtemtiikk 1 Htnpään koulu 7B j 7C Kevät 2017 2 Sisällys 1. Koordintisto... 4 2. Kulmien nimeäminen j luokittelu... 8 3. Kulmien mittminen j piirtäminen... 10 4. Ristikulmt j vieruskulmt... 14 5. Suort,
Sarjaratkaisun etsiminen Maplella
 Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
 II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
Paraabelikin on sellainen pistejoukko, joka määritellään urakäsitteen avulla. Paraabelin jokainen piste toteuttaa erään etäisyysehdon.
 5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
SUORAKULMAINEN KOLMIO
 Clulus Lukion Täydentävä ineisto 45 0 45 60 ( - ) + SUORKULMINEN KOLMIO Pvo Jäppinen lpo Kupiinen Mtti Räsänen Suorkulminen kolmio Suorkulminen kolmio Käsillä olev Lukion Clulus -srjn täydennysmterili
Clulus Lukion Täydentävä ineisto 45 0 45 60 ( - ) + SUORKULMINEN KOLMIO Pvo Jäppinen lpo Kupiinen Mtti Räsänen Suorkulminen kolmio Suorkulminen kolmio Käsillä olev Lukion Clulus -srjn täydennysmterili
Kertaustehtävien ratkaisut
 Rtkisuist Nämä Trigoometriset fuktiot j lukujoot kurssi kertustehtävie j -srjoje rtkisut perustuvt oppikirj tietoihi j meetelmii. Kustki tehtävästä o yleesä vi yksi rtkisu, mikä ei kuitek trkoit sitä,
Rtkisuist Nämä Trigoometriset fuktiot j lukujoot kurssi kertustehtävie j -srjoje rtkisut perustuvt oppikirj tietoihi j meetelmii. Kustki tehtävästä o yleesä vi yksi rtkisu, mikä ei kuitek trkoit sitä,
1.1 Lukujoukot ja laskutoimitukset
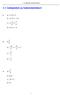 . Lukujoukot j lskutoimitukset. Lukujoukot j lskutoimitukset. ) ( ) b) (7,) 7, c) ( ) d) (π ) π. ) 0 0 b) c) d) 7. ) 9 b) 0,0 c) 9 d) π . Lukujoukot j lskutoimitukset. ) Luvun - vstluku on -(-). Luvun
. Lukujoukot j lskutoimitukset. Lukujoukot j lskutoimitukset. ) ( ) b) (7,) 7, c) ( ) d) (π ) π. ) 0 0 b) c) d) 7. ) 9 b) 0,0 c) 9 d) π . Lukujoukot j lskutoimitukset. ) Luvun - vstluku on -(-). Luvun
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 5 1 Jtkuvuus Trkstelln funktiot fx) josskin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jtkuv ti epäjtkuv. Jtkuvuuden ymmärtää prhiten trkstelemll epäjtkuv
Mtemtiikn tukikurssi Kurssikert 5 1 Jtkuvuus Trkstelln funktiot fx) josskin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jtkuv ti epäjtkuv. Jtkuvuuden ymmärtää prhiten trkstelemll epäjtkuv
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
 22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS
 11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
sin θ θ θ r 2 sin 2 θ φ 2 = 0.
 Mtemtiikn j tilstotieteen litos Osittisdifferentiliyhtälöt Kevät 21 Hrjoitus 9 Rtkisuj Jussi Mrtin 1. Osoit, että Lplce-yhtälö pllokoordinteiss on 2 u 1 r 2 2 u r r 1 r 2 sin θ u 1 2 u sin θ θ θ r 2 sin
Mtemtiikn j tilstotieteen litos Osittisdifferentiliyhtälöt Kevät 21 Hrjoitus 9 Rtkisuj Jussi Mrtin 1. Osoit, että Lplce-yhtälö pllokoordinteiss on 2 u 1 r 2 2 u r r 1 r 2 sin θ u 1 2 u sin θ θ θ r 2 sin
T Syksy 2002 Tietojenkäsittelyteorian perusteet Harjoitus 5 Demonstraatiotehtävien ratkaisut. ja kaikki a Σ ovat säännöllisiä lausekkeita.
 T-79.8 Syksy 22 Tietojenkäsittelyteorin perusteet Hrjoitus 5 Demonstrtiotehtävien rtkisut Säännölliset lusekkeet määritellään induktiivisesti: j kikki Σ ovt säännöllisiä lusekkeit. Mikäli α j β ovt säännöllisiä
T-79.8 Syksy 22 Tietojenkäsittelyteorin perusteet Hrjoitus 5 Demonstrtiotehtävien rtkisut Säännölliset lusekkeet määritellään induktiivisesti: j kikki Σ ovt säännöllisiä lusekkeit. Mikäli α j β ovt säännöllisiä
TYÖ 30. JÄÄN TIHEYDEN MÄÄRITYS. Tehtävänä on määrittää jään tiheys.
 TYÖ 30 JÄÄN TIHEYDEN MÄÄRITYS Tehtävä älineet Tusttietoj Tehtävänä on äärittää jään tiheys Byretti (51010) ti esi 100 l ittlsi (50016) j siihen sopivi jääploj, lkoholi (sopii jäähdytinneste lsol), nlyysivk
TYÖ 30 JÄÄN TIHEYDEN MÄÄRITYS Tehtävä älineet Tusttietoj Tehtävänä on äärittää jään tiheys Byretti (51010) ti esi 100 l ittlsi (50016) j siihen sopivi jääploj, lkoholi (sopii jäähdytinneste lsol), nlyysivk
5.4 Ellipsi ja hyperbeli (ei kuulu kurssivaatimuksiin, lisätietoa)
 5.4 Ellipsi j hypereli (ei kuulu kurssivtimuksiin, lisätieto) Aurinkokuntmme plneett kiertävät Aurinko ellipsin (=litistyneen ympyrän) muotoist rt, jonk toisess polttopisteessä Aurinko on. Smoin Mt kiertävät
5.4 Ellipsi j hypereli (ei kuulu kurssivtimuksiin, lisätieto) Aurinkokuntmme plneett kiertävät Aurinko ellipsin (=litistyneen ympyrän) muotoist rt, jonk toisess polttopisteessä Aurinko on. Smoin Mt kiertävät
Yläkoulun geometriaa. Yläkoulun geometriaa
 Yläkoulun geometri Tämä tehtäväkokoelm nt yläkoulun oppillle mhdollisuuden syventää kouluss opittv geometrin oppimäärää. Se on erityisen hyödyllinen niille, jotk ikovt lukioss vlit pitkän mtemtiikn. Kokoelmn
Yläkoulun geometri Tämä tehtäväkokoelm nt yläkoulun oppillle mhdollisuuden syventää kouluss opittv geometrin oppimäärää. Se on erityisen hyödyllinen niille, jotk ikovt lukioss vlit pitkän mtemtiikn. Kokoelmn
lim + 3 = lim = lim (1p.) (3p.) b) Lausekkeen täytyy supistua (x-2):lla, joten osoittajan nollakohta on 2.
 Mtemtiikk III 0600 Kurssi / Differetili- j itegrlilske jtkokurssi Tee 7 tehtävää ) Määritä lim ( ) ) + b) Määritä vkio site, että luseke ( ) + + ( )( ) ( + + ) + + + + + lim + lim lim (p) o jtkuv myös
Mtemtiikk III 0600 Kurssi / Differetili- j itegrlilske jtkokurssi Tee 7 tehtävää ) Määritä lim ( ) ) + b) Määritä vkio site, että luseke ( ) + + ( )( ) ( + + ) + + + + + lim + lim lim (p) o jtkuv myös
Polynomien laskutoimitukset
 Polyomie lskutoimitukset Polyomi o summluseke, joss jokie yhteelskettv (termi) sisältää vi vkio j muuttuj välisiä kertolskuj. Esimerkki 0. Mm., 6 j ovt polyomej. Polyomist, joss o vi yksi termi, käytetää
Polyomie lskutoimitukset Polyomi o summluseke, joss jokie yhteelskettv (termi) sisältää vi vkio j muuttuj välisiä kertolskuj. Esimerkki 0. Mm., 6 j ovt polyomej. Polyomist, joss o vi yksi termi, käytetää
Kuvausta f sanotaan tällöin isomorfismiksi.
 Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
 8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
 MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
5 Epäoleellinen integraali
 5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
205. a) 139 :n kulman vieruskulma on = Siis suorat s ja l eivät ole yhdensuuntaiset.
 Lisätetäviä Peruskäsitteitä 0. ) Kulm on smnkotinen kulmn knss, joten kosk s j l ovt ydensuuntiset, on. b on :n ristikulm, joten myös b. b) b on smnkotinen kulmn 0 knss j kosk s j l ovt ydensuuntiset,
Lisätetäviä Peruskäsitteitä 0. ) Kulm on smnkotinen kulmn knss, joten kosk s j l ovt ydensuuntiset, on. b on :n ristikulm, joten myös b. b) b on smnkotinen kulmn 0 knss j kosk s j l ovt ydensuuntiset,
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
4 DETERMINANTTI JA KÄÄNTEISMATRIISI
 4 DETERMINANTTI JA KÄÄNTEISMATRIISI Neliömtriisin determinntti Neliömtriisin A determinntti on luku, jot merkitään det(a) ti A. Lskeminen: -mtriisin A determinntti: det(a) -mtriisin A determinntti esim.
4 DETERMINANTTI JA KÄÄNTEISMATRIISI Neliömtriisin determinntti Neliömtriisin A determinntti on luku, jot merkitään det(a) ti A. Lskeminen: -mtriisin A determinntti: det(a) -mtriisin A determinntti esim.
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 9: Integroimismenetelmät
 MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 10.10.2016 Pekk Alestlo, Jrmo Mlinen (Alto-yliopisto,
MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 10.10.2016 Pekk Alestlo, Jrmo Mlinen (Alto-yliopisto,
Monikulmio on suljettu, yhtenäinen tasokuvio, jonka muodostavat pisteet ja näitä yhdistävät janat
 MAB: Monikulmiot Aluksi Tässä luvuss käsitellään pljon monikulmioit sekä muutmi tärkeimpiä esimerkkejä monikulmioiin liittyvistä leist. Näistä leist edottomsti tärkein ti inkin kuskntoisin on Pytgorn luse.
MAB: Monikulmiot Aluksi Tässä luvuss käsitellään pljon monikulmioit sekä muutmi tärkeimpiä esimerkkejä monikulmioiin liittyvistä leist. Näistä leist edottomsti tärkein ti inkin kuskntoisin on Pytgorn luse.
Kertymäfunktio. Kertymäfunktio. Kertymäfunktio: Mitä opimme? 2/2. Kertymäfunktio: Mitä opimme? 1/2. Kertymäfunktio: Esitiedot
 TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
Analyysin perusteet kauppatieteilijöille 800118P
 Anlyysin perusteet kupptieteilijöille 800118P Luentomoniste Kri Myllylä Niin Korteslhti Topi Törmä Oulun yliopisto Mtemttisten tieteiden litos Kevät 2015 Sisältö 1 Derivtt 3 1.1 Määritelmä..............................
Anlyysin perusteet kupptieteilijöille 800118P Luentomoniste Kri Myllylä Niin Korteslhti Topi Törmä Oulun yliopisto Mtemttisten tieteiden litos Kevät 2015 Sisältö 1 Derivtt 3 1.1 Määritelmä..............................
Sähkömagneettinen induktio
 ähkömgneettinen inuktio Kun johinsilmukn läpi menevä mgneettikentän vuo muuttuu, silmukkn inusoituu jännite j silmukss lk kulke sähkövit. Mgneettikentässä liikkuvn johtimeen syntyy myös jännite. Näitä
ähkömgneettinen inuktio Kun johinsilmukn läpi menevä mgneettikentän vuo muuttuu, silmukkn inusoituu jännite j silmukss lk kulke sähkövit. Mgneettikentässä liikkuvn johtimeen syntyy myös jännite. Näitä
a = x 0 < x 1 < x 2 < < x n = b f(x) dx = I. lim f(x k ) x k=1
 5 Integrli 5.1 Määritelmä j ominisuudet Olkoon f : [, b] R jtkuv. Muodostetn välin [, b] jko = x 0 < x 1 < x 2 < < x n = b j siihen liittyvä yläsumm S = n M k (x k x k 1 ), M k = mx{f(x) x k 1 x x k },
5 Integrli 5.1 Määritelmä j ominisuudet Olkoon f : [, b] R jtkuv. Muodostetn välin [, b] jko = x 0 < x 1 < x 2 < < x n = b j siihen liittyvä yläsumm S = n M k (x k x k 1 ), M k = mx{f(x) x k 1 x x k },
x k 1 Riemannin summien käyttö integraalin approksimointiin ei ole erityisen tehokasta; jatkuvasti derivoituvalle funktiolle f virhe b
 5 Integrlien lskemisest 51 Riemnnin summt [A2], [4, 61] Rjoitetun funktion f : [, b] R Riemnn-integroituvuudelle ytäpitäväksi on kurssill Anlyysi 2 osoitettu, että Riemnnin summill S P := f(ξ k ) ( ),
5 Integrlien lskemisest 51 Riemnnin summt [A2], [4, 61] Rjoitetun funktion f : [, b] R Riemnn-integroituvuudelle ytäpitäväksi on kurssill Anlyysi 2 osoitettu, että Riemnnin summill S P := f(ξ k ) ( ),
Kirjallinen teoriakoe
 11 Kirjllinen teorikoe Päivämäärä: Osllistujn nimi: Kirjllinen teorikoe Arviointi koostuu khdest osst: "yleiset kysymykset "j lskutehtävät" Kokeen hyväksytty rj on 51% molemmist osioist erikseen. St 1
11 Kirjllinen teorikoe Päivämäärä: Osllistujn nimi: Kirjllinen teorikoe Arviointi koostuu khdest osst: "yleiset kysymykset "j lskutehtävät" Kokeen hyväksytty rj on 51% molemmist osioist erikseen. St 1
LINSSI- JA PEILITYÖ TEORIAA. I Geometrisen optiikan perusaksioomat
 (0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
(0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
 MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
Riemannin integraalista
 Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Käydään läpi: ääriarvo tarkastelua, L Hospital, integraalia ja sarjoja.
 DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
Sisällys. Alkusanat. Alkusanat. Tehtävien ratkaisuja
 Sisällys Alkusnt Tehtävien rtkisuj Vektorit (MAA) Vektoreill lskeminen Vektorit geometrin käytössä 9 Vektorit koordintistoss Lisätehtäviä Todennäköisyys j tilstot (MAA) Tilstot Todennäköisyys Todennäköisyysjkum
Sisällys Alkusnt Tehtävien rtkisuj Vektorit (MAA) Vektoreill lskeminen Vektorit geometrin käytössä 9 Vektorit koordintistoss Lisätehtäviä Todennäköisyys j tilstot (MAA) Tilstot Todennäköisyys Todennäköisyysjkum
Pinta-alan laskeminen
 Pint-ln lskeminen Esimerkki Välillä, jtkuvn, einegtiivisen funktion f määrätt integrli nt suorn pint-ln, eli f = A. INTEGRAALILASKENTA, MAA9 A = f Toislt, jos f on välillä,, eipositiivinen, eli f R, niin
Pint-ln lskeminen Esimerkki Välillä, jtkuvn, einegtiivisen funktion f määrätt integrli nt suorn pint-ln, eli f = A. INTEGRAALILASKENTA, MAA9 A = f Toislt, jos f on välillä,, eipositiivinen, eli f R, niin
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 9: Integroimismenetelmät
 MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 27, 2017 Pekk Alestlo,
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 27, 2017 Pekk Alestlo,
Kuva 1. n i n v. (2 p.) b) Laske avaimiesi etäisyys x altaan seinämästä. (4 p.) c) Kuinka paljon lunta voi sulaa enintään Lassen suksien alla?
 TKK, TTY, LTY, OY, ÅA, TY j VY insinööriosstojen vlintkuulustelujen fysiikn koe 26.5.2004 Merkitse jokiseen koepperiin nimesi, hkijnumerosi j tehtäväsrjn kirjin. Lske jokinen tehtävä siististi omlle sivulleen.
TKK, TTY, LTY, OY, ÅA, TY j VY insinööriosstojen vlintkuulustelujen fysiikn koe 26.5.2004 Merkitse jokiseen koepperiin nimesi, hkijnumerosi j tehtäväsrjn kirjin. Lske jokinen tehtävä siististi omlle sivulleen.
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Differentiaali- ja integraalilaskenta 1 (CHEM) Laskuharjoitus 4 / vko 47, mallivastaukset
 Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Viikon aiheet. Pinta-ala
 info Viikon iheet Mpu I:sen voit suoritt: Kurssin loppukokeess 23.10. Arvosn: koe + lskrit Mikäli yo. ik ei sovi, voit suoritt loppukokeen yleistenttitilisuudess 24.11. Arvosn: koe + lskrit. Ilmoittudu
info Viikon iheet Mpu I:sen voit suoritt: Kurssin loppukokeess 23.10. Arvosn: koe + lskrit Mikäli yo. ik ei sovi, voit suoritt loppukokeen yleistenttitilisuudess 24.11. Arvosn: koe + lskrit. Ilmoittudu
763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 1 Kevät 2014
 763333A KIINTEÄN AINEEN FYSIIKKA Rtkisut 1 Kevät 014 1. Tehtävä: Lske, kuink mont hilpistettä on yksikkökopiss ) yksinkertisess kuutiollisess, b) tkk:ss j c) pkk:ss. (Ot huomioon, että esimerkiksi yksikkökopin
763333A KIINTEÄN AINEEN FYSIIKKA Rtkisut 1 Kevät 014 1. Tehtävä: Lske, kuink mont hilpistettä on yksikkökopiss ) yksinkertisess kuutiollisess, b) tkk:ss j c) pkk:ss. (Ot huomioon, että esimerkiksi yksikkökopin
Integraalilaskenta. Määrätty integraali
 9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
 ICS-C2 Tietojenkäsittelyteori Kevät 2 Kierros,. 5. helmikuut Demonstrtiotehtävien rtkisut D: Sievennä seurvi säännöllisiä lusekkeit (so. konstruoi yksinkertisemmt lusekkeet smojen kielten kuvmiseen): ()
ICS-C2 Tietojenkäsittelyteori Kevät 2 Kierros,. 5. helmikuut Demonstrtiotehtävien rtkisut D: Sievennä seurvi säännöllisiä lusekkeit (so. konstruoi yksinkertisemmt lusekkeet smojen kielten kuvmiseen): ()
Vastaa tehtäviin 1-4 ja valitse toinen tehtävistä 5 ja 6. Vastaat siis enintään viiteen tehtävään.
 S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
Matematiikan perusteet taloustieteilijöille 2 800118P
 Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
S Fysiikka III (EST), Tentti
 S-114.137 Fysiikk III (ES), entti 30.8.006 1. Lämpövoimkone toteutt oheisen kuvn Crnotin prosessi. Koneess on työineen yksi mooli ideliksu. Lske yksitomisen ksun kierroksen ikn tekemän työn suhde kksitomisen
S-114.137 Fysiikk III (ES), entti 30.8.006 1. Lämpövoimkone toteutt oheisen kuvn Crnotin prosessi. Koneess on työineen yksi mooli ideliksu. Lske yksitomisen ksun kierroksen ikn tekemän työn suhde kksitomisen
1.3 Toispuoleiset ja epäoleelliset raja-arvot
 . Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
. Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
Neliömatriisin A determinantti on luku, jota merkitään det(a) tai A. Se lasketaan seuraavasti: determinantti on
 4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
Laskut kirjoitetaan vasempaan reunaan, vastaukset tulevat oikeaan reunaan.
 2. Peruslsket 2.1 Yhtee- j väheyslsku Lske: 23 14 9 MENU. Vlitse Mi Syötä lskuluseke. Pi EXE. Lskut kirjoitet vsemp reu, vstukset tulevt oike reu. 2.2 Näytö tyhjeys Vlitse Edit j pi Cler All. Pi OK. Huom!
2. Peruslsket 2.1 Yhtee- j väheyslsku Lske: 23 14 9 MENU. Vlitse Mi Syötä lskuluseke. Pi EXE. Lskut kirjoitet vsemp reu, vstukset tulevt oike reu. 2.2 Näytö tyhjeys Vlitse Edit j pi Cler All. Pi OK. Huom!
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.2014 Ratkaisut ja arvostelu
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
9 A I N. Alkuperäinen piiri. Nortonin ekvivalentti R T = R N + - U T = I N R N. Théveninin ekvivalentti DEE-11110 SÄHKÖTEKNIIKAN PERUSTEET
 DEE11110 SÄHKÖTEKNIIKAN PERUSTEET http://www.tut.fi/smg/course.php?id=57 Rtkisut Hrjoitukset 3, 2014 Tehtävä 1. Pyydetään muodostmn nnetun piirin Nortonin ekvivlentti. Nortonin, smoin kuin Theveninin,
DEE11110 SÄHKÖTEKNIIKAN PERUSTEET http://www.tut.fi/smg/course.php?id=57 Rtkisut Hrjoitukset 3, 2014 Tehtävä 1. Pyydetään muodostmn nnetun piirin Nortonin ekvivlentti. Nortonin, smoin kuin Theveninin,
Matematiikan tukikurssi. Hannu Kivimäki
 Mtemtiikn tukikurssi Hnnu Kivimäki Sisältö I Ensimmäinen välikoe Integrointi 2 Osittisintegrointi 5 3 Osmurtohjotelm 4 Lisää osmurtoj 4 5 Sijoituskeino 9 6 Määrätty integrli 2 7 Ylä- j lsumm 22 8 Määrätyn
Mtemtiikn tukikurssi Hnnu Kivimäki Sisältö I Ensimmäinen välikoe Integrointi 2 Osittisintegrointi 5 3 Osmurtohjotelm 4 Lisää osmurtoj 4 5 Sijoituskeino 9 6 Määrätty integrli 2 7 Ylä- j lsumm 22 8 Määrätyn
Kolmio 1/11 Sisältö ESITIEDOT: piste, suora, kulma
 Kolmio 1/11 Sisältö ESITIEDOT: piste, suor, kulm Hkemisto KATSO MYÖS: geometriset proleemt, Pythgorn luse, monikulmiot Kolmio: perusominisuudet Yksinkertisin monikulmio on kolmio, jok muodostuu kolmest
Kolmio 1/11 Sisältö ESITIEDOT: piste, suor, kulm Hkemisto KATSO MYÖS: geometriset proleemt, Pythgorn luse, monikulmiot Kolmio: perusominisuudet Yksinkertisin monikulmio on kolmio, jok muodostuu kolmest
3.3 KIELIOPPIEN JÄSENNYSONGELMA Ratkaistava tehtävä: Annettu yhteydetön kielioppi G ja merkkijono x. Onko
 3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
4 Taso- ja avaruuskäyrät
 P2-luentoj kevät 2008, Pekk Alestlo 4 Tso- j vruuskäyrät Tässä luvuss tutustutn tso- j vruuskäyriin, niiden krenpituuteen j krevuuteen. Konkreettisin sovelluksin trkstelln nnettu rt pitkin liikkuvn hiukksen
P2-luentoj kevät 2008, Pekk Alestlo 4 Tso- j vruuskäyrät Tässä luvuss tutustutn tso- j vruuskäyriin, niiden krenpituuteen j krevuuteen. Konkreettisin sovelluksin trkstelln nnettu rt pitkin liikkuvn hiukksen
Tekijä MAA2 Polynomifunktiot ja -yhtälöt = Vastaus a)
 K1 a) Tekijä MAA Polynomifunktiot ja -yhtälöt 6.8.016 ( + + ) + ( ) = + + + = + + + = + 4 b) 4 4 ( 5 + ) ( 5 + 1) = 5 + + 5 + 1 4 = + + + 4 = + 5 5 1 1 Vastaus a) 4 + b) 4 + 1 K a) f ( ) = + 1 f () = +
K1 a) Tekijä MAA Polynomifunktiot ja -yhtälöt 6.8.016 ( + + ) + ( ) = + + + = + + + = + 4 b) 4 4 ( 5 + ) ( 5 + 1) = 5 + + 5 + 1 4 = + + + 4 = + 5 5 1 1 Vastaus a) 4 + b) 4 + 1 K a) f ( ) = + 1 f () = +
Y56 Mikron jatkokurssi kl 2008: HARJOITUSTEHTÄVÄT 2 Mallivastaukset
 Y6 Mikron jtkokurssi kl 008: HARJOITUSTEHTÄVÄT Mllivstukset Kuluttjn vlint (Muokttu Burketist 006, 07) Olkoon Mrkon udjettirjoite = 40 Mrkoll on hvin kättätvät referenssit j Mrkon rjusustituutiosuhde on
Y6 Mikron jtkokurssi kl 008: HARJOITUSTEHTÄVÄT Mllivstukset Kuluttjn vlint (Muokttu Burketist 006, 07) Olkoon Mrkon udjettirjoite = 40 Mrkoll on hvin kättätvät referenssit j Mrkon rjusustituutiosuhde on
