Juha Aho LEIKKUUPUIMURIN VANTEIDEN GEOMETRIAN TARKASTELU
|
|
|
- Aarne Niemi
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Juha Aho LEIKKUUPUIMURIN VANTEIDEN GEOMETRIAN TARKASTELU Kone- ja tuotantotekniikan koulutusohjelma 2011
2 LEIKKUUPUIMURIN VANTEIDEN GEOMETRIAN TARKASTELU Aho, Juha Satakunnan ammattikorkeakoulu Kone- ja tuotantotekniikan koulutusohjelma Toukokuu 2011 Ohjaaja: Yliopettaja, TkT, Kivinen, Juha-Matti Sivumäärä: 49 Liitteitä: - Asiasanat: leikkuupuimurit, toleranssit, mittaaminen, solidworks, mittalaitteet Opinnäytetyön aiheena oli leikkuupuimurin vanteiden geometrian tarkastelu. Työn toimeksiantajana oli Sampo-Rosenlew Oy. Työn tavoitteena oli saada selville onko uuden mahdollisen toimittajan vanteet tarpeeksi hyviä, että Sampo-Rosenlew Oy voisi vaihtaa vannetoimittajaa. Mitattavat vanteet tulevat Sampo-Rosenlew Oy:n valmistamiin puimureihin. Puimureita on saatavilla erikokoisia ja eri vaatimusasteille, joten vanteitakin on montaa eri kokoa ja muotoa. Vanteet ovat tärkeä osa puimurin toimivuutta, siten oli tärkeää mitata ja varmistaa uuden vannetoimittajan pätevyys vanteiden valmistuksessa. Tässä työssä mitattiin Sampo-Rosenlew Oy:lle myynnin kannalta tärkeimpien vannekokojen, geometristen toleranssien heitot ja tärkeiden mittojen tarkkuus. Mittauksista tehtiin vertailu nykyisen ja mahdollisen uuden vannetoimittajan välillä. Mittaaminen suoritettiin FARO Arm -koordinaattimittalaitteella ja mittaustuloksia tutkittiin käyttäen FARO:n omaa FARO CAM2 measures -mittausohjelmaa ja Solid Works -3D-cad-suunnitteluohjelmaa. Lopputuloksiksi saatiin mittauspöytäkirja jokaisesta vanneparista ja yhteenveto kaikista mittaustuloksista.
3 GEOMETRY EXAMINATION OF COMBINE HARVESTER S RIMS Aho, Juha Satakunnan ammattikorkeakoulu, Satakunta University of Applied Sciences Degree Programme in Mechanical and Production Engineering May 2011 Supervisor: Kivinen, Juha-Matti Number of pages: 49 Appendices: - Keywords: combineharvester, tolerance, measuring, solidworks, measuringdevice The purpose of this thesis was to study geometry of combine harvester rims. Thesis was commissioned by Sampo-Rosenlew Ltd. The goal was to determine whether a potential new supplier of rims are good enough or not so that Sampo-Rosenlew could change the rim supplier. Measured rims are coming to combine harvesters which are manufactured by Sampo- Rosenlew Ltd. Combine harvesters are available in different sizes and for different requirements, so the sizes and shapes of the rims have large variation. Rims are an important part of the combine harvester s functionality, so it was important to measure them and to ensure new rim supplier validity s manufacturing rims. In this thesis, were measured exception in geometry tolerances and accuracy of critical dimensions of best-selling rim sizes. Of the measurements were made comparison between existing and potential new supplier. Measurements were carried out with FARO Arm coordinate measuring device and measurement results were analyzed using FARO s own FARO CAM2 Measures - and Solid Works 3D CAD-software. The end results were a measurement protocol from every rim pairs and a summary of all measurement results.
4 SISÄLLYS 1 JOHDANTO Työn taustat Tavoitteet SAMPO-ROSENLEW MITTAAMINEN Mittaaminen yleisesti Mittalajit Mittayksiköt Mittausvirheet TOLERANSSIT Toleranssit yleisesti Peruskäsitteitä ja määritelmiä toleranssien merkinnöistä Geometriset toleranssit Yleistä geometrisista toleransseista Toleroitavat ominaisuudet Peruskäsitteitä ja määritelmiä Peruselementit Geometristen toleranssien esittäminen MITATTAVAT KAPPALEET Yleistä Valmistus MITTAAMISEN SUORITTAMINEN Yleistä koordinaatiomittaamisesta Mittalaite FARO Arm Portable Coordinate Measuring machine (CMM) Mittausohjelmat Mittaaminen TULOKSET JOHTOPÄÄTÖSET LÄHTEET... 49
5 5 1 JOHDANTO 1.1 Työn taustat Tämän työn tarkoituksena oli tarkastella, Sampo-Rosenlew Oy:lle mahdollisen uuden vannetoimittajan, leikkuupuimurin vanteiden geometrioita ja vertailla niitä vanteiden piirustuksiin, kuin myös nykyisen toimittajan vastaaviin vanteisiin. Työ alkoi suhteellisen pitkällä harjoittelulla, mittaamisen tutkimisella sekä mittalaitteistoon ja mittausohjelmiin perehtymisellä. Työ suoritettiin Satakunnan ammattikorkeakoulun tiloissa, koulun omistamalla FARO Arm koordinaattimittalaitteella. Mittaamiset tehtiin osaksi FARO:n omalla mittausohjelmalla ja osaksi Solid Works 3D-CAD-suunnitteluohjelmalla. Työssä oli alunperin tarkoitus mitata ja vertailla sekä kymmentä uuden toimittajan, että kymmentä nykyisen toimittajan vannetta. Näin työ olisi pitkittynyt, joten rajasimme työn viiteen uuden ja viiteen nykyisen toimittajan vanteeseen, joista saa jo tarpeeksi hyvän hajonnan mittauksista ja on mahdollista tehdä tarvittavat johtopäätökset mittauksista. Sampo-Rosenlew Oy tilasi tämän työn koska heillä itsellään ei ollut tarvittavia mittalaitteita, joilla voisi mitata näinkin isoja vanteita mitä puimureissa käytetään. 1.2 Tavoitteet Työn tavoitteena oli saada selville ovatko uuden mahdollisen toimittajan vanteet tarpeeksi hyviä, että Sampo-Rosenlew Oy voisi vaihtaa vannetoimittajaa. Selville otettiin ovatko vanteet tarpeeksi laadukkaita mitoituksen tarkkuuden osalta, kuin myös heitot osien välillä.
6 6 2 SAMPO-ROSENLEW Sampo-Rosenlew Oy on hallituksen puheenjohtaja Timo Prihtin omistama keskisuuri teollisuusyritys. Yrityksen päätuote on leikkuupuimuri. Puimureita valmistetaan kahteen tuotesarjaan: Sampo-Rosenlew sarjaan sekä suurtehopuimurimallistoa, Sampo-Rosenlew sarjaan. /1/ Kuva 1. Sampo-Rosenlew Oy:n tuotantotilat Porissa. Sampo-Rosenlew Oy perustettiin vuonna 1991 yritysoston myötä Timo Prihtin ostettua liiketoiminnan. Teollinen toiminta tuotantotiloissa on alkanut vuonna 1853, jolloin Oy W Rosenlew Ab perheyritys aloitti toimintansa. Leikkuupuimurivalmistus Porin tehtaalla alkoi vuonna /1/ Sampo-Rosenlew Oy yritystoimintaan kuuluu myös konepajatuotanto ulkopuolisille yrityksille alihankintana, teollisuuspesukonesuunnittelu ja -tuotanto, kuin myös 90- luvun aikana pitkän tuotekehitystyön seurauksena syntynyt uusi tuoteryhmä, metsäkoneet. /2/ Konsernin kotipaikka on Porissa, jossa sijaitsee sen suurin tuotantoyksikkö. Porissa valmistetaan leikkuupuimureita, metsäharvestereita sekä teollisuuspesukoneita. Lisäksi yritys suorittaa metalliteollisuuden alihankintatöitä. Konserniin kuuluvat lisäksi Jyväskylässä toimiva Sampo Hydraulics Oy. Se valmistaa maailmanlaajuiseen myyntiin hydrauliikkamoottoreita sekä rotaattoreita. Sampo-Rosenlew Oy on osakkaana vuonna 2005 perustetussa Sampo Componets Oy:ssa, joka valmistaa metallirakentei-
7 7 ta sekä komponentteja metalliteollisuudelle. Sampo Componentsin toimipaikka ja tuotanto ovat Nakkilassa, Satakunnassa. /1/ Kuva 2. Sampo-Rosenlew 2000-sarjan puimuri. 3 MITTAAMINEN 3.1 Mittaaminen yleisesti Usein ajatellaan väärin, että mittaaminen on nopeaa ja helppoa. Näin voi ollakin jos mittaustyö on rutiinia, hyvin valmisteltua ja ohjelmat helppokäyttöisiä. Mutta useimmiten varsinaista mittausta edeltää, sekä seuraa monenlaisia toimenpiteitä ns. sivuaikoja, joihin hukkuu helposti pääaikaan verrattuna monenkertaisesti aikaa. /3/ Itselläni kului aikaa, esim. siihen että sain mittalaitteen hyvin kiinni. Ettei tulisi mittaheittoja sen takia, että mittalaiteella olisi puutteellinen kiinnitys. Myös mitattavien kappaleiden paikoitus aiheutti myös paljon päänvaivaa. Tässä tapauksessa myös mittausohjelma oli vaikeakäyttöinen. Mittaaminen ei tunnetusti paranna laatua, vaan tuottaa validia, oikeaa ja luotettavaa tietoa hyödynnettäväksi. /3/ Esineen muoto ja koko määritetään koneenpiirustuksissa projektion tai useampien projektioiden sekä mittalukujen ja tunnusten avulla. Projektiot ovat apuna kappaleen mitoituksessa. Piirustusta tulkitaan siis sen muotojen ja mittalukujen avulla. /4/
8 8 Mittauksen perustavoitteena on varmistaa, että mittauksen kohde, olipa se raaka-aine, puolivalmiste, komponentti tai lopputuote, täyttää ne vaatimukset, jotka kohteen tuottaneen prosessin asiakas on asettanut. /5/ Mitat on annettava siten, että osan tai laitteen toiminnan, valmistuksen ja tarkastuksen asettamat vaatimukset tulevat otetuksi huomioon. Mitoitus ei ole yksinomaan kappaleen geometrisen muodon määrittämistä, vaan sen tulee palvella monia tarkoituksia, varsinkin valmistusta ja tarkistamista. Mitoituksen tulee vastata käytettävää työtapaa, sillä on voitava osoittaa tai määrätä kappaleen kiinnityskohdat, jakotasot ja mitoituslähtökohdat, mitoituksen tarkoituksen mukaisella ryhmittelyllä voidaan helpottaa piirustuksen luettavuutta. /4/ Mittalajit Piirustuksen mitat eivät ole merkitykseltään keskenään samanarvoisia. Jotkut mitat ovat koneen toiminnan ja/tai asennuksen kannalta ratkaisevan tärkeitä. Niiden sallitut mittapoikkeamat saattavat olla vain muutaman sadasosamillimetrin verran, kun taas joihinkin mittoihin voidaan sallia jopa useiden millimetrien mittapoikkeamat ilman, että tällainen vaikuttaa haitallisesti koneen toimintaominaisuuksiin ja asennusmahdollisuuksiin. Mitat luokitellaan seuraavasti: - Toimintamitta: Mitta, joka on oleellinen kappaleen toiminnan tai tilan kannalta. Toimintamitoille annetaan lähes aina toleranssi eli sallittu mittavaihtelu. - Ei-toimintamitta: Mitta, joka ei ole tärkeä kappaleen toiminnan tai tilan kannalta. - Apumitta: Mitta, joka on tarkoitettu vain informaation antamiseksi. Tämä mitta ei ohjaa tuotanto- tai tarkastusmittoja ja johtuu muista mitoista, jotka on esitetty piirustuksessa tai piirustukseen liittyvissä asiakirjoissa. Apumitta annetaan sulkeissa tai tähtimerkintänä mitan perässä, eikä siihen sovelleta toleranssia.
9 9 /4/ - Elementti: Kappaleen yksittäinen ominaisuus, kuten esimerkiksi tasopinta, lieriöpinta, kaksi yhdensuuntaista pintaa, olake, kierre, ura, profiili, jne. Tässä työssä keskityttiin vain toiminnallisuuden kannalta tärkeisiin mittoihin (esim. pulttireikien halkaisija), joten työssä ei mitattu ei-toimintamittoja eikä apumittoja (esim. vanteen halkaisijaa, koska se määrittyy geometristen toleranssien mukaan), vaan pelkästään toimintamittoja. Olisi ollut turhaa mitata kaikki mitat vanteista, koska toimintamittojenkin heitto sai olla suhteellisen suurta. Toimintamittojen heittojen suurus johtuu siitä, että puimurit, joihin vanteita käytetään, toimivat epätasaisella pinnalla. Mitat pitivät olla silti piirustusten mukaisessa toleranssissa (kts. luku 4), jotta puimureiden toiminta ei häiriinny. Jos elementille tai elementtiryhmällä on annettu sijainnin, suunnan, muodon tai pinnan muodon toleranssi, niin sijainnin, suunnan, muodon tai pinnan määritteleviä teoreettisesti oikeita perusmittoja kutsutaan teoreettisesti oikeiksi mitoiksi. /10/ Teoreettisesti oikeat koskevat myös mittoja, jotka määrittelevät peruselementtijärjestelmän suhteellisen suunnan. Teoreettisesti oikeita mittoja ei toleroida. Ne on kehystettävä. /10/ Mittayksiköt Jokaisessa yksittäisessä piirustuksessa on käytettävä kaikille mitoille samaa mittayksikköä (esim. mm), ilman että yksikön tunnusta merkitään näkyviin. Pituus mitat ilmoitetaan yleensä millimetreinä. Jos tästä poiketaan, mittayksiköt on merkittävä piirustukseen, esim. µm, cm, in, m. /4/ Kyseisen työn piirustuksissa mittayksiköt olivat aina millimetreinä, ilman poikkeuksia.
10 Mittausvirheet Taulukko 1. Koskettavan koordinaatiomittauksen epävarmuustekijät ja niiden prosentuaaliset osuudet (yleinen arvio). /3/ Tekijä Käyttäjä Kone Ympäristö Työkappale Prosentuaalinen osuus Mitään mittausta ei voida tehdä täysin virheettömästi. Tulos on aina virheellinen, sillä mittaukseen osallistuvat tekijät eivät ole täydellisiä. Näitä tekijöitä ovat mittauksen kohde, perusmitat, mittalaite, mittaustapa, ulkonaiset olosuhteet, mittaaja sekä muutokset, joita kaikissa näissä virhelähteissä tapahtuu mittauksen aikana. /5/ Mittausvirheet voidaan jakaa seuraaviin yleistyyppeihin: /6/ - Systemaattiset virheet, ne esiintyvät toistuvissa mittauksissa säännönmukaisesti suuruudeltaan ja suunnaltaan samanlaisina. Ne voi paljastaa ainoastaan mittausmenetelmän tai välineen muuttaminen, ei mittauksen uudistaminen. - Satunnaiset virheet, joiden suuruus ja etumerkki vaihtelevat. Niiden vaikutus voidaan vähentää suorittamalla mittaus useampia kertoja ja laskemalla mittausarvojen keskiarvo. - Karkeat virheet, ne muodostuvat erilaisista erehdyksistä johtuvan virheryhmän esim. lukemavirhe, ajatusvirhe, väärän mittausmenetelmän käyttö, virhelähteiden huomiotta jättäminen. Niiden suuruusluokka voi olla moninkertainen edellisiin virhetyyppeihin verrattuna. Karkeiden virheiden syntyminen pitäisi voida poistaa riittävän huolellisella työskentelyllä. Kohteen liikkuminen on estettävä mittauksien ajaksi, sillä mitattavan kohteen liikkuminen aiheuttaa mittausvirheen.
11 11 Tunnetuimpia mitattavista kappaleista johtuvia mittavaihteluita ovat lämpötilamuutoksista aiheutuvat mitan- ja muodonmuutokset. Vaihtelua aiheuttavat lisäksi kappaleen pinnan laatu, karheus ja aaltomaisuus sekä puutteellinen puhdistus. Lika ja pöly mitattavalla pinnalla muuttavat suoraan saadun tuloksen arvoa. /5/ Mittalaitteen tarkkuuden kannalta on oleellista säännöllinen kalibrointi. Mittalaitteen eri osien väliset lämpötilaerot voivat aiheuttaa vaihtelua mittaustulokseen. Mittausvoiman vaihtelu saattaa aiheuttaa mittalaitteessa tai mitattavassa kappaleessa taipumia. /5/ Avainasemassa mittausten tarkkuuteen ja luotettavuuteen nähden on mittaaja itse, sillä hänen ajattelukykynsä ovat mittauksen tärkein väline. Mittaaja ratkaisee käyttämänsä mittaustavan ja valitsee mittausvälineet käytettävissä olevien mahdollisuuksien ja omien taitojensa mukaan. Nimenomaan tietojen puutteet koituvat usein myös mittausten puutteellisuudeksi. Mittaajasta aiheutuvat virheet voidaan jakaa kolmeen ryhmään: /5/ - ammattitaito - pysyvät ja muuttuvat ominaisuudet - näkökyky - parallaksipoikkeama Parallaksipoikkeama on virhe, joka syntyy, kun mittalaitetta katsotaan vinoon tarkastelun kohteen pinnalla, jolloin katselukulma aiheuttaa virheen mittaustuloksessa. Kyseistä virhettä ei synny jos käytetään digitaalista mittalaitetta ja silloin siirrytään mittaamisessa suurempiin tarkkuuksiin. /12/ Työ aloittaessa en ollut paljoa käyttänyt ko. mittalaitetta, saati mittaamista harrastanut yleensäkään, mutta pitkän harjoitusjakson ja teoreettisen tutkimisen mittaamisesta suorittaneena, aloitin lopullisten mittauksien teon, niin huomasin kyllä mittaamistaitojeni karttuvan suhteellisen nopeasti.
12 12 4 TOLERANSSIT 4.1 Toleranssit yleisesti Toleranssit ovat rajoja, joiden välillä tietty suure tai ominaisuus saa vaihdella sen silti vielä ollessa käyttökelpoinen. /5/ Näitä ovat mitan, muodon, suunnan ja/tai sijainnin sallittu vaihtelu. Nämä tarkkuuden osatekijät vaikuttavat merkittävästi toisiinsa. /4/ Valmistuksessa työkappaleiden mittoja ei koskaan pystytä saamaan tarkalleen oikeiksi. Kuitenkin koneissa ja laitteissa olevien naapuriosien yhteen liittyvien mittojen tulee olla riittävän oikeita, jotta ne täyttäisivät osilta vaadittavat kolme päävaatimusta: - osien tulee toimia tarkoitetulla tavalla - osien tulee sopia siten yhteen, että kone voidaan kokoonpanna - myöhempää huoltoa yms. varten osien tulee olla vaihtokelpoisia /4/ Nämä vaatimukset täytetään kappaleiden mittojen osalta käyttämällä mitoissa sallittua mittavaihtelua eli toleranssia. /4/ Saavutettu valmistustarkkuus riippuu useista osatekijöistä. Esim. tarkasti valmistettu reiän valmistustarkkuus on riippuvainen (Kuvat 3. a 3. f): - mittatarkkuudesta; eli halkaisijan poikkeamista piirustuksessa annetusta perusmitasta. - muototarkkuudesta; reikä ei ole aivan pyöreä, vaan se saattaa olla muodoltaan esim. soikea, kartiomainen jne. - sijainti tarkkuudesta; reiän keskipiste ei ole aivan piirustuksen mittojen määrittelemässä paikassa - suunnan tarkkuudesta; reiän todellinen akselin suunta poikkeaa piirustuksessa annetusta akselin suunnasta
13 13 /4/ - pinnankarheudesta; vaikkakin toleranssin ja pinnan karheuden välillä ei ole selvää matemaattista riippuvuutta, on niillä kuitenkin keskenään tietty yhteys; esim. tarkasti mittatoleroitu pinta ei saa olla miten karkea tahansa. Yleensä mittatoleranssien suhteen tarkka valmistusmenetelmä tuottaa myös pienen karheuden omaavan pinnan. Kuva 3. Reiän virheellisyyden jaottelu. Yllä esitetyt tekijät on otettava huomioon sekä kappeleiden suunnittelussa että valmistuksessa. Käytännössä tämä merkitsee sitä, että valmistuksessa ei vaaditakaan noudattamaan ehdottomia mittoja, vaan piirustuksessa määritetään se alue, jonka sisäpuolella kappaleen pinnan tai muun kohdan on oltava valmistuksen jälkeen. /4/
14 Peruskäsitteitä ja määritelmiä toleranssien merkinnöistä /4/ Mitta: Luku, joka ilmaisee pituusmitan tiettynä yksikkönä. Perusmitta, nimellismitta: Mitta, josta rajamitat lasketaan käyttäessä ylä- ja alaeromittoja. (kuva 4.) Rajamitat: Suurin ja pienin sallittu mitta. Ylärajamitta: Suurin sallittu mitta. (kuva 4.) Alarajamitta: Pienin sallittu mitta. (kuva 4.) Nollaviiva: Toleranssien graafisessa esityksessä suora viiva, joka kuvaa sitä perusmittaa, johon eromitat ja toleranssi liittyvät. Nollaviiva piirretään vaakasuoraan ja positiiviset eromitat esitetään sen yläpuolella ja negatiiviset sen alapuolella. (kuva 4.) Eromitta: Tietyn mitan ja vastaavan perusmitan algebrallinen erotus. (kuva 4.) Rajaeromitat: Ylä- ja alaeromitta Yläeromitta: Ylärajamitan ja vastaavan perusmitan algebrallinen erotus. (kuva 4.) Alaeromitta: Alarajamitan ja vastaavan perusmitan algebrallinen erotus (kuva 4.) Mittatoleranssi: Ylärajamitan ja alarajamitan erotus, so. yläeromitan ja alaeromitan erotus. Toleranssialue: Toleranssien graafisessa esityksessä ylä- ja alarajamittaa kuvaavien viivojen välinen alue. (kuva 4.) Kuva 4. Toleranssikäsitteitä havainnollistava kuva.
15 Geometriset toleranssit Yleistä geometrisista toleransseista Geometrisilla toleransseilla määritellään ne rajat, joiden sisällä muodon, suunnan ja sijainnin poikkeamien sekä heiton tulee olla. /4/ Geometristen toleranssien käyttö lisääntyi Suomessa vasta koordinaattimittalaitteiden yleistymisen myötä. /5/ Toleroidulla elementillä saa olla mikä muoto tai sijainti tahansa kulloinkin annetun toleranssialueen sisällä, ellei piirustukseen ole merkitty muita rajoittavia tietoja. /8/ Kappaleen mittojen perusmitasta poikkeamiset ilmoitetaan tavallisesti mittatoleransseilla. Jos on annettu vain mittatoleranssi, saavat kappaleen todelliset pinnat silloin poiketa annetusta geometrisesta muodosta sillä edellytyksellä, että pinta on mittatoleranssin määrittelemällä alueella. Jos muotopoikkeamien on sisällyttävä toisiin rajoihin, muototoleranssien avulla on mahdollista asettaa tietyille ominaisuuksille erityisiä mittatoleransseista riippumattomia vaatimuksia. Geometriset toleranssit asetetaan vain silloin, kun se on tarkoituksenmukaista varmistamaan taloudellisella tavalla osien toiminta- ja vaihtokelpoisuus. Toiminnalliset vaatimukset, vaihtokelpoisuus ja todennäköiset valmistusolosuhteet ratkaisevat, miten täydellistä muodon, suunnan ja sijainnin tolerointia kussakin yksittäistapauksessa on tarkoituksen mukaista käyttää. /4/ Toleroitavat ominaisuudet Geometrisin toleranssein on mahdollista antaa elementille (kts. kappale 4.2.3) varsinaisesta mittatoleransseista riippumattomia vaatimuksia. Geometriset toleranssit ovat jaoteltavissa seuraaviin ryhmiin:
16 16 /4/ - Muototoleranssit; näihin kuuluvat seuraavat toleroitavat ominaisuudet o Suoruus o Tasomaisuus o Ympyrämäisyys o Lieriömäisyys o Tasoviivan muoto o Pinnan muoto - Suuntatoleranssit; näihin kuuluvat seuraavat toleroitavat ominaisuudet: o Yhdensuuntaisuus o Kohtisuoruus o Kulma-asento - Sijaintitoleranssit; näihin kuuluvat seuraavat toleroitavat ominaisuudet: o Samankeskisyys ja sama-akselisuus o Symmetrisyys o Paikan sijainti - toleranssit; voivat tarkoittaa joko muoto- tai sijaintitoleransseja taikka molempia yhdessä, ja ne käsittävät seuraavien ominaisuuksien toleransseja: o Kaartioheitto o Säteisheitto o Aksiaalihetto o Kokonaisheitto Tässä työssä geometriset toleranssit olivat mittaamisen pääkohdat, koska niiden tarkkuus oli tärkeintä vanteiden toiminnallisuuden kannalta. Työssä esiintyvät geometriset toleranssit olivat säteis- ja aksiaaliheitto, sama-akselisuus, tasomaisuus ja paikan sijainti. Tärkeimmät näistä oli vanteiden toiminnallisuuden kannalta säteis- ja aksiaaliheitto, koska nämä määrittävät kuinka sulavasti vanne pyörii täyden kierroksen pyörimisakselinsa ympäri. Säteisheitto tässä tapauksessa tarkoittaa sitä kuinka paljon vanteen ulkoreuna heittää suhteessa vanteen keskiöreiän kanssa. Aksiaaliheitto taas tarkoittaa sitä kuinka paljon vanteen ulkoreuna on heittää aksiaalisessa suunnassa vanteen keskilevyn suhteen.
17 17 Sama-akselisuus oli pulttireikien ja keskiöreiän välinen geometrinen toleranssi, eli pulttireikien keskipisteiden akselin heitto suhteessa keskiöreiän akseliin sai olla vain tietyn kokoinen, että vanteet olisivat helppo asentaa paikoilleen. Asennettavuuden helpottamiseksi oli asetettu myös tasomaisuus toleranssi vanteen pintaan, joka on kiinnityskohta puimuriin. Jotta vanne saataisiin sopimaan puimuriin, tulisi kiinnityspinnan olla tarpeeksi tasainen. Se kuinka tasainen pinnan tulee olla, asetetaan tasomaisuus toleranssilla. Pulttireikien paikoille oli myös asetettu geometrinen toleranssi, jolla määriteltiin pulttireikien paikkojen isoin mahdollinen heitto. Toleranssi on asetettu siitä syystä, että puimurissa pulttireikien paikat on tietyissä paikoissa, niin vanteen reikien täytyisi olla melkein samoissa paikoissa, jotta kiinnitys onnistuisi Peruskäsitteitä ja määritelmiä /4/ Geometristen toleranssien yhteydessä käytetään eräitä termejä, joiden ymmärtäminen on välttämätöntä toleranssien käsittelyssä, minkä takia ne määritellään seuraavassa: Elementiksi nimitetään seuraavassa kutakin erillistä pistettä, viivaa, pintaa tai keskitasoa. Toleroitu elementti on piste, viiva tai pinta, jonka muoto, suunta, sijainti tai ulottuvuus halutaan määrittää. Geometrisilla toleransseilla rajataan geometristen viivojen tai pintojen avulla alue tai tila, jonka sisäpuolella toleroitavan elementin pitää kokonaisuudessa ollaan. Riippuen toleroitavasta ominaisuudesta ja toleranssin ilmoittamistavasta toleranssialue voi olla seuraava: - ympyräalue - kahden samankeskisen ympyrän väliin jäävä alue - kahden vakioetäisyydellä toisistaan olevan viivan tai kahden yhdensuuntaisen suoran välinen alue
18 18 - pallon rajoittama tila - lieriön rajoittama tila - kahden samankeskisen lieriön välinen tila - kahden vakioetäisyydellä toisistaan olevan pinnan tai kahden yhdensuuntaisen tason välinen tila - suuntaissärmiön rajoittama tila Peruselementit /4/ Peruselementti: Teoreettisesti oikean muotoinen geometrinen peruslähtökohta (kuten akselit, tasot, suorat, viivat jne.), johon toleroituja elementtejä verrataan. Peruselementtijärjestelmä: Kahden tai useamman erillisen peruselementin muodostama kokonaisuus, jota käytetään toleroidun elementin peruselementtinä. Todellinen peruselementti: Kappaleen todellinen elementti (kuten särmä, pinta tai reikä jne.), jonka avulla peruselementin sijainti on määrätty. Apuperuselementti: Riittävän täsmällisen muotoinen todellinen pinta (kuten mittaustasot, laakeripinnat, tuurnat), joka koskettaa todellista peruselementtiä ja jota käytetään peruselementin asemasta.
19 Geometristen toleranssien esittäminen Tunnukset /4/ Taulukko 2. Toleroitujen ominaisuuksien tunnukset. Taulukko 3. Lisätunnukset (aputunnukset).
20 Toleranssin suuruus ja muoto /4/ Toleranssin suuruus, joka on merkittynä esim. piirustukseen, tarkoittaa kokonaistoleranssia. Toleranssin mittayksikkönä on piirustuksen pituusmittojen yksikkö. Siinä tapauksessa, että toleranssialue on ympyrä tai lieriö, on merkitty tunnus Ø aina toleranssiarvojen eteen Toleranssikehys ja sen merkintä /4/ Kuva 5. Esimerkki toleranssikehyksistä. Toleranssikehykseen tulevat tiedot merkitään vasemmalta alkaen seuraavassa järjestyksessä: 1) Toleroidun ominaisuuden tunnus. Tässä tapauksessa yhdensuuntaisuus. 2) Toleranssin suuruus samassa yksikössä kuin muut piirustusmitat. Jos toleranssi alue on ympyrä, merkitään tunnus Ø ennen toleranssin lukuarvoa. Tässä tapauksessa 0,06 heitto on sallittu yhdensuuntaisuudessa. 3) Tarvittaessa kirjain tai kirjaimet, jotka ilmoittavat peruselementin tai peruselementit. Tässä tapauksessa peruselementti on B Toleranssikehyksen liittäminen elementtiin Toleranssikehys liitetään toleroituun elementtiin viiteviivalla kuvan 6. osoittamalla tavalla. Viiteviiva päätetään toleroituun elementtiin nuolenkärjellä. Kuva 6. Toleranssikehys liitettynä elementtiin.
21 Toleranssikehyksen liittäminen peruselementtiin /4/ Toleranssikehys, jossa viitataan peruselementtiin johon sitä verrataan, niin liittäminen tapahtuu, kuten edellisessä kappaleessa. Toleranssikehys liitetään viiteviivalla ja nuolenkärjellä toleroituun elementtiin ja sen lisäksi myös vertailu- eli peruselementtiin (kuvat 7 ja 8). Liittäminen voi olla joko: - suoraa tai - epäsuoraa. Työhön liittyvissä piirustuksissa käytetään vain epäsuoraa liittämistä, joten keskityn vain epäsuoran liittämisen käsittelyyn. Epäsuora liittäminen Jos toleranssikehystä ei ole voitu yhdistää selvällä ja yksinkertaisella tavalla, käytetään isoa viitekirjainta esittämään peruselementtiä. Jokaiselle peruselementille on valittu eri iso kirjain. Tämä viitekirjain on merkitty neliöön, ja neliö yhdistetty viiteviivalla vastaavaan elementtiin. Viiteviivan peruselementtiä vastaan olevaan päähän on merkitty peruselementillä oleva kolmio (kuvat 7 ja 8). Viitekirjain on merkittynä myös toleranssikehykseen (kuvat 7 ja 8). Kuva 7. Epäsuora liittäminen. Kuva 8. Suora liittäminen.
22 Toleranssin rajoittaminen /4/ Toleranssin rajoituksessa tarkoitetaan, kun toleranssia on tarkoitus noudattaa rajoitetulla alueella. Tällöin toleranssivaatimus koskee vain määrättyä pituutta, pinnan osaa ja niin edelleen. Rajoitettu pituus ilmoitetaan toleranssin suuruutta ilmoittavan luvun jälkeen vinoviivalla erotettuna. Työhön liittyvissä piirustuksissa oli rajoitettu alue ympyrän muotoinen, joten mitan eteen on merkitty tunnus Ø. 5 MITATTAVAT KAPPALEET 5.1 Yleistä Mitattavat kappaleet ovat Sampo-Rosenlew Oy:n valmistamiin puimureihin tulevat vanteet (Kuvat 9 ja 10). Nykyiset Sampo-Rosenlew Oy:n käyttämät vanteet valmistetaan Suomessa (levypyörä), Tanskassa ja Italiassa (GKN Wheels Carpenedolo). Uusi ehdokas vannetoimittajaksi on Ukrainasta (Kremenchug Wheel). Kuva 9. Ukrainalais-valmisteinen vanne. Kuva 10. Tanskalais- ja ukrainalais- valmisteiset vanteet.
23 Valmistus Kuva 11. Vanteen valmistus. Kehäprofiilit valmistetaan useampivaiheisena rullamuovauslinjassa (kuva 12). Rullamuovauksessa rullatyökalujen avulla muovataan kelalla olevasta metallinauhasta profiilia. Profiili voi olla avoin tai tietyissä rajoissa suljettu. Yleensä rullamuovauslinjassa on sarja (esimerkiksi 6 kpl) peräkkäisiä rullapareja tai rullaryhmiä, joilla nauha sen edetessä linjassa vähitellen muovataan lopulliseen muotoonsa. Lopussa profiili hitsataan vielä umpinaiseksi. /13,15/ Kuva 12. Rullamuovauslinja.
24 24 Keskiövalmistuksessa käytetään kylmämuovaustekniikkaa. Kylmämuovauksella eli ohutlevyn muovauksella ymmärretään erilaisia prosesseja, joissa levykappaleelle annetaan kolmiulotteinen muoto. Keskiömuoto ja vakiorei'itykset tehdään epäkeskopuristimilla. /13,14/ Kun molemmat osat vanteesta on saatu valmiiksi, ne hitsataan yhteen. Vanteita hitsataan manuaalisesti, automaatilla ja roboteilla. /13/ Kuva 13. Vanteen hitsausta. 6 MITTAAMISEN SUORITTAMINEN 6.1 Yleistä koordinaatiomittaamisesta Mittaamisessa käytin kouluni, Satakunnan ammattikorkeakoulun, omistamaa koordinaattimittalaitetta. Aluksi haluan kertoa hieman yleisesti koordinaattimittaamisesta, jonka jälkeen tutustutaan paremmin käyttämääni FARO Arm Portable Coordinate Measuring machine (CMM) mittalaitteeseen ja sen omaan FARO CAM2 Measures mittausohjelmaan. Koordinaattimittaaminen tarkoittaa koordinaattien määrittämistä avaruudessa, joskus tasossa. Koordinaattimittalaitteella määritetään anturia liikuttamalla kohteesta pisteiden koordinaatit tasossa tai avaruudessa. Mittalaitteet ovat käsikäyttöisiä, motorisoituja tai numeerisesti ohjattuja. /3/
25 25 Työssä käytetään vain käsikäyttöistä koordinaattimittalaitetta. Kappalegeometria muodostetaan yksittäisistä mitatuista pisteistä. Koskettavalla kärjellä mitattaessa pisteet ovat aina kappaleen geometrioiden pinnalta. /3/ 6.2 Mittalaite FARO Arm Portable Coordinate Measuring machine (CMM) Kuva 14. FARO Arm-koordinaatiomittalaite. FARO Arm - koordinaatiomittalaite on kiinteään alustaan kiinnitettävä käsinohjattava käsivarsi (kuva 14). Mittalaitteessa on kuusi vapausastetta (kuva 15), eli kiertyvää niveltä. Nivelet kiertyvät vapaasti, kun mittausanturia liikutetaan käsin. Samalla
26 26 kunkin nivelen kulma-asento välitetään automaattisesti yhdessä anturin antaman signaalin kanssa ohjelmistolle, joka laskee mittapään paikan XYZ-koordinaateiksi. /3/ Kuva 15. Mittalaitteen kuusi vapausastetta. Mittapäänä toimii halkaisijaltaan 3 mm oleva pallo (Kuva 16), mittapäitä on myös muunlaisia kokoja tarjolla. Mittapää on mekaaninen. Kuva mm mittapää. Mittalaitteeseen kuuluu osana mittaamista tietokone, jolla ohjataan mittaamista. Tietokoneessa pitää olla FARO:n oma mittausohjelma, jotta mittaaminen onnistuisi.
27 27 Mittaaminen aloitetaan siten, että mittausohjelmasta valitaan haluttu mittaamistapa, joita on esim. ympyrän mittaaminen, pisteen mittaaminen ja tason mittaaminen. Kuva 17. Pulttireiän halkaisijan mittaaminen. Itse mittaaminen tapahtuu seuraavalla tavalla, mittapäätä liikutetaan käsin haluttuun paikkaan (Kuva 17) ja painetaan näppäintä mittalaitteen kyljestä (kuva 18), jolloin tietokone tallentaa mittapään pallon keskipisteen koordinaatit. Jotta tulokset tulisivat näkyviin tietokoneelle, täytyy vielä kuitata mittaus painamalla mittalaitteen kyljessä olevasta toisesta näppäimestä (kuva 18). Kuittaaminen tapahtuu aina mittaukselle ominaisella tavalla. Tavat joilla kuitata, löytyvät mittausohjelman omasta oppaasta. Kuittauksen tärkeys tulee esille siinä, että mistä suunnasta mittausohjelma kompensoi mittapään koon, esim. jos mitataan ympyrää, täytyy kuitata ympyrän sisällä jotta kompensointi tapahtuu oikeinpäin.
28 28 Kuva 18. Alemmalla näppäimellä mittapisteen valinta, ylemmällä näppäimellä mittaus kuitataan. Mittalaitetta varten valmistimme sen runkoon kiinnitettävän metallilevyn, jotta kyseisen mittalaitteen voi helposti siirtää paikasta toiseen ja kiinnittää se magneetin kanssa Mittausohjelmat FARO CAM2 Measures FARO CAM2 Measures on Faro Arm -mittalaitteen oma mittausohjelmisto jolla mittauksia ohjataan ja suoritetaan. Mittausohjelmalla kalibroidaan koneen mittauspäät. Se käsittelee mitattuja pisteitä, laskee koneen liikeakseleiden paikka- ja anturitietojen perusteella kosketuskohdat kohteen pinnalla, korjaa mittalaitteen systemaattisia virheitä, muodostaa kosketuspisteistä geometrioita. /3/
29 29 Ohjelmassa on paljon valmiiksi asetettuja mittaustapoja, kuten ympyrän, keskipisteen ja tason mittaus. Osa mitoista, kuten reikien mittausten tulokset, sai suoraan ohjelmasta. Loput mitoituksesta suoritettiin Solid Works- ohjelmalla, josta seuraavassa kappaleessa. Tiedosto tallennetaan IGES -muotoon ohjelmalla, jotta se voidaan avata Solid Works-ohjelmalla. Solid Works Solid Works on 3D -CAD -suunnitteluohjelma, jonka käyttö on itselleni luontevampaa kuin FARO cam2:n käyttö. Osa mitoituksista oli vaikeaa suorittaa FARO cam2:lla, osaksi puutteellisten tietojen FARO cam2:n käytöstä, kuin myös ohjelman vaikeasti toteutetusta mitaamisesta. Joten oli helpompaa käyttää jo hallitsemaani Solid Works-ohjelmaa. Solid Works-ohjelman etuna mittaamisessa oli sen kyky muokata FARO:lta saamia mittaustuloksia ja tehdä niihin mittaamista helpottavia apuviivoja, joiden avulla tarkkuus mittaustuloksissa pysyi hyvänä. 6.3 Mittaaminen Koska kappaleen muodoilla ei ole pääosin mitään tekemistä kappaleen toimivuuden tai asennettavuuden kanssa, en alkanut mittaamaan kappaleesta tuhansittain pisteitä, että saisin kopioitua vanteen muodon. Tämä olisi tullut ehkä kysymykseen jos minulla olisi ollut 3D-kuvat vanteista johon olisin voinut verrat pisteavaruutta. Joten mittasin vain tarkasti valituista pinnoilta pisteitä vähintään viidestä eri paikasta per mittava suure.
30 30 Kuva 19. Mittaaja työnteossa. Kun olin saanut pisteitä tarpeeksi ja oikeisiin paikkoihin, niin vertasin näitä pisteitä luotettavaan tasoon tai elementtiin, jotta tulokset olisivat tarpeeksi lähellä oikeita. Se oli haastavaa koska mitattavat kappaleet olivat joka suunnasta vähän pyöreätä tai kaltevia, jonka takia suoraa ja tasaista pintaa oli vaikea löytää. Pisteet mittasin joka paikasta kolme kertaa. Mittaukset oli hyvä suorittaa useammin kuin yhden kerran, että satunnaiset virheet saatiin eliminoitua. Kuva 20. Kiekko, halkaisijaltaan 16mm ja reikä 3 mm. Nuolet kuvassa esittävät kiekon avulla mitattavat tasot. Mittauksissa apuna käytin koulun laboraatio-insinöörin valmistamaa, 16 mm halkaisijaltaan olevaa kiekkoa jossa oli 3 mm mittapään mentävä reikä keskellä. Sen
31 31 pystyi hyvin sijoittamaan vanteen yhteen mittaustasoon, jonka kaaren säde oli 8 mm. Kiekon avulla sai helposti mittauspisteen oikealle pinnalle (kuva 20). Osa vanteista pystyttiin mittaamaan mittauspöydällä (kuva 21), mutta osaan vanteista kokonsa takia jouduttiin kehittämään erilaisia tukia ja kiinnikkeitä. Kuva 21. pienimmät vanteet voitiin mitata pöydällä. Osa vanteista oli todella leveitä, ne mahtuivat pöydälle, mutta niitä ei voitu mitata pystyasennossa mittalaitteen varren riittämättömyyden takia. Joten vanteille oli keksittävä tuenta jossa vanteet olisivat vinossa kohti mittalaitetta, jotta mittaaminen onnistuisi (kuva 22). Vanteiden suuren painon ansiosta ne pysyivät hyvin paikallaan mittauksen ajan ilman ylimääräisiä kiinnikkeitä ym. Kuva 22. Leveät vanteet mittasin tällä tuennalla.
32 32 Kun vanteiden halkaisija alkoi lähennellä metriä, oli taas keksittävä uusi tuenta vanteille. Joten suunnittelin kaksi tukea, jonka päälle vanne olisi helppo nostaa ja vanne pysyisi paikallaan hyvin ilman ylimääräisiä tukia (kuva 23 ja kuva 24). kuva 23. Tuet isoille vanteille. Kuva 24. Vanne tuilla.
33 33 7 TULOKSET Taulukko 4. Vertailu 1. Kremenchug 9x15.3 Vertailu/current supplier 9x15.3 Aksiaaliheitto Piirustus Max. heitto 2,0 Säteisheitto Piirustus max. 2,0 leveys Vanteen leveys Piirustus 228,5+/- 2,5 Piirustus Max. heitto 2,0 Mittaus 1 1,29 ok Mittaus 1 0,57 ok Mittaus 2 1,06 ok Mittaus 2 0,81 ok Mittaus 3 1,14 ok Mittaus 3 0,67 ok ka 1,16 ka 0,68 Piirustus max. 2,0 Mittaus 1 0,69 ok Mittaus 1 0,68 ok Mittaus 2 0,59 ok Mittaus 2 0,45 ok Mittaus 3 0,55 ok Mittaus 3 0,52 ok ka 0,61 ka 0,55 leveys Piirustus 228,5+/- 2,5 Mittauspiste 1 227,90 ok Mittauspiste 1 227,80 ok Mittauspiste 2 227,83 ok Mittauspiste 2 227,22 ok Mittauspiste 3 228,36 ok Mittauspiste 3 227,67 ok Mittauspiste 4 227,59 ok Mittauspiste 4 227,06 ok Mittauspiste 5 228,89 ok Mittauspiste 5 227,26 ok ka 228,11 ka 227,40 Pituus Piirustus 112,25+ /-2 Mittauspiste 1 118,34 ok Mittauspiste 1 111,96 ok Mittauspiste 2 118,36 ok Mittauspiste 2 112,04 ok Mittauspiste 3 118,39 ok Mittauspiste 3 111,87 ok Mittauspiste 4 118,29 ok Mittauspiste 4 112,17 ok Mittauspiste 5 118,27 ok Mittauspiste 5 112,25 ok ka 118,33 ka 111,95 Pituus Keskeltä sisäreunaan Piirustus 118,3+/- 1,5 Keskiröreikä Piirustus Piirustus ,5 Mittauspiste 1 110,50 ok Mittauspiste 1 109,85 ok Mittauspiste 2 110,45 ok Mittauspiste 2 109,62 ok Mittauspiste 3 110,48 ok Mittauspiste 3 110,05 ok Mittauspiste 4 110,68 ok Mittauspiste 4 109,85 ok Mittauspiste 5 110,26 ok Mittauspiste 5 110,82! ka 110,47 ka 110,04
34 34 Pulttireikä Piirustus 17,00 Piirustus 17+/-0,5 Pulttireikä 1 17,11 Pulttireikä 1 16,90 ok Pulttireikä 2 17,23 Pulttireikä 2 17,02 ok Pulttireikä 3 17,15 Pulttireikä 3 16,96 ok Pulttireikä 4 17,15 Pulttireikä 4 16,98 ok Pulttireikä 5 17,19 Pulttireikä 5 17,01 ok Pulttireikien paikkatol. Piirustus 0,60 Piirustus 0,30 Pulttireikä 1 0,06 ok Pulttireikä 1 0,05 ok Pulttireikä 2 0,35 ok Pulttireikä 2 0,41! Pulttireikä 3 0,24 ok Pulttireikä 3 0,28 ok Pulttireikä 4 0,08 ok Pulttireikä 4 0,20 ok Pulttireikä 5 0,26 ok Pulttireikä 5 0,39! Pulttireikien keskipiste Piirustus Ei ilmoitettu Piirustus 0,50 keskiöreikään verr. Mittaus1 0,32 Mittaus1 0,18 ok Mittaus2 0,31 Mittaus2 0,18 ok Mittaus3 0,31 Mittaus3 0,18 ok ka 0,31 ka 0,18 Venttiilireikä Piirustus 15,7+/- 0,4 Piirustus 15,7+0, 4 Mittaus1 15,92 ok Mittaus1 16,05 ok Mittaus2 15,90 ok Mittaus2 15,95 ok Mittaus3 15,92 ok Mittaus3 15,98 ok ka 15,91 ka 15,99 Huomioita Vanteessa ei huomioitavaa alkavaa ruostetta ja maalipinta näyttää olevan muutenkin hyvässä kunnossa. Vanteessa on merkinnät vanteen koosta, mutta valmistajaa ei ilmoiteta, merkinnät vanteessa olivat todella himmeällä ja ne näkyivät huonosti
35 35 Taulukko 5. Vertailu 2. Kremenchug W12x20 Vertailu/Current supplier W11x20 Aksiaaliheitto Piirustus max. 3,5 Piirustus max. 2,5 Mittaus 1 0,81 Ok Mittaus 1 1,66 Ok Mittaus 2 0,67 Ok Mittaus 2 1,66 Ok Mittaus 3 0,67 Ok Mittaus 3 1,66 Ok ka 0,72 ka 1,66 Säteisheitto Piirustus max. 3,5 Tasomaisuus (Disk's maulding) Piirustus max. 2,5 Mittaus 1 1,27 Ok Mittaus 1 1,78 Ok Mittaus 2 1,27 Ok Mittaus 2 2,02 Ok Mittaus 3 1,34 Ok Mittaus 3 1,89 Ok ka 1,29 ka 1,90 Toleranssi/ halk. 320 Toleranssi/ halk. 260 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,73 Ok Mittaus1 0,42 Ok Mittaus2 0,73 Ok Mittaus2 0,41 Ok Mittaus3 0,70 Ok Mittaus3 0,42 Ok ka 0,72 ka 0,42 Toleranssi/ halk. 320 Toleranssi/ halk. 260 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,70 Mittaus1 0,51 Ok Mittaus2 0,72 Mittaus2 0,52 Ok Mittaus3 0,72 Mittaus3 5,32 Ok ka 0,71 ka 2,12 leveys leveys Vanteen leveys Piirustus 305+/- Piirustus 279,40 2,5 Mittauspiste 1 302,61 Ok Mittauspiste 279,15 1 Mittauspiste 2 302,62 Ok Mittauspiste 280,26 2 Mittauspiste 3 302,98 Ok Mittauspiste 279,28 3 Mittauspiste 4 302,54 Ok Mittauspiste 280,74 4 Mittauspiste 5 302,53 Ok Mittauspiste 279,74 5 ka 302,66 ka 279,83
36 36 Pituus Pituus Keskeltä sisäreunaan Piirustus 167+/- 1,5 Piirustus 159,4+/- 1,5 Mittauspiste 1 167,45 Ok Mittauspiste 142,84! 1 Mittauspiste 2 167,55 Ok Mittauspiste 143,14! 2 Mittauspiste 3 168,28 Ok Mittauspiste 142,97! 3 Mittauspiste 4 168,19 Ok Mittauspiste 143,05! 4 Mittauspiste 5 167,51 Ok Mittauspiste 142,95! 5 ka 167,80 ka 142,98 Keskiröreikä Piirustus Piirustus Mittauspiste 1 110,50 Ok Mittauspiste 111,80! 1 Mittauspiste 2 110,45 Ok Mittauspiste 111,91! 2 Mittauspiste 3 110,48 Ok Mittauspiste 112,05! 3 Mittauspiste 4 110,68 Mittauspiste 112,14! 4 Mittauspiste 5 110,26 Mittauspiste 112,29! 5 ka 110,47 ka 112,04 Vanteen sisähalkaisija Piirustus 459,30 Piirustus Ei ilmoitettu Mittauspiste 1 459,30 Ok Mittauspiste 1 Mittauspiste 2 459,22 Ok Mittauspiste 2 Mittauspiste 3 459,40 Ok Mittauspiste 3 Mittauspiste 4 459,25 Mittauspiste 4 Mittauspiste 5 459,35 Mittauspiste 5 ka 459,30 ka Pulttireikä Piirustus 17,00 Piirustus 17,00 Pulttireikä 1 17,16 Pulttireikä 18,52! 1 Pulttireikä 2 17,18 Pulttireikä 18,54! 2 Pulttireikä 3 17,17 Pulttireikä 18,59! 3 Pulttireikä 4 17,15 Pulttireikä 18,54! 4 Pulttireikä 5 17,17 Pulttireikä 18,57! 5 Pulttireikien paikkatol. Piirustus 0,30 Piirustus 0,30
37 37 Pulttireikä 1 0,12 Ok Pulttireikä 0,18 Ok 1 Pulttireikä 2 0,03 Ok Pulttireikä 0,29 Ok 2 Pulttireikä 3 0,13 Ok Pulttireikä 0,01 Ok 3 Pulttireikä 4 0,14 Ok Pulttireikä 0,18 Ok 4 Pulttireikä 5 0,04 Ok Pulttireikä 0,44 5 Pulttireikien keskipiste Piirustus Ei ilmoi- Piirustus 0,80 keskiöreikään verr. tettu Mitattu 0,25 Mitattu 0,62 Ok Venttiilireikä Piirustus 15,7+/- Piirustus 15,7 0,4 Mittaus1 15,96 Ok Mittaus1 15,54 Ok Mittaus2 16,04 Ok Mittaus2 15,56 Ok Mittaus3 16,05 Ok Mittaus3 15,59 Ok ka 16,02 ka 15,56 Huomioita Vanteessa ei huomioitavaa alkavaa ruostetta. Maalipinta rikki muutamasta paikasta.
38 38 Taulukko 6. Vertailu 3. Kremenchug DW25Ax26 Levypyörä DW25Lx26 Aksiaaliheitto Piirustus max. Piirustus max. 5 Mittaus 1 0,68 ok Mittaus 1 1,31 ok Mittaus 2 0,73 ok Mittaus 2 1,03 ok Mittaus 3 0,76 ok Mittaus 3 1,46 ok ka 0,72 ka 1,27 Säteisheitto Piirustus max. 3,5 Tasomaisuus (Disk's maulding) Piirustus max. 5 Mittaus 1 1,09 ok Mittaus 1 1,64 ok Mittaus 2 1,08 ok Mittaus 2 1,66 ok Mittaus 3 1,11 ok Mittaus 3 1,64 ok ka 1,09 ka 1,65 Toleranssi/ halk. 350 Toleranssi/ halk. 325 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,42 ok Mittaus1 0,14 ok Mittaus2 0,35 ok Mittaus2 0,14 ok Mittaus3 0,37 ok Mittaus3 0,14 ok ka 0,38 ka 0,14 Toleranssi/ halk. 350 Toleranssi/ halk. 325 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,23 ok Mittaus1 0,17 ok Mittaus2 0,25 ok Mittaus2 0,17 ok Mittaus3 0,24 ok Mittaus3 0,17 ok ka 0,24 ka 0,17 leveys leveys Vanteen leveys Piirustus 635+/- Piirustus 635,00 6,4 Mittauspiste 1 636,29 ok Mittauspiste 637,42 1 Mittauspiste 2 635,93 ok Mittauspiste 637,87 2 Mittauspiste 3 636,00 ok Mittauspiste 637,92 3 Mittauspiste 4 636,30 ok Mittauspiste 637,58 4 Mittauspiste 5 635,92 ok Mittauspiste 637,66 5 ka 636,09 ka 637,69 Pituus Pituus Keskeltä sisäreunaan Piirustus 259,5+/- 2 Piirustus 259,5 +/- 1,5
39 39 Mittauspiste 1 259,57 ok Mittauspiste 258,45 ok 1 Mittauspiste 2 260,26 ok Mittauspiste 258,55 ok 2 Mittauspiste 3 259,66 ok Mittauspiste 258,35 ok 3 Mittauspiste 4 260,10 ok Mittauspiste 258,23 ok 4 Mittauspiste 5 259,80 ok Mittauspiste 257,81! 5 Mittauspiste 6 259,47 ok Mittauspiste 257,71! 6 Mittauspiste 7 258,95 ok Mittauspiste 257,64! 7 Mittauspiste 8 258,99 ok Mittauspiste 257,60! 8 ka 259,60 ka 258,04 Keskiröreikä Piirustus Piirustus ,5 Mittauspiste 1 221,44 ok Mittauspiste 222,96! 1 Mittauspiste 2 221,44 ok Mittauspiste 222,81! 2 Mittauspiste 3 221,49 ok Mittauspiste 222,68! 3 Mittauspiste 4 221,34 ok Mittauspiste 222,77! 4 Mittauspiste 5 221,39 ok Mittauspiste 222,50! 5 ka 221,42 ka 222,74 Pulttireikä Piirustus Piirustus Pulttireikä 1 24,46 ok Pulttireikä 1 24,12 ok Pulttireikä 2 24,46 ok Pulttireikä 2 24,03 ok Pulttireikä 3 24,55 ok Pulttireikä 3 24,13 ok Pulttireikä 4 24,47 ok Pulttireikä 4 24,16 ok Pulttireikä 5 24,45 ok Pulttireikä 5 24,22 ok Pulttireikä 6 24,47 ok Pulttireikä 6 24,09 ok Pulttireikä 7 24,45 ok Pulttireikä 7 24,04 ok Pulttireikä 8 24,47 ok Pulttireikä 8 24,02 ok Pulttireikien paikkatol. Piirustus 0,30 Piirustus 0,30 Pulttireikä 1 0,04 ok Pulttireikä 1 0,65 ok Pulttireikä 2 0,03 ok Pulttireikä 2 0,23! Pulttireikä 3 0,46! Pulttireikä 3 0,18! Pulttireikä 4 0,36! Pulttireikä 4 0,35 ok Pulttireikä 5 0,69! Pulttireikä 5 0,16! Pulttireikä 6 0,23 ok Pulttireikä 6 0,04! Pulttireikä 7 0,32! Pulttireikä 7 0,68! Pulttireikä 8 0,21 ok Pulttireikä 8 0,48! Pulttireikien keskipiste keskiöreikään Piirustus Ei ilmoitettu Piirustus 0,80
40 40 verr. Mittaus 1 0,50 Mittaus 1 0,48 ok Mittaus 2 0,50 Mittaus 2 0,48 ok Mittaus 3 0,50 Mittaus 3 0,48 ok ka 0,50 ka 0,48 Venttiilireikä Piirustus 15,7+/- Piirustus 15,7 0,4 Mittaus1 15,96 ok Mittaus1 15,74 ok Mittaus2 16,04 ok Mittaus2 15,80 ok Mittaus3 16,05 ok Mittaus3 15,71 ok ka 16,02 ka 15,75 Huomioita Vanteessa kokomerkinnät, mutta valmistajan tietoja tai piir.num. ei ollut levyn hitsauksien reunoissa alkavaa ruostetta, muuten pinta oli hyvässä kunnossa muutamaa pintarikkoutumaa lukuunottamatta. Pulttireikien paikat vähä väärässä paikassa.
41 41 Taulukko 7. Vertailu 4. Kremenchug DW15Lx34 Levypyörä DW16Lx34 Aksiaaliheitto Piirustus Max. heitto 5 Piirustus Max. heitto 5 Mittaus 1 4,16 ok Mittaus 1 1,07 ok Mittaus 2 4,09 ok Mittaus 2 0,87 ok Mittaus 3 4,65 ok Mittaus 3 0,78 ok ka 4,30 ka 0,91 Säteisheitto Piirustus Max. heitto 5 Tasomaisuus (Disk's maulding) Piirustus Max. heitto 5 Mittaus 1 3,15 ok Mittaus 1 1,29 ok Mittaus 2 3,59 ok Mittaus 2 1,28 ok Mittaus 3 3,11 ok Mittaus 3 1,29 ok ka 3,28 ka 1,29 Toleranssi/ halk. 390 Toleranssi/ halk. 390 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,72 ok Mittaus1 1,95! Mittaus2 0,66 ok Mittaus2 2,32! Mittaus3 0,70 ok Mittaus3 1,99! ka 0,69 ka 2,09 Toleranssi/ halk. 390 Toleranssi/ halk. 390 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,59 ok Mittaus1 1,57! Mittaus2 0,67 ok Mittaus2 1,46! Mittaus3 0,62 ok Mittaus3 1,39! ka 0,63 ka 1,47 leveys leveys Vanteen leveys Piirustus 381 +/-5 Piirustus Mittauspiste 1 381,50 ok Mittauspiste 411,28 1 Mittauspiste 2 380,95 ok Mittauspiste 410,11 2 Mittauspiste 3 381,46 ok Mittauspiste 410,37 3 Mittauspiste 4 381,80 ok Mittauspiste 410,27 4 Mittauspiste 5 379,15 ok Mittauspiste 411,09 5 ka 380,97 ka 410,62 Pituus Pituus Keskeltä sisäreunaan Piirustus 147,5 +/- Piirustus 2 Mittauspiste 1 145,58 ok Mittauspiste 161,03 1 Mittauspiste 2 146,34 ok Mittauspiste 2 160,77
42 42 Mittauspiste 3 145,52 ok Mittauspiste 160,06 3 Mittauspiste 4 146,88 ok Mittauspiste 160,42 4 Mittauspiste 5 146,10 ok Mittauspiste 160,98 5 Mittauspiste 6 147,40 ok Mittauspiste 160,94 6 Mittauspiste 7 146,47 ok Mittauspiste 160,52 7 Mittauspiste 8 146,80 ok Mittauspiste 160,25 8 ka 146,38 ka 160,62 Keskiröreikä Piirustus Piirustus ,5 Mittauspiste 1 221,17 ok Mittauspiste 222,80! 1 Mittauspiste 2 221,22 ok Mittauspiste 222,32! 2 Mittauspiste 3 221,12 ok Mittauspiste 222,58! 3 Mittauspiste 4 221,11 ok Mittauspiste 222,80! 4 Mittauspiste 5 221,15 ok Mittauspiste 222,86! 5 ka 221,15 ka 222,67 Pulttireikä Piirustus Piirustus Pulttireikä 1 24,95 ok Pulttireikä 24,38 ok 1 Pulttireikä 2 24,86 ok Pulttireikä 24,43 ok 2 Pulttireikä 3 25,00 ok Pulttireikä 24,49 ok 3 Pulttireikä 4 24,88 ok Pulttireikä 24,39 ok 4 Pulttireikä 5 24,87 ok Pulttireikä 24,38 ok 5 Pulttireikä 6 24,82 ok Pulttireikä 24,18 ok 6 Pulttireikä 7 24,99 ok Pulttireikä 24,31 ok 7 Pulttireikä 8 24,79 ok Pulttireikä 24,40 ok 8 Pulttireikien paikkatol. Piirustus Halk. 0,3 Piirustus Halk. 0,3 Pulttireikä 1 0,12 ok Pulttireikä 0,17 ok 1 Pulttireikä 2 0,14 ok Pulttireikä 0,03 ok 2 Pulttireikä 3 0,09 ok Pulttireikä 0,19 ok 3 Pulttireikä 4 0,07 ok Pulttireikä 0,23 ok 4 Pulttireikä 5 0,08 ok Pulttireikä 0,16 ok 5 Pulttireikä 6 0,07 ok Pulttireikä 0,11 ok
43 43 Pulttireikien keskipiste keskiöreikään verr. 6 Pulttireikä 7 0,06 ok Pulttireikä 0,05 ok 7 Pulttireikä 8 0,06 ok Pulttireikä 0,14 ok 8 Piirustus Ei ilmoitettu Piirustus Halk. 0,8 Mittaus 1 0,08 Mittaus 1 0,11 ok Mittaus 2 0,10 Mittaus 2 0,17 ok Mittaus 3 0,15 Mittaus 3 0,16 ok ka 0,11 ka 0,15 Venttiilireikä Piirustus 15,7 +0,4 Piirustus 15,7 Mittaus1 16,00 ok Mittaus1 15,92 ok Mittaus2 15,89 ok Mittaus2 15,72 ok Mittaus3 15,88 ok Mittaus3 15,71 ok ka 15,92 ka 15,78 Huomioita Vanteessa ei huomioitavaa alkavaa ruostetta. Maalipinta rikki muutamasta paikasta. Vanteesta ei löydy piirustusnumeroa, valmistajan tietoja eikä kokoa.
44 44 Taulukko 8. Vertailu 5. Kremenchug DW18Lx38 Levypyörä DW18Lx38 Aksiaaliheitto Piirustus Max. heitto 4 Piirustus Max. heitto 4 Mittaus 1 1,16 ok Mittaus 1 1,65 ok Mittaus 2 1,22 ok Mittaus 2 1,76 ok Mittaus 3 1,15 ok Mittaus 3 1,74 ok ka 1,18 ka 1,71 Säteisheitto Piirustus Max. heitto 4 Tasomaisuus (Disk's maulding) Piirustus Max. heitto 4 Mittaus 1 2,52 ok Mittaus 1 1,29 ok Mittaus 2 2,43 ok Mittaus 2 1,28 ok Mittaus 3 2,48 ok Mittaus 3 1,29 ok ka 2,48 ka 1,29 Toleranssi/ halk. 330 Toleranssi/ halk. 325 Piirustus 0,75 Piirustus 0,75 Mittaus1 0,25 ok Mittaus1 0,36 ok Mittaus2 0,31 ok Mittaus2 0,39 ok Mittaus3 0,28 ok Mittaus3 0,39 ok ka 0,28 ka 0,38 Toleranssi/ halk. 330 Toleranssi/ halk. 325 Piirustus 0,75 Piirustus 0,75 Mittaus1 1,79! Mittaus1 0,35 ok Mittaus2 1,70! Mittaus2 0,40 ok Mittaus3 1,73! Mittaus3 0,17 ok ka 1,74 ka 0,31 leveys leveys Vanteen leveys Piirustus 457,2 +/- Piirustus 457,20 4,7 Mittauspiste 1 460,28 ok Mittauspiste 458,33 1 Mittauspiste 2 461,39 ok Mittauspiste 458,18 2 Mittauspiste 3 459,75 ok Mittauspiste 458,13 3 Mittauspiste 4 460,52 ok Mittauspiste 458,23 4 Mittauspiste 5 460,33 ok Mittauspiste 457,91 5 ka 460,45 ka 458,16 Pituus Pituus Keskeltä sisäreunaan Piirustus 202,6 +/- 1,5 Piirustus 202,6 +/- 1,5 Mittauspiste 1 202,72 ok Mittauspiste 201,65 ok 1 Mittauspiste 2 201,98 ok Mittauspiste 202,64 ok
45 45 2 Mittauspiste 3 202,16 ok Mittauspiste 202,35 ok 3 Mittauspiste 4 202,79 ok Mittauspiste 201,63 ok 4 Mittauspiste 5 202,27 ok Mittauspiste 201,82 ok 5 Mittauspiste 6 202,20 ok Mittauspiste 202,07 ok 6 Mittauspiste 7 202,59 ok Mittauspiste 201,80 ok 7 Mittauspiste 8 202,76 ok Mittauspiste 201,85 ok 8 ka 202,43 ka 201,98 Keskiröreikä Piirustus Piirustus Mittauspiste 1 221,24 ok Mittauspiste 222,63! 1 Mittauspiste 2 221,09 ok Mittauspiste 222,54! 2 Mittauspiste 3 221,34 ok Mittauspiste 222,09! 3 Mittauspiste 4 221,30 ok Mittauspiste 222,46! 4 Mittauspiste 5 221,26 ok Mittauspiste 222,42! 5 ka 221,25 ka 222,43 Pulttireikä Piirustus Piirustus Pulttireikä 1 24,69 ok Pulttireikä 1 23,94! Pulttireikä 2 24,71 ok Pulttireikä 2 24,05 ok Pulttireikä 3 24,96 ok Pulttireikä 3 24,32 ok Pulttireikä 4 24,80 ok Pulttireikä 4 24,38 ok Pulttireikä 5 24,70 ok Pulttireikä 5 23,99! Pulttireikä 6 24,81 ok Pulttireikä 6 24,09 ok Pulttireikä 7 24,95 ok Pulttireikä 7 23,75! Pulttireikä 8 24,94 ok Pulttireikä 8 24,02 ok Pulttireikien paikkatol. Pulttireikien keskipiste keskiöreikään verr. Piirustus Halk. 0,3 Piirustus Halk. 0,3 Pulttireikä 1 0,17 ok Pulttireikä 1 0,07 ok Pulttireikä 2 0,24 ok Pulttireikä 2 0,59! Pulttireikä 3 0,24 ok Pulttireikä 3 0,57! Pulttireikä 4 0,22 ok Pulttireikä 4 0,19 ok Pulttireikä 5 0,05 ok Pulttireikä 5 0,77! Pulttireikä 6 0,13 ok Pulttireikä 6 0,47! Pulttireikä 7 0,46! Pulttireikä 7 0,33! Pulttireikä 8 0,35! Pulttireikä 8 0,51! Piirustus Ei ilmoitettu Piirustus Halk. 0,8 Mittaus 1 0,20 Mittaus 1 0,13 ok Mittaus 2 0,18 Mittaus 2 0,13 ok Mittaus 3 0,21 Mittaus 3 0,16 ok
46 46 ka 0,20 ka 0,14 Venttiilireikä Piirustus 15,7 +0,4 Piirustus 15,7 Mittaus1 15,96 ok Mittaus1 15,71 ok Mittaus2 15,85 ok Mittaus2 15,72 ok Mittaus3 15,89 ok Mittaus3 15,71 ok ka 15,90 ka 15,71 Huomioita Vanteessa ei huomioitavaa alkavaa ruostetta. Maalipinta rikki muutamasta paikasta. Ainoa suuri huomautuksen aihe oli kiinnityspinnan tasomaisuus. Vanteesta ei löydy piirustusnumeroa, valmistajan tietoja eikä kokoa.
Keskeiset aihepiirit
 TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
Koneistusyritysten kehittäminen. Mittaustekniikka. Mittaaminen ja mittavälineet. Rahoittajaviranomainen: Satakunnan ELY-keskus
 Koneistusyritysten kehittäminen Mittaustekniikka Mittaaminen ja mittavälineet Rahoittajaviranomainen: Satakunnan ELY-keskus Yleistä Pidä työkalut erillään mittavälineistä Ilmoita rikkoutuneesta mittavälineestä
Koneistusyritysten kehittäminen Mittaustekniikka Mittaaminen ja mittavälineet Rahoittajaviranomainen: Satakunnan ELY-keskus Yleistä Pidä työkalut erillään mittavälineistä Ilmoita rikkoutuneesta mittavälineestä
OSA A. MITTATOLERANSSIT
 BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
Standardin ISO 8062 mittatoleranssijärjestelmä
 Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Varausta poistavien lattioiden mittausohje. 1. Tarkoitus. 2. Soveltamisalue. 3. Mittausmenetelmät MITTAUSOHJE 1.6.2001 1 (5)
 1.6.2001 1 (5) Varausta poistavien lattioiden mittausohje 1. Tarkoitus Tämän ohjeen tarkoituksena on yhdenmukaistaa ja selkeyttää varausta poistavien lattioiden mittaamista ja mittaustulosten dokumentointia
1.6.2001 1 (5) Varausta poistavien lattioiden mittausohje 1. Tarkoitus Tämän ohjeen tarkoituksena on yhdenmukaistaa ja selkeyttää varausta poistavien lattioiden mittaamista ja mittaustulosten dokumentointia
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Mittajärjestelmät ja mittasuositukset.
 Mittajärjestelmät ja mittasuositukset. Hannu Hirsi Johdanto: Mittajärjestelmien tarkoitus: Helpottaa eri toimijoiden järjestelmien ja osien yhteensovittamista : suunnittelua, valmistusta, asentamista,
Mittajärjestelmät ja mittasuositukset. Hannu Hirsi Johdanto: Mittajärjestelmien tarkoitus: Helpottaa eri toimijoiden järjestelmien ja osien yhteensovittamista : suunnittelua, valmistusta, asentamista,
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619
 KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN
 PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN Opas laboratorio- ja konepajakäyttöön SUOMIPAINOS Profiilit ja suodattimet (EN ISO 4287 ja EN ISO 16610-21) 01 Varsinainen profiili on profiili, joka syntyy todellisen
PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN Opas laboratorio- ja konepajakäyttöön SUOMIPAINOS Profiilit ja suodattimet (EN ISO 4287 ja EN ISO 16610-21) 01 Varsinainen profiili on profiili, joka syntyy todellisen
Mittaustekniikka (3 op)
 530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
CAD/CAM Software with world class precision and control. What s Uusi
 What s Uusi SURFCAM V5.2 Mitä Uutta Page 1 of 19 Toukokuu 2011 Mitä uutta - SURFCAM V5.2 Sisällysluettelo 1) Uusi - Millturn valikko 3 2) Uusi HSM Z-rouhinta rata 4 3) Uusi - Valintojen multi maskaus 6
What s Uusi SURFCAM V5.2 Mitä Uutta Page 1 of 19 Toukokuu 2011 Mitä uutta - SURFCAM V5.2 Sisällysluettelo 1) Uusi - Millturn valikko 3 2) Uusi HSM Z-rouhinta rata 4 3) Uusi - Valintojen multi maskaus 6
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Tehoa robotiikasta -hanke. 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu
 Tehoa robotiikasta -hanke 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu Sisällys MITTAUSTARPEIDEN MÄÄRITTELY... 2 KOORDINAATTIMITTALAITTEEN JA MUIDEN MITTALAITTEIDEN TUOMAT
Tehoa robotiikasta -hanke 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu Sisällys MITTAUSTARPEIDEN MÄÄRITTELY... 2 KOORDINAATTIMITTALAITTEEN JA MUIDEN MITTALAITTEIDEN TUOMAT
5. Keskustelun jälkeen päätettiin, että purjeiden mittaussäännöt muutetaan SPL:n teknisen lautakunnan suositusten mukaisiksi seuraavasti (liite 1.
 Haipurjehtijat Hajseglare ry. YLIMÄÄRÄISEN KOKOUKSEN PÖYTÄKIRJA Aika: 19.7.2007 Paikka: Pietarsaari 1. Yhdistyksen puheenjohtaja Håkan Forss avasi kokouksen 2. Valittiin Håkan Forss kokouksen puheenjohtajaksi
Haipurjehtijat Hajseglare ry. YLIMÄÄRÄISEN KOKOUKSEN PÖYTÄKIRJA Aika: 19.7.2007 Paikka: Pietarsaari 1. Yhdistyksen puheenjohtaja Håkan Forss avasi kokouksen 2. Valittiin Håkan Forss kokouksen puheenjohtajaksi
TEKNINEN PIIRUSTUS II
 TEKNINEN PIIRUSTUS II Kevät 2015 PINTAMERKIT TkT Harri Eskelinen 1 1 Johdanto 2 Pintamerkillä ilmoitettavia vaatimuksia Pintamerkkejä käytetään ilmaistaessa mm. seuraavia pintaa koskevia vaatimuksia: Pinnan
TEKNINEN PIIRUSTUS II Kevät 2015 PINTAMERKIT TkT Harri Eskelinen 1 1 Johdanto 2 Pintamerkillä ilmoitettavia vaatimuksia Pintamerkkejä käytetään ilmaistaessa mm. seuraavia pintaa koskevia vaatimuksia: Pinnan
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Valukappaleiden koneenpiirustus: Piirustusmerkinnät ja periaatteet alkeista lähtien Tuula Höök, Valimoinstituutti
 Valukappaleiden koneenpiirustus: Piirustusmerkinnät ja periaatteet alkeista lähtien Tuula Höök, Valimoinstituutti Koneenpiirustusta koskevat standardit Koneenpiirustus yleisesti: piirustusarkki: arkin
Valukappaleiden koneenpiirustus: Piirustusmerkinnät ja periaatteet alkeista lähtien Tuula Höök, Valimoinstituutti Koneenpiirustusta koskevat standardit Koneenpiirustus yleisesti: piirustusarkki: arkin
Kelluvien turvalaitteiden. asennus- ja mittausohje
 Kelluvien turvalaitteiden asennus- ja mittausohje 2009 Versio 0.4 Sivu 1 (9) 14.9.2009 Ohjeen infosivu: Kelluvien turvalaitteiden asennus- ja mittausohje Versio: 0.3 / 28.8.2009 laatinut IK Status: Yleisohje
Kelluvien turvalaitteiden asennus- ja mittausohje 2009 Versio 0.4 Sivu 1 (9) 14.9.2009 Ohjeen infosivu: Kelluvien turvalaitteiden asennus- ja mittausohje Versio: 0.3 / 28.8.2009 laatinut IK Status: Yleisohje
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä
 Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
Sustainable steel construction seminaari
 Sustainable steel construction seminaari 18.1.2017 Geometrian mittaaminen ja 3D skannaus Timo Kärppä 2017 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia asioita 2. Mitä on 3D? 3. 3D skannaus, eri menetelmiä,
Sustainable steel construction seminaari 18.1.2017 Geometrian mittaaminen ja 3D skannaus Timo Kärppä 2017 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia asioita 2. Mitä on 3D? 3. 3D skannaus, eri menetelmiä,
Ympyrä 1/6 Sisältö ESITIEDOT: käyrä, kulma, piste, suora
 Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
TTY Mittausten koekenttä. Käyttö. Sijainti
 TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
3. Harjoitusjakso I. Vinkkejä ja ohjeita
 3. Harjoitusjakso I Tämä ensimmäinen harjoitusjakso sisältää kaksi perustason (a ja b) ja kaksi edistyneen tason (c ja d) harjoitusta. Kaikki neljä harjoitusta liittyvät geometrisiin konstruktioihin. Perustason
3. Harjoitusjakso I Tämä ensimmäinen harjoitusjakso sisältää kaksi perustason (a ja b) ja kaksi edistyneen tason (c ja d) harjoitusta. Kaikki neljä harjoitusta liittyvät geometrisiin konstruktioihin. Perustason
761121P-01 FYSIIKAN LABORATORIOTYÖT 1. Oulun yliopisto Fysiikan tutkinto-ohjelma Kevät 2016
 1 76111P-01 FYSIIKAN LABORATORIOTYÖT 1 Oulun yliopisto Fysiikan tutkinto-ohjelma Kevät 016 JOHDANTO Fysiikassa pyritään löytämään luonnosta lainalaisuuksia, joita voidaan mitata kokeellisesti ja kuvata
1 76111P-01 FYSIIKAN LABORATORIOTYÖT 1 Oulun yliopisto Fysiikan tutkinto-ohjelma Kevät 016 JOHDANTO Fysiikassa pyritään löytämään luonnosta lainalaisuuksia, joita voidaan mitata kokeellisesti ja kuvata
Laboratorioraportti 3
 KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
Tuulen nopeuden mittaaminen
 KON C3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma / ryhmä K Tuulen nopeuden mittaaminen Matias Kidron 429542 Toni Kokkonen 429678 Sakke Juvonen 429270 Kansikuva: http://www.stevennoble.com/main.php?g2_view=core.downloaditem&g2_itemid=12317&g2_serialnumber=2
KON C3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma / ryhmä K Tuulen nopeuden mittaaminen Matias Kidron 429542 Toni Kokkonen 429678 Sakke Juvonen 429270 Kansikuva: http://www.stevennoble.com/main.php?g2_view=core.downloaditem&g2_itemid=12317&g2_serialnumber=2
AKK-MOTORSPORT ry Katsastuksen käsikirja ISKUTILAVUUDEN MITTAAMINEN. 1. Tarkastuksen käyttö
 ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
Differentiaali- ja integraalilaskenta
 Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
Mittaaminen projektipäällikön ja prosessinkehittäjän työkaluna
 Mittaaminen projektipäällikön ja prosessinkehittäjän työkaluna Finesse-seminaari 22.03.00 Matias Vierimaa 1 Mittauksen lähtökohdat Mittauksen tulee palvella sekä organisaatiota että projekteja Organisaatiotasolla
Mittaaminen projektipäällikön ja prosessinkehittäjän työkaluna Finesse-seminaari 22.03.00 Matias Vierimaa 1 Mittauksen lähtökohdat Mittauksen tulee palvella sekä organisaatiota että projekteja Organisaatiotasolla
SATAKUNNAN AMMATTIKORKEAKOULU. Hakala Toni Varpelaide Heidi TEKSTINKÄSITTELYN OHJEET CASE: OPINNÄYTETYÖN RAPORTOINTI WORDILLA
 SATAKUNNAN AMMATTIKORKEAKOULU Hakala Toni Varpelaide Heidi TEKSTINKÄSITTELYN OHJEET CASE: OPINNÄYTETYÖN RAPORTOINTI WORDILLA Liiketalous ja tietojenkäsittely Huittinen Liiketalous Taloushallinto 2005 1
SATAKUNNAN AMMATTIKORKEAKOULU Hakala Toni Varpelaide Heidi TEKSTINKÄSITTELYN OHJEET CASE: OPINNÄYTETYÖN RAPORTOINTI WORDILLA Liiketalous ja tietojenkäsittely Huittinen Liiketalous Taloushallinto 2005 1
Sivu 1(2) Aksonometriset kuvannot kappaleesta ja kuvantoihin liittyvät nimellismitat.
 Sivu 1(2) 201 CAD-SUUNNITTELU 16.12.2008 /MMk/JHa 1. KILPAILUPÄIVÄ OSIO A 2D-TEHTÄVÄ KIKKARE 2D-tehtävä: Kestoaika: Annettu: Piirustus: Kappaleen piirustusten laatiminen aksonometrisen luonnoksen avulla.
Sivu 1(2) 201 CAD-SUUNNITTELU 16.12.2008 /MMk/JHa 1. KILPAILUPÄIVÄ OSIO A 2D-TEHTÄVÄ KIKKARE 2D-tehtävä: Kestoaika: Annettu: Piirustus: Kappaleen piirustusten laatiminen aksonometrisen luonnoksen avulla.
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
Ilmanvirtauksen mittarit
 Swema 3000 yleismittari/monitoimimittari sisäilmastomittauksiin Ilmastoinnin yleismittari, Vahva metallirunkoinen Swema 3000 on suunniteltu ilmastoinnin, sisäilmaston ja olosuhdemittausten tarpeisiin erityisesti
Swema 3000 yleismittari/monitoimimittari sisäilmastomittauksiin Ilmastoinnin yleismittari, Vahva metallirunkoinen Swema 3000 on suunniteltu ilmastoinnin, sisäilmaston ja olosuhdemittausten tarpeisiin erityisesti
I Geometrian rakentaminen pisteestä lähtien
 I Geometrian rakentaminen pisteestä lähtien Koko geometrian voidaan ajatella koostuvan pisteistä. a) Matemaattinen piste on sellainen, millä EI OLE LAINKAAN ULOTTUVUUKSIA. Oppilaita voi johdatella pisteen
I Geometrian rakentaminen pisteestä lähtien Koko geometrian voidaan ajatella koostuvan pisteistä. a) Matemaattinen piste on sellainen, millä EI OLE LAINKAAN ULOTTUVUUKSIA. Oppilaita voi johdatella pisteen
Toleranssit ja pinnankarheus Seppo Kivioja
 Toleranssit ja pinnankarheus Seppo Kivioja 4. painos Espoo 2011 2 Sisältö 1 MITTATOLERANSSIT... 3 1.1 Yleisimmät toleranssikäsitteet... 3 1.2 ISOmittatoleranssijärjestelmä... 4 1.3 Sovitteen valinta...
Toleranssit ja pinnankarheus Seppo Kivioja 4. painos Espoo 2011 2 Sisältö 1 MITTATOLERANSSIT... 3 1.1 Yleisimmät toleranssikäsitteet... 3 1.2 ISOmittatoleranssijärjestelmä... 4 1.3 Sovitteen valinta...
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO
 Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003
 EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003 LABORATORIOTÖIDEN OHJEET (Mukaillen työkirjaa "Teknillisten oppilaitosten Elektroniikka";
EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003 LABORATORIOTÖIDEN OHJEET (Mukaillen työkirjaa "Teknillisten oppilaitosten Elektroniikka";
2. Valukappaleiden suunnittelu mallikustannusten kannalta
 2. Valukappaleiden suunnittelu mallikustannusten kannalta Pekka Niemi Tampereen ammattiopisto 2.1. Valukappaleiden muotoilu Valitse kappaleelle sellaiset muodot, jotka on helppo valmistaa mallipajojen
2. Valukappaleiden suunnittelu mallikustannusten kannalta Pekka Niemi Tampereen ammattiopisto 2.1. Valukappaleiden muotoilu Valitse kappaleelle sellaiset muodot, jotka on helppo valmistaa mallipajojen
Tulevaisuuden teräsrakenteet ja vaativa valmistus. 3D-skannaus ja käänteinen suunnittelu
 Tulevaisuuden teräsrakenteet ja vaativa valmistus Hämeenlinnassa 24. - 25.1.2018 3D-skannaus ja käänteinen suunnittelu Timo Kärppä, HAMK Ohutlevykeskus 2018 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia
Tulevaisuuden teräsrakenteet ja vaativa valmistus Hämeenlinnassa 24. - 25.1.2018 3D-skannaus ja käänteinen suunnittelu Timo Kärppä, HAMK Ohutlevykeskus 2018 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia
Koesuunnitelma. Tuntemattoman kappaleen materiaalin määritys. Kon c3004 Kone ja rakennustekniikan laboratoriotyöt. Janne Mattila.
 Kon c3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma Tuntemattoman kappaleen materiaalin määritys Janne Mattila Teemu Koitto Lari Pelanne Sisällysluettelo 1. Tutkimusongelma ja tutkimuksen
Kon c3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma Tuntemattoman kappaleen materiaalin määritys Janne Mattila Teemu Koitto Lari Pelanne Sisällysluettelo 1. Tutkimusongelma ja tutkimuksen
2/3D ELEKTRONINEN MITTAUS. Auton elektroninen. 2/3D-mittalaite. Technology from FINLAND MEASURING SYSTEMS
 2/3D ELEKTRONINEN MITTAUS Auton elektroninen 2/3D-mittalaite Technology from FINLAND MEASURING SYSTEMS 2/3D ELEKTRONINEN MITTAUS Auton elektroninen 2/3D-mittalaite Autorobot Finland Oy on kehittänyt auton
2/3D ELEKTRONINEN MITTAUS Auton elektroninen 2/3D-mittalaite Technology from FINLAND MEASURING SYSTEMS 2/3D ELEKTRONINEN MITTAUS Auton elektroninen 2/3D-mittalaite Autorobot Finland Oy on kehittänyt auton
MACHINERY on laadunvarmistaja
 MACHINERY on laadunvarmistaja Mitä tapahtuu huomenna? entä jos omaisuudelle tapahtuu jotain? entä jos kalustolle tapahtuu jotain? entä jos sinulle tapahtuu jotain? MACHINERY ennakoi, ennaltaehkäisee ja
MACHINERY on laadunvarmistaja Mitä tapahtuu huomenna? entä jos omaisuudelle tapahtuu jotain? entä jos kalustolle tapahtuu jotain? entä jos sinulle tapahtuu jotain? MACHINERY ennakoi, ennaltaehkäisee ja
2.1 Yhdenmuotoiset suorakulmaiset kolmiot
 2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa
 Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
MONISTE 2 Kirjoittanut Elina Katainen
 MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
2. Sähköisiä perusmittauksia. Yleismittari.
 TURUN AMMATTKORKEAKOULU TYÖOHJE 1 TEKNKKA FYSKAN LABORATORO 2.0 2. Sähköisiä perusmittauksia. Yleismittari. 1. Työn tavoite Tutustutaan tärkeimpään sähköiseen perusmittavälineeseen, yleismittariin, suorittamalla
TURUN AMMATTKORKEAKOULU TYÖOHJE 1 TEKNKKA FYSKAN LABORATORO 2.0 2. Sähköisiä perusmittauksia. Yleismittari. 1. Työn tavoite Tutustutaan tärkeimpään sähköiseen perusmittavälineeseen, yleismittariin, suorittamalla
( ) B-B 142 `0,3 28-0,2. 36 Ra1.6. 2x45. 1x45. 2x45. Keskiöporaus sallitaan. 0,5x0,5. Ra3.2. Ra1.6. Koneistusnäyttö Aihio: D50x145 S355
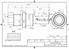 142 `0,3 50 80 M 40 x2 A 20 Ø35 5 n50-0,1 40-0,3 Ø 26-0,05 +0 Ø B + 0,3 55-0 36 Ra1.6 6 2x45 B +0 28-0,2 1x45 0,5x0,5 2x45 b 0,1 A Keskiöporaus sallitaan B-B Ra3.2 Ra1.6 ( ) 3 Designed by Checked by Approved
142 `0,3 50 80 M 40 x2 A 20 Ø35 5 n50-0,1 40-0,3 Ø 26-0,05 +0 Ø B + 0,3 55-0 36 Ra1.6 6 2x45 B +0 28-0,2 1x45 0,5x0,5 2x45 b 0,1 A Keskiöporaus sallitaan B-B Ra3.2 Ra1.6 ( ) 3 Designed by Checked by Approved
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
Säteilijät - aallonpituusnormaalit Stabiloidut laserit rel. 543,5 nm 5 10-10 λ 0
 1/ Säteilijät - aallonpituusnormaalit Stabiloidut laserit 32 nm 1 10-10 λ 0 43, nm 10-10 λ 0 633 nm 1 10-10 λ 0 Pituusmitat Pituuden mittauslaitteet Laser-interferometri 1,0 Peruslaitteisto Kulmapoikkeamien
1/ Säteilijät - aallonpituusnormaalit Stabiloidut laserit 32 nm 1 10-10 λ 0 43, nm 10-10 λ 0 633 nm 1 10-10 λ 0 Pituusmitat Pituuden mittauslaitteet Laser-interferometri 1,0 Peruslaitteisto Kulmapoikkeamien
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET. Jukka-Pekka Rapinoja METSTA
 MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
Suunnitteluohjeita tarkkuusvalukappaleelle
 Suunnitteluohjeita tarkkuusvalukappaleelle Tavoitteena muotoilussa Near-net-shape (NNS) eli mahdollisimman lähelle lopullista muotoa minimi valukappaleen lastuamisella. SFS-ISO 8062 Tarkkuusvalulla saavutettava
Suunnitteluohjeita tarkkuusvalukappaleelle Tavoitteena muotoilussa Near-net-shape (NNS) eli mahdollisimman lähelle lopullista muotoa minimi valukappaleen lastuamisella. SFS-ISO 8062 Tarkkuusvalulla saavutettava
1) Maan muodon selvittäminen. 2) Leveys- ja pituuspiirit. 3) Mittaaminen
 1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
FYSIIKAN LABORAATIOTYÖ 4 LÄMMÖNJOHTAVUUDEN, LÄMMÖNLÄPÄISYKERTOI- MEN JA LÄMMÖNSIIRTYMISKERTOIMEN MÄÄRITYS
 FYSIIKAN LABORAATIOTYÖ 4 LÄMMÖNJOHTAVUUDEN, LÄMMÖNLÄPÄISYKERTOI- MEN JA LÄMMÖNSIIRTYMISKERTOIMEN MÄÄRITYS Työselostuksen laatija: Tommi Tauriainen Luokka: TTE7SNC Ohjaaja: Ari Korhonen Työn tekopvm: 28.03.2008
FYSIIKAN LABORAATIOTYÖ 4 LÄMMÖNJOHTAVUUDEN, LÄMMÖNLÄPÄISYKERTOI- MEN JA LÄMMÖNSIIRTYMISKERTOIMEN MÄÄRITYS Työselostuksen laatija: Tommi Tauriainen Luokka: TTE7SNC Ohjaaja: Ari Korhonen Työn tekopvm: 28.03.2008
1 TYÖNTÖMITTA. sisä mittakärjet tuuma-nonio lukitusruuvi. 1.1 Yleistä työntömitasta
 MITTAVAUNU MATERIAALIA 1( 35) 1 TYÖNTÖMITTA 1.1 Yleistä työntömitasta Työntömitta ( tönäri, mauseri ) kuuluu tekniikan alan perustyökaluihin, joten sen oikeaoppinen käyttö on jokaisen ammattilaisen osattava.
MITTAVAUNU MATERIAALIA 1( 35) 1 TYÖNTÖMITTA 1.1 Yleistä työntömitasta Työntömitta ( tönäri, mauseri ) kuuluu tekniikan alan perustyökaluihin, joten sen oikeaoppinen käyttö on jokaisen ammattilaisen osattava.
geodyna 6800 optima tasapainottamisen uusi standardi
 geodyna 6800 optima tasapainottamisen uusi standardi Täysautomaattinen tasapainotuskone 3 D-laserteknologialla Mikä on GEODYNA 6800 OPTIMA geodyna 6800 optima on täysautomaattinen pyörän tasapainotuskone
geodyna 6800 optima tasapainottamisen uusi standardi Täysautomaattinen tasapainotuskone 3 D-laserteknologialla Mikä on GEODYNA 6800 OPTIMA geodyna 6800 optima on täysautomaattinen pyörän tasapainotuskone
Käyttöopas (ver. 1.29 Injektor Solutions 2006)
 KombiTemp HACCP Elintarviketarkastuksiin Käyttöopas (ver. 1.29 Injektor Solutions 2006) web: web: www.haccp.fi 2006-05-23 KombiTemp HACCP on kehitetty erityisesti sinulle, joka työskentelet elintarvikkeiden
KombiTemp HACCP Elintarviketarkastuksiin Käyttöopas (ver. 1.29 Injektor Solutions 2006) web: web: www.haccp.fi 2006-05-23 KombiTemp HACCP on kehitetty erityisesti sinulle, joka työskentelet elintarvikkeiden
GEOMETRIA MAA3 Geometrian perusobjekteja ja suureita
 GEOMETRI M3 Geometrian perusobjekteja ja suureita Piste ja suora: Piste, suora ja taso ovat geometrian peruskäsitteitä, joita ei määritellä. Voidaan ajatella, että kaikki geometriset kuviot koostuvat pisteistä.
GEOMETRI M3 Geometrian perusobjekteja ja suureita Piste ja suora: Piste, suora ja taso ovat geometrian peruskäsitteitä, joita ei määritellä. Voidaan ajatella, että kaikki geometriset kuviot koostuvat pisteistä.
SwemaAir 5 Käyttöohje
 SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
Kappaleiden tilavuus. Suorakulmainensärmiö.
 Kappaleiden tilavuus Suorakulmainensärmiö. Tilavuus (volyymi) V = pohjan ala kertaa korkeus. Tankomaisista kappaleista puhuttaessa nimitetään korkeutta tangon pituudeksi. Pohjan ala A = b x h Korkeus (pituus)
Kappaleiden tilavuus Suorakulmainensärmiö. Tilavuus (volyymi) V = pohjan ala kertaa korkeus. Tankomaisista kappaleista puhuttaessa nimitetään korkeutta tangon pituudeksi. Pohjan ala A = b x h Korkeus (pituus)
t osatekijät vaikuttavat merkittävästi tuloksen epävarmuuteen Mittaustulosten ilmoittamiseen tulee kiinnittää kriittistä
 Mittausepävarmuuden määrittäminen 1 Mittausepävarmuus on testaustulokseen liittyvä arvio, joka ilmoittaa rajat, joiden välissä on todellinen arvo tietyllä todennäköisyydellä Kokonaisepävarmuusarvioinnissa
Mittausepävarmuuden määrittäminen 1 Mittausepävarmuus on testaustulokseen liittyvä arvio, joka ilmoittaa rajat, joiden välissä on todellinen arvo tietyllä todennäköisyydellä Kokonaisepävarmuusarvioinnissa
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa
 SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
Tasogeometria. Tasogeometrian käsitteitä ja osia. olevia pisteitä. Piste P on suoran ulkopuolella.
 Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
PERUSMITTAUKSIA. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Harjoitus 5: Hitsausmerkinnät Viikko 41, palautus viikko 42
 KON-C3001 Koneenrakennustekniikka A Syksy 2017 Harjoitus 5: Hitsausmerkinnät Viikko 41, palautus viikko 42 Versio 1: Opiskelijanumeron viimeinen numero pariton (All English speaking students, please select
KON-C3001 Koneenrakennustekniikka A Syksy 2017 Harjoitus 5: Hitsausmerkinnät Viikko 41, palautus viikko 42 Versio 1: Opiskelijanumeron viimeinen numero pariton (All English speaking students, please select
z 1+i (a) f (z) = 3z 4 5z 3 + 2z (b) f (z) = z 4z + 1 f (z) = 12z 3 15z 2 + 2
 BM20A5700 - Integraauunnokset Harjoitus 2 1. Laske seuraavat raja-arvot. -kohta ratkeaa, kun pistät sekä yläkerran että alakerran muotoon (z z 1 )(z z 2 ), missä siis z 1 ja z 2 ovat näiden lausekkeiden
BM20A5700 - Integraauunnokset Harjoitus 2 1. Laske seuraavat raja-arvot. -kohta ratkeaa, kun pistät sekä yläkerran että alakerran muotoon (z z 1 )(z z 2 ), missä siis z 1 ja z 2 ovat näiden lausekkeiden
Julkaisun laji Opinnäytetyö. Sivumäärä 43
 OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen
 TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
RKL-, R2KL- ja R3KLkiinnityslevyt
 RKL-, R2KL- ja R3KLkiinnityslevyt Eurokoodien mukainen suunnittelu RKL-, R2KL- ja R3KLkiinnityslevyt 1 TOIMINTATAPA... 2 2 MITAT JA MATERIAALIT... 3 2.1 RKL- ja R2KL-kiinnityslevyjen mitat... 3 2.2 R3KL-kiinnityslevyjen
RKL-, R2KL- ja R3KLkiinnityslevyt Eurokoodien mukainen suunnittelu RKL-, R2KL- ja R3KLkiinnityslevyt 1 TOIMINTATAPA... 2 2 MITAT JA MATERIAALIT... 3 2.1 RKL- ja R2KL-kiinnityslevyjen mitat... 3 2.2 R3KL-kiinnityslevyjen
Monikulmiot 1/5 Sisältö ESITIEDOT: kolmio
 Monikulmiot 1/5 Sisältö Monikulmio Monikulmioksi kutsutaan tasokuviota, jota rajaa perättäisten janojen muodostama monikulmion piiri. Janat ovat monikulmion sivuja, niiden päätepisteet monikulmion kärkipisteitä.
Monikulmiot 1/5 Sisältö Monikulmio Monikulmioksi kutsutaan tasokuviota, jota rajaa perättäisten janojen muodostama monikulmion piiri. Janat ovat monikulmion sivuja, niiden päätepisteet monikulmion kärkipisteitä.
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset
 4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
Mittausten jäljitettävyysketju
 Mittausten jäljitettävyysketju FINAS-päivä 22.1.2013 Sari Saxholm, MIKES @mikes.fi p. 029 5054 432 Mittatekniikan keskus varmistaa kansainvälisesti hyväksytyt mittayksiköt ja pätevyyden arviointipalvelut
Mittausten jäljitettävyysketju FINAS-päivä 22.1.2013 Sari Saxholm, MIKES @mikes.fi p. 029 5054 432 Mittatekniikan keskus varmistaa kansainvälisesti hyväksytyt mittayksiköt ja pätevyyden arviointipalvelut
Mittaamisen maailmasta muutamia asioita. Heli Valkeinen, erikoistutkija, TtT TOIMIA-verkoston koordinaattori
 Mittaamisen maailmasta muutamia asioita Heli Valkeinen, erikoistutkija, TtT TOIMIA-verkoston koordinaattori SISÄLTÖ 1. Mittari vs. indikaattori vs. menetelmä - mittaaminen 2. Luotettavat mittarit 3. Arvioinnin
Mittaamisen maailmasta muutamia asioita Heli Valkeinen, erikoistutkija, TtT TOIMIA-verkoston koordinaattori SISÄLTÖ 1. Mittari vs. indikaattori vs. menetelmä - mittaaminen 2. Luotettavat mittarit 3. Arvioinnin
Mark Summary Form. Taitaja 2012. Skill Number 605 Skill Levy ja hitsaus. Competitor Name
 Summary Form Skill Number 605 Skill Levy ja hitsaus ing Scheme Lock 23-04-2012 13:14:47 Final Lock 26-04-2012 12:04:29 Criterion Criterion Description s Day 1 Day 2 Day 3 Day 4 Award A B C Kuorma-auton
Summary Form Skill Number 605 Skill Levy ja hitsaus ing Scheme Lock 23-04-2012 13:14:47 Final Lock 26-04-2012 12:04:29 Criterion Criterion Description s Day 1 Day 2 Day 3 Day 4 Award A B C Kuorma-auton
ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI. Mikko Kylliäinen
 ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI Mikko Kylliäinen Insinööritoimisto Heikki Helimäki Oy Dagmarinkatu 8 B 18, 00100 Helsinki kylliainen@kotiposti.net 1 JOHDANTO Suomen rakentamismääräyskokoelman
ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI Mikko Kylliäinen Insinööritoimisto Heikki Helimäki Oy Dagmarinkatu 8 B 18, 00100 Helsinki kylliainen@kotiposti.net 1 JOHDANTO Suomen rakentamismääräyskokoelman
Otoskoko 107 kpl. a) 27 b) 2654
 1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
Valukappaleiden koneenpiirustus:
 Valukappaleiden koneenpiirustus: Piirustusmerkinnät ja periaatteet alkeista lähtien Tuula Höök, Valimoinstituutti Koneenpiirustusta koskevat standardit Koneenpiirustus yleisesti: piirustusarkki: arkin
Valukappaleiden koneenpiirustus: Piirustusmerkinnät ja periaatteet alkeista lähtien Tuula Höök, Valimoinstituutti Koneenpiirustusta koskevat standardit Koneenpiirustus yleisesti: piirustusarkki: arkin
Differentiaalilaskennan tehtäviä
 Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Käyttöohjeet Pinta-alamittari Flex Counter
 Käyttöohjeet Pinta-alamittari Flex Counter System Part number Serial number Installed by Installation date Lykketronic Area Counter Standard Page 1 SISÄLLYSLUETTELO 1. YLEISTÄ TIETOA FLEX COUNTERISTA...3
Käyttöohjeet Pinta-alamittari Flex Counter System Part number Serial number Installed by Installation date Lykketronic Area Counter Standard Page 1 SISÄLLYSLUETTELO 1. YLEISTÄ TIETOA FLEX COUNTERISTA...3
Preliminäärikoe Tehtävät Pitkä matematiikka 4.2.2014 1 / 3
 Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
HELSINGIN YLIOPISTON VIIKIN NORMAALIKOULUN
 HELSINGIN YLIOPISTON VIIKIN NORMAALIKOULUN MATEMATIIKAN OPETUSSUUNNITELMA TAVOITTEET 1. LUOKALLE - kykenee keskittymään matematiikan opiskeluun - kykenee kertomaan suullisesti matemaattisesta ajattelustaan
HELSINGIN YLIOPISTON VIIKIN NORMAALIKOULUN MATEMATIIKAN OPETUSSUUNNITELMA TAVOITTEET 1. LUOKALLE - kykenee keskittymään matematiikan opiskeluun - kykenee kertomaan suullisesti matemaattisesta ajattelustaan
A. SMD-kytkennän kokoaminen ja mittaaminen
 A. SMD-kytkennän kokoaminen ja mittaaminen Avaa tarvikepussi ja tarkista komponenttien lukumäärä sekä nimellisarvot pakkauksessa olevan osaluettelon avulla. Ilmoita mahdollisista puutteista tai virheistä
A. SMD-kytkennän kokoaminen ja mittaaminen Avaa tarvikepussi ja tarkista komponenttien lukumäärä sekä nimellisarvot pakkauksessa olevan osaluettelon avulla. Ilmoita mahdollisista puutteista tai virheistä
Päästöjen analysointi ja piirteiden korjaaminen 3
 Päästöjen analysointi ja piirteiden korjaaminen 3 Tampere University of Technology Tuula Höök Ota kappale start_repair_3_1.sldprt. Kappale on kupin muotoinen ja siinä on sivulla vastapäästöllinen muoto.
Päästöjen analysointi ja piirteiden korjaaminen 3 Tampere University of Technology Tuula Höök Ota kappale start_repair_3_1.sldprt. Kappale on kupin muotoinen ja siinä on sivulla vastapäästöllinen muoto.
2016/06/21 13:27 1/10 Laskentatavat
 2016/06/21 13:27 1/10 Laskentatavat Laskentatavat Yleistä - vaakageometrian suunnittelusta Paalu Ensimmäinen paalu Ensimmäisen paalun tartuntapiste asetetaan automaattisesti 0.0:aan. Tämä voidaan muuttaa
2016/06/21 13:27 1/10 Laskentatavat Laskentatavat Yleistä - vaakageometrian suunnittelusta Paalu Ensimmäinen paalu Ensimmäisen paalun tartuntapiste asetetaan automaattisesti 0.0:aan. Tämä voidaan muuttaa
PROJECT X. 2D tarkastuksen standardi Mittausteknologian edelläkävijä
 PROJECT X 2D tarkastuksen standardi Mittausteknologian edelläkävijä 2-dimensioinen kameramittausjärjestelmä Project X.. 2D mittauksen standardi Project X on erilainen. Siinä on otettu käyttöön aivan uusi,
PROJECT X 2D tarkastuksen standardi Mittausteknologian edelläkävijä 2-dimensioinen kameramittausjärjestelmä Project X.. 2D mittauksen standardi Project X on erilainen. Siinä on otettu käyttöön aivan uusi,
Oppilas vahvistaa opittuja taitojaan, kiinnostuu oppimaan uutta ja saa tukea myönteisen minäkuvan kasvuun matematiikan oppijana.
 Tavoitteet S L 3. lk 4. lk 5. lk 6. lk Merkitys, arvot ja asenteet T1 pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta L1, L3, L5
Tavoitteet S L 3. lk 4. lk 5. lk 6. lk Merkitys, arvot ja asenteet T1 pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta L1, L3, L5
Perusteet 5, pintamallinnus
 Perusteet 5, pintamallinnus Juho Taipale, Tuula Höök Tampereen teknillinen yliopisto Ota piirustus fin_basic_4.pdf (Sama piirustus kuin harjoituksessa basic_4). Käytä piirustuksessa annettuja mittoja ja
Perusteet 5, pintamallinnus Juho Taipale, Tuula Höök Tampereen teknillinen yliopisto Ota piirustus fin_basic_4.pdf (Sama piirustus kuin harjoituksessa basic_4). Käytä piirustuksessa annettuja mittoja ja
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE
 Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
Jakopinnat ja liikkuvan keernan pinnat 1, keerna jakopinnan tasalla
 Jakopinnat ja liikkuvan keernan pinnat 1, keerna jakopinnan tasalla Tuula Höök, Tampereen teknillinen yliopisto Teoriatausta Muotin perusrakenne Ruisku tai painevalukappaleen rakenteen perusasiat: päästö,
Jakopinnat ja liikkuvan keernan pinnat 1, keerna jakopinnan tasalla Tuula Höök, Tampereen teknillinen yliopisto Teoriatausta Muotin perusrakenne Ruisku tai painevalukappaleen rakenteen perusasiat: päästö,
Perusopintojen Laboratoriotöiden Työselostus 1
 Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Ratkaisut 2. KJR-C2001 Kiinteän aineen mekaniikan perusteet, IV/2016. Tehtävä 1 Selitä käsitteet kohdissa a) ja b) sekä laske c) kohdan tehtävä.
 Kotitehtävät palautetaan viimeistään keskiviikkoisin ennen luentojen alkua eli klo 14:00 mennessä. Muistakaa vastaukset eri tehtäviin palautetaan eri lokeroon! Joka kierroksen arvostellut kotitehtäväpaperit
Kotitehtävät palautetaan viimeistään keskiviikkoisin ennen luentojen alkua eli klo 14:00 mennessä. Muistakaa vastaukset eri tehtäviin palautetaan eri lokeroon! Joka kierroksen arvostellut kotitehtäväpaperit
Konepajatekniset mittaukset ja kalibroinnit
 Veli-Pekka Esala - Heikki Lehto - Heikki Tikka Konepajatekniset mittaukset ja kalibroinnit T E K N I N E N T I E D O T U S 3 2 0 0 3 A L K U S A N A T Tarkoitus Tämä tekninen tiedotus on tarkoitettu käytettäväksi
Veli-Pekka Esala - Heikki Lehto - Heikki Tikka Konepajatekniset mittaukset ja kalibroinnit T E K N I N E N T I E D O T U S 3 2 0 0 3 A L K U S A N A T Tarkoitus Tämä tekninen tiedotus on tarkoitettu käytettäväksi
AKK-MOTORSPORT ry Katsastuksen käsikirja
 NOKKA-AKSELIEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin nokka-akseli(e)n mittaaminen ja ominaisuuksien laskeminen. Ns. A-(perusympyrä)
NOKKA-AKSELIEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin nokka-akseli(e)n mittaaminen ja ominaisuuksien laskeminen. Ns. A-(perusympyrä)
A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-6. Taulukkokirjaa saa käyttää apuna, laskinta ei.
 PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
Anna jokaisen kohdan vastaus kolmen merkitsevän numeron tarkkuudella muodossa
 Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
