The initial location at the University of Vaasa, Finland
|
|
|
- Ilona Kivelä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 The initial location at the University of Vaasa, Finland Timo Salmi (1977). Mallit suunnittelun ja päätöksenteon apuvälineenä. Lineaarinen optimointimalli huonekalutehtaan vuosibudjetoinnissa CASE. Tietojenkäsittelyn teemapäivät. Valtion koulutuskeskus.
2 KTT Timo Salmi Helsingin kauppakorkeakoulu Lineaarinen optimointimalli huonekalutehtaan vuosibudjetoinnissa CASE Esityksessä tarkastellaan lineaarisen optimointimallin käyttöä huonekalutehtaan vuosibudjetoinnin tukena. Tarkoituksena ei ole käsitellä aihetta yleisesti, vaan esittää käytännön sovellutus mallin soveltamisesta. Sovellutuksessa aikaansaatiin tuloksen (katetuotto) kannalta optimaalinen vuosibudjetti ottaen huomioon samanaikaisesti sekä yrityksen ulkopuolisia että sisäpuolisia rajoituksia. Mallin avulla selvitettiin ensin huonekalutehtaan paras tuotevalikoima lineaarisen optimoinnin mallin ja sen tietokoneratkaisun avulla. Tämän ratkaisun perusteella laadittiin manuaalisesti valmistusohjelma ja budjetit suunnitteluvuodelle. Sovellutuksen kohteena on huonekalutehdas, joka valmistaa jatkuvana sarjatuotantona pehmustamattomia kodin huonekaluja keskittyen erityisesti määrätyn tyyppisiin kalusteisiin (anonymiteettisyistä on tiettyjä tietoja yleistetty tai epämääräistetty). Tuotevakikoiman alkuperäinen määrä oli noin 10 tuotetta. Tuotteiden hintataso on pidetään vakaana sekä kilpailu- että etukäteissitoumussyistä. Tehtaan tuotanto jakautuu kolmeen osastoon,
3 jotka ovat koneistamo, maalaamo ja pakkaamo. Osastot muodostavat tuotannon kustannuspaikat. Työaika- ja valmistuspalkkastandardit on työtutkimuksen avulla määritelty osastoittain kaikille tuotteille. Tämä oli eräs sovellutuksen tekemisen oleellinen edellytys, joka oli jo valmiiksi olemassa. Laajennusinvestointien mahdollisuutta ei aluksi otettu suunnittelussa lainkaan huomioon rahoitusmarkkinoiden kireyden vuoksi, vaan suunnitelma laadittiin aluksi suunnitteluhetken kapasiteetin mukaan. Yrityksen suurimpana ongelmana on ollut niukan valmistuskapasiteetin tehokas ja taloudellinen hyväkskäyttö. Tuotevalikoimaa oli tästä syystä karsittu useampaan otteeseen vähemmän kannattavasta päästä. Valmistussuunnitelman laatimista "tavalliseen tapaan" vaikeutti tuotteiden keskinäinen riippuvuus tuotevalikoimassa. Sen SlJaan tuotteiden markkinointipuoli ei ole tuottanut tehtaalle ongelmia. Parhaan tuotevalikoiman selvittämiseksi ja tuotteiden valmistettavien optimimäärien ratkaisemiseksi rakennettiin yhden vuoden pituista aikaperiodia varten lineaarinen optimointimalli. (Lineaarinen optimointimalli, kuten tunnettua maksimoi annetun lineaarisen tavoitefunktion määriteltyjen lineaaristen rajoitusten vallitessa.) Mallin tavoitteena käytettiin tuotteittaisten katetuottojen summan maksimointia. Kaikille tuotteille on laskettu katetuotto vähentämällä nettomyyntihinnasta raakaaineiden, työpaikkojen ja muuttuvien yleiskustannusten osuus. Jokaisesta tuotteesta on olemassa tuotekalkyyli, jossa raaka-ainekustannukset on eritelty raaka-aineittain
4 ja palkkauskustannukset sekä standardityöajat osastoittain. Seuraavassa käydään käytetty malli läpi pääkohdittain. Mallissa käytettiin seuraavia muuttujia, joiden yhteyteen on merkitty tavoitefunktion muodostamisessa käytetyt laskentatoimen tiedot: Netto- Raaka- Muuttuja Tuotteen nimi myynti- aine hinta X208 X2l0 X2ll X2l2 X254 X266 X267 X268 X270 X27l X290 X400 X406 X40l X402 X403 X404 vuodelaatikko 69 parisänky parisänky II parisänky 111 lastensänky kerrossänky 1 kerrossänky II kerrossänky 111 kerrossänky IV kerrossänky V tikapuut laatikosto 1 laatikosto II Palkat Muutt. yk:t X45l X452 X453 X455 X466 X465 X466 X6l2 X6l6 X620 X650 X65l XLOA XKOR tasolevy 111 kampaustaso 1 kampaustaso II lainan korot otto
5 Tavoitteena on siis maksimoida budjettivuoden kokonaiskatetuotto, josta on vähennetty lainanotosta aiheutuneet korkokulut Mallin rajoitusten muodostamista varten luetteloitiin kunkin osaston (koneistamo, maalaamo, pakkaamo) työaikastandardit, jotka olivk~7~~i~iir~~ selvitettyinä jo ennen sovellutukseen ryhtymistä. Vaikka tuotteiden menekkivaikeuksia ei ollutka~afg~frw~thyt, selvitettiin tuotteitain ja asiakkaittain edellisen vuoden myynti. Tuotteittaisten myyntimäärien ylärajan määräämiseksi suunnittelukaudelle laskettiin kunkin tuotteen kohdalla yhteen myynti eri asiakkaille ja saadut tulokset korjattiin budjettivuodelle ennakoitujen olosuhteiden mukaisiksi. Kysynnän Työ a i kas t a n d a r d i t Tuote yläraja koneistamo maalaamo pakkaamo yhteensä ,62 0,23 0,23 1, ,54 1, ,19 2,00 Lisäksi selvitettiin kunkin osaston kapasiteetti työtunteina ilmaistuna, siten, että kapasiteetilla tarkoitettiin tuntimäärää, joka täysitehoisesti voidaan työskennellä osastolla. Ylityömahdollisuutta ei suunnitelmiin
6 sisällytetty hienoisen työvoimapulan johdosta. Kapasiteetit olivat käytetyllä perusteella laskettuina Koneistamo Maalaamo Pakkaamo.1.1. Kunkin tuotteen osalta rajoitetaan valmistusmäärä korkeintaan kysynnän ylärajaa vastaavaksi X208 < 3000 X2l0 < 1000 jne Tuotteiden välillä on voimakkaita riippuvuussuhteita. Tietyn tuotteen myynti voi vaikuttaa paljonkin toisen tuotteen myyntimäärään, jopa niin, että joidenkin tuotteiden myynnille toisen tuotteen valmistaminen on välttämätön edellytys. Esimerkkinä on vuoteen alla säilytettävä vuodevaatelaatikko, jonka myymiselle vuoteen valmistaminen on välttämätön edellytys. Tällä kohtaa esimerkiksi asetettiin vaatimus, että vuodelaatikon valmistusmäärä eo saa olla yli 30% niiden vuoteiden yhteismäärästä, joiden alla sitä voidaan käyttää. Vastaavia samanlaisia riippuvuussuhteita otettiin lukuun useita muitakin. Erityisesti tällä kohtaa mallin käytön edut tulevat selvästi esiin, koska käypien vaihtoehtojen manuaalinen selvittäminen on hyvin hankala tehtävä.
7 Osastojen valmistuskapasiteetti oli ennen mallin rakentamista todettu eniten toimintaa rajoittavaksi tekijäksi. (Mallin ratkaisemisen jälkeen todettiin asian olevan juuri näin. Sovellutuksen seurauksena syntyikin ehdotus osastoittaisten kapasiteettien lisäämiseksi niiden saattamiseksi mahdollisimman yhteensopiviksi.) Kunkin osaston kohdalle laadittiin rajoitus, jonka mukaan osastolla tapahtuneen valmistuksen yhteistuntimäärä ei saa ylittää osaston kokonaiskapasiteettia. Esimerkiksi koneistamon kohdalla käytettiin rajoitusta Malliin rakennettiin myös rahoitusrajoitus. Sen tehtävänä oli pitää valmistus sellaisissa puitteissa, että budjettikauden kassaanmaksut riittäisivät valmistuksen aiheuttamien muuttuvien kustannusten aiheuttamien kassastamaksujen, kiinteiden kustannusten aiheuttamien kassastamaksujen sekä muiden, ennalta tunnettujen kassastamaksujen kattamiseen. Kassavirtarajoituksen lisäksi malliin sisällytettiin lainanottomahdollisuuden ylärajarajoitus sekä yhtälö joka määritteli lainan (XLOA) johdosta syntyvän korkomaksun (XKOR). Malli ratkaistiin tietokoneella eräällryyi~anomaisella lineaarisen optimoinnin ratkaisuohjelmalla. Tuloksena saatiin mallin ehdottamana kunkin tuotteen tuotantomäärä, lainanotto ehdotus sekä tieto sitovista rajoituksista.
8 Mallin ehdottaman ratkaisun mukaan tuli tuotevalikoimaan ottaa mukaan ainostaan 73% alkuperäisen tuotevalikoiman tuotteista. Aluksi tuntui ehdotettu tuotevalikoiman supistusehdotus aivan liian jyrkältä, mutta yksityiskohtaisemman tarkastelun jälkeen todettiin, että jäljellejäävät tuotteet korvaavat karsitut tuotteet riittävän hyvin. Tätä käsitystä vahvistivat myös jo aikaisemmin tehdyt tuotevalikoiman karsimissuunnitelmat. Ratkaisun perusteella todettiin myös tehtaan osastojen kapasiteetin tulevan hyvin epätasapainoisesti käytettyä. Koneistamon kapasiteetti muodostui valmistuksen pullonkaulaksi, kun taas maalaamoon jäi käyttämätöntä kapasiteettia ratkaisun mukaan 23% ja pakkaamoon 33%. Ratkaisun perusteella todettiin myös eräiden tuotteiden myyntirajoitusten muodostuvan aikaisemmasta poikkeavasti sitovasti toimintaa rajoittavaksi. Tarkempi analyysi osoitti kuitenkin, että rajoittaviksi muodostuneiden myyntimäärien kohdalla ei ollut mahdollisuutta välittömään myynnin lisäykseen. Rahoitus ei muodostunut pullonkaulaksi. Saadun ratkaisun ja sen analyysin perusteella kiinnitettiin seuraavassa vaiheessa huomio erityisesti koneistamon kapasiteettiin. Asiaa tarkemmin tutkittaessa todettiin, että koneistamosta olisi mahdollista saada enemmän kapasiteettia irti hankkimalla porakone ja järjestelemällä joidenkin tuotannossa peräkkäin olevien koneiden paikat paremmin. Näillä toimenpiteillä koneistamon kapa-
9 siteetti olisi saatu kohotettua tunnista tuntiin. Samalla todettiin, että myös muiden osastojen kapasiteetissa voitaisiin saada aikaan vähäistä lisäystä uudelleenjärjestelyillä. Malli ratkaistiin uudelleen ottaen huomioon mahdolliset lisäyksen kapasiteeteissa. Syntyneet muutokset olivat huomattavia. Katetuoton arvo mallin tavoitefunktiossa nousi 16%. Tuotevalikoimaa ratkaisu ehdotti supistettavaksi ainostaan 90%:iin, ensimmäisen ratkaisun 73% asemasta. Rahoitus ei muodostanut tässäkään tapauksessa rajoittavaa tekijää. Sen sijaan koneistamon kapasiteeti osoittautui jälleen rajoittavaksi tekijäksi, kun taas muille osastoille jäi edelleenkin käyttämätöntä kapasiteettia. Koneistamon kapasiteetin tultua todettua oleellisimmaksi pullonkaulatekijäksi, selvitettiin koneistamon laajentemismahdollisuutta. Todettiin, että tehdasrakennuksen yhteydessä oleva varastotila oli mahdollista liittää koneistamoon väliseinän purkamisen jälkeen, jolloin uudella tilajärjestelyllä koneistamon kapasiteetti voitaisiin nostaa tuntiin sekä samalla hieman lisätä muidenkin osastojen kapasiteettia vapautuvan lattiapintaalan sopivalla hyväksikäytöllä. Koska rahoitus ei vieläkään muodostunut pullonkaulaksi, todettiin, että kyseinen laajennus olisi mahdollista suorittaa. Malliin tehtiin asianomaiset muutokset, jolloin saadussa uudessa ratkaisussa ketetuoton arvo lisääntyi vielä 7% edellisestä ratkaisuista. Tuotevalikoiman laajuus pysyi ehdotuksessa ennallaan vaikka edelliseen ratkaisuun verrattuna valikoimassa tapahtui eräitä vaihdoksia.
10 Kolmannen ratkaisun tarkastelu osoitti, ettei mihinkään siinä kriittisiksi muodostuneista rajoituksista enää ollut mahdollista vaikuttaa, joten se valittiin vuosibudjettien laadinnan perustaksi. Budjetit laadittiin manuaalisesti mallin ehdottamista tuotantomääristä liikkeelle lähtien. Näin ollen laadittiin ensimmäiseksi valmistusohjelma ja sen pohjalta myyntibudjetti. Seuraavaksi laadittiin ratkaisun pohjalta tulossuunnitelma. Tämän jälkeen tehtiin rahoitusbudjetti. Viimeiseksi laadittiin vielä edellisten pohjalta suunnitteluvuoden tase-ennuste. Kuvattu sovellutus eli erityisen selväpiirteinen, koska siinä pystyttiin soveltamaan sellaisenaan tuotevalikoiman optimointiongelman "oppikirjaratkausua". Mallin ratkaiseminen kolmessa vaiheessa, johti oleellisen pullonkaulatekijän löytymiseen sekä parannusehdotukseen sen suhteen.
Mertim Oy Tapio Sipponen 3.5.2005 1(6) MYYNNIN JA TUOTANNON BUDJETOINTI. Myynnin budjetointi
 Tapio Sipponen 3.5.2005 1(6) MYYNNIN JA TUOTANNON BUDJETOINTI Myynnin budjetointi Myyntiä budjetoitaessa arvioidaan yhdessä myyntimääriä ja myyntihintoja tuoteryhmittäin tai tuotteittain. Asiakasbudjetit
Tapio Sipponen 3.5.2005 1(6) MYYNNIN JA TUOTANNON BUDJETOINTI Myynnin budjetointi Myyntiä budjetoitaessa arvioidaan yhdessä myyntimääriä ja myyntihintoja tuoteryhmittäin tai tuotteittain. Asiakasbudjetit
Aki Taanila LINEAARINEN OPTIMOINTI
 Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Talousmatematiikan perusteet
 kevät 19 / orms.30 Talousmatematiikan perusteet 8. harjoitus, viikko 11 (11.03..03.19) L Ma 12 A2 R0 Ti 14 16 F43 R01 Ma 12 14 F43 L To 08 A2 R02 Ma 16 18 F43 R06 To 12 14 F140 R03 Ti 08 F42 R07 Pe 08
kevät 19 / orms.30 Talousmatematiikan perusteet 8. harjoitus, viikko 11 (11.03..03.19) L Ma 12 A2 R0 Ti 14 16 F43 R01 Ma 12 14 F43 L To 08 A2 R02 Ma 16 18 F43 R06 To 12 14 F140 R03 Ti 08 F42 R07 Pe 08
1. Lineaarinen optimointi
 0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
Talousmatematiikan perusteet
 kevät 2019 / orms.1030 Talousmatematiikan perusteet 7. harjoitus, viikko 7 1. Oheisessa taulukossa on erään tuotteen hintaindeksejä. Laske hinnan keskimääräinen kasvuvauhti vuosina 2000-2005 vuosi indeksi
kevät 2019 / orms.1030 Talousmatematiikan perusteet 7. harjoitus, viikko 7 1. Oheisessa taulukossa on erään tuotteen hintaindeksejä. Laske hinnan keskimääräinen kasvuvauhti vuosina 2000-2005 vuosi indeksi
Yksikkökate tarkoittaa katetuottoa yhden tuotteen kohdalla. Tämä voidaan määrittää vain jos myytäviä tuotteita on vain yksi.
 KATETUOTTOLASKENTA laskennassa selvitetään onko liiketoiminta kannattavaa. Laskelmat tehdään liiketoiminnasta syntyvien kustannuksien ja tuottojen perusteella erilaisissa tilanteissa. laskennassa käytetään
KATETUOTTOLASKENTA laskennassa selvitetään onko liiketoiminta kannattavaa. Laskelmat tehdään liiketoiminnasta syntyvien kustannuksien ja tuottojen perusteella erilaisissa tilanteissa. laskennassa käytetään
Yritystoiminta Pia Niuta HINNOITTELU
 HINNOITTELU Hinta on keskeinen kilpailukeino. sen muutoksiin asiakkaat ja kilpailijat reagoivat herkästi. toimii tuotteen arvon mittarina. vaikuttaa yrityksen imagoon. on tuotteen/palvelun arvo rahana
HINNOITTELU Hinta on keskeinen kilpailukeino. sen muutoksiin asiakkaat ja kilpailijat reagoivat herkästi. toimii tuotteen arvon mittarina. vaikuttaa yrityksen imagoon. on tuotteen/palvelun arvo rahana
Optimoinnin sovellukset
 Optimoinnin sovellukset Timo Ranta Tutkijatohtori TTY Porin laitos OPTIMI 4.12.2014 Mitä optimointi on? Parhaan ratkaisun systemaattinen etsintä kaikkien mahdollisten ratkaisujen joukosta Tieteellinen
Optimoinnin sovellukset Timo Ranta Tutkijatohtori TTY Porin laitos OPTIMI 4.12.2014 Mitä optimointi on? Parhaan ratkaisun systemaattinen etsintä kaikkien mahdollisten ratkaisujen joukosta Tieteellinen
Laskentatoimen perusteet, harjoituksia (Juha Viljaranta, ekon.,di)
 Laskentatoimen perusteet, harjoituksia (Juha Viljaranta, ekon.,di) Osa 1 Katetuottolaskenta Tuotekustannuslaskenta ja hinnoittelu Osa 2 Kapeikkolaskenta Eroanalyysit 1 Katetuottolaskenta Yksinkertaistettujen
Laskentatoimen perusteet, harjoituksia (Juha Viljaranta, ekon.,di) Osa 1 Katetuottolaskenta Tuotekustannuslaskenta ja hinnoittelu Osa 2 Kapeikkolaskenta Eroanalyysit 1 Katetuottolaskenta Yksinkertaistettujen
LP-mallit, L8. Herkkyysanalyysi. Varjohinta. Tietokoneohjelmia. Aiheet. Yleistä, LP-malleista. Esimerkki, Giapetto.
 LP-mallit, L8 Yleistä 1 LP-mallit on yksi Operaatioanalyysin (Operations Research) perustyökaluista. Perusongelma: Miten pitää suorittaa operaatio mahdollisimman hyvin, kun käytettävissä on rajalliset
LP-mallit, L8 Yleistä 1 LP-mallit on yksi Operaatioanalyysin (Operations Research) perustyökaluista. Perusongelma: Miten pitää suorittaa operaatio mahdollisimman hyvin, kun käytettävissä on rajalliset
Viikkotehtävä 3 Katetuotto-, vaihtoehto- ja kustannuslaskenta Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori
 Viikkotehtävä 3 Katetuotto-, vaihtoehto- ja kustannuslaskenta Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Tehtävän suorittaminen Tehtävänanto sisältää sekä PowerPoint-muodossa
Viikkotehtävä 3 Katetuotto-, vaihtoehto- ja kustannuslaskenta Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Tehtävän suorittaminen Tehtävänanto sisältää sekä PowerPoint-muodossa
Laskentatoimi. Kirjanpito = ulkoinen laskentatoimi Kustannuslaskenta = sisäinen laskentatoimi
 Laskentatoimi Kirjanpito = ulkoinen laskentatoimi Kustannuslaskenta = sisäinen laskentatoimi Kannattavuus, maksuvalmius, vakavaraisuus Yrityksen on huolehdittava: -kannattavuudesta -maksuvalmiudesta -vakavaraisuudesta
Laskentatoimi Kirjanpito = ulkoinen laskentatoimi Kustannuslaskenta = sisäinen laskentatoimi Kannattavuus, maksuvalmius, vakavaraisuus Yrityksen on huolehdittava: -kannattavuudesta -maksuvalmiudesta -vakavaraisuudesta
LP-mallit, L19. Aiheet. Yleistä, LP-malleista. Esimerkki, Giapetto. Graafisen ratkaisun vaiheet. Optimin olemassaolo
 LP-mallit, L19 Yleistä 1 LP-mallit on yksi Operaatioanalyysin (Operations Research) perustyökaluista. Perusongelma: Miten pitää suorittaa operaatio mahdollisimman hyvin, kun käytettävissä on rajalliset
LP-mallit, L19 Yleistä 1 LP-mallit on yksi Operaatioanalyysin (Operations Research) perustyökaluista. Perusongelma: Miten pitää suorittaa operaatio mahdollisimman hyvin, kun käytettävissä on rajalliset
OPERAATIOANALYYSI ORMS.1020
 VAASAN YLIOPISTO Talousmatematiikka Prof. Ilkka Virtanen OPERAATIOANALYYSI ORMS.1020 Tentti 2.2.2008 1. Yrityksen tavoitteena on minimoida tuotannosta ja varastoinnista aiheutuvat kustannukset 4 viikon
VAASAN YLIOPISTO Talousmatematiikka Prof. Ilkka Virtanen OPERAATIOANALYYSI ORMS.1020 Tentti 2.2.2008 1. Yrityksen tavoitteena on minimoida tuotannosta ja varastoinnista aiheutuvat kustannukset 4 viikon
*/* Liitteet: - Vuoden 2016 sanallinen osa koskien Sisäisten palvelujen yksikköä ( ) - kustannusjako kustannuspaikoittain
 Sisäisten palvelujen johtokunta 4 25.01.2016 Sisäisten palvelujen johtokunta 15 21.03.2016 Sisäisten palvelujen johtokunta 31 23.05.2016 Sisäisten palvelujen johtokunta 43 29.08.2016 Sisäisten palvelujen
Sisäisten palvelujen johtokunta 4 25.01.2016 Sisäisten palvelujen johtokunta 15 21.03.2016 Sisäisten palvelujen johtokunta 31 23.05.2016 Sisäisten palvelujen johtokunta 43 29.08.2016 Sisäisten palvelujen
Harjoitus 3 (31.3.2015)
 Harjoitus (..05) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i,j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus (..05) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i,j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus 8: Excel - Optimointi
 Harjoitus 8: Excel - Optimointi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Lineaarisen optimointimallin muodostaminen
Harjoitus 8: Excel - Optimointi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Lineaarisen optimointimallin muodostaminen
30A01000 Taulukkolaskenta ja analytiikka Luku 8: Lineaarinen optimointi ja sen sovellukset
 30A01000 Taulukkolaskenta ja analytiikka Luku 8: Lineaarinen optimointi ja sen sovellukset Mitä on lineaarinen optimointi (LP)? LP= lineaarinen optimointiongelma (Linear Programming) Menetelmä, jolla etsitään
30A01000 Taulukkolaskenta ja analytiikka Luku 8: Lineaarinen optimointi ja sen sovellukset Mitä on lineaarinen optimointi (LP)? LP= lineaarinen optimointiongelma (Linear Programming) Menetelmä, jolla etsitään
KUVAT. Kansainvälisen toiminnan rahoitus
 Kansainvälisen toiminnan rahoitus KUVAT 1 Rahoitussuunnittelu REAALIPROSESSI Tuotannontekijämarkkinat Meno MOBILA OY Tulo Suoritemarkkinat Kassa RAHAPROSESSI Kassastamaksut Kassaanmaksut Korot Verot Osingot
Kansainvälisen toiminnan rahoitus KUVAT 1 Rahoitussuunnittelu REAALIPROSESSI Tuotannontekijämarkkinat Meno MOBILA OY Tulo Suoritemarkkinat Kassa RAHAPROSESSI Kassastamaksut Kassaanmaksut Korot Verot Osingot
Budjetti ja eroanalyysi Ekstralaskuesimerkki
 Budjetti ja eroanalyysi Ekstralaskuesimerkki Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Budjetti, liukuva budjetti ja toteuma Myynnin määräero Budjettiero Toimintapoikkeama
Budjetti ja eroanalyysi Ekstralaskuesimerkki Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Budjetti, liukuva budjetti ja toteuma Myynnin määräero Budjettiero Toimintapoikkeama
Hintakilpailu lyhyellä aikavälillä
 Hintakilpailu lyhyellä aikavälillä Virpi Turkulainen 5.3.2003 Optimointiopin seminaari - Kevät 2003 / 1 Sisältö Johdanto Bertrandin ristiriita ja sen lähestyminen Bertrandin ristiriita Lähestymistavat:
Hintakilpailu lyhyellä aikavälillä Virpi Turkulainen 5.3.2003 Optimointiopin seminaari - Kevät 2003 / 1 Sisältö Johdanto Bertrandin ristiriita ja sen lähestyminen Bertrandin ristiriita Lähestymistavat:
rehtorit ja apulaisrehtorit,
 AMMATILLINEN AIKUISKOULUTUSKESKUS 1 Soveltamisala 1 LIITE T1 Tätä liitettä sovelletaan ten opetushenkilöstöön, johon kuuluvat rehtorit ja apulaisrehtorit, kokoaikaiset opettajat, osa-aikaiset opettajat,
AMMATILLINEN AIKUISKOULUTUSKESKUS 1 Soveltamisala 1 LIITE T1 Tätä liitettä sovelletaan ten opetushenkilöstöön, johon kuuluvat rehtorit ja apulaisrehtorit, kokoaikaiset opettajat, osa-aikaiset opettajat,
Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu
 Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu Merkintöjä := vasen puoli määritellään oikean puolen lausekkeella s.e. ehdolla; siten että (engl. subject to, s.t.) on voimassa
Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu Merkintöjä := vasen puoli määritellään oikean puolen lausekkeella s.e. ehdolla; siten että (engl. subject to, s.t.) on voimassa
Viikkotehtävä 4a Budjetointi ja eroanalyysi
 Viikkotehtävä 4a Budjetointi ja eroanalyysi Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Tehtävän suorittaminen Tehtävänanto sisältää sekä PowerPoint-muodossa esitetyt
Viikkotehtävä 4a Budjetointi ja eroanalyysi Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Tehtävän suorittaminen Tehtävänanto sisältää sekä PowerPoint-muodossa esitetyt
TTY Porin laitoksen optimointipalvelut yrityksille
 TTY Porin laitoksen optimointipalvelut yrityksille Timo Ranta, TkT Frank Cameron, TkT timo.ranta@tut.fi frank.cameron@tut.fi Automaation aamukahvit 28.8.2013 Optimointi Tarkoittaa parhaan ratkaisun valintaa
TTY Porin laitoksen optimointipalvelut yrityksille Timo Ranta, TkT Frank Cameron, TkT timo.ranta@tut.fi frank.cameron@tut.fi Automaation aamukahvit 28.8.2013 Optimointi Tarkoittaa parhaan ratkaisun valintaa
Harjoitus 3 (3.4.2014)
 Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Suominen Yhtymä Oyj. Osavuosikatsaus Suominen Yhtymä Oyj
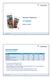 Osavuosikatsaus...6. Esitys 9.7. Suominen yhteensä Osakeanti ylimerkittiin Milj. Q/ Q/9 Q-Q/ Q-Q/9 9 Liikevaihtoiht 44, 4,44 84,88 9, 79,4 Liikevoitto,,6 -,, 6,7 Katsauskauden voitto/tappio -,8, -,9,6,9
Osavuosikatsaus...6. Esitys 9.7. Suominen yhteensä Osakeanti ylimerkittiin Milj. Q/ Q/9 Q-Q/ Q-Q/9 9 Liikevaihtoiht 44, 4,44 84,88 9, 79,4 Liikevoitto,,6 -,, 6,7 Katsauskauden voitto/tappio -,8, -,9,6,9
Lineaarinen optimointitehtävä
 Lineaarinen optimointitehtävä min c 1 x 1 + c 2 x 2 + + c n x n kun a 11 x 1 + a 12 x 2 + + a 1n x n b 1 a 21 x 1 + a 22 x 2 + + a 2n x n b 2. a m1 x 1 + a m2 x 2 + + a mn x n b m x 1, x 2,..., x n 0 1
Lineaarinen optimointitehtävä min c 1 x 1 + c 2 x 2 + + c n x n kun a 11 x 1 + a 12 x 2 + + a 1n x n b 1 a 21 x 1 + a 22 x 2 + + a 2n x n b 2. a m1 x 1 + a m2 x 2 + + a mn x n b m x 1, x 2,..., x n 0 1
Talousmatematiikan perusteet: Luento 11. Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla
 Talousmatematiikan perusteet: Luento 11 Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla Esimerkki Esim. Yritys tekee kahta elintarviketeollisuuden käyttämää puolivalmistetta,
Talousmatematiikan perusteet: Luento 11 Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla Esimerkki Esim. Yritys tekee kahta elintarviketeollisuuden käyttämää puolivalmistetta,
Luento 2: Optimointitehtävän graafinen ratkaiseminen. LP-malli.
 Luento : Optimointitehtävän graafinen ratkaiseminen. LP-malli. LP-malli simerkki: Maalifirma Sateenkaari valmistaa ulko- ja sisämaalia raaka-aineista M ja M. Sisämaalin maksimikysyntä on tonnia/päivä.
Luento : Optimointitehtävän graafinen ratkaiseminen. LP-malli. LP-malli simerkki: Maalifirma Sateenkaari valmistaa ulko- ja sisämaalia raaka-aineista M ja M. Sisämaalin maksimikysyntä on tonnia/päivä.
Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin. Reijo Käki www.reijokaki.com
 Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin Reijo Käki www.reijokaki.com 1. PÄIVÄ I Voitto ja arvopohjainen päätöksenteko? II Kassavirta ja katetuotto III Heikot lenkit IV Marginaalituottavuus
Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin Reijo Käki www.reijokaki.com 1. PÄIVÄ I Voitto ja arvopohjainen päätöksenteko? II Kassavirta ja katetuotto III Heikot lenkit IV Marginaalituottavuus
Ohje yrityksen taloudenohjausjärjestelmään ver3,0
 Ohje yrityksen taloudenohjausjärjestelmään ver3,0 Tässä työkalussa liikutaan välilehdillä täyttäen niitä järjestyksessä vain harmaisiin laatikoihin voi laitta lukuja, muut solut ovat suojattuja Ota muokkaus
Ohje yrityksen taloudenohjausjärjestelmään ver3,0 Tässä työkalussa liikutaan välilehdillä täyttäen niitä järjestyksessä vain harmaisiin laatikoihin voi laitta lukuja, muut solut ovat suojattuja Ota muokkaus
Esimerkki 1 (Rehun sekoitus) 1
 1 Karjankasvattaja käyttää luonnosta saadun nurmirehun lisäksi lisäravinnetta 200kg/päivä. Lisäravinne sekoitetaan maissista ja soijasta. Ravinteen ominaisuuksiin vaikuttaa raaka-aineiden proteiini- ja
1 Karjankasvattaja käyttää luonnosta saadun nurmirehun lisäksi lisäravinnetta 200kg/päivä. Lisäravinne sekoitetaan maissista ja soijasta. Ravinteen ominaisuuksiin vaikuttaa raaka-aineiden proteiini- ja
Tuotantoprosessin optimaalinen aikataulutus (valmiin työn esittely)
 Tuotantoprosessin optimaalinen aikataulutus (valmiin työn esittely) Joona Kaivosoja 01.12.2014 Ohjaaja: DI Ville Mäkelä Valvoja: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
Tuotantoprosessin optimaalinen aikataulutus (valmiin työn esittely) Joona Kaivosoja 01.12.2014 Ohjaaja: DI Ville Mäkelä Valvoja: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
Sosiaali- ja terveysosaston vuoden 2016 talousarvio ja vuosien 2017-2018 taloussuunnitelma
 Sosiaali- ja terveyslautakunta 103 13.10.2015 Sosiaali- ja terveyslautakunta 110 19.10.2015 Sosiaali- ja terveysosaston vuoden 2016 talousarvio ja vuosien 2017-2018 taloussuunnitelma Sosiaali- ja terveyslautakunta
Sosiaali- ja terveyslautakunta 103 13.10.2015 Sosiaali- ja terveyslautakunta 110 19.10.2015 Sosiaali- ja terveysosaston vuoden 2016 talousarvio ja vuosien 2017-2018 taloussuunnitelma Sosiaali- ja terveyslautakunta
HE 78/2011 vp. HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2011 KOLMANNEN LISÄTALOUSARVIOESITYKSEN (HE 38/2011 vp) TÄYDENTÄMISESTÄ
 HE 78/2011 vp HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2011 KOLMANNEN LISÄTALOUSARVIOESITYKSEN (HE 38/2011 vp) TÄYDENTÄMISESTÄ Viitaten tämän esityksen yleisperusteluihin ja yksityiskohtaisten perustelujen
HE 78/2011 vp HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2011 KOLMANNEN LISÄTALOUSARVIOESITYKSEN (HE 38/2011 vp) TÄYDENTÄMISESTÄ Viitaten tämän esityksen yleisperusteluihin ja yksityiskohtaisten perustelujen
Testaa tietosi. 1 c, d 2 a 3 a, c 4 d 5 d
 Testaa tietosi 1 c, d 2 a 3 a, c 4 d 5 d Tehtävä 1 En ole. Taseen vastattavaa-puolen tilien ns. normaalisaldot ovat aina tilin kredit-puolella. Esimerkiksi oma pääoma kasvaa kredit-puolella ja oman pääoma
Testaa tietosi 1 c, d 2 a 3 a, c 4 d 5 d Tehtävä 1 En ole. Taseen vastattavaa-puolen tilien ns. normaalisaldot ovat aina tilin kredit-puolella. Esimerkiksi oma pääoma kasvaa kredit-puolella ja oman pääoma
Vuoden 2013 tilintarkastuskertomus, tilinpäätöksen hyväksyminen ja vastuuvapauden myöntäminen vuodelta 2013
 Raision kaupunki Pöytäkirja 1 (1) Kaupunginhallitus 109 31.3.2014 Asianro 337/02.02.01/2014 52 Vuoden 2013 tilintarkastuskertomus, tilinpäätöksen hyväksyminen ja vastuuvapauden myöntäminen vuodelta 2013
Raision kaupunki Pöytäkirja 1 (1) Kaupunginhallitus 109 31.3.2014 Asianro 337/02.02.01/2014 52 Vuoden 2013 tilintarkastuskertomus, tilinpäätöksen hyväksyminen ja vastuuvapauden myöntäminen vuodelta 2013
RAHOITUS JA RISKINHALLINTA
 RAHOITUS JA RISKINHALLINTA Opintojaksosuunnitelma deadlines 2.9. 9.9. 30.9. 12.11. 2.12. Kohdeyritysvaraus Rahan sitoutuminen yritystoiminnassa käyttöomaisuuteen ja käyttöpääomaan pohdinta Case Rahoitustilanne
RAHOITUS JA RISKINHALLINTA Opintojaksosuunnitelma deadlines 2.9. 9.9. 30.9. 12.11. 2.12. Kohdeyritysvaraus Rahan sitoutuminen yritystoiminnassa käyttöomaisuuteen ja käyttöpääomaan pohdinta Case Rahoitustilanne
Suhdannebarometri. Lounais-Suomi. Suhdanteet. Saldo
 Uusimaa Suhdannearviot hiipuivat hieman alkusyksyn aikana - tilanne edelleen tavanomaista parempi Tuotanto- ja myyntimäärät pysyivät hienoisessa nousussa Henkilökunnan määrä lisääntyi hieman alkusyksyllä
Uusimaa Suhdannearviot hiipuivat hieman alkusyksyn aikana - tilanne edelleen tavanomaista parempi Tuotanto- ja myyntimäärät pysyivät hienoisessa nousussa Henkilökunnan määrä lisääntyi hieman alkusyksyllä
Suhdannebarometri. Suhdanteet. Saldo
 TOUKOKUU 18 Uusimaa oli huhtikuussa 18 tavanomaista parempi Tuotanto lisääntyi lievästi alkuvuoden aikana kasvun ennakoidaan vauhdittuvan lähikuukausina Rekrytointivaikeuksia oli 27 %:lla yrityksistä Lähikuukausien
TOUKOKUU 18 Uusimaa oli huhtikuussa 18 tavanomaista parempi Tuotanto lisääntyi lievästi alkuvuoden aikana kasvun ennakoidaan vauhdittuvan lähikuukausina Rekrytointivaikeuksia oli 27 %:lla yrityksistä Lähikuukausien
SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE ESITYS
 SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE 1.1. - 3.9.24 ESITYS 2.1.24 Liikevaihdon jakautuma 1-9/24 Joustopakkaukset 51,1 milj. euroa 28,5 % Muut (Inka) 6,2 milj. euroa 3,5 % Kosteuspyyhkeet 66,1 milj. euroa 36,9
SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE 1.1. - 3.9.24 ESITYS 2.1.24 Liikevaihdon jakautuma 1-9/24 Joustopakkaukset 51,1 milj. euroa 28,5 % Muut (Inka) 6,2 milj. euroa 3,5 % Kosteuspyyhkeet 66,1 milj. euroa 36,9
MATEMATIIKKA. Matematiikkaa pintakäsittelijöille PAOJ 3. Isto Jokinen 2013
 MATEMATIIKKA Matematiikkaa pintakäsittelijöille PAOJ 3. Isto Jokinen 2013 PROSENTTILASKENTA Prosentti on 1/100 tai 0,01. Esimerkki 40. Lukuarvo % 0,42 42 0,013 1,3 1,002 100,2 1/25 100/25=4 23/45 51,1
MATEMATIIKKA Matematiikkaa pintakäsittelijöille PAOJ 3. Isto Jokinen 2013 PROSENTTILASKENTA Prosentti on 1/100 tai 0,01. Esimerkki 40. Lukuarvo % 0,42 42 0,013 1,3 1,002 100,2 1/25 100/25=4 23/45 51,1
Mikrotaloustiede Prof. Marko Terviö Aalto-yliopiston 31C00100 Syksy 2015 Assist. Salla Simola kauppakorkeakoulu
 Mikrotaloustiede Prof. Marko Terviö Aalto-yliopiston 31C00100 Syksy 2015 Assist. Salla Simola kauppakorkeakoulu Mallivastaukset - Loppukoe 10.12. Monivalinnat: 1c 2a 3e 4a 5c 6b 7c 8e 9b 10a I (a) Sekaniputus
Mikrotaloustiede Prof. Marko Terviö Aalto-yliopiston 31C00100 Syksy 2015 Assist. Salla Simola kauppakorkeakoulu Mallivastaukset - Loppukoe 10.12. Monivalinnat: 1c 2a 3e 4a 5c 6b 7c 8e 9b 10a I (a) Sekaniputus
6.1 Lineaarinen optimointi
 6.1 Lineaarinen optimointi Suora a + b + c = 0 jakaa -tason kahteen puolitasoon. Tason jokainen piste, joka on suoralla, toteuttaa suoran htälön ja kääntäen. Jos siis tason mielivaltaisen pisteen koordinaatit
6.1 Lineaarinen optimointi Suora a + b + c = 0 jakaa -tason kahteen puolitasoon. Tason jokainen piste, joka on suoralla, toteuttaa suoran htälön ja kääntäen. Jos siis tason mielivaltaisen pisteen koordinaatit
 Muutokset henkilökunnan määrässä yrityksen perustamisesta alkaen. 10 % 15 % kasvanut vähintään viidellä henkilöllä 9 % kasvanut 3-4 henkilöllä 44 % 22 % kasvanut 1-2 henkilöllä pysynyt ennallaan vähentynyt
Muutokset henkilökunnan määrässä yrityksen perustamisesta alkaen. 10 % 15 % kasvanut vähintään viidellä henkilöllä 9 % kasvanut 3-4 henkilöllä 44 % 22 % kasvanut 1-2 henkilöllä pysynyt ennallaan vähentynyt
Luento 4: Lineaarisen tehtävän duaali
 Luento 4: Lineaarisen tehtävän duaali Käsittelemme seuraavaksi lineaarisen optimoinnin duaaliteoriaa. Kuten luennossa 2 esitettiin, kohdefunktion optimiarvon herkkyys z, kun rajoitusyhtälön i, 1 i m, oikea
Luento 4: Lineaarisen tehtävän duaali Käsittelemme seuraavaksi lineaarisen optimoinnin duaaliteoriaa. Kuten luennossa 2 esitettiin, kohdefunktion optimiarvon herkkyys z, kun rajoitusyhtälön i, 1 i m, oikea
Demoyritys Oy TASEKIRJA 1.1.2011-31.12.2011
 Sivu1 (13) Demoyritys Oy Oikotie 8 00200 HELSINKI Y-tunnus: 0000000-0 Demoyritys Oy TASEKIRJA 1.1.2011-31.12.2011 . 2 Sisällysluettelo Sivu Hallituksen toimintakertomus 3 Tuloslaskelma 4 Tase (vastaavaa)
Sivu1 (13) Demoyritys Oy Oikotie 8 00200 HELSINKI Y-tunnus: 0000000-0 Demoyritys Oy TASEKIRJA 1.1.2011-31.12.2011 . 2 Sisällysluettelo Sivu Hallituksen toimintakertomus 3 Tuloslaskelma 4 Tase (vastaavaa)
HE 71/2016 vp. Esityksessä ehdotetaan muutettavaksi Kansaneläkelaitoksesta annettua lakia.
 Hallituksen esitys eduskunnalle laiksi Kansaneläkelaitoksesta annetun lain muuttamisesta ESITYKSEN PÄÄASIALLINEN SISÄLTÖ Esityksessä ehdotetaan muutettavaksi Kansaneläkelaitoksesta annettua lakia. Kansaneläkelaitoksen
Hallituksen esitys eduskunnalle laiksi Kansaneläkelaitoksesta annetun lain muuttamisesta ESITYKSEN PÄÄASIALLINEN SISÄLTÖ Esityksessä ehdotetaan muutettavaksi Kansaneläkelaitoksesta annettua lakia. Kansaneläkelaitoksen
Espoon kaupunki Pöytäkirja 265. Kaupunginhallitus 17.09.2012 Sivu 1 / 1
 Kaupunginhallitus 17.09.2012 Sivu 1 / 1 3790/02.05.05/2012 Kaupunginhallituksen konsernijaosto 59 10.9.2012 265 Spinno-Seed Oy:n omistuksesta luopuminen Valmistelijat / lisätiedot: Hindsberg-Karkola Viktoria,
Kaupunginhallitus 17.09.2012 Sivu 1 / 1 3790/02.05.05/2012 Kaupunginhallituksen konsernijaosto 59 10.9.2012 265 Spinno-Seed Oy:n omistuksesta luopuminen Valmistelijat / lisätiedot: Hindsberg-Karkola Viktoria,
Suominen Yhtymä Oyj. Tulostiedote Esitys Suominen Yhtymä Oyj
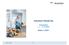 Tulostiedote 1.1. 31.12.2010 Esitys 11.2. 1 Suominen yhteensä Takana vaikea vuosi Milj. Q4/2010 Q4/2009 2010 2009 Liikevaihto 45,3 44,9 173,4 179,4 Liikevoitto -8,7 87 06 0,6-10,8 67 6,7 Katsauskauden
Tulostiedote 1.1. 31.12.2010 Esitys 11.2. 1 Suominen yhteensä Takana vaikea vuosi Milj. Q4/2010 Q4/2009 2010 2009 Liikevaihto 45,3 44,9 173,4 179,4 Liikevoitto -8,7 87 06 0,6-10,8 67 6,7 Katsauskauden
1 PROSENTTILASKENTAA 7
 SISÄLTÖ 1 PROSENTTILASKENTAA 7 Peruskäsitteitä 8 Prosenttiarvo 9 Prosenttiluku 11 Perusarvo 13 Muutosten laskeminen 15 Lisäys ja vähennys 15 Alkuperäisten arvojen laskeminen 17 Muutosprosentti 19 Prosenttiyksikkö
SISÄLTÖ 1 PROSENTTILASKENTAA 7 Peruskäsitteitä 8 Prosenttiarvo 9 Prosenttiluku 11 Perusarvo 13 Muutosten laskeminen 15 Lisäys ja vähennys 15 Alkuperäisten arvojen laskeminen 17 Muutosprosentti 19 Prosenttiyksikkö
Pilkeyrityksen liiketoiminnan kehittäminen
 Pilkeyrityksen liiketoiminnan kehittäminen Mari Hakkarainen, Jyväskylän ammattikorkeakoulu Laskelmapohjat: Timo Värre, JAMK Esimerkki hyvästä tuotteistamisesta Menestyvän yrityksen talous Kasvu - Onko
Pilkeyrityksen liiketoiminnan kehittäminen Mari Hakkarainen, Jyväskylän ammattikorkeakoulu Laskelmapohjat: Timo Värre, JAMK Esimerkki hyvästä tuotteistamisesta Menestyvän yrityksen talous Kasvu - Onko
Projektin arvon määritys
 Projektin arvon määritys Luku 6, s. 175-186 Optimointiopin seminaari - Syksy 2000 / 1 Tehtävä Johdetaan menetelmä projektiin oikeuttavan option määrittämiseksi kohde-etuuden hinnan P perusteella projektin
Projektin arvon määritys Luku 6, s. 175-186 Optimointiopin seminaari - Syksy 2000 / 1 Tehtävä Johdetaan menetelmä projektiin oikeuttavan option määrittämiseksi kohde-etuuden hinnan P perusteella projektin
KOMISSION KERTOMUS EUROOPAN PARLAMENTILLE JA NEUVOSTOLLE. maataloustukirahaston menoista. Varojärjestelmä nro 10-11/2013
 EUROOPAN KOMISSIO Bryssel 13.12.2013 COM(2013) 887 final KOMISSION KERTOMUS EUROOPAN PARLAMENTILLE JA NEUVOSTOLLE maataloustukirahaston menoista Varojärjestelmä nro 10-11/2013 FI FI 1. Johdanto...3 2.
EUROOPAN KOMISSIO Bryssel 13.12.2013 COM(2013) 887 final KOMISSION KERTOMUS EUROOPAN PARLAMENTILLE JA NEUVOSTOLLE maataloustukirahaston menoista Varojärjestelmä nro 10-11/2013 FI FI 1. Johdanto...3 2.
1 PROSENTTILASKENTAA 7
 SISÄLTÖ 1 PROSENTTILASKENTAA 7 Peruskäsitteitä 8 Prosenttiarvo 9 Prosenttiluku 11 Perusarvo 13 Muutosten laskeminen 15 Lisäys ja vähennys 15 Alkuperäisten arvojen laskeminen 17 Muutosprosentti 19 Prosenttiyksikkö
SISÄLTÖ 1 PROSENTTILASKENTAA 7 Peruskäsitteitä 8 Prosenttiarvo 9 Prosenttiluku 11 Perusarvo 13 Muutosten laskeminen 15 Lisäys ja vähennys 15 Alkuperäisten arvojen laskeminen 17 Muutosprosentti 19 Prosenttiyksikkö
Ehdotus NEUVOSTON TÄYTÄNTÖÖNPANOPÄÄTÖS
 EUROOPAN KOMISSIO Bryssel 17.9.2013 COM(2013) 633 final 2013/0312 (NLE) Ehdotus NEUVOSTON TÄYTÄNTÖÖNPANOPÄÄTÖS luvan antamisesta Yhdistyneelle kuningaskunnalle jatkaa yhteisestä arvonlisäverojärjestelmästä
EUROOPAN KOMISSIO Bryssel 17.9.2013 COM(2013) 633 final 2013/0312 (NLE) Ehdotus NEUVOSTON TÄYTÄNTÖÖNPANOPÄÄTÖS luvan antamisesta Yhdistyneelle kuningaskunnalle jatkaa yhteisestä arvonlisäverojärjestelmästä
Valmet Automotiven strategia muuttuvassa toimintaympäristössä. Finnmobile Vaikuttajafoorumi Johtaja Robert Blumberg
 Valmet Automotiven strategia muuttuvassa toimintaympäristössä Finnmobile Vaikuttajafoorumi 8.11.2012 Johtaja Robert Blumberg 1. Autoteollisuus ja markkinat 2. Valmet Automotive muuttuvassa ympäristössä
Valmet Automotiven strategia muuttuvassa toimintaympäristössä Finnmobile Vaikuttajafoorumi 8.11.2012 Johtaja Robert Blumberg 1. Autoteollisuus ja markkinat 2. Valmet Automotive muuttuvassa ympäristössä
Luento 2: Optimointitehtävän graafinen ratkaiseminen. LP-malli.
 Luento 2: Optimointitehtävän graafinen ratkaiseminen. LP-malli. LP-malli Esimerkki. Maalitehdas valmistaa ulko- ja sisämaalia raaka-aineista M1 ja M2. Sisämaalin maksimikysyntä on 2 tonnia/päivä. Sisämaalin
Luento 2: Optimointitehtävän graafinen ratkaiseminen. LP-malli. LP-malli Esimerkki. Maalitehdas valmistaa ulko- ja sisämaalia raaka-aineista M1 ja M2. Sisämaalin maksimikysyntä on 2 tonnia/päivä. Sisämaalin
1. Vastaa seuraavaan tehtävään. Tehtävään liittyvä kuva on seuraavalla sivulla
 A31C00100 Mikrotaloustiede Kevät 2017 HARJOITUKSET 3 1. Vastaa seuraavaan tehtävään. Tehtävään liittyvä kuva on seuraavalla sivulla (i) Alla olevan kuvan kuluttaja A) on riskinkaihtaja B) on riskineutraali
A31C00100 Mikrotaloustiede Kevät 2017 HARJOITUKSET 3 1. Vastaa seuraavaan tehtävään. Tehtävään liittyvä kuva on seuraavalla sivulla (i) Alla olevan kuvan kuluttaja A) on riskinkaihtaja B) on riskineutraali
1. Kuntosalilla on 8000 asiakasta, joilla kaikilla on sama salikäyntien kysyntä: q(p)= P, missä
 A31C00100 Mikrotaloustiede Kevät 2017 1. Kuntosalilla on 8000 asiakasta, joilla kaikilla on sama salikäyntien kysyntä: q(p)= 18 1.5P, missä q on käyntejä kuukaudessa keskimäärin. Yhden käyntikerran rajakustannus
A31C00100 Mikrotaloustiede Kevät 2017 1. Kuntosalilla on 8000 asiakasta, joilla kaikilla on sama salikäyntien kysyntä: q(p)= 18 1.5P, missä q on käyntejä kuukaudessa keskimäärin. Yhden käyntikerran rajakustannus
HE 57/2010 vp HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2010 TOISEKSI LISÄTALOUSARVIOKSI
 HE 57/2010 vp HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2010 TOISEKSI LISÄTALOUSARVIOKSI Viitaten tämän esityksen yleisperusteluihin ja yksityiskohtaisten perustelujen selvitysosiin ehdotetaan, että Eduskunta
HE 57/2010 vp HALLITUKSEN ESITYS EDUSKUNNALLE VUODEN 2010 TOISEKSI LISÄTALOUSARVIOKSI Viitaten tämän esityksen yleisperusteluihin ja yksityiskohtaisten perustelujen selvitysosiin ehdotetaan, että Eduskunta
SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE ESITYS
 SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE 1.1. - 31.12.24 ESITYS 16.2.25 Liikevaihdon jakautuma 1-12/24 Joustopakkaukset 69,2 milj. euroa 29,7 % Muut 7,6 milj. euroa 3,2 % Kosteuspyyhkeet 81,3 milj. euroa 34,9
SUOMINEN YHTYMÄ OYJ TULOSTIEDOTE 1.1. - 31.12.24 ESITYS 16.2.25 Liikevaihdon jakautuma 1-12/24 Joustopakkaukset 69,2 milj. euroa 29,7 % Muut 7,6 milj. euroa 3,2 % Kosteuspyyhkeet 81,3 milj. euroa 34,9
Harjoitus 4: Matlab - Optimization Toolbox
 Harjoitus 4: Matlab - Optimization Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Optimointimallin muodostaminen
Harjoitus 4: Matlab - Optimization Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Optimointimallin muodostaminen
Malliratkaisut Demot
 Malliratkaisut Demot 1 23.1.2017 1. Päätösmuuttujiksi voidaan valita x 1 : tehtyjen peruspöytin lukumäärä x 2 : tehtyjen luxuspöytien lukumäärä. Optimointitehtäväksi tulee max 200x 1 + 350x 2 s. t. 5x
Malliratkaisut Demot 1 23.1.2017 1. Päätösmuuttujiksi voidaan valita x 1 : tehtyjen peruspöytin lukumäärä x 2 : tehtyjen luxuspöytien lukumäärä. Optimointitehtäväksi tulee max 200x 1 + 350x 2 s. t. 5x
Liiketoimintasuunnitelma vuosille
 Liiketoimintasuunnitelma vuosille Yrityskonsultointi JonesCon 2 TAUSTATIEDOT Laatija: Yrityksen nimi: Yrityksen toimiala: Perustajat: Suunnitelman aikaväli: Salassapito: Viimeisimmän version paikka ja
Liiketoimintasuunnitelma vuosille Yrityskonsultointi JonesCon 2 TAUSTATIEDOT Laatija: Yrityksen nimi: Yrityksen toimiala: Perustajat: Suunnitelman aikaväli: Salassapito: Viimeisimmän version paikka ja
Demo 1: Branch & Bound
 MS-C05 Optimoinnin perusteet Malliratkaisut 7 Ehtamo Demo : Branch & Bound Ratkaise lineaarinen kokonaislukuoptimointitehtävä käyttämällä Branch & Boundalgoritmia. max x + x s.e. x + 4x 9 5x + x 9 x Z
MS-C05 Optimoinnin perusteet Malliratkaisut 7 Ehtamo Demo : Branch & Bound Ratkaise lineaarinen kokonaislukuoptimointitehtävä käyttämällä Branch & Boundalgoritmia. max x + x s.e. x + 4x 9 5x + x 9 x Z
Uolevin reitti. Kuvaus. Syöte (stdin) Tuloste (stdout) Esimerkki 1. Esimerkki 2
 Uolevin reitti Kuvaus Uolevi on ruudukon vasemmassa ylänurkassa ja haluaisi päästä oikeaan alanurkkaan. Uolevi voi liikkua joka askeleella ruudun verran vasemmalle, oikealle, ylöspäin tai alaspäin. Lisäksi
Uolevin reitti Kuvaus Uolevi on ruudukon vasemmassa ylänurkassa ja haluaisi päästä oikeaan alanurkkaan. Uolevi voi liikkua joka askeleella ruudun verran vasemmalle, oikealle, ylöspäin tai alaspäin. Lisäksi
Tentissä saa olla mukana vain muistiinpanovälineet ja laskin. Laskut erilliselle konseptille, vastaus selkeästi näkyviin!!! Palauta tenttipaperi!!
 1 School of Business and Management Yliopisto-opettaja, Tiina Sinkkonen Opiskelijanumero ja nimi: CS31A0101 KUSTANNUSJOHTAMISEN PERUSKURSSI Tentti 01.02.2016 Tentissä saa olla mukana vain muistiinpanovälineet
1 School of Business and Management Yliopisto-opettaja, Tiina Sinkkonen Opiskelijanumero ja nimi: CS31A0101 KUSTANNUSJOHTAMISEN PERUSKURSSI Tentti 01.02.2016 Tentissä saa olla mukana vain muistiinpanovälineet
TIEA382 Lineaarinen ja diskreetti optimointi
 TIEA382 Lineaarinen ja diskreetti optimointi Jussi Hakanen Tietotekniikan laitos jussi.hakanen@jyu.fi AgC 426.3 Yleiset tiedot Tietotekniikan kandidaattiopintojen valinnainen kurssi http://users.jyu.fi/~jhaka/ldo/
TIEA382 Lineaarinen ja diskreetti optimointi Jussi Hakanen Tietotekniikan laitos jussi.hakanen@jyu.fi AgC 426.3 Yleiset tiedot Tietotekniikan kandidaattiopintojen valinnainen kurssi http://users.jyu.fi/~jhaka/ldo/
Laskentatoimi, digiaineisto. Esittelyaineisto
 LASKENTATOIMI DIGIAINEISTO Laskentatoimi, digiaineisto Esittelyaineisto Laskentatoimi, digiaineisto sisältää tehtävien ratkaisut Excel-tiedostoina Excel-pohjat tehtävien ratkaisuille opetusdioja Tutustu
LASKENTATOIMI DIGIAINEISTO Laskentatoimi, digiaineisto Esittelyaineisto Laskentatoimi, digiaineisto sisältää tehtävien ratkaisut Excel-tiedostoina Excel-pohjat tehtävien ratkaisuille opetusdioja Tutustu
Prof. Marko Terviö Assist. Jan Jääskeläinen
 Harjoitukset 3. 1. (a) Dismalandissa eri puolueiden arvostukset katusiivoukselle ovat Q A (P ) = 60 6P P A (Q) = 10 Q/6 Q B (P ) = 80 5P P B (Q) = 16 Q/5 Q C (P ) = 50 2P P C (Q) = 25 Q/2 Katusiivous on
Harjoitukset 3. 1. (a) Dismalandissa eri puolueiden arvostukset katusiivoukselle ovat Q A (P ) = 60 6P P A (Q) = 10 Q/6 Q B (P ) = 80 5P P B (Q) = 16 Q/5 Q C (P ) = 50 2P P C (Q) = 25 Q/2 Katusiivous on
Liiketoimintasuunnitelma 01.12.2015 Giganteum. Giganteum 1/11
 Liiketoimintasuunnitelma 01.12.2015 Giganteum Giganteum 1/11 Giganteum 2/11 Perustiedot ja osaaminen Sukunimi Etunimi Leppiaho Mika Osoite Postinumero ja -toimipaikka Kotikunta Puhelinnumero Sähköpostiosoite
Liiketoimintasuunnitelma 01.12.2015 Giganteum Giganteum 1/11 Giganteum 2/11 Perustiedot ja osaaminen Sukunimi Etunimi Leppiaho Mika Osoite Postinumero ja -toimipaikka Kotikunta Puhelinnumero Sähköpostiosoite
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5
 Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5 1. Kotitehtävä. 2. Lasketaan aluksi korkoa korolle. Jos korkoprosentti on r, ja korko maksetaan n kertaa vuodessa t vuoden ajan, niin kokonaisvuosikorko
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5 1. Kotitehtävä. 2. Lasketaan aluksi korkoa korolle. Jos korkoprosentti on r, ja korko maksetaan n kertaa vuodessa t vuoden ajan, niin kokonaisvuosikorko
* Hyödyn maksimointi on ihmisten toimintaa ja valintoja ohjaava periaate.
 KANSANTALOUSTIETEEN PERUSTEET Yrityksen teoria (Economics luvut 13-14) 14) KTT Petri Kuosmanen Optimointiperiaate a) Yksilöt pyrkivät maksimoimaan hyötynsä. * Hyödyn maksimointi on ihmisten toimintaa ja
KANSANTALOUSTIETEEN PERUSTEET Yrityksen teoria (Economics luvut 13-14) 14) KTT Petri Kuosmanen Optimointiperiaate a) Yksilöt pyrkivät maksimoimaan hyötynsä. * Hyödyn maksimointi on ihmisten toimintaa ja
ASIKKALAN KUNTA Tilinpäätös 2014
 ASIKKALAN KUNTA Tilinpäätös 2014 Historiallisen hyvä tulos Ylijäämää kertyi 5,5 miljoonaa euroa, jolloin kumulatiivista ylijäämää taseessa on noin 7,4 miljoonaa euroa. Se on enemmän kuin riittävä puskuri
ASIKKALAN KUNTA Tilinpäätös 2014 Historiallisen hyvä tulos Ylijäämää kertyi 5,5 miljoonaa euroa, jolloin kumulatiivista ylijäämää taseessa on noin 7,4 miljoonaa euroa. Se on enemmän kuin riittävä puskuri
PUUTARHAHARJOITTELURAPORTIN TALOUSLASKELMAT
 PUUTARHAHARJOITTELURAPORTIN TALOUSLASKELMAT Ohjeet perustuvat kululajikohtaiseen tuloslaskelmaan. Lisätietoja tuloslaskelmien ja taseiden esittämisestä löydät esim. http://ktm.elinar.fi/ktm/fin/kirjanpi.nsf/0/ecd13ea878482b8bc22567da002d67f2/$file/tpyleis.pdf
PUUTARHAHARJOITTELURAPORTIN TALOUSLASKELMAT Ohjeet perustuvat kululajikohtaiseen tuloslaskelmaan. Lisätietoja tuloslaskelmien ja taseiden esittämisestä löydät esim. http://ktm.elinar.fi/ktm/fin/kirjanpi.nsf/0/ecd13ea878482b8bc22567da002d67f2/$file/tpyleis.pdf
Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu
 Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu Merkintöjä := vasen puoli määritellään oikean puolen lausekkeella s.e. ehdolla; siten että (engl. subject to, s.t.) vasemman puolen
Luento 1: Optimointimallin muodostaminen; optimointitehtävien luokittelu Merkintöjä := vasen puoli määritellään oikean puolen lausekkeella s.e. ehdolla; siten että (engl. subject to, s.t.) vasemman puolen
EUROOPAN PARLAMENTTI
 EUROOPAN PARLAMENTTI 2004 Vetoomusvaliokunta 2009 7.3.2008 ILMOITUS JÄSENILLE Aihe: Vetoomus nro 849/2004, Bernard Ross, Yhdistyneen kuningaskunnan kansalainen, verotuksesta Ruotsissa ja pääoman vapaasta
EUROOPAN PARLAMENTTI 2004 Vetoomusvaliokunta 2009 7.3.2008 ILMOITUS JÄSENILLE Aihe: Vetoomus nro 849/2004, Bernard Ross, Yhdistyneen kuningaskunnan kansalainen, verotuksesta Ruotsissa ja pääoman vapaasta
Ajatuksia hinnoittelusta. Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin.
 Ajatuksia hinnoittelusta Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin. Hinnoittelu Yritystoiminnan tavoitteena on aina kannattava liiketoiminta ja asiakastyytyväisyys. Hinta
Ajatuksia hinnoittelusta Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin. Hinnoittelu Yritystoiminnan tavoitteena on aina kannattava liiketoiminta ja asiakastyytyväisyys. Hinta
k=0 saanto jokaisen kolmannen asteen polynomin. Tukipisteet on talloin valittu
 LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
Kiinteät kustannukset Vuokrat 1500 Palkat 4200 Poistot 400 Korot 300 Muut Katetuottotavoite (%) 30 %
 Kiinteät kustannukset Vuokrat 1500 Palkat 4200 Poistot 400 Korot 300 Muut 200 6600 Katetuottotavoite (%) 30 % a) Kriittisessä pisteessä katetuottoa pitäisi kertyä kiinteiden kustannusten verran, joka on
Kiinteät kustannukset Vuokrat 1500 Palkat 4200 Poistot 400 Korot 300 Muut 200 6600 Katetuottotavoite (%) 30 % a) Kriittisessä pisteessä katetuottoa pitäisi kertyä kiinteiden kustannusten verran, joka on
Hintadiskriminaatio 2/2
 Hintadiskriminaatio 2/2 Matti Hellvist 12.2.2003 Toisen asteen hintadiskrimiaatio eli tuotteiden kohdennus Toisen asteen hintadiskriminaatio toimii tilanteessa, jossa kuluttajat ovat keskenään erilaisia
Hintadiskriminaatio 2/2 Matti Hellvist 12.2.2003 Toisen asteen hintadiskrimiaatio eli tuotteiden kohdennus Toisen asteen hintadiskriminaatio toimii tilanteessa, jossa kuluttajat ovat keskenään erilaisia
ESITYKSEN PÄÄASIALLINEN SISÄLTÖ PERUSTELUT
 1991 vp - HE 21 Hallituksen esitys Eduskunnalle laiksi tasausverolain muuttamisesta ESITYKSEN PÄÄASIALLINEN SISÄLTÖ Tasausverolakia ehdotetaan muutettavaksi siten, että tasausvero poistetaan kaikilta teollisuuden
1991 vp - HE 21 Hallituksen esitys Eduskunnalle laiksi tasausverolain muuttamisesta ESITYKSEN PÄÄASIALLINEN SISÄLTÖ Tasausverolakia ehdotetaan muutettavaksi siten, että tasausvero poistetaan kaikilta teollisuuden
Anne-Maria Peitsalo, 14.3.2012
 MATERIAALI TEHOKKUUS TUTKIMUS CASE KIDEX Anne-Maria Peitsalo, 14.3.2012 MARTELA LYHYESTI Martela Oyj on työympäristöjen ja julkitilojen muutosten toteuttaja. Martelan sisustusratkaisut tukevat asiakkaan
MATERIAALI TEHOKKUUS TUTKIMUS CASE KIDEX Anne-Maria Peitsalo, 14.3.2012 MARTELA LYHYESTI Martela Oyj on työympäristöjen ja julkitilojen muutosten toteuttaja. Martelan sisustusratkaisut tukevat asiakkaan
omenaraaka-ainetta (KATE) ostetaan omenoita (OMENATAS)
 ALKOHOLITEHDAS Aktiviteettianalyysi mallia varten Raaka-ainelohko 1. Ostetaan omenoita x 1 kg (muuttujana mallissa OMENAT) kulutetaan tuotetaan rahaa omenaraaka-ainetta (KATE) ostetaan omenoita (OMENATAS)
ALKOHOLITEHDAS Aktiviteettianalyysi mallia varten Raaka-ainelohko 1. Ostetaan omenoita x 1 kg (muuttujana mallissa OMENAT) kulutetaan tuotetaan rahaa omenaraaka-ainetta (KATE) ostetaan omenoita (OMENATAS)
(1) Katetuottolaskelma
 (1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
(1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
Piiri K 1 K 2 K 3 K 4 R R
 Lineaarinen optimointi vastaus, harj 1, Syksy 2016. 1. Teollisuuslaitos valmistaa piirejä R 1 ja R 2, joissa on neljää eri komponenttia seuraavat määrät: Piiri K 1 K 2 K 3 K 4 R 1 3 1 2 2 R 2 4 2 3 0 Päivittäistä
Lineaarinen optimointi vastaus, harj 1, Syksy 2016. 1. Teollisuuslaitos valmistaa piirejä R 1 ja R 2, joissa on neljää eri komponenttia seuraavat määrät: Piiri K 1 K 2 K 3 K 4 R 1 3 1 2 2 R 2 4 2 3 0 Päivittäistä
Talousmatematiikan perusteet: Luento 12. Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla
 Talousmatematiikan perusteet: Luento 12 Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla Esimerkki Esim. Yritys tekee kahta elintarviketeollisuuden käyttämää puolivalmistetta,
Talousmatematiikan perusteet: Luento 12 Lineaarinen optimointitehtävä Graafinen ratkaisu Ratkaisu Excel Solverilla Esimerkki Esim. Yritys tekee kahta elintarviketeollisuuden käyttämää puolivalmistetta,
Voitonmaksimointi esimerkkejä, L9
 Voitonmaksimointi esimerkkejä, L9 (1) Yritys Valmistaa kuukaudessa q tuotetta. Kysyntäfunktio on p = 15 0, 05q ja kustannusfunktio on C(q) = 350 + 2q + 0, 05q 2. a) Yritys valmistaa nyt tuotteita kuukaudessa
Voitonmaksimointi esimerkkejä, L9 (1) Yritys Valmistaa kuukaudessa q tuotetta. Kysyntäfunktio on p = 15 0, 05q ja kustannusfunktio on C(q) = 350 + 2q + 0, 05q 2. a) Yritys valmistaa nyt tuotteita kuukaudessa
Oikean hinnan asettaminen
 Oikean hinnan asettaminen Hinnoittelu on yrityksen kannattavuuden kannalta tärkeä tekijä. Tuotteen myyntihintaa voidaan ajatella o markkinoiden kannalta = kuinka paljon asiakkaat ovat valmiita tuotteesta
Oikean hinnan asettaminen Hinnoittelu on yrityksen kannattavuuden kannalta tärkeä tekijä. Tuotteen myyntihintaa voidaan ajatella o markkinoiden kannalta = kuinka paljon asiakkaat ovat valmiita tuotteesta
SUOMINEN YHTYMÄ OYJ OSAVUOSIKATSAUS ESITYS
 SUOMINEN YHTYMÄ OYJ OSAVUOSIKATSAUS 1.1. - 30.6.2006 ESITYS 24.7.2006 Liikevaihdon jakauma 1-6/2006 97,0 milj. euroa Joustopakkaukset 37,1 milj. euroa 38 % Kosteuspyyhkeet 35 % Kuitukankaat 27 % Pyyhkeet
SUOMINEN YHTYMÄ OYJ OSAVUOSIKATSAUS 1.1. - 30.6.2006 ESITYS 24.7.2006 Liikevaihdon jakauma 1-6/2006 97,0 milj. euroa Joustopakkaukset 37,1 milj. euroa 38 % Kosteuspyyhkeet 35 % Kuitukankaat 27 % Pyyhkeet
KANSANTALOUSTIETEEN PÄÄSYKOE 4.6.2015 MALLIVASTAUKSET
 KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
Moduuli 7 Talouden hallinta
 2O16-1-DEO2-KA2O2-003277 Moduuli 7 Talouden hallinta Osa 3 Talouden suunnittelu ja ennusteet Hanke on rahoitettu Euroopan komission tuella. Tästä julkaisusta (tiedotteesta) vastaa ainoastaan sen laatija,
2O16-1-DEO2-KA2O2-003277 Moduuli 7 Talouden hallinta Osa 3 Talouden suunnittelu ja ennusteet Hanke on rahoitettu Euroopan komission tuella. Tästä julkaisusta (tiedotteesta) vastaa ainoastaan sen laatija,
Asiakirjayhdistelmä 2015
 01. Nettolainanotto ja velanhallinta Talousarvioesitys HE 131/2014 vp (15.9.2014) Momentille merkitään nettotuloa 4 467 821 000 euroa. Tuloina otetaan huomioon uusien valtionlainojen nimellisarvot, emissiovoitot,
01. Nettolainanotto ja velanhallinta Talousarvioesitys HE 131/2014 vp (15.9.2014) Momentille merkitään nettotuloa 4 467 821 000 euroa. Tuloina otetaan huomioon uusien valtionlainojen nimellisarvot, emissiovoitot,
Taloudelliset edellytykset Tekes-projektille. Kirsi Leino
 Taloudelliset edellytykset Tekes-projektille Kirsi Leino 28.1.2016 Perusasioiden tulee olla kunnossa Alfa rating Luottotiedot Verovelat Ennakkoperintärekisteri ja työnantajarekisteri (alv-rekisteri) Oma
Taloudelliset edellytykset Tekes-projektille Kirsi Leino 28.1.2016 Perusasioiden tulee olla kunnossa Alfa rating Luottotiedot Verovelat Ennakkoperintärekisteri ja työnantajarekisteri (alv-rekisteri) Oma
Kokonaislukuoptiomointi Leikkaustasomenetelmät
 Kokonaislukuoptiomointi Leikkaustasomenetelmät Systeemianalyysin Laboratorio 19.3.2008 Sisällys Leikkaustasomenetelmät yleisesti Leikkaustasomenetelmät generoivilla kokonaislukujoukoilla Gomoryn leikkaavat
Kokonaislukuoptiomointi Leikkaustasomenetelmät Systeemianalyysin Laboratorio 19.3.2008 Sisällys Leikkaustasomenetelmät yleisesti Leikkaustasomenetelmät generoivilla kokonaislukujoukoilla Gomoryn leikkaavat
Suhdannebarometri. Suhdanteet. Saldo
 ELOKUU 18 Uusimaa on noussut selvästi tavanomasta paremmaksi Tuotanto ja myynti kasvavat yleisesti Henkilökunnan määrä on noususuunnassa, ammattityövoimasta pulaa 31 %:lla alasta himmenivät hieman kesän
ELOKUU 18 Uusimaa on noussut selvästi tavanomasta paremmaksi Tuotanto ja myynti kasvavat yleisesti Henkilökunnan määrä on noususuunnassa, ammattityövoimasta pulaa 31 %:lla alasta himmenivät hieman kesän
1 Rajoitettu optimointi I
 Taloustieteen mat.menetelmät 2017 materiaali II-1 1 Rajoitettu optimointi I 1.1 Tarvittavaa osaamista Matriisit ja vektorit, matriisien de niittisyys Derivointi (mm. ketjusääntö, Taylorin kehitelmä) Implisiittifunktiolause
Taloustieteen mat.menetelmät 2017 materiaali II-1 1 Rajoitettu optimointi I 1.1 Tarvittavaa osaamista Matriisit ja vektorit, matriisien de niittisyys Derivointi (mm. ketjusääntö, Taylorin kehitelmä) Implisiittifunktiolause
Näytesivut LAATIMINEN. 5.1 Lainaosuuslaskelmamalleja esimerkkien muodossa
 5 LAINAOSUUSLASKELMAN LAATIMINEN 5.1 Lainaosuuslaskelmamalleja esimerkkien muodossa Kuten edellä on todettu, lainaosuuslaskelmat ovat muokkautuneet kentällä nykymuotoonsa. Kirjanpitolautakunnan 7.12.2010
5 LAINAOSUUSLASKELMAN LAATIMINEN 5.1 Lainaosuuslaskelmamalleja esimerkkien muodossa Kuten edellä on todettu, lainaosuuslaskelmat ovat muokkautuneet kentällä nykymuotoonsa. Kirjanpitolautakunnan 7.12.2010
