4. Todennäköisyyslaskennan kertausta
|
|
|
- Tarja Lahtinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 luento04.ppt S Liikenneteorian perusteet - Kevät
2 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 2
3 Otosavaruus, alkeistapaus, tapahtuma Otosavaruus Ω sample space on kaikkien mahdollisten alkeistapausten ω sample muodostama joukko, ω Ω Esim. 0. Rahanheitto: Ω {H,T} Esim. 1. Nopanheitto: Ω {1,2,3,4,5,6} Esim. 2. siakkaiden lkm jonossa: Ω {0,1,2,...} Esim. 3. siakkaan palveluaika esim. minuutteina: Ω { R > 0} Tapahtumat,B,C,... events ovat otosavaruuden Ω mitallisia osajoukkoja,,b,c,... Ω Esim. 1. Nopanheitossa parillinen luku : {2,4,6} Esim. 2. Jono tyhjä : {0} Esim. 3. siakkaan palvelu kestää yli 3 minuuttia : { R > 3.0} Merkitään :llä kaikkien tapahtumien joukkoa, Varma tapahtuma: otosavaruus Ω itse Mahdoton tapahtuma: tyhjä joukko 3
4 Tapahtumien yhdistely Yhdiste union tai B : B {ω Ω ω tai ω B} Leikkaus intersection ja B : B {ω Ω ω ja ω B} Komplementti complement ei : c {ω Ω ω } Tapahtumat ja B ovat toistensa poissulkevia disjoint, jos B Kokoelma tapahtumia {B 1, B 2, } muodostaa tapahtuman osituksen partition, jos i B i B j kaikilla i j ii i B i B 1 Esim. 1. Nopanheitossa parittomat ja parilliset luvut osittavat koko otosavaruuden: B 1 {1,3,5} ja B 2 {2,4,6} B 2 B 3 4
5 Todennäköisyys Tapahtuman todennäköisyyttä tn, probability merkitään :lla, [0,1] Todennäköisyysmitta on siis ns. joukkofunktio, : [0,1] Ominaisuuksia: i 0 1 ii 0 iii Ω 1 iv c 1 v B + B B vi B B + B B vii kokoelma {B i } on tapahtuman ositus Σ i B i viii B B 5
6 6 4. Todennäköisyyslaskennan kertausta Ehdollinen todennäköisyys Oletetaan, että tapahtumalle B: B > 0 Määr. Tapahtuman ehdollinen todennäköisyys conditional probability ehdolla B on Seuraus: B B B B B B B
7 Kokonaistodennäköisyyden kaava Olkoon kokoelma {B i } otosavaruuden Ω ositus Tällöin kokoelma { B i } on tapahtuman ositus, joten kts. kalvo 5 vii Oletaan lisäksi, että B i > 0 kaikilla i. Tällöin kts. kalvo 6 i Bi i Bi Bi Tätä kutsutaan kokonaistodennäköisyyden kaavaksi B 1 B 3 Ω B 2 B4 7
8 8 4. Todennäköisyyslaskennan kertausta Bayesin kaava Olkoon kokoelma {B i } otosavaruuden Ω ositus Oletetaan, että > 0 ja B i > 0 kaikilla i. Tällöin kts. kalvo 6 Näin ollen, kokonaistodennäköisyyden kaavan nojalla kts. kalvo 7, Tätä kutsutaan Bayesin kaavaksi tn:iäb i kutsutaan tapahtumien B i a priori todennäköisyyksiksi tn:iäb i taas sanotaan tapahtumien B i a posteriori todennäköisyyksiksi ehdolla, että tapahtuma tapahtui B B B i i i i B j j j i i B B B B B i
9 9 4. Todennäköisyyslaskennan kertausta Tilastollinen riippumattomuus Määr. Tapahtumat ja B ovat riippumattomia independent, jos Seuraus: Vastaavasti: B B B B B B B B B B B
10 Satunnaismuuttujat Määr. Reaaliarvoinen satunnaismuuttuja sm, random variable on mitallinen kuvaus otosavaruudesta Ω reaalilukujen joukkoon R, : Ω R jokaiseen alkeistapaukseen ω Ω liitetään reaaliluku ω Mitallisuus measurability tarkoittaa, että kaikki tyyppiä { }: { ω Ω ω } Ω olevat otosavaruuden joukot kuuluvat tapahtumien joukkoon, ts. { } Tapahtuman todennäköisyys on siten { } 10
11 Esimerkki Rahaa heitetään kolme kertaa peräkkäin Otosavaruus: Ω { ω1, ω2, ω3 ω i {H,T}, i 1,2,3} Olkoon satunnaismuuttuja, joka kertoo klaavojen T tails lkm:n näissä kolmessa heitossa: ω HHH HHT HTH THH HTT THT TTH TTT ω
12 Tapahtuman indikaattori Olkoon mielivaltainen tapahtuma Määr. Satunnaismuuttujaa 1, joka määritellään kaavalla 1 1, ω 0, ω ω sanotaan tapahtuman indikaattoriksi indicator Selvästikin: {1 {1 1} 0} c 1 12
13 Kertymäfunktio Määr. Sm:n kertymäfunktio kf, cumulative distribution function on kuvaus F : R [0,1], joka määritellään kaavalla F { } Kf määrää täydellisesti ko. sm:n jakauman distribution so. tn:t { B}, missä B Rja { B} Ominaisuuksia: i F on kasvava ii F on oikealta jatkuva iii F 0 iv F 1 0 F 13 1
14 14 4. Todennäköisyyslaskennan kertausta Satunnaismuuttujien tilastollinen riippumattomuus Määr. Sm:t ja Y ovat riippumattomia, jos kaikilla ja y Määr. Sm:t 1,, n ovat täydellisesti riippumattomia, jos kaikilla i ja i } { } { }, { y Y y Y } { } { },..., { n n n n L
15 Riippumattomien satunnaismuuttujien maksimi ja minimi Olkoot sm:t 1,, n täydellisesti riippumattomia Merkitään ma : ma{ 1,, n }. Tällöin ma { 1 } {, K, n } { 1 } L { } Merkitään min : min{ 1,, n }. Tällöin min n { > } { 1 >, K, n > } { 1 > } L { n > } 15
16 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 16
17 Diskreetit satunnaismuuttujat Määr. Joukkoa R sanotaan diskreetiksi discrete, jos se on äärellinen, { 1,, n }, tai numeroituvasti ääretön, { 1, 2, }. Määr. Sm on diskreetti, jos on olemassa sellainen diskreetti joukko S R, että Seuraus: { } 0 kaikilla S { S } 1 { } 0 kaikilla S Joukkoa S sanotaan sm:n arvojoukoksi 17
18 18 4. Todennäköisyyslaskennan kertausta istetodennäköisyysfunktio Olkoon sm diskreetti Sm:n jakauman määräävät pistetodennäköisyydet p i, Määr. Sm:n pistetodennäköisyysfunktio ptnf, probability mass function p : R [0,1] määritellään kaavalla Kf on tässä tapauksessa seuraava porrasfunktio: i i i S p }, { : 0,, } { : i i S S p p i i i p F : } {
19 Esimerkki p F pistetodennäköisyysfunktio ptnf kertymäfunktio kf S { 1, 2, 3, 4 } 19
20 Diskreettien satunnaismuuttujien riippumattomuus Diskreetit sm:t ja Y ovat riippumattomia, jos ja vain jos kaikilla i S ja y j S Y { i, Y y j} { i} { Y y j} 20
21 Odotusarvo Määr. Sm:n odotusarvo mean, epectation määritellään kaavalla µ : E[ ]: { } p S S i p i i Huom. 1. Odotusarvo on hyvin määritelty vain, jos Σ i p i i < Huom. 2. Jos i 0 ja Σ i p i i, niin voidaan merkitä E[] Ominaisuuksia: i c R E[c] ce[] ii E[ + Y] E[] + E[Y] iii ja Y riippumattomia E[Y] E[]E[Y] 21
22 Varianssi Määr. Sm:n varianssi variance määritellään kaavalla σ 2 : D 2 [ ]: Var[ ]: E[ E[ ] 2 ] Kätevä kaava todista!: D 2 2 [ ] E[ ] E[ ] 2 Ominaisuuksia: i c R D 2 [c] c 2 D 2 [] ii ja Y riippumattomia D 2 [ + Y] D 2 [] + D 2 [Y] 22
23 Kovarianssi Määr. Sm:ien ja Y välinen kovarianssi covariance määr. kaavalla σ 2 Y : Cov[, Y ]: E[ E[ ] Y E[ Y ]] Kätevä kaava todista!: Cov[, Y ] E[ Y ] E[ ] E[ Y ] Ominaisuuksia: i Cov[,] Var[] ii Cov[,Y] Cov[Y,] iii Cov[+Y,Z] Cov[,Z] + Cov[Y,Z] iv ja Y riippumattomia Cov[,Y] 0 23
24 Muita jakaumaan liittyviä tunnuslukuja Määr. Sm:n hajonta standard deviation: σ : D [ ]: D 2 [ ] Määr. Sm:n variaatiokerroin coefficient of variation: c : C[ ]: D[ ] E[ ] Määr. Sm:n k:s momentti moment, k 1,2,...: µ k k : E[ ] 24
25 25 4. Todennäköisyyslaskennan kertausta Riippumattomien satunnaismuuttujien keskiarvo Olkoot sm:t 1,, n riippumattomia ja samoin jakautuneita IID odotusarvonaan µ ja varianssinaan σ 2 Merkitään näiden sm:ien keskiarvoa sample mean seuraavasti: Tällöin todista! n i i n n 1 1 : n n n n n D D E σ σ µ ] [ ] [ ] [ 2 2
26 Suurten lukujen laki SLL Olkoot sm:t 1,, n riippumattomia ja samoin jakautuneita IID odotusarvonaan µ ja varianssinaan σ 2 Heikko suurten lukujen laki: kaikilla ε > 0 { µ > ε} n Vahva suurten lukujen laki: todennäköisyydellä 1 0 n µ Seuraus: Suurilla n:n arvoilla n µ 26
27 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 27
28 Bernoulli-jakauma Bernoulli p, p 0,1 kuvaa yksittäistä satunnaiskoetta, jonka tuloksena joko onnistuminen 1 tai epäonnistuminen 0; vrt. rahanheitto onnistuminen tn:llä p ja epäonnistuminen tn:llä 1 p rvojoukko: S {0,1} istetodennöisyydet: { 0} 1 p, { 1} p Odotusarvo: E[] 1 p 0 + p 1 p Toinen momentti: E[ 2 ] 1 p p 1 2 p Varianssi: D 2 [] E[ 2 ] E[] 2 p p 2 p1 p 28
29 Binomijakauma Bin n, p, n {1,2,...}, p 0,1 onnistumisten lkm n:ssä perättäisessä ja toisistaan riippumattomassa satunnaiskokeessa; n missä i Bernoullip n satunnaiskokeiden lkm p onnistumisen tn yksittäisessä satunnaiskokeessa rvojoukko: S {0,1,,n} istetodennäköisyydet: { n i n i p 1 p i} Odotusarvo: E[] E[ 1 ] + + E[ n ] np i n n! i! n i! n! n n 1 L2 1 Varianssi: D 2 [] D 2 [ 1 ] + + D 2 [ n ] np1 p riippumattomuus! i 29
30 Geometrinen jakauma Geom p, p 0,1 peräkkäisten onnistumisten lkm ennen ensimmäistä epäonnistumista sarjassa peräkkäisiä ja toisistaan riippumattomia satunnaiskokeita p onnistumisen tn yksittäisessä satunnaiskokeessa rvojoukko: S {0,1, } istetodennäköisyydet: { i} p 1 p Odotusarvo: E[] i ip i 1 p p/1 p Toinen momentti: E[ 2 ] i i 2 p i 1 p 2p/1 p 2 + p/1 p Varianssi: D 2 [] E[ 2 ] E[] 2 p/1 p 2 i 30
31 Geometrisen jakauman unohtavaisuusominaisuus Geometrisella jakaumalla on ns. unohtavaisuusominaisuus memoryless property: kaikilla i,j {0,1,...} Todista! { i + j i} { j} Ohje: Todista ensin, että { i} p i 31
32 Geometrisesti jakautuneiden satunnaismuuttujien minimi Olkoot sm:t 1 Geomp 1 ja 2 Geomp 2 riippumattomia Tällöin min : min{ 1, 2} Geom p1 p2 ja { min i } 1 pi 1 p p 1 2, i {1,2} Todista! Ohje: Kts. kalvo 15 32
33 oisson-jakauma oisson a, a > 0 binomijakauman rajatapaus, kun n ja p 0 siten, että np a rvojoukko: S {0,1, } istetodennäköisyydet: { i} a i a e i! Odotusarvo: E[] a Toinen momentti: E[ 1] a 2 E[ 2 ] a 2 + a Varianssi: D 2 [] E[ 2 ] E[] 2 a 33
34 Esimerkki Oletetaan, että paikalliskeskukseen on kytkettynä 200 tilaajaa yksittäisen tilaajan ominaisliikenne on 0.01 erlangia tilaajat toimivat toisistaan riippumattomasti Tällöin käynnissäolevien puhelujen lkm Bin200,0.01 Vastaava oisson-approksimaatio: oisson2.0 istetodennäköisyyksien vertailua: Bin200, oisson
35 oisson-jakauman ominaisuuksia i Summa: Olkoot sm:t 1 oissona 1 ja 2 oissona 2 riippumattomia. Tällöin oisson a1 + a2 ii Satunnaisotanta: Olkoon oissona alkioiden lkm jossakin satunnaisen kokoisessa joukossa. Valitaan näistä alkioista satunnainen osajoukko jokainen yksittäinen alkio otetaan mukaan tn:llä p, jonka kokoa merkitään Y:llä. Tällöin Y oisson pa iii Satunnaislajittelu: Olkoot sm:t ja Y kuten yllä ii. Merk. Z Y. Tällöin Y ja Z ovat riippumattomia ehdolla, että :ä ei tunneta, Z oisson1 p a 35
36 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 36
37 Jatkuvat satunnaismuutujat Määr. Sm on jatkuva continuous, jos on olemassa sellainen integroituva funktio f : R R +, että kaikilla Rpätee F Funktiota f sanotaan sm:n tiheysfunktioksi tf, probability density function Joukkoa S, missä f > 0, sanotaan sm:n arvojoukoksi Ominaisuuksia: : { i { } 0 kaikilla R ii {a < < b} {a b} a b f d iii { } f d } iv { R} - f d S f d 1 f y dy 37
38 Esimerkki f F tiheysfunktio tf kertymäfunktio kf S 1, 3 38
39 Odotusarvo ja muita jakaumaan liittyviä tunnuslukuja Määr. Sm:n odotusarvo mean määritellään kaavalla µ : E[ ]: f d Huom. 1. Odotusarvo on hyvin määritelty vain, jos - f d < Huom. 2. Jos S R + ja 0 f, niin voidaan merkitä E[] Jatkuvan sm:n odotusarvolla on samat ominaisuudet kuin diskreetin sm:n odotusarvolla kts. kalvo 21 Muut jakaumaan liittyvät tunnusluvut varianssi, kovarianssi,... määritellään odotusarvon avulla täsmälleen samoin kuin diskreetin sm:n tapauksessa Näin ollen myös näiden tunnuslukujen ominaisuudet säilyvät kts. kalvot
40 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 40
41 Tasajakauma U a, b, a < b jatkuva vastine nopanheitolle kaikki arvot yhtä todennäköisiä rvojoukko: S a,b Tiheysfunktio tf: Kertymäfunktio kf: F f 1, a, b b a a b a : { }, a, b Odotusarvo: E[] b a /b a d a + b/2 Toinen momentti: E[ 2 ] b a 2 /b a d a 2 + ab + b 2 /3 Varianssi: D 2 [] E[ 2 ] E[] 2 b a 2 /12 41
42 Eksponenttijakauma Ep λ, λ > 0 geometrisen jakauman jatkuva vastine epäonnistuminen tn:llä λdt { t,t+h] > t} λh + oh, missä oh/h 0, kun h 0 rvojoukko: S 0, Tiheysfunktio tf: Kertymäfunktio kf: F f λ λe, > : { } 1 e, > 0 λ 0 Odotusarvo: E[] 0 λ ep λ d 1/λ Toinen momentti: E[ 2 ] 0 λ 2 ep λ d 2/λ 2 Varianssi: D 2 [] E[ 2 ] E[] 2 1/λ 2 42
43 Eksponenttijakauman unohtavaisuusominaisuus Eksponenttijakaumalla on ns. unohtavaisuusominaisuus memoryless property: kaikilla,y 0, Todista! Ohje: Todista ensin, että { > } e λ Sovellus: { > + y > } { > y} Oletetaan, että puhelujen pitoajat ovat eksponentiaalisesti jakautuneita odotusarvonaan h minuuttia. Tarkastellaan puhelua, joka on jo kestänyt ajan minuuttia. Unohtavaisuusominaisuuden nojalla tällä ei ole mitään merkitystä puhelun jäljellä olevan keston kannalta: keskimäärin tällainen puhelu kestää vielä h minuuttia siis + h minuuttia kaikenkaikkiaan! 43
44 Eksponentiaalisesti jakautuneiden satunnaismuuttujien minimi Olkoot sm:t 1 Epλ 1 ja 2 Epλ 2 riippumattomia. Tällöin ja min : min{ 1, 2} Ep λ 1 + λ2 { min i } λi λ1 + λ2, i {1,2} Todista! Ohje: Kts. kalvo 15 44
45 Normeerattu normaalijakauma N0,1 riippumattomien ja samoin jakautuneiden odotusarvona 0 ja varianssina 1 sm:ien normeeratun summan rajatapaus kts. kalvo 48 rvojoukko: S, Tiheysfunktio tf: f ϕ : 1 2π e Kertymäfunktio kf: F Odotusarvo: E[] 0 tf symmetrinen! Varianssi: D 2 [] 1 : { } Φ : ϕ y dy 45
46 Normaalijakauma N µ, σ 2, µ R, σ > 0 jos µ/σ N0,1 rvojoukko: S, Tiheysfunktio tf: Kertymäfunktio kf: f : F ' 1 σ ϕ µ σ F : { } { µ µ } µ Φ Odotusarvo: E[] µ+σe[ µ/σ] µ tf symmetr. µ:n suhteen Varianssi: D 2 [] σ 2 D 2 [ µ/σ] σ 2 σ σ σ 46
47 Normaalijakauman ominaisuuksia i Lineaarimuunos: Olk. Nµ,σ 2 ja α,β R. Tällöin Y : α + β N αµ + β, α 2 σ 2 ii Summa: Olkoot sm:t 1 Nµ 1,σ 2 1 ja 2 Nµ 2,σ 2 2 riippumattomia. Tällöin N µ 1 + µ 2, σ1 + σ 2 iii Otoskeskiarvo: Olkoot sm:t i Nµ,σ 2, i 1, n, riippumattomia ja samoin jakautuneita IID noudattaen normaalijakaumaa. Tällöin niiden keskiarvolle vrt. kalvo 25 pätee n 2 : 1 N, 1 n i µ n σ n i 1 47
48 Keskeinen raja-arvolause KRL Olkoot sm:t 1,, n riippumattomia ja samoin jakautuneita IID odotusarvonaan µ ja varianssinaan σ 2 ja lisäksi kolmas momentti olemassa Keskeinen raja-arvolause: σ 1 / n n µ i.d. N0,1 Seuraus: Suurilla n:n arvoilla n N µ, n 1 σ 2 48
49 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat Muut satunnaismuuttujat 49
50 Muita satunnaismuuttujia uhtaasti diskreettien ja jatkuvien sm:ien lisäksi on olemassa näiden sekamuotoja Esimerkki: Merk. W:llä asiakkaan odotusaikaa M/M/1 jonossa. Sm:n W jakaumalla on ns. atomi nollassa ts. {W 0} 1 ρ>0, mutta muuten jakauma on jatkuva F W 1 1 ρ
51 Sanastoa otosavaruus sample space tapahtuma event todennäköisyys probability ehdollinen tn conditional probability riippumattomuus independence satunnaismuuttuja random variable indikaattori indicator jakauma distribution kertymäfunktio cumulative distribution function diskreetti discrete pistetodennäköisyysfunktio probability mass function odotusarvo mean value epectation varianssi variance kovarianssi covariance hajonta standard deviation variaatiokerroin coefficient of variation suurten lukujen laki law of large numbers jatkuva continuous tiheysfunktio probability density function unohtavaisuusominaisuus memoryless property keskeinen raja-arvolause central limit theorem 51
52 THE END 52
4. Todennäköisyyslaskennan kertausta
 Sisältö Peruskäsitteet Diskreetit satuaismuuttujat Diskreetit jakaumat (lkm-jakaumat) Jatkuvat satuaismuuttujat Jatkuvat jakaumat (aikajakaumat) Muut satuaismuuttujat lueto04.ppt S-38.45 - Liikeeteoria
Sisältö Peruskäsitteet Diskreetit satuaismuuttujat Diskreetit jakaumat (lkm-jakaumat) Jatkuvat satuaismuuttujat Jatkuvat jakaumat (aikajakaumat) Muut satuaismuuttujat lueto04.ppt S-38.45 - Liikeeteoria
TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä
 J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
AB TEKNILLINEN KORKEAKOULU
 B TEKNILLINEN KORKEKOULU Tetoverkkolaboratoro luento05.ppt S-38.45 - Lkenneteoran perusteet - Kevät 00 Ssältö eruskästteet Dskreett satunnasmuuttujat Dskreett jakaumat lkm-jakaumat Jatkuvat satunnasmuuttujat
B TEKNILLINEN KORKEKOULU Tetoverkkolaboratoro luento05.ppt S-38.45 - Lkenneteoran perusteet - Kevät 00 Ssältö eruskästteet Dskreett satunnasmuuttujat Dskreett jakaumat lkm-jakaumat Jatkuvat satunnasmuuttujat
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
30A02000 Tilastotieteen perusteet
 30A02000 Tilastotieteen perusteet Kertaus 1. välikokeeseen Lauri Viitasaari Tieto- ja palvelujohtamisen laitos Kauppatieteiden korkeakoulu Aalto-yliopisto Syksy 2019 Periodi I-II Sisältö Välikokeesta Joukko-oppi
30A02000 Tilastotieteen perusteet Kertaus 1. välikokeeseen Lauri Viitasaari Tieto- ja palvelujohtamisen laitos Kauppatieteiden korkeakoulu Aalto-yliopisto Syksy 2019 Periodi I-II Sisältö Välikokeesta Joukko-oppi
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Todennäköisyyslaskun kertaus. Heliövaara 1
 Todennäköisyyslaskun kertaus Heliövaara 1 Satunnaismuuttujat ja todennäköisyysjakaumat Heliövaara 2 Stunnaismuuttujat ja todennäköisyysjakaumat Jos satunnaisilmiötä halutaan mallintaa matemaattisesti,
Todennäköisyyslaskun kertaus Heliövaara 1 Satunnaismuuttujat ja todennäköisyysjakaumat Heliövaara 2 Stunnaismuuttujat ja todennäköisyysjakaumat Jos satunnaisilmiötä halutaan mallintaa matemaattisesti,
Todennäköisyyden ominaisuuksia
 Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
4.1. Olkoon X mielivaltainen positiivinen satunnaismuuttuja, jonka odotusarvo on
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Otosavaruus ja todennäköisyys Otosavaruus Ë on joukko, jonka alkiot ovat kokeen tulokset Tapahtuma on otosavaruuden osajoukko
 ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
031021P Tilastomatematiikka (5 op) viikko 3
 031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
Ilkka Mellin Todennäköisyyslaskenta. Osa 3: Todennäköisyysjakaumia. Diskreettejä jakaumia. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Diskreettejä jakaumia TKK (c) Ilkka Mellin (2007) 1 Diskreettejä jakaumia >> Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Diskreettejä jakaumia TKK (c) Ilkka Mellin (2007) 1 Diskreettejä jakaumia >> Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia
 Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3A Normaaliapproksimaatio Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3A Normaaliapproksimaatio Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
031021P Tilastomatematiikka (5 op) viikko 2
 031021P Tilastomatematiikka (5 op) viikko 2 Jukka Kemppainen Mathematics Division Satunnaismuuttuja Useissa luonnon- tai teknistieteellisissä sovellutuksissa satunnaiskokeen lopputulos on numeerinen lukuarvo.
031021P Tilastomatematiikka (5 op) viikko 2 Jukka Kemppainen Mathematics Division Satunnaismuuttuja Useissa luonnon- tai teknistieteellisissä sovellutuksissa satunnaiskokeen lopputulos on numeerinen lukuarvo.
Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia TKK (c) Ilkka Mellin (2005) 1 Diskreettejä jakaumia Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma Geometrinen jakauma Negatiivinen
Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia TKK (c) Ilkka Mellin (2005) 1 Diskreettejä jakaumia Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma Geometrinen jakauma Negatiivinen
Todennäköisyysjakaumia
 8.9.26 Kimmo Vattulainen Todennäköisyysjakaumia Seuraavassa esitellään kurssilla MAT-25 Todennäköisyyslaskenta esille tulleita diskreettejä todennäköisyysjakaumia Diskreetti tasajakauma Bernoullijakauma
8.9.26 Kimmo Vattulainen Todennäköisyysjakaumia Seuraavassa esitellään kurssilla MAT-25 Todennäköisyyslaskenta esille tulleita diskreettejä todennäköisyysjakaumia Diskreetti tasajakauma Bernoullijakauma
Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia: Mitä opimme?
 TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
D ( ) Var( ) ( ) E( ) [E( )]
![D ( ) Var( ) ( ) E( ) [E( )] D ( ) Var( ) ( ) E( ) [E( )]](/thumbs/55/37411593.jpg) Mat-.2620 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Diskreettejä jakaumia Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Eksponenttijakauma, Geometrinen jakauma, Hypergeometrinen
Mat-.2620 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Diskreettejä jakaumia Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Eksponenttijakauma, Geometrinen jakauma, Hypergeometrinen
ABTEKNILLINEN KORKEAKOULU
 ABTEKNILLINEN KORKEAKOULU Tietoverkkolaboratorio Sisältö Peruskäsitteitä Poisson-prosessi Luento05.ppt S-38.45 - Liikenneteorian perusteet - Kevät 2005 2 Stokastiset prosessit () Stokastiset prosessit
ABTEKNILLINEN KORKEAKOULU Tietoverkkolaboratorio Sisältö Peruskäsitteitä Poisson-prosessi Luento05.ppt S-38.45 - Liikenneteorian perusteet - Kevät 2005 2 Stokastiset prosessit () Stokastiset prosessit
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3A Satunnaismuuttujien summa ja keskihajonta Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3A Satunnaismuuttujien summa ja keskihajonta Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
5. Stokastiset prosessit (1)
 luento05.ppt S-38.45 - Liikenneteorian perusteet - Kevät 2006 Sisältö Peruskäsitteitä Poisson-prosessi 2 Stokastiset prosessit () Tarkastellaan jotakin (liikenneteorian kannalta tai sitten muuten) kiinnostavaa
luento05.ppt S-38.45 - Liikenneteorian perusteet - Kevät 2006 Sisältö Peruskäsitteitä Poisson-prosessi 2 Stokastiset prosessit () Tarkastellaan jotakin (liikenneteorian kannalta tai sitten muuten) kiinnostavaa
Miten hyvin mallit kuvaavat todellisuutta? Tarvitaan havaintoja.
 Luku 1 Johdanto 1.1 Todennäköisyys ja tilastotiede Kurssi käsittelee todennäköisyyslaskentaa ja tilastotiedettä. Laaditaan satunnaisilmiöille todennäköisyysmalleja. Miten hyvin mallit kuvaavat todellisuutta?
Luku 1 Johdanto 1.1 Todennäköisyys ja tilastotiede Kurssi käsittelee todennäköisyyslaskentaa ja tilastotiedettä. Laaditaan satunnaisilmiöille todennäköisyysmalleja. Miten hyvin mallit kuvaavat todellisuutta?
Inversio-ongelmien laskennallinen peruskurssi Luento 7
 Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio
 Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio KE (2014) 1 Satunnaismuuttujat ja niiden todennäköisyysjakaumat Satunnaismuuttujat
Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio KE (2014) 1 Satunnaismuuttujat ja niiden todennäköisyysjakaumat Satunnaismuuttujat
Matemaattinen tilastotiede. Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto
 Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
8.1 Ehdolliset jakaumat
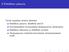 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella:
 8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
11 Raja-arvolauseita ja approksimaatioita
 11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
5/11 6/11 Vaihe 1. 6/10 4/10 6/10 4/10 Vaihe 2. 5/11 6/11 4/11 7/11 6/11 5/11 5/11 6/11 Vaihe 3
 Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
031021P Tilastomatematiikka (5 op) viikot 5 6
 031021P Tilastomatematiikka (5 op) viikot 5 6 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
031021P Tilastomatematiikka (5 op) viikot 5 6 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos)
 J. Virtamo 38.3143 Jonoteoria / Diskreetit jakaumat 1 DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos) Määritelmä Olkoon X diskreetti sm, jonka arvot ovat ei-negatiivisia kokonaislukuja, X {0, 1, 2,...}.
J. Virtamo 38.3143 Jonoteoria / Diskreetit jakaumat 1 DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos) Määritelmä Olkoon X diskreetti sm, jonka arvot ovat ei-negatiivisia kokonaislukuja, X {0, 1, 2,...}.
Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä palamisaikaa?
 21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
Olkoon R S otosavaruuksien R ja S karteesinen tulo: Satunnaismuuttujien X ja Y järjestetty pari (X, Y) määrittelee kaksiulotteisen satunnaismuuttujan:
 Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
Odotusarvo. Odotusarvon ominaisuuksia Satunnaismuuttujien ominaisuuksia 61
 3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos)
 J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Kertymäfunktio. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/73 Johdanto Moderni yhteiskunta: Todellisuuden tilastollinen malli Kolme
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/73 Johdanto Moderni yhteiskunta: Todellisuuden tilastollinen malli Kolme
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-200 Todennäköisyyslaskenta Tentti 29.04.20 / Kimmo Vattulainen Funktiolaskin sallittu.. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi kuutosen. A aloittaa
MAT-200 Todennäköisyyslaskenta Tentti 29.04.20 / Kimmo Vattulainen Funktiolaskin sallittu.. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi kuutosen. A aloittaa
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia TKK (c) Ilkka Mellin (2006) 1 Jatkuvia jakaumia >> Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia TKK (c) Ilkka Mellin (2006) 1 Jatkuvia jakaumia >> Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen
Tilastollinen päättely II, kevät 2017 Harjoitus 1A
 Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
D ( ) E( ) E( ) 2.917
 Mat-2.091 Sovellettu todennäköisyyslasku 4. harjoitukset/ratkaisut Aiheet: Diskreetit jakaumat Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen jakauma, Kertymäfunktio,
Mat-2.091 Sovellettu todennäköisyyslasku 4. harjoitukset/ratkaisut Aiheet: Diskreetit jakaumat Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen jakauma, Kertymäfunktio,
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg 1 Todennäköisyys Satunnaismuuttujat Keskeinen raja-arvolause Aalto-yliopisto. tammikuuta 015 Kaksiulotteiset satunnaismuuttujat
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg 1 Todennäköisyys Satunnaismuuttujat Keskeinen raja-arvolause Aalto-yliopisto. tammikuuta 015 Kaksiulotteiset satunnaismuuttujat
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg Aalto-yliopisto 2. tammikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0502 Todennäköisyyslaskennan ja tilastotieteen
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg Aalto-yliopisto 2. tammikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0502 Todennäköisyyslaskennan ja tilastotieteen
Tilastollinen aineisto Luottamusväli
 Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
5 Tärkeitä yksiulotteisia jakaumia
 5 Tärkeitä yksiulotteisia jakaumia Jakaumista löytyy lisätietoja ja kuvaajia Wikipediasta. Kirjallisuudessa käytetään useille näistä jakaumista monia erilaisia parametrointeja. Kussakin lähteessä käytetty
5 Tärkeitä yksiulotteisia jakaumia Jakaumista löytyy lisätietoja ja kuvaajia Wikipediasta. Kirjallisuudessa käytetään useille näistä jakaumista monia erilaisia parametrointeja. Kussakin lähteessä käytetty
Todennäköisyyslaskenta I. Ville Hyvönen
 Todennäköisyyslaskenta I Ville Hyvönen Kesä 2016 Sisältö 1 Todennäköisyys 3 1.1 Klassinen todennäköisyys............................ 3 1.2 Kombinatoriikkaa................................ 6 1.2.1 Tuloperiaate...............................
Todennäköisyyslaskenta I Ville Hyvönen Kesä 2016 Sisältö 1 Todennäköisyys 3 1.1 Klassinen todennäköisyys............................ 3 1.2 Kombinatoriikkaa................................ 6 1.2.1 Tuloperiaate...............................
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Tilastotieteen kertaus. Vilkkumaa / Kuusinen 1
 Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Luento KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja
 1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-2.090 Sovellettu todennäköisyyslasku A Harjoitus 4 (vko 41/2003) (Aihe: diskreettejä satunnaismuuttujia ja jakaumia, Laininen luvut 4.1 4.7) 1. Kone tekee
TKK / Systeemianalyysin laboratorio Nordlund Mat-2.090 Sovellettu todennäköisyyslasku A Harjoitus 4 (vko 41/2003) (Aihe: diskreettejä satunnaismuuttujia ja jakaumia, Laininen luvut 4.1 4.7) 1. Kone tekee
Moniulotteiset satunnaismuuttujat ja jakaumat
 Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Harjoitus 2: Matlab - Statistical Toolbox
 Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Todennäköisyyslaskenta IIa, syyslokakuu 2019 / Hytönen 2. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syyslokakuu 019 / Hytönen. laskuharjoitus, ratkaisuehdotukset 1. Kurssilla on 0 opiskelijaa, näiden joukossa Jutta, Jyrki, Ilkka ja Alex. Opettaja aikoo valita umpimähkään opiskelijan
Todennäköisyyslaskenta IIa, syyslokakuu 019 / Hytönen. laskuharjoitus, ratkaisuehdotukset 1. Kurssilla on 0 opiskelijaa, näiden joukossa Jutta, Jyrki, Ilkka ja Alex. Opettaja aikoo valita umpimähkään opiskelijan
Johdatus todennäköisyyslaskentaan Kertymäfunktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
Mat Sovellettu todennäköisyyslasku A. Moniulotteiset jakaumat. Avainsanat:
 Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015
 12.1.2016/1 MTTTP5, luento 12.1.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
12.1.2016/1 MTTTP5, luento 12.1.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Bayesläiset piste- ja väliestimaatit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Bayesläiset piste- ja väliestimaatit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia TKK (c) Ilkka Mellin (2005) 1 Jatkuvia jakaumia Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen raja-arvolause TKK (c) Ilkka Mellin
Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia TKK (c) Ilkka Mellin (2005) 1 Jatkuvia jakaumia Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen raja-arvolause TKK (c) Ilkka Mellin
Satunnaismuuttujien summa ja keskiarvo
 Luku 5 Satunnaismuuttujien summa ja keskiarvo Lasse Leskelä Aalto-yliopisto 21. syyskuuta 2017 5.1 Satunnaismuuttujien summa Satunnaismuuttujien summa S n = X 1 + +X n ja keskiarvo n 1 S n ovat satunnaismuuttujia,
Luku 5 Satunnaismuuttujien summa ja keskiarvo Lasse Leskelä Aalto-yliopisto 21. syyskuuta 2017 5.1 Satunnaismuuttujien summa Satunnaismuuttujien summa S n = X 1 + +X n ja keskiarvo n 1 S n ovat satunnaismuuttujia,
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
Luku 10. Bayesläiset estimaattorit Bayesläiset piste-estimaatit. Lasse Leskelä Aalto-yliopisto 18. lokakuuta 2017
 Luku 1 Bayesläiset estimaattorit Lasse Leskelä Aalto-yliopisto 18. lokakuuta 217 1.1 Bayesläiset piste-estimaatit Tarkastellaan datalähdettä, joka tuottaa tiheysfunktion f(x θ) mukaan jakautuneita riippumattomia
Luku 1 Bayesläiset estimaattorit Lasse Leskelä Aalto-yliopisto 18. lokakuuta 217 1.1 Bayesläiset piste-estimaatit Tarkastellaan datalähdettä, joka tuottaa tiheysfunktion f(x θ) mukaan jakautuneita riippumattomia
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3
 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
Tutkimustiedonhallinnan peruskurssi
 Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
TKK @ Ilkka Mellin (2008) 1/5
 Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Osa 1: Todennäköisyys ja sen laskusäännöt. Todennäköisyyden aksioomat
 Ilkka Mellin Todennäköisyyslaskenta Osa 1: Todennäköisyys ja sen laskusäännöt Todennäköisyyden aksioomat TKK (c) Ilkka Mellin (2007) 1 Todennäköisyyden aksioomat >> Todennäköisyyden määritteleminen Todennäköisyyden
Ilkka Mellin Todennäköisyyslaskenta Osa 1: Todennäköisyys ja sen laskusäännöt Todennäköisyyden aksioomat TKK (c) Ilkka Mellin (2007) 1 Todennäköisyyden aksioomat >> Todennäköisyyden määritteleminen Todennäköisyyden
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I
 HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Tehtävä 1 on klassikko. 1. Tässä tehtävässä tapahtumat A ja B eivät välttämättä
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Tehtävä 1 on klassikko. 1. Tässä tehtävässä tapahtumat A ja B eivät välttämättä
5. laskuharjoituskierros, vko 8, ratkaisut
 Mat-.09 Sovellettu todennäköisyyslasku, kevät -05 5. laskuharjoituskierros, vko 8, ratkaisut D. Eräässä maata kiertävällä radalla olevassa satelliitissa on ilmaisin, jonka elinikä X yksikkönä vuosi noudattaa
Mat-.09 Sovellettu todennäköisyyslasku, kevät -05 5. laskuharjoituskierros, vko 8, ratkaisut D. Eräässä maata kiertävällä radalla olevassa satelliitissa on ilmaisin, jonka elinikä X yksikkönä vuosi noudattaa
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
&idx=2&uilang=fi&lang=fi&lvv=2015
 20.10.2015/1 MTTTP5, luento 20.10.2015 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
20.10.2015/1 MTTTP5, luento 20.10.2015 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015
 25.10.2016/1 MTTTP5, luento 25.10.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
25.10.2016/1 MTTTP5, luento 25.10.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg Aalto-yliopisto 2. tammikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0502 Todennäköisyyslaskennan ja tilastotieteen
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa I G. Gripenberg Aalto-yliopisto 2. tammikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0502 Todennäköisyyslaskennan ja tilastotieteen
Satunnaismuuttujien tunnusluvut
 Sisältö 1 Johdanto 1 1.1 Todennäköisyys ja tilastotiede.................. 1 1.2 Havaitut frekvenssit ja empiiriset jakaumat........... 1 1.3 Todennäköisyysmallit....................... 4 1.3.1 Satunnaiskoe.......................
Sisältö 1 Johdanto 1 1.1 Todennäköisyys ja tilastotiede.................. 1 1.2 Havaitut frekvenssit ja empiiriset jakaumat........... 1 1.3 Todennäköisyysmallit....................... 4 1.3.1 Satunnaiskoe.......................
Verkot ja todennäköisyyslaskenta Verkko Verkko eli graafi muodostuu pisteiden joukosta V, särmien joukosta A ja insidenssikuvauksesta : A V V jossa
 Mat-.6 Sovellettu todennäköisyyslaskenta B Mat-.6 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Verkot ja todennäköisyyslaskenta Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio Jakaumien
Mat-.6 Sovellettu todennäköisyyslaskenta B Mat-.6 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Verkot ja todennäköisyyslaskenta Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio Jakaumien
