5 Tärkeitä yksiulotteisia jakaumia
|
|
|
- Marja Hiltunen
- 5 vuotta sitten
- Katselukertoja:
Transkriptio
1 5 Tärkeitä yksiulotteisia jakaumia Jakaumista löytyy lisätietoja ja kuvaajia Wikipediasta. Kirjallisuudessa käytetään useille näistä jakaumista monia erilaisia parametrointeja. Kussakin lähteessä käytetty parametrointi paljastuu tavallisesti vasta tutkimalla lähemmin siinä käytettyjä kaavoja. Eri lähteet käyttävät jakaumille eri tunnuksia.
2 5.1 Diskreettejä jakaumia Kaikilla tämän jakson jakaumilla on se ominaisuus, että niitä noudattavat satunnaismuuttujat voivat saada vain kokonaislukuarvoja. Tämä on tyypillistä sovelluksissa. Binomijakauma Hypergeometrinen jakauma Geometrinen jakauma Negatiivinen binomijakauma Poissonin jakauma
3 5.1.1 Binomijakauma Synty Onnistumisten lkm n-kertaisessa toistetussa Bernoullin kokeessa, kun onnistumistn on p. Tunnus X Bin(n, p), jossa n 1 kokonaisluku (otoskokoparametri) ja 0 p 1 (onnistumistn; todennäköisyysparametri). Ptnf f (x) = f (x n, p) = ( ) n p x (1 p) n x, x x = 0, 1,..., n.
4 Binomijakauma (jatkoa) Odotusarvo, varianssi ja momenttiemäfunktio EX = np, var X = np(1 p), M(t) = (pe t +1 p) n. Yhteyksiä Bin(1, p) on Bernoulli(p). Yhteenlaskuominaisuus Jos X Bin(m, p) ja Y Bin(n, p) (sama onnistumistn) ja X Y, niin X + Y Bin(n + m, p). Yhteenlaskuominaisuuden voi perustella joko toistokoetulkinnan avulla tai momenttiemäfunktiota tarkastelemalla.
5 Esimerkki: binomijakauma ja poiminta takaisinpanolla Olkoon laatikossa N palloa, joista 0 K N on valkoista ja loput mustia. Laatikosta poimitaan umpimähkään n palloa takaisinpanolla. Tällöin nostettujen valkoisten pallojen lukumäärällä X on jakauma Bin(n, K/N).
6 5.1.2 Hypergeometrinen jakauma Synty Laatikossa on N palloa, joista 0 K N on valkoista ja loput ovat mustia. Laatikosta nostetaan umpimähkäisesti n N palloa ilman takaisinpanoa. Ptnf Jos X kertoo, kuinka moni nostetuista palloista on valkoinen, niin X :n ptnf on ( K ) ( N K ) x n x f (x) = f (x N, K, n) = ( N, x = 0, 1,..., n. n) Tämä on hypergeometrinen jakauma parametreilla N, K ja n. Muista, että ( ) m k = 0 ellei 0 k m. Tämän takia f (x N, K, n) 0 vain, kun 0 x min(n, K) ja n x N K.
7 Hypergeometrinen jakauma: ptnf:n johto kombinatoriikan tuloperiaattella Ajattele, että pallot on numeroitu, mutta että ainoastaan pallon väristä ollaan kiinnostuneita. Symmetrisiä alkeistapauksia ovat N pallon n-osajoukot, joiden lukumäärä on ( N n). Sellaisen osajoukon valinta, jossa on x valkoista ja n x mustaa palloa, voidaan ajatella tehtävän kahdessa vaiheessa. 1 valitaan x:n valkoisen pallon osajoukko K valkoisesta pallosta: eri mahdollisuuksia on ( ) K x 2 valitaan n x mustan pallon osajoukko N K mustasta pallosta: eri mahdollisuuksia on ( ) N K n x. f (x) saadaan jakamalla suotuisten alkeistapauksien lukumäärä kaikkien alkeistapausten lukumäärällä.
8 Huomautuksia hypergeometrisesta jakaumasta Hypergeometrisen jakauman käsittely on hankalahkoa. Suurten populaatioiden tapauksessa (N suuri ja n N) sitä mielellään approksimoidaan vastaavalla binomijakaumalla Bin(n, K/N), joka syntyisi otannasta takaisinpanolla. Odotusarvo ja varianssi ovat (vrt. binomijakauman Bin(n, K/N) kaavoihin) EX = n K N, var X = n K N (1 K N ) N n N 1. Nämä tulokset johdetaan esim. Tuomisen kirjassa.
9 Lisää huomautuksia Binomijakauma ja hypergeometrinen jakauma ovat lähisukulaisia. Hypergeometrisella jakaumalla ja seuraavaksi esitettävällä geometrisella jakaumalla ei ole helposti huomattavaa yhteyttä. Hypergeometrisen jakauman nimen tarkka alkuperä on hieman hämärän peitossa, mutta... se ilmeisesti johtuu jakauman tietyistä löyhistä yhteyksistä ns. hypergeometriseen funktioon, joka on eräs klassinen erikoisfunktio. (Historiaa: Wallis, Euler, Pfaff, Gauss...)
10 5.1.3 Geometrinen jakauma Synty Toistetaan riippumattomasti Bernoullin koetta, jossa onnistumistn on 0 < p < 1. Olkoon X = epäonnistumisten lkm ennen ensimmäistä onnistumista. Tällöin X :llä on geometrinen jakauma parametrilla p, eli X Geom(p).
11 Geometrinen jakauma (jatkoa) Ptnf f (x) = f (x p) = P(X = x) = p (1 p) x, x = 0, 1, 2,... Perustelu Epäonnistumisia ennen ensimmäistä onnistumista on X = x kpl jos ja vain jos koetta vastaavat riippumattomat Bernoullin muuttujat Y 1,..., Y x, Y x+1 saavat arvot Y 1 = 0, Y 2 = 0,..., Y x = 0 ja Y x+1 = 1. Riippumattomuuden nojalla tämän tapahtuman tn on (1 p) x p.
12 Geometrinen jakauma (jatkoa) Tarkistus Se, että f (x) = p (1 p) x on ptnf voidaan tarkistaa geometrisen sarjan avulla, r j = 1 + r + r 2 + = 1, r < 1, 1 r j=0 jonka seurauksena 1 f (x) = p 1 (1 p) = 1. x=0 Lisäksi jokainen termeistä f (x) = p (1 p) x on positiivinen. Momenttiemäfunktio saadaan geometrisen sarjan avulla, p M(t) =, t < ln(1 p). 1 (1 p)et
13 Geometrinen jakauma (jatkoa) Odotusarvo ja varianssi lasketaan helposti momenttiemäfunktiosta, EX = 1 p p, var X = 1 p p 2. Huomautus Toisinaan geometrinen jakauma määritellään edellisesti poikkeavasti niin, että se on satunnaismuuttujan Y jakauma, jossa Y = sen toiston järjestysnumero, jolla onnistutaan ensimmäisen kerran.
14 5.1.4 Negatiivinen binomijakauma Synty Toistetaan riippumattomasti Bernoullin koetta, jossa onnistumistn on 0 < p < 1. Olkoon r > 0 kokonaisluku, ja tarkastellaan sm:a X = epäonnistumisten lkm, ennen kuin onnistutaan r:nnen kerran. Parametrit ovat p ja r; geometrinen jakauma saadaan, kun r = 1.
15 Negatiivisen binomijakauman ptnf:n johto Tapahtuma X = x eli että on x epäonnistumista ennen r:ttä onnistumista on sama kuin että r 1 + x ensimmäisessä toistossa epäonnistutaan x kertaa ja onnistutaan r 1 kertaa ja toistossa numero r + x onnistutaan. Koska toistot ovat riippumattomia, on ( ) r + x 1 f (x) = f (x r, p) = p r (1 p) x, x = 0, 1, 2,... x Tässä p r (1 p) x on sellaisen jonon onnistumisia ja epäonnistumisia tn, joka toteuttaa ylläolevat ehdot, ja binomikerroin kertoo tällaisten jonojen lukumäärän.
16 Negatiivisen binomijakauman momenttiemäfunktio Momenttiemäfunktio saadaan suoraviivaisesti binomisarjan avulla ( ) r + x 1 ( M(t) = p r (1 p) x e xt p ) r =, x 1 (1 p)e t x=0 kun t < ln(1 p).
17 Huomautuksia negatiivisesta binomijakaumasta Geometrinen jakauma on negatiivisen binomijakauman erikoistapaus. Sen sijaan binomijakaumalla ja negatiivisella binomijakaumalla ei ole mitään ilmeistä yhteyttä keskenään.
18 Lisää huomautuksia negatiivisesta binomijakaumasta Negatiivinen binomijakauma voidaan yleistää tilanteeseen, jossa r > 0 ei ole kokonaisluku. Tällöin toistokoetulkinta menetetään. Negatiivista binomijakaumaa käytetään usein Poissonin jakauman sijasta lukumäärien mallina, jos aineistossa niillä näyttää olevan suurempi varianssi kuin mitä Poissonin jakaumalla olisi. Laskemme myöhemmin kurssilla negatiivisen binomijakauman odotusarvon ja varianssin, mutta täysin erilaisella tekniikalla kuin mikä selitetään tässä jaksossa luentomonisteessa.
19 5.1.5 Poissonin jakauma Tunnus X Poi(θ), jossa θ > 0. Ptnf θ θx f (x) = f (x θ) = e, x = 0, 1, 2,... x! Tarkistus Tämä on ptnf, sillä kaikki arvot ovat ei-negatiivisia, ja eksponenttifunktion sarjakehitelmän mukaan e u = exp(u) = j=0 u j j!, u R. Mikäli u > 0, niin sarjan kaikki termit ovat positiivisia. Siksi luvut e θ θ j /j! muodostavat pistetodennäköisyysfunktion, kun j = 0, 1, 2,....
20 Poissonin jakauma (jatkoa) Momenttiemäfunktio saadaan eksponenttifunktion sarjakehitelmän avulla, M(t) = x=0 e xt θ θx e x! = exp(θ(et 1)). Odotusarvo ja varianssi saadaan tästä helposti derivoimalla, EX = var X = θ. Yhteenlaskuominaisuus Jos X Poi(θ 1 ) ja Y Poi(θ 2 ), ja X Y, niin M X +Y (t) = M X (t) M Y (t) = exp((θ 1 + θ 2 )(e t 1)), joten X + Y Poi(θ 1 + θ 2 ).
21 Poissonin prosessi: johdattelua Poissonin prosessilla mallinnetaan diskreettejä tapahtumia jatkuvalla aika- tai pituusvälillä tai tasossa tai avaruudessa. Sillä saateetaisiin mallintaa esimerkiksi sitä, kuinka monta asiakasta palvelupisteeseen saapuu tietyllä aikavälillä, kuinka monta fotonia osuu tiettyyn filmin alueeseen, kuinka monta valkosolua löytyy tietystä veripisarasta.
22 Poissonin prosessi Mikäli välin pituus (tai tasoalueen pinta-ala, avaruuden osan tilavuus) on s yksikköä, niin Poissonin prosessissa siinä havaittavien tapahtumien lukumäärällä on Poissonin jakauma Poi(sλ). Lisäksi erillisillä väleillä (tasoalueilla, avaruuden osilla) havaittavat lukumäärät ovat keskenään riippumattomia. Keskimääräinen tapahtumien lukumäärä yhtä (pituus-, pinta-ala- tai tilavuus-)yksikköä kohti on sλ/s = λ. Ts. λ > 0 eli Poissonin prosessin intensiteetti on tapahtumien odotusarvo yhtä (pituus-, pinta-ala-, tilavuus-)yksikköä kohti.
23 5.2 Gamma- ja beetafunktio Eulerin gammafunktio Γ voidaan määritellä positiivisilla argumenteilla integraalilla Γ(t) = 0 x t 1 e x dx, t > 0. (5.3) Jos t 1, niin tämä integraali on epäoleellinen vain ylärjallaan, mutta jos 0 < t < 1, niin integraali on epäoleellinen myös alarajalla, koska tällöin integrandi kasvaa rajatta, kun t lähestyy nollaa. Integraali (5.3) on äärellinen jos ja vain jos t > 0.
24 Gammafunktion Γ(t) = 0 x t 1 e x dx ominaisuuksia Osittaisintegroinnilla nähdään, että Γ(t + 1) = 0 x t e x dx = 0 / x t e x + t 0 x t 1 e x dx. Tämän takia Γ(t + 1) = t Γ(t), kaikilla t > 0. (5.4) Koska lisäksi Γ(1) = 1, niin kokonaislukuargumenteilla n pätee Γ(n) = (n 1)!, kun n = 1, 2, 3,... (5.5) Tässä mielessä gammafunktio on kertoman yleistys.
25 Standardinormaalijakauman normalisointivakio Tarkastellaan integraalia I = e 1 2 x2 dx. Ottamalla huomioon, että integrandi on parillinen funktio ja tekemällä sitten muuttujanvaihto t = 1 2 x 2, saadaan I = 2 0 e 1 2 x2 dx = 2 Kohta nähdään, että Γ( 1 2 ) = π. Tämän jälkeen on tarkistettu, että 0 1 2π e 1 2 x2 e t 1 dt = 2 Γ( 1 ). (5.6) 2t 2 on tiheysfunktio, standardinormaalijakauman tiheysfunktio.
26 Beetafunktion esitys gammafunktion avulla Luentomonisteessa näytetään napakoordinaattien ja muuttujanvaihtojen avulla, että B(a, b) = Γ(a) Γ(b) Γ(a + b), jossa B(a, b) on (Eulerin) beetafunktio, joka määritellään integraalina B(a, b) = 1 0 u a 1 (1 u) b 1 du, a, b > 0. (5.7) Integraali (5.7) on äärellinen jos ja vain jos a > 0 ja b > 0. Erityisesti B( 1 2, 1 2 ) = (Γ( 1 2 ))2.
27 Γ( 1 2 ) = π Määritelmän nojalla B( 1 2, ) = u 1 2 (1 u) 1 2 du Sijoituksella u = sin 2 θ saadaan B( 1 2, 1 2 ) = π sin 2 θ 1 2 sin θ cos θ dθ = π. cos 2 θ Koska Γ( 1 2 ) = B( 1 2, 1 2 ), saadaan Γ( 1 2 ) = π.
28 5.3 Jatkuvia jakaumia Skaalaus ja siirto Tasajakauma Eksponenttijakauma Gammajakauma Beetajakauma Normaalijakauma Normaalijakaumasta johdettuja jakaumia: χ 2 -jakauma t-jakauma F -jakauma.
29 5.3.1 Skaalaus ja siirto Jos sm:lla Z on jatkuva jakauma tiheysfunktiolla f 0, ja sm X määritellään kaavalla X = µ + σz, σ > 0, niin tiheysfunktion muuntokaavan nojalla sm:n X tf on f X (x µ, σ) = 1 ( ) x µ σ f 0. σ Jos erityisesti σ = 1 ja µ = 0, niin X :n tf on f 0. Tällä tavoin saadaan perhe jakaumia, jossa parametria µ kutsutaan sijaintiparametriksi (engl. location parameter) ja parametria σ > 0 skaalaparametriksi (engl. scale parameter).
30 Skaalaus: skaalaparametri vai rate-parametri? Erityisesti jos µ = 0, jolloin X = σ Z, saadaan jakaumaperhe, jonka tiheysfunktiot ovat muotoa 1 σ f 0(x/σ), σ > 0. Jotkin jakaumaperheet parametroidaan muodossa λ f 0 (λx), λ > 0, jossa f 0 on tf. Tällöin σ = 1/λ on skaalaparametri, ja parametria λ voidaan kutsua rate-parametriksi. Sana rate voidaan kääntää, asiayhteydestä riippuen, esim. sanoilla intensiteetti, vauhti, osuus, aste, taajuus jne.
31 5.3.2 Tasajakauma Jos a < b, niin välin (a, b) tasajakaumalla, X U(a, b) on tiheysfunktio f (x) = f (x a, b) = 1 b a 1 (a,b)(x), x R. Kaksi ensimmäistä momenttia lasketaan helposti integroimalla, EX = 1 2 (a + b), EX 2 = 1 3 (a2 + ab + b 2 ), Tästä nähdään, että var X = (b a)2. 12
32 5.3.3 Eksponenttijakauma X noudattaa eksponenttijakaumaa parametrilla λ > 0, eli X Exp(λ), jos sen tf on f (x) = f (x λ) = λe λx, x > 0. Tässä λ on rate-parametri. Jakauman odotusarvo ja varianssi ovat Momenttiemäfunktio on EX = 1 λ, var X = 1 λ 2 = (EX )2. M(t) = λ λ t, t < λ. Usein parametriksi valitaan λ:n sijasta odotusarvo, θ = 1/λ. Tällöin varianssi on θ 2.
33 Eksponenttijakauman muistinmenetysominaisuus Eksponenttijakaumaa käytetään usein komponentin eliniän mallina. Tällöin tehdään se oletus, että komponentti ei kulu käytössä. Eksponenttijakaumalla on nimittäin ns. muistinmenetysominaisuus. Oletetaan, että komponentin elinikä X Exp(λ). Lasketaan todennäköisyys, että elinikä on suurempi kuin x + h, jos se on suurempi kuin x, kun x, h > 0. P(X > x + h X > x) = = 1 F (x + h) 1 F (x) P(X > x + h ja X > x) P(X > x) = e λ(x+h) e λx = P(X > x + h) P(X > x) = e λh = P(X > h). Todennäköisyys ei riipu siitä, kuinka kauan komponenttia on jo käytetty.
34 5.3.4 Gammajakauma Gammafunktion määritelmästä (5.3) nähdään, että g(x) = 1 Γ(α) x α 1 e x, x > 0 on tiheysfunktio, kun parametri α > 0. Kutsumme vastaavaa jakaumaa gammajakaumaksi parametreilla α ja 1, ja merkitsemme sitä tunnuksella Gam(α, 1).
35 Gammajakauman Gam(α, λ) tiheysfunktio Jos α > 0, λ > 0 ja Z Gam(α, 1), niin tällöin määrittelemme, että satunnaismuuttuja X = Z/λ noudattaa gammajakaumaa parametrein α > 0 (muotoparametri) ja λ > 0 (rate-parametri). Tällöin X :llä on tiheysfunktio f (x α, λ) = λ g(λx), jossa g on jakauman Gam(α, 1) tiheysfunktio.
36 Gammajakauman Gam(α, λ) tiheysfunktio 2 Helpolla laskulla nähdään, että gammajakauman Gam(α, λ) tiheysfunktio on f (x) = f (x α, λ) = λα Γ(α) x α 1 e λx, x > 0 (5.11) Huomaa, että gammajakauma ja gammafunktio ovat eri asioita; gammajakauman tiheysfunktion lausekkeessa esiintyy gammafunktio.
37 Integroidaan tilastotieteilijän tapaan Jakauman Gam(α, λ) momenttiemäfunktio saadaan laskettua, kun huomataan, että siinä tarvittava integraali on erään toisen gammajakauman normalisointivakio, e xt 0 λ α M(t) = Ee Xt = Γ(α) x α 1 e λx dx λ α (λ t) α = (λ t) α x α 1 e (λ t)x dx 0 Γ(α) ( ) λ α =, t < λ. λ t Tässä laskussa integroimme kuten tilastotietielijä. Tunnistamme että integrandi on vakiota vaille tutun jakauman tiheysfunktio, jota integroidaan kantajansa yli. Tällöin osaamme suoraan kirjoittaa lausekkeen integraalin arvolle katsomalla ko. tiheysfunktion normalisointivakiota.
38 Gammajakauman Gam(α, λ) ominaisuuksia Odotusarvo ja varianssi Momenttiemäfunktion lausekkeesta nähdään, että EX = α λ, var X = α λ 2. Yhteyksiä muihin jakaumiin Exp(λ) on Gam(1, λ). χ 2 n (khiin neliön jakauma n:llä vapausasteella) on Gam(n/2, 1/2). Yhteenlaskuominaisuus Jos X Gam(α 1, λ) ja Y Gam(α 2, λ) (jälkimmäinen parametri sama) ja X Y, niin X + Y Gam(α 1 + α 2, λ).
39 Varoitus gammajakauma parametroinneista Gammajakauma parametroidaan usein myös käyttämällä parametreja α ja skaalaparametria 1/λ. Kummassakin parametroinnissa jälkimmäistä parametria (rate-parametri tai skaalaparametri) on tapana merkitä symbolilla β. Se, kummasta parametroinnista on kyse selviää, mikäli jakauman tiheysfunktion tai odotusarvon kaava annetaan.
40 5.3.5 Beetajakauma Kun α, β > 0, niin beetafunktion määritelmän nojalla funktio f (x) = f (x α, β) = on tiheysfunktio. 1 B(α, β) x α 1 (1 x) β 1, 0 < x < 1, Ko. jakauma on beetajakauma parametrein α ja β. Käytämme sille tunnusta Be(α, β). Välin (0, 1) tasajakauma U(0, 1) on sama kuin Be(1, 1).
41 Beetajakauman ominaisuuksia Beetajakauman momentit on helppo laskea, sillä ne saadaan suoraan erään toisen beetajakauman normalisointivakiosta (ts. integroimalla kuten tilastotieteilijä). Jos r > 0, on Erityisesti Tästä EX = EX r = α α + β, EX 2 = var X = EX 2 (EX ) 2 = B(α + r, β). B(α, β) α(α + 1) (α + β)(α + β + 1). αβ (α + β) 2 (α + β + 1).
42 5.3.6 Normaalijakauma Standardinormaalijakaumaa N(0, 1) noudattavan sm:n Z N(0, 1) tf on f Z (z) = φ(z) = 1 2π exp( 1 2 z2 ), z R. (5.12) Standardinormaalijakuman tiheysfunktiolle käytetään yleisesti merkintää φ ja sen kertymäfunktiolle merkintää Φ. Tämä on tiheysfunktio sen takia, että funktio on ei-negatiivinen (peräti aidosti positiivinen) ja sen integraali koko reaaliakselin yli on yksi.
43 Standardinormaalijakauman N(0, 1) momenttiemäfunktio M Z (t) = Ee tz = 1 2π exp( 1 2 z2 + tz) dz. Täydennetään eksponenttifunktion argumentti neliöksi, 1 2 z2 + tz = 1 2 (z t) t2, minkä jälkeen (sijoituksella u = z t) nähdään, että M Z (t) = exp( t2 ) exp ( 12 ) u2 du = exp( 1 2π 2 t2 ). Laskemalla kumulanttiemäfunktion K Z (t) = 1 2 t2 derivaatat nähdään, että EZ = 0, var Z = 1.
44 Normaalijakauma N(µ, σ 2 ) Sm X noudattaa normaalijakaumaa parametrein µ, σ 2, eli X N(µ, σ 2 ), jos se voidaan esittää muodossa Tällöin X = µ + σ Z, Z N(0, 1). (5.13) EX = µ, var X = σ 2 var Z = σ 2, joten µ on N(µ, σ 2 )-jakauman odotusarvo ja σ 2 sen varianssi. Jos σ > 0, niin jakauman tf on f X (x) = 1 ( ) x µ σ φ = 1 σ σ 1 2π exp ( 1 2 (x µ) 2 σ 2 ), x R. (5.14)
45 Normaalijakauman ominaisuuksia N(µ, σ 2 )-jakauman momenttiemäfunktio on M X (t) = M µ+σz (t) = E exp((µ + σz)t) = exp(µt) M Z (σt) = exp(µt σ2 t 2 ). (5.15) Yhteenlaskuominaisuus. Jos X N(µ 1, σ 2 1 ) ja Y N(µ 2, σ 2 2 ), ja ne ovat riippumattomia, niin M X +Y (t) = M X (t) M Y (t) = exp((µ 1 + µ 2 )t (σ2 1 + σ 2 2)t 2 ), joten X + Y N(µ 1 + µ 2, σ σ2 2 ).
46 5.3.7 Normaalijakaumasta johdettuja jakaumia Määritelmä 5.1 (Khiin neliön jakauma) Jos X 1,..., X n N(0, 1) ja ne ovat riippumattomia, niin niiden neliöiden summalla sanotaan olevan χ 2 n-jakauma eli khiin neliön jakauma n:llä vapausasteella (tai vapausasteluvulla n). Seuraavaksi nähdään, että khiin neliön jakauma on erikoistapaus gammajakaumasta.
47 χ 2 yhdellä vapausasteella on Gam( 1 2, 1 2 ) Olkoon X N(0, 1), ja Y = X 2. Tietysti Y 0. Jos y 0, niin F Y (y) = P(Y y) = P(X 2 y) = P( y X y) = Φ( y) Φ( y). F Y (y) = 0, jos y < 0. Kf F Y on jatkuva pisteessä y = 0 ja jatkuvasti derivoituva, kun y 0. Jakauma on jatkuva (ks. lause 2.7), joten tf:n saa laskea derivoimalla kf:n. Jos y > 0, niin f Y (y) = [φ( y) + φ( y)] = ( 1 2 )1/2 Γ( 1 2 ) y e 1 2 y 1 2 y
48 χ 2 n on Gam( n 2, 1 2 ) Olk. X 1,..., X n N(0, 1) riippumattomia. Gammajakauman yhteenlaskuominaisuuden perusteella X X 2 2 Gam( , 1 2 ), (X X 2 2 ) + X 2 3 Gam( , 1 2 ), samaa päättelyä jatkamalla X X 2 n Gam( n 2, 1 2 ). Ts. χ 2 n on sama kuin Gam( n 2, 1 2 ). Yleistys. Jos ν > 0 ei ole kokonaisluku, niin määrittelemme, että χ 2 ν-jakauma on gammajakauma Gam( ν 2, 1 2 ).
49 t-jakauma Määritelmä 5.2 (t-jakauma) Jos Z N(0, 1) ja V χ 2 ν (jollekin ν > 0) ja Z V, niin satunnaismuuttujalla T = Z V /ν on jakauma, jota kutsutaan (Studentin) t-jakaumaksi ν:llä vapausasteella tai vapausasteluvulla ν (engl. degrees of freedom, df), eli T t ν.
50 F -jakauma Määritelmä 5.3 (F-jakauma.) Jos U χ 2 k ja V χ2 m ja U V, niin sm:lla Y = U/k V /m on jakauma, jota kutsutaan F -jakaumaksi parametreilla k (osoittajan vapausasteluku) ja m (nimittäjän vapausasteluku), eli Y F k,m.
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia
 Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Satunnaismuuttujien muunnokset ja niiden jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia TKK (c) Ilkka Mellin (2006) 1 Jatkuvia jakaumia >> Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Jatkuvia jakaumia TKK (c) Ilkka Mellin (2006) 1 Jatkuvia jakaumia >> Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen
Todennäköisyysjakaumia
 8.9.26 Kimmo Vattulainen Todennäköisyysjakaumia Seuraavassa esitellään kurssilla MAT-25 Todennäköisyyslaskenta esille tulleita diskreettejä todennäköisyysjakaumia Diskreetti tasajakauma Bernoullijakauma
8.9.26 Kimmo Vattulainen Todennäköisyysjakaumia Seuraavassa esitellään kurssilla MAT-25 Todennäköisyyslaskenta esille tulleita diskreettejä todennäköisyysjakaumia Diskreetti tasajakauma Bernoullijakauma
Tilastollinen päättely II, kevät 2017 Harjoitus 1A
 Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
0 kun x < 0, 1/3 kun 0 x < 1/4, 7/11 kun 1/4 x < 6/7, 1 kun x 1, 1 kun x 6/7,
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia TKK (c) Ilkka Mellin (2005) 1 Jatkuvia jakaumia Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen raja-arvolause TKK (c) Ilkka Mellin
Johdatus todennäköisyyslaskentaan Jatkuvia jakaumia TKK (c) Ilkka Mellin (2005) 1 Jatkuvia jakaumia Jatkuva tasainen jakauma Eksponenttijakauma Normaalijakauma Keskeinen raja-arvolause TKK (c) Ilkka Mellin
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu. f(x, y) = k x y, kun 0 < y < x < 1,
 Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Ilkka Mellin Todennäköisyyslaskenta. Osa 3: Todennäköisyysjakaumia. Diskreettejä jakaumia. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Diskreettejä jakaumia TKK (c) Ilkka Mellin (2007) 1 Diskreettejä jakaumia >> Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Diskreettejä jakaumia TKK (c) Ilkka Mellin (2007) 1 Diskreettejä jakaumia >> Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma
4.1. Olkoon X mielivaltainen positiivinen satunnaismuuttuja, jonka odotusarvo on
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia TKK (c) Ilkka Mellin (2005) 1 Diskreettejä jakaumia Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma Geometrinen jakauma Negatiivinen
Johdatus todennäköisyyslaskentaan Diskreettejä jakaumia TKK (c) Ilkka Mellin (2005) 1 Diskreettejä jakaumia Diskreetti tasainen jakauma Bernoulli-jakauma Binomijakauma Geometrinen jakauma Negatiivinen
JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos)
 J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
k S P[ X µ kσ] 1 k 2.
![k S P[ X µ kσ] 1 k 2. k S P[ X µ kσ] 1 k 2.](/thumbs/92/110318530.jpg) HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
Todennäköisyyden ominaisuuksia
 Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Generointi yksinkertaisista diskreeteistä jakaumista
 S-38.148 Tietoverkkojen simulointi / Satunnaismuuttujien generointi 1(18) Generointi yksinkertaisista diskreeteistä jakaumista Seuraavassa U, U 1,..., U n tarkoittavat riippumattomia U(0,1)-jakautuneita
S-38.148 Tietoverkkojen simulointi / Satunnaismuuttujien generointi 1(18) Generointi yksinkertaisista diskreeteistä jakaumista Seuraavassa U, U 1,..., U n tarkoittavat riippumattomia U(0,1)-jakautuneita
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Epäyhtälöt ovat yksi matemaatikon voimakkaimmista
 6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
30A02000 Tilastotieteen perusteet
 30A02000 Tilastotieteen perusteet Kertaus 1. välikokeeseen Lauri Viitasaari Tieto- ja palvelujohtamisen laitos Kauppatieteiden korkeakoulu Aalto-yliopisto Syksy 2019 Periodi I-II Sisältö Välikokeesta Joukko-oppi
30A02000 Tilastotieteen perusteet Kertaus 1. välikokeeseen Lauri Viitasaari Tieto- ja palvelujohtamisen laitos Kauppatieteiden korkeakoulu Aalto-yliopisto Syksy 2019 Periodi I-II Sisältö Välikokeesta Joukko-oppi
D ( ) E( ) E( ) 2.917
 Mat-2.091 Sovellettu todennäköisyyslasku 4. harjoitukset/ratkaisut Aiheet: Diskreetit jakaumat Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen jakauma, Kertymäfunktio,
Mat-2.091 Sovellettu todennäköisyyslasku 4. harjoitukset/ratkaisut Aiheet: Diskreetit jakaumat Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen jakauma, Kertymäfunktio,
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
4. laskuharjoituskierros, vko 7, ratkaisut
 4. laskuharjoituskierros, vko 7, ratkaisut D1. Kone valmistaa kuulalaakerin kuulia, joiden halkaisija vaihtelee satunnaisesti. Halkaisijan on oltava tiettyjen rajojen sisällä, jotta kuula olisi käyttökelpoinen.
4. laskuharjoituskierros, vko 7, ratkaisut D1. Kone valmistaa kuulalaakerin kuulia, joiden halkaisija vaihtelee satunnaisesti. Halkaisijan on oltava tiettyjen rajojen sisällä, jotta kuula olisi käyttökelpoinen.
8.1 Ehdolliset jakaumat
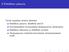 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Todennäköisyyslaskun kertaus. Heliövaara 1
 Todennäköisyyslaskun kertaus Heliövaara 1 Satunnaismuuttujat ja todennäköisyysjakaumat Heliövaara 2 Stunnaismuuttujat ja todennäköisyysjakaumat Jos satunnaisilmiötä halutaan mallintaa matemaattisesti,
Todennäköisyyslaskun kertaus Heliövaara 1 Satunnaismuuttujat ja todennäköisyysjakaumat Heliövaara 2 Stunnaismuuttujat ja todennäköisyysjakaumat Jos satunnaisilmiötä halutaan mallintaa matemaattisesti,
3. laskuharjoituskierros, vko 6, ratkaisut
 Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
5. laskuharjoituskierros, vko 8, ratkaisut
 Mat-.09 Sovellettu todennäköisyyslasku, kevät -05 5. laskuharjoituskierros, vko 8, ratkaisut D. Eräässä maata kiertävällä radalla olevassa satelliitissa on ilmaisin, jonka elinikä X yksikkönä vuosi noudattaa
Mat-.09 Sovellettu todennäköisyyslasku, kevät -05 5. laskuharjoituskierros, vko 8, ratkaisut D. Eräässä maata kiertävällä radalla olevassa satelliitissa on ilmaisin, jonka elinikä X yksikkönä vuosi noudattaa
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
LUKU 3. Ulkoinen derivaatta. dx i 1. dx i 2. ω i1,i 2,...,i k
 LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
4. Todennäköisyyslaskennan kertausta
 luento04.ppt S-38.1145 - Liikenneteorian perusteet - Kevät 2006 1 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat
luento04.ppt S-38.1145 - Liikenneteorian perusteet - Kevät 2006 1 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat
Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2005) 1 Normaalijakaumasta johdettuja jakaumia Johdanto χ 2 -jakauma F-jakauma t-jakauma TKK (c) Ilkka Mellin
Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2005) 1 Normaalijakaumasta johdettuja jakaumia Johdanto χ 2 -jakauma F-jakauma t-jakauma TKK (c) Ilkka Mellin
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
D ( ) Var( ) ( ) E( ) [E( )]
![D ( ) Var( ) ( ) E( ) [E( )] D ( ) Var( ) ( ) E( ) [E( )]](/thumbs/55/37411593.jpg) Mat-.2620 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Diskreettejä jakaumia Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Eksponenttijakauma, Geometrinen jakauma, Hypergeometrinen
Mat-.2620 Sovellettu todennäköisyyslaskenta B / Ratkaisut Aiheet: Diskreettejä jakaumia Avainsanat: Binomijakauma, Diskreetti tasainen jakauma, Eksponenttijakauma, Geometrinen jakauma, Hypergeometrinen
Tilastollinen aineisto Luottamusväli
 Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
031021P Tilastomatematiikka (5 op) viikko 3
 031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
11 Raja-arvolauseita ja approksimaatioita
 11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
Gripenberg. MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta
 MS-A00 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta 7.. Gripenberg Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot ja minkä kokeen suoritat! Laskin,
MS-A00 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta 7.. Gripenberg Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot ja minkä kokeen suoritat! Laskin,
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-2.090 Sovellettu todennäköisyyslasku A Harjoitus 4 (vko 41/2003) (Aihe: diskreettejä satunnaismuuttujia ja jakaumia, Laininen luvut 4.1 4.7) 1. Kone tekee
TKK / Systeemianalyysin laboratorio Nordlund Mat-2.090 Sovellettu todennäköisyyslasku A Harjoitus 4 (vko 41/2003) (Aihe: diskreettejä satunnaismuuttujia ja jakaumia, Laininen luvut 4.1 4.7) 1. Kone tekee
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Kertymäfunktio. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella:
 8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 5 (vko 4/003) (Aihe: jatkuvia satunnaismuuttujia ja jakaumia, sekamalli, Laininen luvut 5.1 5.7, 6.1 6.3)
TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 5 (vko 4/003) (Aihe: jatkuvia satunnaismuuttujia ja jakaumia, sekamalli, Laininen luvut 5.1 5.7, 6.1 6.3)
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Otosavaruus ja todennäköisyys Otosavaruus Ë on joukko, jonka alkiot ovat kokeen tulokset Tapahtuma on otosavaruuden osajoukko
 ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos)
 J. Virtamo 38.3143 Jonoteoria / Diskreetit jakaumat 1 DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos) Määritelmä Olkoon X diskreetti sm, jonka arvot ovat ei-negatiivisia kokonaislukuja, X {0, 1, 2,...}.
J. Virtamo 38.3143 Jonoteoria / Diskreetit jakaumat 1 DISKREETIT JAKAUMAT Generoiva funktio (z-muunnos) Määritelmä Olkoon X diskreetti sm, jonka arvot ovat ei-negatiivisia kokonaislukuja, X {0, 1, 2,...}.
Tilastollinen päättömyys, kevät 2017 Harjoitus 6B
 Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
l (φ; y) = l(θ(φ); y) Toinen derivaatta saadaan tulon derivaatan laskusäännöllä Uudelleenparametroidun mallin Fisherin informaatio on
 HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
Normaalijakaumasta johdettuja jakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2007) 1 Normaalijakaumasta johdettuja jakaumia >> Johdanto χ 2 -jakauma F-jakauma
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2007) 1 Normaalijakaumasta johdettuja jakaumia >> Johdanto χ 2 -jakauma F-jakauma
Juuri 10 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
Matemaattinen tilastotiede. Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto
 Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X Y Bin(Y, θ) Y Poi(λ) λ y. f X (x) (λθ)x
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
031021P Tilastomatematiikka (5 op) viikot 5 6
 031021P Tilastomatematiikka (5 op) viikot 5 6 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
031021P Tilastomatematiikka (5 op) viikot 5 6 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
2. Jatkoa HT 4.5:teen ja edelliseen tehtavään: Määrää X:n kertymäfunktio F (x) ja laske sen avulla todennäköisyydet
 Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
(b) Onko hyvä idea laske pinta-alan odotusarvo lähetmällä oletuksesta, että keppi katkeaa katkaisukohdan odotusarvon kohdalla?
 6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
Johdatus todennäköisyyslaskentaan Kertymäfunktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Kertausluento. Tilastollinen päättely II - 2. kurssikoe
 Kertausluento Tilastollinen päättely II - 2. kurssikoe Yleistä tietoa TP II -2. kurssikokeesta 2. kurssikoe maanantaina 6.5.2019 klo 12.00-14.30 jossakin Exactumin auditoriossa Kurssikokeeseen ilmoittaudutaan
Kertausluento Tilastollinen päättely II - 2. kurssikoe Yleistä tietoa TP II -2. kurssikokeesta 2. kurssikoe maanantaina 6.5.2019 klo 12.00-14.30 jossakin Exactumin auditoriossa Kurssikokeeseen ilmoittaudutaan
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
y x1 σ t 1 = c y x 1 σ t 1 = y x 2 σ t 2 y x 2 x 1 y = σ(t 2 t 1 ) x 2 x 1 y t 2 t 1
 1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
6. laskuharjoitusten vastaukset (viikot 10 11)
 6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
F(x) = 1. x x 0 + F(x) = F(x 0) kaikilla x 0 R.
 Luku 5 Jatkuvat jakaumat Sellaiset suureet kuten esimerkiksi aika, lämpötila, pituus ja paino ajatellaan tavallisesti jatkuviksi muuttujiksi, ts. muuttujiksi, jotka voivat saada mitä tahansa reaaliarvoja
Luku 5 Jatkuvat jakaumat Sellaiset suureet kuten esimerkiksi aika, lämpötila, pituus ja paino ajatellaan tavallisesti jatkuviksi muuttujiksi, ts. muuttujiksi, jotka voivat saada mitä tahansa reaaliarvoja
Harjoitus 2: Matlab - Statistical Toolbox
 Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
Suotuisien tapahtumien lukumäärä Kaikki alkeistapahtumien lukumäärä
 Todennäköisyys 1 Klassinen todennäköisyys: p = Suotuisien tapahtumien lukumäärä Kaikki alkeistapahtumien lukumäärä Esimerkkejä: Nopan heitto, kolikon heitto Satunnaismuuttuja Tilastollisesti vaihtelevaa
Todennäköisyys 1 Klassinen todennäköisyys: p = Suotuisien tapahtumien lukumäärä Kaikki alkeistapahtumien lukumäärä Esimerkkejä: Nopan heitto, kolikon heitto Satunnaismuuttuja Tilastollisesti vaihtelevaa
3.6 Su-estimaattorien asymptotiikka
 3.6 Su-estimaattorien asymptotiikka su-estimaattorit ovat usein olleet puutteellisia : ne ovat usein harhaisia ja eikä ne välttämättä ole täystehokkaita asymptoottisilta ominaisuuksiltaan ne ovat yleensä
3.6 Su-estimaattorien asymptotiikka su-estimaattorit ovat usein olleet puutteellisia : ne ovat usein harhaisia ja eikä ne välttämättä ole täystehokkaita asymptoottisilta ominaisuuksiltaan ne ovat yleensä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 12 1 Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan
Matematiikan tukikurssi Kurssikerta 12 1 Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan
Poisson-prosessien ominaisuuksia ja esimerkkilaskuja
 4B Poisson-prosessien ominaisuuksia ja esimerkkilaskuja Tuntitehtävät 4B1 Eksponentiaalisten odotusaikojen toistuva odottaminen. Satunnaisluvun X sanotaan noudattavan Gamma-jakaumaa parametrein k ja λ,
4B Poisson-prosessien ominaisuuksia ja esimerkkilaskuja Tuntitehtävät 4B1 Eksponentiaalisten odotusaikojen toistuva odottaminen. Satunnaisluvun X sanotaan noudattavan Gamma-jakaumaa parametrein k ja λ,
031021P Tilastomatematiikka (5 op) viikko 2
 031021P Tilastomatematiikka (5 op) viikko 2 Jukka Kemppainen Mathematics Division Satunnaismuuttuja Useissa luonnon- tai teknistieteellisissä sovellutuksissa satunnaiskokeen lopputulos on numeerinen lukuarvo.
031021P Tilastomatematiikka (5 op) viikko 2 Jukka Kemppainen Mathematics Division Satunnaismuuttuja Useissa luonnon- tai teknistieteellisissä sovellutuksissa satunnaiskokeen lopputulos on numeerinen lukuarvo.
Lisätehtäviä ratkaisuineen luentomonisteen lukuihin 2-4 liittyen
 MTTTP5, kevät 2016 4.2.2016/RL Lisätehtäviä ratkaisuineen luentomonisteen lukuihin 2-4 liittyen 1. Laitosneuvostoon valitaan 2 professoria, 4 muuta henkilökuntaan kuuluvaa jäsentä sekä 4 opiskelijaa. Laitosneuvostoon
MTTTP5, kevät 2016 4.2.2016/RL Lisätehtäviä ratkaisuineen luentomonisteen lukuihin 2-4 liittyen 1. Laitosneuvostoon valitaan 2 professoria, 4 muuta henkilökuntaan kuuluvaa jäsentä sekä 4 opiskelijaa. Laitosneuvostoon
F dr = F NdS. VEKTORIANALYYSI Luento Stokesin lause
 91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
V ar(m n ) = V ar(x i ).
 Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
4.1 Diskreetin satunnaismuuttujan odotusarvo
 4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
Estimointi. Vilkkumaa / Kuusinen 1
 Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 10: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali.
 MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
