KIMMOKERROIN. 1 Johdanto. Perustietoa työstä
|
|
|
- Arto Korhonen
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 1 KIMMOKERROIN Perueoa yöä Mhn fykan oa-aueeeen yö yy? Kneden aneden mekankkaan. Mä öyyy yöä arvava eora? Kakk mauuoen käeyä arvava eora on eey yöohjeea. Läeoa öyyy emerkk krjaa Young H. D. ja Freedman R. A.: Unvery Phyc. Mä eeoja yöä arvaan? Sekä abouuen eä uheeen vrheen arvon kokonadfferenaameneemän avua ja 15 ykkön äänö oeeaan unneuk. Tuoen käeyä käyeään penmmän neöumman uoran ovua. Mä maaea yöä käyeään? Mekankan perumauväneä e mermaa, yönömaa, mkromerruuva ja ekunkeoa, joden käyön oeeaan oevan nue uua. Manen eou yöä ehdään? Työä ehdään avanomanen eou, johon öyyy ohjea emerkk kurn noppavua. Seou ehdään eokoneea ja jo LaTex ohjema on nue uu, on uoeavaa käyää ä. 1 Johdano Mona fykan öä ajaeaan kappaeden oevan jäykkä, joon ne äyävä muoona emerkk kkueaan koko ajan. Todee kappaee vova kuenkn apua, venyä, purua kokoon a väänyä nhn vakuaven vomen vakuukea. Jo kappaee ova äyn eaa, ne paauuva akuperäeen muooona vomen akaua vakuamaa. Kun muodonmuuoka aheuava voma ova rävän penä, odee kappaee vodaan ajaea eak. Kappaeden eauuden mana käyeään eaa keroma. Nää keroma on kuekn kappaeee oemaa kome: Kmmokerron, joka kuvaa kappaeen kykyä vauaa venymä a kokoon puruma, ukukerron, joka maee kappaeen kyvyn vauaa ä keräven ekkauvomen aheuama muodonmuuoka ja purukerron, joka kuvaa kappaeen kykyä vauaa hen aae kaka uunna vakuaven vomen ynnyämä muuoka. Eae kerome määreään kappaeeeen kohduvan jännyken ja kappaeen uheeeen muodonmuuoken uheena,. =. (1) Yhäö (1) on nmeään Hooken ak ja nä enyvä jänny arkoaa kappaeeeen vakuavan voman uuruua pna-aaykkköä koh. Jännyken ykkkö on en N/m e Pa.
2 KIMMOKERROIN Suheenen muodonmuuo aa aadaan eve emerkk akemaa kappaeen uheenen venymä e puuden muuoken uhde akuperäeen puueen. Suheeea muodonmuuokea e en oe ykkköä, joen eaen keromen ykkök aadaan myö Pa. Tää yöä määrä eräken kmmokeromen venyämää ohua eräankaa eruurua voma ja määrämää angan uheee venymä veojännyken funkona. Määrä myö eräken ukukeromen käyämää hyväk keroheura, jonka anka on erää. Maamaa heurn jakonajan, angan puuden ja hakajan ekä heurkappaeen maan ja hakajan aa akeuk angan ukukeromen. Kmmokeromen ja ukukeromen avua vo akea myö eräangan ohenemen ja venymen uhdea kuvaavan Poonn uvun. Läk määrä unemaoman mean kmmokeromen avuamaa moemma päään ueua, meaa vameua ohua auvaa. Maamaa auvan apumaa kuormavan voman uuruuden funkona pyy akemaan auvamaeraan kmmokeromen, kun äk maa auvan hakajan ja ukpeden vämakan.
3 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja Teora.1 Eae kerome Tarkaeaan ähemmn kappaeden eran muodonmuuokn yvä eaa keroma. Kuva 1 a) ja b) kappaeeeen vakuaa akenuunanen, pokkpna-aaa vaaan kohuora voma, joka pyrk venyämään (a) a puramaan kokoon (b) kappaea /1/. Jo kappae e ku ämän voman vakuukea, äyyy vaakkaeen pnaan vakuaa kuvan 1 mukae yhä uur, mua vaakkauunanen voma. Kmmokerron Y, joa kuuaan myö nmä kmmomoduu a Youngn moduu, kuvaa kappaeen kykyä vauaa venymä a kokoon puruma kuvan 1 apaea aneea. Hooken aka oveamaa kmmokerron Y aadaan veojännyken ja uheeen puuden muuoken avua euraava joa Y = = F A, () F on kappaeeeen kohduvan, pnaa vaaan kohuoran voman uuruu, A on kappaeen pokkpna-aa, on kappaeen akuperänen puu ja on puuden muuo. a) b) Kuva 1. Kappaeen pnaa vaaan kohuora voma pyrk a) venyämään ja b) puramaan kokoon kappaea.
4 KIMMOKERROIN Kuvaa kappaeen yäpnaan vakuaa pnnan uunanen voma, jonka uuruu on F ja aapnaan vakuaa yhä uur, mua vaakkauunanen voma. Lukukerron a ekkaukerron S kuvaa kappaeen kykyä vauaa kuvan apaen ekkauvomen aheuama muodonmuuoka. Kappaeen yäpnnan pokkeama uheea aapnaan on ny x, joon Hooken ak anaa ukukeromek S kero- e ekkaujännyken ja kerovenyyken avua auuuna F S = = x A, () h joa F on kappaeen pnnan uunaen voman uuruu, A on kappaeen vaakauoran pnnan aa ja h on kappaeen korkeu kuvan mukae. Kuva. Kappaeen pnnan uunanen ekkauvoma pyrk kerämään kappaea. /1/ Kuvaa arkaeaan annea, joa kappae on upoeu neeeeen. Täön kappaeeeen kohduu kaka uunna yhä uur puruvoma, joka pyrk muuamaan kappaeen avuua. Purukerron kuvaa kappaeen kykyä vauaa puruvomen aheuama muuoka. Hooken an avua purukeromek B aadaan p B =, () V V joa p on kappaeeeen kohduvan paneen muuo, V on kappaeen avuuden muuo ja V on kappaeen akuperänen avuu. Kuva. Kappaeeeen kohduu kaka uunna yhä uur puruvoma. /1/. Poonn uku Kun kappaea pureaan kokoon yhdeä uunnaa, nn e yeenä pyrk aajenemaan puruuunaa vaaan kohuora uunna. Vaaava, jo kappaea venyeään, e pyrk upumaan venyyuunaa vaaan kohuora uunna. Tää möä kuuaan Poonn mök ja en mana käyeään Poonn ukua. Poonn uku määreään
5 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 5 yee kokoonpurumen aheuaman uheeen uppeuman ja venyyken akaanaaman uheeen venymän uheena. Emerkk ää yöä venyeävä eräanka ohenee venyeään. Jo angan akuperänen puu on ja puuden muuo, nn angan uheenen venymä on =. Jo aa angan akuperänen hakaja on d ja hakajan muuo on d, nn uheenen uppeuma on d = d d. Poonn uvuk aaan ää apaukea d =. Yeenä anne on eanen, eä odee kappaee Poonn uku vodaan määrää van kokeee. Jo ukavan kappaeen ajaeaan koouvan orooppea ja äyn eaa maeraaa, nn Poonn uvun ja eaen kerronen Y, S ja B vää rppuvuuka vodaan arkaea myö eoreee. Emerkk ää yöä käyöä oevaa ohua venyeävää ja kerreävää eräankaa vodaan pää pokan orooppena. Täön vodaan ajaea, eä anka on ekä orooppnen eä äyn eanen aoa, joa venyy ja kero apahuva. Täaen maeraan Poonn uvue on vomaa yhäö joa Y ja S ova maeraan kmmokerron ja ukukerron. // = Y S 1, (5). Sauvan avuu N/ N/ Kuvaa vaakaaoon aeeua, moemma pää ueua ohua ja aapakua meaauvaa kuormeaan kekeä pyyuoraa vomaa, jonka uuruu on F. Täön auva apuu, koka en er kerroke evä veny yhä pajon. Vodaan ooaa (kao yöohjeen opua oeva Le 1), eä kuvan aneea auvan apuma y kuormavan voman kohdaa, ukpeden puoea vää on // F y =, (6) Y joa on ukpeden vämaka, Y m on auvamaeraan kmmokerron ja d on auvan hakaja. y F Kuva. Sauvan avuu. md
6 6 KIMMOKERROIN Mauaeo ja mauke.1 Langan venyy Teräken kmmokerron määreään rpuamaa eräankaan erpanoa punnuka ja maamaa kunkn punnuken aheuama angan puuden muuo. Venyymauken peraae on en amanapanen kun kuvaa 1 a). Homogeenen, aapakun angan pokkpna-aa on A ja puu on. Langan pähn vakuava aken uunae pokkpna-aaa vaaan kohuora yhä uure mua vaakkauunae voma. Teräken kmmokerron Y aadaan en eve edeä anneua yhäöä (). Kuva 5. Langan venyyaeo. a) Lanka, punnuene ja perupunnu. b) Pekevy, vaupa ja mkromerruuv. Akuaneea ankaan on rpueu perupunnu, joka pää angan uorana. Säädä evy vaakauorak pyörämää mkromerruuva en, eä vaupan puken makupa on kekeä pukea ja ue vaaava mkromerruuvn ukema 1. Rpua en ankaan,5 kg:n punnuke yk kerraaan ja äädä jokaen kohdaa makupa kekee vaupan pukea ja ue kuakn maaa vaaava mkromern ukema 1. Tämän jäkeen poa punnuke yk kerraaan ja havae amaa a- mermaa ja hakaja vaa mkromerruuvn ukema. Maa opuk angan puu D mkromerruuva. Teräangan venyymauka käyeävää aeo on kuvaa 5. Tukava anka on knney pekevyyn, jonka päää on vevaaka e vaupa. Levyn oen pään aapuoea on mkromerruuv, joa ääämää evy aadaan vaupaa apuna käyäen vaakauorak.. Keroheur Teräangan ukukeromen määrykeä käyeään kuvaa 6 eeyä keroheura, joa ohuen angan varaan rpueu mk maanen kekko, jonka äde on r k, pääee kerymään
7 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 7 angan ympär. Kekon keryeä kuman verran angan kaua kukevan aken uheen, anka kohdaa kekkoon väänömomenn = c, mä c on angan omnauuka rppuva vako e angan drekomomen //. Soveamaa pyörmen peruaka = I, joa Ik on kekon haumomen en maakekpeen kaua kukevan aken uheen ja on kumakhyvyy, keroheurn keyhäök aadaan k d d c = c = Ik = Ik + =. mk d d Ik Kuva 6. Keroheur. Tämä vodaan rakaa emerkk kokeemaa yreä ( ) = co( + ), joa on heurn ampud e uurn pokkeama aapanoaemaa, on kumaaajuu ja on vahekuma. Kun anneu yre joeaan heurn keyhäöön, aadaan uo c I + = =. k c I k rk Keroheurn jakonajak T aadaan T I = = k, c 1 joa Ik on kekon haumomen aken uheen e I k = mkrk. Jo joamme heahduajan auekkeeeen veä yöohjeen opua oevaa eeä johdeun angan drekomomenn auekkeen SR c =, joa S on angan ukukerron, R on angan äde ja L L on angan puu, aamme keroheurn heahduajae yhäön T I =. (7) k L SR Krjaa yö kekon maa mk vrherajoneen ja maa kekon hakaja d k yönömaa. L mermaa ja Mua määrää myö yönöman ukemaarkkuu. Maa angan puu määrä puuden mauarkkuu. Keroheurn eräanka on amanaa kun venymämauen anka, joen vo käyää angan hakajana venymämauka määreyä hakajaa vrherajoneen. Pane en heur heaheemaan kerämää ankaa kekon avua nn, eä ampud e uurn kerokuma on pen. Maa 1 peräkkäen heahduken heahduaka 1 keraa. (Huom.! Jo oe ehny Heur -yön aemmn, vo hauea käyää eä maama keroheurn heahduakoja myö ää yöä.)
8 8 KIMMOKERROIN. Tavuumauke Sauvan avuumauka käyeään kuvaa 7 näkyvää aeoa. Vae ohjaajan anama vahoehdoa ukava auva ja yrä pääeä, mä maeraaa e on. Aea auva eneeä oeven vaakauoren eren varaan, joon e on ueu moemma päään. Pane auvan varaan rpun ja kao, eä rpun on oken mkromerruuvn kohdaa. Kerrä en mkromerruuva en, eä mapää kkuu aapän, kunne e oaa knn rpumeen. Täön mkromerruuvn kykey vrapr ukeuuu ja merkkvao yyy. Havae enmmänen mkromerruuvn ukema 1. Kuva 7. Tavuumauen aeo. Lää auvaa kuormavaa panoa aeamaa rpumeen 1 g:n punnuka yk kerraaan. Kerrä mkromerruuva nn, eä merkkvao yyy ja havae vaaava mkromerruuvn ukema 1. Toa en mauke pänvaaea järjeykeä poamaa yk punnu kerraaan ja havaemaa ukema. Tää vaheea mkromerruuvn mapäää on yyä kerää yöpän ennen punnuken poama, joa auvaa e avuea mkromerruuvn avua. Maa opuk auvan ukpeden e vaakauoren eren vämaka mermaa ja auvan hakaja d mkromerruva ja määrä myö näden uureden mauarkkuude.
9 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 9 Mauuoen käey.1 Teräken kmmokerron Määrä enn kuakn maukea käyeyä maaa F m g = =, A D m vaaava veojänny yhäöä joa g on maan veovoman aheuama puoamkhyvyy 9,8 m/. Lake en maoja vaaava mkromerruuvn ukema havaujen ukemen 1 ja kekarvona. Muua ukema angan puuden muuokk vähenämää kekarvoa perupunnukea 1 havaujen ukemen kekarvo. Kuakn maaa vaaava uheee puuden muuoke e uheee venymä aa ny jakamaa puuden muuoke angan puudea,. =. Eä aadu, ) pepar koordnaaoa, ova nhn penmmän neöumman uora ja ( määrä en kumakerron vrherajoneen. Krjoamaa yhäö () muooon 1 = Y huomaaan, eä aadun uoran u kukea orgon kaua ja en kumakerron on kmmokeromen kääneuku. Määrä eräken kmmokerron Y ja en abouuen ja uheeen vrheen yäraja uoran kumakeromen ja en vrherajan avua. Lä eoukee myö prämä kuvaaja, edo ovukea ekä käyämä akenaauuko.. Teräken ukukerron ja Poonn uku Määrä keroheurn jakonaka akemaa 1 havaun heahduajan kekarvo ja muuamaa e yhden heahduken ajak. Heahduajan vrheen aa eve emää uurmman pokkeaman kekarvoa. Lake eräken ukukerron ja en uheeen vrheen yäraja ennakkoehävä 1 ja johama yhäöä. Määrä myö ukukeromen abouuen vrheen yäraja. Lake en eräken Poonn uku yhäöä (5).. Tunemaoman mean kmmokerron Mean kmmokeromen määrämek ake enn kuakn maaa M vaaava mkromern ukema kahden havaun ukeman kekarvona. Sauvan apuma y aa eve vähenämää ukemen kekarvoa pekän rpumen kana havaujen ukemen kekarvon. Kun oeaan huomoon, eä avuumauka kuormava voma on F M g, vomme krjoaa yhäön (6) muooon g =. y M Y md =
10 1 KIMMOKERROIN Eä auvan apuma y maan M funkona ( M, y) koordnaaoa, ova pen penmmän neöumman uora ja määrä uoran kumakerron vrherajoneen. Lake auvamaeraan kmmokerron Y m uoran kumakeromen ( kk = y / M ) avua ja muden yä anneua yhäöä enyven vakoden ja maujen auvan omnauuken avua. Määrä myö kmmokeromen uheeen ja abouuen vrheen yäraja käyämää hyväk ennakkoehävää johamaa yhäöä. Lä kuvaaja, edo ovukea ekä akenaauuko eoukeen. 5 Loppuuoke Imoa oppuuokna eräken kmmokerron ja ukukerron vrherajoneen ekä eräken Poonn uku. Veraa uoka krjauuarvohn. Anna avuumauken oppuuokena mean kmmokerron vrherajoneen ja yrä pääeä en ja käyämä auvan ukonäön ja mahdoen muden omnauuken avua, mä maeraaa auva o. Krjauu /1/ Young H. D. ja Freedman R. A.: Unvery Phyc, Pearon Educaon Inc., San Francco CA, 8. // Sephenon, R. J.: Mechanc and propere of maer, Wey & Son, New Jerey, // Vaar, J.: Fykan aboraoroyö, Gummeru, Jyväkyä, 199. // Aono M. ja Fnn E. J.: Fundamena Unvery Phyc, Voume 1, Addon-Weey, Readng, Maachue, 198.
11 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 11 LIITE 1: SAUVAN TAIVUTUS Aa oeva kuva L1.1 a) eää annea, joa aapakua, moemma pää ueua auvaa kuormeaan kekeä. Täön auva apuu, koka auvan er kerroke evä veny yhä pajon. Sauvan kekeä on n. neuraakerro, joka e veny ekä puru kokoon. Neuraakerroken aapuoea oeva kerroke venyvä, kun aa en yäpuoea oeva kerroke puruva kokoon. Jo apuma oeeaan penk, vodaan maeran dovoma pää harmonna ja oeaa, eä neuraakerro kukee auvan pokkekkauken panopeen kaua. Kuvaa L 1.1 b) auvan apumaa on oeu, joa arkaeava kohee uva evemmn en. Oeeaan, eä auva on apunu kaaree, jonka kaarevuuäde on R. Tarkaeaan kerroa DD, joka on eäyydeä e neuraakerrokea CC. Kerroken DD peneen pnaakoon da vakuaa pnnan uunanen jännyvoma, jonka uuruu on df. Kerroken DD uheenen venymä aadaan jakamaa kerroken uuden puuden ( R + e) ja akuperäen puuden uo R erou akuperäeä puudea. Soveamaa Hooken aka (1) aadaan Y m = df da = ( R + e) R R RdF Yme df = da, eda R joa Y m on auvamaeraan kmmokerron. a) N/ y N/ x F dy dx b) R C A C D D e Kuva L1.1 a) Moemma päään ueun auvan avuu b) Neuraakerro CC ekä venyny kerro DD. da Jo momenpeek vaaan kerroken CC pe ( x, y), pna-akoon da vakuavan jännyvoman df momen d F on yä johdeun yhäön perueea Yme = edf = da. R d F
12 1 KIMMOKERROIN Sauvan pokkekkaukeen vakuaven jännyvomen momenk F aadaan nän oen joa I A = e Yme Ym Ym F = d F da e da I = = A R R =, R da on auvan pokkekkaupnnan pnahaumomen pnnan panopeen kaua kukevan aken uheen. Yä oevaa momenn F yhäöä huomaaan, eä kmmokeromen Ym eve aamek o unneava myö kaarevuuäde R. Vodaan ooaa, eä jo kuvan L1.1 mukaea aneea apuma ova penä, kaarevuuäeen kääneuvue on vomaa 1 R d y dx. Nän oen jännyvomen momenk aadaan d y F = Y I A. m dx Kun auva on aaea aapanoa, jännyvomen momen ja ukoen vomen momen kumoava oena. Kuvaa L1.1 a) nähdään, eä ukoen vomen momen F peen ( x, y) uheen on N N F F = ( + x) Fx + ( x) = Fx = F( x), koka ukoen vomen aapanoehdon mukaan N = F. Taapanoaneea aadaan d y F + Ym I F( x) F = A =. dx Inegromaa ämä kak keraa aadaan yhäö y = ( Fx Nx C1x C), I Y 6 A m joa C1 ja C ova vakoa. Näden vakoden arvo aadaan eve, koka auvan apuma pää on noa. Jo arkaeaan auvan okeaa päää, joa x =, aamme ehdoa dy = ja y = dx funkona on vakok C1 = F ja C = F. Nän oen auvan apuma y pakan x y = ( Fx Fx + F x F ). I Y A m Työä maamme apumaa auvan kekkohdaa, joa x =. Tää kohdaa aamme auvan apumak
13 Ouun yopo Fykan opeuaboraoro Fykan aboraoroyö ja 1 F y = -. 8I Y A m Lakeaan veä auvan pnahaumomen I A = e da auvan panopeen kaua kukevan aken uheen. Sjoeaan auva koordnaaoon aa oevan kuvan L1. mukae. Vaaan pna-akok da kuvan mukanen ukae, joon da= rdrd. Kuvaa nähdään myö, eä e = r n. Pnahaumomenk aadaan e da r x I A = = r r r n rdrd = 1 1 r ( ) rdr = r = r r 1 6 ( d 1 1 ( co ) d) rdr. Kuva L1. Sauvan pnahaumomenn määry. Kun joamme apuman yhäöön pnahaumomenn apumae yhäön (6) mukaen uoken I A = 1 d, aamme maavae 6 6F F y = - =. 8d d Ym Ym
14 1 KIMMOKERROIN LIITE : LANGAN DIREKTIOMOMENTTI Tarkaeaan aa oevan kuvan L.1 mukaa aapakua ja homogeena ankaa, jonka puu on L ja jonka pokkekkaupna on R äenen ympyrä. Kuvaa L.1 a) angan päähän vakuaa pokkekkaupnnan uunanen ekkauvoma, jonka uuruu on F. Voman vakuukea ankaa keryy kuman verran en, eä kuvaa näkyvä pe B ryy kohaan C. Vaaan angan pokkekkaupnnaa pna-akok kuvan L.1 b) mukae r-äenen ympyrärenga, jonka pakuu on dr. Tähän pna-akoon vakuava ekkaujänny d on en d = df A = df (rdr). F a) b) Langan apaukea kerovenyyä vodaan eää kuvaa L.1 a) näkyvän kuman = r L avua. Työohjeen yhäön () perueea ukukeromek S aadaan df (rdr) LdF = = =. r L r dr S Voma F kohdaa arkaeavaan pna-akoon väänömomenn d = rdf. Sjoamaa ähän yä oevaa ukukeromen auekkeea rakau voma df väänömomenk aadaan B C F R L Kuva L.1. a) Langan kerymnen. b) Vau pna-ako. r dr R d d Sr dr =, L joa okean puoen eumerkk johuu ä, eä väänömomen vauaa kuman kavua. Koko ankaan vakuava väänömomen on = R Sr L SR dr = L = c. Yä oevaa yhäöä nähdään, eä angan drekomomen c on SR c =. L
Rak-54.116 Rakenteiden mekaniikka C, RM C (4 ov) Tentti 30.8.2007
 Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
Tässä harjoituksessa käsitellään Laplace-muunnosta ja sen hyödyntämistä differentiaaliyhtälöiden ratkaisemisessa.
 DEE-00 Lneaare järjeelmä Harjou 0, rakauehdouke Tää harjoukea käellään Laplace-muunnoa ja en hyödynämä dfferenaalyhälöden rakaemea Tehävä Laplace-muunno on käevä yökalu dfferenaalyhälöryhmen rakaemea,
DEE-00 Lneaare järjeelmä Harjou 0, rakauehdouke Tää harjoukea käellään Laplace-muunnoa ja en hyödynämä dfferenaalyhälöden rakaemea Tehävä Laplace-muunno on käevä yökalu dfferenaalyhälöryhmen rakaemea,
MUODONMUUTOKSET. Lähtöotaksumat:
 MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
12. ARKISIA SOVELLUKSIA
 MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
Koulutus- ja kehittämispalvelu Aducate 1 (6) KOPSU -hanke 10.10.2011
 Kouluu- ja khämpalvlu Aduca 1 (6) Pykooaal ohjauk ja uvoa rkoumopo (35 op), - kogv ja rakaukk yöklyapa - pykorapu valmuk opo TOTEUTUSPAIKKA Jouu TAVOITE JA KOHDERYHMÄ Kouluu aaa oallujll valmud ouaa ohjau-
Kouluu- ja khämpalvlu Aduca 1 (6) Pykooaal ohjauk ja uvoa rkoumopo (35 op), - kogv ja rakaukk yöklyapa - pykorapu valmuk opo TOTEUTUSPAIKKA Jouu TAVOITE JA KOHDERYHMÄ Kouluu aaa oallujll valmud ouaa ohjau-
Telecommunication engineering I A Exercise 3
 Teleouao egeerg I 5359A xere 3 Proble elaodulaaor lohkokaavo o eey oppkrja kuvaa 3.63. Pulodulaaor ääuloa o aoagaal ja reeregaal erou d. Tää gaal kerroaa pulgeeraaor gaallla rajouke, el erouke erk elväe,
Teleouao egeerg I 5359A xere 3 Proble elaodulaaor lohkokaavo o eey oppkrja kuvaa 3.63. Pulodulaaor ääuloa o aoagaal ja reeregaal erou d. Tää gaal kerroaa pulgeeraaor gaallla rajouke, el erouke erk elväe,
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA 2 OV. Isto Jokinen 2012. 1. Mekaniikka 2
 OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
RATKAISUT: 3. Voimakuvio ja liikeyhtälö
 Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
1. välikoe
 Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
11. Takaisinkytketyt vahvistimet
 Kar berg Kar berg. akankykey vahvme. ahvn yyppejä Jännevahvn Ohjaun läheen pääyyppejä Jänne hjau jännelähde ra hjau jännelähde Jänne hjau vralähde ra hjau vralähde v kun >> v kun >> ja >> njänne n en uraan
Kar berg Kar berg. akankykey vahvme. ahvn yyppejä Jännevahvn Ohjaun läheen pääyyppejä Jänne hjau jännelähde ra hjau jännelähde Jänne hjau vralähde ra hjau vralähde v kun >> v kun >> ja >> njänne n en uraan
Käyttövarmuuden ja kunnossapidon perusteet, KSU-4310: Tentti ma
 KSU-430/Ten 4..2008/Prof. Seppo Vranen /3 Käyövarmuuden ja kunnossapdon perusee, KSU-430: Ten ma 4..2008 Huom. Vasaus van veen kysymykseen. Funko- ja/a ohjelmoavan laskmen, musnpanojen, luenomonseden ja
KSU-430/Ten 4..2008/Prof. Seppo Vranen /3 Käyövarmuuden ja kunnossapdon perusee, KSU-430: Ten ma 4..2008 Huom. Vasaus van veen kysymykseen. Funko- ja/a ohjelmoavan laskmen, musnpanojen, luenomonseden ja
Soorrea. OUTC'KUMPU Oy.' Malminetsintä. O. POhjamies/pAL ,4 1 (3) VLF -MI'ITAUS. Periaate. Lähetysase.mat
 - OUTCKUMPU Oy Malmnesnä O POhames/pAL 94 (3) VLF -MTAUS Peraae Läheysasema VU (= Very M Frequency) -ruauks$sa käyeään apuna 5-0 khz aauusaueea omva asea Näden asemen anenrrl ova pysyä a nssä kulkeva vra
- OUTCKUMPU Oy Malmnesnä O POhames/pAL 94 (3) VLF -MTAUS Peraae Läheysasema VU (= Very M Frequency) -ruauks$sa käyeään apuna 5-0 khz aauusaueea omva asea Näden asemen anenrrl ova pysyä a nssä kulkeva vra
Korjausrakentaminen Maiju Kianta Metropolia 2014
 p y ö r ä k e k u Korjurkenmnen Mju Kn Meropo 2014 M m n v n h e m r k e n n u Rkenneu v. 1934 Arkkeh Thure Heröm TAVOITTEET - äyää rkennu rvoen kunno ueve ukupove - muuoke oeuev oem oev rkennu kunnoen
p y ö r ä k e k u Korjurkenmnen Mju Kn Meropo 2014 M m n v n h e m r k e n n u Rkenneu v. 1934 Arkkeh Thure Heröm TAVOITTEET - äyää rkennu rvoen kunno ueve ukupove - muuoke oeuev oem oev rkennu kunnoen
Rak Rakenteiden mekaniikka C, RM C 4ov Tentti
 Rk-5.6 Rkeneden meknkk RM ov Ten.. 7 Krjo jokeen koeppern elvä - koko nme puhuelunm llevvun - oo vuokur enn pävämäärä ekä enävä opnojko koodeneen - opkeljnumero (muknluken rkukrjn) - moneko ker ole ko.
Rk-5.6 Rkeneden meknkk RM ov Ten.. 7 Krjo jokeen koeppern elvä - koko nme puhuelunm llevvun - oo vuokur enn pävämäärä ekä enävä opnojko koodeneen - opkeljnumero (muknluken rkukrjn) - moneko ker ole ko.
"h 'ffi: ,t^-? ùf 'J. x*r:l-1. ri ri L2-14. a)5-x:8-7x b) 3(2x+ l) :6x+ 1 c) +* +5 * I : 0. Talousmatematiikan perusteet, onus to o.
 1 Vaasan yopso, kev a 0 7 Taousmaemakan perusee, onus o o R1 R R3 R ma 1-1 ma 1-1 r 08-10 r -1 vkko 3 F9 F53 F5 F53 1.-0..01 R5 R o R7 pe R8 pe - r-1 08-10 10-1 F53 F10 F5 F9 1. Sevennä seuraava ausekkee.
1 Vaasan yopso, kev a 0 7 Taousmaemakan perusee, onus o o R1 R R3 R ma 1-1 ma 1-1 r 08-10 r -1 vkko 3 F9 F53 F5 F53 1.-0..01 R5 R o R7 pe R8 pe - r-1 08-10 10-1 F53 F10 F5 F9 1. Sevennä seuraava ausekkee.
8 USEAN VAPAUSASTEEN SYSTEEMIN VAIMENEMATON PAKKOVÄRÄHTELY
 Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
F Y S I I K K A KERTAUSTEHTÄVIÄ 1-20
 F Y S I I K K A KERTAUSTEHTÄVIÄ - 0 Oalla eieyiä kyyykiä vaauke ova huoaavai pidepiä kuin iä eierkiki kokeea vaaukela vaadiaan. Kokeea on oaava vain olennainen aia per ehävä. . Muua SI järjeelän ykiköihin
F Y S I I K K A KERTAUSTEHTÄVIÄ - 0 Oalla eieyiä kyyykiä vaauke ova huoaavai pidepiä kuin iä eierkiki kokeea vaaukela vaadiaan. Kokeea on oaava vain olennainen aia per ehävä. . Muua SI järjeelän ykiköihin
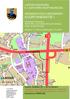
HERNESAARI OSAYLEISKAAVAEHDOTUS VESIHUOLLON YLEISSUUNNITELMA
 HERNESAAR OSAYLESKAAAEHDOTUS ESHUOLLON YLESSUUNNTELMA KS/TEK SSÄLLYSLUETTELO Yä S- v p äöd d ävvä Hvvä K äää ää Nyy S Yä d ävvä Hvvä v v L: L y HELSNGN KAUUNK KAUUNKSUUNNTTELURASTO Y Td Yä y vää H yv-
HERNESAAR OSAYLESKAAAEHDOTUS ESHUOLLON YLESSUUNNTELMA KS/TEK SSÄLLYSLUETTELO Yä S- v p äöd d ävvä Hvvä K äää ää Nyy S Yä d ävvä Hvvä v v L: L y HELSNGN KAUUNK KAUUNKSUUNNTTELURASTO Y Td Yä y vää H yv-
gallup gallup potentiaali ja voima potentiaali ja voima potentiaali ja voima potentiaali ja voima
 aup Kuinka pajon käytät kurikirjaa (tai jotain muuta oppikirjaa)? a) Tututun aiheeeen ennen uentoja b) Luen kirjaa uentojen jäkeen c) Luen oppikirjaa ähinnä akareita tehdeä d) n koke oppikirjaan aup Kappae
aup Kuinka pajon käytät kurikirjaa (tai jotain muuta oppikirjaa)? a) Tututun aiheeeen ennen uentoja b) Luen kirjaa uentojen jäkeen c) Luen oppikirjaa ähinnä akareita tehdeä d) n koke oppikirjaan aup Kappae
tt + ZMn-0. b) Laske liikeyhtälöiden avulla kuinka suuritien kaltevuuden (kulman a)tulee olla, jotta auto pysyisi tiellä nastattomilla renkailla?
 FYSKKA (FY515. KURSS Pvörmnen a eravaao vasraa KUUTEEN (6)TEHTÄVÄÄN KOE 31.01.2014 1. a) Men askeaan normaakhyvyys a angenkhyvyys. Anna kaava a seä kaavoen suuree. b) Määree sanases a maemaases pyörmsmäärä.
FYSKKA (FY515. KURSS Pvörmnen a eravaao vasraa KUUTEEN (6)TEHTÄVÄÄN KOE 31.01.2014 1. a) Men askeaan normaakhyvyys a angenkhyvyys. Anna kaava a seä kaavoen suuree. b) Määree sanases a maemaases pyörmsmäärä.
SAVONLINNAN KAUPUNKI KAAVOITUSKATSAUS Tekninen toimiala
 ONLINNN UUNI OITUTU T T g OITUTU Jd LITU OLET T IEILLÄ OLET T ä y - ä, ä d UUDET HNEET, EI OITUÄÄTÖTÄ NÄYTTÖOIUET UNTOITU OLLITUINEN LIITTEET:,, y, - Eä- yä yö yyd: T / O: O, ONLINN d:, Fx: - äö: ()f :wwwf
ONLINNN UUNI OITUTU T T g OITUTU Jd LITU OLET T IEILLÄ OLET T ä y - ä, ä d UUDET HNEET, EI OITUÄÄTÖTÄ NÄYTTÖOIUET UNTOITU OLLITUINEN LIITTEET:,, y, - Eä- yä yö yyd: T / O: O, ONLINN d:, Fx: - äö: ()f :wwwf
Luento 6 Luotettavuus ja vikaantumisprosessit
 Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
FCG Planeko Oy HELSINGIN KAUPUNKI MUNKKINIEMEN KÄYTTÄJÄKYSELY. Yhteenveto ja johtopäätökset 0100-D1194
 FCG P Oy HELSINGIN AUPUNI UNINIEEN ÄYÄJÄYSELY Yhv hääö -D9..9 FCG P Oy Yhv hääö () SISÄLLYSLUEELO YLEISÄ... YSELY.... V d.... Y d h....3 Ad v.... Ad äyö.... Lh.... Eöyy v... LIIEE (CD)...... yyyh v...
FCG P Oy HELSINGIN AUPUNI UNINIEEN ÄYÄJÄYSELY Yhv hääö -D9..9 FCG P Oy Yhv hääö () SISÄLLYSLUEELO YLEISÄ... YSELY.... V d.... Y d h....3 Ad v.... Ad äyö.... Lh.... Eöyy v... LIIEE (CD)...... yyyh v...
4.3 Liikemäärän säilyminen
 Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Mekaniikan jatkokurssi Fys102
 Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
DEE-53000 Sähkömagneettisten järjestelmien lämmönsiirto
 DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
AIKAKAUSLEHDET. tammik. Suomen Suurin SiSuStuSlehti. Kevään. värikkäät astiat. Talvi 1/0. arke. herkut. retkel MAK
 1 UU mmk 2006 AIKAKAUSLHDT 75 : O R V A I L m U J Am I M Kää JAS ä M A KU r 0 1 ä y ö d K h h H r Sm Sr SSSSh ärkkää RUOKA, JUOM A, KITT IÖ, M AT K A ILU, HY VIVO ITI r y, y 3 ää & r h r d 2008 öö r g
1 UU mmk 2006 AIKAKAUSLHDT 75 : O R V A I L m U J Am I M Kää JAS ä M A KU r 0 1 ä y ö d K h h H r Sm Sr SSSSh ärkkää RUOKA, JUOM A, KITT IÖ, M AT K A ILU, HY VIVO ITI r y, y 3 ää & r h r d 2008 öö r g
INTERFERENSSIN VAIKUTUS LINEAARISESSA MODULAATIOSSA
 INTERFERENSSIN VIUTUS LINERISESS MOULTIOSS Teolkenneeknkka I 521359 a äkkänen Osa 15 1 19 Inefeenssn vakuus lneaasessa odulaaossa Radoaausa nefeenssä RFI sn usa äeselsä, kun oa kanoaaloaauus on lähellä
INTERFERENSSIN VIUTUS LINERISESS MOULTIOSS Teolkenneeknkka I 521359 a äkkänen Osa 15 1 19 Inefeenssn vakuus lneaasessa odulaaossa Radoaausa nefeenssä RFI sn usa äeselsä, kun oa kanoaaloaauus on lähellä
KOE 2 Ympäristöekonomia
 Helingin yliopio Valinakoe.5. Maaalou-meäieeellinen iedekuna KOE Ympäriöekonomia Sekä A- eä B-oioa ulee aada vähinään 5 pieä. Mikäli A-oion piemäärä on vähemmän kuin 5 pieä B-oio jäeään arvoelemaa. B-OSIO
Helingin yliopio Valinakoe.5. Maaalou-meäieeellinen iedekuna KOE Ympäriöekonomia Sekä A- eä B-oioa ulee aada vähinään 5 pieä. Mikäli A-oion piemäärä on vähemmän kuin 5 pieä B-oio jäeään arvoelemaa. B-OSIO
RATKAISUT: 8. Momentti ja tasapaino
 Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
PARTIKKELIN KINETIIKKA
 PTKKELN KNETKK Newonin laki ma m& - on paikkeliin aikuaien oimien eulani - m on paikkelin maa - a & on paikkelin aboluuinen kiih Suoaiiaien liikkeen liikehälö (liikeuuna : m a 0 z 0 Taoliikkeen liikehälö
PTKKELN KNETKK Newonin laki ma m& - on paikkeliin aikuaien oimien eulani - m on paikkelin maa - a & on paikkelin aboluuinen kiih Suoaiiaien liikkeen liikehälö (liikeuuna : m a 0 z 0 Taoliikkeen liikehälö
HYVINKÄÄN KAUPUNKI KUNTATEKNIIKKA
 USUNTO X.. HYNÄÄN UUN UNTTEN o Hgo h y Coygh öyy Fd Oy X X SSÄYS YESTÄ... OHJ J OHJESOOSUHTEET... To j... To j... To, j... To j... To j... To j U... UEEN RENNETTUUS UONNOSEEN ERUSTUEN.... Yä.... R....
USUNTO X.. HYNÄÄN UUN UNTTEN o Hgo h y Coygh öyy Fd Oy X X SSÄYS YESTÄ... OHJ J OHJESOOSUHTEET... To j... To j... To, j... To j... To j... To j U... UEEN RENNETTUUS UONNOSEEN ERUSTUEN.... Yä.... R....
r i m i v i = L i = vakio, (2)
 4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
Viivakuormituksen potentiaalienergia saadaan summaamalla viivan pituuden yli
 hum.9. oiman potentiaalienergia Potentiaalienergiata puhutaan, kun kappaleeeen vaikuttaa jokin konervatiivinen voima. oima on konervatiivinen, jo en tekemä tö vaikutupieen iirteä tiettä paikata toieen
hum.9. oiman potentiaalienergia Potentiaalienergiata puhutaan, kun kappaleeeen vaikuttaa jokin konervatiivinen voima. oima on konervatiivinen, jo en tekemä tö vaikutupieen iirteä tiettä paikata toieen
RATKAISUT: 17. Tasavirtapiirit
 Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Mat Koesuunnittelu ja tilastolliset mallit
 Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
Vuoden Beauceron -säännöt (voimassa alkaen) Yleisiä periaatteita
 Vuoden Beauceron -äännöt (vomaa 1.1.2017 alkaen) Yleä peraatteta Klpalukau on kalentervuo. Mukaan hyväkytään van KoraNetta löytyvät tuloket pl. erkeen pteytetyt arvoklpalut. Yhden uortuken pteet muodotuvat
Vuoden Beauceron -äännöt (vomaa 1.1.2017 alkaen) Yleä peraatteta Klpalukau on kalentervuo. Mukaan hyväkytään van KoraNetta löytyvät tuloket pl. erkeen pteytetyt arvoklpalut. Yhden uortuken pteet muodotuvat
PD-säädin PID PID-säädin
 -äädin - äätö on ykinkertainen äätömuoto, jota voidaan kutua myö uhteuttavaki äädöki. Sinä lähtöignaali on uoraa uhteea tuloignaalin. -äätimen uhdealue kertoo kuinka paljon mittauuure aa muuttua ennen
-äädin - äätö on ykinkertainen äätömuoto, jota voidaan kutua myö uhteuttavaki äädöki. Sinä lähtöignaali on uoraa uhteea tuloignaalin. -äätimen uhdealue kertoo kuinka paljon mittauuure aa muuttua ennen
C B A. Kolmessa ensimmäisessä laskussa sovelletaan Newtonin 2. ja 3. lakia.
 Jako 4: Dynamiikan peruteet jatkuu, työ ja energia Näiden tehtävien viimeinen palautu- tai näyttöpäivä on tiitaina 23.5.2017. Ektra-tehtävät vataavat kolmea tehtävää, kun kurin lopua laketaan lakuharjoitupiteitä.
Jako 4: Dynamiikan peruteet jatkuu, työ ja energia Näiden tehtävien viimeinen palautu- tai näyttöpäivä on tiitaina 23.5.2017. Ektra-tehtävät vataavat kolmea tehtävää, kun kurin lopua laketaan lakuharjoitupiteitä.
TPE AIRRPORT VAIHE 2 MISSIO
 MISSIO ARRpor onepn voeen on edää j luod lplueu elnenoelämälle oo eeläeä j eeeä Suome Hyvä meju j omv nnväle yheyde Eurooppn edeuv eä yryä eä nl edämään enää vuorovuu Yheyde j hyvä meju edeuv myö mlun
MISSIO ARRpor onepn voeen on edää j luod lplueu elnenoelämälle oo eeläeä j eeeä Suome Hyvä meju j omv nnväle yheyde Eurooppn edeuv eä yryä eä nl edämään enää vuorovuu Yheyde j hyvä meju edeuv myö mlun
Taiteen ja kulttuurin yleissuunnitelma Kuopion Saaristokaupunki
 Taeen ja kuuurn yessuunnema Kuopon Saarsokaupunk 2.4.2007 HL Taeen ja kuuurn yessuunnema Kuopon Saarsokaupunk Johdano Kuopon Saarsokaupungn Taeen kaava yhdsää aeen, kuuurn ja rakenamsen avan uudea avaa.
Taeen ja kuuurn yessuunnema Kuopon Saarsokaupunk 2.4.2007 HL Taeen ja kuuurn yessuunnema Kuopon Saarsokaupunk Johdano Kuopon Saarsokaupungn Taeen kaava yhdsää aeen, kuuurn ja rakenamsen avan uudea avaa.
LUKION FYSIIKKAKILPAILU 8.11.2005 avoimen sarjan vast AVOIN SARJA
 LKION FYSIIKKAKILPAIL 8..5 avoien arjan vat AVOIN SARJA Kirjoita tektaten koepaperiin oa niei, kotiooitteei, ähköpotiooitteei, opettajai nii ekä koului nii. Kilpailuaikaa on inuuttia. Sekä tehtävä- että
LKION FYSIIKKAKILPAIL 8..5 avoien arjan vat AVOIN SARJA Kirjoita tektaten koepaperiin oa niei, kotiooitteei, ähköpotiooitteei, opettajai nii ekä koului nii. Kilpailuaikaa on inuuttia. Sekä tehtävä- että
BINÄÄRINEN SYNKRONINEN TIEDONSIIRTO KAISTARAJOITTAMATTOMILLA MIELIVALTAISILLA PULSSIMUODOILLA SOVITETTU SUODATIN JA SEN SUORITUSKYKY AWGN-KANAVASSA
 BINÄÄRINN SYNKRONINN IDONSIIRO KAISARAJOIAMAOMILLA MILIVALAISILLA PULSSIMUODOILLA SOVIU SUODAIN JA SN SUORIUSKYKY AWGN-KANAVASSA Millaiia aalomuooja perupuleja yypilliei käyeään? 536A ieoliikenneekniikka
BINÄÄRINN SYNKRONINN IDONSIIRO KAISARAJOIAMAOMILLA MILIVALAISILLA PULSSIMUODOILLA SOVIU SUODAIN JA SN SUORIUSKYKY AWGN-KANAVASSA Millaiia aalomuooja perupuleja yypilliei käyeään? 536A ieoliikenneekniikka
INTERFERENSSIN VAIKUTUS LINEAARISISSA MODULAATIOISSA
 1 INTERFERENSSIN VIKUTUS LINERISISS MOULTIOISS Men yksaajunen häökanoaalo haaa lasua? 521357 Teolkenneeknkka I Osa 18 Ka Käkkänen Kevä 2015 KERTUST 2 Kanoaaloodulaaolle: os[2πf φ] Lneaanen odulaao Vahee
1 INTERFERENSSIN VIKUTUS LINERISISS MOULTIOISS Men yksaajunen häökanoaalo haaa lasua? 521357 Teolkenneeknkka I Osa 18 Ka Käkkänen Kevä 2015 KERTUST 2 Kanoaaloodulaaolle: os[2πf φ] Lneaanen odulaao Vahee
Täydennetään teoriaa seuraavilla tuloksilla tapauksista, joissa moninkertaisen ominaisarvon geometrinen kertaluku on yksi:
 77 Aemmn oleen, eä mars A on dagonalsouva. Tällanen on lanne äsmälleen sllon, un joasen omnasarvon geomernen eraluu on sama un algebrallnen. Täydenneään eoraa seuraavlla uloslla apaussa, jossa monnerasen
77 Aemmn oleen, eä mars A on dagonalsouva. Tällanen on lanne äsmälleen sllon, un joasen omnasarvon geomernen eraluu on sama un algebrallnen. Täydenneään eoraa seuraavlla uloslla apaussa, jossa monnerasen
Luento 6 Luotettavuus Koherentit järjestelmät
 Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Flow shop, työnvaiheketju, joustava linja, läpivirtauspaja. Kahden koneen flow shop Johnsonin algoritmi
 Flow shop önvaheeju jousava lnja läpvrauspaja Flow shopssa önvaheden järjess on sama alla uoella Kosa vahea vo edelää jono vova ö olla vaheleva ja ö vova ohaa osensa äl ö evä oha osaan puhuaan permuaaoaaaulusa
Flow shop önvaheeju jousava lnja läpvrauspaja Flow shopssa önvaheden järjess on sama alla uoella Kosa vahea vo edelää jono vova ö olla vaheleva ja ö vova ohaa osensa äl ö evä oha osaan puhuaan permuaaoaaaulusa
Helka-neiti kylvyssä
 Helkanet kylvyssä Frtz Grunbaum suom. M. A. ummnen Solo Tenor???? m Fred Raymond sov. G. Ventur 2001 Tä män täs tä p Bass Uu m g Wow uu uu uu uu uu uu uu, uu p wow wow wow wow wow wow wow, wow uu wow Mart
Helkanet kylvyssä Frtz Grunbaum suom. M. A. ummnen Solo Tenor???? m Fred Raymond sov. G. Ventur 2001 Tä män täs tä p Bass Uu m g Wow uu uu uu uu uu uu uu, uu p wow wow wow wow wow wow wow, wow uu wow Mart
Derivoimalla ensimmäinen komponentti, sijoittamalla jälkimmäisen derivaatta siihen ja eliminoimalla x. saadaan
 87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
OSALLISTUMIS- JA ARVIOINTISUUNNITELMA. Hakanpään asemakaavan muutos, kortteli 360. Liite Suunnittelualue
 OSLLSTUMS- J RVONTSUUNNTLM Liie Hakanpään aemakaan muuo, korei 0. Suunnieuaue Tämä oaiumi- a ioiniuunniema kokee Uian kaupungin Nummean kaupunginoaa () iaien Hakanpään aemakaan koreia 0. Hakanpään.. hieua
OSLLSTUMS- J RVONTSUUNNTLM Liie Hakanpään aemakaan muuo, korei 0. Suunnieuaue Tämä oaiumi- a ioiniuunniema kokee Uian kaupungin Nummean kaupunginoaa () iaien Hakanpään aemakaan koreia 0. Hakanpään.. hieua
Ura- / kouluttautumisprosessi Avoin ammattiopistotarjonta: Henkilökohtainen ohjaus ja tukiprosessi. T y ö e l ä m ä l ä h t ö i s y y s
 Avn aap Ojaa (5 pv): Jauunna uuun auua, pua, pnjn ppuunaaaa, pppuuuun aaa Hnann jau ja up Ua- / uuauup Avn aapajna: unnn a Anauua unnn a YO-ana Kuuua unn n a Ojaa (vnn 10 pv): Onunn aaan, aan ja uuuaduun
Avn aap Ojaa (5 pv): Jauunna uuun auua, pua, pnjn ppuunaaaa, pppuuuun aaa Hnann jau ja up Ua- / uuauup Avn aapajna: unnn a Anauua unnn a YO-ana Kuuua unn n a Ojaa (vnn 10 pv): Onunn aaan, aan ja uuuaduun
2.4 Erikoistapaus kantalukuna 10 eli kymmenen potenssit
 2.4 Kyenen potenit 2.4 Erikoitapau kantaukuna ei kyenen potenit Potenin kantaukuna käytetään kyentä erityieti, kun uku on erittäin uuri tai erittäin pieni. Tää auttaa näitten ääritapauten hahottaiea. Tarkateaan
2.4 Kyenen potenit 2.4 Erikoitapau kantaukuna ei kyenen potenit Potenin kantaukuna käytetään kyentä erityieti, kun uku on erittäin uuri tai erittäin pieni. Tää auttaa näitten ääritapauten hahottaiea. Tarkateaan
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
Jaetut resurssit. Tosiaikajärjestelmät Luento 5: Resurssien hallinta ja prioriteetit. Mitä voi mennä pieleen? Resurssikilpailu ja estyminen
 Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Markovin ketju. Stokastinen prosessi. Markovin ketju. Markovin malli: DNA esimerkki. M-ketju:homogeeninen ja ei-homogeeninen
 Soke roe Mkäl lmöö lyy uuu (okuu), uhu ok roee. Soke roe vod myö ähdä oukko umuuu X() oll o ey relo x(). Proe o oääre, o e lolle omuude evä muuu myöä (em. odourvo, vr). Ak vo oll kuv dkree, mo X() Mrkov
Soke roe Mkäl lmöö lyy uuu (okuu), uhu ok roee. Soke roe vod myö ähdä oukko umuuu X() oll o ey relo x(). Proe o oääre, o e lolle omuude evä muuu myöä (em. odourvo, vr). Ak vo oll kuv dkree, mo X() Mrkov
AVARUUSGEOMETRIA. Suorat ja tasot avaruudessa
 VRUUSGEOMERI varuusgeometria tarkasteee kuvioita, joiden kaikki osat eivät oe samassa tasossa. Sana avaruus tarkoittaa yeisesti n-uotteista, n 3, avaruutta. (Lukiossa ähes aina n = 3.) Suorat ja tasot
VRUUSGEOMERI varuusgeometria tarkasteee kuvioita, joiden kaikki osat eivät oe samassa tasossa. Sana avaruus tarkoittaa yeisesti n-uotteista, n 3, avaruutta. (Lukiossa ähes aina n = 3.) Suorat ja tasot
Jakso 4: Dynamiikan perusteet jatkuu, työ ja energia Näiden tehtävien viimeinen palautus- tai näyttöpäivä on maanantaina
 Jako 4: Dynamiikan peruteet jatkuu, työ ja energia Näiden tehtävien viimeinen palautu- tai näyttöpäivä on maanantaina 8.8.2016. Kolmea enimmäieä lakua ovelletaan Newtonin 2. ja 3. lakia. T 4.1 (pakollinen):
Jako 4: Dynamiikan peruteet jatkuu, työ ja energia Näiden tehtävien viimeinen palautu- tai näyttöpäivä on maanantaina 8.8.2016. Kolmea enimmäieä lakua ovelletaan Newtonin 2. ja 3. lakia. T 4.1 (pakollinen):
Mat-2.090 Sovellettu todennäköisyyslasku A
 Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
/If# Lu.ErTeL.a It?.?. /~.3
 040/Magn.omna./SMOY/73 /f# Lu.ErTeL.a t?.?. /~.3 ~~,u~~ - ~,~ ()~.4~~- ~ ;(t-1 ~ ~ tf*#?~/ ~ #~. ~ KVNAYTTEDEN MAGNEETTSTEN OMNASUUKSEN. MAARTYKSA v. 1973 Otanem 28.1 2.1 973 Pea Lappaa nen Rautaruu Oy:n
040/Magn.omna./SMOY/73 /f# Lu.ErTeL.a t?.?. /~.3 ~~,u~~ - ~,~ ()~.4~~- ~ ;(t-1 ~ ~ tf*#?~/ ~ #~. ~ KVNAYTTEDEN MAGNEETTSTEN OMNASUUKSEN. MAARTYKSA v. 1973 Otanem 28.1 2.1 973 Pea Lappaa nen Rautaruu Oy:n
Valmistaminen tai ostaminen varastoon tasainen kysyntä
 Valmsamnen varasoon Make-o-sock (MTS) -uoanoapaa käyävä yrykse, joka valmsava loppuuoea a osa erssä ja valmsuksen jälkeen varasova uoee varasoon odoamaan kysynää MTS-uoanomalln euna ova lyhye omusaja asakkaalle,
Valmsamnen varasoon Make-o-sock (MTS) -uoanoapaa käyävä yrykse, joka valmsava loppuuoea a osa erssä ja valmsuksen jälkeen varasova uoee varasoon odoamaan kysynää MTS-uoanomalln euna ova lyhye omusaja asakkaalle,
Tekes: Korjausrakentamisen kehittäminen -teema TEEMAN TILANNEKUVA
 eke: Krurkee kehäe ee EEMN ILNNEKUV J Sre, kvr, V llce Prer Oy 20.11.2013 J Sre Älykä rkeeu elypärö: V Lkee Rkeuke Su edelläkävä älykkää re plvelu eklg, k udv u ue, yö vp kkuuk. eke edää käyäe, yrye ekä
eke: Krurkee kehäe ee EEMN ILNNEKUV J Sre, kvr, V llce Prer Oy 20.11.2013 J Sre Älykä rkeeu elypärö: V Lkee Rkeuke Su edelläkävä älykkää re plvelu eklg, k udv u ue, yö vp kkuuk. eke edää käyäe, yrye ekä
Öljynvaihtohuolto 7 500 km:n/1 vuoden välein
 Sivu 1/5 Huooauuko Seuraavassa uvussa on Vokswagen-merkin uu huooauuko ja -ohjee. Koska ennen useia myyniaueia käyeiin omia huoo-ohjeia, useimmien eriyisoosuheisa johuen, nämä on ueeu huooauukoissa markkinakohaisin
Sivu 1/5 Huooauuko Seuraavassa uvussa on Vokswagen-merkin uu huooauuko ja -ohjee. Koska ennen useia myyniaueia käyeiin omia huoo-ohjeia, useimmien eriyisoosuheisa johuen, nämä on ueeu huooauukoissa markkinakohaisin
Eo C)sl. oarl. d to E= J. o-= o cy) =uo. f,e. ic v. .o6. .9o. äji. :ir. ijo 96. {c o o. ';i _o. :fe. C=?i. t-l +) (- c rt, u0 C.
 C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
LÄNSI-LAAJASALON KÄYTTÄJÄKYSELY
 FCG P Oy HELINGIN AUPUNI LÄNI-LAAJAALON ÄYTTÄJÄYELY Yv ö -D.. FCG P Oy Yv ö () Hg.. L-L yyy -D IÄLLYLUETTELO YLEITÄ... YELY.... V d.... Y d.... Ad v.... Ad yö.... Eöyy v... LIITTEET... T... FCG P Oy Yv
FCG P Oy HELINGIN AUPUNI LÄNI-LAAJAALON ÄYTTÄJÄYELY Yv ö -D.. FCG P Oy Yv ö () Hg.. L-L yyy -D IÄLLYLUETTELO YLEITÄ... YELY.... V d.... Y d.... Ad v.... Ad yö.... Eöyy v... LIITTEET... T... FCG P Oy Yv
KAAVOITUSKATSAUS VALMISTUMASSA OLEVAT KAAVAT 3 VIREILLÄ OLEVAT KAAVAT 6 UUDET KAAVAHANKKEET, EI KAAVOITUSPÄÄTÖSTÄ 18 MAAKUNTAKAAVOITUS 18
 OIUU LIU OLE IEILLÄ OLE ä - ä, ä d UUDE HNEE, EI OIUÄÄÖÄ UNOIU OLLIUINEN LIIEE:,,, - d: / O: O, ONLINN d:, Fx: - äö: ()f :wwwf / / Höö, ääö B ä, - H, äö, H, N E,,, OIUU ää ä ä ää d ä ää ä, dää g äö- :
OIUU LIU OLE IEILLÄ OLE ä - ä, ä d UUDE HNEE, EI OIUÄÄÖÄ UNOIU OLLIUINEN LIIEE:,,, - d: / O: O, ONLINN d:, Fx: - äö: ()f :wwwf / / Höö, ääö B ä, - H, äö, H, N E,,, OIUU ää ä ä ää d ä ää ä, dää g äö- :
KVANTISOINTIKOHINA JA KANAVAN AWGN- KOHINA PULSSIKOODIMODULAATIOSSA
 KVANTIOINTIKOHINA JA KANAVAN AWGN- KOHINA PULIKOODIMODULAATIOA Teolkenneeknkka I 5359A Kar Kärkkänen Osa 6 5 Kvansonkohna PCM-järjeselmässä PCM:ssa on kaks vrhelähdeä:. kvansonkohna,. kanavan kohnan aheuama
KVANTIOINTIKOHINA JA KANAVAN AWGN- KOHINA PULIKOODIMODULAATIOA Teolkenneeknkka I 5359A Kar Kärkkänen Osa 6 5 Kvansonkohna PCM-järjeselmässä PCM:ssa on kaks vrhelähdeä:. kvansonkohna,. kanavan kohnan aheuama
12. laskuharjoituskierros, vko 16, ratkaisut
 1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
Mallivastaukset KA5-kurssin laskareihin, kevät 2009
 Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
a. Varsinainen prosessi on tuttua tilaesitysmuotoa:
 ELEC-C Sääöeniia 7. lauharjoiu Vaaue. r - K u K C y a. Varinainen proei on uua ilaeiymuooa: A Bu y C Kuvaa nähdään, eä ilamallin iäänmenona on u r K. Salaaria ei voi vähenää mariiia, joen un on n -veori,
ELEC-C Sääöeniia 7. lauharjoiu Vaaue. r - K u K C y a. Varinainen proei on uua ilaeiymuooa: A Bu y C Kuvaa nähdään, eä ilamallin iäänmenona on u r K. Salaaria ei voi vähenää mariiia, joen un on n -veori,
MO-teoria ja symmetria
 MO-teora ja symmetra () Kaks atomorbtaaa vovat muodostaa kaks moekyyorbtaaa - Stova orbtaa - ajottava orbtaa () Atomorbtaaen energoden otava keskenään samansuurusa () Atomorbtaaen symmetravaatmukset LCAO
MO-teora ja symmetra () Kaks atomorbtaaa vovat muodostaa kaks moekyyorbtaaa - Stova orbtaa - ajottava orbtaa () Atomorbtaaen energoden otava keskenään samansuurusa () Atomorbtaaen symmetravaatmukset LCAO
SUOMEN AKTUAARIYHDISTYS THE ACTUARIAL SOCIETY OF FINLAND
 97 SUOMEN AKTUAARIYHDISTYS THE ACTUARIAL SOCIETY OF FINLAND WORKING PAPERS ISSN 0781-4410 SUOMEN AKTUAARIYHDISTYS The Acuarial Sociey o Finland 97 Auranen, Ani Omavauueu (2009) Omavauueu SHV-yö Ani Auranen
97 SUOMEN AKTUAARIYHDISTYS THE ACTUARIAL SOCIETY OF FINLAND WORKING PAPERS ISSN 0781-4410 SUOMEN AKTUAARIYHDISTYS The Acuarial Sociey o Finland 97 Auranen, Ani Omavauueu (2009) Omavauueu SHV-yö Ani Auranen
KOHINAN JA VAIHEVIRHEEN VAIKUTUS VAIHEKOHERENTEILLA JÄRJESTELMILLÄ
 KOHINAN JA VAIHVIRHN VAIKUTUS VAIHKOHRNTILLA JÄRJSTLMILLÄ Mie vaihee epävaruu vaikuaa kohereia ilaiua? Mikä o piloiigaali? 557A Tieoliikeeekiikka I Oa 6 Kari Kärkkäie Kevä 05 VAIHVIRHN YLINN ANALYYSI QSB
KOHINAN JA VAIHVIRHN VAIKUTUS VAIHKOHRNTILLA JÄRJSTLMILLÄ Mie vaihee epävaruu vaikuaa kohereia ilaiua? Mikä o piloiigaali? 557A Tieoliikeeekiikka I Oa 6 Kari Kärkkäie Kevä 05 VAIHVIRHN YLINN ANALYYSI QSB
- lzcht Frwaria ;:h'5ensuuntaisprc j sktioita
 Krjallsuuden kdytto kelletty.,p,,':. Kun prustuksessa on estetty osen muodot ja asennust..,;,!:/ j Zrj estys, on sllon.kyseessd..' + '. cb. ksyttdohj eprustus. : *'. patenttprustus'. tydprustus :. : G
Krjallsuuden kdytto kelletty.,p,,':. Kun prustuksessa on estetty osen muodot ja asennust..,;,!:/ j Zrj estys, on sllon.kyseessd..' + '. cb. ksyttdohj eprustus. : *'. patenttprustus'. tydprustus :. : G
Puupintaisen sandwichkattoelementin. lujuuslaskelmat. Sisältö:
 Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
menetelmän laskennalliset tekniikat Epäkäyvän kantaratkaisun parantaminen
 Smpex-menetemän menetemän askennaset teknkat 8. ento: Prmaa-smpex S ysteemanayysn Laboratoro Teknnen korkeako Matemaattsten agortmen ohemont Kevät 8 / Epäkäyvän kantaratkasn parantamnen. vaheen yenen smpex-menetemä
Smpex-menetemän menetemän askennaset teknkat 8. ento: Prmaa-smpex S ysteemanayysn Laboratoro Teknnen korkeako Matemaattsten agortmen ohemont Kevät 8 / Epäkäyvän kantaratkasn parantamnen. vaheen yenen smpex-menetemä
CHEVROLET JA FORD OSIEN
 1939 CHEVROLET JA FORD OSEN HNNASTO SUOMEN AUTOVARUSTE TURKU YLOPSTONKATU 7 PUH: KONTTOR 3908, MYYMÄLÄ JA VARASTO 3907, 3917 SÄHKÖ O S: AUTOVARUSTE :60 335285 335446-7-8(84018) 335679 335977 335978 337709
1939 CHEVROLET JA FORD OSEN HNNASTO SUOMEN AUTOVARUSTE TURKU YLOPSTONKATU 7 PUH: KONTTOR 3908, MYYMÄLÄ JA VARASTO 3907, 3917 SÄHKÖ O S: AUTOVARUSTE :60 335285 335446-7-8(84018) 335679 335977 335978 337709
Usko, toivo ja rakkaus
 Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Sinusta Kvantin. toimittaja?
 j? jö j jj j j j IO j j j j yj jj föö j y j j j j j - j ö ö j j H j j 05! A ö j ö @fyyf! jj y j Ey fy j! O j! 3 & Pjj 5 Pj 6 yy 8 JU: & H 5 y 8 Q 0 M y j j J : III/ II - /0 P 50 P C Φ- Mj A O H H J J M
j? jö j jj j j j IO j j j j yj jj föö j y j j j j j - j ö ö j j H j j 05! A ö j ö @fyyf! jj y j Ey fy j! O j! 3 & Pjj 5 Pj 6 yy 8 JU: & H 5 y 8 Q 0 M y j j J : III/ II - /0 P 50 P C Φ- Mj A O H H J J M
15.8.2005 KUORMITUSKÄYRÄSTÖT... 16 5. VALMISTUS JA LAADUNVALVONTA... 17
 SUUNNITTELUOHJE 1 () SISÄLLYS 1. YLEISTÄ... 1.1 ESIJÄNNITETTY TERÄSBETONI-YHDISTELMÄRAKENNE... 1.1.1 LBL-pa... 1.1. LB-pa... 1. KÄYTTÖKOHTEET... 1. REUNA- JA KESKIPALKKITYYPIT.... LIITOSTAVAT... 7.1 LIITOS
SUUNNITTELUOHJE 1 () SISÄLLYS 1. YLEISTÄ... 1.1 ESIJÄNNITETTY TERÄSBETONI-YHDISTELMÄRAKENNE... 1.1.1 LBL-pa... 1.1. LB-pa... 1. KÄYTTÖKOHTEET... 1. REUNA- JA KESKIPALKKITYYPIT.... LIITOSTAVAT... 7.1 LIITOS
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
MONIKAPPALEMEKANIIKAN MALLINTAMINEN PARAMETRISOIMALLA SIDOSMONISTO
 IIVISELMÄ MONIKAPPALEMEKANIIKAN MALLINAMINEN PARAMERISOIMALLA SIDOSMONISO J. MÄKINEN & H. MARJAMÄKI eknllen ekankan a optonnn lato apereen teknllnen ylopto PL 589 33101 AMPERE ää etykeä kuvataan lyhyet
IIVISELMÄ MONIKAPPALEMEKANIIKAN MALLINAMINEN PARAMERISOIMALLA SIDOSMONISO J. MÄKINEN & H. MARJAMÄKI eknllen ekankan a optonnn lato apereen teknllnen ylopto PL 589 33101 AMPERE ää etykeä kuvataan lyhyet
Kiinteän omaisuuden hankinta- ja luovutusohjeisto 2019
 S ä d - T T SISÄLLYSLUETTELO RATAISUVALTA JA ALLEIRJOITTAINEN V ää dg YLEISET PERIAATTEET YLEISET HINNOITTELUPERUSTEET Hyöy Idd Hy V yy P YLEISET VARAUSSOPIUSEHDOT V L V ä O y d RAENTAISVELVOITE R VUORASOPIUSEN
S ä d - T T SISÄLLYSLUETTELO RATAISUVALTA JA ALLEIRJOITTAINEN V ää dg YLEISET PERIAATTEET YLEISET HINNOITTELUPERUSTEET Hyöy Idd Hy V yy P YLEISET VARAUSSOPIUSEHDOT V L V ä O y d RAENTAISVELVOITE R VUORASOPIUSEN
Sähköstaattinen energia
 ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
LAPUAN KAUPUNKI 8. LIUHTARIN KAUPUNGINOSA ASEMAKAAVAN KUMOAMINEN KUORTANEENTIE I
 . G ä y, ä y-, y-.., äydy.... äyö- ö.. yäyy g xx.xx. xx yäyy g xx.xx. xx - . - D.. d.. ääyä. ä y-, - y., ö ---, ---, ---, --- (ä) - --... - g - -. y - y d ä. - -,. - .., Ä, yydä g d ää :., ä äy äää ä-.
. G ä y, ä y-, y-.., äydy.... äyö- ö.. yäyy g xx.xx. xx yäyy g xx.xx. xx - . - D.. d.. ääyä. ä y-, - y., ö ---, ---, ---, --- (ä) - --... - g - -. y - y d ä. - -,. - .., Ä, yydä g d ää :., ä äy äää ä-.
3 m kaava-alueen rajan ulkopuolella oleva viiva. Korttelin, korttelinosan ja alueen raja.
 Aevmerkin Auiniloj korelilue. Urheilu- j virkiylveluj lue. Alueel voidn ijoi golf-kä. Meänkäielyä j -hoido ue o huomioon miemn eriyiiiree. - Riviloj j muid kykeyj uinrknu korelilue. Veilue. m kv-lue rjn
Aevmerkin Auiniloj korelilue. Urheilu- j virkiylveluj lue. Alueel voidn ijoi golf-kä. Meänkäielyä j -hoido ue o huomioon miemn eriyiiiree. - Riviloj j muid kykeyj uinrknu korelilue. Veilue. m kv-lue rjn
Ohjelmiston testaus ja laatu. Ohjelmistotekniikka dokumentointi
 Ohjelmson esaus ja laau Ohjelmsoeknkka dokumenon Ohjelmsoyöhön kuuluu oleellsena osana dokumenen krjoamnen laadukkaden dokumenen uoamnen vakeaa akaaulujen panaessa päälle, dokumenonnsa on helppo npsää
Ohjelmson esaus ja laau Ohjelmsoeknkka dokumenon Ohjelmsoyöhön kuuluu oleellsena osana dokumenen krjoamnen laadukkaden dokumenen uoamnen vakeaa akaaulujen panaessa päälle, dokumenonnsa on helppo npsää
TILATYYPPILUONNOKSIA Alustavat luonnokset keskustelun pohjaksi. Luonnos
 TILATYYPPILUONNOKSIA Auv u uu hj Lu Työyu V yöy, d hc-v, u Säyy 74,3 m2 HELPOSTI HUOLLETAVAA VERSTAS Mäyö ud 8 Bäd Väyymyö, hjyö yö 106,7 m2 Säyy 74,3 m2 SIIVOUSKEKSUS 7 14,9 m2 7,5 m2 Bäd 3 6,2 m2 S 85,0
TILATYYPPILUONNOKSIA Auv u uu hj Lu Työyu V yöy, d hc-v, u Säyy 74,3 m2 HELPOSTI HUOLLETAVAA VERSTAS Mäyö ud 8 Bäd Väyymyö, hjyö yö 106,7 m2 Säyy 74,3 m2 SIIVOUSKEKSUS 7 14,9 m2 7,5 m2 Bäd 3 6,2 m2 S 85,0
':(l,i l) 'iac: (å ;) (x 2v + z- o. I o, * 4z:20. 12, +8y 3z: l0. Thlousmatematiikan perusteet, onus ro 0 opettaja: Matti Laaksonen.
 Vaasan kesäyps, kesä 2013 Thusmaemakan perusee, nus r 0 peaja: Ma aaksnen 2. väke, (a 31.8.2013 Rakase 3 ehävää. Kun käsee ehävän, nn käsee sen kakk aakhda. Kkeessa saa a mukana askn (myös graanen ja auukkkrja
Vaasan kesäyps, kesä 2013 Thusmaemakan perusee, nus r 0 peaja: Ma aaksnen 2. väke, (a 31.8.2013 Rakase 3 ehävää. Kun käsee ehävän, nn käsee sen kakk aakhda. Kkeessa saa a mukana askn (myös graanen ja auukkkrja
l, ; i.'s ä E.ä E o gäästaefiiä,ggäeäeää;äggtää EI ;äe E H * eaä* E E 8EP.E .e= äe eääege F EEE;säääg lee sa 8NY ExE öe äec E= : ;H ä a(ü
 ,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
Pyörimisliike. Haarto & Karhunen.
 Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
ELÄKEKASSAN LASKUPERUSTEET TYÖNTEKIJÄN ELÄKELAIN MUKAISTA ELÄKETURVAA VARTEN
 ELÄKEKAAN LAKUPERUEE YÖNEKJÄN ELÄKELAN UKAA ELÄKEURAA AREN Kokooma 4.2.204. mesn kokoomaan ssällyey perusemuuos on ahseu 8..204. Eläkekassa oa erkseen hakea sosaal- ja ereysmnserön ahsusa laskuperuselleen.
ELÄKEKAAN LAKUPERUEE YÖNEKJÄN ELÄKELAN UKAA ELÄKEURAA AREN Kokooma 4.2.204. mesn kokoomaan ssällyey perusemuuos on ahseu 8..204. Eläkekassa oa erkseen hakea sosaal- ja ereysmnserön ahsusa laskuperuselleen.
TALVIKAUDEN LINJASTOSUUNNITELMALUONNOS
 1 () död 10 TIUDE -1 IJTOUUITEUOO öd J - d T g g d 09 - -d 1 %: 18 %: g J % d 09 11, d 0 % ö ö, d d, g d ö T - b ö d, d, ö T d T d d T, d ö J 11 (://f/f///), d, d -, ö d T 8, Fc 2 B, 1 T, 0-11, fx 0- @f,
1 () död 10 TIUDE -1 IJTOUUITEUOO öd J - d T g g d 09 - -d 1 %: 18 %: g J % d 09 11, d 0 % ö ö, d d, g d ö T - b ö d, d, ö T d T d d T, d ö J 11 (://f/f///), d, d -, ö d T 8, Fc 2 B, 1 T, 0-11, fx 0- @f,
YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY 1 YRITYSKOHTAISEN TEHOSTAMISPOTENTIAALIN MITTAAMINEN
 ENERGIAMARKKINAVIRASTO 1 Le 2 Säkön jakeluverkkoomnnan yryskoasen eosamsavoeen määrely YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY Asanosanen: Vaasan Säköverkko Oy Lyy pääökseen dnro 491/424/2007 Energamarkknavraso
ENERGIAMARKKINAVIRASTO 1 Le 2 Säkön jakeluverkkoomnnan yryskoasen eosamsavoeen määrely YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY Asanosanen: Vaasan Säköverkko Oy Lyy pääökseen dnro 491/424/2007 Energamarkknavraso
HF-TAAJUISEN ANTENNIN INTEGROINTI MOBIILIIN RFID-LUKIJAAN
 Toknkan oao Ju Numma HF-TAAJUISEN ANTENNIN INTEGROINTI MOBIILIIN RFID-LUKIJAAN Dpomyö Ah hyväkyy oknkan oaon oaonuvoon kokouka 11.9.2006 Takaaja: Pofo Pkka Loua Akuana Tämä dpomyö on hy Tampn knn yopon
Toknkan oao Ju Numma HF-TAAJUISEN ANTENNIN INTEGROINTI MOBIILIIN RFID-LUKIJAAN Dpomyö Ah hyväkyy oknkan oaon oaonuvoon kokouka 11.9.2006 Takaaja: Pofo Pkka Loua Akuana Tämä dpomyö on hy Tampn knn yopon
7. Pyörivät sähkökoneet
 Pyörivät ähkökoneet 7-1 7. Pyörivät ähkökoneet Mekaanien energian muuntamieen ähköenergiaki ekä ähköenergian muuntamieen takaiin mekaanieki energiaki käytetään ähkökoneita. Koneita, jotka muuntavat mekaanien
Pyörivät ähkökoneet 7-1 7. Pyörivät ähkökoneet Mekaanien energian muuntamieen ähköenergiaki ekä ähköenergian muuntamieen takaiin mekaanieki energiaki käytetään ähkökoneita. Koneita, jotka muuntavat mekaanien
Kirjainkiemurat - mallisivu (c)
 Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Tehtävän 1 moottorin kuormana an työkone, jonka momentti on vakio T=30 Nm. Laske
 SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
KUNTA KÄRÄJÄOIKEUS ULOSOTTOVIRASTO MAISTRAATTI LÄÄNI HOVI
 EUSPAA UNA ÄÄJÄEUS MASAA ÄÄN H UNAN EUS HA.N AAA 020 682 PANMAAN Ä EPNAU 5 A 33101 AMPEE PANMAAN AEASEN SUMPAA P 38, APANAU 5 37601 AEAS FAX 029 562 3669 SSÄSUMEN MASAA JYÄSYÄN YSÖ YPSNAU 28 FAX info.sisasuomi@maistraatti.fi
EUSPAA UNA ÄÄJÄEUS MASAA ÄÄN H UNAN EUS HA.N AAA 020 682 PANMAAN Ä EPNAU 5 A 33101 AMPEE PANMAAN AEASEN SUMPAA P 38, APANAU 5 37601 AEAS FAX 029 562 3669 SSÄSUMEN MASAA JYÄSYÄN YSÖ YPSNAU 28 FAX info.sisasuomi@maistraatti.fi
