Johdatus L A TEXiin. 7. Taulukot ja kuvat Markus Harju. Matemaattiset tieteet
|
|
|
- Arttu Lehtinen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Johdtus L A TEXiin 7. Tulukot j kuvt Mrkus Hrju Mtemttiset tieteet
2 7. Tulukot j kuvt Johdtus LTeXiin (2/11) Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr
3 Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr Ympäristön rgumentiksi nnetn srkemäärittely, jok on kirjimist l, c j r muodostuv jono. Sillä ilmoitetn srkkeiden lukumäärän lisäksi kunkin srkkeen tsus joko vsemmlle, keskelle ti oikelle (left, center, right). 7. Tulukot j kuvt Johdtus LTeXiin (2/11)
4 Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr Ympäristön rgumentiksi nnetn srkemäärittely, jok on kirjimist l, c j r muodostuv jono. Sillä ilmoitetn srkkeiden lukumäärän lisäksi kunkin srkkeen tsus joko vsemmlle, keskelle ti oikelle (left, center, right). Rivit erotelln khdell kenoviivll \\ j srkkeet merkillä & (vrt. mtriisit). 7. Tulukot j kuvt Johdtus LTeXiin (2/11)
5 7. Tulukot j kuvt Johdtus LTeXiin (2/11) Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr Ympäristön rgumentiksi nnetn srkemäärittely, jok on kirjimist l, c j r muodostuv jono. Sillä ilmoitetn srkkeiden lukumäärän lisäksi kunkin srkkeen tsus joko vsemmlle, keskelle ti oikelle (left, center, right). Rivit erotelln khdell kenoviivll \\ j srkkeet merkillä & (vrt. mtriisit). Esim. \begin{tbulr}{lccc} JYP &31 &12 &15\\ KlP &31 &11 &16\\ Lukko &30 &12 &16\\ HIFK &30 &8 &20 \end{tbulr} JYP KlP Lukko HIFK
6 7. Tulukot j kuvt Johdtus LTeXiin (2/11) Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr Ympäristön rgumentiksi nnetn srkemäärittely, jok on kirjimist l, c j r muodostuv jono. Sillä ilmoitetn srkkeiden lukumäärän lisäksi kunkin srkkeen tsus joko vsemmlle, keskelle ti oikelle (left, center, right). Rivit erotelln khdell kenoviivll \\ j srkkeet merkillä & (vrt. mtriisit). Esim. \begin{tbulr}{lccc} JYP &31 &12 &15\\ JYP KlP &31 &11 &16\\ KlP Lukko &30 &12 &16\\ Lukko HIFK &30 &8 &20 HIFK \end{tbulr} Jokisell rivillä tulee oll yhtä mont & merkkiä!
7 7. Tulukot j kuvt Johdtus LTeXiin (3/11) Tulukot II Srkkeet voi erott toisistn viivll lisäämällä srkemäärittelyyn pystyviivn hluttuun kohtn
8 7. Tulukot j kuvt Johdtus LTeXiin (3/11) Tulukot II Srkkeet voi erott toisistn viivll lisäämällä srkemäärittelyyn pystyviivn hluttuun kohtn Esim. \begin{tbulr}{l ccc} JYP &31 &12 &15\\ KlP &31 &11 &16\\ Lukko &30 &12 &16\\ HIFK &30 &8 &20 \end{tbulr} JYP KlP Lukko HIFK
9 7. Tulukot j kuvt Johdtus LTeXiin (3/11) Tulukot II Srkkeet voi erott toisistn viivll lisäämällä srkemäärittelyyn pystyviivn hluttuun kohtn Esim. \begin{tbulr}{l ccc} JYP &31 &12 &15\\ KlP &31 &11 &16\\ Lukko &30 &12 &16\\ HIFK &30 &8 &20 \end{tbulr} JYP KlP Lukko HIFK Rivien väliin voi lisätä vkviivoj komennoll \hline
10 Tulukot II Srkkeet voi erott toisistn viivll lisäämällä srkemäärittelyyn pystyviivn hluttuun kohtn Esim. \begin{tbulr}{l ccc} JYP &31 &12 &15\\ KlP &31 &11 &16\\ Lukko &30 &12 &16\\ HIFK &30 &8 &20 \end{tbulr} JYP KlP Lukko HIFK Rivien väliin voi lisätä vkviivoj komennoll \hline Esim. \begin{tbulr}{lccc} JYP &31 &12 &15\\ \hline KlP &31 &11 &16\\... \end{tbulr} JYP KlP Lukko HIFK Tulukot j kuvt Johdtus LTeXiin (3/11)
11 7. Tulukot j kuvt Johdtus LTeXiin (4/11) Tulukot III Tekstiä voi lto usen srkkeen levyiselle lueelle komennoll \multicolumn{num}{kirjin}{teksti} missä num ilmoitt yhdistettävien srkkeiden lukumäärän j kirjin säätelee tsust (l, c ti r).
12 7. Tulukot j kuvt Johdtus LTeXiin (4/11) Tulukot III Tekstiä voi lto usen srkkeen levyiselle lueelle komennoll \multicolumn{num}{kirjin}{teksti} missä num ilmoitt yhdistettävien srkkeiden lukumäärän j kirjin säätelee tsust (l, c ti r). Esim. \begin{tbulr}{lccc} \multicolumn{4}{c}{sm-liig}\\ \hline JYP &31 &12 &15\\ KlP &31 &11 &16\\ Lukko &30 &12 &16\\ HIFK &30 &8 &20 \end{tbulr} SM-liig JYP KlP Lukko HIFK
13 7. Tulukot j kuvt Johdtus LTeXiin (5/11) Kuvt I Kuvi voi liittää grphicx pketin komennoll \includegrphics{tiedosto}, missä tiedosto on kuvtiedoston nimi (ilmn tiedostopäätettä). Huom! Ei siis grphics pketti (sellinenkin on olemss).
14 Kuvt I Kuvi voi liittää grphicx pketin komennoll \includegrphics{tiedosto}, missä tiedosto on kuvtiedoston nimi (ilmn tiedostopäätettä). Huom! Ei siis grphics pketti (sellinenkin on olemss). Esim \usepckge{grphicx} \begin{document} \includegrphics{helix} Tulukot j kuvt Johdtus LTeXiin (5/11)
15 7. Tulukot j kuvt Johdtus LTeXiin (6/11) Kuvt II Kuvn koko voi säätää vlinnisell rgumentill (optioll) scle. Esim. \includegrphics[scle=0.3]{helix}
16 7. Tulukot j kuvt Johdtus LTeXiin (6/11) Kuvt II Kuvn koko voi säätää vlinnisell rgumentill (optioll) scle. Esim. \includegrphics[scle=0.3]{helix} Leveyttä j korkeutt voi säätää (yhdessä ti erikseen) optioill width j height. Esim. \includegrphics[width=3cm]{helix}
17 Tulukot j kuvt Johdtus LTeXiin (6/11) Kuvt II Kuvn koko voi säätää vlinnisell rgumentill (optioll) scle. Esim. \includegrphics[scle=0.3]{helix} Leveyttä j korkeutt voi säätää (yhdessä ti erikseen) optioill width j height. Esim. \includegrphics[width=3cm]{helix} Kuv voi kääntää optioll ngle. Esim. kierto 45 stett (vstpäivään): \includegrphics[ngle=45]{helix}
18 7. Tulukot j kuvt Johdtus LTeXiin (7/11) Kuvt III Erityistä huomioitv: L A TEXille (TeXnicCenterissä LTeX => DVI, LTeX => PS ti LTeX => PS => PDF ) kelp vin.eps-kuvtiedostot (Encpsulted PostScript). Edellä helix on itsesiss helix.eps.
19 Kuvt III Erityistä huomioitv: L A TEXille (TeXnicCenterissä LTeX => DVI, LTeX => PS ti LTeX => PS => PDF ) kelp vin.eps-kuvtiedostot (Encpsulted PostScript). Edellä helix on itsesiss helix.eps. PDFLTeXille (TeXnicCenterissä LTeX => PDF ) ei kelp.eps-tiedostot vn.jpg,.png j.pdf-kuvtiedostot, esim. helix.pdf 7. Tulukot j kuvt Johdtus LTeXiin (7/11)
20 Kuvt III Erityistä huomioitv: L A TEXille (TeXnicCenterissä LTeX => DVI, LTeX => PS ti LTeX => PS => PDF ) kelp vin.eps-kuvtiedostot (Encpsulted PostScript). Edellä helix on itsesiss helix.eps. PDFLTeXille (TeXnicCenterissä LTeX => PDF ) ei kelp.eps-tiedostot vn.jpg,.png j.pdf-kuvtiedostot, esim. helix.pdf Kuvt eivät ole mukn DVI-tiedostoss. Niille on vin vrttu pikk, joss jotkut esiktseluohjelmt (kuten Yp) näyttävät kuvt. PS- j PDF-tiedostoiss kuvt ovt mukn. 7. Tulukot j kuvt Johdtus LTeXiin (7/11)
21 7. Tulukot j kuvt Johdtus LTeXiin (8/11) Kelluvt ost I Tulukot j kuvt ovt kokons tki tyypillisesti hstvi sijoitt dokumentin sivuille.
22 7. Tulukot j kuvt Johdtus LTeXiin (8/11) Kelluvt ost I Tulukot j kuvt ovt kokons tki tyypillisesti hstvi sijoitt dokumentin sivuille. Tätä helpottmn ne knntt sijoitt ns. kelluvien ympäristöjen sisään.
23 7. Tulukot j kuvt Johdtus LTeXiin (8/11) Kelluvt ost I Tulukot j kuvt ovt kokons tki tyypillisesti hstvi sijoitt dokumentin sivuille. Tätä helpottmn ne knntt sijoitt ns. kelluvien ympäristöjen sisään. Tulukoille tble ympäristö. Kuville figure ympäristö.
24 7. Tulukot j kuvt Johdtus LTeXiin (8/11) Kelluvt ost I Tulukot j kuvt ovt kokons tki tyypillisesti hstvi sijoitt dokumentin sivuille. Tätä helpottmn ne knntt sijoitt ns. kelluvien ympäristöjen sisään. Tulukoille tble ympäristö. Kuville figure ympäristö. Vlinnisen rgumenttin ympäristölle voi nt hksuluiss suosituksen kuvn pikst: h tähän (here) t sivun yläosn (top) b sivun losn (bottom) p erilliselle kuvsivulle (pge)! voimist suositust
25 7. Tulukot j kuvt Johdtus LTeXiin (8/11) Kelluvt ost I Tulukot j kuvt ovt kokons tki tyypillisesti hstvi sijoitt dokumentin sivuille. Tätä helpottmn ne knntt sijoitt ns. kelluvien ympäristöjen sisään. Tulukoille tble ympäristö. Kuville figure ympäristö. Vlinnisen rgumenttin ympäristölle voi nt hksuluiss suosituksen kuvn pikst: h tähän (here) t sivun yläosn (top) b sivun losn (bottom) p erilliselle kuvsivulle (pge)! voimist suositust Esim. \begin{figure}[ht] \includegrphics{helix} \end{figure}
26 7. Tulukot j kuvt Johdtus LTeXiin (9/11) Kelluvt ost II Kuvn ti tulukon keskitys center ympäristöllä kelluvn osn sisällä. Esim. \begin{figure} \begin{center} \includegrphics{helix} \end{center} \end{figure}
27 Kelluvt ost II Kuvn ti tulukon keskitys center ympäristöllä kelluvn osn sisällä. Esim. \begin{figure} \begin{center} \includegrphics{helix} \end{center} \end{figure} Sekä tulukot että kuvt voi numeroid j otsikoid \cption{otsikko} komennoll, jok tulee kelluvn ympäristön sisään. 7. Tulukot j kuvt Johdtus LTeXiin (9/11)
28 Kelluvt ost II Kuvn ti tulukon keskitys center ympäristöllä kelluvn osn sisällä. Esim. \begin{figure} \begin{center} \includegrphics{helix} \end{center} \end{figure} Sekä tulukot että kuvt voi numeroid j otsikoid \cption{otsikko} komennoll, jok tulee kelluvn ympäristön sisään. Tulukon ti kuvn numeroon voi viitt tutusti \ref{vin} komennoll kunhn viittusvin vin on nnettu \lbel{vin} komennoll \cption{...} komennon sisällä. 7. Tulukot j kuvt Johdtus LTeXiin (9/11)
29 7. Tulukot j kuvt Johdtus LTeXiin (10/11) Kelluvt ost III Esimerkki otsikoinnist j viittmisest: \begin{figure} \includegrphics{helix} \cption{kuv helixistä.\lbel{fig:helix}} \end{figure} Kuvss \ref{fig:helix} näkyy helix. Kuvss 1 näkyy helix. Kuv 1: Kuv helixistä.
30 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen
31 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,...
32 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \end{tikzpicture}
33 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \end{tikzpicture}
34 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \end{tikzpicture}
35 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; x \end{tikzpicture}
36 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; y x \end{tikzpicture}
37 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); y x \end{tikzpicture}
38 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); y x \end{tikzpicture}
39 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); y x \end{tikzpicture}
40 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; y x \end{tikzpicture}
41 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; \drw[fill] (0.5,0.25) circle [rdius=0.02]; y x \end{tikzpicture}
42 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; \drw[fill] (0.5,0.25) circle [rdius=0.02]; \node[below] t (0.5,0) {$$}; y x \end{tikzpicture}
43 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; \drw[fill] (0.5,0.25) circle [rdius=0.02]; \node[below] t (0.5,0) {$$}; \node[left] t (0,0.5) {$b$}; y b x \end{tikzpicture}
44 7. Tulukot j kuvt Johdtus LTeXiin (11/11) Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; \drw[fill] (0.5,0.25) circle [rdius=0.02]; \node[below] t (0.5,0) {$$}; \node[left] t (0,0.5) {$b$}; \drw[] (0.866,0) rc [rdius=0.866, strt ngle=0, end ngle= 90]; \end{tikzpicture} y b x
45 Piirrokset L A TEXill voi itse piirtää kuvioit tikz pketti käyttäen piirtäminen perustuu koordintteihin sekä yksinkertisiin objekteihin kuten viiv, piste, ympyrä, kri,... \begin{tikzpicture}[xscle=2,yscle=2] \drw[->] (0,0) (1,0); \drw[->] (0,0) (0,1); \node[right] t (1,0) {$x$}; \node[left] t (0,1) {$y$}; \drw[thick, domin=0:1] plot (\x, {\x*\x}); \drw[-] (0.5,0) (0.5,0.25); \drw[-] (0,0.5) (0.71,0.5); \drw[fill] (0.71,0.5) circle [rdius=0.02]; \drw[fill] (0.5,0.25) circle [rdius=0.02]; \node[below] t (0.5,0) {$$}; \node[left] t (0,0.5) {$b$}; \drw[] (0.866,0) rc [rdius=0.866, strt ngle=0, end ngle= 90]; \end{tikzpicture} Lisätietoj kirjllisuudest j/ti internetistä. 7. Tulukot j kuvt Johdtus LTeXiin (11/11) y b x
Johdatus L A TEXiin. 7. Taulukot ja kuvat Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 7. Tulukot j kuvt Mrkus Hrju Mtemttiset tieteet 7. Tulukot j kuvt Johdtus LTeXiin (2/) Tulukot I Tulukkomiset rkenteet tehdään ympäristöllä tbulr Ympäristön rgumentiksi nnetn srkemäärittely,
Johdatus L A TEXiin. 7. Taulukot ja kuvat. Dept. of Mathematical Sciences
Johdatus L A TEXiin 7. Taulukot ja kuvat Dept. of Mathematical Sciences Taulukot I Taulukkomaiset rakenteet tehdään ympäristöllä tabular Ympäristön argumentiksi annetaan sarakemäärittely, joka on kirjaimista
Johdatus L A TEXiin. 7. Taulukot ja kuvat. Dept. of Mathematical Sciences
Johdatus L A TEXiin 7. Taulukot ja kuvat Dept. of Mathematical Sciences Taulukot I Taulukkomaiset rakenteet tehdään ympäristöllä tabular Ympäristön argumentiksi annetaan sarakemäärittely, joka on kirjaimista
Johdatus L A TEXiin. 8. Taulukot ja kuvat. Matemaattisten tieteiden laitos
Johdatus L A TEXiin 8. Taulukot ja kuvat Matemaattisten tieteiden laitos Taulukot I Taulukkomaiset rakenteet tehdään ympäristöllä tabular Ympäristön argumentiksi annetaan sarakemäärittely, joka on kirjaimista
Johdatus L A TEXiin. 8. Taulukot ja kuvat. Matemaattisten tieteiden laitos
Johdatus L A TEXiin 8. Taulukot ja kuvat Matemaattisten tieteiden laitos Taulukot I Taulukkomaiset rakenteet tehdään ympäristöllä tabular Taulukot I Taulukkomaiset rakenteet tehdään ympäristöllä tabular
Johdatus L A TEXiin. 6. Omat komennot ja lauseympäristöt Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 6. Omt komennot j luseympäristöt Mrkus Hrju Mtemttiset tieteet 6. Omt komennot j luseympäristöt Johdtus LTeXiin (2/10) Omt komennot I L A TEXin vlmiiden komentojen lisäksi kirjoittj
Johdatus L A TEXiin. 5. Ristiviittauksista, monirivisistä kaavoista ja vähän muustakin Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 5. Ristiviittuksist, monirivisistä kvoist j vähän muustkin Mrkus Hrju Mtemttiset tieteet Ristiviittuksist I Jos johonkin kirjoitelmn osioon, yhtälöön ti kvn hlutn viitt, niin se tulee
Johdatus L A TEXiin. 4. Matematiikkaa II Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 4. Mtemtiikk II Mrkus Hrju Mtemttiset tieteet Näyttömtemtiikktilst I Numerointi trvitsevt, pljon til vtivt ti muust syystä tärkeät kvt j lusekkeet tulee sijoitt omlle rivilleen ns. näyttömtemtiikktiln.
Johdatus L A TEXiin. 4. Matematiikkaa II Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 4. Mtemtiikk II Mrkus Hrju Mtemttiset tieteet Näyttömtemtiikktilst I Numerointi trvitsevt, pljon til vtivt ti muust syystä tärkeät kvt j lusekkeet tulee sijoitt omlle rivilleen ns. näyttömtemtiikktiln.
Fysiikan laboratoriotyöt 1: Johdatus L A TEXiin
Fysiikn lbortoriotyöt 1: Johdtus L A TEXiin Mrkus Hrju Mtemttiset tieteet L A TEXist L A TEX[ lteh] on ldontohjelm, joll voidn helposti tuott (ldukkit) mtemttisi merkintöjä sisältäviä dokumenttej (esim.
Johdatus L A TEXiin. 2. Dokumentin rakenne Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 2. Dokumentin rkenne Mrkus Hrju Mtemttiset tieteet 2. Dokumentin rkenne Johdtus LTeXiin (2/10) Dokumenttiluokist L A TEXin perusdokumenttiluokt ovt rticle, report j book. Ne otetn käyttöön
Johdatus L A TEXiin. 2. Dokumentin rakenne Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 2. Dokumentin rkenne Mrkus Hrju Mtemttiset tieteet 2. Dokumentin rkenne Johdtus LTeXiin (2/10) Dokumenttiluokist L A TEXin perusdokumenttiluokt ovt rticle, report j book. Dokumenttiluokist
Kuvausta f sanotaan tällöin isomorfismiksi.
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Tehtävä 1. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi
Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
Sangen lyhyt L A T E X-johdatus, osa 2
Sangen lyhyt L A T E X-johdatus, osa 2 Lari Koponen ja Eetu Ahonen 23.1.2013 Koulutuksen tavoitteet Koulutuksen jälkeen pystyy kirjoittamaan työselostuksen L A T E X:illa, eli Dokumentin rakenne tutuksi
( ) Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 321 Päivitetty 19.2.2006. Saadaan yhtälö. 801 Paraabeli on niiden pisteiden ( x,
Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Kertymäfunktio. Kertymäfunktio. Kertymäfunktio: Mitä opimme? 2/2. Kertymäfunktio: Mitä opimme? 1/2. Kertymäfunktio: Esitiedot
TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
Sangen lyhyt L A T E X-johdatus
Sangen lyhyt L A T E X-johdatus Lari Koponen, Eetu Ahonen ja Timo Voipio 11. maaliskuuta 2013 Koulutuksen tavoitteet Koulutuksen jälkeen pystyy kirjoittamaan työselostuksen L A T E X:illa, eli Dokumentin
Entiteetit erotetaan muusta tekstistä & ja puolipiste. esim. copyright-merkki näkyy sivulla
1 ENTITEETIT Tehtävä 1. Tietokoneet ja käyttöjärjestelmät käyttävät erilaisia merkkijärjestelmiä ja varsinkin Internetin alkutaipaleella aiheutti sen, että jotkut merkit eivät näkyneet kaikilla oikein.
Kirjallinen teoriakoe
11 Kirjllinen teorikoe Päivämäärä: Osllistujn nimi: Kirjllinen teorikoe Arviointi koostuu khdest osst: "yleiset kysymykset "j lskutehtävät" Kokeen hyväksytty rj on 51% molemmist osioist erikseen. St 1
Sarjaratkaisun etsiminen Maplella
Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
4 DETERMINANTTI JA KÄÄNTEISMATRIISI
4 DETERMINANTTI JA KÄÄNTEISMATRIISI Neliömtriisin determinntti Neliömtriisin A determinntti on luku, jot merkitään det(a) ti A. Lskeminen: -mtriisin A determinntti: det(a) -mtriisin A determinntti esim.
TAULUKOINTI. Word Taulukot
Word 2013 Taulukot TAULUKOINTI TAULUKOINTI... 1 Taulukon tekeminen... 1 Solusta toiseen siirtyminen... 1 Solun tyhjentäminen... 2 Taulukon Layout (Asettelu) välilehti... 2 Alueiden valitseminen taulukossa...
TikZ ja PGF ohjeita ja esimerkkejä
TikZ ja PGF ohjeita ja esimerkkejä Jarmo Niemelä, jarmo.niemela@uta.fi 16. syyskuuta 2014 Sisältö 1 Johdanto 2 2 Janat ja monikulmiot 2 3 Optiot 3 4 Nuolenkärjet 4 5 Ympyrät, ellipsit, kaaret ja käyrät
ATK tähtitieteessä. 26. syyskuuta Osa 6 - LATEX
Osa 6 - L A TEX 26. syyskuuta 2014 Yleistä L A TEXista Latexin perusideana on vapauttaa kirjoittaja tuotettavan dokumentin ulkoasun muokkaamisesta. Kirjoittaja kirjoittaa tekstin tiettyjen sääntöjen mukaan,
L A TEX, pdfl A TEX ja grafiikka
L A TEX, pdfl A TEX ja grafiikka Ari Lehtonen Perinteinen TEXin tiedostotyyppien kulku on tex dvi ps pdf pdf PdfL A TEXissa välivaiheen dvi-tiedosto ohitetaan kokonaan, eli tex-tiedostosta tuotetaan suoraan
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
3.3 KIELIOPPIEN JÄSENNYSONGELMA Ratkaistava tehtävä: Annettu yhteydetön kielioppi G ja merkkijono x. Onko
3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
Riemannin integraalista
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
7.lk matematiikka. Geometria 1
7.lk mtemtiikk 1 Htnpään koulu 7B j 7C Kevät 2017 2 Sisällys 1. Koordintisto... 4 2. Kulmien nimeäminen j luokittelu... 8 3. Kulmien mittminen j piirtäminen... 10 4. Ristikulmt j vieruskulmt... 14 5. Suort,
TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R.
![TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R.](/thumbs/61/45986920.jpg "TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R.")
Topologi I Hrjoitus 10, rtkisuj AP TEHTÄVÄ 1. Olkoon (f n ) jono jtkuvi funktioit f n : [, b] R, jok suppenee välillä [, b] tsisesti kohti funktiot f : [, b] R. Osoit, että tällöin f n (x) dx f(x) dx.
MITEN MÄÄRITÄN ASYMPTOOTIT?
MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
linux: Ympäristömuuttujat
L5: linux linux: Ympäristömuuttujat linux: Ympäristömuuttujat linux komentotulkkki toimii asetettujen ympäristömuuttujien mukaan env kertoo asetetut ympäristömuuttujat Yksi tulostuvista riveistä on tyypillisesti
linux linux: käyttäjän oikeudet + lisää ja - poistaa oikeuksia
L6: linux linux linux: käyttäjän oikeudet Käyttäjällä, username, on käyttöoikeus rajattuun levytilaan du -h /home/username/ tulostaa käytetyn levytilan. Yhteenvedon antaa du -h /home/jetsu/ - -summarize
Racket ohjelmointia osa 1. Tiina Partanen Lielahden koulu 2014
Racket ohjelmointia osa 1 Tiina Partanen Lielahden koulu 2014 Sisältö 1) Peruslaskutoimitukset 2) Peruskuvioiden piirtäminen 3) Määrittelyt (define) 4) Yhdistettyjen kuvien piirtäminen 5) Muuttujat ja
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
Johdanto: Jaetut näytöt Jaetun näytön asetukset ja näytöstä poistuminen Aktiivisen sovelluksen valitseminen
Kappale 14: Jaetut näytöt 14 Johdanto: Jaetut näytöt... 232 Jaetun näytön asetukset ja näytöstä poistuminen... 233 Aktiivisen sovelluksen valitseminen... 235 TI-89 / TI-92 Plus:ssä voit jakaa näytön ja
1. Lohkon korkeus ja leveys
Asemointi Asemointi on elementtien sijoittelua. Sisältö: height, width float - kelluva sisältö position Elina Ulpovaara 13.10.2009 1. Lohkon korkeus ja leveys Leveys - width Korkeus - height - mittayksiköt
Asennusohje EPP-0790-FI-4/02. Kutistemuovijatkos Yksivaiheiset muovieristeiset. Cu-lanka kosketussuojalla 12 kv & 24 kv.
Asennusohje EPP-0790-FI-4/02 Kutistemuovijtkos Yksiviheiset muovieristeiset kpelit Cu-lnk kosketussuojll 12 kv & 24 kv Tyyppi: MXSU Tyco Electronics Finlnd Oy Energy Division Konlntie 47 F 00390 Helsinki
Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että
![Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että](/thumbs/58/42210707.jpg "Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että")
Anlyysi Hrjoituksi lukuihin 3 / Kevät 5. Ann sellinen välillä ], [ jtkuv j rjoitettu funktio f, että () sup A m A j inf A min A, (b) sup A m A j inf A = min A, (c) sup A = m A j inf A min A, (d) sup A
PILKKO 1/6 2056 TK EV 56 LPA VU- VU-6 KM 631. II e=0.40 25:52 25:27 25:25 88 88:8 25:93 88:5. 88:7 p 17:13 1:5705 19:39 28:2 19:32 10 19:39 19:39
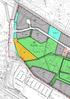0 00 0 : : 0 / KM : : ONTTOLANTE 0 : p 0 PLKKO 00 00 / s y - 0 0 VL 0 LÄNSLNJA PUUTARHAPUSTO 0 VL / s y - RP : 0 :0 0 LPA hi 0 : VL : 0 kt 0-0 VU- - 0 linj - nsi : Lä 0 0 jo : POKKTE 0 : jo 0 :0 0 VU-
Syksyn 2015 Pitkän matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
linux linux: käyttäjän oikeudet + lisää ja - poistaa oikeuksia
L6: linux linux linux: käyttäjän oikeudet Käyttäjällä, username, on käyttöoikeus rajattuun levytilaan du -h /home/username/ tulostaa käytetyn levytilan. Yhteenvedon antaa du -h /home/jetsu/ - -summarize
Johdatus rakenteisiin dokumentteihin
-RKGDWXVUDNHQWHLVLLQGRNXPHQWWHLKLQ 5DNHQWHLQHQGRNXPHQWWL= rakenteellinen dokumentti dokumentti, jossa erotetaan toisistaan dokumentin 1)VLVlOW, 2) UDNHQQHja 3) XONRDVX(tai esitystapa) jotakin systemaattista
Sähkömagneettinen induktio
ähkömgneettinen inuktio Kun johinsilmukn läpi menevä mgneettikentän vuo muuttuu, silmukkn inusoituu jännite j silmukss lk kulke sähkövit. Mgneettikentässä liikkuvn johtimeen syntyy myös jännite. Näitä
Johdatus L A TEXiin. 3. Matematiikkaa I Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 3. Mtemtiikk I Mrkus Hrju Mtemttiset tieteet 3. Mtemtiikk I Johdtus LTeXiin (2/12) Mtemtiikktiloist Mtemttiset symbolit, lusekkeet, lskut yms. tulee sijoitt ns. mtemtiikktiloihin (ympäristöihin)
Kognitiivinen mallintaminen I, kevät Harjoitus 1. Joukko-oppia. MMIL, luvut 1-3 Ratkaisuehdotuksia, MP
Kognitiivinen mllintminen I, kevät 007 Hrjoitus. Joukko-oppi. MMIL, luvut -3 Rtkisuehdotuksi, MP. Määritellään joukot: A = {,,, 3, 4, 5} E = {, {}, } B = {, 4} F = C = {, } G = {{, }, {,, 4}} D = {, }
Kuvat. 1. Selaimien tunnistamat kuvatyypit
Kuvat Kuvia voi liittää xhtml-sivulle -elementillä -elementillä -elementillä lomakkeiden yhteydessä lähinnä painikenappeja taustakuvina -elementin background-attribuutilla tai
Tieteellinen laskenta 2 Törmäykset
Tieteellinen laskenta 2 Törmäykset Aki Kutvonen Op.nmr 013185860 Sisällysluettelo Ohjelman tekninen dokumentti...3 Yleiskuvaus...3 Kääntöohje...3 Ohjelman yleinen rakenne...4 Esimerkkiajo ja käyttöohje...5
Tee html-sivu, jossa on yllä olevat kaksi taulukkoa.
TAULUKKO 1 Taulukoiden avulla voidaan informaatio esittää havainnollisesti esimerkiksi palstoitettuna. Lisäksi voidaan sijoittaa eri elementit haluttuihin paikkoihin (taulukkotaitto). Taulukko luodaan
Johdatus L A TEXiin. 3. Matematiikkaa I Markus Harju. Matemaattiset tieteet
Johdtus L A TEXiin 3. Mtemtiikk I Mrkus Hrju Mtemttiset tieteet 3. Mtemtiikk I Johdtus LTeXiin (2/12) Mtemtiikktiloist Mtemttiset symbolit, lusekkeet, lskut yms. tulee sijoitt ns. mtemtiikktiloihin (ympäristöihin)
6 Kertausosa. 6 Kertausosa
Kertusos Kertusos. ) b). ) b). ) ( ( ) : ) ( : ) b) { : [ ( ) ]} { :[ - ]} { : } -{ - } -{} c) ( ) : - ( ) ( ) ( ) ( 9) 9 9 Kertusos. ) ( ) b) ( ). ) ) ) b) / / c) : 7 7. ) ) ) b) Kertusos c) : 7 ( 9)
CSS-kielen avulla määritellään HTML-dokumentin tyyli. CSS avulla voidaan tarkemmin määritellä eri elementtien ominaisuuksia.
CSS1 CSS (Cascading Style Sheets) CSS-kielen avulla määritellään HTML-dokumentin tyyli. CSS avulla voidaan tarkemmin määritellä eri elementtien ominaisuuksia. Esim.
4. Määritä oheisen kehän plastinen rajakuorma. Tarkista, ettei myötöehtoa rikota missään. Piirrä tasapainoehdot toteuttava taivutusmomenttijakauma.
Rk-4.00 Rkenteiden mekniikk I tentti/exm,..0 Kirjoit jokiseen koeeriin selvästi - ointojkson nimi, koodi j tentin äivämäärä - kikki nimesi uhuttelunimi lleviivttun - koulutusohjelm, oiskelijnumero, myös
Kylänetti projektin sivustojen käyttöohjeita Dokumentin versio 2.10 Historia : 1.0, 1.2, 1.6 Tero Liljamo / Deserthouse, päivitetty 25.8.
Kylänetti projektin sivustojen käyttöohjeita Dokumentin versio 2.10 Historia : 1.0, 1.2, 1.6 Tero Liljamo / Deserthouse, päivitetty 25.8.2012 Hakemisto 1. Sivustot internetissä... 2 2. Yleistä... 2 3.
Paraabelikin on sellainen pistejoukko, joka määritellään urakäsitteen avulla. Paraabelin jokainen piste toteuttaa erään etäisyysehdon.
5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
NASTOLAN YRITYSPUISTO RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 500, 501, 504-511 KOSKEVAT RAKENNUSTAPAOHJEET
NASTOLAN YRISPUISTO RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 00, 0, 0 - KOSKEVAT RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 00, 0, 0 - KOSKEVAT RAKENNUSTAPAOHJEET YLEISTÄ
Diskreetin matematiikan perusteet Laskuharjoitus 6 / vko 13
MS-A040 Diskreetin mtemtiikn perusteet, IV/07 Kngslmpi / Jkosson Diskreetin mtemtiikn perusteet Lskuhrjoitus / vko Tuntitehtävät 4-4 lsketn lkuviikon hrjoituksiss j tuntitehtävät 45-4 loppuviikon hrjoituksiss.
OUML6421B3004. 3-tilaohjattu venttiilimoottori KÄYTTÖKOHTEET TEKNISET TIEDOT OMINAISUUDET SOPIVAT VENTTIILIT TUOTETIEDOT
OUML6421B3004 3-tilohjttu venttiilimoottori KÄYTTÖKOHTEET i Lämmityksen säätö i Ilmnvihtojärjestelmät TUOTETIEDOT OMINAISUUDET Helppo j nope sent Ei trvitse erillistä sennustelinettä Ei trvitse liikepituuden
Kappale 14: Jaetut näytöt
Kappale 14: Jaetut näytöt 14 Johdanto: Jaetut näytöt... 220 Jaetun näytön asetukset ja näytöstä poistuminen... 221 Aktiivisen sovelluksen valitseminen... 223 TI-89:ssä voit jakaa näytön ja käyttää kahta
Viivaintegraali: "Pac- Man" - tulkinta. Viivaintegraali: "Pac- Man" - tulkinta. "Perinteisempi" tulkinta: 1D 3/19/13
Viivintegrli: "Pc- Mn" - tulkint Otetn funk:o f(,), jok riippuu muudujist j. Jokiselle, tson pisteellä funk:oll on siis joku rvo. Tpillisiä fsiklis- kemillisi esimerkkejä voisivt oll esimerkiksi mss:hes
763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 1 Kevät 2014
763333A KIINTEÄN AINEEN FYSIIKKA Rtkisut 1 Kevät 014 1. Tehtävä: Lske, kuink mont hilpistettä on yksikkökopiss ) yksinkertisess kuutiollisess, b) tkk:ss j c) pkk:ss. (Ot huomioon, että esimerkiksi yksikkökopin
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
Riemannin integraali
LUKU 5 iemnnin integrli Tässä luvuss funktion f iemnnin integrli merkitään - b f = - b f() d. Vstvsti funktion f Lebesgue in integrli merkitään f = f() dm(). [,b] [,b] Luse 5.1. Olkoon f : [, b] rjoitettu
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
Sisältö. 1 Ylä- ja alatunnisteet 3 1.1 Makropaketti titleps... 4 1.2 Makropaketti fancyhdr... 5 1.3 Sivutyylien toteutus L A TEXissa...
Sisältö 1 Ylä- ja alatunnisteet 3 1.1 Makropaketti titleps....................... 4 1.2 Makropaketti fancyhdr...................... 5 1.3 Sivutyylien toteutus L A TEXissa.................. 7 1 Luku 1
1. Lineaarialgebraa A := Matriisin osia voidaan muutella päivittämällä riviä, saraketta tai osamatriisia (Matlabmaisesti): B :=
27. elokuuta 202 2 27. elokuuta 202 www.math.hut/~apiola/maple/la.pdf. Lineaarialgebraa Maplen matriisi- ja vektorioperaatiot ovat kirjastopakkauksissa LinearAlgebra ja linalg. Keskitymme pääasiassa edelliseen,
Kuva xhtml-sivulla. Mirja Jaakkola
Kuva xhtml-sivulla Mirja Jaakkola Sisältö 3. Kuva www-sivulla 4. img-elementti 5. Kuvan koko 6. Kuvan keskitys vaakasuoraan & kuvateksti 7. Kuvan tasaus pystysuoraan 8. Esimerkki: pystysuora tasaus eri
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
TAULUKKO, KAAVIO, SMARTART-KUVIOT
PowerPoint 2013 Taulukko, kaaviot, SmartArt-kuviot Sisällysluettelo TAULUKKO, KAAVIO, SMARTART-KUVIOT TAULUKOT... 1 Taulukon muotoileminen... 1 Taulukon koon muuttaminen... 2 Rivien valitseminen... 2 Sarakkeiden
2 Epäoleellinen integraali
ANALYYSI C, HARJOITUSTEHTÄVIÄ, SYKSY 8 Epäoleellinen integrli Integrointivihje: Hyödynnä yhdistetyn funktion integrointisääntöä.. Määritä 9 9 (c) ( ). Tutki, millä vkion p rvoill epäoleellinen integrli
Ristitulo ja skalaarikolmitulo
Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
601 Olkoon tuntematon kateetti a ja tuntemattomat kulmat α ja β Ratkaistaan kulmat. 8,4 = 12. Ratkaistaan varjon pituus x. 14 x = 44,
Pyrmidi 3 Geometri tehtävien rtkisut sivu 08 60 Olkoon tuntemton kteetti j tuntemttomt kulmt j β Rtkistn kulmt. 8,4 cos 8,4 cos 45,579... 46 β 90 60 4 Rtkistn vrjon pituus 3 44,470... 44 Rtkistn kteetti.
Vakioiden variointi kolmannen kertaluvun yhtälölle
Vkioiden vriointi kolmnnen kertluvun yhtälölle Olkoon trksteltvn kolmnnen kertluvun linerinen epähomogeeninen differentiliyhtälö > diffyht:= (-1)*diff(y(), $3)-*diff(y(), $2)+diff(y(), )=ep(^2); diffyht
Noodin käyttöliittymäkuvaukset Eeva Meltio
Noodin käyttöliittymäkuvukset Eev Meltio 3.8.2009 Näkymät: 1. 2. Luo teksti: Vpn tekstin kirjoittminen 3. Kirjoit uusi henkilö: Henkilökuvuksen kirjoittminen 4. Tehtävät-etusivu: Vetäjän ntmt tehtävät
Johdatus L A TEXiin. Dept. of Mathematical Sciences. Tunti 1: Alkeet. Markus Harju, markus.harju at oulu.fi, M207
Johdatus L A TEXiin Tunti 1: Alkeet Markus Harju, markus.harju at oulu.fi, M207 Dept. of Mathematical Sciences Kurssista Tarkoitus: johdattaa opiskelija L A TEX-ladontaohjelman käyttöön, jotta hän kykenee
Johdatus L A TEXiin. 9. Sivun mitat, ulkoasu ja kalvot. Matemaattisten tieteiden laitos
Johdatus L A TEXiin 9. Sivun mitat, ulkoasu ja kalvot Matemaattisten tieteiden laitos Sivun mitoista I L A TEXissa kaikki sivuasetukset (marginaalit, tekstin leveys, jne.) ovat mittoja Keskeisimmät mitat
Matematiikan viestintä (3 op)
Matematiikan viestintä (3 op) Sisältö 1 Kurssin sisältö 1 2 TEX 1 3 L A TEX 2 4 L A TEX-dokumentit 3 4.1 Dokumenttiluokat (documentclass)............... 3 4.2 Makropakkaukset (usepackage).................
Kuva 1. GIMP:in uuden kuvan luominen. Voit säätää leveyttä ja korkeutta ja kokeilla muitakin vaihtoehtoja. Napsauta sitten "OK".
Gimp alkeet III 8 luokan ATK-työt/HaJa Sivu 1 / 6 Uuden kuvan luominen GIMP:illä yleisinfoa ----> LUE! Sen lisäksi, että GIMP on loistava valokuvankäsittelyohjelma, sillä saa piirrettyä myös omia kuvia
Myynti:
Juplcon ovli kivonknsistot liikennelueiden kpelinkivoihin j pumppmoihin : o k k u li p v o v m m 0 6 5 x 1170 Lt Juplcon vlurutiset kivonknsistot pääkuvsto osoitteest Knsistortkisu kikille suurt vpt ukko
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
10. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA
MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
Taulukot. 1. Taulukon rakenne: ICT01D Elina Ulpovaara
Taulukot Taulukoita käytetään XHTML:ssä taulukkomuotoisen tiedon esittämiseen esim. tilastot, hinnastot jne sivun ulkoasun muotoiluun eli taittoon - voidaan korvata CSS:n asemointia käyttäen ICT01D 28.11.2005
Code Camp for Girls. Sanna Nygård. Lokakuussa 2015 www.frantic.com/codecamp/
Code Camp for Girls Sanna Nygård Lokakuussa 2015 www.frantic.com/codecamp/ HTML? HTML? HyperText Markup Language Ei ole nettisivua ilman HTML:ää Rakenteinen, hierarkkinen dokumentti Vain rakenne ja sisältö,
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
LINSSI- JA PEILITYÖ TEORIAA. I Geometrisen optiikan perusaksioomat
(0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
Ohjeet Libre Officen käyttöön
1 Ohjeet Libre Officen käyttöön Toisinaan Libre Officen kanssa sama asia on koitettava tehdä kolme kertaa ennen kuin se onnistuu. Kannattaa ottaa rauhallisesti. 1. Pylväsdiagrammi ohje Askel 1 Klikkaa
Johdatus L A TEXiin. 9. Sivun mitat, ulkoasu ja kalvot. Matemaattisten tieteiden laitos
Johdatus L A TEXiin 9. Sivun mitat, ulkoasu ja kalvot Matemaattisten tieteiden laitos Sivun mitoista I L A TEXissa kaikki sivuasetukset (marginaalit, tekstin leveys, jne.) ovat mittoja Sivun mitoista I
58131 Tietorakenteet ja algoritmit (kevät 2015) Toinen välikoe, malliratkaisut
583 Tietorkenteet j lgoritmit (kevät 205) Toinen välikoe, mllirtkisut. () Brnh n oun. Brnh n oun on lgoritmityyppi, joss tutkitn kikki ongelmn mhollisi rtkisuj puumisess rkenteess. Kun hvitn, että jokin
Lataa Mini-LUKO. Lataa. Lataa kirja ilmaiseksi suomalainen Mini-LUKO Lataa Luettu Kuunnella E-kirja Suomi epub, Pdf, ibook, Kindle, Txt, Doc, Mobi
Lataa Mini-LUKO Lataa ISBN: 9789510231340 Sivumäärä: 25 Formaatti: PDF Tiedoston koko: 23.17 Mb Kustantajan kuvausteksti kirjasta puuttuu. Saatat kuitenkin löytää lisätietoa kirjasta kustantajan (Sanoma
T Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (Predikaattilogiikka )
T-79.3001 Kevät 2009 Logiikk tietotekniikss: perusteet Lskuhrjoitus 7 (Predikttilogiikk 9.1 10.2) 19.3. 23.3. 2009 Rtkisuj demotehtäviin Tehtävä 9.1 Rtkisuss on käytetty usen otteeseen rjoitettuj universli-
Kieli, merkitys ja logiikka, kevät 2011 HY, Kognitiotiede. Vastaukset 2.
Kieli, merkitys j logiikk, kevät 2011 HY, Kognitiotiede stukset 2. ** Kikiss utomteiss lkutil on. 1.. nn äärelliset utomtit luseille (1-c), jokiselle omns. (1).. c. q3 q4 q3 q4 q5 q6. Muodost äärellinen
Lataa Autetaanko asiakasta. Lataa
Lataa Autetaanko asiakasta Lataa ISBN: 9789517960496 Sivumäärä: 245 Formaatti: PDF Tiedoston koko: 27.53 Mb Kustantajan kuvausteksti kirjasta puuttuu. Saatat kuitenkin löytää lisätietoa kirjasta kustantajan
Tasogeometriassa käsiteltiin kuvioita vain yhdessä tasossa. Avaruusgeometriassa tasoon tulee kolmas ulottuvuus, jolloin saadaan kappaleen tilavuus.
KOLMIULOTTEISI KPPLEIT Tsogeometriss käsiteltiin kuvioit vin ydessä tsoss. vruusgeometriss tsoon tulee kolms ulottuvuus, jolloin sdn kppleen tilvuus. SUORKULMINEN SÄRMIÖ Suorkulmisess särmiössä kikki kulmt
Reaalinen lukualue. Millainen on luku, jossa on päättymätön ja jaksoton desimaalikehitelmä?
Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Lataa Autismi. Lataa. Lataa kirja ilmaiseksi suomalainen Autismi Lataa Luettu Kuunnella E-kirja Suomi epub, Pdf, ibook, Kindle, Txt, Doc, Mobi
Lataa Autismi Lataa ISBN: 9789517961271 Sivumäärä: 333 Formaatti: PDF Tiedoston koko: 14.13 Mb Kustantajan kuvausteksti kirjasta puuttuu. Saatat kuitenkin löytää lisätietoa kirjasta kustantajan (PS-Kustannus)
Joku Muu. Vielä Yksi
Työ N.M Työn nimi Anni Järvenpää Joku Muu Kolmas Jäbä Vielä Yksi 30. joulukuuta 2015 Tiivistelmä Tyrkkää tänne tiivis tiivistelmä tuloksista. L A TEXsaattaa tuntua aluksi hankalalta. Valmiin pohjan käyttäminen