9 PÄÄTTELY PREDIKAATTILOGIIKASSA SAMAISTUS L. UNIFIKAATIO
|
|
|
- Kirsi Aaltonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 9 PÄÄTTELY PREDIKAATTILOGIIKASSA Jos predikaattilogiikan lauseista eliminoidaan kvanttorit, niin jäljelle jääneitä lauseita voidaan käsitellä propositiologiikan päättelymenetelmillä. Menetelmää kutsutaan propositionalisoinniksi (propositionalization) Eksistenssilauseet korvataan lauseilla joissa sidotut muuttujat on korvattu Skolem-vakioilla eli uusilla vakiosymboleilla, joita ei ole tietämyskannassa ennestään. Universaalilauseet korvataan kaikilla mahdollisilla lauseilla jotka saadaan kun muuttujat korvataan tietämyskannassa esiintyvillä vakio- ja funktiotermeillä eli perustermeillä (ground term), joissa ei esiinny muuttujia. Universaalikvantifioidun lauseen v α muuttuja v voidaan korvata millä tahansa perustermillä (ground term), eli vakiotai funktiotermillä, joka ei sisällä muuttujia. Sijoitus eli substituutio θ on sidontalista, jossa kullekin muuttujalle annetaan sen korvaava perustermi. Merk. α(θ) on lause, joka saadaan kun sijoitusta θ sovelletaan lauseeseen α. Universaalikvanttorin eliminoimiseksi voimme päätellä v α α({ v/g }), missä v on mikä tahansa muuttuja ja g mielivaltainen perustermi. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.1/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.2/38 Eksistenssikvanttorin eliminoimisessa muuttuja v korvataan Skolem-vakiolla k, joka ei ennestään esiinny tietämyskannassa v α α({ v/k }), Esimerkiksi voimme lauseesta x Isä(Jussi) = x päätellä instantiaation Isä(Jussi) = F 1, missä F 1 on uusi vakio. Eliminoimalla eksistenssikvanttorit korvaamalla muuttujat Skolem-vakioilla ja universaalikvanttorit kaikilla mahdollisilla instantiaatioillaan, muuttuu tietämyskanta oleellisesti propositionaaliseksi. Muuttujattomat atomilauseet kuten Opiskelija(Jussi) ja Äiti(Jussi, Meeri) on vain nähtävä propositiosymboleina. Täten propositiologiikan päättelyä voidaan soveltaa predikaattilogiikan lauseisiin. Jos tietämyskannassa kuitenkin käytetään funktiosymboleita, niin mahdollisten korvaavien perustermien lkm on ääretön: Isä(Isä(Isä(Jussi))) jne Herbrandin kuuluisan tuloksen mukaan 1. kertaluvun teorian loogisilla seurauksilla on todistus propositionalisoidussa teoriassa, joka käsittelee vain äärellistä osaa siitä. Täten sisäkkäisiä funktioita voidaan käsitellä etenemällä ikään kuin leveyssuuntaisesti kokeilemalla ensin vakiotermejä, sitten yhteen kertaan sovellettuja funktioita jne kunnes todistus löytyy. Päättely on siis täydellistä. Analogia Turingin koneiden pysähtymisongelmaan kuitenkin osoittaa, että ongelma on ratkeamaton. Tarkemmin: ongelma on osittain ratkeava: jos lause on looginen seuraus, todistus löytyy, mutta muuten algoritmi voi jatkaa todistuksen etsintää ikuisesti. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.3/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.4/38 SAMAISTUS L. UNIFIKAATIO Em. menetelmä ei kuitenkaan ole kovin tehokas, koska siinä universaalilauseista tuotetaan erilaisilla sijoituksilla monta ilmentymää vaikka usein vain yhtä tarvitaan todistuksessa. Universaalilauseiden kaikkien muuttujasijoitusten aukikirjoittaminen vaikuttaa turhalta. Parempi olisi käyttää vain sellaisia sijoituksia, joista on hyötyä todistamisessa. Jos meillä on sijoitus θ s.e. p i (θ) = p i(θ), kaikilla i, missä p i ja p i ovat atomilauseita kuten myös q, niin voimme käyttää yleistettyä Modus Ponensia p 1,..., p n, (p 1 p n q) q(θ) Esim. lauseista Opiskelija(Jussi), x Ahkera(x) ja y Opiskelija(y) Ahkera(y) Valmistuu2007(y) voimme päätellä Valmistuu2007(Jussi) sidonnan { y/jussi, x/jussi } perusteella Jätetään universaalikvanttorit merkitsemättä ja saadaan Opiskelija(Jussi), Ahkera(x), (Opiskelija(y) Ahkera(y) Valmistuu2007(y)) Valmistuu2007(y)({y/Jussi, x/jussi}) Yleistetty Modus Ponens on eheä päättelysääntö Samaan tapaan kuin yleistetty MP voidaan "korottaa" propositiologiikasta predikaattilogiikkaan, voidaan muokata myös eteen- ja taaksepäinketjutus sekä resoluutiosääntö. Päättelyalgoritmeissa keskeinen käsite on lauseiden samaistus (unification) Samaistusalgoritmi UNIFY palauttaa syötteenä annetut lauseet samaistavan sijoituksen, jos sellainen on olemassa UNIFY(p, q) = θ, s.e. p(θ) = q(θ) muuten samaistus epäonnistuu (fail) luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.5/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.6/38 UNIFY(Tuntee(Jussi, x), Tuntee(Jussi, Jaana)) = { x/jaana } UNIFY(Tuntee(Jussi, x), Tuntee(y, P ekka)) = { x/p ekka, y/jussi } UNIFY(Tuntee(Jussi, x), Tuntee(y, Äiti(y))) = { y/jussi, x/äiti(jussi) } UNIFY(Tuntee(Jussi, x), Tuntee(x, Elina)) = fail Viimeinen samaistus epäonnistuu, koska muuttujaa x ei voida samanaikaisesti sitoa sekä Jussiin että Elinaan Koska muuttujat ovat universaalikvantifioituja, niin Tuntee(x, Elina) tarkoittaa, että kaikki tuntevat Elinan Näin ollen samaistuksen pitäisi onnistua Ongelman edellä aiheuttaa saman muuttujanimen käyttö Toisaalta eri lauseiden muuttujanimillä ei ole merkitystä (ennen sidontaa) joten voidaan uudelleennimetä muuttujat: jälkimmäinen lausee korvataan sellaisella jossa x on korvattu muuttujalla jota ei ole käytetty ennestään, esim x 1 7. Jos samastus voidaan tehdä usealla eri sijoituksella, valitaan se joka asettaa vähiten rajoituksia (sitomisia vakioihin) muuttujille, siis yleisin samaistus (most general unifier). UNIFY(Tuntee(Jussi, x), Tuntee(y, z)) { y/jussi, z/x } { y/jussi, x/jussi, z/jussi } luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.7/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.8/38
2 ETEENPÄINKETJUTUS Yleisimmän unifioijan etsivä algoritmi on esitetty kirjan kuvassa 9.1: Kumpaakin termiä edetään ja tutkitaan rekursiivisesti samastaen aina kummassakin esiintyviä termejä mikäli mahdollista. Jos ei ole mahdollista, niin samastus epäonnistuu. Mikäli verrataan yksittäistä muuttujaa monimutkaiseen termiin, täytyy tehdä esiintymistarkistus (occur check), jossa katsotaan ettei muuttuja esiinny monimutkaisen termin sisällä. Jos esiintyy niin sijoitusta ei löydy ja samastus epäonnistuu. Esiintymistarkistuksen takia algoritmin aikavaatimus on neliöllinen, mutta asia voidaan tehdä lineaarisestikin monimutkaisemmilla algoritmeilla. Usein esiintymistarkistus tosin jätetään tekemättä kokonaan, mikä johtaa eheyden menettämiseen mutta ei usein ole ongelma käytännössä. Eteenpäinketjutus toimii, vastaavasti kuin propositionaalisessa tapauksessa, Hornin lauseille eli literaalien disjunktioille, joissa korkeintaan yksi literaali on positiivinen. Jokainen lause on siis atomilause tai implikaatio, jonka runko on positiivisten atomilauseiden konjunktio ja kärki on yksittäinen positiivinen atomilause Opiskelija(Jussi) Ahkera(x) Opiskelija(y) Ahkera(y) Valmistuu2007(y) (Tarkkaan ottaen Hornin lause: korkeintaan yksi positiivinen literaali, definite clause: täsmälleen yksi positiivinen literaali) Literaalimuodossa universaalikvanttorit jätetään usein kirjoittamatta ja muuttujat vain oletetaan universaalisti kvantifioiduiksi. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.9/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.10/38 Kuten propositiologiikassa lähtien liikkeelle faktoista, soveltaen yleistettyä Modus Ponensia voidaan tehdä eteenpäin ketjuttavaa päättelyä: käydään läpi sääntöjä ja jos löytyy sellainen jonka ehdot täyttyvät, lisätään sen takajäsenen tietämyskantaan. Jatketaan kunnes kyselyn tavoitteenna ollut lause saadaan todistettua tai uusia faktoja ei saada lisättyä. Nyt on huolehdittava siitä, ettei "uusi" fakta ole pelkkä tunnetun faktan uudelleennimentä, esim. Pitää(x, Karkki) Pitää(y, Karkki) Kun päästään vaiheeseen, jossa kaikki pääteltävät lauseet ovat jo tietämyskannassa, kantaa kutsutaan päättelyprosessin kiintopisteeksi (fixed point). Yleistetyn Modus Ponensin sovelluksena eteenpäin ketjutus on eheä päättelyalgoritmi. Se on myös täydellinen siinä mielessä, että tietämyskannan mitä tahansa loogista seurausta koskevaan kyselyyn saadaan vastaus. Datalog-tietämyskannassa ei esiinny laisinkaan funktiosymboleja ja eteenpäinketjutuksessa polynominen askelten lkm riittää kaikkien loogisten seurausten generoimiseen. Yleisessä tapauksessa joudumme vetoamaan Herbrandin tulokseen; päättely vain osittain ratkeavaa. Kirjan (amerikkalainen) esimerkki: USAn lain mukaan amerikkalaiset eivät saa myydä aseita vihamielisille valtioille. Valtio nimeltä Nono on vihollisvaltio, joka omistaa ohjuksia jotka on myynyt amerikkalainen eversti nimeltä West. Todistettava että eversti West on rikollinen. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.11/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.12/38... amerikkalaiset eivät saa myydä aseita vihamielisille valtioille: American(x) W eapon(y) Sells(x, y, z) Criminal(x) Nono omistaa ohjuksia ( x Owns(Nono, x) Missile(x)) Owns(Nono, M 1 ) ja Missile(M 1 )... jotka on myynyt amerikkalainen eversti nimeltä West: x Missile(x) Owns(Nono, x) Sells(W est, x, Nono) Ohjukset ovat aseita: Missile(x) W eapon(x) Amerikan viholliset ovat vihamielisiä: Enemy(x, America) Hostile(x) West on amerikkalainen: American(W est) Nono on Amerikan vihollinen: Enemy(Nono, America) luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.13/38 function FOL-FC-ASK(KB, α) returns a substitution or false repeat until new is empty new for each sentence r in KB do ( p 1... p n = q) STANDARDIZE-APART(r) for each θ such that (p 1... p n)θ = (p 1... p n)θ for some p 1,..., p n in KB q SUBST(θ, q) if q is not a renaming of a sentence already in KB or new then do add q to new φ UNIFY(q, α) if φ is not fail then return φ add new to KB return false luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.14/38 Weapon(M1) Sells(West,M1,Nono) luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.15/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.16/38
3 Eteenpäinketjutusalgoritmia käytetään nk. deduktiivisissa tietokannoissa (deductive databases) ja sääntöjärjestelmissä (production systems). Tämä algoritmi on kuitenkin tehoton kolmesta syystä: Weapon(M1) Sells(West,M1,Nono) 1. Algoritmin sisäsilmukassa generoidaan kaikki mahdolliset unifikaatiot, joilla säännön premissi saadaan samastettua sopivien faktojen kanssa. 2. Jokainen sääntö tarkistetaan jokaisella iteraatiokerralla, vaikka vain yksikin uusi fakta olisi lisätty tietämyskantaan. 3. Algoritmi generoi runsaasti faktoja, joilla ei ole merkitystä todistettavana olevan lauseen kannalta. Näitä ongelmia voidaan korjata eri menetelmillä ja parhaimmillaan eteenpäinketjutus toimii polynomisessa ajassa. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.17/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.18/38 TAAKSEPÄINKETJUTUS Predikaattilogiikassa taaksepäinketjutuksessa maaliksi otetaan ensin todistettava lause ja katsotaan minkä säännön kärjen kanssa maali voidaan samaistaa. Kun tällainen sääntö löytyy, sen rungon kaikki konjunktit lisätään uusiksi maaleiksi ja jatketaan yhdistetyn sijoituksen (composition of substitutions) etsimistä jatkamalla sääntöjen läpikäyntiä uusilla maaleilla kunnes päästään faktoihin asti. Yhdistetty sijoitus määritellään perättäin sovelletuksi sijoitukseksi: Subst(Compose(θ 1, θ 2 ), p) = Subst(θ 2, Subst(θ 1, p)). Kun maali samaistuu faktaan, ei uusia (ali)maaleja tarvitse generoida Syvyyssuuntainen haku tilavaatimus on lineaarinen ja sen ongelmaksi tulee toistuvat tilat ja epätäydellisyys jos syvyys voi olla ääretön. Näitä ongelmia voidaan jossain määrin korjata. function FOL-BC-ASK(KB, goals, θ) returns a set of substitutions inputs: KB, a knowledge base goals, a list of conjuncts forming a query (θ already applied) θ, the current substitution, initially the empty substitution local variables: answers, a set of substitutions, initially empty if goals is empty then return {θ} q SUBST(θ, FIRST(goals)) for each sentence r in KB where STANDARDIZE-APART(r) = ( p 1... p n q) and θ UNIFY(q, q ) succeeds new goals [ p 1,..., p n REST(goals)] answers FOL-BC-ASK(KB, new goals, COMPOSE(θ, θ)) answers return answers luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.19/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.20/38 American(x) Sells(x,y,z) luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.21/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.22/38 Sells(x,y,z) Sells(x,y,z) luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.23/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.24/38
4 {x/west, y/m1} {x/west, y/m1, z/nono} Sells(x,y,z) { z/nono } { y/m1} { y/m1} luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.25/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.26/38 LOGIIKKAOHJELMOINTI { z/nono } {x/west, y/m1, z/nono} { y/m1} Taaksepäinketjutus on logiikkaohjelmoinnin (logic programming) perusta. Logiikkaohjelmoinnin tavoitteena on deklaratiivinen tiedonesitys, jossa tietämys ja päättelyprosessit on erotettu toisistaan. Tunnetuin logiikkaohjelmointikieli on Prolog (Alain Colmerauer, 1972), jossa ohjelma muodostuu Hornin lauseina ilmaistusta tietämyskannasta. Siihen kohdistetaan kyselyitä, jotka sitten käsitellään taaksepäinketjutuksella. Prologin syntaksi on erilainen kuin logiikan: predikaattisymbolit alkavat pienellä kirjaimella ja muuttujat isolla, ensin kirjoitetaan klausuulin kärki, sitten ":-" (implikaatio oikealta vasemmalle) ja runko, missä literaalit on erotettu pilkulla (konjunktio) ja koko lause päättyy pisteeseen: criminal(x) :- american(x), weapon(y), sells(x,y,z), hostile(z). luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.27/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.28/38 Tämä siis vastaa predikaattilogiikan lausetta x, y, z American(x) Sells(x, y, z) Criminal(x) Prologissa on lisäksi määritelty operaatiot listojen käsittelyä ja aritmetiikkaa varten. Esimerkiksi listojen yhdistämiseen on määritelty predikaatti append(x,y,z), joka on tosi, kun Z on X:n ja Y:n yhdiste: append([],y,y). append([a X],Y,[A Z]) :- append(x,y,z). Ensimmäisen mukaan Y saadaan yhdistämällä tyhjä lista Y:hyn ja toinen sanoo, että jos Z saadaan yhdistämällä X:ään Y, niin Z, jonka alusta on poistettu A saadaan yhdistämällä Y X:ään jonka alusta on poistettu A. Nyt voimme suorittaa kyselyn append([1],[2],z), joka kysyy mitä saamme yhdistämällä listat [1] ja [2], ja saamme vastauksen Z=[1,2]. Jos kyselyn maalina on lause append(a,b,[1,2]), siis mitkä kaksi listaa yhdistämällä saadaan lista [1,2], saadaan vastaukseksi mahdolliset muuttujasidonnat eli parit A=[] B=[1,2] A=[1] B=[2] A=[1,2] B=[]. Prolog-lauseiden evaluointi perustuu syvyyssuuntaiseen taaksepäinketjutukseen, missä lauseita kokeillaan siinä järjestyksessä, jossa ne on talletettu tietämyskantaan. Syvyyssuuntaisen päättelyn seurauksena voi olla ikuinen silmukka joten päättely ei ole täydellistä: Korjaus: path(x,z):- path(x,y), link(y,z). path(x,z):- link(x,z). path(x,z):- link(x,z). path(x,z):- path(x,y), link(y,z). luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.29/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.30/38 RESOLUUTIO Prologissa on joitain piirteitä joita ei ole tavallisessa loogisessa päättelyssä: sisäänrakennetut aritmeettiset funktiot, predikaateilla voi olla sivuvaikutuksia (esim. I/O), negation as failure: negatiivinen predikaatti not P saa arvon true, jos positiivista predikaattia P ei onnistuta todistamaan. Esim. alive(x) :- not dead(x) joten kaikki joiden ei voi todistaa kuolleen ovat elossa. Prologissa on yhtäsuuruusmerkki =, mutta se ei ole yhtä vahva kuin identiteettirelaatio logiikassa vaan toteutuu ainoastaan jos kaksi termiä voidaan samastaa. Ei ole mahdollista antaa faktoja tai sääntöjä joissa identtisyyttä olisi käytetty. Kaikkia tarkistuksia (occur check) ei ole toteutettu Prologin unifikaatioalgoritmissa, joten päättely ei ole eheää. Tämä ei kuitenkaan yleensä johda ongelmiin. Kurt Gödelin täydellisyyslause (1930) 1. kertaluvun logiikalle: jokaisella loogisella seurauksella on äärellinen todistus T = φ T φ Vasta Robinsonin (1965) resoluutioalgoritmi antoi käytännöllisen menetelmän todistusten muodostamiseksi Gödelin tuloksista tunnetumpi on tietysti epätäydellisyyslause: matemaattisen induktion omaavan teorian kaikkia loogisia seurauksia ei voida todistaa aksioomista Erityisesti tämä koskee lukuteoriaa, jota siis ei voi aksiomatisoida luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.31/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.32/38
5 1. kertaluvun logiikan kaksi literaalia ovat komplementaarisia, jos yksi voidaan samaistaa toisen negaation kanssa Resoluutiosääntö predikaattilogiikalle: l 1 l k, m 1 m n (l 1 l i 1 l i+1 l k m 1 m j 1 m j+1 m n )θ missä UNIFY(l i, m j ) = θ. Esimerkiksi Rich(x) Unhappy(x) Rich(Ken) missä θ = {x/ken} Unhappy(Ken) Resoluutiossa premissien muuttujat täytyy tarvittaessa standardoida. Johtopäätöksestä täytyy poistaa samaistuvat literaalit. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.33/38 Resoluutiota varten lauseet on muutettava konjunktiiviseen normaalimuotoon. Esim. x [ y Eläin(y) Rakastaa(x, y)] [ y Rakastaa(y, x)] Implikaation poisto x [ y Eläin(y) Rakastaa(x, y)] [ y Rakastaa(y, x)] Negaation siirto sisään x, p x p, x, p x p: x [ y ( Eläin(y) Rakastaa(x, y))] [ y Rakastaa(y, x)] x [ y Eläin(y) Rakastaa(x, y)] [ y Rakastaa(y, x)] x [ y Eläin(y) Rakastaa(x, y)] [ y Rakastaa(y, x)] Muuttujanimien standardointi x [ y Eläin(y) Rakastaa(x, y)] [ z Rakastaa(z, x)] luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.34/38 Skolemisointi x [Eläin(F (x)) Rakastaa(x, F (x))] Rakastaa(G(x), x) Universaalikvanttorin poisto [Eläin(F (x)) Rakastaa(x, F (x))] Rakastaa(G(x), x) Distributiivisuuden soveltaminen [Eläin(F (x)) Rakastaa(G(x), x)] [ Rakastaa(x, F (x)) Rakastaa(G(x), x)] Lopputulos ei enää ole helposti ymmärrettävä, mutta se ei haittaa, koska muunnosproseduuri on automatisoitavissa Resoluutio on myös predikaattilogiikalle (refutaatio)täydellinen päättelyjärjestelmä siinä mielessä, että sen avulla voidaan tarkastaa tietämyskannan loogiset seuraukset KB = α todistetaan osoittamalla, että KB α johtaa ristiriitaan. luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.35/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.36/38 LAmerican(x) LMissile(x) L LSells(x,y,z) LMissile(x) LOwns(Nono,x) Weapon(x) LEnemy(x,America) Sells(West,x,Nono) Hostile(x) Criminal(x) L L L L L L L L L L L L Teoreemantodistimissa logiikkaohjelmoinnin Hornin lauseisiin rajoitettu kieli on laajennettu täyteen 1. kertaluvun logiikkaan Myös esim. Prologin tapa antaa kontrollin sekoittaa lauseiden logiikkaa on yleensä poistettu Päättely ei riipu lauseiden tai niiden osien kirjoitusjärjestyksestä Sovelluskohde: ohjelmien ja laitteiston verifiointi Matematiikassa teoreemantodistimet ovat nousseet näkyvään asemaan Esimerkiksi 1996 Otter-ohjelman seuraaja ensimmäisenä todisti, että Robbinsin 1933 esittämät aksioomat määrittävät Boolen algebran luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.37/38 luku09.tex Tekoäly (4 ov / 8 op) Raul Hakli 10/11/ :14 p.38/38
PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS
 67 PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS Jo äärimmäisen yksinkertaisessa peliesimerkissämme propositiologiikan ilmaisuvoima osoittautuu riittämättömäksi Tietämyskannan alustamiseksi pelin säännöillä meidän
67 PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS Jo äärimmäisen yksinkertaisessa peliesimerkissämme propositiologiikan ilmaisuvoima osoittautuu riittämättömäksi Tietämyskannan alustamiseksi pelin säännöillä meidän
Unify( Tuntee(Jussi, x), Tuntee(y, z) ) { y/jussi, z/x } { y/jussi, x/jussi, z/jussi }
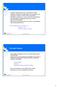 98 Ongelman edellä aiheuttaa saman muuttujanimen käyttö Toisaalta eri lauseiden muuttujanimillä ei ole merkitystä (ennen sidontaa) ja muuttujien nimentä voidaan standardoida Mahdollisia samaistuksia on
98 Ongelman edellä aiheuttaa saman muuttujanimen käyttö Toisaalta eri lauseiden muuttujanimillä ei ole merkitystä (ennen sidontaa) ja muuttujien nimentä voidaan standardoida Mahdollisia samaistuksia on
Ohjelmistotekniikan laitos OHJ-2550 Tekoäly, kevät
 96 Prolog voi päätyä samaan ratkaisuun monen päättelypolun kautta Tällöin sama ratkaisu palautetaan useita kertoja minimum(x,y,x):- X=Y. Molempien sääntöjen kautta löytyyy sama
96 Prolog voi päätyä samaan ratkaisuun monen päättelypolun kautta Tällöin sama ratkaisu palautetaan useita kertoja minimum(x,y,x):- X=Y. Molempien sääntöjen kautta löytyyy sama
815338A Ohjelmointikielten periaatteet
 815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
Lause on validi eli tautologia jos se on tosi kaikissa malleissa P P Jokainen validi lause on loogisesti ekvivalentti arvon T kanssa
 63 Lauseet ja ovat loogisesti ekvivalentteja,, jos ne ovat tosia samoissa malleissa: joss ja Lause on validi eli tautologia jos se on tosi kaikissa malleissa P P Jokainen validi lause on loogisesti ekvivalentti
63 Lauseet ja ovat loogisesti ekvivalentteja,, jos ne ovat tosia samoissa malleissa: joss ja Lause on validi eli tautologia jos se on tosi kaikissa malleissa P P Jokainen validi lause on loogisesti ekvivalentti
1. Johdanto (I, 1) Taustaa Tekoälyn historia. 2. Logiikka, tietämys ja päättely
 TEKOÄLY syksy 4 ov, jatko-opintokelpoinen Luennot ti 12 14 S1, to 12 14 TB109 2. 9. 11. 12. ( viikkoa) prof. Tapio Elomaa Harjoitustyöt 3 kpl tekn.yo. Minna Ruuska Viikkoharjoitukset ti ja to 10 12, pe
TEKOÄLY syksy 4 ov, jatko-opintokelpoinen Luennot ti 12 14 S1, to 12 14 TB109 2. 9. 11. 12. ( viikkoa) prof. Tapio Elomaa Harjoitustyöt 3 kpl tekn.yo. Minna Ruuska Viikkoharjoitukset ti ja to 10 12, pe
LOGIIKKA, TIETÄMYS JA PÄÄTTELY
 36 LOGIIKKA, TIETÄMYS JA PÄÄTTELY Ryhdymme nyt tarkastelemaan tietämyskannan (knowledge base, KB omaavia agentteja KB:n avulla agentti pyrkii pitämään yllä tietoa vain osittain havainnoimastaan maailmasta
36 LOGIIKKA, TIETÄMYS JA PÄÄTTELY Ryhdymme nyt tarkastelemaan tietämyskannan (knowledge base, KB omaavia agentteja KB:n avulla agentti pyrkii pitämään yllä tietoa vain osittain havainnoimastaan maailmasta
Tehtävä 1. Päättele resoluutiolla seuraavista klausuulijoukoista. a. 1 {p 3 } oletus. 4 {p 1, p 2, p 3 } oletus. 5 { p 1 } (1, 2) 7 (4, 6)
 Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
Insinöörimatematiikka A
 Insinöörimatematiikka A Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2018 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 3 1 of 23 Kertausta Määritelmä Predikaattilogiikan
Insinöörimatematiikka A Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2018 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 3 1 of 23 Kertausta Määritelmä Predikaattilogiikan
Logiikan kertausta. TIE303 Formaalit menetelmät, kevät Antti-Juhani Kaijanaho. Jyväskylän yliopisto Tietotekniikan laitos.
 TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
815338A Ohjelmointikielten periaatteet: Logiikkaohjelmointi. Logiikkaohjelmointi
 Logiikkaohjelmointi Tässä osassa käsitellään toista deklaratiivisen ohjelmoinnin paradigmaa eli logiikkaohjelmointia. Pääasiallisena lähteenä on käytetty Sebestan ([Seb]) lukua 16. Maarit Harsun teoksen
Logiikkaohjelmointi Tässä osassa käsitellään toista deklaratiivisen ohjelmoinnin paradigmaa eli logiikkaohjelmointia. Pääasiallisena lähteenä on käytetty Sebestan ([Seb]) lukua 16. Maarit Harsun teoksen
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset 1. Päättele resoluutiolla seuraavista klausuulijoukoista: (a) {{p 0 }, {p 1 }, { p 0, p 2 },
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset 1. Päättele resoluutiolla seuraavista klausuulijoukoista: (a) {{p 0 }, {p 1 }, { p 0, p 2 },
Toinen muotoilu. {A 1,A 2,...,A n,b } 0, Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun 1 / 13
 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
T Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet )
 T-79.144 Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3-3.4) 2 5.11.2005 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio R A
T-79.144 Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3-3.4) 2 5.11.2005 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio R A
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet )
 T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi
 Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
T Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut
 T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
-Matematiikka on aksiomaattinen järjestelmä. -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi
 -Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
-Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
ALGORITMI- MATEMATIIKKA. Keijo Ruohonen
 ALGORITMI- MATEMATIIKKA Keijo Ruohonen 1993 Kirjallisuutta ANDERSON, I.: A First Course in Combinatorial Mathematics. Oxford University Press (1979) GRAHAM, R.L. & KNUTH, D.E. & PATASHNIK, O.: Concrete
ALGORITMI- MATEMATIIKKA Keijo Ruohonen 1993 Kirjallisuutta ANDERSON, I.: A First Course in Combinatorial Mathematics. Oxford University Press (1979) GRAHAM, R.L. & KNUTH, D.E. & PATASHNIK, O.: Concrete
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Etsi lauseen (p 0 (p 1 p 0 )) p 1 kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Etsi lauseen (p 0 (p 1 p 0 )) p 1 kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa
TIEA241 Automaatit ja kieliopit, syksy Antti-Juhani Kaijanaho. 8. syyskuuta 2016
 TIEA241 Automaatit ja kieliopit, syksy 2016 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. syyskuuta 2016 Sisällys a https://tim.jyu.fi/view/kurssit/tie/ tiea241/2016/videoiden%20hakemisto Matemaattisen
TIEA241 Automaatit ja kieliopit, syksy 2016 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. syyskuuta 2016 Sisällys a https://tim.jyu.fi/view/kurssit/tie/ tiea241/2016/videoiden%20hakemisto Matemaattisen
 LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
T kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut
 T-79.5101 kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun juureen
T-79.5101 kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun juureen
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Taulumenetelmä modaalilogiikalle K
 / Kevät 2004 ML-6 1 Taulumenetelmä modaalilogiikalle On vaikeaa löytää Hilbert-tyylisiä todistuksia: Käytössä Modus Ponens -sääntö: jotta voidaan johtaa Q, täytyy johtaa P ja P Q. Mutta mikä on sopiva
/ Kevät 2004 ML-6 1 Taulumenetelmä modaalilogiikalle On vaikeaa löytää Hilbert-tyylisiä todistuksia: Käytössä Modus Ponens -sääntö: jotta voidaan johtaa Q, täytyy johtaa P ja P Q. Mutta mikä on sopiva
Logiikka 1/5 Sisältö ESITIEDOT:
 Logiikka 1/5 Sisältö Formaali logiikka Luonnollinen logiikka muodostaa perustan arkielämän päättelyille. Sen käyttö on intuitiivista ja usein tiedostamatonta. Mikäli logiikka halutaan täsmällistää esimerkiksi
Logiikka 1/5 Sisältö Formaali logiikka Luonnollinen logiikka muodostaa perustan arkielämän päättelyille. Sen käyttö on intuitiivista ja usein tiedostamatonta. Mikäli logiikka halutaan täsmällistää esimerkiksi
T Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka )
 T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka 14.1 14.5) 23. 25.4.2008 Ratkaisuja demotehtäviin Tehtävä 14.1 Herbrand-universumi U muodostuu termeistä,
T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka 14.1 14.5) 23. 25.4.2008 Ratkaisuja demotehtäviin Tehtävä 14.1 Herbrand-universumi U muodostuu termeistä,
Todistusteoriaa. Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan.
 Todistusteoriaa Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan. Todistusteoriassa annetaan joukko aksioomia ja päättely- sääntöjä,
Todistusteoriaa Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan. Todistusteoriassa annetaan joukko aksioomia ja päättely- sääntöjä,
Johdatus logiikkaan I Harjoitus 4 Vihjeet
 Johdatus logiikkaan I Harjoitus 4 Vihjeet 1. Etsi lauseen ((p 0 p 1 ) (p 0 p 1 )) kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa normaalimuodossa, (b) konjunktiivisessa normaalimuodossa.
Johdatus logiikkaan I Harjoitus 4 Vihjeet 1. Etsi lauseen ((p 0 p 1 ) (p 0 p 1 )) kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa normaalimuodossa, (b) konjunktiivisessa normaalimuodossa.
T Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka )
 T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka 10.3. 11.4) 26. 30.3. 2009 Ratkaisuja demotehtäviin Tehtävä 10.5 Allaolevat kolme graafia pyrkivät selventämään
T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka 10.3. 11.4) 26. 30.3. 2009 Ratkaisuja demotehtäviin Tehtävä 10.5 Allaolevat kolme graafia pyrkivät selventämään
T Tietojenkäsittelyteorian seminaari
 p.1/25 T-79.194 Tietojenkäsittelyteorian seminaari Krzysztof R. Apt: Principles of Constraint Programming: 4. luku, ss. 103 118 Jakub Jarvenpaa jakub.jarvenpaa@hut.fi p.2/25 Sisältö Termiyhtälöt Martelli-Montanari-algoritmi
p.1/25 T-79.194 Tietojenkäsittelyteorian seminaari Krzysztof R. Apt: Principles of Constraint Programming: 4. luku, ss. 103 118 Jakub Jarvenpaa jakub.jarvenpaa@hut.fi p.2/25 Sisältö Termiyhtälöt Martelli-Montanari-algoritmi
FI3 Tiedon ja todellisuuden filosofia LOGIIKKA. 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan:
 LOGIIKKA 1 Mitä logiikka on? päättelyn tiede o oppi muodollisesti pätevästä päättelystä 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan: sisältö, merkitys: onko jokin premissi
LOGIIKKA 1 Mitä logiikka on? päättelyn tiede o oppi muodollisesti pätevästä päättelystä 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan: sisältö, merkitys: onko jokin premissi
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Ratkaisu: Käytetään induktiota propositiolauseen A rakenteen suhteen. Alkuaskel. A = p i jollain i N. Koska v(p i ) = 1 kaikilla i N, saadaan
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 2 Ratkaisuehdotukset 1. Olkoon totuusjakauma v sellainen että v(p i ) = 1 kaikilla i N ja A propositiolause, jossa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 2 Ratkaisuehdotukset 1. Olkoon totuusjakauma v sellainen että v(p i ) = 1 kaikilla i N ja A propositiolause, jossa
Luonnollisen päättelyn luotettavuus
 Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
Diskreetit rakenteet. 3. Logiikka. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1
 811120P 3. 5 op Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 ja laskenta tarkastelemme terveeseen järkeen perustuvaa päättelyä formaalina järjestelmänä logiikkaa sovelletaan
811120P 3. 5 op Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 ja laskenta tarkastelemme terveeseen järkeen perustuvaa päättelyä formaalina järjestelmänä logiikkaa sovelletaan
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 3. Logiikka 3.1 Logiikka tietojenkäsittelyssä Pyritään formalisoimaan terveeseen järkeen perustuva päättely Sovelletaan monella alueella tietojenkäsittelyssä, esim.
811120P Diskreetit rakenteet 2016-2017 3. Logiikka 3.1 Logiikka tietojenkäsittelyssä Pyritään formalisoimaan terveeseen järkeen perustuva päättely Sovelletaan monella alueella tietojenkäsittelyssä, esim.
Nimitys Symboli Merkitys Negaatio ei Konjuktio ja Disjunktio tai Implikaatio jos..., niin... Ekvivalenssi... jos ja vain jos...
 2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
Ratkaisu: Yksi tapa nähdä, että kaavat A (B C) ja (A B) (A C) ovat loogisesti ekvivalentit, on tehdä totuustaulu lauseelle
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Olkoot A, B ja C propositiolauseita. Näytä, että A (B C) (A B) (A C). Ratkaisu: Yksi tapa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Olkoot A, B ja C propositiolauseita. Näytä, että A (B C) (A B) (A C). Ratkaisu: Yksi tapa
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
T Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet )
 T-79.3001 Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3 3.4) 21. 24.3.2006 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio
T-79.3001 Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3 3.4) 21. 24.3.2006 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio
7 LOOGISET AGENTIT. (reasoning) maailman tilasta. Tämä on erityisen tärkeää osittain havaittavissa
 7 OOGIET GENTIT Tarkastelemme nyt tietämyskannan (knowledge base, K) omaavia agentteja, joita kutsumme tietämyspohjaisksi toimijoiksi (knowledge-based agents) Tietämyspohjaiset toimijat käyttävät tietämyskantaa
7 OOGIET GENTIT Tarkastelemme nyt tietämyskannan (knowledge base, K) omaavia agentteja, joita kutsumme tietämyspohjaisksi toimijoiksi (knowledge-based agents) Tietämyspohjaiset toimijat käyttävät tietämyskantaa
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
ja λ 2 = 2x 1r 0 x 2 + 2x 1r 0 x 2
 Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Roosa Niemi. Riippuvuuslogiikkaa
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Roosa Niemi Riippuvuuslogiikkaa Informaatiotieteiden yksikkö Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden yksikkö ROOSA NIEMI: Riippuvuuslogiikkaa
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Roosa Niemi Riippuvuuslogiikkaa Informaatiotieteiden yksikkö Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden yksikkö ROOSA NIEMI: Riippuvuuslogiikkaa
Entscheidungsproblem
 Entscheidungsproblem Antti-Juhani Kaijanaho 24. kesäkuuta 2013 Entscheidungsproblem eli ratkaisuongelma kysyy, millä mekaanisella menetelmällä voisi selvittää, onko mielivaltainen annettu ensimmäisen kertaluvun
Entscheidungsproblem Antti-Juhani Kaijanaho 24. kesäkuuta 2013 Entscheidungsproblem eli ratkaisuongelma kysyy, millä mekaanisella menetelmällä voisi selvittää, onko mielivaltainen annettu ensimmäisen kertaluvun
T Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka ) A ( B C) A B C.
 T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka 6.1 7.2) 27. 29.2.2008 Ratkaisuja demotehtäviin Tehtävä 6.1 a) A (B C) Poistetaan lauseesta ensin implikaatiot.
T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka 6.1 7.2) 27. 29.2.2008 Ratkaisuja demotehtäviin Tehtävä 6.1 a) A (B C) Poistetaan lauseesta ensin implikaatiot.
on rekursiivisesti numeroituva, mutta ei rekursiivinen.
 6.5 Turingin koneiden pysähtymisongelma Lause 6.9 Kieli H = { M pysähtyy syötteellä w} on rekursiivisesti numeroituva, mutta ei rekursiivinen. Todistus. Todetaan ensin, että kieli H on rekursiivisesti
6.5 Turingin koneiden pysähtymisongelma Lause 6.9 Kieli H = { M pysähtyy syötteellä w} on rekursiivisesti numeroituva, mutta ei rekursiivinen. Todistus. Todetaan ensin, että kieli H on rekursiivisesti
Pikapaketti logiikkaan
 Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
815338A Ohjelmointikielten periaatteet Harjoitus 6 Vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
Todistusmenetelmiä Miksi pitää todistaa?
 Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen:
 Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen: S A S B Samaan jäsennyspuuhun päästään myös johdolla S AB Ab ab: S A S B Yhteen jäsennyspuuhun liittyy aina tasan yksi vasen
Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen: S A S B Samaan jäsennyspuuhun päästään myös johdolla S AB Ab ab: S A S B Yhteen jäsennyspuuhun liittyy aina tasan yksi vasen
Predikaattilogiikkaa
 Predikaattilogiikkaa UKUTEORIA JA TO- DISTAMINEN, MAA11 Kertausta ogiikan tehtävä: ogiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat
Predikaattilogiikkaa UKUTEORIA JA TO- DISTAMINEN, MAA11 Kertausta ogiikan tehtävä: ogiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat
SAT-ongelman rajoitetut muodot
 SAT-ongelman rajoitetut muodot olemme juuri osoittaneet että SAT on NP-täydellinen perusidea on nyt osoittaa joukolle kiinnostavia ongelmia A NP että SAT p m A, jolloin kyseiset A myös ovat NP-täydellisiä
SAT-ongelman rajoitetut muodot olemme juuri osoittaneet että SAT on NP-täydellinen perusidea on nyt osoittaa joukolle kiinnostavia ongelmia A NP että SAT p m A, jolloin kyseiset A myös ovat NP-täydellisiä
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset
 815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
LOGIIKKA johdantoa
 LOGIIKKA johdantoa LUKUTEORIA JA TO- DISTAMINEN, MAA11 Logiikan tehtävä: Logiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat päättelyt
LOGIIKKA johdantoa LUKUTEORIA JA TO- DISTAMINEN, MAA11 Logiikan tehtävä: Logiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat päättelyt
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
Entscheidungsproblem
 Entscheidungsproblem Antti-Juhani Kaijanaho 10. joulukuuta 2015 Entscheidungsproblem eli ratkaisuongelma kysyy, millä mekaanisella menetelmällä voisi selvittää, onko mielivaltainen annettu ensimmäisen
Entscheidungsproblem Antti-Juhani Kaijanaho 10. joulukuuta 2015 Entscheidungsproblem eli ratkaisuongelma kysyy, millä mekaanisella menetelmällä voisi selvittää, onko mielivaltainen annettu ensimmäisen
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2017-2018 Yhteenveto Yleistä kurssista Kurssin laajuus 5 op Luentoja 30h Harjoituksia 21h Itsenäistä työskentelyä n. 80h 811120P Diskreetit rakenteet, Yhteenveto 2 Kurssin
811120P Diskreetit rakenteet 2017-2018 Yhteenveto Yleistä kurssista Kurssin laajuus 5 op Luentoja 30h Harjoituksia 21h Itsenäistä työskentelyä n. 80h 811120P Diskreetit rakenteet, Yhteenveto 2 Kurssin
Predikaattilogiikan malli-teoreettinen semantiikka
 Predikaattilogiikan malli-teoreettinen semantiikka February 4, 2013 Muistamme, että predikaattilogiikassa aakkosto L koostuu yksilövakioista c 0, c 1, c 2,... ja predikaattisymboleista P, R,... jne. Ekstensionaalisia
Predikaattilogiikan malli-teoreettinen semantiikka February 4, 2013 Muistamme, että predikaattilogiikassa aakkosto L koostuu yksilövakioista c 0, c 1, c 2,... ja predikaattisymboleista P, R,... jne. Ekstensionaalisia
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho. 16. maaliskuuta 2011
 TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 16. maaliskuuta 2011 Sisällys Sisällys Väitelauseet lause (tai virke), joka sanoo jonkin asian pitävän paikkaansa
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 16. maaliskuuta 2011 Sisällys Sisällys Väitelauseet lause (tai virke), joka sanoo jonkin asian pitävän paikkaansa
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (opetusmoniste, lauselogiikka )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
Matematiikan mestariluokka, syksy 2009 7
 Matematiikan mestariluokka, syksy 2009 7 2 Alkuluvuista 2.1 Alkuluvut Määritelmä 2.1 Positiivinen luku a 2 on alkuluku, jos sen ainoat positiiviset tekijät ovat 1 ja a. Jos a 2 ei ole alkuluku, se on yhdistetty
Matematiikan mestariluokka, syksy 2009 7 2 Alkuluvuista 2.1 Alkuluvut Määritelmä 2.1 Positiivinen luku a 2 on alkuluku, jos sen ainoat positiiviset tekijät ovat 1 ja a. Jos a 2 ei ole alkuluku, se on yhdistetty
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
 ICS-C2000 Tietojenkäsittelyteoria Kevät 206 Kierros 0, 2. 24. maaliskuuta Huom! Perjantaina 25. maaliskuuta ei ole laskareita (pitkäperjantai), käykää vapaasti valitsemassanne ryhmässä aiemmin viikolla.
ICS-C2000 Tietojenkäsittelyteoria Kevät 206 Kierros 0, 2. 24. maaliskuuta Huom! Perjantaina 25. maaliskuuta ei ole laskareita (pitkäperjantai), käykää vapaasti valitsemassanne ryhmässä aiemmin viikolla.
Kirjoita käyttäen propositiosymboleita, konnektiiveja ja sulkeita propositiologiikan lauseiksi:
 1 Logiikan paja, kevät 2011 Ratkaisut viikolle I Thomas Vikberg Merkitään propopositiosymboleilla p i seuraavia atomilauseita: p 0 : vettä sataa p 1 : tänään on perjantai p 2 : olen myöhässä Valitaan konnektiiveiksi,
1 Logiikan paja, kevät 2011 Ratkaisut viikolle I Thomas Vikberg Merkitään propopositiosymboleilla p i seuraavia atomilauseita: p 0 : vettä sataa p 1 : tänään on perjantai p 2 : olen myöhässä Valitaan konnektiiveiksi,
Pysähtymisongelman ratkeavuus [Sipser luku 4.2]
![Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Pysähtymisongelman ratkeavuus [Sipser luku 4.2]](/thumbs/59/42645644.jpg) Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
Ehto- ja toistolauseet
 Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 3 Mikko Salo 1.9.2017 Sisältö 1. Logiikasta 2. Suora ja epäsuora todistus 3. Jaollisuus ja alkuluvut Todistus Tähän asti esitetyt todistukset ovat olleet esimerkinomaisia.
Johdatus matematiikkaan Luento 3 Mikko Salo 1.9.2017 Sisältö 1. Logiikasta 2. Suora ja epäsuora todistus 3. Jaollisuus ja alkuluvut Todistus Tähän asti esitetyt todistukset ovat olleet esimerkinomaisia.
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
5.1 Semanttisten puiden muodostaminen
 Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 ari.vesanen (at) oulu.fi 5. Rekursio ja induktio Rekursio tarkoittaa jonkin asian määrittelyä itseensä viittaamalla Tietojenkäsittelyssä algoritmin määrittely niin,
811120P Diskreetit rakenteet 2016-2017 ari.vesanen (at) oulu.fi 5. Rekursio ja induktio Rekursio tarkoittaa jonkin asian määrittelyä itseensä viittaamalla Tietojenkäsittelyssä algoritmin määrittely niin,
3. Predikaattilogiikka
 3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
4 Matemaattinen induktio
 4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
Perinnöllinen informaatio ja geneettinen koodi.
 Tehtävä A1 Kirjoita essee aiheesta: Perinnöllinen informaatio ja geneettinen koodi. Vastaa esseemuotoisesti, älä käytä ranskalaisia viivoja. Piirroksia voi käyttää. Vastauksessa luetaan ansioksi selkeä
Tehtävä A1 Kirjoita essee aiheesta: Perinnöllinen informaatio ja geneettinen koodi. Vastaa esseemuotoisesti, älä käytä ranskalaisia viivoja. Piirroksia voi käyttää. Vastauksessa luetaan ansioksi selkeä
Todistus: Aiemmin esitetyn mukaan jos A ja A ovat rekursiivisesti lueteltavia, niin A on rekursiivinen.
 Lause: Tyhjyysongelma ei ole osittain ratkeava; ts. kieli ei ole rekursiivisesti lueteltava. L e = { w { 0, 1 } L(M w ) = } Todistus: Aiemmin esitetyn mukaan jos A ja A ovat rekursiivisesti lueteltavia,
Lause: Tyhjyysongelma ei ole osittain ratkeava; ts. kieli ei ole rekursiivisesti lueteltava. L e = { w { 0, 1 } L(M w ) = } Todistus: Aiemmin esitetyn mukaan jos A ja A ovat rekursiivisesti lueteltavia,
1 Logiikkaa. 1.1 Logiikan symbolit
 1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
Esimerkkejä polynomisista ja ei-polynomisista ongelmista
 Esimerkkejä polynomisista ja ei-polynomisista ongelmista Ennen yleisempiä teoriatarkasteluja katsotaan joitain tyypillisiä esimerkkejä ongelmista ja niiden vaativuudesta kaikki nämä ongelmat ratkeavia
Esimerkkejä polynomisista ja ei-polynomisista ongelmista Ennen yleisempiä teoriatarkasteluja katsotaan joitain tyypillisiä esimerkkejä ongelmista ja niiden vaativuudesta kaikki nämä ongelmat ratkeavia
1 Lineaariavaruus eli Vektoriavaruus
 1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Heidi Luukkonen. Sahlqvistin kaavat
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Luukkonen Sahlqvistin kaavat Informaatiotieteiden yksikkö Matematiikka Maaliskuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö LUUKKONEN, HEIDI: Sahlqvistin
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Luukkonen Sahlqvistin kaavat Informaatiotieteiden yksikkö Matematiikka Maaliskuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö LUUKKONEN, HEIDI: Sahlqvistin
2. Minkä joukon määrittelee kaava P 0 (x 0 ) P 1 (x 0 ) mallissa M = ({0, 1, 2, 3}, P M 0, P M 1 ), kun P M 0 = {0, 1} ja P M 1 = {1, 2}?
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan II, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Mitkä muuttujat esiintyvät vapaina kaavassa x 2 ( x 0 R 0 (x 1, x 2 ) ( x 3 R 0 (x 3, x 0
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan II, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Mitkä muuttujat esiintyvät vapaina kaavassa x 2 ( x 0 R 0 (x 1, x 2 ) ( x 3 R 0 (x 3, x 0
Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E.
 Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E. Perusaksioomat: Laki 1: Kukin totuusfunktio antaa kullekin propositiolle totuusarvoksi joko toden T tai epätoden
Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E. Perusaksioomat: Laki 1: Kukin totuusfunktio antaa kullekin propositiolle totuusarvoksi joko toden T tai epätoden
Modus Ponens. JosAjaA B ovat tosia, niin välttämättä myösb on tosi 1 / 15. Modus Ponens. Ketjusääntö. Päättelyketju.
 JosAjaA B ovat tosia, niin välttämättä myösb on tosi 1 / 15 JosAjaA B ovat tosia, niin välttämättä myösb on tosi (A (A B)) B on tautologia eli (A (A B)) B. 1 / 15 JosAjaA B ovat tosia, niin välttämättä
JosAjaA B ovat tosia, niin välttämättä myösb on tosi 1 / 15 JosAjaA B ovat tosia, niin välttämättä myösb on tosi (A (A B)) B on tautologia eli (A (A B)) B. 1 / 15 JosAjaA B ovat tosia, niin välttämättä
M = (Q, Σ, Γ, δ, q 0, q acc, q rej )
 6. LASKETTAVUUSTEORIAA Churchin Turingin teesi: Mielivaltainen (riittävän vahva) laskulaite Turingin kone. Laskettavuusteoria: Tarkastellaan mitä Turingin koneilla voi ja erityisesti mitä ei voi laskea.
6. LASKETTAVUUSTEORIAA Churchin Turingin teesi: Mielivaltainen (riittävän vahva) laskulaite Turingin kone. Laskettavuusteoria: Tarkastellaan mitä Turingin koneilla voi ja erityisesti mitä ei voi laskea.
Luku 11. Logiikkaohjelmoinnin idea Logiikkakieli
 Luku 11 Logiikkaohjelmoinnin idea Logiikkaohjelmoinnin perusidea on esittää ohjelmointiongelma faktoina (aksioomina) ja päättelysääntöinä sekä kyselynä, joka kohdistuu näiden muodostamaan tietojoukkoon.
Luku 11 Logiikkaohjelmoinnin idea Logiikkaohjelmoinnin perusidea on esittää ohjelmointiongelma faktoina (aksioomina) ja päättelysääntöinä sekä kyselynä, joka kohdistuu näiden muodostamaan tietojoukkoon.
4.3. Matemaattinen induktio
 4.3. Matemaattinen induktio Matemaattinen induktio: Deduktion laji Soveltuu, kun ominaisuus on osoitettava olevan voimassa luonnollisilla luvuilla. Suppea muoto P(n) : Ominaisuus, joka joka riippuu luvusta
4.3. Matemaattinen induktio Matemaattinen induktio: Deduktion laji Soveltuu, kun ominaisuus on osoitettava olevan voimassa luonnollisilla luvuilla. Suppea muoto P(n) : Ominaisuus, joka joka riippuu luvusta
Algoritmit 2. Luento 4 To Timo Männikkö
 Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Taas laskin. TIES341 Funktio ohjelmointi 2 Kevät 2006
 Taas laskin TIES341 Funktio ohjelmointi 2 Kevät 2006 Rakennepuutyyppi data Term = C Rational T F V String Term :+: Term Term : : Term Term :*: Term Term :/: Term Term :==: Term Term :/=: Term Term :
Taas laskin TIES341 Funktio ohjelmointi 2 Kevät 2006 Rakennepuutyyppi data Term = C Rational T F V String Term :+: Term Term : : Term Term :*: Term Term :/: Term Term :==: Term Term :/=: Term Term :
Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. ( ) Jeremias Berg
 Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. (14.3-18.3) Jeremias Berg 1. Luettele kaikki seuraavien joukkojen alkiot: (a) {x Z : x 3} (b) {x N : x > 12 x < 7} (c) {x N : 1 x 7} Ratkaisu:
Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. (14.3-18.3) Jeremias Berg 1. Luettele kaikki seuraavien joukkojen alkiot: (a) {x Z : x 3} (b) {x N : x > 12 x < 7} (c) {x N : 1 x 7} Ratkaisu:
802320A LINEAARIALGEBRA OSA I
 802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
Lause 5. (s. 50). Olkoot A ja B joukkoja. Tällöin seuraavat ehdot ovat
 jen Kahden joukon A ja B samuutta todistettaessa kannattaa usein osoittaa, että A on B:n osajoukko ja että B on A:n osajoukko. Tällöin sovelletaan implikaation ja ekvivalenssin yhteyttä. Lause 5. (s. 50).
jen Kahden joukon A ja B samuutta todistettaessa kannattaa usein osoittaa, että A on B:n osajoukko ja että B on A:n osajoukko. Tällöin sovelletaan implikaation ja ekvivalenssin yhteyttä. Lause 5. (s. 50).
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
(p j b (i, j) + p i b (j, i)) (p j b (i, j) + p i (1 b (i, j)) p i. tähän. Palaamme sanakirjaongelmaan vielä tasoitetun analyysin yhteydessä.
 Loppu seuraa suoralla laskulla: n n Tave TR = p j (1 + b (i, j)) j=1 = 1 + 1 i
Loppu seuraa suoralla laskulla: n n Tave TR = p j (1 + b (i, j)) j=1 = 1 + 1 i
Ratkeavuus ja efektiivinen numeroituvuus
 Luku 6 Ratkeavuus ja efektiivinen numeroituvuus Proseduurit Olkoon A aakkosto. Proseduuri aakkoston A sanoille on mikä hyvänsä prosessi (algoritmi) P, jolle annetaan syötteeksi sana w A, ja joka etenee
Luku 6 Ratkeavuus ja efektiivinen numeroituvuus Proseduurit Olkoon A aakkosto. Proseduuri aakkoston A sanoille on mikä hyvänsä prosessi (algoritmi) P, jolle annetaan syötteeksi sana w A, ja joka etenee
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa.
 Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
