Empiirinen näkökulma divergenssin ja roottorin käsitteiden opetuksessa
|
|
|
- Elli Heikkilä
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lisensiaatintutkimus Fysiikka Empiirinen näkökulma divergenssin ja roottorin käsitteiden opetuksessa Ossi Pasanen 2009 Ohjaaja: Tarkastajat: prof. Heimo Saarikko prof. Jukka Maalampi prof. Heimo Saarikko HELSINGIN YLIOPISTO FYSIIKAN LAITOS PL 64 (Gustaf Hällströmin katu 2a) Helsingin yliopisto
2
3 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Matemaattis-luonnontieteellinen Tekijä Författare Author Ossi Pasanen Työn nimi Arbetets titel Title Fysiikan laitos Empiirinen näkökulma divergenssin ja roottorin käsitteiden opetuksessa Oppiaine Läroämne Subject Fysiikka Työn laji Arbetets art Level Aika Datum Month and year Sivumäärä Sidoantal Number of pages Lisensiaatintutkimus Toukokuu Tiivistelmä Referat Abstract Aiempien tutkimusten mukaan derivaatan oppimistuloksia voidaan parantaa käyttämällä opetuksessa erilaisia derivaatan esitystapoja ja käsittelemällä derivaattaa konkreettisia ominaisuuksia omaavana objektina. Opetusteknologinen tutkimus on puolestaan tuonut näyttöä siitä, että animaatioista ja interaktiivisista tietokonesimulaatioista on etua staattisiin kuviin nähden tarkasteltaessa dynaamisia ilmiöitä ja kolmiulotteisten objektien rakennetta. Divergenssi ja roottori ovat vektorianalyysin derivaattakäsitteitä, jotka ovat tärkeitä matemaattisia työkaluja fysiikassa. Tässä tutkimuksessa selvitettiin opetuskokeilulla, miten visualisaatiot ja fysikaaliset analogiat soveltuvat divergenssin ja roottorin empiiristen merkitysten opettamiseen yliopisto-opintojaan aloittaville fysiikan opiskelijoille. Kokeilu tehtiin Helsingin yliopiston Fysiikan laitoksella yliopistokurssien Matemaattiset apuneuvot I ja II yhteydessä vuonna Tutkimusaineisto koostuu 97:stä analysoidusta koevastauksesta sekä viidelle opiskelijalle tehdyistä toiminnallisista haastatteluista. Havaittiin, että divergenssin ja roottorin empiirinen ymmärrys voi kehittyä myös niille opiskelijoille, joilta laskutekniset tavoitteet jäävät saavuttamatta. Koetehtävän avoimista vastauksista saatiin näyttöä, että visualisaatioilla on ollut vaikutusta ainakin joidenkin opiskelijoiden käsitteenmuodostukselle. Ymmärryksen esteinä havaittiin virhekäsityksiä, joista osa on peräisin sanojen lähteisyys ja pyörteisyys arkipäivän merkityksistä. Visualisaatiot osoittautuivat toimivaksi menetelmäksi opetuksen monipuolistamisessa. Tällä voi olla merkitystä esimerkiksi opiskelumotivaation kohottajana. Vektorianalyysin matemaattinen rakenne antaa mahdollisuuden etenemisjärjestykseen, joka seuraa fysiikassa tyypillistä abstraktioketjua makroskooppisista mikroskooppisiin käsitteisiin. Fysikaalisten analogioiden korostaminen opetuksessa saattaa tarjota oikoteitä matemaattisten käsitteiden ymmärtämiselle aiemmin tutkitun matematiikan oppimishierarkian ohitse. Avainsanat Nyckelord Keywords divergenssi, roottori, visualisointi, käsitteiden merkitykset, korkeakouludidaktiikka Säilytyspaikka Förvaringsställe Where deposited Kumpulan tiedekirjasto Muita tietoja övriga uppgifter Additional information
4
5 Sisällys 1 Johdanto Taustaa Matematiikan suhde empiriaan Tavoitteiden asettelu Tutkimuksen toteutuksesta Käsitteiden määrittely Usean muuttujan funktiot Funktion raja-arvo Matemaattinen käsite Fysikaalinen näkökulma Osittaisderivaatta Fysikaalinen merkitys Nablaoperaattori Divergenssin fysikaalinen tulkinta Roottorin fysikaalinen tulkinta Gaussin ja Stokesin lause Teoreettinen viitekehys Matemaattisen kehityksen kognitiivisia teorioita Operationaalis-rakenteellinen teoria APOS-teoria matematiikan oppimisesta Matemaattisen ajattelun kolme maailmaa Teorioiden merkitys tämän tutkimuksen kannalta Vastaustiedon kognitiivinen luokittelu SOLO-taksonomia Empiirinen käsitteenmuodostus Divergenssin ja roottorin empiirisen merkityksen rakentuminen
6 vi SISÄLLYS 3.4 Matematiikan opetuksen menetelmiä Visualisaatiot Animaatiot Tutkimuksia derivaatan opetuksesta Vektorianalyysin opetus eri oppikirjoissa Tutkimusongelmat ja tutkimuksen toteutus Opetuskokeilun tavoitteet Tutkimuksen tavoite Opetushypoteesi Tutkimusongelmat Tutkimuksen rakenne ja käytännön toteutus Otanta Empiirisen ymmärryksen mittari Opetuskokeilu Mapu -kurssien yleisiä piirteitä Opetuskokeilu Opetusidean taustaa Käytännön toteutus Lähtötasotesti Opetuskokeilun harjoitustehtävät Opetuskokeilussa käytetyt havaintomenetelmät Animaatiot Styrox-pallo-demonstraatio Java-simulaatiot Empiirisiä merkityksiä tukeva opetusjärjestys Empiirisen ymmärryksen mittaaminen koetehtävällä Koetehtävän analyysi Empiirisen ymmärryksen nelikenttä Nelikentän tarkastelua Koeanalyysin tulokset Haastattelututkimus Haastattelun suunnittelu Haastateltavien valinta Haastattelun kulku Haastattelujen analyysimenetelmä
7 SISÄLLYS vii 7.5 Koehenkilöiden suoritusten arviointi Ymmärryksen mittarit Opiskelijoiden ymmärryksen analyysi Haastatteluarvioinnin tulokset Luotettavuuden ja laadun arviointi Reliabiliteetti ja validiteetti Sisäinen validiteetti Ulkoinen validiteetti Reliabiliteetti Objektiivisuus Tutkimuksen tärkeys Johtopäätökset ja suositukset Johtopäätökset Opetushypoteesin toteutumisen arvio Opetuskokeilun positiiviset vaikutukset Opetuskokeilun kokemukset opettajan näkökulmasta Suositukset ja pohdintaa Lähteet 107 A Luentorungot 113 A.1 Mapu I -kurssin luentorunko B Opetuskokeilumateriaalit 115 B.1 Kuvaus opetuskokeilun oppitunneista B.2 Opetuskokeilun animaatioita B.3 Divergenssin fysikaalinen merkitys B.4 Roottorin fysikaalinen merkitys C Haastattelumateriaalit 125 C.1 Haastattelupyyntö C.2 Haastatteluohjeet C.3 Haastattelun käsikirjoitus C.4 Haastattelukysymyspapereita C.4.1 Koehenkilö 1 (KH 1) C.4.2 Koehenkilö 2 (KH 2) C.4.3 Koehenkilö 5 (KH 5)
8 viii SISÄLLYS D Mapu II -kurssin harjoitustehtäviä 137 D.1 Kotiharjoitus D.2 Kotiharjoitus D.3 Ex tempore -harjoitus D.4 Lisäharjoitus D.5 Harjoitus 7 (lähteisyyden ja pyörteisyyden käsite) E Koetehtävä ja mallivastaus 145 E.1 Koetehtävän pistematriisi
9 Kuvat 1.1 Derivoinnin ketjusäännön hammasratasanalogia Siipiratas pyörteisyysdetektorina Kaavio matematiikan oppimisen kolmesta maailmasta Kaavio tutkimuksen vaiheista Empiirisen ymmärryksen luokittelussa käytetyt tasot Empiiristen merkitysten kytkeytyminen matematiikan 3 maailman teoriaan Kaavio opetuskokeilun ajoittumisesta Mapu -kurssilla Kuvasarja animaatiosta, jolla havainnollistettiin vuota ja lähteisyyden mittaamista Kuvasarja, jolla havainnollistettiin Faradayn lakia Pyörteisyystestipallo Java-demonstraatio laminaarisesta virtauksesta Kaavio roottoriin liittyvien matemaattisten käsitteiden yhteyksistä Koetehtävän 4 pistejakauma Koetehtävän 4 b- ja c-kohtien vastausten välinen nelikenttä Haastattelun tominnallisen osan tutkimuslaitteisto Haastattelutehtävän toiminnallisen osan mittausvälineet Esimerkkikuva virtauksen tutkimisesta silkkipaperilla ja siipirattaalla Yleisluontoinen käsitekartta hiustenkuivaimen virtauskentän mallintamisesta Mallikäsitekartta hiustenkuivaimen virtauksen pyörteisyydeestä 78
10 x KUVAT 7.6 Yksityiskohtainen käsitekartta pyörteisyyden tutkimisesta siipirattaalla Käsitekartta osittaisderivaattojen määrittämisestä silkkipaperilla Koehenkilöiden empiirisen ymmärryksen luokittelu Empiiristen polkujen muodostuminen matematiikan käsitteiden välille B.1 Kuvasarja osittaisderivaatta-animaatiosta B.2 Kuvasarja gradienttianimaatiosta B.3 Animaatio 2. kl. osittaisderivaatoista (osa 1) B.4 Animaatio 2. kl. osittaisderivaatoista (osa 2) B.5 Animaatio 2d-pinnan arvioinnista Taylorin polynomeilla B.6 Kuvasarja sombreropinnan arvioimisesta Taylorin polynomeilla 121 B.7 Vektorikentän vuo tilavuusalkion läpi
11 Taulukot 3.1 Matematiikan oppimistasot APOS-teorian mukaan Matematiikan vastaustiedon SOLO-taksonomia Vektorianalyysin oppikirjakuvausten koodaus Vektorianalyysin opetus eri oppikirjoissa Matemaattisen ajattelun luokittelun YSOLO-taksonomia Mapu II -kurssin luentorunko Koehenkilöiden kurssisuoritusten pisteet Pyörteisyyden käsitteen empiirisen ymmärryksen luokittelu A.1 Mapu I -kurssin luentorunko B.1 Kuvaus Mapu II -kurssin vektorianalyysin luennoista E.1 Koetehtävän 4 pistematriisi E.1 Koetehtävän 4 pistematriisi (jatkuu)
12
13 Luku 1 Johdanto 1.1 Taustaa Matematiikka on fysiikan perustyökalu ja äidinkieli, jonka avulla lainalaisuudet ja mallit esitetään täsmällisen tarkasti. Suureiden välisiä kokeellisesti mitattuja riippuvuuksia kuvataan yhtälöillä ja niitä yhdistelemällä luodaan uusia malleja. Malleista voidaan taas johtaa tuloksia, jotka liittyvät yksittäiseen sovellustilanteeseen. Mallin pätevyyttä voidaan jälleen testata kokeellisesti. Tällaisessa uuden tiedon kehittelyssä ja menestyksellisessä soveltamisessa on ymmärrettävä käytettyjä matemaattisia käsitteitä pintaa syvemmältä ja etenkin niiden empiirisiä merkityksiä. Matematiikan opetuksen jatkuva haaste on uusien opetusmenetelmien kehittäminen ja niiden toimivuuden testaaminen. Vaikka Suomen peruskoulun matematiikan opetuksen tasoa on kehuttu OECD-maiden PISA-tutkimuksessa (Kupari et al., 2004), on alan opettajakunnan sisällä kuitenkin käyty kriittistä keskustelua siitä, mitä tutkimustulokset käytännössä tarkoittavat. Varsinkin korkea-asteen opettajat ovat havainneet, että opiskelijoiden perusmatematiikan taidoissa on sellaisia keskeisiä uuden asian oppimista haittaavia puutteita, jotka eivät PISA-tutkimuksessa ole tulleet näkyviin (Astala et al., 2005; Martio, 2005). Opetuksen tutkimus on Suomessa painottunut perusopetukseen. Koska korkeakouluissakin törmätään opetuksellisiin haasteisiin, on tarpeen saada tutkimustietoa myös korkeakouluopetuksen kehityksen tueksi. Yliopisto-opetuksen kehitystarpeesta onkin ollut viime vuosina yhä enemmän keskustelua (Borko et al., 1992). Matematiikan opetuksen tärkeyttä teollisuuden ja tutkimuksen kilpailukyvyn edistämisessä korostetaan myös Valtion Tiede- ja teknologianeuvoston raportissa (Valtion tiede- ja teknologianeuvosto, 2003).
14 2 LUKU 1. Johdanto 1.2 Matematiikan suhde empiriaan Tutkimusaihe kehittyi kirjoittajan omassa opetustyössään tekemien havaintojen pohjalta. Hän on työskennellyt vuodesta 2000 Helsingin yliopiston teoreettisen fysiikan kurssin Matemaattiset apuneuvot (lyhyesti Mapu) parissa ensin kaksi vuotta laskuharjoitusassistenttina, sitten kyselytuntien pitäjänä ja vuodesta 2004 lähtien kurssin luennoitsijana. Erityisesti hänen vuosina pitämänsä kyselytunnit tarjosivat aitiopaikan kuulla opiskelijoiden käsityksiä ja etenkin virhekäsityksiä kurssin aihepiiriin liittyen, sillä kyselytunneilla opiskelijoilla oli mahdollisuus esittää kysymyksiä epäselväksi jääneistä asioista. Yksi perimmäinen piirre kysymyksien taustalla tuntui olevan halu ymmärtää opetettujen matemaattisten käsitteiden yhteys todellisuuteen. Monet kysymykset esitettiin muodossa mitä se tarkoittaa käytännössä (Pasanen, 2003). Tämä sai huomaamaan, että opiskelijoilla on halu konkretisoida opetettuja matematiikan asioita ja tarve kiinnittää ne jotenkin havaittavaan maailmaan. Alun alkujaankin matematiikalla on varsin konkreettiset empiiriset juuret. Matematiikka on kehittynyt luonnon tutkimuksen pohjalta. Yksinkertaisimmallaan matematiikka on lukumäärän laskemista. Tuo kyky meillä ihmisillä näyttää olevan aivoihin jo valmiiksi rakennettuna, kuten vauvojen aivotutkimuksissa on selvinnyt (Wynn, 1992). Peruslaskennon lisäksi geometriset ongelmat ja ajanlaskun tarpeet ohjasivat matematiikan kehitystä muinaiskulttuureissa (Lehtinen, 2000; Teerikorpi ja Valtonen, 1990). Monet matematiikan historian merkkihenkilöt ovat tehneet tutkimusta myös muilla luonnontieteen aloilla. Matematiikkaa opetetaan kuitenkin kaikilla kouluasteilla erillisenä oppiaineena, jolloin yhteys matematiikan ja fysikaalisen luonnontutkimuksen välillä jää paikoin hämäräksi. Tästä syystä on kiinnostavaa tutkia, miten fysiikan laitoksella tapahtuvassa matematiikan opetuksessa voitaisiin paremmin tukea opiskelijoiden kykyä ymmärtää matematiikan empiirisiä merkityksiä etenkin vaikeana koetun usean muuttujan dierentiaalilaskennan tapauksessa. Myös Kaarle Kurki-Suonio korostaa kolmessa luennossaan (Kurki-Suonio, 2006) matematiikan käsitteiden empiiristä perustaa. Matematiikan voidaan nähdä syntyvän fysiikan kanssa rinta rinnan tarkasteltaessa luonnollisten lukujen käsitettä, joka perustuu fysikaalisen suureeseen lukumäärä ja yhteenlaskun empiiriseen lakiin. Matematiikka voidaan irrottaa omaksi rakenteelliseksi järjestelmäkseen, jossa oleellista ovat vain osasten keskinäiset suhteet. Matematiikan ja fysiikan kehityksessä on kuitenkin koko historian ajan ollut paljon keskinäisiä linkkejä, joista Kurki-Suonio käyttää nimitystä empirian portit. Fysiikka tarjoaa matematiikan käsitteille empiirisiä merkityksiä, joiden avul-
15 1.2. Matematiikan suhde empiriaan 3 la käsitteet voidaan kiinnittää. Kurki-Suonio esittää, että tie matemaattiseen käsitteeseen saattaa olla pitkä, jos sinne joudutaan kulkemaan koko matka matematiikan maailmassa. Sen sijaan empirian kautta käsitteeseen päästään ehkä helpommin. (Kurki-Suonio, 2006) Empirian etuihin matematiikan opetukselle on havahduttu muuallakin. Korkeakouluihin tarkoitetuissa uusissa matematiikan oppikirjoissa (esim. Stewart, 2003; Weir et al., 2008) matematiikan käsitteiden empiiriset merkitykset ovat voimakkaasti edustettuna. Etenkin kirjassa Weir et al. (2008) käytetään fysikaalisia esimerkkejä matematiikan käsitteiden ja relaatioiden jos ei aivan empiirisinä todistuksina niin vähintäänkin empiirisinä analogioina matemaattisen esityksen rinnalla. Yksi onnistunut analogia on derivoinnin ketjusäännön ja hammasratasmallin välinen analogia, jonka kirjoittaja itsekin mainitusta kirjasta riippumattomasti on kehittänyt havainnollistamaan luento-opetustaan (ks. kuva 1.1). Tämän tutkimuksen tavoitteet on koettu tärkeiksi muuallakin. Esimerkiksi Oregon State Universityn fysiikan ja matematiikan laitosten välinen Bridging the Vector Calculus Gap -projekti rakentaa siltaa perinteisen matemaatikoiden opettaman vektorianalyysin ja fyysikoiden käyttämän matematiikan välille (Dray ja Manogue, 1999, 2002). Kuva 1.1: Matemaattiset apuneuvot -kurssilla näytetty kuva derivoinnin ketjusäännön analogiasta mekaanisen hammasratasmallin kanssa (Pasanen, 2006).
16 4 LUKU 1. Johdanto 1.3 Tavoitteiden asettelu Isaac Newtonin ja Gottfried Wilhelm Leibnizin ja 1700-lukujen vaihteessa kehittämä dierentiaali- ja integraalilaskenta on keskeisin fysiikassa tarvittava matematiikan osa-alue. Se pohjautuu derivaatan ja dierentiaalin käsitteisiin. Lukio-opetuksen kehittämiseksi tehdyt tutkimukset ovat osoittaneet, että derivaattaan liittyvien käsitteiden oppimistuloksia voidaan tehostaa representaatioilla (Hähkiöniemi, 2006) eli käsittelemällä derivaattaa objektina, johon liittyy tiettyjä konkreettisesti havaittavia piirteitä, kuten funktion kuvaajan jyrkkyys. Tutkimusten mukaan myös visualisointi ja muu konkretisointi auttavat useita opiskelijoita, joten näitä oppimista tukevia menetelmiä on pyritty lisäämään lukio-opetuksessa (Hähkiöniemi, 2006). Pidemmälle menevän fysiikan opiskelun tarpeisiin on derivaatan käsitettä laajennettava useamman riippumattoman muuttujan tapaukseen ja vektoriarvoisiin funktioihin. Näiden laajennettujen käsitteiden opetukseen soveltuvia opetusmenetelmiä ei ole kuitenkaan kehitetty tutkimuslähtöisesti, vaikka uudistusprosessi on oppikirjoissa ollutkin havaittavissa. Tässä lisensiaatintutkimuksessa käsitellään Helsingin yliopiston fysiikan laitoksella tehtyä tutkimustyötä, jossa pyrittiin kehittämään ja testaamaan uusia runsaisiin visualisointeihin ja konkreettisiin havaintoesimerkkeihin perustuvia opetusmenetelmiä usean muuttujan dierentiaalilaskennan opettamisessa. Näiden opetusmenetelmien todellista toimivuutta ei ole ennen kartoitettu tieteellisesti. Tutkimuksen oheistuotteena on syntynyt uudenlaista opetusmateriaalia, joka pohjautuu aiemmissa tutkimuksissa tehdyille havainnoille opiskelijoiden käsitteenmuodostusprosessin toiminnasta. Materiaali koostuu erityisistä kurssia varten kehitetyistä opetusvälineistä kuten pyörteisyystestipallo, tietokoneanimaatiot ja visualisoinnit. 1.4 Tutkimuksen toteutuksesta Tutkimustyön toiminnallinen osuus ajoittui syksyn 2007 yliopistokursseihin Matemaattiset apuneuvot I ja II (lyhyesti Mapu I ja II). Mapu I -kurssin alussa tehty lähtötasotesti antoi yleiskäsityksen juuri opintonsa aloittaneiden 130 opiskelijan matemaattisfysikaalisen ymmärryksen tasosta. Tutkimuksen kannalta olennaisin uusien opetusideoiden testausvaihe alkoi Mapu I -kurssin loppupuoliskolla. Varsinainen opetuskokeilu pidettiin Mapu II -kurssin keskivaiheilla. Kurssin lopussa joulukuussa opiskelijoille annettiin tehtävämoniste, jonka avulla opiskelijat pääsivät omakohtaisesti pohtimaan käsitteiden merki-
17 1.4. Tutkimuksen toteutuksesta 5 tyksiä. Opetettujen asioiden lopputestinä toimi yksi aihepiirin ymmärtämistä syväluotaava koetehtävä. Keväällä 2008 viidelle opiskelijalle tehtiin tarkempi empiiristä toimintaa sisältävä haastattelututkimus, jolla kartoitettiin opiskelijoiden kognitiivisen kehityksen tasoa usean muuttujan dierentiaalilaskennan käsitteiden ymmärtämisessä sekä formaalin matematiikan että empiiristen merkitysten näkökulmista. Tutkimus kytkeytyy läheisesti aiempiin lukiotasolle keskittyneisiin tutkimuksiin (erityisesti Hähkiöniemi, 2006), joiden tuloksia pyritään hyödyntämään ja kehittämään pidemmälle menevään dierentiaalilaskennan opetukseen soveltuvaksi. Tarkoitus on myös kartoittaa mihin dierentiaalilaskennan ymmärtämisen keskeiset puutteet liittyvät ja miten käsitteiden ymmärtämistä voidaan vahvistaa siten, että opiskelijoilla on kurssin jälkeen selkeä kuva työkalujen käyttökohteista opinnoissaan ja tulevaisuudessa fyysikon työssään. Perustyökalujen parempi ymmärtäminen lisää myös myöhempien opintojen mielekkyyttä ja vaikuttaa näin ehkäisevästi opintojen keskeytyshaluihin.
18
19 Luku 2 Käsitteiden määrittely Tämän tutkielman pääteema on erilaisten derivaatan käsitteiden ymmärtäminen fysikaalisesta näkökulmasta ja näiden käsitteiden opettaminen fysiikan opiskelijoille. Tässä luvussa käydään läpi tärkeimmät tutkielmassa käsiteltävät matemaattiset käsitteet ja tarkastellaan erityisesti niiden tulkintoja ja merkitystä fysiikan kannalta. Esitys edustaa kirjoittajan opetuskokeilun aikaista näkemystä tutkittavista käsitteistä ja niiden empiirisistä merkityksistä. Tutkimuksen tuloksena jäsentyi uusi näkemys aihepiirin käsitehierarkiasta erityisesti empiiristen merkitysten näkökulmasta. Tätä esitellään myöhemmin kappaleessa Usean muuttujan funktiot Tutkielman aihepiiri on vektorianalyysi, joka käsittelee usean muuttujan funktioiden dierentiaali ja integraalilaskentaa. Tarvittavat funktiotyypit ovat: Usean muuttujan reaalifunktiot y = f(x 1, x 2,..., x n ) = f(x), missä määrittelyjoukkona ovat järjestetyt lukujonot eli vektorit 1 x = (x 1, x 2,..., x n ), x i R ja arvojoukkona reaalilukujen joukko y A f = R. Vektorifunktiot y = F(x), missä määrittelyjoukko on n-ulotteinen reaalinen vektoriavaruus ja arvojoukko m-ulotteinen vektoriavaruus. Vektorifunktio F on funktiokokoelma, joka sisältää m kappaletta usean muuttujan funktioita F i (x) eli vektorin komponentteja. Funktio voidaan kirjoittaa vektorimuodossa F = (F 1 (x), F 2 (x),..., F m (x)). Tässä tutkimuksessa tärkeimpiä näistä ovat vektorifunktiot 3-ulotteisessa karteesisessa 1 Vektorisuureet kirjoitetaan tässä tutkielmassa lihavoitua fonttia käyttäen. Esimerkiksi 3-ulotteisen karteesisen koordinaatiston paikkavektori on r = xi + yj + zk.
20 8 LUKU 2. Käsitteiden määrittely koordinaatistossa, jossa M f = A f = R 3. Fysiikassa funktioilla kuvataan skalaari- tai vektorisuureiden riippuvuutta toisista skalaari- ja vektorisuureesta. Esimerkiksi sähködynamiikassa vektorisuure magneettivuon tiheys B riippuu paikasta ja ajasta B(r, t). Nestevirtauksia mallinnettaessa tarvitaan funktiota v(r, t), joka esittää avaruuden pisteessä r olevan nestealkion virtausnopeutta hetkellä t. 2.2 Funktion raja-arvo Matemaattinen käsite Funktion raja-arvo on peruskäsite, johon dierentiaalilaskenta perustuu. Epäformaalisti raja-arvo voidaan määritellä seuraavasti (Adams, 2003). Määritelmä (epäformaali) Olkoon funktio f(x) määritelty pisteen x = x 0 ympäristössä. Jos funktion arvo f(x) lähestyy mielivaltaisen lähelle lukua L, kunhan x valitaan riittävän läheltä pistettä x 0, on funktion raja-arvo pisteessä x = x 0 yhtä kuin L. Merkitään: lim x x 0 f(x) = L. Usein tämä epäformaali määritelmä on matematiikan soveltajalle täysin riittävä, sillä raja-arvo on pohjakäsite, johon seuraavan tason käsitteet perustuvat, mutta raja-arvoa ei sellaisenaan juuri tarvita sovelluksissa. Määritelmässä esiintyy kuitenkin kaksi epämääräistä ilmaisua: lähestyy mielivaltaisen lähelle ja valitaan riittävän läheltä, joiden matemaattinen merkitys on tarpeen täsmentää. Formaalisti raja-arvo määritellään seuraavasti (Adams, 2003; Lahtinen ja Pehkonen, 1992). Määritelmä (formaali) Funktion f(x) raja-arvo pisteessä x 0 on L, merkitään lim x x0 f(x) = L, jos kaikille luvuille ɛ > 0 on olemassa jokin sellainen luku δ ɛ > 0 siten, että ehdon 0 < x x 0 < δ ɛ toteuttavilla x:n arvoilla pätee f(x) L < ɛ. Mielivaltaisen lähellä ja riittävän lähellä tarkoittavat näitä kahta lukua ɛ ja δ ɛ. Koska reaaliluvut täyttävät lukusuoran aukottomasti (Adams, 2003), on matemaattisesta näkökulmasta täysin mielekästä valita luku avoimelta väliltä ]0, [ vaikka miten läheltä nollaa. Tarkastellaan määritelmää seuraavaksi fysikaalisesta näkökulmasta.
21 2.3. Osittaisderivaatta Fysikaalinen näkökulma Olkoon tarkasteltavana kahden fysikaalisen suureen x ja y välistä riippuvuutta kuvaava funktio f eli y = f(x). Tällöin funktion f raja-arvolla pisteessä x 0 tarkoitetaan sitä suureen y arvoa, jota f(x) lähestyy mielivaltaisen lähelle, kun suureen x arvo valitaan riittävän läheltä arvoa x 0, kuitenkin niin, että erotus x x 0 on dimensiollisten lukuarvojen 0 ja δ ɛ välissä, 0 < x x 0 < δ ɛ. Määritelmä siis olettaa, että kahden mittauksen välinen erotus voisi olla miten pieni tahansa olematta kuitenkaan nolla. Tämä on fysikaalisesti mieletön ajatus. Yhtäältä absoluuttisen tarkat mittaukset ovat fysikaalisesti mahdottomia mittaustarkkuus on aina jotain minimirajaa δ min karkeampi. Toisaalta tutkimus on paljastanut, että pienessä mittakaavassa luonto näyttäytyy mittauksissa epäjatkuvana eli suureiden arvot ovat kvantittuneet. Mitattavissa olevat suureiden arvot eivät siis täytä lukusuoraa samalla tavalla aukottomasti kuin reaaliluvut. (Kurki-Suonio ja Kurki-Suonio, 1998) Fysikaalisten ilmiöiden mallintamiseen käytetyt matemaattiset mallit sisältävät siten jatkuvuuden idealisaation, jolle ei ole fysikaalista vastinetta. Mallin hyvyys riippuukin siitä, voidaanko empiirisesti rajallisen kokoiset erotukset ɛ ja δ ɛ valita tarkasteltavassa systeemissä niin pieniksi, että tulos on mittaustarkkuuden rajoissa sama kuin matemaattista määritelmää käytettäessä (Kurki- Suonio ja Kurki-Suonio, 1998). 2.3 Osittaisderivaatta Usean muuttujan funktion arvo voi muuttua minkä tahansa muuttujan muuttuessa. Tällaisen funktion riippuvuutta yksittäisestä muuttujasta kuvataan osittaisderivaatoilla kyseisen muuttujan suhteen kaikkien muiden muuttujien pysyessä muuttumattomina. Kyseessä on yhden muuttujan funktion derivaatan käsitteen laajennus. Määritelmä Usean muuttujan funktion g(x 1, x 2,..., x n ) osittaisderivaatta muuttujan x i suhteen pisteessä (x 1, x 2,..., x n ) on g x i = lim (x1,x 2,...,x n) x 0 g(x 1, x 2,..., x i + x,..., x n ) g(x 1, x 2,..., x n ). x (2.1) Osittaisderivaatan käsitteessä on siis mukana sama raja-arvon avulla määritelty rajankäyntiprosessi kuin tavallisessa yhden muuttujan derivaatassakin.
22 10 LUKU 2. Käsitteiden määrittely Pidetään vain huolta siitä, että useista muuttujista tutkitaan aina yhden muuttujan muutosta kerrallaan. Funktion g osittaisderivaattaa muuttujan x i suhteen merkitään usein lyhyesti i g Fysikaalinen merkitys Monissa fysikaalisissa ilmiöissä tutkittava suure riippuu useamman kuin yhden suureen arvosta. Sopivasti suunnitellussa koetilanteessa saattaa kuitenkin olla mahdollista rajoittaa tutkittavaa ilmiötä siten, että riippuvuutta määritettäessä muutellaan vain yhtä suuretta kerrallaan. Tällöin tilanne vastaa käytännössä yhdestä muuttujasta riippuvaa tapausta ja derivaatta g x voidaan tulkita kahden toisistaan riippuvan suureen absoluuttista muutosta kuvaavien dierentiaalien osamääränä. Kahden muuttujan funktio h(x, y) voidaan esittää pintana kaksiulotteisessa koordinaatistossa. Osittaisderivaatan h(x,y) geometrinen merkitys on pinnan x jyrkkyys liikuttaessa x-akselin suunnassa eli pinnalle piirretyn x-akselin suuntaisen tangenttisuoran kulmakerroin. Osittaisderivaatta y-akselin suhteen on vastaava jyrkkyys y-akselin suuntaisessa siirtymässä. 2.4 Nablaoperaattori Usean muuttujan dierentiaalilaskennassa usein vastaantulevat derivaatat voidaan kirjoittaa yksinkertaisessa helposti käsiteltävässä symbolisessa muodossa ns. nablaoperaattorin (symboli ) avulla. Operaattori on vektorimuotoinen kokoelma edellä määritellyistä osittaisderivaattaoperaattoreista x i, missä indeksi i viittaa koordinaattiakselin järjestysnumeroon avaruudessa, jonka kanta on {ê 1, ê 2,..., ê n }. Nablaoperaattorin määritelmä on ( = ê 1 ) + ê ê n, (2.2) x 1 x 2 x n missä ê i tarkoittaa koordinaattiakselin x i suuntaista yksikkövektoria. Kolmiulotteisessa karteesisessa koordinaatistossa nabla on ( = i x + j y + k ) z (2.3) standardikantavektoreiden {i, j, k} avulla lausuttuna. Koska nabla on muodoltaan vektori, voidaan sillä operoida sekä skalaari- että vektorifunktioihin muodollisesti eri kertolaskutoimitusten avulla. 3-ulotteisessa avaruudessa nablan
23 2.4. Nablaoperaattori 11 avulla määriteltävät peruslaskutoimitukset ovat (Lahtinen ja Pehkonen, 1994) gradientti h, (2.4) divergenssi F, (2.5) roottori F, (2.6) missä h on skalaarifunktio ja F vektorifunktio kolmiulotteisessa avaruudessa. Tässä tutkielmassa keskitymme vain divergenssiin ja roottoriin 2- tai 3- ulotteisessa avaruudessa. Koska kyse on vektorimuotoisten funktioiden dierentiaalilaskennasta eli analyysistä, käytetään tästä aihepiiristä myös lyhyttä nimitystä vektorianalyysi Divergenssin fysikaalinen tulkinta Vektorifunktion F(x, y, z) divergenssi eli lähteisyys F = F x x + F y y + F z z (2.7) on muodoltaan skalaarisuure. Kyseessä on muodollisesti kahden vektorin pistetulo. Tässä divergenssin lauseke on esitetty karteesisessa standardikannassa. Se on kuitenkin suureena koordinaatistovalinnasta riippumaton. Sovelluksissa tarvitaan myös divergenssin esitystä sylinteri- ja pallokoordinaatistomuodossa. Divergenssillä on sama tulkinta sekä kahdessa että kolmessa ulottuvuudessa. Olkoon v(x, y, z) nesteen virtausnopeus. Tällöin divergenssin v arvo pisteessä (x, y, z) tarkoittaa nettovuota tilavuusyksikköä kohti eli vuon tiheyttä tarkasteltavassa pisteessä (ks. liitte B.3 ja lähde Weir et al. (2008)). Jos divergenssi on positiivinen, on tarkastelupisteessä lähde ja virtaus ulos on suurempi kuin sisään eli pisteestä pulppuaa nestettä ulos tai neste laajenee tarkastelupisteessä. Jos taas vuo on negatiivinen, on kyseessä nielu ja piste imee nestettä sisäänsä tai neste puristuu kokoon. Kun divergenssi on nolla, on kenttä tarkastelupisteessä lähteetön. Piste tulee tässä ymmärtää fysikaalisessa mielessä dierentiaalisena tilavuusalkiona. Toinen fysikaalinen esimerkki lähteisyydestä on Maxwellin I laki, joka voidaan esittää muodossa D(r) = ρ(r). (2.8) Laki kertoo varaustiheyden toimivan sähkövuon tiheyden lähteisyytenä (Kurki- Suonio ja Kurki-Suonio, 1999).
24 12 LUKU 2. Käsitteiden määrittely Roottorin fysikaalinen tulkinta Vektorifunktion F(x, y, z) roottori eli pyörteisyys i j k F = x y z = i( y F z z F y ) j( x F z z F x )+k( x F y y F x ). (2.9) F x F y F z on muodoltaan vektorisuure. Lauseke on muodollisesti kahden vektorin vektoritulo. Tämäkin suure voidaan lausua sylinteri- tai pallokoordinaatistossa sovellustilanteen tarpeiden mukaan. Roottoria voidaan käsitellä myös kaksiulotteisena versiona rajoittamalla tarkasteltava vektorikenttä tasoon. Esimerkiksi xy-tasossa roottori on muotoa F = k ( x F y y F x ). (2.10) Divergenssin tapaan myös roottorin fysikaalinen tulkinta voidaan esittää nestevirtauksen avulla. Jos pyörteiseen nestevirtaukseen asetetaan pieni testipallo, se lähtee pyörimään (ks. tarkemmin liite B.4). Pyörteisyysvektorin suunta määräytyy ns. oikean käden säännöllä 2 pallon pyörimisakselista ja kiertosuunnasta. Pyörteisyysvektorin pituus kuvaa pyörteisyyden voimakkuutta ja se on verrannollinen testipallon pyörimisnopeuteen. Pyörteisyysvektori vastaa siten fysikaalisesti kerrointa vaille testipallon kulmanopeusvektoria. Jos testipallo pyörii, esiintyy kyseisessä mittauspisteessä pyörteisyyttä ja pyörteisyysvektorin pituus on suurempi kuin nolla. Rajatapauksessa, jossa testipallo pysyy paikallaan eli F = 0, sanotaan kenttää pyörteettömäksi. Koska pyörteisyys on vektorisuure, ei sen sijaan ole oikein puhua positiivisesta tai negatiivisesta pyörteisyydestä muutoin kuin 2-ulotteisen tarkastelun tapauksessa. Kaksiulotteisessa tilanteessa on vain kaksi mahdollista pyörimissuuntaa. Testipallo voidaan tässä tilanteessa korvata siipirattaalla (Weir et al., 2008), jonka akseli on kohtisuorassa tarkastelutasoa vastaan. Kun tehdään valinta positiivisesta kiertosuunnasta tasossa, voidaan pyörrettä kuvata pelkällä reaaliluvulla, jonka etumerkki ilmaisee pyörteen suunnan. Tieto pyörteisyyden vektorialkuperästä on kätketty positiivisen kiertosuunnan valintaan ja oikean käden sääntöön. Kuvassa 2.1 on esitetty siipirattaan pyörimissuunnan ja pyörteisyysvektorin välinen yhteys oikean käden säännön mukaisesti. 2 Kun oikean käden sormet etusormesta pikkurilliin asetetaan kaarelle osoittamaan pallon kiertosuuntaa, niin pyörimisakselin suuntaisesti pystyyn nostettu peukalo määrää pyörteisyysvektorin suunnan.
25 2.5. Gaussin ja Stokesin lause 13 Kuva 2.1: Tasoon rajoittuneessa kaksiulotteisessa virtauskentässä pyörteisyyden detektorina voidaan käyttää siipiratasta. Pyörteisyysvektorin suunta määräytyy rattaan kiertosuunnasta oikean käden säännön mukaisesti. Hyviä fysikaalisia esimerkkejä pyörteisyydestä ovat myös sähködynamiikkaan kuuluvat Maxwellin III ja IV laki, jotka voidaan esittää muodossa (Kurki- Suonio ja Kurki-Suonio, 1999) B(r, t) E(r, t) =, t (Maxwellin III laki) (2.11) D(r, t) H(r, t) = J(r, t) +, t (Maxwellin IV laki), (2.12) missä E on sähkökentän voimakkuus, B magneettivuon tiheys, H magneettikentän voimakkuus, D sähkövuon tiheys ja J virrantiheys tarkastelupisteessä. Esimerkiksi Maxwellin IV lain staattinen osa (ilman viimeistä termiä), että stationaarinen virtajakauma synnyttää ympärilleen pyörteisen magneettikentän. Magneettikentän pyörteisyys tarkastelupisteessä on yhtä suuri kuin virrantiheys, joten virrantiheysvektori määrää pyörteisyysakselin suunnan. 2.5 Gaussin ja Stokesin lause Tutkimuksen aihepiiriin liittyvät myös viiva-, pinta- ja tilavuusintegraalit sekä Gaussin ja Stokesin lause. Niiden perinpohjaiseen esittelyyn ei tämän tutkielman puitteissa kuitenkaan ryhdytä. Moderni esittely näistä on esimeriksi
26 14 LUKU 2. Käsitteiden määrittely kirjassa Weir et al. (2008) ja klassinen suomenkielinen fysikaalista merkitystä korostava esitys kirjassa Väisälä (1961). Tässä todetaan lyhyesti, että Gaussin lause (käytetään myös nimeä divergenssiteoreema) kytkee yhteen suljetun pinnan S läpi lasketun vektorikentän F vuon F da ja pinnan S rajaaman S tilavuuden V yli lasketun vektorikentän lähteisyyden (Weir et al., 2008) S F da = V ( F) dv, (2.13) missä esiintyy vektoriaalinen pinta-ala-alkio da = n da (n on pinnan normaali tarkastelupisteessä). Kun tarkasteltavaa tilavuutta pienennetään, voidaan lähteisyys kyseisessä kentän pisteessä lausua raja-arvona (Adams, 2003) 1 F = lim V 0 V S F da. (2.14) Tämä antaa lähteisyydelle suoran tulkinnan vektorikentän vuon keskitiheytenä suljetun tilavuutta V ympäröivän pinnan S läpi (Adams, 2003; Väisälä, 1961). Stokesin lause yhdistää vektorikentän reittiä C pitkin lasketun kiertämäintegraalin F dr ja vektorikentän pyörteisyyden pintaintegraalin yli käyrän C C rajaaman pinnan S: C F dr = ( F) n ds. (2.15) S Vastaavasti kutistamalla aluetta S, saadaan pyörteisyyden vektorin n suuntaiselle komponentille raja-arvomuoto (Adams, 2003) 1 ( F) n = lim F dr, (2.16) A 0 A C missä A on alueen S pinta-ala. Tästä paljastuu puolestaan pyörteisyyden n- komponentin yhteys keskimääräiseen kiertämätiheyteen vektorin n suunnassa (Adams, 2003; Väisälä, 1961; Weir et al., 2008).
27 Luku 3 Teoreettinen viitekehys 3.1 Matemaattisen kehityksen kognitiivisia teorioita Vuonna 1965 Piaget oli yksi ensimmäisiä lasten matemaattisen ajattelun kehitystä tutkineita teoreetikoita. Piaget'n mukaan matemaattisen ajattelun kehitys on kolmitasoinen (Tall, 2004): empiirisen abstraktion tasolla lapsi konstruoi objektien ominaisuuksille merkityksiä pseudo-empiirisen abstraktion tasolla lapsi konstruoi merkityksiä niille ominaisuuksille, joita erilaiset toimenpiteet aiheuttavat tarkasteltaville objekteille reektiivisen abstraktion tasolla toimenpiteistä ja operaatioista tulee itsenäisiä ajattelun välineitä. Piaget'n ajatuksia on sittemmin laajennettu ja kehitetty kuvaamaan muidenkin kuin lasten matematiikan opiskelulle ominaisia kognitiivisia rakenteita. Varsinkin Yhdysvalloissa matematiikan korkeakouluopetuksen kehityksen ja arvioinnin yhtenä välineenä käytetään ns. APOS-teoriaa (Dubinsky ja McDonald, 2001), jossa ajattelun kehittymistä kuvataan neliportaisena tienä toimenpiteiden ja prosessien kautta mieleen rakentuviksi objekteiksi ja vähitellen näiden ympärille rakentuvaksi kartaksi. APOS-teoriaan liittyvistä tutkimuksesta riippumatta Sfard (1991) kehitti samankaltaisen operationaalis-rakenteellisen kognitiivisen teorian, joka korostaa matematiikan operationaalisen ja rakenteellisen puolen dualistisuutta. Gray ja Tall (1994) katsovat asiaa symbolien
28 16 LUKU 3. Teoreettinen viitekehys näkökulmasta ja korostavat symbolien merkitystä linkkinä prosessin ja ajateltavan käsitteen välillä. He käyttävät tästä linkistä nimitystä prosepti (eng. procept). Myöhemmin Tall (2004) päätyi aiempien tutkimustensa perusteella uuteen kolmihaaraisen matematiikan oppimista kuvaavan teorian, jota hän kutsuu nimellä matematiikan kolme maailmaa. Seuraavassa tarkastellaan yksityiskohtaisemmin näiden teorioiden piirteitä Operationaalis-rakenteellinen teoria Sfard (1991) esittää, että on olemassa kahdenlaisia matemaattisia käsitteitä. Objektin tyyppiset käsitteet ovat olemassa käsitteinä vain omassa matematiikan maailmassaan. Niitä voidaan esittää paperilla symboleina, mutta matematiikan kannalta objektien konkreettinen olemassaolo ei ole kiinnostavaa. Kiinnostavaa on ainoastaan se, millaisia näitä objekteja koskevat säännöt ja lait ovat. Matematiikan opiskelijan täytyy kehittää kyky nähdä ja kuvitella nämä näkymättömät matemaattiset objektit. Tästä Sfard käyttää nimitystä matematiikan strukturaalinen eli rakenteellinen puoli. Toisenlainen tapa ajatella matemaattisia käsitteitä ovat prosesseina määriteltävät käsitteet. Esimerkiksi luonnolliset luvut voidaan määritellä lukumäärän laskemisen prosessin avulla. Tämä kuvastaa matematiikan operationaalista puolta. Rakenteellinen puoli on staattinen ja ajaton, operationaalinen puoli on dynaaminen tapahtumaketju. Sfard (1991) väittää, että rakenteellinen ja operationaalinen matematiikan näkemys ovat toisilleen komplementaarisia eli kaikki matemaattiset käsitteet voidaan ajatella joko operationaalisina tai rakenteellisina käsitteinä. Rakenteellinen puoli on hänen mielestään abstraktimpi ja vaikeampi hahmottaa kuin operationaalinen. Sfardin artikkelissa on esimerkkejä, miten sama matemaattinen käsite voidaan määritellä näillä kahdella eri tavalla. Esimerkiksi funktio on rakenteellisena käsitteenä joukko järjestettyjä pareja. Operationaaliselta kannalta funktio on laskennallinen prosessi tai sääntö, jolla päästään yhdestä systeemistä toiseen systeemiin. Vastaavasti edellä mainitut luonnolliset luvut voidaan operationaalisen lukumäärän laskemisen sijasta määritellä myös rakenteellisena joukko-opillisena käsitteenä (Sfard, 1991). Strukturaaliset ja operationaaliset käsitteet näkyvät myös siinä, miten ihmiset käsittelevät niitä mielessään (Sfard, 1991). Toisinaan matemaattisia käsitteitä havainnollistetaan mielikuvina toisinaan niistä käytetään mielessä verbaalista kuvausta. Mielikuvat liittyvät strukturaaliseen ja verbaaliset kuvaukset operationaaliseen käsitteeseen. Visualisaatio tekee abstrakteista käsitteistä helpommin tartuttavia ja niistä tulee melkein materiaalisia olioita. Visuaa-
29 3.1. Matemaattisen kehityksen kognitiivisia teorioita 17 linen informaatio on välitöntä, jolloin mielikuvan ominaisuudet ovat välittömästi saatavilla. Verbaaliseen käsitteeseen pääsee käsiksi vasta purkamalla sen tapahtumaketjuna auki mielessä (Sfard, 1991). Oleellinen ero näiden kahden näkökulman välillä on (Sfard, 1991) mukaan niiden erilainen kognitiivinen taso. Hän argumentoi, että rakenteelliset käsitteet ovat abstraktimman tason käsitteitä kuin operationaaliset käsitteet ja käsitteenmuodostuksessa operationaalinen käsite edeltää yleensä rakenteellista käsitettä. Rakenteelliset käsitteet ovat teorian mukaan operationaalisten prosessien tuotoksia. Sfard (1991) perustelee esimerkein, että näin tapahtuu sekä yksilön käsitteen muodostuksessa, että matematiikan kehityksessä yleisemminkin. 1 Tärkeät matemaattiset edistysaskeleet ovat tapahtuneet Sfardin mukaan vasta siinä vaiheessa, kun operationaalinen käsite on pystytty ilmaisemaan rakenteellisessa asussa. Esimerkiksi alunperin prosessina määriteltyjen funktioiden esittäminen rakenteellisena objektina mahdollisti uudenlaiset operaatiot funktioilla ja johti funktionaaleihin ja funktionaalianalyysiin. Sfardin teoria esittää opetukseen selkeän ohjenuoran: operationaaliset käsitteet ennen rakenteellisia käsitteitä (Sfard, 1991). Sfardin mallia soveltaen esimerkiksi pyörteisyys voidaan ymmärtää ensin prosessina, jossa virtauskenttään laitettu testikappale lähtee pyörimään. Pyörimisen prosessi toimii pyörteisyyden operationaalisena mallina. Rakenteellisena mallina pyörteisyyden ominaisuuksiin voidaan kiinnittää abstrakti objekti, vektori, jonka suunta kertoo pyörteisyysakselin ja pituus pyörteisyyden voimakkuuden tarkastelupisteessä. Sfardin teorian mukaan käsitteiden oppiminen tapahtuu kolmessa vaiheessa (Hähkiöniemi, 2006; Sfard, 1991): Ensimmäisellä tasolla opiskelija sisäistää (interiorize) prosessin, joka suoritetaan jo olemassa olevalle objektille. Opiskelija tulee taitavaksi prosessin suorittamisessa ja voi ajatella prosessia suorittamatta sitä. Toisessa vaiheessa pitkät toimintojonot tiivistetään (condense) helpommin hallittavaksi kokonaisuudeksi. Pystytään ajattelemaan prosessia kokonaisuutena tarvitsematta ajatella yksityiskohtia. Kolmannella tasolla matemaattinen hahmo esineellistetään (reify). Tämä tarkoittaa, että käsite ymmärretään objektina, joka on irrotettu siitä 1 Sfard (1991) huomauttaa, että tämä teoria ei välttämättä päde geometriassa, jossa rakenteelliset käsitteet voi olla helpompi hahmottaa kuin proseduraaliset käsitteet. Geometrian opiskelun erilaisesta käsitteenmuodostuksesta kirjoittaa myös Tall (2004).
30 18 LUKU 3. Teoreettinen viitekehys prosessista, joka sen tuotti. Objekti saa itsenäisen merkityksen olemalla tietyn kategorian jäsen eikä viittausta alkuperäisen prosessiin tarvita. Tähän uuteen objektiin voidaan nyt kohdistaa erilaisia prosesseja ja sykli alkaa alusta. Sfard on sitä mieltä, että käsitteiden oppiminen ei aina noudata tätä kehitystä. Voi käydä niin, että opiskelija luo käsitteen ikään kuin tyhjästä alkaen manipuloida käsitettä tiettyjen sääntöjen mukaan aivan kuin se olisi objekti. Tuolla objektilla ei kuitenkaan ole minkäänlaista kiinnitystä operationaaliseen rakenteeseen. Matemaattisen käsitteen representaatio on rakentunut itsenäisenä ilman minkäänlaista tarkoitusta. Tästä oppimisen esteenä olevasta käsitetyypistä Sfard käyttää nimitystä pseudo-rakenteellinen (pseudo-structural tai quasi-structural) käsite (Sfard, 1991). Hähkiöniemi (2006) soveltaa tätä derivaatan oppimiseen ja toteaa, että derivaatta saatetaan helposti oppia pseudorakenteellisena objektina pelkkiä derivointisääntöjä opettelemalla ilman mitään merkitystä. Tätä tukevia havaintoja oli Berryn ja Newmanin tutkimuksessa (Berry ja Nyman, 2003). Saman pseudo-rakenteellisen oppimisen ongelman voi nähdä esiintyvän myös usean muuttujan dierentiaalilaskennassa. Esimerkiksi divergenssin ja roottorin voi oppia pelkkänä symbolisena operaationa vailla minkäänlaista yhteyttä niiden perustana oleviin osittaisderivaattoihin kuuluvaan rajankäyntiprosessiin. Tätä käsitteiden pseudo-oppimista voidaan verrata fysiikan oppimista häiritsevään kaavatautiin, jossa fysiikkaa opetetaan ja opiskellaan kaavojen kokoelmana vailla kiinnitystä empiiriseen todellisuuteen (Kurki-Suonio ja Kurki-Suonio, 1998) APOS-teoria matematiikan oppimisesta APOS-teoria on Piaget'n reektoivan abstraktion teorian sovellus korkeamman tason matematiikan käsitteiden oppimisen mallintamiseksi (Dubinsky ja McDonald, 2001). Sen mukaan matemaattisen käsitteenmuodostuksen alussa opiskelija tekee konemaisesti vaadittuja toimenpiteitä aiemmin konstruoiduille mielikuvarakennelmille tai fyysisille objekteille. Tämä on toimenpiteiden (Action) taso. Vähitellen opiskelija kykenee irrottamaan toimenpiteet kohteestaan ja muodostaa niistä ajatusmallin, jota kutsutaan prosessiksi (Process). Prosessi sisältää ajatuksen toimenpiteiden rakenteesta, muttei ole enää sidottu kohteeseen. Seuraavalla tasolla prosessit ruumiillistuvat objekteiksi (Object), joita voidaan käsitellä kokonaisina yksikköinä. Eri objekteilla nähdään ominaisuuksia,
31 3.1. Matemaattisen kehityksen kognitiivisia teorioita 19 Taulukko 3.1: APOS-teorian mukainen käsitys matematiikan oppimisen eri kehitystasoista Hähkiöniemi (2006) ja Dubinsky ja McDonald (2001) mukaan esitettynä. Action, toimenpidetaso Process, prosessitaso Object, objektitaso Schema, toimintamallitaso Opiskelija oppii yksinkertaisia perustoimintoja, joita voidaan tehdä mentaaliselle tai fyysiselle objektille. Toimenpiteitä tehdään konemaisesti annettuja ohjeita seuraten. Toimenpiteillä on selkeä kohde ja niillä on lopputulos. Toimenpidettä toistettaessa opiskelija alkaa hallita sitä tietoisesti ja muodostaa siitä prosessimallin. Prosessin vaiheita osataan kuvailla sitä toteuttamatta. Prosessi voidaan irrottaa esimerkkitilanteista eikä kohdetta enää tarvita. Prosessi aletaan nähdä kokonaisena objektina, jolle voidaan tehdä muunnoksia. Objekteja voidaan ryhmitellä niiden ominaisuuksien perusteella. Toimintamalli on kokoelma toisiinsa liittyviä toimenpiteitä, prosesseja ja objekteja. Ne muodostavat viitekehyksen, jota käytetään ratkottaessa tietyn aihepiirin ongelmia. jotka mahdollistavat niiden keskinäisen vertaamiseen. Opiskelija ymmärtää, että nämä objektit voivat olla itse muunnoksen kohteita. Objektit on myös mahdollista palauttaa takaisin alkuperäisiksi prosesseiksi, joista ne syntyivät. Viimeisellä tasolla toimenpiteet, prosessit ja objektit jäsentyvät mielessä toimintamalliksi (Schema). Se on opiskelijan muodostama viitekehys opiskeltavasta käsitteestä. Opiskelijalle on muodostunut valmiudet erottaa, mitkä ilmiöt kuuluvat viitekehykseen ja mitkä eivät. Tätä nelitasoisen kehityksen englanninkielisten alkukirjainten mukaan nimettyä mallia kutsutaan APOS-teoriaksi. Tasojen luokittelu on esitetty kootusti taulukossa 3.1. Teoriaa voidaan käyttää esimerkiksi paloiteltaessa yliopistokurssien käsitteitä ns. geneettisiin osiinsa, joiden avulla opetusta voidaan suunnitella siten, että se seuraa opiskelijoiden matemaattisen käsitteenmuodostuksen etenemistä (Artigue, 2001; Dubinsky ja McDonald, 2001). APOSteoria voidaan nähdä yhtenä haarana seuraavana käsiteltävässä matematiikan kolmen maailman teoriassa (Tall, 2008) Matemaattisen ajattelun kolme maailmaa Tall esitti vuonna 2004 mallin, josta hän käyttää nimitystä kolme matematiikan maailmaa (Tall, 2004). Tässä mallissa kognitiivinen kehitys jaetaan kolmeen erilliseen, mutta keskenään vuorovaikuttavaan kehityksen kategoriaan (ks. kuva 3.1). Ensimmäinen maailma lähtee havainnoista, joita teemme ajatte-
32 20 LUKU 3. Teoreettinen viitekehys lemalla ja aistimalla erilaisia asioita sekä fysikaalisessa maailmassa että omassa ajatusmaailmassamme. Voimme kiinnittää huomiota tiettyihin havaintojemme ominaisuuksiin, joiden pohjalta näemme mielessämme idealisoituja käsitteitä, joille ei ole enää vastinetta ympäröivässä maailmassamme. Tall käyttää tästä nimitystä `käsitteellisesti ilmentynyt maailma' 2 (conceptual-embodied world) tai lyhyesti `ilmentynyt maailma'. Tämä käsite sisältää oikeiden reaalimaailman objektien havaintojen lisäksi kaikki matemaattiset käsitteet, jotka pystytään rakentamaan visuaalisina mielikuvina tai muiden aistihavaintojen avulla. Toinen maailma on niiden symbolien maailma, joita käytämme laskutoimituksissa ja operaatioissa algebrassa ja analyysissä sekä muilla matematiikan alueilla. Tähän maailmaan päädytään, kun matemaattisten toimenpiteiden kuten osoittamisen ja lukumäärän laskemisen käsitteet kiinnitetään matemaattisiin symboleihin. Tällöin matemaattiset prosessit muunnetaan yksinkertaisemmiksi symbolisten käsitteiden avulla tapahtuvaksi ajatteluksi. Esimerkiksi lukujen 2 ja 3 summa voidaan ajatella lukumäärän laskemisesta ja joukkojen yhdistämisestä koostuvina prosessina tai symboleiden tasolla tapahtuvana laskutoimituksena, jossa on irtauduttu lukumäärään laskemisen prosessista (Gray ja Tall, 1994). (Gray ja Tall, 1994) käyttää tällaisista prosesseista muodostettujen objektien maailmasta englanninkielistä termiä `proceptual-symbolic world' (procept = process + concept) tai lyhyesti `proceptual world', mikä kuvastaa sitä, että symboleihin on kätketty sekä prosessien, että käsitteiden ominaisuuksia. Koska suomennetuista termeistä prosessi ja konsepti voidaan samaan tapaan muodostaa termi prosepti, otetaan tässä käyttöön tämä ilmaisu sanan procept suomennoksena. Matemaattisen ajattelun kehittyminen tapahtuu proseptuaalisen maailman kannalta laajentamalla symbolisia käsitteitä uusiin asiayhteyksiin esimerkiksi ottamalla yhteenlaskussa käyttöön negatiiviset luvut, murtoluvut, reaaliluvut, vektorit jne. Tall (2008) mukaan edellä käsitelty APOS-teoria koskee matematiikan oppimista juuri tässä proseptuaalisessa maailmassa. Kolmas matemaattisen ajattelun maailma perustuu formaalien määritelmien ja aksioomien avulla ilmaistuihin ominaisuuksiin, jotka määrittelevät matemaattisia rakennelmia kuten ryhmä, vektoriavaruus jne. Tästä käytetään nimitystä `aksiomaattisformaali maailma', lyhyesti `formaali maailma'. Tämä maailma ei perustu tuttuihin olemassa oleviin objekteihin, vaan maailma rakentuu aksioomien avulla lausuttujen matemaattisten ominaisuuksien rakennelmana. Aksiomaattisen systeemin sisällä voidaan luoda uusia käsitteitä ja 2 Haapasalo (2004) suomentaa termin `embodied object' objektin ilmentymäksi.
33 3.1. Matemaattisen kehityksen kognitiivisia teorioita 21 formaali määritelmiin perustuvat formaalit objektit ilmentynyt formaali täysin integroitunut symbolinen formaali tuttuihin käsitteisiin perustuvat määritelmät kognitiivinen kehitys ilmentynyt symbolismi symbolisoitunut ilmentymä symbolinen objektin ilmentymä (embodied) Monet kaavion termit ovat kirjoittajan omia suomennoksia, koska tiedossa ei ole vakiintunutta terminologiaa. Kuva 3.1: Matematiikan oppimisen kolme maailmaa. Kuva piirretty ja suomennettu lähteen (Tall, 2008) mukaan. niiden ominaisuuksia voidaan tutkia. Näiden kolmen matematiikan oppimisen maailman suhdetta ja rakentumisprosessia havainnollistaa kuva 3.1 (piirretty lähteen Tall (2008) mukaan). Ihminen rakentaa ilmentyneiden käsitteiden ja symbolisten proseptien maailmoja ympäristöstä tekemiensä havaintojen ja symboleille tehtyjen toimenpiteiden kautta. Näiden symbolisten proseptien ja ilmentyneiden käsitteiden ominaisuuksista rakennetaan reektoimalla abstraktimman tason aksiomaattisten matemaattisten käsitteiden formaalia maailmaa. Käsitteet voivat rakentua myös näiden yhdistelmänä ilmentyneiden symboleiden tai symbolisoituneiden ilmentymien (kuvassa keskellä) avulla. Tästä on esimerkkinä esimerkiksi derivaatan oppiminen siten, että tarkastellaan funktion kuvaajan (ilmentynyt maailma) kulmakertoimen lukuarvon määrittämistä (symbolinen maailma) (Tall, 2008). Yksilöiden välillä on eroja siinä, miten he rakentavat tätä kolmen maailman järjestelmää. Tall (2004) mukaan tunnistamalla ongelmakohdat tässä käsitteiden rakentumisessa eri maailmoissa, voidaan tukea opiskelijoiden kognitiivista prosessia heidän oman matemaattisen käsitejärjestelmänsä luomisessa. Tall (2004, 2008) esittää, että yksi mahdollinen oppimisen ongelma voi tulla vastaan, kun vanhasta kokemuksesta tuttuja symbolisia esityksiä laajennetaan uuteen ympäristöön. Esimerkiksi symbolit tai b 2 4ac edustavat näkökulmasta riippuen sekä suoritettavaa laskutoimenpidettä tai tällaisen las-
34 22 LUKU 3. Teoreettinen viitekehys kutoimenpiteen tulosta. Kun opiskelija tutustuu merkintään 2 + 3x, häntä voi jäädä vaivaamaan, mikä kyseisen laskutoimituksen vastaus on. Opiskelija näkeekin nyt tilanteen, jossa + -operaatiota ei pystytä suorittamaan, kun x:ää ei tunneta (Tall, 2004) Teorioiden merkitys tämän tutkimuksen kannalta Operationaalis-rakenteellinen teoria (Sfard, 1991) tarjoaa yhden mahdollisen selitysmallin matematiikan oppimisen vaikeuksista pseudo-rakenteellisten objektien muodossa ja ehdotuksen, millaisilla toimilla ongelman syntymistä voidaan estää opetuksessa. Uusien tutkimusten valossa (Hähkiöniemi, 2006; Tall, 2008) näyttää kuitenkin siltä, että kyseinen teoria ei täysin vastaa matematiikan oppimista nykyaikana. Tall (2008) esittää, että osaksi tähän ovat syynä teknologiset mahdollisuudet: esimerkiksi derivaatta voidaan nähdä ensin rakenteellisena ominaisuutena tietokoneen piirtämän kuvaajan kulmakertoimena. Tämän jälkeen voidaan siirtyä operationaaliseen vaiheeseen, jossa pohditaan, miten kulmakerroin voidaan määrittää. Tämä on päinvastoin kuin (Sfard, 1991) esittää. Tallin prosepti-käsite sen sijaan korostaa juuri sitä, että matemaattinen symboli voi tarkoittaa samanaikaisesti sekä operationaalista että rakenteellista käsitettä. Tutkijan oman opetuskokemuksen mukaan Sfard (1991) esittämä havainto operationaalisen puolen helpommasta omaksuttavuudesta vaikuttaa kuitenkin monessa tilanteessa toimivalta ja se kannattaa pitää mielessä opetusta suunniteltaessa. Tällaisia viitteitä saatiin esimerkiksi tutkimuksessa Pasanen (2008). Matematiikan kolmen maailman teorian mukaan oppimista voi tapahtua kolmea eri reittiä pitkin (ks. kuva 3.1). Tall (2008) suosittelee ottamaan nämä eri reitit huomioon matemaattisten käsitteiden opetuksessa. Käytännössä sen voidaan katsoa tarkoittavan symbolisen ja numeerisen laskennan sekä kuvaajien käytön yhdistämistä opetuksessa. 3.2 Vastaustiedon kognitiivinen luokittelu Harjoitustehtävien ja opiskelijoiden suoritusten kognitiivisen tason luokitteluun on kehitetty erilaisia teorioita. Edellä tarkasteltiin APOS-teoriaa, joka on alunperin kehitetty tuntisuunnittelun välineeksi harjoitustehtävien luokitteluun. Sitä voidaan käyttää luokiteltaessa harjoitustehtäviä niiden kognitiivis- 3 Myös kirjoittaja on kohdannut sellaisia opetustilanteita, jossa opiskelija yrittää jatkaa kirjainlausekkeen sieventämistä niin pitkälle, että vastaukseksi tulee vain yksi luku.
35 3.3. Empiirinen käsitteenmuodostus 23 ten tavoitteiden mukaisiin luokkiin. Luokittelua voidaan näin käyttää apuna, kun halutaan laatia monipuolisia harjoitustehtäväkokonaisuuksia, jotka tukevat oppimista erilaisilla kognitiivisilla tavoitetasoilla (Dubinsky ja McDonald, 2001). Toinen luokittelun näkökulma on opiskelijoiden esimerkiksi avoimissa vastauksissa osoittaman ajattelun kognitiivinen luokittelu. Tähän tarkoitukseen APOS-teoria soveltuu kuitenkin huonosti. Koska tässä tutkimuksessa luokitellaan nimenomaan opiskelijoiden vastauksissa osoittamaa kognitiivista tasoa, soveltuu työn tarpeisiin paremmin SOLO-taksonomia SOLO-taksonomia SOLO-taksonomia (Structure of Observed Learning Outcomes) on viisiportainen taksonomia, joka on kehitetty opiskelijoiden vastaustiedon kognitiiviseen luokitteluun (Yrjönsuuri, 1994). SOLO-taksonomia on yleinen luokitteluteoria, jonka katsotaan olevan oppiaineesta riippumaton. Sen pohjalta on kuitenkin kehitetty paremmin matematiikan tehtävien analysoimiseen käyvä muunnos, josta käytetään nimeä vastaustiedon luokittelu (Yrjönsuuri, 1990, 1994). Se on arvojärjestys, joka kuvaa tehtävän ratkaisemisessa esiintyvää oletetun ajattelun laatua. Tämä luokittelu on esitetty taulukossa 3.2. APOS- ja SOLO-taksonomian mukaisessa luokitteluissa on paljon samoja piirteitä, mutta tasojen hienorakenne ja kuvailevat piirteet eroavat toisistaan (ks. esim. Pegg ja Tall (2005)). Tässä tutkimuksessa käytetään empiirisen ymmärryksen tasojen luokittelussa SOLO-taksonomiaan perustuvaa luokittelua. 3.3 Empiirinen käsitteenmuodostus Tämän tutkimuksen aiheena ovat matemaattisten käsitteiden divergenssi ja roottori empiiristen merkitysten hahmottaminen. Tästä syystä tutkimuksen teoreettiseen viitekehykseen kuuluu oleellisesti myös empiirinen käsitteenmuodostus. Fysiikan käsitteenmuodostus on empiiristä, millä tarkoitetaan käsitteenmuodostuksen perustumista kokeellisuuteen. Käsitteenmuodostus alkaa Kurki- Suonio ja Kurki-Suonio (1998, s. 160) mukaan kvalitatiivisen tason perushahmotuksesta, jossa luonnossa havaittavista olioista, ilmiöistä ja niiden ominaisuuksista muodostetaan perushahmoja. Hahmojen merkitys syntyy tunnistamalla ja luokittelemalla näitä perushahmoja sekä jäsentämällä hahmojen keskinäisiä suhteita. Tätä ensimmäistä perushahmotuksen tasoa Kurki-Suonio ja
36 24 LUKU 3. Teoreettinen viitekehys Taulukko 3.2: SOLO-taksonomiaan perustuva matematiikan vastaustiedon luokittelu (Yrjönsuuri, 1994). Tiedon taso 1. Esirakenteinen tieto Näkemys on sattumanvarainen. 2. Yksirakenteinen tieto Käsitys muodostuu jostakin tiedosta. 3. Monirakenteinen tieto Käsitys muodostuu monista osista. 4. Konkreettien yleistysten tietämisen taso Käsitys, jossa ilmiön osia on jo suhteutettu, reektiivinen yleistys ja konkreettien yleistysten taso. 5. Abstraktin tiedon käyttämisen taso Laaja-alainen käsitys ilmiöstä, abstraktin vastauksen taso. Kuvaus toiminnasta Toiminta on epäjohdonmukaista. Ominaista on tehtävän välttäminen asiaan kuulumattomalla toiminnalla. Päätelmä perustuu yhteen näkökulmaan. Ei ole tarvetta johdonmukaisuuteen. Tieto koostuu irrallisista, mutta asiaankuuluvista osista. Epäjohdonmukainen toiminta on mahdollista, yleistäminen on mahdollista vain tietyissä tilanteissa, samoin induktiivinen päättely. Yleistäminen on mahdollista vain opetetussa ja koetussa ympäristössä. Konkreettien yleistysten taso. Opitussa järjestelmässä ei ole ristiriitoja, mutta järjestelmän ulkopuolella voidaan kohdata ongelmia. Ominaista on yleistäminen hypoteettisiin tilanteisiin eli sellaisiin, joita ei ole opetettu tai koettu. Voidaan päätyä useisiin pohdittuihin vaihtoehtoihin. Kurki-Suonio (1998) kuvailee havaitsemisen, tarkkailun ja kvalitatiivisten kokeiden empiriaksi. Seuraava empiirisen käsitteenmuodostuksen vaihe on kvantiointi, jossa ilmiöiden havaittavista ominaisuuksista rakennetaan mitattavia suureita. Ylimmällä hierarkian tasolla käsitteen rakentumisessa on ymmärtämisen ja selittävien mallien taso, johon kuuluvat fysikaaliset teoriat ja mallit (Kurki-Suonio ja Kurki-Suonio, 1998). Suureet ovat fysiikan käsitteenmuodostuksen perusta. Niiden empiiristen merkityksen rakentuminen edellä kuvatun hierarkian mukaan voidaan jäsentää neljään vaiheeseen (Kurki-Suonio ja Kurki-Suonio, 1998, s ): 1. Empiirisen merkityksen synty on kvalitatiivisen perushahmotuksen vaihe, jossa olioiden ja ilmiöiden ominaisuudet käsitteistyvät. Tälle tasolle kuuluvan esikvantioinnin kautta valmistellaan tietä seuraavalle tasolle luokittelemalla ja vertailemalla ominaisuuksia esimerkiksi voimakkuuden tai asteen mukaan. 2. Kvantiointi rakentaa empiirisestä merkityksestä mitattavan kvantitatiivisen suuren.
37 3.4. Matematiikan opetuksen menetelmiä Teoreettinen merkitys muodostuu strukturoinnin kautta, kun suure saa aseman fysiikan teorioiden joukossa. 4. Yleistyminen on suureen käyttöalueen laajentumista ja abstrahoitumista. Suureen merkitys yleistyy kuvaamaan laajempaa ilmiöjoukkoa, kuin mihin se oli alunperin perushahmotusvaiheessa kytketty. Fysiikan opetuksen hahmottava lähestymistapa perustuu oleellisesti juuri tähän hahmotusprosessin hierarkiaan (Kurki-Suonio ja Kurki-Suonio, 1998, s. 265) Divergenssin ja roottorin empiirisen merkityksen rakentuminen Fysikaalisen vektorikentän divergenssi ja roottori kuvaavat tiettyjä kentän havaittavia ominaisuuksia. Ne ovat siten kenttään liittyviä suureita, joiden merkityksen kehittymistä voidaan tarkastella empiirisen käsitteenmuodostuksen näkökulmasta. Erityisesti ilmaisulla divergenssin ja roottorin empiirinen merkitys tarkoitetaan tässä työssä sitä fysikaalista merkitystä, joka divergenssiin ja roottoriin liittyy, kun niitä tarkastellaan fysikaalisen vektorikentän yhteydessä. Tähän työhön liittyvässä opetuskokeilussa divergenssin ja roottorin opetus ei noudattanut hahmottavaa lähestymistapaa, vaan opetus tapahtui käyttämällä perushahmotukseen ja esikvantiointiin kuuluvia demonstraatioita normaalin perinteisemmän matematiikan opetuksen tukena. Näillä demonstraatioilla divergenssi ja roottori kytkettiin fysikaalisiin suureisiin. Vaikka opetus ei siis seurannut edellä olevaa hierarkiaa, voidaan kyseistä jaottelua kuitenkin käyttää hieman soveltaen opiskelijoiden empiirisen ymmärryksen kehittymisen luokitteluun. Tämän mittarin luomista tarkastellaan luvussa Matematiikan opetuksen menetelmiä Visualisaatiot Opiskelumotivaatio on keskeinen oppimistuloksiin vaikuttava tekijä (Joutsenlahti, 2005; Yrjönsuuri, 1990, 1994). On esitetty, että tietotekniikan hyödyntäminen opetusvälineenä voi tarjota mahdollisuuden kohentaa opiskelumotivaatiota (Meisalo et al., 2003). Erityisesti video-otoksia tai demonstraatioita voidaan käyttää apuna huomion kiinnittämisessä opetettavan asian kannalta olennaisiin seikkoihin. Visualisaatioiden käyttöä käsitteiden havainnollistamisessa perustellaan näkökyvyn suurimmalla kaistanleveydellä. Visualisaatiolla tarkoitetaan abstraktin datan esittämistä graaseen muotoon muunnettuna
38 26 LUKU 3. Teoreettinen viitekehys (Meisalo et al., 2003). Tässä tutkimuksessa käsiteltävän aihepiirin yhteydessä esimerkiksi vektorikentän esittäminen hiukkasten virtauksena on visualisaatio. Visualisaatoiden käyttöä opetuksessa tukee myös kasvatuspsykologinen tietämys. Opiskelijoilla on erilaisia oppimistyylejä. Joillekin visuaalinen esitys on tehokkain tapa omaksua käsitteitä, toisille tekstimuotoinen esitys sopii paremmin. Käyttämällä opetuksessa erilaisia medioita saman informaation välittämiseen on siten mahdollista ottaa huomioon oppijoiden erilaiset oppimistyylit (Meisalo et al., 2003) Animaatiot Animaatio määritellään peräkkäisten kuvien sarjana, jossa jokaisessa ruudussa tapahtuu muutos edelliseen ruutuun nähden. Video poikkeaa animaatiosta siinä, että video koostuu oikeiden objektien liikkeestä, kun taas animaatio esittää simuloitujen objektien liikettä (Ainsworth, 2008). Animaatioiden vaikutuksesta oppimistuloksiin on tehty vertailututkimuksia. Esimerkiksi tutkimuksessa Rieber (1991) opetettiin Newtonin lakeja osalle oppilaista animaatioiden ja osalle staattisten kuvien avulla. Tutkimuksessa havaittiin, että animaatioita nähneet oppilaat oppivat tiedostamattaan animaatioissa esitettyjä lainalaisuuksia. Toisaalta kyseisillä opiskelijoilla oli myös suurempi riski väärinkäsitysten riski (Rieber, 1991). Ainsworth (2008) esittää seuraavia tämän tutkimuksen opetuskokeiluun liittyviä näkökohtia animaatioiden avulla tapahtuvasta oppimisesta: kuusi näkökohtaa, jotka liittyvät animaatioiden avulla tapahtuvaan oppimiseen: Animaatioilla on ilmaisuvoimaa, kun on tarve esittää toimintaa, joka ilmenee tietynlaisena tapahtumaketjuna. Animaatioista voi olla tällaisessa tilanteessa apua opiskelijoille, kun esitettävä dynaaminen toiminta on tarpeen ymmärtää juuri määrätynlaisena ketjuna, mutta muissa tapauksissa vastaavaa hyötyä ei välttämättä ole. On todettu, että animaatioiden avulla tapahtuvassa dynaamisten ilmiöiden oppimisessa kognitiivisten resurssien tarve vähentyy muihin oppimistapoihin verrattuna. Toisaalta animaatioiden käyttö myös luo merkittäviä havaintojen käsittelyyn ja muistamiseen liittyviä ongelmia siitä syystä, että animaatiot ovat ajallisesti nopeasti ohikiitäviä. On viitteitä, että animaatioiden käytöllä voi olla vaikutuksia opiskelijoiden aektiiviseen asennoitumiseen matematiikan opetukseen lisäten opiskelijoiden tyytyväisyyttä ja motivaatiota oppimiseen.
39 3.5. Tutkimuksia derivaatan opetuksesta 27 Yksi syy animaatioiden käyttöön tässä opetuskokeilussa oli se, että tarkasteltavat käsitteet liittyvät kolmiulotteiseen avaruuteen. Kolmiulotteisten objektien ja ilmiöiden hahmottaminen staattisista kuvista voi olla hankalaa. Animaatio antaa mahdollisuuden muuttaa objektin tai katsojan kuvakulmaa ja tarkastella näin objektia eri suunnista. Tämä saattaa helpottaa objektin kolmiulotteisen rakenteen hahmottamista. Animaatioiden avulla voidaan myös tarkastella dynaamisen ilmiön kehittymistä ajan muuttuessa. Kriittisessä artikkelissa (Tversky et al., 2002) animaatioiden hyödyllisyydestä opetuksessa todetaan, että juuri tällainen animaatioiden käyttö reaaliaikaiseen paikan ja ajan muutosten kuvaamiseen on tehokasta animaatioiden käyttöä. Tversky et al. (2002) esittävät ns. kongruenssiperiaatteen (Congruence Principle), jonka mukaan visualisaatioiden rakenteen ja sisällön tulisi vastata sitä rakennetta ja sisältöä, joka opiskelijan halutaan esityksestä sisäistävän. Fysikaalista ilmiötä simuloivan animaation tapauksessa näin juuri on, sillä animaatiolla halutaan esittää totuudenmukainen kuva tarkasteltavasta ilmiöstä. Interaktiivisuuden avulla on mahdollista välttää animaatioiden käytössä esiintyviä ongelmia ja tehostaa animaatioiden hyötyjä (Tversky et al., 2002). Esimerkkeinä tällaisista tehostavista interaktiivisuuden muodoista on mainittu mahdollisuus säätää animaation nopeutta, käynnistys, pysäytys, uudelleen katselu ja zoomaaminen. Näitä ominaisuuksia on esimerkiksi interaktiivisiin java-demonstraatioihin perustuvissa visualisaatioissa. 3.5 Tutkimuksia derivaatan opetuksesta Yhden muuttujan funktioiden derivaatan opetuksesta ja oppimisesta on paljon aiempia tutkimuksia sekä Suomessa että ulkomailla. Esimerkiksi Markus Hähkiöniemi tutki väitöskirjassaan (Hähkiöniemi, 2006) opiskelijoiden derivaatan opiskelussa käyttämiä representaatioita. Tutkimusten mukaan derivaatan oppimista voi tukea ottamalla opiskelijoiden erilaiset representaatiot huomioon. Representaatioilla tarkoitetaan yleisesti erilaisia ajattelun apuvälineitä. Ne voivat olla esimerkiksi symbolisia, graasia tai kinesteettisiä (Hähkiöniemi, 2006). Hähkiöniemen tutkimuksen opetuskokeilu perustui ajatukselle, että derivaatan havaitseminen funktion kuvaajasta auttaa derivaatan oppimista. Tätä ovat tutkineet esimeriksi Berry ja Nyman (2003). He selvittivät Yhdysvaltalaisten yliopisto-opintoja aloittavien opiskelijoiden ymmärrystä derivaatan käsitteestä. Heidän havaintonsa oli, että monilla opiskelijoilla oli algebrallissymbolinen käsitys derivaatasta ja heidän oli vaikea löytää yhteyttä derivoidun funk-
40 28 LUKU 3. Teoreettinen viitekehys tion kuvaajan ja alkuperäisen funktion välillä. Opiskelijoilta näytti puuttuvan derivaatan intuitiivinen idea. Opiskelijat pääsevät läpi kursseista tietäen, että heidän `täytyy etsiä derivaatan nollakohta' kuitenkaan ymmärtämättä, miksi se on tärkeää. (Berry ja Nyman, 2003) Gray ja Tall (1994) käsittelevät asiaa teoreettisemmin. He esittävät, että oppiminen voi tapahtua siten, että opittava käsite omaksutaan ensin mielikuvaobjektina. Esimerkiksi derivaatan hahmo voidaan oppia tutkimalla funktion kuvaajaan jyrkkyyttä. Tämä konkreettinen derivaatan hahmo muuntuu vähitellen mielessä abstraktimmaksi ja lopulta se voidaan irrottaa alkuperäisestä konkreettisesta kiinnityksestä. Symbolitasolla oppiminen tapahtuu puolestaan prosessien kautta oppimalla derivaatan ominaisuuksia symbolisia laskutoimenpiteitä tehden, kuten tutkimalla, mitä symbolisen funktion lausekkeen derivaattana saadaan. Tässä esiteltävä tutkimus kohdistuu yhden muuttujan funktioiden sijasta useamman muuttujan funktioiden derivaattoihin ja laajentaa siten aiempien tutkimusten kenttää. Edellä mainitut tutkimukset on tehty matematiikan opetuksen näkökulmasta. Tässä tutkimuksessa sen sijaan korostetaan fysiikan näkökulmaa. Fysiikan sovellusten kannalta derivaatan empiiristen merkitysten ymmärtäminen on tärkeää. Tämä fysiikan tarve on sopusoinnussa tässä luvussa käsiteltyjen kognitiivisten teorioiden kanssa. Tutkimusten mukaan uusien matemaattisten käsitteiden opiskelu on hyvä aloittaa juuri operationaalisista käsitteistä, jossa korostuvat derivaatan empiirisesti tärkeät ominaisuudet. 3.6 Vektorianalyysin opetus eri oppikirjoissa Seuraavaksi tutustutaan erilaisiin oppikirjoista löytyviin vektorianalyysin opetustyyleihin. Tarkoitus on antaa yleiskuva ja tuoda esiin oleellisimmat erot tarkasteltujen oppikirjojen opetustavan ja etenemisjärjestyksen välillä. Kyseessä ei ole tieteelliset kriteerit täyttävä oppikirja-analyysi, vaan kirjoittajan näiden oppikirjojen aktiiviseen käyttöön pohjautuva näkemys. Kirjoittajan mielestä valitut kirjat antavat kuvailevaa tarkoitusta varten riittävän hyvän läpileikkauksen erilaisista opetustyyleistä. 4 Tarkasteltavat kirjat ovat: Calculus (Adams, 2003), Engineering Mathema- 4 Suomenkielisten vektorianalyysin oppikirjojen klassikoihin kuuluu Väisälä (1961), jonka esitystavalla on ollut vaikutusta uudenpiin suomalaisiin vektorianalyysiä käsitteleviin oppikirjoihin. Kyseisessä kirjassa käsitellään hyvin laajasti vektorianalyysin käsitteiden fysikaalista merkitystä. Koska kirja ei ole enää yleisessä oppikirjakäytössä, ei sitä ole tarkasteltu tässä lähemmin.
41 3.6. Vektorianalyysin opetus eri oppikirjoissa 29 tics (Croft et al., 2001), Fysiikan matemaattiset apuneuvot (Honkonen et al., 2003), Matematiikkaa soveltajille (Lahtinen ja Pehkonen, 1992, 1994; Lahtinen et al., 1989) ja Thomas' calculus (Weir et al., 2008). Näissä oppikirjoissa on nähtävissä kaksi äärimmäistä opetustyyliä. Matematiikan teorialähtöisessä esityksessä on tyypillistä, että ensin esitetään teoreema, joka sen jälkeen todistetaan. Teoreeman hyödyllisyys voidaan esittää jälkikäteen esimerkkien ja sovellusten avulla. Tästä formaalista opetustyylistä käytetään tässä nimitystä deduktiivinen opetustyyli. Tämän vastakohta on täydellisesti todistuksia kaihtava opetustapa, jossa matemaattiset käsitteet ja laskutoimitukset esitetään annettuna tietona ja niiden käyttöä opetetaan yksityiskohtaisilla esimerkeillä. Tätä kuvaa hyvin nimitys esimerkkipohjainen opetustyyli. Näiden ääripäiden välimaastossa on ongelmapohjainen opetustyyli, jossa käsiteltävän aiheen johdantona esitetään sovellusten kannalta tärkeä ongelma. Ongelman ratkaisua yritettäessä tullaan kehittäneeksi uusia matemaattisia menetelmiä, jotka voidaan sitten niin haluttaessa esittää myös formaalisti. Käytännössä kaikissa arvioiduissa oppikirjoissa riittää lukijan lähtötasoksi hyvät tiedot lukion matematiikan laajasta oppimäärästä. Kirjassa Fysiikan matemaattiset apuneuvot lähtötaso on kuitenkin selvästi muita kirjoja korkeampi. Thomas' calculus (Weir et al., 2008) erottuu tarkastelluista oppikirjoista teorian käsittelytavaltaan. Teoria esitetään eksaktisti ja formaalisti, mutta esityksessä on merkittävästi painotettu hahmottavaa ja intuitiivista käsittelyä. Eksaktit määritelmät ja käsitteet esitetään vasta siinä vaiheessa, kun ne on kehitelty johdonmukaisesti sovelluksia ja käytännön ongelmia painottaen hahmottavalla tasolla riittävän pitkälle. Graasia ja hahmottavia epäformaaleja todistuksia käytetään laajasti eksaktien todistusten tukena. Kirjassa Matematiikkaa soveltajille (Lahtinen ja Pehkonen, 1992, 1994) kaikki lauseet todistetaan ja määritelmät esitetään eksaktisti matemaattisesti. Käsitteitä ei perustella tai kehitellä hahmottavalla tasolla, vaan esitys on täysin teorialähtöinen ja etenee johdonmukaisesti eksaktin teoriamuodostuksen tarpeiden mukaan. Kirjasarjaan kuuluu myös 3. osa (Lahtinen et al., 1989), joka sisältää aihepiiriin kuuluvia esimerkkitehtäviä fysiikasta, kemiasta ja matematiikasta. Esimerkit ovat kyllä perusteellisia, mutta niitä ei ole erityisesti suunniteltu tukemaan kirjassa opetettavien käsitteiden konkreettista hahmotusta, vaan ne vaikuttavat enemmänkin laskudemonstraatioilta. Fysiikan matemaattiset apuneuvot -kirjassa (Honkonen et al., 2003) monet lauseet jätetään todistamatta tai käytetään intuitiivisia perusteluita täsmällisten todistusten sijasta. Esitys on hyvin kompakti ja nopeasti etenevä.
42 30 LUKU 3. Teoreettinen viitekehys Käsitteitä ei juurikaan kehitellä hahmottavasti. Soveltavia esimerkkejä on hyvin vähän. Vektorianalyysin yhteydessä puhutaan tulkinnoista ja käytetään soveltavia esimerkkejä. Esimerkit ja harjoitukset pääasiassa täysin symbolisia. Muutama symbolisnumeerinen tehtävä joukossa. Engineering mathematics -kirja (Croft et al., 2001) on tarkoitettu elektroniikan ja sähkö- ja tietoliikennetekniikan insinööriopiskelijoille. Kirjassa on tästä syystä lukuisia esimerkkejä näiltä tekniikan aloilta. Yleispiirteeltään kirja etenee siten, että aihepiiriin käsitteet esitellään kappaleen alussa lyhyesti esimerkkien kautta. Sitten määritellään matemaattiset käsitteet ja operaatiot ja tämän jälkeen opetetaan laskutekniikkaa esimerkkien avulla. Konkreettisia esimerkkejä ei kuitenkaan käytetä varsinaisten laskuoperaatioiden johtamisessa, vaan tulkinnat ja esimerkit ovat selkeästi erillään matemaattisista määritelmistä. Kirja ei ole aivan riittävän syvällinen kaikkia Matemaattiset apuneuvot kurssin tavoitteita ajatellen, mutta perusasiat ja laskutekniikan se kattaa hyvin arvosanatasolle 34 vaadittuihin asioihin asti. Kirjaa suositeltiin kurssin oheislukemistoksi juuri laajan esimerkkivalikoiman takia.
43 3.6. Vektorianalyysin opetus eri oppikirjoissa 31 Taulukko 3.3: Oppikirjojen vektorianalyysiosuuden kuvaamisessa käytettävä koodaus Opetustyyli F I E Formaali, opetus etenee deduktiivisesti (ensin teoreema, sitten todistus) Intuitiivinen, opetuksessa käytetään intuitiivisia ja hahmottavia perusteluja Esimerkkilähtöinen, opetus perustuu yksityiskohtaisiin esimerkkeihin Painotus selviää koodauksen järjestyksestä, esim. F I Pääpaino formaalissa esityksessä. Intuitiivisuutta tukena. I F Painotettu merkittävästi intuitiivisuutta, mutta asiat esitetään myös formaalisti. Vektorianalyysin etenemisjärjestys V viivaintegraali K kiertämäintegraali P pinta- ja tilavuusintegraali F vuointegraali D divergenssin määritelmä nablan avulla R roottorin määritelmä nablan avulla G Gaussin lause S Stokesin lause Taulukko 3.4: Vektorianalyysin opetus eri matematiikan oppikirjoissa. Calculus Thomas' Matematiikkaa Fysiikan ma- Engineering calculus soveltajille temaattiset Mathematics apuneuvot Julkaisuvuosi Sivuja (vektorian.) a Opetustyyli F I I F F F (I) E (I) Visuaalisuus b + Tehtävät c Etenemisjärjestys VKPFDRGS VK d PFRSDG DRV e PSGF DRVPFGKS DRV e PFGS a b c d e Mukaan ei ole luettu kirjasarjan 3. osaa. Kuvien määrä on valtava. Visualisointeja hyödynnetään opetusmenetelmänä. Sisältää lähinnä mekaanisia perustehtäviä. Divergenssi ja roottori esitellään kaksiulotteisina versioina jo viivaintegraalin kohdalla, jolloin käsitellään Greenin lauseita. Kiertämän käsitettä ei mainita kirjassa lainkaan.
44
45 Luku 4 Tutkimusongelmat ja tutkimuksen toteutus 4.1 Opetuskokeilun tavoitteet Fysiikan metodisina perusteina ovat kokeellisuus ja eksaktisuus (Kurki-Suonio ja Kurki-Suonio, 1998, s. 118). Käytännössä fysiikan eksaktisuus toteutetaan ilmaisemalla lainalaisuudet matematiikan kielellä. Kirjoittaja on opetustyössään havainnut että osalla yliopisto- ja ammattikorkeakoulu- opiskelijoista on vaikeuksia käyttää näitä metodeja yhdessä. Metodien välinen kuilu korostuu puhuttaessa kokeellisesta ja teoreettisesta fysiikasta kuin kahdesta toisistaan erillisestä oppialasta. Kurki-Suonio ja Kurki-Suonio (1998, s ) korostaa, että fysiikan käsiterakennelmassa ei ole puhtaasti teoreettisia tai kokeellisia käsitteitä, vaan käsitteiden merkitykset rakentuvat prosessissa, joka sulauttaa empirian ja teorian yhdeksi kokonaisuudeksi, niin että niiden empiiriset ja teoreettiset komponentit eivät enää ole erotettavissa. Dierentiaali- ja integraalilaskenta on fysiikassa tärkeä työkalu. Tavallisen yhden muuttujan funktion derivaatan opetuksesta on tehty jo paljon tutkimuksia ja opetuskokeiluja (ks. esimerkiksi väitöskirja Hähkiöniemi, 2006, ja viitteet siinä). Matemaattiset apuneuvot II -kurssilla dierentiaali- ja integraalilaskenta laajenee usean muuttujan funktioihin, missä esiintyy uutena peruskäsitteenä osittaisderivaatta, joka on tavallisen derivaatan yleistys. Opetuskokeilun aihepiiri on rajattu vektorifunktioihin, joiden tapauksessa keskeiset derivaattakäsitteet ovat divergenssi ja roottori. Perinteisesti Mapu -kurssi on keskittynyt vain symboliseen laskentaan, mikä on nähtävissä esimerkiksi kurssin vanhasta oppikirjasta Honkonen et al. (2003). Tavoitteena on ollut lähinnä formaali symbolien käsittelytaito, jota on
46 34 LUKU 4. Tutkimusongelmat ja tutkimuksen toteutus tuettu formaalia puolta korostavilla laskuharjoitustehtävillä 1. Tämä tavoite on jo itsessään vaikea osalle opiskelijoista, minkä kirjoittaja on todennut lukuisia kertoja kurssin kokeita korjatessaan. Osa opiskelijoista ei ole tajunnut divergenssistä ja roottorista käytännöllisesti katsoen mitään. Varmasti osasyy heikkoon menestykseen on puhtaasti opiskelijoiden omassa opiskeluorientaatiossa. Tutkija on kuitenkin nähnyt, että vektorianalyysin käsitteiden omaksuminen voi tuottaa ongelmia muuten hyvin menestyneille opiskelijoillekin. 4.2 Tutkimuksen tavoite Tutkimuksen yleistavoitteena on ymmärtää fysiikan opiskelijoiden ajattelua ja oppimista vektorianalyysistä ja samalla kehittää kyseisen aihepiirin opetusta tutkimukseen perustuen. Spesimpänä tavoitteena on selvittää visualisaatioita ja fysikaalisia analogioita korostavien opetusmenetelmien toimivuutta divergenssin ja roottorin käsitteiden empiiristen merkitysten opettamisessa. 4.3 Opetushypoteesi Opetushypoteesi Visualisaatioita ja fysikaalisia analogioita painottava opetus tukee divergenssin ja roottorin käsitteiden empiiristen merkitysten oppimista. Tässä fysikaalisilla analogioilla tarkoitetaan konkreettisia tai idealisoituja fysikaalisia tilanteita, joissa ilmenee tutkittavaan matemaattiseen käsitteeseen samaistettavia piirteitä. Analogiat voidaan esittää kerrottuna, demonstraatioina tai visuaalisessa muodossa animaatioiden, kuvasarjojen ja simulaatioiden avulla. Hypoteesissa korostetaan erityisesti visualisaatioita opetusmenetelmänä. Hypoteesin teoreettisena perusteluna ovat edellä tarkastellut tutkimustulokset derivaatan oppimisesta ja opetusteknologioiden käytöstä (ks. Luku 3.4). Empiirisillä merkityksillä tarkoitetaan luvussa kuvailtua käsitteenmuodostusta kvalitatiivisesti ja kvantitatiivisesti. 1 Vanhoja tehtäviä on nähtävillä arkistoiduilla kurssisivuilla osoitteessa
47 4.4. Tutkimusongelmat 35 Kriteeristö hypoteesin toteutumiselle Hypoteesin toteutumisen kriteereiksi asetetaan seuraavat saavutetut tavoitteet: 1. Opiskelija osaa kiinnittää divergenssin ja roottorin käsitteet empiirisiin olioihin tai ilmiöihin. 2. Opiskelija osaa luonnehtia divergenssin ja roottorin arvoa kvalitatiivisten havaintojen pohjalta. 3. Opiskelija osaa määrittää divergenssin ja roottorin numeerisen arvon mittaamalla määrittelylausekkeeseen perustuen. Empiiriset oliot ja ilmiöt ovat fysikaalisen suureen muodostamia vektorikenttiä, kuten sähkökenttä tai nesteen virtauskenttä. Ne voivat myös olla suureiden esityksenä käytettäviä vektorikarttakuvia. Näiden kriteerien täyttyminen tarkoittaa käytännössä sitä, että opiskelija kykenee tarkastelemaan käsitteitä matematiikan kolmen maailman teorian mielessä ilmentymien ja symbolien maailmoista käsin ja pystyy siirtymään niiden välillä. 4.4 Tutkimusongelmat Hypoteesin testaaminen tapahtuu seuraavien tutkimusongelmien kautta. Kysymys A liittyy hypoteesin mukaisen opetuskokeilun järjestämiseen. Kysymys B pitää sisällään mittareiden laadinnan sekä aineiston keruun ja analyysin hypoteesin toteutumisen selvittämiseksi. Tutkimuskysymyksen C avulla syvennetään opetuskokeilun käytännön merkitystä pyrkien löytämään suosituksia aihepiirin opetuksen suunnittelulle. A Miten divergenssin ja roottorin empiirisiä merkityksiä voidaan opettaa visualisaatioita ja fysikaalisia analogioita käyttäen? B Toteutuvatko hypoteesin kriteerit opetuskokeilun jälkeen? B.1 Osaako opiskelija kiinnittää divergenssin ja roottorin käsitteet empiirisiin olioihin tai ilmiöihin? B.2 Osaako opiskelija luonnehtia divergenssin ja roottorin arvoa kvalitatiivisten havaintojen pohjalta? B.3 Osaako opiskelija määrittää divergenssin ja roottorin numeerisen arvon mittaamalla määrittelylausekkeeseen perustuen?
48 36 LUKU 4. Tutkimusongelmat ja tutkimuksen toteutus C Miten opetusta voidaan tehostaa opetuskokeilusta saatujen kokemusten perusteella? C.1 Millaisia mahdollisuuksia aihepiirin matemaattinen rakenne antaa empiiristä ymmärtämistä tukevalle opetusjärjestykselle? C.2 Mitä ongelmia opiskelijoilla ilmenee divergenssin ja roottorin käsitteiden oppimisessa? 4.5 Tutkimuksen rakenne ja käytännön toteutus Kuvan 4.1 kaavio esittää tutkimusprosessia. Siinä on myös esitetty pääpiirteittäin tutkimuksen eri osien nivoutuminen toisiinsa ja niiden vaikutus päätöksien tekoon tutkimuksen edetessä. Opetuskokeilu Kuva 4.1: Kaavio tutkimuksen vaiheista
49 4.5. Tutkimuksen rakenne ja käytännön toteutus 37 Tutkimuksen alkuperäinen idea syntyi tutkijan omista opettajana tehdyistä havainnoista sekä mielenkiinnosta uusien havainnollistusmenetelmien kehittämiseen. Tutkimuksen teoreettinen viitekehys pohjautuu matemaattisen käsitteen muodostumisen teorioihin ja tutkimustietoon uusien opetusteknologioiden vaikutuksista oppimiseen. Tämä tausta kiteytyy opetushypoteesissa, jonka toteutumisen testaaminen on tutkimuksen toteutusta ohjaava päätavoite. Tutkimuksen metodin valintaan ja teoreettisen pohjan kokoamiseen vaikuttivat aiemmat derivaatan käsitteen oppimista koskevat teoriat ja tutkimukset (Berry ja Nyman, 2003; Hähkiöniemi, 2006). Tutkimus toteutettiin empiirisenä tutkimuksena hankkimalla opetuskokeiluun osallistuneiden opiskelijoiden käsityksistä tietoa harjoitus- ja koetehtävillä sekä haastatteluilla. Pääasiallinen tutkimusote on fenomenogranen toimintatutkimus. Fenomenograassa tutkitaan ihmisten käsityksiä asioista pyrkimyksenä selvittää, miten käsitykset eroavat yksilöiden välillä. Toimintatutkimus puolestaan viittaa osallistuvaan tutkimukseen, jossa tutkija pyrkii itse vaikuttamaan havaittavaan ilmiöön. Toimintatutkimuksen piirteisiin kuuluu myös, että pyritään kehittämään olemassa olevaa käytäntöä paremmaksi. (Metsämuuronen, 2005) Tutkimusta voidaan luonnehtia myös tapaustutkimukseksi, sillä kohteena oli yhdelle ryhmälle tehty opetuskokeilu ilman vertailuryhmää. Verrokkiryhmän puute johtui sekä tutkimusetiikasta että käytännön syistä. Tutkimuseettisesti olisi arveluttavaa jakaa opiskeluryhmä paloihin ja kieltää osaa opiskelijoista saamasta opettajan itse parempana pitämää opetusta. Erityisesti tutkimuksen yhtenä mittarina toimii koetehtävä. Jos tutkimuksessa käytettäisiin vertailuryhmiä ja ryhmien välillä havaittaisiin eroja, osoittaisi tämä, että eri ryhmien opiskelijat eivät ole olleet samanarvoisessa asemassa. Toisaalta osa tutkimuksen kohteena olevista opetusmenetelmistä on vuosia jatkuneen kehitystyön takia ehtinyt integroitua niin luontevaksi osaksi tutkijan opetusta, ettei aidosti vertailukelpoista näistä menetelmistä vapaata ryhmää ole mahdollista järjestää. Opetustutkimuksissa yksi mahdollisuus olisi valita vertailuryhmä toisesta oppilaitoksesta (Metsämuuronen, 2005). Lukio- ja peruskouluopetuksessa tämä on mahdollista toteuttaa, kun kurssien tavoitteet ja sisällöt on määritelty virallisessa opetussuunnitelman perusteissa. Korkeakouluopetuksessa ei ole standardoitua opetussuunnitelmaa, jonka nojalla vertailuryhmä voitaisiin valita. Kvalitatiivinen tutkimusote valittiin siitä syystä, että divergenssin ja roottorin käsitteiden empiiristen merkitysten oppimisesta ei ole tutkijan tiedossa
50 38 LUKU 4. Tutkimusongelmat ja tutkimuksen toteutus aiempia julkaistuja tutkimuksia. Ennen kuin kvantitatiiviseen tutkimukseen tarvittavia testejä ja kysymyksiä voidaan laatia, on tunnettava opiskelijoiden ajattelun piirteitä tutkittavasta aiheesta riittävästi. Tutkimuksen yhtenä tavoitteena onkin kerätä tietoa näiden käsitteiden ajattelusta. Pääosa aineistosta hankittiin kirjallisessa muodossa opiskelijoille pidetyn alkutestin, harjoitustehtäv ja kokeen avulla. Opetuskokeiluun liittyvässä tutkimuksessa koe- ja harjoitustehtävät ovat luonnollisia tiedonkeruumenetelmiä, joita käyttäen on mahdollista laatia myös selkeät mittarit. Koeanalyysissä tehtävien havaintojen validioimiseksi ja näiden pohjalta nousseiden uusien kysymysten tarkemman tutkimisen välineenä käytettiin toiminnallista haastattelua. Se on osoittautunut hyväksi tiedonkeruumenetelmäksi vastaavissa matematiikan oppimista koskevissa tutkimuksissa (Berry ja Nyman, 2003; Hähkiöniemi, 2006). Haastattelu on perusteltu menetelmä silloin, kun halutaan tietää, miten ihmiset ymmärtävät ja ajattelevat asioista (Kvale, 1996). Haastattelun käyttöä puoltaa myös se, että tutkimuksessa halutaan luoda kuvaavia esimerkkejä opiskelijoiden saavuttamista erilaisista kognitiivisista tasoista tarkasteltavien käsitteiden oppimisessa (Metsämuuronen, 2005). Haastattelussa tietoa kerättiin sekä paperilla esitettävinä tehtävinä että videonauhoituksena. Varmistuksena haastattelut äänitettiin myös nauhurilla. Videonauhoitukseen päädyttiin siksi, että haastattelussa annetut tehtävät sisälsivät tutkimuksen kannalta oleellista fyysistä toiminnallisuutta. Videonauhoitus oli helpoin ja informatiivisin tapa toteuttaa tämän tiedon keruu Otanta Tutkimuksen otantana oli Helsingin yliopiston Fysiikan laitoksella syyslukukaudella 2007 pidettyjen teoreettisen fysiikan kurssien Matemaattiset apuneuvot I ja II opiskelijat. Tutkija on toiminut itse kyseisten kurssien luennoitsijana syksystä Lähtötasotesti pidettiin kurssin ensimmäisellä luennolla. Testin palautti noin 130 opiskelijaa, joista 50 valittiin analysoitavaksi. Lähtötasotestin tuloksia esitellään lyhyesti kappaleessa Tarkempi analyysi testistä on esitetty tutkijan laudaturtutkielmassa (Pasanen, 2008). Kaikki kurssin aloittaneet eivät kuitenkaan suorittaneet kurssia aktiivisesti, vaan Mapu I -kurssin loppukokeeseen osallistui 118 opiskelijaa ja Mapu II kokeeseen 97 opiskelijaa. Mapu II -kurssin loppupuolella annettiin opiskelijoille tehtäväksi harjoitus, jonka tavoitteena oli sekä opettaa tutkittavia käsitteitä että mitata opiskelijoiden ymmärrystä niistä. Harjoitustehtävän palautti yhteensä 81 opiskelijaa,
51 4.6. Empiirisen ymmärryksen mittari 39 mikä on 84 % loppukokeeseen osallistuneista. Harjoitustehtävän vastauksia käsitellään lähemmin luvussa Tutkimuksen tärkeimpänä aineistolähteenä toimi Mapu II -kurssin loppukokeessa ollut tehtävä. Tämän koevastauksen otanta oli kaikki Mapu II kokeeseen osallistuneet 97 opiskelijaa. Toinen keskeinen tutkimusmateriaalin lähde oli haastattelu, joka tehtiin 5 opiskelijalle. 4.6 Empiirisen ymmärryksen mittari Tutkimuksessa ollaan erityisesti kiinnostuneita opiskelijan empiirisen ymmärryksen tasosta. Tämän tutkimuksen kannalta oleellisimmat empiirisen hahmotuksen vaiheet ovat teorialuvussa 3.3 esitetyn rakentumisprosessin 1. ja 2. vaihe. Otetaan niille käyttöön nimitykset E1 ja E2 -vaihe. Näiden vaiheiden täsmentämiseen Kurki-Suonio ja Kurki-Suonio (1998, s.183) esittää joukon jäsentelykysymyksiä, joita on sovellettu ja täydennetty tähän työhön sopivaksi: E1 Kiinnitys ja luonnehdinta (kvalitatiivinen): E1.1 Perushahmotus: Mihin olioihin ja ilmiöihin suure liittyy? Millaista niiden ominaisuutta se esittää? E1.2 Esikvantiointi: Miten ominaisuuden astetta tai voimakkuutta voidaan luonnehtia? E2 Kokeellinen määritelmä (kvantitatiivinen): Miten suuree mitataan sen määrittelylausekkeeseen perustuen? Suurin ero Kurki-Suonio ja Kurki-Suonio (1998) esittämään on kohdan 2 rajoittaminen tässä vain suureen mittaamiseen sen määrittelylausekkeeseen perustuen, kun taas Kurki-Suonio ja Kurki-Suonio (1998) tarkastelevat myös ns. suureen kvantiointikoetta. Opetushypoteesin toteutumiseksi asetetut kriteerit 1-3 (kpl 4.3) on laadittu siten, että ne vastaavat empiirisen hahmotuksen vaiheita E1.1, E1.2 ja E2. E1 on empiirisen hahmotuksen vaihe, jolla suureen merkitys ymmärretään kvalitatiivisesti. E2 on kvantiointivaihe, jolla ymmärretään lisäksi, miten suure voidaan mitata empiirisesti. Näiden vaiheiden alapuolelle voidaan luoda vielä taso E0, joka on näennäisen ymmärryksen vaihe. Sillä tarkoitetaan sellaista esirakenteista tietoa, joka ei ole vielä jäsentynyt oikeaksi asian ymmärrykseksi ja perustuu naiiveihin määritelmiin, kuten pyörteisyys on vektoreiden kaartumista. On mahdollista, että ymmärrys etenee tasoilla E1 ja E2 osittain sa-
52 40 LUKU 4. Tutkimusongelmat ja tutkimuksen toteutus Taulukko 4.1: YSOLO-taksonomia on lähteissä Yrjönsuuri (1990, 1994) esitetty muunnos SOLO-taksonomiasta. Tässä tutkimuksessa luokittelua käytetään opiskelijoiden vastausten osoittaman kognitiivisen tason luokittelussa. YSOLO -taso Kuvaus toiminnasta Y0. Rakenteeton tieto Tiedon puuttuminen ja satunnainen vastaus. (SOLO-taso 1) Y1. Yksirakenteinen tieto Vastaukseen liittyy oppimisen kohteena olevan käsitteen ominaisuuden, matemaattisen rakenteen tai tehtävän ratkaisemiseen vaadittavan toiminnan osittainen ymmärtäminen. (SOLO-taso 2) Y2. Monirakenteinen tieto Sisältää oikean vastaustiedon. (SOLOtasot 35) E1 hahmottava ymmärrys Y2 Y1 Y0 suurempi ymmärrys E2 kvantitatiivinen ymmärrys Y2 Y1 Y0 Kuva 4.2: Empiirisen ymmärryksen luokittelu päätasojen E1 ja E2 ja niiden sisäisten YSOLO-tasojen mukaan manaikaisesti. Tätä voidaan mitata selvittämällä, kuinka pitkälle yksilöt ovat edenneet kummallakin ymmärtämisen tasolla. Päätasojen E1 ja E2 sisäisen hienorakenteen tutkimisessa hyödynnetään tässä tutkimuksessa SOLO-taksonomiaan (ks. luku 3.2.1) pohjautuvaa luokitusta. SOLO-taksonomian viisiportaisen luokituksen soveltaminen täydessä laajuudessaan on vaikeaa. Yrjönsuuri (1990, 1994) esittääkin luokituksesta yksinkertaisemman version, jossa on vain kolme tasoa. Tässä tutkimuksessa siitä käytetään nimeä YSOLO, missä kirjain Y viittaa muunnelman tekijän nimeen. YSOLO -taksonomia on esitetty taulukossa 4.1. Ymmärryksen luokittelua päävaiheisiin E1 ja E2 ja niiden sisäisiin tasoihin Y0Y2 esittelee kuva 4.2. Luvussa tarkastellussa matematiikan kolmen maailman teoriassa (Tall, 2008) sanalliset määritelmät, käsitteiden kuvailut ja mielikuvat toimivat linkkeinä empiiristen merkitysten muodostumisen vaiheeseen E1 (ks. kuva 4.3). Jäsentymisprosessin vaiheen E2 kysymys suureen mittaamisesta on puoles-
53 4.6. Empiirisen ymmärryksen mittari 41 aksiomaattiset geometriat aksiomaattisformaali käsitteiden määritelmät, formaali todistus formaalit aksiomaatiset järjestelmät määritelmiin perustuvat formaalit objektit epäeuklidisten geometrioiden ilmentymät euklidinen todistus kuvaajan paikallinen suoruus funktion paikallinen lineaarisuus raja-arvo tuttuihin objekteihin perustuvat määritelmät lukuarvon määritys Empiirinen käsitteenmuodostus Empiirinen todellisuus kvantifiointi E2 E1 empiirinen merkitys määritelmä konstruktio kuvailu havainto matemaattinen käsite ilmentymien ja symbolien sekoittuminen algebra aritmetiikka numero proseptuaalissymbolinen lukumäärän laskeminen matemaattinen kognitiivinen kehitys käsitteellisilmentynyt Monet kaavion termit ovat kirjoittajan omia suomennoksia, koska tiedossa ei ole vakiintunutta terminologiaa. Kuva 4.3: Empiirisen käsitteenmuodostuksen vaiheiden kytkeytyminen matematiikan kolmen maailman teoriaan. Kuva piirretty ja suomennettu lähteen (Tall, 2008) mukaan. Empiiriset merkitykset ja siihen liittyvät yhteydet ovat tutkijan tekemiä lisäyksiä. E1 tarkoittaa kvalitatiivisen vaiheen ja E2 kvantitatiivisen vaiheen empiiristä jäsentymistä. taan matemaattiselta kannalta numeerisen laskennan hallitsemiseen liittyvä kysymys. Erityisesti divergenssin ja roottorin tapauksessa se tarkoittaa niiden symbolisissa lausekkeissa esiintyvien osittaisderivaattojen määrityksen hallitsemista. Tämä määritys voidaan tehdä joko kokeellisesti mittaamalla tarkasteltavan vektorisuureen muuttumista tai se voidaan tehdä kuvaajasta määrittämällä aivan kuten yhden muuttujan funktion derivaatan tapauksessa. Kyseessä on vastaava kvantiointiaskel kuin esimerkiksi määritellessä suuretta nopeus. Tämän tason jäsentelyssä toimitaan puolestaan kolmen maailman teorian mukaisessa symbolien maailmassa, johon numeerinen laskenta kuuluu (ks. kuva 4.3).
54
55 Luku 5 Opetuskokeilu 5.1 Mapu -kurssien yleisiä piirteitä Tutkimuksen opetuskokeilu suoritettiin Helsingin yliopiston Fysiikan laitoksella syyslukukaudella 2007 pidetyn Matemaattiset apuneuvot II kurssin aikana. Matemaattiset apuneuvot (lyhyesti Mapu) on teoreettisen fysiikan oppialaan kuuluva kaksiosainen kurssisarja, joka käsittelee kaikilla fysiikan aloilla tarvittavaa perusmatematiikkaa. Uusia fysiikan opiskelijoita suositellaan suorittamaan Mapu -kurssit heti ensimmäisenä opiskelusyksynä. Mapu I pidettiin aikavälillä ja se sisälsi 14 kaksoistunnin mittaista luentoa eli yhteensä 28 luentotuntia. Harjoitustilaisuuksia kurssiin kuului yhteensä 26 tuntia (4 tuntia viikossa, ensimmäisellä viikolla vain 2 tuntia). Mapu II alkoi väliviikon jälkeen ja sijoittui aikavälille sisältäen 26 luentotuntia ja 26 tuntia harjoituksia. Vuonna 2007 Mapu I kurssikokeeseen osallistui 118 opiskelijaa ja Mapu II kokeeseen 97 opiskelijaa. Mapu -kurssin ja opetuskokeilun ajoitusta on esitetty kuvassa 5.1. Tutkija oli itse täydessä vastuussa luentojen pitämisestä sekä luentomateriaalin, harjoitustehtävien ja kokeen laatimisesta. Kotiharjoitusten tarkastaminen ja sekä harjoitustilaisuuksien pitäminen oli 7 suomenkielisen, yhden englanninkielisen ja yhden ruotsinkielisen assistentin vastuulla. Osa assistenteista oli joko edistyneitä fysiikan tai teoreettisen fysiikan perustutkintoopiskelijoita osa jo väitöskirjaa tekeviä jatko-opiskelijoita. Harjoitukset olivat kurssilla korostuneessa roolissa. Niistä saadut pisteet vaikuttivat arvosanaan yhden kolmasosan painolla. Harjoituksia oli kahta tyyppiä. Kotiharjoitukset jätettiin assistenteille tarkastettavaksi viikoittain. Tehtävät käytiin ohjatusti läpi seuraavan viikon kotiharjoitustilaisuuksissa, joihin osallistuminen ei ollut pakollista harjoituspisteiden saamiseksi. Tehtäviin ei pääsääntöisesti jaettu mallivastauksia. Mapu I -kurssilla oli 6 ja Mapu II
56 44 LUKU 5. Opetuskokeilu Mapu I luento = 2 h 1 vko KOE Mapu II opetuskokeilu (6.12.) animaatiot: demonstraatio: 1, harjoitus 7 palautus KOE simulaatiot: 1,2 2 Kuva 5.1: Opetuskokeilun ajoittuminen vuoden 2007 Mapu -kurssilla, sekä havaintomenetelmien (animaatiot, demonstraatiot ja simulaatiot) sijoittuminen luennoille. Havaintomenetelmien numerointi vastaa kappaleessa 5.3 ja liitteissä B.1 ja B.2 käytettyä numerointia. -kurssilla 7 kotiharjoitusta. Näiden lisäksi Mapu II -kurssilla jaettiin vapaaehtoinen lisäharjoitustehtävä usean muuttujan funktioiden dierentiaali- ja integraalilaskennasta. Toinen harjoitusmuoto olivat nk. ex tempore -harjoitukset, joihin oli osallistuttava henkilökohtaisesti saadakseen harjoituspisteitä. Näissä harjoituksissa tehtävät jaettiin vasta itse harjoitustilaisuudessa. Tehtävien ratkomiseen oli käytössä aikaa noin tunti, jonka jälkeen tehtävät käytiin ohjatusti läpi. Ex tempore -harjoituksissa oli sallittua ratkoa tehtäviä ryhmissä. Myös harjoitusta pitävältä assistentilta oli lupa kysyä apua. Ryhmätyötä pyrittiin jopa aktiivisesti kannustamaan kurssin alussa, mutta osoittautui, että osa opiskelijoista halusi tästä huolimatta ratkoa tehtäviä itsenäisesti. Ex tempore -harjoituksia oli 7 kertaa molemmilla kursseilla. Luennoitsija lähetti assistenteille viikoittain harjoitustehtävät ja tehtävien oikeat vastaukset kommentteineen. Kommenteilla luennoitsija pyrki ohjaamaan assistenttien työtä ja tuomaan esiin, mikä harjoitustehtävissä oli opetuksellisena ideana ja mihin harjoituksissa tulisi kiinnittää huomiota. Viikoittain yksi harjoitusassistentti korjasi vuorollaan kaikki palautetut harjoitustehtävät. Tällä pyrittiin takaamaan pisteytyksen yhdenmukaisuus kunkin harjoituskerran arvostelussa. Esimerkkejä harjoitustehtävistä löytyy liitteestä D. Kurssilla pidettiin lisäksi viikoittain ns. laskupajaa, jonka tarkoitus oli tukea opiskelijoita kotiharjoitustehtävien tekemisessä. Tilaisuudessa oli paikalla harjoitusassistentti näyttämässä harjoitustehtävien kaltaisia esimerkkejä ja vastaamassa opiskelijoiden kysymyksiin. Tutkija ei itse kontrolloinut millään
57 5.2. Opetuskokeilu 45 tavoin laskupajoissa käsiteltävien asioiden sisältöä. Kurssimateriaalina käytettiin luennoitsijan itse valmistelemia luentomuistiinpanoja. Kaikki muistiinpanot olivat saatavilla myös digitaalisessa muodossa kurssin kotisivuilta. Kurssin oheislukemistoksi suositeltiin erityisesti kirjaa Croft et al. (2001), mutta myös Adamsin Calculus -kirjaan (Adams, 2003) kehotettiin tutustumaan. Kumpaakaan ei kuitenkaan käytetty virallisena kurssimateriaalina. Myös muusta oheislukemistosta oli informoitu kurssin alussa. 5.2 Opetuskokeilu Opetusidean taustaa Tämän kirjoittaja on itse visuaalinen oppija, jolle kaaviot, kuvat ja kuvaajat aukeavat helposti ja joka käyttää mielikuvia ja analogioita oppimiskeinona. Tällöin spontaanisti syntyvät mielikuva-animaatiot tukevat uuden asian oppimista ja opettaessakin tämä ajattelutapa ohjaa asian esittämistä uusista näkökulmista. Tietokoneiden ja dataprojektorien tultua luokkiin ja luentosaleihin oli johdonmukaista alkaa miettiä tarjotun teknologian käyttöä opetuksen apuna. Vuonna 2004 kirjoittaja laati Maple-ohjelmalla yksinkertaisia animaatioita funktion kuvaajista, derivoinnista ja integroinnista sekä staattisen kuvasarjan lineaarikuvauksista. Vuonna 2005 hän käytti ensimmäisen kerran luennoilla interaktiivista kuvaajien piirto-ohjelmaa sekä ennalta suunniteltuihin että spontaaneihin demonstraatioihin. Kokemuksen kasvaessa ja alun virheistä oppineena kirjoittaja oli halukas edelleen lisäämään opetusteknologian ja kehittämiensä hahmottavien demonstraatioiden käyttöä vuoden 2007 Matemaattiset apuneuvot -kurssilla. Tästä muodostui opetusidea, joka toimi pohjana tutkimukselle ja siihen kuuluvalle opetuskokeilulle. Opetustavoitteeksi asetettiin tukea matemaattisten käsitteiden empiiristen merkitysten hahmottamista. Tämä oli tarkoitus toteuttaa sekä tietokoneella esitettävien visualisointien ja demonstraatioiden avulla että perinteisin apuvälinein (liitutaulu, piirtoheitin, konkreettiset välineet). Tavoite toimi taustavaikuttajana koko Mapu -kurssien toteutukselle. Opetusidean tieteelliseksi testaamiseksi oli kuitenkin tarpeen rajata pienempi osa kurssista varsinaiseksi opetuskokeiluksi. Opiskelijapalautteen ja käytännön opetuskokemuksen pohjalta kirjoittaja tietää, että vektorianalyysiä pidetään yhtenä vaikeimmista asioista Mapu II -kurssilla. Tutkimus täsmentyi vielä erityisesti divergenssin ja roottorin käsitteiden opettamiseen. Opetuskokeilun suunnittelu oli enemmänkin intuitiivista kuin tarkkojen periaatteiden mukaan tapahtuvaa toimintaa. Vaikka suunnittelu olikin intuitii-
58 46 LUKU 5. Opetuskokeilu vista oli kaikella opetustoiminnalla opetuksellisia tavoitteita. Seuraavissa kappaleissa esitellään opetuskokeilun etenemistä ja sitä varten kehitettyjä uusia opetusmateriaaleja sekä näiden taustalla vallinneita opetuksellisia tavoitteita Käytännön toteutus Useina aiempina vuosina vektorianalyysi on ajoittunut Mapu II -kurssin loppuun. Tällöin on vaarana, että kiireen takia asiat joudutaan käymään nopeasti läpi, eikä opiskelijoille jää omaksumiseen riittävästi aikaa. Koska opiskelijapalautteen perusteella matriisilaskenta koetaan helposti omaksuttavaksi ja se on mahdollista opettaa irrallisena kokonaisuutena, oli luonnollista vaihtaa vektorianalyysin ja matriisilaskennan keskinäistä järjestystä. Tämä muutos toteutettiin jo vuoden 2005 kurssilla. Sen lisäksi, että järjestely poisti kiireen vektorianalyysin osuudesta, teki se myös mahdolliseksi laajemman aihepiirin käsittelyn harjoitustehtävissä. Vuoteen 2007 mennessä muutettu järjestys oli jo vakiintunut ja hyväksi havaittu. Vektorianalyysin sisäinen etenemisjärjestys on seurannut tutkijan pitämillä kursseilla pääosin luentomuistiinpanoissa lähteenä käytettyjä kirjoja Honkonen et al. (2003); Lahtinen ja Pehkonen (1994). Sama järjestys on myös kurssin oheislukemistona käytetyssä kirjassa Croft et al. (2001), vaikka sitä ei varsinaisena lähteenä ole käytettykään. Tälle käsittelyjärjestykselle on ominaista, että gradientti, divergenssi ja roottori opetetaan ensin symbolisina lausekkeina dierentiaalioperaattori nablan avulla. 1 Tämän jälkeen käsitteiden merkitystä pyritään tulkitsemaan dierentiaalisilla tarkasteluilla. Seuraavaksi käydään läpi viiva-, pinta-, vuo- ja tilavuusintegraalit. Lopuksi divergenssi ja vuointegraali kytketään yhteen Gaussin lauseella ja roottori ja kiertämäintegraali yhdistetään Stokesin lauseella. Tämä etenemisjärjestys päätettiin säilyttää opetuskokeilussa pääosin muuttumattomana pieniä integraaliesimerkkien uudelleen järjestelyjä lukuun ottamatta. Suurempien muutosten tekeminen olisi vaatinut muistiinpanojen uudelleenkirjoittamista ja olisi siten vienyt aikaa varsinaisten tutkittavien opetusideoiden valmistelulta. Opetusjärjestyksen suunnittelua tarkastellaan tutkimusongelmaan C liittyen kappaleessa 5.4. Mapu II -kurssin sisältö ja etenemisjärjestys on esitetty taulukossa 5.1. Tarkempi kuvaus opetuskokeilun luentojen sisällöstä on liitteessä B.1. Koska Mapu II -kurssi rakentuu Mapu I -kurssilla opittujen asioiden pohjalta, on myös Mapu I -kurssin luentorunko esitetty liitteessä olevassa taulukossa A.1. Kaikki 1 Vektorianalyysin opetusta eri oppikirjoissa on esitelty luvussa 3.6 olevassa taulukossa 3.4.
59 5.2. Opetuskokeilu 47 Taulukko 5.1: Mapu II -kurssin luentorunko. Opetuskokeiluun liittyvät aihepiirit on esitetty varjostettuina. viikko päivä sisältö 44 Ti johdatus mapu II sisältöön, integraalien sovelluksia, yhden muuttujan avaruusintegraaleja To kompleksiluvut 45 Ti 1. kertaluvun tavalliset dierentiaaliyhtälöt, 2. kertaluvun dierentiaaliyhtälöt To dierentiaaliyhtälöt, vektoreiden lineaarinen riippuvuus 46 Ti yleiset vektoriavaruudet, ortogonalisointi, osittaisderivaatta To nabla, gradientti, suunnattu derivaatta, divergenssi, roottori 47 Ti osittaisderivaattojen fys. tulkinta, Taylor-kehitelmä, viivaintegraali To viivaintegraali, skalaaripotentiaali, pintaintegraali, tilavuusintegraali 48 Ti pinta- ja tilavuusintegraalit, käyräviivaiset koordinaatistot To vuointegraali, Gaussin ja Stokesin lause, skalaari- ja vektoripotentiaalit, Helmholtzin teoreema, Maxwellin yhtälöt, matriisilaskennan alkeita 49 Ti determinantti, käänteismatriisi, ominaisarvot, jakobiaanien ja lineaarikuvausten yhteys, rotaatiomatriisit 3-ulotteisesssa avaruudessa (To Itsenäisyyspäivä, ei luentoa) 50 Ti similariteettimuunnokset, matriisin diagonalisointi To kertausta ja aihepiirin kokoamista opetuskokeiluun liittyvät luennot nauhoitettiin ja luentojen jälkeen kirjattiin huomioita opetuspäiväkirjaan. Näitä käytettiin materiaalina tutkimuksessa. Yleisenä piirteenä tutkijan opettamilla Mapu -kursseilla on käytetty paljon kerrottua empiriaa ja analogioita kiinnitettäessä opetettuja asioita fysikaalisiin sovellustilanteisiin. Luentojen teoria on esitetty pääosin kalvojen, tietokonedokumenttien ja dokumenttiprojektorin avulla. Esimerkkejä ja selventäviä huomautuksia on tehty liitu- ja tussitauluille. Hahmottavia demonstraatioita konkreettisilla havaintovälineillä on myös ollut käytössä. Esimerkkinä tästä ovat vektorilaskennan havainnollistamisen tukena käytetyt metrin pituiset alumiiniputket. Opetuksessa on tarkasteltu käsitteitä sekä symboliselta puolelta, että hahmottavasta näkökulmasta. Sen sijaan numeerista laskentaa ei ole kurssilla juurikaan käsitelty. Tässä mielessä opetus ei siis vastaa täysin matematiikan kolmen maailman teorian mukaisia opetussuosituksia Lähtötasotesti Matemaattiset apuneuvot I -kurssin opiskelijoiden lukiotaustaa ja lähtötasoa selvitettiin kurssin ensimmäisellä luennolla lähtötasotestillä. Testillä saatua tietoa käytettiin pohdittaessa kurssin tavoitteiden realistisuutta ja etsittäessä
60 48 LUKU 5. Opetuskokeilu mahdollisia syitä oppimisongelmille ja virhekäsityksille. Koska opetuskokeilu ajoittui vasta Mapu II -kurssin keskivaiheille, ei Mapu I -kurssin alussa tehtyä lähtötasotestiä katsottu kuitenkaan kovin merkittäväksi tutkimuksen kannalta olihan Mapu II -kurssin alkaessa jo tuoretta tietoa opiskelijoiden osaamisesta Mapu I -kurssin osalta. Lähtötasotestin oleellisimmat kysymykset koskivat dierentiaalikäsitteen empiiristä ristiriitaa 2 ja derivaatan kokeellista määrittämistä. Testin suunnittelua ja analyysiä on käsitelty tarkemmin tutkijan laudaturtutkielmassa (Pasanen, 2008). Seuraavassa esitellään lyhyesti opetuskokeilun näkökulmasta tärkeimmät tulokset. Lähtötasotestiin palautettiin noin 130 vastausta, joista 50 valittiin analysoitavaksi satunnaisotannalla. Testin perusteella suurin osa kurssilaisista oli aloittanut yliopisto-opintonsa syksyllä 2007 ja Matemaattiset apuneuvot oli yksi heidän ensimmäisistä yliopistokursseistaan. Pääsääntöisesti opiskelijat olivat kirjoittaneet ylioppilaaksi vuoden sisällä opintojensa aloituksesta. Suoritettujen matematiikan kurssien keskiarvo oli 13 kurssia ja fysiikan kurssien keskiarvo lähes 9 kurssia. Suurin osa kurssilaisista oli siten suorittanut kaikki opetussuunnitelmaan kuuluvat pakolliset ja syventävät kurssit (Opetushallitus, 1994) niin matematiikassa kuin fysiikassa ja osa oli käynyt tämän lisäksi koulukohtaisia kursseja. Analysoitujen 50 vastauksen joukossa oli vain 4 opiskelijaa, joilla oli pohjana matematiikan lyhyt oppimäärä. Testin tärkein kysymys koski derivaatan empiiristä merkitystä: Eräässä fysikaalisessa ilmiössä suure A riippuu suureen B arvosta. Halutaan määrittää kokeellisesti suureen A derivaatta suureen B suhteen siinä tilanteessa, kun suureen B arvo on B 0. Kerro lyhyesti, mitkä mittaukset on tehtävä, jotta derivaatta saadaan määritettyä. Mitä kyseinen derivaatta kuvaa? Vain 28 % vastauksista osoitti derivaatan empiirisen merkityksen hyvää tai kohtalaista ymmärrystä. 38 % perusteluista oli epämääräisiä tai puutteellisia ja peräti 34 % ei vastannut lainkaan kysymykseen. Tulos oli yllättävä. Tästä syystä derivaatan käsitteellisen hahmotuksen tukemiseen käytettiin paljon aikaa Mapu I-kurssin luennoilla ja harjoituksissa. 2 Dierentiaalikäsite pitää sisällään rajankäyntiprosessin, johon liittyy fysikaalisen todellisuuden ja matemaattisen käsitteen välinen ristiriita. Luonnossa ei ole mielivaltaisen pieniä mitattavia suureita (Kurki-Suonio ja Kurki-Suonio, 1998, s ).
61 5.3. Opetuskokeilussa käytetyt havaintomenetelmät Opetuskokeilun harjoitustehtävät Opetuskokeilun aihepiiriin liittyviä vektorianalyysin tehtäviä oli yhteensä viidessä Mapu II -kurssin harjoituksessa. Osa tehtävistä on useita vuosia Mapukursseilla käytettyjä tehtäviä, osa uudempia tutkijan kehittämiä tehtäviä. Ne on laadittu kurssin yleiset tavoitteet silmällä pitäen ja niissä on mukana myös konkreettista hahmotusta kehittäviä tehtäviä. Harjoitustehtäviä esitellään tarkemmin liitteessä D. Opetuskokeiluun liittyi myös yksi täysin uusi käsitteitä opettava harjoitustehtävä (ks. liite D.4). Teoriaosassa esiteltyjen aiempien tutkimusten mukaan derivaatan oppimista voidaan tukea käsittelemällä derivaattaa konkreettisia piirteitä omaavana objektina erilaisia representaatioita käyttäen ja niiden ominaisuuksia tutkien (Hähkiöniemi, 2006). Tämän tiedon pohjalta laadittiin opetuskokeiluun uudenlainen harjoitustehtävä, jossa opiskelija joutuu symbolisten laskuoperaatioiden sijaan tarkastelemaan lähteisyyttä ja pyörteisyyttä vektorikenttään liittyvinä konkreettisina kvalitatiivisina ominaisuuksina. Tällöin opiskelija työskentelee matematiikan kolmen maailman teorian mukaisessa ilmentymien maailmassa (ks. kpl 3.1.3). Teorian mukaan tämän pitäisi tukea lähteisyyden ja pyörteisyyden käsitteiden hahmottavaa ymmärtämistä. Tehtävän kysymykset oli muotoiltu avoimiksi, jotta ne kannustaisivat opiskelijoita pohtimaan kysymyksiä monelta eri kannalta. Harjoituksen palautti 84% kokeeseen osallistuneista opiskelijoista. Sen vastausten analyysi on tehty laudaturtutkielmassa (Pasanen, 2008). Tässä tutkimuksessa harjoitustehtävästä saatua materiaalia käytetään tukena analysoitaessa opiskelijoiden haastatteluja. 5.3 Opetuskokeilussa käytetyt havaintomenetelmät Teoriaosassa tarkasteltiin käsitteiden empiiristen merkitysten rakentumisprosessia (kpl 3.3). Empiiriset merkitykset rakentuvat matematiikan kolmen maailman teorian mukaisen ilmentymien maailman kautta. Ilmentymät voivat olla konkreettisia fysikaalisia hahmoja tai mielikuvia. Opetuskokeilun aiheena olevan vektorianalyysin käsitteet ovat luonnostaan sellaisia, että niitä voidaan havainnollistaa hyvin konkreettisina objekteina. Koska kyse on 2- ja 3-ulotteisista pinnoista ja kappaleista avaruudessa on niiden tarkan muodon esittämiseksi voitava tarkastella objekteja eri suunnista. Tutkimusten mukaan animaatiot ja muut visualisaatiot soveltuvat juuri tällaisiin esityksiin, kuten kappaleessa 3.4 todetaan. Animaatioita, visualisaatioita ja havainnollistavaa demonstraa-
62 50 LUKU 5. Opetuskokeilu tiota käytettiinkin opetuskokeilussa varsin paljon havaintomenetelminä. Runsaiden visualisaatioiden toivottiin kiinnittävän opiskelijoiden huomiota matemaattisten kaavojen sijasta merkitysten pohtimiseen. Aihepiiri on koettu vaikeaksi ja opiskelijalta saattaa puuttua uskallusta lähteä ajattelemaan käsitteitä tarkemmin. Normaalisti ne saatetaan nähdä abstrakteina matemaattisina derivointioperaatioina vailla kunnollista kiinnitystä havaittaviin käsitteisiin. Esiin tulevat uudet käsitteet pyrittiin kytkemään konkreettisiin ja tuttuihin käsitteisiin. Esimerkiksi kahden muuttujan funktioiden esitystä samanarvon käyrillä verrattiin maastokarttoihin ja meteorologian isobaareihin. Esitettäessä maastoproileja kolmiulotteisina kuvina, puhuttiin konkreettisesti mäistä ja laaksoista. Gradientin merkitystä esitettäessä pohdittiin kiipeilijän tai laskettelijan liikkumista vuoristossa. Opetuskokeilussa tutkittavat uudet havaintomenetelmät perustuivat animaatioiden (10 erilaista) ja simulaatioiden käyttöön sekä konkreettiseen havainnollistukseen. Näiden osuus koko vektorianalyysiin opetusjaksoon käytetystä luentoajasta oli noin 16%. Tässä tutkimuksessa on rajoituttu tarkastelemaan divergenssin ja roottorein käsitteitä, joiden opetukseen liittyvät seuraavat opetustuokiot: Animaatiot 8-10 Demonstraatio Java-demonstraatiot 1-2 Opetustuokioiden sijoittumien opetuskokeilun aikana näkyy kuvassa 5.1. Seuraavassa esitellään näitä opetustuokioita tarkemmin Animaatiot Animaatio -nimikkeen alle kuuluvat sekä varsinaiset tietokoneanimaatiot että pienemmästä kuvamäärästä koostuvat vaiheittaiset kuvasarjat, joiden esitysnopeutta säädetään manuaalisesti. Opetuskokeilussa käytetyt 10 animaatiota olivat kaikki tutkijan itse laatimia. Animaatioiden esitys luennoilla tapahtui siten, että ensimmäistä kertaa animaatiota näytettäessä se pysäytettiin ennalta määritellyissä kohdissa, jolloin kerrottiin, mihin animaatiossa tulee kiinnittää huomiota. Kun animaatio oli katsottu kerran läpi tällä tavalla, näytettiin se vähintään kerran uudestaan katkeamattomana esityksenä. Seuraavassa esitellään kaikkien näytettyjen animaatioiden opetuksellinen tavoite ja niiden suunnitteluun ja laadintaan liittyneitä näkökohtia.
63 5.3. Opetuskokeilussa käytetyt havaintomenetelmät 51 Animaatioiden suunnittelu ja laadinta Usean muuttujan funktiot ja vektorikentät ovat opiskelijoille uusia aihepiirejä, joiden omaksuminen vaatii aikaa. Jotta niiden konkreettinen ja visuaalinen hahmottaminen kehittyisi, on tällaista ajattelua perusteltua tukea määrätietoisesti eri suunnilta. Animaatioita päätettiin käyttää heti vektorianalyysin alusta lähtien. Aluksi niitä käytettiin funktioiden esittämiseen pintoina ja osittaisderivaatan käsitteen konkretisointiin. Samalla myös tutkijan itsensä animointitaidot kehittyivät. Yleisperiaatteena animaatioiden laadinnassa oli pyrkimys luoda linkkejä symbolisen ja konkreettisen esityksen maailmojen välillä. Tähän kuului muun muassa animaatioiden kanssa rinnakkaisesti tehdyt symboliset laskutoimitukset, joiden tuloksia verrattiin animaatiossa näkyviin piirteisiin. Animaatioita päätettiin kehittää sellaisista aiheista, jotka ovat vaikeasti havainnollistettavia muilla keinoin. Animaatiot laadittiin Blender-ohjelmalla ( joka on ilmainen avoimeen lähdekoodiin perustuva kolmiulotteinen mallinnus- ja animaatio-ohjelma. Seuraavassa kuvataan tutkittavaan aiheeseen liittyvien animaatioiden 810 sisältöä. Animaatioide 17 esittelyt löytyvät liitteestä B.2. Animaatiot 89 Divergenssin opettamista varten laadittiin kaksi animaatiota. Animaatioiden suunnittelun lähtökohtana oli tavoite opettaa divergenssin määritystä Gaussin lauseeseen perustuen määrittämällä vektorikentän vuota suljetun pinnan läpi. Katsottiin, että helpoiten hahmotettava tilanne on hiukkasvirtaus suorakulmaisen särmiön tahkojen läpi. Ensimmäisessä animaatiossa esiintyi vaakasuunnassa tapahtuva hiukkavirtaus. Virtaus kulki sisään yhden särmiön tahkon läpi ja poistui vastapäisen tahkon läpi. Koska kokonaisvuo oli nolla, pääteltiin tästä, että lähteisyys särmiön sisällä on nolla särmiön koon määräämällä mittaustarkkuudella. Ajatuskokeena esitettiin, että särmiön kokoa pienentämällä saadaan yhä tarkempi arvio vektorikentän lähteisyydestä särmiön sisäpuolella. Symbolisella tarkastelulla näytettiin, että divergenssi voidaan lausua särmiön läpi lasketun kokonaisvuon tiheyden raja-arvona. Toisessa animaatiossa tarkasteltavana oli pistemäisen lähteen synnyttämä hiukkasvirtaus. Mittaussärmiö oli ensin sijoitettu lähteen ympärille, jolloin voidaan todeta, että vuo sen tahkojen läpi on positiivinen. Tämä on sopusoinnussa sen kanssa, että särmiön sisällä on positiivinen lähde. Kun särmiö siirretään lähteen ulkopuolelle havaitaan, että sisääntuleva ja ulosvirtaava vuo ovat yhtä suuria. Kokonaisvuo ja divergenssin likiarvo
64 52 LUKU 5. Opetuskokeilu on näin ollen nolla. Animaation opetuksellinen tavoite oli opettaa Gaussin lausetta ja divergenssin käsitettä mikroskooppisesta ja makroskooppisesta näkökulmasta. Erityisesti animaatiolla pyrittiin korostamaan, että divergenssi on pisteeseen liittyvä käsite. Tätä animaatiota esitellään kuvassa 5.2. Animaatio 10 Vektorianalyysin opetuskokeilun viimeiseksi demonstraatioksi otettiin roottorin fysikaalinen merkitys sähkömagnetismissa. Esimerkiksi päätettiin ottaa Faradayn induktiolaki, sillä se on lukiokurssista opiskelijoille tuttu ilmiö. Matemaattisesti laki voidaan esittää muodossa E = B t, (5.1) missä B on magneettivuon tiheys, t aika ja E sähkökentän voimakkuus. Kuvasarjana laadittava demonstraatio suunniteltiin esitettäväksi vaiheittain siten, että opiskelijoilla on ennen seuraavaa kuvaa aikaa pohtia luennoitsijan esittämiä kysymyksiä. Päätettiin ottaa esimerkiksi homogeeninen magneettikenttä, jonka voimakkuus heikkenee. Kuvasarjan ensimmäisessä vaiheessa esitettiin magneettikentän heikkenemistä, jonka pohjalta voidaan päätellä yhtälön 5.1 oikealla puolella olevan derivaattavektorin suunta. Koska lain mukaan tämä on yhtä suuri kuin vasemmalla oleva sähkökentän pyörteisyys, voidaan syntyvän sähkökentän muoto päätellä tunnetusta pyörteisyysvektorista oikean käden säännöllä. Kuvasarjaa esitellään kuvassa Styrox-pallo-demonstraatio Styrox-pallo-demonstraatio oli konkreettinen havainnollistus, jolla pyrittiin auttamaan opiskelijoita sopivien mielikuvamallien muodostamisessa. Oikealla konkreettisella kappaleella ihmisen esittämänä sen toivottiin jäävän elävämpänä mieleen kuin tietokoneen ruudulta näytettynä. Teoriaosassa (2.4.2) kerrottiin, että pyörteisyyden konkreettisena makroskooppisena mittarina voidaan käyttää testipalloa tai siipiratasta, jos vektorikentän ajatellaan esittävän ainevirtausta. Tämä on tärkeä empiirinen yhteys, jonka ymmärtäminen auttaa pyörteisyyden hahmottamista. Ymmärtämisen tueksi kehitettiin konkreettinen demonstraatio. Havainnollistuksen tarkoituksena oli esittää kuviteltua koetilanteita, jonka avulla opiskelija voi luoda idealisoidun mallin käsitteen konkreettisesta merkityksestä.
65 5.3. Opetuskokeilussa käytetyt havaintomenetelmät 53 Kuva 5.2: Kuvasarja animaatiosta, jolla havainnollistettiin kokonaisvuota sellaisen särmiön tahkojen läpi, joka sisältää hiukkaslähteen (kuva 3, vuo >0) ja tilanteessa, jossa lähde sijaitsee särmiön ulkopuolella (kuva 4, vuo = 0). Kuva 5.3: Kuvasarja, jolla havainnollistettiin Faradayn lakia. Muuttuva magneettikenttä indusoi pyörteisen sähkökentän. Vektorianalyysin termein tämä tarkoittaa, että magneettikentän muutosnopeusvektori on yhtä suuri kuin sähkökentän pyörteisyysvektori. Pyörteisyysvektorista voidaan päätellä syntyvän pyörteisen sähkökentän suunta oikean käden säännöllä.
66 54 LUKU 5. Opetuskokeilu Kuva 5.4: Vektorikentän pyörteisyyden kokeellista mittaamista havainnollistettiin ajatuskokeella, jossa käytetään virtauskenttään asetettavaa testipalloa. Ajatuskoetta elävöitettiin raidoitetulla styrox-pallolla, jonka halkaisija oli noin 10 cm. Pyörteisyysdetektorina käytettiin halkaisijaltaan 10 cm mittaista styroxpalloa (ks. kuva 5.4). Pyörimisen havaitsemiseksi palloon piirrettiin tussilla raitoja. Pallon läpi työnnettiin puutikku, jonka avulla sitä oli helppo pidellä ja joka muodosti pallon pyörimisakselin. Piirtoheitinkalvolle oli tulostettu laminaarista vektorikenttää F = yi kuvaavia nuolia. Kyseessä on kenttä, joka on kaikkialla x-akselin suuntainen, mutta voimistuu positiivisen y-akselin suunnassa. Vektorikentän kuva heijastettiin valkokankaalle. Testipalloa pideltiin valkokankaan edessä siten, että sen akseli oli kohtisuorassa kangasta vastaan. Palloa alettiin pyörittää akselinsa ympäri ikään kuin se olisi vektorikentän kaltaisessa virtauskentässä. Kerrottiin, että pallon pyöriminen indikoi vektorikentän pyörteisyyttä ja pyörteisyysvektorin suunta saadaan oikean käden säännöllä pallon pyörimisestä. Tämä tapahtuu asettamalla oikean käden koukistetut sormet osoittamaan pallon pyörimissuuntaa. Pystyyn nostettu peukalo osoittaa tällöin pyörteisyysvektorin suuntaan. Vastaavanlaista oikean käden sääntöä oli käsitelty aiemmin jo vektorilaskennan osuudessa ristitulon yhteydessä Java-simulaatiot Java-demonstraatioiden ja havainnollistusten opetuksellinen tarkoitus oli demonstroida erilaisia konkreettisia tai helposti kuviteltavia menetelmiä, joilla voidaan hahmottaa divergenssin ja roottorin fysikaalista merkitystä. Javaohjelmat ovat web-sivujen kautta ladattavia java-kielellä toteutettuja yleensä interaktiivisia demonstraatio- ja simulaatio-ohjelmia. Opetuskokeilussa käytet-
67 5.3. Opetuskokeilussa käytetyt havaintomenetelmät 55 tiin Paul Falstadin laatimaa vektorikenttiä havainnollistavaa java-ohjelmaa 3. Esimerkkikuvia ohjelmasta on kuvassa 5.5. Ohjelma on interaktiivinen, mikä tarjoaa mahdollisuuden ohjata simulaation kulkua. Tversky et al. (2002) mainitsee juuri interaktiivisuuden yhtenä keinona parantaa animaatioiden opetustuloksia. Ohjelmalla voidaan tarkastella joko valmiiksi määriteltyjä tai käyttäjän itse syöttämiä kaksiulotteisia vektorikenttiä. Vektorikentän muotoa havainnollistetaan suuntaa osoittavilla nuolilla ja voimakkuutta kuvaavalla värikoodauksella. Vaihtoehtoisesti esityksenä voidaan käyttää virtausviivoja. Konkreettisen hahmotuksen kannalta tärkein esitystapa on kuitenkin dynaaminen virtausmalli. Virtauksen dynaamiseen tutkimiseen on käytettävissä kaksi menetelmää, joista toinen soveltuu divergenssin tutkimiseen ja toinen roottorin tutkimiseen. Simulaatio 1 Divergenssiä tutkittaessa käytetään esityksenä hiukkasia kuvaavia pieniä ympyröitä. Ohjelma simuloi hiukkasten liikkumista vektorikentän esittämässä virtauskentässä. Tarkasteltiin virtauksen luonnetta kolmea erilaista ohjelmaan valmiiksi määriteltyä vektorikenttää käyttäen. Simulaatio 2 Roottorin demonstrointia varten ohjelmassa on mahdollisuus käyttää vektorikentän esityksessä rastin ( ) muotoisia pyörteisyysdetektoreita (eng. curl detector). Jos detektori pyörii, se kertoo virtauskentässä olevasta pyörteisyydestä. Tämä on vastaavanlainen konkretisoiva esitys kuin luennoilla esitetty konkreettinen styrox-pallo-havainnollistus. Ohjelmassa on myös toiminto, jolla voidaan laskea kuvaan vektorikentän numeerinen reitti-integraali kuvaan piirrettävän suorakulmion reunaa pitkin. Stokesin lauseen mukaisesti tämä reitti-integraali on yhteydessä vektorikentän pyörteisyyteen suorakulmion sisällä. Tämän demonstraation avulla voitiin näin kiinnittää pyörteisyyden mikroskooppinen ja makroskooppinen näkökulma toisiinsa. Pyörteisyyden likiarvo on vektorikentän suljetun reitti-integraalin ja reitin sisään jäävän pinta-alan suhdeluku. Tätä yhteyttä tarkasteltiin kolmen eri vektorikentän tapauksessa. Demonstraatiolla vahvistettiin muun muassa aiemmin teoreettisesti tarkasteltu ominaisuus, että suljetun reitti-integraalin ollessa nolla kenttä on pyörteetön, mikä ilmenee niin, että pyörteisyysdetektorit eivät pyöri. 3 Ohjelma on saatavilla ilmaiseksi osoitteesta
68 56 LUKU 5. Opetuskokeilu Kuva 5.5: Esimerkkikuvia laminaarisen virtauksen demonstroimisesta javaohjelmalla. Ylemmässä kuvassa vektorikentän suunta on esitetty nuolina ja kentän voimakkuus on koodattu värillä. Alempi kuva on pysäytyskuva animaatiosta, jossa rastien esittämät ns. pyörteisyysdetektorit liikkuvat vektorikentän mukana. Detektoreiden pyöriminen ilmaisee kentän pyörteisyyden.
69 5.4. Empiirisiä merkityksiä tukeva opetusjärjestys Empiirisiä merkityksiä tukeva opetusjärjestys Kuten aiemmin todettiin, seurasi kurssilla käytetty vektorianalyysin etenemisjärjestys pääpiirteiltään luentomateriaalien lähteenä käytettyjen teosten esitysjärjestystä. Opetuskokeilussa päätettiin keskittyä ainoastaan uusien havaintomenetelmien käyttöön, eikä koko aihepiirin opetusjärjestystä lähdetty muuttamaan opetuskokeilua varten. Aihepiirin opetuksen kehittämisen kannalta on kuitenkin relevanttia esittää kysymys, mikä on empiiristen merkitysten opettamisen kannalta hyvä opetusjärjestys?. Tämä kysymys on kirjattu tutkimusongelmaksi C.2. (ks. luku 4.4). Vastausta kysymykseen etsitään tässä aihepiiristä laaditun käsitekartan avulla. Käsittely rajataan tässä vain roottorin käsitteeseen. Divergenssin tapauksessa tarkastelu on hyvin samantapainen: Kiertämän käsitteen tilalla on vektorikentän vuo suljetun pinnan läpi ja mikroskooppista ja makroskooppista maailmaa yhdistämässä on Gaussin lause. Kuvassa 5.6 on esitetty roottoriin liittyvien käsitteiden rakentuminen makroskooppisesta ja mikroskooppisesta näkökulmasta. Mapu II -kurssilla roottori on opetettu perinteisesti mikroskooppisesta näkökulmasta. Tällöin pohjakäsitteeksi voidaan ottaa kentän mikroskooppinen kiertämä. Se on kuitenkin hankalasti konkretisoitava käsite, sillä mikroskooppinen kiertämä on idealisoitu innitesimaaliseen pinta-alkioon liittyvä käsite. Tämän etenemistavan mukaisissa oppikirjoissa käsitettä ei ole yleensä edes mainittu (ks. oppikirjakuvaukset kappaleesta 3.6). Esimerkiksi kirjassa Honkonen et al. (2003) dierentiaalista tarkastelua ei esitetä lainkaan, vaan roottori määritellään ensin dierentiaalioperaattorin nabla avulla. Sen jälkeen käsitettä perustellaan esimerkillä makroskooppisen jäykän kappaleen pyörimisestä. Fysikaalisen käsitteenmuodostuksen näkökulmasta tämä on nurinkurinen järjestys. Kvalitatiivisten merkitysten tulisi olla hahmotusprosessissa ennen suureen määrittelevää kvantitatiivista lauseketta (Kurki-Suonio ja Kurki-Suonio, 1998, s. 182). Toinen ongelma mikroskooppisesta määritelmästä lähtemisessä on, että fysikaalinen käsitteenmuodostus etenee tyypillisesti päinvastaiseen suuntaan makroskooppisesta mikroskooppiseen (Kurki-Suonio ja Kurki-Suonio, 1998, s ). Kun tällä tavalla etenevässä opetuksessa käsitellään Stokesin lausetta ja makroskooppisia vektorikentän integraalilausekkeita, saattaa esimerkiksi fysikaalisesti tärkeä kiertämän käsite jäädä vähälle huomiolle. Tästä ovat esimerkkinä kirjat Croft et al. (2001); Lahtinen ja Pehkonen (1994), joissa kiertämää ei ole mainittu erillisenä käsitteenä lainkaan.
70 58 LUKU 5. Opetuskokeilu Makroskooppinen näkökulma Mikroskooppinen näkökulma Kuva 5.6: Kaavio roottoriin liittyvien matemaattisten käsitteiden yhteyksistä
71 5.4. Empiirisiä merkityksiä tukeva opetusjärjestys 59 Käsitekartasta nähdään, että tämä aihepiiri on täysin mahdollista opettaa makroskooppisista käsitteistä lähtien, jolloin opetus voidaan kytkeä tuttuihin empiirisiin merkityksiin ja se noudattaa fysiikassa tavanomaista abstraktiosuuntaa makroskooppisesta mikroskooppiseen. Avainkäsitteeksi nousee tällöin vektorikentän kiertämä. Tutuin empiirinen lähtökohta kiertämälle on voiman kappaleeseen tekemä työ suljetulla reitillä. Muita tulkintoja on esimerkiksi meteorologiassa jatkuvan aineen virtauskentän vortisiteetti Holton (2004). Tässä järjestyksessä etenevässä opetuksessa tulee opettaa ensin käyrä- ja pintaintegraalit. Roottori määritellään kiertämätiheytenä suljetun reitin rajaamaan pinta-alaan nähden. Yhteys mikroskooppiseen muotoon tapahtuu Stokesin lauseen kautta ja tarkastelemalla kiertämätiheyden raja-arvoa, kun reitin rajaama pinta-ala lähestyy nollaa. Myös divergenssi voidaan opettaa tässä järjestyksessä makroskooppisen vuon tilavuustiheyden avulla. Mikroskooppiselle rajalle päästään tällöin Gaussin lauseen kautta. Makroskooppisesta mikroskooppiseen seuraavaa etenemisjärjestystä on käytetty meteorologian oppikirjassa Holton (2004) pyörteisyyden yhteydessä. Differentiaali- ja integraalilaskennan oppikirjassa Weir et al. (2008) opetetaan sekä divergenssin että roottorin käsitteet johdonmukaisesti makroskooppisen kiertämän pintatiheyden ja vuon tilavuustiheyden käsitteistä lähtien. Sähkömagnetismin oppikirjassa Kurki-Suonio ja Kurki-Suonio (1999) selostetaan seikkaperäisesti dierentiaali- ja integraalimuotoisten esitysten fysikaalisia merkityksiä, mutta käsittely ei kaikilta osin seuraa järjestystä makroskooppisesta mikroskooppiseen. Esimerkiksi divergenssi opetetaan ensimmäisen kerran innitesimaalista särmiötä tarkastellen.
72
73 Luku 6 Empiirisen ymmärryksen mittaaminen koetehtävällä Pääosa empiirisen ymmärryksen tutkimisesta tehtiin Mapu II -kurssin loppukokeessa olevalla koetehtävällä numero 4. Koetehtävän käyttöä puoltaa se, että kokeen vaikutus arvosanaan motivoi opiskelijoita vastaamaan koekysymykseen parhaan tietonsa mukaisesti. Näin mittarin voidaan katsoa antavan tietoa opiskelijoiden todellisesta ajattelusta koehetkellä. Kokeeseen laadittiin yksi numeerista laskentaa ja graasta päättelyä yhdistävä tehtävä (ks. liite E), josta saatavan aineiston pohjalta yritetään löytää vastaus tutkimuskysymyksiin B.2 ja B.3. Koetehtävässä (ks. liite E) on annettu taulukossa vektorikentän arvoja yhdeksässä eri pisteessä suorakulmion muotoisella alueella. Tehtävä on jaettu kolmeen osaan; a-kohta on yksinkertainen piirtotehtävä, jossa vektorikenttä hahmotellaan annettuun koordinaatistoon, b-kohdassa pyydetään laskemaan likiarvo vektorikentän divergenssille ja roottorille suorakulmion keskellä olevassa pisteessä, c-kohdassa tulee vertailla perustellen, ovatko b-kohdassa lasketut arvot sopusoinnussa a-kohdan kuvaajasta tehtyjen kvalitatiivisten päätelmien kanssa. Tehtävän b-kohdan vastaukset antavat materiaalia tutkimuskysymykseen B.3 ja c-kohta puolestaan kysymykseen B.2 vastaamiseksi. Tehtävästä tehtiin sellainen, ettei sitä voi ratkaista pelkän ulkoa opitun tiedon ja mekaanisten laskutoimitusten avulla, vaan tehtävä vaatisi aitoa ymmärtämistä ja soveltamista. Tehtävän c-kohdassa tarvittavaa numeerista osittaisderivointia ei opetettu kurssilla, eikä sitä käsitellä alan oppikirjoissakaan (ks. luku 3.6). Siirtyminen yhden muuttujan funktion derivaatasta osittaisderivaattaan on muodollisesti hyvin yksinkertainen ja opiskelijat ovat ymmärtäneet sen yleensä hyvin nopeasti symbolisella tasolla. Koska yhden muuttujan funktion derivaatan numeerista määritystä oli tarkasteltu esimerkeissä Mapu I -kurssilla, katsottiin, ettei asiaa tarvitse käsitellä enää osittaisderivoinnin yh-
74 62 LUKU 6. Empiirisen ymmärryksen mittaaminen koetehtävällä 6 5 Tehtäväpisteet Lukumäärä Kuva 6.1: Koetehtävän 4 pistejakauma. Mukana kaikki 97 kokeessa ollutta opiskelijaa. teydessä. Numeerisen osittaisderivoinnin ymmärtäminen koetehtävässä vaatii siten opiskelijalta kykyä yleistää aiemmin oppimaansa. 6.1 Koetehtävän analyysi Tehtävän c-kohdan osaaminen kertoo hahmottavasta ymmärtämisestä, joka on empiirisen ymmärryksen tasolla E1. (ks. luku 3.3.1). Vastaukset b-kohdan numeerista laskentaa vaativaan kysymykseen antavat puolestaan tietoa, ymmärtääkö opiskelija divergenssin ja roottorin mittaustekniseltä puolelta. Tämä osaaminen on luokittelussa empiirisen ymmärryksen tasolla E2. Osaamista näissä kummassakin osa-alueessa mitataan luonnolliseen tapaan koetehtävän pisteytyksellä. Tehtävän mallivastaus ja arvosteluperusteet on esitetty liitteessä E. Koetehtävä osoittautui yleisesti hyvin vaikeaksi. Lähes kaikki tehtävää yrittäneet osasivat kyllä piirtää a-kohdan kuvaajan oikein, mutta vastoin odotuksia, tehtävän b-kohta osoittautui erittäin vaikeaksi. C-kohta oli sen sijaan osattu paremmin. Tehtävän b-kohdan keskiarvo 1 oli 0,4 (02), c-kohdan keskiarvo 1,1 (03) ja kokonaispisteiden keskiarvo 2,4 (06) pistettä. Yhteensä 36 opiskelijaa (37 %) sai tehtävästä vain 1 pisteen. Tehtävän pistejakauma on esitetty kuvassa 6.1 ja koepisteiden havaintomatriisi liitteenä (liite E.1) Empiirisen ymmärryksen nelikenttä Koetehtävästä saatujen pisteiden painottuessa voimakkaasti 1 ja 2 pistettä saaneiden ryhmään, ei ole perusteltua tehdä kovin yksityiskohtaista luokittelua 1 Tässä käytetään keskiarvolle ja minimi- ja maksimiarvoille merkintää: k.a. (minmax).
75 6.1. Koetehtävän analyysi 63 b- ja c-kohtien osaamisesta. Suurin osa opiskelijoista tulee joka tapauksessa sijoittumaan luokittelun alimpiin ryhmiin. Myöskään tehtävän pisteytys ei ole kovin erotteleva. Näistä syistä on perusteltua käyttää empiirisen ymmärryksen tutkimisessa karkeaa luokittelua, jossa b- ja c-kohtien osaaminen jaetaan kahteen ryhmään: osaa, ei osaa ja ymmärtää, ei ymmärrä. Näin syntyy neljä erilaista b- ja c-kohtien keskinäistä osaamista kuvaavaa koepisteryhmää. Niitä on havainnollista esittää ristiintaulukoituna nelikentässä (Metsämuuronen, 2005). Nelikentästä saadaan hyvä käsitys siitä, miten kurssilaiset saavuttivat empiirisen ymmärryksen eri tasojen tavoitteita. Analyysin luotettavuuden varmistamiseksi on osaamisen luokittelussa syytä olla varovainen. Valitaan b-kohdassa ei osaa -ryhmäksi 01 pistettä saaneet suoritukset ja osaa -ryhmäksi vain täydet 2 pistettä saaneet. Vastaavasti c- kohdassa ymmärtää -ryhmään luokitellaan vain sellaiset vastaukset, joissa on hyviä perusteluita ja selkeää osoitusta kvalitatiivisesta ymmärryksestä. Tällä perustella c-kohdan ymmärtää ryhmään pääsevät vain 23 pistettä saaneet, ja loput laitetaan ei ymmärrä -ryhmään. Tällä luokittelulla laadittu nelikenttä on esitetty kuvassa 6.2. Merkitään nelikentän soluja koodeilla R1R4. Vertailuluvuksi nelikenttään on laskettu solujen odotetut frekvenssit 2 (merkitty E:llä), jotka vastaavat tilannetta, jossa tarkasteltavat muuttujat olisivat täysin riippumattomia. Kuhunkin soluun liittyvän opiskelijaryhmän kurssipisteiden keskiarvo minimi- ja maksimirajoineen on myös ilmoitettu. Kurssipisteiden keskiarvo kaikkien kokeessa olleiden osalta oli 60 (9111) ja mediaani Kurssin läpipääsyraja oli 40 pistettä ja korkeimman arvosanan (5) raja 85 pistettä Nelikentän tarkastelua Yleisenä piirteenä nelikentässä nähdään, että b- ja c-kohdan osaamisen välillä on selvä yhteys. Havainto perustuu siihen, että havaitut frekvenssit (H) poikkeavat paljon vertailuarvoista (E), jotka on laskettu tilastollisina todennäköi- 2 Rivillä i sarakkeessa j olevan solun odotettu frekvenssi E ij lasketaan kaavalla (Metsämuuronen, 2005) E ij = m n H mn m H im H mj, missä H ij on solun i, j havaittu frekvenssi. 3 Vertailun vuoksi syksyllä 2008 tutkijan pitämällä hyvin samankaltaisesti toteutetulla kurssilla kurssipisteiden keskiarvo oli 62 (9106) ja mediaani 66. Vuoden 2007 kurssi ei tämän perusteella ollut mitenkään poikkeuksellinen. m
76 64 LUKU 6. Empiirisen ymmärryksen mittaaminen koetehtävällä hahmottava ymmärrys, E1 (c-kohta) ei ymmärrä ymmärtää R2 R1 H = 19 (20%) (E = 27) kurssipisteet 69 (32101) H = 12 (12%) (E = 4) kurssipisteet 86 (39111) R3 R4 H = 66 (68%) H = 0 (0%) (E = 58) (E = 8) kurssipisteet 53 (994) ei osaa osaa kvantitatiivinen osaaminen, E2 (b-kohta) Kuva 6.2: Koetehtävän 4 b- ja c-kohtien osaamisen välinen nelikenttä. H = havaittu frekvenssi (soluun kuuluvien suoritusten lukumäärä), E = odotettu frekvenssi. Kuhunkin soluun kuuluvan opiskelijaryhmän osalta on ilmoitettu kurssipisteiden keskiarvo sekä minimi- ja maksimipisteet, jotka on esitetty muodossa: k.a. (minmax). Arvoissa ovat mukana kaikki 97 kokeen tehnyttä opiskelijaa. syyksinä olettaen b- ja c-kohdan osaaminen riippumattomiksi 4. Kun tarkastellaan ensin b-kohdan osaamisen yhteyttä c-kohtaan, havaitaan, että b-kohdan osaajat ovat poikkeuksetta osanneet vastata myös hahmottavalla tasolla oikein tehtävän c-kohdassa, sillä ryhmässä R4 ei ole yhtäkään opiskelijaa. Nelikenttää voidaan tutkia myös toisesta näkökulmasta vertaamalla c-kohdan ymmärtäjä-ryhmää b-kohdan vastausluokkiin. Tässä suunnassa ei nähdä selkeää yhteyttä: hahmottava ymmärtäminen c-kohdassa ei suoraan takaa b- kohdan osaamista. Tarkastellaan nelikentän ryhmiin kuuluvien koevastausten piirteitä lähemmin. Ryhmä R1 Ryhmä R1 koostuu todellisista osaajista. Tiukan luokittelun mukaisesti b- ja c-kohdan osaa ja ymmärtää luokkiin valittiin vain sellaiset, jotka osoittivat selkeästi hallitsevansa kyseisen tehtävän osan. Ryhmään kuuluvien kurssi- 4 Koska tutkimus on laadullista ja mittari karkea, ei ole mieltä laskea varsinaisia tilastollisia tunnuslukuja.
77 6.1. Koetehtävän analyysi 65 pisteistä nähdään, että nämä opiskelijat koostuivat hyvin menestyneistä opiskelijoista. Ryhmän kurssipisteiden keskiarvo 86 ylitti korkeimman arvosanan pisterajan 85 pistettä. Tämä on varsin triviaali havainto: Hyvin menestyneet opiskelijat osaavat parhaiten. Merkityksellisempää onkin kiinnittää huomio mahdollisiin poikkeamiin tästä pääpiirteestä. Tarkemmin tutkittaessa havaittiin, että ryhmään kuuluu yksi opiskelija, jonka 39 kurssipistettä johtivat suorituksen hylkäämiseen. Kyseisen opiskelijan harjoituspisteet olivat alle keskiarvon, joten opiskelijan kurssiaktiivisuutta voidaan luonnehtia keskimääräistä alhaisemmaksi. Opiskelija sai kokeen tehtävästä 4 täydet 6 pistettä kokonaispisteiden jäädessä vain 12 pisteeseen (maksimi 36). Toinen ryhmän R1 opiskelija, joka oli selvästi alle ryhmän keskiarvon, sai 67 kurssipisteellä arvosanan 3. Hänen harjoitusaktiivisuutensa oli hieman yli keskimääräisen. Hän sai niin ikään koetehtävästä 4 täydet 6 pistettä, mutta kokonaispisteet kokeesta olivat 22 pistettä. Kaikki muut tähän ryhmään kuuluvat opiskelijat saivat arvosanaksi 4 tai 5. Muutama ryhmän opiskelija käytti ansiokkaasti c-kohdassa Gaussin ja Stokesin lausetta graasessa perustellussaan. Tämä osoittaa jo pitkälle edennyttä aihepiirin jäsentelyä ja hyvää käsitteiden hallintaa empiiriseltä kannalta. Vain yhdelle ryhmän opiskelijalle divergenssi ja roottori olivat tuttuja aiemmista opinnoista. Ryhmän R1 opiskelijat käyttivät koetehtävän c-kohdassa mm. seuraavia perusteluita: Esimerkki Gaussin lauseen käytöstä päättelyssä Kenttää ei näytä syntyvän laatikossa.. Esimerkki mekaanisen pyörteisyysdetektorin käytöstä Roottorin arvo näyttää järkevältä, koska vektorit näyttäisivät pyörittävän kuviteltua indikaattoria myötäpäivään. Esimerkki roottorivektorin suunnan ja suuruuden päättelystä...kun tarkastelumittakaava on varsin pieni, saatu lukuarvo ( 2000 k) vaikuttaa jossain määrin realistiselta. (Ja koska sen arvo on negatiivinen, kentän tulisi pyöriä myötäpäivään, mikä pitää paikkansa.) Nämä R1 ryhmän koevastausten piirteet tukevat tulkintaa, että tämän ryhmän opiskelijat ovat saavuttaneet divergenssin ja roottorin empiirisen merkityksen ymmärtämisessä sekä vaiheen E1 että vaiheen E2.
78 66 LUKU 6. Empiirisen ymmärryksen mittaaminen koetehtävällä Ryhmä R2 Osa ryhmän R2 opiskelijoista on niitä, jotka ovat laskeneet b- kohdan väärin ja toteavat sen olevan ristiriidassa kuvaajasta tekemiensä päätelmien kanssa. Koepisteiden maksimoimiseksi nämä opiskelijat ovat joutuneet pohtimaan ristiriidan syytä ja sen korjaamista. Ristiriidan myöntäminen kertoo siitä, että hahmottavalla ymmärryksellä on opiskelijalle niin vahva merkitys, että hän uskaltaa luottaa siihen tuloksen järkevyyttä arvioidessaan. Samalla opiskelija myöntää itselleen ja kokeen tarkastajalle, että b-kohdan tuloksessa on virhe, jota ei ole kyennyt korjaamaan. Tällainen ristiriidan havaitseminen omassa toiminnassa on tärkeä tekijä oppimiseen ja ymmärtämiseen tähtäävän toiminnan kannalta (Merenluoto ja Lehtinen, 2004). Tämän ryhmän vastauksissa on myös paljon niitä, joissa b-kohta on laskettu sillä tavalla väärin, että virheellinen tulos on sopusoinnussa c-kohdan päätelmien kanssa. Vaikka pääosin ryhmän R2 vastausten yleisenä piirteenä on kuvasta tehtyjen päätelmien varmuus, oli vastausten joukossa myös sellaisia, jotka empivät päätelmiensä kanssa. Esiintyi myös muutamia epävarmoja vastauksia, joissa opiskelija ei tiennyt, oliko ristiriidan aiheuttava virhe b-kohdan laskusuorituksessa vai opiskelijan kuvasta tekemissä päätelmissä. Kategoriaan R2 kuuluvien opiskelijoiden kurssipisteiden keskiarvo 69 vastaa kurssiarvosanaa 3 eli keskitasoa. Kurssipisteiden jakauma on kuitenkin laaja. Arvosanan 45 saaneita on 9 kappaletta ja hylätyn tai arvosanan 1 saaneita viisi. Hyvä osaaminen koetehtävän c-kohdassa on siis ollut täysin mahdollista, vaikka opiskelija ei olisi saavuttanut muita kurssin läpipääsyn kriteereinä olleita laskennallisia tavoitteita. Tähän nelikentän ryhmään kuuluvissa vastauksissa käytettiin c-kohdassa mm. seuraavia perusteluja: Esimerkki ristiriidasta Kentän kuvaajassa on selkeää pyörteisyyttä, joten roottorin arvo ei saisi olla nolla. Tässä on siis jotain pielessä....laskussa roottorin arvo on positiivinen, mutta kentän kuvaajaa tarkastellen sen tulisi osoittaa toiseen suuntaan....joko lasku on väärin, tai pyörteisyys on toiseen suuntaan. Esimerkki pyörteisyysdetektorin avulla tehdystä päätelmästä Roottorin arvo ei kyllä tunnu järkevältä, koska jos tuonne sellaisen Ossin roottoridetektorin 5 ymppäisi, niin eiköhän se pyörisi. 5 viittaus tutkijan luennoilla esittämään demonstraatioon
79 6.1. Koetehtävän analyysi 67 Jos roottoridetektori asetettaisiin (2,00; 1,00) Se alkaisi pyöriä myötäpäivään eli F olisi k:n suuntainen. (Havaitaan myös, että) jos pisteeseen (2,00; 1,00) kuviteltaisiin pallo, ja kyseessä olevat vektorit kuvaisivat voimia, alkaisi pallo pyörimään. Yleispiirteenä voidaan edellä esitettyjen perustelujen pohjalta todeta, että ryhmän R2 opiskelijat ovat divergenssin ja roottorin empiiristen merkitysten ymmärtämisessä vaiheessa E1. Ryhmä R3 Peräti 68% opiskelijoista kuuluu luokkaan R3. Ryhmä koostuu vastauksista, joissa ei ole nähtävissä aitoa ymmärrystä kummassakaan tehtävän osassa. Lähes kaikissa tämän ryhmän vastauksissa esiintyi b-kohdassa täsmälleen sama virhe: Vektorikentän osittaisderivaattaa laskettiin derivoimalla symbolisesti kentän yksittäistä numeroarvoa. Arvoksi saatiin tietenkin nolla sekä divergenssille että roottorille, jos derivointi oli muodollisesti oikein toteutettu. Kategoriaan R3 kuuluvien opiskelijoiden koepisteiden keskiarvo oli 53, joka vastasi alinta hyväksyttyä arvosanaa 1. Tähän ryhmään kuului suhteellisesti enemmän heikon arvosanan tai hylätyn saaneita opiskelijoita kuin ryhmiin R1 ja R2. Ryhmässä on kuitenkin myös muutama arvosanan 5 saanut opiskelija. Ryhmään kuului kolme sellaista opiskelijaa, jotka kertoivat harjoitustehtävän yhteydessä divergenssin ja roottorin olleen tuttuja käsitteitä aiemmista opinnoista. Koetehtävään vastaamisessa siitä ei kuitenkaan näyttänyt olleen etua. R3 -ryhmän päätelmille on tyypillistä epäjohdonmukaisuus ja virhekäsitykset. Perusteluissa esiintyy sanojen lähteisyys ja pyörteisyys arkipäiväisistä merkityksistä peräisin olevia virhekäsitteitä ja näihin liittyviä virheellisiä analogioita. Ohessa esimerkkejä koevastauksista. Esimerkkejä arkipäivän merkityksiin perustuvista virhekäsityksistä...ei ole pyörrettä eikä lähdettä. Kuvaaja vahvistaa tämän... Intuitiivinen analogia: tyyntä myrskyn silmässä....koska se (piste) on pyörteisyyden keskipisteessä, voisi ajatella että siinä ei ole pyörteisyyttä. pisteessä (2,00; 1,00) on pyörteisen vektorikentän lähde Esimerkkejä virheistä, joissa päättely tehdään yhden pisteen perusteella
80 68 LUKU 6. Empiirisen ymmärryksen mittaaminen koetehtävällä Kuvaajasta nähdään, että kohdassa (2,00; 1,00) vektorikenttä kulkee vaakasuorassa eli siinä ei ole pyörrettä Pisteessä (2,00; 1,00) kentän vektori on 3i, eli pisteessä syntyy ainetta, se on siis lähteinen. Esimerkki vuohon liittyvästä virhekäsityksestä (opiskelija oli laskenut b-kohdassa divergenssin arvoksi 3) Divergenssi tarkoittaa kentän vuota kyseisen pisteen (2,00; 1,00) läpi, ja pisteessä kenttävektorin pituus on 3. Näillä perusteluilla ryhmän R3 opiskelijat eivät vielä ymmärrä divergenssin ja roottorin empiirisiä merkityksiä, joten luokitus on E0. Ryhmä R4 Nelikentän ryhmä R4 jäi täysin tyhjäksi. Kaikki b-kohdan osanneet opiskelijat osasivat varmistaa saamansa tuloksen oikeellisuuden myös kuvan avulla. Assistenttien vastaukset koetehtävään Koetehtävän toimivuuden varmistamiseksi myös kurssin assistentteja pyydettiin tekemään koetehtävä. Tehtävän palautti 5 assistenttia. Heistä neljä 4 sijoittui nelikentän ryhmään R1 ja yksi ryhmään R2. Ryhmään R1 sijoittuvissa vastauksissa tehtävä oli ymmärretty täydellisesti ja vastaukset olivat hyviä esimerkkejä empiirisen ymmärryksen varmuudesta. Tämän perusteella tehtävässä ei näytä olevan sellaista sisäistä ongelmaa, mikä estäisi sen ratkaisemisen, jos todella ymmärtää divergenssin ja roottorin käsitteet perin pohjin. Nämä havainnot eivät kuitenkaan vielä takaa sitä, että tehtävä todella mittaa empiiristä ymmärrystä. Mittarin validiutta pohditaan tarkemmin kappaleessa Koeanalyysin tulokset Koetehtävän b- ja c-kohdat oli suunniteltu mittaamaan kvantitatiivista ja kvalitatiivista empiiristä ymmärrystä divergenssistä ja roottorista. Kummankin tehtävän osan vastaukset jaettiin kahteen ryhmään. B- ja c-kohdan vastaukset esitettiin tämän luokittelu mukaan nelikentässä (kuva 6.2). Tätä nelikenttää tarkastellessa havaittiin, että b- ja c-kohdan osaaminen näyttää muodostavan hierarkian, jossa kvantitatiivisen b-kohdan osaaminen on ylimpänä, sillä kaikki kvantitatiivisen tason E2 saavuttaneet opiskelijat ovat saavuttaneet myös hahmottavan ymmärryksen tason E1, mutta ei päinvastoin. Toinen koetehtävän
81 6.2. Koeanalyysin tulokset 69 avoimen c-kohdan vastauksiin perustuva havainto oli, että osa opiskelijoista käyttää divergenssin ja roottorin perusteluissaan suoria viittauksia luennoilla esitettyihin demonstraatioihin. Kolmantena havaittiin, että myös heikosti kurssilla menestyneet opiskelijat voivat saavuttaa empiirisen ymmärryksen tason E1 ja E2. Neljäs havainto koskee virhekäsityksiä. Havaittiin, että opiskelijoiden perusteluissa esiintyy sanojen lähteisyys ja pyörteisyys arkipäiväisistä merkityksistä peräisin olevia virhekäsitteitä ja näihin liittyviä virheellisiä analogioita. Viides ja ehkä yllättävin havainto oli koetehtävän b-kohdassa esiintynyt tyyppivirhe: Vektorikentän osittaisderivaattaa laskettiin derivoimalla symbolisesti kentän yksittäistä numeroarvoa. Näitä tuloksia tarkastellaan tutkimusongelman valossa johtopäätöksien yhteydessä luvussa 9.
82
83 Luku 7 Haastattelututkimus Empiirisen ymmärryksen mittarina käytetyn koetehtävän analyysissä tehtiin odottamaton havainto, että 68 % kurssin opiskelijoista ei ole saavuttanut empiirisen ymmärryksen tavoitteita. Havainto saa toisaalta epäilemään mittarin luotettavuutta ja toisaalta pohtimaan, miksi koetehtävä oli niin vaikea. Näihin kysymyksiin pyrittiin etsimään vastausta 5 opiskelijan haastattelututkimuksella. Koska haastattelulla on mahdollista saada yksityiskohtaisempaa tietoa kuin kokeella, on tavoitteena tehdä hienojakoisempi luokittelu E1- ja E2-vaiheen ymmärryksestä YSOLO-taksonomian mukaisiin luokkiin Y0Y2. Tutkimushaastattelut päätettiin toteuttaa toiminnallisina haastatteluina. Menetelmän valinta perustui siihen, että aiemmissa derivaatan oppimista koskevissa tutkimuksissa (esim. Hähkiöniemi (2006)) on käytetty samaa menetelmää. Toisaalta nyt tutkimusaiheena oli erityisesti fysiikan opiskelijoiden empiiristen merkitysten ymmärtäminen. Tästä näkökulmasta on perusteltua käyttää haastattelussa konkreettista fysikaalista mittaus- ja mallinnustehtävää. Tiedonkeruu suoritettiin haastattelussa videoimalla. 7.1 Haastattelun suunnittelu Haastattelututkimuksella haluttiin ensisijaisesti löytää tarkempia vastauksia tutkimusongelmiin B (kpl 4.4). Koetehtävässä tarkasteltiin jo näitä kysymyksiä kirjallisen tehtävän muodossa. Haastattelussa on mahdollista tutkia ymmärtämistä vielä konkreettisemmin aidon empiirisen tutkimustehtävän avulla. Kriteereinä haastattelun suunnittelussa oli, että tutkittavan ilmiön on oltava käsitteellisesti mahdollisimman yksinkertainen, jotta se on ymmärrettävissä opiskelijoiden taustatiedoilla. Lisäksi ilmiön tulee olla myös helposti toteutettavissa tutuilla, mahdollisesti arkipäiväisillä, välineillä. Haastattelumetodin ongelma on se, että materiaalia syntyy paljon ja merkityksellinen tiedon löytäminen on vaikeaa. Tästä syystä haastattelussa on pyritty rajaamaan aihetta
84 72 LUKU 7. Haastattelututkimus tiukasti. Haastattelussa keskitytään erityisesti roottorikäsitteeseen. Luennoilla käytettiin vektorianalyysin aihepiiriä havainnollistettaessa usein esimerkkinä konkreettisia jatkuvan aineen virtauskenttiä kuten ilma- ja nestevirtaukset. Päädyttiin laatimaan tutkimustehtävä, jossa mitataan hiustenkuivaimen ilmavirtausta. Tämän katsottiin täyttävän hyvin kaikki asetetut kriteerit. Varsinainen analysoitava tutkimustehtävä on periaatteeltaan samanlainen kuin koetehtävä. Opiskelijan on määritettävä mittauksiin ja mahdollisiin numeerisiin laskuihin perustuen hiustenkuivaimen ilmavirtauksen pyörteisyys annetussa mittauspisteessä. Haastattelussa käytetty koelaitteisto on esitetty kuvassa 7.1. Hiustenkuivain oli asennettu kiinni statiiviin siten, että kuivaimen suutin oli suunnattu vaakasuuntaisesti. Statiivi sijaitsi pienen apupöydän päällä. Apupöydän nurkkaan oli sijoitettu koordinaatistomerkki, joka kiinnitti oikeakätisen koordinaatiston x-,y- ja z-akselit. Opiskelijoiden käytettävissä olevat mittalaitteet on esitetty kuvassa 7.2. Näilä välineillä tapahtuvaa mittaustapahtumaa demonstroidaan kuvassa 7.3. Tehtävänä oli ensin tutkia ilmavirtausta suuttimen korkeudella kulkevassa vaakasuorassa tasossa. Yleisen tarkastelun jälkeen keskityttiin tutkimaan virtauksen mahdollista pyörteisyyttä. Erityisesti huomio kiinnitettiin yhteen tiettyyn pisteeseen, jonka sijainti oli kiinnitetty pienellä statiivitangon palalla (näkyy kuvassa hiustenkuivaimen suuttimen edessä). Tehtävänä oli määrittää virtauksen pyörteisyys kyseisessä pisteessä. Tätä kysyttiin sekä mittausten kannalta, että matemaattista lauseketta tarkastelemalla. Näin tarkasteltiin pyörteisyyden käsitettä kahdelta eri kannalta. Kuva 7.1: Haastattelun toiminnallisessa osassa käytetty tutkimuslaitteisto. Hiustenkuivain on kiinnitetty statiiviin. Kuivaimen virtausta tarkastellaan tarkemmin statiivitangolla osoitetussa mittauspisteessä.
85 7.2. Haastateltavien valinta 73 Kuva 7.2: Haastattelutehtävän toiminnallisessa vaiheessa opiskelijoilla oli käytössä mittavälineinä erilaisia silkkipaperisuikaleita, siipiratas ja mittanauhoja. Kuva 7.3: Esimerkkikuva hiustenkuivaimen virtauksen tutkimisesta silkkipaperin ja siipirattaan avulla. 7.2 Haastateltavien valinta Syksyn 2007 Mapu II -kurssin pistelistasta poimittiin arpomalla 4 opiskelijaa jokaisesta arvosanaryhmästä 1-5. Tutkimuksen painopisteenä olivat ensi kertaa kurssilla mukana olevat ja aktiivisesti kurssille osallistuneet opiskelijat. Tähän nojaten arvottujen joukosta poistettiin yksi opiskelija, joka osallistui kurssille jo toista kertaa ja kaksi opiskelijaa, jotka eivät olleet osallistuneet lainkaan kurssin ex tempore -harjoituksiin. Poistettujen tilalle arvottiin uudet opiskelijat samasta arvosanaryhmästä. Näin saatiin 20 opiskelijan lista, joille lähetettiin ( ) sähköpostilla haastattelupyyntö (ks. liite C.1). Haastatteluun osallistuneille luvattiin palkkioksi elokuvalippu. Haastattelut pidettiin aikavälillä Haastattelupyyntöön vastasi myöntävästi 5 opiskelijaa. Heidän taustatietonsa on esitetty taulukossa 7.1. Katsottiin, että otos sisältää tutkimuksen laadullisten tavoitteiden näkökulmasta riittävästi erilaisia osaamisen tasoja. Haastateltavia oli varauduttu hankkimaan lisää, jos katsottiin, että aineistoksi tarvitaan uusia näkökulmia. 7.3 Haastattelun kulku Haastattelun kulku seurasi ennalta laadittua käsikirjoitusta (ks. liite C.3). Haastattelu koostui eri vaiheista, joiden merkitystä tutkimuksen kannalta tarkastellaan seuraavassa.
86 74 LUKU 7. Haastattelututkimus Taulukko 7.1: Koehenkilöiden suoritusten pistemäärät ja kurssin loppuarvosana. Suluissa maksimiarvot. Koehenkilön numero Mapu II arvosana (5) Koepisteet (36) Tehtävä 4 b) pisteet (2) Tehtävä 4 c) pisteet (3) nelikentän ryhmä R1 R3 R2 R3 R3 OSA 1: Ennen varsinaisen haastattelun alkua haastateltavalle kerrottiin haastattelun luottamuksellisuudesta sekä tiedon tallentamisesta ja sen käsittelemisestä. Samalla annettiin myös ohjeita haastattelutehtäviin ja kysymyksiin vastaamiseen liittyen. Haastatteluohjeet ovat liitteessä C.2. OSA 2: Nauhoitus käynnistettiin käsikirjoitukseen merkityn osan 2 alussa. Tämän osan tarkoitus oli toimia lähinnä lämmittelynä ja jännityksen poistajana. Kysymyksillä pohjustettiin aihepiiriä, johon varsinainen haastattelu kuuluu. Tämän osuuden analysoiminen ei ole tarpeen tutkimuksen kannalta. OSA 3: Tästä alkoivat haastattelun varsinaiset toiminnalliset osuudet. Opiskelijalle annettiin moniste, jossa oli tehtävä yhden muuttujan funktion numeerisesta derivoinnista. Tehtävällä selvitetään, osaako opiskelija määrittää suureen derivaatan toisen suureen suhteen kuvaajan avulla. Testauksen lisäksi tehtävän on tarkoitus aktivoida opiskelijaa ajattelemaan, että derivaatan määrityksessä on kyse kahden muutoksen vertaamisesta toisiinsa. Tehtävän osaaminen kertoo, onko opiskelijalla pohjatiedot kunnossa korkeampien käsitteiden osaamiselle. Jos tässä ilmenee ongelmia, ovat edellytykset varsinaisen tutkimustehtävän suorittamiselle hyvin heikot. Koska tehtävä oli lähinnä itsenäistä työskentelyä paperilla, on tämän osan analyysi luontevinta tehdä haastateltavien paperille tekemän suorituksen perusteella. Transkriptioresurssien kohdentamiseksi varsinaiseen tutkimustehtävään, on tästä osasta tehty transkriptio vain siinä tapauksessa, että opiskelija selitti tehtävän aikana sellaista oleellista, mikä ei ole paperivastauksesta nähtävissä. OSA 4: Tämä osa haastattelusta käsittää tutkimuksen pääaiheen hiustenkuivaimen ilmavirtauksen määrityksen ja roottorin arvon määrityksen tietyssä
87 7.4. Haastattelujen analyysimenetelmä 75 mittauspisteessä. Tutkimusmateriaalia saatiin sekä videon välityksellä opiskelijan toiminnasta että paperimuodossa opiskelijan paperille tekemien merkintöjen kautta. Tutkimustehtävä oli luonteeltaan hyvin avoin. Opiskelijan tuli tehdä itse päätös siitä, mikä on paras tapa vastata esitettyyn kysymykseen. Haastattelija ei juurikaan ohjannut opiskelijoita eteenpäin tehtävän suorituksessa. Jos näytti siltä, ettei opiskelija pääse kysymyksessä lainkaan eteenpäin, esitti haastattelija lisäkysymyksiä tai antoi pieniä vihjeitä. Tämän ohjauksen tarkoitus oli varmistaa, että opiskelijan pysähtyminen johtuu siitä, että on todella tunnistettu opiskelijan ymmärryksen raja. Toisaalta jos näytti siltä, että opiskelija ei pysty vastaamaan esitettyyn kysymykseen, pyrittiin kysymystä muotoilemaan uudestaan ja mahdollisesti esittämään se eri näkökulmasta. Näin voitiin varmistaa, johtuiko vastauksen puute kysymyksen muotoilusta vai kuvasiko se opiskelijan ymmärrystä asiasta. Ensimmäisenä tässä osassa oli hiustenkuivaimen virtauskentän mallintaminen siipirattaalla ja silkkipaperinauhoilla tehtyjen mittausten avulla. Tämän tarkoitus oli, että opiskelijoille syntyisi konkreettinen itse muodostettu kuva siitä, millainen virtauskenttä on rakenteeltaan. Myöhemmin haastattelussa tutkittiin tämän konkreettisen virtauskentän roottoria ja sen mittaamista sekä lukuarvon määrittämistä derivaattalausekkeen avulla. 7.4 Haastattelujen analyysimenetelmä Haastattelujen analyysin tukena käytetään käsitekarttamenetelmää (Novak ja Gowin, 1995) jäsentämässä tutkittavien käsitteiden keskinäisiä riippuvuuksia. Tutkija laati haastattelutehtävässä esiintyvistä olennaisista käsitteistä ja toimintavaiheista käsitekarttoja. Käsitekarttoja hyödynnetään haastattelun analyysissä siten, että opiskelijoiden toimintaa, sanoja ja tehtäväpaperiin tehtyjä merkintöjä vertaillaan tutkijan laatimiin mallikarttoihin (ks. kuvat 7.4, 7.6 ja 7.7). Yksi videohaastattelun ongelmista on saadun materiaalin valtava määrä ja sen merkityksellisen tulkinnan vaikeus (Kvale, 1996; Powell et al., 2003). Tästä syystä haastattelututkimuksen kohdetta on tarpeen rajata voimakkaasti. Haastattelussa keskityttiin tästä syystä ainoastaan roottorin käsitteeseen. Haastatteluaineiston käsittelylle on erilaisia metodeja. Yksi tapa on tehdä haastattelusta tarkka kirjallinen transkriptio, jonka pohjalta analyysi toteutetaan. Transkriptiolla pyritään kuvaamaan haastattelutilanteessa tapahtunutta vuo-
88 76 LUKU 7. Haastattelututkimus vaiko? Kuva 7.4: Yleisluontoinen käsitekartta hiustenkuivaimen virtauskentän mallintamisesta silkkipaperilla tehtävien mittausten avulla.
89 7.5. Koehenkilöiden suoritusten arviointi 77 rovaikutusta. Puheen lisäksi vuorovaikutuksessa esiintyvien eleiden ja ilmeiden kuvaaminen saattaa olla kirjallisessa muodossa vaikeaa (Powell et al., 2003). Toinen näkökulma on tehdä analyysi suoraan videotallenteiden avulla. Molempiin lähestymistapoihin liittyy hyviä ja huonoja puolia. Tässä tutkimuksessa analyysi toteutettiin menetelmällä, joka oli edellä kuvattujen hybridi. Videohaastatteluista tehtiin valikoitu transkriptio, jossa keskityttiin tutkimuskysymysten kannalta oleellisiin seikkoihin. Transkription tukena käytettiin analyysivaiheessa myös itse videonauhoituksia. Tehtyjä päätelmiä perustellaan transkriptioista tehdyillä lainauksilla. Haastattelut käytiin ensimmäisen kerran läpi keväällä 2008, jolloin tehtiin alustavat transkriptiot. Materiaalin pariin palattiin uudestaan noin vuoden päästä keväällä 2009, kun tutkimustulosten kokoaminen alkoi. Tällöin haastatteluaineisto käytiin uudestaan läpi tarkastellen kriittisesti aiemmin tehtyjä havaintoja. Menetelmäkirjallisuudessa tuetaan tällaista toimintatapaa keinona lisätä tulkinnan objektiivisuutta ja mahdollisuutena nähdä materiaali uudesta näkökulmasta (Kvale, 1996). Haastattelun transkripitiossa ei kiinnitetty erityistä huomiota sanojen painotukseen tai muihin ilmaisun yksityiskohtiin. Niissä kohdissa, missä painotuksella haluttiin korostaa jotain erityistä asiaa, on tämä kirjattu haastattelun transkriptiossa. Kvale (1996) ohjeistaa, että käyttökelpoisten materiaalin varmistamiseksi on kiinnitettävä haastattelun aikana huomiota syntyvän materiaalin laatuun. Tämä otettiin huomioon siten, että haastattelija pyrki ymmärtämään jo haastattelun kuluessa koehenkilöiden ajattelua. Jos tutkijasta vaikutti siltä, että koehenkilöllä on aukkoja kysyttävän käsitteen ymmärryksessä, pyrittiin tätä havaintoa varmistamaan sopivasti muotoilluilla tarkentavilla kysymyksillä. 7.5 Koehenkilöiden suoritusten arviointi Ymmärryksen mittarit Haastattelun tavoite tutkimuksen kannalta on empiirisen ymmärryksen vaiheiden E1 ja E2 sisäisen hienorakenteen tutkiminen YSOLO-asteikon mukaisilla tasoilla Y0Y2 luokiteltuna (ks. kuva 4.2 kappaleessa 4.6). Tässä tarkennettaan, miten luokittelu E1 ja E2 vaiheeseen ja näiden YSOLO-luokituksen mukaisiin alatasoihin Y0Y2 tehdään käytännössä, kun arviointi on rajoittunut roottorin käsitteeseen ja mallikartan (kuva 7.5) pääreitteihin 1 ja 2.
90 78 LUKU 7. Haastattelututkimus Kuva 7.5: Mallikäsitekartta hiustenkuivaimen ilmavirran pyörteisyyden määrittämisestä haastattelutehtävässä. Koehenkilöiden haastattelujen analysointi tapahtui tämän käsitekartan pohjalta. Kartta sisältää ainoastaan tutkimuksen kannalta oleelliset käsitteet ja niiden väliset yhteydet.
91 7.5. Koehenkilöiden suoritusten arviointi 79 YSOLO-luokitus ei sisällä tietoa tarkasteltavasta aiheesta, vaan sen tasojen kuvailut ovat luonteeltaan yleisiä. Jotta analyysi saisi täsmällisemmän pohjan, on perusteltua tehdä YSOLO-tasojen tarkempia kiinnityksiä roottorin käsitteen empiiriseen ymmärtämiseen liittyviin piirteisiin. Tällaiset kiinnitykset pyritään tekemään YSOLO-taksonomian hengessä käyttäen sitä ohjenuorana. Luokituksen ensisijainen tarkoitus on kuvata empiirisen ymmärryksen askeleita, joten viime kädessä luokittelun kriteerit perustuvat tähän käyttötarkoitukseen. Luokitus on esitetty taulukossa 7.2. Analyysiä rajataan tässä osassa vektorikentän roottorin empiiriseen merkitykseen, jonka hahmotusprosessia kuvataan käsitekartassa 7.5. Tarkasteltavaksi on valikoitu kaksi karttaan numeroitua pääreittiä, joita pitkin käsitteen jäsentyminen voi tapahtua. Haastateltavan ymmärryksen jäsentymistä näillä reiteillä selvitetään vertaamalla haastatteluista sekä koe- ja harjoitusvastauksista saatua tietoa tarkasteltavasta hahmotusreitistä laadittuun käsitekarttaan. Jos opiskelija käyttää siipiratasta tai muuta detektoria vektorikentän pyörteisyyden tunnistamiseen, käyttää hän kuvaan 7.5 merkittyä reittiä 1. Siipirattaan pyöriminen on yksinkertainen fysikaalinen ilmiö, joka luo pyörteisyydelle empiirisen merkityksen. Tämä kuuluu siis hahmottavalle tasolle E1.1. Kun opiskelija ymmärtää myös detektorin pyörimissuunnan merkityksen ja päättelee sen avulla pyörteisyysvektorin suunnan, on hän esikvantioinnin tasolla E1.2. Reittiä 1 tapahtuvan hahmotuksen yksityiskohtaisempi käsitekartta on kuvassa 7.6. Pyörteisyyden tunnistaminen pelkkien virtausnopeusmittausten avulla on sen sijaan hankalaa. Tunnistamiseen ei riitä kvalitatiivinen havainto nopeuden suunnan ja suuruuden muutoksesta niin kuin osa opiskelijoista valitettavasti kuvittelee sillä kenttävektoreiden suunta ja suuruus voivat muuttua pyörteettömässä kentässäkin. Koska reittiä 1 tapahtuva pyörteisyyden tunnistaminen fysikaalisen pyörteisyysdetektorin avulla on oleellisesti yksinkertaisempaa kuin reittiä 2 tapahtuva tunnistaminen, voidaan reitistä 1 käyttää nimitystä empiirinen oikotie. Kurki-Suonio (2006) kutsuu tätä empirian portiksi. E2 -vaihe on pyörteisyyden arvon mittaamista. Sen voi tehdä sekä reittiä 1 ja 2. Siipirattaan käyttäminen pyörteisyyden lukuarvon mittaamiseen (reitti 1) perustuu siihen, että rattaan virtauksessa saavuttama kulmanopeus on verrannollinen virtauskentän kiertämään. Jos kulmanopeudelle saadaan lukuarvo, voidaan pyörteisyys määrittää Stokesin lauseeseen perustuen. Käytännössä kukaan haastateltavista ei kuitenkaan esittänyt pyörteisyyden arvon määritystä tällä menetelmällä.
92 80 LUKU 7. Haastattelututkimus Taulukko 7.2: Pyörteisyyden käsitteen empiirisen ymmärryksen luokittelu YSOLO-taksonomiaa soveltaen YSOLO -taso E1: Hahmotusvaihe Kuvaus toiminnasta Y0. Rakenteeton tieto Opiskelijalla on paljon virhekäsityksiä ja naiiveja arkikäsityksiä pyörteisyydestä (pyörteisyys on vektoreiden suunnan muuttumista), jotka muodostavat esteen syvemmälle hahmotukselle. Käsitykset eivät ole johdonmukaisia, vaan vaikuttavat satunnaisilta. Y1. Perushahmotus Ilmiön tunnistaminen on johdonmukaista: pyörteisyysdetektori lähtee pyörimään. Ymmärrys on kuitenkin vain osittaista, eikä opiskelija ymmärrä esimerkiksi pyörteisyyden suunnan merkitystä. Osaa vastata jäsentelykysymyksiin E1.1. Y2. Esikvantiointi Sisältää oikeaa tietoa, joka on jäsentynyttä ja muodostaa johdonmukaisen kokonaisuuden. Opiskelija ymmärtää, että pyörteisyysdetektorin pyörimissuunta määrää oikean käden säännön avulla pyörteisyysvektorin suunnan. Osaa vastata jäsentelykysymyksiin E1.2. E2: Kvantifiointi Y0. Opiskelijalla on virhekäsityksiä osittaisderivaattojen fysikaalisesta merkityksestä. Ei osaa päätellä kvalitatiivisesti, mitä derivaatoista saadaan vastauksena. Y1. Opiskelija ymmärtää osittaisderivaatan mittausteknisesti. Hän pystyy päättelemään tekemiensä havaintojen avulla osittaisderivaatan positiivisuuden tai negatiivisuuden ja tämän avulla roottorin positiivisuuden tai negatiivisuuden. Y2. Opiskelija osaa määrittää pyörteisyyden lukuarvon konkreettisten mittausten tai kuvasta tai taulukosta saatujen lukuarvojen avulla ja osaa verrata tulosta hahmottavan E1 -vaiheen havaintoon. Pyörteisyyden lukuarvon määrittämiseen virtausnopeusmittausten avulla (reitti 2) tarvitaan useita erillisiä mittauksia, joiden arvojen avulla voidaan määrittää likiarvot virtausnopeuden osittaisderivaatoille ja niiden avulla itse pyörteisyyden likiarvo. Pyörteisyyden määrittämistä tällä menetelmällä esittää käsitekartta 7.7.
93 7.5. Koehenkilöiden suoritusten arviointi 81 Kuva 7.6: Yksityiskohtainen käsitekartta pyörteisyyden määrittämisestä hiustenkuivaimen virtauskentässä siipirattaan avulla Opiskelijoiden ymmärryksen analyysi Seuraavassa tarkastellaan sekä haastattelusta että koe- ja harjoitusvastauksista saadun aineiston pohjalta, mille hahmotuksen tasoille opiskelijan osoittamat vastaukset sijoittuvat. Haastattelukuvausten esittämisessä noudatetaan (Kvale, 1996, s ) esittämiä ohjeita. Vain tulkintojen kannalta oleellisimmat kohdat on lainattu ja niiden kontekstia selvennetään kehyskertomuksen avulla. Vuorosanat on muokattu kirjalliseen ilmaisuun soveltuvaan asuun alkuperäiset merkitykset säilyttäen. Haastattelulainauksissa T tarkoittaa tutkijaa (haastattelija) ja KH koehenkilöä. Analyysin tukena on käytetty myös haastateltavien vastauksia koe- ja harjoitustehtävään.
94 82 LUKU 7. Haastattelututkimus Kuva 7.7: Käsitekartta osittaisderivaattojen määrittämisestä silkkipaperilla hiustenkuivaimen virtauskentässä. Koehenkilö 1 (KH 1) Vaiheen E1 hahmotus Koehenkilö osoitti haastattelussa ymmärtävänsä siipirattaan käytön pyörteisyyden hahmon tunnistamiseen sekä perushahmotuksen että esikvantioinnin tasolla. Opiskelija suoritti ensin mittauksia silkkipapereilla vaikuttaen itsevarmalta ja tietävänsä, mitä oli tekemässä. Siipirattaalla hän kertoi mittaavansa pyörteisyyttä ja piti sitä sormiensa välissä oikeal-
95 7.5. Koehenkilöiden suoritusten arviointi 83 la tavalla eli akseli pystyasennossa. Hän havaitsi, että pyörteisyyden suunta on erilainen virtauksen vastakkaisilla reunoilla: KH 1: Siipiratas pyörii täällä myötäpäivään ja täällä vastapäivään. Haastattelija pyysi koehenkilöä tutkimaan pyörteisyyttä statiivitangolla osoitetussa mittauspisteessä. Koehenkilö piti siipirattaan akselia pystysasennossa ja kertoi havainnostaan: KH 1: Tässä tilanteessa pyörteisyys on k-vektorin suuntainen. Se on siis ylöspäin tästä tasosta. Empiirisen ymmärryksen tasojen luokituksen mukaan nämä piirteet kuuluvat tason Y2 saavuttaneeseen hahmotukseen. Opiskelijan koe- ja harjoitusvastauksista ei löytynyt aineistoa luokittelun puolesta eikä sitä vastaan. Vaihe E2 Kun tarkastellaan kvantitatiivista ymmärtämistä, antavat haastattelu ja koevastaus hieman ristiriitaisen kuvan siitä, miten hyvin opiskelija ymmärtää osittaisderivaatan mittausten kannalta. Haastattelun yhteydessä opiskelija kertoi olevansa epävarma osittaisderivaatan fysikaalisesta merkityksestä. T: Tarkastellaan näitä yksittäisiä termejä. Selitä, mitä ensimmäinen termi x v y tarkoittaa. KH 1: Se on kentän y-akselin suuntaisen komponentin derivaatta x:n suhteen. Jos kentän y-komponentti riippuu x:stä, niin derivaatta on nollasta poikkeava. KH 1: On vaikea sanoa, mitä se tarkoittaa fysikaalisesti tässä tilanteessa. Ymmärrän kyllä, mitä se tarkoittaa matemaattisesti. Haastattelun aikana oli voimakas tunne siitä, että oikean mittausmenetelmän keksiminen oli vain pienestä kiinni. Tämän testaamiseksi haastattelija antoi vihjeen palata tutkimaan haastattelun lämmittelyvaiheessa tehtyä tehtävää, jossa pyydettiin määrittämään yhden muuttujan funktion derivaatta kuvaajan avulla. Vihjeen jälkeen haastateltava pohti osittaisderivaatan mittaamista näin: KH 1: Pyörteisyyden arvoja pitää mitata eri pisteissä y-akselin suunnassa. Siipirattaalla voi määrittää kierrosmäärän tässä virtauksessa.
96 84 LUKU 7. Haastattelututkimus Opiskelija toteutti ehdotuksensa mittaamalla siipirattaalla arvoja (vapaavalintaisella keksimällään asteikolla) eri kohdissa y-suunnassa ja esittämällä ne taulukossa (ks. liitteessä C.4.1 oleva kuva). Saamiensa arvojen avulla hän määritti osittaisderivaatan lukuarvon. Vaikka menetelmä oli lähellä oikeaa, tarkoitti siipirattaan käyttö kuitenkin sitä, että todellisuudessa hän määritti pyörteisyyden derivaatan y-koordinaatin suhteen. Oikein tehtynä olisi pitänyt mitata nopeuden x-komponentin muuttumista y-suunnassa. Kokeessa sen sijaan opiskelija ratkaisi b-kohdan täydellisesti oikein taulukoitujen arvojen avulla ja osasi c-kohdassa todeta tuloksen olevan sopusoinnussa kuvasta tehtyihin päätelmiin, osoittaen hyvää ymmärrystä reitin 2 mukaisesta pyörteisyyden kvantitatiivisesta määrittämisestä. Ristiriita koe- ja haastattelusuorituksen välillä saattaa tosin johtua myös opiskelijan epävarmuudesta haastattelutilanteessa. Varovaisuuden periaatetta noudattaen katsotaan kuitenkin, että käytettävissä oleva aineisto mahdollistaa E2 tason ymmärryksen luokittelun varmuudella vain tasolle Y1. Koehenkilö 2 (KH 2) Vaihe E1 Opiskelija ymmärsi, että siipirattaan pyöriminen on ilmiö, joka kertoo virtauksen pyörteisyydestä. Aluksi hän piti kuitenkin siipirattaan akselia y-akselin suunnassa mitaten käytännössä xz-tason suuntaista pyörteisyyttä. Havainto pyörteisyydestä on tässäkin tapauksessa täysin oikea, mutta tutkimussuunta ei ole ohjeiden mukainen. Opiskelija ihmetteli, miksi siipiratas pyörii eri suuntiin eri kohdissa. Haastattelija kysyi tästä lisää: T: Mitä suunnalla tarkoitetaan? KH 2: Pyörteisyys voi olla vasta- tai myötäpäivään. Vastaus ei vielä tyydyttänyt haastattelijaa ja koehenkilökin tuntui vielä mietiskelevän käsitteitä mallia piirtäessään. Niinpä haastattelija kysyi, pystyisikö pyörteisyyttä tutkimaan vielä tarkemmin kokeellisesti. Tällöin koehenkilö ehdotti: KH 2: Auttaisiko jos kääntäisin propellin toisinpäin? T: Kerro tuosta ajatuksesta lisää. [innostuneesti] KH 2: Pohdin, mitä vaikutusta sillä olisi, että siipirattaan kääntäisi toisinpäin. Äsken tutkin siipirattaalla vaakatasossa. Mitä, jos olisin tutkinut pystytasoa?
97 7.5. Koehenkilöiden suoritusten arviointi 85 Kuullessaan haastateltavan ehdotuksesta haastattelija innostui, mikä oli havaittavissa myös haastattelijan äänen sävyssä. Koska opiskelija oli jo luopumassa ideastaan todeten ei sillä suunnalla ole vaikutusta, päätti tutkija vielä rohkaista häntä: T: Kerrotko vielä, mikä merkitys asennolla sinun mielestäsi on? KH 2: Siipirattaan pyöriminen vain muistuttaa pyörteisyyttä, mutta ei se välttämättä todellisuudessa ole sitä. Opiskelija tuntuu pitävän siipirattaan pyörimistä vain pyörteisyyden indikaattorina, mutta epäilee, ettei sillä ole muuta yhteyttä pyörteisyyteen. Haastattelija pyysi opiskelijaa tutkimaan vielä asennon merkitystä kokeellisesti. Tämä paljasti virhekäsityksiä: KH 2: Tässä on kaksi pyörteisyyden lähdettä. Täällä olisi ensimmäinen ja täällä sitten toinen T: Käytit sanaa pyörteisyyden lähde. Mitä tarkoitat sillä? KH 2: Tarkoitan sitä paikkaa, mistä pyörteisyys lähtee liikkeelle. En tiedä, mitä se on käsitteellisesti. Näiden opiskelijan vastausten ja opiskelijan kuvaan (ks. kuva liitteessä C.4.2) piirtämän virtauskentän perusteella (kuvaan on piirretty lähteitä paikkoihin, joissa hän kertoi näkevänsä pyörteisyyttä) vaikuttaa siltä, että pyörteisyyden käsite ja sen ilmeneminen vektorikentässä ei ole opiskelijalla vielä jäsentynyt kunnolla. Tätä tulkintaa tukee myös opiskelijan harjoitusvastaus, jossa hän pitää pyörteisyyden tunnusmerkkinä vektoreiden suunnan muuttumista. Näiden havaintojen perusteella luokitellaan E1-vaiheen ymmärrys tasolle Y0. Haastateltavan koevastauksessa ei ole materiaalia luokittelun puolesta eikä sitä vastaan. Vaihe E2 Myös kvantitatiivisen tason ymmärrystä arvioitaessa nähdään, että opiskelijalla on sekä oikean tiedon pirstaleita että virhekäsityksiä. Haastattelija kirjoitti paperille roottorin symbolisen lausekkeen xy-tasossa ( x F y y F x )k ja kysyi siinä esiintyvien osittaisderivaattojen merkitystä mittausten kannalta. T: Pystytäänkö tämän lausekkeen arvo mittaamaan jotenkin? KH 2: Kun derivaatta kuvasi kasvunopeutta, niin tuo ensimmäinen kuvaa funktion F y-komponentin kasvunopeutta x-akselin suunnassa.
98 86 LUKU 7. Haastattelututkimus T: Voitko selittää tai näyttää kuvasta, mitä ajattelit? KH 2: Voisiko se olla kulmakerrointa tuosta vektorista? Opiskelija yrittää yhdistellä aiemmin haastattelussa yhden muuttujan derivaattatehtävässä tekemäänsä kulmakertoimen määritystä osittaisderivaatan tapaukseen. Se johtaa kuitenkin virheelliseen päätelmään vektorin kulmakertoimen määrittämisestä. Virhekäsitys voimistuu haastattelun loppua kohti, kun opiskelija ehdottaa, että derivaatta y:n suhteen saadaan kääntämällä vektoria. KH 2: Ehkä derivaatta y:n suhteen saadaan kääntämällä vektori toisinpäin. En tiedä, kun en ole koskaan miettinyt tällaista. Myös koetehtävän analyysi osoittaa, ettei tälle koehenkilölle ole hyvin selvillä, miten osittaisderivaatan numeerisen arvon määritys tehdään. Koevastaus edusti aiemmin tarkasteltua tyyppivirhettä, jossa derivaatta yritetään laskea symbolisesti (ks. luku 6.1). Haastattelussa syntyi kokonaisvaikutelma, että opiskelijalla on selviä oikean tiedon palasia, mutta ne eivät ole jäsentyneet vielä mielekkääksi kokonaisuudeksi. Käytettävissä olevan aineiston pohjalta varovaisuusperiaatetta noudattaen päädytään luokittelemaan kvantitatiivisen vaiheen ymmärryksen tasoksi Y0. Koehenkilö 3 (KH 3) Vaihe E1 Tälle koehenkilölle vaikutti olevan hyvin selvillä, mihin siipiratasta voidaan käyttää ilmavirtauksen tutkimisessa: KH 3: Tällä siipirattaalla voi mitata pyörteisyyttä. Täällä se pyörii myötäpäivään ja täällä vastapäivään. Tässä on kohta, jossa se ei pyöri lainkaan. Samalla hän osoitti ymmärtävänsä, että rattaan pyörimissuunta on tärkeä pyörteisyyteen liittyvä ominaisuus. Myös harjoitusvastauksessa opiskelijan käyttämä ilmaisu piste A lähtisi kiertämään negat.suuntaan kertoo siitä, että hän on oppinut käyttämään detektoreiden pyörimistä pyörteisyyden osoittavina empiirisinä ilmiöinä. Samanaikaisesti opiskelija kuitenkin määrittelee pyörteisyyden sanallisesti seuraavasti: Vektorikentän pyörteisyys kertoo, ovatko kentän vektorit samansuuntaisia. Haastattelussa vastaus oli samanlainen: T: Miten pyörteisyyden tunnistaa kuvasta? KH 3: Tässä kuvassa sen näkee siitä, että kaikki nuolet eivät ole samansuuntaisia.
99 7.5. Koehenkilöiden suoritusten arviointi 87 Vaikka opiskelijalla on osittain jopa tasolle Y2 luokiteltavaa tietoa E1 -vaiheen hahmotuksessa, on havaittujen virhekäsitysten johdosta perusteltua katsoa tasoksi Y1, koska näyttö ei ole riittävän vakuuttava korkeamman luokituksen puolesta. Luokituksen perusteluna voidaan käyttää myös vertailua muihin koehenkilöihin. Koehenkilö 1 kykeni kuvailemaan pyörteisyyttä kvalitatiivisesti paljon koehenkilöä 3 tarkemmin käyttäen mm. oikean käden sormisääntöä pyörteisyysvektorin suunnan päättelyyn. Koehenkilön 3 kvalitatiivisen hahmotuksen taso vaikutti oleva lähempänä koehenkilön 4 tasoa kuin koehenkilön 1, joten luokitus tuntuu tässä mielessä oikealta. Vaihe E2 Haastattelussa opiskelijalta kysyttiin, miten pyörteisyyden lausekkeessa esiintyvät osittaisderivaatat voidaan määrittää mittaamalla. Koska opiskelija ei osannut vastata kysymykseen, yritti tutkija johdatella eteenpäin yhden muuttujan funktion derivaatan avulla. T: Mitä yhden muuttujan funktion derivaatta kuvaa? KH 3: Hetkellistä muutosta. T: Kuvaako tämä pyörteisyyden lausekkeessa esiintyvä osittaisderivaatta jotain vastaavanlaista? KH 3: Yhden muuttujan derivaatta oli kulmakerroin. Onhan näilläkin nuolilla kulmakerroin... Opiskelija vaikutti kuitenkin epävarmalta lähtiessään pohtimaan kulmakerrointa vektorien tapauksessa. Hän ei osannut kertoa, miten osittaisderivaattojen mittaaminen toteutettaisiin kokeellisesti. Myös koetehtävän b-kohdan vastaus tukee havaintoa, ettei opiskelijalle ole selvää, miten vektorikentän pyörteisyyden likiarvo voidaan määrittää eri pisteissä mitattujen vektorikentän arvojen avulla. Koevastaus oli tämänkin koehenkilön tapauksessa aiemmasta tuttu tyyppivirhe, jossa derivoidaan vektorikentän pisteittäistä numeerista arvoa symbolisesti. E2-vaiheen ymmärrys on näiden havaintojen pohjalta helppo määrittää Y0:ksi. Koehenkilö 4 (KH 4) Vaihe E1 Mielenkiintoinen piirre koehenkilön 4 haastattelussa oli se, että haastateltavan ymmärrys tarkasteltavista käsitteistä vaikutti selvästi parantuvan haastattelun kuluessa. Aluksi hän ei tiennyt, miten pyörteisyyden voi tun-
100 88 LUKU 7. Haastattelututkimus nistaa hiustenkuivaimen ilmavirtauksesta. Hetken päästä hän alkoi muistella luentodemonstraatioita: KH 4: On muistikuvia, että luennoilla oli tuollainen pyörteisyysdetektori, jonka pyörimistä vektorikentässä tarkasteltiin. Opiskelija jatkaa vielä pyörteisyyden pohdiskelua piirtämäänsä kuvaa katsoen ja arvelee, että pyörteisyyttä saattaisi esiintyä. Välillä tarkasteltiin käsitettä matemaattiselta kannalta, kunnes haastattelun loppupuolella palattiin vielä kvalitatiiviseen tarkasteluun. Haastattelija kysyi tällöin, miten derivaattalausekkeesta päättelemällä saadun tuloksen voisi tarkistaa mittaamalla. Koehenkilö vastasi empien KH 4: Ehkä siinä tarvitaan tuota siipiratasta. En tiedä. Haastattelija pyysi vielä opiskelijaa näyttämään sen konkreettisesti. Sitä kokeillessaan opiskelija totesi innostuneesti: KH 4: Kyllä tämä näinpäin pyörii! Syntyi vaikutelma, että pyörimissuunta oli hänen oletuksensa mukainen. Opiskelija kuitenkin jatkoi vielä mittaamista kääntäen siipirattaan akselin vaakasuuntaiseksi. Kokeillessaan lisää hän muuttui epävarmemmaksi, eikä lopulta halunnut sanoa mitään varmaa pyörimissuunnan merkityksestä. Varmaksi havainnoksi hän sanoi ainoastaan siipirattaan pyörimisen. Opiskelijan käsitteiden jäsentymisen vaihetta kuvaa se, että hänen sanansa olivat epävarmoja ja ajoittain ristiriitaisia sen kanssa, mitä kuvanauhalla nähdään tapahtuvan. Harjoitustehtävässä opiskelija määrittelee pyörteisyyden seuraavasti: Pyörteisyys kertoo siitä, joutuuko vektorikentän läpi virtaavien hiukkasten vuo pyörivään liikkeeseen kentässä. Tässä ilmenevät virhekäsitykset tukevat arviota, että käsitteiden jäsentyminen on vielä alkutekijöissä. Toisaalta haastattelun perusteella erityisesti tämän opiskelijan käsitteiden jäsentyminen oli niin nopeassa muutosvaiheessa, että voidaan kyseenalaistaa kaksi kuukautta ennen haastattelua tehdyn harjoitustehtävän käyttöä opiskelijan ymmärryksen arviointiin. Koska harjoituksen perusteella kvalitatiivinen ymmärrys luokiteltaisiin tasolle Y0 ja haastattelussa havaittiin paikoitellen tasolle Y2 yltävää, joskin epävarmaa, pohdintaa pyörteisyyden suunnasta, on turvallisinta luokitella haastatteluhetken ymmärrys tasolle Y1. Vaihe E2 Haastattelija kysyi, miten paperille kirjoitetussa lausekkeessa ( x v y y v x )k olevien osittaisderivaattojen arvot voidaan määrittää. Opiskelija päätteli piirtämänsä vektorikartan avulla näin:
101 7.5. Koehenkilöiden suoritusten arviointi 89 KH 4: Kun siirrytään x-suunnassa, niin virtaus on melkein vakio. Muutosnopeus on siis lähellä nollaa. Y-suunnassa muutosnopeus on paljon suurempi. Opiskelija pohdiskeli merkintöjä aikansa ja pystyi vähän kerrallaan lisäämään ymmärrystään lausekkeesta. Jonkun ajan päästä hän oli jo valmis esittämään päätelmiä, mitä derivaatoista saadaan lukuarvoiksi. KH 4: Virtauskomponenttia y-suunnassa ei ole käytännössä ollenkaan. Silloin termiä x v y ei tarvitse ajatella. Katsotaan vain termiä y v x. Siinä v x muuttuu y-suunnassa paljon. Se pienenee paljon. Se on siis negatiivinen. Roottorin arvon hän päätteli positiiviseksi jälkimmäisen derivaattatermin edessä olevan miinusmerkin takia: KH 4: Jos tuo x v y on nolla ja y v x on miinus, siitä tulee miinus miinus eli plus. Tulos on aivan oikein. Haastattelija uteli vielä opiskelijan käsitystä siitä, mitä vastaus tarkoittaa fysikaalisesti: KH 4: Se tarkoittaa, että esiintyy pyörteisyyttä. Haastattelija huomauttaa, että lausekkeessa oli vielä k-kirjain, jonka merkitystä opiskelija ei selittänyt. Siihen opiskelija vastasi: KH 4: Se tarkoittaa, että vastaukseksi tulee vektori. Koska saatiin positiivinen luku, on vektori k-suunnassa eli tasosta ylöspäin. T: Mitä vektorin suunta tarkoittaa? Onko sillä joku merkitys? KH 4: Ehkä se kertoo siitä, mihin suuntaan se pyörii? En tiedä. Koehenkilö osoitti kvantitatiivista ymmärrystä mittaavassa haastatteluosassa ymmärtävänsä, miten osittaisderivaattojen lukuarvoista voidaan esittää päätelmiä konkreettisen vektorikentän tapauksessa. Luokittelukriteerien (taulukko 7.2) perusteella taso on siten Y1. Jos edellä kuvattua verrataan opiskelijan koetehtävän b-kohdan suoritukseen, havaitaan tältäkin osin selvä ristiriita. Opiskelijan koevastaus b-kohtaan on variaatio aiemmin kuvatusta tyyppivirheestä, jossa tehtävää yritetään ratkaista symbolisesti. Joko opiskelijan ymmärrys on syventynyt kokeen ja haastattelun välisenä aikana tai sitten haastattelumenetelmä soveltui koetehtävää paremmin tämän opiskelijan ymmärryksen esiintuomiseen.
102 90 LUKU 7. Haastattelututkimus Koehenkilö 5 (KH 5) Vaihe E1 Haastattelussa tutkija kysyi opiskelijan ymmärrystä pyörteisyyden käsitteestä. Opiskelijan vastaus oli tyypillinen Y0-tason virhekäsitys: T: Mitä pyörteisyys tarkoittaa? KH 5: Syntyy pyörteitä. Virtaus ei kulje suoraan vaan kaartaa tiettyyn suuntaan. Haastattelija pyysi kertomaan tarkemmin pyörteisyyden mittaamisesta: T: Jos pitäisi selvittää pyörteisyys tietyssä virtauksen pisteessä, niin miten mittaisit sitä? KH 5: Ehkä tällaisella silkkipaperilla. Katsoisin lähteekö se kaartamaan tarkastelupisteessä johonkin suuntaan vai asettuuko se suoraan. Haastateltava ei kuitenkaan pystynyt sanomaan varmuudella mittauksen perusteella, esiintyykö tarkastelupisteessä pyörteisyyttä. T: Pystytkö sanomaan varmuudella, esiintyykö tarkastelupisteessä pyörteisyyttä? KH 5: En ihan varmuudella sano, mihin päin tuo silkkipaperi lähtee pyörimään. Opiskelija kokeili siipiratasta lyhyesti virtauskentässä, muttei osoittanut ymmärtävänsä, että pyörteisyyden voi tunnistaa sen avulla. Haastateltavalla ei ollut toimivaa käsitystä siitä, miten pyörteisyys voidaan havaita konkreettisessa virtauskentässä. Harjoitus- ja koevastauksista ei löydy tietoa siitä, miten opiskelija perustelee pyörteisyyden esiintymisen. Koska opiskelijalla ei ollut oikeaa tietoa pyörteisyyden hahmosta, on kvalitatiivisen ymmärryksen taso perustellusti Y0. Vaihe E2 Testatessaan opiskelijan kvantitatiivista ymmärrystä haastattelija kysyi, mitä osittaisderivaatta tarkoittaa konkreettisesti. Koska opiskelija ei osannut aluksi vastata mitään, johdatteli haastattelija yhden muuttujan funktion derivaatan avulla. T: Mitä tavallinen yhden muuttujan funktion derivaatta tarkoittaa?
103 7.5. Koehenkilöiden suoritusten arviointi 91 KH 5: Funktion muutosnopeutta. T: Entäs osittaisderivaatta? Liittyykö sekin jollain tavalla muutokseen? KH 5: Kyllä sekin kuvaa muutosnopeutta. Siihen liittyy myös suunta. Opiskelija ei kuitenkaan tiennyt, miten osittaisderivaatta voitaisiin määrittää mittaamalla. Opiskelija oli kirjoittanut paperille matemaattisesti virheellinen lausekkeen (ks. liite C.4.3) F = F x x + F y y + F z z = ai + bj + ck, joka hänen mielestään esitti vektorikentän pyörteisyyttä. Kysyttäessä, miten opiskelija määrittäisi kirjoittamansa lausekkeen arvon mittaamalla, opiskelija vastasi: KH 5: Yrittäisin mitata, miten paljon joku suunta muuttuu suorasta linjasta. Opiskelija ei siis pystynyt selittämään, mitä osittaisderivaatat tarkoittavat ja miten ne määritetään. Selitys oli sattumanvarainen ja virheellinen. Lisäksi koetehtävän b-kohdassa opiskelija esittää vastauksen, joka on aiemmin kuvattu tyyppiesimerkki tehtävään annetuista virheellisistä vastauksista. Opiskelijan E2-vaiheen jäsentäminen on perustellusti tasolla Y Haastatteluarvioinnin tulokset Haastattelun perusteella tehty koehenkilöiden luokittelu empiirisen ymmärryksen tasojen mukaan on koottu ristitaulukkoon, joka on esitetty kuvassa 7.8. Pienessä kuvassa näkyy samojen koehenkilöiden sijoittuminen koearvioinnin mukaisessa nelikentässä, joka esiteltiin luvussa Uuden luokituksen mukaan koehenkilö 1 on roottorin käsitteen ymmärryksessä edelleen pisimmällä. Vastaavasti koehenkilöiden 2 ja 5 empiirinen ymmärrys vaikuttaa haastattelujenkin valossa heikolta. Oleellisin ja tämän tutkimuksen kannalta mielenkiintoisin tulos on koehenkilöiden 3 ja 4 sijoittumien uudessa luokittelussa. Haastattelututkimus paljasti, että koehenkilön 3 kvalitatiivisen tason empiirinen ymmärrys ei ole niin varmalla pohjalla kuin nelikenttäluokituksen mukaan voisi odottaa. Häntä voi kuitenkin luonnehtia opiskelijaksi, jolla empiiristen merkitysten ymmärtäminen on hyvällä alullaan. Kyseisen opiskelijan saama arvosana kurssista oli 2. Tämä tekee opiskelijasta erityisen mielenkiintoisen
104 92 LUKU 7. Haastattelututkimus Y2 KH1 Nelikenttäluokitus E1 (hahmottava ymmärrys) Y1 Y0 KH3 KH2, KH5 KH4 E1 KH3 KH2, KH4, KH5 E2 KH1 Y0 Y1 Y2 E2 (kvantitatiivinen ymmärrys) Kuva 7.8: Tutkimusaineiston pohjalta tehty koehenkilöiden empiirisen ymmärtämisen luokittelu hahmottavan ja kvantitatiivisen ymmärryksen tasoilla E1 ja E2. Tasojen hienorakenne (Y0Y2) on luokiteltu YSOLO-tasojen mukaan (ks. taulukko 4.1). Oikealla olevassa pikkukuvassa on vertailtavana koehenkilöiden sijoittuminen alkuperäisessä pelkän koeanalyysin pohjalta tehdyssä karkeassa nelikenttäluokittelussa (ks. kpl 6.1.1). haastatteluun osallistuneiden opiskelijoiden joukossa. Hän on esimerkkitapaus opiskelijasta, jonka menestyminen kurssilla oli alle keskitason, mutta joka saavutti alustavaa kvalitatiivisen tason empiiristä ymmärrystä roottorista. Koehenkilön 4 tapaus on mielenkiintoinen siitä syystä, että koenelikentän perusteella hän ei ole saavuttanut kvalitatiivista eikä kvantitatiivista ymmärrystä roottorin käsitteestä. Haastattelun yhteydessä opiskelija kykeni kuitenkin palauttamaan mieleen kurssilla oppimiaan asioita ja osoitti alustavaa empiiristä ymmärrystä sekä vaiheessa E1 että E2. Erityisesti merkillepantavaa on, että palauttaessaan mieleen opittuja asioita, opiskelija muisteli luennoilla esitettyjä demonstraatioita. Havaittiin, että koehenkilöillä 2 ja 5 oli vaikeuksia osittaisderivaatan empiirisen merkityksen ymmärtämisessä. He ymmärsivät osittaisderivaatan kuvaavan muutosta, mutta eivät kyenneet kertomaan, mitä se haastattelun konkreettisen ilmiön tapauksessa tarkoitti. Koehenkilö 2 käytti termiä pyörteisyyden lähde kuvatessaan pisteitä, joissa hänen mukaansa virtauskenttään
105 7.5. Koehenkilöiden suoritusten arviointi 93 syntyi pyörteisyyttä. Toinen havaittu virhekäsitys oli ajatus osittaisderivaatan x F y määrittämisestä vektorinuolten kulmakertoimiin perustuen. Yleisenä piirteenä haastatteluissa havaittiin, että vektorifunktion komponenttien ymmärtäminen tuotti vaikeuksia osittaisderivaatan yhteydessä. Tutkijalle syntyi haastatteluissa yleisvaikutelma, että asian ymmärtämistä mutkistaa se, että roottorin lausekkeessa x- ja y-suunnat esiintyvät ristiin: tutkitaan kentän y- komponentin muuttumista x-suunnassa ja päinvastoin.
106
107 Luku 8 Luotettavuuden ja laadun arviointi Tässä luvussa tarkastellaan tutkimuksen laatua ja luotettavuutta. Niiden arvioinnissa seurataan Kilpatrik (1993) esittämiä matematiikan opetuksen tutkimusta varten laadittuja ohjeita soveltuvin osin sekä kirjan Metsämuuronen (2005) käsittelyä reliabiliteetin ja validiteetin arvioinnista. 8.1 Reliabiliteetti ja validiteetti Validiteetti on tutkimuksen luotettavuuden arviointia siinä mielessä, ollaanko tutkittu sitä, mitä on ollut tarkoitus tutkia (Metsämuuronen, 2005). Validiteetti voi olla joko sisäistä tai ulkoista. Sisäinen validius tarkoittaa tutkimuksen omaa luotettavuutta. Siihen vaikuttavat mm. käytetyt käsitteet, valittu teoria ja mittarit. Ulkoisella validiteetilla tarkoitetaan tutkimuksen yleistettävyyttä muihin tilanteisiin ja asiayhteyksiin Sisäinen validiteetti Tutkimuksessa tarkasteltiin divergenssin ja roottorin käsitteenmuodostusta matematiikan ja fysiikan opetuksen sekä opetusteknologioiden tutkimuksen näkökulmista. Matematiikan käsitteenmuodostuksen osalta teoreettinen viitekehys on luotu tutustumalla aiempien derivaatan oppimista käsittelevien tutkimusten teoriapohjaan (Berry ja Nyman, 2003; Hähkiöniemi, 2006) kuin myös yleisiin matemaattista ajattelua koskeviin tutkimuksiin (Joutsenlahti, 2005; Yrjönsuuri, 1990, 1994). Fysiikan osalta tutkimus liittyy empiiriseen käsitteenmuodostukseen, jonka teoreettinen pohja perustuu kirjan Kurki-Suonio ja Kurki- Suonio (1998) perinpohjaiseen käsittelyyn aiheesta. Myös Meisalo ja Erätuuli (1985) antoi perspektiiviä aiheeseen, vaikkei sitä varsinaisena teoreettisena läh-
108 96 LUKU 8. Luotettavuuden ja laadun arviointi teenä käytettykään. Opetusteknologian käyttöä koskevista tutkimuksista valittiin teoreettiseen taustaan mukaan yleiskatsaus moderneista oppimisympäristöistä (Meisalo et al., 2003) sekä erityisesti animaatioiden käyttöä koskevien julkaisujen (Ainsworth, 2008; Tversky et al., 2002) keskeisimpiä tuloksia. Erityisesti Tversky et al. (2002) kriittinen katsaus animaatioiden käytöstä katsottiin tärkeäksi teoreettisen taustan objektiivisuuden parantajana. Tutkimuksessa väitetään mitattavan opiskelijoiden empiiristä ymmärrystä divergenssin ja roottorin käsitteistä. Empiirinen ymmärrys on määritelty fysiikan empiirisen käsitteenmuodostuksen näkökulmasta (Kurki-Suonio ja Kurki-Suonio, 1998). Sen mittareina on käytetty koe- ja harjoitustehtäviä sekä toiminnallisia haastattelutehtäviä. Koetehtävän analyysi osoitti, että tehtävän kvalitatiiviseksi ja kvantitatiiviseksi laadituista osioista saadut pistemäärät noudattivat odotettua käsitteenmuodostuksen hierarkiaa kvalitatiivisesta kvantitatiiviseen siten että kaikki kvantitatiivisessa osassa menestyneet hallitsivat myös kvalitatiivisen puolen. Pelkästään kvantitatiivisessa osassa menestyneitä ei löytynyt. Koetehtävän toimivuuden varmistamiseksi myös kurssin assistentteja pyydettiin tekemään koetehtävä. Viidestä tehtävän palauttaneesta assistentista 4 sijoittui ryhmään R1 (ks. kpl 6.1.1) ja yksi ryhmään R2. Ryhmään R1 sijoittuvissa vastauksissa tehtävä oli ymmärretty täydellisesti ja perinpohjaiset vastaukset olivat hyviä esimerkkejä empiirisen ymmärryksen varmuudesta. Tämä havainto ei kuitenkaan vielä todista, että tehtävä todella mittaa empiiristä ymmärrystä. Tarkempaa tietoa koetehtävän validiudesta saatiin vertaamalla siitä saatuja tuloksia haastattelumenetelmällä saatuihin tuloksiin. Havaittiin, että haastattelun ja saman henkilön koevastauksen välillä oli paikoin ristiriitaisuutta. Tämä saattaa johtua esimerkiksi siitä, että koetilanteessa voi esiintyä kiirettä ja jännitystä tai koekysymyksen muotoilu ei ole ollut riittävän selkeä. Haastattelussa samaa asiaa voidaan kysyä eri sanoin ja haastattelija voi käyttää johdattelua. Toisaalta eron syynä voi olla myös se, että kokeen ja haastattelun välillä oli kaksi kuukautta aikaa. Ainakin kaksi haastattelussa ollutta koehenkilöä valitti asioiden alkaneen unohtua tässä ajassa. Kaikissa luokittelutilanteissa on pyritty noudattamaan varovaisuuden periaatetta: Jos luokituksessa käytetyissä havainnoissa nähdään voimakkaita perusteita sekä korkeamman että matalamman luokituksen puolesta, on luokittelu tehty alaspäin.
109 8.1. Reliabiliteetti ja validiteetti Ulkoinen validiteetti Yksi tutkimuksessa tehdyn opetuskokeilun luotettavuuden uhka ovat harjoitustilaisuudet. Harjoitustunteja oli kurssilla yhtä paljon kuin luentojakin. Harjoituksia pitäviä assistentteja ei oltu erikseen opastettu tutkimuksen tavoitteita silmällä pitäen. Tämä johtui toisaalta assistenttien suuresta määrästä ja toisaalta luontaisen ilmaisutyylien eroista. Tutkija kontrolloin assistenttien työtä ainoastaan kurssin alussa pidetyssä yleispalaverissa käytyjen yleisten linjausten ja tehtävien mallivastauksissa mainittujen lyhyiden selitysten muodossa. Siitä, miten harjoitustunnit käytännössä sujuivat, ei ole yksityiskohtaista tietoa. Jokainen kurssin opiskelija osallistui sekä koti- että ex tempore-harjoituksiin. Opiskelijat jaettiin ryhmiin harjoitusaikatoiveiden mukaisesti. Näin ollen suuri osa opiskelijoista oli koko kurssin ajan kahden eri assistentin opetuksessa (vain harvat opiskelijat olivat saman assistentin ryhmässä sekä koti- että ex tempore-harjoituksissa). Tämä tasoittaa hieman harjoitusassistentin vaikutusta mittausasetelmaan. Tutkimuksen otanta oli koevastausten osalta kaikki loppukokeeseen osallistuneet. Haastateltavat pyrittiin valikoimaan niin, että he edustaisivat mahdollisimman monipuolisesti erilaisia esimerkkitapauksia kurssin opiskelijoista. Tämän onnistumista on vaikea arvioida. Saatujen tulosten valossa näyttää kuitenkin siltä, että otanta oli onnistunut, sillä opiskelijat jakautuivat eri luokkiin haastattelun perusteella. On tärkeää tiedostaa, että kurssin opiskelijajoukko on valikoitunut. Opiskelijat ovat pääosin fysiikan pääaineopiskelijoita, jotka ovat lähtökohtaisesti matemaattisesti suuntautuneita. Tästä kertoo myös lähtötasotesti, jonka mukaan suurin osa opiskelijoista on suorittanut kaikki pakolliset ja syventävät matematiikan lukiokurssit. Syksyn 2007 Matemaattiset apuneuvot II -kurssin arvosanajakauma oli kaksihuippuinen. Huippuina oli kiitettävästi osanneet ja hylätyn arvosanan saaneet. Joukossa on paljon matemaattisesti lahjakkaita opiskelijoita. Tämä saattaa asettaa rajoituksia tutkimuksen yleistettävyydelle. Tuloksissa havaittiin kuitenkin, että tavoiteltuja oppimistuloksia saavutettiin kaikissa arvosanaryhmissä. Jos havainto pitää paikkansa, voidaan katsoa, että tutkimuksen tuloksia voi yleistää myös tapauksiin, joissa opiskelijaryhmän matemaattisen osaamisen lähtötaso on rakenteeltaan erilainen kuin tässä tarkastellulla kurssilla 1 1 Tutkija on jo itse soveltanut tässä tutkimuksessa käytettyjä opetusmenetelmiä ammattikorkeakouluopetuksessa.
110 98 LUKU 8. Luotettavuuden ja laadun arviointi Reliabiliteetti Reliabiliteetilla tarkoitetaan mittauksen toistettavuutta (Metsämuuronen, 2005). Tutkimuksessa käytetyt mittarit on pyritty esittämään niin seikkaperäisesti, että mittaukset olisi periaatteessa mahdollista toistaa niiden avulla. Koe- ja harjoitustehtävät ja analyysimenetelmät kuin myös haastattelun käsikirjoitus, koeasetelma ja analyysimenetelmät on dokumentoitu yksityiskohtaisesti tässä raportissa. Itse opetuskokeilu ei luonnollisesti ole yksityiskohdiltaan täydellisesti toistettavissa, sillä opettajat ovat yksilöitä ja kurssin käytännön puitteet olivat vahvasti sidoksissa kurssin opetuspaikkaan. 8.2 Objektiivisuus Tutkimuksen objektiivisuus on tavoite, jota kohti on pyrittävä, vaikka kokonaisobjektiivisuutta on mahdotonta saavuttaa opetuksen tutkimuksessa (Kilpatrik, 1993). Tärkeää on tunnistaa tutkijan oma puolueellisuus ja ennakkoasenteet, jotka voivat vaikuttaa tutkimustuloksiin. Tässä tarkasteltavassa tutkimuksessa tehtiin opetuskokeilu, jossa tutkija toimi itse opettajana. Kirjoittaja on itse positiivisesti asennoitunut visualisaatioiden ja demonstraatioiden hyötyihin opetuksessa. Tämän vaikutusta voidaan testata kyseenalaistamalla tehtyjä johtopäätöksiä. Tarkastellaan vastahypoteesiä visualisaatioilla ei ollut mitään vaikutusta opiskelijoiden divergenssin ja roottorin empiiristen merkitysten hahmottamiseen. Opiskelijoiden koe- ja harjoitusvastauksissa ja haastatteluissa kuitenkin selvästi havaittiin, että jotkut opiskelijat käyttävät suoraan luennoilla esitettyjä demonstraatioita perusteluina määrittäessään esimerkiksi roottorin arvoa. Tällä perusteella kyseessä on objektiivinen ja aito havainto. Tutkija tutustui myös kriittisiin kannanottoihin uusien opetusteknologioiden käytöstä (Tversky et al., 2002). 8.3 Tutkimuksen tärkeys Tutkimuksen tärkeyttä (relevance) voidaan arvioida vastaamalla kysymyksiin (Kilpatrik, 1993) Onko tutkimuksesta hyötyä? Ja kenelle? Mahdollista hyötyä on syytä pohtia sekä opettajien että alan tutkijoiden näkökulmasta. Tutkimuksen yleistavoitteena oli parantaa vektorianalyysin opetusta niin, että opetus tukisi opiskelijoiden hahmotusprosessia divergenssin ja roottorin empiirisistä merkityksistä. Työhön liittyi opetuskokeilu, jonka yhteydessä testattiin uusien tämän aihepiirin opetusta varten laadittujen menetelmien toimi-
111 8.3. Tutkimuksen tärkeys 99 mista tavoitteen saavuttamisessa. Tuloksina saatiin tietoa opiskelijoiden empiirisen ymmärryksen tasosta. Havaittiin myös virhekäsityksiä, joiden huomioiminen aihepiirin opetuksessa voi auttaa oppimisprosessissa. Lisäksi esitetään aiemmin tutkittuun fysiikan käsitteenmuodostusprosessiin pohjautuva suositus aihepiirin opetuksen järjestämiseksi niin, että se tukee empiirisiä merkityksiä. Edellä mainituista syistä tutkimuksella on välitöntä käytännön merkitystä matematiikan korkeakouluopetukselle. Työ on jatkoa aiemmille dierentiaalilaskennan oppimista ja opettamista koskeville tutkimuksille. Sillä on myös yhteyksiä opetusteknologiatutkimuksiin aiempia havaintoja testaavassa mielessä. Tutkimuksessa yhdistetään matematiikan oppimisen kognitiivisia teorioita ja fysiikan hahmottavan käsitteen muodostuksen teoria saman viitekehyksen alle.
112
113 Luku 9 Johtopäätökset ja suositukset Tässä luvussa tarkastellaan tutkimusongelmien (kpl 4.4) vastauksia sekä tutkimushypoteesin (kpl 4.3) toteutumista kokeen ja haastattelun analyysissä saatujen tulosten (kappaleet 6.2 ja 7.5.3) valossa. Esitetään myös suosituksia, joihin johtopäätökset antavat aihetta. 9.1 Johtopäätökset Opetushypoteesin toteutumisen arvio Opetushypoteesin toteutumiselle asetettiin kolme kriteeriä (kpl 4.3), jotka kuvaavat empiirisen hahmotusprosessin vaiheita. Näiden kriteereiden täyttymisen mittausta varten oli asetettu tutkimusongelmat B.1B.3 (kpl 4.4), jotka olivat B.1 Osaako opiskelija kiinnittää divergenssin ja roottorin käsitteet empiirisiin olioihin tai ilmiöihin? B.2 Osaako opiskelija luonnehtia divergenssin ja roottorin arvoa kvalitatiivisten havaintojen pohjalta? B.3 Osaako opiskelija määrittää divergenssin ja roottorin numeerisen arvon mittaamalla määrittelylausekkeeseen perustuen? Näiden vastaavuus empiirisen ymmärryksen luokituksen kanssa on seuraava: B.1 = E1 (taso Y1) B.2 = E1 (taso Y2) B.3 = E2 (tasot Y1 ja Y2). Tasot Y1 ja Y2 viittaavat haastattelun yhteydessä tehtyyn tarkempaan YSOLOtasojen mukaiseen luokitukseen.
114 102 LUKU 9. Johtopäätökset ja suositukset Opiskelijoiden koevastausten analyysi paljasti, että 20 % opiskelijoista saavutti kvalitatiivisen ymmärryksen tason E1 ja 12 % kvantitatiivisen ymmärryksen tason E2. Näin ollen 32 % kurssin opiskelijoista saavutti vähintään kvalitatiivisen (hahmottavan) empiirisen ymmärryksen tason divergenssin ja roottorin käsitteistä. Loput 68 % opiskelijoista ei koetehtävän luokituksen mukaan juurikaan ymmärtänyt divergenssiä ja roottoria empiirisesti, vaan heidät luokiteltiin tasolle E0. Haastattelussa paljastui, että yksi alunperin tasolle E0 luokiteltu opiskelija hallitsi kvalitatiivista hahmotusta E1 tasolla Y1 ja myös kvantitatiivista hahmotusta E2 tasolla Y1. Tämä antaa viitteitä siitä, että osa tasolle E0 luokitelluista opiskelijoista saattaisi tarkemmassa luokituksessa kuulua alkuperäistä luokitusta korkeammalle tasolle. Siitäkin huolimatta on hyvin kyseenalaista, voidaanko edes hypoteesin osittaisesta toteutumisesta puhua. Tutkijan odotuksena oli, että huomattavasti useampi opiskelija olisi päässyt kvantitatiivisen hahmotuksen tasolle. Nyt kuitenkin 68 % vastauksista esiintyi vakava virhe, jossa opiskelija laskee vektorikentän osittaisderivaattaa derivoimalla symbolisesti kentän yksittäistä numeroarvoa Opetuskokeilun positiiviset vaikutukset Vaikka opetushypoteesin toteutuminen on saatujen tulosten valossa kyseenalaista, löydettiin tutkimuksessa myös positiivisia merkkejä opetuskokeilun vaikutuksista. Ensiksikin havaittiin, että empiirisen hahmotuksen tason E1 saavuttaneiden joukossa on myös heikon kurssiarvosanan saaneita opiskelijoita. Empiirinen hahmotus on siis mahdollista opiskelijan kurssimenestyksestä riippumatta. koe- ja harjoitustehtävien avointen kysymysten kautta saatiin toisaalta myös näyttöä siitä, että kurssilla käytetyillä opetusmenetelmillä on ollut suora yhteys ainakin joidenkin opiskelijoiden empiirisen ymmärryksen kehittymiseen. Tämän osoittavat vastaukset, joissa opiskelija perustelee päätelmiään vektorikentän divergenssistä ja roottorista ajatuskokeilla, jotka perustuvat opetuskokeilun aikana esitettyihin visualisaatioihin ja fysikaalisiin analogioihin. Esimerkkejä ovat: Kuvitteellinen pyörredetektori pyörii myötäpäivään, tällöin roottori on negatiivinen. Jos pisteeseen kuviteltaisiin pallo, ja kyseessä olevat vektorit kuvaisivat voimia, alkaisi pallo pyöriä.
115 9.1. Johtopäätökset 103 aksiomaattisformaali Stokesin lause empiiriset merkitykset pyörteisyys kiertämätiheys E2 E1 kiertämä kulmanopeus siipirattaan pyöriminen hiukkasvirta Esitys: vektorikartta proseptuaalissymbolinen käsitteellisilmentynyt F Kuva 9.1: Empiiristen polkujen muodostuminen matematiikan käsitteiden välille matematiikan kolmen maailman teoriaan sovellettuna (ks. kpl 4.6, kuva 4.3). Esimerkkinä virtauskentän pyörteisyyden empiirinen havaitseminen siipirattaan avulla. Vektorikentän pyörteisyyden havaitsemisessa käytettävä kuvitteellinen tai konkreettinen pyörteisyysdetektori ei ole matematiikan käsitteisiin kuuluva objekti. Se on empiirinen mittalaite, jonka toiminta perustuu fysikaaliseen ilmiöön. Tällaisen empiirisen mittalaitteen käyttö voi tarjota uuden tavan oppia matematiikan käsitteitä. Kuvassa 9.1 on esitetty, kuinka empiiriset havainnot luovat uusia reittejä matematiikan käsitteiden välille matematiikan kolmen maailman teoriassa. On mahdollista, että käsitteenmuodostuminen tällaista empiiristä oikotietä pitkin, on toisinaan yksinkertaisempaa kuin normaalia matemaattista reittiä, kuten myös Kurki-Suonio (2006) esittää luennossaan. Pyörteisyysdetektori voidaan nähdä yhtenä esimerkkinä tällaista empiiristä oikotietä tapahtuvasta käsitteenmuodostuksesta (ks. kpl 7.5.1) Opetuskokeilun kokemukset opettajan näkökulmasta Tutkimusongelma A liittyi opetuksen suunnitteluun. Tarkoituksena oli toteuttaa opetuskokeilu, jossa hyödynnetään visualisaatioita ja fysikaalisia analogioi-
116 104 LUKU 9. Johtopäätökset ja suositukset ta. Opetuskokeilun kuvaus oli jo itsessään vastaus tähän kysymykseen, mutta tässä esitellään kokeilun toteuttamiseen liittyvää pohdintaa. Konkreettisten fysikaalisten havainnollistusvälineiden käyttö (styrox-pallo ja alumiiniputket) ei vaatinut opettajalta erityistä valmistelua. Ne olivat osa normaalia rutiinia ja kulkivat luennoilla aina mukana valmiina spontaania käyttöä varten. Sen sijaan opetuskokeilua varten laaditut opetusanimaatiot vaativat valtavasti esityötä. Opetusohjelmien todellista hyötyä arvioitaessa on kustannus-hyötysuhde yksi kriteeri (Meisalo et al., 2003). Kukin animaatio oli kestoltaan vain 12 minuuttia, mutta niiden valmisteluun kului kertaisesti aikaa. Tämä aika sisältää vain animaation laatimiseen kuluneen ajan, joka vietettiin tietokoneen ääressä. Sen jälkeen ohjelma piirsi animaation ruutu kerrallaan mallintamalla valonkulkua virtuaalimaailmassa. Kahden minuutin animaatio koostuu 3000 ruudusta, joiden piirtämiseen saattoi kulua jopa 4 tuntia 1. Tästä syystä tietokoneajot suoritettiinkin usein yöaikaan. Valmiita animaatioita voidaan kuitenkin käyttää lukuisia kertoja, mikä pienentää valmisteluajan osuutta käyttöaikaan nähden pitkällä aikavälillä. Esimerkiksi joitakin tässä opetuskokeilussa laadittuja animaatioita on jo ehditty käyttää opetuksessa myöhemmillä yliopisto- ja ammattikorkeakoulukursseilla. Animaatio-ohjelmaa valitessa oli tärkeä kriteeri, että satoja työtunteja vaativat työtiedostot säilyisivät käyttökelpoisina kehityspohjina pitkälle tulevaisuuteen. Avoimeen lähdekoodiin perustuva Blender-ohjelma vaikutti tässä mielessä hyvältä valinnalta. Avoimuutensa takia sen käyttämälle tallennusformaatille on mahdollista laatia konvertointiohjelmia, vaikka ohjelman kehitys joskus lakkaisikin. Lisäksi Blenderin käyttöä puolsi tieto siitä, että sitä on käytetty muuallakin fysikaalisten opetusanimaatioiden tekoon ja ohjelma sisältää fysikaaliseen mallinnukseen vaadittavia toimintoja. Hyvän selkeän ja toimivan animaation tekeminen on valtava urakka ja vaatii paljon suunnittelua, kokeilua ja opiskelua. Matkalla ideasta valmiiseen animaatioon joutuu todennäköisesti tekemään monta kompromissia. Lienee selvää, että tällainen uhrautuminen vaatii opettajalta kärsivällisyyden lisäksi suurta henkilökohtaista mielenkiintoa aiheeseen. Tämän opetuskokeilun jälkeen tutkija on sitä mieltä, että animaatioiden käytöllä on potentiaalia vektorianalyysin opetuksessa, kunhan niiden valmisteluun on käytettävissä riittävästi resursseja. Kokeilussa saatiin erinomaisia ko- 1 Käytössä oli vuoden 2007 mittapuun mukaan suhteellisen moderni 2,4 GHz taajuudella toimiva kaksiytiminen Intel Core 2 Duo -prosessori.
117 9.2. Suositukset ja pohdintaa 105 kemuksia myös interaktiivisten java-simulaatioiden käytöstä. Kun otetaan huomioon animaatioiden hyötyjä kohtaan esitetty kritiikki (Tversky et al., 2002) ja esitetty parannusehdotus juuri interaktiivisuuden muodossa, on tulevaa opetusta suunnitellessa syytä myös pohtia, pystyisikö animaation opetusidean toteuttamaan kenties paremmin java-ohjelmana. 9.2 Suositukset ja pohdintaa Tutkimusongelmien C -kohdassa esitetään kysymyksiä, miten opetusta voidaan tehostaa saatujen kokemusten perusteella. Tulevan opetuksen järjestämisen kannalta on kiinnostavaa, miksi 68 % opiskelijoista ei saavuttanut empiirisen hahmotuksen tasoa E1. Haastattelututkimuksissa nähtiin, että osa opiskelijoista ei ymmärtänyt osittaisderivaatan empiiristä merkitystä. Vaikka koehenkilöt hallitsivat yhden muuttujan funktion derivaatan graasen määrityksen vaiheet, eivät he ymmärtäneet, mitä vektorikentän osittaisderivaatta tarkoittaa tai miten sitä voidaan mitata. On mahdollista, että myös vektorifunktion käsite on opiskelijoille vaikea. Tätä päätelmää tukee koetehtävän vastauksissa kohdattu tyyppivirhe: Opiskelijat eivät ole ymmärtäneet eroa vektorifunktion pisteittäisen arvon ja vektorifunktion symbolisen lausekkeen välillä. Näihin ongelmiin voitaneen vaikuttaa tarkastelemalla osittaisderivaatan määritystä myös numeerisesti ja kiinnittämällä opetuksessa huomiota vektorifunktion eri esitystapoihin ja niiden välillä siirtymiseen. Tällainen suositus vastaa matematiikan kolmen maailman teorian mukaista oppimiskäsitystä. Oppikirjojen vektorianalyysin opetusta tarkastellessa nähtiin, että empiiristen merkitysten ymmärtämistä tuetaan kirjoissa vaihtelevasti. On epätodennäköistä, että opetus, jossa analogioita ei käytetä, johtaisi divergenssin ja roottorin empiiristen merkitysten muodostumiseen. Matematiikan kolmen maailman teorian mukaisesti käsitteiden oppiminen voi alkaa joko symbolien maailmasta tai objektien ilmentymien maailmasta. Objektien maailmassa oppiminen vastaa divergenssin ja roottorin oppimista symbolisina laskuoperaatioina vailla selvää yhteyttä konkreettisiin ilmentymiin. Tällöin matematiikan soveltajan on tehtävä käsitteiden kiinnitysprosessi jälkikäteen löytämällä symbolisten lausekkeiden ja ilmentymien välillä vastaavuus. Fysiikan näkökulmasta divergenssi ja roottori voidaan nähdä vektorikenttäsuureeseen liittyvinä johdannaissuureina. Tällöin kentän divergenssin ja roottorin merkitysten rakentuminen lähtee emosuureeseen liittyvien ominaisuuksien ymmärtämisestä. Yksinkertainen fysikaalinen esimerkki, joka voi toimia
118 106 LUKU 9. Johtopäätökset ja suositukset näiden käsitteiden esihahmotuksen välineenä ovat nestevirtaukset. Tällöin luonnollinen tapa edetä suureen hahmotuksessa on edetä makroskooppisesta suureesta kohti mikroskooppista. Luvussa (5.4) todettiin, että vektorianalyysin opetus on mahdollista järjestää makroskooppisista vektorikentän kiertämän ja vektorikentän vuon suureista lähtien. Suosituksena esitetään, että empiirisiä merkityksiä korostava vektorianalyysin opetus noudattaisi tätä fysiikasta tuttua käsitteenmuodostuksen reittiä. Tutkimuksessa tarkastelluista oppikirjoista etenkin Weir et al. (2008) soveltuu hyvin käytettäväksi tällaiseen empiriaa korostavaan opetukseen. Tässä tutkimuksessa hahmoteltiin aiempiin matematiikan ja fysiikan käsitteenmuodostuksen tutkimustuloksiin pohjautuen uutta empiiristä lähestymistapaa vektorianalyysin opetukseen. Tutkimus tarjoaa uusia mielenkiintoisia mahdollisuuksia tuleville opetuskokeilulle ja jatkotutkimukselle tässä esitettyjen suositusten testaamisen ja jatkokehityksen muodossa.
119 Lähteet Adams, R. A. (2003). Calculus: a complete course. Addison Wesley, 5. painos. Ainsworth, S. (2008). How Do Animations Inuence Learning? Kirjassa D. Robinson & G. Schraw (toim.), Current Perspectives on Cognition, Learning, and Instruction: Recent Innovations in Educational Technology that Facilitate Student Learning, ss Information Age Publishing. Artigue, M. (2001). What can we learn from educational research at the university level? Kirjassa Holton, D. et al. (toim.), The Teaching and Learning of Mathematics at University Level: An ICMI study, ss Kluwer Academic Publishers. Astala, K., Kivelä, S. K., et al. (2005). Pisa-tutkimus vain osatotuus suomalaisten matematiikan taidoista. Matematiikkalehti Solmu, 1/2005. Berry, J. S. ja Nyman, M. A. (2003). Promoting students' graphical understanding of the calculus. Journal of Mathematical Behavior, 22(4): Borko, H. et al. (1992). Learning to teach hard mathematics: Do novice teachers and their instructors give up too easily. Journal for Research in Mathematics Education, 23(3): Croft, A., Davison, R. ja Hargreaves, M. (2001). Prentice-Hall, 3. painos. Engineering Mathematics. Dray, T. ja Manogue, C. A. (1999). The vector calculus gap: Mathematics physics. PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 1. Dray, T. ja Manogue, C. A. (2002). Bridging the vector (calculus) gap. Kirjassa Sternheim, M. M. (toim.), Pathways to Change: An International Conference on Transforming Math and Science Education in the K16 Continuum.
120 108 LÄHTEET Dubinsky, E. ja McDonald, M. A. (2001). APOS: A constructivist theory of learning in undergraduate mathematics education research. Kirjassa Holton, D. et al. (toim.), The Teaching and Learning of Mathematics at University Level: An ICMI study, ss Kluwer Academic Publishers. Gray, E. M. ja Tall, D. O. (1994). Duality, ambiguity and exibility: A proceptual view of simple arithmetic. The Journal for Research in Mathematics Education, 25(2): Haapasalo, L. (2004). Pitääkö ymmärtää voidakseen tehdä vai pitääkö tehdä voidakseen ymmärtää? Kirjassa P. Räsänen, P. Kupari et al. (toim.) Matematiikka näkökulmia opettamiseen ja oppimiseen, ss Niilo Mäki Instituutti. Hähkiöniemi, M. (2006). The Role of Representations in Learning the Derivative. PhD thesis, University of Jyväskylä. Holton, J. R. (2004). An Introduction to Dynamic Meteorology. Elsevier, 4. painos. Honkonen, J., Perko, T. ja Pitkänen, M. (2003). Fysiikan matemaattiset apuneuvot. Limes ry, 6. painos. Joutsenlahti, J. (2005). Lukiolaisten matemaattisen ajattelun piirteitä luvun pitkän matematiikan opiskelijoiden matemaattisen osaamisen ja uskomusten ilmentämänä. Väitöskirja, Tampereen yliopisto. Kilpatrik, J. (1993). Beyond Face Value: Assessing Research in Mathematics Education. Kirjassa G. Nissen ja M. Blomhøj (toim.) Criteria for Scientic Quality and Relevance in the Didactics of Mathematics, ss Danish Research Council for the Humanities. Kupari, P., Välijärvi, J., et al. (2004). Nuoret osaajat: Pisa tutkimuksen ensituloksia. Kurki-Suonio, K. (2006). Kolme luentoa käsitteenmuodostuksesta: Fysiikan täydennyskoulutuskurssi, fysiikan historia ja losoa http: //per.physics.helsinki.fi/kurkisuo/4/06-kolmeluentoa.pdf (haettu ). Kurki-Suonio, K. ja Kurki-Suonio, R. (1998). Fysiikan merkitykset ja rakenteet. Limes ry.
121 LÄHTEET 109 Kurki-Suonio, K. ja Kurki-Suonio, R. (1999). sähkömagnetismin perusteet. Limes ry. Vuorovaikutuksista kenttiin Kvale, S. (1996). InterViews: An Introduction to Qualitative Research Interviewing. Sage Publications. Lahtinen, A. ja Pehkonen, E. (1992). Matematiikkaa soveltajille: peruskurssi korkeakouluja varten, osa 1. Kirjayhtymä. Lahtinen, A. ja Pehkonen, E. (1994). Matematiikkaa soveltajille: peruskurssi korkeakouluja varten, osa 2. Kirjayhtymä. Lahtinen, A., Pehkonen, E., Kalliorinne, K. ja Manninen, S. (1989). Matematiikkaa soveltajille: peruskurssi korkeakouluja varten, osa 3. Kirjayhtymä. Lehtinen, M. (2000). Matematiikan historia. Matematiikkalehti Solmu, http: //solmu.math.helsinki.fi/. Martio, O. (2005). Pisa-tutkimus, matematiikan oppisisällöt ja opettajat. Matematiikkalehti Solmu, Erikoisnumero 1/ Meisalo, V. ja Erätuuli, M. (1985). Fysiikan ja kemian didaktiikka. Kustannusosakeyhtiö Otava. Meisalo, V., Sutinen, E. ja Tarhio, J. (2003). Tietosanoma. Modernit oppimisympäristöt. Merenluoto, K. ja Lehtinen, E. (2004). Käsitteellisen muutoksen näkökulma matematiikan oppimiseen ja opettamiseen. Kirjassa P. Räsänen, P. Kupari et al. (toim.) Matematiikka näkökulmia opettamiseen ja oppimiseen, ss Niilo Mäki Instituutti. Metsämuuronen, J. (2005). Tutkimuksen tekemisen perusteet ihmistieteissä. International Methelp, 3. laitos. Novak, J. D. ja Gowin, D. B. (1995). Opi oppimaan. Gaudeamus. Opetushallitus (1994). Lukion opetussuunnitelman perusteet. Pasanen, O. (2006). Matemaattiset apuneuvot I. Luentomuistiinpanot, Helsingin yliopisto, Fysiikan laitos. Pasanen, O. (2008). Opiskelijoiden käsityksiä divergenssistä ja roottorista. Laudaturtutkielma, Helsingin yliopisto.
122 110 LÄHTEET Pasanen, O. (2003). [Opiskelijoiden toiveita Mapu-kurssin kyselytunneilla käsiteltävistä aiheista vuosina ]. Julkaisemattomat muistiinpanot. Pegg, J. ja Tall, D. (2005). The fundamental cycle of concept construction underlying various theoretical frameworks. International Reviews on Mathematical Education (Zentralblatt für Didaktik der Mathematik), 37(6): Powell, A. B., Francisco, J. M. ja Maher, C. A. (2003). An analytical model for studying the development of learners' mathematical ideas and reasoning using videotape data. Journal of Mathematical Behavior, 22: Rieber, L. P. (1991). Animation, incidental learning, and continuing motivation. Journal of Educational Psychology, 83(3): Sfard, A. (1991). On the dual nature of mathematical conceptions: Reections on processes and objects as dierent sides of the same coin. Educational Studies in Mathematics, 22(1):136. Stewart, J. (2003). Single Variable Calculus: early transcendentals. Brooks/Cole, 5. painos. Tall, D. (2004). Thinking through three worlds of mathematics. Kirjassa The 28th International Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway July 2004, ss Tall, D. (2008). The transition to formal thinking in mathematics. Mathematics Education Research Journal, 20(2):524. Teerikorpi, P. ja Valtonen, M. (1990). Kosmos maailmamme muuttuva kuva. Tähtitieteellinen yhdistys Ursa. Tversky, B., Morrison, J. B. ja Betrancourt, M. (2002). Animation: Can it facilitate? International Journal of Human-Computer Studies, 57: Valtion tiede- ja teknologianeuvosto (2003). Osaaminen, innovaatiot ja kansainvälistyminen. Väisälä, K. (1961). Vektorianalyysi. WSOY, 3. painos. Weir, M. D. et al. (2008). Thomas' Calculus: Media Upgrade. Pearson Addison- Wesley, 11. painos.
123 LÄHTEET 111 Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358: Yrjönsuuri, R. (1990). Lukiolaisten matemaattisen ajattelun oppiminen. Helsingin yliopiston opettajankoulutuslaitos. Tutkimuksia nro 88. Helsingin yliopisto. Yrjönsuuri, R. (1994). Opiskelulla laatua matematiikan oppimiseen. Yliopistopaino.
124
125 Liite A Luentorungot A.1 Mapu I -kurssin luentorunko Taulukko A.1: Mapu I -kurssin luentorunko viikko päivä sisältö 36 Ti kurssin yleisiä asioita, johdattelua ja kertausta To geometrinen sarja, induktio, funktiot, yhdistetty funktio, käänteisfunktio, funktioiden esitysmuodot, funktioiden muunnokset 37 Ti alkeisfunktiot, logaritmi- ja eksponenttifunktiot, sovelluksia To trigonometriaa, hyperboliset funktiot 38 Ti vektorialgebraa, skalaaritulo, vektoreiden projektiot To vektoritulo, skalaarikolmitulo 39 Ti raja-arvo ja jatkuvuus To derivaatta 40 Ti implisiittinen ja eksplisiittinen derivointi, logaritminen derivointi, käänteisfunktion derivaatta To parametrimuotoinen derivointi, l'hospitalin sääntö, sovellukset, lineaarinen approksimointi 41 Ti Taylorin sarja, määräämätön integraali To Integrointimenetelmiä: sijoitusmenetelmä, osittaisintegrointi 42 Ti integraalien palautuskaavat, rationaalifunktion integrointi To integrointikeinoja, määrätty integraali, yksiköt matemaattisissa lausekkeissa
126
127 Liite B Opetuskokeilumateriaalit B.1 Kuvaus opetuskokeilun oppitunneista Oheisessa taulukossa (taulukko B.1) on esitelty opetuskokeiluun kuuluvien oppituntien etenemistä, käsiteltyä sisältöä ja käytettyjä havainnollistusmenetelmiä. Taulukko B.1: Selostus Mapu II -kurssin vektorianalyysin luento-osuudesta päivä sisältö Havaintomenetelmät: tietokoneanimaatiot, näytelty havainnollistus Usean muuttujan funktioiden dierentiaali- ja integraalilaskennan osuus alkoi tällä luennolla. Funktiokäsitettä laajennettiin usean muuttujan funktioihin. Esimerkkinä erilaisista funktiotyypeistä tutkittiin mm. sääkartassa nähtäviä paikasta riippuvia suureita. Funktion muutoksen tutkimiseen johdateltiin näytellyllä havainnollistuksella, jossa lämpötila luentosalin eri pisteissä toimi esimerkkinä. Koska avaruuden pisteestä voidaan liikkua äärettömän moneen suuntaan, tarvitaan muutoksen tutkimiseen tehokas työkalu, osittaisderivaatta, jolla tehtävä yksinkertaistuu. Osittaisderivaatan määritelmä esitettiin ja todettiin, että symbolinen derivointi tapahtuu kuten aiemmin yhden muuttujan funktioilla osittaisderivoinnissa tarkastellaan vain yhden muuttujan muutosta kerrallaan. Osittaisderivaatan käyttöön tutustuttiin esimerkkien avulla. Tarkasteltiin ensimmäisenä esimerkkinä tietokoneanimaatiota (animaatio 1, kuva B.1). Toisena esimerkkinä oli ns. satulapinta, jonka muotoa esitettiin sekä animaation 2 avulla että symbolisesti. Lopuksi opetettiin alustavasti toisen kertaluvun osittaisderivaatat. jatkuu seuraavalla sivulla
128 116 LUKU B. Opetuskokeilumateriaalit jatkoa edelliseltä sivulta päivä sisältö Havaintomenetelmät: demonstraatio dokumenttikameralla, tietokoneanimaatiot Dokumenttikameran avulla näytetyllä demonstraatiolla kerrattiin kahden muuttujan skalaarifunktion esittämisestä pintana 3-ulotteisessa avaruudessa. Päädyttiin gradientin ja suunnatun derivaatan käsitteeseen tutkimalla kahden muuttujan skalaarifunktion arvon muuttumista pienessä siirtymässä alkupisteeseen nähden. Myös nabla-operaattori esiteltiin tässä yhteydessä. Suunnattua derivaattaa ja gradienttia demonstroitiin animoidulla esimerkillä satulapinnasta (animaatio 3, kuva B.2). Käytiin läpi erilaisia nabla-operaattorin käyttömahdollisuuksia: gradientti, divergenssi ja roottori. Gradienttivektorin tulkintaa käsiteltiin formaalisti. Sovelluksena tarkasteltiin tasa-arvopinnan normaalivektorin muodostamista. Lopuksi pohjustettiin divergenssin fysikaalista merkitystä johtamalla lauseke nestevirtauksen vuon muutokselle pienen dierentiaalisen särmiön tahkojen läpi Havaintomenetelmät: tietokoneanimaatiot, java-simulaatio, kerrottu empiria, havainnollistus styrox-pallolla Toisen kertaluvun sekaderivaattojen merkitystä käytiin läpi kahden animaatioon perustuvan esimerkin avulla (animaatiot 45, kuvat B.3 ja B.4). Myös Taylorin sarjoja demonstroitiin animaatioilla (animaatiot 6 7, kuvat B.5 ja B.6). Esitettiin usean muuttujan funktion ketjusääntö ja dierentiaalien muodostaminen sen avulla. Kerrotun empirian kautta tarkasteltiin liikkuvan havaitsijan mittaaman lämpötilan muutosnopeutta. Luennon jälkimmäisellä puoliskolla jatkettiin divergenssin ja roottorin käsittelyä. Esiteltiin käsitteet lähde ja nielu. Käsiteltiin lyhyesti sähködynamiikkaa Maxwellin I ja II lain avulla ja kerrottiin kenttäviivaesityksestä. Maxwellin lakeihin viitaten opetettiin käsitteet lähteinen ja lähteetön vektorikenttä ja mainittiin alustavasti, että lähteettömässä kentässä kenttäviivat muodostavat suljettuja silmukoita kuten magneettikentän voimaviivat. Esitettiin havainnollistus vektorikentän pyörteisyyden tunnistamisesta styrox-pallolla, jota käytettiin pyörteisyysdetektorina (demonstraatio). Pohdittiin ajatuskokeena, että pallo lähtisi pyörimään seinälle projisoidussa vektorikentässä, jos kyseessä olisi oikea virtauskenttä. Javaohjelmia käytettiin divergenssin ja roottorin käsitteellisen merkityksen syventämiseen (simulaatiot 12). Näytettiin havainnollistuksia lähteisistä ja pyörteisistä vektorikentistä ohjelman hiukkasvirtausta ja pyörteisyysdetektoreita käyttäen. Luennon lopuksi pohjustettiin tulevaa usean muuttujan funktioiden integrointilaskennan käsitteistöä. jatkuu seuraavalla sivulla
129 B.1. Kuvaus opetuskokeilun oppitunneista 117 jatkoa edelliseltä sivulta päivä sisältö Havaintomenetelmät: havainnollistus styrox-pallolla, javasimulaatiot Tarkasteltiin erilaisten nabla-operaattorin sievennyssääntöjen käyttöä. Jatkettiin usean muuttujan funktioiden integrointilaskentaa. Esitettiin viivaintegraali annettua reittiä pitkin ja sen tulkinta voiman tekemänä työnä kyseisellä reitillä. Opetettiin potentiaalifunktion käsite ja tarkasteltiin potentiaalin määrittämistä sekä työn laskemista potentiaalifunktion avulla. Tarkasteltiin vektorikentän pyörteettömyyden yhteyttä potentiaalin olemassaoloon. Palautettiin mieleen pyörteisyyden havaitseminen kenttään asetetun testipallon pyörimisenä (demonstraatio). Tärkeänä käsitteellisenä asiana tarkasteltiin pyörteisyyden käsitettä makroskooppiselta ja mikroskooppiselta kannalta (simulaatiot 12). Näytettiin simulaatio-ohjelmalla, että suljetun reitti-integraalin ollessa nolla pyörteisyysdetektorit eivät pyöri. Luennon lopuksi käytiin alustavasti läpi pinta- ja tilavuusintegraalien laskemista Havaintomenetelmät: ei erityisiä havaintomenetelmiä Pinta- ja tilavuusintegraaleja jatkettiin. Käsiteltiin integrointialueen valinnan merkitystä ja integrointijärjestystä. Toisella puoliskolla laskettiin esimerkkinä tilavuusintegraali tetraedrin läpi. Tutustuttiin muuttujanvaihtoon usean muuttujan funktioiden tapauksessa Jakobin determinantin avulla. Esiteltiin käyräviivaisen koordinaatiston ideaa ja erityisesti tarkasteltiin fysiikassa tarpeellisia sylinteri- ja pallokoordinaatistoja Havaintomenetelmät: animaatiot, havainnollistus styroxpallolla Luennon aiheena olivat ensisijaisesti Gaussin ja Stokesin lause. Gaussin lauseeseen johdateltiin humoristisella analogialla. Yleistajuisin termein perusteltiin että suljetun pinnan yli laskettu vuointegraali on yhtä suuri kuin pinnan sisään jäävän kappaleen läpi laskettu integraali lähteistä ja nieluista. Gaussin ja Stokesin lauseet esitettiin sekä mikroskooppisessa että makroskooppisessa muodossa. Käsiteltiin Stokesin lauseessa olevaa kiertämäintegraalia. Divergenssille ja roottorille esitettiin raja-arvomuotoiset määritelmät. Animaation avulla esitettiin, miten lähteisyyttä voidaan mitata suorakulmaisen särmiön läpi kulkevaa vuota tarkastelemalla (animaatiot 89). Helmholtzin teoreemalla koottiin vektorikenttien aihepiiri yhdeksi kokonaisuudeksi. Tarkasteltiin kuvasarjalla (animaatio 10) sähkömagneettista induktiota ja sitä kuvaavan Faradayn induktiolain esitystä roottorimuodossa. Syntyvän sähkökentän suunta voitiin päätellä pohtimalla kvalitatiivisesti lausekkeessa olevien termien merkitystä. Styrox-palloa käytettiin palauttamaan mieleen aiemmilla luennoilla esitettyjä demonstraatioita (demonstraatio).
130 118 LUKU B. Opetuskokeilumateriaalit Kuva B.1: Kuvia animaatiosta, jota käytettiin kahden muuttujan funktion pintaesityksen ja osittaisderivaatan käsitteen opettamisessa. B.2 Opetuskokeilun animaatioita Varsinaiset divergenssin ja roottorin opetusta varten laaditut animaatiot (animaatiot 810) on kuvattu kappaleessa Opetuskokeiluun liittyi muitakin animaatioita, jotka mm. tutustuttivat opiskelijoita usean muuttujan funktioihin ja osittaisderivaattaan toimien pohjustuksena divergenssin ja roottorin käsitteiden opetukselle. Tässä kuvaillaan tarkemmin näiden animaatioiden sisältöä ja tarkoitusta. Animaatiot 13 Näiden animaatioiden opetuksellisena tavoitteena oli demonstroida opiskelijoille kahden muuttujan funktioiden esittämistä avaruuspintoina. Animaatioita käytettiin myös osittaisderivaatan, suunnatun derivaatan ja gradientin geometrisen merkityksen havainnollistamiseen. Animaatioissa esiintyviä funktioita käsiteltiin rinnakkaisesti symbolisessa muodossa liitutaululla ja todettiin vastaavuus symbolisesti laskettujen osittaisderivaattojen ja kuvaajista havaittavien ominaisuuksien välillä. Näin luotiin yhteyksiä symbolisen ja konkreettisten ilmentymien matemaattisen maailman välille. Tutkijan omana tavoitteena oli harjoitella animaatio-ohjelman käyttöä ennen vaativampien animaatioiden valmistelua ja toisaalta testata esitysvälineistön toimivuutta. Otteita näistä animaatioista löytyy kuvista B.1 ja B.2. Kuvasarjassa B.1 esitetyn animaation opetuksellisena tavoitteena oli totuttaa opiskelijoita kahden muuttujan funktioiden havainnollistamiseen avaruuspintoina ja opettaa osittaisderivaatan merkitystä kuvaajien avulla. Tutkijan omana tavoitteena oli harjoitella animaatio-ohjelman käyt-
131 B.2. Opetuskokeilun animaatioita 119 Kuva B.2: Kuvia gradientin geometrista merkitystä esittelevästä animaatiosta. töä ennen vaativampien animaatioiden valmistelua ja toisaalta testata esitysvälineistön toimivuutta. Satulapinnan muodon ja osittaisderivaattojen selventämistä varten laadittiin ensin yksinkertainen animaatio (animaatio 2), jonka pohjalta tehtiin laajempi opetusanimaatio gradientin geometrisesta merkityksestä (animaatio 3). Kyseiset animaatiot ovat ulkoasultaan hyvin samanlaisia. Kuva B.2 esittelee animaatiota 3, jossa satulapinnalle piirrettiin vaiheittain osittaisderivaattojen avulla lasketut x- ja y-akselin suuntaiset tangenttisuorat ja näitä mukaileva tangenttitaso. Gradientti opetettiin sellaisena suuntana xy-tasossa, jonne kuljettaessa kyseinen tangenttitaso nousee jyrkimmin. Animaatiot 45 Ensimmäisen kertaluvun osittaisderivaatta on verraten helppo ymmärtää yhden muuttujan funktion derivaatan yleistyksenä. Toisen kertaluvun osittaisderivaatoissa opitaan uutena käsitteenä sekaderivaatat, joilla ei ole tuttua aiempaa vastinetta. Toisen kertaluvun sekaderivaattojen geometristä merkitystä tukemaan laadittiin kaksi animaatiota (kuvat B.3 ja B.4), joissa tarkasteltavina pintoina olivat pyörähdysparaboloidi ja elliptinen paraboloidi. Animaatioissa pinnat leikattiin xz-tason suuntaisiin viipaleisiin kolmella eri y-koordinaatin arvolla. Demonstraatiossa osoitettiin yhteys poikkileikkauksina saatavien paraabelien sijainnin muuttumisen ja toisen kertaluvun sekaderivaattojen välillä. Animaatiot oli jälleen integroitu liitutaululla tapahtuvan symbolisen tarkastelun kanssa.
132 120 LUKU B. Opetuskokeilumateriaalit Kuva B.3: Valikoituja kuvia paraboloidipinnan viipalointianimaatiosta, jolla opetettiin toisen kertaluvun osittaisderivaattojen konkreettista merkitystä. Kuva B.4: Valikoituja kuvia elliptisen paraboloidipinnan viipalointianimaatiosta, jolla opetettiin toisen kertaluvun osittaisderivaattojen konkreettista merkitystä.
133 B.2. Opetuskokeilun animaatioita 121 Kuva B.5: Kuvia kaksiulotteisen pinnan approksimoinnista Taylorin sarjan 1. ja 2. kertaluvun polynomeilla. Kuva B.6: Otteita kuvasarjasta, jolla havainnollistettiin sombreropinnan approksimointia 2. ja 4. kertaluvun Taylorin polynomeilla. Animaatiot 67 Kuvasarjat B.5 ja B.6 esittävät animaatioita, jotka havainnollistivat kahden muuttujan Taylorin sarjaa. Animaatioissa esitettiin, miten avaruuspintaa voidaan approksimoida Taylorin polynomeilla ensin tangenttitasolla, sitten paraboloideilla ja muilla korkeamman asteen pinnoilla. Vaikka tämä aihe ei suoranaisesti liity tutkimuksessa tarkasteltaviin käsitteisiin, noudattavat animaatiot havainnollistusten laadinnassa käytettyä yleisperiaatetta luoda linkkejä symbolisen maailman ja konkreettisen esityksen välillä.
Dierentiaalilaskennan käsitteistä
 Dierentiaalilaskennan käsitteistä Ossi Pasanen 13. marraskuuta 2008 1 Funktio Funktio on matemaattinen käsite, joka kuvaa kahden alkion välistä riippuvuutta. Erityisesti, kun fysiikassa jonkin suureen
Dierentiaalilaskennan käsitteistä Ossi Pasanen 13. marraskuuta 2008 1 Funktio Funktio on matemaattinen käsite, joka kuvaa kahden alkion välistä riippuvuutta. Erityisesti, kun fysiikassa jonkin suureen
Opiskelijoiden käsityksiä divergenssistä ja roottorista
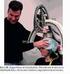 Laudaturtutkielma Fysiikan opettajan suuntautumisvaihtoehto Opiskelijoiden käsityksiä divergenssistä ja roottorista Ossi Pasanen 2008 Ohjaaja: Tarkastajat: Heimo Saarikko Heimo Saarikko Kaarle Kurki-Suonio
Laudaturtutkielma Fysiikan opettajan suuntautumisvaihtoehto Opiskelijoiden käsityksiä divergenssistä ja roottorista Ossi Pasanen 2008 Ohjaaja: Tarkastajat: Heimo Saarikko Heimo Saarikko Kaarle Kurki-Suonio
Derivaatta: funktion approksimaatio lineaarikuvauksella.
 Viikko 5 Tällä viikolla yleistetään R 2 :n ja R 3 :n vektorialgebran peruskäsitteet n-ulotteiseen avaruuteen R n, ja määritellään lineaarikuvaus. Tarkastellaan funktioita, joiden määrittelyjoukko on n-ulotteisen
Viikko 5 Tällä viikolla yleistetään R 2 :n ja R 3 :n vektorialgebran peruskäsitteet n-ulotteiseen avaruuteen R n, ja määritellään lineaarikuvaus. Tarkastellaan funktioita, joiden määrittelyjoukko on n-ulotteisen
F x y z. F voidaan ymmärtää kahden vektorin. Divergenssi. Vektorikentän F( x, y, z ) divergenssi määritellään
 31 VEKTORIANALYYSI Luento 5 Divergenssi F Vektorikentän F(, y, z ) divergenssi määritellään F F F y z y F z. Divergenssistä käytetään usein myös merkintää div, Divergenssi pistetulona, F div F. F voidaan
31 VEKTORIANALYYSI Luento 5 Divergenssi F Vektorikentän F(, y, z ) divergenssi määritellään F F F y z y F z. Divergenssistä käytetään usein myös merkintää div, Divergenssi pistetulona, F div F. F voidaan
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause.
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
2 Osittaisderivaattojen sovelluksia
 2 Osittaisderivaattojen sovelluksia 2.1 Ääriarvot Yhden muuttujan funktiolla f(x) on lokaali maksimiarvo (lokaali minimiarvo) pisteessä a, jos f(x) f(a) (f(x) f(a)) kaikilla x:n arvoilla riittävän lähellä
2 Osittaisderivaattojen sovelluksia 2.1 Ääriarvot Yhden muuttujan funktiolla f(x) on lokaali maksimiarvo (lokaali minimiarvo) pisteessä a, jos f(x) f(a) (f(x) f(a)) kaikilla x:n arvoilla riittävän lähellä
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio.
 MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
Vektorien pistetulo on aina reaaliluku. Esimerkiksi vektorien v = (3, 2, 0) ja w = (1, 2, 3) pistetulo on
 13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina klo
 HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina 10.8.2015 klo 16.15. Tehtäväsarja I Tutustu lukuun 15, jossa vektoriavaruuden
HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina 10.8.2015 klo 16.15. Tehtäväsarja I Tutustu lukuun 15, jossa vektoriavaruuden
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 23.2.2016 Susanna Hurme Tervetuloa kurssille! Mitä on statiikka? Mitä on dynamiikka? Miksi niitä opiskellaan? Päivän aihe: Voiman käsite ja partikkelin tasapaino
KJR-C1001 Statiikka ja dynamiikka Luento 23.2.2016 Susanna Hurme Tervetuloa kurssille! Mitä on statiikka? Mitä on dynamiikka? Miksi niitä opiskellaan? Päivän aihe: Voiman käsite ja partikkelin tasapaino
F dr = F NdS. VEKTORIANALYYSI Luento Stokesin lause
 91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
TUKIMATERIAALI: Arvosanan kahdeksan alle jäävä osaaminen
 1 FYSIIKKA Fysiikan päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta fysiikan opiskeluun T2 ohjata
1 FYSIIKKA Fysiikan päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta fysiikan opiskeluun T2 ohjata
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit
 MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento : Moniulotteiset integraalit Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 26 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy
MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento : Moniulotteiset integraalit Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 26 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
12. Derivointioperaattoreista geometrisissa avaruuksissa
 12. Derivointioperaattoreista geometrisissa avaruuksissa 12.1. Gradientti, divergenssi ja roottori 328. Laske u, kun u on vektorikenttä a) (z y)i + (x z)j + (y x)k, b) e xyz (i + xlnyj + x 2 zk), c) (x
12. Derivointioperaattoreista geometrisissa avaruuksissa 12.1. Gradientti, divergenssi ja roottori 328. Laske u, kun u on vektorikenttä a) (z y)i + (x z)j + (y x)k, b) e xyz (i + xlnyj + x 2 zk), c) (x
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
Joukot. Georg Cantor ( )
 Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Antti Rasila. Kevät Matematiikan ja systeemianalyysin laitos Aalto-yliopisto. Antti Rasila (Aalto-yliopisto) MS-A0204 Kevät / 16
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitusviikkoon 5 /
 M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 24 Mikä on pinta?
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 24 Mikä on pinta?
Opetusperiodi:I, suunnattu hakukohteille:
 Kurssin nimi ja koodi Muut kommentit MS-A0001 Matriisilaskenta 5 op (Matrisräkning, Kuvaus: kurssi Teknillinen fysiikka ja matematiikka käsittelee lineaarisia yhtälöryhmiä sekä vektoreita ja matriiseja
Kurssin nimi ja koodi Muut kommentit MS-A0001 Matriisilaskenta 5 op (Matrisräkning, Kuvaus: kurssi Teknillinen fysiikka ja matematiikka käsittelee lineaarisia yhtälöryhmiä sekä vektoreita ja matriiseja
Sivu 1 / 8. A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste. Olli Kauppi
 Sivu 1 / 8 A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste Olli Kauppi Monisteen ensimmäinen luku käsittelee derivointia hieman yleisemmästä näkökulmasta. Monisteen lopussa on kurssilla
Sivu 1 / 8 A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste Olli Kauppi Monisteen ensimmäinen luku käsittelee derivointia hieman yleisemmästä näkökulmasta. Monisteen lopussa on kurssilla
Polkuintegraali yleistyy helposti paloitain C 1 -poluille. Määritelmä Olkoot γ : [a, b] R m paloittain C 1 -polku välin [a, b] jaon
![Polkuintegraali yleistyy helposti paloitain C 1 -poluille. Määritelmä Olkoot γ : [a, b] R m paloittain C 1 -polku välin [a, b] jaon Polkuintegraali yleistyy helposti paloitain C 1 -poluille. Määritelmä Olkoot γ : [a, b] R m paloittain C 1 -polku välin [a, b] jaon](/thumbs/71/65388066.jpg) Polkuintegraali yleistyy helposti paloitain C 1 -poluille. Määritelmä 4.1.3. Olkoot : [a, b] R m paloittain C 1 -polku välin [a, b] jaon P = {a = t 1 < < t k = b} ja joukko D R m sellainen, että ([a, b])
Polkuintegraali yleistyy helposti paloitain C 1 -poluille. Määritelmä 4.1.3. Olkoot : [a, b] R m paloittain C 1 -polku välin [a, b] jaon P = {a = t 1 < < t k = b} ja joukko D R m sellainen, että ([a, b])
5 Differentiaalilaskentaa
 5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
Gaussin lause eli divergenssilause 1
 80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
Oppimistavoitematriisi
 Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Arvosanaan 1 2 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä ja yhtälöpareja Osaan muokata
Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Arvosanaan 1 2 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä ja yhtälöpareja Osaan muokata
Oppimistavoitematriisi
 Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Esitiedot Arvosanaan 1 2 riittävät Arvosanaan 3 4 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä
Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Esitiedot Arvosanaan 1 2 riittävät Arvosanaan 3 4 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
Aika/Datum Month and year Kesäkuu 2012
 Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos/Institution Department Filosofian, historian, kulttuurin ja taiteiden tutkimuksen laitos Humanistinen tiedekunta Tekijä/Författare Author Veera Lahtinen
Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos/Institution Department Filosofian, historian, kulttuurin ja taiteiden tutkimuksen laitos Humanistinen tiedekunta Tekijä/Författare Author Veera Lahtinen
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
hyvä osaaminen
 MERKITYS, ARVOT JA ASENTEET FYSIIKKA T2 Oppilas tunnistaa omaa fysiikan osaamistaan, asettaa tavoitteita omalle työskentelylleen sekä työskentelee pitkäjänteisesti. T3 Oppilas ymmärtää fysiikkaan (sähköön
MERKITYS, ARVOT JA ASENTEET FYSIIKKA T2 Oppilas tunnistaa omaa fysiikan osaamistaan, asettaa tavoitteita omalle työskentelylleen sekä työskentelee pitkäjänteisesti. T3 Oppilas ymmärtää fysiikkaan (sähköön
VEKTORIKENTÄN ROTAATIO JA DIVERGENSSI, MAXWELLIN YHTÄLÖT
 VEKTORIKENTÄN ROTAATIO JA DIVERGENSSI, MAXWELLIN YHTÄLÖT 1/32 2 VEKTORIKENTÄN ROTAATIO JA DIVERGENSSI, MAXWELLIN YHTÄLÖT Kenttäilmiöt Sähkö- ja magneettikentät Vaikeasti havaittavissa ihmisen aistein!
VEKTORIKENTÄN ROTAATIO JA DIVERGENSSI, MAXWELLIN YHTÄLÖT 1/32 2 VEKTORIKENTÄN ROTAATIO JA DIVERGENSSI, MAXWELLIN YHTÄLÖT Kenttäilmiöt Sähkö- ja magneettikentät Vaikeasti havaittavissa ihmisen aistein!
Selvästi. F (a) F (y) < r x d aina, kun a y < δ. Kolmioepäyhtälön nojalla x F (y) x F (a) + F (a) F (y) < d + r x d = r x
 Seuraavaksi tarkastellaan C 1 -sileiden pintojen eräitä ominaisuuksia. Lemma 2.7.1. Olkoon S R m sellainen C 1 -sileä pinta, että S on C 1 -funktion F : R m R eräs tasa-arvojoukko. Tällöin S on avaruuden
Seuraavaksi tarkastellaan C 1 -sileiden pintojen eräitä ominaisuuksia. Lemma 2.7.1. Olkoon S R m sellainen C 1 -sileä pinta, että S on C 1 -funktion F : R m R eräs tasa-arvojoukko. Tällöin S on avaruuden
VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4
 VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4 Jokaisen tehtävän jälkeen on pieni kommentti tehtävään liittyen Nämä eivät sisällä mitään kovin kriittistä tietoa tehtävään liittyen, joten niistä ei tarvitse välittää
VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4 Jokaisen tehtävän jälkeen on pieni kommentti tehtävään liittyen Nämä eivät sisällä mitään kovin kriittistä tietoa tehtävään liittyen, joten niistä ei tarvitse välittää
arvostelija OSDA ja UDDI palveluhakemistoina.
 Hyväksymispäivä Arvosana arvostelija OSDA ja UDDI palveluhakemistoina. HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty/Section Laitos Institution
Hyväksymispäivä Arvosana arvostelija OSDA ja UDDI palveluhakemistoina. HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty/Section Laitos Institution
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
POHDIN - projekti. Funktio. Vektoriarvoinen funktio
 POHDIN - projekti Funktio Funktio f joukosta A joukkoon B tarkoittaa sääntöä, joka liittää jokaiseen joukon A alkioon jonkin alkion joukosta B. Yleensä merkitään f : A B. Usein käytetään sanaa kuvaus synonyymina
POHDIN - projekti Funktio Funktio f joukosta A joukkoon B tarkoittaa sääntöä, joka liittää jokaiseen joukon A alkioon jonkin alkion joukosta B. Yleensä merkitään f : A B. Usein käytetään sanaa kuvaus synonyymina
Funktiot ja raja-arvo P, 5op
 Funktiot ja raja-arvo 800119P, 5op Pekka Salmi 15. syyskuuta 2017 Pekka Salmi FUNK 15. syyskuuta 2017 1 / 122 Yleistä Luennot: ke 810, to 1214 (ensi viikosta lähtien) Luennoitsija: Pekka Salmi, MA327 Laskupäivä:
Funktiot ja raja-arvo 800119P, 5op Pekka Salmi 15. syyskuuta 2017 Pekka Salmi FUNK 15. syyskuuta 2017 1 / 122 Yleistä Luennot: ke 810, to 1214 (ensi viikosta lähtien) Luennoitsija: Pekka Salmi, MA327 Laskupäivä:
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit
 MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy 215 1 / 24 Skalaarikenttä Olkoon R
MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy 215 1 / 24 Skalaarikenttä Olkoon R
Vastausehdotukset analyysin sivuainekurssin syksyn välikokeeseen
 Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
Johdatus tekoälyn taustalla olevaan matematiikkaan
 Johdatus tekoälyn taustalla olevaan matematiikkaan Informaatioteknologian tiedekunta Jyväskylän yliopisto 3. luento 17.11.2017 Neuroverkon opettaminen (ohjattu oppiminen) Neuroverkkoa opetetaan syöte-tavoite-pareilla
Johdatus tekoälyn taustalla olevaan matematiikkaan Informaatioteknologian tiedekunta Jyväskylän yliopisto 3. luento 17.11.2017 Neuroverkon opettaminen (ohjattu oppiminen) Neuroverkkoa opetetaan syöte-tavoite-pareilla
Injektio (1/3) Funktio f on injektio, joss. f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f )
 Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
kaikki ( r, θ )-avaruuden pisteet (0, θ ) - oli θ
 58 VEKTORIANALYYSI Luento 9 Ortogonaaliset käyräviivaiset koordinaatistot Olemme jo monta kertaa esittäneet karteesiset x, y ja z koordinaatit uusia koordinaatteja käyttäen: x= xuvw (,, ), y= yuvw (,,
58 VEKTORIANALYYSI Luento 9 Ortogonaaliset käyräviivaiset koordinaatistot Olemme jo monta kertaa esittäneet karteesiset x, y ja z koordinaatit uusia koordinaatteja käyttäen: x= xuvw (,, ), y= yuvw (,,
Mapusta. Viikon aiheet
 Infoa Mapusta Tiistaina: Ongelmanratkaisu ryhmässä luento klo 8-10 D101. Tähän liittyviä tehtäviä tehään myöhemmin perusopintojen laboratoriotöihin integroituna. Mikäli luento menee ex-temporen päälle,
Infoa Mapusta Tiistaina: Ongelmanratkaisu ryhmässä luento klo 8-10 D101. Tähän liittyviä tehtäviä tehään myöhemmin perusopintojen laboratoriotöihin integroituna. Mikäli luento menee ex-temporen päälle,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 7 1 Useamman muuttujan funktion raja-arvo Palautetaan aluksi mieliin yhden muuttujan funktion g(x) raja-arvo g(x). x a Tämä raja-arvo kertoo, mitä arvoa funktio g(x)
Matematiikan tukikurssi Kurssikerta 7 1 Useamman muuttujan funktion raja-arvo Palautetaan aluksi mieliin yhden muuttujan funktion g(x) raja-arvo g(x). x a Tämä raja-arvo kertoo, mitä arvoa funktio g(x)
Opetusperiodi:I, suunnattu hakukohteille: Teknillinen fysiikka ja matematiikka
 Kurssin nimi ja koodi MS-A0001 Matriisilaskenta 5 op (Matrisräkning, Kuvaus: kurssi käsittelee lineaarisia yhtälöryhmiä sekä vektoreita ja matriiseja sovelluksineen. Sisältö: vektorilaskentaa, matriisit
Kurssin nimi ja koodi MS-A0001 Matriisilaskenta 5 op (Matrisräkning, Kuvaus: kurssi käsittelee lineaarisia yhtälöryhmiä sekä vektoreita ja matriiseja sovelluksineen. Sisältö: vektorilaskentaa, matriisit
BM20A0300, Matematiikka KoTiB1
 BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 17 R. Kangaslampi Vektoriavaruudet Vektoriavaruus
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 17 R. Kangaslampi Vektoriavaruudet Vektoriavaruus
Matematiikan tukikurssi, kurssikerta 1
 Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
TUKIMATERIAALI: Arvosanan kahdeksan alle jäävä osaaminen
 KEMIA Kemian päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta kemian opiskeluun T2 ohjata ja
KEMIA Kemian päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta kemian opiskeluun T2 ohjata ja
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA. Karoliina Ljungberg
 Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
FUNKTIONAALIANALYYSIN PERUSKURSSI 1. 0. Johdanto
 FUNKTIONAALIANALYYSIN PERUSKURSSI 1. Johdanto Funktionaalianalyysissa tutkitaan muun muassa ääretönulotteisten vektoriavaruuksien, ja erityisesti täydellisten normiavaruuksien eli Banach avaruuksien ominaisuuksia.
FUNKTIONAALIANALYYSIN PERUSKURSSI 1. Johdanto Funktionaalianalyysissa tutkitaan muun muassa ääretönulotteisten vektoriavaruuksien, ja erityisesti täydellisten normiavaruuksien eli Banach avaruuksien ominaisuuksia.
Lineaarialgebra ja matriisilaskenta II. LM2, Kesä /141
 Lineaarialgebra ja matriisilaskenta II LM2, Kesä 2012 1/141 Kertausta: avaruuden R n vektorit Määritelmä Oletetaan, että n {1, 2, 3,...}. Avaruuden R n alkiot ovat jonoja, joissa on n kappaletta reaalilukuja.
Lineaarialgebra ja matriisilaskenta II LM2, Kesä 2012 1/141 Kertausta: avaruuden R n vektorit Määritelmä Oletetaan, että n {1, 2, 3,...}. Avaruuden R n alkiot ovat jonoja, joissa on n kappaletta reaalilukuja.
f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y 2.
 13. Erityyppisten integraalien väliset yhteydet 13.1. Gaussin lause 364. Laske A f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y
13. Erityyppisten integraalien väliset yhteydet 13.1. Gaussin lause 364. Laske A f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
1. Logiikan ja joukko-opin alkeet
 1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
1. Osoita, että joukon X osajoukoille A ja B on voimassa toinen ns. de Morganin laki (A B) = A B.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
KJR-C1001: Statiikka L2 Luento : voiman momentti ja voimasysteemit
 KJR-C1001: Statiikka L2 Luento 21.2.2018: voiman momentti ja voimasysteemit Apulaisprofessori Konetekniikan laitos Luennon osaamistavoitteet Tämän päiväisen luennon jälkeen opiskelija Pystyy muodostamaan,
KJR-C1001: Statiikka L2 Luento 21.2.2018: voiman momentti ja voimasysteemit Apulaisprofessori Konetekniikan laitos Luennon osaamistavoitteet Tämän päiväisen luennon jälkeen opiskelija Pystyy muodostamaan,
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
hyvä osaaminen. osaamisensa tunnistamista kuvaamaan omaa osaamistaan
 MERKITYS, ARVOT JA ASENTEET FYSIIKKA 8 T2 Oppilas asettaa itselleen tavoitteita sekä työskentelee pitkäjänteisesti. Oppilas harjoittelee kuvaamaan omaa osaamistaan. T3 Oppilas ymmärtää lämpöilmiöiden tuntemisen
MERKITYS, ARVOT JA ASENTEET FYSIIKKA 8 T2 Oppilas asettaa itselleen tavoitteita sekä työskentelee pitkäjänteisesti. Oppilas harjoittelee kuvaamaan omaa osaamistaan. T3 Oppilas ymmärtää lämpöilmiöiden tuntemisen
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot Harri Hakula Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2018 1 Perustuu Antti Rasilan luentomonisteeseen
MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot Harri Hakula Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2018 1 Perustuu Antti Rasilan luentomonisteeseen
= ( F dx F dy F dz).
 17 VEKTORIANALYYSI Luento 2 3.4 Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin
17 VEKTORIANALYYSI Luento 2 3.4 Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin
MS-C1340 Lineaarialgebra ja
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi kevät 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Idea Lineaarisen systeemin ratkaiseminen Olkoon
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi kevät 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Idea Lineaarisen systeemin ratkaiseminen Olkoon
Tehtävä 1. Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja.
 Tehtävä 1 Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja. 1 Jos 1 < y < 3, niin kaikilla x pätee x y x 1. 2 Jos x 1 < 2 ja y 1 < 3, niin x y
Tehtävä 1 Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja. 1 Jos 1 < y < 3, niin kaikilla x pätee x y x 1. 2 Jos x 1 < 2 ja y 1 < 3, niin x y
Derivointiesimerkkejä 2
 Derivointiesimerkkejä 2 (2.10.2008 versio 2.0) Parametrimuotoisen funktion erivointi Esimerkki 1 Kappale kulkee pitkin rataa { x(t) = sin 2 t y(t) = cos t. Määritetään raan suuntakulma positiiviseen x-akseliin
Derivointiesimerkkejä 2 (2.10.2008 versio 2.0) Parametrimuotoisen funktion erivointi Esimerkki 1 Kappale kulkee pitkin rataa { x(t) = sin 2 t y(t) = cos t. Määritetään raan suuntakulma positiiviseen x-akseliin
Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2014
 Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2014 Hestenes (1992): The great game of science is modelling the real world, and each scientific theory lays down a system of rules for
Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2014 Hestenes (1992): The great game of science is modelling the real world, and each scientific theory lays down a system of rules for
Matematiikka vuosiluokat 7 9
 Matematiikka vuosiluokat 7 9 Matematiikan opetuksen ydintehtävänä on tarjota oppilaille mahdollisuus hankkia sellaiset matemaattiset taidot, jotka antavat valmiuksia selviytyä jokapäiväisissä toiminnoissa
Matematiikka vuosiluokat 7 9 Matematiikan opetuksen ydintehtävänä on tarjota oppilaille mahdollisuus hankkia sellaiset matemaattiset taidot, jotka antavat valmiuksia selviytyä jokapäiväisissä toiminnoissa
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 6 Mikko Salo 6.9.2017 Sisältö 1. Kompleksitaso 2. Joukko-oppia Kompleksiluvut Edellisellä luennolla huomattiin, että toisen asteen yhtälö ratkeaa aina, jos ratkaisujen annetaan
Johdatus matematiikkaan Luento 6 Mikko Salo 6.9.2017 Sisältö 1. Kompleksitaso 2. Joukko-oppia Kompleksiluvut Edellisellä luennolla huomattiin, että toisen asteen yhtälö ratkeaa aina, jos ratkaisujen annetaan
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
b) Määritä/Laske (ei tarvitse tehdä määritelmän kautta). (2p)
 Matematiikan TESTI, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
Matematiikan TESTI, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
5.6.3 Matematiikan lyhyt oppimäärä
 5.6.3 Matematiikan lyhyt oppimäärä Matematiikan lyhyen oppimäärän opetuksen tehtävänä on tarjota valmiuksia hankkia, käsitellä ja ymmärtää matemaattista tietoa ja käyttää matematiikkaa elämän eri tilanteissa
5.6.3 Matematiikan lyhyt oppimäärä Matematiikan lyhyen oppimäärän opetuksen tehtävänä on tarjota valmiuksia hankkia, käsitellä ja ymmärtää matemaattista tietoa ja käyttää matematiikkaa elämän eri tilanteissa
Matemaattisen analyysin tukikurssi
 Matemaattisen analyysin tukikurssi 4. Kurssikerta Petrus Mikkola 4.10.2016 Tämän kerran asiat Funktion raja-arvo Raja-arvon määritelmä Toispuolinen raja-arvo Laskutekniikoita Rationaalifunktion esityksen
Matemaattisen analyysin tukikurssi 4. Kurssikerta Petrus Mikkola 4.10.2016 Tämän kerran asiat Funktion raja-arvo Raja-arvon määritelmä Toispuolinen raja-arvo Laskutekniikoita Rationaalifunktion esityksen
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos. MS-A0203 Differentiaali- ja integraalilaskenta 2, kevät 2016
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A23 Differentiaali- ja integraalilaskenta 2, kevät 216 Laskuharjoitus 2A (Vastaukset) Alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A23 Differentiaali- ja integraalilaskenta 2, kevät 216 Laskuharjoitus 2A (Vastaukset) Alkuviikolla
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
KESKEISET SISÄLLÖT Keskeiset sisällöt voivat vaihdella eri vuositasoilla opetusjärjestelyjen mukaan.
 VUOSILUOKAT 6 9 Vuosiluokkien 6 9 matematiikan opetuksen ydintehtävänä on syventää matemaattisten käsitteiden ymmärtämistä ja tarjota riittävät perusvalmiudet. Perusvalmiuksiin kuuluvat arkipäivän matemaattisten
VUOSILUOKAT 6 9 Vuosiluokkien 6 9 matematiikan opetuksen ydintehtävänä on syventää matemaattisten käsitteiden ymmärtämistä ja tarjota riittävät perusvalmiudet. Perusvalmiuksiin kuuluvat arkipäivän matemaattisten
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas Tampereen teknillinen yliopisto Elektroniikan laitos
 SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 Sähköstatiikka Coulombin laki ja sähkökentän
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 Sähköstatiikka Coulombin laki ja sähkökentän
Koht dialogia? Organisaation toimintaympäristön teemojen hallinta dynaamisessa julkisuudessa tarkastelussa toiminta sosiaalisessa mediassa
 Kohtdialogia? Organisaationtoimintaympäristönteemojenhallinta dynaamisessajulkisuudessatarkastelussatoiminta sosiaalisessamediassa SatuMariaPusa Helsinginyliopisto Valtiotieteellinentiedekunta Sosiaalitieteidenlaitos
Kohtdialogia? Organisaationtoimintaympäristönteemojenhallinta dynaamisessajulkisuudessatarkastelussatoiminta sosiaalisessamediassa SatuMariaPusa Helsinginyliopisto Valtiotieteellinentiedekunta Sosiaalitieteidenlaitos
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei.
 5.5 Surjektio Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei. Määritelmä 5.5.1. Kuvaus f : X æ Y on surjektio, jos jokaisella
5.5 Surjektio Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei. Määritelmä 5.5.1. Kuvaus f : X æ Y on surjektio, jos jokaisella
Fr ( ) Fxyz (,, ), täytyy integroida:
 15 VEKTORIANALYYSI Luento Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin ja voima
15 VEKTORIANALYYSI Luento Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin ja voima
sin(x2 + y 2 ) x 2 + y 2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
8 KANNAT JA ORTOGONAALISUUS. 8.1 Lineaarinen riippumattomuus. Vaasan yliopiston julkaisuja 151
 Vaasan yliopiston julkaisuja 151 8 KANNAT JA ORTOGONAALISUUS KantaOrthogon Sec:LinIndep 8.1 Lineaarinen riippumattomuus Lineaarinen riippumattomuus on oikeastaan jo määritelty, mutta kirjoitamme määritelmät
Vaasan yliopiston julkaisuja 151 8 KANNAT JA ORTOGONAALISUUS KantaOrthogon Sec:LinIndep 8.1 Lineaarinen riippumattomuus Lineaarinen riippumattomuus on oikeastaan jo määritelty, mutta kirjoitamme määritelmät
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
