|
|
|
- Juha Jaakkola
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 OPTINEN PAIKANMÄÄRITYS 12.1 YLEISTÄ Liikuttaessa rannikon tuntumassa tai saaristossa aluksen paikanmääritys tapahtuu havainnoimalla maissa olevia tunnistettuja kohteita. Menetelmästä käytetään nimitystä optinen paikanmääritys, koska havaintoja tehdään pääasiassa optisin keinoin. Joitakin apuvälineitä kuitenkin tarvitaan silmän avuksi. Näitä ovat esimerkiksi kiikari, kello, kompassi, loki ja sen nollattava matkamittari, suuntimalaite, sekstantti ja etäisyyttä määritettäessä myös tutka (tai etäisyysmittari). Optisten havaintojen perusteella saadaan kartalle piirretyksi viiva tai tarkemmin kaari, jonka jossain pisteessä alus sijaitsee. Tällaista kaarta kutsutaan sijoittajaksi SIJOITTAJA Sijoittaja on todellisuudessa aina kaari, koska kaikki optiset havainnot ovat osa isoympyrää. Kaarevuus on pienimittakaavaisella kartalla kuitenkin erittäin vähäistä, jolloin sijoittaja voidaan useimmiten piirtää suorana viivana. Poikkeuksena tästä ovat vaakakulmat ja tutkaetäisyys, joiden sijoittajat ovat suhteellisen pieniä ympyröitä (sikäli, kun niitä kartalle edes kokonaisuudessaan piirretään). Sijoittaja voidaan määrittää havaitsemalla kaksi kohdetta linjassa päällekäin (suora) mittaamalla kahden kohteen välinen vaakasuora kulma (kaari) mittaamalla suuntima tunnettuun kohteeseen (suora) mittaamalla etäisyys kohteeseen (kaari) luotaamalla (käyrä). On huomattava, että yksi sijoittaja ei riitä aluksen tarkan paikan määrittämiseksi, vaan silloin tiedetään vasta suora/kaari, jolla alus sijaitsee. Tarkan paikannuksen saamiseksi sijoittajia on oltava ainakin kaksi ja niiden tulee olla mahdollisimman samanaikaisten havaintojen tuloksia. Sijoittajien yhdistämisestä on tarkemmin kohdassa MENETELMÄT A. YHDYSLINJA Yhdyslinjalla tarkoitetaan kahden kiinteän, peräkkäin olevan kohteen muodostamaa suoraa. Kun ne aluksesta katsottaessa ovat päällekkäin, on aluksen paikka jossain kohteiden kautta kulkevalla suoralla.
2 233 Kohteet voivat olla joko luonnon merkkejä (saarten reunat, korkeat rinteet) tai merimerkkejä (majakat, loistot, kummelit, reunamerkit, linjataulut). Yhdyslinja on sijoittajana tarkka. Tarkkuus on suurin kun kohteiden välinen etäisyys on suuri ja aluksen ja lähemmän kohteen välinen etäisyys on pieni. Yhdyslinjaa voidaan käyttää esimerkiksi aluksen kulkureitin (linjataulut), tai turvalinjan määrittämiseen. Turvalinjalla tarkoitetaan linjaa, jonka toiselle puolelle ei saa mennä. Esimerkiksi alus on liikaa väylän oikealla puolella, jos reunamerkki ja sen takana olevan saaren vasen reuna ovat päällekkäin (turvalinja). (9,5) Kuva 152. Yhdyslinja sijoittajana (linjataulut) ja turvalinja. B. VAAKAKULMA Kahden tunnetun kohteen välinen vaakasuora kulma (vaakakulma) mitataan sekstantilla tai suuntimalaitteella. Alus sijaitsee ympyrän kaarella, joka kulkee kohteiden kautta ja sisältää mitatun kulman. Sekstantilla mitattu vaakakulma on suuntimalaiteella mitattua tarkempi, koska suuntimalaitteeseen vaikuttavat myös kompassin virheet ja laitteen linjausvirhe. 1. Runko 2. Liikkuva säde (Alhidadi) 3. Kaari (Limbi) ja astejaotus 4. Isopeili 5. Pikkupeili 6. Näköputki 7. Himmennyslasit 8. Lukitussalpa 9. Rumpu ja sen minuuttijaotus 10. Rummun sekuntiasteikko Kuva 153. Sekstantti.
3 234 Sekstantin näyttämän tarkkuuteen vaikuttavat peilien asennot. Jos peilit ovat väärässä asennossa, eivät peilien kautta kulkevat säteet ole yhdensuuntaisia eikä kulmia saada mitattua tarkasti. Sekstanteissa on yleensä indeksivirhettä, jolle määritetään indeksikorjaus (i). Kun mitataan kulmia, tulee aina ensin määrittää laitteen indeksivirhe ja -korjaus. Jos indeksivirhe vaakakulmamittauksessa on pienempi kuin 0,25 sitä ei tarvitse ottaa huomioon. Tämä sen vuoksi, että kulmanasettimen (station pointer; laite, jolla kulma siirretään kartalle) tarkkuus ei mahdollista sen käyttämistä. Jos taas korjaus on suurempi kuin edellämainittu, on se ottava aina huomioon. Indeksivirhe aiheutuu sekstantin asteikkovirheestä tai peilien väärästä asennosta. Myös laitteen metallinen runko voi aiheutta virhettä reagoimalla lämpötilan muutoksiin. Tämän vuoksi sekstantti on vietävä käyttölämpötilaan muutamia minuutteja ennen virheen määritystä ja varsinaista mittausta. On myös huomioitava, että eri mittaajat saavat yleensä eri tuloksen indeksikorjaukseksi. Indeksikorjauksen määrittäminen (katso kuva 154): Kun sekstantti on käyttövalmiina, aseta liikkuva säde ja rummun osoitinpiiru nollakohtaan. Pidä laitetta pystyasennossa. Katso jotain kaukaista kohdetta näköputken läpi (esimerkiksi horisontti). Kohteen tulisi olla vähintään 1 mpk:n etäisyydellä, jotta parallaksivirhettä ei synny (peilien ja kohteen välinen kulma mahdollisimman pieni). Jos näköputken läpi näkyvät iso- ja pikkupeilien kuvat yhtyvät ja horisontti näkyy tasaisena, sekstantissa EI OLE indeksivirhettä. Jos iso- ja pikkupeilien kuvat eivät yhdy, vaan horisontti näkyy kahtena eri tasossa olevana kuvana, sekstantissa ON indeksivirhettä. Indeksivirhe määritetään kääntämällä rumpua niin, että kuvat yhtyvät. Virheen suuruus luetaan rummun asteikolta. Asteikolla yksi piirtoväli on 1 minuutti. Minuutit luetaan rummun asteikolta ja kymmenykset rungossa olevalta kymmenysasteikolta. Jos nollakohta on liikkunut kaaren nollakohdan oikealle puolelle on indeksikorjaus positiivinen, koska mitattu kulma on todellista pienempi, ja päinvastoin.
4 Kuva 154. Indeksivirheen määrittäminen sekstantilla. Vasemalla olevassa kuvassa indeksivirhe on - 0,6 ja oikealla + 0,8. Indeksivirhe voidaan määrittää myös auringon tai kaukana olevan pystytolpan (savupiippu) avulla. Pystyssä olevasta kohteesta mitattaessa sekstantti käännetään vaaka-asentoon. Indeksivirhe voidaan poistaa kääntämällä sekstantin pikkupeiliä sen takana olevista säätöruuveista, mutta käytännössä siihen ei kannata ryhtyä, koska sekstanttiin saattaa syntyä vain lisää virhettä. Vaakakulman mittaaminen: Kuva 155. Vaakakulman mittaaminen. Sekstantti nollataan, käännetään vaaka-asentoon ja katsotaan näköputken läpi ensin oikean puoleista kohdetta. Sekstantin runkoa aletaan liikuttaa vartaloa kääntäen hitaasti vasempaan. Kääntöliikkeen aikana liikkuvaa sädettä käännetään niin, että isossa peilissä säilyy koko ajan oikeanpuoleinen kohde. Kun vasemmanpuoleinen kohde ilmestyy pikkupeiliin liikkuva säde lukitaan. Nyt molemmat kohteet näkyvät näköputken läpi ja ne siirretään tarkasti päällekkäin rummun avulla. Kulma voidaan tämän jälkeen lukea kaaren ja rummun asteikoilta. Täydet asteet kaarelta, minuutit rummulta ja asteen kymmenykset rummun asteikolta.
5 236 Vaakakulma voidaan mitata myös katsomalla ensin vasemmanpuoleista kohdetta ja hakemalla ison peilin avulla toinen kohteista näkyviin. Se, kumpaa menetelmää käytetään, ei ole vaakakulmissa tärkeää, mutta mitattaessa korkeuskulmia (taivaankappaleista) on ensimmäinen keino ainoa oikea, koska haluttu taivaankappale (esimerkiksi tähti) on pidettävä isossa peilissä koko ajan. Kahdesta vaakakulmasta tulee mitata ensin se, johon kulmanopeus on suurempi. Mitattu vaakasuora kulma kohteiden välillä siirretään kartalle joko astelevyn tai asemanosoittimen avulla. Asemanosoitinta tarvitaan jos vaakakulmia määritetään kaksi. Tällöin kohteita on kolme. Yksi vaakakulma antaa sijoittajaksi vain ympyrän, eikä sitä voi yksin käyttää paikanmääritykseen. Jos toinen kohteista suunnitaan, saadaan näiden yhdistelmästä paikka. Kohtuullisen tarkan paikan määrittämiseksi vaakakulmien avulla tarvitaan aina kolmesta kohteesta mitatut kaksi vaakakulmaa º - 076º (10,0) º - 042º 57 (10,0) M 33 Kallbåda Helikopteritaso V - B (3) 20 sek º º 05 24º 10 Kehyksen sisäreuna 699,7 x 999,5 mm Kuva 156. Vaakakulma merikartalla ja asemanosoitin. Asemanosoittimen tarkkuus voidaan tarkastaa avaamalla viivaimet esimerkiksi 60 kulmaan. Viivaimien sivuja pitkin piirretään viivat paperille tai kartalle, ja merkitään piste asemanosoittimen keskipisteessä olevan reiän kohdalle. Asemanosoitin otetaan pois, ja piirrettyjä viivoja jatketaan kunnes viivat leikkaavat toisensa. Mikäli viivat leikkaavat merkityssä keskipisteessä, on asemanosoitin kunnossa ja tarkka. Asemanosoittimessa esiintyvät virheet voidaan ottaa huomioon kulmia kartalle vietäessä. C. SUUNTIMA Suuntimalla tarkoitetaan havaitsijan meridiaanin ja havaitun kohteen yhdistävän isoympyrän kaaren välistä kulmaa. Suuntima on todellisuudessa aina kaari, koska se on osa isoympyrää. Mutta koska kaarevuus pienimittakaavaisella kartalla on erittäin vähäistä, se voidaan piirtää suorana viivana. Piirretty viiva on sijoittaja, jonka jossain pisteessä alus sijaitsee. On muistettava, että kartalle viedään vain tosisuuntimia. Tämän vuoksi suuntima on aina muutettava tosisuuntimaksi ennen sen piirtämistä kartalle. Suuntimia on käsitelty tarkemmin tämän kirjan luvussa 8.
6 237 Suuntimat otetaan yleensä kompassin päällä olevalla suuntimalaitteella. Suuntimalaitteet voivat olla valolla varustettuja (asteikkovalo), jolloin niitä voidaan käyttää pimeälläkin. Yleensä suuntimalaitteilla voidaan suuntia myös taivaankappaleita peilien ja suodattimien avulla. Joillakin aluksilla on kuitenkin käytössä vain parrassuuntimalaitteet. Suuntima kohteeseen saadaan kääntämällä suuntimalaitteen päällä oleva viivain kohdetta kohti ja lukemalla arvo kompassista tai levyltä. Suuntimien luotettavuus riippuu olennaisesti käytetyn laitteen lukematarkkuudesta, kompassin tai suuntimislevyn virheistä ja havaitsijan tarkkuudesta. Virheiden takia aluksen paikka on sektorissa, jonka leveys kasvaa, mitä kauemmaksi kohteesta mennään (katso myös kohta 12.5). Yhden asteen virhe suuntimassa aiheuttaa 6 mpk:n etäisyydellä noin yhden kaapelinmitan (tarkemmin 193,93 metrin) virheen paikannukseen. 193,9 m 1 6 mpk Kuva 157. Suuntima kohteeseen º - 076º (10,0) º - 042º 57 (10,0) M 33 Kallbåda Helikopteritaso V - B (3) 20 sek º º 05 Kehyksen sisäreuna 699,7 x 999,5 mm 24º 10 Kuva 158. Suuntimalla saadun sijoittajan piirtäminen merikarttaan.
7 238 D. ETÄISYYS Mittaamalla etäisyys tunnettuun kohteeseen saadaan sijoittajaksi ympyrä, jonka keskipisteenä kohde on. Säteenä on mitattu etäisyys. Alus sijaitsee jossakin ympyrän kehän pisteessä. Etäisyys voidaan mitata tutkalla tai etäisyysmittarilla sekstantilla määrittämällä horisontin etäisyys (kohde horisontissa). Kun määritetään etäisyyttä kohteeseen tutkalla on aluksen tutka-antenni ympyrän keskipisteenä ja mitattu etäisyys säteenä. Tutkan säädettävä etäisyysrengas (VRM, Variable Range Marker) asetetaan sivuamaan kohdetta, jolloin etäisyys kyseiseen kohteeseen voidaan lukea näytöltä. Mahdollisimman tarkka tulos saadaan kun etäisyysrenkaan etureuna sivuaa kohdetta eikä ole sen päällä. Koska tutkasäteet taipuvat myös horisontin taakse, ei kohteen tarvitse välttämättä olla optisesti näkyvissä. Cursor BRG RNG 000 0,67 DEG NM EBL VRM 328 0,42 DEG NM Etäisyys (7,2) Kuva 159. Etäisyyden määrittäminen tutkalla. Etäisyysmittarit eivät ole yleisessä käytössä merenkulussa, koska taajuudeltaan etäisyysmittaukseen soveltuva lasersäde on silmälle vahingollinen. Mittaustarkkuus niillä on huippuluokkaa mutta vain sillä edellytyksellä, että kohde näkyy optisesti. Etäisyys voidaan mitata myös kulmamittaukseen perustuen sekstantilla. Edellytyksenä on, että kohteen korkeus tunnetaan. Kohteina voidaan käyttää esimerkiksi loistoluetteloissa mainittuja turvalaitteita. Kun kohteen korkeus on tiedossa ja sen korkeuskulma vedenpinnasta on sekstantilla mitattu, saadaan etäisyys laskettua seuraavasta kaavasta:
8 239 Etäisyys (mpk) = 1,86 x h k missä 1,86 = vakio, jolloin etäisyys saadaan meripeninkulmina, h = kohteen korkeus metreinä ja k = mitattu kulma kaariminuutteina. Huomattava on, että korkeus on mitattava esimerkiksi majakan valon keskikohtaan, koska sen korkeus vedenpinnasta on mainittu loistoluettelossa. Kun kohde nähdään merihorisontissa, saadaan etäisyys siihen laskettua seuraavasti: Etäisyys (mpk) = 2,08 x (Öh + ÖH) missä 2,08 = vakio, jolloin etäisyys saadaan meripeninkulmina, h = havaitsijan silmän korkeus metreinä ja H = havaintokohteen korkeus metreinä, molemmat merenpinnasta mitattuna. Kaavan kertoimessa on huomioitu valon taipumisesta johtuva näköpiirin laajeneminen, joka on noin 7,7 %. Käytännön merenkulussa voidaan kertoimena käyttää tasalukua 2 ilman suurta virhettä ja laskutoimitus on helpompi suorittaa. Tätä menetelmää käytettäessä sääolosuhteiden tulisi olla mahdollisimman normaalit, koska valo taipuu eri tavoin eri olosuhteissa. Edellä mainittu kaava on periaatteessa sama, jolla horisontin etäisyys lasketaan. Horisontin etäisyyttä määritettäessä kaavaan ei vain oteta mukaan kohteen korkeutta. Kaavan perusteet selviävät seuraavasta: a } h r r Kuva 160. Horisontin etäisyys.
9 240 Kuvasta selviää, että horisontin etäisyyttä havaitsijasta voidaan tarkastella suorakulmaisen kolmion avulla. Kuvan mukaisen suorakulmaisen kolmion sivun pituus saadaan kaavasta: a 2 = (r + h) 2 - r 2 joka voidaan esittää muodossa a 2 = r 2 + 2rh + h 2 - r 2 ja edelleen muodossa a = Ö h x (2r + h). Koska tekijässä (2r + h) on h erittäin pieni verrattuna maan säteeseen r, voidaan se ilman suurta virhettä jättää huomiotta. Tällöin kaava on muotoa: a = Ö 2r x Ö h Sijoittamalla kaavaan maapallon säde r (noin m) metreinä ja pitämällä myös h (havaitsijan silmänkorkeus) samassa yksikössä, saadaan näköpiirin etäisyydeksi metreinä lausuttuna: a = 3568,47 x Ö h ja meripeninkulmina a = 3568,47 / 1852 x Ö h = 1,927 x Ö h Valonsäteiden taipumisen vuoksi näköpiirin etäisyys on kuitenkin noin 7,7% suurempi, jolloin todellisen näköpiirin etäisyydeksi saadaan: a = 1,927 x Ö h + 0,077 x 1,927 x Ö h = 2,08 x Ö h E. LUOTAAMINEN Sijoittajan määritys luotaamalla suoritetaan vertaamalla kaikuluodin näyttämää merikartalla oleviin syvyysmerkintöihin. Menetelmänä se on epätarkka ja antaa sijoittajaksi käyrän. Menetelmää voidaan käyttää esimerkiksi lähestyttäessä rannikkoa avomereltä. Tällöin syvyyssuhteiden nopea muuttuminen on helposti havaittavissa kaikuluodilta. Edellytyksenä on, että karttaan painetut syvyyskäyrät ovat samansuuntaisia ja lähes rannikon suuntaisia. Luotaamisen käyttäminen sijoittajan määrittämiseen on riippuvainen merenmittauksen tarkkuudesta. Yhdeksänkymmentäluvulla painetuissa ja mitatuissa merikartoissa syvyystiedot ovat luotettavia ainakin kulkuväylillä, vaikka kaikkia syvyysarvoja ei karttoihin ole painettukaan. Yleisesti merikarttaan voi luottaa, kun liikutaan väyläalueella. Sen sijaan väyläalueen ulkopuolella liikkuminen voi olla hyvinkin riskialtista. Väyläalueet on aina harattu, kun taas ulkopuolinen alue vain luodattu. Kaikuluotia tulee käyttää aina liikuttaessa väyläalueen ulkopuolella. Väyläalueen ulkopuolella joudutaan liikkumaan esimerkiksi aluksen ankkuroides-
10 241 sa. Huomioitavaa suoraan pohjan alle mittaavan kaikuluodin käytössä on, että se ei anna syvyysinformaatiota ennakkoon. Koska kaikuluoti näyttää veden syvyyttä jatkuvasti (varsinkin piirtävä kaikuluoti), muodostuu merenpohjasta kuva, joka yhdessä muiden sijoittajien kanssa antaa vähintään tyydyttävän paikanmääritystarkkuuden. Luotaaminen voidaan suorittaa myös käsiluodin avulla. Tällöin luoti heitetään kulkusuunnassa aluksen keulan eteen ja syvyystieto luetaan, kun käsiluodin naru on pystysuoraan kohti merenpohjaa. Käsiluotia käytettäessä aluksen tulee liikkua erittäin hitaasti SUUNTIMIEN MÄÄRITTÄMINEN Kuten jo aiemmin mainittiin, suuntimat määritetään yleensä kompassin päällä olevalla suuntimalaitteella. Joillakin aluksilla on kuitenkin käytössä vain parrassuuntimalaitteet, joilla saadaan vain keulasuuntimia. Suuntima kohteeseen saadaan kääntämällä suuntimislevyn päällä oleva viivain kohdetta kohti. Viivaimen päissä on yleensä diopterit tarkkaa suuntimista varten. Suuntimien luotettavuus riippuu olennaisesti suuntimiseen käytetyn laitteen lukematarkkuudesta, kompassin tai suuntimislevyn virheistä ja havaitsijan tarkkuudesta. Kahdella tai useammalla suuntimalla määritetyn paikan tarkkuus riippuu sekä sijoittajien tarkkuudesta että siitä kulmasta, jossa sijoittajat leikkaavat toisensa. Sijoittajien leikkauspisteeseen muodostuu virhealue, jonka sisällä alus teoriassa sijaitsee. Mikäli suuntimia (sijoittajia) on kaksi, on optimaalisin leikkauskulma 90. Kolme sijoittajaa tulee mahdollisuuksien mukaan valita siten, että niiden välinen leikkauskulma on 120 (katso myös kohta 12.5). Kuva 161. Virhealueen muodostuminen suuntimalla.
11 242 A. PAIKANMÄÄRITYS SUUNTIMALAITTEEN AVULLA 1. Kaksi suuntimaa samaan kohteeseen. Sama kohde suunnitaan kaksi kertaa sellaisin väliajoin, että suuntimien arvot (keulasuuntimia) poikkeavat toisistaan vähintään 40. Suuntimien välillä aluksen tulee ajaa samaa suuntaa ja nopeutta mahdollisimman tarkasti Väylä Sijoittajan siirtäminen, kuljettu suunta ja matka. Kuva 162. Kaksi suuntimaa samaan kohteeseen. 1. Ensimmäinen suuntima. Samalla luetaan tai nollataan loki tai kello, joilla kuljettu matka voidaan myöhemmin määrittää. Piirretään sijoittaja kartalle. 2. Toinen suuntima. Samalla määritetään suuntimien välillä kuljettu matka (lokin tai kellon ja nopeuden avulla). Piirretään sijoittaja kartalle. 3. Ensimmäinen sijoittaja siirretään yhdensuuntaissiirtona kuljetun matkan verran kulkusuuntaan. 4. Aluksen havaittu paikka on siirretyn ja jälkimmäisen sijoittajan leikkauspisteessä. 5. Matkaa jatketaan havaitusta paikasta haluttuun suuntaan. Tämän menetelmän epätarkkuudet syntyvät yleensä siitä, että alus ei kulje suuntimien välillä samaa suuntaa ja nopeutta, vaan esimerkiksi sortuu tuulen ja/tai virran vaikutuksesta (katso kohta 5.5). Pitkä havaintojen välinen aika vaikuttaa virheen muodostumiseen, koska silloin lokilaitteeseen kertyy enemmän virhettä. Hyvissä olosuhteissa ja muutaman harjoituskerran jälkeen tämä on suhteellisen tarkka menetelmä, joka soveltuu hyvin paikanmääritykseen liikuttaessa rannikon läheisyydessä.
12 Kipparin suuntima (neljän piirun suuntima). Tämä menetelmä on erikoistapaus suuntimasta samaan kohteeseen. Suuntimista (ensimmäinen 45 ja toinen 90, keulasuuntimina) muodostuu suorakulmainen kolmio, jonka sivut ovat yhtä pitkät. Jos alus kulkee suuntimien välillä 0,7 meripeninkulmaa, on myös sivuutusetäisyys suunnittavaan kohteeseen sama. Jos halutaan tietää ennakkoon tuleva sivuutusetäisyys kohteeseen, on ensimmäisen suuntiman oltava 26,5 ja toisen 45 (tan 26,5 = 0,5). Sivuutusetäisyys voidaan määrittää myös jälkikäteen siten, että ensimmäinen suuntima on 90 ja jälkimmäinen 135. Seuraavassa kuvassa ja tekstissä on esitetty kipparinsuuntiman suorittaminen käytännössä. Suuntimiseen soveltuu mikä tahansa suuntimislaite, jolla voidaan määrittää keulasuuntimia. (1) 1 (2) 2 a Väylä 26,5 a 45 a 90 3 Kuva 163. Kipparin suuntima. 1. Suunnitaan kohde ensimmäisen kerran, kun se on 45 (neljä piirua) (tai 26,5 ) keulasuuntimassa ja luetaan tai nollataan loki tai kello, joilla kuljettu matka voidaan myöhemmin määrittää. 2. Suunnitaan kohde uudestaan, kun se on 90 keulasuuntimassa (suoraan sivulla) (tai 45, jos ensimmäinen oli 26,5 ). Samalla määritetään suuntimien välillä kuljettu matka (lokin tai kellon ja nopeuden avulla). 3. Sivuutusetäisyys on sama kuin suuntimien välillä kuljettu matka (kuvassa a). Havaittu paikka piirretään kartalle kohteen sivuutuskohtaan määritetyn sivuutusetäisyyden päähän siitä. MIKÄLI ALUS SORTUU TUULEN JA/TAI VIRRAN VAIKUTUKSESTA, ON SOR- TOKULMA OTETTAVA HUOMIOON SUUNTIMISSA, KOSKA VIRHE MUODOS- TUU VARSINKIN SUUREMMALLA ETÄISYYDELLÄ SUUREKSI!
13 SIJOITTAJIEN YHDISTELMÄT Kuten aiemmin on korostettu, vain yhtä sijoittajaa käyttämällä ei saada aluksen tarkkaa paikkaa, vaan alus sijaitsee jossakin kohtaa kyseistä sijoittajaa. Tarkan paikannuksen saamiseksi sijoittajia on oltava ainakin kaksi. Niiden tulee leikata toisensa ja olla mahdollisimman samanaikaisten havaintojen tuloksia. Poikkeuksena tästä on vain siirretty sijoittaja, jota käytetään esimerkiksi tähtitieteellisessä paikanmäärityksessä sekä suunnittaessa samaa kohdetta kaksi kertaa. Erilaisia sijoittajien yhdistelmiä ovat muun muassa kaksi linjaa suuntima ja etäisyys suuntima ja luotaus kaksi suuntimaa samaan kohteeseen ristisuuntimat suuntima ja vaakakulma kaksi vaakakulmaa kaksi tai useampia etäisyyksiä. Kaksi linjaa, kun alus sijaitsee niiden leikkauspisteessä, muodostavat erittäin tarkan ja helpon menetelmän paikanmääritykseen. Sijoittajatkin ovat jo valmiiksi piirrettynä merikarttaan jos linjoina käytetään linjatauluja. Linjat voidaan muodostaa itsekin. Kohteet voivat tällöin olla joko luonnon merkkejä (saarten reunat, korkeat rinteet ), merimerkkejä (majakat, loistot, kummelit, reunamerkit, linjataulut ) tai muita selvästi merelle näkyviä rakenteita. Jos sijoittajat on muodostettu itse valituista kohteista, piirretään sijoittajat kartalle astelevyn ja yhdensuuntaisviivaimen avulla. Suuntima ja etäisyys voidaan mitata joko samaan kohteeseen tai myöskin eri kohteisiin. Edellytyksenä on, että sijoittajat leikkaavat toisensa. Käytännössä etäisyys mitataan tutkalla. Suuntima voidaan määrittää joko suuntimalaitteella tai tutkan elektronisella suuntimaviivalla (EBL, Electronic Bearing Line). Etäisyys on näistä kahdesta tarkempi, vaikka tutkalla määritetty etäisyys ei olekaan absoluuttinen totuus. Tutkapulssin pituudesta riippuen mitattu etäisyys voi olla muutamia kymmeniä metrejä todellista suurempi tai pienempi.
14 245 Cursor BRG RNG DEG NM EBL VRM 000 0, ,42 DEG NM Kuva 164. Suuntima ja etäisyys. Suuntima ja luotaus antavat tyydyttävän paikanmääritystarkkuuden jos veden syvyyssuhteet muuttuvat tasaisesti, syvyyskäyrät ovat luotettavia, kaikuluoti toimii oikein eikä alus kulje syvyyskäyrän suuntaisesti. Suuntima on näistä kahdesta tarkempi. Kaksi suuntimaa samaan kohteeseen on selvitetty edellisellä sivulla. Tämän menetelmän epätarkkuudet syntyvät yleensä siitä, että alus ei kulje suuntimien välillä samaa suuntaa ja nopeutta, vaan esimerkiksi sortuu tuulen ja/tai virran vaikutuksesta. Lisäksi pitkä havaintojen välinen aika vaikuttaa virheen muodostumiseen, koska silloin lokilaitteeseen kertyy enemmän virhettä tai nopeuden arviointi tulee vaikeaksi. Kaksi suuntimaa voidaan valita myös siten, että ensimmäisen keulasuuntiman arvo tuplataan toiseen suuntimaan. Tässä tapauksessa kolmiosta muodostuu tasasivuinen, jolloin suuntimien välillä kuljettu matka on sama kuin etäisyys kohteeseen toisen suuntiman hetkellä. Jälkimmäinen keulasuuntima muutetaan tosisuuntimaksi ja piirretään merikarttaan. Lokilaitteelta tai kellon ja nopeuden avulla määritetty matka asetetaan harppiin ja etäisyyssijoittaja piirretään leikkaamaan suuntimasijoittajaa, kuten suuntima ja etäisyys. Ristisuuntimalla tarkoitetaan kahta tai useampaa toisiaan leikkaavaa sijoittajaa, jotka on määritetty suuntimalla. Kahdella tai useammalla suuntimalla määritetyn paikan tarkkuus riippuu sekä sijoittajien tarkkuudesta että siitä kulmasta, jossa sijoittajat leikkaavat toisensa. Kuten aiemmin kohdassa 12.4 on mainittu, sijoittajien leikkauspisteeseen voi muodostua virhealue, jonka sisällä alus teoriassa sijaitsee. Jos suuntimia (sijoittajia) on kaksi, on optimaalisin leikkauskulma 90. Kolme sijoittajaa tulisi mahdollisuuksien mukaan valita siten, että niiden välinen leikkauskulma olisi 120. Mikäli määritetyt sijoittajat leikkaavat toisensa samassa pisteessä on aluksen paikka kyseisessä pisteessä. Mutta jos sijoittajien leikkauksista muodostuu virhekolmio (kolme sijoittajaa) tiedetään, että yhdessä tai useammassakin suuntimissa on virhettä.
15 246 Virhekolmion syntyyn vaikuttavat havaintojen välinen aika havaintoetäisyys kompassin tarkkuus ja rajoitukset (lukematarkkuus) väärin huomioitu kompassin eksymä (tai etumerkki) epätarkkuus sijoittajien kartalle piirtämisessä mahdollisesti väärä kohde. Kaikkiin muihin paitsi kompassista johtuviin virheisiin voidaan vaikuttaa (ne voidaan eliminoida) suhteellisen helposti. Havaintojen välillä kuljettu aika voidaan huomioida siirtämällä kahta ensimmäistä sijoittajaa yhdensuuntaisena kulkusuuntaan kuljetun matkan verran (aika/nopeus). Kompassista johtuvia virheitä on huomattavasti vaikeampi huomioida paikannuksessa, koska ne ovat joko systemaattisia tai satunnaisia. Systemaattinen virhe voi aiheutua esimerkiksi virheellisestä erannosta tai eksymästä. Virhe vaikuttaa kaikkiin suuntimiin samanmerkkisenä ja -suuruisena. Kun sijoittajat piirretään kartalle muodostuu niiden leikkauskohtaan virhekolmio, jonka sisällä aluksen pitäisi teoriassa olla, mutta käytännössä niin ei kuitenkaan välttämättä ole. Esimerkiksi yhden asteen virheellisellä eksymällä (a) saadaan kohteisiin A, B ja C kuvan osoittama virhekolmio, kun todelliset suuntimat ovat A = 255, B = 285 ja C = 310. Mikäli kohteiden väliset etäisyydet ovat seuraavat: AB 5 mpk, BC 4 mpk ja AC 9 mpk, ja suuntimien väliset leikkauskulmat (Φ) ovat vastaavasti 30, 25 ja 55, saadaan aluksen todelliseksi paikaksi piste F. C a B a F = 25 Y F = 55 F = 30 Z X F a A Kuva 165. Aluksen todellinen paikka sekä virhekolmio kolmella suuntimalla, joissa on yhden asteen vakiovirhe. Kuvassa virhe suuntimiin on suurennettu 5 asteeseen selvyyden vuoksi.
16 247 Pisteen F etäisyys virhekolmion eri pisteistä voidaan määrittää kaavasta: ZF = AB x sin a (tämä kaava antaa etäisyyden välillä ZF) sin F ZF = (5 x (sin 1 ) / sin 30 ) = 0, mpk Sijoittamalla kukin arvo kaavaan saadaan tulokseksi, että ZF = 0,175 mpk, XF = 0,165 mpk ja YF = 0,192 mpk. Kun etäisyydet ovat pieniä, eikä kiinteä virhe ylitä yhtä astetta, voidaan syntynyttä virheellisyyttä paikannuksessa pitää merkityksettömänä, varsinkin liikuttaessa rannikon tuntumassa avomerellä. On hyvä kuitenkin pitää mielessä, että paikka ei välttämättä sijaitse virhekolmion sisällä. Todennäköisimmäksi paikaksi on aina hyvä olettaa epäedullisin, jolloin suunta voidaan valita turvallisimmin. Satunnaiset virheet voivat johtua esimerkiksi suuntimavirheestä ja piirtämisen aiheuttamista virheistä. Satunnaisvirheiden aiheuttamaa virheellisyyttä paikannukseen on mahdotonta määrittää tai laskea. Tämä tukeekin epäedullisimman paikan valintaa todennäköiseksi paikaksi, koska jo pelkkä virhekolmion syntyminen osoittaa, että joissakin tai kaikissa suuntimissa on virhettä. Virhealueen muodostumista teoreettisesti tarkasteltuna on käsitelty myös kohdassa Suuntimisessa on tärkeää suorittamisjärjestys. Koska kahden tai useamman suuntiman välillä kuluu aikaa, on ensin suunnittava kohteista se, johon suuntima muuttuu hitaammin. Suuntima muuttuu hitaammin kohteisiin, jotka sijaitsevat aluksen keulan tai perän puolella (kulmanopeus pieni) ja nopeammin kohteisiin jotka ovat sivulla (kulmanopeus suuri). Tarkkuutta voidaan parantaa siten, että jälkimmäisen suuntiman jälkeen suunnitaan vielä kerran ensimmäinen kohde ja kartalle piirretään näiden kahden suuntiman (1. kohteeseen) keskiarvo. Toinen tapa on siirtää ensimmäistä suuntimaa yhdensuuntaissiirtona suuntimien välillä kuljetun matkan verran. Kuten aiemmin on todettu, yksi vaakakulma antaa sijoittajaksi ympyrän, eikä sitä yksin voi käyttää paikanmääritykseen. Mikäli toinen kohteista vielä suunnitaan, saadaan näiden yhdistelmästä aluksen paikka, koska suuntima osoittaa ympyräsijoittajalta kohdan, jossa vaakakulma pitää paikkaansa. Näistä kahdesta vaakakulma on tarkempi sijoittaja. Vaakakulma 053 Suuntima Kuva 166. Aluksen kulkusuunta Suuntima ja vaakakulma.
17 248 Kaksi vaakakulmaa menetelmänä antaa kohtalaisen tarkan paikan. Koska vaakakulmia käytetään liikuttaessa rannikon läheisyydessä, muuttuvat kohteiden väliset kulmat suhteellisen hitaasti. Kuitenkin jos toinen kulmista muuttuu nopeammin, on se määritettävä jälkimmäisenä. Kulmanopeus voidaan määrittää silmämääräisesti arvioimalla. Vaakakulman mittaaminen on selvitetty kohdassa 12.3 B. Mitatut vaakakulmat asetetaan asemanosoittimeen, ja viedään kartalle siten, että osoittimen sivut sivuavat kyseisiä kohteita. Kartalle viedyt vaakakulmat antavat aluksen paikan keskelle asemanosoittimen levyä. Levyssä on yleensä reikä, josta kynällä voidaan paikka piirtää kartalle. Kaksi tai useampia etäisyyksiä antavat myös kohtalaisen tarkan paikanmäärityksen, koska etäisyys voidaan määrittää suhteellisen luotettavasti. Edellytyksenä tässäkin menetelmässä on, että sijoittajat leikkaavat toisensa. Mikäli kohteet, joista etäisyys on määritetty, sijaitsevat vastakkaisilla puolilla alusta, sijoittajat leikkaavat kahdessa kohtaa. Tällöin toinen leikkauspisteistä on suljettava pois varmistamalla paikannus esimerkiksi mittaamalla kolmas etäisyys tai suuntimalla toinen kohteista. Voi käydä myös niin, että määritetyt etäisyyssijoittajat eivät leikkaa toisiaan lainkaan (esimerkiksi kohteet vastakkaisilla puolilla alusta). Tällöin toinen etäisyyksistä on määritettävä siten että kohde sijaitsee 90 kulmassa ensimmäiseen nähden SIJOITTAJIEN LUOTETTAVUUS Eri menetelmillä saadut sijoittajat voidaan asettaa luotettavuusjärjestykseen sen perusteella, mitä virheitä sijoittajissa esiintyy. Kaikissa sijoittajissa on otettava huomioon se, että merikarttakaan ei ehkä ole aivan tarkka. Sijoittaja saattaa olla oikea, mutta kartalle siirron yhteydessä siihen voi muodostua virhettä esimerkiksi kartan projisointitavasta johtuen. Eri menetelmät tarkkuusjärjestyksessä ovat (tarkimmasta alkaen): yhdyslinja etäisyys vaakakulma suuntima luotaus sekä niiden yhdistelmät: kaksi linjaa kaksi tai useampia etäisyyksiä kaksi vaakakulmaa suuntima ja etäisyys suuntima ja vaakakulma kaksi suuntimaa samaan kohteeseen (edellyttäen, että etäisyydet ovat pieniä)
18 249 ristisuuntimat suuntima ja luotaus. Sijoittajan luotettavuuteen vaikuttaa myös se, että se piirretään kartalle suorana viivana, vaikka sijoittaja todellisuudessa on kaari. Optinen sijoittaja on osa isoympyrää, joka Mercatorin kartalla on aina kaareva. Tämän vaikutus näköpiirin alueella on kuitenkin käytännössä mitätön. Siirretyn sijoittajan virhe kasvaa ajan myötä. Tämä johtuu siitä, että aluksen kulkusuunnassa ja nopeudessa esiintyy ajan kuluessa virheitä, joita ei voida ennustaa tarkasti ALUKSEN OHJAILU OPTISIN SUUNTIMIN Mikäli alusta halutaan ohjata pelkästään optisia suuntimia apuna käyttäen, tulee suunnittavat kohteet valita huolella jo reittisuunnitteluvaiheessa. Kohteiden tulee olla selvästi erottuvia ja yksiselitteisiä. Tämä sen vuoksi, että ohjailija ei yleensä itse suorita suuntimista, vaan sen tekee tähystäjä. Tähystäjille on tehtävä selkeä taulukko suunnittavista kohteista ja ilmoitettavista suuntimista. Ohjailua optisin suuntimin tarvitaan esimerkiksi silloin, kun alus ei syystä tai toisesta voi käyttää tutkaa tai elektronisia paikanmäärityslaitteita. Turvalliseen optisin menetelmin suoritettavaan ohjailuun kuuluu aina merimaastosta valitun kohteen (ohjailumerkki) ja kartalla olevan väylän tosisuunnan käyttö. Jos keula ei osoita ohjailumerkkiin silloin kun kulkusuunta on oikein tai päinvastoin, alus on pysäytettävä paikanmääritystä varten. Ajettavalle reitille suunnitellaan tarkastuspisteet (reitillä pysyminen), käännösten ennakkopisteet sekä muut halutut pisteet suuntimin. Suuntimia suunnitellaan otettavaksi molemmin puolin yhtäaikaa, jolloin niistä saadaan ristisuuntima ja näin ollen havaittu paikka. Käytännössä ohjailu suoritetaan esimerkiksi seuraavasti (kuva 167): 1. Alus ajaa suuntaa 202 ja varmistaa paikkansa suuntimalla kohteen Ohjailija ilmoittaa tähystäjille suuntimishetken ( valmiina suuntimaan kohde 1, lähestyy LUE ). 3. LUE- komennolla ruorimies lukee hyrräkompassin näyttämän suunnan ohjailijalle (mikäli käytetään parrassuuntimalaitetta) ja tähystäjät suuntivat suunnitellut kohteensa. 4. Ohjailija ilmoittaa tähystäjille suuntimishetken hyrräsuunnan, jonka tähystäjät asettavat parrassuuntimalaitteen levyyn (kääntämällä levyä, mutta ei enää osoitinta). 5. Tähystäjät ilmoittavat ohjailijalle hyrräsuuntimat, jotka ohjailija merkitsee muistiin (esimerkiksi kartan reunaan) ja muuttaa ne tosisuuntimiksi. 6. Ohjailija piirtää määritetyt sijoittajat kartalle ja merkitsee niiden leikkauspisteeseen havaitun paikan. 7. Havaitun paikan perusteella ohjattavaa suuntaa korjataan haluttuun suuntaan, mikäli siihen on tarvetta.
19 Suuntimista jatketaan samalla tavalla kaikissa ennalta suunnitelluissa pisteissä ja tarpeen mukaan myös muulloin. 9. Koko ohjailun ajan on käytettävä väyläosuuksille valittuja ohjailumerkkejä ja tosisuuntia sekä tarvittaessa esimerkiksi kipparin suuntimia. Lisäksi paikanmääritystä varmennetaan lokilaitteen trippimittarin avulla. Näin ohjailijalla on kolme toisiaan varmistavaa ja täydentävää menetelmää. suuntimat (päämenetelmä) ohjailumerkki ja tosisuunta (käytetään aina ja kaikissa ohjailumenetelmissä) trippimittari (tukeva menetelmä) Kallbåda Helikopteritaso V - B (3) 20 sek 12 M º - 022º (10,0) º (10,0) 202º - 022º º 05 Kehyksen sisäreuna 699,7 x 999,5 mm 24º 10 Kuva 167. Esimerkki optisin suuntimin toteutettavaan ohjailuun. Suuntimien arvot (keula-, hyrrä- tai tosisuuntimat) tulee merkitä varsinaiseen suunnitelmaan. Mikäli aluksella on hyrräsuuntimalaite ja nopeusvirheen korjaus toimii oikein, voidaan ilmoitetut suuntimat piirtää suoraan kartalle tosisuuntimina. Muussa tapauksessa nopeusvirhe tulee huomioida ja muuttaa hyrräsuuntimat tosisuuntimiksi ennen niiden siirtämistä merikartalle (katso kohta 5.4 C). Näin suuntimista jatketaan kullakin väyläosuudella paikannuksen varmistamiseksi sekä ennakko- ja käännöspisteen määrittämiseksi. Ennakkopiste tulee valita siten, että pisteessä aloitetaan kääntyminen tai, käännöksen varmistamiseksi, nollataan matkamittari ja käännös aloitetaan sen perusteella. Uudelle suunnalle kääntymisen jälkeen tarkistetaan välittömästi suuntimalla aluksen paikka väylän suhteen. Jos aluksen keula käännöksen jälkeen osoittaa ohjailumerkkiä kohti ja alus on väylän tosisuunnalla, voidaan aluksen kulkusuuntaa käyttää toisena suuntimana.
20 251 Suuntiminen voidaan suorittaa myös siten, että suuntijat ilmoittavat ennalta suunnitellut suuntimat: Kohde 1, suuntima 202 lähestyy - NYT. Jos suuntijat ilmoittavat suuntimat eri aikaan, on alus tällöin sivussa suunnitellulta reitiltä. Mikäli esimerkiksi oikeanpuoleinen suuntima ilmoitetaan ensin, on alus vasemmalla suunnitellulta reitiltä ja päinvastoin. 13. ELEKTRONINEN PAIKANMÄÄRITYS 13.1 YLEISTÄ Elektronisella paikanmäärityksellä tarkoitetaan aluksen paikannusta erilaisin elektronisin apuvälinein. Jotta merenkulkija voi luottaa välineidensä tuottamaan paikannukseen tai mittausarvoihin, tulee hänen tarkasti tuntea ne perusteet, joiden mukaan kyseiset laitteet toimivat, mitä virheitä niissä mahdollisesti voi esiintyä sekä miten niiden luotettavuutta voidaan seurata ja arvioida. Lisäksi tulee tuntea laitteiden eri käyttömahdollisuudet merellä liikuttaessa. Elektronisia paikanmääritysjärjestelmiä käytettiin aiemmin vain avomerenkulussa ja rannikon lähellä sekä lähestyttäessä rannikkoa. Rannikkomerenkulussa elektroninen paikanmääritys yleistyi vasta GPS:n ja erityisesti DGPS:n tultua käyttöön. Merivoimissa käytettiin rannikkomerenkulussa jo näitä aiemmin Syledis -radiopaikannusjärjestelmää. Elektronisessa paikanmäärityksessä käytettävistä maajärjestelmistä käsitellään tässä Decca, Loran C ja Syledis. Satelliittijärjestelmistä käsitellään GPS, Glonass ja DGPS. Näiden lisäksi oma lukunsa on myös tutkalaitteesta. Maajärjestelmistä on merivoimissa nykyään käytössä ainoastaan Syledis. Decca korvattiin 90- luvun puolivälissä GPS- ja DGPS-järjestelmällä eikä Loran C-laitteita ole enää ollenkaan käytössä. Eri paikannuslaitteita on tässä käsitelty vain niiden kehityksen, toimintaperiaatteen, virheiden ja käyttömahdollisuuksien kannalta. Varsinainen laitteen käyttö ja näppäintekniikka on suurimmalta osaltaan jätetty tehtäväksi käytännön harjoituksina, koska laitteet ovat toiminnoiltaan hyvinkin erilaisia. Muutamia käytännössä hyviksi havaittuja keinoja on tähän kuitenkin otettu mukaan. Koska kaikki paikannuslaitteet käyttävät hyväkseen radiotiellä etenevää sähkömagneettista säteilyä, tarkastellaan ensin signaalin käyttäytymistä ilmakehässä SIGNAALIN KÄYTTÄYTYMINEN ILMAKEHÄSSÄ Elektronisten paikannuslaitteiden tai järjestelmiin kuuluvien osien lähettämät signaalit ovat elektromagneettista säteilyä. Käytännössä säteily synnytetään suuritaajuisesta vaihtosähköstä, joka suunnataan antennin kautta ilmaan. Nämä säteet muodostavat radioaaltoja, joiden taajuus eri laitteilla on erilainen. Radioaallot etenevät ilmakehässä lähes km/s optiikan lakien mukaisesti joka suuntaan. Käytetystä taajuudesta ja signaalin lähtökulmasta riippuen se joko taipuu tai
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla
 AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla Tähtitieteellinen merenkulkuoppi on oppi, jolla määrätään aluksen sijainti taivaankappaleiden perusteella. Paikanmääritysmenetelmänäon ristisuuntiman
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla Tähtitieteellinen merenkulkuoppi on oppi, jolla määrätään aluksen sijainti taivaankappaleiden perusteella. Paikanmääritysmenetelmänäon ristisuuntiman
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Satelliittipaikannus
 Kolme maailmalaajuista järjestelmää 1. GPS (USAn puolustusministeriö) Täydessä laajuudessaan toiminnassa v. 1994. http://www.navcen.uscg.gov/gps/default.htm 2. GLONASS (Venäjän hallitus) Ilmeisesti 11
Kolme maailmalaajuista järjestelmää 1. GPS (USAn puolustusministeriö) Täydessä laajuudessaan toiminnassa v. 1994. http://www.navcen.uscg.gov/gps/default.htm 2. GLONASS (Venäjän hallitus) Ilmeisesti 11
RATKAISUT: 16. Peilit ja linssit
 Physica 9 1 painos 1(6) : 161 a) Kupera linssi on linssi, jonka on keskeltä paksumpi kuin reunoilta b) Kupera peili on peili, jossa heijastava pinta on kaarevan pinnan ulkopinnalla c) Polttopiste on piste,
Physica 9 1 painos 1(6) : 161 a) Kupera linssi on linssi, jonka on keskeltä paksumpi kuin reunoilta b) Kupera peili on peili, jossa heijastava pinta on kaarevan pinnan ulkopinnalla c) Polttopiste on piste,
d sinα Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila
 Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
Yhtälön oikealla puolella on säteen neliö, joten r. = 5 eli r = ± 5. Koska säde on positiivinen, niin r = 5.
 Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
 MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
Geometrian kertausta. MAB2 Juhani Kaukoranta Raahen lukio
 Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
Työn tavoitteita. 1 Teoriaa
 FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinto 14.12.2012
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinto 14.12.2012 Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi, kiinteä
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinto 14.12.2012 Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi, kiinteä
YMPYRÄ. Ympyrä opetus.tv:ssä. Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne
 YMPYRÄ Ympyrä opetus.tv:ssä Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne KAPPALEEN TERMEJÄ 1. Ympyrä Ympyrä on niiden tason pisteiden joukko, jotka ovat yhtä kaukana
YMPYRÄ Ympyrä opetus.tv:ssä Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne KAPPALEEN TERMEJÄ 1. Ympyrä Ympyrä on niiden tason pisteiden joukko, jotka ovat yhtä kaukana
FYSIIKAN LABORATORIOTYÖT 2 HILA JA PRISMA
 FYSIIKAN LABORATORIOTYÖT HILA JA PRISMA MIKKO LAINE 9. toukokuuta 05. Johdanto Tässä työssä muodostamme lasiprisman dispersiokäyrän ja määritämme työn tekijän silmän herkkyysrajan punaiselle valolle. Lisäksi
FYSIIKAN LABORATORIOTYÖT HILA JA PRISMA MIKKO LAINE 9. toukokuuta 05. Johdanto Tässä työssä muodostamme lasiprisman dispersiokäyrän ja määritämme työn tekijän silmän herkkyysrajan punaiselle valolle. Lisäksi
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 21.4.2017 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 21.4.2017 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Ympyrä 1/6 Sisältö ESITIEDOT: käyrä, kulma, piste, suora
 Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Heijastuminen ionosfääristä
 Aaltojen eteneminen Etenemistavat Pinta-aalto troposfäärissä Aallon heijastuminen ionosfääristä Lisäksi joitakin erikoisempia heijastumistapoja Eteneminen riippuu väliaineen ominaisuuksista, eri ilmiöt
Aaltojen eteneminen Etenemistavat Pinta-aalto troposfäärissä Aallon heijastuminen ionosfääristä Lisäksi joitakin erikoisempia heijastumistapoja Eteneminen riippuu väliaineen ominaisuuksista, eri ilmiöt
Merenkulku. Onnea matkaan aikaa 10 minuuttia
 Merenkulku Onnea matkaan aikaa 10 minuuttia Tehtävä 1 Minkälaisen äänimerkin konealus antaa, kun se liikkuu veden halki, näkyvyyden ollessa rajoittunut? A. Yksi lyhyt enintään 1min välein B. Yksi pitkä
Merenkulku Onnea matkaan aikaa 10 minuuttia Tehtävä 1 Minkälaisen äänimerkin konealus antaa, kun se liikkuu veden halki, näkyvyyden ollessa rajoittunut? A. Yksi lyhyt enintään 1min välein B. Yksi pitkä
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Työ 2324B 4h. VALON KULKU AINEESSA
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/5 Työ 2324B 4h. VALON KULKU AINEESSA TYÖN TAVOITE Työssä perehdytään optisiin ilmiöihin tutkimalla valon kulkua linssisysteemeissä ja prismassa. Tavoitteena on saada
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/5 Työ 2324B 4h. VALON KULKU AINEESSA TYÖN TAVOITE Työssä perehdytään optisiin ilmiöihin tutkimalla valon kulkua linssisysteemeissä ja prismassa. Tavoitteena on saada
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Luento 5: Stereoskooppinen mittaaminen
 Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 5: Stereoskooppinen mittaaminen AIHEITA Etäisyysmittaus stereokuvaparilla Esimerkki: "TKK" Esimerkki: "Ritarihuone"
Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 5: Stereoskooppinen mittaaminen AIHEITA Etäisyysmittaus stereokuvaparilla Esimerkki: "TKK" Esimerkki: "Ritarihuone"
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Työ 31A VAIHTOVIRTAPIIRI. Pari 1. Jonas Alam Antti Tenhiälä
 Työ 3A VAIHTOVIRTAPIIRI Pari Jonas Alam Antti Tenhiälä Selostuksen laati: Jonas Alam Mittaukset tehty: 0.3.000 Selostus jätetty: 7.3.000 . Johdanto Tasavirtapiirissä sähkövirta ja jännite käyttäytyvät
Työ 3A VAIHTOVIRTAPIIRI Pari Jonas Alam Antti Tenhiälä Selostuksen laati: Jonas Alam Mittaukset tehty: 0.3.000 Selostus jätetty: 7.3.000 . Johdanto Tasavirtapiirissä sähkövirta ja jännite käyttäytyvät
yleisessä muodossa x y ax by c 0. 6p
 MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-6. Taulukkokirjaa saa käyttää apuna, laskinta ei.
 PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
Suomen Navigaatioliitto Finlands Navigationsförbund rf
 1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 22.4.2016 tehtävien ratkaisut Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,0 metriä ja
1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 22.4.2016 tehtävien ratkaisut Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,0 metriä ja
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Lauri Karppi j82095. SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI.
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Oskari Uitto i78966 Lauri Karppi j82095 SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI Sivumäärä: 14 Jätetty tarkastettavaksi: 25.02.2008 Työn
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Oskari Uitto i78966 Lauri Karppi j82095 SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI Sivumäärä: 14 Jätetty tarkastettavaksi: 25.02.2008 Työn
SEISOVA AALTOLIIKE 1. TEORIAA
 1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut. Rannikkomerenkulkuoppi
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 20.4.2018 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 20.4.2018 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut. Rannikkomerenkulkuoppi
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 12.4.2019 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 12.4.2019 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Ratkaisut vuosien tehtäviin
 Ratkaisut vuosien 1958 1967 tehtäviin 1958 Pyörähtäessään korkeusjanansa ympäri tasakylkinen kolmio muodostaa kartion, jonka tilavuus on A, ja pyörähtäessään kylkensä ympäri kappaleen, jonka tilavuus on
Ratkaisut vuosien 1958 1967 tehtäviin 1958 Pyörähtäessään korkeusjanansa ympäri tasakylkinen kolmio muodostaa kartion, jonka tilavuus on A, ja pyörähtäessään kylkensä ympäri kappaleen, jonka tilavuus on
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
MAA4 - HARJOITUKSIA. 1. Esitä lauseke 3 x + 2x 4 ilman itseisarvomerkkejä. 3. Ratkaise yhtälö 2 x 7 3 + 4x = 2 (yksi ratkaisu, eräs neg. kokon.
 MAA4 - HARJOITUKSIA 1. Esitä lauseke 3 + 4 ilman itseisarvomerkkejä.. Ratkaise yhtälö a ) 5 9 = 6 b) 6 9 = 0 c) 7 9 + 6 = 0 3. Ratkaise yhtälö 7 3 + 4 = (yksi ratkaisu, eräs neg. kokon. luku) 4. Ratkaise
MAA4 - HARJOITUKSIA 1. Esitä lauseke 3 + 4 ilman itseisarvomerkkejä.. Ratkaise yhtälö a ) 5 9 = 6 b) 6 9 = 0 c) 7 9 + 6 = 0 3. Ratkaise yhtälö 7 3 + 4 = (yksi ratkaisu, eräs neg. kokon. luku) 4. Ratkaise
Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 19.4.2013
 1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 19.4.2013 Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä.
1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 19.4.2013 Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä.
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa
 Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
x 5 15 x 25 10x 40 11x x y 36 y sijoitus jompaankumpaan yhtälöön : b)
 MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 14.12.2007 tutkinnon ratkaisut Tehtävät on ratkaistu Microsoft PowerPoint ohjelmalla. Karttakuvat ovat skannattuja kuvia harjoitusmerikartasta
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 14.12.2007 tutkinnon ratkaisut Tehtävät on ratkaistu Microsoft PowerPoint ohjelmalla. Karttakuvat ovat skannattuja kuvia harjoitusmerikartasta
Kolmioitten harjoituksia. Säännöllisten monikulmioitten harjoituksia. Pythagoraan lauseeseen liittyviä harjoituksia
 Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 14.12.2012
 1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 14.12.2012 Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä.
1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinto 14.12.2012 Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä.
! 7! = N! x 8. x x 4 x + 1 = 6.
 9. 10. 2008 1. Pinnalta punaiseksi maalattu 3 3 3-kuutio jaetaan 27:ksi samankokoiseksi kuutioksi. Mikä osuus 27 pikkukuution kokonaispinta-alasta on punaiseksi maalattu? 2. Positiivisen kokonaisluvun
9. 10. 2008 1. Pinnalta punaiseksi maalattu 3 3 3-kuutio jaetaan 27:ksi samankokoiseksi kuutioksi. Mikä osuus 27 pikkukuution kokonaispinta-alasta on punaiseksi maalattu? 2. Positiivisen kokonaisluvun
Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti!
 MAA3 Koe 1.4.2014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
MAA3 Koe 1.4.2014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
Merikarttanavigointikilpailu Finaali 2018, Kouvola
 Merikarttanavigointikilpailu Finaali 2018, Kouvola Vene: 11 metrinen uppoumarunkoinen moottorivene. Varusteet: mangneettikompassi, loki, kaiku, käsisuuntimakompassi. Eranto: +7,2 Sää: tuuli alle 5 m/s,
Merikarttanavigointikilpailu Finaali 2018, Kouvola Vene: 11 metrinen uppoumarunkoinen moottorivene. Varusteet: mangneettikompassi, loki, kaiku, käsisuuntimakompassi. Eranto: +7,2 Sää: tuuli alle 5 m/s,
Juuri 3 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K1. a) Ratkaistaan suorakulmaisen kolmion kateetin pituus x tangentin avulla. tan9 x,5,5 x,5 tan 9 x 2,8... x» 2,8 (cm) Kateetin pituus x on 2,8 cm. b) Ratkaistaan vinokulmaisen kolmion sivun pituus
Kertaus K1. a) Ratkaistaan suorakulmaisen kolmion kateetin pituus x tangentin avulla. tan9 x,5,5 x,5 tan 9 x 2,8... x» 2,8 (cm) Kateetin pituus x on 2,8 cm. b) Ratkaistaan vinokulmaisen kolmion sivun pituus
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
MATEMATIIKKA 5 VIIKKOTUNTIA. PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009
 EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon tehtävien ratkaisu
 1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 20.04.2012 tehtävien ratkaisu Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja
1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 20.04.2012 tehtävien ratkaisu Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja
VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ
 56 VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ Hyvällä havaitsijalla keskimääräinen virhe tähdenlennon kirkkauden arvioimisessa on noin 0.4 magnitudia silloin, kun meteori näkyy havaitsijan näkökentän keskellä.
56 VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ Hyvällä havaitsijalla keskimääräinen virhe tähdenlennon kirkkauden arvioimisessa on noin 0.4 magnitudia silloin, kun meteori näkyy havaitsijan näkökentän keskellä.
Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 20.04.2007 tehtävien ratkaisu
 1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 20.04.2007 tehtävien ratkaisu Tehtävät on ratkaistu Microsoft PowerPoint ohjelmalla. Apuna on käytetty Carta Marina
1 Suomen Navigaatioliitto Finlands Navigationsförbund rf Saaristomerenkulkuopin tutkinnon 20.04.2007 tehtävien ratkaisu Tehtävät on ratkaistu Microsoft PowerPoint ohjelmalla. Apuna on käytetty Carta Marina
MAB3 - Harjoitustehtävien ratkaisut:
 MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Vastaus: Määrittelyehto on x 1 ja nollakohta x = 1.
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.
![Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot. Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.](/thumbs/61/46046056.jpg) 7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 25.04.2014 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 25.04.2014 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 9.12.2016 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 9.12.2016 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Ratkaisu: Maksimivalovoiman lauseke koostuu heijastimen maksimivalovoimasta ja valonlähteestä suoraan (ilman heijastumista) tulevasta valovoimasta:
 LASKUHARJOITUS 1 VALAISIMIEN OPTIIKKA Tehtävä 1 Pistemäinen valonlähde (Φ = 1000 lm, valokappaleen luminanssi L = 2500 kcd/m 2 ) sijoitetaan 15 cm suuruisen pyörähdysparaboloidin muotoisen peiliheijastimen
LASKUHARJOITUS 1 VALAISIMIEN OPTIIKKA Tehtävä 1 Pistemäinen valonlähde (Φ = 1000 lm, valokappaleen luminanssi L = 2500 kcd/m 2 ) sijoitetaan 15 cm suuruisen pyörähdysparaboloidin muotoisen peiliheijastimen
Tasogeometria. Tasogeometrian käsitteitä ja osia. olevia pisteitä. Piste P on suoran ulkopuolella.
 Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
4.1 Kaksi pistettä määrää suoran
 4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
Tehtävä 3.1. Kuinka pitkän matkan kuljet a) 26 minuutissa, jos nopeutesi on 10,7 solmua? b) 38 minuutissa, jos nopeutesi on 6,5 solmua?
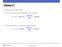 Tehtävä 3.1 Kuinka pitkän matkan kuljet a) 26 minuutissa, jos nopeutesi on 10,7 solmua? 26 min s = vt = 10,7 kn = 4,6 M 60 b) 38 minuutissa, jos nopeutesi on 6,5 solmua? s = vt = 6,5 kn 38 min = 4,1 M
Tehtävä 3.1 Kuinka pitkän matkan kuljet a) 26 minuutissa, jos nopeutesi on 10,7 solmua? 26 min s = vt = 10,7 kn = 4,6 M 60 b) 38 minuutissa, jos nopeutesi on 6,5 solmua? s = vt = 6,5 kn 38 min = 4,1 M
4. Varastossa on 24, 23, 17 ja 16 kg:n säkkejä. Miten voidaan toimittaa täsmälleen 100 kg:n tilaus avaamatta yhtään säkkiä?
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Harjoituksia MAA4 - HARJOITUKSIA. 6. Merkitse lukusuoralle ne luvut, jotka toteuttavat epäyhtälön x 2 < ½.
 MAA4 - HARJOITUKSIA 1 Esitä lauseke 3 x + x 4 ilman itseisarvomerkkejä Ratkaise yhtälö a ) 5x 9 = 6 b) 6x 9 = 0 c) 7x 9 + 6 = 0 3 Ratkaise yhtälö x 7 3 + 4x = 4 Ratkaise yhtälö 5x + = 3x 4 5 Ratkaise yhtälö
MAA4 - HARJOITUKSIA 1 Esitä lauseke 3 x + x 4 ilman itseisarvomerkkejä Ratkaise yhtälö a ) 5x 9 = 6 b) 6x 9 = 0 c) 7x 9 + 6 = 0 3 Ratkaise yhtälö x 7 3 + 4x = 4 Ratkaise yhtälö 5x + = 3x 4 5 Ratkaise yhtälö
Vanhoja koetehtäviä. Analyyttinen geometria 2016
 Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
3 TOISEN ASTEEN POLYNOMIFUNKTIO
 3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
1 Laske ympyrän kehän pituus, kun
 Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Rannikkomerenkulkuoppi
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 15.12.2017 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 15.12.2017 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
TTY Mittausten koekenttä. Käyttö. Sijainti
 TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin tutkinnon ratkaisut. Rannikkomerenkulkuoppi
 Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 14.12.2018 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Suomen Navigaatioliitto Finlands Navigationsförbund Rannikkomerenkulkuopin 14.12.2018 tutkinnon ratkaisut Tutkinto tehdään 12 m pituisella merikelpoisella moottoriveneellä, jossa on varusteina mm. pääkompassi,
Saaristomerenkulun tutkinto Ratkaisuesimerkkejä
 Saaristomerenkulun tutkinto 11.12.2015 Ratkaisuesimerkkejä Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä. Veneen varustukseen kuuluu pääkompassin
Saaristomerenkulun tutkinto 11.12.2015 Ratkaisuesimerkkejä Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,2 metriä ja korkeus 3,4 metriä. Veneen varustukseen kuuluu pääkompassin
Pythagoraan polku 16.4.2011
 Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 2016 Sivu 1 / 4
 Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 06 Sivu / 4 Laske yhteensä enintään 0 tehtävää. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. Osiossa A EI SAA käyttää laskinta. Osiossa
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 06 Sivu / 4 Laske yhteensä enintään 0 tehtävää. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. Osiossa A EI SAA käyttää laskinta. Osiossa
Valitse vain kuusi tehtävää! Tee etusivun yläreunaan pisteytysruudukko! Kaikkiin tehtäviin tarvittavat välivaiheet esille!
 5.4.013 Jussi Tyni 1. Selitä ja piirrä seuraavat lyhyesti: a) Kehäkulma ja keskikulma b) Todista, että kolmion kulmien summa on 180 astetta. Selitä päätelmiesi perustelut.. a) Suorakulmaisen kolmion kateetit
5.4.013 Jussi Tyni 1. Selitä ja piirrä seuraavat lyhyesti: a) Kehäkulma ja keskikulma b) Todista, että kolmion kulmien summa on 180 astetta. Selitä päätelmiesi perustelut.. a) Suorakulmaisen kolmion kateetit
Geometriaa kuvauksin. Siirto eli translaatio
 Geometriaa kuvauksin Siirto eli translaatio Janan AB kuva on jana A B ja ABB A on suunnikas. Suora kuvautuu itsensä kanssa yhdensuuntaiseksi suoraksi. Kulmat säilyvät. Kuva ja alkukuva ovat yhtenevät.
Geometriaa kuvauksin Siirto eli translaatio Janan AB kuva on jana A B ja ABB A on suunnikas. Suora kuvautuu itsensä kanssa yhdensuuntaiseksi suoraksi. Kulmat säilyvät. Kuva ja alkukuva ovat yhtenevät.
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Laudatur 4 MAA4 ratkaisut kertausharjoituksiin
 Laudatur MAA ratkaisut kertausharjoituksiin Yhtälöparit ja yhtälöryhmät 6. a) x y = 7 eli,y+, sijoitetaan alempaan yhtälöön x+ 7y = (, y+, ) + 7y =,y =, y = Sijoitetaan y = yhtälöparin ylempään yhtälöön.,
Laudatur MAA ratkaisut kertausharjoituksiin Yhtälöparit ja yhtälöryhmät 6. a) x y = 7 eli,y+, sijoitetaan alempaan yhtälöön x+ 7y = (, y+, ) + 7y =,y =, y = Sijoitetaan y = yhtälöparin ylempään yhtälöön.,
IL Dnro 46/400/2016 1(5) Majutveden aallokko- ja virtaustarkastelu Antti Kangas, Jan-Victor Björkqvist ja Pauli Jokinen
 IL Dnro 46/400/2016 1(5) Majutveden aallokko- ja virtaustarkastelu Antti Kangas, Jan-Victor Björkqvist ja Pauli Jokinen Ilmatieteen laitos 22.9.2016 IL Dnro 46/400/2016 2(5) Terminologiaa Keskituuli Tuulen
IL Dnro 46/400/2016 1(5) Majutveden aallokko- ja virtaustarkastelu Antti Kangas, Jan-Victor Björkqvist ja Pauli Jokinen Ilmatieteen laitos 22.9.2016 IL Dnro 46/400/2016 2(5) Terminologiaa Keskituuli Tuulen
1 Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Saaristomerenkulun tutkinto Ratkaisuesimerkkejä
 Saaristomerenkulun tutkinto 24.04.2015 Ratkaisuesimerkkejä Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,0 metriä ja korkeus 4,0 metriä. Veneen varustukseen kuuluu pääkompassin
Saaristomerenkulun tutkinto 24.04.2015 Ratkaisuesimerkkejä Tutkinnossa käytetty moottorivene on 13 metriä pitkä, sen syväys on 1,0 metriä ja korkeus 4,0 metriä. Veneen varustukseen kuuluu pääkompassin
Ratkaisuja, Tehtävät
 ja, Tehtävät 988-97 988 a) Osoita, että lausekkeiden x 2 + + x 4 + 2x 2 ja x 2 + - x 4 + 2x 2 arvot ovat toistensa käänteislukuja kaikilla x:n arvoilla. b) Auton jarrutusmatka on verrannollinen nopeuden
ja, Tehtävät 988-97 988 a) Osoita, että lausekkeiden x 2 + + x 4 + 2x 2 ja x 2 + - x 4 + 2x 2 arvot ovat toistensa käänteislukuja kaikilla x:n arvoilla. b) Auton jarrutusmatka on verrannollinen nopeuden
Ota tämä paperi mukaan, merkkaa siihen omat vastauksesi ja tarkista oikeat vastaukset klo 11:30 jälkeen osoitteesta
 MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
1/6 TEKNIIKKA JA LIIKENNE FYSIIKAN LABORATORIO V1.31 9.2011
 1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
Matematiikka ja teknologia, kevät 2011
 Matematiikka ja teknologia, kevät 2011 Peter Hästö 13. tammikuuta 2011 Matemaattisten tieteiden laitos Tarkoitus Kurssin tarkoituksena on tutustuttaa ja käydä läpi eräisiin teknologisiin sovelluksiin liittyvää
Matematiikka ja teknologia, kevät 2011 Peter Hästö 13. tammikuuta 2011 Matemaattisten tieteiden laitos Tarkoitus Kurssin tarkoituksena on tutustuttaa ja käydä läpi eräisiin teknologisiin sovelluksiin liittyvää
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ a) jana, jonka pituus on 3 b) kulma, jonka suuruus on 45 astetta c)
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ a) jana, jonka pituus on 3 b) kulma, jonka suuruus on 45 astetta c)
Kuten aaltoliikkeen heijastuminen, niin myös taittuminen voidaan selittää Huygensin periaatteen avulla.
 FYS 103 / K3 SNELLIN LAKI Työssä tutkitaan monokromaattisen valon taittumista ja todennetaan Snellin laki. Lisäksi määritetään kokonaisheijastuksen rajakulmia ja aineiden taitekertoimia. 1. Teoriaa Huygensin
FYS 103 / K3 SNELLIN LAKI Työssä tutkitaan monokromaattisen valon taittumista ja todennetaan Snellin laki. Lisäksi määritetään kokonaisheijastuksen rajakulmia ja aineiden taitekertoimia. 1. Teoriaa Huygensin
