Putkilokasveilla juuret ottavat veden. Sammalet ottavat vettä koko pinnallaan.
|
|
|
- Laura Järvenpää
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Joensuun yliopisto Metsätieteellinen tiedekunta Mallikysymyksiä ja -vastauksia valintakokeeseen 008 BIOLOGIA1. Veden kulkeutuminen kasveissa. Ydinasiat: Putkilokasveilla juuret ottavat veden. Sammalet ottavat vettä koko pinnallaan. Vesi siirtyy maasta juuren solukoihin osmoosin vaikutuksesta. Soluissa olevat liuenneet aineet aiheuttavat veden siirtymistä solun sisään ja solujen välillä. Veden kuljetus juurista lehtiin tapahtuu muilla putkilokasveilla johtojänteiden putkilo-osassa, havupuilla putkisoluissa. Vettä kulkee myös lehdistä muihin osiin kasvia. Haihtumisimu on tärkein vettä kasvissa nostava ilmiö. Haihtumisimu perustuu vesimolekyylien koheesioon sekä kapillaariilmiöön kapeissa johtojänteissä, eikä vaadi energiaa. Vesi muodostaa johtojänteissä yhtenäisen patsaan, jossa esiintyvät ilmakuplat katkaisevat veden kulun. Juuripaine on toinen vettä nostava ilmiö, ja se vaatii energiaa. Sillä on merkitystä erityisesti lehtipuilla keväisin. Juuripaineen vaikutus näkyy pisarointina lehdillä. Vesi poistuu kasvista haihtumalla ilmaan ilmarakojen kautta. Ilmarakoja avaamalla ja sulkemalla kasvi säätelee haihduttamista. Selkeys ja johdonmukaisuus Pisteitys 1 1
2 BIOLOGIA. Oheisessa kuvasarjassa on esitetty erään tutkimuksen tuloksia hieskoivun (Betula pubescens) eri alkuperien viikoittaisesta pituuskasvusta 60. ja 70. leveysasteilla. Pohdi kuvasarjan avulla miten eri alkuperien pituuskasvuun ja hallatuhoriskiin voi vaikuttaa se, että alkuperä siirretään etelään tai vastaavasti pohjoiseen sen normaaliin kasvuympäristöön nähden ja mitä metsänhoidollisia johtopäätöksiä voit tehdä näiden tulosten perusteella. Ydinasiat: - Siirrettäessä alkuperä pohjoisesta etelään uudelle viljelypaikkakunnalle, havaitaan että sen kasvu kärsii. Kasvu alkaa jopa varhemmin kuin eteläisemmät alkuperät samoissa olosuhteissa, ja se myös päättyy huomattavasti aiemmin. - Vastaavasti viljelypaikkakuntaa eteläisempi alkuperä aloittaa kasvun paikallisen alkuperän kanssa samoihin aikoihin, mutta lopettaa kasvun huomattavasti myöhemmin, mikä voi johtaa syyshallojen riskiin. - Mitä eteläisempi alkuperä siirretään pohjoiseen, sitä suurempi hallariski on syksyllä, vastaavasti pohjoisten alkuperien siirto etelään voi lisätä niiden keväthallariskiä jossain määrin. - Lisääntynyt hallariski em. tapauksessa johtuu siitä, että puut ovat sopeutuneet perimänsä puitteissa tietynlaiseen kasvurytmiin eivätkä kykene uusissa olosuhteissa riittävästi mukautumaan muuttuneisiin olosuhteisiin (esim. kasvukauden lämpösumma, valoilmasto). - Liian suuret siirtomatkat etelästä pohjoiseen tai toisinpäin eivät ole metsänhoidollisesti suositeltavia. - Selkeys ja johdonmukaisuus. Pisteitys 1 Yhteensä 1
3 BIOLOGIA3. Miten puiden ja puuaineksen erilaisia ominaisuuksia voidaan muunnella? Mitkä ovat eri keinojen rajoitteet? Ydinasiat: Valinta: valitaan halutun ominaisuuden omaava puu, pluspuu, jota kloonataan siementuotantoa varten. Rajoitteena hitaus ja pölytyksen hallitsemattomuus laajoilla siemenviljelmillä. Lisäksi raja tulee vastaan eikä sillä varsinaisesti luoda muuntelua. Risteytys: valitaan halutunlainen emopuu, jonka kukat pölytetään toisen valitun puun siitepölyllä, jolloin saadaan risteytys. Jälkeläiset ilmentävät vanhempiensa ominaisuuksia sattumanvaraisesti, joten jälkeläisistä edelleen joudutaan valitsemaan halutunlaiset ja kenties jatkamaan risteytystä. Hidasta ja raja tulee vastaan. Mikrolisäys, kloonaus: suvutonta lisäämistä valitun yksilön soluja lisäämällä, uusia taimia saadaan nopeasti ja paljon. Ei geneettistä muuntelua, nimenomaan yhden tietyn yksilön lisäämistä. Geeniteknologia: geeniperimän muokkaamista, haluttuja ominaisuuksia määräävien geenien siirtämistä ilman lajirajoja. Menetelmä vielä kehitysvaiheessa varsinkin puiden osalta (ei tunneta geenejä, ei osata kunnolla), luontoon siirtämisen rajoitteet ekosysteemien yms. suojelemiseksi arvaamattomilta vaikutuksilta. Kasvupaikan valinta tietylle lajille sopivaksi metsää uudistettaessa; ympäristötekijät yleensäkin. Metsänhoidolliset toimenpiteet: luodaan puiden kasvulle parempia oloja, edistetään puiden kasvua ja terveyttä ym. Selkeys ja johdonmukaisuus Pisteitys 1 Yhteensä 1
4 MATEMATIIKKA1. Aurinko paistaa vaakasuoralla maanpinnalla olevaan puuhun alla olevan kuvan mukaisesti. Puun pituus on 15 m ja pisin oksa on kahden metrin korkeudella. a) Kuinka pitkä voi pisin oksa enintään olla, jotta 30 asteen korkeudelta paistavan auringon valonsäteet osuisivat puun tyveen pisimmästä oksasta huolimatta? (maksimi 7 p) b) Kuinka pitkälle puun varjo ulottuu sen tyveltä, kun auringon korkeuskulma on 5? (maksimi 7 p) c) Miten kaukana viereinen 10 m pituinen puu voi olla, että pitemmän puun varjo näkyy pienemmän puun taakse, kun auringon korkeuskulma on 5? (maksimi 7 p) Voidaan olettaa, että valonsäteet ovat yhdensuuntaisia. Korkeuskulmalla tarkoitetaan maanpinnan ja valonsäteiden välistä terävää kulmaa. a) b) c) r m X X Z Y Yht. 1p a) Merkitään pisimmän oksan pituudeksi r tan 30 = /r tai tan 60 =r/ (p) r= /tan 30 tai r=tan 60 [tai muistikolmion mittasuhteiden perusteella r = 3 metriä] b) Merkitään varjon pituudeksi X tan 5 =15/X X=15/tan 5 [tai muistikolmion perusteella tan 5 =1, joten X=15 metriä] (p) Vaihtoehtoinen ratkaisu tasakylkisen kolmion perusteella, X=15 metriä (7p) c) Merkitään varjon pituudeksi pitemmän puun tyveltä X, varjon pituudeksi lyhyemmän puun tyveltä Y ja puiden väliseksi etäisyydeksi Z tan 5 =15/X X=15/tan 5 =15 (p) tan 5 = 10/Y Y=10/tan 5 =10 (1p) Z=X-Y=(15-10)/tan 5 Z=5/tan 5 [Muistikolmion perusteella Z=5 metriä] (p) Vaihtoehtoinen ratkaisu tasakylkisen kolmion perusteella Z=15-10=5 metriä tai yhdenmukaisten kolmioiden perusteella, esimerkiksi: Z = Z=5 metriä (7p) 15 15
5 MATEMATIIKKA. Puun rungon läpimittaa d (cm) korkeudella h (metriä maan pinnasta) kuvataan paloittain määritellyllä funktiolla h+ 6 0 h 11 d( h) = 5 85 h + h > 11 a) Piirrä rungon läpimitan kuvaaja korkeuden funktiona (ns. runkokäyrä) (maksimi p) b) Kuinka pitkä puu on? (maksimi p) c) Kuinka suuri on puun rinnankorkeusläpimitta, eli läpimitta 1,3 metrin korkeudella maanpinnasta? (maksimi 3 p) d) Läpimitaltaan yli 16 cm vahvuisesta rungonosasta voidaan tehdä sahatukkia. Läpimitaltaan tätä pienemmästä puusta voidaan tehdä kuitua aina 5 cm:n läpimittaan asti. Mitkä ovat rungon tukki- ja kuituosien päättymiskorkeudet (maksimi 10 p) a) Yht. 1 p d, cm h, m (p) b) 5 85 Ratkaistaan yhtälö h + = 0 (p) 5 85 h + = 0 5h + 85= 0 5h = h = 5 h = 17 Puun pituus on 17 metriä. (p)
6 c) Sijoittamalla korkeus h=1,3 (<11) saadaan d( 1, 3 ) = 13, + 6 =, 7 cm Puun läpimitta on,7 cm d) Ensin on selvitettävä onko läpimitta 16 cm korkeuden 11m ylä- vai alapuolella. Liittymäkohdassa h=11m puun läpimitta on -11+6=15 cm. Koska funktio on vähenevä, saa funktio arvon 16 cm välillä 0<h<11 ja arvon 5 cm välillä 11<h<17. (p) Tukkiosan päättymiskorkeus lasketaan käyttäen ylempää osafunktiota. Saadaan h + 6 = 16 h = 6 16 h = 10 Kuituosan päättymiskorkeuden laskemiseksi käytetään alempaa osafunktiota. Saadaan 5 85 h + = 5 5h + 85= 10 5h = h = 5 h = 15 Tukkiosa päättyy siis 10 metrin korkeudella maan pinnasta ja kuituosa 15 metrin korkeudella maan pinnasta. (p)
7 MATEMATIIKKA3. a) Liikkeessä A myytiin raivaussahaa ohjehinnasta lasketulla 30 % alennuksella, ja myöhemmin alennetusta hinnasta vähennettiin vielä 15 käteisalennus. Toisessa liikkeessä B samasta ohjehinnasta annettiin aluksi 0 % alennus ja myöhemmin vielä 30 käteisalennus. Kaikkien alennusten jälkeen raivaussahan hinta liikkeessä A oli 10 % halvempi kuin liikkeessä B. Mikä oli raivaussahan ohjehinta? (maksimi 13 pistettä) b) Täydellisen kilpailun toimistopaperimarkkinoilla markkinavoimat, kysyntä ja tarjonta, määräävät paperin hinnan. Markkinatasapainossa kysytty ja tarjottu paperimäärä ovat yhtä suuret. Yleensä hinnan noustessa kysytty määrä pienenee. Niinpä kysyntä voidaan esittää kysyntäyhtälönä D = 80 5P, missä D on tietyn alueen kysytty toimistopaperin määrä (kg/henkilö/vuosi) ja P on hinta ( /papeririisi, 500 arkkia). Vastaavasti, hinnan kohotessa paperin tarjottu määrä kasvaa tarjontayhtälön S = 5P 10 mukaisesti, missä S on tietyn alueen tarjottu toimistopaperin määrä (kg/henkilö/vuosi) ja P on hinta, ( /papeririisi). Mikä on toimistopaperin markkinahinta ja markkinoilla vaihdettu (tuotettu ja kulutettu) paperimäärä? (maksimi 8 pistettä) a) Olkoon x = ohjehinta; silloin Alennettu hinta liikkeessä A = 0,7x 15 Alennettu hinta liikkeessä B = 0,8x 30 (p) (p) Saadaan 0,7x 15 = 0,9(0,8x 30) (6p) 0,0x = 1 x = 600 Raivaussahan ohjehinta on 600. b) Asettamalla kysynnän ja tarjonnan yhtä suureksi (D=S) saamme P=5P-10 10P=90 P=9 Toimistopaperin markkinahinta on siis 9 /papeririisi. (p) (p) Sijoittamalla markkinahinnan P joko kysyntä- tai tarjontayhtälöön, saamme markkinoilla vaihdetun (kulutetun ja tuotetun) paperimäärän, 35 kg/henkilö/vuosi. (p)
Geometrian kertausta. MAB2 Juhani Kaukoranta Raahen lukio
 Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
Itä-Suomen yliopisto/metsätieteiden osasto Valintakoe 2012/MALLIVASTAUKSET
 Itä-Suomen yliopisto/metsätieteiden osasto Valintakoe 0/MALLIVASTAUKSET BIOLOGIA. Kasvisolun perusrakenne ja solun osien tehtävät. Ydinasiat: Uloimpana pääasiassa selluloosasta koostuva soluseinä, joka
Itä-Suomen yliopisto/metsätieteiden osasto Valintakoe 0/MALLIVASTAUKSET BIOLOGIA. Kasvisolun perusrakenne ja solun osien tehtävät. Ydinasiat: Uloimpana pääasiassa selluloosasta koostuva soluseinä, joka
[MATEMATIIKKA, KURSSI 8]
![[MATEMATIIKKA, KURSSI 8] [MATEMATIIKKA, KURSSI 8]](/thumbs/30/14370320.jpg) 2015 Puustinen, Sinn PYK [MATEMATIIKKA, KURSSI 8] Trigometrian ja avaruusgeometrian teoriaa, tehtäviä ja linkkejä peruskoululaisille Sisällysluettelo 8.1 PYTHAGORAAN LAUSE... 3 8.1.1 JOHDANTOTEHTÄVÄT 1-6...
2015 Puustinen, Sinn PYK [MATEMATIIKKA, KURSSI 8] Trigometrian ja avaruusgeometrian teoriaa, tehtäviä ja linkkejä peruskoululaisille Sisällysluettelo 8.1 PYTHAGORAAN LAUSE... 3 8.1.1 JOHDANTOTEHTÄVÄT 1-6...
Solun toiminta. II Solun toiminta. BI2 II Solun toiminta 6. Kasvien vesi- ja ravinnetalous
 Solun toiminta II Solun toiminta 6. Kasvien vesi- ja ravinnetalous 1. Avainsanat 2. Vesi nousee kasveihin lähes ilman energian kulutusta 3. Putkilokasvin rakenne ja toiminta 4. Ilmarakojen toiminta ja
Solun toiminta II Solun toiminta 6. Kasvien vesi- ja ravinnetalous 1. Avainsanat 2. Vesi nousee kasveihin lähes ilman energian kulutusta 3. Putkilokasvin rakenne ja toiminta 4. Ilmarakojen toiminta ja
OULUN YLIOPISTO, BIOLOGIAN LAITOS Puututkimus
 OULUN YLIOPISTO, BIOLOGIAN LAITOS Puututkimus Puu on yksilö, lajinsa edustaja, eliöyhteisönsä jäsen, esteettinen näky ja paljon muuta. Tässä harjoituksessa lähestytään puuta monipuolisesti ja harjoitellaan
OULUN YLIOPISTO, BIOLOGIAN LAITOS Puututkimus Puu on yksilö, lajinsa edustaja, eliöyhteisönsä jäsen, esteettinen näky ja paljon muuta. Tässä harjoituksessa lähestytään puuta monipuolisesti ja harjoitellaan
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
2.1 Yhdenmuotoiset suorakulmaiset kolmiot
 2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
Luennon 2 oppimistavoitteet RUNGON RAKENNE PUU. Elävä puu ja puuaineksen muodostuminen. Puu-19.210 Puun rakenne ja kemia
 Elävä puu ja puuaineksen muodostuminen Puu-19.210 Puun rakenne ja kemia Luennon 2 oppimistavoitteet Osaat nimetä ja tunnistaa puun eri osat (latvusto, runko, oksat, sisäoksat, juuret). Tunnistat ja osaat
Elävä puu ja puuaineksen muodostuminen Puu-19.210 Puun rakenne ja kemia Luennon 2 oppimistavoitteet Osaat nimetä ja tunnistaa puun eri osat (latvusto, runko, oksat, sisäoksat, juuret). Tunnistat ja osaat
Pitkä matematiikka Suullinen kuulustelu (ma00s001.doc) Tehtävät, jotka on merkitty (V), ovat vaativia.
 Pitkä matematiikka Suullinen kuulustelu (ma00s00doc) Tehtävät, jotka on merkitty (V), ovat vaativia Yleistä Ratkaise yhtälöt n n n n n 5 a) 5 + 5 + 5 + 5 + 5 = 5 b) ( ) ( ) > 0 + = + c) ( ) Suureet ja
Pitkä matematiikka Suullinen kuulustelu (ma00s00doc) Tehtävät, jotka on merkitty (V), ovat vaativia Yleistä Ratkaise yhtälöt n n n n n 5 a) 5 + 5 + 5 + 5 + 5 = 5 b) ( ) ( ) > 0 + = + c) ( ) Suureet ja
Preliminäärikoe Tehtävät Pitkä matematiikka 4.2.2014 1 / 3
 Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Pythagoraan polku 16.4.2011
 Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
PRELIMINÄÄRIKOE. Pitkä Matematiikka 3.2.2015
 PRELIMINÄÄRIKOE Pitkä Matematiikka..5 Vastaa enintään kymmeneen tehtävään. Tähdellä merkittyjen (*) tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6.. a) Ratkaise epäyhtälö >.
PRELIMINÄÄRIKOE Pitkä Matematiikka..5 Vastaa enintään kymmeneen tehtävään. Tähdellä merkittyjen (*) tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6.. a) Ratkaise epäyhtälö >.
Trigonometriaa ja solve-komento GeoGebralla
 Trigonometriaa ja solve-komento GeoGebralla Valitse yläreunasta Näytä-valikosta CAS ja Piirtoalue. CAS-on laskinohjelma, piirtoalueen avulla saat kuviot näkyville tarvittaessa. Harjoitellaan ensiksi CAS-ikkunan
Trigonometriaa ja solve-komento GeoGebralla Valitse yläreunasta Näytä-valikosta CAS ja Piirtoalue. CAS-on laskinohjelma, piirtoalueen avulla saat kuviot näkyville tarvittaessa. Harjoitellaan ensiksi CAS-ikkunan
Lahon aste Yhteensä Pysty- Maa- Yhteensä Pysty- Maa-
 Liitetaulukko 43. Kuolleen puuston tilavuus lahon asteen mukaan metsä- ja kitumaalla. Ahvenanmaa Mänty 110 29 139 16 13 29 10 22 32 0 10 10 6 137 80 216 Kuusi 65 24 89 24 19 43 5 13 18 0 10 10 12 94 78
Liitetaulukko 43. Kuolleen puuston tilavuus lahon asteen mukaan metsä- ja kitumaalla. Ahvenanmaa Mänty 110 29 139 16 13 29 10 22 32 0 10 10 6 137 80 216 Kuusi 65 24 89 24 19 43 5 13 18 0 10 10 12 94 78
Läpäisyehto: Kokeesta saatava 5. Uusintakoe: Arvosana määräytyy yksin uusintakokeen perusteella.
 MAA7 Trigonometriset funktiot Arvosanan perusteet: koe 70 %, harjoitustehtävä 10 %, tuntitestit 20 %, lisäksi oppimisen ja työskentelyn havainnointi opettajan harkinnan mukaan (ks. OPS 6.2). Muu arviointi:
MAA7 Trigonometriset funktiot Arvosanan perusteet: koe 70 %, harjoitustehtävä 10 %, tuntitestit 20 %, lisäksi oppimisen ja työskentelyn havainnointi opettajan harkinnan mukaan (ks. OPS 6.2). Muu arviointi:
15. Suorakulmaisen kolmion geometria
 15. Suorakulmaisen kolmion geometria 15.1 Yleistä kolmioista - kolmion kulmien summa on 180⁰ α α + β + γ = 180⁰ β γ 5.1.1 Tasasivuinen kolmio - jos kaikki kolmion sivut ovat yhtä pitkät, on kolmio tasasivuinen
15. Suorakulmaisen kolmion geometria 15.1 Yleistä kolmioista - kolmion kulmien summa on 180⁰ α α + β + γ = 180⁰ β γ 5.1.1 Tasasivuinen kolmio - jos kaikki kolmion sivut ovat yhtä pitkät, on kolmio tasasivuinen
Taimikonhoitoon vaikuttavat biologiset tekijät
 1.1.1 Taimikonhoitoon vaikuttavat biologiset tekijät Lehtipuiden kasvu ja vesominen Jari Miina, METLA Lehtipuita syntyy aina, - hakkuu/raivauskannot vesovat - haavan ja harmaalepän juurivesat - siemensyntyiset
1.1.1 Taimikonhoitoon vaikuttavat biologiset tekijät Lehtipuiden kasvu ja vesominen Jari Miina, METLA Lehtipuita syntyy aina, - hakkuu/raivauskannot vesovat - haavan ja harmaalepän juurivesat - siemensyntyiset
YMPYRÄ. Ympyrä opetus.tv:ssä. Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne
 YMPYRÄ Ympyrä opetus.tv:ssä Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne KAPPALEEN TERMEJÄ 1. Ympyrä Ympyrä on niiden tason pisteiden joukko, jotka ovat yhtä kaukana
YMPYRÄ Ympyrä opetus.tv:ssä Määritelmä Kehän pituus Pinta-ala Sektori, kaari, keskuskulma, segmentti ja jänne KAPPALEEN TERMEJÄ 1. Ympyrä Ympyrä on niiden tason pisteiden joukko, jotka ovat yhtä kaukana
Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x 1 ja x 2 on voimassa ehto:
 4 Reaalifunktiot 4. Funktion monotonisuus Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x ja x on voimassa ehto: "jos x < x, niin f (x
4 Reaalifunktiot 4. Funktion monotonisuus Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x ja x on voimassa ehto: "jos x < x, niin f (x
Maatalous-metsätieteellinen tiedekunta Metsien ekologia ja käyttö
 Tehtävä 1: Pisteet /5 pistettä Vastaa johdonmukaisesti kokonaisilla lauseilla. Älä ylitä annettua vastaustilaa! 1. Miten kasvit ovat sopeutuneet elämään maalla? (5 p) Kasvien sopeutuminen elämään maalla
Tehtävä 1: Pisteet /5 pistettä Vastaa johdonmukaisesti kokonaisilla lauseilla. Älä ylitä annettua vastaustilaa! 1. Miten kasvit ovat sopeutuneet elämään maalla? (5 p) Kasvien sopeutuminen elämään maalla
LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT KOKEEN JÄLKEEN JA ANNA PISTEESI RUUTUUN!
 Matematiikan TESTI 4, Maa7 Trigonometriset funktiot ATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TAKISTA TEHTÄVÄT
Matematiikan TESTI 4, Maa7 Trigonometriset funktiot ATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TAKISTA TEHTÄVÄT
Tarkastellaan neliötä, jonka sivun pituus on yksi metri. Silloinhan sen pinta-ala on 1m 1m
 MB: Yhdenmuotoisuus luksi Tämän luvun aiheina ovat yhdenmuotoisuus sekä yhdenmuotoisuussuhde. Kaikkein tavallisimmat yhdenmuotoisuuden sovellukset ovat varmasti kartta ja pohjapiirros. loitamme tutuista
MB: Yhdenmuotoisuus luksi Tämän luvun aiheina ovat yhdenmuotoisuus sekä yhdenmuotoisuussuhde. Kaikkein tavallisimmat yhdenmuotoisuuden sovellukset ovat varmasti kartta ja pohjapiirros. loitamme tutuista
yleisessä muodossa x y ax by c 0. 6p
 MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
Pyramidi 9 Trigonometriset funktiot ja lukujonot 15.4.2011 HK1-1. Dsin3 x. 3cos3x. Dsinx. u( x) sinx ja u ( x) cosx. Dsin. Dsin
 Pyramidi 9 Trigonometriset funktiot ja lukujonot 5.4.0 HK- a) Dsin3 us ( ) cos3 3 us( ) s( ) 3cos3 s( ) 3 ja s( ) 3 u( ) sin ja u( ) cos b) Dsin 3 3 Dsin us ( ) s( ) sin ja s( ) cos 3 u( ) ja u( ) 3 3sin
Pyramidi 9 Trigonometriset funktiot ja lukujonot 5.4.0 HK- a) Dsin3 us ( ) cos3 3 us( ) s( ) 3cos3 s( ) 3 ja s( ) 3 u( ) sin ja u( ) cos b) Dsin 3 3 Dsin us ( ) s( ) sin ja s( ) cos 3 u( ) ja u( ) 3 3sin
3 Määrätty integraali
 Määrätty integraali. a) Muodostuva alue on kolmio, jonka kanta on. Kolmion korkeus on funktion arvo kohdassa, eli f() = = 6. Lasketaan A() kolmion pintaalana. 6 A() 6 Vastaus: A() = 6 b) Muodostuva alue
Määrätty integraali. a) Muodostuva alue on kolmio, jonka kanta on. Kolmion korkeus on funktion arvo kohdassa, eli f() = = 6. Lasketaan A() kolmion pintaalana. 6 A() 6 Vastaus: A() = 6 b) Muodostuva alue
 PURO Osahanke 3 Annikki Mäkelä, HY Anu Kantola Harri Mäkinen Edistyminen -mallin adaptointi kuuselle mittaukset kuusen yleisestä rakenteesta, kilpailun vaikutus siihen Anu Kantola kuusen oksamittaukset
PURO Osahanke 3 Annikki Mäkelä, HY Anu Kantola Harri Mäkinen Edistyminen -mallin adaptointi kuuselle mittaukset kuusen yleisestä rakenteesta, kilpailun vaikutus siihen Anu Kantola kuusen oksamittaukset
B. 2 E. en tiedä C. 6. 2 ovat luonnollisia lukuja?
 Nimi Koulutus Ryhmä Jokaisessa tehtävässä on vain yksi vastausvaihtoehto oikein. Laske tehtävät ilman laskinta.. Missä pisteessä suora y = 3x 6 leikkaa x-akselin? A. 3 D. B. E. en tiedä C. 6. Mitkä luvuista,,,
Nimi Koulutus Ryhmä Jokaisessa tehtävässä on vain yksi vastausvaihtoehto oikein. Laske tehtävät ilman laskinta.. Missä pisteessä suora y = 3x 6 leikkaa x-akselin? A. 3 D. B. E. en tiedä C. 6. Mitkä luvuista,,,
MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014
 MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014 KOE 2: Ympäristöekonomia KANSANTALOUSTIEDE JA MATEMATIIKKA Sekä A- että B-osasta tulee saada vähintään 10 pistettä. Mikäli A-osan pistemäärä on vähemmän
MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014 KOE 2: Ympäristöekonomia KANSANTALOUSTIEDE JA MATEMATIIKKA Sekä A- että B-osasta tulee saada vähintään 10 pistettä. Mikäli A-osan pistemäärä on vähemmän
Miten kasvit saavat vetensä?
 Miten kasvit saavat vetensä? 1. Haihtumisimulla: osmoosilla juureen ilmaraoista haihtuu vettä ulos vesi nousee koheesiovoiman ansiosta ketjuna ylös. Lehtien ilmaraot säätelevät haihtuvan veden määrää.
Miten kasvit saavat vetensä? 1. Haihtumisimulla: osmoosilla juureen ilmaraoista haihtuu vettä ulos vesi nousee koheesiovoiman ansiosta ketjuna ylös. Lehtien ilmaraot säätelevät haihtuvan veden määrää.
Napapiirin luontokansio
 Puolipilvistä, sanoi etana ja näytti vain toista sarvea Tutki säätilaa metsässä ja suolla ja vertaa tuloksia. Säätilaa voit tutkia mihin vuodenaikaan tahansa. 1. Mittaa a) ilman lämpötila C b) tuulen nopeus
Puolipilvistä, sanoi etana ja näytti vain toista sarvea Tutki säätilaa metsässä ja suolla ja vertaa tuloksia. Säätilaa voit tutkia mihin vuodenaikaan tahansa. 1. Mittaa a) ilman lämpötila C b) tuulen nopeus
Kun pallojen keskipisteet yhdistetään, muodostuu neliöpohjainen, suora pyramidi (kuva 3), jonka sivusärmien pituudet ovat 2 pallon säde eli 2 1 = 2.
 Hyvän ratkaisun piirteitä: a) Neliöpohjainen rakennelma Kun pallojen keskipisteet yhdistetään, muodostuu neliöpohjainen, suora pyramidi (kuva ), jonka sivusärmien pituudet ovat 2 pallon säde eli 2 1 =
Hyvän ratkaisun piirteitä: a) Neliöpohjainen rakennelma Kun pallojen keskipisteet yhdistetään, muodostuu neliöpohjainen, suora pyramidi (kuva ), jonka sivusärmien pituudet ovat 2 pallon säde eli 2 1 =
Arboristi / Hortonomi Teppo Suoranta puh
 3 4 5 6 1 2 7 Puut tutkittiin ensiksi silmämääräisesti. Tyvet ovat jonkin verran liian syvällä johtuen täyttömaasta. Halkeamia ja laho-onkaloita ei ole. Kasvupaikalla on tiivis maa ja pinta on katettu
3 4 5 6 1 2 7 Puut tutkittiin ensiksi silmämääräisesti. Tyvet ovat jonkin verran liian syvällä johtuen täyttömaasta. Halkeamia ja laho-onkaloita ei ole. Kasvupaikalla on tiivis maa ja pinta on katettu
Viherympäristöliiton hyväksymät
 Viherympäristöliiton hyväksymät Taimitarhakasvien lajitteluohjeet viherrakentamiseen Nämä ovat Viherympäristöliitto ry:n suositus taimitarhakasvien lajittelu- ja niputusohjeiksi. Jos näitä ohjeita sovelletaan
Viherympäristöliiton hyväksymät Taimitarhakasvien lajitteluohjeet viherrakentamiseen Nämä ovat Viherympäristöliitto ry:n suositus taimitarhakasvien lajittelu- ja niputusohjeiksi. Jos näitä ohjeita sovelletaan
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
AMMATTIKORKEAKOULUJEN LUONNONVARA JA YMPÄRISTÖALAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN LUONNONVARA JA YMPÄRISTÖALAN VALINTAKOE Matematiikan koe 7.6.2005 Nimi: Henkilötunnus: Sain kutsun kokeeseen Hämeen amk:lta Jyväskylän amk:lta Kymenlaakson amk:lta Laurea amk:lta
AMMATTIKORKEAKOULUJEN LUONNONVARA JA YMPÄRISTÖALAN VALINTAKOE Matematiikan koe 7.6.2005 Nimi: Henkilötunnus: Sain kutsun kokeeseen Hämeen amk:lta Jyväskylän amk:lta Kymenlaakson amk:lta Laurea amk:lta
1 2 x2 + 1 dx. (2p) x + 2dx. Kummankin integraalin laskeminen oikein (vastaukset 12 ja 20 ) antaa erikseen (2p) (integraalifunktiot
 Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Miten kasvit saavat vetensä?
 Miten kasvit saavat vetensä? 1. Haihtumisimulla: osmoosilla juureen ilmaraoista haihtuu vettä ulos vesi nousee koheesiovoiman ansiosta ketjuna ylös. Lehtien ilmaraot säätelevät haihtuvan veden määrää.
Miten kasvit saavat vetensä? 1. Haihtumisimulla: osmoosilla juureen ilmaraoista haihtuu vettä ulos vesi nousee koheesiovoiman ansiosta ketjuna ylös. Lehtien ilmaraot säätelevät haihtuvan veden määrää.
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Matematiikan ilmiöiden tutkiminen GeoGebran avulla
 Johdatus GeoGebraan Matematiikan ilmiöiden tutkiminen GeoGebran avulla Harjoitus 1B. Konstruoi tasakylkinen kolmio ABC, jonka kyljen pituus on 5. Vihje: käytä Kiinteä jana työvälinettä kahdesti. Ota kolmion
Johdatus GeoGebraan Matematiikan ilmiöiden tutkiminen GeoGebran avulla Harjoitus 1B. Konstruoi tasakylkinen kolmio ABC, jonka kyljen pituus on 5. Vihje: käytä Kiinteä jana työvälinettä kahdesti. Ota kolmion
AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRIS- TÖALAN VALINTAKOE 2008 MATEMATIIKKA
 AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRIS- TÖALAN VALINTAKOE 008 MATEMATIIKKA TEHTÄVIEN RATKAISUT Tehtävä. Maljakossa on 0 keltaista ja 0 punaista tulppaania, joista puutarhuriopiskelijan on määrä
AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRIS- TÖALAN VALINTAKOE 008 MATEMATIIKKA TEHTÄVIEN RATKAISUT Tehtävä. Maljakossa on 0 keltaista ja 0 punaista tulppaania, joista puutarhuriopiskelijan on määrä
MAY1 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 12.4.2016 Julkaiseminen sallittu vain koulun suljetussa verkossa.
 KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRISTÖALAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRISTÖALAN VALINTAKOE Matematiikan koe.6.009 Nimi: Henkilötunnus: VASTAUSOHJEET: 1. Koeaika on tuntia (klo 1.00 14.00). Kokeesta saa poistua aikaisintaan klo 1.0..
AMMATTIKORKEAKOULUJEN LUONNONVARA- JA YMPÄRISTÖALAN VALINTAKOE Matematiikan koe.6.009 Nimi: Henkilötunnus: VASTAUSOHJEET: 1. Koeaika on tuntia (klo 1.00 14.00). Kokeesta saa poistua aikaisintaan klo 1.0..
4 Kysyntä, tarjonta ja markkinatasapaino (Mankiw & Taylor, 2 nd ed., chs 4-5)
 4 Kysyntä, tarjonta ja markkinatasapaino (Mankiw & Taylor, 2 nd ed., chs 4-5) Opimme tässä ja seuraavissa luennoissa että markkinat ovat hyvä tapa koordinoida taloudellista toimintaa (mikä on yksi taloustieteen
4 Kysyntä, tarjonta ja markkinatasapaino (Mankiw & Taylor, 2 nd ed., chs 4-5) Opimme tässä ja seuraavissa luennoissa että markkinat ovat hyvä tapa koordinoida taloudellista toimintaa (mikä on yksi taloustieteen
Lukion. Calculus. Paavo Jäppinen Alpo Kupiainen Matti Räsänen Otava PIKATESTIN JA KERTAUSKOKEIDEN TEHTÄVÄT RATKAISUINEEN
 alculus Lukion M Geometia Paavo Jäppinen lpo Kupiainen Matti Räsänen Otava PIKTESTIN J KERTUSKOKEIEN TEHTÄVÄT RTKISUINEEN Geometia (M) Pikatesti ja ketauskokeet Tehtävien atkaisut 1 Pikatesti (M) 1 Määitä
alculus Lukion M Geometia Paavo Jäppinen lpo Kupiainen Matti Räsänen Otava PIKTESTIN J KERTUSKOKEIEN TEHTÄVÄT RTKISUINEEN Geometia (M) Pikatesti ja ketauskokeet Tehtävien atkaisut 1 Pikatesti (M) 1 Määitä
Kaikki 17 punavaahteraa tutkittiin silmämääräisesti tyviltä latvoihin saakka. Apuna käytettiin kiikaria ja 120 cm:n terässondia.
 Acer rubrum / Punavaahterat Kaikki 17 punavaahteraa tutkittiin silmämääräisesti tyviltä latvoihin saakka. Apuna käytettiin kiikaria ja 120 cm:n terässondia. Tällaisilta leikkausten tulisi näyttää Havainnot
Acer rubrum / Punavaahterat Kaikki 17 punavaahteraa tutkittiin silmämääräisesti tyviltä latvoihin saakka. Apuna käytettiin kiikaria ja 120 cm:n terässondia. Tällaisilta leikkausten tulisi näyttää Havainnot
Etsi Siidan alakerran retkeilynäyttelyn kartasta vastaavat rajat. Vertaa niitä omiin havaintoihisi:
 Nimeni: Metsänrajat Tarkkailutehtävä linja-automatkalle Jos tulet Inariin etelästä, aloita tarkkailu Vuotsosta:Jos tulet Inariin pohjoisesta, aloita tarkkailu lähtöpaikastasi: Käytä värikyniä, jotta saat
Nimeni: Metsänrajat Tarkkailutehtävä linja-automatkalle Jos tulet Inariin etelästä, aloita tarkkailu Vuotsosta:Jos tulet Inariin pohjoisesta, aloita tarkkailu lähtöpaikastasi: Käytä värikyniä, jotta saat
Preliminäärikoe Pitkä Matematiikka 3.2.2009
 Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 23.9.2015 HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.9.05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.9.05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Runko: Tomografiassa halkeamien takia lahoa sensoreitten 3-4 ja 6-7 välissä. Kaksi isoa pintaruhjetta ja lahoa sensori 4-5 alapuolella.
 Pintaruhjeita, lahoa 290. Tilia cordata 290. Tilia cordata 126 cm maasta (sensori 1, pohjoinen) Läpimitta 48,7 cm keskimäärin 48 % Kaivettu juuristoalueella. Pintaruhjeita ja lahoa. Iso, kuollut oksa Asfaltti
Pintaruhjeita, lahoa 290. Tilia cordata 290. Tilia cordata 126 cm maasta (sensori 1, pohjoinen) Läpimitta 48,7 cm keskimäärin 48 % Kaivettu juuristoalueella. Pintaruhjeita ja lahoa. Iso, kuollut oksa Asfaltti
Turun seitsemäsluokkalaisten matematiikkakilpailu 22.1.2014 Ratkaisuita
 Turun seitsemäsluokkalaisten matematiikkakilpailu 22.1.2014 Ratkaisuita 1. Laske 3 21 12 3. a) 27 b) 28 c) 29 d) 30 e) 31 Ratkaisu. 3 21 12 3 = 63 36 = 27. 2. Peräkylän matematiikkakerholla on kaksi tapaa
Turun seitsemäsluokkalaisten matematiikkakilpailu 22.1.2014 Ratkaisuita 1. Laske 3 21 12 3. a) 27 b) 28 c) 29 d) 30 e) 31 Ratkaisu. 3 21 12 3 = 63 36 = 27. 2. Peräkylän matematiikkakerholla on kaksi tapaa
A-osio. Ilman laskinta. MAOL-taulukkokirja saa olla käytössä. Maksimissaan tunti aikaa. Laske kaikki tehtävät:
 MAA3 Geometria Koe 5.2.2016 Jussi Tyni Lue ohjeet ja tee tehtävät huolellisesti! Tee tarvittavat välivaiheet, vaikka laskimesta voikin ottaa tuloksia. Välivaiheet perustelevat vastauksesi. Tee pisteytysruudukko
MAA3 Geometria Koe 5.2.2016 Jussi Tyni Lue ohjeet ja tee tehtävät huolellisesti! Tee tarvittavat välivaiheet, vaikka laskimesta voikin ottaa tuloksia. Välivaiheet perustelevat vastauksesi. Tee pisteytysruudukko
1 ENSIMMÄISEN ASTEEN POLYNOMIFUNKTIO
 1 ENSIMMÄISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Lämpötila maanpinnalla nähdään suoran ja y-akselin leikkauspisteen y- koordinaatista, joka on noin 10. Kun syvyys on 15 km, nähdään suoralta, että lämpötila
1 ENSIMMÄISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Lämpötila maanpinnalla nähdään suoran ja y-akselin leikkauspisteen y- koordinaatista, joka on noin 10. Kun syvyys on 15 km, nähdään suoralta, että lämpötila
x + 1 πx + 2y = 6 2y = 6 x 1 2 πx y = x 1 4 πx Ikkunan pinta-ala on suorakulmion ja puoliympyrän pinta-alojen summa, eli
 BM0A5810 - Differentiaalilaskenta ja sovellukset Harjoitus, Syksy 015 1. a) Funktio f ) = 1) vaihtaa merkkinsä pisteissä = 1, = 0 ja = 1. Lisäksi se on pariton funktio joten voimme laskea vain pinta-alan
BM0A5810 - Differentiaalilaskenta ja sovellukset Harjoitus, Syksy 015 1. a) Funktio f ) = 1) vaihtaa merkkinsä pisteissä = 1, = 0 ja = 1. Lisäksi se on pariton funktio joten voimme laskea vain pinta-alan
Taimikonhoito. Ohjeet omatoimiseen taimikonhoitoon Pekka Riipinen, Jyväskylän ammattikorkeakoulu. Sykettä Keski Suomen metsiin
 Taimikonhoito Ohjeet omatoimiseen taimikonhoitoon Pekka Riipinen, Jyväskylän ammattikorkeakoulu Sykettä Keski Suomen metsiin Raivaussahatyöskentelyn perusteet Varusteet taimikonhoitoon Raivaussaha, valjaat
Taimikonhoito Ohjeet omatoimiseen taimikonhoitoon Pekka Riipinen, Jyväskylän ammattikorkeakoulu Sykettä Keski Suomen metsiin Raivaussahatyöskentelyn perusteet Varusteet taimikonhoitoon Raivaussaha, valjaat
TEHTÄVIEN RATKAISUT. Luku a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5.
 TEHTÄVIEN RATKAISUT Luku 4.1 183. a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5. Lasketaan funktioon syötetyn luvun neliö: 5 = 5. Saatuun arvoon lisätään luku 1:
TEHTÄVIEN RATKAISUT Luku 4.1 183. a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5. Lasketaan funktioon syötetyn luvun neliö: 5 = 5. Saatuun arvoon lisätään luku 1:
dx = L2 (x + 1) 2 dx x ln x + 1 = L 2 1 L + 1 L ( = 1 ((L + 1)ln(L + 1) L) L k + 1 xk+1 = 1 k + 2 xk+2 = 1 10k+1 k + 2 = 7.
 BM2A582 - Integraalilaskenta ja sovellukset Harjoitus 5, Kevät 26. a Lumikuiorman massa-alkio kohdassa on λd L2 + 2 d, joten kokonaismassa on Momentti suoran suhteen on L L 2 L m d L2 + 2 d + 2 / L L 2
BM2A582 - Integraalilaskenta ja sovellukset Harjoitus 5, Kevät 26. a Lumikuiorman massa-alkio kohdassa on λd L2 + 2 d, joten kokonaismassa on Momentti suoran suhteen on L L 2 L m d L2 + 2 d + 2 / L L 2
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Metsänmittausohjeita
 Metsänmittausohjeita 1. PUUN LÄPIMITAN MITTAAMINEN Tilavuustaulukko perustuu siihen, että läpimitta mitataan 1,3 metriä ylintä juurenniskaa korkeammalta eli 1,3 metriä sen kohdan yläpuolelta, mistä metsuri
Metsänmittausohjeita 1. PUUN LÄPIMITAN MITTAAMINEN Tilavuustaulukko perustuu siihen, että läpimitta mitataan 1,3 metriä ylintä juurenniskaa korkeammalta eli 1,3 metriä sen kohdan yläpuolelta, mistä metsuri
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 10.6.2013 klo 10-13 Ratkaisut ja pisteytysohjeet
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo - Ratkaisut ja pisteytysohjeet. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x+ x +9, b) log (x) 7,
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo - Ratkaisut ja pisteytysohjeet. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x+ x +9, b) log (x) 7,
Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.
![Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot. Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.](/thumbs/61/46046056.jpg) 7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
Taimikonhoito kitkemällä
 Taimikonhoito kitkemällä Taimikonhoitoa voi tehdä kitkemällä joko käsin tai koneellisesti. Kitkennässä siis vesakkoa poistetaan repimällä ne maasta juurineen, jolloin seuraavina vuosina ei tapahdu niin
Taimikonhoito kitkemällä Taimikonhoitoa voi tehdä kitkemällä joko käsin tai koneellisesti. Kitkennässä siis vesakkoa poistetaan repimällä ne maasta juurineen, jolloin seuraavina vuosina ei tapahdu niin
Tekijä Pitkä matematiikka a) Ratkaistaan nimittäjien nollakohdat. ja x = 0. x 1= Funktion f määrittelyehto on x 1 ja x 0.
 Tekijä Pitkä matematiikka 6 9.5.017 K1 a) Ratkaistaan nimittäjien nollakohdat. x 1= 0 x = 1 ja x = 0 Funktion f määrittelyehto on x 1 ja x 0. Funktion f määrittelyjoukko on R \ {0, 1}. b) ( 1) ( 1) f (
Tekijä Pitkä matematiikka 6 9.5.017 K1 a) Ratkaistaan nimittäjien nollakohdat. x 1= 0 x = 1 ja x = 0 Funktion f määrittelyehto on x 1 ja x 0. Funktion f määrittelyjoukko on R \ {0, 1}. b) ( 1) ( 1) f (
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset
 4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
8 Yritys kilpailullisilla markkinoilla (Mankiw & Taylor, Ch 14)
 8 Yritys kilpailullisilla markkinoilla (Mankiw & Taylor, Ch 14) Markkinat ovat kilpailulliset silloin, kun siellä on niin paljon yrityksiä, että jokainen pitää markkinoilla määräytyvää hintaa omista toimistaan
8 Yritys kilpailullisilla markkinoilla (Mankiw & Taylor, Ch 14) Markkinat ovat kilpailulliset silloin, kun siellä on niin paljon yrityksiä, että jokainen pitää markkinoilla määräytyvää hintaa omista toimistaan
AURINKO VALON JA VARJON LÄHDE
 AURINKO VALON JA VARJON LÄHDE Tavoite: Tarkkaillaan auringon vaikutusta valon lähteenä ja sen vaihtelua vuorokauden ja vuodenaikojen mukaan. Oppilaat voivat tutustua myös aurinkoenergian käsitteeseen.
AURINKO VALON JA VARJON LÄHDE Tavoite: Tarkkaillaan auringon vaikutusta valon lähteenä ja sen vaihtelua vuorokauden ja vuodenaikojen mukaan. Oppilaat voivat tutustua myös aurinkoenergian käsitteeseen.
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
matematiikka Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola
 798 matematiikka E Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola Helsingissä Kustannusosakeyhtiö Otava Otavan asiakaspalvelu Puh. 0800 17117
798 matematiikka E Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola Helsingissä Kustannusosakeyhtiö Otava Otavan asiakaspalvelu Puh. 0800 17117
LED-tekniikan käyttö kuusen ja männyn taimien tuotannossa Johanna Riikonen, LUKE, Suonenjoki. Kuvat: Pekka Voipio
 LED-tekniikan käyttö kuusen ja männyn taimien tuotannossa Johanna Riikonen, LUKE, Suonenjoki Kuvat: Pekka Voipio LED vs. perinteinen kasvihuonelamppu 400 450 500 550 600 650 700 nm Kasvit käyttävät valoa
LED-tekniikan käyttö kuusen ja männyn taimien tuotannossa Johanna Riikonen, LUKE, Suonenjoki Kuvat: Pekka Voipio LED vs. perinteinen kasvihuonelamppu 400 450 500 550 600 650 700 nm Kasvit käyttävät valoa
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe klo 10-13
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo -. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x +9, b) log (x) 7, c) x + x 4 =.. Määrää kaikki ne
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo -. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x +9, b) log (x) 7, c) x + x 4 =.. Määrää kaikki ne
Pystypuusta lattialankuksi
 Pystypuusta lattialankuksi Naapuripalstallamme tehtiin eräänä talvena avohakkuu, jonka seurauksena seuraavan kesän puhurituulet kaatoivat useita suuria kuusia oman metsäpalstamme suojattomasta reunasta.
Pystypuusta lattialankuksi Naapuripalstallamme tehtiin eräänä talvena avohakkuu, jonka seurauksena seuraavan kesän puhurituulet kaatoivat useita suuria kuusia oman metsäpalstamme suojattomasta reunasta.
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
2. a- ja b-kohdat selviä, kunhan kutakuinkin tarkka, niin a-kohta 1 p b-kohta 1 p
 LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
Lisätehtäviä. Rationaalifunktio. x 2. a b ab. 6u x x x. kx x
 MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
Vaiheittaiset ohjeet Majan rakentaminen puuhun
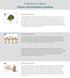 Vaiheittaiset ohjeet Majan rakentaminen puuhun Sopivan puun valitseminen Valitse muodoltaan ja rakenteeltaan sopiva puu ja varmista, että se on terve. Tämä on erittäin tärkeää, jotta majalla on tukeva
Vaiheittaiset ohjeet Majan rakentaminen puuhun Sopivan puun valitseminen Valitse muodoltaan ja rakenteeltaan sopiva puu ja varmista, että se on terve. Tämä on erittäin tärkeää, jotta majalla on tukeva
Symbioosi 2 VASTAUKSET. b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl
 Luku 14 Symbioosi 2 VASTAUKSET 1. Banaanikärpänen dihybridiristeytys a. Mikä on vanhempien genotyyppi? Vastaus: VvLl b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl c.
Luku 14 Symbioosi 2 VASTAUKSET 1. Banaanikärpänen dihybridiristeytys a. Mikä on vanhempien genotyyppi? Vastaus: VvLl b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl c.
Aritmeettinen lukujono
 Aritmeettinen lukujono 315. Aritmeettisen lukujonon kolme ensimmäistä jäsentä ovat 1, 4 ja 7. a) Mikä on jonon peräkkäisten jäsenten erotus d? b) Mitkä ovat jonon kolme seuraavaa jäsentä? a) d = 7 4 =
Aritmeettinen lukujono 315. Aritmeettisen lukujonon kolme ensimmäistä jäsentä ovat 1, 4 ja 7. a) Mikä on jonon peräkkäisten jäsenten erotus d? b) Mitkä ovat jonon kolme seuraavaa jäsentä? a) d = 7 4 =
OHJE PUIDEN ISTUTTAMISEEN LIITO-ORAVIEN KULKUREITEILLE JA ELINALUEILLE ESPOON YMPÄRISTÖKESKUS Kuva: Heimo Rajaniemi, Kuvaliiteri
 OHJE PUIDEN ISTUTTAMISEEN LIITO-ORAVIEN KULKUREITEILLE JA ELINALUEILLE ESPOON YMPÄRISTÖKESKUS 2016 Kuva: Heimo Rajaniemi, Kuvaliiteri 2 OHJE PUIDEN ISTUTTAMISEEN LIITO-ORAVIEN KULKUREITEILLE JA ELINALUEILLE
OHJE PUIDEN ISTUTTAMISEEN LIITO-ORAVIEN KULKUREITEILLE JA ELINALUEILLE ESPOON YMPÄRISTÖKESKUS 2016 Kuva: Heimo Rajaniemi, Kuvaliiteri 2 OHJE PUIDEN ISTUTTAMISEEN LIITO-ORAVIEN KULKUREITEILLE JA ELINALUEILLE
KOTONA, KOULUSSA JA KAUPUNGISSA
 JAKSO ❶2 3 4 5 6 KOTONA, KOULUSSA JA KAUPUNGISSA 4 OLETKO MIETTINYT: Miten sinä voit vaikuttaa omalla toiminnallasi ympäristöösi? Miten kasvit voivat kasvaa niin monenlaisissa paikoissa? Miten kasvien
JAKSO ❶2 3 4 5 6 KOTONA, KOULUSSA JA KAUPUNGISSA 4 OLETKO MIETTINYT: Miten sinä voit vaikuttaa omalla toiminnallasi ympäristöösi? Miten kasvit voivat kasvaa niin monenlaisissa paikoissa? Miten kasvien
Kolmioitten harjoituksia. Säännöllisten monikulmioitten harjoituksia. Pythagoraan lauseeseen liittyviä harjoituksia
 Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti!
 MAA3 Koe 1.4.2014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
MAA3 Koe 1.4.2014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
40VUOTISJUHLARETKEILY
 METSÄNTUTKIMUSLAITOKSEN 40VUOTISJUHLARETKEILY PUNKAHARJUN HEINÄKUUN KOKEILUALUEESSA 1 PÄIVÄNÄ 1958 RETKEILY OHJELMA klo 8.30 10.00 Kahviaamiainen T ervehdyssanat 10.00 12.00 Retkeilyä 12.00 13.15 Kenttälounas
METSÄNTUTKIMUSLAITOKSEN 40VUOTISJUHLARETKEILY PUNKAHARJUN HEINÄKUUN KOKEILUALUEESSA 1 PÄIVÄNÄ 1958 RETKEILY OHJELMA klo 8.30 10.00 Kahviaamiainen T ervehdyssanat 10.00 12.00 Retkeilyä 12.00 13.15 Kenttälounas
Taitaja 2011 finaalitehtävät Metsäkoneenkäyttö
 Taitaja 2011 finaalitehtävät Metsäkoneenkäyttö Tehtävä A: Koneellinen puutavaran valmistus (uudistushakkuu) (John Deere E-sarjan käyttösimulaattori) Tavoitteet Tehtävässä tavoitellaan ammattimaista koneenkäsittelyä
Taitaja 2011 finaalitehtävät Metsäkoneenkäyttö Tehtävä A: Koneellinen puutavaran valmistus (uudistushakkuu) (John Deere E-sarjan käyttösimulaattori) Tavoitteet Tehtävässä tavoitellaan ammattimaista koneenkäsittelyä
Männyn laatukasvatus Jari Hynynen. Metsäntutkimuslaitos Skogsforskningsinstitutet Finnish Forest Research Institute www.metla.fi
 Männyn laatukasvatus Jari Hynynen Metsäntutkimuslaitos Skogsforskningsinstitutet Finnish Forest Research Institute www.metla.fi Johdanto Suomen metsien luontaiset edellytykset soveltuvat hyvin laatupuun
Männyn laatukasvatus Jari Hynynen Metsäntutkimuslaitos Skogsforskningsinstitutet Finnish Forest Research Institute www.metla.fi Johdanto Suomen metsien luontaiset edellytykset soveltuvat hyvin laatupuun
Syksyn 2015 Lyhyen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
 Sksn 015 Lhen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut Tekijät: Olli Karkkulainen ja Markku Parkkonen Ratkaisut on laadittu TI-Nspire CAS -tietokoneohjelmalla kättäen Muistiinpanot -sovellusta.
Sksn 015 Lhen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut Tekijät: Olli Karkkulainen ja Markku Parkkonen Ratkaisut on laadittu TI-Nspire CAS -tietokoneohjelmalla kättäen Muistiinpanot -sovellusta.
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ ESITYS pisteitykseksi
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.9.05 ESITYS pisteitykseksi Yleisohje tarkkuuksista: Ellei tehtävässä vaadittu tiettyä tarkkuutta, kelpaa numeerisissa vastauksissa ohjeen vastauksen lisäksi yksi merkitsevä
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.9.05 ESITYS pisteitykseksi Yleisohje tarkkuuksista: Ellei tehtävässä vaadittu tiettyä tarkkuutta, kelpaa numeerisissa vastauksissa ohjeen vastauksen lisäksi yksi merkitsevä
A Lausekkeen 1,1 3 arvo on 1,13 3,3 1,331 B Tilavuus 0,5 m 3 on sama kuin 50 l 500 l l C Luvuista 2 3, 6 7
 1 Tuotteen hinta nousee ensin 10 % ja laskee sitten 10 %, joten lopullinen hinta on... alkuperäisestä hinnasta. alkuperäisestä hinnasta. YLIOPPILASTUTKINTO- LAUTAKUNTA 23.3.2016 MATEMATIIKAN KOE PITKÄ
1 Tuotteen hinta nousee ensin 10 % ja laskee sitten 10 %, joten lopullinen hinta on... alkuperäisestä hinnasta. alkuperäisestä hinnasta. YLIOPPILASTUTKINTO- LAUTAKUNTA 23.3.2016 MATEMATIIKAN KOE PITKÄ
Graafit ja verkot. Joukko solmuja ja joukko järjestämättömiä solmupareja. eli haaroja. Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria
 Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Helsingin seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut
 Helsingin seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut (1) Laske 6 5 4 5 4 3 + 4 3 2 3 2 1. a) 88 b) 66 c) 78 d) 76 Ratkaisu. Suoralla laskulla: 6 5 4 5 4 3 + 4 3 2 3 2 1
Helsingin seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut (1) Laske 6 5 4 5 4 3 + 4 3 2 3 2 1. a) 88 b) 66 c) 78 d) 76 Ratkaisu. Suoralla laskulla: 6 5 4 5 4 3 + 4 3 2 3 2 1
hinnoitteluun ja puukauppaan
 Työkaluja puutavaran hinnoitteluun ja puukauppaan PUU tutkimus ja kehittämisohjelman väliseminaari 6.9.2012 Sokos Hotel Vaakuna, Hämeenlinna Jukka Malinen Metla / Joensuu Metsäntutkimuslaitos Skogsforskningsinstitutet
Työkaluja puutavaran hinnoitteluun ja puukauppaan PUU tutkimus ja kehittämisohjelman väliseminaari 6.9.2012 Sokos Hotel Vaakuna, Hämeenlinna Jukka Malinen Metla / Joensuu Metsäntutkimuslaitos Skogsforskningsinstitutet
Tehtävä 1. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi
 Tehtävä. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi lyhyesti. a) a, c, e, g, b),,, 7,, Ratkaisut: a) i ja k - oikea perustelu ja oikeat kirjaimet, annetaan
Tehtävä. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi lyhyesti. a) a, c, e, g, b),,, 7,, Ratkaisut: a) i ja k - oikea perustelu ja oikeat kirjaimet, annetaan
Kertausosan ratkaisut. 1. Kulma α on 37 suurempi kuin kulma eli 37. Koska kulmat α ja β ovat vieruskulmia, niiden summa on 180 eli
 Kertausosa 1. Kulma α on 7 suurempi kuin kulma eli 7. Koska kulmat α ja β ovat vieruskulmia, niiden summa on 180 eli 180 7 180 14 : 71,5 Siis 7 71,5 7 108, 5 Vastaus: 108,5, 71, 5. Kuvaan merkityt kulmat
Kertausosa 1. Kulma α on 7 suurempi kuin kulma eli 7. Koska kulmat α ja β ovat vieruskulmia, niiden summa on 180 eli 180 7 180 14 : 71,5 Siis 7 71,5 7 108, 5 Vastaus: 108,5, 71, 5. Kuvaan merkityt kulmat
Tekijä Pitkä matematiikka
 Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
