Taulukko 1 Kiintopiste Lämpötila ( C) Tila He -270,15-268,15 höyrypainepiste e-h 2 (H 2, missä orto- ja paramuodot
|
|
|
- Aurora Rantanen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lämpötila-asteikko ITS- Kansainvälinen lämpötila-asteikko ITS- efeenssi 1) on ollut voimassa vuodesta 19 lähtien. Se poikkeaa hiukan vanhasta asteikosta IPTS-6876), joka edelleen on käytössä monessa lämpötilaa mittaavassa laitteessa. Lämpötila-asteikon lisäksi käytetään IEC-standadit Pt100-antueille ja temoelementeille. Lämpötila-asteikkoon kuuluu kiintopisteitä ja antueita, joilla voi intepoloida kiintopisteiden välillä. Lämpötila-asteikon ITS- kiintopisteet ovat Taulukossa 1. Asteikkoon kuuluvat mittauslaitteet ovat kapselityyppiset platinavastusantuit, standadiplatinavastusantuit, kokean lämpötilan platinavastusantuit ja säteilypyometit. a) Lämpötila-asteikon ITS- kiintopisteet Taulukko 1 Kiintopiste Lämpötila C) Tila He -270,15-268,15 höyypainepiste e-h 2 H 2, missä oto- ja paamuodot -259,3467 kolmoispiste ovat tasapainossa) e-h 2 tai He H 2, missä oto- ja paamuodot ovat tasapainossa) -256,15 höyypainepiste tai kaasulämpömittaipiste) e-h 2 tai He H 2, missä oto- ja paamuodot ovat tasapainossa) -252,85 höyypainepiste tai kaasulämpömittaipiste) Ne -248,5939 kolmoispiste O 2-218,7916 kolmoispiste A -189,3442 kolmoispiste Hg -38,8344 kolmoispiste H 2 O 0,01 kolmoispiste Ga 29,7646 sulamispiste In 156,5985 jähmettymispiste Sn 231,928 jähmettymispiste Zn 419,527 jähmettymispiste Al 660,323 jähmettymispiste Ag 961,78 jähmettymispiste Au 1064,18 jähmettymispiste Cu 1084,62 jähmettymispiste
2 b) Lämpötila-asteikon ITS- efeenssifunktiot Lämpötilat määitellään esistanssin RT ) lämpötilassa T ) ja esistanssin R263,16 K) veden kolmoispisteen lämpötilassa) välisen suhteen avulla: WT ) = RT ) R 27316, K) 1) Lämpötila-alueella 13,8033 K 273,16 K käytetään efeenssifunktiota i ln[ W T )] = A + A{[ln T / 27316, K) + 15, ] / 15, 12 0 i i= 1 Käänteisfunktio, joka antaa saman T -avon kuin yhtälö 2a) 0,1 mk:n takkuudella: 2a) 15 T B B W T 16 / ) 065, i / 27316, K = 0 + i{ i=1 035, Vakioiden A 0, B 0, A i ja B i avot ovat taulukossa 2. 2b) Lämpötila-alueella 0 C 961,78 C on efeenssifunktio: 9 W T C C T / K 754, 15 i ) = 0 + i{ 481 i=1 3a) Käänteisfunktio, joka antaa saman T -avon kuin yhtälö 3a) 0,13 mk:n takkuudella: T D W T 264, i / K 27315, = 0{ 164, 3b) Vakioiden C 0, D 0, C i ja D i avot ovat taulukossa 2.
3 Taulukko 2: Refeenssifunktioiden 2), 2a), 3) ja 3a) vakioiden A 0, B 0, A i ja B i sekä C 0, D 0, C i ja D i avot A 0-2, B 0 0, B 13-0, A 1 3, B 1 0, B 14 0, A 2-1, B 2 0, B 15 0, A 3 0, B 3 0, A 4 0, B 4 0, A 5-0, B 5 0, A 6-0, B 6 0, A 7 0, B 7-0, A 8 0, B 8-0, A 9-0, B 9-0, A 10 0, B 10 0, A 11 0, B 11 0, A 12-0, B 12-0, C 0 2, D 0 439, C 1 1, D 1 472, C 2-0, D 2 37, C 3-0, D 3 7, C 4-0, D 4 2, C 5 0, D 5 0, C 6 0, D 6-0, C 7-0, D 7-0, C 8-0, D 8 0, C 9 0, D 9 0, c) Lämpötila-asteikon ITS- intepolointifunktio agonin kolmoispisteestä veden kolmoispisteeseen Vastuslämpömittai kaliboidaan agonin 83,8054 K), elohopean 234,3156 K) ja veden 273,16 K) kolmoispisteissä. Poikkeamafunktio on: WT ) W T) = awt ) 1] + bwt [ ) ]ln WT ) 4) Vakioiden a ja b avot lasketaan kiintopistekaliboinnin avoilla. d) Lämpötila-asteikon ITS- intepolointifunktiot lämpötilasta 0 C hopean jähmettymispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) sekä tinan 231,928 C), sinkin 419,527 C), alumiinin 660,323 C) ja hopean 961,78 C) jähmettymispisteissä.
4 Poikkeamafunktio on: 2 WT ) W T ) = awt [ ) 1] + bwt [ ) 1] + 3 cw [ T ) 1] + dw [ T ) W 660, 323 C)] 2 5) Kun lämpötila on pienempi kuin 660,323 C on d = 0, ja vakioiden a, b ja c avot lasketaan yhtälöstä 5 3 kalibointipistettä tina, sinkki ja alumiini) kolmen yhtälön yhmä). Alumiinipisteen ja hopeapisteen välisille lämpötiloille käytetään myös vakiota d, joka on laskettu hopeapisteen kalibointiavolla käyttäen edellä lasketut a, b ja c. d1) Lämpötila-asteikon ITS- intepolointifunktio lämpötilasta 0 C alumiinin jähmettymispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) sekä tinan 231,928 C), sinkin 419,527 C), ja alumiinin 660,323 C) jähmettymispisteissä. Poikkeamafunktiona toimii yhtälö 5), kun d = 0. d2) Lämpötila-asteikon ITS- intepolointifunktio lämpötilasta 0 C sinkin jähmettymispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) sekä tinan 231,928 C) ja sinkin 419,527 C jähmettymispisteissä. Poikkeamafunktiona toimii yhtälö 5), kun c = d = 0. d3) Lämpötila-asteikon ITS- intepolointifunktio lämpötilasta 0 C tinan jähmettymispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) sekä indiumin 156,5985 C) ja tinan 231,928 C) jähmettymispisteissä. Poikkeamafunktiona toimii yhtälö 5), kun c = d = 0. d4) Lämpötila-asteikon ITS- intepolointifunktio lämpötilasta 0 C galliumin sulamispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) ja galliumin sulamispisteessä 29,7646 C). Poikkeamafunktiona toimii yhtälö 5), kun b = c = d = 0.
5 d5) Lämpötila-asteikon ITS- intepolointifunktio elohopean kolmoispisteestä galliumin sulamispisteeseen Vastuslämpömittai kaliboidaan veden kolmoispisteissä 0,01 C) sekä elohopean kolmoispisteessä -38,8344 C) ja galliumin sulamispisteessä 29,7646 C). Poikkeamafunktiona toimii yhtälö 5), kun b = c = d = 0. W T )-avot lasketaan yhtälöstä 2b) kun T < 0,01 C ja yhtälöstä 3b) kun T > 0,01 C. e) Lämpötila-asteikon ITS- laskentafunktio hopean jähmettymispisteen yläpuolella: Planckin säteilylaki Lämpötila-asteikko ITS- on hopeapisteen yläpuolella määitelty seuaavasti: Lλ T) e = L [ T X)] e λ c [ λt X)] 2 c [ λt ] 2 1 6) missä T X) on joko hopean, kullan tai kupain kiintopistelämpötila. L λ T ) on mustan kappaleen säteilijän adianssi aallonpituudella λ tyhjiössä) lämpötilassa T, ja L λ T X)) on vastaava adianssi lämpötilassa T X). c 2 = 0, m K. Refeenssit: 1. H. Peston-Thomas, The Intenational Tempeatue Scale of 19 ITS-), Metologia 27 19) R. L. Rusby, R.P. Hudson and M. Duieux, Revised Values fo t - t 68 ) fom 630 C to 1064 C, Metologia )
JAKSOLLINEN JÄRJESTELMÄ
 JASOLLINEN JÄRJESTELMÄ Oppitunnin tavoite: Oppitunnin tavoitteena on opettaa jaksollinen järjestelmä sekä sen historiaa alkuainepelin avulla. Tunnin tavoitteena on, että oppilaat oppivat tieteellisen tutkimuksen
JASOLLINEN JÄRJESTELMÄ Oppitunnin tavoite: Oppitunnin tavoitteena on opettaa jaksollinen järjestelmä sekä sen historiaa alkuainepelin avulla. Tunnin tavoitteena on, että oppilaat oppivat tieteellisen tutkimuksen
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
Liitetaulukko 1/11. Tutkittujen materiaalien kokonaispitoisuudet KOTIMAINEN MB-JÄTE <1MM SAKSAN MB- JÄTE <1MM POHJAKUONA <10MM
 Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Tärkeitä tasapainopisteitä
 Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
KOVAJUOTTEET 2009. Somotec Oy. fosforikupari. hopea. messinki. alumiini. juoksutteet. www.somotec.fi
 KOVAJUOTTEET 2009 fosforikupari hopea messinki alumiini juoksutteet Somotec Oy www.somotec.fi SISÄLLYSLUETTELO FOSFORIKUPARIJUOTTEET Phospraz AG 20 Ag 2% (EN 1044: CP105 ). 3 Phospraz AG 50 Ag 5% (EN 1044:
KOVAJUOTTEET 2009 fosforikupari hopea messinki alumiini juoksutteet Somotec Oy www.somotec.fi SISÄLLYSLUETTELO FOSFORIKUPARIJUOTTEET Phospraz AG 20 Ag 2% (EN 1044: CP105 ). 3 Phospraz AG 50 Ag 5% (EN 1044:
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 9: Fotonit ja relativistiset kaasut Ke 30.3.2016 1 AIHEET 1. Fotonikaasun termodynamiikkaa.
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 9: Fotonit ja relativistiset kaasut Ke 30.3.2016 1 AIHEET 1. Fotonikaasun termodynamiikkaa.
Firan vesilaitos. Laitosanalyysit. Lkm keski- maksimi Lkm keski- maksimi
 Laitosanalyysit Firan vesilaitos Lämpötila C 3 8,3 8,4 4 8,4 9 ph-luku 3 6,5 6,5 4 7,9 8,1 Alkaliteetti mmol/l 3 0,53 0,59 4 1 1,1 Happi 3 2,8 4 4 11,4 11,7 Hiilidioksidi 3 23,7 25 4 1 1,9 Rauta Fe 3
Laitosanalyysit Firan vesilaitos Lämpötila C 3 8,3 8,4 4 8,4 9 ph-luku 3 6,5 6,5 4 7,9 8,1 Alkaliteetti mmol/l 3 0,53 0,59 4 1 1,1 Happi 3 2,8 4 4 11,4 11,7 Hiilidioksidi 3 23,7 25 4 1 1,9 Rauta Fe 3
KJR-C2004 materiaalitekniikka. Harjoituskierros 3
 KJR-C2004 materiaalitekniikka Harjoituskierros 3 Tänään ohjelmassa 1. Tasapainopiirros 1. Tulkinta 2. Laskut 2. Faasimuutokset 3. Ryhmätyöt 1. Esitehtävän yhteenveto (palautetaan harkassa) 2. Ryhmätehtävä
KJR-C2004 materiaalitekniikka Harjoituskierros 3 Tänään ohjelmassa 1. Tasapainopiirros 1. Tulkinta 2. Laskut 2. Faasimuutokset 3. Ryhmätyöt 1. Esitehtävän yhteenveto (palautetaan harkassa) 2. Ryhmätehtävä
17VV VV 01021
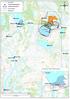 Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
4757 4h. MAGNEETTIKENTÄT
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
Lkm keski- maksimi Lkm keski- maksimi. Lkm keski- maksimi Lkm keski- maksimi
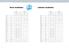 Firan vesilaitos Lahelan vesilaitos Lämpötila C 12 9,5 14,4 12 7,9 8,5 ph-luku 12 6,6 6,7 12 8,0 8,1 Alkaliteetti mmol/l 12 0,5 0,5 12 1,1 1,1 Happi mg/l 12 4,2 5,3 12 11,5 13,2 Hiilidioksidi mg/l 12 21
Firan vesilaitos Lahelan vesilaitos Lämpötila C 12 9,5 14,4 12 7,9 8,5 ph-luku 12 6,6 6,7 12 8,0 8,1 Alkaliteetti mmol/l 12 0,5 0,5 12 1,1 1,1 Happi mg/l 12 4,2 5,3 12 11,5 13,2 Hiilidioksidi mg/l 12 21
Mikroskooppisten kohteiden
 Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Suhteellisuusteorian perusteet, harjoitus 6
 Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde...2 1.2 Mikroskooppiset ja makroskooppiset teoriat...3 1.3 Terminen tasapaino ja lämpötila...5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde...2 1.2 Mikroskooppiset ja makroskooppiset teoriat...3 1.3 Terminen tasapaino ja lämpötila...5 1.4 Termodynamiikan
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 2016 Sivu 1 / 4
 Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 06 Sivu / 4 Laske yhteensä enintään 0 tehtävää. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. Osiossa A EI SAA käyttää laskinta. Osiossa
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 06 Sivu / 4 Laske yhteensä enintään 0 tehtävää. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. Osiossa A EI SAA käyttää laskinta. Osiossa
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
kultaseokset hammaslaboratorioille ja -teknikoille
 kultaseokset hammaslaboratorioille ja -teknikoille K.A.Rasmussen on Pohjoismaiden johtava jalometallialan yritys. Vuodesta 1872 jalometallien asiantuntemusta. 1 SISäLLySLuETTELO laatu on perinteemme 3
kultaseokset hammaslaboratorioille ja -teknikoille K.A.Rasmussen on Pohjoismaiden johtava jalometallialan yritys. Vuodesta 1872 jalometallien asiantuntemusta. 1 SISäLLySLuETTELO laatu on perinteemme 3
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1
 Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1 A B B Piirroksen alue 1: Sularajan yläpuolella on seos aina täysin sula => yksifaasialue (L). Alueet 2 ja 5: Nämä ovat
Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1 A B B Piirroksen alue 1: Sularajan yläpuolella on seos aina täysin sula => yksifaasialue (L). Alueet 2 ja 5: Nämä ovat
Käsitteitä. Hapetusluku = kuvitteellinen varaus, jonka atomi saa elektronin siirtyessä
 Sähkökemia Nopea kertaus! Mitä seuraavat käsitteet tarkoittivatkaan? a) Hapettuminen b) Pelkistyminen c) Hapetusluku d) Elektrolyytti e) Epäjalometalli f) Jalometalli Käsitteitä Hapettuminen = elektronin
Sähkökemia Nopea kertaus! Mitä seuraavat käsitteet tarkoittivatkaan? a) Hapettuminen b) Pelkistyminen c) Hapetusluku d) Elektrolyytti e) Epäjalometalli f) Jalometalli Käsitteitä Hapettuminen = elektronin
17VV VV Veden lämpötila 14,2 12,7 14,2 13,9 C Esikäsittely, suodatus (0,45 µm) ok ok ok ok L. ph 7,1 6,9 7,1 7,1 RA2000¹ L
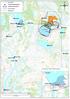 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan
 Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
METROLOGIA osa I Kari Riski, Mittatekniikan keskus, MIKES kari.riski@mikes.fi
 METROLOGIA osa I Kari Riski, Mittatekniikan keskus, MIKES kari.riski@mikes.fi SISÄLTÖ Mitä metrologia on Metrisopimus, MIKES Lämpötilan yksikkö kelvin, lämpötila-asteikko ITS-90 Valovoiman yksikkö kandela,
METROLOGIA osa I Kari Riski, Mittatekniikan keskus, MIKES kari.riski@mikes.fi SISÄLTÖ Mitä metrologia on Metrisopimus, MIKES Lämpötilan yksikkö kelvin, lämpötila-asteikko ITS-90 Valovoiman yksikkö kandela,
JÄTTEET HARVINAISTEN LUONNONVAROJEN LÄHTEENÄ
 JÄTTEET HARVINAISTEN LUONNONVAROJEN LÄHTEENÄ Ari Väisänen 8.5.2019 Sisältö Kriittisten materiaalien tuotanto Potentiaalisia raaka-ainelähteitä Raaka-aineiden talteenotto lietteestä 3D tulostetut metallisiepparit
JÄTTEET HARVINAISTEN LUONNONVAROJEN LÄHTEENÄ Ari Väisänen 8.5.2019 Sisältö Kriittisten materiaalien tuotanto Potentiaalisia raaka-ainelähteitä Raaka-aineiden talteenotto lietteestä 3D tulostetut metallisiepparit
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
9 Klassinen ideaalikaasu
 111 9 Klassinen ideaalikaasu 9-1 Klassisen ideaalikaasun patitiofunktio Ideaalikaasu on eaalikaasun idealisaatio, jossa molekyylien väliset keskimäääiset etäisyydet oletetaan hyvin suuiksi molekyylien
111 9 Klassinen ideaalikaasu 9-1 Klassisen ideaalikaasun patitiofunktio Ideaalikaasu on eaalikaasun idealisaatio, jossa molekyylien väliset keskimäääiset etäisyydet oletetaan hyvin suuiksi molekyylien
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
6*. MURTOFUNKTION INTEGROINTI
 MAA0 6*. MURTOFUNKTION INTEGROINTI Murtofunktio tarkoittaa kahden polynomin osamäärää, ja sen yleinen muoto on P() R : R(). Q() Mikäli osoittajapolynomin asteluku on nimittäjäpolynomin astelukua korkeampi
MAA0 6*. MURTOFUNKTION INTEGROINTI Murtofunktio tarkoittaa kahden polynomin osamäärää, ja sen yleinen muoto on P() R : R(). Q() Mikäli osoittajapolynomin asteluku on nimittäjäpolynomin astelukua korkeampi
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Matematiikan kurssikoe, Maa 9 Integraalilaskenta RATKAISUT Torstai A-OSA
 Matematiikan kussikoe, Maa 9 Integaalilaskenta RATKAISUT Tostai..8 A-OSA Sievin lukio. a) Integoi välivaiheineen i) (x t ) dt ii) x dx. b) Määittele integaalifunktio. c) i) Olkoon 5 f(x) dx =, f(x) dx
Matematiikan kussikoe, Maa 9 Integaalilaskenta RATKAISUT Tostai..8 A-OSA Sievin lukio. a) Integoi välivaiheineen i) (x t ) dt ii) x dx. b) Määittele integaalifunktio. c) i) Olkoon 5 f(x) dx =, f(x) dx
Määräys STUK SY/1/ (34)
 Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Juottaminen J O H D A N T O... D 1. 2. J u o k s u t t e e n v a l i n t a t a u l u k k o... D 1. 3
 J O H D A N T O.......................................... D 1. 2 J u o k s u t t e e n v a l i n t a t a u l u k k o............... D 1. 3 I M P O W E L D, C H E M E T, F E L D E R j a S T E L L A - j
J O H D A N T O.......................................... D 1. 2 J u o k s u t t e e n v a l i n t a t a u l u k k o............... D 1. 3 I M P O W E L D, C H E M E T, F E L D E R j a S T E L L A - j
SMG-4200 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen 3 ratkaisuiksi
 SMG-4 Sähkömagneettisten jäjestelmien lämmönsiito Ehdotukset hajoituksen 3 atkaisuiksi 1. Voidaan kohtuullisella takkuudella olettaa, että pallonmuotoisessa säiliössä lämpötila muuttuu vain pallon säteen
SMG-4 Sähkömagneettisten jäjestelmien lämmönsiito Ehdotukset hajoituksen 3 atkaisuiksi 1. Voidaan kohtuullisella takkuudella olettaa, että pallonmuotoisessa säiliössä lämpötila muuttuu vain pallon säteen
Kansalaisnäytteet paljastavat vakavia puutteita Talvivaaran valvonnassa
 1 Kansalaisnäytteet paljastavat vakavia puutteita Talvivaaran valvonnassa Seuraavassa taulukossa on Ylä-Lumijärven keltaisen herkkäliikkeisen sekä sen alla olevan sakan koostumus kiintoainetta kohden.
1 Kansalaisnäytteet paljastavat vakavia puutteita Talvivaaran valvonnassa Seuraavassa taulukossa on Ylä-Lumijärven keltaisen herkkäliikkeisen sekä sen alla olevan sakan koostumus kiintoainetta kohden.
Muita tyyppejä. Bender Rengas Fokusoitu Pino (Stack) Mittaustekniikka
 Muita tyyppejä Bender Rengas Fokusoitu Pino (Stack) 132 Eri piezomateriaalien käyttökohteita www.ferroperm.com 133 Lämpötilan mittaaminen Termopari Halpa, laaja lämpötila-alue Resistanssin muutos Vastusanturit
Muita tyyppejä Bender Rengas Fokusoitu Pino (Stack) 132 Eri piezomateriaalien käyttökohteita www.ferroperm.com 133 Lämpötilan mittaaminen Termopari Halpa, laaja lämpötila-alue Resistanssin muutos Vastusanturit
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
HAMMASKULTA- SEOKSET
 HAMMASKULTA- SEOKSET LAATU ON PERINTEEMME K.A.Rasmussen on johtava hammaskultaseosten valmistaja ja tavarantoimittaja Skandinaviassa. Tuotevalikoima ja laatu tarjoavat turvallisuutta niin hammasteknikoille,
HAMMASKULTA- SEOKSET LAATU ON PERINTEEMME K.A.Rasmussen on johtava hammaskultaseosten valmistaja ja tavarantoimittaja Skandinaviassa. Tuotevalikoima ja laatu tarjoavat turvallisuutta niin hammasteknikoille,
VILJAVUUSTUTKIMUS s-posti: neuvonta@viljavuuspalvelu.fi Päivämäärä Asiakasnro Tutkimusnro
 1/8 Näytteen numero 1 2 3 4 5 6 7 Peruslohkotunnus 754-07722- 19 754-07334- 19 Pintamaan maalaji a) HeS HeS HeS HeS HsS HsS HeS Multavuus a) rm rm rm rm rm rm rm 0,8 1,0 0,7 0,5 0,4 0,6 0,5 Happamuus ph
1/8 Näytteen numero 1 2 3 4 5 6 7 Peruslohkotunnus 754-07722- 19 754-07334- 19 Pintamaan maalaji a) HeS HeS HeS HeS HsS HsS HeS Multavuus a) rm rm rm rm rm rm rm 0,8 1,0 0,7 0,5 0,4 0,6 0,5 Happamuus ph
10. Toisen kertaluvun lineaariset differentiaaliyhtälöt
 37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
LÄMPÖTILAN VERTAILUMITTAUS L11, PT100-ANTURIN SOVITUSMENETELMÄN KEHITTÄMINEN
 MITTATEKNIIKAN KESKUS Julkaisu J3/2001 LÄMPÖTILAN VERTAILUMITTAUS L11, PT100-ANTURIN SOVITUSMENETELMÄN KEHITTÄMINEN Thua Weckström Helsinki 2001 SUMMARY The interlaboratory comparison on calculating coefficients
MITTATEKNIIKAN KESKUS Julkaisu J3/2001 LÄMPÖTILAN VERTAILUMITTAUS L11, PT100-ANTURIN SOVITUSMENETELMÄN KEHITTÄMINEN Thua Weckström Helsinki 2001 SUMMARY The interlaboratory comparison on calculating coefficients
1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ
![1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ 1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ](/thumbs/67/57751673.jpg) Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
TUTKIMUSSELOSTE. Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: Tarkkailukierros: vko 2. Tutkimuksen lopetus pvm
 TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 2 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 2 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
LIITE nnn GTKn moreeninäytteet Suhangon alueelta.! = analyysitulos epävarma
 LIITE nnn GTKn moreeninäytteet Suhangon alueelta Havnro Vuosi X Y Aines Pvm_511p Al_511p Ba_511p Ca_511p Co_511p Cr_511p Cu_511p Fe_511p K_511p La_511p Li_511p Mg_511p 30759 89 7333802 3461760 MR 19910128
LIITE nnn GTKn moreeninäytteet Suhangon alueelta Havnro Vuosi X Y Aines Pvm_511p Al_511p Ba_511p Ca_511p Co_511p Cr_511p Cu_511p Fe_511p K_511p La_511p Li_511p Mg_511p 30759 89 7333802 3461760 MR 19910128
Jännittävät metallit
 Jännittävät metallit Tästä alkaa tutkimusmatkamme sähkön syntymiseen! Varmaan tiedätkin, että sähköä saadaan sekä pistorasioista että erilaisista paristoista. Pistorasioista saatava sähkö tuotetaan fysikaalisesti,
Jännittävät metallit Tästä alkaa tutkimusmatkamme sähkön syntymiseen! Varmaan tiedätkin, että sähköä saadaan sekä pistorasioista että erilaisista paristoista. Pistorasioista saatava sähkö tuotetaan fysikaalisesti,
Normaalipotentiaalit
 Normaalipotentiaalit MATERIAALIT JA TEKNOLOGIA, KE4 Yksittäisen elektrodin aiheuttaman jännitteen mittaaminen ei onnistu. Jännitemittareilla voidaan havaita ja mitata vain kahden elektrodin välinen potentiaaliero
Normaalipotentiaalit MATERIAALIT JA TEKNOLOGIA, KE4 Yksittäisen elektrodin aiheuttaman jännitteen mittaaminen ei onnistu. Jännitemittareilla voidaan havaita ja mitata vain kahden elektrodin välinen potentiaaliero
NIMI: Luokka: c) Atomin varaukseton hiukkanen on nimeltään i) protoni ii) neutroni iii) elektroni
 Peruskoulun kemian valtakunnallinen koe 2010-2011 NIMI: Luokka: 1. Ympyröi oikea vaihtoehto. a) Ruokasuolan kemiallinen kaava on i) CaOH ii) NaCl iii) KCl b) Natriumhydroksidi on i) emäksinen aine, jonka
Peruskoulun kemian valtakunnallinen koe 2010-2011 NIMI: Luokka: 1. Ympyröi oikea vaihtoehto. a) Ruokasuolan kemiallinen kaava on i) CaOH ii) NaCl iii) KCl b) Natriumhydroksidi on i) emäksinen aine, jonka
Chem-C2400 Luento 3: Faasidiagrammit Ville Jokinen
 Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
 Raportti Sivu 1 (7) K1301600 2BQWOKQ8N98 Vahanen Oy Projekti TT 1099 Kyösti Nieminen Tilausnumero Sisäänkirjattu 2013-11-13 Linnoitustie 5 Raportoitu 2013-11-21 02600 ESPOO Materiaalin analysointi Asiakkaan
Raportti Sivu 1 (7) K1301600 2BQWOKQ8N98 Vahanen Oy Projekti TT 1099 Kyösti Nieminen Tilausnumero Sisäänkirjattu 2013-11-13 Linnoitustie 5 Raportoitu 2013-11-21 02600 ESPOO Materiaalin analysointi Asiakkaan
12. Differentiaaliyhtälöt
 1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
2. Koska f(5) > 8 ja yhdeksän pisteen varaan voidaan virittää kupera viisikulmio, niin f(5) = 9.
 Dimension 1/2018 pulmasivu Ratkaisuja 1. Viiden pisteen joukosta voidaan aina valita neljä, jotka ovat kuperan monikulmion kärkipisteitä, mutta neljästä pisteestä ei muodostu aina kuperaa monikulmiota.
Dimension 1/2018 pulmasivu Ratkaisuja 1. Viiden pisteen joukosta voidaan aina valita neljä, jotka ovat kuperan monikulmion kärkipisteitä, mutta neljästä pisteestä ei muodostu aina kuperaa monikulmiota.
KIERTOTALOUS KEMISTIN NÄKÖKULMASTA
 KIERTOTALOUS KEMISTIN NÄKÖKULMASTA Ari Väisänen 7.6.2019 Sisältö Kriittisten materiaalien tuotanto Potentiaalisia raaka-ainelähteitä Raaka-aineiden talteenotto lietteestä 3D tulostetut metallisiepparit
KIERTOTALOUS KEMISTIN NÄKÖKULMASTA Ari Väisänen 7.6.2019 Sisältö Kriittisten materiaalien tuotanto Potentiaalisia raaka-ainelähteitä Raaka-aineiden talteenotto lietteestä 3D tulostetut metallisiepparit
Juuri 12 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K. a) Polynomi P() = 3 + 8 on jaollinen polynomilla Q() = 3, jos = 3 on polynomin P nollakohta, eli P(3) = 0. P(3) = 3 3 3 + 8 3 = 54 08 + 54 = 0. Polynomi P on jaollinen polynomilla Q. b) Jaetaan
Kertaus K. a) Polynomi P() = 3 + 8 on jaollinen polynomilla Q() = 3, jos = 3 on polynomin P nollakohta, eli P(3) = 0. P(3) = 3 3 3 + 8 3 = 54 08 + 54 = 0. Polynomi P on jaollinen polynomilla Q. b) Jaetaan
KRIITTISTEN RAAKA-AINEIDEN SELEKTIIVINEN TALTEENOTTO SE-ROMUSTA
 KRIITTISTEN RAAKA-AINEIDEN SELEKTIIVINEN TALTEENOTTO SE-ROMUSTA 16.5.2018 Ari Väisänen Kriittisten metallien tuotanto Harvinaisten maametallien tuotanto 95% Kiinassa Pd ja Pt tuotanto keskittynyt Etelä-Afrikkaan
KRIITTISTEN RAAKA-AINEIDEN SELEKTIIVINEN TALTEENOTTO SE-ROMUSTA 16.5.2018 Ari Väisänen Kriittisten metallien tuotanto Harvinaisten maametallien tuotanto 95% Kiinassa Pd ja Pt tuotanto keskittynyt Etelä-Afrikkaan
Fysp240/1 Ising-malli (lyhyt raportti)
 Tiia Monto Työ tehty: 19.1. tiia.monto@jyu. 7515 Fysp/1 Ising-malli (lyhyt apotti) Assistentti: Avostellaan (joko hyväksytty tai hylätty) Työ jätetty: Abstact I simulated paamagnet, feomagnet and antifeomagnet
Tiia Monto Työ tehty: 19.1. tiia.monto@jyu. 7515 Fysp/1 Ising-malli (lyhyt apotti) Assistentti: Avostellaan (joko hyväksytty tai hylätty) Työ jätetty: Abstact I simulated paamagnet, feomagnet and antifeomagnet
Fysiikka 8. Aine ja säteily
 Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Sähkökemia. Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali
 Sähkökemia Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali Esimerkki 1 Pohdi kertauksen vuoksi seuraavia käsitteitä a) Hapettuminen b) Pelkistin c) Hapetusluku d) Elektrolyytti e)
Sähkökemia Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali Esimerkki 1 Pohdi kertauksen vuoksi seuraavia käsitteitä a) Hapettuminen b) Pelkistin c) Hapetusluku d) Elektrolyytti e)
Elektrolyysi Anodilla tapahtuu aina hapettuminen ja katodilla pelkistyminen!
 Elektrolyysi MATERIAALIT JA TEKNOLOGIA, KE4 Monet kemialliset reaktiot ovat palautuvia eli reversiibeleitä. Jo sähkökemian syntyvaiheessa oivallettiin, että on mahdollista rakentaa kahdenlaisia sähkökemiallisia
Elektrolyysi MATERIAALIT JA TEKNOLOGIA, KE4 Monet kemialliset reaktiot ovat palautuvia eli reversiibeleitä. Jo sähkökemian syntyvaiheessa oivallettiin, että on mahdollista rakentaa kahdenlaisia sähkökemiallisia
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Tapa II: Piirretään voiman F vaikutussuora ja lasketaan momentti sen avulla. Kuva 3. d r. voiman F vaikutussuora
 VOIMAN MOMENTTI Takastellaan jäykkää kappaletta, joka pääsee kietymään akselin O ympäi. VOIMAN MOMENTTI on voiman kietovaikutusta kuvaava suue. Voiman momentti määitellään voiman F ja voiman vaen tulona:
VOIMAN MOMENTTI Takastellaan jäykkää kappaletta, joka pääsee kietymään akselin O ympäi. VOIMAN MOMENTTI on voiman kietovaikutusta kuvaava suue. Voiman momentti määitellään voiman F ja voiman vaen tulona:
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
Malmi Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb
 11.2 Malmi % % % ppm ppm % ppm ppm ppm ppm ppm ppm ppm Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb Konttijärvi Kattopuoli 0,20 0,14 0,07 48,97 376,76 4,33
11.2 Malmi % % % ppm ppm % ppm ppm ppm ppm ppm ppm ppm Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb Konttijärvi Kattopuoli 0,20 0,14 0,07 48,97 376,76 4,33
Sovelletun fysiikan pääsykoe
 Sovelletun fysiikan pääsykoe 7.6.016 Kokeessa on neljä (4) tehtävää. Vastaa kaikkiin tehtäviin. Muista kirjoittaa myös laskujesi välivaiheet näkyviin. Huom! Kirjoita tehtävien 1- vastaukset yhdelle konseptille
Sovelletun fysiikan pääsykoe 7.6.016 Kokeessa on neljä (4) tehtävää. Vastaa kaikkiin tehtäviin. Muista kirjoittaa myös laskujesi välivaiheet näkyviin. Huom! Kirjoita tehtävien 1- vastaukset yhdelle konseptille
1 Perussuureiden kertausta ja esimerkkejä
 1 Perussuureiden kertausta ja esimerkkejä 1.1 Vuontiheys ja pintakirkkaus Vuontiheys ( flux density ) kertoo, kuinka paljon säteilyenergiaa taajuskaistassa [ν,ν+1hz] virtaa 1 m 2 pinta-alan läpi sekunnissa.
1 Perussuureiden kertausta ja esimerkkejä 1.1 Vuontiheys ja pintakirkkaus Vuontiheys ( flux density ) kertoo, kuinka paljon säteilyenergiaa taajuskaistassa [ν,ν+1hz] virtaa 1 m 2 pinta-alan läpi sekunnissa.
TUTKIMUSSELOSTE. Tutkimuksen lopetus pvm. Näkösyv. m
 TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 3 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 3 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
Talousmatematiikan perusteet: Luento 4. Potenssifunktio Eksponenttifunktio Logaritmifunktio
 Talousmatematiikan perusteet: Luento 4 Potenssifunktio Eksponenttifunktio Logaritmifunktio Viime luennolla Funktiolla f: A B kuvataan muuttujan y B riippuvuutta muuttujasta x A A on lähtö- tai määrittelyjoukko
Talousmatematiikan perusteet: Luento 4 Potenssifunktio Eksponenttifunktio Logaritmifunktio Viime luennolla Funktiolla f: A B kuvataan muuttujan y B riippuvuutta muuttujasta x A A on lähtö- tai määrittelyjoukko
Ratkaisu. Tarkastellaan aluksi Fe 3+ - ja Fe 2+ -ionien välistä tasapainoa: Nernstin yhtälö tälle reaktiolle on:
 Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Muutoksen arviointi differentiaalin avulla
 Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
AKKU- JA PARISTOTEKNIIKAT
 AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
Kriittiset metallit uudessa energiateknologiassa. Leena Grandell, Energiasysteemit VTT
 Kriittiset metallit uudessa energiateknologiassa Leena Grandell, Energiasysteemit VTT 2 Euroopan energiasektori murroksessa Talouskasvu lisää energian kysyntää, erityisesti kehittyvissä maissa Tekninen
Kriittiset metallit uudessa energiateknologiassa Leena Grandell, Energiasysteemit VTT 2 Euroopan energiasektori murroksessa Talouskasvu lisää energian kysyntää, erityisesti kehittyvissä maissa Tekninen
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
x = π 3 + nπ, x + 1 f (x) = 2x (x + 1) x2 1 (x + 1) 2 = 2x2 + 2x x 2 = x2 + 2x f ( 3) = ( 3)2 + 2 ( 3) ( 3) + 1 3 1 + 4 2 + 5 2 = 21 21 = 21 tosi
 Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
Alikuoret eli orbitaalit
 Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta
 1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
Sähkökemiaa. Hapettuminen Jännitesarja Elektrolyysi Faradayn laki Korroosio
 Sähkökemiaa Hapettuminen Jännitesarja Elektrolyysi Faradayn laki Korroosio Hapettuminen ja pelkistyminen 1. Hapetin ja pelkistin 2. Hapetusluku Sähkökemiaa 1. Sähköpari 2. Metallien jännitesarja 3. Elektrolyysi
Sähkökemiaa Hapettuminen Jännitesarja Elektrolyysi Faradayn laki Korroosio Hapettuminen ja pelkistyminen 1. Hapetin ja pelkistin 2. Hapetusluku Sähkökemiaa 1. Sähköpari 2. Metallien jännitesarja 3. Elektrolyysi
Analyysi 1. Harjoituksia lukuihin 4 7 / Syksy Tutki funktion f(x) = x 2 + x 2 jatkuvuutta pisteissä x = 0 ja x = 1.
 Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
LIITE 4A 4A LÄMPÖTILAN T LISÄRAKENTEITA
 LIIE 4A 4A LÄMPÖILAN LISÄRAKENEIA ämä kohta 4A perustuu siihen, mitä kohdassa 4 on esitetty. ässä kuitenkin koetetaan mennä vielä syvemmälle lämpötilarakenteeseen ja löytää toisenlaisia rakenteita, joita
LIIE 4A 4A LÄMPÖILAN LISÄRAKENEIA ämä kohta 4A perustuu siihen, mitä kohdassa 4 on esitetty. ässä kuitenkin koetetaan mennä vielä syvemmälle lämpötilarakenteeseen ja löytää toisenlaisia rakenteita, joita
Quality Coated Abrasives. Joustavat hiomatuotteet metallien hiontaan
 Quality Coated Abrasives Joustavat hiomatuotteet metallien hiontaan Quality Coated Abrasives Varmin tapa täydelliseen pinnanlaatuun Ammattimaisesti hiotut työkappaleet erottuvat hyvän pinnanlaatunsa johdosta,
Quality Coated Abrasives Joustavat hiomatuotteet metallien hiontaan Quality Coated Abrasives Varmin tapa täydelliseen pinnanlaatuun Ammattimaisesti hiotut työkappaleet erottuvat hyvän pinnanlaatunsa johdosta,
Esitiedot. Jalometallit. Resistiivisyys 10 8 Ohm m. Hintatietoutta. Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana?
 Esitiedot Jalometallit Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana? Matalalla sulavia metalliseoksia käytetään ainakin juotteina, mutta mitä muita sovelluksia niille on? Mitä on
Esitiedot Jalometallit Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana? Matalalla sulavia metalliseoksia käytetään ainakin juotteina, mutta mitä muita sovelluksia niille on? Mitä on
Esitiedot. Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana?
 Jalometallit Esitiedot Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana? Matalalla sulavia metalliseoksia käytetään ainakin juotteina, mutta mitä muita sovelluksia niille on? Mitä on
Jalometallit Esitiedot Mitä kaikkia ihmisille yritetään myydä hopeana, kultana ja platinana? Matalalla sulavia metalliseoksia käytetään ainakin juotteina, mutta mitä muita sovelluksia niille on? Mitä on
SI-järjestelmä uudistuu
 SI-järjestelmä uudistuu Virpi Korpelainen VTT MIKES 6.10.2018 VTT beyond the obvious 1 Sisällys SI-järjestelmä Uudistus Miksi? Mitä? Milloin? Uudet määritelmät ja toteutus Kysymyksiä? 6.10.2018 VTT beyond
SI-järjestelmä uudistuu Virpi Korpelainen VTT MIKES 6.10.2018 VTT beyond the obvious 1 Sisällys SI-järjestelmä Uudistus Miksi? Mitä? Milloin? Uudet määritelmät ja toteutus Kysymyksiä? 6.10.2018 VTT beyond
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Suomen harvinaisimmat metallirahat 2018
 Suomen harvinaisimmat metallirahat 2018 Turun rahat 1410-1558 Eerik Pommerilainen 1396-1439 Nimellisarvo Kuntoluokka Vuosi 6(1+) 4(1) 2(1?) Aurtua A ilman poikkiviivaa 3 500 2 000 1 000 Aurtua A poikkiviivaalla
Suomen harvinaisimmat metallirahat 2018 Turun rahat 1410-1558 Eerik Pommerilainen 1396-1439 Nimellisarvo Kuntoluokka Vuosi 6(1+) 4(1) 2(1?) Aurtua A ilman poikkiviivaa 3 500 2 000 1 000 Aurtua A poikkiviivaalla
Suomen kaivostoiminta nyt ja mahdollisuudet tulevaisuudessa
 Suomen kaivostoiminta nyt ja mahdollisuudet tulevaisuudessa Olli Breilin Johtaja, operatiivinen toiminta Kokkola Material Week 2018 Kaivostoiminta Suomessa Investoinnit malminetsintään ovat kasvussa Lähde:
Suomen kaivostoiminta nyt ja mahdollisuudet tulevaisuudessa Olli Breilin Johtaja, operatiivinen toiminta Kokkola Material Week 2018 Kaivostoiminta Suomessa Investoinnit malminetsintään ovat kasvussa Lähde:
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia
 Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
sin x cos x cos x = sin x arvoilla x ] π
![sin x cos x cos x = sin x arvoilla x ] π sin x cos x cos x = sin x arvoilla x ] π](/thumbs/88/114931690.jpg) Matematiikan johdantokurssi, syksy 08 Harjoitus 0, ratkaisuista. Todenna, että = + tan x. Mutta selvitäppä millä reaaliarvoilla se oikeasti pitää paikkansa! Ratkaisu. Yhtälön molemmat puolet ovat määriteltyjä
Matematiikan johdantokurssi, syksy 08 Harjoitus 0, ratkaisuista. Todenna, että = + tan x. Mutta selvitäppä millä reaaliarvoilla se oikeasti pitää paikkansa! Ratkaisu. Yhtälön molemmat puolet ovat määriteltyjä
Lyijyttömät juotokset Weller-työkaluilla
 Lyijyttömät juotokset Weller-työkaluilla Miksi lyijytön? Euroopan yhteisön lakien mukaan juotoksissa sallitaan 1.7.2006 alkaen ainoastaan lyijyttömän tinan käyttö. Muuttuvan lainsäädännön perusteena ovat
Lyijyttömät juotokset Weller-työkaluilla Miksi lyijytön? Euroopan yhteisön lakien mukaan juotoksissa sallitaan 1.7.2006 alkaen ainoastaan lyijyttömän tinan käyttö. Muuttuvan lainsäädännön perusteena ovat
Harjoitus 5 / viikko 7
 DEE-000 Piiianalyysi Hajoitus 5 / viikko 7 5. Laske solmupistemenetelmällä oheisen kuvan esittämän piiin jännite ja vita i. 0k ma k k k i ma Solmupistemenetelmää käytettäessä takasteltavan kytkennän jännitelähteet
DEE-000 Piiianalyysi Hajoitus 5 / viikko 7 5. Laske solmupistemenetelmällä oheisen kuvan esittämän piiin jännite ja vita i. 0k ma k k k i ma Solmupistemenetelmää käytettäessä takasteltavan kytkennän jännitelähteet
M 19/1823/-75/1/10 Enontekiö, Kilpisjärvi Olavi Auranen 1975-10-30. Selostus malmitutkimuksista Enontekiön Kilpisjärvellä v. 1974
 M 19/1823/-75/1/10 Enontekiö, Kilpisjärvi Olavi Auranen 1975-10-30 Selostus malmitutkimuksista Enontekiön Kilpisjärvellä v. 1974 Syksyllä 1973 lähetti rajajääkäri Urho Kalevi Mäkinen geologisen tutkimuslaitoksen
M 19/1823/-75/1/10 Enontekiö, Kilpisjärvi Olavi Auranen 1975-10-30 Selostus malmitutkimuksista Enontekiön Kilpisjärvellä v. 1974 Syksyllä 1973 lähetti rajajääkäri Urho Kalevi Mäkinen geologisen tutkimuslaitoksen
a) Piirrä hahmotelma varjostimelle muodostuvan diffraktiokuvion maksimeista 1, 2 ja 3.
 Ohjeita: Tee jokainen tehtävä siististi omalle sivulleen/sivuilleen. Merkitse jos tehtävä jatkuu seuraavalle konseptille. Kirjoita ratkaisuihin näkyviin tarvittavat välivaiheet ja perustele lyhyesti käyttämästi
Ohjeita: Tee jokainen tehtävä siististi omalle sivulleen/sivuilleen. Merkitse jos tehtävä jatkuu seuraavalle konseptille. Kirjoita ratkaisuihin näkyviin tarvittavat välivaiheet ja perustele lyhyesti käyttämästi
lnx x 1 = = lim x = = lim lim 10 = x x0
 BM0A580 - Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 05. (a) (b) ln = sin(t π ) t π t π = = 0 = = cos(t π = ) = 0 t π (c) e [ = ] = = e e 3 = e = 0 = 0 (d) (e) 3 3 + 6 + 8 + 6 5 + 4 4 + 4
BM0A580 - Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 05. (a) (b) ln = sin(t π ) t π t π = = 0 = = cos(t π = ) = 0 t π (c) e [ = ] = = e e 3 = e = 0 = 0 (d) (e) 3 3 + 6 + 8 + 6 5 + 4 4 + 4
