Lisävaatimuksia aaltofunktiolle
|
|
|
- Ari-Pekka Uotila
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lisävaatimuksia aaltofunktiolle (1) Koska Ψ*Ψ on äärellinen => Ψ on äärellinen. () Koska P = Ψ*Ψdτ => Ψ on yksiselitteinen. (3) Ψ on jatkuva. (4) dψ/dτ on jatkuva. Esimerkki Epäkelpoja aaltofunktioita Aaltofunktion antama informaatio Tarkastellaan yksidimensionaalista aaltofunktiota ψ(x): HΨ = EΨ H = m d dx +V x ( ) Ratkaisu vapaalle hiukkaselle [V(x) = 0], jonka massa on m: Ψ = Ae ikx + Be ikx ja E = k m
2 Osoitus, että kyseessä on aaltoyhtälön ratkaisu: m d Ψ dx = m d dx ( Ae ikx + Be ikx ) = m # A ik = k m ( ) e ikx + B( ik) e ikx ( Aeikx + Be ikx ) = EΨ $ % Ominaisyhtälö: Ωf = ω f (operaattori)(funktio) = (vakio) x (funktio) ominaisarvo ominaisfunktio Esimerkki Osoita, että e ax on operaattorin d/dx ominaisfunktio. Mikä on sen ominaisarvo? Onko e ax operaattorin d/dx ominaisfunktio? Jos tunnetaan systeemin aaltofunktio ja havaittavaa suuretta vastaava operaattori siten, että aaltofunktio on operaattorin ominaisfunktio, havaittavalle suureelle saadaan arvo yhtälön ominaisarvosta Schrödingerin aaltoyhtälö: (energiaoperaattori)(aaltofunktio) = (energia)x(aaltofunktio) havaittava suure
3 Liikemääräoperaattori Tarkastellaan yksiulotteista tapausta: ˆp = i d dx ˆpΨ = pψ Esimerkki Vapaa hiukkanen V(x) = 0 d Ψ m dx = EΨ Ψ = Aeikx + Be ikx ;E = k m (1) B = 0 Ψ = Ae ikx ˆpΨ = i p = k dψ dx = i A deikx dx = kaeikx Johtopäätökset: - Hiukkanen, jonka aaltofunktio on e ikx, liikkuu +x-suuntaan. - Hiukkanen, jonka aaltofunktio on e -ikx, liikkuu x-suuntaan. - Liikemäärä kummassakin tapauksessa on k. () A = 0 Ψ = Be ikx p = k (3) A = B Ψ = A( e ikx + e ikx ) = Acos x ˆpΨ = i d ( coskx) A dx = ka sinkx i Aaltofunktio ei ole ominaisfunktio
4 Odotusarvo Liikemäärällä ei ole täsmällistä arvoa. Ψ = Ψ + Ψ (1) Jos p mitataan, havaitaan yksi arvo liikemäärälle, joka vastaa tilaa Ψ i. () Havainnon todennäköisyys = c i p = k p = k tod. näk. 50 % tod. näk. 50 % Odotusarvo <Ω>: - suuren havaintojoukon keskiarvo Superpositio: => Ψ = Σc i Ψ i Ω = Ψ * ˆΩΨ dτ Odotusarvoja: (1) Olkoon Ψ Ω:n ominaisfunktio ja ω sen ominaisarvo. => Ω = Ψ * ˆΩΨ dτ = Ψ *ωψ dτ = ω Ψ * Ψ dτ = ω () Olkoon φ = c 1 Ψ 1 + c Ψ (Ψ i on ominaisfunktio operaattorille Ω). Ω = ( c 1 Ψ 1 + c Ψ )* ˆΩ ( c 1 Ψ 1 + c Ψ )dτ = ( c 1 Ψ 1 + c Ψ )*( c 1 ˆΩΨ1 + c ˆΩΨ )dτ = ( c 1 Ψ 1 + c Ψ )*( c 1 ω 1 Ψ 1 + c ω Ψ )dτ = c 1 *c 1 ω 1 Ψ 1 * Ψ 1 dτ + c *c ω Ψ * Ψ dτ + c *c 1 ω 1 Ψ * Ψ 1 dτ + c 1 *c ω Ψ 1 * Ψ dτ Ω = c 1 ω 1 + c ω
5 Esimerkki Laske perustilassa olevan vety-atomin 1s-elektronin keskimääräinen etäisyys ytimestä. (3) Hiukkasen kineettinen energia yhdessä dimensiossa E k = Ψ * Êk Ψ dx = m Ψ * d Ψ dx dx Suuri kontribuutio kineettiseen energiaan, kun dψ /dx on suuri ja kun ψ on suuri.
6 Heisenbergin epätarkkuusperiaate Lähtökohta: Ψ = e ikx p = k Werner Heisenberg Ψ * Ψ = ( Ae ikx ) * ( Ae ikx ) = (Ae ikx )(Ae ikx ) = A => Hiukkasen liikemäärä tiedetään tarkasti, sijaintia ei lainkaan. Epätarkkuusperiaate: Δx Δy Hiukkasen sijaintia ja liikemäärää ei koskaan voida määrittää tarkasti yhtäaikaa. Epätarkkuusperiatteen tulkinta: Epämääräinen sijainti: - Aaltofunktioiden superpositio. - Konstruktiivinen interferenssi. Tarkka sijainti tunnetaan: - Aaltofunktion arvo suuri yhdessä pisteessä, nolla muualla. - Aaltofunktio koostuu äärettömästä määrästä erilaisia aaltofunktioita, joiden liikemäärä on erisuuri.
7 Esimerkki (a) Luodin, jonka massa on 1,0 g, nopeuden epätarkkuus on 10-6 m s -1. Mikä on epätarkkuus luodin sijainnissa? (b) Jos elektronin nopeus tunnetaan samalla tarkkuudella, miikä on epätarkkuus elektronin sijainnissa? Esimerkki Hiukkasen aaltofunktio on Ψ(x) = a π 1/4 e ax missä a on vakio ja - < x <. Osoita, että tulo ΔpΔx on sopusoinnussa Heisenbergin epätarkkuusperiaatteen kanssa.
8 Komplementaariset havaittavat muuttujat: Muuttujat ovat komplementaarisia, jos seuraava ehto täyttyy: ˆΩ 1 ( ˆΩ Ψ) ˆΩ ˆΩ1 Ψ ( ) Esimerkki Sijainnin ja liikemäärän komplementaarisuus ˆx = x ˆp = i d dx Kommutaattori: ˆΩ 1, ˆΩ = ˆΩ 1 ˆΩ ˆΩ ˆΩ1 ˆxˆpΨ = x i ˆpˆxΨ = i dψ dx d ( xψ) = dx i $ # Ψ + x dψ dx % ' & ˆxˆpΨ ˆpˆxΨ = x i dψ dx i Ψ x dψ dx = i Ψ = i Ψ Relaksaatioaika ja spektriresoluutio Heisenbergin epätarkkuusperiaate: ΔE Δt! ΔνΔt 1 π missä ΔE = epätarkkuus virittyneen tilan energiassa Δν = spektriviivan leveys (resoluutio) Δt = virittyneen tilan elinikä (relaksaatioaika)
9 Esimerkki Elektronispektrit Δt s (lyhyt elinikä) => ΔE 60 kj mol -1 Johtopäätös: - ΔE tilojen välinen energiaero - Vain muutama leveä absorptihuippu spektrissä; ei vähän hienorakennetta Esimerkki NMR - relaksaatioajat yleensä pitkiä - resoluutio yleensä hyvä 1,,3,4,5-Se 5 S :n 77 Se NMR spektri Esimerkki Mikroaaltospektroskopia Relaksaatio riippuu molekyylien keskinäisten törmäyksien välisestä ajasta (~ P) Johtopäätös: - Nesteissä ja liuoksissa ei MWspektriä voi havaita - Molekyylisäteessä parempi resoluutio
10 Schrödingerin aaltoyhtälön ratkaisuja yksinkertaisissa systeemeissä (1) Vapaa elektroni V(x) = 0 d Ψ m dx = EΨ Ψ = Aeikx + Be ikx ;E = k m Ψ*Ψ itsenäinen x- koordinaatista k voi saada minkä tahansa arvon Elektronin sijainti ei ole ennustettavissa Elektronin energia ei ole kvantittunut () Elektroni yksidimensionaalisessa laatikossa 0 < x < L :V(x) = 0; x 0, x L :V(x) = d Ψ m dx = EΨ Ψ = Aeikx + Be ikx ;E = k m => Kaikki ratkaisut eivät ole mahdollisia Reunaehdot: x = 0, Ψ = 0 ja x = L, Ψ = 0 => Ψ = Csinkx + Dcoskx Ψ = Csin nπ x L (n =1,,3,...) Pisteessä x = 0 ja Ψ = 0 => Ψ = C sin kx (C 0, D = 0) Pisteessä x = L ja Ψ = 0 => sin kl = 0 => kl = nπ E n = n π = n h (n =1,,3,...) ml 8mL
11 Normalisointi: Ψ = Csin nπ x L L # C sin nπ x & % (dx = C L $ L ' =1 C = L 0 Aaltofunktion kaarevuus kasvaa ja aallonpituus lyhenee, kun n kasvaa. Samalla energia kasvaa Ψ = # nπ x & sin% ( Energia kvantittunut L $ L ' (n = kvanttiluku) Huom! n > 0 => E 1 = h (nollapistenergia) 8mL - epätarkkuusperiaate - aaltofunktion kaarevuus Peräkkäisten energiatasojen välinen energiaero: ( E n+1 E n = n +1 ) h n h = 8mL ( n +1) 8mL Huom! ΔE pienenee, kun L kasvaa h 8mL Esimerkki Elektroni on lineaarisessa molekyylissä, jonka pituus on 1,0 nm. (a) Mikä on elektronin minimienergia? (b) Mikä on viritysenergia perustilalta 1. viritetylle tilalle?
12 Todennäköisyystiheys: Ψ * Ψ = Ψ = % $ 'sin nπ x % $ ' # L & # L & ψ Kun n kasvaa, todennäköisyys elektronin sijainnille laatikossa 0 < x < L tasoittuu. Vastaavuusperiaate: ψ Kvanttimekaniikka yhdistyy klassiseen mekaniikkaan korkeilla kvanttiluvuilla. Esimerkki Laske todennäköisyys, millä 10.0 nm pitkässä laatikossa perustilassa oleva hiukkanen sijaitsee (a) välillä 4,95 nm < x < 5,05 nm, (b) välillä 1,95 nm < x <,05 nm, (c) välillä 9,90 < x < 10,00 nm, (d) laatikon keskimmäisessä kolmanneksessa.
13 Ortogonaalisuus: Ψ n' * Ψ n dτ = 0 Esimerkki n = 1 Ψ 1 = L sin π x % $ ' # L & n = 3 Ψ 3 = 3π x % sin$ ' L # L & L 0 Ψ 1 * Ψ 3 dτ = % $ ' # L & L 0 sin π x % $ 'sin 3π x % $ 'dx = 0 # L & # L & (3) Elektroni kaksidimensionaalisessa laatikossa V(x, y) = 0 $ Ψ & m % x + Ψ y ' ) = EΨ ( Muuttujien erottaminen: Ψ = X(x)Y (y) d X m dx = E xx d Y m dy = E yy E = E x + E y
14 ! X n1 = sin n 1π x $ # & L 1 L 1 %! Y n = sin n π y $ # & L % Ψ n1.n = X n1 Y n L Ψ n1,n = sin n 1π x % $ 'sin n π y % $ ' 0 x L 1 ;0 y L L 1 L # & # & L 1 E n1,n = n 1 L + n % $ ' h # 1 L & 8m L ( ) Esimerkki Hiukkanen kaksi-dimensionaalisella pinnalla n 1 = n = n 1 = n = 1 n 1 = 1 n = (3) Elektroni kolmidimensionaalisessa laatikossa 8 % Ψ n1,n,n (x, y, z) = $ ' # L 1 L L 3 & 1/ sin n 1π x % $ 'sin n π y % $ 'sin n3π z % $ ' # & # L & # L3 & E n1,n,n 3 = n 1 L + n 1 L + n % 3 $ ' h # L 3 & 8m (0 x L ;0 y L ;0 z L ) 1 3 L 1 n 1 = 1 n = 1 (3) Degeneraatio Kaksiulotteinen tapaus, jossa L 1 = L = L Ψ n1,n = sin n 1π x sin n π y L L L ( ) E n1,n = n 1 + n h 8mL Esimerkki Tapaus 1: n 1 = 1, n = Ψ 1, = % $ 'sin π x % $ 'sin π y % $ ' # L & # L & # L & E 1, = 5h 8mL Tapaus : n 1 =, n = 1 Ψ 1, = % $ 'sin π x % $ 'sin π y % $ ' # L & # L & # L & E 1, = 5h 8mL
15 Tunneli-ilmiö Tunneli-ilmiöllä ymmärretään hiukkasen läpäisyä klassisen mekaniikan mukaista kiellettyä aluetta joko kokonaan tai osittain. Läpäisyn todennäköisyys: x < 0 : Ψ = Ae ikx + Be ikx k = me k 0 x L : m Ψ = Ce κ x + De κ x κ = d Ψ +VΨ = EΨ (E < V ) dx m( V E) 0 L L > x : Ψ=A'e ikx + B'e ikx (Olkoon B' = 0) ( ) % ' T= 1+ eκl e κl & 16ε ( 1 ε (' ) ) ' * +' 1 0 L Scanning tunneling microscope: Pt, Rh, W e - Sähkövirta riippuu neulan kärjen ja tarkasteltavan pinnan välisestä etäisyydestä: - Sähkövirta-moodi - Vakioetäisyys-moodi Cs-atomeja seostettu GaAs:n pinnalle
16 Esimerkki Vetysidokset 8-hydroxyquiliinissa (8-hq) Science 013 DOI:10.116/science.14603
Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa
 Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Kvanttimekaniikan perusteet
 Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aineaaltokenttä ja todennäköisyystiheys
Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aineaaltokenttä ja todennäköisyystiheys
Aikariippuva Schrödingerin yhtälö
 Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
5.10. HIUKKANEN POTENTIAALIKUOPASSA
 5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
Aineaaltodynamiikkaa
 Aineaaltodynamiikkaa Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit = kuinka hiukkasen fysikaaliset
Aineaaltodynamiikkaa Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit = kuinka hiukkasen fysikaaliset
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
 Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Sidotut tilat. Yliopistonlehtori, TkT Sami Kujala. Kevät Harris luku 5. Mikro- ja nanotekniikan laitos
 Sidotut tilat Harris luku 5 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Johdanto Tähän asti tutkittu aineaaltojen ominaisuuksia Seuraavaksi ryhdytään käyttämään aineaaltoja
Sidotut tilat Harris luku 5 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Johdanto Tähän asti tutkittu aineaaltojen ominaisuuksia Seuraavaksi ryhdytään käyttämään aineaaltoja
Korkeammat derivaatat
 Korkeammat derivaatat Jo kerran derivoitu funk6o voidaan derivoida uudelleen. d! df(x) $ dx " # dx % & = d2 f(x) = f''(x) = f (2) (x) dx 2 Yleisemmin merkitään: d n f(x) dx n = f (n) (x) Esimerkki: 2-
Korkeammat derivaatat Jo kerran derivoitu funk6o voidaan derivoida uudelleen. d! df(x) $ dx " # dx % & = d2 f(x) = f''(x) = f (2) (x) dx 2 Yleisemmin merkitään: d n f(x) dx n = f (n) (x) Esimerkki: 2-
Luku 8: Kvanttimekaniikan soveltaminen eri liiketyyppeihin:
 Luku 8: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Vibraatio eli värähdysliike Rotaatio eli pyörimisliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Luku 8: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Vibraatio eli värähdysliike Rotaatio eli pyörimisliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin:
 Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Rotaatio eli pyörimisliike Vibraatio eli värähdysliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Rotaatio eli pyörimisliike Vibraatio eli värähdysliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Osallistumislomakkeen viimeinen palautuspäivä on maanantai
 Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Tilat ja observaabelit
 Tilat ja observaabelit Maksimaalinen informaatio systeemistä tietyllä ajanhetkellä sisältyy tilaan ψ (ket). Tila = vektori Hilbertin avaruudessa sisätulo ψ ψ C ψ c 1 ψ 1 + c 2 ψ 2 = c 1 ψ ψ 1 + c 2 ψ ψ
Tilat ja observaabelit Maksimaalinen informaatio systeemistä tietyllä ajanhetkellä sisältyy tilaan ψ (ket). Tila = vektori Hilbertin avaruudessa sisätulo ψ ψ C ψ c 1 ψ 1 + c 2 ψ 2 = c 1 ψ ψ 1 + c 2 ψ ψ
1240eV nm. 410nm. Kun kappaleet saatetaan kontaktiin jännite-ero on yhtä suuri kuin työfunktioiden erotus ΔV =
 S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
Korkeammat derivaatat
 Korkeammat derivaatat Jo kerran derivoitu funk1o voidaan derivoida uudelleen. d df(x) dx dx = d2 f(x) dx 2 = f''(x) = f 2 (x) Yleisemmin merkitään: d n f(x) dx n = f n (x) Esimerkki: 2 atominen molekyyli
Korkeammat derivaatat Jo kerran derivoitu funk1o voidaan derivoida uudelleen. d df(x) dx dx = d2 f(x) dx 2 = f''(x) = f 2 (x) Yleisemmin merkitään: d n f(x) dx n = f n (x) Esimerkki: 2 atominen molekyyli
Kvanttifysiikan perusteet, harjoitus 5
 Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
ψ(x) = A cos(kx) + B sin(kx). (2) k = nπ a. (3) E = n 2 π2 2 2ma 2 n2 E 0. (4)
 76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
780392A/782631S Fysikaalinen kemia II, 5 op / 4 op
 78392A/782631S Fysikaalinen kemia II, 5 op / 4 op Luennot: 5.9.-15.11.216 Ma klo 8-1 PR12 Ti klo 12-14 PR12 Risto Laitinen (22.2.-14.3.) Epäorgaanisen kemian tutkimusyksikkö (KE 313) PL 3 914 Oulun yliopisto
78392A/782631S Fysikaalinen kemia II, 5 op / 4 op Luennot: 5.9.-15.11.216 Ma klo 8-1 PR12 Ti klo 12-14 PR12 Risto Laitinen (22.2.-14.3.) Epäorgaanisen kemian tutkimusyksikkö (KE 313) PL 3 914 Oulun yliopisto
Korkeammat derivaatat
 Korkeammat derivaatat Jo kerran derivoitu funk1o voidaan derivoida uudelleen. d dx! " # df(x) dx $ % & = d2 f(x) = f''(x) = f (2) (x) dx 2 Yleisemmin merkitään: d n f(x) dx n = f (n) (x) Esimerkki: 2-
Korkeammat derivaatat Jo kerran derivoitu funk1o voidaan derivoida uudelleen. d dx! " # df(x) dx $ % & = d2 f(x) = f''(x) = f (2) (x) dx 2 Yleisemmin merkitään: d n f(x) dx n = f (n) (x) Esimerkki: 2-
Nyt n = 1. Tästä ratkaistaan kuopan leveys L ja saadaan sijoittamalla elektronin massa ja vakiot
 S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
1 Aaltofunktio, todennäköisyystulkinta ja normitus
 KEMA5 syksy 16 Kertausta keskeisistä asioista 1 Aaltofunktio, todennäköisyystulkinta ja normitus Kvanttimekaniikassa tarkasteltavaa systeemiä kuvaa aaltofunktio ψ. Aaltofunktio on puhtaan matemaattinen
KEMA5 syksy 16 Kertausta keskeisistä asioista 1 Aaltofunktio, todennäköisyystulkinta ja normitus Kvanttimekaniikassa tarkasteltavaa systeemiä kuvaa aaltofunktio ψ. Aaltofunktio on puhtaan matemaattinen
Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2011
 Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2011 Luennot: Henrik Kunttu, Nanoscience Center, huone YN213; puh: 050-5996134; henrik.m.kunttu@jyu.fi Laskuharjoitukset: Lauri Nykänen; lauri.j.a.nykanen@.jyu.fi
Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2011 Luennot: Henrik Kunttu, Nanoscience Center, huone YN213; puh: 050-5996134; henrik.m.kunttu@jyu.fi Laskuharjoitukset: Lauri Nykänen; lauri.j.a.nykanen@.jyu.fi
1. (a) (2p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori
 FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
766326A Atomifysiikka 1 - Syksy 2013
 766326A Atomifysiikka 1 - Syksy 2013 Luennot n. 46 tuntia Torstaisin 8-10 sali IT116 Perjantaisin 8-10 sali L6 Poikkeuksia: to 19.9. luento vain 8-9 to 17.10. luento vain 8-9 to 14.11. luento vain 8-9
766326A Atomifysiikka 1 - Syksy 2013 Luennot n. 46 tuntia Torstaisin 8-10 sali IT116 Perjantaisin 8-10 sali L6 Poikkeuksia: to 19.9. luento vain 8-9 to 17.10. luento vain 8-9 to 14.11. luento vain 8-9
Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2016
 Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2016 Luennot: Henrik Kunttu, Nanoscience Center, huone YN213; puh: 050-5996134; henrik.m.kunttu@jyu.fi Vastaanotto torstaisin klo 13-15 Laskuharjoitukset: FM
Fysikaalinen kemia 2 (KEMA225, 4 op) syksy 2016 Luennot: Henrik Kunttu, Nanoscience Center, huone YN213; puh: 050-5996134; henrik.m.kunttu@jyu.fi Vastaanotto torstaisin klo 13-15 Laskuharjoitukset: FM
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S Fysiikka III (EST) Tentti ja välikoeuusinta
 S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
J 2 = J 2 x + J 2 y + J 2 z.
 FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
S Fysiikka III (EST) (6 op) 1. välikoe
 S-114.1327 Fysiikka III (EST) (6 op) 1. välikoe 1.3.21 Ilkka Tittonen 1. Vastaa seuraaviin kysymyksiin perustellusti, mutta ytimekkäästi (esim. 5-1 lausetta) (2p per kohta). a) Mikä on sidottu tila? Anna
S-114.1327 Fysiikka III (EST) (6 op) 1. välikoe 1.3.21 Ilkka Tittonen 1. Vastaa seuraaviin kysymyksiin perustellusti, mutta ytimekkäästi (esim. 5-1 lausetta) (2p per kohta). a) Mikä on sidottu tila? Anna
pääkiertoakseli #$%%ä 2C 2 C 2!"
 Tehtävä 1 Määritä seuraavien molekyylien pisteryhmät: (a) H 3 N H 3 N l o l NH 3 + NH 3 urataan lohkokaaviota: lineaari!"!" suuri symmetria 2s v #$%%ä 2v!" pääkiertoakseli #$%%ä 2 2 2!" s h Vastaavasti:
Tehtävä 1 Määritä seuraavien molekyylien pisteryhmät: (a) H 3 N H 3 N l o l NH 3 + NH 3 urataan lohkokaaviota: lineaari!"!" suuri symmetria 2s v #$%%ä 2v!" pääkiertoakseli #$%%ä 2 2 2!" s h Vastaavasti:
(1) (2) Normalisointiehdoksi saadaan nytkin yhtälö (2). Ratkaisemalla (2)+(3) saamme
 S-446 Fysiikka IV (Sf) Tentti 3934 Oletetaan, että φ ja φ ovat ajasta riippumattoman Scrödingerin yhtälön samaan ominaisarvoon E liittyviä ominaisfunktioita Nämä funktiot ovat normitettuja, mutta eivät
S-446 Fysiikka IV (Sf) Tentti 3934 Oletetaan, että φ ja φ ovat ajasta riippumattoman Scrödingerin yhtälön samaan ominaisarvoon E liittyviä ominaisfunktioita Nämä funktiot ovat normitettuja, mutta eivät
Esimerkki: 2- atominen molekyyli. Korkeammat derivaatat 1/24/13. Jo kerran derivoitu funk6o voidaan derivoida uudelleen. Yleisemmin merkitään:
 Korkeammat erivaatat Jo kerran erivoitu funk6o voiaan erivoia uuelleen.! f(x) x " # x % & = 2 f(x) = f''(x) = f (2) (x) x 2 Yleisemmin merkitään: n f(x) = f (n) (x) x n erkki: 2- atominen molekyyli Värähtelevän
Korkeammat erivaatat Jo kerran erivoitu funk6o voiaan erivoia uuelleen.! f(x) x " # x % & = 2 f(x) = f''(x) = f (2) (x) x 2 Yleisemmin merkitään: n f(x) = f (n) (x) x n erkki: 2- atominen molekyyli Värähtelevän
Kvanttimekaniikan perusteet
 Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aaltofunktio ja todennäköisyystiheys
Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aaltofunktio ja todennäköisyystiheys
Ch7 Kvanttimekaniikan alkeita. Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset.
 Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
FYSA2031 Potentiaalikuoppa
 FYSA2031 Potentiaalikuoppa Työselostus Laura Laulumaa JYFL YK216 laura.e.laulumaa@student.jyu.fi 16.10-2.11. 2017 Ohjaus Työn ja ohjelman esittely ( 30 min) Harjoitellaan ohjelman käyttöä Harmoninen potentiaali
FYSA2031 Potentiaalikuoppa Työselostus Laura Laulumaa JYFL YK216 laura.e.laulumaa@student.jyu.fi 16.10-2.11. 2017 Ohjaus Työn ja ohjelman esittely ( 30 min) Harjoitellaan ohjelman käyttöä Harmoninen potentiaali
ja KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
FYSA234 Potentiaalikuoppa, selkkarityö
 FYSA234 Potentiaalikuoppa, selkkarityö Jari Partanen, Jani Komppula JYFL FL246, S118 japapepa@jyu.fi, jani.komppula@jyu.fi 16. lokakuuta 2013 Ohjaus Työn ja ohjelman esittely (15-30 min) Harjoitellaan
FYSA234 Potentiaalikuoppa, selkkarityö Jari Partanen, Jani Komppula JYFL FL246, S118 japapepa@jyu.fi, jani.komppula@jyu.fi 16. lokakuuta 2013 Ohjaus Työn ja ohjelman esittely (15-30 min) Harjoitellaan
FYSA234 Potentiaalikuoppa, selkkarityö
 FYSA234 Potentiaalikuoppa, selkkarityö Jari Partanen, Jani Komppula JYFL FL246, S118 japapepa@jyu.fi, jani.komppula@jyu.fi 13. lokakuuta 2014 Ohjaus Työn ja ohjelman esittely (15-30 min) Harjoitellaan
FYSA234 Potentiaalikuoppa, selkkarityö Jari Partanen, Jani Komppula JYFL FL246, S118 japapepa@jyu.fi, jani.komppula@jyu.fi 13. lokakuuta 2014 Ohjaus Työn ja ohjelman esittely (15-30 min) Harjoitellaan
KVANTTIMEKANIIKAN PERUSTEET...57
 KVANTTIMEKANIIKAN PERUSTEET...57.1 Johdanto... 57. Aaltofunktio ja todennäköisyystiheys... 58.3 Schrödingerin yhtälö... 61.3.1 Vapaan hiukkasen aaltofunktio... 6.4 Hiukkasen sironta potentiaaliaskeleesta...
KVANTTIMEKANIIKAN PERUSTEET...57.1 Johdanto... 57. Aaltofunktio ja todennäköisyystiheys... 58.3 Schrödingerin yhtälö... 61.3.1 Vapaan hiukkasen aaltofunktio... 6.4 Hiukkasen sironta potentiaaliaskeleesta...
Todennäköisyys ja epämääräisyysperiaate
 Todennäköisyys ja epämääräisyysperiaate Luento 7 Hiukkas-aaltodualismi vaatii uudenlaisen kielenkäytön omaksumista kuvaamaan iukkasten liikettä ja paikkaa. Newtonin mekaniikassa iukkanen on aina jossain
Todennäköisyys ja epämääräisyysperiaate Luento 7 Hiukkas-aaltodualismi vaatii uudenlaisen kielenkäytön omaksumista kuvaamaan iukkasten liikettä ja paikkaa. Newtonin mekaniikassa iukkanen on aina jossain
3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE
 3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE 3.1. DE BROGLIE AALLOT 1905: Aaltojen hiukkasominaisuudet 1924: Hiukkasten aalto-ominaisuudet: de Broglien hypoteesi Liikkuvat hiukkaset käyttäytyvät aaltojen
3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE 3.1. DE BROGLIE AALLOT 1905: Aaltojen hiukkasominaisuudet 1924: Hiukkasten aalto-ominaisuudet: de Broglien hypoteesi Liikkuvat hiukkaset käyttäytyvät aaltojen
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
kolminkertaisesti tehtäviä tavallisiin harjoituksiin verrattuna, voi sen kokonaan tekemällä saada suunnilleen kolmen tavallisen harjoituksen edestä
 Matematiikkaa kemisteille, kevät 2013 Ylimääräisiä laskuharjoituksia Tällä laskuharjoituksella voi korottaa laskuharjoituspisteitään, mikäli niitä ei ole riittävästi kurssin läpäisemiseen, tai vaihtoehtoisesti
Matematiikkaa kemisteille, kevät 2013 Ylimääräisiä laskuharjoituksia Tällä laskuharjoituksella voi korottaa laskuharjoituspisteitään, mikäli niitä ei ole riittävästi kurssin läpäisemiseen, tai vaihtoehtoisesti
Vapaat tilat. Yliopistonlehtori, TkT Sami Kujala. Kevät Harris luku 6. Mikro- ja nanotekniikan laitos
 Vapaat tilat Harris luku 6 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Potentiaaliaskel Potentiaalivalli ja tunneloituminen Aaltopaketti ja aineaallon eteneminen Potentiaaliaskel
Vapaat tilat Harris luku 6 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Potentiaaliaskel Potentiaalivalli ja tunneloituminen Aaltopaketti ja aineaallon eteneminen Potentiaaliaskel
Johdantoa. 0.1 Mustan kappaleen säteily. Musta kappale (black body): Kvanttimekaniikka. Wienin siirtymälaki jakautuman maksimille on
 MNQT, sl 2015 1 MNQT, sl 2015 2 Johdantoa Kvanttimekaniikka tarvittiin selittämään uusia kokeellisia havaintoja korvaa Newtonin yhtälön Schrödingerin yhtälöllä, joka on tavallaan pienten hiukkasten "liikeyhtälö"
MNQT, sl 2015 1 MNQT, sl 2015 2 Johdantoa Kvanttimekaniikka tarvittiin selittämään uusia kokeellisia havaintoja korvaa Newtonin yhtälön Schrödingerin yhtälöllä, joka on tavallaan pienten hiukkasten "liikeyhtälö"
Aineen aaltoluonne. Yliopistonlehtori, TkT Sami Kujala. Kevät Harris luku 4. Mikro- ja nanotekniikan laitos
 Aineen aaltoluonne Harris luku 4 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Aineaallot Heisenbergin epätarkkuusperiaate Fourier-muunnos ja epätarkkuusperiaate Aineaaltojen
Aineen aaltoluonne Harris luku 4 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Aineaallot Heisenbergin epätarkkuusperiaate Fourier-muunnos ja epätarkkuusperiaate Aineaaltojen
Kvanttimekaniikka: Luento 2. Mar$kainen Jani- Petri
 Kvanttimekaniikka: Luento 2 Mar$kainen Jani- Petri Assarointimainos Fyssa tarvitsee assareita Noin 30 euroa tun$+ lisiä tyypillises$ n. 4h/viikko, muba voi olla enemmän/vähemmän Opintosuoritukset+ lyhyt
Kvanttimekaniikka: Luento 2 Mar$kainen Jani- Petri Assarointimainos Fyssa tarvitsee assareita Noin 30 euroa tun$+ lisiä tyypillises$ n. 4h/viikko, muba voi olla enemmän/vähemmän Opintosuoritukset+ lyhyt
Tfy Fysiikka IIB Mallivastaukset
 Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria
 Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Shrödingerin yhtälön johto
 Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Kvanttimekaniikkaa yhdessä ulottuvuudessa
 Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
766334A Ydin- ja hiukkasfysiikka
 1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
Matematiikkaa kemisteille, kevät 2012 Ylimääräinen laskuharjoitus Palautus 7.5. klo (suositellaan kuitenkin tekemään ennen välikoetta 30.4!
 Matematiikkaa kemisteille, kevät 2012 Ylimääräinen laskuharjoitus Palautus 7.5. klo 16.00 (suositellaan kuitenkin tekemään ennen välikoetta 30.4! Tämä laskuharjoitus ei ole pakollinen, eikä sen pisteitä
Matematiikkaa kemisteille, kevät 2012 Ylimääräinen laskuharjoitus Palautus 7.5. klo 16.00 (suositellaan kuitenkin tekemään ennen välikoetta 30.4! Tämä laskuharjoitus ei ole pakollinen, eikä sen pisteitä
Luku 13: Elektronispektroskopia. 2-atomiset molekyylit moniatomiset molekyylit Fluoresenssi ja fosforesenssi
 Luku 13: Elektronispektroskopia 2-atomiset molekyylit moniatomiset molekyylit Fluoresenssi ja fosforesenssi 1 2-atomisen molekyylin elektronitilan termisymbolia muodostettaessa tärkeä ominaisuus on elektronien
Luku 13: Elektronispektroskopia 2-atomiset molekyylit moniatomiset molekyylit Fluoresenssi ja fosforesenssi 1 2-atomisen molekyylin elektronitilan termisymbolia muodostettaessa tärkeä ominaisuus on elektronien
Kvantittuminen. E = hf f on säteilyn taajuus h on Planckin vakio h = 6, Js = 4, evs. Planckin kvanttihypoteesi
 Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Osittaisdifferentiaaliyhtälöt
 Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
3.6 Feynman s formulation of quantum mechanics
 3.6 Feynman s formulation of quantum mechanics Course MAT-66000: Quantum mechanics and the particles of nature Ilkka Kylänpää Tampere University of Technology 14.10.2010 Sisältö Johdattelua Klassinen action
3.6 Feynman s formulation of quantum mechanics Course MAT-66000: Quantum mechanics and the particles of nature Ilkka Kylänpää Tampere University of Technology 14.10.2010 Sisältö Johdattelua Klassinen action
Kvanttimekaniikka kolmessa ulottuvuudessa Case vetyatomi
 Kvanttimekaniikka kolmessa ulottuvuudessa Case vetyatomi Harris luku 7 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Johdanto Yleistetään viidennen luvun sidottujen tilojen
Kvanttimekaniikka kolmessa ulottuvuudessa Case vetyatomi Harris luku 7 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Johdanto Yleistetään viidennen luvun sidottujen tilojen
T R Hψ = H(r + R)ψ(r + R) = H(r)ψ(r + R) Kahden peräkkäisen translaation vaikutus ei riipu
 Elektronit periodisessa potentiaalissa Tarkastellaan täydellistä Bravais n hilan kuvaamaa kidettä. Vaikka todelliset kiinteät aineet eivät esiinnykään täydellisinä hiloina, voidaan poikkeamat periodisuudesta
Elektronit periodisessa potentiaalissa Tarkastellaan täydellistä Bravais n hilan kuvaamaa kidettä. Vaikka todelliset kiinteät aineet eivät esiinnykään täydellisinä hiloina, voidaan poikkeamat periodisuudesta
Fysikaalinen kemia II kaavakokoelma, osa 1
 Fysikaalinen kemia II kaavakokoelma, osa 1 Wienin siirtymälaki: T λ max = 0.2898 cm K (1) Stefan Boltzmanin laki: M = σt 4 σ = 5.67 10 8 W m 2 K 4 (2) Planckin jakauma ρ = 8πkT λ 4 ( 1 ) e hc/λkt 1 (3)
Fysikaalinen kemia II kaavakokoelma, osa 1 Wienin siirtymälaki: T λ max = 0.2898 cm K (1) Stefan Boltzmanin laki: M = σt 4 σ = 5.67 10 8 W m 2 K 4 (2) Planckin jakauma ρ = 8πkT λ 4 ( 1 ) e hc/λkt 1 (3)
.) (b) Vertaa p :tä vastaavaa kineettistä energiaa perustilan kokonaisenergiaan. ( ) ( ) = = Ek
 S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
ELEC-A3110 Mekaniikka (5 op)
 ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Mikro- ja nanotekniikan laitos Syksy 2016 1 / 21 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Mikro- ja nanotekniikan laitos Syksy 2016 1 / 21 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
Klassisen fysiikan ja kvanttimekaniikan yhteys
 Klassise fysiika ja kvattimekaiika yhteys Scrödigeri yhtälö ei statioäärisistä tiloista muodostuvie aaltopakettie aikakäyttäytymie oudattaa Newtoi lakeja. Newtoi mekaiikka voidaa johtaa Schrödigeri yhtälöstä.
Klassise fysiika ja kvattimekaiika yhteys Scrödigeri yhtälö ei statioäärisistä tiloista muodostuvie aaltopakettie aikakäyttäytymie oudattaa Newtoi lakeja. Newtoi mekaiikka voidaa johtaa Schrödigeri yhtälöstä.
AINEAALTODYNAMIIKKA...105
 AINEAALTODYNAMIIKKA...105 3.1 Aikariippuva Schrödingerin yhtälö... 105 3.1.1 Stationääriset tilat... 108 3.1.. Ei-stationääriset tilat... 109 3.1.3 Aaltofunktioon liittyvä todennäköisyysvirta... 113 3.1.4
AINEAALTODYNAMIIKKA...105 3.1 Aikariippuva Schrödingerin yhtälö... 105 3.1.1 Stationääriset tilat... 108 3.1.. Ei-stationääriset tilat... 109 3.1.3 Aaltofunktioon liittyvä todennäköisyysvirta... 113 3.1.4
Voima ja potentiaalienergia II Energian kvantittuminen
 Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Analyysi 1. Harjoituksia lukuihin 1 3 / Syksy Osoita täsmällisesti perustellen, että joukko A = x 4 ei ole ylhäältä rajoitettu.
 Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina
 Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Kahden suoran leikkauspiste ja välinen kulma (suoraparvia)
 Kahden suoran leikkauspiste ja välinen kulma (suoraparvia) Piste x 0, y 0 on suoralla, jos sen koordinaatit toteuttavat suoran yhtälön. Esimerkki Olkoon suora 2x + y + 8 = 0 y = 2x 8. Piste 5,2 ei ole
Kahden suoran leikkauspiste ja välinen kulma (suoraparvia) Piste x 0, y 0 on suoralla, jos sen koordinaatit toteuttavat suoran yhtälön. Esimerkki Olkoon suora 2x + y + 8 = 0 y = 2x 8. Piste 5,2 ei ole
Jukka Tulkki 8. Laskuharjoitus (ratkaisut) Palautus torstaihin 3.4 klo 12:00 mennessä. x 2
 S 437 Fysiikka III Kevät 8 Jukka Tulkki 8 askuharjoitus (ratkaisut) Palautus torstaihin 34 klo : mennessä Assistentit: Jaakko Timonen Ville Pale Pyry Kivisaari auri Salmia (jaakkotimonen@tkkfi) (villepale@tkkfi)
S 437 Fysiikka III Kevät 8 Jukka Tulkki 8 askuharjoitus (ratkaisut) Palautus torstaihin 34 klo : mennessä Assistentit: Jaakko Timonen Ville Pale Pyry Kivisaari auri Salmia (jaakkotimonen@tkkfi) (villepale@tkkfi)
Numeeriset menetelmät TIEA381. Luento 5. Kirsi Valjus. Jyväskylän yliopisto. Luento 5 () Numeeriset menetelmät / 28
 Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
 Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Demo: Kahden elektronin spintilojen muodostaminen
 Demo: Kahden elektronin spintilojen muodostaminen Tämän demonstraation tarkoituksena on havainnollistaa kvanttimekaniikan operaattoriformalismin soveltamista kahden elektronin systeemin spintilojen muodostamiseen.
Demo: Kahden elektronin spintilojen muodostaminen Tämän demonstraation tarkoituksena on havainnollistaa kvanttimekaniikan operaattoriformalismin soveltamista kahden elektronin systeemin spintilojen muodostamiseen.
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
 6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
Luento Atomin rakenne
 Luento 10 5. Atomin rakenne Vetatomi Ulkoisten kenttien aiheuttama energiatasojen hajoaminen Zeemanin ilmiö Elektronin spin Monen elektronin atomit Röntgensäteiln spektri 1 Schrödingerin htälö kolmessa
Luento 10 5. Atomin rakenne Vetatomi Ulkoisten kenttien aiheuttama energiatasojen hajoaminen Zeemanin ilmiö Elektronin spin Monen elektronin atomit Röntgensäteiln spektri 1 Schrödingerin htälö kolmessa
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
8. MONIELEKTRONISET ATOMIT
 8. MONIELEKTRONISET ATOMIT 8.1. ELEKTRONIN SPIN Epärelativistinen kvanttimekaniikka selittää vetyatomin rakenteen melko tarkasti, mutta edelleen kokeellisissa atomien energioiden mittauksissa oli selittämättömiä
8. MONIELEKTRONISET ATOMIT 8.1. ELEKTRONIN SPIN Epärelativistinen kvanttimekaniikka selittää vetyatomin rakenteen melko tarkasti, mutta edelleen kokeellisissa atomien energioiden mittauksissa oli selittämättömiä
Kvanttidynamiikka Tarkastellaan ensin hieman bra/ket-merkintää ja vertaillaan sitä muihin merkintätapoihin.
 Kvanttidynamiikka 30.10.2010 0.1 Bra- ja Ket-merkinnöistä Tarkastellaan ensin hieman bra/ket-merkintää ja vertaillaan sitä muihin merkintätapoihin. Oletetaan, että ket ψ ja bra φ ovat alkioita, jotka liittyvät
Kvanttidynamiikka 30.10.2010 0.1 Bra- ja Ket-merkinnöistä Tarkastellaan ensin hieman bra/ket-merkintää ja vertaillaan sitä muihin merkintätapoihin. Oletetaan, että ket ψ ja bra φ ovat alkioita, jotka liittyvät
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Energian säilymislain perusteella elektronin rekyylienergia on fotnien energioiden erotus: (1)
 S-11446 Fysiikka IV (Sf), I Väliko 544 1 Osoita, ttä Comptonin sironnassa lktronin suurin mahdollinn rkyylinrgia voidaan sittää muodossa E Kin hf 1 + mc /hf Enrgian säilymislain prustlla lktronin rkyylinrgia
S-11446 Fysiikka IV (Sf), I Väliko 544 1 Osoita, ttä Comptonin sironnassa lktronin suurin mahdollinn rkyylinrgia voidaan sittää muodossa E Kin hf 1 + mc /hf Enrgian säilymislain prustlla lktronin rkyylinrgia
Luento 13: Periodinen liike. Johdanto Harmoninen värähtely Esimerkkejä F t F r
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Monissa fysiikan probleemissa vaikuttavien voimien yksityiskohtia ei tunneta
 8 LIIKEMÄÄRÄ, IMPULSSI JA TÖRMÄYKSET Monissa fysiikan probleemissa vaikuttavien voimien yksityiskohtia ei tunneta Tällöin dynamiikan peruslain F = ma käyttäminen ei ole helppoa tai edes mahdollista Newtonin
8 LIIKEMÄÄRÄ, IMPULSSI JA TÖRMÄYKSET Monissa fysiikan probleemissa vaikuttavien voimien yksityiskohtia ei tunneta Tällöin dynamiikan peruslain F = ma käyttäminen ei ole helppoa tai edes mahdollista Newtonin
6. Kompleksiluvut. Kompleksilukuja esiintyy usein polynomiyhtälöiden ratkaisuina. Esim:
 6. Kompleksiluvut Yhtälöllä x = 1 ei ole reaalilukuratkaisua: tarvitaan uusia lukuja. Kompleksiluku on kahden reaaliluvun järjesteby "pari" (x,y): Z = x +iy Missä i on imaginääriyksikkö, jolla on ominaisuus
6. Kompleksiluvut Yhtälöllä x = 1 ei ole reaalilukuratkaisua: tarvitaan uusia lukuja. Kompleksiluku on kahden reaaliluvun järjesteby "pari" (x,y): Z = x +iy Missä i on imaginääriyksikkö, jolla on ominaisuus
dx = d dψ dx ) + eikx (ik du u + 2ike e ikx u i ike ikx u + e udx
 763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 5 Kevät 2014 1. Tehtävä: Johda luetomateriaali kaavat d 2 u i k du 2 m + Uxu = E k 2 u p = k + u x i d ux. Ratkaisu: Oletetaa, että ψx = e ikx ux, missä ux +
763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 5 Kevät 2014 1. Tehtävä: Johda luetomateriaali kaavat d 2 u i k du 2 m + Uxu = E k 2 u p = k + u x i d ux. Ratkaisu: Oletetaa, että ψx = e ikx ux, missä ux +
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
MEI Kontinuumimekaniikka
 MEI-55300 Kontinuumimekaniikka 1 MEI-55300 Kontinuumimekaniikka 3. harjoitus matemaattiset peruskäsitteet, kinematiikkaa Ratkaisut T 1: Olkoon x 1, x 2, x 3 (tai x, y, z) suorakulmainen karteesinen koordinaatisto
MEI-55300 Kontinuumimekaniikka 1 MEI-55300 Kontinuumimekaniikka 3. harjoitus matemaattiset peruskäsitteet, kinematiikkaa Ratkaisut T 1: Olkoon x 1, x 2, x 3 (tai x, y, z) suorakulmainen karteesinen koordinaatisto
Luento 10: Työ, energia ja teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
Aatofunktiot ja epätarkkuus
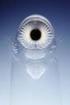 Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
kertausta Boltzmannin jakauma infoa Ideaalikaasu kertausta Maxwellin ja Boltzmannin vauhtijakauma
 infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Fysiikka 8. Aine ja säteily
 Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause.
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Aineaaltodynamiikka. Aikariippuva Schrödingerin yhtälö. Stationääriset tilat. Ei-stationääriset tilat
 Aieaaltodyamiikka Aikariiuva Scrödigeri ytälö Aieaaltoketä aikariiuvuude määrää ytälö Aieaaltokettie riiuvuus ajasta aikariiuva Scrödigeri ytälö Statioääriset ja ei-statioääriset tilat Aaltoaketit Kvattimekaiika
Aieaaltodyamiikka Aikariiuva Scrödigeri ytälö Aieaaltoketä aikariiuvuude määrää ytälö Aieaaltokettie riiuvuus ajasta aikariiuva Scrödigeri ytälö Statioääriset ja ei-statioääriset tilat Aaltoaketit Kvattimekaiika
, m s ) täytetään alimmasta energiatilasta alkaen. Alkuaineet joiden uloimmalla elektronikuorella on samat kvanttiluvut n,
 S-114.6, Fysiikka IV (EST),. VK 4.5.005, Ratkaisut 1. Selitä lyhyesti mutta mahdollisimman täsmällisesti: a) Keskimääräisen kentän malli ja itsenäisten elektronien approksimaatio. b) Monen fermionin aaltofunktion
S-114.6, Fysiikka IV (EST),. VK 4.5.005, Ratkaisut 1. Selitä lyhyesti mutta mahdollisimman täsmällisesti: a) Keskimääräisen kentän malli ja itsenäisten elektronien approksimaatio. b) Monen fermionin aaltofunktion
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
Jatko-opintoseminaari Kevyttä johdattelua kvanttimekaniikkaan: Tila-avaruus. Petteri Laakkonen
 Jatko-opintoseminaari 21-211 Kevyttä johdattelua kvanttimekaniikkaan: Tila-avaruus Petteri Laakkonen 23.9.21 Tämä teksti on tiivistelmä kirjan [1] luvun 2 tekstistä. Pyrkimyksenä on esittää perustellusti
Jatko-opintoseminaari 21-211 Kevyttä johdattelua kvanttimekaniikkaan: Tila-avaruus Petteri Laakkonen 23.9.21 Tämä teksti on tiivistelmä kirjan [1] luvun 2 tekstistä. Pyrkimyksenä on esittää perustellusti
Useita oskillaattoreita yleinen tarkastelu
 Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
