:il. c) putoamismatka 45 sekunnin aikana. c) Miten jarrutusmatka muuttuu a)-kohdan arvosta, jos nopeus 72kmlh puolittuu?
|
|
|
- Anita Seppälä
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 FYSKKA (FY4.2): 4. KURSS: Liikkeen ait våsraa KuurEEN $) rehrävään il KOE 21.1t.20L3 1. Linnun lentonopeus alussa on 64 km/h. Lintu kiihdyttää nopeuttaan tasaisesti kiihtyvyydellä 2,3 mf s2l-,8 sekunnin ajan. a) Laske linnun loppunopeus kiihdytyksen jälkeen. b) Kuinka pitkän matkan lintu kulkee kiihdytyksen aikana? c) Lintu pienentää kiihdytyksessä saavuttamaansa a)-kohdan nopeutta tasaisesti hidastuvuu della -2,4 m/s2. Kuinka kauan kuluu aikaa, kunnes lintu pysähtyy? 2. Laskuvarjohyppääjän nopeus muuttui ajan funktiona vapaan pudotuksen aikana alla olevan kuvaajan osoittamalla tavalla. Määritä kuvaajan avulla laskuvarjohyppääjän a) kiihtyvyys hetkellä t = 10 s b) kiihtyvyys hetkellä t = 30 s. c) putoamismatka 45 sekunnin aikana. ltt T,ås å{i :il 3 il* 5* 7r] Pyöräilijän nopeus 17 metriä korkean mäen päällä on 16 km/h. d, Mäen pituus on 130 m ja pyörän ja pyöräilijän kokonaismassa on 85 kg. Pyöräilijä tulee vapaasti polkematta mäkeä alas. Liikettä vastustavien \ voimien suuruus mäessä on 62 N. Laske pyöräilijän nopeuden suuruus mäen alla Auton massa on 21,000 kg ja nopeus 72km/h. Auto pysäytetään tasaisella tiellä, jossa renkaiden ja tien välinen kitkakerroin on 0,40. a) Kuinka pitkä matka vähintään tarvitaan auton pysäyttämiseksi? b) Kuinka suuri on jarrutusmatka liukkaammalla tiellä, jossa kitkakerroin on 0,20? c) Miten jarrutusmatka muuttuu a)-kohdan arvosta, jos nopeus 72kmlh puolittuu? 5. Pallo, jonka massa on 0,20 kg, osuu lattiaan nopeudella 5,4 mf sja se pomppaa ylöspäin nopeudella 5,2 m/s. a) Laske pallojen liikemäärä ennen ja jälkeen lattiaan törmäystä. b) Laske pallon liikemäärän muutos. l" f j...'.i. i'- v.,? i:.. t:.::{.;l,,t ',tir : i:ä KÄÄNNii l
2 6. Henkilöauto ja kuorma-auto törmäävät toisiinsa suoralla tiellä ja takertuvat toisiinsa kiinni. Henkilöauton massa on 1250 kg ja nopeus 85 km/h. Kuorma-auton massa on kg ja nopeus 65 km/h. a) Millä nopeudella ja mihin suuntaan autot liikkuvat toisiinsa tarttuneina hetitörmäyksen jälkeen? b) Laske autojen yhteinen liike-energia ennen törmäystä ja törmäyksen jälkeen. c) Kuinka monta prosenttia autojen yhteisestä liike-energiasta säilyy törmäyksessä? 7. Varastomies työntää lattiaa pitkin vakionopeudella laatikkoa, jonka massa on 25 kg. Laatikon ja vaa kasuoran lattian väli nen i u ku kitkakerroin on 0,18. Kappaletta liikuttavan työntävän voiman F suunta on kuvan 1 mukainen. Kuvassa 2 on esitetty laatikon voimakuvio eli laatikkoon vaikuttavat voimat. Kuva 1. Laatikon työntö. Kuva 2. Laatikon voimakuvio. F, a) b) Nimeä laatikkoon vaikuttavat voimat ja esitä laatikon liikeyhtälöt komponenttimuodossa x- ja y-suunnassa. Laske työntävän voiman F suuruus, kun laatikko liikkou vakionopeudella.
3 rli li lr FYtttKKA (rv4-t..r*riat.-rut lrl l tl q Fv RJ\r/ j,ro e illi.li ll * Å. tl- &OltJ ea! t]) -;-- 'uo +ot 61 rh J- u,,3 *. ZrG -( - '\) = 21, 7 tllt...? Ä{ ' {4,år 9',[t) r = _t_ 1i, t 64 6 r* ö m. d,1 at ---,,?;.F å å,3 ; 35,71efn,Y 36m, : A fr (rnd' F es F1 ^"lo P ev»e nj np 'k : tt"} = a uf: 11 r,?qp Y g_ 716 g+- l. AVU LLA 2t,?ta-P r n/\r?a J-- 1+'t 77,84 r s - f, P"'.r
4 &. J.tÖ llo t G ea^ F,r &rrl /= Y{. f t NTÅ'-Å ur Na ll lr-'ä = at 1) = l?rp?.= är?$ 0,5 lt O lrf 4o J* rb SQ öal /rf+ -l7,tg 36 (n + 2 l: i '-l li il i -+ ', - " - ---j
5 \i C c') l+e rk llrm Ai lc, tf-f ryvyw f^ DAl,.t N Af O P tv.f l<l Va a.l zt Rr/ *r:tftkla*t; N.t K Ur,r ra t< jl t rl &'Å '- tu l7n{ 6 Ar rl (r,, lr #,) L rt. r T,tza t = lot P t r r? RerÅ,X rv k U vtn-l ÅLd Ko,* r/rn nj ^ ry qs r' rå ö ]- raån ts ct.å kilc.ff fff f rrå, 'ltn. Jn {tss, A # \ /\J l<tthttvyy,r q (to;1 = å f1r - at =2-1r, c( c{ fl,0s) : dt) 2i fl- \)6J /{-s år t rhf{} b ***t, x å, 13 r"1 rl.!, \J4 ) $r. rt.etrå
6 !,&) a(ao'r) r,fr- \./ re. Kod^ k a Yvvrl^.r^LLe Eo t+raån ZCe c) 11 AT-lra TaAAAAN (t,u)-kyyr-ntnåå* / f lf,rod,r/å ffirjlgy4 - r-{.f/17* -4+^Y4- rr,{vrerxitv 4YYYf ry - re L*+ÅÅ; lb-uutu; il loff f4trk^a taf -5,.= fom - l<c,<}arnl.fl^ rzuvtv'tå; SAYPL \.* ot^evv"urå (r fvar-tlcf^tft): lakfl A r l<,r vxtr trå 0s * { r" futahr r-{ ^rtsa Att-.-ar"{a d^/ 5s 4f s FvrvtvtN ( A rn t* &. C /1e \) \ \J -.Jv t, g t lsoclrn = l{ f Ln.:F-ffi-_:_- t;^.rr,t4 t1.trt ^Å
7 t-, o f)= [7rn 11 = 16 knlh { =, l?or l?o fr, (l] z O'4' _l F = -69N r4r= 3 Ne &e(a pe Rt^^:.C.' t-4 trr fir-*"j f _o {- l:.' t t/v = rn ru* *f- n7h+w,-t b+ K + fnvh *VV =.'),r i_ U _,.->> 6-74-lO (1=o) $ rnu2 it. ärn.\a D.= DL = 1}=å
8 / t-r=t/*+ tlh+2w rl o (l VM % = t/\" + *Ah + 3E Yovr:n (r= _ GA^/),,.; {(#?)'* 7'?rnlf-. lynt + J' (*e en)-boy, # {tfl 1;; 12,?? el f (+t b*l h) *m,f *W T.tt hf=-.tf T'r<t W.sff, L o r. vsfr{ lcv r r Fr M Vv =.- 6å A/. 30lfn + *7h +W.= jnnte : {-n" cr... 1 D: rr"f +mah tw b^= bl* tr= + (-).1.' =» l- 7rn L( zl:yi"*ryh t: w) rn ryyltt*tl!3y rn ry [i,f 1l,E! rn +r-f rr] f#fru e rir.u z1g,n (t= e xv) s JlvG -.o
9 it * -1r",,b - 1» =,0 l M ö fr/= = rn7 tä= 7t h,,p': or ' o h a) t- Z \)-e - t4 r<a M ll t<a Fv 6M R G t AP Rl'^'t f G t-q?-q, Q --9 F; +Fr={-w= tr;+r; c:x)l?oj <^ \f^ A l< ^rv o z-a-l A f t N N +LL^ Fr lt Hvul-v [A r i.); nzu rv trr? - Fr J/ efveggt^{'eet;^/-16 {rt) ca.< f1 vooon \^r -s tri q.+ F.{ F \Ar s 4F* KtTl.avorH,^N s Alrlc6- ener W; l-i0 h*k,-q ( r> å r',?f AÅre ) T?ke rrä r> 6r zr tv /*f V vt0r.f
10 - 'r Fr,J = -+rn- s / /Gs P(nqS s /$ ob +- t 0 - å /rt å J*arav1-vrt<tYt-A n4 u-a- 'l) å o * rn bol ;/a rn3 '*1rå Ao "? /4M3 J/4 R evtvr H a l: R^ Vo DA^ Al.l d HT4 / Y Y#r T/\$r4 l rej]:.,!-t ) 4A -rtv{a N LttFFee,nl Avvtt{,' q : {s= \t+ fn $ttr" oa/ v4^ 'sto (r).,,= u, + o't (9 o: J= å r"j (E uo + ^t, år; t, r1 rytl '1r -= o =7v Al :,/4 r'l A s lj_ [r) r6ar ry
11 -r: - 1ro' q nl* +}_ 2a _ åq (o /+r/r0 tv L il lc e y,,1),{ f-ö V* a l<r t,/uf-rna.f,fa \-7=fna./ NllN A=-2 rn ttj- råh,q' yl+rå dö ru GJ_. - - _Uo... å 2- (-E_\ v m/ i,\åm *? \ s-- "1,f rn :' til -lö /u 7*/*3 { lff, J,t G,?v i-vrr P,-t \- Fa
12 f-t J^ f- trur\{ \ 3/6 -f/ L 2" Of?O-?S t# lrn x ai,7e gln,(t) ("- - - å C- raa * ra?4* å-*f.1 e E -Rr3 tr:_r -?L ö /3 i= 9.,f c,p.fo,gg6itn -f"r la»rn ) 'lro ---8, j tr, s; -=,(*å!rl-, e,r.? C --.r + '&- J A eevry F{ JOJ NOPCVJ.*L 'lnl =- 1va : * - A,/l 7 el A i- Sa,?(tt n å: /Jrn lv k,ir P l $ferr/ e {*A'fAA^// ( v Tcr rt1/u r, lil :;,;i nn "-{, *-oj^ ALt&{reeät- *&v o.f fa 5lrn
13 /T) - w 0 rfl l<le*ån rhvjlc.t 4, s ry - ft b Pallo, jonka massa on 0,20 kg, osuu lattiaan nopeudella 5,4 mls ja se pomppaa ylöspäin nopeudella 5,2 m/s. a) Laske pallon liikemäärä ennen ja jälkeen lattiaan törmäystä. b) Laske pallon liikemäärän muutos. Ratkaisu m=0,20kg, vu=5,4m s, v1= 5,2mls, a) Piirretään tilannetta havainnoilistava nen suunta alaspäin. P^=?, Pt =?.' Lp=? _+,il '1:h..,!'# r.;#ffi kuva ja valitaan positiivii. Pallon liikemäärä alussa on pu = miu,)okaskalaarimuodossa on Pu= ffivn= 0,20 kg. 5,4 * =,,0* + = t,t$ Positiivinen tulos tarkoittaa, että liikemäärä on so'nitun positiivisen suunnan suuntainen, siis alaspäin kuvassa. Pallon liikemäärä lopussa on pr = mir,)okaskalaarimuodossa on p,: m{-v1)= 0,20 kg. (-s,z!)= -1,04 kgm = -t,o kg-. SSS Negatiivinen tulos tarkoittaa, että liikemäärä lopussa on ylöspäin. Lukuarvoltaan liikemäärä on pienentynyt, koska liikemäärää on "siirtynyt" lattiaan. tr) Liikemäärän muutos on di = Pt- P^. Skalaarirnuodossa liikemäärän mtiutos on ap=h*pu Vastaus a) Pallon liikemäärä alussa on 1,1 kgm/s alaspäin ja lopussa 1,0 kgmis ylöspäin. b) Liikemäärän muutos on1,l kgm/s ylöspäin.
14 @ v r' a) ri{yr/n.b, - ö'plcf"vf,rrv,f s.rå(-lå7 yr nhoro N rör r*l.äyvl ul" *. -.<-- * M -->> fr,* tlå t*rct\ 85 r h L tt t.e,<,itå eä (/Å Å LvJ0a ft** 'la.ä = fr,\ + ma\ bi 2;000 k? 6 Fån h E luyy '. ' L oloujora ä (r,* fro) lå fn (**l) + fr*t^ G (fi, r nolu fiv roj ^/ Y flte r M e/v t{a re uj rä R,', ÅvF J e N JÅ te e.n :( /*ert ) p\: i-l = f\t f- qj + rneu.l fqr + fnl (-ot#) te- 1\ t a3oao\
15 /L( /'.{ t: Ä \ å6 f o 7 t21 w 1rt? a7? g?å3 # 4 ill s7 + kvocrrå-, vrdn fl " LFu Peei rr N \r/ v N r/^a/,gs ^vtujeev r ) e N rven/ rö,ertävc ri: / F j nn\= +- å **** tfr \\ F*, = o,s-te s-o h " (#S)i 0,. flj taah. ffi #)^ Fkl = 4a2:*7(3,317 J.* tc??sa3j tr-.= 4tt-lo6J = 4,t l"r..j *Ft e) rb' Rn,av rr fnl J Ä LEeefv LP*t E s å (m,+ fra) ^^ tr?--t Er*ÄY 3o6Y3å5J,i 3,1-106J Fr, = 3, l HJ
16 () ut-oj elv Y HrelJ e-rrrt Ll tre; pve 8* ^ G r a{ -a tå t LY y Tt; F H Ä'YF, e.fr/a F L Eg. 3 06s 3*5 J å- 0,74 SS Fp, * asz 163 J t; fr 7s '/, l*t t t - en e 6 r^{' r,t 7t l. rå lev Y f iip HÅ'Y r efcä Flvo nt q * Ko N rr^r.f^ Va t e^?v H e Rrr^ ru Yäs 1ä3 (5 * f.tfe r- ä'l N S fi L^ Artt Y rrra å o N fltr, *l + wtt\ra = (*,* t\]"u,lå = ffi,9 r* fy1* ^ fnr t" {*a \.>e,u -t&{i-?ryh'f5? lå 0h -F ff oua\
17 Ratka isu Laatikon massa on m : 25kg, jatason jalaatikon välinen liukukitkakerroin on # : 0,18. Voiman suuntavaakatasoon nähden on o : 35". a) Laatikkoon vaikuttavat voimat ovatpglq1, kitkl 4,, tukivoima t j"."tåirä *i*" F. Laatikko liikkuu vakionopeudella 7. Sijoitetaan F, ja N edelliseenyhtdlöön, jolloin saadaan Fcosc-p(Fsinc*G):3 Fcosa - Fpsina - FG :0 F(cosc-psina):Wg - pmg cos0 - lrslne Sijoitetaan tunnetut arvot yhtälöön. F_ 0, kg.9,8l cos35" - 0,i8'sin35" = 61,6629 N = 62 N F* : Fcosa Fr : Fsina Dynamiikan peruslain mukaan -= l : ma. Laatikko liikkuu vakionopeudella, joten sen kiihtyvyys on nolla ja F:F+G+N+F;:0. 0 Ratkaistaan ensin tukivoima N /-suunnan yhtälöstä N:Fr*G. Sijoitetaan F, }: Fsina * G. Koskakitkavoima{, : FN, saadaan x-suunnassa yhtåilö { - pn:0.
ääexgäl*ääääe ääg I ä*fre3 I äee iäa ää-äälgü il leääö ää; i ääs äei:ä ä+ i* äfä g u ;; + EF'Hi: 2 ä ; s i r E:;g 8ää-i iää: Ffärg',
 !P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
!P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
äiäää?l älägcläälii äisrä lää äää
 E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
3 *ä;r ä:e 5ä ä{ :i. c oo) S g+;!qg *r; Er ; l[$ E ;;iä F:ä ä :E ä: a bo. =. * gäf$iery g! Eä. a is äg*!=."fl: ä; E!, \ ins:" qgg ;._ EE üg.
 t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
NEN PAINOVOIMAMITTAUS N:o OU 10/7b
 I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
TEHTÄVIEN RATKAISUT. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 712 p m 105 kg
 TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
VOLKER BECK P. =H. o:_ie!r n^: =:l - dö5i6 = '1 arcii - a; +; s*. P <,R< qe 5 +ä a. c g-;i-(d1. ::qp io > iädaa :; 3fE,:E A. Ö!\lo: Y.
 -Tl (D 'f.g) = (,g L! (D =5.T 0) \ (:) ( P. =H ''. @ 5q 9
-Tl (D 'f.g) = (,g L! (D =5.T 0) \ (:) ( P. =H ''. @ 5q 9
Pakkauksen sisältö: Sire e ni
 S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
-lllii;i i Eiää: Iiiii:; ä;äiäeiäi
 I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
SU01\1JEL\I MAINJ[ OY
 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
F_l/ mlmz SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA. Fon. (vetovoima) mr ja lxz välinen gravitaatiovoima. kappaleiden massat ovat mr ja mz (kg)
 SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA ltl ka ppa leiden (vetovoima) m ja lxz välinen gavitaatiovoima Fon F_l/ mlmz 2 kappaleiden massat ovat m ja mz (kg) on kappaleiden keskipisteiden välinen etäisyys
SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA ltl ka ppa leiden (vetovoima) m ja lxz välinen gavitaatiovoima Fon F_l/ mlmz 2 kappaleiden massat ovat m ja mz (kg) on kappaleiden keskipisteiden välinen etäisyys
Luvun 5 laskuesimerkit
 Luvun 5 laskuesimerkit Huom: luvun 4 kohdalla luennolla ei ollut laskuesimerkkejä, vaan koko luvun 5 voi nähdä kokoelmana sovellusesimerkkejä edellisen luvun asioihin! Esimerkki 5.1 Moottori roikkuu oheisen
Luvun 5 laskuesimerkit Huom: luvun 4 kohdalla luennolla ei ollut laskuesimerkkejä, vaan koko luvun 5 voi nähdä kokoelmana sovellusesimerkkejä edellisen luvun asioihin! Esimerkki 5.1 Moottori roikkuu oheisen
Luvun 5 laskuesimerkit
 Luvun 5 laskuesimerkit Esimerkki 5.1 Moottori roikkuu oheisen kuvan mukaisessa ripustuksessa. a) Mitkä ovat kahleiden jännitykset? b) Mikä kahleista uhkaa katketa ensimmäisenä? Piirretäänpä parit vapaakappalekuvat.
Luvun 5 laskuesimerkit Esimerkki 5.1 Moottori roikkuu oheisen kuvan mukaisessa ripustuksessa. a) Mitkä ovat kahleiden jännitykset? b) Mikä kahleista uhkaa katketa ensimmäisenä? Piirretäänpä parit vapaakappalekuvat.
PUTKIKAKSOISNIPPA MUSTA
 Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
l, ; i.'s ä E.ä E o gäästaefiiä,ggäeäeää;äggtää EI ;äe E H * eaä* E E 8EP.E .e= äe eääege F EEE;säääg lee sa 8NY ExE öe äec E= : ;H ä a(ü
 ,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
+ () 4 Abä. o t-{ +J t4. -s. -r) -^.b. L,'iI. o I=={ ) ts{ A L] l--.l. l*4. op{ cta-rff" ii F{ H H. !Jrl) ..:
![+ () 4 Abä. o t-{ +J t4. -s. -r) -^.b. L,'iI. o I=={ ) ts{ A L] l--.l. l*4. op{ cta-rff ii F{ H H. !Jrl) ..: + () 4 Abä. o t-{ +J t4. -s. -r) -^.b. L,'iI. o I=={ ) ts{ A L] l--.l. l*4. op{ cta-rff ii F{ H H. !Jrl) ..:](/thumbs/104/161729100.jpg) \ H + t4 + to t{ F{ O 4, ) e) 4 Abä,.,'i M ^.b 4 r), U) A ] l.l { ) t{ ) C5 t< cff" rl) t{ A p{ H H ii F{ c l4 ä..: v \ \ \ ) ) \ R V) A ) \ g'ä$ää e;'ü ä; {3;t:Hfä F",r ri 3 äääätäää c;{r;l ä:ärugärlsä:h$
\ H + t4 + to t{ F{ O 4, ) e) 4 Abä,.,'i M ^.b 4 r), U) A ] l.l { ) t{ ) C5 t< cff" rl) t{ A p{ H H ii F{ c l4 ä..: v \ \ \ ) ) \ R V) A ) \ g'ä$ää e;'ü ä; {3;t:Hfä F",r ri 3 äääätäää c;{r;l ä:ärugärlsä:h$
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t,
 AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t, v)-koordinaatistossa ruutumenetelmällä. Tehtävä 4 (~YO-K97-1). Tekniikan
AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t, v)-koordinaatistossa ruutumenetelmällä. Tehtävä 4 (~YO-K97-1). Tekniikan
5-2. a) Valitaan suunta alas positiiviseksi. 55 N / 6,5 N 8,7 m/s = =
 TEHTÄVIEN RATKAISUT 5-1. a) A. Valitaan suunta vasemmalle positiiviseksi. Alustan suuntainen kokonaisvoima on ΣF = 19 N + 17 N -- 16 N = 0 N vasemmalle. B. Valitaan suunta oikealle positiiviseksi. Alustan
TEHTÄVIEN RATKAISUT 5-1. a) A. Valitaan suunta vasemmalle positiiviseksi. Alustan suuntainen kokonaisvoima on ΣF = 19 N + 17 N -- 16 N = 0 N vasemmalle. B. Valitaan suunta oikealle positiiviseksi. Alustan
L. Maan ia Auringon vetovoiman yhtäsuuruus
 GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
g - s Eä;t;i;s!itää# EiäErE ii:ääg Eä E *läeäfiäeräsil* E sis $ä äce:;!ääfät ;1*iEs ;tää:gi g;ää*f ;ij !äef ä:e'geä;:ä Elä tä Efiäilii: ; g E
 H!äf ä'gä;ä lä tä fäl ; $ä äc;!ääfät ;1* ;tääg ä;t;;!tää# är ääg ä *läääeräl* tä*äätäääägtätg B g - ü ;;*ä9äää g;ää*f ' g ;j ä u e *; t t ;; t ü t p ä; u ä; e r * g t g U ).l t r A ä O.* 6) l- C ) t n
H!äf ä'gä;ä lä tä fäl ; $ä äc;!ääfät ;1* ;tääg ä;t;;!tää# är ääg ä *läääeräl* tä*äätäääägtätg B g - ü ;;*ä9äää g;ää*f ' g ;j ä u e *; t t ;; t ü t p ä; u ä; e r * g t g U ).l t r A ä O.* 6) l- C ) t n
FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!!
 FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!! 1. Vastaa, ovatko seuraavat väittämät oikein vai väärin. Perustelua ei tarvitse kirjoittaa. a) Atomi ei voi lähettää
FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!! 1. Vastaa, ovatko seuraavat väittämät oikein vai väärin. Perustelua ei tarvitse kirjoittaa. a) Atomi ei voi lähettää
Eo C)sl. oarl. d to E= J. o-= o cy) =uo. f,e. ic v. .o6. .9o. äji. :ir. ijo 96. {c o o. ';i _o. :fe. C=?i. t-l +) (- c rt, u0 C.
 C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
w%i rf* meccanoindex.co.uk
 &, w% r* lr,ryd* kro g ; - C +gä!! r -. ä.;'! dg+s Zt t0, y < 9 -! 8 tü;r" lun.'-y; ',ä lrl;!tä u l - 9 9! - ä 6 ^ 9 b - q - cz * ; *'a! a = ;6 f
&, w% r* lr,ryd* kro g ; - C +gä!! r -. ä.;'! dg+s Zt t0, y < 9 -! 8 tü;r" lun.'-y; ',ä lrl;!tä u l - 9 9! - ä 6 ^ 9 b - q - cz * ; *'a! a = ;6 f
1, MITÄ TARKOITETAAN SEURAAVILLA TERMEILLÄ:
 KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
ä 3 lr;+fä3fää äää+ r
 h. /] fr ff J { 1) -* {s ;; '*J 0 K F * 4 EP f' J d {.l E *e}' -{ ä'r) * fü PE }} ä g {fr ff EW g) f< Q-O -r -l ^= F{ $ $ ä- $FF flü +ä# äf $ E& =4 äh $ F. g ääü f se L ü,,8 g gr- ä äe HSs 9 5 ;n; g Fß;
h. /] fr ff J { 1) -* {s ;; '*J 0 K F * 4 EP f' J d {.l E *e}' -{ ä'r) * fü PE }} ä g {fr ff EW g) f< Q-O -r -l ^= F{ $ $ ä- $FF flü +ä# äf $ E& =4 äh $ F. g ääü f se L ü,,8 g gr- ä äe HSs 9 5 ;n; g Fß;
VUOROVAIKUTUS JA VOIMA
 VUOROVAIKUTUS JA VOIMA Isaac Newton 1642-1727 Voiman tunnus: F Voiman yksikkö: 1 N (newton) = 1 kgm/s 2 Vuorovaikutus=> Voima Miten Maa ja Kuu vaikuttavat toisiinsa? Pesäpallon ja Maan välinen gravitaatiovuorovaikutus
VUOROVAIKUTUS JA VOIMA Isaac Newton 1642-1727 Voiman tunnus: F Voiman yksikkö: 1 N (newton) = 1 kgm/s 2 Vuorovaikutus=> Voima Miten Maa ja Kuu vaikuttavat toisiinsa? Pesäpallon ja Maan välinen gravitaatiovuorovaikutus
Fysiikan perusteet. Voimat ja kiihtyvyys. Antti Haarto
 Fysiikan perusteet Voimat ja kiihtyvyys Antti Haarto.05.01 Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure
Fysiikan perusteet Voimat ja kiihtyvyys Antti Haarto.05.01 Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure
RIIHIMÄEN MELUSELVITYS 2008
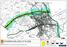 S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh
S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Vedetään kiekkoa erisuuruisilla voimilla! havaitaan kiekon saaman kiihtyvyyden olevan suoraan verrannollinen käytetyn voiman suuruuteen
 4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
Arvio metsd maa n a rvosta
 Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
6. KOKOUKSEN LAILLISUUSEN JA PÄÄTÖSVALTAISUUDEN TOTEAMINEN
 (3) PÖYTÄKIRJA 5..203 SÄÄNTÖMÄÄRÄISEN SYYSKOKOUKSEN PÖYTÄKIRJA Aika Paikka 5..203 klo 9.20 alkaen Ideapark, Kokoustila Kotka. Lempäälä Läsnä Osallistujalista liitteenä (liite ). KOKOUKSEN AVAUS TaLVIn
(3) PÖYTÄKIRJA 5..203 SÄÄNTÖMÄÄRÄISEN SYYSKOKOUKSEN PÖYTÄKIRJA Aika Paikka 5..203 klo 9.20 alkaen Ideapark, Kokoustila Kotka. Lempäälä Läsnä Osallistujalista liitteenä (liite ). KOKOUKSEN AVAUS TaLVIn
1i; i S;Ji'l i. ?::Z+i?; i i räf. i:ä;äi +;la=;iilsi*t li +t ' ?1*1i+;s iii:e: riile s:: : ri;-r2=" ii1js:?i_?7-i17;i i
 ,.24 1,? V ) J.,, q " < ^ ; > ). p. Ä I +, 1. ) d. + 1 \ d ; t l r Y ^ L j. 1 > \ 7. r 7 5 r r E,^.. l, 2 9 ; r t 9 j J l 2 1 ; Y,7, ) r 4.. ; G / ) ^ ^ ^ 7 ^ t. r P l t L ) 2 4 P? D 9 ; F I*, 1.. ) /
,.24 1,? V ) J.,, q " < ^ ; > ). p. Ä I +, 1. ) d. + 1 \ d ; t l r Y ^ L j. 1 > \ 7. r 7 5 r r E,^.. l, 2 9 ; r t 9 j J l 2 1 ; Y,7, ) r 4.. ; G / ) ^ ^ ^ 7 ^ t. r P l t L ) 2 4 P? D 9 ; F I*, 1.. ) /
Fysiikka 1. Dynamiikka. Voima tunnus = Liike ja sen muutosten selittäminen Physics. [F] = 1N (newton)
![Fysiikka 1. Dynamiikka. Voima tunnus = Liike ja sen muutosten selittäminen Physics. [F] = 1N (newton) Fysiikka 1. Dynamiikka. Voima tunnus = Liike ja sen muutosten selittäminen Physics. [F] = 1N (newton)](/thumbs/91/107282868.jpg) Dynamiikka Liike ja sen muutosten selittäminen Miksi esineet liikkuvat? Physics Miksi paikallaan oleva 1 esine lähtee liikkeelle? Miksi liikkuva esine hidastaa ja pysähtyy? Dynamiikka käsittelee liiketilan
Dynamiikka Liike ja sen muutosten selittäminen Miksi esineet liikkuvat? Physics Miksi paikallaan oleva 1 esine lähtee liikkeelle? Miksi liikkuva esine hidastaa ja pysähtyy? Dynamiikka käsittelee liiketilan
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 1.6.2005, malliratkaisut.
 1 Kuvaan 1 on piiretty kahden suoraviivaisesti samaan suuntaan liikkuvan auton ja B nopeudet ajan funktiona. utot ovat rinnakkain ajanhetkellä t = 0 s. a) Kuvaile auton liikettä ajan funktiona. Kumpi autoista
1 Kuvaan 1 on piiretty kahden suoraviivaisesti samaan suuntaan liikkuvan auton ja B nopeudet ajan funktiona. utot ovat rinnakkain ajanhetkellä t = 0 s. a) Kuvaile auton liikettä ajan funktiona. Kumpi autoista
v = Δs 12,5 km 5,0 km Δt 1,0 h 0,2 h 0,8 h = 9,375 km h 9 km h kaava 1p, matkanmuutos 1p, ajanmuutos 1p, sijoitus 1p, vastaus ja tarkkuus 1p
 2. Pyöräilijä lähti Pietarsaaresta kohti Kokkolaa, jonne on matkaa 33 km. Hän asetti tavoitteeksi ajaa edestakaisen matkan keskinopeudella 24 km/h. Vastatuulen takia hän joutui käyttämään menomatkaan aikaa
2. Pyöräilijä lähti Pietarsaaresta kohti Kokkolaa, jonne on matkaa 33 km. Hän asetti tavoitteeksi ajaa edestakaisen matkan keskinopeudella 24 km/h. Vastatuulen takia hän joutui käyttämään menomatkaan aikaa
Luvun 8 laskuesimerkit
 Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
Määräys STUK SY/1/ (34)
 Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Diplomi-insino o rien ja arkkitehtien yhteisvalinta - dia-valinta 2015 Insino o rivalinnan fysiikan koe 27.5.2015, malliratkaisut
 Diplomi-insino o rien ja arkkitehtien yhteisalinta - dia-alinta 15 Insino o rialinnan fysiikan koe 7.5.15, malliratkaisut A1 Pallo (massa m = 1, kg, sa de r =, cm) nojaa kur an mukaisesti pystysuoraan
Diplomi-insino o rien ja arkkitehtien yhteisalinta - dia-alinta 15 Insino o rialinnan fysiikan koe 7.5.15, malliratkaisut A1 Pallo (massa m = 1, kg, sa de r =, cm) nojaa kur an mukaisesti pystysuoraan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2013 Insinöörivalinnan fysiikan koe 29.5.2013, malliratkaisut
 A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
4rrr. PYSwvYoesrÄ. 0809-cPR-1115. Tarvasjoen Teräsovi Oy Junnaronkatu 16 24100 Salo SE RTI FI KAATTI TUOTTEE N SUORITUSTASON EN 12101-2:2003
 4rrr VTT XPRT SRVCS Y llmeu ls r 0809 VTT XPRT SRVCS Y P 1001.02044\TT S RT KAATT TUTT SURTUSTAS PYSwvYesrÄ 0809PR1115 urpn prlmenn j neuvsn seuksen : 305/201 1 (rkennusueseus el CPR), jk n nneu mlskuun
4rrr VTT XPRT SRVCS Y llmeu ls r 0809 VTT XPRT SRVCS Y P 1001.02044\TT S RT KAATT TUTT SURTUSTAS PYSwvYesrÄ 0809PR1115 urpn prlmenn j neuvsn seuksen : 305/201 1 (rkennusueseus el CPR), jk n nneu mlskuun
on hidastuvaa. Hidastuvuus eli negatiivinen kiihtyvyys saadaan laskevan suoran kulmakertoimesta, joka on siis
 Fys1, moniste 2 Vastauksia Tehtävä 1 N ewtonin ensimmäisen lain mukaan pallo jatkaa suoraviivaista liikettä kun kourun siihen kohdistama tukivoima (tässä tapauksessa ympyräradalla pitävä voima) lakkaa
Fys1, moniste 2 Vastauksia Tehtävä 1 N ewtonin ensimmäisen lain mukaan pallo jatkaa suoraviivaista liikettä kun kourun siihen kohdistama tukivoima (tässä tapauksessa ympyräradalla pitävä voima) lakkaa
> 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db
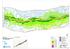 Pet jr t Kvm Kr Hyyr yl Sr m Hm Ko e o LIITE.. Mtede melelvty 0 Yömelto (etore: m) Ortmp Petmo Immo Kop Rto Tehr Rö Voe Lepelto Pr Ptlh Rm Kymht Netytem Vroj Prorp Sem Rto Tlllo Vtter Sotmp It-Sto M Korvet
Pet jr t Kvm Kr Hyyr yl Sr m Hm Ko e o LIITE.. Mtede melelvty 0 Yömelto (etore: m) Ortmp Petmo Immo Kop Rto Tehr Rö Voe Lepelto Pr Ptlh Rm Kymht Netytem Vroj Prorp Sem Rto Tlllo Vtter Sotmp It-Sto M Korvet
PUUT T E H TÄV. käyttää hyödyksi.
 PUU / j j l Y / E H ÄÄ l l l l r r Ä E H Ä l l j l j H rl r j K PUU j r r j r IE OA P P r j r l J rj r P r l j r l l j l r r j r j r P P l r j r l j P j Ml r j rg j r r l M A R JA r l l O E H ÄÄ l / l
PUU / j j l Y / E H ÄÄ l l l l r r Ä E H Ä l l j l j H rl r j K PUU j r r j r IE OA P P r j r l J rj r P r l j r l l j l r r j r j r P P l r j r l j P j Ml r j rg j r r l M A R JA r l l O E H ÄÄ l / l
sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639
 DLL sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639 *************************** ISO 639 *************************** () ab aa af sq am ar hy as ay az ba eu bn dz bh bi br bg my be 299 ( ) ( ) () () km ca zh
DLL sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639 *************************** ISO 639 *************************** () ab aa af sq am ar hy as ay az ba eu bn dz bh bi br bg my be 299 ( ) ( ) () () km ca zh
Kitka ja Newtonin lakien sovellukset
 Kitka ja Newtonin lakien sovellukset Haarto & Karhunen Tavallisimpia voimia: Painovoima G Normaalivoima, Tukivoima Jännitysvoimat Kitkavoimat Voimat yleisesti F f T ja s f k N Vapaakappalekuva Kuva, joka
Kitka ja Newtonin lakien sovellukset Haarto & Karhunen Tavallisimpia voimia: Painovoima G Normaalivoima, Tukivoima Jännitysvoimat Kitkavoimat Voimat yleisesti F f T ja s f k N Vapaakappalekuva Kuva, joka
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
 YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
g-kentät ja voimat Haarto & Karhunen
 g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
Jakotukit / tarvikkeet
 Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi VIRTAUSMITTARI UPONOR SMART S 2022148 BT40 JAKOTUKKIIN PALUUVENTTIILI UPONOR SMART S JAKOTUKKIIN JAKOTUKKI DANFOSS FBH-F RST 2+2 LATTIALÄMMITYS 2+2 VIRTAUKSEN
Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi VIRTAUSMITTARI UPONOR SMART S 2022148 BT40 JAKOTUKKIIN PALUUVENTTIILI UPONOR SMART S JAKOTUKKIIN JAKOTUKKI DANFOSS FBH-F RST 2+2 LATTIALÄMMITYS 2+2 VIRTAUKSEN
POISTOILMAVENTTIILI HALTON
 Venttiilit Tuote LVI-numero Pikakoodi 8707702 AT09 URH/A-100 URH/A-125 URH/A-160 URH/A-200 URH/B-100 URH/B-125 URH/B-160 URH/B-200 PEITELEVY HALTON CS/ULA-160 TULOVENTTIILI HALTON ULA-100 TULOVENTTIILI
Venttiilit Tuote LVI-numero Pikakoodi 8707702 AT09 URH/A-100 URH/A-125 URH/A-160 URH/A-200 URH/B-100 URH/B-125 URH/B-160 URH/B-200 PEITELEVY HALTON CS/ULA-160 TULOVENTTIILI HALTON ULA-100 TULOVENTTIILI
NEWTONIN LAIT MEKANIIKAN I PERUSLAKI MEKANIIKAN II PERUSLAKI MEKANIIKAN III PERUSLAKI
 NEWTONIN LAIT MEKANIIKAN I PERUSLAKI eli jatkavuuden laki tai liikkeen jatkuvuuden laki (myös Newtonin I laki tai inertialaki) Kappale jatkaa tasaista suoraviivaista liikettä vakionopeudella tai pysyy
NEWTONIN LAIT MEKANIIKAN I PERUSLAKI eli jatkavuuden laki tai liikkeen jatkuvuuden laki (myös Newtonin I laki tai inertialaki) Kappale jatkaa tasaista suoraviivaista liikettä vakionopeudella tai pysyy
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
-d;'$ d{ee lr a ;{*.v. ii{:i; rtl i} dr r/ r ) i a 4 a I p ;,.r.1 il s, Karttatuloste. Maanmittauslaitos. Page 1 of 1. Tulostettu 22.08.
 Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
=*' igäiäigä$jii,äägääggägääfä. E'EEEEiäs*'ääääEäggägäiiläägäääägäää. i;giggggäggg äg;gfggäiggis. E Ei. ä jggä;fäfäää. e;egelgäf EEE : !
 l d=. ö^ 3k 4rcna lc ' *O\ J * '\ tia.2 t :q(cblz c i;iä ä;fäis il 6! iää; iäiäää 9 S # öt == cf) \n.vdtd &= e;läf ;:c cj '5 'tr=lz ä jä;fäfäää c5 FrO! =*' ":rf : 6 Ä'^üi= iu l n. :S Xn.!.< V,; :;,^?'=.!.=Na'tY
l d=. ö^ 3k 4rcna lc ' *O\ J * '\ tia.2 t :q(cblz c i;iä ä;fäis il 6! iää; iäiäää 9 S # öt == cf) \n.vdtd &= e;läf ;:c cj '5 'tr=lz ä jä;fäfäää c5 FrO! =*' ":rf : 6 Ä'^üi= iu l n. :S Xn.!.< V,; :;,^?'=.!.=Na'tY
Luku 7 Työ ja energia. Muuttuvan voiman tekemä työ Liike-energia
 Luku 7 Työ ja energia Muuttuvan voiman tekemä työ Liike-energia Tavoitteet: Selittää työn käsite Mallittaa voiman tekemä työ Mallittaa liike-energian ja työn keskinäinen riippuvuus Esitiedot Newtonin lait
Luku 7 Työ ja energia Muuttuvan voiman tekemä työ Liike-energia Tavoitteet: Selittää työn käsite Mallittaa voiman tekemä työ Mallittaa liike-energian ja työn keskinäinen riippuvuus Esitiedot Newtonin lait
Liike ja voima. Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä
 Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Luvun 10 laskuesimerkit
 Luvun 10 laskuesimerkit Esimerkki 10.1 Tee-se-itse putkimies ei saa vesiputken kiinnitystä auki putkipihdeillään, joten hän päättää lisätä vääntömomenttia jatkamalla pihtien vartta siihen tiukasti sopivalla
Luvun 10 laskuesimerkit Esimerkki 10.1 Tee-se-itse putkimies ei saa vesiputken kiinnitystä auki putkipihdeillään, joten hän päättää lisätä vääntömomenttia jatkamalla pihtien vartta siihen tiukasti sopivalla
FYSIIKAN HARJOITUSTEHTÄVIÄ
 FYSIIKAN HARJOITUSTEHTÄVIÄ MEKANIIKKA Nopeus ja keskinopeus 6. Auto kulkee 114 km matkan tunnissa ja 13 minuutissa. Mikä on auton keskinopeus: a) Yksikössä km/h 1. Jauhemaalaamon kuljettimen nopeus on
FYSIIKAN HARJOITUSTEHTÄVIÄ MEKANIIKKA Nopeus ja keskinopeus 6. Auto kulkee 114 km matkan tunnissa ja 13 minuutissa. Mikä on auton keskinopeus: a) Yksikössä km/h 1. Jauhemaalaamon kuljettimen nopeus on
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Arvio metsdmaan arvosta
 Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
& # # w. œ œ œ œ # œ œ œ œ œ # œ w. # w nœ. # œ œ œ œ œ # œ w œ # œ œ œ Œ. œ œ œ œ œ œ œ œ # œ w. œ # œ œ œ w œ œ w w w w. W # w
 Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
NÄKYMÄ TURVESUONKADUN JA LIELAHDENKADUN RISTEYKSESTÄ MAANKÄYTTÖSUUNNITELMA TEIVAALANTIELLE LIELAHTEEN LUONNOS ARKKITEHDIT A3 OY
 NÄKYMÄ TURVESUNKADUN JA LELAHDENKADUN RSTEYKSESTÄ MAANKÄYTTÖSUUNNTELMA TEVAALANTELLE LELAHTEEN LUNNS.. ARKKTEHDT A Y ,,,,,, :,, Pelv o,,,,,,,,,,,,,,,,,,,, :,,,,,,,, :,,,,,,, Pol Pl,,,, K,, :,,, :,,,,,,,
NÄKYMÄ TURVESUNKADUN JA LELAHDENKADUN RSTEYKSESTÄ MAANKÄYTTÖSUUNNTELMA TEVAALANTELLE LELAHTEEN LUNNS.. ARKKTEHDT A Y ,,,,,, :,, Pelv o,,,,,,,,,,,,,,,,,,,, :,,,,,,,, :,,,,,,, Pol Pl,,,, K,, :,,, :,,,,,,,
Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta
 1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
PS. Jos vastaanotit Sinulle kuulumattoman viestin, pyydän ilmoittamaan siitä viipymättä allekirjoittaneelle ja tuhoamaan viestin, kiitos.
 Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Ideaalikaasut. 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista?
 Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
Jakotukit / tarvikkeet
 Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
CHEVROLET JA FORD OSIEN
 1939 CHEVROLET JA FORD OSEN HNNASTO SUOMEN AUTOVARUSTE TURKU YLOPSTONKATU 7 PUH: KONTTOR 3908, MYYMÄLÄ JA VARASTO 3907, 3917 SÄHKÖ O S: AUTOVARUSTE :60 335285 335446-7-8(84018) 335679 335977 335978 337709
1939 CHEVROLET JA FORD OSEN HNNASTO SUOMEN AUTOVARUSTE TURKU YLOPSTONKATU 7 PUH: KONTTOR 3908, MYYMÄLÄ JA VARASTO 3907, 3917 SÄHKÖ O S: AUTOVARUSTE :60 335285 335446-7-8(84018) 335679 335977 335978 337709
766323A Mekaniikka, osa 2, kl 2015 Harjoitus 4
 766323A Mekaniikka, osa 2, kl 2015 Harjoitus 4 0. MUISTA: Tenttitehtävä tulevassa päätekokeessa: Fysiikan säilymislait ja symmetria. (Tästä tehtävästä voi saada tentissä kolme ylimääräistä pistettä. Nämä
766323A Mekaniikka, osa 2, kl 2015 Harjoitus 4 0. MUISTA: Tenttitehtävä tulevassa päätekokeessa: Fysiikan säilymislait ja symmetria. (Tästä tehtävästä voi saada tentissä kolme ylimääräistä pistettä. Nämä
= 6, Nm 2 /kg kg 71kg (1, m) N. = 6, Nm 2 /kg 2 7, kg 71kg (3, m) N
 t. 1 Auringon ja kuun kohdistamat painovoimat voidaan saada hyvin tarkasti laksettua Newtonin painovoimalailla, koska ne ovat pallon muotoisia. Junalle sillä saadaan selville suuruusluokka, joka riittää
t. 1 Auringon ja kuun kohdistamat painovoimat voidaan saada hyvin tarkasti laksettua Newtonin painovoimalailla, koska ne ovat pallon muotoisia. Junalle sillä saadaan selville suuruusluokka, joka riittää
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 17.3.2016 Susanna Hurme Päivän aihe: Energian, työn ja tehon käsitteet sekä energiaperiaate (Kirjan luku 14) Osaamistavoitteet: Osata tarkastella partikkelin kinetiikkaa
KJR-C1001 Statiikka ja dynamiikka Luento 17.3.2016 Susanna Hurme Päivän aihe: Energian, työn ja tehon käsitteet sekä energiaperiaate (Kirjan luku 14) Osaamistavoitteet: Osata tarkastella partikkelin kinetiikkaa
3.4 Liike-energiasta ja potentiaalienergiasta
 Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
atr E e, öp = J';i i o bi O() 8.;.E ä '=OOtr 3:E B TJJ I.U EEäH ir> cö
 o O() N r r F F TJJ.U e, P J' o b tr 8.. ä 'OOtr B äh r> c ...\ 'ffuä ut\'o' " "\.\ ' FF rl,c # _ xl r äää1 r *..s5 +_.P eä
o O() N r r F F TJJ.U e, P J' o b tr 8.. ä 'OOtr B äh r> c ...\ 'ffuä ut\'o' " "\.\ ' FF rl,c # _ xl r äää1 r *..s5 +_.P eä
P S. Va r äi n. m m2 2. e a / puistossa säilyvät puut. korko muuttuu, kansi uusitaan SVK asv.
 TI E f as 8 5 5 pu ke lu pi ip iv - le / te AP 1 4 KI +8 8 +8 9 O le lem ht a ip ss uu a st ol oa ev aa rk ki ip met A L 31 6 L AP P LE IK S E T ei l y tu pu r u va liu m k u at m to äk i in u hl M 22
TI E f as 8 5 5 pu ke lu pi ip iv - le / te AP 1 4 KI +8 8 +8 9 O le lem ht a ip ss uu a st ol oa ev aa rk ki ip met A L 31 6 L AP P LE IK S E T ei l y tu pu r u va liu m k u at m to äk i in u hl M 22
Q 17.1/27.2/74/3. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste. T. Jokinen SUSKEPTIBILITEETTIPROFIILI
 Q 171/272/74/3 T Jokinen 1974-12-02 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SUSKEPTIBILITEETTIPROFIILI 4 171 /272/74/3 T Jokinen 1974-12-02 GEOLOGIIVEIV 'i-litkimuslaitos
Q 171/272/74/3 T Jokinen 1974-12-02 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SUSKEPTIBILITEETTIPROFIILI 4 171 /272/74/3 T Jokinen 1974-12-02 GEOLOGIIVEIV 'i-litkimuslaitos
Modulplan. Für die Ausbildung im Fachseminar Bildende Kunst. Stand: Februar 2012
 Mdulplan Für die Ausbildung im Fahseminar Bildende Kunst Stand: Februar 2012 g) g 5 5F. F s r s # 5 P g e ä F g F 9b ; ä: -+ F- -.+ s,t $ ;.e üe ü i ; ö F ä t ä$ lil ä ä H * H äg Hä fiäfä;äf;ää äääägäfi
Mdulplan Für die Ausbildung im Fahseminar Bildende Kunst Stand: Februar 2012 g) g 5 5F. F s r s # 5 P g e ä F g F 9b ; ä: -+ F- -.+ s,t $ ;.e üe ü i ; ö F ä t ä$ lil ä ä H * H äg Hä fiäfä;äf;ää äääägäfi
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN. Fysiikan ja kemian perusteet ja pedagogiikka, luento Kari Sormunen
 VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian perusteet ja pedagogiikka, 1.-2. luento Kari Sormunen Mitä yhteistä? Kirja pöydällä Opiskelijapari Teräskuulan liike magneetin lähellä
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian perusteet ja pedagogiikka, 1.-2. luento Kari Sormunen Mitä yhteistä? Kirja pöydällä Opiskelijapari Teräskuulan liike magneetin lähellä
Pietarsaaren lukio Vesa Maanselkä
 Fys 9 / Mekaniikan osio Liike ja sen kuvaaminen koordinaatistossa Newtonin lait Voimavektorit ja vapaakappalekuvat Työ, teho,työ-energiaperiaate ja energian säilymislaki Liikemäärä ja sen säilymislaki,
Fys 9 / Mekaniikan osio Liike ja sen kuvaaminen koordinaatistossa Newtonin lait Voimavektorit ja vapaakappalekuvat Työ, teho,työ-energiaperiaate ja energian säilymislaki Liikemäärä ja sen säilymislaki,
FYSIIKKA. Mekaniikan perusteita pintakäsittelijöille. Copyright Isto Jokinen; Käyttöoikeus opetuksessa tekijän luvalla. - Laskutehtävien ratkaiseminen
 FYSIIKKA Mekaniikan perusteita pintakäsittelijöille - Laskutehtävien ratkaiseminen - Nopeus ja keskinopeus - Kiihtyvyys ja painovoimakiihtyvyys - Voima - Kitka ja kitkavoima - Työ - Teho - Paine LASKUTEHTÄVIEN
FYSIIKKA Mekaniikan perusteita pintakäsittelijöille - Laskutehtävien ratkaiseminen - Nopeus ja keskinopeus - Kiihtyvyys ja painovoimakiihtyvyys - Voima - Kitka ja kitkavoima - Työ - Teho - Paine LASKUTEHTÄVIEN
- Zj + +i, virittämän suunnikkaan pinta-ala. 2x + Y: 4. 3x 2y:2 -x+y:-1. 3x + y:5. -x +2y:2. 4x + Y: 4. voitto : qr Aq+ rr q. : -!A_'r.
 Vaasan yliopisto, syksy 2014 Lineaarialgebra, MAH. lo4o 7. harjoitus, (viikko 2, 5.1.-9.1.2015 R01: ma 12-14 Dl15, R02: ke 14-16 D115, R03: to 10-12 F651 Viimeisellä luennolla käsiteltiin opetusmonisteen
Vaasan yliopisto, syksy 2014 Lineaarialgebra, MAH. lo4o 7. harjoitus, (viikko 2, 5.1.-9.1.2015 R01: ma 12-14 Dl15, R02: ke 14-16 D115, R03: to 10-12 F651 Viimeisellä luennolla käsiteltiin opetusmonisteen
Kiiännö!! b) Fysiikan tunnilla tutkittiin lääkeruiskussa olevan ilman paineen riippuvuutta lämpötilasta vakiotilavuudessa ruiskuun kiinnitetyn
 FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
Muunnokset ja mittayksiköt
 Muunnokset ja mittayksiköt 1 a Mitä kymmenen potenssia tarkoittavat etuliitteet m, G ja n? b Mikä on massan (mass) mittayksikkö SI-järjestelmässäa? c Mikä on painon (weight) mittayksikkö SI-järjestelmässä?
Muunnokset ja mittayksiköt 1 a Mitä kymmenen potenssia tarkoittavat etuliitteet m, G ja n? b Mikä on massan (mass) mittayksikkö SI-järjestelmässäa? c Mikä on painon (weight) mittayksikkö SI-järjestelmässä?
b) '5555z-?:lo -1:7 ' 5 ',r+i (i-å) n- r*or i+i- sl4-4 s-5-''- (å) 2:+ 2 r t I 3-3 a)23+42 Ð'+., (, -:), u)j++ b)2-1 "i
 Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
2.2 Principia: Sir Isaac Newtonin 1. ja 2. laki
 Voima se on joka jyllää!, sanottiin ennen. Fysiikassakin voimalla tarkoitetaan jokseenkin juuri sitä, mikä ennenkin jylläsi, joskin täytyy muistaa, että voima ja teho ovat kaksi eri asiaa. Fysiikan tutkimuksen
Voima se on joka jyllää!, sanottiin ennen. Fysiikassakin voimalla tarkoitetaan jokseenkin juuri sitä, mikä ennenkin jylläsi, joskin täytyy muistaa, että voima ja teho ovat kaksi eri asiaa. Fysiikan tutkimuksen
Peitelevy ja peitelaippa
 Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN. Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen
 VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen Vuorovaikutus on yksi keskeisimmistä fysiikan peruskäsitteistä
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen Vuorovaikutus on yksi keskeisimmistä fysiikan peruskäsitteistä
)x -)! ^i, + lu" x---',!^,y+je+ov. z'?+t' -t e +v A,ft1 = ffi*- my. Am= ft1x- fhy. A R-*t+AJa^HtNeN. lla.f J^ YA r e. LAtTE^l,NeN YDtMFffi
 Yl ast.qvaj lv zrn Ja Re/4Frto M pg,4f{_g LAtTE^l,NeN YDtMFffi lla.f J^ YA r e Ä^W: frtxhrä- Yrr;rer rn Tulo 6- Y7' r, T' t? Atcrr o,vg R CIA a elt H^J o*>1r M n AÅ = R
Yl ast.qvaj lv zrn Ja Re/4Frto M pg,4f{_g LAtTE^l,NeN YDtMFffi lla.f J^ YA r e Ä^W: frtxhrä- Yrr;rer rn Tulo 6- Y7' r, T' t? Atcrr o,vg R CIA a elt H^J o*>1r M n AÅ = R
J u s s i N ie m i-p y n ttä ri, y lilä ä k ä ri, M a lm in p s y k ia tria n p o lik lin ik k a T o rs ta i 1.1 2.2 0 1 1
 M IT E N O S A A M IS T A V O I J O H T A A? jo ita k in a ja tu k s ia J u s s i N ie m i-p y n ttä ri, y lilä ä k ä ri, M a lm in p s y k ia tria n p o lik lin ik k a T o rs ta i 1.1 2.2 0 1 1 E s ity
M IT E N O S A A M IS T A V O I J O H T A A? jo ita k in a ja tu k s ia J u s s i N ie m i-p y n ttä ri, y lilä ä k ä ri, M a lm in p s y k ia tria n p o lik lin ik k a T o rs ta i 1.1 2.2 0 1 1 E s ity
L a = L l. rv a = Rv l v l = r R v a = v a 1, 5
 Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut 1 Huvipuiston vuoristoradalla vaunu (massa m v = 1100 kg) lähtee levosta liikkeelle
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut 1 Huvipuiston vuoristoradalla vaunu (massa m v = 1100 kg) lähtee levosta liikkeelle
Voiman ja liikemäärän yhteys: Tämä pätee kun voima F on vakio hetken
 Liikemäärä Henkilöauto törmää tukkirekkaan, miksi henkilöautossa olijat loukkaantuvat vakavasti, mutta rekan kuljettaja selviää yleensä aina vammoitta? Mihin suuntaan ja millä nopeudella rekka ja henkilöauto
Liikemäärä Henkilöauto törmää tukkirekkaan, miksi henkilöautossa olijat loukkaantuvat vakavasti, mutta rekan kuljettaja selviää yleensä aina vammoitta? Mihin suuntaan ja millä nopeudella rekka ja henkilöauto
Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti
 MAA8 Ko 5..04 T konsptiin pisttsruudukko! Muista kirjata nimsi ja rhmäsi. Lu ohjt huolllissti A-Osio: Ei saa kättää laskinta. MAOL saa olla alusta asti kätössä. Maksimissaan h aikaa suorittaa A- Osio.
MAA8 Ko 5..04 T konsptiin pisttsruudukko! Muista kirjata nimsi ja rhmäsi. Lu ohjt huolllissti A-Osio: Ei saa kättää laskinta. MAOL saa olla alusta asti kätössä. Maksimissaan h aikaa suorittaa A- Osio.
HARJOITUS 4 1. (E 5.29):
 HARJOITUS 4 1. (E 5.29): Työkalulaatikko, jonka massa on 45,0 kg, on levossa vaakasuoralla lattialla. Kohdistat laatikkoon asteittain kasvavan vaakasuoran työntövoiman ja havaitset, että laatikko alkaa
HARJOITUS 4 1. (E 5.29): Työkalulaatikko, jonka massa on 45,0 kg, on levossa vaakasuoralla lattialla. Kohdistat laatikkoon asteittain kasvavan vaakasuoran työntövoiman ja havaitset, että laatikko alkaa
Sisäpiirintiedon syntyminen
 Kai Kotiranta Sisäpiirintiedon syntyminen Kontekstuaalinen tulkinta Y liopistollinen väitöskirja, jo k a Lapin yliopiston oikeustieteiden tiedekunnan suostum uksella esitetään julkisesti tarkastettavaksi
Kai Kotiranta Sisäpiirintiedon syntyminen Kontekstuaalinen tulkinta Y liopistollinen väitöskirja, jo k a Lapin yliopiston oikeustieteiden tiedekunnan suostum uksella esitetään julkisesti tarkastettavaksi
Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census
 Suomen virallinen tilasto Finlands officiella Statistik Official Statistics of Finland VI C:106 Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census 1980 Osa XV Del XV Volume
Suomen virallinen tilasto Finlands officiella Statistik Official Statistics of Finland VI C:106 Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census 1980 Osa XV Del XV Volume
ole vastaanottotiloja.
 Kiinteistd Oy Kalajoen Keidas Karhuojantie 2 90460 Oulunsalo TOIMINTAKERTOMUS TILIKAUDELTA 1.1.-3122009 1 Yleistai yhtidstii Yhtion omistamissa rakennuksissa huoneistot varattu osakkeenomistajille lomaasunnoiksi.
Kiinteistd Oy Kalajoen Keidas Karhuojantie 2 90460 Oulunsalo TOIMINTAKERTOMUS TILIKAUDELTA 1.1.-3122009 1 Yleistai yhtidstii Yhtion omistamissa rakennuksissa huoneistot varattu osakkeenomistajille lomaasunnoiksi.
