Q 17.1/27.2/74/3. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste. T. Jokinen SUSKEPTIBILITEETTIPROFIILI
|
|
|
- Kirsti Auvinen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Q 171/272/74/3 T Jokinen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SUSKEPTIBILITEETTIPROFIILI
2 4 171 /272/74/3 T Jokinen GEOLOGIIVEIV 'i-litkimuslaitos Geofysiikan osasto HP 9820 A-ohjelmaseloste Suskeptibiliteettiprofiili Ohjelmaa voidaan käyttää suskeptibiliteettiprofiilipohjien piirtämiseen ja mittauspisteiden esittämiseen profiileina jolloin samalla mittauspisteet lasketaan 10~~~1-~ksiköiksi Profiilin piirtarnisen jälkeen tulostaa ohjelma myös kaik- kien suskeptibiliteettien keskiarvon keskihajonnan ja vaih- telukertoimen Vaihtoehtoisesti voidaan profiilipohjien piirtäminen jättää pois (FLG61 Profiilin piirtämisessä on eri vaihtoehtoja: 1 Normaalitapauksessa ohjelma piirtää suskeptibiliteetit +:nä ja yhdistää nämä merkit jos mittauspisteiden väli L 7 m (rivillä Suskeptibiliteetit esitetään mustattuina ympyröina (FLG41 3 Kaikki suskeptibiliteettien välit yhdistetään riippumatta mittauspisteiden etäisyyksista (FLG21 Liitteissä 1-5 on esimerkkejä eri piirtämistavoista Toimintaohjeet Clhjelma sijaitsee kahdella pitkällä kortilla 4 sivulla Piirtoalaksi skaalataan 25 x 38 cmz (suuremman HP-paperin nurkat] Jos haluat jättää profiilipohjan piirtämisen pois aseta FLG6 Kysymyksiin vastataan seuraavasti: [suluissa muistirekisteri jonne vastaus menee1 PROFNUMER0 Anna k0 numero (RIO1 KARTTALEHTI (R201 anna alueen 1: karttalehti (6 numeroinen luku1 Seuraaviin kysymyksiin vastataan muodossa PLT "vastaus"
3 MATKAMITTAKAAVA [ R2 1 anna mittakaava muodossa 1/R2 esim 1/ XO =? [ROI ensimmäinen numeroitava x MITTAUSSUUNTA (R11 Mittaussuunta asteina jos k0 luku > 180 piirtää ohjelma profiilin oikealta vasemmalle X-KOCIRDINAATTI Y-KOORDINAATTI Alkupisteen koordinaatit SEURAAVA X anna matkalukema metreinä LI =? L =? anna ilmalukema ja mittauslukema jos samoja kuin edellisellä pisteellä jätä antamatta Virheellisen lukeman korjaaminen Anna kysymykseen L =? vastaukseksi -1 jolloin ohjelma palaa kysymykseen SEURAAVA X Suskeptibiliteetin jättäminen keskiarvon laskemisesta pois Aseta FLG 0 ennen kuin tulee kysymys SEURAAVA X Voit painaa kesken piirtämisen SFG jolloin FLG 0 on asetettu Piirtoalan looouminen Jos piirrettävä X PIIRTOALA LOPPUI <-2 tai >36 tulee näyttötaululle ilmoitus jos haluat jatkaa piirtämistä uudella paperilla vaihda pa-peri ja anna vastaukseksi luku 1 Jos lopetat profiilin piirtamisen jätä vastaus antamatta jolloin ohjelma tulostaa N:n k:n S:n ja C:n Piirtämisen looettaminen Profiilin viimeisen pisteen piirtamisen jälkeen anna kysymykseen vastaukseksi luku -2 Tällöin ohjelma tulostaa kaikkien piirrettyjen suskeptibiliteettien [ellet ole käyttänyt FLG 0:aal lukumäärän (Nl keskiarvon MEAN K (1 O-~SI 1 keski-
4 hajonnan S [IO-~SII ja vaihtelukertoimen C sekä niiden suskeptibiliteettien lukumaaran jotka olet jättänyt keskiarvon laskemisesta pois FLG0:n avulla (Nl) Ohjelman rakenne rivit FXD 0 Skaalausarvot jos FLG 6 ei ole asetettu haarautuminen riville 30 Akselien piirtäminen Y-akselin numerointi Vakiotekstit Profiilin numeron ja karttalehden antaminen Karttalehden ja profiilin numeron plottaus Alue laite PVM Matkamittakaavan XO:n mittaussuunnan ja alkupisteen koordinaattien antaminen X-akselin nurnerointi Mittaussuunnan ja koordinaattien plottaus Eräiden rekisterien nollaus "SEURAAVA X" Piirtämisen lopetustesti Matkalukema muutetaan piirtärnisarvoksi Piirtämisarvojen muutokset jos FLG 3 tai FLG 1 Li =? L =? Jos L = -1 palaa riville 58 AL:n muutos yksiköiksi IO-~SI Piirrettävän Y:n laskeminen((~0~1~-skaala) Jos mittauspisteiden väli i 7 m yhtenäinen viiva k0 pisteen plottaus Jos FLG 0 jää k0 arvo pois keskiarvon laskemisesta Keskiarvon ja -hajonnan laskeminen Paluu riville 58 Piirtoalan loppuminen Piirtamisen lopettaminen keskiarvon ja -hajonnan ja pisteiden lukumaaran plottaus Piirtäminen jatkuu seuraavalla paperilla Alirutiini joka piirtää mustatun ympyrän EIVD
5 Muistitilan käyttö A Sisäänsyötettävä Li 11 C - - matka X Piirrettävä X (cm) 11 Y - - Y (cm) Xo (ensimmäinen numeroitava x) Mittaussuunta (O) X:n mittakaava (muodossa 1/R2) K (IO-~SII r xl -koordinaatti profiilin alkupisteen yl koordinaatit vapaa L - Li= AL 4a 1154 AL AL') = ~~[IO-~SI) Eki Profiilin numero N I k : n laskemiseen käytettyjen mittausten lukumäärä) k (suskeptibiliteettie keskiarv0~10~~~1) Cki 9 S keskihajonta -nk2 = J( n-l 1 R14 R15 C vaihtelukerroin = S/k Cki2 x-akselin numerointi R18 R19 1: karttalehden osanumero R20 karttalehden numero R22 x-akselin numerointi R23 Niiden mittausten lukumäärä joita ei ole käytetty k:n laskemiseen = NI R24 vapaa R25 Paperin vaihto jos R25 # 0 R26 Ympyrän säde jos havaintopisteet esitetään ympyröinä (o15) R27 X (cm) R28 I~i+i - ~ i = ( 1~x1 R29 Xi-1 (edellinen piirretty x) R30 Yi-1 [ Y)
6 FLAGIT FLG 0 : k0 suskeptibiliteetti jää keskiarvon laskemisesta pois FLG 1: Profiilia jatketaan seuraavalla paperilla [sisäinen] FLG 2: Kaikki piirrettävät pisteet yhdistetään yhtenäiseksi profiiliksi (liite 51 FLG 3: Profiilin piirtäminen oikealta vasemmalle (sisäinen] FLG 4: Suskeptibiliteetit esitetään mustattuina ympyröinä FLG 6: Profiilipohjan piirtäminen jää pois
7 - a L LI I= -u Lil u Z
8 m rn - N P B J N N - J J -
9 1 1 \ ;tfl LV LA 8 13 m ; 1 : 4 I I 3- IFJ : 'EJ : m 1 4 : -! 1 * - i j :! ; 1 ' i ' " l d i! ; l L m - - 4! r\l Ln /:II - i m -- - LO :!! : J : I " L : ' < i [U r : -_i 1 :- _-:LI:--r;--:r-ii:! : L_ 1 L ~ ~ - ~ : -: : :! i : I L -1 : L *- 1 - : - a - - : ; : -! : : : ; - : i - IL---!--'-~ 1 i- 3- n1 --- I i!! "! : : - : ---- ;--- -i! l! -: i j ; ; --] - --!- -! 8 * - - i :!! i L 1 - -A i ~ : i 8 / -! -- i! ~-~ - - -l- :- I i 1 M : ; --- e - -- : - --!-; - -: C-- - ; ~- : :~' L- 1P l- 3 8! : w - 'm ;m : L --- : -_- : i- 8 i l 1 : :-- / / i_: -:i: i_ -:::: :-i; - 'VU1 : ' jj : : : ~-< - - :! I i ' i ; :: ' + 8 ' l: :- ~ - : i- " jj j j ' l I < - : t s*ot I < ' 8 ' - : - -: :! - ; -: : : - I:: :: _? j :! i : ; I < :! R;I 1 1!! _ j! " - I - *- i : ;! 1 : I 8 -- i Y!ml> * I I I I 1 I I 1 4 d d I r2j 61 n1 l-3 m m Rl EJ t5j I-51 rsl t4 m m IQ E(1 Ei rn CJ Fu IA N Lrl - - Ju 4bl - t'a El rj;l 1 9 L - J - ~: m- ru mn a MP ru p" X> I
10 ~ ~ i ni v -!- - --!- -~ 1! 8 - ;-! 1: ~ ' : 1 1 : m '! m < - : : Ea B mi i i ~ ~ +!! : l 1 i : -- # j : 1 ' ; : i - : : : 1 - i ' 1 -- ~ : ; + - i 1 : i: -! : i ~ ~ ; ~ + : :! ::! :! : ; I i 1 ~! ~ ~ ~ * ~ I _-- ' : ' I! 8 8! : ;! ~! : : i : ;! i! :!! < - ~ + I! : - 2" ; i ~ : V:! m ' ; -~ :--i ;- -i: - 8 : : 1 : : f'l4 8 f :! I I I 1 I l I 1 1 I 1 d d 6l l;;i IZ! Eil El - EJ - ~4 LI 8 - 'EJ 01 ' m n N t3 El KI El 6l U a1 hlt3 L r N Irl d N - M N - Lr 4 - v -- mm NF? X> ~ '
11
12
13
Q 17.1/24.1/74/1. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste. T. Jokinen SLINGRAM-PROFIILI
 Q 17.1/24.1/74/1 T. Jokinen 1974-12-05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SLINGRAM-PROFIILI Q 17.1/24.1/74/1 T. Jokinen 1974-12-05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
Q 17.1/24.1/74/1 T. Jokinen 1974-12-05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SLINGRAM-PROFIILI Q 17.1/24.1/74/1 T. Jokinen 1974-12-05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
4 17.1/24.34/74/1. Tarmo Jokinen. Geofysiikan osasto GEOLOGINEN TUTKIMUSLAITOS VLF-PRDFIILI
 4 17.1/24.34/74/1 Tarmo Jokinen 1974-1 1-1 9 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto VLF-PRDFIILI 't LJ 17.1/2$.34/74/1 T. Jokinen 1974-1 1-19 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820
4 17.1/24.34/74/1 Tarmo Jokinen 1974-1 1-1 9 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto VLF-PRDFIILI 't LJ 17.1/2$.34/74/1 T. Jokinen 1974-1 1-19 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820
Q 17.1/24.1/73/1. GEOLOGINEN TLITKIIYUSLAITOS Geofysiikan osasto. Tarmo Jokinen SLIINGRAM-PRCIFIILIIN PIIRTÄMINEN
 Q 7/24/73/ Tarmo Jokinen 973-0-03 GEOLOGINEN TLITKIIYUSLAITOS Geofysiikan osasto SLIINGRAM-PRCIFIILIIN PIIRTÄMINEN 24 Q 7/=/73/ T Jokinen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A -0h~emaseloste
Q 7/24/73/ Tarmo Jokinen 973-0-03 GEOLOGINEN TLITKIIYUSLAITOS Geofysiikan osasto SLIINGRAM-PRCIFIILIIN PIIRTÄMINEN 24 Q 7/=/73/ T Jokinen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A -0h~emaseloste
Q 17.1/16.2/73/6. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 9820 A. P. Mikkola Koskee: Q 17.1/22
 Q 171/162/73/6 P Mikkola 1973-12-17 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 9820 A Koskee: Q 171/22 UZIANOMALIAN LASKEMINEN ( malli 17 puolizäretöntä levyä) Q 171/162/73/6 P Mikkola
Q 171/162/73/6 P Mikkola 1973-12-17 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 9820 A Koskee: Q 171/22 UZIANOMALIAN LASKEMINEN ( malli 17 puolizäretöntä levyä) Q 171/162/73/6 P Mikkola
Q 17.1/27/75/2. Risto Puranen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto
 Q 17.1/27/75/2 Risto Puranen 197 5-01-08 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Q 17.1/27/75/2 Risto Puranen 1975-01-08 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste Ohjelman
Q 17.1/27/75/2 Risto Puranen 197 5-01-08 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Q 17.1/27/75/2 Risto Puranen 1975-01-08 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste Ohjelman
PETROFYSIKAALINEN SYVÄKAIRAUSPROFIILI (TULOSTEN ESITTÄMINENI
 Q 17.1/27/74/21 R. Puranen 1974-12-28 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasta HP 9820 A-ohjelrnaseloste PETROFYSIKAALINEN SYVÄKAIRAUSPROFIILI (TULOSTEN ESITTÄMINENI Q 17.1 /27/74/21 Risto Puranen
Q 17.1/27/74/21 R. Puranen 1974-12-28 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasta HP 9820 A-ohjelrnaseloste PETROFYSIKAALINEN SYVÄKAIRAUSPROFIILI (TULOSTEN ESITTÄMINENI Q 17.1 /27/74/21 Risto Puranen
HAVAINTOARVOJEN TLILOSTUS LCIMAKKEELLE PETROFYSIKAALISET LABORA- TURIOMITTAUKSET
 Q 17.1/27/75/3 R. Puranen 1975-01 -22 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste HAVAINTOARVOJEN TLILOSTUS LCIMAKKEELLE PETROFYSIKAALISET LABORA- TURIOMITTAUKSET - 1975. Q 17,1/27/75/3
Q 17.1/27/75/3 R. Puranen 1975-01 -22 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste HAVAINTOARVOJEN TLILOSTUS LCIMAKKEELLE PETROFYSIKAALISET LABORA- TURIOMITTAUKSET - 1975. Q 17,1/27/75/3
R. Puranen Q 17.1 /27/74/23. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste
 Q 17.1 /27/74/23 R. Puranen 1974-03-07 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste HAVAINTOPISTEIDEN PLOTTAUS (1:250001 JA TILASTOLLINEN KÄSITTELY 4 17.1 /27/74/23 R. Puranen
Q 17.1 /27/74/23 R. Puranen 1974-03-07 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste HAVAINTOPISTEIDEN PLOTTAUS (1:250001 JA TILASTOLLINEN KÄSITTELY 4 17.1 /27/74/23 R. Puranen
Q 17,4/21/73/2 GEOLOGINEN TUTKIMUSLAITOS. Seppo Elo. Geofysiikan osasta FORTRAN IV ohjelmaseloste
 Q 17,4/21/73/2 Seppo Elo 19 73-12-05 GEOLOGINEN TUTKIMUSLAITOS 1. Geofysiikan osasta FORTRAN IV ohjelmaseloste FORTRAN IV OHJELMA JOKA LASKEE SARJAN VAAKASUORISTA SUORAKULMAISISTA MONIKULMIOSTA KOOSTUVIEN
Q 17,4/21/73/2 Seppo Elo 19 73-12-05 GEOLOGINEN TUTKIMUSLAITOS 1. Geofysiikan osasta FORTRAN IV ohjelmaseloste FORTRAN IV OHJELMA JOKA LASKEE SARJAN VAAKASUORISTA SUORAKULMAISISTA MONIKULMIOSTA KOOSTUVIEN
GEOLOGINEN TUTKIMUSLAITOS AZ-ANOMALIAN LASKEMINEN (GAY:N MUKAAN) Geofysiikan osasto HP-ohjelmaseloste 9820 A. Koskee: Q 17.1/22
 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 9820 A Koskee: Q 7./22 AZ-ANOMALIAN LASKEMINEN (GAY:N MUKAAN) Q 7,/6.2/73/%4 A. Villareal 973-09-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 9820 A Koskee: Q 7./22 AZ-ANOMALIAN LASKEMINEN (GAY:N MUKAAN) Q 7,/6.2/73/%4 A. Villareal 973-09-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
Q ~ i~.i/z~7a/t R. Puranen
 Q ~ i~.i/z~7a/t R. Puranen 7 976-01 -05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto RAPORTTITI EDOSTO -- P \ Q 17*1/27/76/V 2. Puranen GEOLOGIETEN rputkimusli1itos Geofysiikan osasto HP 9820 A-ohjelmaseloste
Q ~ i~.i/z~7a/t R. Puranen 7 976-01 -05 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto RAPORTTITI EDOSTO -- P \ Q 17*1/27/76/V 2. Puranen GEOLOGIETEN rputkimusli1itos Geofysiikan osasto HP 9820 A-ohjelmaseloste
PETROFYSIKAALINEN KARTOITUS REIKÄNAuHALTA (1:50 000)
 Q 17.1/27/74/3 R. Puranen 1974-06-19 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-oh jelmaseloste PETROFYSIKAALINEN KARTOITUS REIKÄNAuHALTA (1:50 000) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/3 Risto Puranen
Q 17.1/27/74/3 R. Puranen 1974-06-19 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-oh jelmaseloste PETROFYSIKAALINEN KARTOITUS REIKÄNAuHALTA (1:50 000) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/3 Risto Puranen
Q 17.1/27/75/4 Risto Puranen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto SUSKEPTIBILITEETIN RIIPPUVUUS TIHEYDESTÄ. JA KÄSIPLOTTAUS.
 Q 17.1/27/75/4 Risto Puranen 1975-01-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto SUSKEPTIBILITEETIN RIIPPUVUUS TIHEYDESTÄ. JA KÄSIPLOTTAUS. TULOSTUSPDHJA Q 17.1 /27/75/4 R. Puranen 1975-01 -24 GEOLOGINEN
Q 17.1/27/75/4 Risto Puranen 1975-01-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto SUSKEPTIBILITEETIN RIIPPUVUUS TIHEYDESTÄ. JA KÄSIPLOTTAUS. TULOSTUSPDHJA Q 17.1 /27/75/4 R. Puranen 1975-01 -24 GEOLOGINEN
Q 17.1/27/73/2 R. Puranen
 Q 17.1/27/73/2 R. Puranen 1973-07-31 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste MERKKIEN SELTTYKSEN PIIRT#MINEN SUSaPTIBILZTEETTI- JA TIHEYSKARTTQIHIN Q 17 *1/37/73/2 R. Puranen 1973-07-31
Q 17.1/27/73/2 R. Puranen 1973-07-31 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste MERKKIEN SELTTYKSEN PIIRT#MINEN SUSaPTIBILZTEETTI- JA TIHEYSKARTTQIHIN Q 17 *1/37/73/2 R. Puranen 1973-07-31
S-ZSOTOOP DZDATA !SWIA 0 \ S-ISOTOOPPIDATA GTL-78 S AVZA. M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä
 M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
(NYRKKIN~YTTEET) Q 17.1/27/74/6 R. Puranen 1974-05-24. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HAVAINTOARVOJEN ~SITTELY JA TULOSTUS LOMAKKEELLE A
 Q 17.1/27/74/6 R. Puranen 1974-05-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HAVAINTOARVOJEN ~SITTELY JA TULOSTUS LOMAKKEELLE A (NYRKKIN~YTTEET) HP 9 820 A-OHJELMASELOSTE Q 17.1/27/74/6 R. Puranen
Q 17.1/27/74/6 R. Puranen 1974-05-24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HAVAINTOARVOJEN ~SITTELY JA TULOSTUS LOMAKKEELLE A (NYRKKIN~YTTEET) HP 9 820 A-OHJELMASELOSTE Q 17.1/27/74/6 R. Puranen
/27/75/5. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste. R. Puranen
 4 1 7.1/27/75/5 R. Puranen 1975-01 -24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SUSKEPTIBILITEETIN RIIPPUVUUS TIHEYDESTÄ. REIKÄNAUHALTA. TULOSTUS Q 17.1/27/75/5 R. Puranen
4 1 7.1/27/75/5 R. Puranen 1975-01 -24 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste SUSKEPTIBILITEETIN RIIPPUVUUS TIHEYDESTÄ. REIKÄNAUHALTA. TULOSTUS Q 17.1/27/75/5 R. Puranen
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
HP 9820 A-OHJELMASELOSTE
 Q 17.1/27/74/15 R. Puranen 1974-05-28 GEOLOGNEN TUTKMUSLATOS Geofysiikan osasto HP 9820 A-ohjelmaseloste STATSTKKA PETROFYSKAALSELTA REKÄNAUHALTA (PNTANAYTTEET) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/15
Q 17.1/27/74/15 R. Puranen 1974-05-28 GEOLOGNEN TUTKMUSLATOS Geofysiikan osasto HP 9820 A-ohjelmaseloste STATSTKKA PETROFYSKAALSELTA REKÄNAUHALTA (PNTANAYTTEET) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/15
Geofysiikan osasto Q 17.1/27/75/9 1975-03-11 GECILOGINEN TUTKIMUSLAITOS. HP-ohj elmaseloste ALLIEELLINEN STATISTIIKKA REIKÄNAUHALTA IPINTA- IVÄYTTEETI
 Q 17.1/27/75/9 R. Puranen 1975-03-11 GECILOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohj elmaseloste ALLIEELLINEN STATISTIIKKA REIKÄNAUHALTA IPINTA- IVÄYTTEETI Q 17.1/27/75/9 R. Puranen 1975-03-1 1 GEOLOGINEN
Q 17.1/27/75/9 R. Puranen 1975-03-11 GECILOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohj elmaseloste ALLIEELLINEN STATISTIIKKA REIKÄNAUHALTA IPINTA- IVÄYTTEETI Q 17.1/27/75/9 R. Puranen 1975-03-1 1 GEOLOGINEN
R. Puranen. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste 1975-04-13
 Q 17.1/27/75/13 R. Puranen 1975-04-13 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste PETROFYSIKAALINEN KARTOITUS KASETEILTA (1:50 0001 HP 9820 A-OHJELMASELOSTE Q 17.1/27/75/13 Risto Puranen
Q 17.1/27/75/13 R. Puranen 1975-04-13 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste PETROFYSIKAALINEN KARTOITUS KASETEILTA (1:50 0001 HP 9820 A-OHJELMASELOSTE Q 17.1/27/75/13 Risto Puranen
4 17.1/27/75/10 R. Puranen
 4 17.1/27/75/10 R. Puranen 1975-04-12 GEOLOGINEN TUTK:CI/IUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste RAPORTTITIEDOSTO KIVILAJIEN STATISTIIKKA KASETEILTA IPPNTANÄYTTEETI HP 9820 A-OHJELIYASELOSTE
4 17.1/27/75/10 R. Puranen 1975-04-12 GEOLOGINEN TUTK:CI/IUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste RAPORTTITIEDOSTO KIVILAJIEN STATISTIIKKA KASETEILTA IPPNTANÄYTTEETI HP 9820 A-OHJELIYASELOSTE
MITTAUSARVOJEN TULOSTUS PETROFYSIKAALISIKSI REI~NAUHOIKSI
 Q 17.1/27/74/2 Risto Puranen 1974-05-07 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste MITTAUSARVOJEN TULOSTUS PETROFYSIKAALISIKSI REI~NAUHOIKSI (NYRKKINÄYTTEET) I HP 9820 A-OHJELMASELOSTE
Q 17.1/27/74/2 Risto Puranen 1974-05-07 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohjelmaseloste MITTAUSARVOJEN TULOSTUS PETROFYSIKAALISIKSI REI~NAUHOIKSI (NYRKKINÄYTTEET) I HP 9820 A-OHJELMASELOSTE
NEN PAINOVOIMAMITTAUS N:o OU 10/7b
 I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
HP 9820 A-ohjelmaseloste
 GEOLOGINEN TUTKIMUSLAITOS GeoQsiikan osasto HP 9820 A-ohjelmaseloste PETRQPY SIKAALISEN REI~NAUHAN QTSZKOINTI ( FINTAN#YTTEET 1 Q 17,1/27/74/9 R. Puranen 1974-05-03 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
GEOLOGINEN TUTKIMUSLAITOS GeoQsiikan osasto HP 9820 A-ohjelmaseloste PETRQPY SIKAALISEN REI~NAUHAN QTSZKOINTI ( FINTAN#YTTEET 1 Q 17,1/27/74/9 R. Puranen 1974-05-03 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan
HP 9820 A-OHJELMASELQSTE
 Q 17.1/27f 741 14 Risto Puranen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste PETROPY SIKAALISTEN TIETOJEN LAY ISTY S ( P INTAN~YTTEET, P-KOODI = 41 HP 9820 A-OHJELMASELQSTE Q 17.1/27/74/14
Q 17.1/27f 741 14 Risto Puranen GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste PETROPY SIKAALISTEN TIETOJEN LAY ISTY S ( P INTAN~YTTEET, P-KOODI = 41 HP 9820 A-OHJELMASELQSTE Q 17.1/27/74/14
Pakkauksen sisältö: Sire e ni
 S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
3 *ä;r ä:e 5ä ä{ :i. c oo) S g+;!qg *r; Er ; l[$ E ;;iä F:ä ä :E ä: a bo. =. * gäf$iery g! Eä. a is äg*!=."fl: ä; E!, \ ins:" qgg ;._ EE üg.
 t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
Forssan kaupunki Osavuosikatsaus YHDYSKUNTAPALVELUT. Arviointik r iteeri tr mittarit ja tavoitetaso ja t a v o i t e t a s o
 Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
EP 9820 -A-Oh jelmaseloste
 & 17.1/27/74/10 R. Puranen 1974-04-01 Geologinen tutkimuslaitos Geofysiikan osasto d EP 9820 -A-Oh jelmaseloste - PETROFYSIKAALISTEN TIETOJEN LAVISTYS ARKISTOKORTEILTA R. Puranen 1974-04-01 PETROFYSIKAALISTEN
& 17.1/27/74/10 R. Puranen 1974-04-01 Geologinen tutkimuslaitos Geofysiikan osasto d EP 9820 -A-Oh jelmaseloste - PETROFYSIKAALISTEN TIETOJEN LAVISTYS ARKISTOKORTEILTA R. Puranen 1974-04-01 PETROFYSIKAALISTEN
Q 17.1/27/74/7 R. Puranen GEOLOGINEN TUTKIMUSLAITOS. Geofysiikan osasto NÄYTETUNNUSTEN LÄVISTYS (PINTAN~YTTEET) HP 9820 A-OHJELMASELOSTE
 Q 17.1/27/74/7 R. Puranen 1974-05-14 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto NÄYTETUNNUSTEN LÄVISTYS (PINTAN~YTTEET) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/7 R. Puranen 1974-05-14 GEOLOGINEN TUTKIMUSLAITOS
Q 17.1/27/74/7 R. Puranen 1974-05-14 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto NÄYTETUNNUSTEN LÄVISTYS (PINTAN~YTTEET) HP 9820 A-OHJELMASELOSTE Q 17.1/27/74/7 R. Puranen 1974-05-14 GEOLOGINEN TUTKIMUSLAITOS
0 17.1/27/75/14 R. Puranen GECILOGINEN TUTKIMUSLAITOS. Geofysiikan osasto REIKÄNAUHAN LUKEMIIUEN KASETILLE
 0 17.1/27/75/14 R. Puranen 1975-04-10 GECILOGINEN TUTKIMUSLAITOS Geofysiikan osasto REIKÄNAUHAN LUKEMIIUEN KASETILLE IMUSLAITOS R. Puranen GeofjsiSan osasto -. Ohjelman avulla voidôan silrtaa petrofysikaalinen
0 17.1/27/75/14 R. Puranen 1975-04-10 GECILOGINEN TUTKIMUSLAITOS Geofysiikan osasto REIKÄNAUHAN LUKEMIIUEN KASETILLE IMUSLAITOS R. Puranen GeofjsiSan osasto -. Ohjelman avulla voidôan silrtaa petrofysikaalinen
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Q 17.1/27/74/19. HP 9820 A-ohjelmaseloste. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto. R. Puranen
 Q 17.1/27/74/19 R. Puranen 1974-1 2-27 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste PETROFYSIKAALISTEN TIETOJEN LÄVISTYS (SYVÄKAIRAUS- NÄYTTEET, P-KOODI = 4..61 Q 17.1/27/74/19
Q 17.1/27/74/19 R. Puranen 1974-1 2-27 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP 9820 A-ohjelmaseloste PETROFYSIKAALISTEN TIETOJEN LÄVISTYS (SYVÄKAIRAUS- NÄYTTEET, P-KOODI = 4..61 Q 17.1/27/74/19
Q 17.1/27/75/17. Geofysiikan osasto. R. Puranen GEOLOGINEN TUTKIMUSLAITOS PETROFYSIKAALISEN KASETIN EOITOINTI
 Q 17.1/27/75/17 R. Puranen 1975-04-14 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto PETROFYSIKAALISEN KASETIN EOITOINTI - Q 17*1/27/75/17 GZOLOGZiEN TUTKINUSLAITOS 2. Puzanen Geofysiikan osasto 1975-04-1
Q 17.1/27/75/17 R. Puranen 1975-04-14 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto PETROFYSIKAALISEN KASETIN EOITOINTI - Q 17*1/27/75/17 GZOLOGZiEN TUTKINUSLAITOS 2. Puzanen Geofysiikan osasto 1975-04-1
Luento 2: Viivan toteutus
 Tietokonegrafiikan perusteet T-111.4300 3 op Luento : Viivan toteutus Lauri Savioja 11/07 Primitiivien toteutus / 1 GRAAFISTEN PRIMITIIVIEN TOTEUTUS HUOM! Oletuksena on XY-koordinaatisto Suorien viivojen
Tietokonegrafiikan perusteet T-111.4300 3 op Luento : Viivan toteutus Lauri Savioja 11/07 Primitiivien toteutus / 1 GRAAFISTEN PRIMITIIVIEN TOTEUTUS HUOM! Oletuksena on XY-koordinaatisto Suorien viivojen
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla
 Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
ääexgäl*ääääe ääg I ä*fre3 I äee iäa ää-äälgü il leääö ää; i ääs äei:ä ä+ i* äfä g u ;; + EF'Hi: 2 ä ; s i r E:;g 8ää-i iää: Ffärg',
 !P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
!P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
äiäää?l älägcläälii äisrä lää äää
 E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
OUTOKUMPU OY 040/2341 12/~~/83
 Q OUTOKUMPU OY 040/234 2/~~/83 0 K MALMINETSINTX Eero Sandgren/PHM 25..984 GEOFYSIIKAN TUTKIMUKSET VUONNA 98 JA 983 Reisjarvi, Tiaskuru 234 2 Sijainti :400 000 Lähtökohta Kesän 983 aikana tutkimuskohteella
Q OUTOKUMPU OY 040/234 2/~~/83 0 K MALMINETSINTX Eero Sandgren/PHM 25..984 GEOFYSIIKAN TUTKIMUKSET VUONNA 98 JA 983 Reisjarvi, Tiaskuru 234 2 Sijainti :400 000 Lähtökohta Kesän 983 aikana tutkimuskohteella
2 Keminmaa 3 4 5 6. Haaparanta TORNIO. > 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db. Vt 4 Kemi
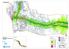 LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
1. Olkoot vektorit a, b ja c seuraavasti määritelty: a) Määritä vektori. sekä laske sen pituus.
 Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
OUTOKUMPU OY 0 K MALMINETSINTA. Eero Sandqren/PHM 11-4.1983 1 GEOFYSIIKAN TUTKIMUKSET VUONNA 1979 JA 19. Sijainti 1:400 000. Vihanti, Kiviharju
 Q OUTOKUMPU OY 0 K MALMINETSINTA Eero Sandqren/PHM 11-4.1983 1 GEOFYSIIKAN TUTKIMUKSET VUONNA 1979 JA 19 Vihanti, Kiviharju 2434 05 Sijainti 1:400 000 Gähtökohta Lampinsaaren malmimuodostuman kulku on
Q OUTOKUMPU OY 0 K MALMINETSINTA Eero Sandqren/PHM 11-4.1983 1 GEOFYSIIKAN TUTKIMUKSET VUONNA 1979 JA 19 Vihanti, Kiviharju 2434 05 Sijainti 1:400 000 Gähtökohta Lampinsaaren malmimuodostuman kulku on
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Tekijä Pitkä matematiikka Pisteen (x, y) etäisyys pisteestä (0, 2) on ( x 0) Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y.
 Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä
 Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Tehtävä 1 2 3 4 5 6 7 Vastaus
 Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Yhtälön oikealla puolella on säteen neliö, joten r. = 5 eli r = ± 5. Koska säde on positiivinen, niin r = 5.
 Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Kattoläpiviennit KATTOLÄPIVIENTISARJA VILPE. Tuote LVI-numero Pikakoodi SOLAR TIILI MUSTA TM85 SOLAR TIILI RUSKEA AD58
 Kattoläpiviennit Tuote LVI-numero Pikakoodi 5289200 WF99 SOLAR TIILI MUSTA 75602 SOLAR TIILI RUSKEA 75604 SOLAR TIILI HARMAA 75607 SOLAR TIILI TIILENPUN. 75609 SOLAR PELTIMUSTA 75612 SOLAR CLASSIC MUSTA
Kattoläpiviennit Tuote LVI-numero Pikakoodi 5289200 WF99 SOLAR TIILI MUSTA 75602 SOLAR TIILI RUSKEA 75604 SOLAR TIILI HARMAA 75607 SOLAR TIILI TIILENPUN. 75609 SOLAR PELTIMUSTA 75612 SOLAR CLASSIC MUSTA
b) '5555z-?:lo -1:7 ' 5 ',r+i (i-å) n- r*or i+i- sl4-4 s-5-''- (å) 2:+ 2 r t I 3-3 a)23+42 Ð'+., (, -:), u)j++ b)2-1 "i
 Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
 Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Q 16/24.34/71/1. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto VLF-m i ttau kset. P. Mikkola 24.6.1971 VLF-MITTAUKSISTA JA TULOSTEN KÄSITTELYSTÄ
 C C Q 16/24.34/71/1 P. Mikkola 24.6.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto VLF-m i ttau kset VLF-MITTAUKSISTA JA TULOSTEN KÄSITTELYSTÄ KÄYTÄNNÖN MITTAUS Vastaanotinta on säilytettävä paikassa,
C C Q 16/24.34/71/1 P. Mikkola 24.6.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto VLF-m i ttau kset VLF-MITTAUKSISTA JA TULOSTEN KÄSITTELYSTÄ KÄYTÄNNÖN MITTAUS Vastaanotinta on säilytettävä paikassa,
Vanhoja koetehtäviä. Analyyttinen geometria 2016
 Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
l, ; i.'s ä E.ä E o gäästaefiiä,ggäeäeää;äggtää EI ;äe E H * eaä* E E 8EP.E .e= äe eääege F EEE;säääg lee sa 8NY ExE öe äec E= : ;H ä a(ü
 ,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
Aluksi. 1.1. Kahden muuttujan lineaarinen yhtälö
 Aluksi Matematiikan käsite suora on tarkalleen sama asia kuin arkikielen suoran käsite. Vai oliko se toisinpäin? Matematiikan luonteesta johtuu, että sen soveltaja ei tyydy pelkkään suoran nimeen eikä
Aluksi Matematiikan käsite suora on tarkalleen sama asia kuin arkikielen suoran käsite. Vai oliko se toisinpäin? Matematiikan luonteesta johtuu, että sen soveltaja ei tyydy pelkkään suoran nimeen eikä
Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Lue tehtävänannot huolellisesti. Tee pisteytysruudukko B-osion konseptin yläreunaan!
 MAA4 koe 1.4.2016 Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Lue tehtävänannot huolellisesti. Tee pisteytysruudukko B-osion konseptin yläreunaan! Jussi Tyni A-osio: Ilman laskinta. Laske kaikki
MAA4 koe 1.4.2016 Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Lue tehtävänannot huolellisesti. Tee pisteytysruudukko B-osion konseptin yläreunaan! Jussi Tyni A-osio: Ilman laskinta. Laske kaikki
yleisessä muodossa x y ax by c 0. 6p
 MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
Ratkaisut vuosien tehtäviin
 Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
4.3 Kehäkulma. Keskuskulma
 4.3 Kehäkulma. Keskuskulma Sellaista kulmaa, jonka kärki on ympyrän kehällä ja kumpikin kylki leikkaa (rajatapauksessa sivuaa) ympyrän kehää, sanotaan kehäkulmaksi, ja sitä vastaavan keskuskulman kyljet
4.3 Kehäkulma. Keskuskulma Sellaista kulmaa, jonka kärki on ympyrän kehällä ja kumpikin kylki leikkaa (rajatapauksessa sivuaa) ympyrän kehää, sanotaan kehäkulmaksi, ja sitä vastaavan keskuskulman kyljet
4 37.1/27/75/ R. Puranen. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto PETROFYSIKAALISTEN TIETOJEN NAUHOITUS (PINTANÄYTTEETI
 4 37.1/27/75/38 R. Puranen 1975-04-3 6 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto PETROFYSIKAALISTEN TIETOJEN NAUHOITUS (PINTANÄYTTEETI i Q?7*1/27/75/18 R. Puranen 197 5-04-1 6 GEOLOGINEN TUTKIMUSLAITOS
4 37.1/27/75/38 R. Puranen 1975-04-3 6 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto PETROFYSIKAALISTEN TIETOJEN NAUHOITUS (PINTANÄYTTEETI i Q?7*1/27/75/18 R. Puranen 197 5-04-1 6 GEOLOGINEN TUTKIMUSLAITOS
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
Ota tämä paperi mukaan, merkkaa siihen omat vastauksesi ja tarkista oikeat vastaukset klo 11:30 jälkeen osoitteesta
 MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
Yl ä -S a von S O TE kunt a yhtym ä en Kuukausiraportti
 Ylä-Savon SOTE K U N T A Y H T Y M A Yl ä -S a von S O TE kunt a yhtym ä en Kuukausiraportti Tammikuu - Heinäkuu 213 Kuukausiraportti heinäkuu 213 Kuntayhtymä Talous Ta 213 Tot.71213 Tot-% Ennuste Toimintatuotot,
Ylä-Savon SOTE K U N T A Y H T Y M A Yl ä -S a von S O TE kunt a yhtym ä en Kuukausiraportti Tammikuu - Heinäkuu 213 Kuukausiraportti heinäkuu 213 Kuntayhtymä Talous Ta 213 Tot.71213 Tot-% Ennuste Toimintatuotot,
VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN-
 Q 16.1/21/73/1 Seppo Elo 1973-11-16 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Painovoimapisteiden korkeuden mittauksesta statoskoopeilla VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN- MÄARITYKSESTA
Q 16.1/21/73/1 Seppo Elo 1973-11-16 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Painovoimapisteiden korkeuden mittauksesta statoskoopeilla VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN- MÄARITYKSESTA
Yhtälöryhmä matriisimuodossa. MS-A0007 Matriisilaskenta. Tarkastellaan esimerkkinä lineaarista yhtälöparia. 2x1 x 2 = 1 x 1 + x 2 = 5.
 2. MS-A000 Matriisilaskenta 2. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2..205 Tarkastellaan esimerkkinä lineaarista yhtälöparia { 2x x 2 = x x 2 =
2. MS-A000 Matriisilaskenta 2. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2..205 Tarkastellaan esimerkkinä lineaarista yhtälöparia { 2x x 2 = x x 2 =
2016/07/05 08:58 1/12 Shortcut Menut
 2016/07/05 08:58 1/12 Shortcut Menut Shortcut Menut Shortcut menut voidaan aktivoida seuraavista paikoista. Shortcut menun sisältö riippuu siitä, mistä se aktivoidaan. 1. Shortcut menu suunnitellusta linjasta
2016/07/05 08:58 1/12 Shortcut Menut Shortcut Menut Shortcut menut voidaan aktivoida seuraavista paikoista. Shortcut menun sisältö riippuu siitä, mistä se aktivoidaan. 1. Shortcut menu suunnitellusta linjasta
v1.2 Huom! Piirto-ohjelmissa asioita voi tehdä todella monella tavalla, tässä esitellään yksi esimerkkitapa tällaisen käyrän piirtämiseen.
 v2 Tehtävä: Piirrä kartalle merkittyjen pisteiden ja välinen korkeusprofiili. Voit käyttää valmista Libre Office Draw koordinaatistopohjaa. Pisteiden välisen janan jakomerkit ovat 100m välein. Vaihtoehtoisesti
v2 Tehtävä: Piirrä kartalle merkittyjen pisteiden ja välinen korkeusprofiili. Voit käyttää valmista Libre Office Draw koordinaatistopohjaa. Pisteiden välisen janan jakomerkit ovat 100m välein. Vaihtoehtoisesti
KSAO Liiketalous 1. Asiakirjan ulkoasuun vaikuttavat tekstin muotoilut ja kappale muotoilut. Kappaleen ulkoasuun vaikuttavia tekijöitä:
 KSAO Liiketalous 1 Asiakirjan ulkoasuun vaikuttavat tekstin muotoilut ja kappale muotoilut. Kappaleen ulkoasuun vaikuttavia tekijöitä: tekstin tasaus sisennys riviväli; kappaleen sisäiset rivivälit kappaleiden
KSAO Liiketalous 1 Asiakirjan ulkoasuun vaikuttavat tekstin muotoilut ja kappale muotoilut. Kappaleen ulkoasuun vaikuttavia tekijöitä: tekstin tasaus sisennys riviväli; kappaleen sisäiset rivivälit kappaleiden
LIITE 1 Jaksoarviointi, Syntymäpäivätaivas Opettaja
 LIITE 1 Jaksoarviointi, Syntymäpäivätaivas Opettaja SYNTYMÄPÄIVÄTAIVAS (aapinen s. 114 125): JAKSOARVIOINTI, opettajan ohjeet Jaksoarvioinnin kolme ensimmäistä tehtävää ovat sanelutehtäviä ja ne tehdään
LIITE 1 Jaksoarviointi, Syntymäpäivätaivas Opettaja SYNTYMÄPÄIVÄTAIVAS (aapinen s. 114 125): JAKSOARVIOINTI, opettajan ohjeet Jaksoarvioinnin kolme ensimmäistä tehtävää ovat sanelutehtäviä ja ne tehdään
ill 'l' L r- i-ir il_i_ lr-+ 1r l
 ir a I - --+,.---+-,- i-ir il_i_ lr-+ 1r l rl ill 'l' L r- T- 'l rl *r- I s. ;l -' --S"[nJ+&L rlr D Ur-r^^;lA_e^ 3. Piirrä indi erenssikäyrät korille ( ; x 2 ); kun on tavallinen hyödyke, ja x 2 on tavallinen
ir a I - --+,.---+-,- i-ir il_i_ lr-+ 1r l rl ill 'l' L r- T- 'l rl *r- I s. ;l -' --S"[nJ+&L rlr D Ur-r^^;lA_e^ 3. Piirrä indi erenssikäyrät korille ( ; x 2 ); kun on tavallinen hyödyke, ja x 2 on tavallinen
A-osio. Tehdään ilman laskinta ja taulukkokirjaa! Valitse tehtävistä A1-A3 kaksi ja vastaa niihin. Maksimissaan tunti aikaa suorittaa A-osiota.
 MAA5.2 Loppukoe 24.9.2013 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A1. A-osio. Tehdään
MAA5.2 Loppukoe 24.9.2013 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A1. A-osio. Tehdään
Tasapainotehta via vaakamallin avulla
 Tasapainotehta via vaakamallin avulla Aihepiiri Luokka-aste Kesto Tarvittavat materiaalit / välineet Asiasanat Lausekkeet ja yhtälöt 7.-8. luokka 20 30 minuuttia Piirtoheitin, 2 kalvoa, erimuotoisia paloja
Tasapainotehta via vaakamallin avulla Aihepiiri Luokka-aste Kesto Tarvittavat materiaalit / välineet Asiasanat Lausekkeet ja yhtälöt 7.-8. luokka 20 30 minuuttia Piirtoheitin, 2 kalvoa, erimuotoisia paloja
Piirrä kuvioita suureen laatikkoon. Valitse ruutuun oikea merkki > tai < tai =.
 Piirrä kuvioita suureen laatikkoon. Valitse ruutuun oikea merkki tai < tai =. 1 Valitse ruutuun oikea merkki tai < tai =. ------------------------------------------------------------------------------
Piirrä kuvioita suureen laatikkoon. Valitse ruutuun oikea merkki tai < tai =. 1 Valitse ruutuun oikea merkki tai < tai =. ------------------------------------------------------------------------------
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla (Opettajan ohje)
 Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla (Opettajan ohje) TAVOITTEET Tämän kokonaisuuden tavoitteena on tutustuttaa oppilaat Pythonilla ohjelmointiin ja erityisesti Turtle moduulin
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla (Opettajan ohje) TAVOITTEET Tämän kokonaisuuden tavoitteena on tutustuttaa oppilaat Pythonilla ohjelmointiin ja erityisesti Turtle moduulin
SU01\1JEL\I MAINJ[ OY
 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
Osa 1: Todennäköisyys ja sen laskusäännöt. Klassinen todennäköisyys ja kombinatoriikka
 Ilkka Mellin Todennäköisyyslaskenta Osa 1: Todennäköisyys ja sen laskusäännöt Klassinen todennäköisyys ja kombinatoriikka TKK (c) Ilkka Mellin (2007) 1 Klassinen todennäköisyys ja kombinatoriikka >> Klassinen
Ilkka Mellin Todennäköisyyslaskenta Osa 1: Todennäköisyys ja sen laskusäännöt Klassinen todennäköisyys ja kombinatoriikka TKK (c) Ilkka Mellin (2007) 1 Klassinen todennäköisyys ja kombinatoriikka >> Klassinen
a) Sievennä lauseke 1+x , kun x 0jax 1. b) Aseta luvut 2, 5 suuruusjärjestykseen ja perustele vastauksesi. 3 3 ja
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
Peitelevy ja peitelaippa
 Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
Kertausosa. 5. Merkitään sädettä kirjaimella r. Kaaren pituus on tällöin r a) sin = 0, , c) tan = 0,
 Kertausosa. a),6 60 576 Peruuttaessa pyörähdyssuunta on vastapäivään. Kulma on siis,4 60 864 a) 576 864 0,88m. a) α b 0,6769... 0,68 (rad) r,m 8cm β,90...,9 (rad) 4cm a) α 0,68 (rad) β,9 (rad). a) 5,0
Kertausosa. a),6 60 576 Peruuttaessa pyörähdyssuunta on vastapäivään. Kulma on siis,4 60 864 a) 576 864 0,88m. a) α b 0,6769... 0,68 (rad) r,m 8cm β,90...,9 (rad) 4cm a) α 0,68 (rad) β,9 (rad). a) 5,0
MAA7 7.3 Koe Jussi Tyni Valitse kuusi tehtävää! Tee vastauspaperiin pisteytysruudukko! Kaikkiin tehtäviin välivaiheet näkyviin!
 MAA7 7. Koe Jussi Tyni 1..01 1. Laske raja-arvot: a) 5 x lim x5 x 10 b) x 8x16 lim x x 9 x. a) Määritä erotusosamäärän avulla funktion f (5). b) Onko funktio f x vastauksesi lyhyesti 1 9 x ( ) x f ( x)
MAA7 7. Koe Jussi Tyni 1..01 1. Laske raja-arvot: a) 5 x lim x5 x 10 b) x 8x16 lim x x 9 x. a) Määritä erotusosamäärän avulla funktion f (5). b) Onko funktio f x vastauksesi lyhyesti 1 9 x ( ) x f ( x)
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Tekijä Pitkä matematiikka b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta.
 Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
Q 17.1/06/71/2. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto. Juha Korhonen HP-ohJ el mase l oste
 Q 17.1/06/71/2 Juha Korhonen 1.4.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohJ el mase l oste SUORAVI IVAISTEN KOORDINAATTIEN MUUNTAMINEN MAANTIETEELLISIKSI OHJELMASELOSTE TRANSFORFAAT I ON
Q 17.1/06/71/2 Juha Korhonen 1.4.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto HP-ohJ el mase l oste SUORAVI IVAISTEN KOORDINAATTIEN MUUNTAMINEN MAANTIETEELLISIKSI OHJELMASELOSTE TRANSFORFAAT I ON
6L61 VSSflfl1V101 - SAAS. f 0 p h l\ vssv13aah 13S1flYllIWVlNfliISflAIS
 6L61 VSSflfl1V101 - SAAS f 0 p h l\ vssv13aah 13S1flYllIWVlNfliISflAIS SIVUSUUNTAMITTAUS HYVELRSSR SYYS-LOKAKUUSSA 1379 1. Yleistä Suomen Malmi Oy on suorittanut Porin pohjoispuolella Hyvelän kohteella
6L61 VSSflfl1V101 - SAAS f 0 p h l\ vssv13aah 13S1flYllIWVlNfliISflAIS SIVUSUUNTAMITTAUS HYVELRSSR SYYS-LOKAKUUSSA 1379 1. Yleistä Suomen Malmi Oy on suorittanut Porin pohjoispuolella Hyvelän kohteella
Kenguru 2013 Student sivu 1 / 7 (lukion 2. ja 3. vuosi)
 Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
 YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
Kuva 1. GIMP:in uuden kuvan luominen. Voit säätää leveyttä ja korkeutta ja kokeilla muitakin vaihtoehtoja. Napsauta sitten "OK".
 Gimp alkeet III 8 luokan ATK-työt/HaJa Sivu 1 / 6 Uuden kuvan luominen GIMP:illä yleisinfoa ----> LUE! Sen lisäksi, että GIMP on loistava valokuvankäsittelyohjelma, sillä saa piirrettyä myös omia kuvia
Gimp alkeet III 8 luokan ATK-työt/HaJa Sivu 1 / 6 Uuden kuvan luominen GIMP:illä yleisinfoa ----> LUE! Sen lisäksi, että GIMP on loistava valokuvankäsittelyohjelma, sillä saa piirrettyä myös omia kuvia
Q 17.1/27.2/71/5. GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto. Risto Puranen REMANENTTI MAGNETOITUMINEN, ERANNON (El LASKENNOLLINEN
 Q 17.1/27.2/71/5 Risto Puranen 22.1.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto REMANENTTI MAGNETOITUMINEN, ERANNON (El LASKENNOLLINEN KORJAAMINEN: J Dr, I ')+(J,D, I;Jx,Jy,Jz; I,m,n) REMAhrENTTI
Q 17.1/27.2/71/5 Risto Puranen 22.1.1971 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto REMANENTTI MAGNETOITUMINEN, ERANNON (El LASKENNOLLINEN KORJAAMINEN: J Dr, I ')+(J,D, I;Jx,Jy,Jz; I,m,n) REMAhrENTTI
Kenguru 2012 Cadet (8. ja 9. luokka)
 sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Scratch ohjeita. Perusteet
 Perusteet Scratch ohjeita Scratch on graafinen ohjelmointiympäristö koodauksen opetteluun. Se soveltuu hyvin alakouluista yläkouluunkin asti, sillä Scratchin käyttömahdollisuudet ovat monipuoliset. Scratch
Perusteet Scratch ohjeita Scratch on graafinen ohjelmointiympäristö koodauksen opetteluun. Se soveltuu hyvin alakouluista yläkouluunkin asti, sillä Scratchin käyttömahdollisuudet ovat monipuoliset. Scratch
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2010 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 4. kesäkuuta 2010 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2010 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 4. kesäkuuta 2010 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
Talousmatematiikan perusteet, L3 Prosentti, yhtälöt Aiheet
 Talousmatematiikan perusteet, L3 Prosentti, t Toisen Prosentti 1 Jos b on p% luvusta a, eli niin b = p 100 a a = perusarvo (Mihin verrataan?) (Minkä sadasosista on kysymys.) p = prosenttiluku (Miten monta
Talousmatematiikan perusteet, L3 Prosentti, t Toisen Prosentti 1 Jos b on p% luvusta a, eli niin b = p 100 a a = perusarvo (Mihin verrataan?) (Minkä sadasosista on kysymys.) p = prosenttiluku (Miten monta
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Valitse Näkymät->Geometria PIIRRETÄÄN KOLMIOITA: suorakulmainen kolmio keksitkö, miten korostat suoraa kulmaa? tasakylkinen kolmio keksitkö,
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Valitse Näkymät->Geometria PIIRRETÄÄN KOLMIOITA: suorakulmainen kolmio keksitkö, miten korostat suoraa kulmaa? tasakylkinen kolmio keksitkö,

