Satunnaismuuttujat Satunnaismuuttuja kuvaa kokeen tuloksen reaaliakselille Satunnaismuuttuja on siis funktio X(s) joka saa reaalisia arvoja Koe s
|
|
|
- Mikael Mäki
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Satunnaismuuttujat Satunnaismuuttuja kuvaa kokeen tuloksen reaaliakselille Satunnaismuuttuja on siis funktio X(s) joka saa reaalisia arvoja Koe s kuuluu todennäköisyysavaruuteen S (s S) Esimerkkejä Kolikonheitossatodennäköisyysavaruus S = {kruunu,klaava} Satunnaismuuttuja voisi olla { 1 (s = kruunu) X(s) = 1 (s =klaava) 50
2 Nopan heitossa S = {1, 2, 3, 4, 5, 6}. Satunnaismuuttuja voi olla X(s) =s, jolloin mahdolliset tulokset ovat 1,2,3,4,5,6 Satunnaismuuttuja voi olla myös X(s) =s 2, jolloin mahdolliset tulokset ovat 1,4,9,16,25,36 Usein merkitään yksinkertaisuuden vuoksi X(s) = X, mutta on syytä muistaa mistä on kysymys Kompleksinen satunnaismuuttuja Z on kahden reaalisen satunnaismuuttujan X ja Y funktio siten että Z = X + jy. Muuttujan Z ominaisuuksia tarkasteltaessa on tiedettävä ko. summan omaisuudet 51
3 Satunnaismuuttuja voi saada äärellisen määrän eri arvoja diskreetti satunnaismuuttuja (kuten edellisissä esimerkeissä) Satunnaismuuttuja voi myös saada kaikkia mahdollisia arvoja joltain tietyltä väliltä reaaliakselilla jatkuva satunnaismuuttuja (kuten elektronisten laitteiden generoiman kohinan amplitudi) 52
4 Käytännön tutkimustyössä tehdään usein seuraavaa: Näytteistetyn satunnaissignaalin (tiedonsiirtokanavasta vastaanotettu signaali) elementit ovat diskreettejä satunnaismuuttujia, mutta analyysissä niitä kohdellaan jatkuvina, koska jatkuvia muuttujia on helpompi käsitellä Jos sananleveys on riittävä (useita bittejä, ei kahta), niin näin tehty analyysi vastaa kokeellisia tuloksia Pienille sananleveyksille (muutama bitti) näin tehty analyysi ei ole tarkka vaan analyysi ja simulaatiotulokset (joissa käytetään ko. sananleveyttä) poikkevat jonkin verran toisistaan 53
5 Satunnaismuuttujat ja todennäköisyys Tarkastellaan tapahtumaa jossa satunnaismuuttuja X on lukua x pienempi eli tarkastellaan tapahtumaa {X x}. x voi olla mikä tahansa reaaliluku väliltä ( < x < ) Tapahtuman todennäköisyys on P(X x) Yleensä se merkitään lyhyesti F (x) (tai F X (x) jos on vaara seikoittaa johonkin muuhun vastaavaan funktioon) eli F (x) =P(X x) ( <x< ) (22) Funktiota F (x) kutsutaan todennäköisyys kertymäfunktioksi tai kumulatiiviseksi kertymäfunktioksi (CDF, cumulative distribution funktion) CDF siis kuvaa millä todennäköisyydellä satunnaismuuttuja X on lukua x pienempi 54
6 CDF on todennäköisyys joten 0 F (x) 1 On myös helppo havaita että F () =0jaF ( ) =1 CDF on kasvava funktio eli F (x 1 ) F (x 2 ), x 1 <x 2 Seuraavassaesimerkkejä diskreetistä ja jatkuvasta kertymäfunktiosta sekä näiden sekoituksesta 55
7 F (x) 1 F (x) jatkuva CDF Nopanheiton CDF kun X(s) =s sekoitus CDF x 0 x Diskreetti CDF Jatkuva ja sekoitus CDF:t 56
8 Kertymäfunktion F (x) derivaattaa p(x)(myös p X (x)) kutsutaan satunnaismuuttujan X todennäköisyys tiheysfunktioksi (PDF, probability density function) Nyt siis pätee p(x) = df(x) ( <x< ) (23a) dx ja F (x) = x p(u) du ( <x< ) (23b) Koska F (x) on kasvava, niin p(x) 0 Selvästi p(x) dx = F ( ) = 1 (pinta-ala on 1) 57
9 Diskreettien muuttujien tapauksessa p(x)sisältää impulssinf (x):n epäjatkuvuuskohdassa x i eli tälläisessa kohdassa p(x) on p(x i )=P(X = x i )δ(x x i ) (24) jossa δ(x) on impulssifunktio eli { 1 x =0 δ(x) = 0 x 0 (25) 58
10 Satunnaismuuttujalla X sanotaan olevan jakauma. Jakaumat on usein nimetty henkilöiden (mahdollisesti keksijä) tai PDF funktion mukaan Esimerkkinä ensimmäisestä on Gaussin jakauma ja toisesta eksponentiaalinen jakauma, jossa PDF on eksponentiaalinen. Kullakin jakaumalla on PDF ja CDF, joista se on tunnistettavissa. 59
11 Usein halutaan tietää todennäköisyys jolla satunnaismuuttuja on jollain välillä eli tapahtuman {x 1 <X x 2 } todennäköisyys (x 1 <x 2 ) Tapahtuma voidaan aina esittää kahden toisensa poissulkevan tapahtuman unionina (usein käytetty temppu) Tapahtuma {X x 2 } on selvästi tapahtumien {X x 1 } ja {x 1 <X x 2 } unioni X x 2 X x 1 x 1 <X X 2 x 1 x 2 x 60
12 Tällöin eli Tästä seuraa x1 P(X x 2 )=P(X x 1 )+P(x 1 <X x 2 ) F (x 2 )=F (x 1 )+P(x 1 <X x 2 ) P(x 1 <X x 2 )=F (x 2 ) F (x 1 ) x2 x 1 x 2 = = x2 x2 p(x) dx x1 p(x) dx x 1 p(x) dx (26) Todennäköisyys että satunaismuuttuja X saa arvoja väliltä x 1 < X x 2 on siis PDF:n integraali yli tuon alueen 61
13 Useita satunnaismuutujia Kun tarkastellaan useita yhtäaikaisia tapahtumia tai peräkkäisiä tapahtumiapitäätietää näiden yhteis kertymä- ja/tai tiheysfunktiot (yhteisjakauma) Useat satunnaismuuttujat muodostavat periaatteessa moniulotteisen funktion, joka on määritelty yhdistetyssä näyteavaruudessa Tarkastellaan ensin kahden muuttujan X 1 ja X 2 yhteisjakaumaa ja yleistetään tulokset sen jälkeen useammille muuttujille 62
14 Yhteiskertymäfunktio (yhteis (joint) CDF) on F (x 1,x 2 )=P(X 1 x 1,X 2 x 2 ) = x1 x2 p(u 1,u 2 ) du 1 du 2 (27) jossa p(x 1,x 2 ) on yhteis todennäköisyys tiheysfunktio (yhteis PDF), joka on p(x 1,x 2 )= 2 x 1 x 2 F (x 1,x 2 ) (28) 63
15 Kun yhteis PDF integroidaan yli toisen satunnaismuuttujan saadaan p(x 1,x 2 ) dx 2 = p(x 1 ) (29) jota kutsutaan marginaaliseksi PDF:ksi (erotukseksi varsinaisesta PDF:stä, jota ei ole saatu integroimalla) On helppo havaita että p(x 1,x 2 ) dx 1 dx 2 =1 F (, ) =F (,x 2 )=F (x 1, ) =0 64
16 Yleistys useampiulotteisiin tapauksiin on suoraviivaista F (x 1,...,x n )=P(X 1 x 1,...,X n x n ) = x1 xn p(u 1,...,u n ) du 1...du n n p(x 1,...,x n )= F (x 1,...,x n ) x 1 x n Marginaaliset PDF:t voidaan generoida mille tahansa määrälle satunnaismuuttujia eli p(x 1,x 2,x 3,x 4,x 5,...,x n ) dx 2 dx 4 = p(x 1,x 3,x 5,...,x n ) Havaitaan myös että F (x 1,,x 3,,x 5,...,x n )=F (x 1,x 3,x 5,...,x n ) F (x 1,,x 2,...,x n )=0 65
17 Ehdollinen tiheysfunktio Ehdollinen todennäköisyyshän oli P(A B) =P (A, B)/P (B) Ehdollisen todennäköisyyden, että muuttuja X 1 on pienempi kuin x 1 kun satunnaismuuttuja X 2 on saanut arvon x 2 eli todennäköisyyden P(X 1 x 1 X 2 = x 2 ) laskeminen ei yleisessä tapauksessa onnistu suoraan, koska tyypillisesti P(X 2 = x 2 )=0 ( 0 vain jos kyseessä distreetti muuttuja jolla jokin arvo ko. pisteessä) Lasketaan siis tapahtuman {X 1 x 1 x 2 <X 2 x 2 } todennäköisyys, jossa on pieni positiivinen luku 66
18 Tällöin x1 x2 x P(X 1 x 1 x 2 <X 2 x 2 )= 2 p(u 1,u 2 ) du 1 du 2 x2 x 2 p(u 2) du 2 = F (x 1,x 2 ) F (x 1,x 2 ) F (x 2 ) F (x 2 ) (30) Olettaen, että vaaditut PDF:t ovat jatkuvia alueella (x 2,x 2 ) voidaan osoittaja ja nimittäjä yhtälössä (30) jakaa :lla ja ottaa raja-arvo 0 ( ) Derivaatan määritelmä: lim h 0 f(x) f(x + h) /h 67
19 Tällöin P(X 1 x 1 X 2 = x 2 ) F (x 1 x 2 ) (31) = F(x 1,x 2 )/ x 2 F(x 2 )/ x 2 = [ x 1 x2 p(u ] 1,u 2 ) du 1 du 2 / x2 [ x 2 p(u ] 2) du 2 / x2 x1 = p(u 1,x 2 ) du 1 p(x 2 ) Derivoimalla tämä x 1 :sen suhteen saadaan p(x 1 x 2 )= p(x 1,x 2 ) p(x 2 ) joka on ehdollinen PDF. (32) (33) 68
20 Selvästi meillä onmyös p(x 1,x 2 )=p(x 1 x 2 )p(x 2 )=p(x 2 x 1 )p(x 1 ) (34) Yhtälön (34) yleistys on joskus hyödyllinen jakaumia määrättäessä. Se on p(x 1,x 2,...,x n )=p(x 1,...,x k x k+1,...,x n )p(x k+1,...,x n ) 69
21 Riippumattomat satunnaismuuttujat Riippumattomuushan tarkoitti että eri kokeiden ulostulot eivät millään lailla vaikuta toisiinsa. Havaittiin, että tällöin P(A 1,...,A n )=P(A 1 ) P(A n ) Koska satunnaismuuttujat liittyvät kokeisiin ja P (X x) = F (x) niin satunnaismuuttujat ovat tilastollisesti riippumattomia jos ja vain jos n F (x 1,...,x n )=F(x 1 ) F(x n )= F (x i ) (35) tai p(x 1,...,x n )=p(x 1 ) p(x n )= i=1 n p(x i ) (36) i=1 70
22 Tämä tarkoittaa siis sitä, että riippumattomien satunnaismuuttujien CDF tai PDF on yksittäisten satunnaismuuttujien CDF:ien tai PDF:ien tulo Tämä on hyvin usein käytetty ja hyödyllinen tieto 71
23 Satunnaismuuttujien funktiot Usein tarvitsee tietää mikä on satunnaismuuttujan/muuttujien funktion jakauma Tämä tarkoittaa, että halutaan tietää muuttujan Y = g(x) jakauma, kun tiedetään muuttujan X jakauma Tämä on varsin suoraviivaista jos kuvaus g on yksi-yhteen (yksikäsitteinen) Jos kuvaus ei ole yksikäsitteinen, esim. Y = X 2, niin jakauman määräämisessätäytyy olla hyvin huolellinen Tätä tietoutta tullaan käyttämään esim. joidenkin tiedonsiirtomenetelmien suorituskyvyn määräämisessä (DTS) 72
24 Esimerkki 1 Tarkastellaan muuttujaa Y = ax + b, jossa a>0jab ovat vakioita Kuvaus on lineaarinen ja monotooninen (= joko kasvava tai vähenevä funktio, nyt kasvava) Kuvaus on siis yksikäsitteinen Olkoon F X (x) jaf Y (y) muuttujien X ja Y CDF:t Selvästi ( F Y (y) =P(Y y) =P(aX + b y) =P X y b ) a ( y b ) (y b)/a = F X = p X (x) dx a Derivoimalla F Y (y) saadaan p Y (y) = 1 ( y b ) a p X a 73
25 Lineaarisessa muunnoksessa muuttujan Y = ax + b jakauma on helposti esitettävissä muuttujan X jakauman avulla y Y = ax + b p X (x) p Y (y) x -1 1 x b a 0 b b + ay siirtää (b) venyttää (a) Esimerkin 1 havainnollistaminen 74
26 Esimerkki 2 Tarkastellaan muuttujaa Y = ax 3 + b Kuvaus on yksikäsitteinen y 5 b Y=aX 3 +b x 75
27 Nyt on siis F Y (y) =P(Y y) =P(aX 3 + b y) ( ( y b ) 1/3 ) (( y b ) 1/3 ) =P X = F X a a josta derivoimalla 1 (( y b ) 1/3 ) p Y (y) = 3a[(y b)/a] p 2/3 X a 76
28 Esimerkki 3 Nyt tarkastellaan muuttujaa Y = ax 2 + b Kuvaus ei ole yksikäsitteinen sillä yhtä Y :n arvoa vastaa kaksi X:n arvoa y 5 4 Y=aX 2 +b 3 b x 77
29 Nyt =P F Y (y) =P(aX 2 + b y) ( y b ) ( y b y b ) X =P <X a a a ( y b ) ( y b ) = F X F X a a Derivoimalla saadaan p Y (y) = p ( ) X (y b)/a 2a (y b)/a + p ( ) X (y b)/a 2a (y b)/a 78
30 Esimerkissä 3 havaittiin, että yhtälöllä g(x) =ax 2 + b on kaksi ratkaisua x 1 = (y b)/a ja x 2 = (y b)/a ja että muuttujan Y = ax 2 + b PDF on muotoa p Y (y) = p X(x 1 ) g (x 1 ) + p X(x 2 ) g (x 2 ) jossa x 1 ja x 2 ovat yhtälön g(x) =ax 2 + b juuret ja g (x) on g(x):än derivaatta x:n suhteen Yleisesti muuttujalle Y = g(x) päteekin p Y (y) = p X(x 1 ) g (x 1 ) + + p X(x n ) g (x n ) = n i=1 p X (x i ) g (x i ) jossa x i,i=1,...,n ovat yhtälön y = g(x) reaaliset juuret (37) 79
31 Sovelletaan edellistä tulosta (37) esimerkkiin 1 Nyt Y = ax + b, mutta ei rajoituta tilanteeseen a>0kuten esimerkkissä 1 Yhtälön y = g(x) juuri on y =(y b)/a ja funktion g(x) = ax + b derivaatta on a. Täten p Y (y) = p ( ) X (y b)/a a 80
32 Usean muuttujan tilanne Olkoon X =[x 1... x n ] n dimensioinen satunnaisvektori Sen CDF on F (X) =F (x 1,...,x n ) ja PDF vastaavasti p(x) = p(x 1,...,x n ). Nämä ovat siis muuttujien X 1,...,X n yhteis CDF ja PDF. Vektorimerkintä on siis oiva tapa yksinkertaistaa merkintöjä Meillä on lisäksi yksiarvoiset (yksi ulostulo) funktiot g i (X) jasatunnaismuuttujat Y i = g i (X), jotka riippuvat muuttujista X i,i= 1,...,n Myös Y i :t ja g i (X):t voidaan vektorisoida eli Y =[Y 1... Y n ]ja g(x) =[g 1 (X)... g n (X)] Lisäksi oletetaan että käänteiskuvaukset x i = g 1 (Y) ovatolemassa ja käänteisfunktiot ovat yksiarvoisia. Lisäksi vaaditaan, että funktioiden osittaisderivaatat ovat jatkuvia 81
33 (seuraava tulos ei siis sovi joka tilanteeseen) Silloin p(y) on ( p Y (Y) =p X g 1 (Y) ) g 1 (Y) (38) Y = p ( X g 1 (Y) ) g(x) (39) X Determinantit g 1 (Y) Y ja g(x) ovat kuvausten g 1 (Y)jag(X) X Jacobiaanit Jacobiaanit ovat g1 1 g1 g 1 y (Y) 1 1 y n Y =..... ja g g(x) 1 g x 1 1 x n gn 1 X =..... (40) g y 1 n g x 1 n x n g 1 n y n 82
34 Jacobiaanit ovat siis muunnosten osittaisderivaatoista muodostettujen matriisien determinatteja Tulos (38) on esitetty oppikirjassa Tulosta (39) ei ole esitetty oppikirjassa mutta se voi olla hyödyllinen, sitähän käytettiin jo yhden muuttujan funktion jakauman löytämisessä eli yksikäsitteisessä tapauksessa tulos (37) on suora seuraus tuloksesta (39) 83
35 Tulos (37) on hieman yleisempi (yhdelle muuttujalle) kuin (39), sillä siinä voiyhtälöllä y = g(x) voi olla useita ratkaisuja, mutta ratkaisussa (39) on oletettu yksi ratkaisu yhtälöryhmälle Y = g(x). Tulos (39) on toki yleistettävissä Otetaan seuraava lineaarisen muunnoksen yleistys esimerkiksi kummankin tavan käytöstä. Kyseistä muunnosta käytetään hyvin usein, joten esimerkki on hyödyllinen Olkoon Y = AX + b, jossa A on ei-singulaarinen n n muunnosmatriisi, Y ja X ovat n 1 satunnaisvektoreita ja b on n 1 vakiovektori Tällöin matriisin A käänteismatriisi A 1 on olemassa Käytetään ensin tapaa (38) Nyt X = A 1 (Y b) =g 1 (Y) Käänteiskuvauksen g 1 (Y) Jacobiaani on A 1 84
36 Näin on koska A 1 (Y b)/ Y = {A 1 Y A 1 b}/ Y = A 1 Miksi näin? Tarkastellaan matriisi vektoritulon Ay i:nettäelementtiä x i = j a ijy j, jossa a ij ja y j ovat m n matriisin A ja n 1 vektorin y elementit. Silloin x i = { j a } ijy j y k y k = { } a i1 y a ik y k a in y n = a ik y k eli matriisin A (i, k) :s elementti Osittaisderivaattoja x i y on m n kpl jotka järjestettynä matriisiin antavat halutun tuloksen eli k x y = {Ay} = A y 85
37 Tuloksen (38) mukaan saadaan siis ( p(y) =p X A 1 (Y b) ) A 1 = p ( X A 1 (Y b) ) A sillä determinanteille pätee A 1 =1/ A Käytetään sitten tapaa (39) Tarkasteltava muunnos on Y = AX + b = g(x) Muunnoksen g(x) Jacobiaani on A Tuloksen (39) mukaan p(y) = p ( X A 1 (Y b) ) A joka on sama kuin tuloksen (38) avulla laskettu tulos 86
38 Tilastolliset keskiarvot Satunnaismuutujien tilastolliset keskiarvot ovat usein tarvittu ominaisuus ja ne ilmenevät useissa eri yhteyksissä, esim. demodulaattorien ja kanavakorjainten suunnittelussa Tärkeimpinä ovat ehkäpä ensimmäinen ja toinen momentti ja 2. keskeismomentti. Satunnaismuuttujan n:s momentti on E{X n } = x n p(x) dx (41) 1. momenttia kutsutaan satunnaismuuttujan tilastolliseksi keskiarvoksi tai odotusarvoksi (mean or expected value) ja se on E{X} m x = xp(x) dx (42) 87
39 Olkoon satunnaismuuttuja Y = g(x). Sen odotusarvo on E{Y } = g(x)p(x) dx (43) Miksi tämä kuvaa (yleisesti) keskiarvoa? Diskreetissä tapauksessa E{Y } = i g(x i)p (x = x i )δ(x x i ) selvästi kuvaa muuttujien g(x i )keskimääräistä arvoa Esim. nopanheitossa, jos g(x) = nopan silmäluku, saadaan 1 1/6+2 1/ /6 =3, 5 eli 1 esiintyy frekvenssillä 1/6, 2 frekvenssillä 1/6 jne. ja keskimääräinen arvo on 3,5 jatkuville muuttujille keskimääräinen arvo vastaa ylläolevaa integraalia 88
40 Olkoon Y =(X m x ) n eli X josta on vähennetty keskiarvo (potenssiin n) Tämän keskiarvo on E{(X m x ) n } = (x m x ) n p(x) dx (44) jota kutsutaan n:ksi keskeismomentiksi Se on momentti keskiarvon suhteen 2. keskeismomenttia kutsutaan varianssiksi ja se on E{(X m x ) 2 } σ 2 x = (x m x ) 2 p(x) dx (45) ja se kuvaa muuttujan arvon heilumista keskiarvon ympärillä eli hajontaa 89
41 Purkamalla neliöinti saadaan σx 2 = (x 2 2xm x + m 2 x)p(x) dx = x 2 2 p(x) dx 2m x xp(x) dx +mx p(x) dx }{{}}{{}}{{} E{X 2 } m x 1 =E{X 2 } m 2 x (46) joka muodostaa yhteyden varianssin sekä ensimmäisen ja toisen momentin välille Nollakeskiarvoiselle satunnaismuuttujalle varianssi ja toinen momentti ovat samat 90
42 Kahden muuttujan tapauksessa saadaan yhteismomentti E{X k 1 X n 2 } = sekä yhteis keskeismomentti E{(X 1 m 1 ) k (X 2 m 2 ) n } = x k 1x n 2p(x 1,x 2 ) dx 1 dx 2 (47) (x 1 m 1 ) k (x 2 m 2 ) n p(x 1,x 2 ) dx 1 dx 2 (48) jossa m i =E{X i }. Kiinnostavin tilanne on kun n = k = 1. Silloin muuttujien X i ja X j yhteismomenttia kutsutaan korrelaatioksi ja yhteiskeskeismomenttia kovarianssiksi 91
43 Korrelaatio on siis ja kovarianssi on E{X i X j } (49) µ ij =E{(X i m i )(X j m j )} (50) eli ne ovat muuttujien tulojen odotusarvot Kovarianssin sekä korrelaation ja keskiarvojen välillä onyhteys µ ij =E{X i X j X i m j m i X j + m i m j } =E{X i X j } E{X i } m }{{} j m i E{X j } +m }{{} i m j m i =E{X i X j } m i m j (51) Nollakeskiarvoisille muuttujille korrelaatio ja kovarianssi ovat samat m j 92
44 Useamman muuttujan tapauksessa voidaan myös määritellä erilaisia yhteismomentteja mutta useimmiten ollaan kiinnostuttu vain korrrelaatiosta ja kovarianssista eri muuttujien välillä. Olkoon meillä satunnaisvektori X = [X 1 X 2... X n ] T jossa yläindeksi T tarkoittaa transpoosia. X on siis n 1 pystyvektori Korrelaattiomatriisi sisältää vektorin X alkioiden väliset korrelaatiot ja kovarianssimatriisi niiden väliset kovarianssit Korrelaatiomatriisi on siis E{X 1 X 1 } E{X 1 X 2 }... E{X 1 X n } E{XX T } = E{X 2 X 1 } E{X 2 X 2 }... E{X 2 X n } (52) E{X n X 1 } E{X n X 2 }... E{X n X n } Diagonaali sisältää kunkin alkion 2. keskeismomentin ja diagonaalin ulkopuoliset elementit alkioiden välisiä yhteismomentteja 93
45 ... m n ] T muuttujien X i keskiarvo- Olkoon m =E{X} =[m 1 vektori Kovarianssimatriisi on E{(X m)(x m) T } = µ 11 µ µ 1n µ 21 µ µ 2n (53) µ n1 µ n2... µ nn Diagonaali sisältää alkioiden varianssit sillä µ ii = σ 2 i Vastaavasti voidaan määrittää satunnaisvektorien X ja Y väliset ristikorrelaatio- ja -kovarianssimatriisi eli E{XY T } ja E{(X m x )(Y m y ) T } 94
46 Korreloimattomuus Kahta satunnaismuuttujaa X i ja X j sanotaan korreloimattomiksi jos niiden välinen kovarianssi on nolla eli µ ij =0 Tästä seuraa se, että korrelaatio on keskiarvojen tulo, silläyhtälöstä µ ij =E{X i X j } m i m j = m i m j =0 saadaan E{X i X j } = m i m j =E{X i } E{X j } Tästä seuraa että tilastollisesti riippumattomat satunnaismuuttujat ovat korreloimattomia Tästä ei seuraa että korreloimattomat satunnaismuuttujat ovat välttämättä riippumattomia (näin toki voi olla) Satunnaismuuttujien sanotaan olevan ortogonaalisia jos E{X i X j } =0 95
47 Näin on esim. jos muuttujat ovat korreloimattomia ja jompi kumpi tai molemmat keskiarvoista ovat nollia 96
48 Karakteristinen funktio Määritelmän mukaan satunnaismuuttujan karakteristinen funktio on E{e jvx } ψ(jv)= e jvx p(x) dx, j = 1 (54) Tämä vastaa Fourier muunnosta (lukuunottamatta eksponentin miinus merkkiä, mutta sillä eioleväliä) Fourier käänteismuunnoksesta seuraa että muuttujan PDF karakteristisen funktion avulla ilmaistuna on p(x) = 1 ψ(jv)e jvx dv (55) 2π Karakteristisen funktion avulla voidaan siis määrittää muuttujan PDF 97
49 Toinen hyödyllinen seikka on yhteys momentteihin Derivoimalla karakteristien funktio muuttujan v suhteen saadaan dψ(jv) = j xe jvx p(x) dx dv Ratkaisemalla tämä pisteessä v = 0 saadaan dψ(jv) = j xp(x) dx dv v=0 eli 1. momentti (keskiarvo) on ilmaistavissa myös muodossa E{X} = j dψ(jv) (56) dv v=0 98
50 Korkeamman asteen derivaatoista saadaan korkeammille momenteille yhtälö E{X n } =( j) ndn ψ(jv) v=0 (57) dv n Karakteristisen funktion avulla voidaan siis määrätä muuttujan momentit 99
51 Karakteristinen funktio voidaan esittää sarjamuodossa Karakteristisen funktion Taylorin sarja pisteen v = 0ympäristössä on d n ψ(jv) v=0 v n ψ(jv)= dv n n! k=0 Sijoittamalla tähän derivaatan paikalle yhtälöstä (56) saatu derivaatta saadaan ψ(jv)= E{X n } (jv)n (58) n! k=0 Karakteristinen funktio voidaan siis esittää myös momenttien avulla 100
52 Karakteristisen funktion avulla on helppo löytää riippumattomien satunnaismuuttujien summan PDF Tarkastellaan usean muuttujan summaa eli muuttujaa n Y = i=1 X i 101
53 Sen karakteristinen funktio on ψ Y (jv)=e{e jvy } { =E exp ( jv n ) } X i i=1 { n ( ) } =E e jvx i (sillä e a+b = e a e b ) = i=1 ( n i=1 ) e jvx i p(x 1,...,x n ) dx 1...,dx n 102
54 Koska muuttujat X i ovat riippumattomia, niin p(x 1,...,x n )= p(x 1 ) p(x n ) jolloin n [ ] ψ Y (jv)= e jvx i p(x i ) dx i = i=1 n ψ Xi (jv) (59) i=1 Riippumattomien muuttujien summan karakteristinen funktio on siis yksittäisten muuttujien karakterististen funktioiden tulo Summan PDF on tämän käänteinen Fourier muunnos Jos muuttujat ovat identtisesti jakautuneita eli p(x i )=p(x j ) i, j niin ψ Y (jv)= [ ψ X (jv)] n (60) 103
55 Fourier muunnoksen ominaisuuksista seuraa, ettäpdf:iäkäyttäen riippumattomien muuttujien summan PDF on yksittäisten PDF:ien konvoluutio Tulo on kuitenkin usein helpompi laskea kuin konvoluutio, joten karakteristisen funktion käyttö ko. summanpdf:n määräämiseen on useimmiten järkevää 104
56 Usean muuttujan yhteisjakauman tapauksessa tarvitaan moniulotteista Fourier muunnosta n:lle muuttujalle karakteristinen funktio on { n } ψ(jv 1,...,jv n )=E exp (j v i X i ) = i=1 exp (j n v i x i )p(x 1,...,x n ) dx 1...dx n i=1 Kahden muuttujan tapauksessa meillä on ψ(jv 1,jv 2 )= e j(v 1x 1 +v 2 x 2 ) p(x 1,x 2 ) dx 1 dx 2 105
57 Momentit saadaan generoitua vastaavasti kuten yhden muuttujan tapauksessa ottamalla osittaisderivaatat muuttujien suhteen ja ratkaisemalla se pisteissä v i =0 i. Esimerkiksi kahden muuttujan tapauksessa saadaan }{{} jj E{X 1 X 2 } = 2 ψ(jv 1,jv 2 ) v1 v 1 v 2 =v 2 =0 1 Korkeammat momentit voidaan käsitellä vastaavasti 106
Nämä ovat siis minimivaatimukset, enemmänkin saa ja suositellaan
 Mitä pitäisi vähintään osata Tässäkäydään läpi asiat jotka olisi hyvä osata Nämä ovat siis minimivaatimukset, enemmänkin saa ja suositellaan osattavan 333 Kurssin sisältö Todennäköisyyden, satunnaismuuttujien
Mitä pitäisi vähintään osata Tässäkäydään läpi asiat jotka olisi hyvä osata Nämä ovat siis minimivaatimukset, enemmänkin saa ja suositellaan osattavan 333 Kurssin sisältö Todennäköisyyden, satunnaismuuttujien
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
TIEDONSIIRRON MATEMAATTISET MENETELMÄT S. Harri Saarnisaari. Centre for Wireless Communications (CWC) University of Oulu, Finland
 TIEDONSIIRRON MATEMAATTISET MENETELMÄT 2005 521309S Harri Saarnisaari Centre for Wireless Communications (CWC) University of Oulu, Finland Luennot Harri Saarnisaari Yhteystiedot puh. 553 2842, email: harri.saarnisaari@ee.oulu.fi
TIEDONSIIRRON MATEMAATTISET MENETELMÄT 2005 521309S Harri Saarnisaari Centre for Wireless Communications (CWC) University of Oulu, Finland Luennot Harri Saarnisaari Yhteystiedot puh. 553 2842, email: harri.saarnisaari@ee.oulu.fi
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Tarkastellaan sitten tilastollisesti riippumattomien identtisesti kuten X edellä jakautuneiden muuttujien summaa Y = X i. 1 p p. Muuttujan X PDF.
 Jakaumia Seuraavassa esitellään digitaalisessa tietoliikenteessäuseinkäytettyjä jakaumia Esitellään jakaumien CDF, PDF ja karakteristiset funktiot sekä joitain momentteja kuten keskiarvo, 2. momentti ja
Jakaumia Seuraavassa esitellään digitaalisessa tietoliikenteessäuseinkäytettyjä jakaumia Esitellään jakaumien CDF, PDF ja karakteristiset funktiot sekä joitain momentteja kuten keskiarvo, 2. momentti ja
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3
 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
0 kun x < 0, 1/3 kun 0 x < 1/4, 7/11 kun 1/4 x < 6/7, 1 kun x 1, 1 kun x 6/7,
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
Odotusarvo. Odotusarvon ominaisuuksia Satunnaismuuttujien ominaisuuksia 61
 3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä
 J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
Satunnaismuuttujien muunnokset ja niiden jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Mat Sovellettu todennäköisyyslasku A. Moniulotteiset jakaumat. Avainsanat:
 Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
031021P Tilastomatematiikka (5 op) viikko 7
 0302P Tilastomatematiikka (5 op) viikko 7 Jukka Kemppainen Mathematics Division Yhteisjakauma Edellä on tarkasteltu yksiulotteista satunnaismuuttujaa. Sovelluksissa joudutaan usein tarkastelemaan samanaikaisesti
0302P Tilastomatematiikka (5 op) viikko 7 Jukka Kemppainen Mathematics Division Yhteisjakauma Edellä on tarkasteltu yksiulotteista satunnaismuuttujaa. Sovelluksissa joudutaan usein tarkastelemaan samanaikaisesti
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
TKK @ Ilkka Mellin (2008) 1/5
 Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
y x1 σ t 1 = c y x 1 σ t 1 = y x 2 σ t 2 y x 2 x 1 y = σ(t 2 t 1 ) x 2 x 1 y t 2 t 1
 1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
Moniulotteiset satunnaismuuttujat ja jakaumat
 Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu. f(x, y) = k x y, kun 0 < y < x < 1,
 Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Epäyhtälöt ovat yksi matemaatikon voimakkaimmista
 6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella:
 8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
Kurssilla esitetään lyhyt katsaus niihin todennäköisyyden ja satunnaisprosessien peruskäsitteisiin ja -ominaisuuksiin, joita tarvitaan digitaalisten
 Todennäköisyys Kurssilla esitetään lyhyt katsaus niihin todennäköisyyden ja satunnaisprosessien peruskäsitteisiin ja -ominaisuuksiin, joita tarvitaan digitaalisten tietoliikennejärjestelmien ymmärtämisessä
Todennäköisyys Kurssilla esitetään lyhyt katsaus niihin todennäköisyyden ja satunnaisprosessien peruskäsitteisiin ja -ominaisuuksiin, joita tarvitaan digitaalisten tietoliikennejärjestelmien ymmärtämisessä
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
k S P[ X µ kσ] 1 k 2.
![k S P[ X µ kσ] 1 k 2. k S P[ X µ kσ] 1 k 2.](/thumbs/92/110318530.jpg) HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 7 (vko 44/003) (Aihe: odotusarvon ja varianssin ominaisuuksia, satunnaismuuttujien lineaarikombinaatioita,
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe (kesto 2h 30 min)
 Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat. Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat
 TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat Johdatus todennäköisyyslaskentaan todennäköisyysjakaumat TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat: Mitä opimme? /5 hden satunnaismuuttujan todennäköisyysjakaumat
TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat Johdatus todennäköisyyslaskentaan todennäköisyysjakaumat TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat: Mitä opimme? /5 hden satunnaismuuttujan todennäköisyysjakaumat
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Luento KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja
 1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
Inversio-ongelmien laskennallinen peruskurssi Luento 7
 Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
3. laskuharjoituskierros, vko 6, ratkaisut
 Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Olkoon R S otosavaruuksien R ja S karteesinen tulo: Satunnaismuuttujien X ja Y järjestetty pari (X, Y) määrittelee kaksiulotteisen satunnaismuuttujan:
 Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
Käänteismatriisi 1 / 14
 1 / 14 Jokaisella nollasta eroavalla reaaliluvulla on käänteisluku, jolla kerrottaessa tuloksena on 1. Seuraavaksi tarkastellaan vastaavaa ominaisuutta matriiseille ja määritellään käänteismatriisi. Jokaisella
1 / 14 Jokaisella nollasta eroavalla reaaliluvulla on käänteisluku, jolla kerrottaessa tuloksena on 1. Seuraavaksi tarkastellaan vastaavaa ominaisuutta matriiseille ja määritellään käänteismatriisi. Jokaisella
Liittomatriisi. Liittomatriisi. Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä. 1) i+j det A ij.
 Liittomatriisi Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä (cof A) ij =( 1) i+j det A ij kaikilla i, j = 1,...,n. Huomautus 8 Olkoon A 2 M(n, n). Tällöin kaikilla
Liittomatriisi Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä (cof A) ij =( 1) i+j det A ij kaikilla i, j = 1,...,n. Huomautus 8 Olkoon A 2 M(n, n). Tällöin kaikilla
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
0 3 y4 dy = 3 y. 15x 2 ydx = 15. f Y (y) = 5y 4 1{0 y 1}.
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Kertymäfunktio. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
 Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
Johdatus tn-laskentaan perjantai 17.2.2012
 Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia: Mitä opimme?
 TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi. Viikko 3. Kaksiulotteiset satunnaismuuttujat
 .9. Kaksiulotteiset satunnaismuuttujat MS-A Todennäköisslaskennan ja tilastotieteen peruskurssi Viikko Moniulotteiset satunnaismuuttujat sekä niiden jakaumat ja tunnusluvut; Moniulotteisia jakaumia Usein
.9. Kaksiulotteiset satunnaismuuttujat MS-A Todennäköisslaskennan ja tilastotieteen peruskurssi Viikko Moniulotteiset satunnaismuuttujat sekä niiden jakaumat ja tunnusluvut; Moniulotteisia jakaumia Usein
4.1 Diskreetin satunnaismuuttujan odotusarvo
 4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
Matriisilaskenta, LH4, 2004, ratkaisut 1. Hae seuraavien R 4 :n aliavaruuksien dimensiot, jotka sisältävät vain
 Matriisilaskenta LH4 24 ratkaisut 1 Hae seuraavien R 4 :n aliavaruuksien dimensiot jotka sisältävät vain a) Kaikki muotoa (a b c d) olevat vektorit joilla d a + b b) Kaikki muotoa (a b c d) olevat vektorit
Matriisilaskenta LH4 24 ratkaisut 1 Hae seuraavien R 4 :n aliavaruuksien dimensiot jotka sisältävät vain a) Kaikki muotoa (a b c d) olevat vektorit joilla d a + b b) Kaikki muotoa (a b c d) olevat vektorit
JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos)
 J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
J. Virtamo 38.3143 Jonoteoria / Jatkuvat jakaumat 1 JATKUVAT JAKAUMAT Laplace-muunnos (Laplace-Stieltjes-muunnos) Määritelmä Ei-negatiivisen satunnaismuuttujan X 0, jonka tiheysfunktio on f(x), Laplace-muunnos
Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä palamisaikaa?
 21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
5 Ominaisarvot ja ominaisvektorit
 5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X Y Bin(Y, θ) Y Poi(λ) λ y. f X (x) (λθ)x
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
1 Ominaisarvot ja ominaisvektorit
 1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
Inversio-ongelmien laskennallinen peruskurssi Luento 2
 Inversio-ongelmien laskennallinen peruskurssi Luento 2 Kevät 2012 1 Lineaarinen inversio-ongelma Määritelmä 1.1. Yleinen (reaaliarvoinen) lineaarinen inversio-ongelma voidaan esittää muodossa m = Ax +
Inversio-ongelmien laskennallinen peruskurssi Luento 2 Kevät 2012 1 Lineaarinen inversio-ongelma Määritelmä 1.1. Yleinen (reaaliarvoinen) lineaarinen inversio-ongelma voidaan esittää muodossa m = Ax +
031021P Tilastomatematiikka (5 op) viikko 3
 031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
031021P Tilastomatematiikka (5 op) viikko 3 Jukka Kemppainen Mathematics Division Jakauman tunnusluvut Jakauman tärkeimmät tunnusluvut ovat odotusarvo ja varianssi. Odotusarvo ilmoittaa jakauman keskikohdan
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Satunnaismuuttujan odotusarvo ja laskusäännöt
 Luku 3 Satunnaismuuttujan odotusarvo ja laskusäännöt Lasse Leskelä Aalto-yliopisto 16. syyskuuta 2017 3.1 Odotusarvon käsite ja suurten lukujen laki Lukuarvoisen satunnaismuuttujan X odotusarvo määritellään
Luku 3 Satunnaismuuttujan odotusarvo ja laskusäännöt Lasse Leskelä Aalto-yliopisto 16. syyskuuta 2017 3.1 Odotusarvon käsite ja suurten lukujen laki Lukuarvoisen satunnaismuuttujan X odotusarvo määritellään
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Johdatus todennäköisyyslaskentaan Kertymäfunktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
V ar(m n ) = V ar(x i ).
 Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
Diskreetin satunnaismuuttujan odotusarvo, keskihajonta ja varianssi
 TOD.NÄK JA TILASTOT, MAA0 Diskreetin satunnaismuuttujan odotusarvo, keskihajonta ja varianssi Kuten tilastojakaumia voitiin esittää tunnuslukujen (keskiarvo, moodi, mediaani, jne.) avulla, niin vastaavasti
TOD.NÄK JA TILASTOT, MAA0 Diskreetin satunnaismuuttujan odotusarvo, keskihajonta ja varianssi Kuten tilastojakaumia voitiin esittää tunnuslukujen (keskiarvo, moodi, mediaani, jne.) avulla, niin vastaavasti
BM20A0300, Matematiikka KoTiB1
 BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
Insinöörimatematiikka D
 Insinöörimatematiikka D M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Luentokalvot 5 1
Insinöörimatematiikka D M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Luentokalvot 5 1
2. Jatkoa HT 4.5:teen ja edelliseen tehtavään: Määrää X:n kertymäfunktio F (x) ja laske sen avulla todennäköisyydet
 Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Satunnaismuuttujat ja jakaumat
 Luku 2 Satunnaismuuttujat ja jakaumat Lasse Leskelä Aalto-yliopisto 2. syyskuuta 207 2. Satunnaismuuttujan käsite Käytännön tilanteissa ei yleensä olla kiinnostuneita satunnaisilmiön kaikista yksityiskohdista,
Luku 2 Satunnaismuuttujat ja jakaumat Lasse Leskelä Aalto-yliopisto 2. syyskuuta 207 2. Satunnaismuuttujan käsite Käytännön tilanteissa ei yleensä olla kiinnostuneita satunnaisilmiön kaikista yksityiskohdista,
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
Ennakkotehtävän ratkaisu
 Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
a 1 y 1 (x) + a 2 y 2 (x) = 0 vain jos a 1 = a 2 = 0
 6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
5 Differentiaaliyhtälöryhmät
 5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
Generointi yksinkertaisista diskreeteistä jakaumista
 S-38.148 Tietoverkkojen simulointi / Satunnaismuuttujien generointi 1(18) Generointi yksinkertaisista diskreeteistä jakaumista Seuraavassa U, U 1,..., U n tarkoittavat riippumattomia U(0,1)-jakautuneita
S-38.148 Tietoverkkojen simulointi / Satunnaismuuttujien generointi 1(18) Generointi yksinkertaisista diskreeteistä jakaumista Seuraavassa U, U 1,..., U n tarkoittavat riippumattomia U(0,1)-jakautuneita
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi on lineaarinen projektio.
 Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Otosavaruus ja todennäköisyys Otosavaruus Ë on joukko, jonka alkiot ovat kokeen tulokset Tapahtuma on otosavaruuden osajoukko
 ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
ÌÓÒÒĐĐÓ ÝÝ ÔÖÙ ØØ Naiiveja määritelmiä Suhteellinen frekvenssi kun ilmiö toistuu Jos tehdas on valmistanut 1000000 kpl erästä tuotetta, joista 5013 ovat viallisia, niin todennäköisyys, että tuote on viallinen
8.1 Ehdolliset jakaumat
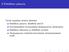 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Differentiaali- ja integraalilaskenta 2 (CHEM) MS-A0207 Hakula/Vuojamo Kurssitentti, 12.2, 2018, arvosteluperusteet
 ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
Harjoitus 2: Matlab - Statistical Toolbox
 Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Jos nyt on saatu havaintoarvot Ü ½ Ü Ò niin suurimman uskottavuuden
 1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
