Hex-pelin matematiikkaa
|
|
|
- Esa Saaristo
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Solmu 3/ Hex-pelin matematiikkaa Tuomas Korppi Johdanto Hex on kahden pelaajan strategiapeli, jonka ovat keksineet toisistaan riippumatta matemaatikot Piet Hein ja taloustieteen Nobelinkin saanut John Nash 1. Peli on siitä mielenkiintoinen, että sitä on mahdollista analysoida matemaattisesti aika pitkälle, mutta ei kuitenkaan niin pitkälle, että käytännön pelaaminen olisi orjallista kaavojen seuraamista. Tässä kirjoitelmassa esittelemme Hexin ja todistamme muutaman peliä koskevan teoreeman. Esityksemme perustuu osin teokseen Browne [1]. Hexin säännöt Hexiä pelataan timantinmuotoisella pelilaudalla, jolla on kuusikulmioista koostuva ruudutus (nk. heksaruudutus). Kaksi vastakkaista pelilaudan sivua on merkitty mustiksi ja toiset kaksi vastakkaista sivua valkoisiksi. (Katso kuva 1.) Piet Hein suositteli peliin kuusikulmiosta eli heksasta koostuvaa lautaa, joka on nykyisin yleisimmin käytetty, ja John Nash puolestaan heksasta koostuvaa lautaa. Allekirjoittaneen suosikkikoko on Kuva 1: 4 4 -lauta. Toinen pelaaja pelaa mustilla pelinappuloilla ja toinen valkoisilla. Pelinappuloita oletetaan olevan tarpeeksi niin, että ne eivät voi loppua kesken. Peli alkaa tyhjältä laudalta. Vuorollaan pelaaja asettaa yhden omanvärisensä pelinappulan johonkin pelilaudan vapaaseen kuusikulmioon. Pelin voittaa se pelaaja, joka saa yhdistettyä omanvärisensä pelilaudan sivut omanvärisistä, vierekkäisissä heksoissa sijaitsevista nappuloista koostuvalla nappulaketjulla. Voittava ketju saa mutkitella kuinka paljon tahansa, kunhan se yhdistää sivut. (Katso kuva 2.) Laudan kulmaheksojen katsotaan kuuluvan kumpaankin viereiseen sivuun. 1 Anekdootin mukaan Nashin keksimänä peli tunnettiin nimellä John (englanninkielinen slangi-ilmaus vessalle), koska pelilauta muistuttaa vessan lattian laatoitusta.
2 2 Solmu 3/2013 Edellisen tuloksen nojalla myös Hexissä jommalla kummalla on voittostrategia tai kummallakin on tasapelistrategia. Hexistä tiedetään kuitenkin hiukan enemmänkin, ja tätä käsittelemme seuraavassa luvussa. Teoreemalle saadaan helposti seuraava korollaari: Korollaari 2. Jos edellisessä teoreemassa peli ei voi päättyä tasapeliin, jommalla kummalla on voittostrategia. Kuva 2: Mustan voittopolku. Ylä- ja alalaidat on yhdistetty. Täyden informaation pelit Tarkoitamme täyden informaation pelillä lauta- tai vastaavaa peliä, joka toteuttaa kaikki seuraavat ehdot: Pelissä ei ole satunnaisuutta (kuten nopanheittoa). Pelissä ei ole tietoa, jonka vain osa pelaajista tietäisi (kuten pelaajan kädessä olevat kortit). Pelaajat tekevät siirrot vuorotellen. (Pelissä ei siis ole kivi-sakset-paperi -pelin tyyppistä yhtaikaista siirtojen valitsemista.) Siis esimerkiksi shakki, go ja hex ovat täyden informaation pelejä. Voittostrategialla tarkoitamme menetelmää, jota seuraamalla pelin voittaa varmasti. Tasapelistrategia tarkoittaa strategiaa, jota seuraamalla saa aikaan varmasti joko voiton tai tasapelin. Voidaan todistaa seuraava teoreema. Todistus jätetään vaikeahkoksi harjoitustehtäväksi. Tehtävää tosin kannattaa yrittää vasta siinä vaiheessa, kun on lukenut tämän kirjoitelman loppuun ja saanut jonkinlaisen kuvan siitä, kuinka tällaisia asioita voidaan todistaa. Teoreema 1. Äärellisessä, kahden pelaajan täyden informaation pelissä jommalla kummalla pelaajalla on voittostrategia tai kummallakin on tasapelistrategia. Shakki on äärellinen peli, koska shakissa on sääntö, jonka mukaan peli on tasapeli, kun laudan asema on toistunut kolme kertaa. Näin ollen meillä on tulos, jonka mukaan shakissakin jommalla kummalla pelaajalla on voittostrategia tai kummallakin on tasapelistrategia. Ei kuitenkaan tiedetä, mikä kyseisistä vaihtoehdoista pätee. On myös mahdollista (ja jopa luultavaa), että kyseiset strategiat ovat niin monimutkaisia, että ihmiset eivät koskaan tule tuntemaan niitä. Huomautamme, että pelin äärellisyysehto on myös olennainen. On olemassa monimutkaisia joukko-opillisia kahden pelaajan täyden informaation pelejä, jotka toteuttavat seuraavat kaikki ehdot: Pelissä tehdään yhteensä ääretön jono siirtoja ja voittaja ratkaistaan tällaisen äärettömän siirtojonon perusteella. Jokainen peli päättyy jomman kumman pelaajan voittoon. Kummallakaan ei ole voittostrategiaa. Jos tässä pelaajat ovat A ja B, jokaiselle A:n strategialle löytyy siis B:n strategia, joka voittaa sen, ja jokaiselle B:n strategialle löytyy A:n strategia, joka voittaa sen. Hexin perustulokset Tässä luvussa todistamme, että Hex-peli ei voi päättyä tasapeliin. Itse asiassa todistamme vahvemman tuloksen, jonka mukaan täyteen pelatulla laudalla toisella ja vain toisella pelaajalla on voittopolku. Todistamme myös, että Hexissä voittostrategia on pelin aloittajalla. Tämä tulos on kuitenkin teoreettinen olemassaolotulos, ja käytännön voittostrategiaa ei tunneta. Teoreema 3. Hex-peli ei voi päättyä tasapeliin. Todistus: Oletetaan, että lauta on pelattu täyteen. Osoitamme, että tässä tilanteessa toisella ja vain toisella pelaajalla on voittava nappulaketju. Teknisistä syistä oletamme, että myös laudan ulkopuolella on nappuloita, mustien sivujen vieressä mustia ja valkoisten sivujen vieressä valkoisia. Oletetaan, että ala- ja yläsivut ovat mustia ja oikea ja vasen sivu valkoisia. Muodostamme tässä todistuksessa polun, joka kulkee heksojen välisiä reunaviivoja pitkin niin, että kaikissa kohdissa polun vasemmalla puolella on valkea nappula ja polun oikealla musta nappula. Tässä siis oikea ja vasen määritellään suhteessa polkua kulkevaan henkilöön. Huomautamme, että jos olemme muodostaneet polkua n askelta ja tulleet kolmen heksan leikkauspisteeseen, voimme aina jatkaa polkua. Jos edessä on valkea nappula, jatkamme polkua oikealle, ja jos edessä on musta nappula, jatkamme polkua vasemmalle.
3 Solmu 3/ Aloitamme polun laudan vasemmasta alanurkasta. Jos siinä on valkoinen nappula, aloitamme sen alapuolelta (tällöin aloituspisteen alla on musta nappula laudan ulkopuolella), ja jos siinä on musta nappula, aloitamme sen vasemmalta puolelta (jolloin sen vasemmalla puolella on valkea nappula laudan ulkopuolella). Jatkamme polkua, kunnes törmäämme laudan ylä- tai oikeaan laitaan. Edellisen kappaleen perusteella polkua voidaan jatkaa näin. Jos törmäämme laudan ylälaitaan, polun oikealla puolella on voittava musta ketju, ja jos törmäämme oikeaan laitaan, polun vasemmalla puolella on voittava valkea ketju. Siis jommalla kummalla pelaajalla on voittava ketju. (Polusta katso kuva 3). Todistuksemme käytti olennaisesti hyväkseen sitä, että lautamme on heksalauta. Tätä käytetään hyväksi siinä vaiheessa, kun todetaan, että polun jommalla kummalla puolella on voittava ketju. Neliöruuduista koostuvalla laudalla olisi mahdollista tehdä nk. ristileikkaus (kuva 4), joka estäisi voittavan ketjun syntymisen. Kuva 4: Ristileikkaus. Ristileikkauksen avulla on mahdollista tehdä neliöruuduilla pelattavalle Hex-pelille tasapelitilanne, joka on esitetty kuvassa 5. Kuva 3: Vahvennettuna polku, joka konstruoitiin Teoreeman 3 todistuksessa. Polkumme tosiaan päätyy lopulta joko oikeaan tai ylälaitaan. Se ei nimittäin voi päättyä silmukkaan, koska tällöin silmukan lopussa olisi vääränvärisiä nappuloita ketjun oikealla tai vasemmalla puolen. Perustelemme vielä sen, että polun toisella puolella on tosiaan voittava ketju. Oletetaan, että törmäsimme ylälaitaan. (Jos törmäsimme oikeaan laitaan, todistus menee samoin.) Jokaisen polkuun kuuluvan heksan sivun oikealla puolella on musta pelinappula. Koska kahdella peräkkäisellä polkuun kuuluvalla heksan sivulla on yhteinen kärki, yhteinen kärki on myös niillä peräkkäisillä heksoilla, joissa on mustat pelinappulat. Kyseisillä heksoilla on myös yhteinen sivu, koska heksalaudalla kahdella heksalla on yhteinen sivu, jos niillä on yhteinen kärki. Siis edellä mainittu musta ketju koostuu heksoista, joista kahdella peräkkäisellä on aina yhteinen sivu, joten kyseessä on voittoketju. Lisäksi havaitsemme, että voittava ketju jakaa pelilaudan kahtia niin, että tilanne, jossa kummallakin on voittava ketju on mahdoton. Todistuksessa mainitut seikat tarkoittavat sitä, että ainoa keino blokata vastustaja Hex-pelissä on muodostaa oma voittava ketju. Käytännön pelissä tämä tarkoittaa sitä, että Hexissä hyökkääminen (oman ketjun muodostaminen) ja puolustaminen (vastustajan estäminen) ovat yksi ja sama asia. Kuva 5: Ruutulaudalla Hex voi päättyä tasapeliin. Teoreema 4. Hex-pelissä ensimmäisenä pelaavalla on voittostrategia. Todistus: Oletetaan, että toisena pelaavalla on voittostrategia S ja johdetaan ristiriita. Ensimmäisenä pelaava muodostaa strategian S, joka on muutoin sama kuin S, mutta siinä mustan ja valkoisen roolit on vaihdettu, ja lautaa on peilattu jomman kumman lävistäjän suhteen niin, että sivujen väritykset vastaavat uusia pelaajien rooleja. Nyt ensimmäisenä pelaava voi pelata seuraavasti: Hän tekee ensimmäisen siirron mielivaltaisesti. Tämän jälkeen hän pelaa strategialla S kuvitellen, ettei ole tehnyt ensimmäistä siirtoaan. Jos hänen jossain kohti peliä täytyy tehdä S :n mukaan ensimmäinen siirtonsa, hän lakkaa kuvittelemasta, ettei ole tehnyt ensimmäistä siirtoaan, tekee mielivaltaisen siirron ja kuvittelee jatkossa, ettei ole tehnyt uutta mielivaltaista siirtoaan. Jos hänen täytyy myöhemmin tehdä S :n mukaan se siirto, jota hän ei kuvittele tehneensä, hän lakkaa kuvittelemasta... Koska S on voittostrategia, sitä on myös S. Koska siitä siirrosta, jota ensimmäinen pelaaja ei kuvittele tehneensä, ei ole ensimmäisenä pelaavalle missään tilanteessa haittaa, ensimmäisenä pelaava voittaa. Ristiriita sen kanssa, että toisena pelaavalla on voittostrategia.
4 4 Solmu 3/2013 Koska kyseessä on äärellinen peli, joka ei voi päättyä tasapeliin, jommalla kummalla on voittostrategia. Koska edellisen argumentin nojalla toisena pelaavalla ei ole voittostrategiaa, voittostrategia on ensimmäisenä pelaavalla. Samanlaisella argumentilla voidaan näyttää, että missä tahansa äärellisessä kahden pelaajan täyden informaation pelissä, joka ei voi päättyä tasapeliin, jossa pelaajien roolit ovat symmetriset, eikä siirrosta ole missään tapauksessa siirron tekijälle haittaa, on ensimmäisenä pelaavalla voittostrategia. Jos muut ehdot pätevät, mutta peli voi päättyä myös tasapeliin, samanlaisella argumentilla voidaan näyttää, että joko ensimmäisenä pelaavalla on voittostrategia tai peli päättyy optimaalisella pelillä tasapeliin. Tässä on huomattava, että ensimmäisen pelaajan voittostrategian olemassaolon todistaminen on puhdas olemassaolotodistus: Se kertoo, että ensimmäisenä pelaavalla on voittostrategia, mutta se ei kerro mitään siitä, millainen tuo voittostrategia on. Hexin tapauksessa sitä ei tiedetäkään, joten käytännön pelaaminen on mielekästä. ja myös jonkinasteinen käytännön etu. Koska voittostrategiaa ei tunneta, ei etu ole paremmalle pelaajalle ylitsepääsemätön. Voisi olla houkutteleva idea antaa heikommalle pelaajalle tasoitusta niin, että hän pelaa ylä- ja alalaitoja yhdistäen, ja lauta on tässä suunnassa kapeampi. Tämä idea ei kuitenkaan toimi, koska tällöin on olemassa tunnettu voittostrategia. Teoreema 5. Oletetaan, että meillä on Hex-lauta, joka on pystysuunnassa n 1 heksan kokoinen ja vaakasuunnassa n heksan kokoinen. Tällöin ylä- ja alalaitoja yhdistävällä pelaajalla on tunnettu voittostrategia, vaikka hän pelaisi toisena. Todistus: Merkitään laudan heksat kirjaimilla kuten kuvassa 6. Reilun pelin aikaansaaminen Kuten edellisessä luvussa totesimme, ensimmäisenä pelaavalla on teoreettinen etu. Pelikokemus on osoittanut, että ensimmäisenä pelaavalla on huomattava etu myös käytännön peleissä. Tämän johdosta Hex-pelin alussa käytetäänkin nk. kakunleikkaussääntöä (englanniksi pie rule), joka toimii seuraavasti: Ensimmäisenä pelaava tekee mustilla aloitussiirron. Tämän jälkeen toisena pelaava valitsee, pelaako hän mustilla vai valkoisilla. Tämän jälkeen peli jatkuu valkean pelaajan siirrolla ja sen jälkeen normaalisti vuorotellen värejä. Tätä protokollaa noudattaen ensimmäisen mustan siirron ei kannata olla liian hyvä, vaan sellainen, että kummallakin on siirron jälkeen suunnilleen yhtä hyvät voitonmahdollisuudet. Kakunleikkaussääntö onkin saanut nimensä operaatiosta, jossa jaetaan kakku kahteen osaan niin, että ensimmäinen ruokailija leikkaa kakun kahtia ja toinen ruokailija valitsee kumman osan ottaa. Toinen osa jää halkaisijalle. Lukijalle jätetään harjoitustehtäväksi osoittaa, että käytettäessä Hexissä kakunleikkaussääntöä on toisena pelaavalla teoreettinen voittostrategia. Jos toinen pelaajista on heikompi, ei kakunleikkaussääntöä yleensä käytetä, vaan heikompi pelaaja yksinkertaisesti aloittaa pelin. Hänellä on teoreettinen etu, Kuva 6: Ylä- ja alasivuja yhdistävän voittostrategia. Oletetaan, että ylä- ja alalaitoja yhdistävä pelaa toisena. Nyt toisena pelaavan voittostrategia on se, että hän pelaa aina heksaan, missä on sama kirjain kuin vastustajan edellisenä pelaamassa heksassa. Todistamme, että tämä on voittostrategia. Oletetaan, että toinen pelaaja pelaa tällä strategialla, ja tehdään vastaoletus, että ensimmäisenä pelaavalla on voittava ketju P. Oletamme, että ketju alkaa vasemmasta laidasta ja päättyy oikeaan laitaan. Voidaan olettaa, että voittoketju on minimaalinen niin, että se ei leikkaa itseään. Olkoon h ketjun ensimmäinen heksa, jossa ketju käy joidenkin oikeanpuoleisten heksojen A, B tai C kautta. Olkoon h ketjun edellinen heksa. Koska h:ssa ja h :ssa ei voi olla samaa kirjainta, on h yläviistoon h :sta. Olkoon h ketjun m:s nappula ja Q ketjun m ensimmäistä nappulaa. Olkoon R toisen pelaajan vastaukset Q:ta edustaviin siirtoihin yllä kuvaillulla voittostrategialla. Nyt Q ja R muodostavat pussin, jonka sisälle h jää, eikä voittoketju voi edetä maaliinsa kulkematta sellaisen heksan läpi, jossa on R:n nappula (mikä on mahdotonta sääntöjen perusteella) tai Q:n nappula (mikä on mahdotonta, koska oletimme, ettei voittoketju leikkaa itseään.) (Pussi on kuvattu kuvassa 7.)
5 Solmu 3/ Kuva 7: Musta on pelannut valkean rastilla merkityn nappulan pussiin. Siis ensimmäisenä pelaavalla ei voi olla voittoketjua. Koska peli ei voi päättyä tasapeliin, toisena pelaava voittaa, joten hänen strategiansa on voittostrategia. Vaikka olemme yllä käsitelleet 4 3 -lautaa, nähdään helposti, että annettu argumentti yleistyy kaikille laudan koille n (n 1). Lukijalle jätetään harjoitustehtäväksi osoittaa, että sama pätee myös siinä tapauksessa, että pysty- ja vaakasuuntien kokojen ero on enemmän kuin 1, sekä se, että sama pätee myös silloin, kun ylä- ja alalaitoja yhdistävä pelaaja aloittaa pelin. Mistä pelivälineet? Siltä varalta, että lukijalle iski kipinä päästä pelaamaan, selitämme tässä luvussa, kuinka hankkia pelivälineet. Hex-settejä ei käsittääkseni myydä missään, joten pelivälineet joutuu valmistamaan itse. Roolipelivälineitä myyvät kaupat myyvät tuotetta nimeltä Battle Mat. Se on ohut vinyylilauta, jossa on toisella puolella tavallinen ruudutus ja toisella puolella heksaruudutus. Siitä on helppo leikata halutun kokoinen Hex-lauta. Suomessa Battle Matia myy mm. Fantasiapelit ( Hex-nappuloina voidaan käyttää Go-pelin pelinappuloita eli kiviä, joita Suomessa myy Gaimport ( Onnekkaan yhteensattuman ansiosta Battle Mat, jossa on yhden tuuman kokoiset heksat, on juuri oikean kokoinen standardeille Go-kiville. Koska Hexissä nappuloita ei koskaan siirretä tai poisteta laudalta, sitä voi pelata myös kynällä ja paperila. Tähän tarkoitukseen lautoja voi tulostaa Hex Wikistä ( Internetissä Hexiä voi pelata esimerkiksi Little Golemissa ( kirjepelin tahtiin. Little Golem tarjoaa ja lautakoot. Kuva 8: Tämän kirjoitelman ohjeilla toteutettu Hexsetti. Pähkinöitä 1. Olkoon P äärellinen, kahden pelaajan täyden informaation peli, jossa tasapeli on mahdoton. Oletetaan, että P :ssä on kakunleikkaussääntö ensimmäisen siirron jälkeen. Osoita, että toisena pelaavalla on voittostrategia. (Voit olettaa tunnetuksi, että kaikissa kahden pelaajan äärellisissä täyden informaation peleissä, joissa tasapeli ei ole mahdollinen, on jommalla kummalla pelaajalla voittostrategia.) 2. Oletetaan, että Hexissä laudan pystykoko on pienempi kuin vaakakoko, ja ylä- ja alalaitoja yhdistävä pelaa toisena. Konstruoi ylä- ja alalaitoja yhdistävälle voittostrategia. 3. Sama kuin edellä, mutta ylä- ja alalaitoja yhdistävä aloittaa pelin. 4. Teoreeman 5 todistuksessa oletettiin, että voidaan valita voittoketju, joka ei leikkaa itseään. Osoita, että tämä on mahdollista. Osoita siis, että jos P on voittoketju, joka leikkaa itseään, P :n sisällä on voittoketju P, joka ei leikkaa itseään. 5. Osoita, että kaikissa kahden pelaajan äärellisissä täyden informaation peleissä jommalla kummalla pelaajalla on voittostrategia tai kummallakin on tasapelistrategia. (Vihje: Induktio pelin mahdollisista lopputiloista taaksepäin.) Viitteet [1] Browne, Cameron, Hex Strategy: Making the Right Connections, A K Peters Ltd, 2000.
Matematiikkalehti 3/2013. http://solmu.math.helsinki.fi
 Matematiikkalehti 3/013 http://solmu.math.helsinki.fi Solmu 3/013 Solmu 3/013 ISSN-L 1458-8048 ISSN 1459-0395 (Painettu) ISSN 1458-8048 (Verkkolehti) Matematiikan ja tilastotieteen laitos PL 68 (Gustaf
Matematiikkalehti 3/013 http://solmu.math.helsinki.fi Solmu 3/013 Solmu 3/013 ISSN-L 1458-8048 ISSN 1459-0395 (Painettu) ISSN 1458-8048 (Verkkolehti) Matematiikan ja tilastotieteen laitos PL 68 (Gustaf
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 4 ratkaisut Tehtävä 1. Määritä suurin aste k, johon saakka kuvan verkot G ja G ovat osittaisesti isomorfisia: Ratkaisu 1. Huomataan aluksi, että G =4 G : Ehrenfeucht-Fraïssé
Äärellisten mallien teoria Harjoituksen 4 ratkaisut Tehtävä 1. Määritä suurin aste k, johon saakka kuvan verkot G ja G ovat osittaisesti isomorfisia: Ratkaisu 1. Huomataan aluksi, että G =4 G : Ehrenfeucht-Fraïssé
SÄÄNNÖT. Language: English / Suomi
 Rules of Coerceo by Coerceo Company Finnish translation by Janne Henriksson SÄÄNNÖT Language: English / Suomi Tekijänoikeus Mitään tämän dokumentin osaa ei saa jäljentää, kopioida tai välittää missään
Rules of Coerceo by Coerceo Company Finnish translation by Janne Henriksson SÄÄNNÖT Language: English / Suomi Tekijänoikeus Mitään tämän dokumentin osaa ei saa jäljentää, kopioida tai välittää missään
Ohjeet ovat työn alla ja kirjaan niitä päivittäen ja edes takaisin lukien pari viikkoa.
 ( 1 ) Hannu Särön lautapelien ohjeita pelaajille - ( 1 ) - Sisältö. ( 2 ) - Jätkänshakki. ( 3 ) - Reversi. ( 4 ) - Tammi. ( 5 ) - Mylly. ( 6 ) - Shakki. ( 7 ) - Shakki, uudet napit ja uudet laudat. Ohjeet
( 1 ) Hannu Särön lautapelien ohjeita pelaajille - ( 1 ) - Sisältö. ( 2 ) - Jätkänshakki. ( 3 ) - Reversi. ( 4 ) - Tammi. ( 5 ) - Mylly. ( 6 ) - Shakki. ( 7 ) - Shakki, uudet napit ja uudet laudat. Ohjeet
Johdatus go-peliin. 25. joulukuuta 2011
 Johdatus go-peliin 25. joulukuuta 2011 Tämän dokumentin tarkoitus on toimia johdatuksena go-lautapeliin. Lähestymistapamme poikkeaa tavallisista go-johdatuksista, koska tässä dokumentissa neuvotaan ensin
Johdatus go-peliin 25. joulukuuta 2011 Tämän dokumentin tarkoitus on toimia johdatuksena go-lautapeliin. Lähestymistapamme poikkeaa tavallisista go-johdatuksista, koska tässä dokumentissa neuvotaan ensin
Matinteko (1 / 10) Matinteko (2 / 10) Helpointa matin tekeminen on kahdella raskaalla upseerilla (esim. kuningattarella ja tornilla).
 Shakkinappuloiden voimasuhteet Matinteko (1 / 10) Kuningas on pelin tärkein nappula, ilman kuningasta peli on hävitty. 1. Kuningas + Daami + Torni vs Kuningas Matinteko (2 / 10) Helpointa matin tekeminen
Shakkinappuloiden voimasuhteet Matinteko (1 / 10) Kuningas on pelin tärkein nappula, ilman kuningasta peli on hävitty. 1. Kuningas + Daami + Torni vs Kuningas Matinteko (2 / 10) Helpointa matin tekeminen
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Pelaajat siirtävät nappuloitaan vastakkaisiin suuntiin pelilaudalla. Peli alkaa näin. Tuplauskuutio asetetaan yhtä kauas kummastakin pelaajasta.
 DVD Backgammon Pelin tavoite Pelin tavoitteena on siirtää kaikki omat pelinappulat omalle sisäkentälle ja sieltä pois laudalta. Se pelaaja, joka ensimmäisenä on poistanut kaikki pelinappulansa pelilaudalta,
DVD Backgammon Pelin tavoite Pelin tavoitteena on siirtää kaikki omat pelinappulat omalle sisäkentälle ja sieltä pois laudalta. Se pelaaja, joka ensimmäisenä on poistanut kaikki pelinappulansa pelilaudalta,
Pelitehtäviä. Helpot tehtävät. Tuomas Korppi
 Solmu 1/2012 1 Pelitehtäviä Tuomas Korppi Tämänkertaisissa tehtävissä analysoimme yksinkertaisia pelejä. Tehtävät 1 6 ovat helppoja, ja soveltuvat arvioni mukaan yläasteelle 1. Tehtävät 7 11 ovat vaikeampia,
Solmu 1/2012 1 Pelitehtäviä Tuomas Korppi Tämänkertaisissa tehtävissä analysoimme yksinkertaisia pelejä. Tehtävät 1 6 ovat helppoja, ja soveltuvat arvioni mukaan yläasteelle 1. Tehtävät 7 11 ovat vaikeampia,
Yhtenäisyydestä. Johdanto. Lähipisteavaruus. Tuomas Korppi
 Solmu 2/2012 1 Yhtenäisyydestä Tuomas Korppi Johdanto Tarkastellaan kuvassa 1 näkyviä verkkoa 1 ja R 2 :n (eli tason) osajoukkoa. Kuvan 2 verkko voidaan jakaa kolmeen osaan niin, että osien välillä ei
Solmu 2/2012 1 Yhtenäisyydestä Tuomas Korppi Johdanto Tarkastellaan kuvassa 1 näkyviä verkkoa 1 ja R 2 :n (eli tason) osajoukkoa. Kuvan 2 verkko voidaan jakaa kolmeen osaan niin, että osien välillä ei
Determinoiruvuuden aksiooma
 Determinoiruvuuden aksiooma Vadim Kulikov Esitelma 12 Maaliskuuta 2008 Tiivistelma. Valinta-aksioomasta seuraa, etta Leb(R) ( P(R), eli on olemassa epamitallisia joukkoja. Tassa esitelmassa nahdaan, etta
Determinoiruvuuden aksiooma Vadim Kulikov Esitelma 12 Maaliskuuta 2008 Tiivistelma. Valinta-aksioomasta seuraa, etta Leb(R) ( P(R), eli on olemassa epamitallisia joukkoja. Tassa esitelmassa nahdaan, etta
Peliteoria luento 1. May 25, 2015. Peliteoria luento 1
 May 25, 2015 Tavoitteet Valmius muotoilla strategisesti ja yhteiskunnallisesti kiinnostavia tilanteita peleinä. Kyky ratkaista yksinkertaisia pelejä. Luentojen rakenne 1 Joitain pelejä ajanvietematematiikasta.
May 25, 2015 Tavoitteet Valmius muotoilla strategisesti ja yhteiskunnallisesti kiinnostavia tilanteita peleinä. Kyky ratkaista yksinkertaisia pelejä. Luentojen rakenne 1 Joitain pelejä ajanvietematematiikasta.
SEKASTRATEGIAT PELITEORIASSA
 SEKASTRATEGIAT PELITEORIASSA Matti Estola 8. joulukuuta 2013 Sisältö 1 Johdanto 2 2 Ratkaistaan sukupuolten välinen taistelu sekastrategioiden avulla 5 Teksti on suomennettu kirjasta: Gibbons: A Primer
SEKASTRATEGIAT PELITEORIASSA Matti Estola 8. joulukuuta 2013 Sisältö 1 Johdanto 2 2 Ratkaistaan sukupuolten välinen taistelu sekastrategioiden avulla 5 Teksti on suomennettu kirjasta: Gibbons: A Primer
Miten osoitetaan joukot samoiksi?
 Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8
 Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
MS-C2105 Optimoinnin perusteet Malliratkaisut 5
 MS-C2105 Optimoinnin perusteet Malliratkaisut 5 Ehtamo Demo 1: Arvaa lähimmäksi Jokainen opiskelija arvaa reaaliluvun välillä [0, 100]. Opiskelijat, joka arvaa lähimmäksi yhtä kolmasosaa (1/3) kaikkien
MS-C2105 Optimoinnin perusteet Malliratkaisut 5 Ehtamo Demo 1: Arvaa lähimmäksi Jokainen opiskelija arvaa reaaliluvun välillä [0, 100]. Opiskelijat, joka arvaa lähimmäksi yhtä kolmasosaa (1/3) kaikkien
Määritelmä, alkuluku/yhdistetty luku: Esimerkki . c) Huomautus Määritelmä, alkutekijä: Esimerkki
 Alkuluvut LUKUTEORIA JA TODISTAMINEN, MAA11 Jokainen luku 0 on jaollinen ainakin itsellään, vastaluvullaan ja luvuilla ±1. Kun muita eri ole, niin kyseinen luku on alkuluku. Määritelmä, alkuluku/yhdistetty
Alkuluvut LUKUTEORIA JA TODISTAMINEN, MAA11 Jokainen luku 0 on jaollinen ainakin itsellään, vastaluvullaan ja luvuilla ±1. Kun muita eri ole, niin kyseinen luku on alkuluku. Määritelmä, alkuluku/yhdistetty
Trafficars - Ruuhkaara
 760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Luonnollisten lukujen induktio-ominaisuudesta
 Solmu 1/2019 19 Luonnollisten lukujen induktio-ominaisuudesta Tuomas Korppi Johdanto Kuten lukija varmaan tietääkin, luonnollisille luvuille voidaan tehdä induktiotodistuksia. Tämä mahdollisuus on ominainen
Solmu 1/2019 19 Luonnollisten lukujen induktio-ominaisuudesta Tuomas Korppi Johdanto Kuten lukija varmaan tietääkin, luonnollisille luvuille voidaan tehdä induktiotodistuksia. Tämä mahdollisuus on ominainen
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Todistusmenetelmiä Miksi pitää todistaa?
 Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Matematiikan tukikurssi, kurssikerta 2
 Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
Toistetut pelit Elmeri Lähevirta. MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly
 Toistetut pelit MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Elmeri Lähevirta The document can be stored and made available to the public on the open internet pages of Aalto University.
Toistetut pelit MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Elmeri Lähevirta The document can be stored and made available to the public on the open internet pages of Aalto University.
LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT
 LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT 1. Alkupohdintaa Mitä lempipelejä oppilailla on? Ovatko ne pohjimmiltaan matemaattisia? (laskeminen, todennäköisyys ) Mitä taktiikoita esimerkiksi
LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT 1. Alkupohdintaa Mitä lempipelejä oppilailla on? Ovatko ne pohjimmiltaan matemaattisia? (laskeminen, todennäköisyys ) Mitä taktiikoita esimerkiksi
Impedanssitomografia-peli
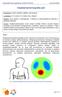 Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Bayesin pelit. Kalle Siukola. MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly
 Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
Tehtävä 8 : 1. Tehtävä 8 : 2
 Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Tehtävä 4 : 2. b a+1 (mod 3)
 Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Shakkiopas vähemmän pelanneille
 Shakkiopas vähemmän pelanneille Sisällysluettelo: 1. Siirtäminen 2. Yleisiä muodollisuuksia 3. Pöytäkirjan pito 4. Avaukset yleensä 5. Siirron miettiminen 6. Vastustajan vuoro 7. Koulumatti ja Preussilainen
Shakkiopas vähemmän pelanneille Sisällysluettelo: 1. Siirtäminen 2. Yleisiä muodollisuuksia 3. Pöytäkirjan pito 4. Avaukset yleensä 5. Siirron miettiminen 6. Vastustajan vuoro 7. Koulumatti ja Preussilainen
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Muinaiset kreikkalaiset uskoivat kaiken maanpäällisen koostuvan neljästä elementistä: maasta, ilmasta, vedestä ja tulesta.
 Johdanto Muinaiset kreikkalaiset uskoivat kaiken maanpäällisen koostuvan neljästä elementistä: maasta, ilmasta, vedestä ja tulesta. Jumalten maailma, kaikki ihmisten maailman yläpuolinen, koostui viidennestä
Johdanto Muinaiset kreikkalaiset uskoivat kaiken maanpäällisen koostuvan neljästä elementistä: maasta, ilmasta, vedestä ja tulesta. Jumalten maailma, kaikki ihmisten maailman yläpuolinen, koostui viidennestä
Helsingin seitsemäsluokkalaisten matematiikkakilpailu Ratkaisuita
 Helsingin seitsemäsluokkalaisten matematiikkakilpailu 22..204 Ratkaisuita. Laske 23 45. a) 4000 b) 4525 c) 4535 d) 5525 e) 5535 Ratkaisu. Lasketaan allekkain: 45 23 35 90 45 5535 2. Yhden maalipurkin sisällöllä
Helsingin seitsemäsluokkalaisten matematiikkakilpailu 22..204 Ratkaisuita. Laske 23 45. a) 4000 b) 4525 c) 4535 d) 5525 e) 5535 Ratkaisu. Lasketaan allekkain: 45 23 35 90 45 5535 2. Yhden maalipurkin sisällöllä
(iv) Ratkaisu 1. Sovelletaan Eukleideen algoritmia osoittajaan ja nimittäjään. (i) 7 = , 7 6 = = =
 JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 7, MALLIRATKAISUT Tehtävä Etsi seuraavien rationaalilukujen ketjumurtokehitelmät: (i) 7 6 (ii) 4 7 (iii) 65 74 (iv) 63 74 Ratkaisu Sovelletaan Eukleideen algoritmia
JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 7, MALLIRATKAISUT Tehtävä Etsi seuraavien rationaalilukujen ketjumurtokehitelmät: (i) 7 6 (ii) 4 7 (iii) 65 74 (iv) 63 74 Ratkaisu Sovelletaan Eukleideen algoritmia
Yhteistyötä sisältämätön peliteoria
 Yhteistyötä sisältämätön peliteoria jarkko.murtoaro@hut.fi Optimointiopin seminaari Kevät 2003 / 1 Sisältö Johdanto Käsitteistö Työkalut Nashin tasapaino Täydellinen tasapaino Optimointiopin seminaari
Yhteistyötä sisältämätön peliteoria jarkko.murtoaro@hut.fi Optimointiopin seminaari Kevät 2003 / 1 Sisältö Johdanto Käsitteistö Työkalut Nashin tasapaino Täydellinen tasapaino Optimointiopin seminaari
Olkoon seuraavaksi G 2 sellainen tasan n solmua sisältävä suunnattu verkko,
 Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Matematiikan tukikurssi, kurssikerta 5
 Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
Näytetään nyt relaatioon liittyvien ekvivalenssiluokkien olevan verkon G lohkojen särmäjoukkoja. Olkoon siis f verkon G jokin särmä.
 Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Topologia Syksy 2010 Harjoitus 11
 Topologia Syksy 2010 Harjoitus 11 (1) Tarkastellaan tason (a, )-topologiaa. (Tässä topologiassa A R 2 on avoin jos ja vain jos A =, A = R 2 tai A = {(x, y) R 2 x > a ja y > b} joillekin a, b R.) Jokaiselle
Topologia Syksy 2010 Harjoitus 11 (1) Tarkastellaan tason (a, )-topologiaa. (Tässä topologiassa A R 2 on avoin jos ja vain jos A =, A = R 2 tai A = {(x, y) R 2 x > a ja y > b} joillekin a, b R.) Jokaiselle
Johdatus matemaattiseen päättelyyn
 Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä Luonnollisten lukujen joukko N on joukko N = {1, 2, 3,...} ja kokonaislukujen
Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä Luonnollisten lukujen joukko N on joukko N = {1, 2, 3,...} ja kokonaislukujen
Tarkastelemme ensin konkreettista esimerkkiä ja johdamme sitten yleisen säännön, joilla voidaan tietyissä tapauksissa todeta kielen ei-säännöllisyys.
 Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Pelit matematiikan opetuksessa
 Pelit matematiikan opetuksessa Vadim Kulikov Helsingin Yliopisto Matematiikan ja tilastotieteen laitos Epsilonit kirjaa tutkimassa, 28.01.2012 Millaisia pelejä? pärjääminen edellyttää ongelmanratkaisukykyä,
Pelit matematiikan opetuksessa Vadim Kulikov Helsingin Yliopisto Matematiikan ja tilastotieteen laitos Epsilonit kirjaa tutkimassa, 28.01.2012 Millaisia pelejä? pärjääminen edellyttää ongelmanratkaisukykyä,
Induktiota käyttäen voidaan todistaa luonnollisia lukuja koskevia väitteitä, jotka ovat muotoa. väite P(n) on totta kaikille n = 0,1,2,...
 Induktiotodistus Induktiota käyttäen voidaan todistaa luonnollisia lukuja koskevia väitteitä, jotka ovat muotoa väite P(n) on totta kaikille n = 0,1,2,.... Tässä väite P(n) riippuu n:n arvosta. Todistuksessa
Induktiotodistus Induktiota käyttäen voidaan todistaa luonnollisia lukuja koskevia väitteitä, jotka ovat muotoa väite P(n) on totta kaikille n = 0,1,2,.... Tässä väite P(n) riippuu n:n arvosta. Todistuksessa
Sisällysluettelo. 1. Johdanto
 Säännöt Sisällysluettelo 1. Johdanto 3 2. Sisältö 4 3. Alkuvalmistelut 5 4. Pelin aloitus ja kulku 6 5. Pelin lopetus 9 6. Vaikea peli ja muut pelimuunnelmat 10 1. Johdanto Pelilauta on 25 ruudusta muodostuva
Säännöt Sisällysluettelo 1. Johdanto 3 2. Sisältö 4 3. Alkuvalmistelut 5 4. Pelin aloitus ja kulku 6 5. Pelin lopetus 9 6. Vaikea peli ja muut pelimuunnelmat 10 1. Johdanto Pelilauta on 25 ruudusta muodostuva
Luento 5: Peliteoriaa
 Luento 5: Peliteoriaa Tässä kappaleessa tutustutaan hieman peliteoriaan. Keskeisiä asioita ovat Nash-tasapaino ja sekastrategia. Cournot n duopolimalli vuodelta 1838 toimii oivallisena havainnollistuksena
Luento 5: Peliteoriaa Tässä kappaleessa tutustutaan hieman peliteoriaan. Keskeisiä asioita ovat Nash-tasapaino ja sekastrategia. Cournot n duopolimalli vuodelta 1838 toimii oivallisena havainnollistuksena
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Johdanto peliteoriaan Kirja kpl. 2
 Aalto-yliopiston TKK Mat-2.4142 K2010 Esitelmä 1 Ilkka Leppänen 1 Johdanto peliteoriaan Kirja kpl. 2 Ilkka Leppänen 20.1.2010 Aalto-yliopiston TKK Mat-2.4142 K2010 Esitelmä 1 Ilkka Leppänen 2 Aiheet Laajennettu
Aalto-yliopiston TKK Mat-2.4142 K2010 Esitelmä 1 Ilkka Leppänen 1 Johdanto peliteoriaan Kirja kpl. 2 Ilkka Leppänen 20.1.2010 Aalto-yliopiston TKK Mat-2.4142 K2010 Esitelmä 1 Ilkka Leppänen 2 Aiheet Laajennettu
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
Nollasummapelit ja bayesilaiset pelit
 Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Ratkaisu: a) Kahden joukon yhdisteseen poimitaan kaikki alkiot jotka ovat jommassakummassa joukossa (eikä mitään muuta).
 Matematiikan laitos Johdatus Diskreettiin Matematiikaan Harjoitus 1 03.11.2010 Ratkaisuehdotuksia Aleksandr Nuija 1. Tarkastellaan joukkoja A = {1,3,4}, B = {2,3,7,9} ja C = {2, 5, 7}. Määritä joukot (a)
Matematiikan laitos Johdatus Diskreettiin Matematiikaan Harjoitus 1 03.11.2010 Ratkaisuehdotuksia Aleksandr Nuija 1. Tarkastellaan joukkoja A = {1,3,4}, B = {2,3,7,9} ja C = {2, 5, 7}. Määritä joukot (a)
KOKO PERHEEN HAUSKA STRATEGIAPELI OHJEET
 KOKO PERHEEN HAUSKA STRATEGIAPELI OHJEET ROBOGEM_Ohjevihko_148x210mm.indd 1 PELIN TAVOITE Robotit laskeutuvat kaukaiselle planeetalle etsimään timantteja, joista saavat lisää virtaa aluksiinsa. Ohjelmoi
KOKO PERHEEN HAUSKA STRATEGIAPELI OHJEET ROBOGEM_Ohjevihko_148x210mm.indd 1 PELIN TAVOITE Robotit laskeutuvat kaukaiselle planeetalle etsimään timantteja, joista saavat lisää virtaa aluksiinsa. Ohjelmoi
Insinöörimatematiikka A
 Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Pelivaihtoehtoja. Enemmän vaihtelua peliin saa käyttämällä erikoislaattoja. Jännittävimmillään Alfapet on, kun miinusruudut ovat mukana pelissä!
 Pelivaihtoehtoja Yksinkertaisin vaihtoehto: lfapetia voi pelata monella eri tavalla. Yksinkertaisimmassa vaihtoehdossa käytetään ainoastaan kirjainlaattoja. Pelilaudan miinusruudut ovat tavallisia ruutuja,
Pelivaihtoehtoja Yksinkertaisin vaihtoehto: lfapetia voi pelata monella eri tavalla. Yksinkertaisimmassa vaihtoehdossa käytetään ainoastaan kirjainlaattoja. Pelilaudan miinusruudut ovat tavallisia ruutuja,
Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. ( ) Jeremias Berg
 Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. (14.3-18.3) Jeremias Berg 1. Luettele kaikki seuraavien joukkojen alkiot: (a) {x Z : x 3} (b) {x N : x > 12 x < 7} (c) {x N : 1 x 7} Ratkaisu:
Diskreetin Matematiikan Paja Ratkaisuhahmotelmia viikko 1. (14.3-18.3) Jeremias Berg 1. Luettele kaikki seuraavien joukkojen alkiot: (a) {x Z : x 3} (b) {x N : x > 12 x < 7} (c) {x N : 1 x 7} Ratkaisu:
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten. Ratkaisuehdotelma
 Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
1 PÖYDÄT JA PALLOT 1. Kilpailuissa tulee käyttää Suomen Biljardiliiton hyväksymiä pöytiä ja palloja.
 KARAMBOLEN SÄÄNNÖT Kolmen vallin kara Yhden vallin kara Suora kara - Cadre YHTEISET SÄÄNNÖT KAIKILLE PELIMUODOILLE 1 PÖYDÄT JA PALLOT 1. Kilpailuissa tulee käyttää Suomen Biljardiliiton hyväksymiä pöytiä
KARAMBOLEN SÄÄNNÖT Kolmen vallin kara Yhden vallin kara Suora kara - Cadre YHTEISET SÄÄNNÖT KAIKILLE PELIMUODOILLE 1 PÖYDÄT JA PALLOT 1. Kilpailuissa tulee käyttää Suomen Biljardiliiton hyväksymiä pöytiä
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 4 Funktion raja-arvo 4. Määritelmä. Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: f) A < ε aina, kun 0 < a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 4 Funktion raja-arvo 4. Määritelmä. Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: f) A < ε aina, kun 0 < a < δ, saadaan kvanttorien järjestystä vaihtamalla
Blackjack on korttipeli, jossa pelaajan tavoitteena on voittaa pelinhoitaja.
 POHDIN projekti Blackjack Blackjack on pelinhoitajaa vastaan pelattava korttipeli mutta myös ns. uhkapeli 1. Kun kyseessä on ns. rahapeli, niin ikäraja Suomessa on tällaiselle pelille K-18. Blackjackissä
POHDIN projekti Blackjack Blackjack on pelinhoitajaa vastaan pelattava korttipeli mutta myös ns. uhkapeli 1. Kun kyseessä on ns. rahapeli, niin ikäraja Suomessa on tällaiselle pelille K-18. Blackjackissä
7 Vapaus. 7.1 Vapauden määritelmä
 7 Vapaus Kuten edellisen luvun lopussa mainittiin, seuraavaksi pyritään ratkaisemaan, onko annetussa aliavaruuden virittäjäjoukossa tarpeettomia vektoreita Jos tällaisia ei ole, virittäjäjoukkoa kutsutaan
7 Vapaus Kuten edellisen luvun lopussa mainittiin, seuraavaksi pyritään ratkaisemaan, onko annetussa aliavaruuden virittäjäjoukossa tarpeettomia vektoreita Jos tällaisia ei ole, virittäjäjoukkoa kutsutaan
Pysähtymisongelman ratkeavuus [Sipser luku 4.2]
![Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Pysähtymisongelman ratkeavuus [Sipser luku 4.2]](/thumbs/59/42645644.jpg) Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
a k+1 = 2a k + 1 = 2(2 k 1) + 1 = 2 k+1 1. xxxxxx xxxxxx xxxxxx xxxxxx
 x x x x x x x x Matematiikan johdantokurssi, syksy 08 Harjoitus, ratkaisuista Hanoin tornit -ongelma: Tarkastellaan kolmea pylvästä A, B ja C, joihin voidaan pinota erikokoisia renkaita Lähtötilanteessa
x x x x x x x x Matematiikan johdantokurssi, syksy 08 Harjoitus, ratkaisuista Hanoin tornit -ongelma: Tarkastellaan kolmea pylvästä A, B ja C, joihin voidaan pinota erikokoisia renkaita Lähtötilanteessa
Matematiikan mestariluokka, syksy 2009 7
 Matematiikan mestariluokka, syksy 2009 7 2 Alkuluvuista 2.1 Alkuluvut Määritelmä 2.1 Positiivinen luku a 2 on alkuluku, jos sen ainoat positiiviset tekijät ovat 1 ja a. Jos a 2 ei ole alkuluku, se on yhdistetty
Matematiikan mestariluokka, syksy 2009 7 2 Alkuluvuista 2.1 Alkuluvut Määritelmä 2.1 Positiivinen luku a 2 on alkuluku, jos sen ainoat positiiviset tekijät ovat 1 ja a. Jos a 2 ei ole alkuluku, se on yhdistetty
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
a b c d
 1. 11. 011!"$#&%(')'+*(#-,.*/103/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + +. 3. 4. 5. 6. + + + + + + + + + + P1. 5 140 8 47 = 5 140 ( 3 ) 47 = 5 140 3 47 = 5 140 141 = (5 ) 140 = 10 140, jossa on
1. 11. 011!"$#&%(')'+*(#-,.*/103/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + +. 3. 4. 5. 6. + + + + + + + + + + P1. 5 140 8 47 = 5 140 ( 3 ) 47 = 5 140 3 47 = 5 140 141 = (5 ) 140 = 10 140, jossa on
Tehtävä: FIL Tiedostopolut
 Tehtävä: FIL Tiedostopolut finnish BOI 2015, päivä 2. Muistiraja: 256 MB. 1.05.2015 Jarkka pitää vaarallisesta elämästä. Hän juoksee saksien kanssa, lähettää ratkaisuja kisatehtäviin testaamatta esimerkkisyötteillä
Tehtävä: FIL Tiedostopolut finnish BOI 2015, päivä 2. Muistiraja: 256 MB. 1.05.2015 Jarkka pitää vaarallisesta elämästä. Hän juoksee saksien kanssa, lähettää ratkaisuja kisatehtäviin testaamatta esimerkkisyötteillä
Matematiikassa väitelauseet ovat usein muotoa: jos P on totta, niin Q on totta.
 Väitelause Matematiikassa väitelauseet ovat usein muotoa: jos P on totta, niin Q on totta. Tässä P:tä kutsutaan oletukseksi ja Q:ta väitteeksi. Jos yllä oleva väitelause on totta, sanotaan, että P:stä
Väitelause Matematiikassa väitelauseet ovat usein muotoa: jos P on totta, niin Q on totta. Tässä P:tä kutsutaan oletukseksi ja Q:ta väitteeksi. Jos yllä oleva väitelause on totta, sanotaan, että P:stä
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
1. Osoita, että joukon X osajoukoille A ja B on voimassa toinen ns. de Morganin laki (A B) = A B.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
Kannan vektorit siis virittävät aliavaruuden, ja lisäksi kanta on vapaa. Lauseesta 7.6 saadaan seuraava hyvin käyttökelpoinen tulos:
 8 Kanta Tässä luvussa tarkastellaan aliavaruuden virittäjävektoreita, jotka muodostavat lineaarisesti riippumattoman jonon. Merkintöjen helpottamiseksi oletetaan luvussa koko ajan, että W on vektoreiden
8 Kanta Tässä luvussa tarkastellaan aliavaruuden virittäjävektoreita, jotka muodostavat lineaarisesti riippumattoman jonon. Merkintöjen helpottamiseksi oletetaan luvussa koko ajan, että W on vektoreiden
Mohrin-Mascheronin lause kolmiulotteisessa harppi-viivaingeometriassa
 Mohrin-Mascheronin lause kolmiulotteisessa harppi-viivaingeometriassa Matematiikka Sakke Suomalainen Helsingin matematiikkalukio Ohjaaja: Ville Tilvis 29. marraskuuta 2010 Tiivistelmä Harppi ja viivain
Mohrin-Mascheronin lause kolmiulotteisessa harppi-viivaingeometriassa Matematiikka Sakke Suomalainen Helsingin matematiikkalukio Ohjaaja: Ville Tilvis 29. marraskuuta 2010 Tiivistelmä Harppi ja viivain
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho. 31. maaliskuuta 2011
 TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 31. maaliskuuta 2011 Sisällys Sisällys Chomskyn hierarkia kieli säännöllinen kontekstiton kontekstinen rekursiivisesti
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 31. maaliskuuta 2011 Sisällys Sisällys Chomskyn hierarkia kieli säännöllinen kontekstiton kontekstinen rekursiivisesti
joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja.
 ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
Pohdiskeleva ajattelu ja tasapainotarkennukset
 Pohdiskeleva ajattelu ja tasapainotarkennukset Sanna Hanhikoski 24.3.2010 Sisältö Pohdiskeleva ajattelu Nashin tasapainotarkennukset Täydellinen tasapaino Täydellinen bayesiläinen tasapaino Vaiheittainen
Pohdiskeleva ajattelu ja tasapainotarkennukset Sanna Hanhikoski 24.3.2010 Sisältö Pohdiskeleva ajattelu Nashin tasapainotarkennukset Täydellinen tasapaino Täydellinen bayesiläinen tasapaino Vaiheittainen
Vieruskaverisi on tämän päivän luennolla työtoverisi. Jos sinulla ei ole vieruskaveria, siirry jonkun viereen. Esittäytykää toisillenne.
 Aloitus Vieruskaverisi on tämän päivän luennolla työtoverisi. Jos sinulla ei ole vieruskaveria, siirry jonkun viereen. Esittäytykää toisillenne. Mitkä seuraavista väitteistä ovat tosia? A. 6 3 N B. 5 Z
Aloitus Vieruskaverisi on tämän päivän luennolla työtoverisi. Jos sinulla ei ole vieruskaveria, siirry jonkun viereen. Esittäytykää toisillenne. Mitkä seuraavista väitteistä ovat tosia? A. 6 3 N B. 5 Z
Cantorin joukon suoristuvuus tasossa
 Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
ja λ 2 = 2x 1r 0 x 2 + 2x 1r 0 x 2
 Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
- 4 aloituslaattaa pelaajien väreissä molemmille puolille on kuvattu vesialtaat, joista lähtee eri määrä akvedukteja.
 AQUA ROMANA Vesi oli elintärkeä ja keskeinen edellytys Rooman imperiumin kehitykselle. Vedensaannin turvaamiseksi taitavimmat rakennusmestarit rakensivat valtavan pitkiä akvedukteja, joita pidetään antiikin
AQUA ROMANA Vesi oli elintärkeä ja keskeinen edellytys Rooman imperiumin kehitykselle. Vedensaannin turvaamiseksi taitavimmat rakennusmestarit rakensivat valtavan pitkiä akvedukteja, joita pidetään antiikin
b) Määritä myös seuraavat joukot ja anna kussakin tapauksessa lyhyt sanallinen perustelu.
 Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
Rekursiolause. Laskennan teorian opintopiiri. Sebastian Björkqvist. 23. helmikuuta Tiivistelmä
 Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Algebra I, Harjoitus 6, , Ratkaisut
 Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
1 Lukujen jaollisuudesta
 Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Salasuhteita. esimerkiksi espanjaksi nimi tarkoittaa pientä pusua.
 Salasuhteita Avioliittopeleistä kehiteltiin edelleen uusia pelejä, joissa varsinaisten avioliittojen lisäksi kohdataan sopimattomia suhteita kuningatarten ja sotilaiden välillä vieläpä maiden rajat ylittäen!
Salasuhteita Avioliittopeleistä kehiteltiin edelleen uusia pelejä, joissa varsinaisten avioliittojen lisäksi kohdataan sopimattomia suhteita kuningatarten ja sotilaiden välillä vieläpä maiden rajat ylittäen!
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
(1) refleksiivinen, (2) symmetrinen ja (3) transitiivinen.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku
 Pasi Leppäniemi OuLUMA, sivu 1 POLYNOMIPELI Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku Luokkataso: 8-9 lk Välineet: pelilauta, polynomikortit, monomikortit, tuloskortit,
Pasi Leppäniemi OuLUMA, sivu 1 POLYNOMIPELI Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku Luokkataso: 8-9 lk Välineet: pelilauta, polynomikortit, monomikortit, tuloskortit,
Kenguru Cadet, ratkaisut (1 / 6) luokka
 Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Yleinen tietämys ja Nashin tasapaino
 Yleinen tietämys ja Nashin tasapaino 24.3.2010 Nashin tasapaino Ratkaisumalli kahden tai useamman pelaajan pelille. Yleisesti: Jos jokainen pelaaja on valinnut strategiansa eikä yksikään pelaaja voi hyötyä
Yleinen tietämys ja Nashin tasapaino 24.3.2010 Nashin tasapaino Ratkaisumalli kahden tai useamman pelaajan pelille. Yleisesti: Jos jokainen pelaaja on valinnut strategiansa eikä yksikään pelaaja voi hyötyä
Platonin kappaleet. Avainsanat: geometria, matematiikan historia. Luokkataso: 6-9, lukio. Välineet: Polydron-rakennussarja, kynä, paperia.
 Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
j(j 1) = n(n2 1) 3 + (k + 1)k = (k + 1)(k2 k + 3k) 3 = (k + 1)(k2 + 2k + 1 1)
 MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
Tehtävä 1. Päättele resoluutiolla seuraavista klausuulijoukoista. a. 1 {p 3 } oletus. 4 {p 1, p 2, p 3 } oletus. 5 { p 1 } (1, 2) 7 (4, 6)
 Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
KuntaVaaliPeli. Tuomo Pekkanen / 2012
 KuntaVaaliPeli Tuomo Pekkanen / 2012 Mistä oikein on kyse? Kuntavaalipelissä koitetaan selvittää mikä neljästä puolueesta onkaan seuraavien vaalien jälkeen se suuri puolue. Jokainen puolue kamppailee kolmesta
KuntaVaaliPeli Tuomo Pekkanen / 2012 Mistä oikein on kyse? Kuntavaalipelissä koitetaan selvittää mikä neljästä puolueesta onkaan seuraavien vaalien jälkeen se suuri puolue. Jokainen puolue kamppailee kolmesta
