Nimi: Ratkaise tehtävät sivun alalaitaan. (paperi nro 1) 1. Valitse oikea toisen asteen yhtälön ratkaisukaava: (a) b ± b 4ac 2a. (b) b ± b 2 4ac 2a
|
|
|
- Ritva Salonen
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 paperi nro 0 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö x 2 + 7x 12 = Ratkaise epäyhtälö 3x 2 30x > 0 4. Ratkaise epäyhtälö 5x < 0
2 paperi nro 1 a b ± b 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 2 + 4ac 2. Ratkaise toisen asteen yhtälö 5x 2 15x 20 = Ratkaise epäyhtälö x 2 10x 0 4. Ratkaise epäyhtälö 4x
3 paperi nro 2 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 5x x = Ratkaise epäyhtälö x 2 + x 0 4. Ratkaise epäyhtälö 5x
4 paperi nro 3 a b ± b 2 + 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö x 2 + x 90 = Ratkaise epäyhtälö 5x 2 + 5x > 0 4. Ratkaise epäyhtälö 2x
5 paperi nro 4 a b ± b 2 + 4ac b b ± b 4ac c b ± b 2 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 2x x + 16 = Ratkaise epäyhtälö 3x 2 + 9x < 0 4. Ratkaise epäyhtälö 5x < 0
6 paperi nro 5 a b ± b 2 4ac b b ± b 2 4ac c b ± b 2 + 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö 3x 2 21x 54 = Ratkaise epäyhtälö 4x x > 0 4. Ratkaise epäyhtälö 3x 2 3 > 0
7 paperi nro 6 a b ± b 2 4ac b b ± b 2 4ac c b ± b 4ac d b ± b 2 + 4ac 2. Ratkaise toisen asteen yhtälö 5x 2 5x = Ratkaise epäyhtälö 4x 2 16x < 0 4. Ratkaise epäyhtälö x 2 64 > 0
8 paperi nro 7 a b ± b 2 4ac b b ± b 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 5x x + 50 = Ratkaise epäyhtälö x 2 2x 0 4. Ratkaise epäyhtälö 4x
9 paperi nro 8 a b ± b 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 2 + 4ac 2. Ratkaise toisen asteen yhtälö 5x 2 15x + 10 = Ratkaise epäyhtälö x 2 5x < 0 4. Ratkaise epäyhtälö 5x
10 paperi nro 9 a b ± b 2 + 4ac b b ± b 4ac c b ± b 2 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 4x x 36 = Ratkaise epäyhtälö 3x 2 + 3x > 0 4. Ratkaise epäyhtälö 4x
11 paperi nro 10 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 4x x 40 = Ratkaise epäyhtälö 4x x 0 4. Ratkaise epäyhtälö 4x < 0
12 paperi nro 11 a b ± b 2 4ac b b ± b 2 4ac c b ± b 2 + 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö x 2 8x + 9 = Ratkaise epäyhtälö 5x 2 25x 0 4. Ratkaise epäyhtälö 3x > 0
13 paperi nro 12 a b ± b 2 4ac b b ± b 2 4ac c b ± b 2 + 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö x 2 + 4x + 12 = Ratkaise epäyhtälö 2x 2 14x 0 4. Ratkaise epäyhtälö 2x
14 paperi nro 13 a b ± b 2 + 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö x 2 3x 54 = Ratkaise epäyhtälö x 2 8x 0 4. Ratkaise epäyhtälö 5x
15 paperi nro 14 a b ± b 2 4ac b b ± b 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 2x x 120 = Ratkaise epäyhtälö 4x x 0 4. Ratkaise epäyhtälö 2x > 0
16 paperi nro 15 a b ± b 4ac b b ± b 2 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 3x x 126 = Ratkaise epäyhtälö 4x x < 0 4. Ratkaise epäyhtälö x 2 81 > 0
17 paperi nro 16 a b ± b 2 4ac b b ± b 4ac c b ± b 2 4ac d b ± b 2 + 4ac 2. Ratkaise toisen asteen yhtälö 2x x + 56 = Ratkaise epäyhtälö 3x x < 0 4. Ratkaise epäyhtälö 4x > 0
18 paperi nro 17 a b ± b 2 4ac b b ± b 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 2x 2 + 6x 20 = Ratkaise epäyhtälö 5x 2 10x 0 4. Ratkaise epäyhtälö x > 0
19 paperi nro 18 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 4x 2 80x 400 = Ratkaise epäyhtälö 4x 2 + 8x 0 4. Ratkaise epäyhtälö 3x > 0
20 paperi nro 19 a b ± b 2 4ac b b ± b 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 2x x 48 = Ratkaise epäyhtälö 2x 2 16x 0 4. Ratkaise epäyhtälö 3x < 0
21 paperi nro 20 a b ± b 2 + 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö 3x x + 72 = Ratkaise epäyhtälö x 2 5x 0 4. Ratkaise epäyhtälö 5x
22 paperi nro 21 a b ± b 4ac b b ± b 2 4ac c b ± b 2 + 4ac d b ± b 2 4ac 2. Ratkaise toisen asteen yhtälö 4x 2 48x + 80 = Ratkaise epäyhtälö 3x 2 21x < 0 4. Ratkaise epäyhtälö 4x
23 paperi nro 22 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö 3x x 72 = Ratkaise epäyhtälö 5x 2 40x 0 4. Ratkaise epäyhtälö 5x
24 paperi nro 23 a b ± b 2 4ac b b ± b 2 + 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö 3x x 60 = Ratkaise epäyhtälö 3x 2 27x > 0 4. Ratkaise epäyhtälö 3x > 0
25 paperi nro 24 a b ± b 2 + 4ac b b ± b 2 4ac c b ± b 2 4ac d b ± b 4ac 2. Ratkaise toisen asteen yhtälö 5x 2 15x = Ratkaise epäyhtälö 2x x > 0 4. Ratkaise epäyhtälö 2x 2 18 > 0
26 Array [0] => Array [0] => 4 [1] => 4 ja 3 [2] => -0 ja -10 [3] => 1 ja -1 [1] => Array [0] => 2 [1] => 4 ja -1 [2] => 0 ja 10 [3] => -10 ja 10 [2] => Array [0] => 4 [1] => -4 ja -6 [2] => -1 ja 0 [3] => -5 ja 5 [3] => Array [0] => 3 [1] => 9 ja -10 [2] => 1 ja -0 [3] => 6 ja -6 [4] => Array [0] => 4 [1] => -8 ja -1 [2] => 3 ja -0 [3] => 6 ja -6
27 [5] => Array [0] => 2 [1] => -2 ja 9 [2] => -5 ja 0 [3] => -1 ja 1 [6] => Array [0] => 1 [1] => -7 ja 6 [2] => -0 ja -4 [3] => -8 ja 8 [7] => Array [0] => 1 [1] => -2 ja -5 [2] => -0 ja -2 [3] => 4 ja -4 [8] => Array [0] => 2 [1] => 1 ja 2 [2] => 0 ja 5 [3] => 4 ja -4 [9] => Array [0] => 4 [1] => -9 ja 1 [2] => -1 ja 0 [3] => -9 ja 9
28 [10] => Array [0] => 4 [1] => -10 ja 1 [2] => -10 ja 0 [3] => 3 ja -3 [11] => Array [0] => 2 [1] => 1 ja -9 [2] => 0 ja 5 [3] => -8 ja 8 [12] => Array [0] => 2 [1] => -2 ja 6 [2] => -0 ja -7 [3] => -10 ja 10 [13] => Array [0] => 3 [1] => -6 ja 9 [2] => 0 ja 8 [3] => 2 ja -2 [14] => Array [0] => 4 [1] => 10 ja 6 [2] => -4 ja 0 [3] => 3 ja -3 [15] => Array
29 [0] => 2 [1] => 6 ja 7 [2] => 6 ja -0 [3] => -9 ja 9 [16] => Array [0] => 1 [1] => -4 ja -7 [2] => 10 ja -0 [3] => 7 ja -7 [17] => Array [0] => 4 [1] => -5 ja 2 [2] => -0 ja -2 [3] => 7 ja -7 [18] => Array [0] => 1 [1] => -10 ja -10 [2] => 2 ja -0 [3] => 5 ja -5 [19] => Array [0] => 4 [1] => -8 ja 3 [2] => -0 ja -8 [3] => 2 ja -2 [20] => Array
30 [0] => 3 [1] => -6 ja -4 [2] => 0 ja 5 [3] => -2 ja 2 [21] => Array [0] => 2 [1] => 10 ja 2 [2] => 0 ja 7 [3] => 7 ja -7 [22] => Array [0] => 3 [1] => 8 ja 3 [2] => -0 ja -8 [3] => 5 ja -5 [23] => Array [0] => 1 [1] => 10 ja 2 [2] => -0 ja -9 [3] => 8 ja -8 [24] => Array [0] => 2 [1] => -9 ja 6 [2] => 10 ja -0 [3] => -3 ja 3
Lukion. Calculus. Polynomifunktiot. Paavo Jäppinen Alpo Kupiainen Matti Räsänen Otava PIKATESTIN JA KERTAUSKOKEIDEN TEHTÄVÄT RATKAISUINEEN
 Calculus Lukion MAA Polynomifunktiot Paavo Jäppinen Alpo Kupiainen Matti Räsänen Otava PIKATESTIN JA KERTAUSKOKEIDEN TEHTÄVÄT RATKAISUINEEN Polynomifunktiot (MAA) Pikatesti ja kertauskokeet Tehtävien ratkaisut
Calculus Lukion MAA Polynomifunktiot Paavo Jäppinen Alpo Kupiainen Matti Räsänen Otava PIKATESTIN JA KERTAUSKOKEIDEN TEHTÄVÄT RATKAISUINEEN Polynomifunktiot (MAA) Pikatesti ja kertauskokeet Tehtävien ratkaisut
30 + x. 15 + 0,5x = 2,5 + x 0,5x = 12,5 x = 25. 27,5a + 27,5b = 1,00 55 = 55. 2,5a + (30 2,5)b (27,5a + 27,5b) = 45 55.
 RATKAISUT, Insinöörimatematiikan koe 1.5.201 1. Kahdessa astiassa on bensiinin ja etanolin seosta. Ensimmäisessä astiassa on 10 litraa seosta, jonka tilavuudesta 5 % on etanolia. Toisessa astiassa on 20
RATKAISUT, Insinöörimatematiikan koe 1.5.201 1. Kahdessa astiassa on bensiinin ja etanolin seosta. Ensimmäisessä astiassa on 10 litraa seosta, jonka tilavuudesta 5 % on etanolia. Toisessa astiassa on 20
2.7 Neliöjuuriyhtälö ja -epäyhtälö
 2.7 Neliöjuuriyhtälö ja -epäyhtälö Neliöjuuren määritelmä palautettiin mieleen jo luvun 2.2 alussa. Neliöjuurella on mm. seuraavat ominaisuudet. ab = a b, a 0, b 0 a a b =, a 0, b > 0 b a2 = a a > b, a
2.7 Neliöjuuriyhtälö ja -epäyhtälö Neliöjuuren määritelmä palautettiin mieleen jo luvun 2.2 alussa. Neliöjuurella on mm. seuraavat ominaisuudet. ab = a b, a 0, b 0 a a b =, a 0, b > 0 b a2 = a a > b, a
Aluksi. 2.1. Kahden muuttujan lineaarinen epäyhtälö
 Aluksi Matemaattisena käsitteenä lineaarinen optimointi sisältää juuri sen saman asian kuin mikä sen nimestä tulee mieleen. Lineaarisen optimoinnin avulla haetaan ihannearvoa eli optimia, joka on määritelty
Aluksi Matemaattisena käsitteenä lineaarinen optimointi sisältää juuri sen saman asian kuin mikä sen nimestä tulee mieleen. Lineaarisen optimoinnin avulla haetaan ihannearvoa eli optimia, joka on määritelty
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
2 Yhtälöitä ja epäyhtälöitä
 2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
Johdatus yliopistomatematiikkaan, 2. viikko (2 op)
 Johdatus yliopistomatematiikkaan, 2. viikko (2 op) Jukka Kemppainen Mathematics Division Yhtälöt ja epäyhtälöt Jokainen osaa ratkaista ensimmäisen asteen yhtälön ax + by + c = 0. Millä parametrien a, b
Johdatus yliopistomatematiikkaan, 2. viikko (2 op) Jukka Kemppainen Mathematics Division Yhtälöt ja epäyhtälöt Jokainen osaa ratkaista ensimmäisen asteen yhtälön ax + by + c = 0. Millä parametrien a, b
Hyvä uusi opiskelija!
 Hyvä uusi opiskelija! Tässä tulee tärkeää tietoa heti syksyn alussa pidettävästä laskutaitotestistä. Tekniikan kieli on matematiikka. Matematiikka tarjoaa perustan tekniikan opiskelulle ja soveltamiselle
Hyvä uusi opiskelija! Tässä tulee tärkeää tietoa heti syksyn alussa pidettävästä laskutaitotestistä. Tekniikan kieli on matematiikka. Matematiikka tarjoaa perustan tekniikan opiskelulle ja soveltamiselle
Numeeriset menetelmät
 Numeeriset menetelmät Luento 1 Ti 6.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 1 Ti 6.9.2011 p. 1/28 p. 1/28 Numeriikan termejä Simulointi: Reaalimaailman ilmiöiden jäljitteleminen (yleensä)
Numeeriset menetelmät Luento 1 Ti 6.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 1 Ti 6.9.2011 p. 1/28 p. 1/28 Numeriikan termejä Simulointi: Reaalimaailman ilmiöiden jäljitteleminen (yleensä)
EUROOPAN YHTEISÖ. Lähetys-/Vientimaan 1 ILMOITUS A LÄHETYS-/VIENTITOIMIPAIKKA. 2 Lähettäjä/Viejä Nro. C 3 Lomakenro BIS.
 Kollit 2 Lähettäjä/Viejä Nro Merkit numerot Konttien numerot Lukumäärä laji 3 Lomake 1 A LÄHETYS-/VIENTITOIMIPAIKKA 33 Tavaran 40 Yleisilmoitus/Edeltävä asiakir Kollit Merkit numerot Konttien numerot Lukumäärä
Kollit 2 Lähettäjä/Viejä Nro Merkit numerot Konttien numerot Lukumäärä laji 3 Lomake 1 A LÄHETYS-/VIENTITOIMIPAIKKA 33 Tavaran 40 Yleisilmoitus/Edeltävä asiakir Kollit Merkit numerot Konttien numerot Lukumäärä
Talousmatematiikan perusteet, ORMS1030
 Tamprn ksäyliopisto, 2015-2016 Talousmatmatiikan prustt, ORMS1030 1. väliko, (ti 15.12.2015) Ratkais 3 thtävää. Kokssa saa olla mukana laskin (myös graafinn laskin on sallittu) ja taulukkokirja (MAOL tai
Tamprn ksäyliopisto, 2015-2016 Talousmatmatiikan prustt, ORMS1030 1. väliko, (ti 15.12.2015) Ratkais 3 thtävää. Kokssa saa olla mukana laskin (myös graafinn laskin on sallittu) ja taulukkokirja (MAOL tai
Epäyhtälön molemmille puolille voidaan lisätä sama luku: kaikilla reaaliluvuilla a, b ja c on voimassa a < b a + c < b + c ja a b a + c b + c.
 Epäyhtälö Kahden lausekkeen A ja B välisiä järjestysrelaatioita A < B, A B, A > B ja A B nimitetään epäyhtälöiksi. Esimerkiksi 2 < 6, 9 10, 5 > a + + 2 ja ( + 1) 2 2 + 2 ovat epäyhtälöitä. Epäyhtälössä
Epäyhtälö Kahden lausekkeen A ja B välisiä järjestysrelaatioita A < B, A B, A > B ja A B nimitetään epäyhtälöiksi. Esimerkiksi 2 < 6, 9 10, 5 > a + + 2 ja ( + 1) 2 2 + 2 ovat epäyhtälöitä. Epäyhtälössä
( ) ( ) ( ) ( ( ) Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 271 Päivitetty 19.2.2006. 701 a) = keskipistemuoto.
 Pyramidi Analyyttinen geometria tehtävien ratkaisut sivu 7 Päivitetty 9..6 7 a) + y = 7 + y = 7 keskipistemuoto + y 7 = normaalimuoto Vastaus a) + y = ( 7 ) + y 7= b) + y+ 5 = 6 y y + + = b) c) ( ) + y
Pyramidi Analyyttinen geometria tehtävien ratkaisut sivu 7 Päivitetty 9..6 7 a) + y = 7 + y = 7 keskipistemuoto + y 7 = normaalimuoto Vastaus a) + y = ( 7 ) + y 7= b) + y+ 5 = 6 y y + + = b) c) ( ) + y
VILJAVUUSTUTKIMUS. Oja Hannu. Tulospalvelu Käyttäjätunnus: 30412 Salasana: Oja Hannu. Valtakatu 4, PL 29 84101 YLIVIESKA. Viljavuustietojen yhteenveto
 VILJAVUUSTUTKIMUS Sammonkatu 8, Oulu p. 08-5145600 f. 08-3113029 Pvm Työ nro As.nro 1.08.2013 96975 30412 Oja Hannu Valtakatu 4, PL 29 84101 YLIVIESKA Tulospalvelu Käyttäjätunnus: 30412 Salasana: Oja Hannu
VILJAVUUSTUTKIMUS Sammonkatu 8, Oulu p. 08-5145600 f. 08-3113029 Pvm Työ nro As.nro 1.08.2013 96975 30412 Oja Hannu Valtakatu 4, PL 29 84101 YLIVIESKA Tulospalvelu Käyttäjätunnus: 30412 Salasana: Oja Hannu
YHTÄLÖ kahden lausekkeen merkitty yhtäsuuruus
 YHTÄLÖ kahden lausekkeen merkitty yhtäsuuruus Ensimmäisen asteen yhtälö: :n korkein eksponentti = 1 + 5 = 4( 3) Toisen asteen yhtälö: :n korkein eksponentti = 3 5 + 4 = 0 Kolmannen asteen yhtälö: :n korkein
YHTÄLÖ kahden lausekkeen merkitty yhtäsuuruus Ensimmäisen asteen yhtälö: :n korkein eksponentti = 1 + 5 = 4( 3) Toisen asteen yhtälö: :n korkein eksponentti = 3 5 + 4 = 0 Kolmannen asteen yhtälö: :n korkein
A-osio: Laske ilman laskinta tälle paperille, aikaa maksimissaan 60 min. MAOL:ia saa käyttää.
 MAA Kurssikoe 9..0 Arto Hekkanen ja Jussi Tyni A-osio: Laske ilman laskinta tälle paperille, aikaa maksimissaan 60 min. MAOL:ia saa käyttää. Nimi:. Kaikki kohdat ½ pisteen arvoisia. a) x x x (x ) b) 0
MAA Kurssikoe 9..0 Arto Hekkanen ja Jussi Tyni A-osio: Laske ilman laskinta tälle paperille, aikaa maksimissaan 60 min. MAOL:ia saa käyttää. Nimi:. Kaikki kohdat ½ pisteen arvoisia. a) x x x (x ) b) 0
Preliminäärikoe Pitkä Matematiikka 3.2.2009
 Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
2.2 Täydellinen yhtälö. Ratkaisukaava
 . Täydellinen yhtälö. Ratkaisukaava Tulon nollasäännöstä näkee silloin tällöin omituisia sovellutuksia. Jotkut näet ajattelevat, että on olemassa myöskin tulon -sääntö tai tulon "mikä-tahansa"- sääntö.
. Täydellinen yhtälö. Ratkaisukaava Tulon nollasäännöstä näkee silloin tällöin omituisia sovellutuksia. Jotkut näet ajattelevat, että on olemassa myöskin tulon -sääntö tai tulon "mikä-tahansa"- sääntö.
VILJAVUUSTUTKIMUS. Oulun Kaupunki Tekn.Keskus Leipivaara Anne Uusikatu 26 90100 OULU. Viljavuustietojen yhteenveto. Pvm Työ nro As.
 VILJAVUUSTUTKIMUS Sammonkatu 8, 90570 Oulu p. 08-5145600 f. 08-3113029 Pvm Työ nro As.nro 19.10.2010 73415 13424 Oulun Kaupunki Tekn.Keskus Leipivaara Anne Uusikatu 26 90100 OULU Tilatunnus saapui 05.10.2010
VILJAVUUSTUTKIMUS Sammonkatu 8, 90570 Oulu p. 08-5145600 f. 08-3113029 Pvm Työ nro As.nro 19.10.2010 73415 13424 Oulun Kaupunki Tekn.Keskus Leipivaara Anne Uusikatu 26 90100 OULU Tilatunnus saapui 05.10.2010
VILJAVUUSTUTKIMUS. Oulun Kaupunki, Yhdyskunta-ja ympäristöp Maa ja mittaus PL 32/ Solistinkatu 2 90015 OULUN KAUPUNKI. Viljavuustietojen yhteenveto
 VILJAVUUSTUTKIMUS Sammonkatu 8, Oulu p. 08-5145600 f. 08-33029 Pvm Työ nro As.nro 9.10.2015 3743 22631 Oulun Kaupunki, Yhdyskunta-ja ympäristöp Maa ja mittaus PL 32 Solistinkatu 2 90015 OULUN KAUPUNKI
VILJAVUUSTUTKIMUS Sammonkatu 8, Oulu p. 08-5145600 f. 08-33029 Pvm Työ nro As.nro 9.10.2015 3743 22631 Oulun Kaupunki, Yhdyskunta-ja ympäristöp Maa ja mittaus PL 32 Solistinkatu 2 90015 OULUN KAUPUNKI
OSA 1: YHTÄLÖNRATKAISUN KERTAUSTA JA TÄYDENNYSTÄ SEKÄ FUNKTIO
 OSA : YHTÄLÖNRATKAISUN KERTAUSTA JA TÄYDENNYSTÄ SEKÄ FUNKTIO Tekijät: Ari Heimonen, Hellevi Kupila, Katja Leinonen, Tuomo Talala, Hanna Tuhkanen ja Pekka Vaaraniemi Alkupala Kolme kaverusta, Olli, Pekka
OSA : YHTÄLÖNRATKAISUN KERTAUSTA JA TÄYDENNYSTÄ SEKÄ FUNKTIO Tekijät: Ari Heimonen, Hellevi Kupila, Katja Leinonen, Tuomo Talala, Hanna Tuhkanen ja Pekka Vaaraniemi Alkupala Kolme kaverusta, Olli, Pekka
3. Kongruenssit. 3.1 Jakojäännös ja kongruenssi
 3. Kongruenssit 3.1 Jakojäännös ja kongruenssi Tässä kappaleessa esitellään kokonaislukujen modulaarinen aritmetiikka (ns. kellotauluaritmetiikka), jossa luvut tyypillisesti korvataan niillä jakojäännöksillä,
3. Kongruenssit 3.1 Jakojäännös ja kongruenssi Tässä kappaleessa esitellään kokonaislukujen modulaarinen aritmetiikka (ns. kellotauluaritmetiikka), jossa luvut tyypillisesti korvataan niillä jakojäännöksillä,
2. Tyyppi-, erä- tai sarjanumero tai muu merkintä, jonka ansiosta rakennustuotteet voidaan tunnistaa, kuten 11 artiklan 4 kohdassa edellytetään:
 SUORITUSTASOILMOITUS No.:001/CPR/2013-07-01 1. Tuotetyypin yksilöllinen tunniste: Lämpölux 2. Tyyppi-, erä- tai sarjanumero tai muu merkintä, jonka ansiosta rakennustuotteet voidaan tunnistaa, kuten 11
SUORITUSTASOILMOITUS No.:001/CPR/2013-07-01 1. Tuotetyypin yksilöllinen tunniste: Lämpölux 2. Tyyppi-, erä- tai sarjanumero tai muu merkintä, jonka ansiosta rakennustuotteet voidaan tunnistaa, kuten 11
Eksponenttifunktio ja Logaritmit, L3b
 ja Logaritmit, L3b eksponentti-funktio Eksponentti-funktio Linkkejä kurssi8, / Etälukio (edu.) kurssi8, logaritmifunktio / Etälukio (edu.) Potenssifunktio y = f (x) = 2 Vakiofunktion y = a kuvaaja on vaakasuora
ja Logaritmit, L3b eksponentti-funktio Eksponentti-funktio Linkkejä kurssi8, / Etälukio (edu.) kurssi8, logaritmifunktio / Etälukio (edu.) Potenssifunktio y = f (x) = 2 Vakiofunktion y = a kuvaaja on vaakasuora
1 2 x2 + 1 dx. (2p) x + 2dx. Kummankin integraalin laskeminen oikein (vastaukset 12 ja 20 ) antaa erikseen (2p) (integraalifunktiot
 Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Käyttöohje Busch-AudioWorld. REG-vahvistin 8208-500 Busch-AudioWorld. 1673-1-8311 Rev. 01 17.12.2012
 Pos: 2 /#Neustruktur#/Online-Dokumentation (+KN)/Titelblätter/AudioVideo/Titelblatt - 8208 - BJE @ 22\mod_1332420093624_174011.docx @ 205176 @ @ 1 === Ende der Liste für Textmarke Cover === 1673-1-8311
Pos: 2 /#Neustruktur#/Online-Dokumentation (+KN)/Titelblätter/AudioVideo/Titelblatt - 8208 - BJE @ 22\mod_1332420093624_174011.docx @ 205176 @ @ 1 === Ende der Liste für Textmarke Cover === 1673-1-8311
Turnauksen otteluohjelma
 - FC Nestehukka Turnauksen otteluohjelma Nro vm Aika aikka Lohko Joukkue A Joukkue B.. : K B Testimuailma FC Jalkala - LT.. : K A Savon Letkeä Kankeus FC Ulkohuussi - LT.. : K C MCMLXIX Mustasurma - LT
- FC Nestehukka Turnauksen otteluohjelma Nro vm Aika aikka Lohko Joukkue A Joukkue B.. : K B Testimuailma FC Jalkala - LT.. : K A Savon Letkeä Kankeus FC Ulkohuussi - LT.. : K C MCMLXIX Mustasurma - LT
Käyttöohje Busch-Infoline. 1510 UC-500 Kutsujärjestelmä inva-wc:tä varten. 1673-1-8322 Rev. 01 17.12.2012
 Pos: 2 /#Neustruktur#/Online-Dokumentation (+KN)/Titelblätter/Infoline/Titelblatt - 1510 @ 25\mod_1339651633537_174011.docx @ 217346 @ @ 1 === Ende der Liste für Textmarke Cover === 1673-1-8322 Rev. 01
Pos: 2 /#Neustruktur#/Online-Dokumentation (+KN)/Titelblätter/Infoline/Titelblatt - 1510 @ 25\mod_1339651633537_174011.docx @ 217346 @ @ 1 === Ende der Liste für Textmarke Cover === 1673-1-8322 Rev. 01
Väestökehitys 1999-2009 ja ennuste vuosille 2014 ja 2019
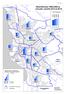 Väestökehitys - ja ennuste vuosille 2014 ja 2019 Koko kaupunki 115538 136936 143500 149500 2014 2019 Keskusta Sanginsuu Väestökehitys - ja ennuste vuosille 2014 ja 2019 20 000 2014 2019 Nuo Suuralueen
Väestökehitys - ja ennuste vuosille 2014 ja 2019 Koko kaupunki 115538 136936 143500 149500 2014 2019 Keskusta Sanginsuu Väestökehitys - ja ennuste vuosille 2014 ja 2019 20 000 2014 2019 Nuo Suuralueen
PRELIMINÄÄRIKOE. Pitkä Matematiikka 3.2.2015
 PRELIMINÄÄRIKOE Pitkä Matematiikka..5 Vastaa enintään kymmeneen tehtävään. Tähdellä merkittyjen (*) tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6.. a) Ratkaise epäyhtälö >.
PRELIMINÄÄRIKOE Pitkä Matematiikka..5 Vastaa enintään kymmeneen tehtävään. Tähdellä merkittyjen (*) tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6.. a) Ratkaise epäyhtälö >.
Esimerkkilaskelma. Mastopilarin perustusliitos liimaruuveilla
 Esimerkkilaskelma Mastopilarin perustusliitos liimaruuveilla.08.014 3.9.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS... - 4-4.1 ULOSVETOKESTÄVYYS (VTT-S-07607-1)...
Esimerkkilaskelma Mastopilarin perustusliitos liimaruuveilla.08.014 3.9.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS... - 4-4.1 ULOSVETOKESTÄVYYS (VTT-S-07607-1)...
Säätökeskus RVA36.531
 Säätökeskus Asennusohje 1. Johdanto Tämä ohje koskee säätökeskusta joka on tarkoitettu lämmönsäätöön pientaloissa jossa on vesikiertoinen lämmitysjärjestelmä.ohje tulee säilyttää lähellä säädintä.. Säätökeskus
Säätökeskus Asennusohje 1. Johdanto Tämä ohje koskee säätökeskusta joka on tarkoitettu lämmönsäätöön pientaloissa jossa on vesikiertoinen lämmitysjärjestelmä.ohje tulee säilyttää lähellä säädintä.. Säätökeskus
Pythagoraan polku 16.4.2011
 Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
Pythagoraan polku 6.4.20. Todista väittämä: Jos tasakylkisen kolmion toista kylkeä jatketaan omalla pituudellaan huipun toiselle puolelle ja jatkeen päätepiste yhdistetään kannan toisen päätepisteen kanssa,
ARVIOINTIPERIAATTEET
 PSYKOLOGIAN YHTEISVALINNAN VALINTAKOE 2012 ARVIOINTIPERIAATTEET Copyright Helsingin yliopisto, käyttäytymistieteiden laitos, Materiaalin luvaton kopiointi kielletty. TEHTÄVÄ 1. (max. 34.5 pistettä) 1 a.i)
PSYKOLOGIAN YHTEISVALINNAN VALINTAKOE 2012 ARVIOINTIPERIAATTEET Copyright Helsingin yliopisto, käyttäytymistieteiden laitos, Materiaalin luvaton kopiointi kielletty. TEHTÄVÄ 1. (max. 34.5 pistettä) 1 a.i)
Lineaarialgebra ja differentiaaliyhtälöt Harjoitus 4 / Ratkaisut
 MS-C34 Lineaarialgebra ja differentiaaliyhtälöt, IV/26 Lineaarialgebra ja differentiaaliyhtälöt Harjoitus 4 / t Alkuviikon tuntitehtävä Hahmottele matriisia A ( 2 6 3 vastaava vektorikenttä Matriisia A
MS-C34 Lineaarialgebra ja differentiaaliyhtälöt, IV/26 Lineaarialgebra ja differentiaaliyhtälöt Harjoitus 4 / t Alkuviikon tuntitehtävä Hahmottele matriisia A ( 2 6 3 vastaava vektorikenttä Matriisia A
monissa laskimissa luvun x käänteisluku saadaan näyttöön painamalla x - näppäintä.
 .. Käänteisunktio.. Käänteisunktio Mikäli unktio : A B on bijektio, niin joukkojen A ja B alkioiden välillä vallitsee kääntäen yksikäsitteinen vastaavuus eli A vastaa täsmälleen yksi y B, joten myös se
.. Käänteisunktio.. Käänteisunktio Mikäli unktio : A B on bijektio, niin joukkojen A ja B alkioiden välillä vallitsee kääntäen yksikäsitteinen vastaavuus eli A vastaa täsmälleen yksi y B, joten myös se
Ohjeita Volvo -kuorma-autojen jarrutarkastuksen suorittamiseen
 Ohjeita Volvo -kuorma-autojen jarrutarkastuksen suorittamiseen Mittauspisteiden sijainti ALB-kilven sijainti Laskentapaineet Yleisesti jarruhidastuvuusmittauksissa käytettävät laskentapaineet ovat VOLVO
Ohjeita Volvo -kuorma-autojen jarrutarkastuksen suorittamiseen Mittauspisteiden sijainti ALB-kilven sijainti Laskentapaineet Yleisesti jarruhidastuvuusmittauksissa käytettävät laskentapaineet ovat VOLVO
ADOBE CONNET (AC) -ALUSTAN KÄYTTÖ
 Kevät 2012 LISÄOHJEET: Lisäohjeet AC:n käytöstä löydät myös Opetusteknologiakeskus Mediamyllyn sivuilta http://diak.screenstepslive.com/s/755/m/adobeconnect8 Fronter-ohjeet: http://diak.screenstepslive.com/s/755/m/2397
Kevät 2012 LISÄOHJEET: Lisäohjeet AC:n käytöstä löydät myös Opetusteknologiakeskus Mediamyllyn sivuilta http://diak.screenstepslive.com/s/755/m/adobeconnect8 Fronter-ohjeet: http://diak.screenstepslive.com/s/755/m/2397
10. Kytkentäohje huonetermostaateille
 . Kytkentäohje huonetermostaateille TERMOSTAATTIE JA TOIMILAITTEIDE KYTKETÄ JA KYT KE TÄ KO TE LOI HI 2 1 2 2 1 WehoFloor-termostaatti 3222 soveltuvaa kaapelia 3 1, mm 2. joh timet keskusyk sikköön käsikirjassa
. Kytkentäohje huonetermostaateille TERMOSTAATTIE JA TOIMILAITTEIDE KYTKETÄ JA KYT KE TÄ KO TE LOI HI 2 1 2 2 1 WehoFloor-termostaatti 3222 soveltuvaa kaapelia 3 1, mm 2. joh timet keskusyk sikköön käsikirjassa
Viljan laatuhinnoittelu
 Sivu 1/19 Voimassa 27.10.2015 alkaen Korvaa 01.10.2015 ilmoitetun laatuhinnoittelun Ver. 5/2015 Viljan laatuhinnoittelu Satokausi 2015 / 2016 Voimassa ostoissa rehutehtaille ja varastoihin. Muutoksia kohdissa:
Sivu 1/19 Voimassa 27.10.2015 alkaen Korvaa 01.10.2015 ilmoitetun laatuhinnoittelun Ver. 5/2015 Viljan laatuhinnoittelu Satokausi 2015 / 2016 Voimassa ostoissa rehutehtaille ja varastoihin. Muutoksia kohdissa:
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4. Koe 8.5.0 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4. Koe 8.5.0 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
Täydellinen kilpailu: markkinoilla suuri määrä yrityksiä. ----> Yksi yritys ei vaikuta hyödykkeen markkinahintaan.
 5. EPÄTÄYDELLINEN KILPAILU Täydellinen kilpailu: markkinoilla suuri määrä yrityksiä. ----> Yksi yritys ei vaikuta hyödykkeen markkinahintaan. Epätäydellinen kilpailu: markkinoilla yksi tai vain muutama
5. EPÄTÄYDELLINEN KILPAILU Täydellinen kilpailu: markkinoilla suuri määrä yrityksiä. ----> Yksi yritys ei vaikuta hyödykkeen markkinahintaan. Epätäydellinen kilpailu: markkinoilla yksi tai vain muutama
ABB-Welcome M. M2301 Mini-järjestelmän keskusyksikkö 30.07.2014
 Pos : 2 /Di na4 - Anleit ung en O nline/i nhalt /KN X/D oorentr y/83220- AP- xxx/titelbl att - 83220-AP- xxx - ABB @ 19\mod_1323249806476_15.docx @ 111084 @ @ 1 === Ende der List e f ür T ext mar ke Cover
Pos : 2 /Di na4 - Anleit ung en O nline/i nhalt /KN X/D oorentr y/83220- AP- xxx/titelbl att - 83220-AP- xxx - ABB @ 19\mod_1323249806476_15.docx @ 111084 @ @ 1 === Ende der List e f ür T ext mar ke Cover
JavaScript alkeet Esimerkkikoodeja moniste 3 (Metropolia 11/2011)
 JavaScript alkeet Esimerkkikoodeja moniste 3 (Metropolia 11/2011) Array (taulukko) olio Esim. 9.1. taulukko eli Array olio kirjataulukko
JavaScript alkeet Esimerkkikoodeja moniste 3 (Metropolia 11/2011) Array (taulukko) olio Esim. 9.1. taulukko eli Array olio kirjataulukko
Testausseloste 2009-2611-1 1(1) Vesinäyte 31.07.2009
 Testausseloste 2009-2611-1 1(1) Vesinäyte 31.07.2009 Ulvilan Näytetiedot Näyte Näyte otettu 28.07.2009 Näytteen ottaja Haanpää Saapunut 28.07.2009 Näytteenoton syy Jatkuva valvonta Tutkimus alkoi 28.07.2009
Testausseloste 2009-2611-1 1(1) Vesinäyte 31.07.2009 Ulvilan Näytetiedot Näyte Näyte otettu 28.07.2009 Näytteen ottaja Haanpää Saapunut 28.07.2009 Näytteenoton syy Jatkuva valvonta Tutkimus alkoi 28.07.2009
110. 111. 112. 113. 114. 4. Matriisit ja vektorit. 4.1. Matriisin käsite. 4.2. Matriisialgebra. Olkoon A = , B = Laske A + B, 5 14 9, 1 3 3
 4 Matriisit ja vektorit 4 Matriisin käsite 42 Matriisialgebra 0 2 2 0, B = 2 2 4 6 2 Laske A + B, 2 A + B, AB ja BA A + B = 2 4 6 5, 2 A + B = 5 9 6 5 4 9, 4 7 6 AB = 0 0 0 6 0 0 0, B 22 2 2 0 0 0 6 5
4 Matriisit ja vektorit 4 Matriisin käsite 42 Matriisialgebra 0 2 2 0, B = 2 2 4 6 2 Laske A + B, 2 A + B, AB ja BA A + B = 2 4 6 5, 2 A + B = 5 9 6 5 4 9, 4 7 6 AB = 0 0 0 6 0 0 0, B 22 2 2 0 0 0 6 5
1. Murtoluvut, murtolausekkeet, murtopotenssit ja itseisarvo
 1. Murtoluvut, murtolausekkeet, murtopotenssit ja itseisarvo Olkoot a, b, c mielivaltaisesti valittuja reaalilukuja eli reaaliakselin pisteitä. Ne toteuttavat seuraavat laskulait (ns. kunta-aksioomat):
1. Murtoluvut, murtolausekkeet, murtopotenssit ja itseisarvo Olkoot a, b, c mielivaltaisesti valittuja reaalilukuja eli reaaliakselin pisteitä. Ne toteuttavat seuraavat laskulait (ns. kunta-aksioomat):
EKOMAKSUT 01.05.2013. Jätetaksa Oy Botniarosk Ab:n toimialueella Jätemaksutaulukko nro 1
 EKOMAKSUT Jätemaksutaulukko nro 1 /vuosi /vuosi Asunnot, joissa asuu 1 henkilö 20,00 24,8 Asunnot, joissa asuu 2 henkilöä 33,00 40,92 Asunnot, joissa asuu 3 henkilöä tai enemmän 38,00 47,12 Rivi- ja kerrostalot/asunto
EKOMAKSUT Jätemaksutaulukko nro 1 /vuosi /vuosi Asunnot, joissa asuu 1 henkilö 20,00 24,8 Asunnot, joissa asuu 2 henkilöä 33,00 40,92 Asunnot, joissa asuu 3 henkilöä tai enemmän 38,00 47,12 Rivi- ja kerrostalot/asunto
WC istuimien huuhtelusäiliöiden testaus
 TESTAUSSELOSTE Nro VTT S 11139 07 20.12.2007 WC istuimien huuhtelusäiliöiden testaus Tuotteet: Mio 828717 ja 827713, Alessi 826971, Form 827673 ja Pro 826953 Tilaaja: Laattapiste Oy TESTAUSSELOSTE NRO
TESTAUSSELOSTE Nro VTT S 11139 07 20.12.2007 WC istuimien huuhtelusäiliöiden testaus Tuotteet: Mio 828717 ja 827713, Alessi 826971, Form 827673 ja Pro 826953 Tilaaja: Laattapiste Oy TESTAUSSELOSTE NRO
Elektroniset sysäysreleet
 Elektroniset sysäysreleet EPS 0B EPS 0B Käyttöpainike Jokaisella painalluksella tästä painikkeestä sysäysreleen lähtökosketin vaihtaa tilaa. min 60 Tilannäyttö LEDin palaessa lähtökosketin on kytketty
Elektroniset sysäysreleet EPS 0B EPS 0B Käyttöpainike Jokaisella painalluksella tästä painikkeestä sysäysreleen lähtökosketin vaihtaa tilaa. min 60 Tilannäyttö LEDin palaessa lähtökosketin on kytketty
PERUSKOULUSTA PITKÄLLE
 Raimo Seppänen Tytti Kiiski PERUSKOULUSTA PITKÄLLE KERTAUSTA JA TÄYDENNYSTÄ LUKION PITKÄLLE MATEMATIIKALLE JA MATEMATIIKKAA VAATIVAAN AMMATILLISEEN KOULUTUKSEEN MFKA-KUSTANNUS OY HELSINKI 2007 SISÄLLYS
Raimo Seppänen Tytti Kiiski PERUSKOULUSTA PITKÄLLE KERTAUSTA JA TÄYDENNYSTÄ LUKION PITKÄLLE MATEMATIIKALLE JA MATEMATIIKKAA VAATIVAAN AMMATILLISEEN KOULUTUKSEEN MFKA-KUSTANNUS OY HELSINKI 2007 SISÄLLYS
Ylioppilastutkintolautakunta S tudentexamensnämnden
 Ylioppilastutintolautaunta S tudenteamensnämnden MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 0..0 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden ja sisältöjen luonnehdinta ei sido ylioppilastutintolautaunnan
Ylioppilastutintolautaunta S tudenteamensnämnden MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 0..0 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden ja sisältöjen luonnehdinta ei sido ylioppilastutintolautaunnan
Lyhyt jyrsin. K2 HM-jyrsimet 105-120. Kaikki hinnat ilman Alv.
 yhyt jyrsin K2 -jyrsimet 105-120 105 Kaikki hinnat iman Av. yhyt jyrsin G 9424 Vaurauta Aumiini Seos m m m Titaani Kupari INCONE Hiii m m m Toeranssiarvot YG STD s. 116 G 9424... h10 3878020...020 2,0
yhyt jyrsin K2 -jyrsimet 105-120 105 Kaikki hinnat iman Av. yhyt jyrsin G 9424 Vaurauta Aumiini Seos m m m Titaani Kupari INCONE Hiii m m m Toeranssiarvot YG STD s. 116 G 9424... h10 3878020...020 2,0
5784-40 LAATTA L1 275.05. TYÖOHJEET Suunniteltu käyttöikä 100 v. Toteutusluokka 2 1:100
 LTT L1 - PLUT Paalun puristuskestävyys Rd.max = Rd.nurj = 799 kn Paalun puristuskestävyys Rd.max = Rd.nurj = 777 kn PLULTT HL = mm Betoni, XC2, XD1 Betoniteräs B500B, B500K (500HW) L2 - lapinnassa 60 mm
LTT L1 - PLUT Paalun puristuskestävyys Rd.max = Rd.nurj = 799 kn Paalun puristuskestävyys Rd.max = Rd.nurj = 777 kn PLULTT HL = mm Betoni, XC2, XD1 Betoniteräs B500B, B500K (500HW) L2 - lapinnassa 60 mm
TESTAUSSELOSTE Talousvesitutkimus^ 29.5.2015
 1 (3) Heinäveden kunta Tekninen lautakunta Kermanrannantie 7 79700 HEINÄVESI Tilausnro 188708 (4232/TALVE), saapunut 11.5.2015, näytteet otettu 11.5.2015 Näytteenottaja: Kuuva Kauko NÄYTTEET Lab.nro Näytteen
1 (3) Heinäveden kunta Tekninen lautakunta Kermanrannantie 7 79700 HEINÄVESI Tilausnro 188708 (4232/TALVE), saapunut 11.5.2015, näytteet otettu 11.5.2015 Näytteenottaja: Kuuva Kauko NÄYTTEET Lab.nro Näytteen
Kompaktisäädin KNX. Kompaktisäädin KNX
 Sertifioitu KNX, S-tilan laite Toiminta-alue.. Pa (mittausalue..5 Pa) Käyntiaika 5s Käyttöjännite AC 24V GDB8.E/KN: vääntömomentti 5 Nm -> pellin ala n..8 m2 GLB8.E/KN: vääntömomentti Nm -> pellin ala
Sertifioitu KNX, S-tilan laite Toiminta-alue.. Pa (mittausalue..5 Pa) Käyntiaika 5s Käyttöjännite AC 24V GDB8.E/KN: vääntömomentti 5 Nm -> pellin ala n..8 m2 GLB8.E/KN: vääntömomentti Nm -> pellin ala
Pitkä matematiikka Suullinen kuulustelu (ma00s001.doc) Tehtävät, jotka on merkitty (V), ovat vaativia.
 Pitkä matematiikka Suullinen kuulustelu (ma00s00doc) Tehtävät, jotka on merkitty (V), ovat vaativia Yleistä Ratkaise yhtälöt n n n n n 5 a) 5 + 5 + 5 + 5 + 5 = 5 b) ( ) ( ) > 0 + = + c) ( ) Suureet ja
Pitkä matematiikka Suullinen kuulustelu (ma00s00doc) Tehtävät, jotka on merkitty (V), ovat vaativia Yleistä Ratkaise yhtälöt n n n n n 5 a) 5 + 5 + 5 + 5 + 5 = 5 b) ( ) ( ) > 0 + = + c) ( ) Suureet ja
OPTIIKAN TYÖ. Fysiikka 1-2:n/Fysiikan peruskurssien harjoitustyöt (mukautettu lukion oppimäärään) Nimi: Päivämäärä: Assistentti:
 Fysiikka 1-2:n/Fysiikan peruskurssien harjoitustyöt (mukautettu lukion oppimäärään) Nimi: Päivämäärä: Assistentti: OPTIIKAN TYÖ Vastaa ensin seuraaviin ennakkotietoja mittaaviin kysymyksiin. 1. Mitä tarkoittavat
Fysiikka 1-2:n/Fysiikan peruskurssien harjoitustyöt (mukautettu lukion oppimäärään) Nimi: Päivämäärä: Assistentti: OPTIIKAN TYÖ Vastaa ensin seuraaviin ennakkotietoja mittaaviin kysymyksiin. 1. Mitä tarkoittavat
Liitetaulukko 1/11. Tutkittujen materiaalien kokonaispitoisuudet KOTIMAINEN MB-JÄTE <1MM SAKSAN MB- JÄTE <1MM POHJAKUONA <10MM
 Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Matematiikan perusteet taloustieteilijöille 1a 802152P
 Matematiikan perusteet taloustieteilijöille 1a 802152P Luentomoniste Kari Myllylä Niina Korteslahti Oulun yliopisto Matemaattisten tieteiden laitos Syksy 2013 Sisältö 1 Perusmatematiikkaa 3 1.1 Lukujoukot..............................
Matematiikan perusteet taloustieteilijöille 1a 802152P Luentomoniste Kari Myllylä Niina Korteslahti Oulun yliopisto Matemaattisten tieteiden laitos Syksy 2013 Sisältö 1 Perusmatematiikkaa 3 1.1 Lukujoukot..............................
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2008
 ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2008 Harjoitus 5 Ratkaisuehdotuksia Näissä harjoituksissa viljellään paljon sanaa paradoksi. Sana tulee ymmärtää laajassa mielessä. Suppeassa mielessähän
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2008 Harjoitus 5 Ratkaisuehdotuksia Näissä harjoituksissa viljellään paljon sanaa paradoksi. Sana tulee ymmärtää laajassa mielessä. Suppeassa mielessähän
HQ-PURE150/12 (F) HQ-PURE150/24 (F) 150 WATIN DC-AC SINIAALTOINVERTTERI
 SUOMI KÄYTTÖOPAS HQ-PURE150/12 (F) HQ-PURE150/24 (F) 150 WATIN DC-AC SINIAALTOINVERTTERI LUE OHJEET ENNEN KÄYTTÖÄ! Hyödylliset sovellukset Kannettavat, radiot, pienet televisiot, VCR-nauhurit, DVD-soittimet,
SUOMI KÄYTTÖOPAS HQ-PURE150/12 (F) HQ-PURE150/24 (F) 150 WATIN DC-AC SINIAALTOINVERTTERI LUE OHJEET ENNEN KÄYTTÖÄ! Hyödylliset sovellukset Kannettavat, radiot, pienet televisiot, VCR-nauhurit, DVD-soittimet,
Robotisointi ja mekanisointi. Orbitaalihitsaus. Kalervo Leino VTT Tuotteet ja tuotanto
 Robotisointi ja mekanisointi. Orbitaalihitsaus. Kalervo Leino VTT Tuotteet ja tuotanto HITSAUSAUTOMAATION TAVOITTEET hitsauksen tuottavuuden paraneminen tuottavien hitsausprosessien käyttö parempi työhygienia
Robotisointi ja mekanisointi. Orbitaalihitsaus. Kalervo Leino VTT Tuotteet ja tuotanto HITSAUSAUTOMAATION TAVOITTEET hitsauksen tuottavuuden paraneminen tuottavien hitsausprosessien käyttö parempi työhygienia
JET-Power, ALU-Power ja D-Power HM-jyrsimet
 JET-Power, ALU-Power ja -Power HM-jyrsimet JET-Power. Erikoisjyrsin ruostumattomille teräksille (alle HRc 45) ALU-Power. Erikoisjyrsin alumiinille ja kupariseoksille. -Power. Erikoisjyrsin grafiittia varten.
JET-Power, ALU-Power ja -Power HM-jyrsimet JET-Power. Erikoisjyrsin ruostumattomille teräksille (alle HRc 45) ALU-Power. Erikoisjyrsin alumiinille ja kupariseoksille. -Power. Erikoisjyrsin grafiittia varten.
Fluke Connect -moduulit Tekniset tiedot
 Fluke Connect -moduulit Tekniset tiedot Joustavuutta langattomien järjestelmien rakentamiseen - miten haluat - milloin haluat. Langattomat Fluke 3000 FC -mittauslaitteet ovat joukkue, jossa moduulit pelaavat
Fluke Connect -moduulit Tekniset tiedot Joustavuutta langattomien järjestelmien rakentamiseen - miten haluat - milloin haluat. Langattomat Fluke 3000 FC -mittauslaitteet ovat joukkue, jossa moduulit pelaavat
Nimike Hinta EUR/kpl 1-10 kpl Hinta EUR/kpl 10-100 kpl 1A5600 0,252 0,1764
 Sulakepitimet autosulakkeelle Cooper 1A5600-sarjan sulakepidin Autosulakkeelle 0-20A. 1A5600 0,252 0,1764 Cooper 1A1119-sarjan sulakepidin Sulakepidin 6,3 x 32 mm sulakkeelle 0-15A Nimike Pitimen materiaali
Sulakepitimet autosulakkeelle Cooper 1A5600-sarjan sulakepidin Autosulakkeelle 0-20A. 1A5600 0,252 0,1764 Cooper 1A1119-sarjan sulakepidin Sulakepidin 6,3 x 32 mm sulakkeelle 0-15A Nimike Pitimen materiaali
Fluke 279 FC -yleismittari/lämpökamera
 TEKNISET TIEDOT Fluke 279 FC -yleismittari/lämpökamera Etsi. Korjaa. Tarkasta. Raportoi. 279 FC, digitaalisen yleismittarin ja lämpökameran yhdistelmä, lisää mittausten tuottavuutta ja luotettavuutta.
TEKNISET TIEDOT Fluke 279 FC -yleismittari/lämpökamera Etsi. Korjaa. Tarkasta. Raportoi. 279 FC, digitaalisen yleismittarin ja lämpökameran yhdistelmä, lisää mittausten tuottavuutta ja luotettavuutta.
Tekniset tiedot. Kontaktorit ja moottorikäynnistimet CI-TI TM Aikareleet ATI, BTI, MTI 520B11309
 Kontaktorit ja moottorikäynnistimet CI-TI TM Elokuu 2002 DKACT.PD.Coo.J2.20 520B11309 Johdanto MTI: - päästöhidastus - vetohidastus - Pulssitoiminnot - Tähti/kolmio vaihtokytkentä Toimintojen valinta AV
Kontaktorit ja moottorikäynnistimet CI-TI TM Elokuu 2002 DKACT.PD.Coo.J2.20 520B11309 Johdanto MTI: - päästöhidastus - vetohidastus - Pulssitoiminnot - Tähti/kolmio vaihtokytkentä Toimintojen valinta AV
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
Ikkunan ja oven tärkeimmät teknilliset ominaisuudet
 Ikkunan ja oven tärkeimmät teknilliset ominaisuudet 12.2.2015 Jorma S. Tiiri Tuotekehityspäällikkö Domus Yhtiöt Oy LOIMAA CE-merkintä Rakennustuoteasetuksen N:o 305/2011 ja tuotestandardin SFS-EN 14351-1
Ikkunan ja oven tärkeimmät teknilliset ominaisuudet 12.2.2015 Jorma S. Tiiri Tuotekehityspäällikkö Domus Yhtiöt Oy LOIMAA CE-merkintä Rakennustuoteasetuksen N:o 305/2011 ja tuotestandardin SFS-EN 14351-1
(x 0 ) = lim. Derivoimissääntöjä. Oletetaan, että funktiot f ja g ovat derivoituvia ja c R on vakio. 1. Dc = 0 (vakiofunktion derivaatta) 2.
 Derivaatta kuvaa funktion hetkellistä kasvunopeutta. Geometrisesti tulkittuna funktion derivaatta kohdassa x 0 on funktion kuvaajalle kohtaan x 0 piirretyn tangentin kulmakerroin. Funktio f on derivoituva
Derivaatta kuvaa funktion hetkellistä kasvunopeutta. Geometrisesti tulkittuna funktion derivaatta kohdassa x 0 on funktion kuvaajalle kohtaan x 0 piirretyn tangentin kulmakerroin. Funktio f on derivoituva
SÄHKE-hanke. Tekninen mallintamisen Esimerkit siirtotiedoston metatiedoista Esimerkki, Metatied.xml.
 04.02.2005 1 (12) SÄHKE-hanke Tekninen mallintamisen Versio ja pvm Laatinut Tarkpvm Tarkastanut Hyvpvm Hyväksynyt 2.0 / 04.02.2005 Lasse Akselin 15.02.2005 Markus Merenmies 18.02.2005 Ohjausryhmä 04.02.2005
04.02.2005 1 (12) SÄHKE-hanke Tekninen mallintamisen Versio ja pvm Laatinut Tarkpvm Tarkastanut Hyvpvm Hyväksynyt 2.0 / 04.02.2005 Lasse Akselin 15.02.2005 Markus Merenmies 18.02.2005 Ohjausryhmä 04.02.2005
( ) Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 321 Päivitetty 19.2.2006. Saadaan yhtälö. 801 Paraabeli on niiden pisteiden ( x,
 Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Mitä riskiperusteisuus on? Veli-Mikko Niemi Elintarvikevalvonnan päivät Tampere 24.1.2012
 Mitä riskiperusteisuus on? Veli-Mikko Niemi Elintarvikevalvonnan päivät Tampere 24.1.2012 Riskiperusteisuus kuulostaa helpolta paperilla ja pomojen juhlapuheissa Jaana Husu-Kallio, 17.1.2012 Riskipohjainen
Mitä riskiperusteisuus on? Veli-Mikko Niemi Elintarvikevalvonnan päivät Tampere 24.1.2012 Riskiperusteisuus kuulostaa helpolta paperilla ja pomojen juhlapuheissa Jaana Husu-Kallio, 17.1.2012 Riskipohjainen
KOMPONENTIT JA ERIKOISKAAPELIT 9
 HÄLYTYS- LAITTEET KOMPONENTIT JA ERIKOISKAAPELIT 9 SKS-automaatio Oy Martinkyläntie 50, PL 122, 01721 Vantaa, sähköposti: automaatio@sks.fi, faksi 852 6820, puh. *852 661 Etelä-Suomi Martinkyläntie 50
HÄLYTYS- LAITTEET KOMPONENTIT JA ERIKOISKAAPELIT 9 SKS-automaatio Oy Martinkyläntie 50, PL 122, 01721 Vantaa, sähköposti: automaatio@sks.fi, faksi 852 6820, puh. *852 661 Etelä-Suomi Martinkyläntie 50
Kuusakoski Oy:n rengasrouheen kaatopaikkakelpoisuus.
 Kuusakoski Oy:n rengasrouheen kaatopaikkakelpoisuus. 2012 Envitop Oy Riihitie 5, 90240 Oulu Tel: 08375046 etunimi.sukunimi@envitop.com www.envitop.com 2/5 KUUSAKOSKI OY Janne Huovinen Oulu 1 Tausta Valtioneuvoston
Kuusakoski Oy:n rengasrouheen kaatopaikkakelpoisuus. 2012 Envitop Oy Riihitie 5, 90240 Oulu Tel: 08375046 etunimi.sukunimi@envitop.com www.envitop.com 2/5 KUUSAKOSKI OY Janne Huovinen Oulu 1 Tausta Valtioneuvoston
Lahden kaupungin vapaat omakotitontit 8.6. - 29.7.2016
 1 (7) KYTÖLÄ Rukkikatu 4 10272 3 860 250 II 30 590 1 529,50 Rämekuja 3 12402 13 865 250 I u2/3 25 570 1 278,50 Lehväkuja 4 12402 14 872 250 I u2/3 25 766 1 288,30 Rämekuja 2 12402 19 1 004 250 I 29 462
1 (7) KYTÖLÄ Rukkikatu 4 10272 3 860 250 II 30 590 1 529,50 Rämekuja 3 12402 13 865 250 I u2/3 25 570 1 278,50 Lehväkuja 4 12402 14 872 250 I u2/3 25 766 1 288,30 Rämekuja 2 12402 19 1 004 250 I 29 462
PIIRIANALYYSI. Harjoitustyö nro 7. Kipinänsammutuspiirien mitoitus. Mika Lemström
 PIIRIANAYYSI Harjoitustyö nro 7 Kipinänsammutuspiirien mitoitus Mika emström Sisältö 1 Johdanto 3 2 RC-suojauspiiri 4 3 Diodi suojauspiiri 5 4 Johtopäätos 6 sivu 2 [6] Piirianalyysi Kipinänsammutuspiirien
PIIRIANAYYSI Harjoitustyö nro 7 Kipinänsammutuspiirien mitoitus Mika emström Sisältö 1 Johdanto 3 2 RC-suojauspiiri 4 3 Diodi suojauspiiri 5 4 Johtopäätos 6 sivu 2 [6] Piirianalyysi Kipinänsammutuspiirien
Sisäverkon peittotuotteet
 Sisäverkon peittotuotteet Laatuantennin sisäverkon peittotuotteilla voitte helposti parantaa kuuluvuutta tai nostaa mobiililaajakaistan nopeutta. Ulkoantennin avulla hitaasti toimivan laajakaistaliittymän
Sisäverkon peittotuotteet Laatuantennin sisäverkon peittotuotteilla voitte helposti parantaa kuuluvuutta tai nostaa mobiililaajakaistan nopeutta. Ulkoantennin avulla hitaasti toimivan laajakaistaliittymän
Tilastollinen päättely. 5. Väliestimointi. 5.1. Johdanto. 5.2. Luottamusvälien konstruointi. 5.3. Luottamusvälien vertailu
 ilastollinen päättely 5.. Johdanto Estimointi, Joukkoestimointi, Kriittinen alue, uottamusjoukko, uottamustaso, uottamusväli, Otos, Parametri, Peittotodennäköisyys, Piste estimointi, Väliestimaatti, Väliestimaattori,
ilastollinen päättely 5.. Johdanto Estimointi, Joukkoestimointi, Kriittinen alue, uottamusjoukko, uottamustaso, uottamusväli, Otos, Parametri, Peittotodennäköisyys, Piste estimointi, Väliestimaatti, Väliestimaattori,
Oulun seudulla kiertävien nopeusnäyttötaulujen mittaukset ajalla 8/2014-7/2015. Pohjois-Pohjanmaan ELY-keskuksen maantieverkon kohteet
 Oulun seudulla kiertävien nopeusnäyttötaulujen mittaukset ajalla 8/2014-7/2015 Pohjois-Pohjanmaan ELY-keskuksen maantieverkon kohteet Mittauspisteet MittausID Suuralue tai kunta Sijainti Tietoja 108 Haukipudas
Oulun seudulla kiertävien nopeusnäyttötaulujen mittaukset ajalla 8/2014-7/2015 Pohjois-Pohjanmaan ELY-keskuksen maantieverkon kohteet Mittauspisteet MittausID Suuralue tai kunta Sijainti Tietoja 108 Haukipudas
XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut
 XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut 1. Avaruusalus sijaitsee tason origossa (0, 0) ja liikkuu siitä vakionopeudella johonkin suuntaan, joka ei muutu. Tykki
XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut 1. Avaruusalus sijaitsee tason origossa (0, 0) ja liikkuu siitä vakionopeudella johonkin suuntaan, joka ei muutu. Tykki
SCOTT PRO 2 SUODATTIMET TEKNISET TIEDOT
 SCOTT PRO 2 SUODATTIMET TEKNISET TIEDOT Testitulokset HUOM: Kaksoissuodattimisten puolinaamarien suodattimet testataan yksitellen, ja testissä käytetään puolitettua virtausta, esim. vaatimuksissa esitetty
SCOTT PRO 2 SUODATTIMET TEKNISET TIEDOT Testitulokset HUOM: Kaksoissuodattimisten puolinaamarien suodattimet testataan yksitellen, ja testissä käytetään puolitettua virtausta, esim. vaatimuksissa esitetty
testo 610 Käyttöohje
 testo 610 Käyttöohje FIN 2 Pikaohje testo 610 Pikaohje testo 610 1 Suojakansi: käyttöasento 2 Kosteus- ja lämpötilasensori 3 Näyttö 4 Toimintonäppäimet 5 Paristokotelo (laitteen takana) Perusasetukset
testo 610 Käyttöohje FIN 2 Pikaohje testo 610 Pikaohje testo 610 1 Suojakansi: käyttöasento 2 Kosteus- ja lämpötilasensori 3 Näyttö 4 Toimintonäppäimet 5 Paristokotelo (laitteen takana) Perusasetukset
ei jakoventtiileinä. Laipallista venttiiliä M3P...FY on saatavana kahta eri kokoa: laipallinen venttiili DN100
 Magneettitoimimoottorilla varustetut moduloivat säätöventtiilit PN kylmä- ja lämminvesilaitoksia varten; varustettu asennon säädöllä ja asennon takaisinkytkennällä MP80FY MP00FY Magneettisella toimimoottorilla
Magneettitoimimoottorilla varustetut moduloivat säätöventtiilit PN kylmä- ja lämminvesilaitoksia varten; varustettu asennon säädöllä ja asennon takaisinkytkennällä MP80FY MP00FY Magneettisella toimimoottorilla
Nämä toimitusehdot korvaavat aikaisemmat Mäntypuisten ratapölkkyjen tekniset toimitusehdot 1281/731/97, 1.11.1997. kunnossapitoyksikön päällikkö
 RATAHALLINTO- KESKUS BANFÖRVALTNINGS- CENTRALEN 1717/731/02 8.11.2002 1 (7) MÄNTYPUISTEN RATAPÖLKKYJEN TEKNISET TOIMITUSEHDOT Ratahallintokeskus on vahvistanut Mäntypuisten ratapölkkyjen tekniset toimitusehdot
RATAHALLINTO- KESKUS BANFÖRVALTNINGS- CENTRALEN 1717/731/02 8.11.2002 1 (7) MÄNTYPUISTEN RATAPÖLKKYJEN TEKNISET TOIMITUSEHDOT Ratahallintokeskus on vahvistanut Mäntypuisten ratapölkkyjen tekniset toimitusehdot
JÄTEJAKEIDEN YMPÄRISTÖKELPOISUUS MAARAKENTAMISESSA. RAMBOLL FINLAND OY 28.1.2016 marjo.ronkainen@ramboll.fi
 JÄTEJAKEIDEN YMPÄRISTÖKELPOISUUS MAARAKENTAMISESSA RAMBOLL FINLAND OY 28.1.2016 marjo.ronkainen@ramboll.fi UUSIOMATERIAALIT MAANRAKENNUKSESSA UUMA2-OHJELMA 2013-2017 Tavoite Tavoitteena on saada uusiomateriaalit
JÄTEJAKEIDEN YMPÄRISTÖKELPOISUUS MAARAKENTAMISESSA RAMBOLL FINLAND OY 28.1.2016 marjo.ronkainen@ramboll.fi UUSIOMATERIAALIT MAANRAKENNUKSESSA UUMA2-OHJELMA 2013-2017 Tavoite Tavoitteena on saada uusiomateriaalit
TA-Slider 160. Toimilaitteet Digitaalisesti määriteltävä, suhteellisesti säätävä, yksitoiminen (push) toimilaite 160/200 N
 TA-Slider 160 Toimilaitteet Digitaalisesti määriteltävä, suhteellisesti säätävä, yksitoiminen (push) toimilaite 160/200 N TA-Slider 160 Digitaalisesti määriteltävät toimilaitteet usealla asettelumahdollisuudella
TA-Slider 160 Toimilaitteet Digitaalisesti määriteltävä, suhteellisesti säätävä, yksitoiminen (push) toimilaite 160/200 N TA-Slider 160 Digitaalisesti määriteltävät toimilaitteet usealla asettelumahdollisuudella
Sähkötekniikka ja elektroniikka
 Sähkötekniikka ja elektroniikka Kimmo Silvonen (X) Kokeet, harjoitustehtävät, palaute 2. välikoe ja tentti ma 7.12. klo 10.15-13, S1 Valitset kokeen aikana, suoritatko tentin Ilmoittaudu joka tapauksessa
Sähkötekniikka ja elektroniikka Kimmo Silvonen (X) Kokeet, harjoitustehtävät, palaute 2. välikoe ja tentti ma 7.12. klo 10.15-13, S1 Valitset kokeen aikana, suoritatko tentin Ilmoittaudu joka tapauksessa
MATEMATIIKAN JAOS Kompleksianalyysi
 MATEMATIIKAN JAOS Kompleksianalyysi Harjoitustehtäviä, syksy 00. Määrää kompleksiluvun a) = 3 j + 3j, b) = j, + j c) = ( 3 3 3 j)( j) itseisarvo ja argumentti.. Määrää sellaiset reaaliluvut x ja y, että
MATEMATIIKAN JAOS Kompleksianalyysi Harjoitustehtäviä, syksy 00. Määrää kompleksiluvun a) = 3 j + 3j, b) = j, + j c) = ( 3 3 3 j)( j) itseisarvo ja argumentti.. Määrää sellaiset reaaliluvut x ja y, että
KESKUSAKKUJÄRJESTELMÄ FZLV. Valvottu 24 V:n keskusakkujärjestelmä VER 16-03
 KESKUSAKKUJÄRJESTELMÄ FZLV Valvottu 24 V:n keskusakkujärjestelmä VER 16-03 Reitti selväksi se on fi losofi amme ja liikeideamme. Accenta AB markkinoi ja myy laajaa opasvalaisin-, turvavalaistus- ja varavalaistusvarusteiden
KESKUSAKKUJÄRJESTELMÄ FZLV Valvottu 24 V:n keskusakkujärjestelmä VER 16-03 Reitti selväksi se on fi losofi amme ja liikeideamme. Accenta AB markkinoi ja myy laajaa opasvalaisin-, turvavalaistus- ja varavalaistusvarusteiden
HIV-POSITIIVISTEN POTILAIDEN KUOLINSYYT 2000-LUVUN HELSINGISSÄ. 11.2.2015 XVI valtakunnallinen HIV-koulutus Jussi Sutinen Dos, Joona Lassila LL
 HIV-POSITIIVISTEN POTILAIDEN KUOLINSYYT 2000-LUVUN HELSINGISSÄ 11.2.2015 XVI valtakunnallinen HIV-koulutus Jussi Sutinen Dos, Joona Lassila LL Changes in the cause of death among HIV positive subjects
HIV-POSITIIVISTEN POTILAIDEN KUOLINSYYT 2000-LUVUN HELSINGISSÄ 11.2.2015 XVI valtakunnallinen HIV-koulutus Jussi Sutinen Dos, Joona Lassila LL Changes in the cause of death among HIV positive subjects
Matematiikan tukikurssi. Syksy 2009
 Matematiikan tukikurssi Syksy 2009 Sisältö I Ensimmäinen välikoe 5 Matemaattisesta päättelystä 5 2 Toisen asteen yhtälöistä 6 3 Joukko-oppia 8 4 Funktiokäsitteestä 5 Määrittelyjoukoista 6 6 Relaatioista
Matematiikan tukikurssi Syksy 2009 Sisältö I Ensimmäinen välikoe 5 Matemaattisesta päättelystä 5 2 Toisen asteen yhtälöistä 6 3 Joukko-oppia 8 4 Funktiokäsitteestä 5 Määrittelyjoukoista 6 6 Relaatioista
a b c d + + + + + + + + +
 28. 10. 2010!"$#&%(')'+*(#-,.*/1032/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + + + 2. 3. 4. 5. 6. + + + + + + + + + + P1. Valitaan kannaksi sivu, jonka pituus on 4. Koska toinen jäljelle jäävistä sivuista
28. 10. 2010!"$#&%(')'+*(#-,.*/1032/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + + + 2. 3. 4. 5. 6. + + + + + + + + + + P1. Valitaan kannaksi sivu, jonka pituus on 4. Koska toinen jäljelle jäävistä sivuista
Lattiabetonin valinta eri käyttökohteisiin. Vesa Anttila
 Lattiabetonin valinta eri käyttökohteisiin Vesa Anttila 29.10.2015 Lattioiden teko haastava betonityö! Laajat avoimet pinnat Olosuhteet rajaavat usein valintoja Paljon käsityötä työmiehillä suuri vaikutus
Lattiabetonin valinta eri käyttökohteisiin Vesa Anttila 29.10.2015 Lattioiden teko haastava betonityö! Laajat avoimet pinnat Olosuhteet rajaavat usein valintoja Paljon käsityötä työmiehillä suuri vaikutus
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 18.3.2015 HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 8..5 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 8..5 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Sisällysluettelo. PREXISO P80 788508b 1
 Sisällysluettelo Kojeen asennus - - - - - - - - - - - - - - - - - - - - - - - - - - -2 Yleiskuva - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2 Näyttö - - - - - - - - - - - - - - -
Sisällysluettelo Kojeen asennus - - - - - - - - - - - - - - - - - - - - - - - - - - -2 Yleiskuva - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2 Näyttö - - - - - - - - - - - - - - -
TALOUSTIETEEN LUENTOJEN TEHTÄVÄT
 TALOUSTIETEEN LUENTOJEN TEHTÄVÄT 1. Suhteellisen edun periaate 1. Maassa A: 1 maito ~ 3 leipää 1 leipä ~ 0,33 maitoa Maassa B: a. b. 3 maitoa ~ 5 leipää 1 maito ~ 1,67 leipää 1 leipä ~ 0,6 maitoa i. Maalla
TALOUSTIETEEN LUENTOJEN TEHTÄVÄT 1. Suhteellisen edun periaate 1. Maassa A: 1 maito ~ 3 leipää 1 leipä ~ 0,33 maitoa Maassa B: a. b. 3 maitoa ~ 5 leipää 1 maito ~ 1,67 leipää 1 leipä ~ 0,6 maitoa i. Maalla
Lataa ilmaiseksi mafyvalmennus.fi/mafynetti. Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla!
 Miten opit parhaiten? Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla! n Harjoittelu tehdään aktiivisesti tehtäviä ratkomalla. Tehtävät kattavat kaikki yo-kokeessa
Miten opit parhaiten? Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla! n Harjoittelu tehdään aktiivisesti tehtäviä ratkomalla. Tehtävät kattavat kaikki yo-kokeessa
