AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä
|
|
|
- Timo-Jaakko Lattu
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä 1
2 Marika Toivola ja Tiina Härkönen AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä Sisältö kuvituksineen on lisensoitu avoimella CC BY 3.0 -lisenssillä. Kirjan alkuperäiseen docx-muotoiseen versioon löytyy linkki sivulta Graafinen suunnittelu ja kuvitus: Taira Vehkasalo, Hanna Inkilä, Helmi Folkersma 2
3 Tilastoja ja todennäköisyyksiä 1. Kuvaajien tulkintaa Pylväs- ja viivadiagrammi Sektoridiagrammi Tilastomuuttujan tyypit ja frekvenssi Aineiston luokittelu Keskiarvon laskeminen Tyyppiarvon ja mediaanin määrittäminen Hajontalukujen määrittäminen Taulukkolaskentaa Tuotetaan ja havainnollistetaan tilastotietoja Joukko-oppia Todennäköisyyden määrittäminen Klassinen todennäköisyys Tilastollinen ja geometrinen todennäköisyys Malleja alkeistapausten muodostamiseksi Riippumattomien tapahtumien kertosääntö Yleinen kertosääntö Erillisten tapahtumien yhteenlaskusääntö Vastatapahtuma Kertaustehtäviä Vastaukset Taulukko-osio
4 Miten tilastot liittyvät koleraepidemian taltuttamiseen? 4
5 Lontoossa oli 1800-luvulla useita koleraepidemioita. Ihmiset olivat kauhuissaan ja yrittivät päästä pakoon tuota tappavaa suolistosairautta. Suurimmat seuraukset olivat vuoden 1949 epidemialla, joka laantui vasta kun ihmistä oli menehtynyt. Koleraan ei ollut parannuskeinoa, eikä kukaan tiennyt, mikä aiheutti tämän sairauden. Koleran uskottiin johtuvan maaperästä kohoavista höyryistä. Lontoolainen lääkäri John Snow aavisti, että tartuntalähde oli pilaantunut vesi. Vuoden 1854 koleraepidemia tarjosi Snow lle mahdollisuuden todistaa arvauksensa oikeaksi. Hän merkitsi karttaan kaikki tietoonsa tulleet tautitapaukset. Tämä kartta oli tehokkain ase koleraa vastaan, koska se osoitti, että lähes kaikki tartunnan saaneet asuivat saman vesiyhtiön, Vauxhall Water Companyn, toimialueella. Muista vesiyhtiöistä poiketen, se otti veden Thamesjoen alajuoksulta. Vesi ei ollut siis puhdasta vaan ulosteiden ja muiden jätteiden saastuttamaa jokivettä. Koleran yhteys epäpuhtaaseen veteen vahvistui entisestään, kun tohtori Snow löysi erään kolerakuoleman kaukaa Broad Streetin pumpusta. Eräs nainen oli pitänyt niin paljon Broad Streetin vedestä, että hän maksoi, että sai sitä kotiin toimitettuna. Oli selvää, että jokin oli saastuttanut tämän pumpun veden ja surmannut tuhansia ihmisiä. Kun saastuneet kaivot suljettiin, koleraepidemia alkoi nopeasti laantua. Snow n tutkimukset osoittivat viemäröinnin tärkeyden kaupungeissa. Seuraava suuri edistysaskel juomaveden turvallisuudelle oli kloorauksen aloittaminen 1900-luvun alussa. Silloin oltiin jo selvillä bakteerien yhteydestä tauteihin. Snow n tutkimukset osoittivat myös sen, miten hyödyllistä tiedon kerääminen, järjestämien ja analysoiminen on. Tilastojen hyödyntäminen pelasti tuhansia ihmishenkiä koleralta. Nykyisin tiedetään, että koleran aiheuttaa Vibrio cholerae- bakteeri. Koleraa esiintyy edelleen monissa Aasian ja Afrikan maissa. Sitä on esiintynyt myös Latinalaisessa Amerikassa. Koska länsimaalaisilta puuttuu suoja koleraa vastaan, suositellaan rokotetta kolera-alueelle matkustaville henkilöille, jotka asuvat siellä kauan ja alkeellisissa oloissa. Kolerabakteeri kuolee normaalisti mahalaukun happamassa ympäristössä, mutta henkilöt, joilla mahahapon määrä on tavallista pienempi, ovat erityisen herkkiä tartunnalle. Kolera on ehkäistävissä hyvällä käsi- ja ruokahygienialla. 5
6 1 Tilastotietoja havainnollistetaan usein graafisesti eli erilaisten kuvaajien avulla. Kuvaajista Kuvaajien tulkintaa käytetään nimitystä diagrammit ja niiden tehtävänä on kertoa uutisoitavasta asiasta tärkeimmät seikat yksinkertaisesti ja selkeästi. Kuvaajia kannattaa kuitenkin tarkastella kriittisesti, koska joskus ne voivat vääristää tietoa. Esimerkki 1. Tarkastellaan alla olevaa kuvaajaa. a) Mihin kellonaikaan kamelin ruuminlämpö oli korkeimmillaan? b) Paljonko ruumiinlämpö oli klo: 20.00? c) Milloin ruuminlämpö nousi eniten? d) Paljonko ruumiinlämpö oli alimmillaan? Ratkaisu: a) b) 37 C c) klo: d) 34 C Ruumiinlämpö ( C) Kamelin ruumiinlämpö eri vuorokauden aikoina Kellonaika
7 Esimerkki 2. Tarkastellaan allaolevaa kuvaajaa. a) Mikä on hiihtoladun korkeusero? b) Monennenko kilometrin kohdalla tulee jyrkin nousu? c) Kuinka pitkä on pisin laskuosuus? d) Montako nousuosuutta ladulla on? korkeus 5 km hiihdon latuprofiili matka km Ratkaisu: a) noin 38 m b) 3,5 km c) noin 600 m d) 9 7
8 Tehtäviä 1. Vastaa kuvaajan perusteella kysymyksiin. a) Kuinka paljon tarvitset kuvaajan mukaan unta? b) Paljonko 20-vuotias tarvitsee unta? c) Paljonko 90-vuotias tarvitsee unta? d) Minkä ikäisille riittää kuuden tunnin yöunet? Tuntia vuorokaudessa Keskimääräinen unentarve vuorokaudessa iän mukaan Ikä (vuotta) 2. Suoran y= x + 3 kuvaaja Tarkastellaan y koordinaatistoon piirrettyä suoran kuvaajaa. a) Kun x = 0, mikä on 6 4 y-koordinaatti? b) Kun y = 6, mikä on x-koordinaatti? c) Kun x = -4, mikä on y-koordinaatti? x -6 8
9 3. Vastaa kuvaajaa käyttämällä kysymyksiin. a) Milloin brittejä asui vähiten Suomessa? b) Montako brittiä vuonna 2000 asui Suomessa? c) Montako brittiä enemmän Suomessa asui vuonna 2003 kuin vuonna 1996? Suomessa vuosina asuneiden Britannian kansalaisten lukumäärä lukumäärä vuosi (Lähde: Tilastokeskus) 4. Kuvaaja esittää celsius- ja fahrenheitasteiden välistä riippuvuutta. Ilmoita fahrenheitasteina a) lämpötila, jossa vesi jäätyy, b) lämpötila, jossa vesi kiehuu, ºF c) ihmisen normaali ruumiinlämpötila ºC 9
10 5. Vastaa kuvaajan perusteella kysymyksiin. a) Minkä ikäisenä murrosiän kasvupyrähdys on tytöillä huipussaan, entä pojilla? b) Kuinka monta vuotta murrosiän kasvupyrähdys kestää? c) Minkä ikäisenä tyttöjen pituuskasvu pysähtyy, entä pojilla? d) Kummatko ovat pidempia kahdeksan vuoden iässä? pituuden lisäys (cm vuodessa) Tyttöjen ja poikien keskimääräinen vuotuinen pituuskasvu ikä vuosina pojat tytöt 6. Oppilaat tekivät kokeen, jonka maksimipistemäärä oli 42 pistettä. Opettaja päätti arvostella kokeen seuraavasti: kymppiin vaadittiin 42 pistettä ja jos puolet oli oikein, sai arvosanaksi 6 ½. Opettaja piirsi näiden kahden pisteen avulla suoran, jolloin muodostui kuvaaja, josta määräytyivät muut arvosanat. Pistemäärä a) Mitkä arvosanat saa pisteillä 24, 30 ja 38? b) Paljonko pisteitä vaaditaan arvosanoihin 7-, 8 ½ ja 9? c) Millä pistemäärällä saa arvosanan 5-? Arvosana 10
11 Soveltavat tehtävät 7. Mikä kuvaajista sopisi kuvaamaan seuraavia asioita? a) Kangas maksaa 10 / metri. b) Auton vuokra koostuu 100 perusmaksusta sekä joka kilometriltä velotettavasta 0,35 kilometrikorvauksesta. c) Mansikat maksavat 3 /kg, mutta, jos ostat yli 10 kg, on kilohinta 2,5. A B C 8. Taksimaksun hinta määräytyy hinta hinta seuraavasti: Perusmaksu on 3,87 ja lisävelotus on 1,00 kilometriä kohti. Jos taksi joutuu pysähtymään välillä, on odotusmaksu 28,59 tunnilta. Aune menee taksilla pankkiin. Taksi odottaa, hinta A matka hinta B matka kunnes Aune on saanut asiansa hoidettua ja kyyditsee vanhuksen takaisin kotiin. Mikä seuraavista kuvaajista sopii tilanteen kuvaamiseen? C matka D matka 11
12 9. Suomessa on kesä, kun vuorokauden keskilämpötila on pysyvästi +10 C yläpuolella. Syksyllä keskilämpötila on pysyvästi +10 C ja 0 C välillä. Talvella keskilämpötila on pysyvästi alle 0 C ja keväällä pysyvästi 0 C ja +10 C välillä. Termiset vuodenajat määräytyvät lämpötilan tasoitetun vuosikäyrän avulla. a) Mitä voit sanoa kesän ja talven pituudesta Turussa ja Sodankylässä? b) Kummassa kaupungissa on suuremmat lämpötilaerot vuodessa? Montako astetta lämpötila voi siellä vaihdella? Turku Talvi Kevät Kesä Syksy Talvi terminen kasvukausi Sodankylä Talvi Kevät Kesä Syksy Talvi terminen kasvukausi (Lähde: Ilmatieteenlaitos) 12
13 10. Mikä kuvaajista sopii tarinoihin? a) Puoli vuotta sitten aloin käymään lenkillä iltaisin. Aluksi kuntoni kohosi huimasti. Nyt kehitys on hidastunut, mutta juoksen kuitenkin viiden kilometrin lenkkini yhä nopeammin. b) Lenkkeilyn myötä painoni putosi ilahduttavasti. Jouluna nautiskelin hyvästä ruuasta ja lenkit jäivät viikoksi väliin, joten lihoin hieman takaisin, mutta sen jälkeen olen pysynyt hoikassa kunnossa. A B C D 11. Kuvaajassa on esitetty väkivaltaisesti tai tapaturmaisesti kuolleiden miesten ja naisten lukumäärät eri ikäryhmittäin vuonna a) Kirjoita muutama lause siitä, mitä kuvaaja kertoo väkivaltaan tai tapaturmaisesti kuolleista b) Mihin ikään asti väkivaltaan tai tapaturmaisesti kuolleiden miesten ja naisten määrä oli suunnilleen sama? c) Paljonko kuolleista oli vuotiaita naisia? Entä miehiä? d) Paljonko kuolleista oli vuotiaita naisia? Entä miehiä? Huom! Miehet joutuvat maksamaan tapaturmavakuutuksistaan melkein kaksi kertaa niin paljoin kuin naiset vastaavista vakuutuksista. Keksitkö syytä? kuolemantapauksia Väkivaltaisesti tai tapaturmaisesti kuolleiden miesten ja naisten lukumäärät eri ikäryhmittäin vuonna ikä (vuotta) miehet (Lähde: Tilastokeskus) naiset 13
14 12. Suomessa väkiluku oli henkilöä tilastokeskuksen mukaan Väestön jakautuminen on esitetty seuraavassa pylväsdiagrammin avulla. Mitä kaikkea voit väestöstä kuvaajan perusteella kertoa? Väestö iän ja sukupuolten mukaan Väestö Naiset Miehet _ Ikä (Vuosina) 13. Pylväsdiagrammin avulla on esitetty EU:n jäsenmaissa vuonna 1996 niiden yli 16-vuotiaiden osuus väestöstä, joilla on toimintakykyä haittaava pitkäaikaissairaus. a) Missä maissa on miehillä enemmän haittaavaa pitkäaikaissairastavuutta, kuin naisilla? b) Monellako prosentilla naisista on Suomessa haittaava pitkäaikaissairaus entä miehistä? c) Missä maassa naiset ovat keskimääräisesti terveempiä entä miehet? d) Miten kuvailisit Suomalaisia pylväsdiagrammin perusteella? (Lähde: Tilastokeskus) 14. Alankomaat Belgia Britannia Espanja Irlanti Italia Itävalta Kreikka Luxemburg Portugali Ranska Saksa Suomi Tanska Haittaava pitkäaikaissairastuvuus (%) 14 Miehet Naiset (Lähde: Tilastokeskus)
15 Vaativat tehtävät 14. Vieressä on kuvaaja, johon on piirretty Mikon pyöräilemä matka ajan suhteen. a) Millä nopeudella Mikko pyöräilee? b) Kuinka pitkän matkan Mikko on pyöräillyt 7 tunnin kuluttua? c) Kuinka pitkän matkan Mikko on pyöräillyt 10 tunnin kuluttua? d) Pyöräileekö Mikko tasaisella nopeudella vai vaihteleeko nopeus? Matka (km) Aika (h) 15. Alla oleva kuvaaja osoittaa, miten kilpa-auton nopeus vaihtelee tasaisella 3 kilometrin radalla sen toisen ratakierroksen aikana. Nopeus (km/h) Kilpa-auton nopeus 3 km radalla (toinen ratakierros) ,5 1,5 2, ,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 Lähtöviiva Radan pituus (km) 15
16 a) Miten pitkä matka on arviolta lähtöviivalta radan pisimmän suoran osan alkuun? b) Missä nopeus oli alhaisimmillaan toisen kierroksen aikana? c) Mitä voit sanoa auton nopeudesta 2,6 km ja 2,8 km välillä? d) Millä näistä radoista autoa ajettiin, jotta tuloksena oli aiemmin esitetty kuvaaja? B A C D = Lähtöviiva E (Lähde: Kansainvälinen oppimistulosten arviointiohjelma, Pisa) 16
17 16. Simpukka -diagrammi esittää ajoneuvon teoreettisen pysäytysmatkan hyvissä jarrutusolosuhteissa sekä nopeuden ja pysähtymismatkan riippuvuuden. Määritä ajoneuvon etenemä matka kuljettajan reaktioaikana, kokonaisuudessaan edetty matka ennen pysähtymistä, pysähtymiseen kuluva aika ja jarrutuksen aikana edetty matka seuraavissa nopeuksissa: a) 90 km/h b) 120 km/h c) 180 km/h d) Miten käy jarrutusmatkalle, kun nopeus kaksinkertaistuu? 219 m 5,62 s 245,5 m 9,08 s Ajoneuvon pysäytysmatka Ajoneuvon pysäytysaika 197,6 m 8,15 s Jarrutuksen aikana edetty matka 175,4 m 7,69 s 152,2 m 7,23 s 135,6 m 6,76 s 118 m 6,30 s 31,3 m 29,2 m 27,1 m 5,84 s 101 m 33,3 m 37,5 m 35,4 m km/h m ,9 m 14,6m 20,8 m 18,7 m 16,7m 3,99 s 4,6 s 5,38 s 8,3m 10,3m 12,5m 46 m 4,92 s 57,7 m 70,7 m 85,4 m Kuljettajan reaktioaikana edetty matka 18,6 m 2,60 s 26,5 m 3,06 s 35,7 m 3,53 s (Lähde: Kansainvälinen oppimistulosten arviointiohjelma, Pisa) 17
18 2 Pylväs- ja viivadiagrammi Pylväsdiagrammi muodostuu pystypylväistä. Jos pylväät on piirretty vaakasuoraan, puhutaan usein palkkidiagrammista. Diagrammin piirtäminen Merkitse käytetyt mitta-asteikot ja yksiköt näkyviin. Laita kuvaajaan otsikko. Tee graafisesta esityksestä niin selkeä, että siitä tulee ilmi kaikki tarpeelliset asiat. Kuvaajaa pitää pystyä tulkitsemaan ilman muuta asianyhteyteen liittyvää tekstiä. Pylväsdiagrammilla havainnollistetaan kokonaisuuden jakautumista osiin tai vertaillaan suuruussuhteita. nimi lukumäärä Veeti 481 Esimerkki 1. Eetu 475 Taulukossa on esitetty suosituimmat poikien esimmäiset etunimet vuonna Aleksi 464 Elias 433 Onni 420 (Lähde: Väestörekisterikeskus)
19 Piirretään tiedoista pylväsdiagrammi, jonka vaaka-akselilla on nimi ja pystyakselilla annettujen nimien lukumäärä. Suosituimmat poikien nimet 2007 lukumäärä Veeti Eetu Aleksi Elias Onni nimi Viivadiagrammissa havaintoarvot on yhdistetty toisiinsa viivalla. Viivadiagrammeja käytetään samanlaisissa tilanteissa kuin pylväsdiagrammia. Viivadiagrammi soveltuu kuitenkin paremmin kuvaamaan kehityssuuntaa. Esimerkki 2. Helsingin väkiluku vuosina vuosi väkiluku Helsingin väkiluku on viime vuosina kasvanut huomattavasti. Piirretään oheisen taulukon pohjalta viivadiagrammi väestön määrästä
20 Sijoitetaan vuosiluvut vaaka-akselille ja väestön määrät pystyakselille. Jos viivadiagrammi piirretään kuten pylväsdiagrammi, alkavat pystyakselin arvot nollasta. Viivadiagrammilla halutaan kuitenkin yleensä kuvata muutosta ja tällöin muutoksen suuruus ei ole selvästi nähtävissä. Jotta muutos nähtäisiin selvemmin ja kuvaajasta saataisiin tarkempi, on pystyakselin asteikko valittava uudestaan. Suurin pystyriville tuleva arvo on , joten maksimiarvon tulee olla tätä vähän suurempi. Pienin arvo on , joten minimin tulee olla tätä vähän pienempi. väkiluku väkiluku Helsingin asukasluku vuosi Helsingin asukasluku vuosi 20
21 Tehtäviä 17. Taulukossa on esitetty suosituimmat tyttöjen esimmäiset etunimet vuonna Piirrä taulukon tiedoista pylväsdiagrammi. nimi lukumäärä Ella 456 Emma 411 Aino 407 Anni 406 Venla 386 (Lähde: Väestörekisterikeskus) 18. Ulla Uimari tarkkaili kesällä järviveden lämpötilaa ja sai oheiset mittaustulokset Piirrä mittaustuloksista viivadiagrammi, joka kuvaa päivämäärän ja veden lämpötilan välistä riippuvuutta. Päivämäärä Lämpötila [ C] viikonpäivä lämpötila [ C] 19. Janne seurasi yhden viikon ajan ulkolämpötiloja aamuisin ja sai seuraavanlaisia mittaustuloksia. Piirrä tiedoista viivadiagrammi. maanantai 2 tiistai -3 keskiviikko 0 torstai -6 perjantai -15 lauantai -8 sunnuntai
22 20. Taulukossa on Suomessa olevien matkapuhelinliittymien lukumääriä. Piirrä taulukon tiedoista pylväsdiagrammi. vuosi matkapuhelinliittymät (Lähde: Tilastokeskus) (Lähde: Tilastokeskus) Soveltavat tehtävät 21. Vieressä on esitetty taulukoituna tutkinnon suorittaneiden osuus prosentteina eri ikäluokista vuonna Mukaan on otettu lukiossa, ammatillisissa oppilaitoksissa, ammattikorkeakouluissa tai yliopistoissa tutkinnon suorittaneet. Piirrä pylväsdiagrammi prosentuaalisista tutkinnon suorittaneista ikäluokittain. Mitä voit päätellä tutkinnon suorittamisen tarpeesta? 22 Ikäluokka Tutkinnon suorittanut ikäluokasta [%] , , , , , , , , , ,4 (Lähde: Tilastokeskus) (Lähde: Tilastokeskus)
23 22. Seuraavassa taulukossa on esitetty Suomessa asuvien henkilöiden määrä sekä keskimäärin kotitalouksissa asuvien henkilöiden lukumäärä vuosina a) Piirrä viivadiagrammi väestön määrästä vuosittain. b) Piirrä viivadiagrammi kotitalouksien keskikoosta vuosittain. c) Mitä tästä voi päätellä? Vuosi Väestö [ 1000 hlö] Kotitalouksien keskikoko [hlö] , , , , , , , , ,15 (Lähde: Tilastokeskus) 23. Itävaltalaisella Adam Rainerilla on havaittu suurin pituuden muutos maailmassa. Adam oli 21-vuotiaana vain 118 cm mittainen. Nopean kasvun jälkeen hänen pituutensa oli 32-vuotiaana 218 cm. Tämän ainutlaatuisen kasvun vuoksi hän oli niin heikko, että joutui pysyttelemään vuoteessaan loppuikänsä. Kuollessaan 51-vuotiaana v.1950 Rainer oli kasvanut vielä 16 cm. Piirrä tietojen pohjalta viivadiagrammi Adamin pituudesta. 23
24 Vaativat tehtävät 24. Liikkeestä raportoitiin, että myymälässä oli vuonna 1997 CD-levyjä seuraavan taulukon mukaisesti. Myymälä sai 10.7 lähetyksen, joka sisälsi CD-levyä. Esitä graafisesti CD-levyjen lukumäärät liikkeessä vuoden 1997 aikana (kuukaudet vaaka-akselilla ja määrät pystyakselilla). Kuinka monta CD-levyä myytiin keskimäärin yhden kuukauden aikana? (yo syksy 1999) päivämäärä levyjä [kpl] Luokan oppilaiden pituudet ovat seuraavat: 139 cm, 144 cm, 148 cm, 160 cm, 161 cm, 146 cm, 155 cm, 170 cm, 166 cm, 153 cm, 155 cm, 152 cm, 163 cm, 165 cm, 169 cm, 147 cm, 159 cm, 160 cm, 157 cm, 172 cm. Luokittele pituudet oheisen taulukon avulla ja piirrä pylväsdiagrammi. pituus [cm] oppilaiden lukumäärä
25 26. Taulukossa on esitetty miesten vuorokautisen energiatarpeen (MJ) riippuvuus ruumiinpainosta ja iästä. (1 megajoule (MJ) = 239 kilokaloria (kcal)) Piirrä samaan kuvaan kolme viivadiagrammia ikien 25 v, 45 v ja 65 v mukaan. paino ikä kg 25 v 45 v 65 v 50 9,6 8,8 7, ,3 9,2 7, ,9 9,8 8, ,5 10,5 8, ,1 10,9 9, ,8 11,5 9, ,4 12,1 10,3 27. Naisten energiatarpeen arvot ovat 15 % pienemmät kuin miesten. Piirrä 25 vuotiaan naisen energiatarpeesta viivadiagrammi painon mukaan ,8 10,7 kuukausi miehiä naisia koko väestö maaliskuu helmikuu Piirrä viivadiagrammi, joka kuvaa Helsingin väestömäärän muutosta taulukon pohjalta. tammikuu joulukuu marraskuu lokakuu syyskuu elokuu heinäkuu kesäkuu toukokuu (Lähde: Väestörekisterikeskus) 25
26 29. Piirrä edellisen tehtävän taulukon pohjalta yksi pylväsdiagrammi, josta käy ilmi Helsingissä asuvien miesten ja naisten määrä. Olisiko jokin muu diagrammityyppi sopinut kuvaajaan paremmin, miksi? Kannattaako mielestäsi sekä miesten että naisten määrät sijoittaa samaan kuvaajaan? 30. Piirrä Suomen valtionvelan määrän kuvaaja ajan suhteen. Minä vuonna velka kasvoi a) määrällisesti eniten? b) määrällisesti vähiten? c) suhteellisesti eniten (velan kasvuprosentti suurin)? d) suhteellisesti vähiten? Suomen valtionvelka vuosi velan määrä [miljardia ] , , , , , , , , , , , ,8 (Lähde: Tilastokeskus) 26
27 Sektoridiagrammi 3 Sektori- eli piirakkakuvio on ympyrän muotoinen kaavio, jossa ympyrä on jaettu osiin eli sektoreihin. Sektoridiagrammia käytetään kuvattaessa kokonaisuuden jakautumista osiin, jotka on yleensä ilmoitettu prosenttilukuna. Jokaista prosenttilukua vastaa ympyräsektori, jonka keskuskulma on yhtä monta prosenttia koko ympyrän 360 asteesta. Esimerkki 1. Piirretään sektoridiagrammi siten, että että 70 % kuviosta on sinistä ja 30 % vihreää. 108º 252º 70 % 30 % Lasketaan 70 % täysi ympyrän 360 asteesta º = 252º ja vastaavasti 30 % on º = 108º 100 ruoka-aine suositeltu osuus päivittäisestä ravinnosta [%] Esimerkki 2. Taulukossa on suositukset päivittäisistä ruokaaineista. Piirretään tiedoista sektoridiagrammi, jota kutsutaan ruokaympyräksi. kasvikset, hedelmät, marjat 31 viljatuotteet, peruna 26 maitotuotteet 20 kala, liha, kananmuna 18 rasvat 5
28 Lasketaan aluksi prosenttilukuja vastaavat keskuskulmat: Koska 100 % vastaa keskuskulmaa 360, niin silloin 1 % vastaa keskuskulmaa 360 º 100 = 3,6º Tämän avulla voidaan laskea muiden keskuskulmien suuruudet. prosenttiosuus keskuskulma 31 % 31 3,6 111,5 26 % 26 3,6 93,5 20 % 20 3,6 =72 18 % 18 3, % 5 3,6 = 18 yhteensä 100 % yhteensä 360 Piirretään sitten ympyrä ja jaetaan se sektoreihin ,5 93,5 Lisätään sektoridiagrammiin vielä otsikko, prosenttiluvut ja niiden selitteet Ruokaympyrä 5 % Rasvat 18 % Kala, liha, kananmuna 31 % Kasvikset, hedelmät, marjat 20 % Maitotuotteet 26 % Viljatuotteet, peruna 28
29 Tehtäviä 31. Piirrä sektoridiagrammi, joka on jaettu neljään osaan siten, että osioiden koot ovat 1, 1, 1 ja 1 koko ympyrästä Piirrä sektoridiagrammi, joka on jaettu kolmeen osaan siten, että osien koot ovat 50, 20 ja 30 prosenttia koko ympyrästä. 33. Oheisessa sektoridiagrammissa on esitetty suomalaisten vuonna 2000 tekemien 27,6 miljoonan matkan jakautuminen matkatyypeittäin. Tee taulukko, josta näkyy eri matkakohteisiin tehtyjen matkojen kappalemäärät. Matkat sukulaisten ja tuttavien luo 44 % Vapaa-ajanmatkat kotimaassa maksullisessa majoituksessa 14 % Yöpymisen ulkomailla sisältäneet matkat ml. Työ- ja kokousmatkat 12 % Matkat omalle mökille 11 % Työ- ja kokousmatkat kotimaassa 10 % Risteilyt 9 % (Lähde: Tilastokeskus) 29
30 34. Maapallon kokonaispinta-ala on km², josta maa-ala on km² ja loput on vettä. Kuvaa sektoridiagrammilla vesien ja maan osuutta koko maapallon pinta-alasta. 35. Suomalaisista 31 % kuuluu O-veriryhmään, A-ryhmään kuuluu 44 %, B-ryhmään 17 % ja ABryhmään 8 %. Piirrä tiedoista sektoridiagrammi. Soveltavat tehtävät 36. Kuinka suuri osuus ympyrästä on kyseessä prosentteina ilmaistuna, jos sektorin keskuskulman suuruus on a) 360º b) 180º c) 90º d) 45º e) 10º 37. Minkä diagrammityypin valitsisit kuvaamaan seuraavia asioita? a) Myytävien elintarvikkeiden määrän jakautuminen kotimaisiin ja ulkomaisiin tuotteisiin. b) Öljyn hinnanmuutokset kymmenen vuoden aikana. c) Kotimaasta ostetun auton hinnanvertailu muualta ostettuihin vastaaviin autoihin. 38. Energian loppukäyttö vuonna 2000 on seuraava: teollisuus käyttää energiasta 51 %, rakennusten lämmitykseen menee 21 %, liikenteeseen 16 % ja muuhun 11 %. Piirrä energian käyttöä kuvaava sektoridiagrammi. (Lähde: Tilastokeskus) 30
31 39. Kuvaa taulukon tietoja sektoridiagrammin avulla. Koulutettu väestö Suomessa koulutusaloittain 1999 koulutusala yhteensä Terveys- ja sosiaaliala Kasvatustieteellinen ja opettajankoulutus Palvelualat Humanistinen, taideala Kaupallinen ja yhteiskuntatieteellinen Luonnontieteet Maa- ja metsätalousala Tekniikka (Lähde: Tilastokeskus) Vaativat tehtävät 40. Oheinen diagrammi esittää hiilidioksidipäästöjen jakautumista eri alojen kesken Suomessa vuonna Montako prosenttia hiilidioksidin kokonaispäästö vähenisi, jos a) sektori, johon kuuluvat kotitaloudet, palvelut, maatalous ym., vähentäisi päästöjään 20 % ja muut pysyisivät ennallaan? b) teollisuus ja liikenne kumpikin vähentäisivät päästöjään 20 % ja muut pysyisivät ennallaan? (yo kevät 1998) Hiilidioksidipäästöt kulutussektoreittain Teollisuus 38 % Kotitaloudet, palvelut, maatalous ym. 15 % Liikenne 20 % Lämmitys 27 % 31
32 4 Tilastomuuttujan tyypit ja frekvenssi Tilastokuvaajan eli diagrammin tyyppi valitaan sen mukaan millainen tilastomuuttuja on kyseessä. Diskreetti tilastomuuttuja voi saada vain erillisiä arvoja. Jatkuva tilastomuuttuja voi saada kaikkia arvoja joltakin väliltä. Histogrammi muodostuu toisissaan kiinni olevista pystypylväistä. Frekvenssi on tietyn havaintoarvon esiintymiskertojen lukumäärä tilastoaineistossa. Diskreettiä muuttujaa kuvataan yleensä pylväsdiagrammin avulla. Jatkuvaa muuttujaa kuvataan sen sijaan yleensä viivadigrammilla tai histogrammilla. Diskreetin tilastomuuttujan arvot voidaan laskea. Jatkuvan tilastomuuttujan arvot voidaan mitata. Frekvenssi voidaan ilmaista myös prosentteina kokonaismäärästä, jolloin käytetään nimitystä suhteellinen frekvenssi. Suhteellisien frekvenssien havainnollistamiseen sopii hyvin sektoridiagrammi. Suhteellinen frekvenssi on luku, joka ilmoittaa, kuinka suuri osuus havainnoista saa tietyn arvon. Se voidaan ilmoittaa murto-, desimaali- tai prosenttilukuna. suhteellinen frekvenssi = frekvenssi frekvenssien summa Suhteellisten frekvenssien summa on aina 1 tai 100 %, laskuissa summa voi hieman poiketa johtuen pyöristyksistä.
33 Esimerkki 1. Luokan oppilaiden sisarusten lukumäärää kuvaava tilasto on seuraava: Tilastomuuttuja on tässä tapauksessa sisarusten lukumäärä ja kyseessä on diskreetti muuttuja, koska sisarusten lukumäärä saadaan selville laskemalla. Ryhmitellään tiedot sisarusten lukumäärästä. Merkitään taulukkoon kuinka monella ei ole sisaruksia, kuinka monella on 1 sisarus jne. Näin saadaan selville sisarusten lukumäärien frekvenssit. Suhteellinen frekvenssi puolestaan ilmoittaa, monellako prosentilla koko luokan oppilaista on tietty määrä sisaruksia. sisarusten lkm frekvenssi, f suhteellinen frekvenssi [%] !100% = 12,5% 16 4!100% = 25% yhteensä:
34 Frekvenssien perusteella voidaan piirtää pylväsdiagrammi. Frekvenssi 6 5 Esimerkissä 1 pylväsdiagrammi sisältää kaiken alkuperäisen informaation. Se on kuitenkin paljon havainnollisempi tapa sisarusten lukumäärän kuvaamiseen kuin pelkkä taulukointi. Pylväsdiagrammista nähdään lisäksi, että sisaruksien lukumäärän jakauman kuvaaja on yksihuippuinen ja se laskee lähes symmetrisesti huipun kummallakin puolella. Jakauman kuvaaja voi olla myös epäsymmetrinen tai monihuippuinen Sisarusten lukumäärä Tasainen jakauma Epäsymmetrinen, kaksihuippuinen jakauma
35 Tehtäviä 41. Mitkä seuraavista ovat jatkuvia ja mitkä diskreettejä muuttujia? a) lämpötila b) sukupuoli c) puoluekanta d) ihmisen paino 42. Mitä tilastotietoja sinusta on vuosien aikana kerätty? Mitkä näistä tiedoista ovat julkisia? 43. Mitä tilastotietoja voit löytää sanomalehdistä? Mitä niissä on tilastomuuttujina? Mikä niissä on perusjoukkona? 44. Mitä tietoja keräisit, jos aikoisit ryhtyä pitämään kotipaikkakunnallasi a) kahviota b) kuntosalia c) lemmikkieläinkauppaa? 45. Mikä ero on histogrammilla ja pylväsdiagrammilla? 35
36 46. Kasvitieteilijä tutki erään lannoitteen vaikutusta herneiden kasvuun. Hän piirsi viivadiagrammit herneiden määrästä yhdessä herneenpalkossa ja herneiden koosta. Mikä vaikutus lannoitteella oli herneiden a) määrään b) kokoon? frekvenssi lannoitteeton lannoitteellinen hemeiden lukumäärä 47. Alla on lueteltu erään 8. luokan matematiikan arvosanat syksyn todistuksissa. Muodosta tietojen pohjalta taulukko, jossa näkyy arvosanojen frekvenssit ja kuvaa arvosanojen jakaumaa sopivalla diagrammilla. frekvenssi hemeiden koko
37 48. Kolmessa eri luokassa suoritettiin kysely oppilaiden lempihedelmistä. Seuraavassa taulukossa on esitetty kuinka moni oppilas piti mitäkin hedelmää parhaimpana. a) Kirjoita jokaisen luokan suhteelliset frekvenssit erikseen. b) Kirjoita suhteelliset frekvenssit siten, että yhdistät kaikkien hedelmämieltymykset. c) Jos kysely olisi tehty sadalle ihmiselle, niin arvioi moniko olisi valinnut lempihedelmäkseen appelsiinin. banaani omena päärynä appelsiini luokka 8A luokka 8B luokka 8C Tehkää luokassa pikagallup jokaisen perheessä olevien lasten lukumäärästä. Laatikaa tietojen perusteella taulukko, jossa näkyy frekvenssit ja suhteelliset frekvenssit lasten määrästä. Havainnollistakaa tietoja sopivan diagrammin avulla. Esimerkki 1. Esimerkki 1. 37
38 5 Jos muuttujan arvoja on paljon, tilastoaineiston tulkintaa helpottaa muuttujan arvojen Aineiston luokittelu luokittelu ryhmiin. Luokittelemalla menetetään osa aineiston informaatiosta, mutta useissa tapauksissa sillä lisätään tulosten havainnollisuutta. Jos kyseessä on jatkuva tilastomuuttuja, havainnollistetaan sitä histogrammilla, jossa pylvään keskikohta edustaa luokkakeskusta. Koripalloseuraan kuuluvien naisten pituudet senttimetreinä ovat: Kyseessä on jatkuva muuttuja, koska pituudet on saatu selville mittaamalla. Ne on pyöristetty lähimpään senttimetriin. Pituudet ovat hajautuneet melko laajalle välille ja osa niistä esiintyy aineistossa vain muutamia kertoja. Ryhmitellään pelaajien pituudet seitsemään luokkaan ja lasketaan niiden luokkakeskus, frekvenssi ja suhteellinen frekvenssi.
Ma8 Todennäköisyys ja tilastot
 Ma8 Todennäköisyys ja tilastot H1 Tilastollisen aineiston kuvaaminen 1.1 Vastaa kuvaajan perusteella kysymyksiin. a) Kuinka paljon tarvitset kuvaajan mukaan unta? b) Paljonko 20-vuotias tarvitsee unta?
Ma8 Todennäköisyys ja tilastot H1 Tilastollisen aineiston kuvaaminen 1.1 Vastaa kuvaajan perusteella kysymyksiin. a) Kuinka paljon tarvitset kuvaajan mukaan unta? b) Paljonko 20-vuotias tarvitsee unta?
Ma8 Todennäköisyys ja tilastot
 Ma8 Todennäköisyys ja tilastot Arvioitavat tehtävät 1. Kuvaajassa on esitetty väkivaltaisesti tai tapaturmaisesti kuolleiden miesten ja naisten lukumäärät eri ikäryhmittäin vuonna 1999. (Lähde: Tilastokeskus)
Ma8 Todennäköisyys ja tilastot Arvioitavat tehtävät 1. Kuvaajassa on esitetty väkivaltaisesti tai tapaturmaisesti kuolleiden miesten ja naisten lukumäärät eri ikäryhmittäin vuonna 1999. (Lähde: Tilastokeskus)
AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä
 Marika Toivola ja Tiina Härkönen AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä Sisältö on lisensoitu avoimella CC BY 3.0 -lisenssillä. 1 Tilastoja ja todennäköisyyksiä 1. Kuvaajien tulkintaa... 4 2.
Marika Toivola ja Tiina Härkönen AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä Sisältö on lisensoitu avoimella CC BY 3.0 -lisenssillä. 1 Tilastoja ja todennäköisyyksiä 1. Kuvaajien tulkintaa... 4 2.
AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä
 Marika Toivola ja Tiina Härkönen AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä Sisältö on lisensoitu avoimella CC BY 3.0 -lisenssillä. 1 Tilastoja ja todennäköisyyksiä 1. Kuvaajien tulkintaa... 4 2.
Marika Toivola ja Tiina Härkönen AVOIN MATEMATIIKKA Tilastoja ja todennäköisyyksiä Sisältö on lisensoitu avoimella CC BY 3.0 -lisenssillä. 1 Tilastoja ja todennäköisyyksiä 1. Kuvaajien tulkintaa... 4 2.
1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet
 VAASAN YLIOPISTO/AVOIN YLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia 1 KURSSIKYSELYAINEISTO: 1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
VAASAN YLIOPISTO/AVOIN YLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia 1 KURSSIKYSELYAINEISTO: 1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet
 VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: 1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: 1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
Esimerkki 1: auringonkukan kasvun kuvailu
 GeoGebran LASKENTATAULUKKO Esimerkki 1: auringonkukan kasvun kuvailu Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi aurinkoisina kesinä hyvissä kasvuolosuhteissa Suomessakin
GeoGebran LASKENTATAULUKKO Esimerkki 1: auringonkukan kasvun kuvailu Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi aurinkoisina kesinä hyvissä kasvuolosuhteissa Suomessakin
Tilastolliset toiminnot
 -59- Tilastolliset toiminnot 6.1 Aineiston esittäminen graafisesti Tilastollisen aineiston tallentamisvälineiksi TI-84 Plus tarjoaa erityiset listamuuttujat L1,, L6, jotka löytyvät 2nd -toimintoina vastaavilta
-59- Tilastolliset toiminnot 6.1 Aineiston esittäminen graafisesti Tilastollisen aineiston tallentamisvälineiksi TI-84 Plus tarjoaa erityiset listamuuttujat L1,, L6, jotka löytyvät 2nd -toimintoina vastaavilta
1.9 Harjoituksia. Frekvenssijakaumien harjoituksia. MAB5: Tilastotieteen lähtökohdat. a) Kaikki aakkoset b) Kirjaimet L, E, M, C, B, A ja i.
 MAB5: Tilastotieteen lähtökohdat 1.9 Harjoituksia 1.1 Ulkolämpömittari näytti eilen 10 C ja tänään 20 C. Onko tänään kaksi kertaa niin kylmä kuin eilen? Miksi tai miksi ei? 1.2 Minkä luokkien muuttujia
MAB5: Tilastotieteen lähtökohdat 1.9 Harjoituksia 1.1 Ulkolämpömittari näytti eilen 10 C ja tänään 20 C. Onko tänään kaksi kertaa niin kylmä kuin eilen? Miksi tai miksi ei? 1.2 Minkä luokkien muuttujia
1. Kymmenjärjestelmä ja desimaalilukujen yhteen- ja vähennyslaskua
 . Kymmenjärjestelmä ja desimaalilukujen yhteen- ja vähennyslaskua. Jatka. + 00 000 0 0 0 0 0 0 0 000 + 0 000 0 0 0 0 0 0 0 + 0,0,,,,,,0 0,,,,,,, + 0,,,0,,0,,00. Merkitse laskutapa ja laske. a), +, + 0,,
. Kymmenjärjestelmä ja desimaalilukujen yhteen- ja vähennyslaskua. Jatka. + 00 000 0 0 0 0 0 0 0 000 + 0 000 0 0 0 0 0 0 0 + 0,0,,,,,,0 0,,,,,,, + 0,,,0,,0,,00. Merkitse laskutapa ja laske. a), +, + 0,,
Matin alkuvuoden budjetti
 1 TILASTOJEN TULKINTAA 1. euroa Matin alkuvuoden budjetti 600 500 400 300 200 100 0 tammikuu helmikuu maaliskuu huhtikuu a) Milloin Matti on kuluttanut eniten rahaa ostoksiin? Arvioi, kuinka paljon vaatteisiin
1 TILASTOJEN TULKINTAA 1. euroa Matin alkuvuoden budjetti 600 500 400 300 200 100 0 tammikuu helmikuu maaliskuu huhtikuu a) Milloin Matti on kuluttanut eniten rahaa ostoksiin? Arvioi, kuinka paljon vaatteisiin
KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun se kelpaa kyllä!
 VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun
VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun
Järvi 1 Valkjärvi. Järvi 2 Sysijärvi
 Tilastotiedettä Tilastotieteessä kerätään tietoja yksittäisistä asioista, ominaisuuksista tai tapahtumista. Näin saatua tietoa käsitellään tilastotieteen menetelmin ja saatuja tuloksia voidaan käyttää
Tilastotiedettä Tilastotieteessä kerätään tietoja yksittäisistä asioista, ominaisuuksista tai tapahtumista. Näin saatua tietoa käsitellään tilastotieteen menetelmin ja saatuja tuloksia voidaan käyttää
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 11. lokakuuta 2007 Antti Rasila () TodB 11. lokakuuta 2007 1 / 15 1 Johdantoa tilastotieteeseen Peruskäsitteitä Tilastollisen kuvailun ja päättelyn menetelmiä
Sovellettu todennäköisyyslaskenta B Antti Rasila 11. lokakuuta 2007 Antti Rasila () TodB 11. lokakuuta 2007 1 / 15 1 Johdantoa tilastotieteeseen Peruskäsitteitä Tilastollisen kuvailun ja päättelyn menetelmiä
MONISTE 2 Kirjoittanut Elina Katainen
 MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas JAKAUMAN MUOTO Vinous, skew (g 1, γ 1 ) Kertoo jakauman symmetrisyydestä Vertailuarvona on nolla, joka vastaa symmetristä jakaumaa (mm. normaalijakauma)
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas JAKAUMAN MUOTO Vinous, skew (g 1, γ 1 ) Kertoo jakauman symmetrisyydestä Vertailuarvona on nolla, joka vastaa symmetristä jakaumaa (mm. normaalijakauma)
Til.yks. x y z
 Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
MATEMATIIKAN KOE. AMMATIKKA top 17.11.2005. 2. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu. Oppilaitos:.
 AMMATIKKA top 17.11.005 MATEMATIIKAN KOE. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu Nimi: Oppilaitos:. Koulutusala:... Luokka:.. Sarjat: MERKITSE OMA SARJA 1. Tekniikka
AMMATIKKA top 17.11.005 MATEMATIIKAN KOE. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu Nimi: Oppilaitos:. Koulutusala:... Luokka:.. Sarjat: MERKITSE OMA SARJA 1. Tekniikka
Matemaatikot ja tilastotieteilijät
 Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus
 GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus Mitä jäi mieleen viime viikosta? Mitä mieltä olet tehtävistä, joissa GeoGebralla työskentely yhdistetään paperilla jaettaviin ohjeisiin
GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus Mitä jäi mieleen viime viikosta? Mitä mieltä olet tehtävistä, joissa GeoGebralla työskentely yhdistetään paperilla jaettaviin ohjeisiin
Matemaattista mallintamista
 Johdatus GeoGebraan Matemaattista mallintamista Harjoitus 2A. Tutkitaan eksponentiaalista kasvua ja eksponenttifunktioita Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi
Johdatus GeoGebraan Matemaattista mallintamista Harjoitus 2A. Tutkitaan eksponentiaalista kasvua ja eksponenttifunktioita Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi
Tilastoja yleisurheillen
 Koostanut Elina Viro Opettajalle Tilastoja yleisurheillen Kohderyhmä: Luokat 7-9 Esitiedot: Prosenttilaskenta Taustalla oleva matematiikka: Frekvenssi, suhteellinen frekvenssi, moodi, mediaani, keskiarvo,
Koostanut Elina Viro Opettajalle Tilastoja yleisurheillen Kohderyhmä: Luokat 7-9 Esitiedot: Prosenttilaskenta Taustalla oleva matematiikka: Frekvenssi, suhteellinen frekvenssi, moodi, mediaani, keskiarvo,
Hannu mies LTK 180 Johanna nainen HuTK 168 Laura nainen LuTK 173 Jere mies NA 173 Riitta nainen LTK 164
 86118P JOHDATUS TILASTOTIETEESEEN Harjoituksen 3 ratkaisut, viikko 5, kevät 19 1. a) Havaintomatriisissa on viisi riviä (eli tilastoyksikköä) ja neljä saraketta (eli muuttujaa). Hannu mies LTK 18 Johanna
86118P JOHDATUS TILASTOTIETEESEEN Harjoituksen 3 ratkaisut, viikko 5, kevät 19 1. a) Havaintomatriisissa on viisi riviä (eli tilastoyksikköä) ja neljä saraketta (eli muuttujaa). Hannu mies LTK 18 Johanna
Kenguru 2012 Student sivu 1 / 8 (lukion 2. ja 3. vuosi)
 Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Merkitse yhtä puuta kirjaimella x ja kirjoita yhtälöksi. Mikä tulee vastaukseksi? 3x + 2x = 5x + =
 Mikä X? Esimerkki: Merkitse yhtä puuta kirjaimella ja kirjoita yhtälöksi. Mikä tulee vastaukseksi? 3 + 2 = 5 + = 5 + = 1. Merkitse yhtä päärynää kirjaimella ja kirjoita yhtälöksi? Mikä tulee vastaukseksi?
Mikä X? Esimerkki: Merkitse yhtä puuta kirjaimella ja kirjoita yhtälöksi. Mikä tulee vastaukseksi? 3 + 2 = 5 + = 5 + = 1. Merkitse yhtä päärynää kirjaimella ja kirjoita yhtälöksi? Mikä tulee vastaukseksi?
A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-6. Taulukkokirjaa saa käyttää apuna, laskinta ei.
 PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
Tehtävät 1/11. TAMPEREEN YLIOPISTO Informaatiotieteiden tiedekunta Valintakoe Matematiikka ja tilastotiede. Sukunimi (painokirjaimin)
 1/11 Tehtävä 1 2 3 4 5 6 7 8 9 10 Yhteensä Pisteet (tarkastaja merkitsee) Kokeessa on kymmenen tehtävää, joista jokainen on erillisellä paperilla. Jokaisen tehtävän maksimipistemäärä on 6 pistettä. Ratkaise
1/11 Tehtävä 1 2 3 4 5 6 7 8 9 10 Yhteensä Pisteet (tarkastaja merkitsee) Kokeessa on kymmenen tehtävää, joista jokainen on erillisellä paperilla. Jokaisen tehtävän maksimipistemäärä on 6 pistettä. Ratkaise
LASKUTOIMITUKSET. Montako ötökkää on kussakin ruudussa? Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos:
 LASKUTOIMITUKSET Montako ötökkää on kussakin ruudussa? Nimi: 1 Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Jos laskit ötökät yksitellen, harjoittele ja mieti, miten voit tehdä laskun
LASKUTOIMITUKSET Montako ötökkää on kussakin ruudussa? Nimi: 1 Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Jos laskit ötökät yksitellen, harjoittele ja mieti, miten voit tehdä laskun
2. a- ja b-kohdat selviä, kunhan kutakuinkin tarkka, niin a-kohta 1 p b-kohta 1 p
 LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
MITEN TEET AIKAAN LIITTYVIÄ KYSYMYKSIÄ JA MITEN VASTAAT NIIHIN?
 MITEN TEET AIKAAN LIITTYVIÄ KYSYMYKSIÄ JA MITEN VASTAAT NIIHIN? 1. MILLOIN? KOSKA? 2. MIHIN AIKAAN? 3. MINÄ PÄIVÄNÄ? 4. MILLÄ VIIKOLLA? 5. MISSÄ KUUSSA? 6. MINÄ VUONNA? 7. MILLÄ VUOSIKYMMENELLÄ? 8. MILLÄ
MITEN TEET AIKAAN LIITTYVIÄ KYSYMYKSIÄ JA MITEN VASTAAT NIIHIN? 1. MILLOIN? KOSKA? 2. MIHIN AIKAAN? 3. MINÄ PÄIVÄNÄ? 4. MILLÄ VIIKOLLA? 5. MISSÄ KUUSSA? 6. MINÄ VUONNA? 7. MILLÄ VUOSIKYMMENELLÄ? 8. MILLÄ
1 TILASTOMATEMATIIKKA... 2 2 TILASTOTIETEEN PERUSKÄSITTEITÄ... 3 3 MUUTTUJAT... 6 4 FREKVENSSIJAKAUMA... 8 5 AINEISTON LUOKITTELU...
 SISÄLLYSLUETTELO 1 TILASTOMATEMATIIKKA... 2 1.1 JOHDANTO... 2 1.2 LINKKEJÄ... 2 1.3 LÄHTEET... 2 2 TILASTOTIETEEN PERUSKÄSITTEITÄ... 3 2.1 HAVAINTOAINEISTO... 3 2.2 POPULAATIO... 3 2.3 OTOS... 3 2.4 HAVAINTOAINEISTON
SISÄLLYSLUETTELO 1 TILASTOMATEMATIIKKA... 2 1.1 JOHDANTO... 2 1.2 LINKKEJÄ... 2 1.3 LÄHTEET... 2 2 TILASTOTIETEEN PERUSKÄSITTEITÄ... 3 2.1 HAVAINTOAINEISTO... 3 2.2 POPULAATIO... 3 2.3 OTOS... 3 2.4 HAVAINTOAINEISTON
TILASTO- JA TALOUSMATEMATIIKKA s. 1
 TILASTO- JA TALOUSMATEMATIIKKA s. 1 Käsitteitä: Tilastoja voidaan havainnollistaa: o Tilastokuvioilla eli diagrammeilla Tavallisimmin käytettyjä tilastokuvioita ovat pylväsdiagrammit Muodostuu erillisistä
TILASTO- JA TALOUSMATEMATIIKKA s. 1 Käsitteitä: Tilastoja voidaan havainnollistaa: o Tilastokuvioilla eli diagrammeilla Tavallisimmin käytettyjä tilastokuvioita ovat pylväsdiagrammit Muodostuu erillisistä
Määrällisen aineiston esittämistapoja. Aki Taanila
 Määrällisen aineiston esittämistapoja Aki Taanila 24.4.2017 1 Kategoriset muuttujat Lukumääriä Prosentteja (muista n-arvot) Pylväitä 2 Yhteenvetotaulukko (frekvenssitaulukko) TAULUKKO 1. Asunnon tyyppi
Määrällisen aineiston esittämistapoja Aki Taanila 24.4.2017 1 Kategoriset muuttujat Lukumääriä Prosentteja (muista n-arvot) Pylväitä 2 Yhteenvetotaulukko (frekvenssitaulukko) TAULUKKO 1. Asunnon tyyppi
Metsämuuronen: Tilastollisen kuvauksen perusteet ESIPUHE... 4 SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 2. AINEISTO...
 Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA...9 1.2 AIHEESEEN PEREHTYMINEN...9 1.3
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA...9 1.2 AIHEESEEN PEREHTYMINEN...9 1.3
Kvantitatiiviset menetelmät
 Kvantitatiiviset menetelmät HUOM! Tentti pidetään tiistaina.. klo 6-8 Vuorikadulla V0 ls Muuttujien muunnokset Usein empiirisen analyysin yhteydessä tulee tarve muuttaa aineiston muuttujia Esim. syntymävuoden
Kvantitatiiviset menetelmät HUOM! Tentti pidetään tiistaina.. klo 6-8 Vuorikadulla V0 ls Muuttujien muunnokset Usein empiirisen analyysin yhteydessä tulee tarve muuttaa aineiston muuttujia Esim. syntymävuoden
Juuri 10 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
3. kappale (kolmas kappale) AI KA
 3. kappale (kolmas kappale) AI KA 3.1. Kellonajat: Mitä kello on? Kello on yksi. Kello on tasan yksi. Kello on kaksikymmentä minuuttia vaille kaksi. Kello on kymmenen minuuttia yli yksi. Kello on kymmenen
3. kappale (kolmas kappale) AI KA 3.1. Kellonajat: Mitä kello on? Kello on yksi. Kello on tasan yksi. Kello on kaksikymmentä minuuttia vaille kaksi. Kello on kymmenen minuuttia yli yksi. Kello on kymmenen
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
7. laskuharjoituskierros, vko 10, ratkaisut
 7. laskuharjoituskierros, vko 10, ratkaisut D1. a) Oletetaan, että satunnaismuuttujat X ja Y noudattavat kaksiulotteista normaalijakaumaa parametrein E(X) = 0, E(Y ) = 1, Var(X) = 1, Var(Y ) = 4 ja Cov(X,
7. laskuharjoituskierros, vko 10, ratkaisut D1. a) Oletetaan, että satunnaismuuttujat X ja Y noudattavat kaksiulotteista normaalijakaumaa parametrein E(X) = 0, E(Y ) = 1, Var(X) = 1, Var(Y ) = 4 ja Cov(X,
AJANILMAISUT AJAN ILMAISUT KOULUTUSKESKUS SALPAUS MODUULI 3
 AJAN ILMAISUT AJAN ILMAISUT 1. PÄIVÄ, VIIKONPÄIVÄ 2. VUOROKAUDENAIKA 3. VIIKKO 4. KUUKAUSI 5. VUOSI 6. VUOSIKYMMEN, VUOSISATA, VUOSITUHAT 7. VUODENAIKA 8. JUHLAPÄIVÄT MILLOIN? 1. 2. 3. 4. maanantai, tiistai,
AJAN ILMAISUT AJAN ILMAISUT 1. PÄIVÄ, VIIKONPÄIVÄ 2. VUOROKAUDENAIKA 3. VIIKKO 4. KUUKAUSI 5. VUOSI 6. VUOSIKYMMEN, VUOSISATA, VUOSITUHAT 7. VUODENAIKA 8. JUHLAPÄIVÄT MILLOIN? 1. 2. 3. 4. maanantai, tiistai,
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
A-OSA. Kyseessä on binomitodennäköisyys. 30 P(Tasan 10 sadepäivää ja muut 20 poutapäiviä) 0,35 (1 0,35) ,35 0, ,
 MAB8-harjoituskoe RATKAISUT A-OSA 1. Eräänä kuukautena yksittäisen sadepäivän todennäköisyys on 35 %. Millä todennäköisyydellä kuukauden päivistä 10 on sadepäiviä ja 20 poutapäiviä, kun kuukaudessa on
MAB8-harjoituskoe RATKAISUT A-OSA 1. Eräänä kuukautena yksittäisen sadepäivän todennäköisyys on 35 %. Millä todennäköisyydellä kuukauden päivistä 10 on sadepäiviä ja 20 poutapäiviä, kun kuukaudessa on
AMMATIKKA top 16.11.2006
 AMMATIKKA top 16.11.2006 Toisen asteen ammatillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU Nimi Oppilaitos Koulutusala Luokka Sarjat: MERKITSE OMA SARJA 1. Tekniikka ja liikenne: O 2.
AMMATIKKA top 16.11.2006 Toisen asteen ammatillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU Nimi Oppilaitos Koulutusala Luokka Sarjat: MERKITSE OMA SARJA 1. Tekniikka ja liikenne: O 2.
Kandidaatintutkielman aineistonhankinta ja analyysi
 Kandidaatintutkielman aineistonhankinta ja analyysi Anna-Kaisa Ylitalo M 315, anna-kaisa.ylitalo@jyu.fi Musiikin, taiteen ja kulttuurin tutkimuksen laitos Jyväskylän yliopisto 2018 2 Havaintomatriisi Havaintomatriisi
Kandidaatintutkielman aineistonhankinta ja analyysi Anna-Kaisa Ylitalo M 315, anna-kaisa.ylitalo@jyu.fi Musiikin, taiteen ja kulttuurin tutkimuksen laitos Jyväskylän yliopisto 2018 2 Havaintomatriisi Havaintomatriisi
1.1 Tilastotieteen peruskäsitteitä
 Tilastotieteen peruskäsitteitä 1.1 Tilastotieteen peruskäsitteitä 1. Muodostetaan taulukon perusteella suhteellinen frekvenssijakauma. Lehti Levikki f % Helsingin 365994 365 994 0,13579... 13,6% Sanomat
Tilastotieteen peruskäsitteitä 1.1 Tilastotieteen peruskäsitteitä 1. Muodostetaan taulukon perusteella suhteellinen frekvenssijakauma. Lehti Levikki f % Helsingin 365994 365 994 0,13579... 13,6% Sanomat
1. Muunna seuraavat yksiköt. Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu. Oppilaitos:.. Koulutusala:...
 MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. Sarjat: LAITA MERKKI OMAAN SARJAASI. Tekniikka ja liikenne:..
MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. Sarjat: LAITA MERKKI OMAAN SARJAASI. Tekniikka ja liikenne:..
TILASTOKATSAUS 15:2016
 Tilastokatsaus 6:2012 TILASTOKATSAUS 15:2016 1 25.8.2016 TYÖTTÖMÄT VANTAALLA 31.12.2015 Työttömyysaste oli Vantaalla 12,4 prosenttia vuoden 2015 lopussa. Työttömien määrä kasvoi kaikilla suuralueilla,
Tilastokatsaus 6:2012 TILASTOKATSAUS 15:2016 1 25.8.2016 TYÖTTÖMÄT VANTAALLA 31.12.2015 Työttömyysaste oli Vantaalla 12,4 prosenttia vuoden 2015 lopussa. Työttömien määrä kasvoi kaikilla suuralueilla,
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Tehtävä 1 2 3 4 5 6 7 Vastaus
 Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Tilaston esittäminen frekvenssitaulukossa ja graafisesti. Keskiluvut luokittelemattomalle ja luokitellulle aineistolle: moodi, mediaani, keskiarvo.
 Kertaus Tilaston esittäminen frekvenssitaulukossa ja graafisesti. Luokiteltu aineisto. Keskiluvut luokittelemattomalle ja luokitellulle aineistolle: moodi, mediaani, keskiarvo. Hajontaluvut luokittelemattomalle
Kertaus Tilaston esittäminen frekvenssitaulukossa ja graafisesti. Luokiteltu aineisto. Keskiluvut luokittelemattomalle ja luokitellulle aineistolle: moodi, mediaani, keskiarvo. Hajontaluvut luokittelemattomalle
MATEMATIIKKAKILPAILU
 Tekniikan Opettajat TOP ry Teknologiateollisuuden Kustannusosakeyhtiö Opetushallitus 100-vuotissäätiö Otava AMMATIKKA top 15.11.2012 Toisen asteen ammattillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU
Tekniikan Opettajat TOP ry Teknologiateollisuuden Kustannusosakeyhtiö Opetushallitus 100-vuotissäätiö Otava AMMATIKKA top 15.11.2012 Toisen asteen ammattillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU
EI MIKÄÄN NÄISTÄ. KUVITETTU MINI-MENTAL STATE EXAMINATION Ohjeet viimeisellä sivulla. 1. Mikä vuosi nyt on? 2. Mikä vuodenaika nyt on?
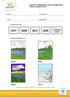 POTILAS: SYNTYMÄAIKA: TUTKIJA: PÄIVÄMÄÄRÄ: 1. Mikä vuosi nyt on? 2000 2017 2020 1917 EI MIKÄÄN NÄISTÄ 2. Mikä vuodenaika nyt on? KEVÄT KESÄ SYKSY TALVI 3. Monesko päivä tänään on? 1 2 3 4 5 6 7 8 9 10
POTILAS: SYNTYMÄAIKA: TUTKIJA: PÄIVÄMÄÄRÄ: 1. Mikä vuosi nyt on? 2000 2017 2020 1917 EI MIKÄÄN NÄISTÄ 2. Mikä vuodenaika nyt on? KEVÄT KESÄ SYKSY TALVI 3. Monesko päivä tänään on? 1 2 3 4 5 6 7 8 9 10
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Totta vai tarua matematiikan paradokseja
 Totta vai tarua matematiikan paradokseja Onko intuitio aina oikeassa todennäköisyyksiä pohdittaessa? Tilastot eivät valehtele, eiväthän? Työohjeet: 1) Muodostetaan noin 3 henkilön ryhmät. 2) Valitkaa yhden
Totta vai tarua matematiikan paradokseja Onko intuitio aina oikeassa todennäköisyyksiä pohdittaessa? Tilastot eivät valehtele, eiväthän? Työohjeet: 1) Muodostetaan noin 3 henkilön ryhmät. 2) Valitkaa yhden
Määrällisen aineiston esittämistapoja. Aki Taanila
 Määrällisen aineiston esittämistapoja Aki Taanila 7.11.2011 1 Muuttujat Aineiston esittämisen kannalta muuttujat voidaan jaotella kolmeen tyyppiin: Kategoriset (esimerkiksi sukupuoli, koulutus) Asteikolla
Määrällisen aineiston esittämistapoja Aki Taanila 7.11.2011 1 Muuttujat Aineiston esittämisen kannalta muuttujat voidaan jaotella kolmeen tyyppiin: Kategoriset (esimerkiksi sukupuoli, koulutus) Asteikolla
PRELIMINÄÄRIKOE. Lyhyt Matematiikka 3.2.2015
 PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
Til.yks. x y z 1 2 1 20.3 2 2 1 23.5 9 2 1 4.7 10 2 2 6.2 11 2 2 15.6 17 2 2 23.4 18 1 1 12.5 19 1 1 7.8 24 1 1 9.4 25 1 2 28.1 26 1 2-6.2 33 1 2 33.
 Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE
 LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän alla olevaan tilaan. Mikäli
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän alla olevaan tilaan. Mikäli
Yksityishenkilöiden tulot ja verot vuonna 2012
 2014:28 Yksityishenkilöiden tulot ja verot vuonna 2012 Helsingissä mediaanitulo 26 300 euroa Helsinkiläisen vuositulot keskimäärin 32 800 euroa Pääomatuloja huomattavasti edellisvuotta vähemmän Veroja
2014:28 Yksityishenkilöiden tulot ja verot vuonna 2012 Helsingissä mediaanitulo 26 300 euroa Helsinkiläisen vuositulot keskimäärin 32 800 euroa Pääomatuloja huomattavasti edellisvuotta vähemmän Veroja
matematiikka Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola
 9 E matematiikka Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola Helsingissä Kustannusosakeyhtiö Otava Yhteenlaskumenetelmän harjoittelua Joskus
9 E matematiikka Martti Heinonen Markus Luoma Leena Mannila Kati Rautakorpi-Salmio Timo Tapiainen Tommi Tikka Timo Urpiola Helsingissä Kustannusosakeyhtiö Otava Yhteenlaskumenetelmän harjoittelua Joskus
TILASTOKATSAUS 4:2015
 Tilastokatsaus 6:212 TILASTOKATSAUS 4:2 1 12.8.2 TIETOJA TYÖVOIMASTA JA TYÖTTÖMYYDESTÄ Työvoiman määrä kasvoi 1 3:lla (,9 %) vuoden 213 aikana Vantaalla työvoimaan kuuluvien joukko on suurentunut vuodesta
Tilastokatsaus 6:212 TILASTOKATSAUS 4:2 1 12.8.2 TIETOJA TYÖVOIMASTA JA TYÖTTÖMYYDESTÄ Työvoiman määrä kasvoi 1 3:lla (,9 %) vuoden 213 aikana Vantaalla työvoimaan kuuluvien joukko on suurentunut vuodesta
Aluksi. 1.1. Kahden muuttujan lineaarinen yhtälö
 Aluksi Matematiikan käsite suora on tarkalleen sama asia kuin arkikielen suoran käsite. Vai oliko se toisinpäin? Matematiikan luonteesta johtuu, että sen soveltaja ei tyydy pelkkään suoran nimeen eikä
Aluksi Matematiikan käsite suora on tarkalleen sama asia kuin arkikielen suoran käsite. Vai oliko se toisinpäin? Matematiikan luonteesta johtuu, että sen soveltaja ei tyydy pelkkään suoran nimeen eikä
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas TEOREETTISISTA JAKAUMISTA Usein johtopäätösten teko helpottuu huomattavasti, jos tarkasteltavan muuttujan perusjoukon jakauma noudattaa
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas TEOREETTISISTA JAKAUMISTA Usein johtopäätösten teko helpottuu huomattavasti, jos tarkasteltavan muuttujan perusjoukon jakauma noudattaa
Valitse aineisto otsikoineen maalaamalla se hiirella ja kopioimalla (Esim. ctrl-c). Vaihtoehtoisesti, Lataa CSV-tiedosto
 Versio k15 Näin laadit ilmastodiagrammin Libre Officen taulukkolaskentaohjelmalla. Ohje on laadittu käyttäen Libre Officen versiota 4.2.2.1. Voit ladata ohjelmiston omalle koneellesi osoitteesta fi.libreoffice.org.
Versio k15 Näin laadit ilmastodiagrammin Libre Officen taulukkolaskentaohjelmalla. Ohje on laadittu käyttäen Libre Officen versiota 4.2.2.1. Voit ladata ohjelmiston omalle koneellesi osoitteesta fi.libreoffice.org.
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa. Luentokuulustelujen esimerkkivastauksia. Pertti Palo. 30.
 FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa Luentokuulustelujen esimerkkivastauksia Pertti Palo 30. marraskuuta 2012 Saatteeksi Näiden vastausten ei ole tarkoitus olla malleja vaan esimerkkejä.
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa Luentokuulustelujen esimerkkivastauksia Pertti Palo 30. marraskuuta 2012 Saatteeksi Näiden vastausten ei ole tarkoitus olla malleja vaan esimerkkejä.
MAA1.1 Koe Jussi Tyni Kastellin lukio Tee pisteytysruudukko! Vastaa yhteensä 6 tehtävään. Muista kirjoittaa selkeät välivaiheet
 MAA. Koe Jussi Tyni 0.9.0 Tee pisteytysruudukko! Vastaa yhteensä tehtävään. Muista kirjoittaa selkeät välivaiheet A-OSIO Vastaa tehtävistä A A kahteen ja palauta vastaukset. Tähän osioon on käytettävissä
MAA. Koe Jussi Tyni 0.9.0 Tee pisteytysruudukko! Vastaa yhteensä tehtävään. Muista kirjoittaa selkeät välivaiheet A-OSIO Vastaa tehtävistä A A kahteen ja palauta vastaukset. Tähän osioon on käytettävissä
Äidinkielen valtakunnallinen koe 9.luokka
 Keväällä 2013 Puumalan yhtenäiskoulussa järjestettiin valtakunnalliset kokeet englannista ja matematiikasta 6.luokkalaisille ja heille tehtiin myös äidinkielen lukemisen ja kirjoittamisen testit. 9.luokkalaisille
Keväällä 2013 Puumalan yhtenäiskoulussa järjestettiin valtakunnalliset kokeet englannista ja matematiikasta 6.luokkalaisille ja heille tehtiin myös äidinkielen lukemisen ja kirjoittamisen testit. 9.luokkalaisille
TEHTÄVIEN RATKAISUT. Luku a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5.
 TEHTÄVIEN RATKAISUT Luku 4.1 183. a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5. Lasketaan funktioon syötetyn luvun neliö: 5 = 5. Saatuun arvoon lisätään luku 1:
TEHTÄVIEN RATKAISUT Luku 4.1 183. a) Merkintä f (5) tarkoittaa lukua, jonka funktio tuottaa, kun siihen syötetään luku 5. Lasketaan funktioon syötetyn luvun neliö: 5 = 5. Saatuun arvoon lisätään luku 1:
14 Jatkuva jakauma. Käsitellään kuitenkin ennen täsmällisiä määritelmiä johdatteleva
 4 Jatkuva jakauma Edellä määriteltiin diskreetiksi satunnaismuuttujaksi sellainen, joka voi saada vain (hyppäyksittäin) erillisiä arvoja. Jatkuva satunnaismuuttuja voi saada mitä hyvänsä arvoja yleensä
4 Jatkuva jakauma Edellä määriteltiin diskreetiksi satunnaismuuttujaksi sellainen, joka voi saada vain (hyppäyksittäin) erillisiä arvoja. Jatkuva satunnaismuuttuja voi saada mitä hyvänsä arvoja yleensä
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
ikä (vuosia) on jo muuttanut 7 % 46 % 87 % 96 % 98 % 100 %
 Testaa taitosi 1 1. Noppaa heitetään kahdesti. Merkitse kaikki alkeistapaukset koordinaatistoon. a) Millä todennäköisyydellä ainakin toinen silmäluvuista on 3? b) Mikä on a-kohdan tapahtuman vastatapahtuma?
Testaa taitosi 1 1. Noppaa heitetään kahdesti. Merkitse kaikki alkeistapaukset koordinaatistoon. a) Millä todennäköisyydellä ainakin toinen silmäluvuista on 3? b) Mikä on a-kohdan tapahtuman vastatapahtuma?
Tarkista vielä ennen analysoinnin aloittamista seuraavat seikat:
 Yleistä Tilastoapu on Excelin sisällä toimiva apuohjelma, jonka avulla voit analysoida tilastoaineistoja. Tilastoapu toimii Excelin Windows-versioissa Excel 2007, Excel 2010 ja Excel 2013. Kun avaat Tilastoavun,
Yleistä Tilastoapu on Excelin sisällä toimiva apuohjelma, jonka avulla voit analysoida tilastoaineistoja. Tilastoapu toimii Excelin Windows-versioissa Excel 2007, Excel 2010 ja Excel 2013. Kun avaat Tilastoavun,
A-Osio. Ei saa käyttää laskinta, maksimissaan tunti aikaa. Valitse seuraavista kolmesta tehtävästä kaksi, joihin vastaat:
 MAA6 Loppukoe 26..203 Jussi Tyni Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! Lue ohjeet huolella! A-Osio. Ei saa
MAA6 Loppukoe 26..203 Jussi Tyni Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! Lue ohjeet huolella! A-Osio. Ei saa
MAY1 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 12.4.2016 Julkaiseminen sallittu vain koulun suljetussa verkossa.
 KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
Opetusmateriaali. Fermat'n periaatteen esittely
 Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen kuudennen luokan matematiikan koe 2014
 Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen kuudennen luokan matematiikan koe 2014 MFKA-Kustannus Oy Rautatieläisenkatu 6, 0020 HELSINKI, puh. (09) 102 378 http://www.mfka.fi Peruskoulun
Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen kuudennen luokan matematiikan koe 2014 MFKA-Kustannus Oy Rautatieläisenkatu 6, 0020 HELSINKI, puh. (09) 102 378 http://www.mfka.fi Peruskoulun
1 Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin!
 MAA6 Kurssikoe 1.11.14 Jussi Tyni ja Juha Käkilehto Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-OSIO: Laske kaikki
MAA6 Kurssikoe 1.11.14 Jussi Tyni ja Juha Käkilehto Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-OSIO: Laske kaikki
Syksyn 2015 Lyhyen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
 Sksn 015 Lhen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut Tekijät: Olli Karkkulainen ja Markku Parkkonen Ratkaisut on laadittu TI-Nspire CAS -tietokoneohjelmalla kättäen Muistiinpanot -sovellusta.
Sksn 015 Lhen matematiikan YO-kokeen TI-Nspire CAS -ratkaisut Tekijät: Olli Karkkulainen ja Markku Parkkonen Ratkaisut on laadittu TI-Nspire CAS -tietokoneohjelmalla kättäen Muistiinpanot -sovellusta.
TILASTOKATSAUS 4:2017
 Tilastokatsaus 6:2012 TILASTOKATSAUS 4:201 1.10.201 TYÖTTÖMÄT VANTAALLA 200 2016 Työttömyysaste oli Vantaalla 11, prosenttia vuoden 2016 lopussa. Laskua edellisvuoteen oli 0,5 prosenttiyksikköä, mikä johtui
Tilastokatsaus 6:2012 TILASTOKATSAUS 4:201 1.10.201 TYÖTTÖMÄT VANTAALLA 200 2016 Työttömyysaste oli Vantaalla 11, prosenttia vuoden 2016 lopussa. Laskua edellisvuoteen oli 0,5 prosenttiyksikköä, mikä johtui
MATEMATIIKKAKILPAILU
 Tekniikan Opettajat TOP ry Teknologiateollisuuden Kustannusosakeyhtiö Opetushallitus 100-vuotissäätiö Otava AMMATIKKA top 13.11.2008 Toisen asteen ammattillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU
Tekniikan Opettajat TOP ry Teknologiateollisuuden Kustannusosakeyhtiö Opetushallitus 100-vuotissäätiö Otava AMMATIKKA top 13.11.2008 Toisen asteen ammattillisen koulutuksen kaikkien alojen yhteinen MATEMATIIKKAKILPAILU
Tilastojen tulkintatehtäviä lukion 2. ja 3. vuosikursseille
 Yhteystiedot: Tilastokeskus tilastokoulu@tilastokeskus.fi Tilastojen tulkintatehtäviä lukion 2. ja 3. vuosikursseille Oppilaan nimi: Vastaa suoraan tähän koepaperiin. Hyödynnä koepaperille jätettyjä vastausviivoja
Yhteystiedot: Tilastokeskus tilastokoulu@tilastokeskus.fi Tilastojen tulkintatehtäviä lukion 2. ja 3. vuosikursseille Oppilaan nimi: Vastaa suoraan tähän koepaperiin. Hyödynnä koepaperille jätettyjä vastausviivoja
Millaisia maksuvaikeudet ovat eri-ikäisillä suomalaisilla?
 PERINTÄASIAKKAAT IKÄRYHMITTÄIN Millaisia maksuvaikeudet ovat eri-ikäisillä suomalaisilla? 1. TILASTOSELVITYS Tilastotarkastelun tarkoituksena on selvittää, miten perintään päätyneet laskut jakautuvat eri-ikäisille
PERINTÄASIAKKAAT IKÄRYHMITTÄIN Millaisia maksuvaikeudet ovat eri-ikäisillä suomalaisilla? 1. TILASTOSELVITYS Tilastotarkastelun tarkoituksena on selvittää, miten perintään päätyneet laskut jakautuvat eri-ikäisille
Kynä-paperi -harjoitukset. Taina Lehtinen Taina I Lehtinen Helsingin yliopisto
 Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
1 Jalkapallo 100 0,806 81 % Vastaus: 81 % Esimerkki 1. Desimaaliluvun muuntaminen prosenttiluvuksi: 0,81 = 81 % 2 Prosentti- ja potenssilaskenta
 1 Jalkapallo Esimerkki 1 Desimaaliluvun muuntaminen prosenttiluvuksi: 0,81 = 81 % Tampere Utd:n maalivahti Mikko Kavén torjui 100 maalia kaudella 2004. Kohti maalia laukauksia oli 124. Kuinka monta prosenttia
1 Jalkapallo Esimerkki 1 Desimaaliluvun muuntaminen prosenttiluvuksi: 0,81 = 81 % Tampere Utd:n maalivahti Mikko Kavén torjui 100 maalia kaudella 2004. Kohti maalia laukauksia oli 124. Kuinka monta prosenttia
Tilastoja yleisurheillen
 Tilastoja yleisurheillen Millainen mehupurkki on halvin valmistaa? Voisiko kaupan mehupurkki olla muodoltaan pallo? Entä lieriö? Opettaja jakaa luokan oppilaat noin kolmen henkilön ryhmiin. Työohjeet:
Tilastoja yleisurheillen Millainen mehupurkki on halvin valmistaa? Voisiko kaupan mehupurkki olla muodoltaan pallo? Entä lieriö? Opettaja jakaa luokan oppilaat noin kolmen henkilön ryhmiin. Työohjeet:
Ma4 Yhtälöt ja lukujonot
 Ma4 Yhtälöt ja lukujonot H4 Lukujonot 4.1 Kirjoita lukujonon seuraavat viisi termiä, kun ensimmäinen termi on 1 ja muut muodostuvat seuraavien sääntöjen mukaan. a) Lisää edelliseen termiin 3. b) Kerro
Ma4 Yhtälöt ja lukujonot H4 Lukujonot 4.1 Kirjoita lukujonon seuraavat viisi termiä, kun ensimmäinen termi on 1 ja muut muodostuvat seuraavien sääntöjen mukaan. a) Lisää edelliseen termiin 3. b) Kerro
Kuvioita, taulukoita ja tunnuslukuja. Aki Taanila 2.2.2011
 Kuvioita, taulukoita ja tunnuslukuja Aki Taanila 2.2.2011 1 Tilastokuviot Pylväs Piirakka Viiva Hajonta 2 Kuviossa huomioitavia asioita 1 Kuviolla tulee olla tarkoitus ja tehtävä (minkä tiedon haluat välittää
Kuvioita, taulukoita ja tunnuslukuja Aki Taanila 2.2.2011 1 Tilastokuviot Pylväs Piirakka Viiva Hajonta 2 Kuviossa huomioitavia asioita 1 Kuviolla tulee olla tarkoitus ja tehtävä (minkä tiedon haluat välittää
MATEMATIIKKA 5 VIIKKOTUNTIA. PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009
 EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
5.3 Ensimmäisen asteen polynomifunktio
 Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
SPSS-pikaohje. Jukka Jauhiainen OAMK / Tekniikan yksikkö
 SPSS-pikaohje Jukka Jauhiainen OAMK / Tekniikan yksikkö SPSS on ohjelmisto tilastollisten aineistojen analysointiin. Hyvinvointiteknologian ATK-luokassa on asennettuna SPSS versio 13.. Huom! Ainakin joissakin
SPSS-pikaohje Jukka Jauhiainen OAMK / Tekniikan yksikkö SPSS on ohjelmisto tilastollisten aineistojen analysointiin. Hyvinvointiteknologian ATK-luokassa on asennettuna SPSS versio 13.. Huom! Ainakin joissakin
1.1 Funktion määritelmä
 1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
1.3 Prosenttilaskuja. pa b = 100
 1.3 Prosenttilaskuja Yksi prosentti jostakin luvusta tai suureesta on tämän sadasosa ja saadaan siis jakamalla ao. luku tai suure luvulla. Jos luku b on p % luvusta a, toisin sanoen jos luku b on p kpl
1.3 Prosenttilaskuja Yksi prosentti jostakin luvusta tai suureesta on tämän sadasosa ja saadaan siis jakamalla ao. luku tai suure luvulla. Jos luku b on p % luvusta a, toisin sanoen jos luku b on p kpl
Pehmopapereiden matematiikkaa
 Koostanut Iida Hirn ja Elina Viro Opettajalle Pehmopapereiden matematiikkaa Kohderyhmä: 9.luokka Esitiedot: Pinta-ala, tilavuus, tilastomatematiikka, Excel, verranto, koordinaatisto Taustalla oleva matematiikka:
Koostanut Iida Hirn ja Elina Viro Opettajalle Pehmopapereiden matematiikkaa Kohderyhmä: 9.luokka Esitiedot: Pinta-ala, tilavuus, tilastomatematiikka, Excel, verranto, koordinaatisto Taustalla oleva matematiikka:
