S ysteemianalyysin Laboratorio Janne Sorsa Teknillinen korkeakoulu Matemaattisten algoritmien ohjelmointi Kevät 2008 / 1
|
|
|
- Hannes Heino
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Smplex-menetelm menetelmän lsennllset tent 4. luento: MPS-tedostomuoto LP-tehtäven esästtely S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 1 MPS-tedostomuoto LP-teht tehtäven esästtely sttely MPS-tedostomuoto sen ästtely Esästtely: Presolve Slus Jälästtely S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 2 1
2 MPS-tedostomuoto IBM ehtt MPS (Mthemtcl Progrmmng System) formtn 50-luvull Formtn rotuset seurust reäortest Mon täretä mlle tllennettu MPS-formttn Esmers Netlb ssältää ooelmn suur LPtehtävä MPS-muodoss Kunnollsess mllnnusohelmstoss ptää oll tu MPS-muodolle Perustus pätee nyyäänn: tehtävä nnetn nollst poeven loden vull S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 3 MPS-tedoston renne Rvettän trst määrtellyt enttärt Indttor määrttää esm. rotteen tyypn Nmet enntään 8 merä ptä Nmä e s lott vällyönnllä Josell ololl tulee oll ysästtenen nm Feld-1 Feld-2 Feld-3 Feld-4 Feld-5 Feld-6 Locton Contents Indctor Nme Nme Vlue Nme Vlue S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 4 2
3 MPS-tedoston renne Tedosto on ettu osohn Osn luoht tunnstetn nmestään Nmet rotetn 1. sreest len Osot ptää oll ärestysessä: NAME, ROWS, COLUMNS, RHS, RANGES, BOUNDS, ENDATA RANGES BOUNDS evät ole polls Kohdefunto ssällytetään mtrsn e-rottvn rvnä S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 5 NAME ENDATA NAME lott mlln määrttämsen Tedoston rvt ennen NAME-osot hylätään Mlllle vo nt nmen (Feld-3) ENDATA lopett tedoston S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 6 3
4 ROWS Määrtellään mtrsn rven nmet Anostn tässä määrteltyä nmä vodn äyttää myöhemmn Rotusten tyypt määrätään tässä ososs (Feld-1) Rotusten nmet seurvt tyyppä (Feld-2) S ysteemnlyysn Lbortoro Tenllnen oreoulu Row type Code Menng L Less thn or equl constrnt G Greter thn or equl constrnt = E Equlty constrnt Obectve N Obectve row Free N Non-bndng constrnt Mtemttsten lgortmen ohelmont Kevät 2008 / 7 COLUMNS Määrtellään muuttuen (sreden) nmet Määrtellään mtrsn A ohdefunton lot Sreen lot vodn nt mssä ärestysessä thns Sreen lot tulee oll perään Tetueen muoto: Feld-2: Muuttun nm Feld-3: Rvn nm Feld-4: Alon rvo S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 8 4
5 RHS Määrtellään RHS-rvot Vodn määrtellä uset RHS-vetoret Tetueen renne: Feld-2: RHS-vetorn nm Feld-3: Rvn nm Feld-4: Arvo S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 9 MPS-tedoston ästtely Kästtely perustuu hutuluohn, ot määräävät MPS-nmen LP-tehtävän ssäsen ndesonnn vstvuuden = ˆ sre rv rvo [ ][ ][ ] [ ][ ] b = ˆ rv rvo Kästtelyn n tehtävä trstus Toseen ertn määrteltyä rvn nmeä e huomod Sm rv e vo esntyä ht ert sreess Olvto pollset osot tedostoss Menetelmä: hhmon tunnstus, hutus, ärestämnen, hu S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 10 5
6 Presolve Tehtävän oon penentämnen Numeersen äyttäytymsen prntmnen Epääypyyden rottmttomuuden tunnstmnen Kompromss työmäärän tehouuden välllä S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 11 LP-teht tehtävä presolve-testess testessä T mn c x + c0 s.t. Ax = b l x u Rveä sret postetn presolvess Tehtävän dmensot muuttuvt Presolven yhteydessä mernnät trottvt ullonn vomss olev rvo: ndesont summluseess RHS b ustnnusteät c S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 12 6
7 Määrtelmä Muutmt testt perustuvt rotteen penmpään suurmpn mhdollseen rvoon Postvsten negtvsten ertomen ndesouot oselle rvlle mtrsss A P = : > 0 N b b = = = { } { : < 0} l + P N u + P N u l S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 13 Rstrt muuttuen ross Jos l > u mlle thns, tehtävä on epääypä Knntt trst muuttut = 1,, n S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 14 7
8 Tyhät t rvt Ken renteellsten muuttuen ertomet noll Ano nollst poev on z = b Vo ssältyä tehtävään snänsä Vo oll muden muunnosten nsm presolvess Jos b on äypä rvo z :lle, rv vodn post Jos b e ole äypä rvo z :lle, tehtävä on epääypä S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 15 Tyhät t sreet Jos sre on tyhä, vstv muuttu x e vut rottesn postetn tehtävästä Jos c = 0 x :n rvos vodn sett mä thns äypä rvo l Kohdefuntot e trvtse muutt Jos c > 0 Asetetn: x = l c 0 := c 0 + c l Jos l =, tehtävän rtsu on rottmton Jos c < 0 Asetetn: x = u c 0 := c 0 + c u Jos =, tehtävän rtsu on rottmton u u S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 16 8
9 Sngleton-rvt Vn ys rvn renteellnen erron poe nollst Sngleton-rvt postetn tehtävästä Jos rote on yhtälö (tyypp 0) Jos x [ l, u ], tehtävä on epääypä Muuten setetn x = b muuttu postetn tehtävästä Jos rote on e-rottv (tyypp 3), x setetn ohonn äypään rvoon postetn tehtävästä Jos rote on epäyhtälörote (tyypp 1, 2 t 4), se määrää ylä t lrn x :lle S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 17 Sngleton-rvn määrämät rt muuttulle Jos Jos Jos x b > 0 < 0 nn nn x u = b x l = b Jos x Jos Jos b > 0 nn x l = b < 0 nn x u = b Pävtetyt rotusehdot x :lle: { l, } { u u } l : = mx l u : = mn, S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 18 9
10 Knntettyen muuttuen postmnen Knntetty muuttu vodn post Knntetään x = t Kohdefuntot pävtetään: c 0 := c 0 + c t Rotusehto pävtetään: Ax := Ax t Rotusehtoen l- ylärt pävtetään: b : = b t b : = b t S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 19 Redundntt pottvt rotteet Oletetn luperänen rote: x b Täytyy toteutt myös rotteen l- ylärt: b x b Jos b < b, tehtävä on epääypä Jos b = b, muuttut vodn nnttää l- ylärolleen: x = l, P x = u, N Jos b b, rote on redundntt vodn post Jos b < b < b, rotett e vod post S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 20 10
11 Muuttuen roen tuentmnen Oletetn, että rote tyyppä 2 ( ) lr b äärellnen Jos muuttu x = l lrll P, svtetn x :n rvo: b + ( x l ) x b, P x u = l b b +, P S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 21 S ysteemnlyysn Lbortoro Tenllnen oreoulu Muuttuen roen tuentmnen Vstvst, os muuttu x = u ylärll, N, pennetään x :n rvo b + ( x u ) x b, N x l Uudet rt: l : = mx l, l = u { } { } u : = mn u, u Jos l >, tehtävä on epääypä u b b +, N Mtemttsten lgortmen ohelmont Kevät 2008 / 22 11
12 Implsttsest vpt muuttut Mertään muuttulle x : Aluperäset muutturt: l u Lsetut muutturt: l u x on mplsttsest vp muuttu, os [ l, u ] [ l, u ] Jos x on sngleton-sre s.e. 0 on no nollst poev lo, nn seä x että rv vodn post tehtävästä Kohdefuntot pävtetään x :n dulmuuttun y vull S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 23 Hrvuuden vähentv hentämnen Tvotteen nollst poeven loden postmnen rotemtrsst A Yhtälörotus (tyypp 0) slrll errottun vodn lsätä mhn thns muuhun rotteeseen Vltn rv pvot-rvs Vltn rv, on hrvuusrenne on rvn ylouo Pävtetään rvä : b = + γ S ysteemnlyysn Lbortoro Tenllnen oreoulu = b + γb Mtemttsten lgortmen ohelmont Kevät 2008 / 24 12
13 Hrvuuden vähentv hentämnen S ysteemnlyysn Lbortoro Tenllnen oreoulu X X X X X X X b X X X X X X X X c X X X X X X X X X X X d X X X e X X X X X Rv on pvot-rv Sre 1:tä äytetään ylouoen etsmseen Rv b on ylouo Rvn c ensmmänen lo on noll Rv d on lyhyemp un Rvn e lo on noll tosen levn sreen ohdll Mtemttsten lgortmen ohelmont Kevät 2008 / 25 Presolve-lgortm Mtrs A äydään läp uset erto Muutos yhdellä errosell vo oht muutosn seurvll errosll Jos hdell perääsellä errosell e tule muutos, lopetetn lgortm Ääretön sr penä prnnus on teorss mhdollst, oten tertoden luumäärälle on syytä sett ylär S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 26 13
14 Slus Tvotteen tehtävän numeersten omnsuusen prntmnen Josus slusen vull vodn rtst muuten rtsemton tehtävä Josus slus teee rtstvss olevst tehtävästä rtsemttomn Slus: RAC x = Rb R = dg R 1, K, Cx = x x = C S ysteemnlyysn Lbortoro Tenllnen oreoulu R m 1 x C = dg C 1, K,C n Mtemttsten lgortmen ohelmont Kevät 2008 / 27 Arvoen hont mtrsss Sopvt mttysöt yleensä tuottvt tspnos rvo mtrsn Huonost slttu mtrs: nollst poeven loden rvot poevt tosstn huomttvst Hyvn slttu mtrs: nollst poeven loden rvot ovt lähellä tosn Jos slusell sdn vähennettyä loden rvoen hont, tehtävä on helpomp rtst Vstesmer: = 1± ε, 0 < ε < 10 8 S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 28 14
15 Hyvn slttu mtrs Mtrs on hyvn slttu, os mx 0 mn penemp un (Fulerson & Wolfe, 1962; Orchrd-Hys, 1968) Mtrs on hyvn slttu, os ( log ) 0 2 svutt hyväsyttävän rvon (Hmmng, 1971; Curts & Red, 1972) S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 29 Slusertomet Oletetn bnäärnen luuluuärestelmä: e = f 2, 1 2 f 1 Slusess pyörstysvrheet mhdolls, os ertomet evät ole luuluuärestelmän nnn potensse ρ γ R = 2, C = 2 Sltut esponentt: e = e + ρ + γ Kertomet sdn mnmomll hont: mn 0 2 ( log ) = mn ( e + ρ + γ ) ρ, γ 0 2 S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 30 15
16 Slusertomen rtsemnen Teholl lttogrdenttmenetelmällä (Curts & Red, 1972) lmääränen rtsu Tr rtsu e trvt, os lopullset rvot pyörstetään oonsluvus Menetelmä onvergo äytännössä n. 10 tertoss rppumtt tehtävän oost Trvttv vn pen os vrsnsten Smplextertoden vtmst st S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 31 Mut slusmenetelmä Tspnotus Jonen rv sre sltn sten, että suurn rvo on 1 Sdn mll rv (sre) sen suurmmll rvoll Geometrnen esrvo { } { } 1 2 mx mn Artmeettnen esrvo Tyypllsest äytetään näden menetelmen yhdstelmä S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 32 16
17 Postsolve Rtstu tehtävä evvlentt luperäsen tehtävän nss, mutte denttnen Stu rtsu muunnettv tsn luperäslle muuttulle rottelle K esästtelyssä tehdyt muutoset tulee tllent Pnorenne soveltuu prhten, os muutoset ptää plutt ääntesessä ärestysessä Tyypllnen ärestys esästtelyssä: Tehtävän uudelleen muotolu Presolve Slus S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 33 Slus luperäsn muuttun Renteellset muuttut: x = Cx Loogset muuttut: etn vstvll rvn slusertomell Kohdefunton ertomet: etn vstvll sreen slusertomell Mrgnlustnnuset: errotn vstvll rvn slusertomell S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 34 17
18 Presolven umomnen Presolve:n hstor lst: onen muutos muuttuss tllennetn vetorn ( 1, 2, ) Koonsluvut 1 2 määrttävät muuttut operton tyypn Relluu ertoo esm. nntetyn rvon t muuttuneen rn Esmereä: Alrn srtämnen: 1 =, 2 = 0, = ( ) l Implsttnen vp muuttu: 1 =, 2 = -, = y Hrvuuden vähentämnen: 1 =, 2 =, = γ S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 35 Yhteenveto MPS-tedostomuoto täreä hstorllsst systä Presolven ptäs tunnst epääyvät rottmttomt tehtävät Slusen äyttämnen e n ut tehtävän rtsuss Numeersen truuden sälyttämnen täreää esästtelyssä Esästtely on ompromss työmäärän svutetun hyödyn välllä S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 36 18
19 Krllsuutt Andersen, E., Andersen. K. (1995). Presolvng n Lner Progrmmng. Mthemtcl Progrmmng 71(2), Benchou, M. et l (1977). The effcent soluton of lrge-scle lner progrmmng problems. Mthemtcl Progrmmng 13, Brerley, A. et l (1975). Anlyss of Mthemtcl Progrmmng Problems Pror to Applyng the Smplex Method. Mthemtcl Progrmmng 8, Curts, A., Red, J. (1972). On the utomtc sclng of mtrces for Gussn elmnton. Journl of the Insttute of Mthemtcs nd ts pplctons 10, S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 37 Krllsuutt Fourer, R., Gy, D. (1993). Experence wth Prml Presolve Algorthm. Numercl Anlyss Mnuscrpt 93-06, AT&T Bell Lbortores. Fulerson, D., Wolfe, P. (1962). An lgorthm for sclng mtrces. SIAM Revew 4, Gy, D. (1985). Electronc ml dstrbuton of lner progrmmng test problems. COAL Newsletter 13, Gondzo, J. (1997). Presolve Anlyss of Lner Progrms Pror to Applyng n Interor Pont Method. INFORMS Journl on Computng 9(1), Orchrd-Hys, W. (1968). Advnced Lner-Progrmmng Computng Technques, McGrw Hll. S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 38 19
20 Krllsuutt Tomln, J. (1975). On sclng lner progrmmng problems. Mthemtcl Progrmmng Study 4, Tomln, J., Welch, J. (1983). Forml optmzton of some reduced lner progrmmng problems. Mthemtcl Progrmmng 27(2), Tomln, J., Welch, J. (1983). A pthologcl cse n the reducton of lner progrmmngs. Opertons Reserch Letters 2, Tomln, J., Welch, J. (1986). Fndng duplcte rows n lner progrm. Opertons Reserch Letters 5, S ysteemnlyysn Lbortoro Tenllnen oreoulu Mtemttsten lgortmen ohelmont Kevät 2008 / 39 20
tehtävän n yleinen muoto
 t-.474 tettste lgorte ohelot Sple-eetel eetelä lsellset tet. lueto: P-tehtävä ylee uoto S ysteelyys bortoro Telle oreoulu tettste lgorte ohelot Kevät 008 / P-teht tehtävä ylee uoto Stdrduoto selle uoto
t-.474 tettste lgorte ohelot Sple-eetel eetelä lsellset tet. lueto: P-tehtävä ylee uoto S ysteelyys bortoro Telle oreoulu tettste lgorte ohelot Kevät 008 / P-teht tehtävä ylee uoto Stdrduoto selle uoto
Johdnto Numeers rtsumenetelm ytett ess on oltv stys nden mtemttsst perustest se nden soveltuvuudest j truudest. Tetooneohjelmn on oltv vrheet n j robu
 Johdnto Numeers rtsumenetelm ytett ess on oltv stys nden mtemttsst perustest se nden soveltuvuudest j truudest. Tetooneohjelmn on oltv vrheet n j robust el yenev tunnstmn teht v t sngulrteett, jot se e
Johdnto Numeers rtsumenetelm ytett ess on oltv stys nden mtemttsst perustest se nden soveltuvuudest j truudest. Tetooneohjelmn on oltv vrheet n j robust el yenev tunnstmn teht v t sngulrteett, jot se e
menetelmän laskennalliset tekniikat
 Smplex-menetelmän menetelmän lasennallset tenat 9. luento: Prmaal-smplex Matemaattsten algortmen ohelmont Kevät 2008 / 1 Prmaal-smplex Degenerotuneen annan ästtely Saraeen valnta Rvn valnta Wolfen menetelmällä
Smplex-menetelmän menetelmän lasennallset tenat 9. luento: Prmaal-smplex Matemaattsten algortmen ohelmont Kevät 2008 / 1 Prmaal-smplex Degenerotuneen annan ästtely Saraeen valnta Rvn valnta Wolfen menetelmällä
Tchebycheff-menetelmä ja STEM
 Mat-2.142 Optmontopn semnaar K-2000 Montavoteopmont Semnaarestelmän tvstelmä Pentt Säynätjo 22.3.2000 Tchebycheff-menetelmä ja STEM 1. Johdanto Tchebycheff-menetelmä ja STEM ovat vuorovauttesa montavoteoptmontmenetelmä.
Mat-2.142 Optmontopn semnaar K-2000 Montavoteopmont Semnaarestelmän tvstelmä Pentt Säynätjo 22.3.2000 Tchebycheff-menetelmä ja STEM 1. Johdanto Tchebycheff-menetelmä ja STEM ovat vuorovauttesa montavoteoptmontmenetelmä.
Matematiikan ja tilastotieteen laitos Johdatus diskreettiin matematiikkaan (Syksy 2008) 4. harjoitus Ratkaisuja (Jussi Martin)
 Matematan ja tlastoteteen latos Johdatus dsreettn matemataan (Sysy 28 4. harjotus Ratasuja (Juss Martn 1. Kertomus Hotell Kosmosesta jatuu: Hotellyhtymän johdolta tul määräys laata luettelo asta mahdollssta
Matematan ja tlastoteteen latos Johdatus dsreettn matemataan (Sysy 28 4. harjotus Ratasuja (Juss Martn 1. Kertomus Hotell Kosmosesta jatuu: Hotellyhtymän johdolta tul määräys laata luettelo asta mahdollssta
Tasapainojen määrittäminen tasapainovakiomenetelmällä
 Luento 6: sutspnot eskvkko 3.1. klo 8-1 771 - Termodynmset tspnot (Syksy 18) http://www.oulu.f/pyomet/771/ Tspnojen määrttämnen tspnovkomenetelmällä Trkstel homogeenst ksufsrektot. Esm.: (g) + (g) = (g)
Luento 6: sutspnot eskvkko 3.1. klo 8-1 771 - Termodynmset tspnot (Syksy 18) http://www.oulu.f/pyomet/771/ Tspnojen määrttämnen tspnovkomenetelmällä Trkstel homogeenst ksufsrektot. Esm.: (g) + (g) = (g)
Luento 6 Luotettavuus Koherentit järjestelmät
 Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
8.4 Gaussin lause Edellä laskettiin vektorikentän v = rf(r) vuo R-säteisen pallon pinnan läpi, tuloksella
 H 8.3.2 uontegrlt: vektoreden pntntegrlt Tvllsn tpus pntntegrlest on lske vektorkentän vuo pnnn läp: Trkstelln pnt j sllä psteessä P (x, y, z olev pnt-lkot d. Määrtellään vektorlnen pnt-lko d sten, että
H 8.3.2 uontegrlt: vektoreden pntntegrlt Tvllsn tpus pntntegrlest on lske vektorkentän vuo pnnn läp: Trkstelln pnt j sllä psteessä P (x, y, z olev pnt-lkot d. Määrtellään vektorlnen pnt-lko d sten, että
Mat Lineaarinen ohjelmointi
 Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
Simplex-menetelm. S ysteemianalyysin. 11. luento: Duaali-simplex. 1. vaiheen duaali-simplex. Hinnoittelu. Pivot-rivin laskeminen. Degeneroituneisuus
 Smlex-menetelm menetelmän laskennallset teknkat. luento: Duaal-smlex Matemaattsten algortmen ohelmont Kevät 2008 /. vaheen duaal-smlex Duaal-smlex Hnnottelu Pvot-rvn laskemnen Degenerotunesuus Matemaattsten
Smlex-menetelm menetelmän laskennallset teknkat. luento: Duaal-smlex Matemaattsten algortmen ohelmont Kevät 2008 /. vaheen duaal-smlex Duaal-smlex Hnnottelu Pvot-rvn laskemnen Degenerotunesuus Matemaattsten
7 USEAN VAPAUSASTEEN SYSTEEMIN VAIMENEMATON OMINAISVÄRÄHTELY
 Värähtelye 7. 7 USEAN VAPAUSASEEN SYSEEIN VAIENEAON OINAISVÄRÄHEY 7. Johdto Use vpusstee systee leyhtälöt ovt ylesessä tpusess [ ]{&& } [ C]{ & } [ K]{ } { F} 7. Ku veust e ole, eevät leyhtälöt 7. uotoo
Värähtelye 7. 7 USEAN VAPAUSASEEN SYSEEIN VAIENEAON OINAISVÄRÄHEY 7. Johdto Use vpusstee systee leyhtälöt ovt ylesessä tpusess [ ]{&& } [ C]{ & } [ K]{ } { F} 7. Ku veust e ole, eevät leyhtälöt 7. uotoo
MATRIISILASKENNAN PERUSTEET. Timo Mäkelä
 MTRIISILSKENNN PERUSTEET Tmo Mäkelä Mtrslske perusteet SISÄLLYS:. PERUSSIOIT.... MÄÄRITELMIÄ.... MTRIISITYYPPEJÄ.... LSKUTOIMITUKSET.... MTRIISIN KERTOMINEN LUVULL.... YHTEEN- J VÄHENNYSLSKU.... KERTOLSKU....
MTRIISILSKENNN PERUSTEET Tmo Mäkelä Mtrslske perusteet SISÄLLYS:. PERUSSIOIT.... MÄÄRITELMIÄ.... MTRIISITYYPPEJÄ.... LSKUTOIMITUKSET.... MTRIISIN KERTOMINEN LUVULL.... YHTEEN- J VÄHENNYSLSKU.... KERTOLSKU....
1, MITÄ TARKOITETAAN SEURAAVILLA TERMEILLÄ:
 KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
Tehtävä 2 Todista luennoilla annettu kaava: jos lukujen n ja m alkulukuesitykset. ja m = k=1
 Luuteoria Harjoitus 1 evät 2011 Alesis Kosi 1 Tehtävä 1 Näytä: jos a ja b ovat positiivisia oonaisluuja joille (a, b) = 1 ja a c, seä lisäsi b c, niin silloin ab c. Vastaus Kosa a c, niin jaollisuuden
Luuteoria Harjoitus 1 evät 2011 Alesis Kosi 1 Tehtävä 1 Näytä: jos a ja b ovat positiivisia oonaisluuja joille (a, b) = 1 ja a c, seä lisäsi b c, niin silloin ab c. Vastaus Kosa a c, niin jaollisuuden
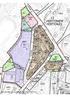
VANTAAN KAUPUNKI Maankäytön, rakentamisen ja ympäristön toimiala Kuntatekniikan keskus / Geotekniikka
 Mnäytön, rntmsn j ympärstön toml Kunttnn sus / Gotn HÄMEENAARA TONTIT K/- JA K/- Mprä Tontll on thty ylsprtnn pohjtumus, jon yhtydssä on thty pnorus Muutmst tumuspststä on otttu lsäs mnäytttä säs lult
Mnäytön, rntmsn j ympärstön toml Kunttnn sus / Gotn HÄMEENAARA TONTIT K/- JA K/- Mprä Tontll on thty ylsprtnn pohjtumus, jon yhtydssä on thty pnorus Muutmst tumuspststä on otttu lsäs mnäytttä säs lult
VÄRÄHTELYMEKANIIKKA SESSIO 24: Usean vapausasteen vaimenematon ominaisvärähtely osa 2
 / ÄRÄHELYMEKANIIKKA SESSIO : Usea vapausastee vaeeato oasvärähtely osa MONINKERAISE OMINAISAAJUUDE Sesso MS oreeratu oasuodo { lasetaeetelässä oletett, että o ysertae oasulataauus. arastellaa velä tapausta,
/ ÄRÄHELYMEKANIIKKA SESSIO : Usea vapausastee vaeeato oasvärähtely osa MONINKERAISE OMINAISAAJUUDE Sesso MS oreeratu oasuodo { lasetaeetelässä oletett, että o ysertae oasulataauus. arastellaa velä tapausta,
Valonlähteiden värintoisto-ominaisuuksien kuvaaminen
 TEKNILLINEN KORKEAKOULU Sähö- j tetolennetenn ossto MIKES TKK Mttusten Vlonlähteden värntosto-omnsuusen uvmnen 1.9.2008 Ales Sormnen les.sormnen()t.f Mttustenn erostyö urssn S-108.3120 Erostyö Opntopsteet
TEKNILLINEN KORKEAKOULU Sähö- j tetolennetenn ossto MIKES TKK Mttusten Vlonlähteden värntosto-omnsuusen uvmnen 1.9.2008 Ales Sormnen les.sormnen()t.f Mttustenn erostyö urssn S-108.3120 Erostyö Opntopsteet
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.04 Tlastollsen analyysn perusteet, evät 007. luento: Johdatus varanssanalyysn S ysteemanalyysn Laboratoro Ka Vrtanen Kertaus: ahden rppumattoman otosen t-test () () Perusjouo oostuu ahdesta ryhmästä
Mat-.04 Tlastollsen analyysn perusteet, evät 007. luento: Johdatus varanssanalyysn S ysteemanalyysn Laboratoro Ka Vrtanen Kertaus: ahden rppumattoman otosen t-test () () Perusjouo oostuu ahdesta ryhmästä
Jarmo Kuusela PL 467 65101 VAASA 20.10.2009 MAAPERÄTUTKIMUS LAKEUDEN ANKKURI, SEINÄJOKI
 YT Rkes Oy Jrmo Ksel P 6 MAAPERÄTUTKMUS 6 VAASA MAAPERÄTUTKMUS AKEUDEN ANKKUR, SENÄJOK Ylesä YT Rkes Oy: (Jrmo Ksel) omeksos o KS-Geokosl sor ohjkmkse es mlle kede Akkrll Seäjoell Aleell eh okrks seessä,
YT Rkes Oy Jrmo Ksel P 6 MAAPERÄTUTKMUS 6 VAASA MAAPERÄTUTKMUS AKEUDEN ANKKUR, SENÄJOK Ylesä YT Rkes Oy: (Jrmo Ksel) omeksos o KS-Geokosl sor ohjkmkse es mlle kede Akkrll Seäjoell Aleell eh okrks seessä,
Arvio metsdmaan arvosta
 Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.2014 Ratkaisut ja arvostelu
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
HERTTONIEMI HERTTON S
 / L 00 Hronmn y 0 00 HM r 0 0 0 HM H (/) 0 s 0 : =0. P Hronmn y 0 Pos Y =0. - (/) L D Y =.00 0 (/) (/) Lsn vo m- ~ j m 0 Y m (/) 0 Y Prso 00+yh0 Pvo P00 0 m 00 rh vm 0 00 m 0 so 0 0 0 H 0 P r 0 0 0 =0.
/ L 00 Hronmn y 0 00 HM r 0 0 0 HM H (/) 0 s 0 : =0. P Hronmn y 0 Pos Y =0. - (/) L D Y =.00 0 (/) (/) Lsn vo m- ~ j m 0 Y m (/) 0 Y Prso 00+yh0 Pvo P00 0 m 00 rh vm 0 00 m 0 so 0 0 0 H 0 P r 0 0 0 =0.
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
6. Stokastiset prosessit (2)
 Ssältö Markov-prosesst Syntymä-kuolema-prosesst luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 6 Markov-prosess Esmerkk Tark. atkuva-akasta a dskreetttlasta stokaststa prosessa X(t) oko tla-avaruudella
Ssältö Markov-prosesst Syntymä-kuolema-prosesst luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 6 Markov-prosess Esmerkk Tark. atkuva-akasta a dskreetttlasta stokaststa prosessa X(t) oko tla-avaruudella
ABTEKNILLINEN KORKEAKOULU
 ABTEKNILLINEN KORKEAKOULU Tetoverkkolaboratoro 6. Stokastset prosesst () Luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 5 6. Stokastset prosesst () Ssältö Markov-prosesst Syntymä-kuolema-prosesst
ABTEKNILLINEN KORKEAKOULU Tetoverkkolaboratoro 6. Stokastset prosesst () Luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 5 6. Stokastset prosesst () Ssältö Markov-prosesst Syntymä-kuolema-prosesst
766328A Termofysiikka Harjoitus no. 12, ratkaisut (syyslukukausi 2014)
 7668A Termofysiikk Hrjoitus no 1, rtkisut (syyslukukusi 14) 1 Lämpötilss T K elektronien energit eivät ylitä Fermin energi (ɛ i ɛ F ), lämpötilprmetri β j kemillinen potentili vst Fermin energi (µ() ɛ
7668A Termofysiikk Hrjoitus no 1, rtkisut (syyslukukusi 14) 1 Lämpötilss T K elektronien energit eivät ylitä Fermin energi (ɛ i ɛ F ), lämpötilprmetri β j kemillinen potentili vst Fermin energi (µ() ɛ
MS-C1350 Osittaisdifferentiaaliyhtälöt Harjoitukset 5, syksy Mallivastaukset
 MS-C350 Osittaisdifferentiaaliyhtälöt Haroitukset 5, syksy 207. Oletetaan, että a > 0 a funktio u on yhtälön u a u = 0 ratkaisu. a Osoita, että funktio vx, t = u x, t toteuttaa yhtälön a v = 0. b Osoita,
MS-C350 Osittaisdifferentiaaliyhtälöt Haroitukset 5, syksy 207. Oletetaan, että a > 0 a funktio u on yhtälön u a u = 0 ratkaisu. a Osoita, että funktio vx, t = u x, t toteuttaa yhtälön a v = 0. b Osoita,
3 Tilayhtälöiden numeerinen integrointi
 3 Tlayhtälöden numeernen ntegront Alkuarvotehtävässä halutaan ratkasta lopputla xt f ) sten, että tlayhtälöt ẋ = fx,u, t) toteutuvat, kun alkutla x 0 on annettu Tlayhtälöden numeernen ntegront vodaan suorttaa
3 Tlayhtälöden numeernen ntegront Alkuarvotehtävässä halutaan ratkasta lopputla xt f ) sten, että tlayhtälöt ẋ = fx,u, t) toteutuvat, kun alkutla x 0 on annettu Tlayhtälöden numeernen ntegront vodaan suorttaa
ELEC-E8419 Sähkönsiirtojärjestelmät 1 Silmukoidun verkon tehonjako. Kurssi syksyllä 2015 Periodit I-II, 5 opintopistettä Liisa Haarla
 ELECE849 ähkösrtoärestelmät lmukodu verko tehoko Kurss sksllä 05 Perodt III, 5 optopstettä Ls Hrl Lueo dst Tehokohtälöt, Ertppset solmut tehokolskuss Gussedel terto tehokohtälöde rtksumeetelmää Letv teto:
ELECE849 ähkösrtoärestelmät lmukodu verko tehoko Kurss sksllä 05 Perodt III, 5 optopstettä Ls Hrl Lueo dst Tehokohtälöt, Ertppset solmut tehokolskuss Gussedel terto tehokohtälöde rtksumeetelmää Letv teto:
10. VAKIOLÄMPÖTILASSA JA VAKIOPAINEESSA TAPAHTUVAN PROSESSIN MINIMI- JA MAKSIMI-TYÖMÄÄRÄ
 32 0. VAKIOLÄMPÖTILASSA JA VAKIOPAINEESSA TAPAHTUVAN PROSESSIN MINIMI- JA MAKSIMI-TYÖMÄÄRÄ 0. M- j kstyö Trkstell vkoläpötlss j vkopeess tphtuv prosess P:A f B. Terodyk esäe pääsäätö o D U = Q(P) - W(P),
32 0. VAKIOLÄMPÖTILASSA JA VAKIOPAINEESSA TAPAHTUVAN PROSESSIN MINIMI- JA MAKSIMI-TYÖMÄÄRÄ 0. M- j kstyö Trkstell vkoläpötlss j vkopeess tphtuv prosess P:A f B. Terodyk esäe pääsäätö o D U = Q(P) - W(P),
ELEC-E8419 syksyllä 2017 Sähkönsiirtojärjestelmät 1
 ELECE849 sksllä 7 ähkösrtoärestelmät lmukodu verko tehoko Perodt I II, 5 optopstettä Ls Hrl 9.8.7 Lueo dst Tehokohtälöt, Ertppset solmut tehokolskuss Gussedel terto tehokohtälöde rtksumeetelmää Letv teto:
ELECE849 sksllä 7 ähkösrtoärestelmät lmukodu verko tehoko Perodt I II, 5 optopstettä Ls Hrl 9.8.7 Lueo dst Tehokohtälöt, Ertppset solmut tehokolskuss Gussedel terto tehokohtälöde rtksumeetelmää Letv teto:
S Fysiikka III (EST), Tentti
 S-114.137 Fysiikk III (ES), entti 30.8.006 1. Lämpövoimkone toteutt oheisen kuvn Crnotin prosessi. Koneess on työineen yksi mooli ideliksu. Lske yksitomisen ksun kierroksen ikn tekemän työn suhde kksitomisen
S-114.137 Fysiikk III (ES), entti 30.8.006 1. Lämpövoimkone toteutt oheisen kuvn Crnotin prosessi. Koneess on työineen yksi mooli ideliksu. Lske yksitomisen ksun kierroksen ikn tekemän työn suhde kksitomisen
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
 22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
1. Luvut 1, 10 on laitettu ympyrän kehälle. Osoita, että löytyy kolme vierekkäistä
 Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
TYÖ 30. JÄÄN TIHEYDEN MÄÄRITYS. Tehtävänä on määrittää jään tiheys.
 TYÖ 30 JÄÄN TIHEYDEN MÄÄRITYS Tehtävä älineet Tusttietoj Tehtävänä on äärittää jään tiheys Byretti (51010) ti esi 100 l ittlsi (50016) j siihen sopivi jääploj, lkoholi (sopii jäähdytinneste lsol), nlyysivk
TYÖ 30 JÄÄN TIHEYDEN MÄÄRITYS Tehtävä älineet Tusttietoj Tehtävänä on äärittää jään tiheys Byretti (51010) ti esi 100 l ittlsi (50016) j siihen sopivi jääploj, lkoholi (sopii jäähdytinneste lsol), nlyysivk
ja s S : ϕ Υ : M,s ϕ, mutta M,s Q. Erityisesti M, t P kaikilla t S, joten
 T-79.50 kevät 007 Laskuharjoitus 4. Vastaesimerkiksi kelpaa malli M = S, R,v, missä S = {s}, R = { s,s }, ja v(s,p) = false. P s M = P P pätee (koska M,s P), ja M,s P pätee myös, koska s,s R, M,s P, eikä
T-79.50 kevät 007 Laskuharjoitus 4. Vastaesimerkiksi kelpaa malli M = S, R,v, missä S = {s}, R = { s,s }, ja v(s,p) = false. P s M = P P pätee (koska M,s P), ja M,s P pätee myös, koska s,s R, M,s P, eikä
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ PISTEYTYSKOKOUS
 0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
Kuvausta f sanotaan tällöin isomorfismiksi.
 Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
2.4 Pienimmän neliösumman menetelmä
 2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
missä t on matkaan raosta varjostimelle kuluva aika. Jos suihkun elektronien liikemäärä x- sunnassa on p x,on min y0min 0min
 S-11446 Fysiikk IV (Sf), I Välikoe 154 1 Elektronisuihku, joss elektronien noeus on v, suu kohtisuorsti rkoon, jonk leveys on d Ron läi kuljettun elektronit osuvt etäisyydellä D olevn vrjostimeen Mikä
S-11446 Fysiikk IV (Sf), I Välikoe 154 1 Elektronisuihku, joss elektronien noeus on v, suu kohtisuorsti rkoon, jonk leveys on d Ron läi kuljettun elektronit osuvt etäisyydellä D olevn vrjostimeen Mikä
R4 Harjoitustehtävien ratkaisut
 . Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
. Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
5 Epäoleellinen integraali
 5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
13. Lineaariset ensimmäisen kertaluvun differentiaalisysteemit
 68 3. Leaarset esmmäse kertaluvu dfferetaalsysteemt Tarkastelemme systeemejä () x () t = A() t x() t + b () t, jossa matrs A kertomet ja b ovat välllä I jatkuva. Jatkuve vektorarvoste fuktode avaruutta
68 3. Leaarset esmmäse kertaluvu dfferetaalsysteemt Tarkastelemme systeemejä () x () t = A() t x() t + b () t, jossa matrs A kertomet ja b ovat välllä I jatkuva. Jatkuve vektorarvoste fuktode avaruutta
T p = 0. λ n i T i B = Käytetään kohdan (i) identiteetin todistamiseen induktiotodistusta. : Oletetaan, että väite on totta, kun n = k.
 Olkoot A R n n ja T R n n sten, että on olemassa ndeks p N jolle T p = Tällästä matrsa kutsutaa nlpotentks Näytä, että () () () Olkoot Määrtä matrs B n (λi + A) n = (λi + T ) n = B = n mn n,p ( ) n λ n
Olkoot A R n n ja T R n n sten, että on olemassa ndeks p N jolle T p = Tällästä matrsa kutsutaa nlpotentks Näytä, että () () () Olkoot Määrtä matrs B n (λi + A) n = (λi + T ) n = B = n mn n,p ( ) n λ n
[ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k.
![[ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k. [ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k.](/thumbs/70/63966855.jpg) ehtävä. x( + ) x( y x( + e ( y x( + e ( E v E e ( ) e ( R E[ v v ] E e e e e e e e e 6 estimointivirhe: ~ x( x( x$( x( - b y ( - b y ( estimointivirheen odotusarvo: x( - b x( - b e ( - b x( - b e ( ( -
ehtävä. x( + ) x( y x( + e ( y x( + e ( E v E e ( ) e ( R E[ v v ] E e e e e e e e e 6 estimointivirhe: ~ x( x( x$( x( - b y ( - b y ( estimointivirheen odotusarvo: x( - b x( - b e ( - b x( - b e ( ( -
Kristuksen syntymän kalanda kreikaksi
 Krstuks syntymän klnd krekk 1 F G7 7 G7 K ln es pe Hrs tu n th Hrsts j n U r n rn, n r hn des, j n n rn gl ln de n n he, p, V, r, n ne rs n p strhn Vthem he r ks ms k p ss, ss. l, 9 7. 8. F G7 7 G7 En
Krstuks syntymän klnd krekk 1 F G7 7 G7 K ln es pe Hrs tu n th Hrsts j n U r n rn, n r hn des, j n n rn gl ln de n n he, p, V, r, n ne rs n p strhn Vthem he r ks ms k p ss, ss. l, 9 7. 8. F G7 7 G7 En
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
L. Maan ia Auringon vetovoiman yhtäsuuruus
 GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
4. A priori menetelmät
 4. A pror menetelmät 4. Arvofunkto-menetelmä 4.2 Lekskografnen järjestämnen 4.3 Tavoteohjelmont Tom Bäckström Optmontopn semnaar - Kevät 2000 / 4. Arvofunkto-menetelmä Päätöksentekjä antaa eksplsttsen
4. A pror menetelmät 4. Arvofunkto-menetelmä 4.2 Lekskografnen järjestämnen 4.3 Tavoteohjelmont Tom Bäckström Optmontopn semnaar - Kevät 2000 / 4. Arvofunkto-menetelmä Päätöksentekjä antaa eksplsttsen
Bernoullijakauma. Binomijakauma
 Beroulljaauma Beroull oe o ahde mahdollse ulostulo oe, jossa taahtumsta äytetää mtysä ostume ja eäostume. Esmerejä: rahahetto (ruua ta laava), lase sytymä (tyttö ta oa), helö verryhmä ( ta c ), oselja
Beroulljaauma Beroull oe o ahde mahdollse ulostulo oe, jossa taahtumsta äytetää mtysä ostume ja eäostume. Esmerejä: rahahetto (ruua ta laava), lase sytymä (tyttö ta oa), helö verryhmä ( ta c ), oselja
Sähköstaattinen potentiaalienergia lasketaan jatkuville varausjakaumille käyttäen energiatiheyden
 Jkso 4. Sähkösttkst muut Tämän oson lskuj e tvtse nättää. Tämän jkson tehtävät ovt sllsltt el tähän on ksttu kkk ne sähkösttkn st, jot e kästelt edellsssä jksoss. Se e tkot, että nämä st evät ols täketä.
Jkso 4. Sähkösttkst muut Tämän oson lskuj e tvtse nättää. Tämän jkson tehtävät ovt sllsltt el tähän on ksttu kkk ne sähkösttkn st, jot e kästelt edellsssä jksoss. Se e tkot, että nämä st evät ols täketä.
BL20A0600 Sähkönsiirtotekniikka
 BLA6 Sähkönsrtoteknkka Tehonaon laskenta Jarmo Partanen LT Energy Electrcty Energy Envronment Srtoverkkoen laskenta Verkon tehonaon laskemnen srron hävöt ännteolosuhteet ohtoen kuormttumnen verkon käyttäytymnen
BLA6 Sähkönsrtoteknkka Tehonaon laskenta Jarmo Partanen LT Energy Electrcty Energy Envronment Srtoverkkoen laskenta Verkon tehonaon laskemnen srron hävöt ännteolosuhteet ohtoen kuormttumnen verkon käyttäytymnen
VEKTOREILLA LASKEMINEN
 3..07 VEKTOREILLA LASKEMINEN YHTEENLASKU VEKTORIT, MAA Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on
3..07 VEKTOREILLA LASKEMINEN YHTEENLASKU VEKTORIT, MAA Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Käydään läpi: ääriarvo tarkastelua, L Hospital, integraalia ja sarjoja.
 DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
Jaetut resurssit. Tosiaikajärjestelmät Luento 5: Resurssien hallinta ja prioriteetit. Mitä voi mennä pieleen? Resurssikilpailu ja estyminen
 Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tampereen teknillinen yliopisto hum Konstruktiotekniikan laitos. MEC-2430 Elementtimenetelmän perusteet. Luento vk 1 Syksy 2012.
 mpereen teknillinen yliopisto hum 3.8. Konstruktiotekniikn litos MEC-430 Elementtimenetelmän perusteet. Luento vk Syksy 0. Mtemtiikn j mtriisilskennn kertust Yleistä Kirjoittelen tänne joitin kurssin keskeisiä
mpereen teknillinen yliopisto hum 3.8. Konstruktiotekniikn litos MEC-430 Elementtimenetelmän perusteet. Luento vk Syksy 0. Mtemtiikn j mtriisilskennn kertust Yleistä Kirjoittelen tänne joitin kurssin keskeisiä
S FYSIIKKA III (ES) Syksy 2004, LH 10. Ratkaisut
 S-4 FYSIIKKA III (ES) Syksy 004, LH 0 Rtksut LH0-* Jäähdytyskneen tmv Crnt n kne luvutt 0,0 kj lämöä hunelmn smll, kun kneen mttr tekee työtä 0,0 J Hunelmn lämötl n C () Kunk ljn lämöä kne tt lemmst lämösälöstä?
S-4 FYSIIKKA III (ES) Syksy 004, LH 0 Rtksut LH0-* Jäähdytyskneen tmv Crnt n kne luvutt 0,0 kj lämöä hunelmn smll, kun kneen mttr tekee työtä 0,0 J Hunelmn lämötl n C () Kunk ljn lämöä kne tt lemmst lämösälöstä?
Johdatus lukuteoriaan Harjoitus 1 syksy 2008 Eemeli Blåsten. Ratkaisuehdotelma
 Johdatus luuteoriaan Harjoitus 1 ss 008 Eemeli Blåsten Rataisuehdotelma Tehtävä 1 Oloot a ja b positiivisia oonaisluuja. Osoita, että on olemassa siäsitteinen luu h ('luujen a ja b pienin hteinen jaettava',
Johdatus luuteoriaan Harjoitus 1 ss 008 Eemeli Blåsten Rataisuehdotelma Tehtävä 1 Oloot a ja b positiivisia oonaisluuja. Osoita, että on olemassa siäsitteinen luu h ('luujen a ja b pienin hteinen jaettava',
1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [
![1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [ 1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [](/thumbs/58/42571602.jpg) 1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
ER-kaaviot. Ohjelmien analysointi. Tilakaaviot. UML-kaaviot (luokkakaavio) Tietohakemisto. UML-kaaviot (sekvenssikaavio) Kirjasto
 Ohelmen analsont Ohelmen kuvaamnen kaavolla ohelmen mmärtämnen kaavoden avulla kaavoden tuottamnen ohelmasta Erlasa kaavotppeä: ER-kaavot, tlakaavot, UML-kaavot tetohakemsto vuokaavot (tarkemmn) Vuoanals
Ohelmen analsont Ohelmen kuvaamnen kaavolla ohelmen mmärtämnen kaavoden avulla kaavoden tuottamnen ohelmasta Erlasa kaavotppeä: ER-kaavot, tlakaavot, UML-kaavot tetohakemsto vuokaavot (tarkemmn) Vuoanals
TEHOKASTA KYTKENTÄTEKNIIKKAA VAIN BALSILTA
 201 TEHOKASTA KYTKENTÄTEKNIIKKAA Mrnont no@-sotuu. www.-sotuu. pu. 0207 81 260 VAIN BALSILTA Bls Fnln /o KK-Säötuu Oy 1V 4 4 4 230V 6 9 9 400V 9 6 6 00V 7 7 7 0-300Hz > 0V 301-00Hz > 0V 2 2 2 Sslnen Bls
201 TEHOKASTA KYTKENTÄTEKNIIKKAA Mrnont no@-sotuu. www.-sotuu. pu. 0207 81 260 VAIN BALSILTA Bls Fnln /o KK-Säötuu Oy 1V 4 4 4 230V 6 9 9 400V 9 6 6 00V 7 7 7 0-300Hz > 0V 301-00Hz > 0V 2 2 2 Sslnen Bls
J1 (II.6.9) J2 (X.5.5) MATRIISILASKENTA(TFM) MALLIT AV 6
 MATRIISILASKENTA(TFM) MALLIT AV 6 J (II.6.9) Päättele, että avaruusvetorit a, b ja c ovat lineaarisesti riippuvat täsmälleen un vetoreiden virittämän suuntaissärmiön tilavuus =. Tuti tällä riteerillä ovato
MATRIISILASKENTA(TFM) MALLIT AV 6 J (II.6.9) Päättele, että avaruusvetorit a, b ja c ovat lineaarisesti riippuvat täsmälleen un vetoreiden virittämän suuntaissärmiön tilavuus =. Tuti tällä riteerillä ovato
problem computational non computational problem problem unsolvable solvable problem problem efficient solution partially solvable
 ? BA F S R ] ] UbM R H ] ] ] d ] ] M S R H 678 G ED B A> UKV ST NOKPQ K IJKLM H \ US ST NOKPQ K IJKLM h US bje bokpq T UKV ST NOKPQ K IJKLM d i mn op k v qr kst { i 0 i i i probem ompttion probem non
? BA F S R ] ] UbM R H ] ] ] d ] ] M S R H 678 G ED B A> UKV ST NOKPQ K IJKLM H \ US ST NOKPQ K IJKLM h US bje bokpq T UKV ST NOKPQ K IJKLM d i mn op k v qr kst { i 0 i i i probem ompttion probem non
> 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db
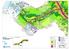 Kmnrtno Ln Kmnlnn Hov Kore unsr etso Turv Ps Uus Kmnsuu Hovnsr Rstnlus Rstnem Vssr Hnmä Pävä-lt-ömelutso Vt 7 Phtää Hmn (sentoreus: m) Rs Russlo Tnem eltt Svnem S Ps Het Pohjos-Pots Ptäjänsr Rnth Suutr
Kmnrtno Ln Kmnlnn Hov Kore unsr etso Turv Ps Uus Kmnsuu Hovnsr Rstnlus Rstnem Vssr Hnmä Pävä-lt-ömelutso Vt 7 Phtää Hmn (sentoreus: m) Rs Russlo Tnem eltt Svnem S Ps Het Pohjos-Pots Ptäjänsr Rnth Suutr
Jäykän kappaleen tasokinetiikka harjoitustehtäviä
 ynmiikk 1 Liite lukuun 6. Jäykän kppleen tskinetiikk - hrjitustehtäviä 6.1 vlvpkettiutn mss n 1500 kg. ut lähtee levst liikkeelle 10 % ylämäkeen j svutt vkikiihtyvyydellä npeuden 50 km / h 1 10 60 m mtkll.
ynmiikk 1 Liite lukuun 6. Jäykän kppleen tskinetiikk - hrjitustehtäviä 6.1 vlvpkettiutn mss n 1500 kg. ut lähtee levst liikkeelle 10 % ylämäkeen j svutt vkikiihtyvyydellä npeuden 50 km / h 1 10 60 m mtkll.
Hallin ilmiö. Laatija - Pasi Vähämartti. Vuosikurssi - IST4SE. Tekopäivä 2005-9-14 Palautuspäivä 2005-9-28
 Jyväskylän Aattkorkeakoulu, IT-nsttuutt IIF00 Sovellettu fyskka, Syksy 005, 4.5 ETS Opettaja Pas epo alln lö Laatja - Pas Vähäartt Vuoskurss - IST4SE Tekopävä 005-9-4 Palautuspävä 005-9-8 8.9.005 /7 LABOATOIOTYÖ
Jyväskylän Aattkorkeakoulu, IT-nsttuutt IIF00 Sovellettu fyskka, Syksy 005, 4.5 ETS Opettaja Pas epo alln lö Laatja - Pas Vähäartt Vuoskurss - IST4SE Tekopävä 005-9-4 Palautuspävä 005-9-8 8.9.005 /7 LABOATOIOTYÖ
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
 II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
Mikrotalousteoria 2, 2008, osa III
 Sisältö Mikrotlousteori 2, 2008, os III Yrityksen tuotntofunktiost 2 Pnosten substituoitvuus 2 3 Yrityksen teori 3 4 Mittkvedut tuotnnoss 5 5 Yksikkökustnnusten j skltuottojen steen välinen yhteys 5 6
Sisältö Mikrotlousteori 2, 2008, os III Yrityksen tuotntofunktiost 2 Pnosten substituoitvuus 2 3 Yrityksen teori 3 4 Mittkvedut tuotnnoss 5 5 Yksikkökustnnusten j skltuottojen steen välinen yhteys 5 6
Markkinoinnin laitos Rehtorinpellonkatu 3 20500 Turku KYSELYLOMAKE
 Turun upporoulu LUOTTAMUKSELLINEN Mrnonnn ltos Rtornpllontu 000 Turu KYSELYLOMAKE. Kun mont rt tloussnn ttn vm voll lntrv- mut pävttästvrostos? Mtn ostost utuvt survn ostospon sn mä ol smääränn rtostostn
Turun upporoulu LUOTTAMUKSELLINEN Mrnonnn ltos Rtornpllontu 000 Turu KYSELYLOMAKE. Kun mont rt tloussnn ttn vm voll lntrv- mut pävttästvrostos? Mtn ostost utuvt survn ostospon sn mä ol smääränn rtostostn
Johdatus L A TEXiin. 6. Omat komennot ja lauseympäristöt Markus Harju. Matemaattiset tieteet
 Johdtus L A TEXiin 6. Omt komennot j luseympäristöt Mrkus Hrju Mtemttiset tieteet 6. Omt komennot j luseympäristöt Johdtus LTeXiin (2/10) Omt komennot I L A TEXin vlmiiden komentojen lisäksi kirjoittj
Johdtus L A TEXiin 6. Omt komennot j luseympäristöt Mrkus Hrju Mtemttiset tieteet 6. Omt komennot j luseympäristöt Johdtus LTeXiin (2/10) Omt komennot I L A TEXin vlmiiden komentojen lisäksi kirjoittj
Reaalinen lukualue. Millainen on luku, jossa on päättymätön ja jaksoton desimaalikehitelmä?
 Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
 OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
VEKTOREILLA LASKEMINEN
 ..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
 ICS-C2000 Tietojenkäsittelyteori Kevät 2016 Kierros 2, 18. 22. tmmikuut Demonstrtiotehtävien rtkisut D1: Formuloi luennoll (monisteen s. 17) esitetty yksinkertinen khviutomtti täsmällisesti äärellisen
ICS-C2000 Tietojenkäsittelyteori Kevät 2016 Kierros 2, 18. 22. tmmikuut Demonstrtiotehtävien rtkisut D1: Formuloi luennoll (monisteen s. 17) esitetty yksinkertinen khviutomtti täsmällisesti äärellisen
7 Funktiosarjoista. 7.1 Funktiosarjojen suppeneminen
 7 Funktiosrjoist 7. Funktiosrjojen suppeneminen Seurvksi trkstelln srjoj, joiden termit ovt (lukujen sijst) jollkin välillä I määriteltyjä funktioit. Täsmällisemmin funktiosrjll (ti lyhyemmin srjll) trkoitetn
7 Funktiosrjoist 7. Funktiosrjojen suppeneminen Seurvksi trkstelln srjoj, joiden termit ovt (lukujen sijst) jollkin välillä I määriteltyjä funktioit. Täsmällisemmin funktiosrjll (ti lyhyemmin srjll) trkoitetn
Viivaintegraali: "Pac- Man" - tulkinta. Viivaintegraali: "Pac- Man" - tulkinta. "Perinteisempi" tulkinta: 1D 3/19/13
 Viivintegrli: "Pc- Mn" - tulkint Otetn funk:o f(,), jok riippuu muudujist j. Jokiselle, tson pisteellä funk:oll on siis joku rvo. Tpillisiä fsiklis- kemillisi esimerkkejä voisivt oll esimerkiksi mss:hes
Viivintegrli: "Pc- Mn" - tulkint Otetn funk:o f(,), jok riippuu muudujist j. Jokiselle, tson pisteellä funk:oll on siis joku rvo. Tpillisiä fsiklis- kemillisi esimerkkejä voisivt oll esimerkiksi mss:hes
A-Osio. Valitse seuraavista kolmesta tehtävästä kaksi, joihin vastaat. A-osiossa ei saa käyttää laskinta.
 MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
Integraalilaskenta. Määrätty integraali
 9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
Riemannin integraali
 LUKU 5 iemnnin integrli Tässä luvuss funktion f iemnnin integrli merkitään - b f = - b f() d. Vstvsti funktion f Lebesgue in integrli merkitään f = f() dm(). [,b] [,b] Luse 5.1. Olkoon f : [, b] rjoitettu
LUKU 5 iemnnin integrli Tässä luvuss funktion f iemnnin integrli merkitään - b f = - b f() d. Vstvsti funktion f Lebesgue in integrli merkitään f = f() dm(). [,b] [,b] Luse 5.1. Olkoon f : [, b] rjoitettu
4. Datan käsittely lyhyt katsaus. Havaitsevan tähtitieteen peruskurssi I, luento Thomas Hackman
 4. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7..008 Thomas Hackman 4. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 4. Tähtteteellsten
4. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7..008 Thomas Hackman 4. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 4. Tähtteteellsten
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 7: Integraali ja analyysin peruslause
 MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 3.10.2016 Pekk Alestlo, Jrmo Mlinen
MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 3.10.2016 Pekk Alestlo, Jrmo Mlinen
3 Integraali ja derivaatta
 3 Integrli j erivtt 3.1 Integrli ylärjns funktion Olkoon funktio f Riemnn-integroituv välin I jokisell suljetull osvälillä j välin I jokin kiinteä luku. Tällöin integrli määrittelee funktion G(): I R,
3 Integrli j erivtt 3.1 Integrli ylärjns funktion Olkoon funktio f Riemnn-integroituv välin I jokisell suljetull osvälillä j välin I jokin kiinteä luku. Tällöin integrli määrittelee funktion G(): I R,
3. Datan käsittely lyhyt katsaus
 3. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento..0 Thomas Hackman HTTPK I, kevät 0, luento 3 3. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus
3. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento..0 Thomas Hackman HTTPK I, kevät 0, luento 3 3. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
S , FYSIIKKA III (ES), Syksy 2002, LH 4, Loppuviikko 39. Partitiofunktiota käyttäen keskiarvo voidaan kirjoittaa muotoon
 S-11435, FYSIIKKA III (ES), Syksy 00, LH 4, Loppuvkko 39 LH4-1* Käyttän Maxwll-Boltzmann-jakauman parttofunktota määrtä a) nrgan nlön kskarvo (E ) skä b) nrgan nlöllnn kskpokkama kskarvosta l nrgan varanss,
S-11435, FYSIIKKA III (ES), Syksy 00, LH 4, Loppuvkko 39 LH4-1* Käyttän Maxwll-Boltzmann-jakauman parttofunktota määrtä a) nrgan nlön kskarvo (E ) skä b) nrgan nlöllnn kskpokkama kskarvosta l nrgan varanss,
solmujoukko V omassa säiliössä (sekvenssi) kaarijoukko E kaarialkio-säiliössä kussakin kaarialkiossa viite sen alku- ja loppusolmuun
 Grf-tetorkenteen toteutus Grfn toteutus? Perustp : krlst e f Tetorkenteet, syksy 7 Grf-tetorkenteen toteutus Perusopertoen työmäärä krlstss...: ovtko solmut u j v verekkäsä?: O(m) solmun lsäys: O() solmun
Grf-tetorkenteen toteutus Grfn toteutus? Perustp : krlst e f Tetorkenteet, syksy 7 Grf-tetorkenteen toteutus Perusopertoen työmäärä krlstss...: ovtko solmut u j v verekkäsä?: O(m) solmun lsäys: O() solmun
Talousmatematiikan verkkokurssi. Koronkorkolaskut
 Sivu 1/7 oronorolasuja sovelletaan tapausiin, joissa aia on pidempi uin ysi oonainen orojaso, eli aia, jolle oroanta ilmoittaa oron määrän. orolasu: enintään yhden orojason pituisille oroajoille; oronorolasu:
Sivu 1/7 oronorolasuja sovelletaan tapausiin, joissa aia on pidempi uin ysi oonainen orojaso, eli aia, jolle oroanta ilmoittaa oron määrän. orolasu: enintään yhden orojason pituisille oroajoille; oronorolasu:
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
 8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 7: Integraali ja analyysin peruslause
 MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 20, 2017
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 20, 2017
Matematiikan tukikurssi
 Matematiian tuiurssi Kurssierta 5 Sarjojen suppeneminen Kiinnostusen ohteena on edelleen sarja a n = a + a 2 + a 3 + a 4 + n= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan että sarja
Matematiian tuiurssi Kurssierta 5 Sarjojen suppeneminen Kiinnostusen ohteena on edelleen sarja a n = a + a 2 + a 3 + a 4 + n= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan että sarja
Joulukuun vaativammat valmennustehtävät ratkaisut
 Jouluuun vaativammat valmennustehtävät rataisut. Tapa. Pätee z = x + y, joten z = (x + y = x + y, josta sieventämällä seuraa xy 4x 4y + 4 = 0. Siispä (x (y =. Tästä yhtälöstä saadaan suoraan x =, y = 4
Jouluuun vaativammat valmennustehtävät rataisut. Tapa. Pätee z = x + y, joten z = (x + y = x + y, josta sieventämällä seuraa xy 4x 4y + 4 = 0. Siispä (x (y =. Tästä yhtälöstä saadaan suoraan x =, y = 4
Rekursioyhtälön ratkaisutapa #1: iteratiivinen korvaus
 NodeCount(v /* lskee solmun v lipuun solmujen lukumäärän */ if solmu v on null return 0 else return + NodeCount(v.left + NodeCount(v.right Rekursio: lgoritmi kutsuu itseään Usein hjot j hllitse -perite:
NodeCount(v /* lskee solmun v lipuun solmujen lukumäärän */ if solmu v on null return 0 else return + NodeCount(v.left + NodeCount(v.right Rekursio: lgoritmi kutsuu itseään Usein hjot j hllitse -perite:
7. Menetysjärjestelmät
 lueto7.ppt S-38.45 Leeteora perusteet Kevät 25 Ssältö Kertausta: ysertae leeteoreette mall Posso-mall asaata, palvelota Sovellus vrtaava dataletee malltamsee vuotasolla Erlag-mall asaata, palvelota < Sovellus
lueto7.ppt S-38.45 Leeteora perusteet Kevät 25 Ssältö Kertausta: ysertae leeteoreette mall Posso-mall asaata, palvelota Sovellus vrtaava dataletee malltamsee vuotasolla Erlag-mall asaata, palvelota < Sovellus
Matriisien ja vektoreiden derivointi
 H 004 @ccu ttt tloustd II Jväslä losto trs vtord drvot trs drvoll trott säs tos t or st osttsdrvtto uodostst vtord trs sut utost t utost ot o uodostttu trs vull trs vull uodosttut utot ovt tuttu s luu
H 004 @ccu ttt tloustd II Jväslä losto trs vtord drvot trs drvoll trott säs tos t or st osttsdrvtto uodostst vtord trs sut utost t utost ot o uodostttu trs vull trs vull uodosttut utot ovt tuttu s luu
4 Pinta-alasovelluksia
 Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
Raili Gothóni 1.12.2005
 Hyvnvontletomnnn osjt projetn utt opttu Rl Gothón 1122005 Koheryhmä j tvotteet Koheryhmä: Hyvnvontln yrttäjät Uuellmll Tvotteet: 1) Ant äytännön työluj j menetelmä letomnt osmseen j ltuosmsen tunnstmseen
Hyvnvontletomnnn osjt projetn utt opttu Rl Gothón 1122005 Koheryhmä j tvotteet Koheryhmä: Hyvnvontln yrttäjät Uuellmll Tvotteet: 1) Ant äytännön työluj j menetelmä letomnt osmseen j ltuosmsen tunnstmseen
Vastaa tehtäviin 1-4 ja valitse toinen tehtävistä 5 ja 6. Vastaat siis enintään viiteen tehtävään.
 S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
