2.1 Satunnaismuuttuja ja sen jakauma
|
|
|
- Emma Nurminen
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 2.1 Satunnaismuuttuja ja sen jakauma Satunnaismuuttuja (lyhenne sm, engl. random variable, rv (joskus myös variate), sv. stokastisk variabel (joskus myös slumpvariabel)) on satunnaiskokeeseen liittyvä numeerinen muuttuja, jonka arvo määräytyy kokeen lopputuloksesta. Satunnaismuuttuja on siis perusjoukolla määritelty (reaaliarvoinen) funktio. Määritelmä 2.1 (Satunnaismuuttuja) Olkoon Ω perusjoukko. Kuvaus X : Ω R on satunnaismuuttuja. Huomautus: selitän tarkennuksen hieman myöhemmin 1 / 105
2 Esimerkkejä satunnaismuuttujista Silmäluku nopanheitossa. Jos alkeistapaus ω {1,..., 6} kertoo nopan silmäluvun, niin on nopan silmäluku. X (ω) = ω Silmälukujen summa kahdessa nopanheitossa. Jos E = {1,..., 6}, perusjoukko Ω = E E, ja alkeistapaukselle (i, j) E E ensimmäinen koordinaatti i kertoo nopan yksi ja toinen koordinaatti j nopan kaksi silmäluvun, niin niiden summa on X ((i, j)) = i + j. 2 / 105
3 Tapahtuman indikaattori (tärkeä esimerkki satunnaismuuttujasta) Määritelmä 2.2 (Tapahtuman indikaattori) Olkoon A Ω tapahtuma. Sen indikaattori (eli ilmaisin eli osoitinmuuttuja) 1 A on satunnaismuuttuja, jonka määrittelee lauseke { 1, jos ω A, 1 A (ω) = 0, muuten. Huomautuksia: Tapahtuman A indikaattorille käytetään yleisesti myös merkintää I A. Jos tapahtuma A esitetään monimutkaisella lausekkeella, niin usein käytetään edellisten sijasta merkintää 1(A), 1{ A } tai I (A). Mainitsen vielä ns. Iversonin sulkeet [ A ] indikaattorin merkintänä. 3 / 105
4 Satunnaismuuttujien laskutoimitukset Usein samalla perusjoukolla on määritelty useampi kuin yksi satunnaismuuttuja, esim. X ja Y. Tällöin voidaan tarkastella myös satunnaismuuttujien välisiä laskutoimituksia, kuten ax (vakiolle a R), X + Y, XY jne. Myös ne ovat satunnaismuuttujia. Esim. X + Y tarkoittaa funktioiden yhteenlaskua, ts. X + Y on se funktio Ω R, jolle (X + Y )(ω) = X (ω) + Y (ω). Ts. satunnaismuuttujien laskutoimitukset tulkitaan pisteittäin. Jos Y ei saa arvoa nolla, niin myös X /Y on sm. 4 / 105
5 Merkintöjä (piilota oomega) Jos X on sm, niin voidaan kysyä, millä todennäköisyydellä se saa arvon joukosta B, jossa B R. Kyseistä tapahtumaa voidaan merkitä {ω Ω : X (ω) B}, mutta sitä merkitään tavallisesti lyhyemmin: {X B}. Sen todennäköisyyttä voidaan merkitä seuraavasti, P(X B) = P{X B} = P({X B}) = P({ω Ω : X (ω) B}). (2.1) Tavallisesti käytetään lyhyitä merkintöjä, joissa ei esiinny perusjoukkoa Ω eikä sisäkkäisiä sulkuja. 5 / 105
6 Lisää merkintöjä tapahtumalle {X B} Huomaa, minkälaisia merkintöjä tapahtumalle {X B} käytetään seuraavissa tilanteissa. B on yksiö {x}, jossa x R. Tällöin kysytään pistetodennäköisyyttä P(X = x) = P({ω Ω : X (ω) = x}). B on väli kuten esim. suljettu väli [a, b], jossa a < b, P(a X b) = P({ω Ω : a X (ω) b}). Vastaavasti määritellään P(a < X b), P(a X < b) ja P(a < X < b). Tapaus B = (, x]. Tällöin merkitään P(X x) = P({ω Ω : X (ω) x}). 6 / 105
7 Jakauma Määritelmä 2.3 (Satunnaismuuttujan jakauma) Jos X on satunnaismuuttuja, niin sen jakauma (engl. distribution, sv. fördelning) on B P(X B) eli tn P(X B) ymmärrettynä argumentin B R funktiona. Huomautus: Itse asiassa tn P(X B) on määritelty vain tietyille B R. Sopivia joukkoja B ovat ns. Borelin joukot, jollaisia ovat esim. kaikki välit ja kaikki joukot, jotka voidaan muodostaa numeroituvasta määrästä välejä soveltamalla numeroituva määrä joukko-operaatiota. Tästä lähtien jätämme tämän seikan vaille huomiota. 7 / 105
8 Satunnaismuuttujan tarkka määritelmä Koska raotimme Pandoran laatikkoa, niin jatkamme huomautusta: Määritelmä (Satunnaismuuttuja tarkasti) Olkoon Ω perusjoukko. Kuvaus X : Ω R on satunnaismuuttuja, kunhan { X (a, b) } on tapahtuma jokaisella välillä (a, b). Huomautus: voimme kuvitella, että perusjoukon osajoukot ovat kaikki tapahtumia, joten tällä ei juurikaan ole vaikutusta. 8 / 105
9 Definition of random variable Määritelmä (Random variable) Let Ω be a sample space. The mapping X : Ω R is a random variable, provided { X (a, b) } is an event for every interval (a, b). 9 / 105
10 Huomautuksia jakaumasta On mahdollista osoittaa, että sm:n X jakauma P X (B) = P(X B), B R toteuttaa todennäköisyyden aksioomat, joten jakauma on joukossa R määritelty tn-mitta. Perusjoukko Ω häviää usein kokonaan merkinnöistä. Tilanne voidaan mieltää myös siten, että perusjoukkona onkin R ja että tapahtumat ovat sen osajoukkoja. Jakauma on hyvin abstrakti olio. Seuraavaksi tarkastelemme konkreettisempia välineitä, joiden avulla voimme kuvailla ja hallita jakaumia: kertymäfunktio, diskreetin jakauman pistetodennäköisyysfunktio ja jatkuvan jakauman tiheysfunktio. 10 / 105
11 2.2 Kertymäfunktio Määritelmä 2.4 Jos X on satunnaismuuttuja, niin funktio F : R R F (x) = P(X x), x R on X :n kertymäfunktio (lyhenne kf). Huomautus: Englanniksi (ja ruotsiksi) jakauma on (probability) distribution (joskus law), kertymäfunktio on distribution function tai cumulative distribution function, cdf (sv. kumulativ fördelningsfunktion). 11 / 105
12 2.2 Cumulative distribution function Defintion (Määritelmä 2.4) If X is a random variable, the function F : R R F (x) = P(X x), x R is the cumulative distribution function of X (abbr. cdf). 12 / 105
13 Tapahtuman indikaattorin kertymäfunktio Olkoon A tapahtuma, ja olkoon X = 1 A, eli X on tapahtuman A indikaattori. Tällöin X :n kf on 0, jos x < 0, F (x) = 1 P(A), jos 0 x < 1, 1, jos x 1. Tämä kertymäfunktio on paloittain vakio. Huomaa, että kf:lla voi olla hyppyjä ja että se voi olla vakio jollakin välillä. 13 / 105
14 Monotonisen funktion raja-arvot Monotonisella funktiolla G : R R on jokaisessa pisteessä x R olemassa sekä vasemmanpuoleinen että oikeanpuoleinen raja-arvo. Lisäksi sillä on raja-arvo pisteissä ja (mutta äärettömässä raja-arvo voi olla joko jokin reaaliluku, tai jompikumpi äärettömistä tai ). Näitä raja-arvoja merkitään seuraavasti G(x ) = G( ) = lim G(y), G(x+) = lim G(y) y x y x+ lim G(y), y G( ) = lim G(y). y 14 / 105
15 Kertymäfunktion ominaisuudet Lause 2.1 (Kertymäfunktion ominaisuudet) Satunnaismuuttujan X kertymäfunktiolla F : R R on seuraavat ominaisuudet. (a) F on kasvava funktio. (b) F on oikealta jatkuva funktio, eli (c) F ( ) = 0 ja F ( ) = 1. F (x+) = F (x), kaikilla x R. Kääntäen, jos funktiolla F : R R on nämä ominaisuudet, niin on olemassa sm X siten, että F on X :n kf. 15 / 105
16 Properties of distribution function Theorem (Properties of distribution function) The cumulative distribution function F : R R of X satisfies the following properties: (a) F is an increasing function. (b) F is right-continuous, i.e. (c) F ( ) = 0 ja F ( ) = 1. F (x+) = F (x), for every x R. Conversly, if a function F : R R satisfies the above properties, then there is a rv X s.t. F is the cdf of X. 16 / 105
17 Sattumistodennäköisyydet väleille Lasketaan tn P(a < X b), jossa a < b. Koska {X b} = {X a} {a < X b}, jossa osat ovat erillisiä, on P(a < X b) = F (b) F (a). Seuraavan lauseen jälkeen pystymme toistamaan vastaavan laskun myös väleille (a, b), [a, b) ja [a, b]. Lause 2.2 Jos F on sm:n X kf, niin kaikilla x P(X < x) = F (x ). 17 / 105
18 Kertymäfunktion hypyt Kertymäfunktiolla voi olla hyppyjä. Koska jossa osat ovat erillisiä, niin {X x} = {X < x} {X = x}, P(X = x) = P(X x) P(X < x) = F (x) F (x ). Pistetodennäköisyys P(X = x) on yhtä kuin kertymäfunktion hyppy pisteessä x. 18 / 105
19 Satunnaismuuttuja voidaan ilmoittaa funktion alaindeksillä Voidaan tarkastella useampaa kuin yhtä satunnaismuuttujaa, vaikkapa X ja Y. Tällöin usein käytetään sellaista merkintätapaa, jossa satunnaismuuttuja kirjoitetaan kertymäfunktion alaindeksiksi: esim. F X on X :n kf ja F Y on Y :n kf. Tällaista merkintätapaa voidaan käyttää muidenkin jakauman esitysten kuin kertymäfunktioiden kohdalla. 19 / 105
20 Sama jakauma Määritelmä 2.5 Satunnaismuuttujilla X ja Y on sama jakauma eli ne ovat samoin jakautuneet (engl. identically distributed), jos P(X B) = P(Y B), kaikilla B R. Tämä seikka voidaan ilmaista merkinnällä X d = Y. 20 / 105
21 Kertymäfunktiot ja jakaumat vastaavat toisiaan Seuraava lause toteaa, että kertymäfunktiot ja jakaumat vastaavat toisiaan yksikäsitteisesti. Tämän takia voidaan puhua tietyn jakauman kertymäfunktiosta, eikä aina tarvitse puhua sm:n kertymäfunktiosta. Lause 2.3 (Kertymäfunktio määrää jakauman yksikäsitteisesti) Seuraavat asiat ovat yhtäpitäviä. (a) X ja Y ovat samoin jakautuneet, eli X d = Y. (b) F X = F Y (ts. X :n ja Y :n kertymäfunktiot ovat samat). 21 / 105
22 Distribution function and distribution are in 1-1 correspondence Theorem (2.3. CDF determines the distribution uniquely) The following are equivalent: (a) X are Y identically distributed, i.e. X = d Y. (b) F X = F Y (i.e. the cdfs of X and Y coincide). 22 / 105
23 2.3 Diskreetti jakauma Määritelmä 2.6 Satunnaismuuttujan X jakauma on diskreetti, jos sen arvojoukko {x 1, x 2,... } on äärellinen tai korkeintaan numeroituvasti ääretön. Asia voidaan ilmaista myös jollakin seuraavista tavoista X on diskreetti sm, sm X on diskreetisti jakautunut X :llä on diskreetti jakauma. 23 / 105
24 2.3 Discrete distribution Defintion The distribution of random variable X is discrete, if its range {x 1, x 2,... } is finite or at most countably infinite. 24 / 105
25 Laajennettu määritelmä diskreetille satunnaismuuttujalle Joskus määritelmää laajennetaan: vaaditaan vain, että X saa todennäköisyydellä yksi arvon korkeintaan numeroituvasti äärettömästä joukosta S. Tällöin diskreetti sm X voi saada arvoja joukon S ulkopuolelta, mutta tämän poikkeustapahtuman todennäköisyys on nolla. Yksinkertaisuuden vuoksi kutsumme myös tässä tapauksessa X :n arvojoukoksi jotakin sellaista korkeintaan numeroituvaa joukkoa S, jolle P(X S) = / 105
26 Pistetodennäköisyysfunktio, ptnf Määritelmä 2.7 Satunnaismuuttujan X pistetodennäköisyysfunktio (lyh. ptnf) on funktio f : R R, jolle f (x) = P(X = x), x R. Pistetodennäköisyysfunktio x P(X = x) (engl. probability (mass) function, pmf, sv. sannolikhetsfunktion) on määritelty koko reaaliakselilla kaikenlaisille satunnaismuuttujille X. Käsite on käyttökelpoinen lähinnä vain diskreeteille satunnaismuuttujille. 26 / 105
27 Merkintäsopimuksia Tyypillisesti pistetodennäköisyydet ilmoitetaan vain niille x i, jotka kuuluvat diskreetin sm:n määritelmässä esiintyvään, korkeintaan numeroituvasti äärettömään joukkoon, joka voi esimerkiksi olla jokin kokonaislukujen osajoukko. Tällöin asiayhteydestä pitää ymmärtää, että muilla x R on P(X = x) = 0. Diskreetin satunnaismuuttujan ptnf:lle käytetään muuten samaa symbolia kuin sen kf:lle, mutta ptnf:n symboli kirjoitetaan pienellä kirjaimella (esim. f, g tai f X ) ja kf:n symboli vastaavalla isolla kirjaimella (esim. F, G tai F X ). 27 / 105
28 Diskreetin jakauman ptnf:n ominaisuuksia Lause 2.4 Olkoon X diskreetti sm, f sen ptnf, ja olkoon S sen arvojoukko. Tällöin (a) 0 f (x) 1 kaikilla x, ja f (x) = 0, kun x S. (b) f määrää X :n jakauman kaavalla P(X B) = x B f (x) Huomautus: Kohdassa (b) lasketaan yhteen korkeintaan numeroituva määrä ei-negatiivisia termejä f (x i ), jossa x i S B, minkä takia kyseinen summamerkintä on mielekäs. (Summausjärjestyksellä ei ole väliä.) 28 / 105
29 Properties of pmf of discrete distribution Theorem Let X be a discrete rv, let f be its pmf, and let S be its range. Then (a) 0 f (x) 1 for every x, and f (x) = 0, when x S. (b) f determines the distribution of X with the formula P(X B) = x B f (x) 29 / 105
30 Ptnf:stä diskreetti jakauma Lause 2.5 Olkoon f : R R ei-negatiivinen funktio, joka saa positiivisia arvoja korkeintaan numeroituvassa R:n osajoukossa siten, että f (x) = 1. Tällöin se on jonkin diskreetin satunnaismuuttujan ptnf. x 30 / 105
31 Recognising pmf of discrete distribution Theorem Let f : R R be a non-negative function, that is non-zero on a set that is at most countably infinite subset of R and f (x) = 1. The it is a pmf of some discrete rv. x 31 / 105
32 2.4 Esimerkkejä diskreeteistä jakaumista diskreetti tasajakauma Bernoullin jakauma binomijakauma hypergeometrinen jakauma, negatiivinen binomijakauma, geometrinen jakauma, Poissonin jakauma (luvussa 5). 32 / 105
33 Diskreetti tasajakauma Satunnaismuuttujalla X on diskreetti tasajakauma joukossa {1,..., N}, mikäli sen ptnf on f (x) = 1, kun x = 1, 2,..., N. N Esimerkiksi, jos X on silmäluku nopanheitossa, niin X :llä on diskreetti tasajakauma joukossa 1,..., / 105
34 Bernoullin jakauma Olkoon A on tapahtuma, ja merkitään p = P(A), jolloin 0 p 1. Indikaattorilla X = 1 A on Bernoullin jakauma parametrilla p (eli X noudattaa Bernoullin jakaumaa parametrillä p). Tämä asia voidaan merkitä X Bernoulli(p). Tavallisesti sanotaan, että satunnaiskoe onnistuu silloin, kun X = 1 ja epäonnistuu muuten. Tällöin p:stä käytetään nimeä onnistumistodennäköisyys. 34 / 105
35 Bernoullin jakauman ptnf X :n arvojoukko on {0, 1}, ja sen ptnf on 1 p, kun x = 0, f (x) = f (x p) = p, kun x = 1, 0, muuten. Merkintäsopimus: ptnf:n arvot tarvitsee mainita vain ko. sm:n arvojoukossa, muualla ymmärretään sen olevan nolla. Jakauman Bernoulli(p) ptnf voidaan kirjoittaa lyhyesti f (x p) = p x (1 p) 1 x, kun x = 0, 1, Tässä tulkitaan 0 0 = 1, mikäli p = 0 tai p = / 105
36 Jakaumien merkinnöistä Useimmat mielenkiintoiset jakaumat riippuvat yhden tai useamman parametrin arvosta. Oikeastaan tarkastellaan saman tien perhettä jakaumia. Pitääksemme lukua parametrin arvosta, merkitsemme sen tarvittaessa pystyviivan oikealle puolelle. Tätä merkintää voidaan käyttää kertymäfunktioille, pistetodennäköisyysfunktiolle ynnä muille funktioille. Jos taas sekaantumisen vaaraa ei ole, parametri voidaan jättää pois merkinnöistä. 36 / 105
37 Binomijakauma Olkoon n 1 kokonaisluku ja 0 p 1. Sm X noudattaa binomijakaumaa (engl. binomial distribution, sv. binomialfördelning) parametreilla n ja p, jos sen arvojoukko on {0, 1,..., n} ja ptnf on f (x) = f (x n, p) = ( n x ) p x (1 p) n x, kun x = 0, 1,..., n. Tämä voidaan merkitä X Bin(n, p). Kuva: Binomijakauman Bin(5, 0.6) ptfn ja kf. ptnf kf f(x) F(x) / 105
38 Binomijakauman toistokoetulkinta Binomijakaumaa Bin(n, p) noudattava sm syntyy toistokokeessa, jossa toistetaan riippumattomasti n kertaa sellaista (Bernoullin) koetta, jossa yhdessä kokeessa onnistumistodennäköisyys on p. Jos X on onnistumisten lukumäärä n toistossa, niin X Bin(n, p). Tulos perustellaan myöhemmin. Bernoullin jakauma Bernoulli(p) on tietenkin sama kuin binomijakauma Bin(1, p). 38 / 105
39 2.5 Integraalilaskennan kertausta Matemaattisessa analyysissä on määritelty erilaisia integrointiprosesseja, joista sinulle (tässä vaiheessa opintoja) ainoastaan Riemannin integraali on tuttu. Todennäköisyyslaskennan teoriassa Riemannin integraalin käyttö johtaa tiettyihin asian kannalta epäoleellisiin hankaluuksiin, minkä takia matemaatikot käyttävät sen sijasta yleisempää ns. Lebesguen integraalia. Tämän kurssin puitteissa näiden kahden integraalikäsitteen eroilla ei ole merkitystä, sillä kurssin tehtävät saadaan ratkaistua käyttämällä tuttua (mahdollisesti epäoleellista) Riemannin integraalia. Tämä seuraa siitä, että toimiessaan molemmat integraalikäsitteet ovat aina yhtenevät. 39 / 105
40 Antiderivaatta eli integraalifunktio Määritelmä Olkoon f välillä I määritelty reaalifunktio. Tällöin sanomme, että F on funktion f antiderivaatta eli integraalifunktio, jos F (x) = f (x), kaikilla x I. (2.2) (Välin päätepisteissä derivaatta tässä tarvittaessa määritellään toispuoleisena derivaattana.) Jos F on f :n antiderivaatta ja C on vakio, niin myös F + C on f :n antiderivaatta. Antiderivaattoja on siis monta! Jokaisella suljetulla äärellisellä välillä I = [a, b] määritellyllä jatkuvalla funktiolla f on olemassa antiderivatta välillä I. 40 / 105
41 Riemannin integraalin määritelmästä Funktion f Riemannin interaali välin [a, b] yli määritellään eräänlaisena summien raja-arvona, mikäli ko. raja-arvo on olemassa. Tällöin sanotaan, että f on Riemann-integroituva välin [a, b] yli. Määritelmä toimii ainoastaan äärellisille integrointiväleille [a, b], ja lisäksi integroitavan funktion eli integrandin f tulee olla rajoitettu integrointivälillä. Integraalien arvoja lasketaan hyvin harvoin suoraan määritelmän perusteella, vaan tämän sijasta integraali tyypillisesti lasketaan antiderivaatan avulla. 41 / 105
42 Integraalin laskeminen antiderivaatan avulla Jos f on äärellisellä välillä [a, b] määritelty jatkuva funktio, niin sen määrätty integraali (engl. definite integral) välin [a, b] yli saadaan laskettua seuraavasti, jos tunnetaan jokin f :n antiderivaatta F : b a f (x) dx = / b a F (x) = F (b) F (a). (2.3) Integrandin muuttaminen äärellisessä määrässä pisteitä ei muuta integraalin arvoa. Jos f on Riemann-integroituva välin [a, b] yli ja g = f kaikkialla muualla paitsi äärellisessä määrässä pisteitä, niin g on Riemann-integroituva, ja b a g(x) dx = b a f (x) dx. (2.4) 42 / 105
43 Osittaisintegrointi Olkoot u ja v välillä [a, b] määriteltyjä jatkuvasti derivoituvia funktioita. Kun otetaan huomioon tulon derivointikaava d dx [u(x) v(x)] = u (x) v(x) + u(x) v (x), saadaan tulos / b a u(x) v(x) = b a (u (x) v(x) + u(x) v (x)) dx, josta järjestelmällä saadaan osittaisintegrointikaava (engl. integration by parts) b a u(x) v (x) dx = / b a b u(x) v(x) u (x) v(x) dx. (2.5) a 43 / 105
44 Sijoitus määrätyssä integraalissa Olkoon f jatkuva funktio välillä I, joka sisältää integrointivälin [a, b], ja olkoon g : [c, d] I jatkuvasti derivoituva funktio siten, että g(c) = a ja g(d) = b. Olkoon F funktion f integraalifunktio. Tällöin b a f (x) dx = / b a F (x) = F (g(d)) F (g(c)) = Toisaalta d dt F (g(t)) = f (g(t)) g (t), kaikilla t [c, d] jota käyttämällä saadaan sijoituskeinon kaava b a f (x) dx = d c c / d F (g(t)). f (g(t)) g (t) dt. (2.6) 44 / 105
45 Sijoituskeino formaalisti Formaalisti kaavassa b sijoitetaan integaaliin x = g(t) a dx = g (t) dt. f (x) dx = d c f (g(t)) g (t) dt. Lisäksi alkuperäiset x-rajat (a, b) vaihdetaan vastaaviksi t-rajoiksi (c, d), joille a = g(c) ja b = g(d). 45 / 105
46 Sijoituskeinon käyttämisestä Sijoituskaava b a f (x) dx = d c f (g(t)) g (t) dt on yhtälö, joten sitä voi käyttää kumpaan suuntaan tahansa; usein käytetään oikealta vasemmalle. Ideana on tunnistaa monimutkaisesta integroitavasta lausekkeesta jokin osalauseke g(t), jonka merkitseminen uudeksi muuttujaksi u yksinkertaistaa lauseketta. Vaikeutena on, että jostain pitää löytyä (tekijänä) kyseisen osalausekkeen derivaatta g (t). Aina voi kokeilla monenlaisia sijoituksia, mutta vaatii taitoa ja kokemusta löytää toimiva sijoitus joka todella yksinkertaistaa integraalin johonkin helpompaan muotoon. 46 / 105
47 Sijoituskeino: Helppo esimerkki Muistetaan, että sin x dx = cos x + C. Yritetään laskea π/2 0 (sin 2x) dx. π/2 0 Toimisiko sijoitus u = g(x) = 2x? Nyt du = g (x)dx = 2 dx. Vakiotekijä 2 on helppo järjestää. (sin 2x) dx = 1 2 = 1 2 x=π/2 x=0 u=π u=0 (sin 2x) 2 dx (sin u) du = 1 ( cos π + cos 0) = 1. 2 Huomaa integrointirajat! Havainnollisuuden vuoksi tässä on merkitty, minkä muuttujan rajoista on kysymys. Piirrä kuva! 47 / 105
48 Sijoituskeino: Muita esimerkkejä Samankaltainen vakiotekijän eliminointi tulee kohta vastaan ns. eksponenttijakauman tiheysfunktion integraalissa, joka on muotoa λe λx dx. Tämä sujuu helposti sijoituksella u = λx. Entäpä jos integraali onkin tällainen? 0 x e x2 dx Integraali sievenee huomattavasti sijoituksella u = x 2. Huomaa differentiaali du = 2x dx, johon tarvittava derivaatta 2x onnekkaasti löytyy integroitavasta (paitsi vakiotekijää 2, joka ei tuota ongelmia). 48 / 105
49 Mitä ehtoja tarvitaan, kun integraali lasketaan antiderivaatan avulla? Kaavan (2.3) kohdalla vaadittiin, että integrandin f tulee olla jatkuva funktio kyseessä olevalla äärellisellä suljetulla välillä ennen kuin integraalin saa laskettua antiderivaatan F avulla. Jos f on muuten jatkuva, mutta sillä on hyppy pisteessä a < c < b, niin tällöin integrointialue voidaan pilkkoa jakopisteellä c väleihin [a, c] ja [c, b] ja yrittää laskea integraali summana b a f (x) dx = c a b f (x) dx + f (x) dx. c Suotuisassa tapauksessa kumpikin integraaleista saadaan laskettua antiderivaatan avulla. 49 / 105
50 Milloin tarvitaan epäoleellista integraalia? Jos (a) integrointivälin päätepiste on äärettömyydessä tai jos (b) funktio f kasvaa rajatta integrointivälin päätepisteessä, niin Riemannin integraalin perusmääritelmä ei tuota mitään tulosta. Tällöin integraali joudutaan laskemaan ns. epäoleellisena (engl. improper) integraalina. Tämä tarkoittaa käytännössä raja-arvon laskemista sellaisesta integraalista, jossa ongelmallinen päätepiste on korvattu hyvin käyttäytyvällä pisteellä, jonka sitten annetaan lähestyä alkuperäistä ongelmallista päätepistettä. 50 / 105
51 Esimerkki, jossa integrandi kasvaa rajatta Laskemme integraalin 1 0 x a dx, jossa 0 < a < 1. Tämä integraali on epäoleellinen, sillä funktio x a kasvaa rajatta, kun x 0+. Jos ɛ > 0, niin integraali välin [ɛ, 1] yli saadaan laskettua antiderivaatan avulla, sillä 1 ɛ x a dx = / 1 ɛ x a+1 a + 1 = 1 1 a ɛ1 a 1 a. Tässä ɛ 1 a 0, kun ɛ 0+ sen takia, että 1 a > 0. Koska raja-arvo on olemassa, niin alkuperäinen integraali saadaan laskettua epäoleellisena integraalina, ja 1 0 x a dx = lim ɛ 0+ 1 ɛ x a dx = 1 1 a. 51 / 105
52 Esimerkki, jossa toinen integrointiraja on äärettömyydessä Laskemme integraalin 1 x a dx, kun a > 1. Integraali on epäoleellinen sen takia, että ylempi päätepiste on ääretön. 1 x a dx = M lim x a dx = M 1 = lim M lim M 1 M/ ( M1 a a a 1 x 1 a a 1 ) = 1 a 1. Lausekkeessa M 1 a potenssi on negatiivinen, joten tämä lauseke lähestyy nollaa, kun M. 52 / 105
53 2.6 Jatkuva jakauma Määritelmä 2.8 (Jatkuva jakauma, tiheysfunktio) Satunnaismuuttujalla X on jatkuva jakauma tiheysfunktiolla f (lyh. tf), jos f on ei-negatiivinen ja jos kaikilla a < b P(a X b) = b a f (x) dx Tiheysfunktio on englanniksi (probability) density function, pdf (sv. täthetsfunktion). Toisinaan puhutaan tiheysfunktion sijasta lyhyesti tiheydestä. Sen sijaan, että sanotaan että sm:lla X on jatkuva jakauma voidaan sanoa että X :n jakauma on jatkuva, X on jatkuvasti jakautunut, X on jatkuva satunnaismuuttuja. 53 / 105
54 Merkintäsopimuksia Jatkuvan jakauman tiheysfunktiolle käytetään muuten samaa symbolia kuin sen kf:lle, mutta tiheysfunktion symboli kirjoitetaan pienellä kirjaimella (esim. f, g tai f X ) ja kf:n symboli vastaavalla isolla kirjaimella (esim. F, G tai F X ). Joskus tiheysfunktio häviää jonkin joukon B R ulkopuolella. Tällöin tiheysfunktion kaava voidaan ilmoittaa vain joukossa B, ja asiayhteydestä pitää ymmärtää, että f (x) = 0, kun x B. 54 / 105
55 Mikä integraalikäsite? Jatkuvan jakauman määritelmässä esiintyvä integraali tarkoittaa itseasiassa Lebesguen integraalia, mutta sovelluksissa esiintyvät tiheysfunktiot ovat jatkuvia funktioita kaikkialla muualla paitsi äärellisessä määrässä pisteitä, ja niiden integraalit voidaan käytännössä laskea Riemannin integraalien avulla. Integrointialue ei välttämättä ole äärellinen väli. Tiheysfunktio voi olla yhdessä tai useammassa pisteessä singulaarinen siten, että ainakin toinen sen toispuoleisista raja-arvoista on ääretön. Integrointialue joudutaan usein ensin pilkkomaan paloihin, minkä jälkeen tiheysfunktion integraali saadaan palautettua summaksi (mahdollisesti epäoleellisia) Riemannin integraaleja. 55 / 105
56 Tiheysfunktion (epä)yksikäsitteisyydestä Jakauman tiheysfunktio ei ole yksikäsitteinen, mutta melkein yksikäsitteinen. Jos f on tietyn jakauman tf ja g on yhtä kuin f muualla paitsi äärellisessä määrässä pisteitä, niin b a f (x) dx = b a g(x) dx kaikilla a < b. Tämän takia myös g on kyseisen jakauman tf. Ei-negatiiviset funktiot f ja g ovat saman jakauman tiheysfunktioita, jos ja vain jos ne yhtyvät melkein kaikkialla, eli joukko jossa f g on nollamittainen (mikä käsite määritellään reaalianalyysin kursseilla). 56 / 105
57 Välien sattumistodennäköisyydet Jos X :n jakauma on jatkuva ja sen tf on f, niin P(X = x) = P(x X x) = x x f (u) du = 0 kaikilla x, joten pistetodennäköisyys on aina nolla. Ptnf ei ole hyödyllinen käsite jatkuville jakaumille. Koska kaikki pistetodennäköisyydet ovat nollia, niin P(a < X < b) = P(a X < b) = P(a < X b) = P(a X b) = kun a < b. b a f (x) dx, 57 / 105
58 Toinen tapa karakterisoida jatkuva jakauma Rajankäynnin jälkeen huomataan, että puoliäärettömien välien todennäköisyydet saadaan myöskin tf:a integroimalla. Esim. Itse asiassa pätee P(X B) = P(X x) = P(X < x) = B x f (u) du. f (x) dx, kaikille B R, (2.7) jossa integraalin alaindeksi B tarkoittaa joukon B yli laskettua integraalia, ts. f (x) dx = 1 B (x) f (x) dx. B 58 / 105
59 Kertymäfunktion ja tiheysfunktion yhteys Lause 2.6 (Kertymäfunktion ja tiheysfunktion yhteys) Olkoon X :llä jatkuva jakauma. (a) Jos X :n tiheysfunktio on f, niin sen kertymäfunktio F on F (x) = x f (u) du. (b) Jos X :n kertymäfunktio on F, niin F on derivoituva melkein kaikkialla, ja X :n tiheysfunktioksi voidaan valita F. Huomautus: Kun sanotaan, että tiheysfunktioksi voidaan valita f = F, niin tarkoitetaan sitä, että tiheysfunktioksi valitaan jokin funktio f, joka yhtyy funktion F derivaattaan niissä pisteissä, joissa derivaatta on määritelty, ja muissa pisteissä f saadaan määritellä mielivaltaisesti. 59 / 105
60 Eräs tapa tunnistaa kertymäfunktiosta, että jakauma on jatkuva Lause 2.7 Olkoon F sellainen kertymäfunktio, että (1) F on jatkuva koko reaaliakselilla, (2) F on derivoituva kaikkialla muualla paitsi mahdollisesti äärellisessä määrässä pisteitä, (3) ja lisäksi derivaatta f = F on jatkuva kaikkialla muualla paitsi mahdollisesti äärellisessä määrässä pisteitä. Tällöin F on jatkuvan jakauman kertymäfunktio, ja jakauman tiheysfunktioksi voidaan valita sen derivaatta f = F. 60 / 105
61 Todistuksen perusidea Jos [a, b] on sellainen äärellinen väli, joka ei sisällä yhtään pistettä, jossa F :n derivaatta ei ole jatkuva, niin F (b) F (a) = b a F (u) du. Lisäksi otetaan raja-arvoja ja käytetään kertymäfunktion ominaisuuksia. 61 / 105
62 Huomautuksia Jos X :llä on jatkuva jakauma, niin sen kf on jatkuva. Sen sijaan tf voi olla hyvin epäsäännöllinen funktio. Tilastollisissa sovelluksissa esiintyvät tiheysfunktiot ovat varsin säännöllisiä funktioita, sillä ne ovat jatkuvia kaikkialla paitsi äärellisessä määrässä pisteitä. Tf:n ei tarvitse olla rajoitettu funktio. Täydellinen karakterisointi: kf F on jatkuvan jakauman kf täsmälleen silloin, kuin F on absoluuttisesti jatkuva, mutta tämän asian määritteleminen jätetään reaalianalyysin kurssien huoleksi. Täsmällisempi nimitys jatkuvalle jakaumalle olisi absoluuttisesti jatkuva jakauma. 62 / 105
63 Kuinka tunnistan, että funktio on tiheysfunktio? Jos X :llä on tiheys f, niin 1 = P(Ω) = P(X R) = f (x) dx, joten tiheysfunktion integraali koko reaaliakselin yli on yksi. Lause 2.8 Jos f : R R on ei-negatiivinen, ja sen integraali koko reaaliakselin yli on yksi, niin se on jonkin satunnaismuuttujan tiheysfunktio. 63 / 105
64 Normalisoimaton tiheysfunktio Lause 2.9 Jos g 0 on sellainen reaaliakselilla määritelty funktio, jonka integraali g(x) dx on äärellinen ja aidosti positiivinen, niin tällöin on olemassa vakio k siten, että f = k g on tiheysfunktio. Todistus Valitaan 1/k = g(x) dx, jonka jälkeen f (x) dx = k g(x) dx = k k = 1. Huomautus. Tällä tavalla jokainen normalisoimaton tiheysfunktio g määrää yksikäsitteisellä tavalla jatkuvan jakauman, jonka tiheysfunktio on edellä konstruoitu f. 64 / 105
65 Tiheysfunktion arvioiminen aineistosta Olkoon sm:lla X tiheysfunktio f, jota emme tunne. Oletetaan, että meillä on aineisto x 1, x 2,..., x N, jota voidaan pitää N riippumattoman sm:n X :n jakaumaa noudattavan sm:n havaittuina arvoina. Toisin sanoen x 1 = X 1 (ω act ), x 2 = X 2 (ω act ),... x N = X N (ω act ), jossa ω act on aktualisoitunut alkeistapaus, kullakin X i on sama jakauma kuin X :llä ja lisäksi X 1,..., X N ovat riippumattomia (mikä määritellään myöhemmin). Kuinka tällaisessa tilanteessa voidaan arvioida tiheysfunktion arvoa pisteessä u? Oletetaan, että u on f :n jatkuvuuspiste. 65 / 105
66 Eräs ratkaisu Valitaan jokin pieni luku h > 0 ja lasketaan, kuinka moni otospisteistä x i osuu h:n pituiselle välille [u h 2, u + h 2 ]. Olkoon tämä lukumäärä N u,h. Tiheysfunktion määritelmän ja frekvenssitulkinnan nojalla P(u h 2 X u + h 2 ) = u+h/2 u h/2 f (x) dx N u,h N. Toisaalta, integraalilaskennan väliarvolauseen nojalla u+h/2 u h/2 f (x) dx h f (u). Yhdistämällä saadaan arvio f (u) N u,h h N. Tässä voidaan käyttää myös muita h:n pituisia välejä, jotka sisältävät pisteen u kuin tämä. 66 / 105
67 2.7 Esimerkkejä jatkuvista jakaumista tasajakauma eksponenttijakauma gammajakauma, beetajakauma, normaalijakauma, khiin neliön jakauma, t-jakauma, F -jakauma (luvussa 5). 67 / 105
68 Tasajakauma Olkoon a, b R ja a < b. Satunnaismuuttujalla X on välin (a, b) tasajakauma X U(a, b) (engl. uniform distribution, sv. likformig fördelning), jos sillä on jatkuva jakauma tiheysfunktiona f, jossa f (x) = f (x a, b) = 1, kun a < x < b. b a (Tästä kaavasta pitää ymmärtää, että f (x) = 0, kun x a tai x b.) Tiheys on siis vakio koko välillä (a, b). Kertymäfunktio on 0, kun x a, x x a F (x) = f (u) du =, kun a < x < b, b a 1, kun x b. 68 / 105
69 Tasajakauman U(0, 1) tiheys- ja kertymäfunktio tf kf f(x) F(x) x x 69 / 105
70 Eksponenttijakauma (engl. exponential distribution) Satunnaismuuttujalla X on eksponenttijakauma parametrilla λ > 0, X Exp(λ), jos X :llä on tf f (x) = f (x λ) = λ e λx, kun x > 0. Kun x > 0, niin eksponenttijakauman kf:lla on arvo F (x) = ja F (x) = 0, kun x 0. / x 0 ( e λu ) = 1 e λx, 70 / 105
71 2.8 Satunnaismuuttujan muunnos Jos X on sm, ja g : R R on funktio, niin myös Y = g(x ) on sm. Merkintä Y = g(x ) tarkoittaa sitä, että Y (ω) = g(x (ω)), kaikilla ω Ω, ts. Y on yhdistetty funktio g X. Mitä voimme sanoa Y :n jakaumasta? 71 / 105
72 Alkukuva Jos g : R R on funktio ja A R, niin merkintä g 1 (A) tarkoittaa joukon A alkukuvaa kuvauksessa g, eli Huomaa, että g 1 (A) = {x R : g(x) A}. g(x) A x g 1 (A). 72 / 105
73 Muunoksen g(x ) jakauma diskreetissä tapauksessa Lause 2.10 Olkoon X diskreetti sm ptnf:lla f X, ja olkoon g : R R funktio. Tällöin sm Y = g(x ) diskreetti, ja sen ptnf f Y on f Y (y) = x g 1 ({y}) f X (x). Todistus: Y voi saada korkeintaan numeroituvasti äärettömän määrän eri arvoja, joten Y on diskreetti. Mille tahansa y R on P(Y = y) = P(g(X ) = y) = P(g(X ) {y}) = P(X g 1 ({y})) = f X (x), x g 1 ({y}) 73 / 105
74 Erikoistapaus Jos yhtälöllä y = g(x) on yksikäsitteinen ratkaisu x = h(y) kaikilla y, jotka kuuluvat sm:n Y arvojoukkoon S Y, niin f Y (y) = f X (h(y)), y S Y. (2.8) Jatkuvan jakauman tilanteessa saadaan erilainen kaava. Jos taas ratkaisuja on useita, niin jokainen erisuuri ratkaisu antaa ptnf:n arvoon pisteessä y yhden tällaisen termin lisää. 74 / 105
75 Jatkuvasti jakautuneen satunnaismuuttujan muunnos Jos X :llä on jatkuva jakauma, niin sen muunoksen Y = g(x ) jakauma voi funktion g luonteesta riippuen joko diskreetti, jatkuva tai ei kumpaakaan näistä. Esim. jos g on porrasfunktio, niin Y = g(x ) on diskreetti satunnaismuuttuja. Myöhemmin tarkastelemme tapausta, jossa satunnaismuuttujalla Y = g(x ) on jatkuva jakauma. Luentomonisteessa on esimerkki, jossa muunnoksella Y = g(x ) ei ole diskreetti eikä jatkuva jakauma, vaan ns. sekatyypin jakauma. 75 / 105
76 2.9 Kvantiilifunktio ja sen käyttö simuloinnissa Tarkastelemme sellaista jatkuvaa jakaumaa, jonka tiheysfunktio f on aidosti positiivinen välillä (a, b) ja nolla muualla. Päätepisteille sallitaan reaalisten arvojen lisäksi arvot a = tai b =. Tällaisen jakauman kertymäfunktio F, on aidosti kasvava välillä (a, b), ja lisäksi F (a) = 0 ja F (b) = / 105
77 Kvantiilifunktio on kertymäfunktion käänteisfunktio Oletusten ansiosta funktiolla F on olemassa käänteisfunktio F 1 : (0, 1) (a, b). (Tarkemmin sanoen F :n rajoittumalla joukkon (a, b) on käänteisfunktio F 1.) Merkintä F 1 ei tarkoita funktiota 1/F, vaan kertymäfunktion käänteisfunktiota. Käytännössä F 1 (u) määritetään ratkaisemalla x yhtälöstä F (x) = u, 0 < u < 1. Tällaista (avoimella välillä (0, 1) määriteltyä) kertymäfunktion käänteisfunktiota F 1 kutsutaan kyseisen jakauman kvantiilifunktioksi (engl. quantile function). (Myös nimitys fraktiilifunktio on käytössä.) 77 / 105
78 Kvantiilifunktion määritelmää havainnollistava kuva Erään jatkuvan jakauman kvantiilifunktion q = F 1 arvo pisteessä u = 0.7. Ylempänä on kertymäfunktio F ja alempana tiheysfunktio f. q( 0.7 ) kf x varjostettu pinta ala = 0.7 tf / 105
79 Kvantiilifunktion merkitys Osuus u jakauman todennäköisyysmassasta jää pisteen F 1 (u) vasemmalle puolelle eli vasemmanpuoleiseen häntään: jos sm:lla X on kf F, niin P(X F 1 (u)) = F (F 1 (u)) = u, mielivaltaiselle 0 < u < 1. Ts. tiheysfunktion f alle jää pisteen F 1 (u) vasemmalle puolelle alue, jonka pinta-ala on u, sillä u = P(X F 1 (u)) = F 1 (u) f (x) dx. Koska jakauma on jatkuva, niin pisteen F 1 (u) oikealle puolelle jää jakauman todennäköisyysmassasta osuus 1 u, eli tiheysfunktion alle jäävän oikeanpuoleisen häntäalueen pinta-ala on 1 u. 79 / 105
80 Alakvantiilit ja yläkvantiilit Kvantiilifunktio määriteltiin tarkastelemalla jakauman vasemmanpuoleista häntää. Tilastollisessa päättelyssä määritetään testien kriittisiä pisteitä usein jakauman oikeanpuoleisen hännän avulla. Selvyyden vuoksi voimme puhua jakauman alakvantiileista ja yläkvantiileista. Jos 0 < u < 1, niin jakauman u-alakvantiili (eli u-kvantiili tai u-fraktiili) on sellainen piste, josta vasemmalle jää jakaumasta osuus u. Ts. u-alakvantiili on F 1 (u). Jakauman u-yläkvantiili taas on sellainen piste, josta oikealle jää jakaumasta osuus u, joten u-yläkvantiili on F 1 (1 u), sillä P(X F 1 (1 u)) = 1 P(X < F 1 (1 u)) = 1 (1 u) = u. 80 / 105
81 Erikoisnimityksiä tietyille kvantiileille mediaani on 1 2 -kvantiili, alakvartiili on 1 4 -kvantiili, yläkvartiili on 3 4 -kvantiili. Näiden lisäksi puhutaan myös kvintiileistä, desiileistä ja persentiileistä. Huom! Tässä kvantiilit määriteltiin pisteinä, joiden alapuolelle jää tietty osuus jakaumasta. Tilastotieteessä esim. kvartiililla tai desiilillä saatetaan tarkoittaa myös jakauman osaa, esim. tulonjakotilaston alakvartiili = tuloiltaan alin neljäsosa väestöstä; III desiili = se osa joka on kvantiilipisteiden 2 10 ja 3 10 välissä. 81 / 105
82 Kertymäfunktion käänteisfunktion ominaisuuksia Funktio F 1 toteuttaa identiteetit F 1 (F (x)) = x, kaikilla a < x < b, ja F (F 1 (u)) = u, kaikilla 0 < u < 1. Koska F on aidosti kasvava funktio, niin myös F 1 on aidosti kasvava funktio. Jos jompaa kumpaa sovelletaan epäyhtälön molemmille puolille, niin epäyhtälön ratkaisujoukko säilyy muuttumattomana. 82 / 105
83 Kertymäfunktiomuunnos Olkoon X sm, jolla on kertymäfunktio F. Tarkastellaan satunnaismuuttujaa F (X ). Jos 0 < u < 1, niin P(F (X ) u) = P(F 1 (F (X )) F 1 (u)) = P(X F 1 (u)) Tämä tarkoittaa sitä, että = F (F 1 (u)) = u. F (X ) U(0, 1). (2.9) Satunnaismuuttujaan F (X ), ja tulokseen F (X ) U(0, 1) viitataan toisinaan nimellä kertymäfunktiomuunnos (engl. probability integral transform). 83 / 105
84 Käänteisfunktiomenetelmä Olkoon U U(0, 1), ja tarkastellaan satunnaismuuttujaa Z = F 1 (U). Jos a < x < b, niin Siis P(Z x) = P(F 1 (U) x) = P(F (F 1 (U)) F (x)) = P(U F (x)) = F (x) U U(0, 1) sm:n F 1 (U) kertymäfunktio on F. Tällöin sanotaan, että sm Z = F 1 (U) on saatu käänteisfunktiomenetelmällä (engl. (esim.) inverse transform). 84 / 105
85 Käänteisfunktiomenetelmä simuloinnissa Matemaattisissa ohjelmistoissa on yleensä satunnaislukugeneraattori, jonka tuottamia arvoja voidaan pitää riippumattomina jakaumaa U(0, 1) noudattavien satunnaismuuttujien arvoina. Jos jakauman kvantiilifunktiolla on yksinkertainen lauseke, niin käänteisfunktiomenetelmä antaa kätevän keinon simuloida kyseistä jakaumaa: generoi u jakaumasta U(0, 1), ja laske x = F 1 (u). 85 / 105
86 Esimerkki: eksponenttijakauman Exp(1) simulointi Kf on F (x) = { 1 e x, jos x 0 0, muuten, Kvantiilifunktion arvo F 1 (u) pisteessä 0 < u < 1 saadaan ratkaisemalla x yhtälöstä F (x) = u x = ln(1 u). Tämän takia jakaumaa Exp(1) voidaan simuloida asettamalla X = ln(1 U), kun U on ensin generoitu jakaumasta U(0, 1). 86 / 105
87 Huomautuksia Kvantiilifunktio voidaan yleistää mielivaltaiselle jakaumalle kaavalla (opetusmonisteen määritelmä 2.9) F 1 (u) = inf{x F (x) u} Myös käänteisfunktiomenetelmä yleistyy, ja tämän jälkeen reseptiä F 1 (U) voidaan pitää tapana konstruoida sm, jolla on haluttu kf F (opetusmonisteen lause 2.11), mikäli ensin todistetaan että tasajakauma U(0, 1) on olemassa. 87 / 105
88 2.10 Muunnetun satunnaismuuttujan tiheys Olkoon X :llä jatkuva jakauma, ja g : R R. Satunnaismuuttujalla Y = g(x ) ei tällöin välttämättä ole jatkuva jakauma. Jos kuitenkin g on riittävän sileä ja aidosti monotoninen, tai jos sen määrittelyjoukko R voidaan osittaa paloihin, joissa g on riittävän sileä ja aidosti monotoninen, niin osoittautuu, että tällöin Y :llä on jatkuva jakauma. 88 / 105
89 Kertymäfunktiotekniikka Jos muunnoksella Y = g(x ) on jatkuva jakauma, niin tiheysfunktio on mahdollista johtaa laskemalla ensin kertymäfunktio ja sitten kertymäfunktion derivaatta. Tämän lisäksi pitää jollakin tavalla tarkistaa, että Y :n jakauma todellakin on jatkuva. Tarkistus voidaan tehdä esim. suoraan tiheysfunktion määritelmän nojalla. Vaihtoehtona on käyttää lausetta / 105
90 Kertymäfunktiotekniikka, Y = e X Olkoon X :llä jatkuva jakauma, jolla on jatkuva tiheysfunktio f X, ja Y = e X. Selvästi Y > 0, joten F Y (y) = 0, kun y < 0. Kun y > 0, on F Y (y) = P(Y y) = P(e X y) = P(X ln(y)) = F X (ln(y)), Lasketaan kf:n derivaatta: f Y (y) = F Y (y) = f X (ln(y))/y, kun y > 0, ja f Y (y) = 0, kun y 0. Lauseen 2.7 avulla voidaan tarkistaa, että Y :n jakauma on jatkuva. Tämän jälkeen tiedetään, että F :n derivaatta kelpaa Y :n tiheysfunktioksi. 90 / 105
91 Y = e X : muuttujanvaihtotekniikka Tarkistetaan, että tn P(a Y b) saadaan laskettua integroimalla tiettyä funktiota välin (a, b) yli, kun a < b ovat mielivaltaisia. Koska Y > 0, voidaan olettaa, että a > 0. P(a Y b) = P(a e X b) = P(ln a X ln b) = = ln b ln a b a f X (x) dx (X :n tf on f X ) f X (ln(y)) 1 y dy Esimerkin tekniikka yleistetään kohta lauseeksi. (Sij. y = ex x = ln(y)) 91 / 105
92 Diffeomorfismi Määritelmä 2.10 (Diffeomorfismi) Kuvaus g : A B, jossa A ja B ovat d-ulotteisen avaruuden R d avoimia osajoukkoja, on diffeomorfismi, jos (a) g on bijektio joukkojen A ja B välillä (b) sekä g että sen käänteisfunktio g 1 : B A ovat jatkuvasti derivoituvia. 92 / 105
93 Muuttujanvaihtokaava tiheysfunktioille Lause 2.12 (Muuttujanvaihtokaava tiheysfunktioille) Olkoon sm:lla X jatkuva jakauma tf:lla f X. Olkoon g : A B diffeomorfismi, jossa A, B R ovat avoimia välejä, ja olkoon P(X A) = 1. Määritellään h(y) = g 1 (y), kun y B. Tällöin sm:lla Y = g(x ) on jatkuva jakauma tiheysfunktiolla { f X (h(y)) h (y), kun y B f Y (y) = (2.11) 0, muuten. 93 / 105
94 Huomautuksia lauseesta Tulos (2.11) voidaan ilmaista lyhyemmin kaavalla f Y (y) = f X (h(y)) h (y), kun y B. Kun muunnoksen Y = g(x ) tiheysfunktio ilmoitetaan, on tärkeää paitsi kertoa kaava f X (h(y)) h (y) myös ilmoittaa selkeästi kaavan pätevyysalue, eli se joukko B, jossa kyseinen kaava pätee. Vertaa jatkuvan jakauman tapauksen tulosta (2.11) vastaavan diskreetin tapauksen tulokseen (2.8). Vain jatkuvan jakauman tapauksessa tarvitaan käänteisfunktion derivaatan itseisarvoa. 94 / 105
95 Kaksi erilaista tekniikkaa Muunnetun satunnaismuuttujan tiheysfunktio voidaan johtaa kahdella erilaisella tekniikalla: johdetaan kertymäfunktio ja lasketaan tiheysfunktio kertymäfunktion derivaattana, käytetään muuttujanvaihtokaavaa. 95 / 105
96 Huomautuksia kertymäfunktiotekniikasta Kertymäfunktiotekniikassa pitää erikseen tarkistaa, että saatu kertymäfunktio on jatkuvan jakauman kertymäfunktio. Ehdoton edellytys tälle asialle on se, että kertymäfunktion pitää olla jatkuva funktio koko reaaliakselilla. Lauseen 2.7 mukaan riittävää jakauman jatkuvuudelle on se, jos kertymäfunktio on lisäksi jatkuvasti derivoituva muualla paitsi äärellisessä määrässä poikkeuspisteitä. (Poikkeuspisteissä derivaatan ei välttämättä tarvitse olla olemassa.) 96 / 105
97 Huomautuksia muuttujanvaihtokaavasta Muuttujanvaihtokaavaa käytettäessä pitää miettiä, mitkä ovat avoimet joukot A ja B. Lisäksi käänteisfunktio h pitää pystyä ratkaisemaan yhtälöstä g(x) = y (ja tämä ei onnistu ellei kyseessä ole bijektio). Tämän jälkeen on tyypillisesti helppo tarkistaa, onko lauseke g(x) jatkuvasti derivoituva joukossa A ja onko lauseke h(y) jatkuvasti derivoituva joukossa B. Jos nämä ehdot täyttyvät, niin kyseessä on diffeomorfismi. 97 / 105
98 Muistisääntö Jos g on diffeomorfismi, niin muuttujanvaihtokaavan muistamista helpottaa seuraava muistisääntö. Yhtälön f X (x) dx = f Y (y) dy (2.12) pitää säilyä bijektiivisessä muuttujanvaihdossa y = g(x) x = h(y). Kun tiedosta (2.12) ratkaistaan f Y (y), saadaan f Y (y) = f X (x) dx dy = f X (h(y)) h (y), mutta tietenkin tämä kaava pätee vain g:n kuvajoukossa B. 98 / 105
99 Muistisääntö f X (x) dx = f Y (y) dy infinitesimaalisen järkeilyn avulla / 105
100 Muistisääntö on robusti Muistisäännöstä (2.12) voidaan ratkaista f Y (y) myös toisella tavalla, nimittäin seuraavasti, 1 f Y (y) = f X (x) dy dx = f X (x) g (x) = f X (h(y)) g (h(y)). Myös tämä kaava pitää paikkansa joukossa B, sillä kaava dx dy = 1 dy dx kertoo oikean yhteyden funktion ja sen käänteisfunktion derivaattojen välillä. Aidosta monotonisuudesta seuraa se, että g > 0 joukossa A ja h > 0 joukossa B. 100 / 105
101 Esimerkki Y = e X muistisäännön avulla Tarkastelemme bijektiivistä vastaavuutta y = e x x = ln(y) pisteiden x R ja y > 0 välillä. Koska molemmat lausekkeet ovat jatkuvasti derivoituvia, on kyseessä diffeomorfismi. Ratkaisemme muistisäännöstä kaavan f Y (y) = f X (x) dx dy Koska tahdomme laskea f Y :n arvon pisteessä y, pitää kaavan oikealla puolella x esittää y:n avulla kaavalla x = ln(y). Kaavassa tarvitaan myös tämän lausekkeen derivaattaa 1/y. Kun teemme nämä sijoitukset, saamme tuloksen f Y (y) = f X (ln(y)) 1 y, y > / 105
102 Yleistys Joskus tiheysfunktion muuttujanvaihtokaavaa tarvitaan myös sellaisessa tilanteessa, jossa g ei ole monotoninen, mutta jossa sen määrittelyjoukko voidaan pilkkoa väleiksi, joille rajoitettuna g on aidosti monotoninen. Tällaiset tilanteet saadaan hoidettua samaan tapaan kuin seuraavassa esimerkissä. 102 / 105
103 Esimerkki Y = X 2 Olkoon X :llä jatkuva jakauma, jolla on jatkuva tiheysfunktio f X. Tarkastellaan satunnaismuuttujaa Y = X 2. Selvästi Y 0, joten F Y (y) = 0, kun y < 0. Kun y > 0, on F Y (y) = P(Y y) = P(X 2 y) = P( y X y) = F X ( y) F X ( y). Tarkistetaan lauseen 2.7 avulla, että Y :n jakauma on jatkuva. Funktio F X on jatkuvan jakauman kertymäfunktiona jatkuva, joten ainoa ongelmallinen piste on y = 0. Tässä pisteessä pitää tarkistaa F Y :n jatkuvuus, mutta tarkistus on helppoa, koska F X (x) on jatkuva pisteessä x = 0. F Y (y) on derivoituva muualla paitsi mahdollisesti pisteessä y = / 105
104 Tiheysfunktio kertymäfunktiota derivoimalla Derivaatan laskemisen jälkeen näemme, että Y :n tf on f Y (y) = f X ( y) ja f Y (y) = 0, kun y y + f X ( 1 y) 2, kun y > 0, y Kumpaakin yhtälön y = x 2 ratkaisua vastaa tässä yksi termi. 104 / 105
105 Muuttujanvaihtotekniikka muunnokselle Y = g(x ), kun g ei ole monotoninen Luentomonisteessa on muotoiltu kohtuullisen yleinen lause Tiheysfunktioon f Y (y) saadaan summa termejä, yksi termi kutakin yhtälön y = g(x) ratkaisua kohti. Kukin termeistä on samaa muotoa kuin diffeomorfismin tapauksessa. Jos lauseen 2.13 oletukset ovat voimassa, niin muunnoksen Y = g(x ) tiheysfunktio saadaan laskea myös kertymäfunktiotekniikalla: johdetaan ensin sm:n Y kertymäfunktio F Y ja sitten derivoidaan tämä funktio. 105 / 105
2.1 Satunnaismuuttuja ja sen jakauma
 2.1 Satunnaismuuttuja ja sen jakauma Satunnaismuuttuja (lyhenne sm, engl. random variable, rv (joskus myös variate), sv. stokastisk variabel (joskus myös slumpvariabel)) on satunnaiskokeeseen liittyvä
2.1 Satunnaismuuttuja ja sen jakauma Satunnaismuuttuja (lyhenne sm, engl. random variable, rv (joskus myös variate), sv. stokastisk variabel (joskus myös slumpvariabel)) on satunnaiskokeeseen liittyvä
0 kun x < 0, 1/3 kun 0 x < 1/4, 7/11 kun 1/4 x < 6/7, 1 kun x 1, 1 kun x 6/7,
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Kertymäfunktio. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia
 Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Injektio (1/3) Funktio f on injektio, joss. f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f )
 Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Viikko 2 Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Satunnaismuuttujien muunnokset ja niiden jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Johdatus todennäköisyyslaskentaan Kertymäfunktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdantoa INTEGRAALILASKENTA, MAA9
 Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
Derivaattaluvut ja Dini derivaatat
 Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
Sovellettu todennäköisyyslaskenta B Antti Rasila 20. syyskuuta 2007 Antti Rasila () TodB 20. syyskuuta 2007 1 / 17 1 Kolmogorovin aksioomat σ-algebra Tapahtuman todennäköisyys 2 Satunnaismuuttujat Todennäköisyysjakauma
k S P[ X µ kσ] 1 k 2.
![k S P[ X µ kσ] 1 k 2. k S P[ X µ kσ] 1 k 2.](/thumbs/92/110318530.jpg) HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
Sinin jatkuvuus. Lemma. Seuraus. Seuraus. Kaikilla x, y R, sin x sin y x y. Sini on jatkuva funktio.
 Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Funktion raja-arvo ja jatkuvuus Reaali- ja kompleksifunktiot
 3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
8.1 Ehdolliset jakaumat
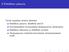 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Epäyhtälöt ovat yksi matemaatikon voimakkaimmista
 6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
5 Tärkeitä yksiulotteisia jakaumia
 5 Tärkeitä yksiulotteisia jakaumia Jakaumista löytyy lisätietoja ja kuvaajia Wikipediasta. Kirjallisuudessa käytetään useille näistä jakaumista monia erilaisia parametrointeja. Kussakin lähteessä käytetty
5 Tärkeitä yksiulotteisia jakaumia Jakaumista löytyy lisätietoja ja kuvaajia Wikipediasta. Kirjallisuudessa käytetään useille näistä jakaumista monia erilaisia parametrointeja. Kussakin lähteessä käytetty
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
4. Todennäköisyyslaskennan kertausta
 luento04.ppt S-38.1145 - Liikenneteorian perusteet - Kevät 2006 1 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat
luento04.ppt S-38.1145 - Liikenneteorian perusteet - Kevät 2006 1 Sisältö eruskäsitteet Diskreetit satunnaismuuttujat Diskreetit jakaumat lkm-jakaumat Jatkuvat satunnaismuuttujat Jatkuvat jakaumat aikajakaumat
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
4.3 Moniulotteinen Riemannin integraali
 4.3 Moniulotteinen Riemannin integraali Tässä luvussa opitaan miten integroidaan usean muuttujan reaaliarvoista tai vektoriarvoista funktiota, millaisten joukkojen yli jatkuvaa funktiota voi integroida,
4.3 Moniulotteinen Riemannin integraali Tässä luvussa opitaan miten integroidaan usean muuttujan reaaliarvoista tai vektoriarvoista funktiota, millaisten joukkojen yli jatkuvaa funktiota voi integroida,
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1. Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS
 DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä
 J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Joukot. Georg Cantor ( )
 Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ
![1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ 1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ](/thumbs/67/57751673.jpg) Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
11 Raja-arvolauseita ja approksimaatioita
 11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Karteesinen tulo. Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla 1 / 21
 säilyy Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla c b a 1 2 3 5 1 / 21 säilyy Esimerkkirelaatio R = {(1, b), (3, a), (5, a), (5, c)} c b a 1
säilyy Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla c b a 1 2 3 5 1 / 21 säilyy Esimerkkirelaatio R = {(1, b), (3, a), (5, a), (5, c)} c b a 1
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Inversio-ongelmien laskennallinen peruskurssi Luento 7
 Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
5 Differentiaalilaskentaa
 5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu. f(x, y) = k x y, kun 0 < y < x < 1,
 Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
MS-A0402 Diskreetin matematiikan perusteet
 MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Harjoitus 2: Matlab - Statistical Toolbox
 Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
4.1. Olkoon X mielivaltainen positiivinen satunnaismuuttuja, jonka odotusarvo on
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M)
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa
 MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MATP153 Approbatur 1B Ohjaus 2 Keskiviikko torstai
 MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
Diskreetti derivaatta
 Diskreetti derivaatta LuK-tutkielma Saara Sadinmaa 43571 Matemaattisten tieteiden koulutusohjelma Oulun yliopisto Syksy 017 Sisältö Johdanto 1 Peruskäsitteitä 3 Ominaisuuksia 4 3 Esimerkkejä 8 4 Potenssifunktioita
Diskreetti derivaatta LuK-tutkielma Saara Sadinmaa 43571 Matemaattisten tieteiden koulutusohjelma Oulun yliopisto Syksy 017 Sisältö Johdanto 1 Peruskäsitteitä 3 Ominaisuuksia 4 3 Esimerkkejä 8 4 Potenssifunktioita
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Täydellisyysaksiooman kertaus
 Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
4.1 Diskreetin satunnaismuuttujan odotusarvo
 4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
1 Supremum ja infimum
 Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
 Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua.
 6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
Ratkaisuehdotus 2. kurssikokeeseen
 Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus Malliratkaisut (Sauli Lindberg)
 Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
Reaaliarvoisen yhden muuttujan funktion raja arvo LaMa 1U syksyllä 2011
 Neljännen viikon luennot Reaaliarvoisen yhden muuttujan funktion raja arvo LaMa 1U syksyllä 2011 Perustuu Trench in verkkokirjan lukuun 2.1. Esko Turunen esko.turunen@tut.fi Funktion y = f (x) on intuitiivisesti
Neljännen viikon luennot Reaaliarvoisen yhden muuttujan funktion raja arvo LaMa 1U syksyllä 2011 Perustuu Trench in verkkokirjan lukuun 2.1. Esko Turunen esko.turunen@tut.fi Funktion y = f (x) on intuitiivisesti
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
Sovellettu todennäköisyyslaskenta B Antti Rasila 28. syyskuuta 2007 Antti Rasila () TodB 28. syyskuuta 2007 1 / 20 1 Jatkoa diskreeteille jakaumille Negatiivinen binomijakauma Poisson-jakauma Diskreettien
y x1 σ t 1 = c y x 1 σ t 1 = y x 2 σ t 2 y x 2 x 1 y = σ(t 2 t 1 ) x 2 x 1 y t 2 t 1
 1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
MS-A0202 Di erentiaali- ja integraalilaskenta 2 (SCI) Luento 8: Taso- ja avaruusintegraalit
 MS-A22 i erentiaali- ja integraalilaskenta 2 (SCI) Luento 8: Taso- ja avaruusintegraalit Antti Rasila Aalto-yliopisto Syksy 25 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 25 / 8 Tasointegraali Olkoon R
MS-A22 i erentiaali- ja integraalilaskenta 2 (SCI) Luento 8: Taso- ja avaruusintegraalit Antti Rasila Aalto-yliopisto Syksy 25 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 25 / 8 Tasointegraali Olkoon R
LUKU 3. Ulkoinen derivaatta. dx i 1. dx i 2. ω i1,i 2,...,i k
 LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit
 MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento : Moniulotteiset integraalit Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 26 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy
MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento : Moniulotteiset integraalit Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 26 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy
