3 Ohjelmointi On-line help Piirtäminen Tasografiikka Avaruusgrafiikka Piirto-optiot... 20
|
|
|
- Timo-Jaakko Jaakkola
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Maxima-pikaopas Sisältö Aritmetiikka ja algebra. Luvut Funktiot Matriisit ja vektorit Yhtälöiden ratkaiseminen Algebrallinen sieventäminen Trigonometrinen sieventäminen Lausekkeen osan poimiminen ja korvaaminen Summat ja tulot Joukot Differentiaali- ja integraalilaskenta 9. Differentiointi ja raja-arvot Integrointi Tavalliset differentiaaliyhtälöt Laplace- ja Fourier-muunnos Vektorianalyysi Ohjelmointi 5 4 On-line help 6 5 Piirtäminen 8 5. Tasografiikka Avaruusgrafiikka Piirto-optiot Yleistä Maxima on laaja symboliseen laskentaan suunniteltu ohjelma, joka on nykyisin vapaasti saatavissa ja jaettavissa GNU GPL). Maximalla voidaan sieventää lausekkeita, jakaa polynomeja tekijöihin, ratkaista yhtälöitä, derivoida, integroida, kehittää funktioita taylorin sarjoiksi, ratkaista differentiaaliyhtälöitä. Vaikka Maximan vahvuusalueita on nimenomaan symbolinen laskenta, on siinä paljon numeeriseen laskemiseen liittyviä toimintoja laskeminen tarkoilla arvoilla ja likiarvoilla, suurilla kokonaisluvuilla ja suurtarkkuuslikiarvoilla, jne) sekä varsin monipuoliset piirto-ominaisuudet. Maximassa on lisäksi ohjelmointikieli, jolla Maximan toimintoja voidaan laajentaa. Maxima on siis täysiverinen matemaattinen yleisohjelmisto ja siinä käytettävissä olevan matematiikan tietämyksen nojalla sitä voidaan kutsua matemaattiseksi asiantuntijajärjestelmäksi tosin sen käyttäjänkin pitää olla matematiikan asiantuntija).
2 Maximan käyttäjä on tavallisesti kosketuksissa ainakin) kolmen ohjelman kanssa. Varsinainen Maximaohjelma jää yleensä taustalle, mutta se on näistä kolmesta tärkein, Maximan komentoja käsittelevä laskentaydin. Käyttäjä näkee lähinnä jonkin monista käyttöliittymistä, joista näillä sivuilla käsitellään vain wxmaximaa. Muihin löytyy linkkejä Maximan kotisivulta []; näyttökuvia eri käyttöliittymistä löytyy Maximan screenshots.html-sivulta [4]. Kolmas tarpeellinen ohjelma on Gnuplot [9], joka hoitaa Maximan kuvien tekemisen. Gnuplot-ohjelmaa voi käyttää suoraankin, mutta aluksi kuvien tekeminen Maximasta käsin lienee helpointa. Erikoismerkkejä ; puolipiste päättää komennon ja palauttaa tuloksen $ dollarimerkki päättää komennon, mutta estää tuloksen näkymisen % prosenttimerkki viittaa edellisen laskun tulokseen, pilkku erottaa muuttujat tai listan/joukon alkiot; erottaa useita samalla komentorivillä annettuja komentoja toisistaan : kaksoispistettä käytetään arvon tallettamiseksi muuttujaan = yhtäsuuruusmerkkiä käytetään yhtälöiden esittämiseen := pari kaksoispiste-yhtäsuuruusmerkki määrittelee funktion ) kaarisulut ilmoittavat funktion argumentit; ryhmittävät useita komentoja samalle komentoriville [ ] hakasulut ilmaisevat listoja tai vektoreita, tai indeksoituja muuttujia { } aaltosulut ilmaisevat joukkoja lainausmerkki estää seuraavan symbolin arvon laskemisen tarpeen mm. differentiaaliyhtälöitä esitettäessä) kahdennettu lainausmerkki ei kaksoislainausmerkki) pakottaa seuraavan symbolin arvon laskemisen kaksoislainausmerkkiä käytetään merkkijonojen ilmaisemiseen /* */ /* tämä on kommentti */ Huomio: ääkkösiä ei tule käyttää muuttujien tai funktioiden nimissä eikä niitä ilmeisesti ole syytä käyttää merkkijonoissakaan. Pienet ja isot kirjaimet tarkoittavat eri asiaa eli tarkkana komentojen kirjoittamisessa ja muuttujien nimeämisessä).
3 Aritmetiikka ja algebra. Luvut %i) %e^%i*%pi); %o) %i) 0^0-0^0-; %o) %i) 00!/0!; %o) %i4) %o4) %i5) 0 luku:457/4656; luku, numer; %o5) %i6) bfloatluku); %o6) b %i7) %i8) fpprec:00$ bfloatluku); %o8) [44digits] b %i9) fpprec:6$ %i0) bfloatluku), fpprec:00; %o0) [44digits] b Kompleksiluvun reaali- ja imaginaariosa, itseisarvo eli moduli), vaihekulma eli argumentti) sekä muunnokset karteesisiin koordinaatteihin ja napakoordinaatteihin: %i) realpartx+%i*y); %o) x %i) imagpartx+%i*y); %o) y %i) cabsx+%i*y); %o) y + x %i4) cargx+%i*y); %o4) atan y, x)
4 %i5) rectformx+%i*y); %o5) i y + x %i6) polarformx+%i*y); %o6) y + x e i atany,x) %i7) realpartsinx+%i*y)); %o7) sin x) cosh y) %i8) imagpartsinx+%i*y)); %o8) cos x) sinh y) %i9) cabssin+%i*)); %o9) cos ) sinh ) + sin ) cosh ) %i0) cargsin+%i*)); ) cos ) sinh ) %o0) atan sin ) cosh ) %i) rectformsin+%i*)); %o) i cos ) sinh ) + sin ) cosh ) %i) polarformsin+%i*)); %o) cos ) sinh ) + sin ) cosh ) cos) sinh) i e atan sin) cosh)). Funktiot %i) fx,y):=x^y+y^x; %o) f x, y) := x y + y x %i4) lambda[x,y], x^y+y^x); %o4) lambda [x, y], x y + y x ) %i5) f,); %o5) 7 %i6) evx^y+y^x, x=, y=); %o6) 7 Maximan käsikirjassa v. 5.4): Logaritmit 4, trigonometriset funktiot 5, erikoisfunktiot 6, elliptiset funktiot 7, paketti orthopoly 74. Huomaa: log = luonnollinen logaritmi; arkusfunktiot: asin, acos, atan, acot, asec, acsc; areafunktiot: asinh, acosh, atanh, acoth, asech, acsch 4
5 . Matriisit ja vektorit %i7) mat:matrix[a,b],[c,d]); ) a b %o7) c d %i8) mat[]; %o8) [a, b] %i9) mat.[x,y]; ) b y + a x %o9) d y + c x %i0) [x,y].mat; %o0) c y + a x d y + b x ) Matriisin muodostaminen, kun matriisin paikassa [i, j] olevalle alkiolle on kaava huomaa, että indeksoidun funktion h muuttujat ovat hakasuluissa): %i) h[i,j]:=i+j*x, genmatrixh,,)); ) x + x + %o) x + x + %i) mat:mat^^-, detout; ) d b %o) c a a d b c %i) mat.mat, ratsimp; ) 0 %o) 0 %i4) mat^^; ) b c + a b d + a b %o4) c d + a c d + b c %i5) determinantmat - diagmatrix,x)); %o5) a x) d x) b c.4 Yhtälöiden ratkaiseminen %i6) solve[x^+y*x=,x+y=a-],[x,y]); %o6) [[x = a, y = a a a ]] %i7) allrootsx^+x+=0); %o7) [x = i , x = i, x = ] 5
6 %i8) sol:solvex^+x+=0,x); ) %o8) [x = ) i i ) x = ) i i ), %i9) maplambda[j], evx^+x+, sol[j])), [,,]); ) %o9) [ ) i i ), x = i ) ) ) i +, ) ) i i ) + ) ) ) + %i40) mapratsimp, %); %o40) [0, 0, 0] %i4) realrootsx^5/895+x^+), numer; %o4) [x = ] %i4) sol:allrootsx^5/895+x^+); ) ) i ) ) + + ] ) ) ] i %o4) [x = i , x = i, x = , x = i , x = i ] %i4) maplambda[j], evx^5/895+x^+, sol[j])), [,,,4,5]); i )5 %o4) [ i ) +, i) i) +, 0.0, 895 ) i i ) +, 895 ) i i ) + ] 895 %i44) expand%); %o44) [ i , i , 0.0, i , i ] ) +, 6
7 %i45) mapcabs, %); %o45) [ , , 0.0, , ].5 Algebrallinen sieventäminen %i46) factorx^+%i*x^-5*x^-5*%i*x+4*x+4*%i); %o46) x 4) x ) x + i) %i47) expand%); %o47) x + i x 5 x 5 i x + 4 x + 4 i %i48) partfrac/x+a)*x-b)),x); %o48) b + a) x b) b + a) x + a) %i49) ratsimp%); %o49) x + a b) x a b %i50) xthrux/x+a)-b/x+b)); %o50) x x + b) b x + a) x + a) x + b) %i5) radcansqrtx^-)/sqrtx-)); %o5) x + %i5) integrate/cost), t), logabs:true; %o5) log sin t) + ) %i5) logcontract*%); ) sin t) + %o5) log sin t) %i54) %, logexpand:all; log sin t) ) %o54) log sin t) + ) log sin t) ).6 Trigonometrinen sieventäminen %i55) exponentializecosy)); %o55) ei y + e i y %i56) trigexpandsin*x)+cos*y)); %o56) sin y) + cos y) + cos x) sin x) 7
8 %i57) trigreduce%,x); %o57) sin y) + cos y) + sin x) %i58) trigrat%); %o58) cos y) + sin x) %i59) trigsimpsinx)^+cosx)^); %o59) %i60) trigsimp+tanx)^); %o60) cos x).7 Lausekkeen osan poimiminen ja korvaaminen %i6) partz+y+x^r,,); %o6) r Listan osiin voi viitata kuten indeksoituihin funktioihin yleisen lausekeen osat pitää poimia komennolla part): %i6) l:[z, y, x^r], l[]); %o6) x r %i6) substcat,dog,tail+dog); %o6) tail + cat %i64) lhsb+a=c+d); %o64) b + a.8 Summat ja tulot %i65) %pi/0)*sumsini*%pi/0),i,0,0); ) + sin 4 ) 5 + sin 7 ) 0 + sin 5 %o65) sin 9 0 %i66) numer:true$ %i67) %pi/0)*sumsini*%pi/0),i,0,0); %o67) %i68) numer:false$ %i69) *sum/^i,i,,inf), simpsum:true; %o69) ) + sin 5 0 ) + sin ) 0 + sin ) 5 + sin ) 0) + 8
9 %i70) summa:sumi/^i,i,,inf), simpsum:true; %o70) i= i i %i7) loadsimplify_sum)$ %i7) simplify_sumsumma); %o7) %i7) nusum^i*i^,i,,n); 4 n 6 n + n ) n+ %o7) 8 + %i74) nusum-)^k*k / 4*k^ - ), k,, n); solve: dependent equations eliminated: ) %o74) ) n 4 n + ) %i75) producta[i],i,,5); %o75) a a a a 4 a 5.9 Joukot %i76) union{cat, dog, bird}, {fish, cat}); %o76) bird, cat, dog, fish %i77) intersect{cat, dog, bird}, {fish, cat}); %o77) cat %i78) setdifference{cat, dog, bird}, {fish, cat}); %o78) bird, dog Huomaa ero listan ja joukon välillä: %i79) [[,,,], {,,,}]; %o79) [[,,, ], {,, }] Differentiaali- ja integraalilaskenta. Differentiointi ja raja-arvot %i80) diffx^x,x,); %o80) x x log x) + ) + x x %i8) diffelliptic_et,m), t); %o8) m sin t) 9
10 %i8) limittanx),x,%pi/,plus); %o8) %i8) taylorsina*x),x,0,5); %o8)/t/ a x a x 6 + a5 x %i84) taylorelliptic_et,m),t,0,5); %o84)/t/ t m t m 4 m ) t %i85) taylortanx),x,0,5); %o85)/t/ x + x + x %i86) pade%,,); %o86) [ x 5 x 6 x 5 ] Pade-approksimaatio on toisinaan paljon tarkempi kuin Taylorin polynomiapproksimaatio: %i87) t:taylortanx),x,0,5); %o87)/t/ x + x + x %i88) t:pade%,,); %o88) [ x 5 x 6 x 5 ] %i89) t:expandt), t:t[]); %o89) x 5 x 6 x 5 %i90) wxplotd[tanx),t,t],[x,-.5,.5])$ %t90) %i9) wxplotd[tanx)-t, tanx)-t],[x,-.5,.5])$ 0
11 %t9). Integrointi %i9) integrate/y^/4)/y-),y); ) ) ) %o9) log y 4 + atan y 4 + log y 4 %i9) *integratesinx)/x,x,0,inf); %o9) %i94) logabs:true$ %i95) fx):= integrate/cosx), x)); %o95) f x) := %i96) logabs:false$ log sin x) + ) %i97) integratelogx)/x, x); %o97) log x) %i98) integratex/logx), x); %o98) gamma incomplete 0, log x)) %i99) assumea>0)$ log sin x) ) %i00) integratet^a-)*%e^-t), t,0, inf); %o00) γ a) %i0) forgeta>0)$ Integraalin numeerisen likiarvon laskeminen on rombergf, x, a, b) käsikirja 76) ja QUADPACK-kirjaston käsikirja ) quad qagf, x, a, b, key): %i0) rombergexp-x^),x,0.0,.4); %o0)
12 %i0) integrateexp-x^),x,0,4/0); erf 7 ) 5 %o0) %i04) float%); %o04) %i05) rombergsin/x),x,0.0,.0); romberg failed to converge an error. To debug this try: debugmodetrue); %i06) quad_qagsin/x),x,0.0,.0,); %o06) [ , , 65, 0] %i07) quad_qagsin/x),x,0.00,.0,6); %o07) [ , , 867, 0]. Tavalliset differentiaaliyhtälöt Huomaa ero: %i08) [diffy,x), diffy,x)]; %o08) [0, d d x y] %i09) eq: diffy,x)=*x*y*y-); %o09) d y = x y ) y d x %i0) sol:odeeq,y,x); %o0) %i) method; %o) separable log y) log y ) %i) icsol,x=0,y=/); %o) log y) log y ) = x + %c = x + log ) + log %i) eq: diffy,x,)+y* diffy,x))^; %o) ) d d d x y + y d x y %i4) sol:odeeq,y,x); %o4) y + 6 %k y 6 = x + %k %i5) icsol,x=0,y=0, diffy,x)=); ) %o5) y + y 6 = x
13 %i6) bcsol,x=0,y=,x=,y=); %o6) y 0 y 6 = x Rungen ja Kuttan menetelmä alkuarvotehtävälle y x) = fx, yx)), yx 0 ) = y 0, x 0 x x muutos dx:n välein = rkfx,y), y, y0, [x, x0, x, dx]). Esimerkiksi alkuarvotehtävä y = erfy ), y0) =, 0 x, dx = 0.5: %i7) rkerfy^),y,,[x,0,,0.5]); %o7) [[0, ], [0.5, ], [.0, ]] Lineaarisen differentiaaliyhtälöryhmän ratkaiseminen Laplace-muunnoksen avulla: %i8) eq: diffxt),t)= diffyt),t)+sint)$ %i9) eq: diffyt),t,)= diffxt),t)-cost)$ %i0) atvalue diffyt),t),t=0,a)$ %i) desolve[eq,eq],[xt),yt)]); %o) [x t) = a e t a + x 0), y t) = cos t) + a e t a + y 0) ] %i) ode diffy,x)=%e^x-y)/+%e^x),y,x); %o) e y log e x + ) = %c %i) odex*x+)* diffy,x,)+x+5)* diffy,x,)+-4)*y,y,x); %o) false %i4) loadcontrib_ode)$ %i5) contrib_odex*x+)* diffy,x,)+x+5)* diffy,x,)+-4)*y,y,x); %o5) [y = %i6) method; %o6) odelin gauss b 6,,, x) %k gauss a 6,,, x) %k x 4 + x 4 ] Funktio gauss aa,a,b,t) Gaussin hypergeometrinen funktio, joka Maximasta löytyy myös nimillä hypergeometric[a,a], [b], t) ja %f[,][a,a], [b], t). Nimelle hypergeometric[a,a], [b], t) määritelty versio tuntee numeeriset arvot ja sievennyssäätöjä..4 Laplace- ja Fourier-muunnos %i7) laplacesint),t,s); %o7) s + %i8) ilt%,s,t); %o8) sin t)
14 %i9) loadfourie)$ %i0) totalfourierabsx),x,%pi); %t0) a 0 = %t) a n = %t) b n = 0 %t) a 0 = %t4) a n = )n ) n %t5) b n = 0 ) sin n) cos n) n + n n %o5) ) n ) cosn x) n= n + %i6) totalfourierexpx),x,%pi); %t6) %t7) a n = a 0 = e e n sin n) e n +e + e n sin n) n + cos n) e n +e + e cos n) n + sin n) e %t8) b n = n +e + e sin n) n cos n) n + + e n +e e n cos n) n + %t9) a 0 = e e ) e + ) %t40) a n = e e ) e + ) ) n n + ) %t4) b n = e e ) e + ) n ) n n + ) %o4) e e ) e + ) n ) n sinn x) n= n + e e ) e + ) %i4) totalfourierexpabsx)),x,%pi); %t4) a 0 = e ) e n sin n) n %t4) a n = + + e cos n) n + n + %t44) b n = 0 %t45) a 0 = e %t46) a n = e ) n ) n + ) %t47) b n = 0 %o47) e ) n ) cosn x) n= n + + e 4 + e e ) e + ) ) n cosn x) n= n + +
15 .5 Vektorianalyysi %i48) loadvect); %o48) /Applications/Maxima/... /5.4.0/share/vector/vect.mac Sisätulo e.b tavallinen piste), ristitulo e b näppäile mato-aksentti välilyönnin päälle) %i49) declare[e,b,j],nonscalar); %o49) done %i50) j~b~e)+b.e; %o50) b.e b e) j %i5) vectorsimp%); %o5) b.e b e) j %i5) curlgradf))+divcurle)); %o5) 0 %i5) vectorsimpcurlcurlb))), expandall; %o5) grad div b)) laplacian b) %i54) scalefactors[[r*costh),r*sinth),z],r,th,z]); %o54) done %i55) expressdivb)); %o55) d d z r b z) + d d th b th + d d r b r r ) r Ohjelmointi %i56) plist:[], lkm:0, for n: step while lkm<0 do if primepn) then plist:appendplist,[n]), lkm:lkm+) ), plist); %o56) [, 5, 7,,, 7, 9,, 9, ] %i57) p:, plist:[p], for n: thru 0 do p:next_primep), plist:appendplist,[p]) ), plist); %o57) [, 5, 7,,, 7, 9,, 9,, 7] %i58) maplambda[n], n^), %); %o58) [9, 5, 49,, 69, 89, 6, 59, 84, 96, 69] 5
16 4 On-line help %i59) apropos"integ"); %o59) [askinteger, beta args sum to integer, expintegral chi, expintegral ci, expintegral e, expintegral e, expintegral ei, expintegral e simp, expintegral hyp, expintegral li, expintegral shi, expintegral si, expintegral trig, freeof integrate, integer, integerp, integervalued, integer partitions, integfactor, integral, integrate, integrate use rootsof, integration constant, integration constant counter, lie integrating factor, nointegrate, noninteger, nonnegintegerp, ode riccati original not integrable, require integer, require posinteger, split integer part, sum by integral, sum by integral transforms, use integral, integerlinear, e-integer-coeff] %i60) describeintegerp); Function: integerp expr ) Returns true if expr is a literal numeric integer, otherwise false. integerp returns false if its argument is a symbol, even if the argument is declared integer. Examples: %i) integerp 0); %o) true %i) integerp ); %o) true %i) integerp -7); %o) true %i4) integerp 0.0); %o4) false %i5) integerp.0); %o5) false %i6) integerp %pi); %o6) false %i7) integerp n); %o7) false %i8) declare n, integer); %o8) done %i9) integerp n); %o9) false There are also some inexact matches for integerp. Try?? integerp to see them. %o60) true %i6) examplecombine); %i6)combineb/y+a/y+b/x+a/x) %o6) b + a y %o6) done + b + a x %i6) demo"trgsmp.dem"); read and interpret file: /Applications/Maxima/... /5.4.0/demo/trgsmp.dem At the prompt, type ; and enter to get next demonstration. sin x) ) cos x) %i64)tan x) sec x) + cos x) %o64) sec x) tan x) + sin x) cos x) ; 6
17 %i65)trigsimp %) %o65) sin x) + cos x)4 cos x) ; sec x) %i66) + tan x) tan x) sec x) %o66) sec x) sec x) tan x) + tan x) ; %i67)trigsimp %) %o67) sin x) 4 + sin x) cos x) sin x) cos x) 4 ; + cos x) sin x) + 4 %i68) cos x) sin x) ) 6 cos x) sin x) + sin x) 4 8 cos x) sin x) 4 6 cos x) sin x) + 4 cos x) sin x) ) + 8 sin x) + cos x) 4 + %o68) 8 cos x) ; %i69)trigsimp %) %o69) sin x) + cos x)4 cos x) ; %i70) sech x) tanh x) coth x) + %o70) sech x) sinh x) tanh x) coth x) %i7)trigsimp %) cosh x) sech x) tanh x) sech x) sinh x) tanh x) coth x) + coth x) + cosh x) sech x) tanh x) sech x) tanh x) coth x) + coth x) ; %o7) sinh x)5 + sinh x) 4 + sinh x) cosh x) 5 ; %i7) sech x) sinh x) + 5 cosh x) 4 sinh x) 8 cosh x) + sinh x) ) + 0 cosh x) sinh x) cosh x) sinh x) + sinh x) ) + cosh x) cosh x) sinh x) + sinh x) 4) + sinh x) 5 ))/ 6 %o7) sech x) 5 sinh x) cosh x) sinh x) 8 %i7)trigsimp %) sinh x) cosh x) sinh x) + cosh x) 4) sinh x) + cosh x) ) + 5 cosh x) 4 sinh x) + 4 sinh x) + 6))/ 6 ; %o7) sinh x)5 + sinh x) 4 sinh x) cosh x) 5 ; ) %i74) cos x) sec x) sin x) + cos x) + sec x) tan x) ) %o74) cos x) sec x) tan x) + sec x) sin x) cos x) ; %i75)trigsimp %) %o75) 0 ; ) d %i76) d x v %o76) v cos x) sec x) tan x)+ ) d d cos x)+ d x v cos x) sec x)+ d x v )) v sec x) d d x v 7 sinh x) + cosh x) sinh x) ) ) v sec x) sin x)+v cos x) sec x) tan x) ) ) d d sin x)+ d x v cos x) sec x)+ d x v cos x) ; ) +
18 %i77)trigsimp %) ) d %o77) d x v ) d sin x) + d x v cos x) + d d x v ; %o77) /Applications/Maxima/... /5.4.0/demo/trgsmp.dem 5 Piirtäminen 5. Tasografiikka Alla olevissa muodoissaan piirtokomentojen muodostama kuva tulee omaan, Gnuplot-ohjelman luomaan ikkunaan. Lisää komennon alkuun wx, jos haluat kuvan tulevan wxmaxima-dokumentti-ikkunaan. Tähän pdf-versioon kuvien tulostus on suunnattu eps-tiedostoon, jotta dokumenttiin liitettty kuva olisi tulostuskelpoinen. Lisää komentoihin rivit [gnuplot_term, ps] ja [gnuplot_out_file, "tiedoston_nimi.eps"]. %i78) plotdexp-x^),[x,-,])$ %e - x x %i79) plotd[parametric,cost),sin*t),[t,-%pi,%pi]], [nticks,00], [gnuplot_preamble,"set size ratio -"])$ sin*t) cost) 8
19 5. Avaruusgrafiikka %i80) plotdsinx)*siny), [x,-*%pi,*%pi], [y,-*%pi,*%pi])$ sinx)*siny) z x y 6 %i8) plotdsinx)*siny), [x,-*%pi,*%pi], [y,-*%pi,*%pi], [gnuplot_preamble,"set view 60, 0,,.5"])$ z sinx)*siny) x y %i8) contour_ploty^-x^+x, [x,-,], [y,-,])$ y x 9
20 5. Piirto-optiot Komento plot options näyttää piirto-optiot ja niiden oletusarvot. Piirtoalue: [x,x,x], [y,y,y]. Käyrän jakopisteiden määrä: [nticks,n]. Tasoalueen ruudukon jakopisteiden määrä: [grid,nx,ny]. Gnuplot-ohjelmalle välitettäviä arvoja [gnuplot preamble, parametriteksti ]. Esimerkiksi [gnuplot preamble, set size ratio - ] määrää akseleille saman mittakaavan; [gnuplot preamble, set view rotx, rotz, skaala, skaalaz ] d-grafiikassa katselukulman asettaminen; rotx: kierto x-akselin suhteen, rotz: kierto z-akselin suhteen, skaala: kuvan skaalaus, skaalaz: kuvan skaalaus z- akselin suunnassa. %i8) plot_options; %o8) [[t, -, ], [grid, 0, 0], [transform xy, false], [run viewer, true], [axes, true], [plot format, gnuplot pipes], [color, blue, red, green, magenta, black, cyan], [point type, bullet, circle, plus, times, asterisk, box, square, triangle, δ, wedge, nabla, diamond, lozenge], [palette, [hue, 0.5, 0.7, 0.8, 0.5], [hue, 0.65, 0.8, 0.9, 0.55], [hue, 0.55, 0.8, 0.9, 0.4], [hue, 0.95, 0.7, 0.8, 0.5]], [gnuplot term, x], [gnuplot out file, false], [nticks, 9], [adapt depth, 5], [gnuplot preamble, ], [gnuplot default term command, set term pop], [gnuplot dumb term command, set term dumb 79 ], [gnuplot ps term command, set size.5,.5; set term postscript eps enhanced color solid 4], [plot realpart, false]] Kirjallisuutta [] luettu kesäkuussa 0). [] luettu kesäkuussa 0). [] luettu kesäkuussa 0). [4] luettu kesäkuussa 0). [5] Richard H. Rand: Introduction to Maxima, 005, pdf-dokumentti osoitteessa luettu kesäkuussa 0). [6] Robert Dodier: Minimal Maxima, 005, luettu kesäkuussa 0). [7] Paulo Ney de Souza, Richard J. Fateman, Joel Moses ja Cliff Yapp: The Maxima book, 004, luettu kesäkuussa 0). [8] Wilhelm Haager: Graphics with MAXIMA, 0, pdf-dokumentti osoitteessa with Maxima.pdf luettu kesäkuussa 0). [9] 4.4/gnuplot.pdf luettu kesäkuussa 0). [0] Leon Q. Brin: Maxima and the calculus, 00, brin/papers/maxima and calculus.pdf luettu kesäkuussa 0). 0
wxmaxima-pikaopas Ari Lehtonen
 wxmaxima-pikaopas Ari Lehtonen. Yleistä Maxima on laaja symboliseen laskentaan suunniteltu ohjelma. Maximalla voidaan sieventää lausekkeita, jakaa polynomeja tekijöihin, ratkaista yhtälöitä, derivoida,
wxmaxima-pikaopas Ari Lehtonen. Yleistä Maxima on laaja symboliseen laskentaan suunniteltu ohjelma. Maximalla voidaan sieventää lausekkeita, jakaa polynomeja tekijöihin, ratkaista yhtälöitä, derivoida,
1 Johdantoa. 1.1 Help: example, apropos ja describe. 1.2 Peruslaskutoimitukset + - * / ^ 1.3 Tärkeät erikoismerkit
 SL_esim_L1.wxm 1 / 8 1 Johdantoa 1.1 Help: example, apropos ja describe Lista olemassa olevista erillisistä esimerkeistä saadaan komennolla example(); Esimerkiksi komentoon diff liiittyviä esimerkkejä
SL_esim_L1.wxm 1 / 8 1 Johdantoa 1.1 Help: example, apropos ja describe Lista olemassa olevista erillisistä esimerkeistä saadaan komennolla example(); Esimerkiksi komentoon diff liiittyviä esimerkkejä
Harjoitus 10: Mathematica
 Harjoitus 10: Mathematica Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon Mathematican
Harjoitus 10: Mathematica Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon Mathematican
plot(f(x), x=-5..5, y=-10..10)
 [] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
[] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
wxmaxima opas 1 Mikä wxmaxima on 2 wxmaximan käyttö Petri Sallasmaa 13. toukokuuta 2014
 wxmaxima opas Petri Sallasmaa 13. toukokuuta 2014 1 Mikä wxmaxima on wxmaxima on yksinkertainen graanen käyttöliittynä Maxima CAS(computer algebra system)-järjestelmälle, joka on luotu wxwidgets nimisen
wxmaxima opas Petri Sallasmaa 13. toukokuuta 2014 1 Mikä wxmaxima on wxmaxima on yksinkertainen graanen käyttöliittynä Maxima CAS(computer algebra system)-järjestelmälle, joka on luotu wxwidgets nimisen
DIFFERENTIAALI- JA INTEGRAALILASKENTA
 DIFFERENTIAALI- JA INTEGRAALILASKENTA Timo Mäkelä Tässä tekstissä esitellään yhden muuttujan reaaliarvoisten funktioiden differentiaalilaskentaa sekä sarjoja. Raja-arvot Raja-arvoja voidaan laskea käyttämällä
DIFFERENTIAALI- JA INTEGRAALILASKENTA Timo Mäkelä Tässä tekstissä esitellään yhden muuttujan reaaliarvoisten funktioiden differentiaalilaskentaa sekä sarjoja. Raja-arvot Raja-arvoja voidaan laskea käyttämällä
1 Kertausta ja täydennystä
 SL_esim_lin_alg.wxm / 9 Kertausta ja täydennystä. "assume" (%i) integrate(/(a+x^), x); Is a positive or negative? pos; x atan a (%o) a (%i) assume(a>); (%o) [ a > ] (%i) integrate(/(a+x^), x); x atan a
SL_esim_lin_alg.wxm / 9 Kertausta ja täydennystä. "assume" (%i) integrate(/(a+x^), x); Is a positive or negative? pos; x atan a (%o) a (%i) assume(a>); (%o) [ a > ] (%i) integrate(/(a+x^), x); x atan a
Matriiseista. Emmi Koljonen
 Matriiseista Emmi Koljonen 3. lokakuuta 22 Usein meillä on monta systeemiä kuvaavaa muuttujaa ja voimme kirjoittaa niiden välille riippuvaisuuksia, esim. piirin silmukoihin voidaan soveltaa silmukkavirtayhtälöitä.
Matriiseista Emmi Koljonen 3. lokakuuta 22 Usein meillä on monta systeemiä kuvaavaa muuttujaa ja voimme kirjoittaa niiden välille riippuvaisuuksia, esim. piirin silmukoihin voidaan soveltaa silmukkavirtayhtälöitä.
Valitse ruudun yläosassa oleva painike Download Scilab.
 Luku 1 Ohjeita ohjelmiston Scilab käyttöön 1.1 Ohjelmiston lataaminen Ohjeet ohjelmiston lataamiseen Windows-koneelle. Mene verkko-osoitteeseen www.scilab.org. Valitse ruudun yläosassa oleva painike Download
Luku 1 Ohjeita ohjelmiston Scilab käyttöön 1.1 Ohjelmiston lataaminen Ohjeet ohjelmiston lataamiseen Windows-koneelle. Mene verkko-osoitteeseen www.scilab.org. Valitse ruudun yläosassa oleva painike Download
TIEA341 Funktio-ohjelmointi 1, kevät 2008
 TIEA341 Funktio-ohjelmointi 1, kevät 2008 Luento 11 Antti-Juhani Kaijanaho Jyväskylän yliopisto Tietotekniikan laitos 21. tammikuuta 2008 Listakomprehensio Uusi tapa luoda (ja muokata) listoja: [ lauseke
TIEA341 Funktio-ohjelmointi 1, kevät 2008 Luento 11 Antti-Juhani Kaijanaho Jyväskylän yliopisto Tietotekniikan laitos 21. tammikuuta 2008 Listakomprehensio Uusi tapa luoda (ja muokata) listoja: [ lauseke
Harjoitus 1: Matlab. Harjoitus 1: Matlab. Mat Sovelletun matematiikan tietokonetyöt 1. Syksy 2006
 Harjoitus 1: Matlab Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Matlab-ohjelmistoon Laskutoimitusten
Harjoitus 1: Matlab Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Matlab-ohjelmistoon Laskutoimitusten
Kevään 2011 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä /
 Kevään 0 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä / 8.7.0 a) b) c) a) Tehtävä Yhtälö ratkaistaan yleensä Solve-funktiolla: Solve x 3 x, x x 4 Joissakin tapauksissa
Kevään 0 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä / 8.7.0 a) b) c) a) Tehtävä Yhtälö ratkaistaan yleensä Solve-funktiolla: Solve x 3 x, x x 4 Joissakin tapauksissa
Matlab- ja Maple- ohjelmointi
 Perusasioita 2. helmikuuta 2005 Matlab- ja Maple- ohjelmointi Yleistä losoaa ja erityisesti Numsym05-kurssin tarpeita palvellee parhaiten, jos esitän asian rinnakkain Maple:n ja Matlab:n kannalta. Ohjelmien
Perusasioita 2. helmikuuta 2005 Matlab- ja Maple- ohjelmointi Yleistä losoaa ja erityisesti Numsym05-kurssin tarpeita palvellee parhaiten, jos esitän asian rinnakkain Maple:n ja Matlab:n kannalta. Ohjelmien
Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica
 Simo K. Kivelä Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica Symbolinen laskenta ei aina toimi, kuten voisi odottaa. Parempi onkin ajatella, että se elää omaa elämäänsä, jolla
Simo K. Kivelä Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica Symbolinen laskenta ei aina toimi, kuten voisi odottaa. Parempi onkin ajatella, että se elää omaa elämäänsä, jolla
Matriisit ovat matlabin perustietotyyppejä. Yksinkertaisimmillaan voimme esitellä ja tallentaa 1x1 vektorin seuraavasti: >> a = 9.81 a = 9.
 Python linkit: Python tutoriaali: http://docs.python.org/2/tutorial/ Numpy&Scipy ohjeet: http://docs.scipy.org/doc/ Matlabin alkeet (Pääasiassa Deni Seitzin tekstiä) Matriisit ovat matlabin perustietotyyppejä.
Python linkit: Python tutoriaali: http://docs.python.org/2/tutorial/ Numpy&Scipy ohjeet: http://docs.scipy.org/doc/ Matlabin alkeet (Pääasiassa Deni Seitzin tekstiä) Matriisit ovat matlabin perustietotyyppejä.
Funktion määrittely (1/2)
 Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
Integroimistekniikkaa Integraalifunktio
 . Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
. Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
Harjoitus 3 -- Ratkaisut
 Harjoitus 3 -- Ratkaisut 1 ' '-merkki kirjoitetaan =, ' '-merkki!=, ' '-merkki ==. Yhtälöiden ratkaisusta puhutaan lisää myöhemmin. a f x, y : If ehtolauseke x y, y tämä palautetaan, jos
Harjoitus 3 -- Ratkaisut 1 ' '-merkki kirjoitetaan =, ' '-merkki!=, ' '-merkki ==. Yhtälöiden ratkaisusta puhutaan lisää myöhemmin. a f x, y : If ehtolauseke x y, y tämä palautetaan, jos
Harjoitus 4 -- Ratkaisut
 Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio: In[15]:= f x : x 1 x Sin x ; Plot f x, x, 0, 3 Π, PlotRange All Out[159]= Luodaan tasavälinen pisteistö välille 0 x 3 Π. Tehdään se ensin kiinnitetyllä
Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio: In[15]:= f x : x 1 x Sin x ; Plot f x, x, 0, 3 Π, PlotRange All Out[159]= Luodaan tasavälinen pisteistö välille 0 x 3 Π. Tehdään se ensin kiinnitetyllä
1 Lausekkeiden sieventäminen: kertausta ja täydennystä
 SL_esim_L.wxm / 4 Lausekkeiden sieventäminen: kertausta ja täydennystä. Rationaalilausekkeet (%i) p:product(x(random(0)5), j,0,4); (%o) x x x (%i) expand(p); (%o) x 5 8 x 4 x 4 x x (%i) ratsimp(p); (%o)
SL_esim_L.wxm / 4 Lausekkeiden sieventäminen: kertausta ja täydennystä. Rationaalilausekkeet (%i) p:product(x(random(0)5), j,0,4); (%o) x x x (%i) expand(p); (%o) x 5 8 x 4 x 4 x x (%i) ratsimp(p); (%o)
cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti. Piirrä integroitavan funktion kuvaaja. Mikä itse asiassa on integraalin arvo?
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
Mathematica Sekalaista asiaa
 Mathematica Sekalaista asiaa Asetusoperaattorit Mathematicassa voi käyttää omia muuttujasymboleja melko rajattomasti ja niiden nimeämisessä voi käyttää miltei mitä tahansa merkkejä. Käytännössä nimeämisessä
Mathematica Sekalaista asiaa Asetusoperaattorit Mathematicassa voi käyttää omia muuttujasymboleja melko rajattomasti ja niiden nimeämisessä voi käyttää miltei mitä tahansa merkkejä. Käytännössä nimeämisessä
Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua.
 6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
MATEMATIIKAN LATOMINEN LA T EXILLA, OSA 1
 MATEMATIIKAN LATOMINEN LA T EXILLA, OSA 1 PEKKA SALMI Tämä dokumentti on johdatus matemaattisten termien kirjoittamiseen L A TEXilla. Tarkoituksena on esitellä yksinkertaisia matemaattisia konstruktioita
MATEMATIIKAN LATOMINEN LA T EXILLA, OSA 1 PEKKA SALMI Tämä dokumentti on johdatus matemaattisten termien kirjoittamiseen L A TEXilla. Tarkoituksena on esitellä yksinkertaisia matemaattisia konstruktioita
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 28.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 28.9.2016 Pekka Alestalo,
Funktionimien kuormitus. TIES341 Funktio ohjelmointi 2 Kevät 2006
 Funktionimien kuormitus TIES341 Funktio ohjelmointi 2 Kevät 2006 Kertausta ongelma Mikä on (+) operaattorin tyyppi? Num a => a -> a -> a Mikä on (==) operaattorin tyyppi? Eq a => a -> a -> a Mikä on show
Funktionimien kuormitus TIES341 Funktio ohjelmointi 2 Kevät 2006 Kertausta ongelma Mikä on (+) operaattorin tyyppi? Num a => a -> a -> a Mikä on (==) operaattorin tyyppi? Eq a => a -> a -> a Mikä on show
Ratkaisu: Tutkitaan derivoituvuutta Cauchy-Riemannin yhtälöillä: f(x, y) = u(x, y) + iv(x, y) = 2x + ixy 2. 2 = 2xy xy = 1
 1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MS-A0104 Differentiaali- ja integraalilaskenta 1 (ELEC2) MS-A0106 Differentiaali- ja integraalilaskenta 1 (ENG2)
 MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
mlvektori 1. Muista, että Jacobin matriisi koostuu vektori- tai skalaariarvoisen funktion F ensimmäisistä
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mlvektori 1. Muista, että Jacobin matriisi koostuu vektori- tai skalaariarvoisen funktion F ensimmäisistä osittaisderivaatoista: y 1... J F =.
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mlvektori 1. Muista, että Jacobin matriisi koostuu vektori- tai skalaariarvoisen funktion F ensimmäisistä osittaisderivaatoista: y 1... J F =.
TRIGONOMETRISET JA HYPERBOLISET FUNKTIOT
 TRIGONOMETRISET JA HYPERBOLISET FUNKTIOT ARI LEHTONEN. Trigonometriset funktiot.. Peruskaavat. tan x := sin x cos x, cos x cot x := sin x Anglosaksisissa maissa käytössä ovat myös funktiot sekantti sec
TRIGONOMETRISET JA HYPERBOLISET FUNKTIOT ARI LEHTONEN. Trigonometriset funktiot.. Peruskaavat. tan x := sin x cos x, cos x cot x := sin x Anglosaksisissa maissa käytössä ovat myös funktiot sekantti sec
f[x i ] = f i, f[x i,..., x j ] = f[x i+1,..., x j ] f[x i,..., x j 1 ] x j x i T n+1 (x) = 2xT n (x) T n 1 (x), T 0 (x) = 1, T 1 (x) = x.
![f[x i ] = f i, f[x i,..., x j ] = f[x i+1,..., x j ] f[x i,..., x j 1 ] x j x i T n+1 (x) = 2xT n (x) T n 1 (x), T 0 (x) = 1, T 1 (x) = x. f[x i ] = f i, f[x i,..., x j ] = f[x i+1,..., x j ] f[x i,..., x j 1 ] x j x i T n+1 (x) = 2xT n (x) T n 1 (x), T 0 (x) = 1, T 1 (x) = x.](/thumbs/64/52007594.jpg) Kaavakokoelma f[x i ] = f i, f[x i,..., x j ] = f[x i+,..., x j ] f[x i,..., x j ] x j x i T n+ (x) = 2xT n (x) T n (x), T (x) =, T (x) = x. n I,n = h f(t i + h 2 ), E,n = h2 (b a) f (2) (ξ). 24 i= I,n
Kaavakokoelma f[x i ] = f i, f[x i,..., x j ] = f[x i+,..., x j ] f[x i,..., x j ] x j x i T n+ (x) = 2xT n (x) T n (x), T (x) =, T (x) = x. n I,n = h f(t i + h 2 ), E,n = h2 (b a) f (2) (ξ). 24 i= I,n
Tässä dokumentissa on ensimmäisten harjoitusten malliratkaisut MATLABskripteinä. Voit kokeilla itse niiden ajamista ja toimintaa MATLABissa.
 Laskuharjoitus 1A Mallit Tässä dokumentissa on ensimmäisten harjoitusten malliratkaisut MATLABskripteinä. Voit kokeilla itse niiden ajamista ja toimintaa MATLABissa. 1. tehtävä %% 1. % (i) % Vektorit luodaan
Laskuharjoitus 1A Mallit Tässä dokumentissa on ensimmäisten harjoitusten malliratkaisut MATLABskripteinä. Voit kokeilla itse niiden ajamista ja toimintaa MATLABissa. 1. tehtävä %% 1. % (i) % Vektorit luodaan
Harjoitus 7 -- Ratkaisut
 Harjoitus 7 -- Ratkaisut 1 Solve osaa ratkaista polynomiyhtälöitä, ainakin astelukuun 4 asti. Erikoistapauksissa korkeammankin asteen yhtälöt ratkeavat. Clear a, b, c, d, e, x ; Solve a x 3 b x 2 c 0,
Harjoitus 7 -- Ratkaisut 1 Solve osaa ratkaista polynomiyhtälöitä, ainakin astelukuun 4 asti. Erikoistapauksissa korkeammankin asteen yhtälöt ratkeavat. Clear a, b, c, d, e, x ; Solve a x 3 b x 2 c 0,
Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37
 Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37 Tehtävä 1: Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37 Tehtävä 1: Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
Differentiaaliyhtälöryhmä
 Differentiaaliyhtälöryhmä Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti täsmälleen samanlaisilla kaavoilla
Differentiaaliyhtälöryhmä Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti täsmälleen samanlaisilla kaavoilla
Mat-1.C Matemaattiset ohjelmistot
 Mat-.C Matemaattiset ohjelmistot Luento ma 9.3.0 $z; Error, (in rtable/product) invalid arguments.z; z C z C z3 3 C z4 4 C z5 5.Tr z ; z C z C z3 3 C z4 4 C z5 5 ; Error, (in rtable/power) eponentiation
Mat-.C Matemaattiset ohjelmistot Luento ma 9.3.0 $z; Error, (in rtable/product) invalid arguments.z; z C z C z3 3 C z4 4 C z5 5.Tr z ; z C z C z3 3 C z4 4 C z5 5 ; Error, (in rtable/power) eponentiation
Ensimmäisen kertaluvun yhtälön numeerinen ratkaiseminen
 nummen.nb 1 Ensimmäisen kertaluvun yhtälön numeerinen ratkaiseminen Eulerin menetelmä alkaurvoprobleeman y' = f Hx, yl, yhx 0 L = y 0 ratkaisemiseksi voidaan ohjelmoida Mathematicalle euler-nimiseksi funktioksi
nummen.nb 1 Ensimmäisen kertaluvun yhtälön numeerinen ratkaiseminen Eulerin menetelmä alkaurvoprobleeman y' = f Hx, yl, yhx 0 L = y 0 ratkaisemiseksi voidaan ohjelmoida Mathematicalle euler-nimiseksi funktioksi
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
Värähtelevä jousisysteemi
 Mathematican version 8 mukainen. (5.10.01 SKK) Värähtelevä jousisysteemi Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla m d x k x, d t missä x on jousen
Mathematican version 8 mukainen. (5.10.01 SKK) Värähtelevä jousisysteemi Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla m d x k x, d t missä x on jousen
1. Viikko. K. Tuominen MApu II 1/17 17
 1. Viikko Keskeiset asiat ja tavoitteet: 1. Kompleksiluvut, kompleksitaso, polaariesitys, 2. Kompleksilukujen peruslaskutoimitukset, 3. Eulerin ja De Moivren kaavat, 4. Potenssi ja juuret, kompleksinen
1. Viikko Keskeiset asiat ja tavoitteet: 1. Kompleksiluvut, kompleksitaso, polaariesitys, 2. Kompleksilukujen peruslaskutoimitukset, 3. Eulerin ja De Moivren kaavat, 4. Potenssi ja juuret, kompleksinen
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio
 MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
y z = (x, y) Kuva 1: Euklidinen taso R 2
 Kompleksiluvut. Määritelmä Tarkastellaan euklidista tasoa R = {(, y), y R}. y y z = (, y) R Kuva : Euklidinen taso R Suorakulmaisessa koordinaatistossa on -akseli ja y-akseli. Luvut ja y ovat pisteen z
Kompleksiluvut. Määritelmä Tarkastellaan euklidista tasoa R = {(, y), y R}. y y z = (, y) R Kuva : Euklidinen taso R Suorakulmaisessa koordinaatistossa on -akseli ja y-akseli. Luvut ja y ovat pisteen z
1.1 Vektorit. MS-A0007 Matriisilaskenta. 1.1 Vektorit. 1.1 Vektorit. Reaalinen n-ulotteinen avaruus on joukko. x 1. R n. 1. Vektorit ja kompleksiluvut
 ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0007 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 26.10.2015 Reaalinen
ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0007 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 26.10.2015 Reaalinen
Harjoitus 1 -- Ratkaisut
 Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
Fortran 90/95. + sopii erityisesti numeriikkaan:
 Fortran 90/95 + sopii erityisesti numeriikkaan: + optimoivat kääntäjät tehokas koodi + mukana valmiiksi paljon varusfunktioita + kompleksiluvut + taulukko-operaatiot + operaattorit laajennettavissa myös
Fortran 90/95 + sopii erityisesti numeriikkaan: + optimoivat kääntäjät tehokas koodi + mukana valmiiksi paljon varusfunktioita + kompleksiluvut + taulukko-operaatiot + operaattorit laajennettavissa myös
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pystyakselin
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pystyakselin
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 1 / vko 44
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko Tehtävä (L): Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko Tehtävä (L): Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Hannu Mäkiö. kertolasku * jakolasku / potenssiin korotus ^ Syöte Geogebran vastaus
 Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)
![mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011) mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)](/thumbs/91/107207023.jpg) Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan Plots/Insert Plot/XY plot Huomaa - ja y-akselin paikanvaraajat (ja näissä valmiina yksikön syöttöruutu). Siirrä - akselia ylös/alas. Palauta origo perinteiseen
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan Plots/Insert Plot/XY plot Huomaa - ja y-akselin paikanvaraajat (ja näissä valmiina yksikön syöttöruutu). Siirrä - akselia ylös/alas. Palauta origo perinteiseen
1.1 Vektorit. MS-A0004/A0006 Matriisilaskenta. 1.1 Vektorit. 1.1 Vektorit. Reaalinen n-ulotteinen avaruus on joukko. x 1. R n.
 ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
1 Plot. 1.1 Funktion kuvaaja: y=f(x)
 SL_esim_grafiikkaa.wxm 1 / 13 1 Plot Maximan sisäänrakennetut piirtokomennot sopivat "kevyeen" työskentelyyn. Komennot tunnistaa nimistä, joiden osana on plot. Avuksi Maximan käsikirjan luku "Plotting"
SL_esim_grafiikkaa.wxm 1 / 13 1 Plot Maximan sisäänrakennetut piirtokomennot sopivat "kevyeen" työskentelyyn. Komennot tunnistaa nimistä, joiden osana on plot. Avuksi Maximan käsikirjan luku "Plotting"
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit
 MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy 215 1 / 24 Skalaarikenttä Olkoon R
MS-A35 ifferentiaali- ja integraalilaskenta 3 Luento 1: Moniulotteiset integraalit Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A35 Syksy 215 1 / 24 Skalaarikenttä Olkoon R
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Harjoitus 1 -- Ratkaisut
 Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Kompleksiluvut Riikka Korte (muokannut Riikka Kangaslammen materiaalin pohjalta) Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.11.2015 1 /
MS-A0102 Differentiaali- ja integraalilaskenta 1 Kompleksiluvut Riikka Korte (muokannut Riikka Kangaslammen materiaalin pohjalta) Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.11.2015 1 /
Kompleksiluvut., 15. kesäkuuta /57
 Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Mat Matematiikan peruskurssi K2
 Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
Differentiaali- ja integraalilaskenta 2 Ratkaisut: loppuviikko 2
 Differentiaali- ja integraalilaskenta 2 Ratkaisut: loppuviikko 2 Harjoitustehtävät 11-13 lasketaan alkuviikon harjoituksissa, 15-17 loppuviikon harjoituksissa. Kotitehtävä 14 palautetaan MyCourses-sivulle
Differentiaali- ja integraalilaskenta 2 Ratkaisut: loppuviikko 2 Harjoitustehtävät 11-13 lasketaan alkuviikon harjoituksissa, 15-17 loppuviikon harjoituksissa. Kotitehtävä 14 palautetaan MyCourses-sivulle
JYVÄSKYLÄN YLIOPISTO. Integraalilaskenta 2 Harjoitus Olkoon A := {(x, y) R 2 0 x π, sin x y 2 sin x}. Laske käyräintegraali
 JYVÄSKYLÄN YLIOPISTO MTEMTIIKN J TILSTOTIETEEN LITOS Integraalilaskenta Harjoitus 4 5.4.4. Olkoon := {(x, y) R x π, sin x y sin x}. Laske käyräintegraali + (y dx + x dy) a) suoraan; ja b) Greenin lauseen
JYVÄSKYLÄN YLIOPISTO MTEMTIIKN J TILSTOTIETEEN LITOS Integraalilaskenta Harjoitus 4 5.4.4. Olkoon := {(x, y) R x π, sin x y sin x}. Laske käyräintegraali + (y dx + x dy) a) suoraan; ja b) Greenin lauseen
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
Opiskelijan pikaopas STACK-tehtäviin. Lassi Korhonen, Oulun yliopisto
 Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Numeeriset menetelmät
 Numeeriset menetelmät Luento 3 Ti 13.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 3 Ti 13.9.2011 p. 1/37 p. 1/37 Epälineaariset yhtälöt Newtonin menetelmä: x n+1 = x n f(x n) f (x n ) Sekanttimenetelmä:
Numeeriset menetelmät Luento 3 Ti 13.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 3 Ti 13.9.2011 p. 1/37 p. 1/37 Epälineaariset yhtälöt Newtonin menetelmä: x n+1 = x n f(x n) f (x n ) Sekanttimenetelmä:
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
Fysiikan matematiikka P
 Fysiikan matematiikka 763101P Luennoija: Kari Rummukainen, Fysikaalisten tieteiden laitos Tavoite: tarjota opiskelijalle nopeasti fysikaalisten tieteiden tarvitsemia matematiikan perustietoja ja taitoja.
Fysiikan matematiikka 763101P Luennoija: Kari Rummukainen, Fysikaalisten tieteiden laitos Tavoite: tarjota opiskelijalle nopeasti fysikaalisten tieteiden tarvitsemia matematiikan perustietoja ja taitoja.
dt 2. Nämä voimat siis kumoavat toisensa, jolloin saadaan differentiaaliyhtälö
 Mathematican version 8 mukainen. (25.10.2012 SKK) Tavallinen heiluri Otetaan tarkastelun kohteeksi tavallinen yksinkertainen heiluri. Tämä koostuu kitkattomaan niveleen kiinnitetystä (massattomasta) varresta
Mathematican version 8 mukainen. (25.10.2012 SKK) Tavallinen heiluri Otetaan tarkastelun kohteeksi tavallinen yksinkertainen heiluri. Tämä koostuu kitkattomaan niveleen kiinnitetystä (massattomasta) varresta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
Matemaattiset ohjelmistot A. Osa 2: MATLAB
 Matemaattiset ohjelmistot 802364A Osa 2: MATLAB Mikko Orispää 30. lokakuuta 2013 Sisältö 1 MATLAB 2 1.1 Peruslaskutoimitukset......................... 2 1.2 Muuttujat................................ 3
Matemaattiset ohjelmistot 802364A Osa 2: MATLAB Mikko Orispää 30. lokakuuta 2013 Sisältö 1 MATLAB 2 1.1 Peruslaskutoimitukset......................... 2 1.2 Muuttujat................................ 3
Differentiaaliyhtälöryhmän numeerinen ratkaiseminen
 numryh.nb Differentiaaliyhtälöryhmän numeerinen ratkaiseminen Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti
numryh.nb Differentiaaliyhtälöryhmän numeerinen ratkaiseminen Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
6 Eksponentti- ja logaritmifunktio
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 019 6 Eksponentti- ja logaritmifunktio 6.1 Eksponenttifunktio 1. Määritä (a) e 3 e + 5, (b) e, (c) + 3e e cos.. Tutki, onko funktiolla f() = 1 e tan + 1 ( π + nπ, n
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 019 6 Eksponentti- ja logaritmifunktio 6.1 Eksponenttifunktio 1. Määritä (a) e 3 e + 5, (b) e, (c) + 3e e cos.. Tutki, onko funktiolla f() = 1 e tan + 1 ( π + nπ, n
Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu!
 Lineaarialgebra a, kevät 2018 Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu! Klikkaa kappaleet auki kolmiosta restart; # Tämä unohduttaa aikaisemmat
Lineaarialgebra a, kevät 2018 Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu! Klikkaa kappaleet auki kolmiosta restart; # Tämä unohduttaa aikaisemmat
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
(b) = x cos x 1 ( cos x)dx. = x cos x + cos xdx. = sin x x cos x + C, C R.
 Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
Maxima ja Maple. millaan lailla sukua muuttujille a ja b. 1 Ohjelmat eivät yleensä pahastu turhista välilyönneistä, joten niitä
 Maxima ja Maple Maple on symbolisen matematiikan laskentaohjelma jota käytetään esim. Joensuun yliopistossa; siihen on törmätty mestariluokan laskuharjoituksissa. Koska Maple on kaupallinen ohjelma ja
Maxima ja Maple Maple on symbolisen matematiikan laskentaohjelma jota käytetään esim. Joensuun yliopistossa; siihen on törmätty mestariluokan laskuharjoituksissa. Koska Maple on kaupallinen ohjelma ja
Lineaarialgebra a, kevät 2019
 Lineaarialgebra a, kevät 2019 Kotilaskut 1 yms. Maple:lla Tämä on vanha Maple 6 -versio, joka avautunee uudemmissa - kuten Maple 2018 - Classic Worksheet - versiona. Työarkkien yhteensopivuus taaksepäin
Lineaarialgebra a, kevät 2019 Kotilaskut 1 yms. Maple:lla Tämä on vanha Maple 6 -versio, joka avautunee uudemmissa - kuten Maple 2018 - Classic Worksheet - versiona. Työarkkien yhteensopivuus taaksepäin
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Kompleksilukujen kunnan konstruointi
 Kompleksilukujen kunnan konstruointi Seuraava esitys osoittaa, miten kompleksilukujoukko voidaan määritellä tunnetuista reaalisista käsitteistä lähtien. Määrittelyjen jälkeen on helppoa osoittaa Mathematican
Kompleksilukujen kunnan konstruointi Seuraava esitys osoittaa, miten kompleksilukujoukko voidaan määritellä tunnetuista reaalisista käsitteistä lähtien. Määrittelyjen jälkeen on helppoa osoittaa Mathematican
Differentiaali- ja integraalilaskenta 1 Ratkaisut 2. viikolle /
 MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
Kompleksiluvut Kompleksitaso
 . Kompleksiluvut.. Kompleksitaso 8. Todista kompleksilukujen yhteen- ja kertolaskun (lukuparien avulla annettuihin) määritelmiin perustuen osittelulaki: z (z + z ) = z z + z z. 8. Todista kompleksilukujen
. Kompleksiluvut.. Kompleksitaso 8. Todista kompleksilukujen yhteen- ja kertolaskun (lukuparien avulla annettuihin) määritelmiin perustuen osittelulaki: z (z + z ) = z z + z z. 8. Todista kompleksilukujen
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2 3
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pstakselin
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pstakselin
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Matlabin perusteita Grafiikka
 BL40A0000 SSKMO KH 1 Seuraavassa esityksessä oletuksena on, että Matlabia käytetään jossakin ikkunoivassa käyttöjärjestelmässä (PC/Win, Mac, X-Window System). Käytettäessä Matlabia verkon yli joko tekstipäätteeltä,
BL40A0000 SSKMO KH 1 Seuraavassa esityksessä oletuksena on, että Matlabia käytetään jossakin ikkunoivassa käyttöjärjestelmässä (PC/Win, Mac, X-Window System). Käytettäessä Matlabia verkon yli joko tekstipäätteeltä,
linux linux: käyttäjän oikeudet + lisää ja - poistaa oikeuksia
 L6: linux linux linux: käyttäjän oikeudet Käyttäjällä, username, on käyttöoikeus rajattuun levytilaan du -h /home/username/ tulostaa käytetyn levytilan. Yhteenvedon antaa du -h /home/jetsu/ - -summarize
L6: linux linux linux: käyttäjän oikeudet Käyttäjällä, username, on käyttöoikeus rajattuun levytilaan du -h /home/username/ tulostaa käytetyn levytilan. Yhteenvedon antaa du -h /home/jetsu/ - -summarize
Mat-C.1 harj2. Alustuksia f d 1 C sin x 1 C x 2 f := 1 C sin x
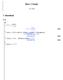 Mat-C.1 harj2 21.3. 2012 Alustuksia 1. a) f d 1 C sin 1 C 2 f := 1 C sin 1 C 2 subs =K2.0, f ; evalf % # Sijoita :n paikalle -2.0 lausekkeessa f. 1 C 0.2000000000 sin K2.0 eval f, =K2.0 plot f, =K5..5
Mat-C.1 harj2 21.3. 2012 Alustuksia 1. a) f d 1 C sin 1 C 2 f := 1 C sin 1 C 2 subs =K2.0, f ; evalf % # Sijoita :n paikalle -2.0 lausekkeessa f. 1 C 0.2000000000 sin K2.0 eval f, =K2.0 plot f, =K5..5
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Harjoitus Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia:
 Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 /
 MS-A3x Differentiaali- ja integraalilaskenta 3, IV/6 Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 / 9..-.3. Avaruusintegraalit ja muuttujanvaihdot Tehtävä 3: Laske sopivalla muunnoksella
MS-A3x Differentiaali- ja integraalilaskenta 3, IV/6 Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 / 9..-.3. Avaruusintegraalit ja muuttujanvaihdot Tehtävä 3: Laske sopivalla muunnoksella
Johdatus f90/95 ohjelmointiin. H, R & R luvut 1-3
 Johdatus f90/95 ohjelmointiin H, R & R luvut 1-3 Fortran-kieli ( 3.1-3) IBM 1954, FORmula TRANslator ISO/ANSI standardit f90, f95, f2003 tieteellinen & teknillinen laskenta rinnakkaislaskenta (HPF, openmp)
Johdatus f90/95 ohjelmointiin H, R & R luvut 1-3 Fortran-kieli ( 3.1-3) IBM 1954, FORmula TRANslator ISO/ANSI standardit f90, f95, f2003 tieteellinen & teknillinen laskenta rinnakkaislaskenta (HPF, openmp)
Mathcad Prime. Kaur Jaakma
 Mathcad Prime Miksi dokumentoidaan Teknisellä dokumentoinnilla saadaan tallennettua tämänhetkinen tilanne CAD, CAE, vaatimuslistat, tuotantosuunnitelmat, suunnittelulaskelmat Mahdollistaa työn jatkamisen
Mathcad Prime Miksi dokumentoidaan Teknisellä dokumentoinnilla saadaan tallennettua tämänhetkinen tilanne CAD, CAE, vaatimuslistat, tuotantosuunnitelmat, suunnittelulaskelmat Mahdollistaa työn jatkamisen
Ville Turunen: Mat Matematiikan peruskurssi P1 1. välikokeen alueen teoriatiivistelmä 2007
 Ville Turunen: Mat-1.1410 Matematiikan peruskurssi P1 1. välikokeen alueen teoriatiivistelmä 2007 Materiaali: kirjat [Adams R. A. Adams: Calculus, a complete course (6th edition), [Lay D. C. Lay: Linear
Ville Turunen: Mat-1.1410 Matematiikan peruskurssi P1 1. välikokeen alueen teoriatiivistelmä 2007 Materiaali: kirjat [Adams R. A. Adams: Calculus, a complete course (6th edition), [Lay D. C. Lay: Linear
