wxmaxima opas 1 Mikä wxmaxima on 2 wxmaximan käyttö Petri Sallasmaa 13. toukokuuta 2014
|
|
|
- Pauliina Tamminen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 wxmaxima opas Petri Sallasmaa 13. toukokuuta Mikä wxmaxima on wxmaxima on yksinkertainen graanen käyttöliittynä Maxima CAS(computer algebra system)-järjestelmälle, joka on luotu wxwidgets nimisen käyttöliittymäkirjaston avulla. wxmaximassa voidaan Maximan komennot syöttää valikkojen tai dialogien avulla, jolloin ei ainakaan alkuun ole välttämätöntä opetella kaikkea komentorivillä käytettävän Maximan komentoja. Perustoimintoja ja muitakin komentoja voi ja kannataa kuitenkin kirjoittaa suoraan dokumentin kirjoitusalueelle. wxmaximan käyttöliittymä on seuraavanlainen: Käyttöliittymän ylälaidassa on tuttu valikko, josta voidaan valita komentoja, jotka sitten suoritetaan dokumentin kirjoitustilassa. wxmaximassa tuotetaan tavallaan tekstidokumenttia johon Maxima tuottaa haluttuja laskennallisia tuloksia. Dokumentti ja näin myös kirjoitusalue on jaettu pienempiin osiin soluihin. Perussoluja ovat syöteet, tulosteen ja erilaiset tekstityyppiset solut. Kirjoitusalueella syötesolut merkitään tunnisteella (%i#), missä # on syötteen järjestysnumero, ja tulosteet (%o#), missä taas # on tulosteen järjestysnumero. Tekstityyppisellä soluilla ei ole numeroituja tunnisteita. Kirjoitusalueella on myös ruudun poikki kulkeva musta viiva, joka on kirjoitusalueen kohdistin (kursori), siis kohta johon ollaan seuraavaksi lisäämässä jotain. 2 wxmaximan käyttö Koska itse Maxima on suhteellisen laaja ohjelma, jolla voidaan laskea vaikeitakin mateemaattisia laskuja, tässä oppaassa keskitytään perustoimintojen suorittamiseen ja lähinnä käyttäen wxmaximan käyttöliittymää. Ihan vertailun vuoksi Maksiman version 5.30, joka tässäkin wxmaximassa on taustalla, virallisessa oppaassa on 1048 sivua. Eli Tässä oppaassa Maximan käytöstä käydään läpi vain murto-osa. 1
2 2.1 Syöttäminen ja peruslaskutoimitukset Söytesolu saadaa kirjoitusalueelle kohdistimen osoittamaan paikkaan valitsemalla valikosta jokin toimenpide tai yksinkertaisesti alkamalla kirjoittaa jotain. Cell-valikossa on myös valittavissa Insert Input Cell, mutta tämä vastaa sitä kun aloittaa kirjoittamaan vain näppäimistöltä tekstiä. Harjoitus 1. Kirjoita syötteeksi 1+1. Nyt Kirjoitusalueella on syöte > 1+1. Tätä syötettä ei ole vielä annettu Maximan prosessoitavaksi ja se tehdään painamalla shift+enter. Pelkkä enter näppäimen painaminen tekee syötteeseen rivinvaihdon, koska syöte saa olla myös monella eri rivilllä. Harjoitus 2. Paina shift+enter, jolloin syöte syötetään Maximalle suoritettavaksi. Nyt kirjoitusalueelle tulee ensimmäinen syöte-tuloste solupari Tässä ensimmäinen syöte on on tunnisteella (%i1) ja sitä vastaava tuloste (%o1). Huomaa että syötteen perään tulee puolipiste(;). Jokainen komento päätetään aina puolipisteeseen tai dollari($)-merkkiin. Nyt kun kirjoitettiin syötteeksi perus laskutoimitus tulosteeksi tulee suoraan sen laskun tulos. Harjoitus 3. Kirjoita syötteeksi 1+1$ ja suorita se (painamalla shift+enter) Nyt kirjoitusalueelle tulee toinen syöte %i2, mutta jos komennon päättää puolipisteen sijaan dollarimerkkiin tuloste ei tule näkyviin. Jossain tilanteessa, esimerkiksi kun määritellään kerralla paljon omia muuttujia tai ketjutettaessa syötteitä ja tulosteita, ei haluta tulostusta tai välitulosta näkyviin ruudulle, niin silloin sen voi tehdä lisäämällä komentojen perään dollarimerkin. Perus laskutoimitukset syötetään niitä vastaavilla operaatioilla. Taulukossa on tyypillisimmät operaatiot ja niitä vastaavat merkit lueteltuna Toiminto Merkki yhteenlasku + vähennyslasku - kertolasku * jakolasku / potenssi ^ sulkeet ( ja ) nelijuuri x sqrt( x ) kertoma! Harjoitus 4. Syötä lasku 1/3+4/7 Huomaa, että laskettaessa kokonaisluvuilla tulosteet ovat rationaalilukuja siis tarkkoja arvoja. Harjoitus 5. Syötä laskut 1/3 ja 1/3.0. Tee se samaa syötteeseen kirjoittamalla laskujen väliin puolipiste siis 1/3;1/3.0; (Huomaa että Maximassa on desimaalipilkun tilalla käytössä desimaalipiste) Nyt tulostelohkossa on kaksi tulostetta %o4 ja %o5. Koska jälkimmäisessä laskussa käytettiin desimaalilukua kokonaisluvun sijaan, vastauskin annettiin kokonaislukuna. Toinen tapa saada vastaus desimaalilukuna on käyttää komentoa oat. Harjoitus 6. Syötä lasku 1/3. Kun saat tuloksen 1 3 valitse valikosta numeric komento To Float. (Saman lopputuloksen saat jos kirjoitat suoraan syötteksi oat(1/3) ) 2
3 Kun valikosta valittiin To Float komento se kohdistettiin edelliseen tulosteeseen. Tämän merkkinä syötteessä %i7 on oat komennon parametri %. Siis aina jos halutaan viitata edelliseen tulokseen sen voi tehdä kirjoittamalla lausekkeeseen tai komentoon yksinkertaisesti %-merkin. Laskuissa ja lausekkeissa voidaan viitata myös mihin tahansa syöteeseen tai tulosteseen käyttämällä niiden nimiä %i# tai #o#, missä # on syötteen tai tulosteen järjestysnumero. Numeerisen laskennan lisäksi perulaskutoimisuksia voidaan tehdä muuttujille. Harjoitus 7. Syötä lasku x+x. Tulokseksi saadaan Harjoitus 8. Syötä lasku 3x+4x. Nyt tulostukseen tulee seuraavanlainen virheilmoitus Maxima, kuten ei yleisesti muutkaan CAS-järjestelmät, ymmärrä impisiittistä kertomerkkiä siis 3x pitää aina kirjoittaa muodossa 3*x. Samoin pitää toimia sulkeiden kanssa siis (x-1)(x+1) pitää kirjoittaa muodoss (x- 1)*(x+1). Muuttuja ovat kirjainkokoherkkiä siis a ja A ovat ei muuttujia. Muuttujat voivat olla myös merkkijonoja siis useamman kirjaimen mittasia. Harjoitus 9. Syötä lasku 3*Petri+4*Petri. Kun kertomerkin ovat paikallaan ja muuttuja on Petri niin tulokseksi tulee 2.2 Vakiot ja omat muuttujat Kuten edellä muuttujia voidaan käyttää niitä sen paremmin määrittelemättä. Mutta kun muuttujalle halutaan määrätä jokin arvo tai lauseke, se tehdään määrittelymerkin : (kaksoispiste) avulla esimerkiksi a : 5 jolloin sijoitetaan muuttujaan a arvo 5 Harjoitus 10. Määrittele muuttuja a siten että sen arvo on 5. Määrittele myös että x on b+c. Siis kirjoitamme syötteeksi a : 5; d : b+c;. Syöttenä on määrittelyt ja kahtena eri tulosteena niiden arvot Tällöin siis seuraavaksi kun lausekkeessa on a niin se korvautuu luvulla 5 ja d lausekkeella b+c. Tieto siitä mitä muuttujia on määritelty saadaan Maxima-valikosta komennolla Show Variables. Niiden arvot saadaan yksinkertaisesti syöttämällä muuttuja niin tulosteena on sen arvo. 3
4 Maximassa on sisäänrakennettuna vakiota ja niitä voi myös käyttää laskuissa ja lausekkeissa. Tärkeimpiä vakiota seuraavassa taulukossa Vakio Maximassa π %pi Eulerin vakio e %e ääretön( ) inf - ääretön( ) minf tosi true epätosi false imaginääriyksikkö i %i Harjoitus 11. Tarkastele vakion π desimaaliarvoa. (Syötä %pi ja muuta se desimaaliesitykseen) 2.3 Funktiot ja funktion määritteleminen Maximassa on paljon sisäänrakennettuja funktiota, siis trigonometrisiä funktiota, itseisravo, minimiä, maksimia, tilastollisiafunktioita ym... Perusfunktiota ja niiden käyttöohjeita löytyy enemmän valikosta Help ja sieltä Maxima Help (tai painamalla F1) valikosta otsikolla Mathematical functions. Funktiota käytetään kuten normaalistikin kirjoittaessa esim sin(x), log(4), abs(-3) (asb on itseisarvo). Harjoitus 12. Kirjoita syötteeksi sin( %pi ) + log( %e); Oman funktion voi määritellä vähän kuten muuttujankin nyt vaan funktiolla pitää olla nimi, muuttujat sulkeissa pilkulla eroteltuna, määrittelymerkkinä kaksoispiste ja yhtäsuuruus ( : = ) ja sitten itse funktion lauseke. Siis f(x) : = 2*x + 1 ja nyt funktion f on määritelty. Harjoitus 13. Määrittele funktio f (x) = 2x 5. Kokeile määrittelemääsi funktiota kysymällä sen arvoja esim f ( -1 ) ja f ( 5 ). Funtioon tai tulosteeseen voi tehdä myös sijoituksen arvon saamiseksi. Sijoituskomento löytyy Simplify valikosta Substitute... Harjoitus 14. Kirjoita syötteeksi x^2. Tämän jälkeen valitse Simplify valikosta Substitute... Nyt Dialogi kysyy mistä lausekkeesta (tai funktiosta), mitä korvataan ja millä korvataan. Korvaa edelisen tulosteen % muuttuja x muttujalla y Näin tulosteessa kaikki muuttujan x esiintymät korvattiin muuttujalla y. Harjoitus 15. Valitse Simplify valikosta uudelleen Substitute... Kijoita nyt dialogiin lausekkeeksi %o18 (eli 18 tuloste joka on tuo x 2 ), muuttuja x korvatan jälleen, mutta nyt luvulla 5. 4
5 Näin lausekkeen x 2 muuttujan paikalle sijoitettiin luku 5 ja sen arvo laskettiin samalla 2.4 Factor, Expand ja simplify Jatketaan tutustumalla Simplify valikon komentoihin Factor Expression ja Expand Expression. Niillä voidaan lausekkeita tai lukuja jakaa tekijöihin tai laajentaa esimerkiksi polymoniksi. Harjoitus 16. Kirjoita syötteeksi 30!. Tulosteeseen tulee kertoman arvo. Tämän jälkeen valitse Simplify valikosta Factor Expression. Näin edellinen tuloste eli 30! saadaan alkulukuhajoitelmana. Tekijöihinjako toimii myös polynomeilla. Harjoitus 17. Kirjoita syötteeksi x^4+2*x^3-x^2-2*x. Tämän jälkeen valitse Simplify valikosta Factor Expression. Näin edellinen tuloste eli neljännenasteen polynomi jakautuu tekijöihin. Toisaalta välillä pitää saada polynimit kerrottua auki. Tämä onnistuu valitsemalla Simplify valikon komennon Expand Expression. Harjoitus 18. Kirjoita syötteeksi (x+3)^4. Tämän jälkeen valitse Simplify valikosta Expand Expression. Näin edellinen tuloste kerrotaan auki summamuotoon Simplify valikossa myös komento lausekkeen sieventämiselle Simlify Expression. Tällä komennolla voidaan sieventää esimerkiksi rationaalilausekkeita. Harjoitus 19. Kirjoita syötteeksi (x^2-4) / (x+2). Tämän jälkeen valitse Simplify valikosta Simplify Expression. Näin edellinen tuloste eli rationaalilauseke sievennetään Huomaa, että sievennys ei ota huomioon määrittelyehtoja siis tässä tapauksessa x 2! 5
6 Edelliset komennot eivät toimi trigonometrisillä funktioilla, mutta niitä varten on Simplify valikossa oma työkalukokoelma Triconometric Simplication jossa on vastaavat komennot trigonometrisille funktioille Harjoitus 20. Kirjoita syötteeksi cos(x)^2 + sin(x)^2; Tämän jäkeen Simplify valikon Trigonometric Simpli- cation valikosta Simplify Trigonometric Harjoitus 21. Kirjoita syötteeksi sin(2*x); Tämän jäkeen Simplify valikon Trigonometric Simplication valikosta Expand Trigonometric 2.5 Yhtälöt ja yhtälöparit Yhtälön ratkaisemiseksi avataan dialogi valikosta Equations ja sieltä komento Solve... Dialogin Equation(s) kenttään syötetään yhtälö. Jos kenttään ei syötetä yhtäruusuusmerkkiä ohjelma tulkitsee että silloin lauseke on nolla siis 2*x+3 syöte vastaa syötettä 2*x+3=0. Variable(s) kenttään syötetään minkä muuttujan suhteen yhtälö ratkaistaan. Harjoitus 22. Avaa yhtälön ratkaisu Equations ja Solve.. ja syötä lauseke x^4+2*x^3-x^2-2*x ja ratkaise se muuttujan x suhteen. (Huomaaa että lauseke on sama joka oli harjoituksessa 17 joten voit myös viitata siihen harjoituksessa olevan syötekentän tunnisteella tässä %i23) Näin saatiin yhtälön ratkaisut 6
7 Jos joku ratkaisuista pitää poimia ratkaisujoikosta se ommistuu kirjoittamalla tulosteen tunnisteen ja hakasulkeisiin ([ ]) halutun ratkaisun järjestysnumero Harjoitus 23. Poimi edellisestä tuloksesta negatiivinen ratkaisu eli toinen ratkaisuista. (Voit nyt viitata tulokseen pelkällä %-merkillä koska se viimeinen tuloste, mutta aina varmenpaa on käyttää oikeea tunnistetta eli tässä %o34 ) Näin esimerkiksi voidaan käyttää yhtä ratkaisua sijoituksessa toiseen lausekkeeseen tai jatkaa laskua siitä ratkaisusta eteenpäin. Yhtälöpari tai yleisemmin yhtälöryhmän ratkaiseminen on yhtä vaivatonta. Nyt vaan Solve... dialogin Equation(s) kenttään syötetään useampi yhtälö pilkulla (, ) eroteltuna. Variable(s) kenttään syötetään ne muuttujat jotka halutaan ratkaista. Harjoitus 24. Avaa yhtälön ratkaisu Equations ja Solve.. ja syötä yhtälöryhmän yhtälot x+y+z=3, -x+y+2*z=3, 3*x+y-2*z=-5 ja ratkaise yhtälöryhmän muuttujat x, y ja z. 2.6 Derivointi ja integrointi Komennot derivointiin ja integrointiin löytyvät Calculus valikosta. Funktion tai lausekkeen derivaatan voi laskea kun valitsee Calculus valikosta Dierentiate... komennon. Derivoitava funktio tai lauseke kirjoitetaan Expression kenttään, Variable(s) kenttään syötetään minkä muuttujan suhteen derivoidaan ja Times kenttää monesko derivaatta lasketaan. Harjoitus 25. Määritä funktio f(x) := x^3 + 5*x^2-2*x + 7. Avaa sitten Calculus valikon Dierentiate.. komento ja derivoi funktio f muuttujan x suhteen kerran. Avaa dialogi uudelleen ja laske funktion f toinen derivaatta muuttujan x suhteen. Integrointi tapahtuu samaisen Calculus valikon komennolla Integrate... Inegroitava funktio tai lauseke kirjoitetaan Expression kenttään, Variable kenttään syötetään minkä muuttujan suhteen integroidaan. Saman dialogin avulla voidaan laskea määrätty integraali. Tällöin valitaan Denite integration valinta ja syötetään integroinille alaja ylärajat. Special napin takaa löytyy rajojen arvoksi erikoisarvoja kuten ääretöntä, pi, ym.. Harjoitus 26. Avaa sitten Calculus valikon Integrate.. komento ja integroi funktio f muuttujan x suhteen. Avaa dialogi uudelleen ja laske funktion f määrätty integraali välillä [0,5]. 7
8 2.7 Kuvaajat Maxima ei itsessään osaa piirtää kuvaajia, mutta ohjelman mukana on ohjelmia, joita Maxima kutsuu kuvaajien piirtämiseksi. Kuvaajat voivat olla kaksi tai kolmeulotteisia. Kaksi ulotteisen kuvaajan piitrtämiseksi valitaan Plot valikosta Plot 2d... Avautuvaan dialogiin Expression(s) kenttään kirjoitetaan funktio tai lauseke, jonka kuvaaja piirretää. Niitä voi taas olla useampia ja ne erotetaan toisistaan pilkulla. Seuraavaksi määrätään piirtoalueen muuttujat Variable vaaka ja pystysuuntaan, sekä niille arvoalueet. Ticks kertoo kuvan piirtotarkkuudesta. Format kertoo piirretäänkö kuva maximadokumentiin (inline) vai tulostetaanko se apuohjelmaan (gnuplot, open math). Options valikolla voidaan säätää esimerkiksi näytetäänko koordinaattiakseleita ja sen sellaista. File kentän avulla kuvan voi tulostaa tiedostoon jos kuvaajan haluaa liittää johonkin muuhun dokumenttiin. Harjoitus 27. Avaa Plot valikosta Plot 2d.. ja syötä lausekkeet -3*x^2+4*x ja -5*x+3 Expression(s) kenttään valitse muuttujiksi x ja y, sekä niille rajoiksi muuttujalle x [-10,10], sekä muuttujalle y [-30,10]. Piirrä kuvaaja. 8
9 Kolmeulotteisten kuvaajan piitrtämiseksi valitaan Plot valikosta Plot 3d... Avautuvaan dialogiin Expression(s) kenttään kirjoitetaan funktio tai lauseke, jonka kuvaaja piirretää. Niitä voi taas olla useampia ja ne erotetaan toisistaan pilkulla. Seuraavaksi määrätään piirtoalueen muuttujat Variable vaaka ja pystysuuntaan, sekä niille arvoalueet. Grid kertoo kuvan kolmiulotteisen ruudukon suuruuden. Format kertoo piirretäänkö kuva maximadokumentiin (inline) vai tulostetaanko se apuohjelmaan (gnuplot, open math). Options valikolla voidaan säätää lisäasetuksia. Plot to le kentän avulla kuvan voi tulostaa tiedostoon jos kuvaajan haluaa liittää johonkin muuhun dokumenttiin. Harjoitus 28. Avaa Plot valikosta Plot 3d.. ja syötä lauseke 2^(-x^2-y^2) Expression kenttään valitse muuttujiksi x ja y, sekä niille rajoiksi -2 ja 2. Piirrä kuvaaja. Harjoitus 29. Avaa Plot valikosta Plot 3d.. ja syötä uudelleen lauseke 2^(-x^2-y^2) Expression kenttään valitse muuttujiksi x ja y, sekä niille rajoiksi -2 ja 2. Valitse Format valikosta gnuplot. Piirrä kuvaaja. Nyt kuvaaja avautuu gnuplot ohjelmaan ja siellä sitä voi esimerkiksi pöyritellä ja zoomailla 2.8 Tekstikentät Cell valikossa on Text, Title, Section ja Subsection tyyppisiä teksti kenttiä joita voi laittaa Maxima-dokumenttiin syötteiden väliin. Näiden avulla voi kirjoitta itselleen tai muille sanallista informaatiota siitä, mitä dokumentissa ollaan laskemassa. Harjoitus 30. Liisää erilaisia teksisyötteitä dokumenttiin 9
10 2.9 Apupanelit Maxima valikosta löytyy valikko Panels. Sieltä esimerkiksi General Math paneelin voi avata näkyviin. Tässä paneelissa on perusmatematiikka komennot kootusti eli tällöin niitä ei tarvitse valikoista hakea. Jos ohjelmaa kuitenkin käytää enemmän alkaa komennot oppia ulkoa ja ne on paljon helpompi kirjoittaa syötteeseen kuin kayttää valikoita. 10
wxmaxima-pikaopas Ari Lehtonen
 wxmaxima-pikaopas Ari Lehtonen. Yleistä Maxima on laaja symboliseen laskentaan suunniteltu ohjelma. Maximalla voidaan sieventää lausekkeita, jakaa polynomeja tekijöihin, ratkaista yhtälöitä, derivoida,
wxmaxima-pikaopas Ari Lehtonen. Yleistä Maxima on laaja symboliseen laskentaan suunniteltu ohjelma. Maximalla voidaan sieventää lausekkeita, jakaa polynomeja tekijöihin, ratkaista yhtälöitä, derivoida,
Harjoitus 10: Mathematica
 Harjoitus 10: Mathematica Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon Mathematican
Harjoitus 10: Mathematica Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon Mathematican
plot(f(x), x=-5..5, y=-10..10)
 [] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
[] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
DIFFERENTIAALI- JA INTEGRAALILASKENTA
 DIFFERENTIAALI- JA INTEGRAALILASKENTA Timo Mäkelä Tässä tekstissä esitellään yhden muuttujan reaaliarvoisten funktioiden differentiaalilaskentaa sekä sarjoja. Raja-arvot Raja-arvoja voidaan laskea käyttämällä
DIFFERENTIAALI- JA INTEGRAALILASKENTA Timo Mäkelä Tässä tekstissä esitellään yhden muuttujan reaaliarvoisten funktioiden differentiaalilaskentaa sekä sarjoja. Raja-arvot Raja-arvoja voidaan laskea käyttämällä
Matriisit ovat matlabin perustietotyyppejä. Yksinkertaisimmillaan voimme esitellä ja tallentaa 1x1 vektorin seuraavasti: >> a = 9.81 a = 9.
 Python linkit: Python tutoriaali: http://docs.python.org/2/tutorial/ Numpy&Scipy ohjeet: http://docs.scipy.org/doc/ Matlabin alkeet (Pääasiassa Deni Seitzin tekstiä) Matriisit ovat matlabin perustietotyyppejä.
Python linkit: Python tutoriaali: http://docs.python.org/2/tutorial/ Numpy&Scipy ohjeet: http://docs.scipy.org/doc/ Matlabin alkeet (Pääasiassa Deni Seitzin tekstiä) Matriisit ovat matlabin perustietotyyppejä.
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pystyakselin
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pystyakselin
Opiskelijan pikaopas STACK-tehtäviin. Lassi Korhonen, Oulun yliopisto
 Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Hannu Mäkiö. kertolasku * jakolasku / potenssiin korotus ^ Syöte Geogebran vastaus
 Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
KAAVAT. Sisällysluettelo
 Excel 2013 Kaavat Sisällysluettelo KAAVAT KAAVAT... 1 Kaavan tekeminen... 2 Kaavan tekeminen osoittamalla... 2 Kaavan kopioiminen... 3 Kaavan kirjoittaminen... 3 Summa-funktion lisääminen... 4 Suorat eli
Excel 2013 Kaavat Sisällysluettelo KAAVAT KAAVAT... 1 Kaavan tekeminen... 2 Kaavan tekeminen osoittamalla... 2 Kaavan kopioiminen... 3 Kaavan kirjoittaminen... 3 Summa-funktion lisääminen... 4 Suorat eli
Harjoitus 1: Matlab. Harjoitus 1: Matlab. Mat Sovelletun matematiikan tietokonetyöt 1. Syksy 2006
 Harjoitus 1: Matlab Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Matlab-ohjelmistoon Laskutoimitusten
Harjoitus 1: Matlab Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen Matlab-ohjelmistoon Laskutoimitusten
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan Plots/Insert Plot/XY plot Huomaa - ja y-akselin paikanvaraajat (ja näissä valmiina yksikön syöttöruutu). Siirrä - akselia ylös/alas. Palauta origo perinteiseen
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan Plots/Insert Plot/XY plot Huomaa - ja y-akselin paikanvaraajat (ja näissä valmiina yksikön syöttöruutu). Siirrä - akselia ylös/alas. Palauta origo perinteiseen
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
GeoGebra-harjoituksia malu-opettajille
 GeoGebra-harjoituksia malu-opettajille 1. Ohjelman kielen vaihtaminen Mikäli ohjelma ei syystä tai toisesta avaudu toivomallasi kielellä, voit vaihtaa ohjelman käyttöliittymän kielen seuraavasti: 2. Fonttikoon
GeoGebra-harjoituksia malu-opettajille 1. Ohjelman kielen vaihtaminen Mikäli ohjelma ei syystä tai toisesta avaudu toivomallasi kielellä, voit vaihtaa ohjelman käyttöliittymän kielen seuraavasti: 2. Fonttikoon
Harjoitus 1 -- Ratkaisut
 Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
MATP153 Approbatur 1B Ohjaus 2 Keskiviikko torstai
 MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
Differentiaali- ja integraalilaskenta 1. Tietokoneharjoitus: ratkaisut
 Johdanto Kokeile tavallista numeroilla laskemista: yhteen-, kerto- ja jakolaskuja sekä potenssiinkorotusta. 5 (3.1) Differentiaali- ja integraalilaskenta 1 Tietokoneharjoitus: ratkaisut Kurssin 1. alkuviikon
Johdanto Kokeile tavallista numeroilla laskemista: yhteen-, kerto- ja jakolaskuja sekä potenssiinkorotusta. 5 (3.1) Differentiaali- ja integraalilaskenta 1 Tietokoneharjoitus: ratkaisut Kurssin 1. alkuviikon
Excel syventävät harjoitukset 31.8.2015
 Yleistä Excel on taulukkolaskentaohjelma. Tämä tarkoittaa sitä että sillä voi laskea laajoja, paljon laskentatehoa vaativia asioita, esimerkiksi fysiikan laboratoriotöiden koetuloksia. Excel-ohjelmalla
Yleistä Excel on taulukkolaskentaohjelma. Tämä tarkoittaa sitä että sillä voi laskea laajoja, paljon laskentatehoa vaativia asioita, esimerkiksi fysiikan laboratoriotöiden koetuloksia. Excel-ohjelmalla
Valitse ruudun yläosassa oleva painike Download Scilab.
 Luku 1 Ohjeita ohjelmiston Scilab käyttöön 1.1 Ohjelmiston lataaminen Ohjeet ohjelmiston lataamiseen Windows-koneelle. Mene verkko-osoitteeseen www.scilab.org. Valitse ruudun yläosassa oleva painike Download
Luku 1 Ohjeita ohjelmiston Scilab käyttöön 1.1 Ohjelmiston lataaminen Ohjeet ohjelmiston lataamiseen Windows-koneelle. Mene verkko-osoitteeseen www.scilab.org. Valitse ruudun yläosassa oleva painike Download
Python-ohjelmointi Harjoitus 2
 Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)
![mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011) mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)](/thumbs/91/107207023.jpg) Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
Kevään 2011 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä /
 Kevään 0 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä / 8.7.0 a) b) c) a) Tehtävä Yhtälö ratkaistaan yleensä Solve-funktiolla: Solve x 3 x, x x 4 Joissakin tapauksissa
Kevään 0 pitkän matematiikan ylioppilastehtävien ratkaisut Mathematicalla Simo K. Kivelä / 8.7.0 a) b) c) a) Tehtävä Yhtälö ratkaistaan yleensä Solve-funktiolla: Solve x 3 x, x x 4 Joissakin tapauksissa
Harjoitus 1 -- Ratkaisut
 Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
Kun teet harjoitustyöselostuksia Mathematicalla, voit luoda selkkariin otsikon (ja mahdollisia alaotsikoita...) määräämällä soluille erilaisia tyylejä. Uuden solun tyyli määrätään painamalla ALT ja jokin
12. Differentiaaliyhtälöt
 1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
Luento 5. Timo Savola. 28. huhtikuuta 2006
 UNIX-käyttöjärjestelmä Luento 5 Timo Savola 28. huhtikuuta 2006 Osa I Shell-ohjelmointi Ehtolause Lausekkeet suoritetaan jos ehtolausekkeen paluuarvo on 0 if ehtolauseke then lauseke
UNIX-käyttöjärjestelmä Luento 5 Timo Savola 28. huhtikuuta 2006 Osa I Shell-ohjelmointi Ehtolause Lausekkeet suoritetaan jos ehtolausekkeen paluuarvo on 0 if ehtolauseke then lauseke
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Javan perusteet. Ohjelman tehtävät: tietojen syöttö, lukeminen prosessointi, halutun informaation tulostaminen tulostus tiedon varastointi
 1 Javan perusteet Ohjelmointi IPO-malli Java lähdekoodista suoritettavaksi ohjelmaksi Vakio Muuttuja Miten Javalla näytetään tietoa käyttäjälle, miten Javalla luetaan käyttäjän antama syöte Miten Javalla
1 Javan perusteet Ohjelmointi IPO-malli Java lähdekoodista suoritettavaksi ohjelmaksi Vakio Muuttuja Miten Javalla näytetään tietoa käyttäjälle, miten Javalla luetaan käyttäjän antama syöte Miten Javalla
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
2. Lisää Java-ohjelmoinnin alkeita. Muuttuja ja viittausmuuttuja (1/4) Muuttuja ja viittausmuuttuja (2/4)
 2. Lisää Java-ohjelmoinnin alkeita Muuttuja ja viittausmuuttuja Vakio ja literaalivakio Sijoituslause Syötteen lukeminen ja Scanner-luokka 1 Muuttuja ja viittausmuuttuja (1/4) Edellä mainittiin, että String-tietotyyppi
2. Lisää Java-ohjelmoinnin alkeita Muuttuja ja viittausmuuttuja Vakio ja literaalivakio Sijoituslause Syötteen lukeminen ja Scanner-luokka 1 Muuttuja ja viittausmuuttuja (1/4) Edellä mainittiin, että String-tietotyyppi
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Luvuilla laskeminen. Esim. 1 Laske 6 21 7
 Luvuilla laskeminen TI-84 Plus käyttää laskujen suorittamiseen ns. yhtälönkäsittelyjärjestelmää (EOS TM, Equation Operating System), jonka avulla lausekkeiden syöttö tapahtuu matemaattisessa kirjoitusjärjestyksessä.
Luvuilla laskeminen TI-84 Plus käyttää laskujen suorittamiseen ns. yhtälönkäsittelyjärjestelmää (EOS TM, Equation Operating System), jonka avulla lausekkeiden syöttö tapahtuu matemaattisessa kirjoitusjärjestyksessä.
PERUSLASKUJA. Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +5^2
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/4+^2 3 4+ 2 Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +^2 3 + 4 2 Kopioi
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/4+^2 3 4+ 2 Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +^2 3 + 4 2 Kopioi
Maxima ja Maple. millaan lailla sukua muuttujille a ja b. 1 Ohjelmat eivät yleensä pahastu turhista välilyönneistä, joten niitä
 Maxima ja Maple Maple on symbolisen matematiikan laskentaohjelma jota käytetään esim. Joensuun yliopistossa; siihen on törmätty mestariluokan laskuharjoituksissa. Koska Maple on kaupallinen ohjelma ja
Maxima ja Maple Maple on symbolisen matematiikan laskentaohjelma jota käytetään esim. Joensuun yliopistossa; siihen on törmätty mestariluokan laskuharjoituksissa. Koska Maple on kaupallinen ohjelma ja
Yhtälöryhmät 1/6 Sisältö ESITIEDOT: yhtälöt
 Yhtälöryhmät 1/6 Sisältö Yhtälöryhmä Yhtälöryhmässä on useita yhtälöitä ja yleensä myös useita tuntemattomia. Tavoitteena on löytää tuntemattomille sellaiset arvot, että kaikki yhtälöt toteutuvat samanaikaisesti.
Yhtälöryhmät 1/6 Sisältö Yhtälöryhmä Yhtälöryhmässä on useita yhtälöitä ja yleensä myös useita tuntemattomia. Tavoitteena on löytää tuntemattomille sellaiset arvot, että kaikki yhtälöt toteutuvat samanaikaisesti.
Valokuvien matematiikkaa
 Valokuvien matematiikkaa Avainsanat: valokuva, pikseli, päättely Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: Kynä, tehtävämonisteet (liitteenä), mahdollisiin jatkotutkimuksiin tietokone
Valokuvien matematiikkaa Avainsanat: valokuva, pikseli, päättely Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: Kynä, tehtävämonisteet (liitteenä), mahdollisiin jatkotutkimuksiin tietokone
YKSIKÖT Tarkista, että sinulla on valittuna SI-järjestelmä. Math/Units Ohjelma tulostaa/käyttää laskennassaan valittua järjestelmää.
 YKSIKÖT Tarkista, että sinulla on valittuna SI-järjestelmä. Math/Units Ohjelma tulostaa/käyttää laskennassaan valittua järjestelmää. HUOM! Käytettäessä yksikköjä on huomioitava dokumentissa käytettävät
YKSIKÖT Tarkista, että sinulla on valittuna SI-järjestelmä. Math/Units Ohjelma tulostaa/käyttää laskennassaan valittua järjestelmää. HUOM! Käytettäessä yksikköjä on huomioitava dokumentissa käytettävät
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Rationaalilauseke ja -funktio
 4.8.07 Rationaalilauseke ja -funktio Määritelmä, rationaalilauseke ja funktio: Kahden polynomin ja osamäärä, 0 on rationaalilauseke, jonka osoittaja on ja nimittäjä. Huomaa, että pelkkä polynomi on myös
4.8.07 Rationaalilauseke ja -funktio Määritelmä, rationaalilauseke ja funktio: Kahden polynomin ja osamäärä, 0 on rationaalilauseke, jonka osoittaja on ja nimittäjä. Huomaa, että pelkkä polynomi on myös
Harjoitus 3 -- Ratkaisut
 Harjoitus 3 -- Ratkaisut 1 ' '-merkki kirjoitetaan =, ' '-merkki!=, ' '-merkki ==. Yhtälöiden ratkaisusta puhutaan lisää myöhemmin. a f x, y : If ehtolauseke x y, y tämä palautetaan, jos
Harjoitus 3 -- Ratkaisut 1 ' '-merkki kirjoitetaan =, ' '-merkki!=, ' '-merkki ==. Yhtälöiden ratkaisusta puhutaan lisää myöhemmin. a f x, y : If ehtolauseke x y, y tämä palautetaan, jos
Lineaarinen yhtälöryhmä
 Lineaarinen yhtälöryhmä 1 / 39 Lineaarinen yhtälö Määritelmä 1 Lineaarinen yhtälö on muotoa a 1 x 1 + a 2 x 2 + + a n x n = b, missä a i, b R, i = 1,..., n ovat tunnettuja ja x i R, i = 1,..., n ovat tuntemattomia.
Lineaarinen yhtälöryhmä 1 / 39 Lineaarinen yhtälö Määritelmä 1 Lineaarinen yhtälö on muotoa a 1 x 1 + a 2 x 2 + + a n x n = b, missä a i, b R, i = 1,..., n ovat tunnettuja ja x i R, i = 1,..., n ovat tuntemattomia.
FUNKTION KUVAAJAN PIIRTÄMINEN
 FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pstakselin
FUNKTION KUVAAJAN PIIRTÄMINEN Saat kuvapohjan painamalla @-näppäintä tai Insert/Graph/X-Y-POT. Kuvapohjassa on kuusi paikanvaraaja: vaaka-akselin keskellä muuttuja ja päissä minimi- ja maksimiarvot pstakselin
Python-ohjelmointi Harjoitus 5
 Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
Alkuarvot ja tyyppimuunnokset (1/5) Alkuarvot ja tyyppimuunnokset (2/5) Alkuarvot ja tyyppimuunnokset (3/5)
 Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 21.1.2009 T-106.1208 Ohjelmoinnin perusteet Y 21.1.2009 1 / 32 Tyypeistä Monissa muissa ohjelmointikielissä (esim. Java ja C) muuttujat on määriteltävä ennen
Ohjelmoinnin perusteet Y Python T-106.1208 21.1.2009 T-106.1208 Ohjelmoinnin perusteet Y 21.1.2009 1 / 32 Tyypeistä Monissa muissa ohjelmointikielissä (esim. Java ja C) muuttujat on määriteltävä ennen
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 20.1.2010 T-106.1208 Ohjelmoinnin perusteet Y 20.1.2010 1 / 40 Arvon pyytäminen käyttäjältä Käyttäjän antaman arvon voi lukea raw_input-käskyllä. Käskyn sulkujen
Ohjelmoinnin perusteet Y Python T-106.1208 20.1.2010 T-106.1208 Ohjelmoinnin perusteet Y 20.1.2010 1 / 40 Arvon pyytäminen käyttäjältä Käyttäjän antaman arvon voi lukea raw_input-käskyllä. Käskyn sulkujen
Ohjelmassa henkilön etunimi ja sukunimi luetaan kahteen muuttujaan seuraavasti:
 1 (7) Tiedon lukeminen näppäimistöltä Scanner-luokan avulla Miten ohjelma saa käyttöönsä käyttäjän kirjoittamaa tekstiä? Järjestelmässä on olemassa ns. syöttöpuskuri näppäimistöä varten. Syöttöpuskuri
1 (7) Tiedon lukeminen näppäimistöltä Scanner-luokan avulla Miten ohjelma saa käyttöönsä käyttäjän kirjoittamaa tekstiä? Järjestelmässä on olemassa ns. syöttöpuskuri näppäimistöä varten. Syöttöpuskuri
Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica
 Simo K. Kivelä Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica Symbolinen laskenta ei aina toimi, kuten voisi odottaa. Parempi onkin ajatella, että se elää omaa elämäänsä, jolla
Simo K. Kivelä Mitä symbolilaskentaohjelmalta voi odottaa ja mitä ei? Tapaus Mathematica Symbolinen laskenta ei aina toimi, kuten voisi odottaa. Parempi onkin ajatella, että se elää omaa elämäänsä, jolla
Aki Taanila LINEAARINEN OPTIMOINTI
 Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
Mukavia kokeiluja ClassPad 330 -laskimella
 Mukavia kokeiluja ClassPad 330 -laskimella Tervetuloa tutustumaan Casio ClassPad laskimeen! Jos laskin ei ole yksin omassa käytössäsi, on hyvä tyhjentää aluksi muistit ja näytöt valikosta Edit->Clear All
Mukavia kokeiluja ClassPad 330 -laskimella Tervetuloa tutustumaan Casio ClassPad laskimeen! Jos laskin ei ole yksin omassa käytössäsi, on hyvä tyhjentää aluksi muistit ja näytöt valikosta Edit->Clear All
Geogebra -koulutus. Ohjelmistojen pedagoginen hyödyntäminen
 Geogebra -koulutus Ohjelmistojen pedagoginen hyödyntäminen Geogebra Ilmainen dynaaminen matematiikkaohjelmisto osoitteessa http://www.geogebra.org Geogebra-sovellusversion voi asentaa tietokoneilla ja
Geogebra -koulutus Ohjelmistojen pedagoginen hyödyntäminen Geogebra Ilmainen dynaaminen matematiikkaohjelmisto osoitteessa http://www.geogebra.org Geogebra-sovellusversion voi asentaa tietokoneilla ja
Fx-CP400 -laskimella voit ratkaista yhtälöitä ja yhtälöryhmiä eri tavoin.
 3. Yhtälöt Fx-CP400 -laskimella voit ratkaista yhtälöitä ja yhtälöryhmiä eri tavoin. 3.1 Ensimmäisen asteen yhtälöt Ratkaise yhtälö. 3 x ( x 3) 4x 5 Kirjoita tehtävä sellaisenaan, maalaa se ja käytä Interactive
3. Yhtälöt Fx-CP400 -laskimella voit ratkaista yhtälöitä ja yhtälöryhmiä eri tavoin. 3.1 Ensimmäisen asteen yhtälöt Ratkaise yhtälö. 3 x ( x 3) 4x 5 Kirjoita tehtävä sellaisenaan, maalaa se ja käytä Interactive
n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa.
 MAA 12 kertaus Funktion kuvaaja n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa. Funktion nollakohta on piste, jossa f () = 0, eli kuvaaja leikkaa -akselin. Kuvaajan avulla
MAA 12 kertaus Funktion kuvaaja n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa. Funktion nollakohta on piste, jossa f () = 0, eli kuvaaja leikkaa -akselin. Kuvaajan avulla
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Mathcad Prime. Kaur Jaakma
 Mathcad Prime Miksi dokumentoidaan Teknisellä dokumentoinnilla saadaan tallennettua tämänhetkinen tilanne CAD, CAE, vaatimuslistat, tuotantosuunnitelmat, suunnittelulaskelmat Mahdollistaa työn jatkamisen
Mathcad Prime Miksi dokumentoidaan Teknisellä dokumentoinnilla saadaan tallennettua tämänhetkinen tilanne CAD, CAE, vaatimuslistat, tuotantosuunnitelmat, suunnittelulaskelmat Mahdollistaa työn jatkamisen
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 27.1.2010 T-106.1208 Ohjelmoinnin perusteet Y 27.1.2010 1 / 37 If-käsky toistokäskyn sisällä def main(): HELLERAJA = 25.0 print "Anna lampotiloja, lopeta -300:lla."
Ohjelmoinnin perusteet Y Python T-106.1208 27.1.2010 T-106.1208 Ohjelmoinnin perusteet Y 27.1.2010 1 / 37 If-käsky toistokäskyn sisällä def main(): HELLERAJA = 25.0 print "Anna lampotiloja, lopeta -300:lla."
Harjoitus 5: Symbolinen laskenta I (Mathematica)
 Harjoitus 5: Symbolinen laskenta I (Mathematica) SCI-C0200 Fysiikan ja matematiikan menetelmien studio SCI-C0200 Fysiikan ja matematiikan menetelmien studio 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon
Harjoitus 5: Symbolinen laskenta I (Mathematica) SCI-C0200 Fysiikan ja matematiikan menetelmien studio SCI-C0200 Fysiikan ja matematiikan menetelmien studio 1 Harjoituksen aiheita Tutustuminen Mathematica-ohjelmistoon
Merkitse kertolasku 3 3 3 3 potenssin avulla ja laske sen arvo.
 13 Luvun potenssi Kertolasku, jonka kaikki tekijät ovat samoja, voidaan merkitä lyhyemmin potenssin avulla. Potenssimerkinnässä eksponentti ilmaisee, kuinka monta kertaa kantaluku esiintyy tulossa. Potenssin
13 Luvun potenssi Kertolasku, jonka kaikki tekijät ovat samoja, voidaan merkitä lyhyemmin potenssin avulla. Potenssimerkinnässä eksponentti ilmaisee, kuinka monta kertaa kantaluku esiintyy tulossa. Potenssin
Johdatus Ohjelmointiin
 Johdatus Ohjelmointiin Syksy 2006 Viikko 2 13.9. - 14.9. Tällä viikolla käsiteltävät asiat Peruskäsitteitä Kiintoarvot Tiedon tulostus Yksinkertaiset laskutoimitukset Muuttujat Tiedon syöttäminen Hyvin
Johdatus Ohjelmointiin Syksy 2006 Viikko 2 13.9. - 14.9. Tällä viikolla käsiteltävät asiat Peruskäsitteitä Kiintoarvot Tiedon tulostus Yksinkertaiset laskutoimitukset Muuttujat Tiedon syöttäminen Hyvin
2 Yhtälöitä ja epäyhtälöitä
 2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti. Piirrä integroitavan funktion kuvaaja. Mikä itse asiassa on integraalin arvo?
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2 3
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
Derivaatta graafisesti, h- ja keskeisdifferenssimuodot GeoGebralla Valokuva-albumi
 Derivaatta graafisesti, h- ja keskeisdifferenssimuodot GeoGebralla Valokuva-albumi Jussi Kytömäki Lisätiedot ja tekijä: PPT-tiedoston jussi tilaus Jussi.kytomaki@ylojarvi.fi 15.12.2015 GeoGebra-tiedosto
Derivaatta graafisesti, h- ja keskeisdifferenssimuodot GeoGebralla Valokuva-albumi Jussi Kytömäki Lisätiedot ja tekijä: PPT-tiedoston jussi tilaus Jussi.kytomaki@ylojarvi.fi 15.12.2015 GeoGebra-tiedosto
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 6.3.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 6.3.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Java-kielen perusteet
 Java-kielen perusteet Tunnus, varattu sana, kommentti Muuttuja, alkeistietotyyppi, merkkijono, literaalivakio, nimetty vakio Tiedon merkkipohjainen tulostaminen 1 Tunnus Java tunnus Java-kirjain Java-numero
Java-kielen perusteet Tunnus, varattu sana, kommentti Muuttuja, alkeistietotyyppi, merkkijono, literaalivakio, nimetty vakio Tiedon merkkipohjainen tulostaminen 1 Tunnus Java tunnus Java-kirjain Java-numero
MAY01 Lukion matematiikka 1
 MAY01 Lukion matematiikka 1 - Oppikirja: Yhteinen tekijä, Lukion matematiikka 1: Luvut ja lukujonot (paperisena tai sähköisenä ) - Kurssilla tarvitaan myös tietokone, TI-laskinohjelma, geogebraohjelma,
MAY01 Lukion matematiikka 1 - Oppikirja: Yhteinen tekijä, Lukion matematiikka 1: Luvut ja lukujonot (paperisena tai sähköisenä ) - Kurssilla tarvitaan myös tietokone, TI-laskinohjelma, geogebraohjelma,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu!
 Lineaarialgebra a, kevät 2018 Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu! Klikkaa kappaleet auki kolmiosta restart; # Tämä unohduttaa aikaisemmat
Lineaarialgebra a, kevät 2018 Kotilaskut 1 yms. Maple:lla Maple 2017 versio. Työarkkien yhteensopivuus taaksepäin ei ole taattu! Klikkaa kappaleet auki kolmiosta restart; # Tämä unohduttaa aikaisemmat
Matriiseista. Emmi Koljonen
 Matriiseista Emmi Koljonen 3. lokakuuta 22 Usein meillä on monta systeemiä kuvaavaa muuttujaa ja voimme kirjoittaa niiden välille riippuvaisuuksia, esim. piirin silmukoihin voidaan soveltaa silmukkavirtayhtälöitä.
Matriiseista Emmi Koljonen 3. lokakuuta 22 Usein meillä on monta systeemiä kuvaavaa muuttujaa ja voimme kirjoittaa niiden välille riippuvaisuuksia, esim. piirin silmukoihin voidaan soveltaa silmukkavirtayhtälöitä.
Jypelin käyttöohjeet» Ruutukentän luominen
 Jypelin käyttöohjeet» Ruutukentän luominen Pelissä kentän (Level) voi luoda tekstitiedostoon "piirretyn" mallin mukaisesti. Tällöin puhutaan, että tehdään ns. ruutukenttä, sillä tekstitiedostossa jokainen
Jypelin käyttöohjeet» Ruutukentän luominen Pelissä kentän (Level) voi luoda tekstitiedostoon "piirretyn" mallin mukaisesti. Tällöin puhutaan, että tehdään ns. ruutukenttä, sillä tekstitiedostossa jokainen
Harjoitus 4 -- Ratkaisut
 Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio: In[15]:= f x : x 1 x Sin x ; Plot f x, x, 0, 3 Π, PlotRange All Out[159]= Luodaan tasavälinen pisteistö välille 0 x 3 Π. Tehdään se ensin kiinnitetyllä
Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio: In[15]:= f x : x 1 x Sin x ; Plot f x, x, 0, 3 Π, PlotRange All Out[159]= Luodaan tasavälinen pisteistö välille 0 x 3 Π. Tehdään se ensin kiinnitetyllä
815338A Ohjelmointikielten periaatteet Harjoitus 2 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
Kerta 2. Kerta 2 Kerta 3 Kerta 4 Kerta 5. 1. Toteuta Pythonilla seuraava ohjelma:
 Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
OpenOffice.org Base 3.1.0
 OpenOffice.org Base 3.1.0 Sisällysluettelo 1 Tietokannan luominen...1 2 Taulukon eli taulun luominen...3 3 Kysely...9 4 Raportti...14 1 Tietokannan luominen Tietokanta on kokoelma tietoja, joilla on yhteys
OpenOffice.org Base 3.1.0 Sisällysluettelo 1 Tietokannan luominen...1 2 Taulukon eli taulun luominen...3 3 Kysely...9 4 Raportti...14 1 Tietokannan luominen Tietokanta on kokoelma tietoja, joilla on yhteys
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
1 Peruslaskuvalmiudet
 1 Peruslaskuvalmiudet 11 Lukujoukot N {1,, 3, 4,} on luonnollisten lukujen joukko (0 mukana, jos tarvitaan), Z {, 3,, 1, 0, 1,, 3,} on kokonaislukujen joukko, Q m n : m, n Z, n 0 on rationaalilukujen joukko,
1 Peruslaskuvalmiudet 11 Lukujoukot N {1,, 3, 4,} on luonnollisten lukujen joukko (0 mukana, jos tarvitaan), Z {, 3,, 1, 0, 1,, 3,} on kokonaislukujen joukko, Q m n : m, n Z, n 0 on rationaalilukujen joukko,
Seuraavassa on esitetty seuraavien laskutoimitusten suoritukset eri laskinmalleilla
 Seuraavassa on esitetty seuraavien laskutoimitusten suoritukset eri laskinmalleilla Muuttuja Frekvenssi 7 12 8 16 9 11 10 8 Tilastomoodin valinta. Tilastomuistin tyhjennys. Keskiarvon ja keskihajonnan
Seuraavassa on esitetty seuraavien laskutoimitusten suoritukset eri laskinmalleilla Muuttuja Frekvenssi 7 12 8 16 9 11 10 8 Tilastomoodin valinta. Tilastomuistin tyhjennys. Keskiarvon ja keskihajonnan
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Luvun π irrationaalisuus. Ilari Vallivaara
 Luvun π irrationaalisuus Ilari Vallivaara 27. marraskuuta 24 Sisältö 1 Esipuhe 2 2 Todistuksen pääpiirteinen kulku 3 3 Todistus 4 Lähdeluettelo 9 1 1 Esipuhe Luvun π irrationaalisuus seuraa suoraan sen
Luvun π irrationaalisuus Ilari Vallivaara 27. marraskuuta 24 Sisältö 1 Esipuhe 2 2 Todistuksen pääpiirteinen kulku 3 3 Todistus 4 Lähdeluettelo 9 1 1 Esipuhe Luvun π irrationaalisuus seuraa suoraan sen
Ohjeita LINDOn ja LINGOn käyttöön
 Ohjeita LINDOn ja LINGOn käyttöön LINDOn tärkeimmät komennot ovat com (command), joka tuloaa käytettävissä olevat komennot ruudulle, ja help, jonka avulla saa tietoa eri komennoia. Vaaukset kursiivilla
Ohjeita LINDOn ja LINGOn käyttöön LINDOn tärkeimmät komennot ovat com (command), joka tuloaa käytettävissä olevat komennot ruudulle, ja help, jonka avulla saa tietoa eri komennoia. Vaaukset kursiivilla
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Vektorit. Vektorin luominen... 192 Vektorin tuominen näyttöön... 195 Vektorin koon ja alkioiden muokkaaminen... 195 Vektorin poistaminen...
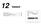 12 Vektorit Vektorin luominen... 192 Vektorin tuominen näyttöön... 195 Vektorin koon ja alkioiden muokkaaminen... 195 Vektorin poistaminen... 196 TI -86 M1 M2 M3 M4 M5 F1 F2 F3 F4 F5 192 Luku 12: Vektorit
12 Vektorit Vektorin luominen... 192 Vektorin tuominen näyttöön... 195 Vektorin koon ja alkioiden muokkaaminen... 195 Vektorin poistaminen... 196 TI -86 M1 M2 M3 M4 M5 F1 F2 F3 F4 F5 192 Luku 12: Vektorit
MATHCAD. Kokeilemalla voi tarkistaa tunnistaako MATHCAD halutun kerrannaisyksikön: Siis ei tunnistanut millinewtonia
 YKSIKÖT Valitsemalla Tools/Worksheet Options/Unit System nähdään, että Mcad:ssa on käytettävissä SI,MKS-, CGS-, U.S- yksikkövalikoimat sekä vaihtoehto None, jolloin käytettävät yksiköt voi määritellä itse.
YKSIKÖT Valitsemalla Tools/Worksheet Options/Unit System nähdään, että Mcad:ssa on käytettävissä SI,MKS-, CGS-, U.S- yksikkövalikoimat sekä vaihtoehto None, jolloin käytettävät yksiköt voi määritellä itse.
Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37
 Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37 Tehtävä 1: Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
Matriisilaskenta Laskuharjoitus 1 - Ratkaisut / vko 37 Tehtävä 1: Käynnistä Matlab-ohjelma ja kokeile laskea sillä muutama peruslaskutoimitus: laske jokin yhteen-, vähennys-, kerto- ja jakolasku. Laske
Ohjelmointitaito (ict1td002, 12 op) Kevät 2008. 1. Java-ohjelmoinnin alkeita. Tietokoneohjelma. Raine Kauppinen raine.kauppinen@haaga-helia.
 Ohjelmointitaito (ict1td002, 12 op) Kevät 2008 Raine Kauppinen raine.kauppinen@haaga-helia.fi 1. Java-ohjelmoinnin alkeita Tietokoneohjelma Java-kieli ja Eclipse-ympäristö Java-ohjelma ja ohjelmaluokka
Ohjelmointitaito (ict1td002, 12 op) Kevät 2008 Raine Kauppinen raine.kauppinen@haaga-helia.fi 1. Java-ohjelmoinnin alkeita Tietokoneohjelma Java-kieli ja Eclipse-ympäristö Java-ohjelma ja ohjelmaluokka
Zeon PDF Driver Trial
 Matlab-harjoitus 2: Kuvaajien piirto, skriptit ja funktiot. Matlabohjelmoinnin perusteita Numeerinen integrointi trapezoidaalimenetelmällä voidaan tehdä komennolla trapz. Esimerkki: Vaimenevan eksponentiaalin
Matlab-harjoitus 2: Kuvaajien piirto, skriptit ja funktiot. Matlabohjelmoinnin perusteita Numeerinen integrointi trapezoidaalimenetelmällä voidaan tehdä komennolla trapz. Esimerkki: Vaimenevan eksponentiaalin
Funktiot. 3.1 Itse määritellyn funktion lauseke Y = Funktio määritellään Y= -editorissa, jonne päästään näppäilemällä Y =.
 0 Funktiot 3.1 Itse määritellyn funktion lauseke Y = Funktio määritellään Y= -editorissa, jonne päästään näppäilemällä Y =. Esim. 1 a) Kirjoita lauseke Y 1 = + 3 (kuva 1) ja paina ENTER. Muuttuja (suuri
0 Funktiot 3.1 Itse määritellyn funktion lauseke Y = Funktio määritellään Y= -editorissa, jonne päästään näppäilemällä Y =. Esim. 1 a) Kirjoita lauseke Y 1 = + 3 (kuva 1) ja paina ENTER. Muuttuja (suuri
MAY1 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 12.4.2016 Julkaiseminen sallittu vain koulun suljetussa verkossa.
 KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
KERTAUS Lukujono KERTAUSTEHTÄVIÄ K1. Ratkaisussa annetaan esimerkit mahdollisista säännöistä. a) Jatketaan lukujonoa: 2, 4, 6, 8, 10, 12, 14, 16, Rekursiivinen sääntö on, että lukujonon ensimmäinen jäsen
Java-kielen perusteet
 Java-kielen perusteet Tunnus, varattu sana, kommentti Muuttuja, alkeistietotyyppi, merkkijono, Vakio Tiedon merkkipohjainen tulostaminen Ohjelmointi (ict1tx006) Tunnus (5.3) Javan tunnus Java-kirjain Java-numero
Java-kielen perusteet Tunnus, varattu sana, kommentti Muuttuja, alkeistietotyyppi, merkkijono, Vakio Tiedon merkkipohjainen tulostaminen Ohjelmointi (ict1tx006) Tunnus (5.3) Javan tunnus Java-kirjain Java-numero
Värähtelevä jousisysteemi
 Mathematican version 8 mukainen. (5.10.01 SKK) Värähtelevä jousisysteemi Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla m d x k x, d t missä x on jousen
Mathematican version 8 mukainen. (5.10.01 SKK) Värähtelevä jousisysteemi Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla m d x k x, d t missä x on jousen
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 2.3.2009 T-106.1208 Ohjelmoinnin perusteet Y 2.3.2009 1 / 28 Puhelinluettelo, koodi def lue_puhelinnumerot(): print "Anna lisattavat nimet ja numerot." print
Ohjelmoinnin perusteet Y Python T-106.1208 2.3.2009 T-106.1208 Ohjelmoinnin perusteet Y 2.3.2009 1 / 28 Puhelinluettelo, koodi def lue_puhelinnumerot(): print "Anna lisattavat nimet ja numerot." print
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 3 Supremum ja infimum Tarkastellaan aluksi avointa väliä, ) = { : < < }. Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen. Kuitenkaan päätepisteet
Matematiikan tukikurssi Kurssikerta 3 Supremum ja infimum Tarkastellaan aluksi avointa väliä, ) = { : < < }. Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen. Kuitenkaan päätepisteet
Muuttujien määrittely
 Tarja Heikkilä Muuttujien määrittely Määrittele muuttujat SPSS-ohjelmaan lomakkeen kysymyksistä. Harjoitusta varten lomakkeeseen on muokattu kysymyksiä kahdesta opiskelijoiden tekemästä Joupiskan rinneravintolaa
Tarja Heikkilä Muuttujien määrittely Määrittele muuttujat SPSS-ohjelmaan lomakkeen kysymyksistä. Harjoitusta varten lomakkeeseen on muokattu kysymyksiä kahdesta opiskelijoiden tekemästä Joupiskan rinneravintolaa
Differentiaali- ja integraalilaskenta 2 (CHEM) MS-A0207 Hakula/Vuojamo Kurssitentti, 12.2, 2018, arvosteluperusteet
 ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
Opiskelun ja työelämän tietotekniikka (DTEK1043)
 Opiskelun ja työelämän tietotekniikka (DTEK1043) pääaine- ja sivuaineopiskelijat Taulukkolaskennan perusteet Yleistä Tämä harjoitus käsittelee taulukkolaskentaohjelman perustoimintoja. Harjoituksissa opetellaan
Opiskelun ja työelämän tietotekniikka (DTEK1043) pääaine- ja sivuaineopiskelijat Taulukkolaskennan perusteet Yleistä Tämä harjoitus käsittelee taulukkolaskentaohjelman perustoimintoja. Harjoituksissa opetellaan
