PÄIVÄNVALO. Lue alla oleva teksti ja vastaa sen jäljessä tuleviin kysymyksiin.
|
|
|
- Riitta-Liisa Myllymäki
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 ÄIVÄNVALO Lue alla oleva teksti ja vastaa sen jäljessä tuleviin kysymyksiin. ÄIVÄNVALO 22. KSÄKUUTA 2002 Tänään, kun pohjoisella pallonpuoliskolla juhlitaan vuoden pisintä päivää, viettävät australialaiset lyhintään. Melbournessa*, Australiassa, aurinko nousee aamulla klo 7.36 ja laskee 17.08, joten päivänvaloa saadaan yhdeksän tuntia ja 32 minuuttia. Vertaapa tätä päivää vuoden pisimpään päivään eteläisellä pallonpuoliskolla, jonka lasketaan olevan 22. joulukuuta, jolloin aurinko nousee klo 5.55 ja laskee 20.42, ja päivänvaloa saadaan 14 tuntia ja 47 minuuttia. Tähtitieteellisen seuran puheenjohtaja erry Vlahos sanoi vuodenaikojen vaihtelun pohjoisella ja eteläisellä pallonpuoliskolla olevan yhteydessä maapallon 23 asteen kallistumaan. *Melbourne on kaupunki Australiassa ja sijaitsee suunnilleen 38. leveyspiirillä päiväntasaajalta etelään. Tehtävä 1: ÄIVÄNVALO S129Q01 Mikä seuraavista väittämistä selittää, miksi maapallolla on päivänvaloa ja pimeyttä? A Maapallo pyörii akselinsa ympäri. B Aurinko pyörii akselinsa ympäri. C Maan akseli on kallellaan. D Maapallo kiertää Auringon ympäri. ÄIVÄNVALO ISTITYS 1 Täydet pisteet Koodi 1: A. Maapallo pyörii akselinsa ympäri. i pisteitä Koodi 0: Muut vastaukset. Koodi 9: uuttuva vastaus.
2 Tehtävä 2: ÄIVÄNVALO S129Q Kuvassa Auringosta lähtevät valosäteet valaisevat maapalloa. Auringosta tuleva valo Maapallo Kuva: valonsäteet Auringosta Oletetaan, että on vuoden lyhin päivä Melbournessa. Merkitse kuvaan Maan pyörimisakseli, pohjoinen ja eteläinen pallonpuolisko sekä päiväntasaaja. Nimeä nämä kaikki. ÄIVÄNVALO ISTITYS 2 Huom. Tätä tehtävää tarkastettaessa kiinnitä huomio seuraaviin tärkeisiin seikkoihin: 1. Oikeassa vastauksessa Maan pyörimisakseli on piirretty kallistuneena Aurinkoon päin kallistuskulman ollessa välillä pystysuorasta tasosta katsottuna. Katso oheinen kuva: 10 O 23 O 45 O AKSLI OIKIN Mikäli kallistuskulma välin ulkopuolella: ei pisteitä. 2. ohjoinen ja eteläinen pallonpuolisko on nimetty selvästi, tai vain toinen näistä on nimetty ja toinen ilmaistu epäsuorasti. S129Daylt_NG3.doc
3 3. Oikeassa vastauksessa päiväntasaaja on piirretty kallistuneena Aurinkoon päin kallistuskulman ollessa välillä vaakasuorasta tasosta katsottuna. Katso oheinen kuva: voidaan piirtää joko ellipsin muotoisena tai suorana viivana. ÄIVÄNTASAAJA OIKIN 23 O 10 O 45 O Mikäli välin ulkopuolella: ei pisteitä. Täydet pisteet Koodi 21: Kuva, jossa päiväntasaaja on kallistunut vaakatasosta Aurinkoon päin ja pyörimisakseli on kallistunut Aurinkoa kohti :n kulmassa pystysuorasta. teläinen ja pohjoinen pallonpuolisko on nimetty oikein (tai toinen nimetty ja toiseen viitattu muulla tavoin). A Osittaiset pisteet Koodi 11: yörimisakselin kallistuskulma on välillä 10 45, pohjoinen ja/tai eteläinen pallonpuolisko on nimetty oikein (tai toinen nimetty ja toiseen viitattu muulla tavoin), mutta päiväntasaajan kallistuskulma ei ole virherajojen sisäpuolella, tai päiväntasaaja puuttuu kokonaan. yörimisakseli S129Daylt_NG3.doc
4 Koodi 12: n kallistuskulma on välillä 10 45, pohjoinen ja/tai eteläinen pallonpuolisko on nimetty oikein (tai toinen nimetty ja toiseen viitattu muulla tavoin), mutta pyörimisakselin kallistuskulma ei ole virherajojen sisäpuolella, tai pyörimisakseli puuttuu kokonaan. N Koodi 13: n kallistuskulma on välillä ja pyörimisakselin kallistuskulma välillä 10 45, mutta pohjoista ja eteläistä pallonpuoliskoa ei ole merkitty oikein (tai toinen merkitty ja toiseen viitattu muulla tavoin tai molemmat puuttuvat). i pisteitä Koodi 01: Ainoastaan pohjoisen ja/tai eteläisen pallonpuoliskon merkintä on oikein (tai toinen merkitty ja toiseen viitattu muulla tavoin). Koodi 02: Ainoastaan päiväntasaajan kallistuskulma välillä on oikein. S129Daylt_NG3.doc
5 Koodi 03: Ainoastaan pyörimisakselin kallistuskulma välillä on oikein. Koodi 04: Mikään kohdista ei ole oikein ja muut vastaukset. Koodi 99: uuttuva vastaus. S129Daylt_NG3.doc
AURINKO VALON JA VARJON LÄHDE
AURINKO VALON JA VARJON LÄHDE Tavoite: Tarkkaillaan auringon vaikutusta valon lähteenä ja sen vaihtelua vuorokauden ja vuodenaikojen mukaan. Oppilaat voivat tutustua myös aurinkoenergian käsitteeseen.
PIKAOPAS 1. Kellotaulun kulma säädetään sijainnin leveys- asteen mukaiseksi.
Käyttöohje PIKAOPAS 1. Kellotaulun kulma säädetään sijainnin leveysasteen mukaiseksi. Kellossa olevat kaupungit auttavat alkuun, tarkempi leveysasteluku löytyy sijaintisi koordinaateista. 2. Kello asetetaan
SÁME JÁHKI - saamelainen vuosi
6789067890678901267890678906789012678906 6789067890678901267890678906789012678906 6789067890678901267890678906789012678906 67890 67890 678906 678906 678906 67890 67890 67890 67890 67890 678906 678906 678906
Tähtitieteelliset koordinaattijärjestelemät
Tähtitieteelliset Huom! Tämä materiaali sisältää symbolifontteja, eli mm. kreikkalaisia kirjaimia. Jos selaimesi ei näytä niitä oikein, ole tarkkana! (Tällä sivulla esiintyy esim. sekä "a" että "alpha"-kirjaimia,
Juha Ojanperä Har javalta
Tähtitaivaan alkeet Juha Ojanperä Harjavalta 06.10. - 08.12.2016 Kurssin sisältö 1. Kerta Taivaanpallo ja tähtitaivaan liike opitaan lukemaan ja ymmärtämään tähtikarttoja 2. kerta Tärkeimmät tähdet ja
AURINKOENERGIA. Auringon kierto ja korkeus taivaalla
AURINKOENERGIA Auringon kierto ja korkeus taivaalla Maapallo kiertää aurinkoa hieman ellipsin muotoista rataa pitkin, jonka toisessa polttopisteessä maapallo sijaitsee. Maapallo on lähinnä aurinkoa tammikuussa
1 Laske ympyrän kehän pituus, kun
Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
LAINAUSJÄRJESTELMÄ. Kyllä. Vihermetsän lukion kirjastossa on samankaltainen, mutta monimutkaisempi lainausjärjestelmä:
LAINAUSJÄRJESTELMÄ Holopaisten lukion kirjastossa on yksinkertainen kirjojen lainausjärjestelmä: henkilökunnalle laina-aika on 28 päivää, ja opiskelijoille laina-aika on 7 Alla on tätä yksinkertaista järjestelmää
1) Maan muodon selvittäminen. 2) Leveys- ja pituuspiirit. 3) Mittaaminen
1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
TAIVAANMEKANIIKKA IHMISEN PERSPEKTIIVISTÄ
TAIVAANMEKANIIKKA IHMISEN PERSPEKTIIVISTÄ ARKIPÄIVÄISTEN ASIOIDEN TÄHTITIETEELLISET AIHEUTTAJAT, FT Metsähovin Radio-observatorio, Aalto-yliopisto KOPERNIKUKSESTA KEPLERIIN JA NEWTONIIN Nikolaus Kopernikus
RATKAISUT: 19. Magneettikenttä
Physica 9 1. painos 1(6) : 19.1 a) Magneettivuo määritellään kaavalla Φ =, jossa on magneettikenttää vastaan kohtisuorassa olevan pinnan pinta-ala ja on magneettikentän magneettivuon tiheys, joka läpäisee
Ajan osasia, päivien palasia
Ajan osasia, päivien palasia Ajan mittaamiseen tarvitaan liikettä. Elleivät taivaankappaleet olisi määrätyssä liikkeessä keskenään, ajan mittausta ei välttämättä olisi syntynyt. Säännöllinen, yhtäjaksoinen
DEE Tuulivoiman perusteet
DEE-53020 Tuulivoiman perusteet Aihepiiri 2 Tuuli luonnonilmiönä: Ilmavirtoihin vaikuttavien voimien yhteisvaikutuksista syntyvät tuulet Globaalit ilmavirtaukset 1 VOIMIEN YHTEISVAIKUTUKSISTA SYNTYVÄT
Syntyikö maa luomalla vai räjähtämällä?
Syntyikö maa luomalla vai räjähtämällä? Tätä kirjoittaessani nousi mieleeni eräs tuntemani insinööri T. Palosaari. Hän oli aikansa lahjakkuus. Hän oli todellinen nörtti. Hän teki heti tietokoneiden tultua
SMG-4500 Tuulivoima. Toisen luennon aihepiirit VOIMIEN YHTEISVAIKUTUKSISTA SYNTYVÄT TUULET
SMG-4500 Tuulivoima Toisen luennon aihepiirit Tuuli luonnonilmiönä: Ilmavirtoihin vaikuttavien voimien yhteisvaikutuksista syntyvät tuulet Globaalit ilmavirtaukset 1 VOIMIEN YHTEISVAIKUTUKSISTA SYNTYVÄT
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla Tähtitieteellinen merenkulkuoppi on oppi, jolla määrätään aluksen sijainti taivaankappaleiden perusteella. Paikanmääritysmenetelmänäon ristisuuntiman
766323A Mekaniikka, osa 2, kl 2015 Harjoitus 4
766323A Mekaniikka, osa 2, kl 2015 Harjoitus 4 0. MUISTA: Tenttitehtävä tulevassa päätekokeessa: Fysiikan säilymislait ja symmetria. (Tästä tehtävästä voi saada tentissä kolme ylimääräistä pistettä. Nämä
Tähtitieteen LUMA-työpaja
Tähtitieteen LUMA-työpaja (Ohje työpajaan, jota käsiteltiin MAOL:in syyspäivillä 2016) Pertti Rautiainen Tähtitieteen tutkimusyksikkö Oulun yliopisto Tähtitieteen LUMA-työpaja: Maa on planeetta taustatietoa
Kenguru 2012 Cadet (8. ja 9. luokka)
sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kartografian historiaa ja perusteita. Taru Tiainen
Kartografian historiaa ja perusteita Taru Tiainen 18.4.2016 Alkutehtävä Piirrä Joensuun kartta Aikaa n. 5 minuuttia Alkutehtävä Mikä vaikuttaa karttasi tekoon? Miksi kartta on näköisensä? Mitä tämän tehtävän
Etäisyyden yksiköt tähtitieteessä:
Tähtitiedettä Etäisyyden yksiköt tähtitieteessä: Astronominen yksikkö AU = 149 597 870 kilometriä. Tämä vastaa sellaisen Aurinkoa kiertävän kuvitellun kappaleen etäisyyttä, jonka kiertoaika on sama kuin
Pimennys- yms. lisäsivut Maailmankaikkeus nyt -kurssi
Pimennys- yms. lisäsivut Maailmankaikkeus nyt -kurssi Asko Palviainen Matemaattis-luonnontieteellinen tiedekunta Ajanlasku Kuukalenteri vuodessa 12 kuu-kuukautta ei noudata vuodenaikoja nykyisistä kalentereista
Liike pyörivällä maapallolla
Liike pyörivällä maapallolla Voidaan olettaa: Maan pyöriminen tasaista Maan rataliikkeen näennäisvoimat tasapainossa Auringon vetovoiman kanssa Riittää tarkastella Maan tasaisesta pyörimisestä akselinsa
monta rautaa. Toimi ohjaajan antamien ohjeiden mukaan.
keskittyminen monta rautaa. Toimi ohjaajan antamien ohjeiden mukaan. KESKITTYMINEN 9 Kuulaana pilvettömänä yönä voimme nähdä taivaankannen tähtikuviot. Meille tutuin tähtikuvio lienee Otava, joka on osa
7. Resistanssi ja Ohmin laki
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
FAI/F3A Radio-ohjatut taitolennokit TUOMAROINTIESITYS F3A Team Finlandille
FAI/F3A Radio-ohjatut taitolennokit TUOMAROINTIESITYS F3A Team Finlandille Produced by Bob Skinner, September 2004 F3A Liikkeiden TUOMAROINTI ARKKUUS RAUHALLISUUS & NÄYTTÄVYYS SIJOITTELU KOKO (Suhteessa
B. 2 E. en tiedä C. 6. 2 ovat luonnollisia lukuja?
Nimi Koulutus Ryhmä Jokaisessa tehtävässä on vain yksi vastausvaihtoehto oikein. Laske tehtävät ilman laskinta.. Missä pisteessä suora y = 3x 6 leikkaa x-akselin? A. 3 D. B. E. en tiedä C. 6. Mitkä luvuista,,,
Tervetuloa Aikuisten suunnistuskouluun 2019
Tervetuloa Aikuisten suunnistuskouluun 2019 Koskaan ei eksy helpommin kuin silloin kun luulee tietävänsä tien Kiinalainen sananlasku Suunnistaminen on koko ajan tapahtuvaa havainnointia, analysointia ja
Lauseen erikoistapaus on ollut kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa seuraavassa muodossa:
Simo K. Kivelä, 13.7.004 Frégier'n lause Toisen asteen käyrillä ellipseillä, paraabeleilla, hyperbeleillä ja niiden erikoistapauksilla on melkoinen määrä yksinkertaisia säännöllisyysominaisuuksia. Eräs
Pimennys- yms. lisäsivut Maailmankaikkeus nyt -kurssi
Pimennys- yms. lisäsivut Maailmankaikkeus nyt -kurssi Asko Palviainen Matemaattis-luonnontieteellinen tiedekunta Ajanlasku Kuukalenteri vuodessa 12 kuu-kuukautta ei noudata vuodenaikoja nykyisistä kalentereista
Esimerkkejä kuvasarjan piirtämisestä
Esimerkkejä kuvasarjan piirtämisestä Tässä esimerkki kuvasarjasta, joka on piirretty 20 minuutissa (jäänyt lopusta keskeneräiseksi) Kokeessa design-tehtävän kuvasarjan piirtämistä varten kannattaa varata
Miksi meillä on talvi? Kirsti Jylhä Ilmatieteen laitos Ilmastotutkimus ja -sovellukset
Miksi meillä on talvi? Kirsti Jylhä Ilmatieteen laitos Ilmastotutkimus ja -sovellukset Esityksen pääaiheet Miksei talvea 12 kk vuodessa? Terminen ja tähtitieteellinen talvi Jääkausista Entä talvi tulevaisuudessa?
SolarView. Käyttäjän opas. AR Software
SolarView Käyttäjän opas AR Software Sisällysluettelo 1. Johdanto...3 2. Sovelluksen yleiskuvaus...4 2.1 Laitteisto- ja ohjelmistovaatimukset...4 3. Keskeiset käsitteet...5 3.1. Paikkakoordinaatit...5
MAAPALLON GEOMETRIA JA SEN SELVITTÄMINEN
STRUVEN KETJULLA MAAPALLOA MITTAAMAAN: MAAPALLON GEOMETRIA JA SEN SELVITTÄMINEN Joonas Ilmavirta Matematiikan ja tilastotieteen laitos Jyväskylän yliopisto 3.10.2017 OSA I: MAAPALLON GEOMETRIA MAAPALLON
PL 186, 01531 VANTAA, FINLAND, puh. 358 (0)9 4250 11, Faksi 358 (0)9 4250 2898
OPS M2-1, Liite 1 21.12.2007 PL 186, 01531 VANTAA, FINLAND, puh. 358 (0)9 4250 11, Faksi 358 (0)9 4250 2898 www.ilmailuhallinto.fi LENTOKONEEN VALOT Huom. Katso luku 6 1. MÄÄRITELMIÄ Kun tässä luvussa
VALONTAITTOMITTARIN KÄYTTÖ
VALONTAITTOMITTARIN KÄYTTÖ MERKITSE KUVAAN VALONTAITTOMITTARIN OSAT. 1. Okulaarin säätörengas 2. Asteikkorengas 3. Käyttökatkaisin 4. Linssipitimen vapautin 5. Linssialusta 6. Linssipidin 7. Linssipöytä
4.1 Kaksi pistettä määrää suoran
4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
Kokeiden kuvaus/ohjekirja. Tellurium N
Kokeiden kuvaus/ohjekirja Sisällys Yleiset ohjeet... 3 Telluriumin tärkeät osat ja niiden käyttö... 4 Opetus-yksiköt työskentelyyn Telluriumilla:... 6 1 Maa, gyroskooppi avaruudessa... 8 2 Päivä ja yö...
Mikä määrää maapallon sääilmiöt ja ilmaston?
Mikä määrää maapallon sääilmiöt ja ilmaston? Ilmakehä Aurinko lämmittää epätasaisesti maapalloa, joka pyörii kallellaan. Ilmakehä ja sen ominaisuudet vaikuttavat siihen, miten paljon lämpöä poistuu avaruuteen.
Työ 2324B 4h. VALON KULKU AINEESSA
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/5 Työ 2324B 4h. VALON KULKU AINEESSA TYÖN TAVOITE Työssä perehdytään optisiin ilmiöihin tutkimalla valon kulkua linssisysteemeissä ja prismassa. Tavoitteena on saada
Materiaalifysiikan perusteet P Ratkaisut 1, Kevät 2017
Materiaalifysiikan perusteet 51104P Ratkaisut 1, Kevät 017 1. Kiderakenteen alkeiskopin hahmottamiseksi pyritään löytämään kuvitteellisesta rakenteesta sen pienin toistuva yksikkö (=kanta). Kunkin toistuvan
8a. Kestomagneetti, magneettikenttä
Nimi: LK: SÄHKÖ-OPPI 8. Kestomagneetti, magneettikenttä (molemmat mopit) Tarmo Partanen 8a. Kestomagneetti, magneettikenttä Tee aluksi testi eli ympyröi alla olevista kysymyksistä 1-8 oikeaksi arvaamasi
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Vanhoja koetehtäviä. Analyyttinen geometria 2016
Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Puzzle SM 2005 15. 25.7.2005. Pistelasku
Puzzle SM 005 5. 5.7.005 Pistelasku Jokaisesta oikein ratkotusta tehtävästä saa yhden () pisteen, minkä lisäksi saa yhden () bonuspisteen jokaisesta muusta ratkojasta, joka ei ole osannut ratkoa tehtävää.
a) Montako rasiaa täyttyy 35 karkista 63 karkista 49 karkista 70 karkista 56 karkista
5) Yhteen rasiaan mahtuu 7 suklaakarkkia. 8 a) Montako rasiaa täyttyy 35 karkista 63 karkista 49 karkista 7 karkista 56 karkista b) Monestako karkista täyttyy 3 rasiaa 6 rasiaa rasiaa rasiaa 2 rasiaa 4
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
Kenguru 2019 Benjamin 6. ja 7. luokka
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai
AquaPro IP 54. Laser 635 nm. auto man man DE 02 GB 09 NL 16 DK 23 FR 30 ES 37 IT 44 PL 51 FI 58 PT 65 SE 72 NO 79 TR 86 RU 93 UA 100 CZ 107 EE 114
Laser 635 nm IP 54 auto man man AquaPro DE 02 GB 09 NL 16 DK 23 FR 30 ES 37 IT 44 PL 51 58 PT 65 SE 72 NO 79 TR 86 RU 93 UA 100 CZ 107 EE 114 LV 121 LT 128 RO 135 BG 142 GR 149 58 Lue käyttöohje kokonaan.
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty c) sin 50 = sin ( ) = sin 130 = 0,77
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty.5.07 Kertaus K. a) sin 0 = 0,77 b) cos ( 0 ) = cos 0 = 0,6 c) sin 50 = sin (80 50 ) = sin 0 = 0,77 d) tan 0 = tan (0 80 ) = tan 0 =,9 e)
Tornio 24.5.2012 RAMK Petri Kuisma
Tornio 24.5.2012 RAMK Petri Kuisma Sisältö Aurinko Miten aurinkoenergiaa hyödynnetään? Aurinkosähkö ja lämpö Laitteet Esimerkkejä Miksi aurinkoenergiaa? N. 5 miljardia vuotta vanha, fuusioreaktiolla toimiva
Kenguru 2014 Benjamin (6. ja 7. luokka) sivu 1 / 7 ja Pakilan ala-aste
(6. ja 7. luokka) sivu 1 / 7 ja Pakilan ala-aste NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä
Tekijä Pitkä matematiikka
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Tähtitieteen historiaa, avaruusgeometrian tehtäviä ja muita tehtäviä
Tähtitieteen historiaa, avaruusgeometrian tehtäviä ja muita tehtäviä A1. Antiikin kreikkalainen monitieteilijä Eratosthenes (276-194) eaa. onnistui ensimmäisenä mittaamaan 240 eaa. maapallon ympärysmitan
2.1 Yksinkertaisen geometrian luonti
2.1 Yksinkertaisen geometrian luonti Kuva 2.1 Tiedon portaat Kuva 2.2 Ohjelman käyttöliittymä suoran luonnissa 1. Valitse Luo, Suora, Luo suora päätepistein. 2. Valitse Pystysuora 3. Valitse Origo Origon
Aluksi. 1.1. Kahden muuttujan lineaarinen yhtälö
Aluksi Matematiikan käsite suora on tarkalleen sama asia kuin arkikielen suoran käsite. Vai oliko se toisinpäin? Matematiikan luonteesta johtuu, että sen soveltaja ei tyydy pelkkään suoran nimeen eikä
3D-kuvauksen tekniikat ja sovelluskohteet. Mikael Hornborg
3D-kuvauksen tekniikat ja sovelluskohteet Mikael Hornborg Luennon sisältö 1. Optiset koordinaattimittauskoneet 2. 3D skannerit 3. Sovelluskohteet Johdanto Optiset mittaustekniikat perustuvat valoon ja
Ensimmäinen osa: Rautalankamallinnus. Rautalankamallinnus
Ensimmäinen osa: Rautalankamallinnus Rautalankamallinnus Tampereen ammattiopisto - CAD -perusharjoitukset Rautalankamallinnus I: Jana, suorakulmio ja ympyrä Harjoitusten yleisohje Valitse suunnittelutilan
2.3 Voiman jakaminen komponentteihin
Seuraavissa kappaleissa tarvitaan aina silloin tällöin taitoa jakaa voima komponentteihin sekä myös taitoa suorittaa sille vastakkainen operaatio eli voimien resultantin eli kokonaisvoiman laskeminen.
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
ESIMERKKEJÄ JA HARJOITUKSIA
ESIMERKKEJÄ JA HARJOITUKSIA OSA I: MATEMAATTISTEN MERKINTÖJEN JA KIRJAINSYMBOLIEN KÄYTTÖÄ (ja tutustumista tilinpitoon ja keynesiläiseen malliin) Harjoitellaan seuraavassa kirjainsymbolien käyttöä ja yhtälöiden
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
GeoGebran 3D paketti
GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
on hidastuvaa. Hidastuvuus eli negatiivinen kiihtyvyys saadaan laskevan suoran kulmakertoimesta, joka on siis
Fys1, moniste 2 Vastauksia Tehtävä 1 N ewtonin ensimmäisen lain mukaan pallo jatkaa suoraviivaista liikettä kun kourun siihen kohdistama tukivoima (tässä tapauksessa ympyräradalla pitävä voima) lakkaa
SMG-4500 Tuulivoima. Ensimmäisen luennon aihepiirit. Ilmavirtojen liikkeisiin vaikuttavat voimat TUULEN LUONNONTIETEELLISET PERUSTEET
SMG-4500 Tuulivoima Ensimmäisen luennon aihepiirit Tuuli luonnonilmiönä: Ilmavirtojen liikkeisiin vaikuttavat voimat 1 TUULEN LUONNONTIETEELLISET PERUSTEET Tuuli on ilman liikettä suhteessa maapallon pyörimisliikkeeseen.
MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Turvallisuus. Asennuksessa tarvittavat työkalut. Kuomun asentamisessa tarvitaan kaksi (2) henkilöä.
Kuomun asennusohje Turvallisuus Kuomun asentamisessa tarvitaan kaksi (2) henkilöä.! kuomun nostaminen, siirtäminen ja kääntäminen kevennysjousien asentaminen tuulihaan asentaminen varmistettava peräkärryn
Kenguru 2014 Student sivu 1 / 8 (lukion 2. ja 3. vuosi)
Kenguru 2014 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2013 Junior sivu 1 / 9 (lukion 1. vuosikurssi)
Kenguru 2013 Junior sivu 1 / 9 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Sampomuunnos, kallistuneen lähettimen vaikutuksen poistaminen Matti Oksama
ESY Q16.2/2006/4 28.11.2006 Espoo Sampomuunnos, kallistuneen lähettimen vaikutuksen poistaminen Matti Oksama GEOLOGIAN TUTKIMUSKESKUS KUVAILULEHTI 28.11.2006 Tekijät Matti Oksama Raportin laji Tutkimusraportti
Mikä neljästä numeroidusta kuviosta jatkaa alkuperäistä kuviosarjaa? Perustele lyhyesti
Tehtävä 1. Mikä neljästä numeroidusta kuviosta jatkaa alkuperäistä kuviosarjaa? Perustele lyhyesti a) 1 4 b) 1 4 a) - kuvio, annetaan 1,5 p - ympyrä täyttyy neljänneksen kerrallaan, annetaan 1,5 p b) -
Mb8 Koe Kuopion Lyseon lukio (KK) sivu 1/2
Mb8 Koe 0.11.015 Kuopion Lyseon lukio (KK) sivu 1/ Kokeessa on kaksi osaa. Osa A ratkaistaan tehtäväpaperille ja osa B ratkaistaan konseptipaperille. Osa A: saat käyttää taulukkokirjaa mutta et laskinta.
Taitaja2010, Iisalmi Suunnittelutehtävä, teoria osa
Taitaja2010, Iisalmi Suunnittelutehtävä, teoria osa Nimi: Pisteet: Koulu: Lue liitteenä jaettu artikkeli Solar Lamp (Elector Electronics 9/2005) ja selvitä itsellesi laitteen toiminta. Tätä artikkelia
Luku 3. Ilmakehä suojaa ja suodattaa. Manner 2
Luku 3 Ilmakehä suojaa ja suodattaa Sisällys Ilmakehä eli atmosfääri Ilmakehän kerrokset Ilmakehä kaasukoostumuksen mukaan Ilmakehä lämpötilan mukaan Säteilytase ja säteilyn absorboituminen Kasvihuoneilmiö
Kolmioitten harjoituksia. Säännöllisten monikulmioitten harjoituksia. Pythagoraan lauseeseen liittyviä harjoituksia
Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
x + 1 πx + 2y = 6 2y = 6 x 1 2 πx y = x 1 4 πx Ikkunan pinta-ala on suorakulmion ja puoliympyrän pinta-alojen summa, eli
BM0A5810 - Differentiaalilaskenta ja sovellukset Harjoitus, Syksy 015 1. a) Funktio f ) = 1) vaihtaa merkkinsä pisteissä = 1, = 0 ja = 1. Lisäksi se on pariton funktio joten voimme laskea vain pinta-alan
Avaruuslävistäjää etsimässä
Avaruuslävistäjää etsimässä Avainsanat: avaruusgeometria, mittaaminen Luokkataso: 6.-9. lk, lukio Välineet: lankaa, särmiön muotoisia kartonkisia pakkauksia(esim. maitotölkki tms.), sakset, piirtokolmio,
EI MIKÄÄN NÄISTÄ. KUVITETTU MINI-MENTAL STATE EXAMINATION Ohjeet viimeisellä sivulla. 1. Mikä vuosi nyt on? 2. Mikä vuodenaika nyt on?
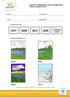POTILAS: SYNTYMÄAIKA: TUTKIJA: PÄIVÄMÄÄRÄ: 1. Mikä vuosi nyt on? 2000 2017 2020 1917 EI MIKÄÄN NÄISTÄ 2. Mikä vuodenaika nyt on? KEVÄT KESÄ SYKSY TALVI 3. Monesko päivä tänään on? 1 2 3 4 5 6 7 8 9 10
Kenguru 2015 Benjamin (6. ja 7. luokka)
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Pelivaihtoehtoja. Enemmän vaihtelua peliin saa käyttämällä erikoislaattoja. Jännittävimmillään Alfapet on, kun miinusruudut ovat mukana pelissä!
Pelivaihtoehtoja Yksinkertaisin vaihtoehto: lfapetia voi pelata monella eri tavalla. Yksinkertaisimmassa vaihtoehdossa käytetään ainoastaan kirjainlaattoja. Pelilaudan miinusruudut ovat tavallisia ruutuja,
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 2016 Sivu 1 / 4
Preliminäärikoe Tehtävät A-osio Pitkä matematiikka kevät 06 Sivu / Laske yhteensä enintään 0 tehtävää. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. Osiossa A EI SAA käyttää laskinta. Osiossa A
Kenguru 2010, Benjamin, ratkaisut sivu 1 / 9
Kenguru 2010, Benjamin, ratkaisut sivu 1 / 9 3 pistettä 1. Kun tiedetään, että + + 6 = + + +, mikä luku voidaan sijoittaa kolmion paikalle? A) 2 B) 3 C) 4 D) 5 E) 6 Ratkaisu: Kun poistetaan kummaltakin
Naps Systems Oy. Näkökulma aurinkoatlaksen merkityksestä järjestelmätoimittajalle. TkT Mikko Juntunen, Teknologiajohtaja
1 Naps Systems Oy Näkökulma aurinkoatlaksen merkityksestä järjestelmätoimittajalle TkT Mikko Juntunen, Teknologiajohtaja Copyright Naps Systems, Inc. 2013 2 Naps Systems lyhyesti Suomalainen, yksityisomistuksessa
= 6, Nm 2 /kg kg 71kg (1, m) N. = 6, Nm 2 /kg 2 7, kg 71kg (3, m) N
t. 1 Auringon ja kuun kohdistamat painovoimat voidaan saada hyvin tarkasti laksettua Newtonin painovoimalailla, koska ne ovat pallon muotoisia. Junalle sillä saadaan selville suuruusluokka, joka riittää
Kenguru 2016 Benjamin (6. ja 7. luokka)
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Navigointi/suunnistus
Navigointi/suunnistus Aiheita Kartan ja kompassin käyttö Mittakaavat Koordinaatistot Karttapohjoinen/neulapohjoinen Auringon avulla suunnistaminen GPS:n käyttö Reitin/jäljen luonti tietokoneella Reittipisteet
3D-kuva A B C D E Kuvanto edestä Kuvanto sivulta Kuvanto päältä. Nimi Sotun loppuosa - Monimuotokoulutuksen soveltavat tehtävät 20 p. Tehtävä 1 3p.
Nimi Sotun loppuosa - Monimuotokoulutuksen soveltavat tehtävät 20 p. Tehtävä 1 3p. Viiden oheisen 3D-kappaleen kuvannot kolmesta suunnasta katsottuna on esitetty seuraavalla sivulla. Merkitse oheiseen
a) on lokaali käänteisfunktio, b) ei ole. Piirrä näiden pisteiden ympäristöön asetetun neliöruudukon kuva. VASTAUS:
6. Käänteiskuvaukset ja implisiittifunktiot 6.1. Käänteisfunktion olemassaolo 165. Määritä jokin piste, jonka ympäristössä funktiolla f : R 2 R 2, f (x,y) = (ysinx, x + y + 1) a) on lokaali käänteisfunktio,
v = Δs 12,5 km 5,0 km Δt 1,0 h 0,2 h 0,8 h = 9,375 km h 9 km h kaava 1p, matkanmuutos 1p, ajanmuutos 1p, sijoitus 1p, vastaus ja tarkkuus 1p
2. Pyöräilijä lähti Pietarsaaresta kohti Kokkolaa, jonne on matkaa 33 km. Hän asetti tavoitteeksi ajaa edestakaisen matkan keskinopeudella 24 km/h. Vastatuulen takia hän joutui käyttämään menomatkaan aikaa
KUVASARJA AVOSINKKAUKSEN VALMISTAMISESTA KÄSITYÖVÄLINEILLÄ Kari Koski 1 LITRAN MITTA (KAPPALEEN MITAT 10X100X120mm (paksuus*leveys*pituus).
KUVASARJA AVOSINKKAUKSEN VALMISTAMISESTA KÄSITYÖVÄLINEILLÄ Kari Koski 1 LITRAN MITTA (KAPPALEEN MITAT 10X100X120mm (paksuus*leveys*pituus). 3. Tappikappale jaetaan merkistä lovikappaleen tappien lukumäärällä
3. kappale (kolmas kappale) AI KA
3. kappale (kolmas kappale) AI KA 3.1. Kellonajat: Mitä kello on? Kello on yksi. Kello on tasan yksi. Kello on kaksikymmentä minuuttia vaille kaksi. Kello on kymmenen minuuttia yli yksi. Kello on kymmenen
Kenguru 2015 Ecolier (4. ja 5. luokka)
sivu 1 / 13 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Ratkaisu: Maksimivalovoiman lauseke koostuu heijastimen maksimivalovoimasta ja valonlähteestä suoraan (ilman heijastumista) tulevasta valovoimasta:
LASKUHARJOITUS 1 VALAISIMIEN OPTIIKKA Tehtävä 1 Pistemäinen valonlähde (Φ = 1000 lm, valokappaleen luminanssi L = 2500 kcd/m 2 ) sijoitetaan 15 cm suuruisen pyörähdysparaboloidin muotoisen peiliheijastimen
annettu 20 päivänä toukokuuta 1975,
13/N de 04 Euroopan yhteisöjen virallinen lehti 113 375L0322 N:o L 147/28 EUROOPAN YHTEISÖJEN VIRALLINEN LEHTI 9.6.75 NEUVOSTON DIREKTIIVI, annettu 20 päivänä toukokuuta 1975, pyörillä varustettuihin maatalous-
5.3 Ensimmäisen asteen polynomifunktio
Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;