OH CHOOH (2) 5. H2O. OH säiliö. reaktori 2 erotus HCOOCH 3 11.
|
|
|
- Anna-Leena Nieminen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Kemian laieekniikka 1 Koilasku Jarmo Vesola Tuoee ja reakio: hiilimonoksidi, meanoli, meyyliformiaai C HC (1) vesi, meyyliformiaai, meanoli, muurahaishappo HC CH (2) hiilimonoksi, vesi, muurahaishappo C CH (3) Kuva prosessisa C 2. C 3. HC 4. HC 5. H2 HC reakori 1 erous reakori 2 erous HC 6. HC CH erous 1. HC 7. CH säiliö leukse Muurahaishappoa (CH) valmiseaan 6,6 onnia/h (1%), eli säiliöön menevässä virrassa 7 on muurahaishappoa 6,6 onnia unnissa. Meyyliformiaain (HC ) konversio muurahaishapoksi 52 % Meanolia syöeään 19 mol-% ylimäärä reakoriin 1 Varasosäiliön liuos sisälää muurahaishappo 58 mol-% ja meanoli,8 mol-%, lopu veä Tuoresyööjen suuruuksia ja kaikkia virran komponeneja laskeaessa kuviellaan asealue jokaisen prosessilaieen ympärille ja virojen riseyskohiin. Reakioyhälöiden 1,2 ja 3 peruseella nähdään, eä jokaisa uoeua moolimäärää kohi arviaan asan yksi mooli lähöaineia. Massavirojen sijasa voidaan siis laskea moolivirroilla. Käyeään laskuissa merkinäapaa: n virran numero, komponeni (moolivira merkiään kirjoiamisen helpoamiseksi ilman yläpiseä)
2 Virra komponeneiain Laskeaan ensiksi uoeiden moolimassa aulukkokirjan avulla hiilimonoksidi M(C) = (12,1+16) g/mol 28,1 g/mol meanoli M( ) = (12,1+4*1,8+16) g/mol 32,42 g/mol meyyliformiaai M(HC ) = (4*1,8+2*12,1+2*16) g/mol 6,52 g/mol vesi M( ) = (2*1,8+16) g/mol 18,16 g/mol muurahaishappo M(CH) = (12,1+1,8+2*16) g/mol 46,26 g/mol Jos (1%) muurahaishappoa haluaan valmisaa 66 kg/h, niin n 6, CH = m/m = (6 6 g)/(46, 2 g/mol) = ,21 mol = n 7, CH Varasosäiliön liuos sisälää 58 mol-% muurahaishappoa, yheensä säiliössä on siis ainea: n*,58 = ,21 mol n = ( ,21 mol)/,58 = ,57 mol Lähöieojen mukaan ämä varasosäiliössä oleva liuos sisälää myös,8 mol-% meanolia, n 7, CH3 = ,57 mol *,8 = 1977,89 mol Lopu varasosäiliön liuoksesa on siis veä: n 7, H2 = ,57 mol 1977,89 mol ,21 mol = ,47 mol Ny voidaan laskea viroja aaksepäin. n 7, H2 = n 6, H2 = ,49 mol Meyyliformiaain konversio muurahaishapoksi on 52 mol-%. Meyyliformiaaia on siis muuunu muurahaishapoksi 52 %. n 5, HCCH3 *,52 = n 6, CH n 5, HCCH3 *,52 = ,21 mol n 5, HCCH3 = ,86 mol Meyyliformiaaia on siis jäljellä 48 mol-%. n 6, HCCH3 =,48 * n 5, HCCH3 n 6, HCCH3 =,48 * ,86 mol = ,65 mol n 1, HCCH3 = n 6, HCCH3 = n 9, HCCH3 = ,65 mol n 5, HCCH3 n 9, HCCH3 = n 4, HCCH3 n 4, HCCH3 = ( , ,65) mol = ,21 mol n 3, HCCH3 = n 4, HCCH3 = ,21 mol Reakioyhälö 2 keroo, eä veden kuluus on sama kuin meyyliformiaain. Veä kuluu siis yhä paljon kuin meyyliformiaaia on reakori 2:ssa kulunu. n 5, H2 = n 6,H2 + (n 5, HCCH3 n 6, HCCH3 ) = ,49 mol + ( , ,65) mol = ,7 mol
3 Veden uoresyöö on siis sama. n 13, H2 = n 5, H2 = ,7 mol Reakioyhälön 2 mukaan meanolin kuluus on yhä suuri kuin meyyliformiaain. Meanolia synyy siis yhä paljon, kuin meyyliformiaaia on kulunu reakorissa 2. n 6, CH3 = n 5, HCCH3 n 6,HCCH3 = ,86 mol ,65 mol = ,21 mol n 1, CH3 = n 6, CH3 n 7, CH3 = ( , ,89) mol = ,32 mol n 11, CH3 = n 1, CH3 = ,32 mol Reakioyhälön 1 mukaan 1 mooliin meyyliformiaaia arviaan 1 mooli hiilimonoksidia, eli n 2, C = n 3, HCCH3 = ,21 mol ja n 1, C = n 2, C = ,21 mol Meanolia syöeään 19 mol-% ylimäärä reakoriin 1, eli ylimäärä hiilimonoksidiin nähden: n 2, CH3 = 1,19 * n 2, C = 1,19 * ,21 mol = ,68 mol Virrassa kolme meanolia on siis jäljellä vain ylimäärä, eli,19 * alkuperäinen meanolin määrä: n 3, CH3 =,19 * n 2, Co =,19 * ,21 mol = ,47 mol n 8, CH3 = n 3, CH3 = ,47 mol n 12, CH3 = n 8, CH3 + n 11, CH3 = (27 245, ,32) mol = ,79 mol n 1, CH3 = n 2, CH3 - n 12, CH3 = (17 642, ,79 ) mol = 1977,89 mol n 1,CH3 = n 7,CH3 = 1977,89 mol B) Virra komponeneiain aulukoiuna (kmol/h) Vira C HC CH 1 143,4 1, ,4 17,6 3 27,2 143, , ,8 245, ,4 132,4 11,9 143,4 7 1,98 11,9 143,4 8 27, , ,4 132, , , ,3
4 A) Tuoresyööjen suuruude (kg/h) Hiilimonoksi (C) = ,21 mol/h * 28,1 g/mol 416,6 kg/h Vesi ( ) = ,7 mol * 18,16 g/mol 4418,6 kg/h Meanoli ( ) = 1977,89 mol * 32,42 g/mol 63,4 kg/h Koha C Muodoseaan ilavuusvirran muuokselle yhälö ulosvirauksen kaavan avulla. Ulosviraus noudaaa kaavaa kh, jossa h on nesepinnan korkeus mereissä ja k on iey poisokerroin (ehävässä,72 m 2 /s). Kuviellaan, eä ilavuuden muuos on siis negaiivisa. d = kh Joa separoiuva differeniaaliyhälö voidaan rakaisa, ilavuusvirran muuos piää lausua sien, eä yhälössä olevan korkeus-ermi korvaaan ilavuudella. Nesepinnan korkeus piää siis lausua ilavuuden avulla, käyäen muunnosa: V = r 2 h h= V V D h= 2 2 D2 4 h= 4V D 2,617 V meriä Tilavuusvirran muuosa kuvaa ny siis yhälö: d =,72,617V d =,4332V Laskeaan inegroimisraja: Alaraja: loppuilavuus = alkuperäinen ilavuus*äyöase = 11 m 3 *,83 = 91,3 m 3 = Yläraja: lähöilavuus = alkuperäinen ilavuus*äyöase = 11 m 3 *,12 = 13,2 m 3 = Inegroiava yhälö on ny muooa: V =,4332 d, josa inegroimalla saadaan: ln =,4332 ln 13,2 =,4332 1,93393=, ,3 446,4 sekunia Tyhjennys kesää siis noin 7 minuuia ja 3 sekunia.
5 Koha D Säiliöön syöeään ny samanaikaisesi uua liuosa 3 dm 3 /s. Tilavuuden pieneneminen kuviellaan edelleenkin negaiiviseksi ja inegroimisraja ova sama kuin kohdassa C. Lasku on siis muuen aivan samanlainen, mua siihen on vain lisäy mukaan sisäänulovira, josa käyän merkinää in-ermi. Tilavuusvirran muuosa kuvaa ny yhälö: d = ou in d d = m3 m3 = kh,3 s,4332v,3 s =,4332V m3 d s,4332v,3 =,3 m3 s d Kerroaan ylempi yhälö ermillä -,4332, joa voidaan käyää kaavaa f ' f dx=ln f C,4332V,3 =,4332 d,4332v,3 =,4332 d,4332=ln,4332,3 ln.4332,3, sijoieaan inegroimisraja,4332=ln, ,2,3 ln ,3,3,4332 =ln,272 ln,3655,4332 = 3,6 1 = 2,6 6,2 sekunia,4332 Tyhjennys kesää siis noin 1 minuuia. Tyhjennykseen kulunu aika kasvoi siis vain noin reilu kaksi minuuia.
W dt dt t J.
 DEE-11 Piirianalyysi Harjoius 1 / viikko 3.1 RC-auon akku (8.4 V, 17 mah) on ladau äyeen. Kuinka suuri osa akun energiasa kuluu ensimmäisen 5 min aikana, kun oleeaan mooorin kuluavan vakiovirran 5 A? Oleeaan
DEE-11 Piirianalyysi Harjoius 1 / viikko 3.1 RC-auon akku (8.4 V, 17 mah) on ladau äyeen. Kuinka suuri osa akun energiasa kuluu ensimmäisen 5 min aikana, kun oleeaan mooorin kuluavan vakiovirran 5 A? Oleeaan
Huomaa, että aika tulee ilmoittaa SI-yksikössä, eli sekunteina (1 h = 3600 s).
 DEE- Piirianalyysi Ykkösharkan ehävien rakaisuehdoukse. askeaan ensin, kuinka paljon äyeen ladaussa akussa on energiaa. Tämä saadaan laskeua ehäväpaperissa anneujen akun ieojen 8.4 V ja 7 mah avulla. 8.4
DEE- Piirianalyysi Ykkösharkan ehävien rakaisuehdoukse. askeaan ensin, kuinka paljon äyeen ladaussa akussa on energiaa. Tämä saadaan laskeua ehäväpaperissa anneujen akun ieojen 8.4 V ja 7 mah avulla. 8.4
Tasaantumisilmiöt eli transientit
 uku 12 Tasaanumisilmiö eli ransieni 12.1 Kelan kykeminen asajännieeseen Kappaleessa 11.2 kykeiin reaalinen kela asajännieeseen ja ukiiin energian varasoiumisa kelan magneeikenään. Tilanne on esiey uudelleen
uku 12 Tasaanumisilmiö eli ransieni 12.1 Kelan kykeminen asajännieeseen Kappaleessa 11.2 kykeiin reaalinen kela asajännieeseen ja ukiiin energian varasoiumisa kelan magneeikenään. Tilanne on esiey uudelleen
Diskreetillä puolella impulssi oli yksinkertainen lukujono:
 DEE-00 ineaarise järjeselmä Harjoius 5, rakaisuehdoukse [johdano impulssivaseeseen] Jakuva-aikaisen järjeselmän impulssivase on vasaavanlainen järjeselmäyökalu kuin diskreeillä puolellakin: impulssivase
DEE-00 ineaarise järjeselmä Harjoius 5, rakaisuehdoukse [johdano impulssivaseeseen] Jakuva-aikaisen järjeselmän impulssivase on vasaavanlainen järjeselmäyökalu kuin diskreeillä puolellakin: impulssivase
Monisilmukkainen vaihtovirtapiiri
 Monisilmukkainen vaihovirapiiri Oeaan arkaselun koheeksi RLC-vaihovirapiiri jossa on käämejä, vasuksia ja kondensaaoreia. Kykenä Tarkasellaan virapiiriä, jossa yksinkeraiseen RLC-piiriin on kodensaaorin
Monisilmukkainen vaihovirapiiri Oeaan arkaselun koheeksi RLC-vaihovirapiiri jossa on käämejä, vasuksia ja kondensaaoreia. Kykenä Tarkasellaan virapiiriä, jossa yksinkeraiseen RLC-piiriin on kodensaaorin
( ) 5 t. ( ) 20 dt ( ) ( ) ( ) ( + ) ( ) ( ) ( + ) / ( ) du ( t ) dt
 SMG-500 Verolasennan numeerise meneelmä Ehdouse harjoiusen 4 raaisuisi Haeaan ensin ehävän analyyinen raaisu: dx 0 0 0 0 dx 00e = 0 = 00e 00 x = e + = 5e + alueho: x(0 = 0 0 x 0 = 5e + = 0 = 5 0 0 0 5
SMG-500 Verolasennan numeerise meneelmä Ehdouse harjoiusen 4 raaisuisi Haeaan ensin ehävän analyyinen raaisu: dx 0 0 0 0 dx 00e = 0 = 00e 00 x = e + = 5e + alueho: x(0 = 0 0 x 0 = 5e + = 0 = 5 0 0 0 5
Mittaustekniikan perusteet, piirianalyysin kertausta
 Miausekniikan perusee, piirianalyysin kerausa. Ohmin laki: =, ai = Z ( = ännie, = resisanssi, Z = impedanssi, = vira). Kompleksiluvu Kompleksilukua arviaan elekroniikassa analysoiaessa piireä, oka sisälävä
Miausekniikan perusee, piirianalyysin kerausa. Ohmin laki: =, ai = Z ( = ännie, = resisanssi, Z = impedanssi, = vira). Kompleksiluvu Kompleksilukua arviaan elekroniikassa analysoiaessa piireä, oka sisälävä
A-osio. Ei laskinta! Valitse seuraavista kolmesta tehtävästä vain kaksi joihin vastaat!
 MAA Koe 7..03 A-osio. Ei laskina! Valise seuraavisa kolmesa ehäväsä vain kaksi joihin vasaa! A. a) Mikä on funkion f(x) määrieljoukko, jos f( x) x b) Muua ulomuooon: 4a 8a 4 A. a) Rakaise hälö: x 4x b)
MAA Koe 7..03 A-osio. Ei laskina! Valise seuraavisa kolmesa ehäväsä vain kaksi joihin vasaa! A. a) Mikä on funkion f(x) määrieljoukko, jos f( x) x b) Muua ulomuooon: 4a 8a 4 A. a) Rakaise hälö: x 4x b)
( ) ( ) x t. 2. Esitä kuvassa annetun signaalin x(t) yhtälö aikaalueessa. Laske signaalin Fourier-muunnos ja hahmottele amplitudispektri.
 ELEC-A7 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS Sivu 1/11 1. Johda anneun pulssin Fourier-muunnos ja hahmoele ampliudispekri. Käyä esim. derivoinieoreemaa, ja älä unohda 1. derivaaan epäjakuvuuskohia!
ELEC-A7 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS Sivu 1/11 1. Johda anneun pulssin Fourier-muunnos ja hahmoele ampliudispekri. Käyä esim. derivoinieoreemaa, ja älä unohda 1. derivaaan epäjakuvuuskohia!
x v1 y v2, missä x ja y ovat kokonaislukuja.
 Digiaalinen videonkäsiel Harjoius, vasaukse ehäviin 4-0 Tehävä 4. Emämariisi a: V A 0 V B 0 Hila saadaan kanavekorien (=emämariisin sarakkee) avulla. Kunkin piseen paikka hilassa on kokonaisluvulla kerroujen
Digiaalinen videonkäsiel Harjoius, vasaukse ehäviin 4-0 Tehävä 4. Emämariisi a: V A 0 V B 0 Hila saadaan kanavekorien (=emämariisin sarakkee) avulla. Kunkin piseen paikka hilassa on kokonaisluvulla kerroujen
9. Epäoleelliset integraalit; integraalin derivointi parametrin suhteen. (x + y)e x y dxdy. e (ax+by)2 da. xy 2 r 4 da; r = x 2 + y 2. b) A.
 9. Epäoleellise inegraali; inegraalin derivoini paramerin suheen 9.. Epäoleellise aso- ja avaruusinegraali 27. Olkoon = {(x, y) x, y }. Osoia hajaanuminen ai laske arvo epäoleelliselle asoinegraalille
9. Epäoleellise inegraali; inegraalin derivoini paramerin suheen 9.. Epäoleellise aso- ja avaruusinegraali 27. Olkoon = {(x, y) x, y }. Osoia hajaanuminen ai laske arvo epäoleelliselle asoinegraalille
( ) ( ) 2. Esitä oheisen RC-ylipäästösuotimesta, RC-alipäästösuotimesta ja erotuspiiristä koostuvan lineaarisen järjestelmän:
 ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
DEE Lineaariset järjestelmät Harjoitus 4, ratkaisuehdotukset
 D-00 ineaarise järjeselmä Harjoius 4, rakaisuehdoukse nnen kuin mennään ämän harjoiuksen aihepiireihin, käydään läpi yksi huomionarvoinen juu. Piirianalyysin juuri suorianee opiskelija saaava ihmeellä,
D-00 ineaarise järjeselmä Harjoius 4, rakaisuehdoukse nnen kuin mennään ämän harjoiuksen aihepiireihin, käydään läpi yksi huomionarvoinen juu. Piirianalyysin juuri suorianee opiskelija saaava ihmeellä,
12. ARKISIA SOVELLUKSIA
 MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
2. Matemaattinen malli ja funktio 179. a) f (-2) = -2 (-2) = = -6 b) f (-2) = 2 (-2) 2 - (-2) = (-8) + 7 = = 23
 LISÄTEHTÄVÄT. Maemaainen malli ja funkio 9. a) f (-) = - (-) + = - + = -6 b) f (-) = (-) - (-) + = - (-8) + = 8 + 8 + = 80. a) f ( ) = + f ( ) = 0 + = 0 ( ) = ± = ± = ai = Vasaus: = - ai = b) + = + = 0
LISÄTEHTÄVÄT. Maemaainen malli ja funkio 9. a) f (-) = - (-) + = - + = -6 b) f (-) = (-) - (-) + = - (-8) + = 8 + 8 + = 80. a) f ( ) = + f ( ) = 0 + = 0 ( ) = ± = ± = ai = Vasaus: = - ai = b) + = + = 0
ETERAN TyEL:n MUKAISEN VAKUUTUKSEN ERITYISPERUSTEET
 TRAN TyL:n MUKASN AKUUTUKSN RTYSPRUSTT Tässä peruseessa kaikki suuree koskea eraa, ellei oisin ole määriely. Tässä peruseessa käyey lyhenee: LL Lyhyaikaisissa yösuheissa oleien yönekijäin eläkelaki TaL
TRAN TyL:n MUKASN AKUUTUKSN RTYSPRUSTT Tässä peruseessa kaikki suuree koskea eraa, ellei oisin ole määriely. Tässä peruseessa käyey lyhenee: LL Lyhyaikaisissa yösuheissa oleien yönekijäin eläkelaki TaL
joka on separoituva yhtälö, jolla ei ole reaalisia triviaaliratkaisuja. Ratkaistaan: z z(x) dx =
 HY / Maemaiikan ja ilasoieeen laios Differeniaalihälö I kevä 09 Harjois 4 Rakaisehdoksia. Rakaise differeniaalihälö = (x + + Rakais: Tehdään differeniaalihälöön lineaarinen mnnos z(x = x + (x + jolloin
HY / Maemaiikan ja ilasoieeen laios Differeniaalihälö I kevä 09 Harjois 4 Rakaisehdoksia. Rakaise differeniaalihälö = (x + + Rakais: Tehdään differeniaalihälöön lineaarinen mnnos z(x = x + (x + jolloin
f x dx y dy t dt f x y t dx dy dt O , (4b) . (4c) f f x = ja x (4d)
 Tehävä 1. Oleeaan, eä on käössä jakuva kuva, jossa (,, ) keroo harmaasävn arvon paikassa (, ) ajanhekenä. Dnaaminen kuva voidaan esiää Talor sarjana: d d d d d d O ( +, +, + ) = (,, ) + + + + ( ). (4a)
Tehävä 1. Oleeaan, eä on käössä jakuva kuva, jossa (,, ) keroo harmaasävn arvon paikassa (, ) ajanhekenä. Dnaaminen kuva voidaan esiää Talor sarjana: d d d d d d O ( +, +, + ) = (,, ) + + + + ( ). (4a)
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.4 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vasausen piireiden, sisälöjen ja piseiysen luonnehdina ei sido ylioppilasukinolauakunnan arvoselua. Lopullisessa arvoselussa
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.4 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vasausen piireiden, sisälöjen ja piseiysen luonnehdina ei sido ylioppilasukinolauakunnan arvoselua. Lopullisessa arvoselussa
Luento 4. Fourier-muunnos
 Lueno 4 Erikoissignaalien Fourier-muunnokse Näyeenoo 4..6 Fourier-muunnos Fourier-muunnos Kääneismuunnos Diricle n edo Fourier muunuvalle energiasignaalille I: Signaali on iseisesi inegroiuva v ( d< II:
Lueno 4 Erikoissignaalien Fourier-muunnokse Näyeenoo 4..6 Fourier-muunnos Fourier-muunnos Kääneismuunnos Diricle n edo Fourier muunuvalle energiasignaalille I: Signaali on iseisesi inegroiuva v ( d< II:
S Signaalit ja järjestelmät Tentti
 S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
järjestelmät Luento 4
 DEE- Lineaarise järjeselmä Lueno 4 Lineaarise järjeselmä Riso Mionen 3.7.4 Lueno 3 - Recap Lineaarisen differenssiyhälöiden raaiseminen Impulssivaseen äsie Impulssivase ja onvoluuiosumma Lineaarise järjeselmä
DEE- Lineaarise järjeselmä Lueno 4 Lineaarise järjeselmä Riso Mionen 3.7.4 Lueno 3 - Recap Lineaarisen differenssiyhälöiden raaiseminen Impulssivaseen äsie Impulssivase ja onvoluuiosumma Lineaarise järjeselmä
VÄRÄHTELYMEKANIIKKA SESSIO 18: Yhden vapausasteen pakkovärähtely, transienttikuormituksia
 8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
Seoksen pitoisuuslaskuja
 Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
2. Suoraviivainen liike
 . Suoraviivainen liike . Siirymä, keskinopeus ja keskivauhi Aika: unnus, yksikkö: sekuni s Suoraviivaisessa liikkeessä kappaleen asema (paikka) ilmoieaan suoralla olevan piseen paikkakoordinaain (unnus
. Suoraviivainen liike . Siirymä, keskinopeus ja keskivauhi Aika: unnus, yksikkö: sekuni s Suoraviivaisessa liikkeessä kappaleen asema (paikka) ilmoieaan suoralla olevan piseen paikkakoordinaain (unnus
1. Todista/Prove (b) Lause 2.4. käyttäen Lausetta 2.3./by using Theorem b 1 ; 1 b + 1 ; 1 b 1 1
 KETJUMURTOLUVUT Harjoiuksia 209. Todisa/Prove Lause 2.2. käyäen Lausea 2.3./by using Theorem 2.3. Lause 2.4. käyäen Lausea 2.3./by using Theorem 2.3. 2. Määrää Canorin kehielmä luvuille 0,, 2, 3, 4, 5,
KETJUMURTOLUVUT Harjoiuksia 209. Todisa/Prove Lause 2.2. käyäen Lausea 2.3./by using Theorem 2.3. Lause 2.4. käyäen Lausea 2.3./by using Theorem 2.3. 2. Määrää Canorin kehielmä luvuille 0,, 2, 3, 4, 5,
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
Puolijohdekomponenttien perusteet A Ratkaisut 2, Kevät 2017
 OY/PJKOMP R 017 Puolijohdekomoeie erusee 571A Rakaisu, Kevä 017 1. Massavaikuuslai mukaisesi eemmisö- ja vähemmisövarauksekuljeajie ulo o vakio i, joka riiuu uolijohdemaeriaalisa ja lämöilasa. Kuvasa 1
OY/PJKOMP R 017 Puolijohdekomoeie erusee 571A Rakaisu, Kevä 017 1. Massavaikuuslai mukaisesi eemmisö- ja vähemmisövarauksekuljeajie ulo o vakio i, joka riiuu uolijohdemaeriaalisa ja lämöilasa. Kuvasa 1
b) Ei ole. Todistus samaan tyyliin kuin edellinen. Olkoon C > 0 ja valitaan x = 2C sekä y = 0. Tällöin pätee f(x) f(y)
 Maemaiikan ja ilasoieeen osaso/hy Differeniaaliyhälö II Laskuharjoius 1 malli Kevä 19 Tehävä 1. Ovako seuraava funkio Lipschiz-jakuvia reaaliakselilla: a) f(x) = x 1/3, b) f(x) = x, c) f(x) = x? a) Ei
Maemaiikan ja ilasoieeen osaso/hy Differeniaaliyhälö II Laskuharjoius 1 malli Kevä 19 Tehävä 1. Ovako seuraava funkio Lipschiz-jakuvia reaaliakselilla: a) f(x) = x 1/3, b) f(x) = x, c) f(x) = x? a) Ei
Dynaaminen optimointi ja ehdollisten vaateiden menetelmä
 Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Mallivastaukset KA5-kurssin laskareihin, kevät 2009
 Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
Silloin voidaan suoraan kirjoittaa spektrin yhtälö käyttämällä hyväksi suorakulmaisen pulssin Fouriermuunnosta sekä viiveen vaikutusta: ( ) (
 TT/TV Inegraalimuunnokse Fourier-muunnos, ehäviä : Vasauksia Meropolia/. Koivumäki v(. Määriä oheisen signaalin Fourier-muunnos. Vinkki: Superposiio, viive. Voidaan sovelaa superposiioperiaaea, koska signaalin
TT/TV Inegraalimuunnokse Fourier-muunnos, ehäviä : Vasauksia Meropolia/. Koivumäki v(. Määriä oheisen signaalin Fourier-muunnos. Vinkki: Superposiio, viive. Voidaan sovelaa superposiioperiaaea, koska signaalin
2. Reaktioyhtälö 3) CH 3 CH 2 COCH 3 + O 2 CO 2 + H 2 O
 2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
ẍ(t) q(t)x(t) = f(t) 0 1 z(t) +.
 Diffrniaaliyhälö II, harjoius 3, 8 228, rakaisu JL, kuusi sivua a On muunnava linaarinn oisn kraluvun diffrniaaliyhälö ẍ qx f yhäpiäväksi nsimmäisn kraluvun linaarisksi kahdn skalaariyhälön sysmiksi Rak
Diffrniaaliyhälö II, harjoius 3, 8 228, rakaisu JL, kuusi sivua a On muunnava linaarinn oisn kraluvun diffrniaaliyhälö ẍ qx f yhäpiäväksi nsimmäisn kraluvun linaarisksi kahdn skalaariyhälön sysmiksi Rak
Derivoimalla ensimmäinen komponentti, sijoittamalla jälkimmäisen derivaatta siihen ja eliminoimalla x. saadaan
 87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Mallivastaukset KA5-kurssin laskareihin, kevät 2009
 Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 8 (viikko 14) Tehävä 1 LAD-käyrä siiryy ylöspäin. Ulkomaisen hinojen nousessa oman maan reaalinen vaihokurssi heikkenee 1 vaihoase vahvisuu IS-käyrä
Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 8 (viikko 14) Tehävä 1 LAD-käyrä siiryy ylöspäin. Ulkomaisen hinojen nousessa oman maan reaalinen vaihokurssi heikkenee 1 vaihoase vahvisuu IS-käyrä
Tehtävä I. Vaihtoehtotehtävät.
 Kem-9.7 Prosessiauomaaion perusee Teni 5.9.5 TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN MUKANA NIMI: (OS: ) OPINTOKIRJA: VIERAILULUENNOT KUUNNELTU: VALV. LASK: Tehävä I. Vaihoehoehävä. Oikea vasaus
Kem-9.7 Prosessiauomaaion perusee Teni 5.9.5 TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN MUKANA NIMI: (OS: ) OPINTOKIRJA: VIERAILULUENNOT KUUNNELTU: VALV. LASK: Tehävä I. Vaihoehoehävä. Oikea vasaus
DEE Lineaariset järjestelmät Harjoitus 6, harjoitustenpitäjille tarkoitetut ratkaisuehdotukset
 DEE- ineaarie järjeelmä Harjoiu 6, harjoiuenpiäjille arkoieu rakaiuehdouke Tää harjoiukea käiellään aplace-muunnoa ja en hyödynämiä differeniaaliyhälöiden rakaiemiea Tehävä Määrielmän mukaan funkion f
DEE- ineaarie järjeelmä Harjoiu 6, harjoiuenpiäjille arkoieu rakaiuehdouke Tää harjoiukea käiellään aplace-muunnoa ja en hyödynämiä differeniaaliyhälöiden rakaiemiea Tehävä Määrielmän mukaan funkion f
KOMISSION VALMISTELUASIAKIRJA
 EUROOPAN UNIONIN NEUVOSTO Bryssel, 23. oukokuua 2007 (24.05) (OR. en) Toimielinen välinen asia: 2006/0039 (CNS) 9851/07 ADD 2 N 239 RESPR 5 CADREN 32 LISÄYS 2 I/A KOHTAA KOSKEVAAN ILMOITUKSEEN Läheäjä:
EUROOPAN UNIONIN NEUVOSTO Bryssel, 23. oukokuua 2007 (24.05) (OR. en) Toimielinen välinen asia: 2006/0039 (CNS) 9851/07 ADD 2 N 239 RESPR 5 CADREN 32 LISÄYS 2 I/A KOHTAA KOSKEVAAN ILMOITUKSEEN Läheäjä:
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe
 Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
a. Varsinainen prosessi on tuttua tilaesitysmuotoa:
 ELEC-C Sääöeniia 7. lauharjoiu Vaaue. r - K u K C y a. Varinainen proei on uua ilaeiymuooa: A Bu y C Kuvaa nähdään, eä ilamallin iäänmenona on u r K. Salaaria ei voi vähenää mariiia, joen un on n -veori,
ELEC-C Sääöeniia 7. lauharjoiu Vaaue. r - K u K C y a. Varinainen proei on uua ilaeiymuooa: A Bu y C Kuvaa nähdään, eä ilamallin iäänmenona on u r K. Salaaria ei voi vähenää mariiia, joen un on n -veori,
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
DEE Lineaariset järjestelmät Harjoitus 3, harjoitustenpitäjille tarkoitetut ratkaisuehdotukset
 DEE- ineaarise järjeselmä Harjoius 3, harjoiusenpiäjille arkoieu rakaisuehdoukse Ennen kuin mennään ämän harjoiuksen aihepiireihin, käydään läpi yksi huomionarvoinen juu Piirianalyysin juuri suorianee
DEE- ineaarise järjeselmä Harjoius 3, harjoiusenpiäjille arkoieu rakaisuehdoukse Ennen kuin mennään ämän harjoiuksen aihepiireihin, käydään läpi yksi huomionarvoinen juu Piirianalyysin juuri suorianee
DVC. VARIZON Piennopeuslaite säädettävällä hajotuskuviolla. Pikavalintataulukko
 VARIZON Piennoeuslaie säädeävällä hajouskuviolla Lyhyesi Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Eri värivaihoehoja Pikavalinaaulukko
VARIZON Piennoeuslaie säädeävällä hajouskuviolla Lyhyesi Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Eri värivaihoehoja Pikavalinaaulukko
DEE-53000 Sähkömagneettisten järjestelmien lämmönsiirto
 DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
Suunnitteluharjoitus s-2016 (...k-2017)
 1 Suunnieluharjoius s-2016 (...k-2017) HAKKURITEHOLÄHDE Seuraavan push-pull-yyppisen hakkurieholäheen komponeni ulisi valia (muunajaa lukuunoamaa). V1 iin 230 V ± 10 % 50 Hz V3 Perusieoja kykennäsä Verkkoasasuunauksen
1 Suunnieluharjoius s-2016 (...k-2017) HAKKURITEHOLÄHDE Seuraavan push-pull-yyppisen hakkurieholäheen komponeni ulisi valia (muunajaa lukuunoamaa). V1 iin 230 V ± 10 % 50 Hz V3 Perusieoja kykennäsä Verkkoasasuunauksen
MUODONMUUTOKSET. Lähtöotaksumat:
 MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
5 LIUOKSEN PITOISUUS Lisätehtävät
 LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
4. Integraalilaskenta
 4. Inegrlilsken Joh8elev esimerkki: kun hiukksen pikk s( erivoin jn suheen, sn hiukksen nopeus: v( = s'( Kun nopeus erivoin jn suheen sn kiihyvyys ( = v'( Kääneinen ongelm: hiukksen kiihyvyys on (. Mikä
4. Inegrlilsken Joh8elev esimerkki: kun hiukksen pikk s( erivoin jn suheen, sn hiukksen nopeus: v( = s'( Kun nopeus erivoin jn suheen sn kiihyvyys ( = v'( Kääneinen ongelm: hiukksen kiihyvyys on (. Mikä
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA 2 OV. Isto Jokinen 2012. 1. Mekaniikka 2
 OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
MAT-02450 Fourier n menetelmät. Merja Laaksonen, TTY 2014
 MAT-45 Fourier n meneelmä Merja Laaksonen, TTY 4..4 Sisälö Johano 3. Peruskäsieiä................................... 4.. Parillinen ja parion funkio....................... 7.. Heavisien funkio............................
MAT-45 Fourier n meneelmä Merja Laaksonen, TTY 4..4 Sisälö Johano 3. Peruskäsieiä................................... 4.. Parillinen ja parion funkio....................... 7.. Heavisien funkio............................
Rahoitusriskit ja johdannaiset Matti Estola. luento 12 Stokastisista prosesseista
 Rahoiusriski ja johdannaise Mai Esola lueno Sokasisisa prosesseisa . Markov ominaisuus Markov -prosessi on sokasinen prosessi, missä ainoasaan muuujan viimeinen havaino on relevani muuujan seuraavaa arvoa
Rahoiusriski ja johdannaise Mai Esola lueno Sokasisisa prosesseisa . Markov ominaisuus Markov -prosessi on sokasinen prosessi, missä ainoasaan muuujan viimeinen havaino on relevani muuujan seuraavaa arvoa
luku 1.notebook Luku 1 Mooli, ainemäärä ja konsentraatio
 Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
2. Taloudessa käytettyjä yksinkertaisia ennustemalleja. ja tarkasteltavaa muuttujan arvoa hetkellä t kirjaimella y t
 Tilasollinen ennusaminen Seppo Pynnönen Tilasoieeen professori, Meneelmäieeiden laios, Vaasan yliopiso. Tausaa Tulevaisuuden ennusaminen on ehkä yksi luoneenomaisimpia piireiä ihmiselle. On ilmeisesi aina
Tilasollinen ennusaminen Seppo Pynnönen Tilasoieeen professori, Meneelmäieeiden laios, Vaasan yliopiso. Tausaa Tulevaisuuden ennusaminen on ehkä yksi luoneenomaisimpia piireiä ihmiselle. On ilmeisesi aina
Copyright Isto Jokinen MATEMATIIKKA. Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017
 AEAKKA aeaiikkaa piakäsielijöille Ogelarakaisu so Jokie 207 SSÄLÖ. aeaaise ogelie rakaisu laskukaaoilla 2. ekijäyhälö 3. Laskukaaoje yhdisäie 4. Yhälöide uodosaie aeaaisee ogelaa Käyöoikeus opeuksessa
AEAKKA aeaiikkaa piakäsielijöille Ogelarakaisu so Jokie 207 SSÄLÖ. aeaaise ogelie rakaisu laskukaaoilla 2. ekijäyhälö 3. Laskukaaoje yhdisäie 4. Yhälöide uodosaie aeaaisee ogelaa Käyöoikeus opeuksessa
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Sopimuksenteon dynamiikka: johdanto ja haitallinen valikoituminen
 Soimukseneon dynamiikka: johdano ja haiallinen valikoiuminen Ma-2.442 Oimoinioin seminaari Elise Kolola 8.4.2008 S yseemianalyysin Laboraorio Esielmä 4 Elise Kolola Oimoinioin seminaari - Kevä 2008 Esiyksen
Soimukseneon dynamiikka: johdano ja haiallinen valikoiuminen Ma-2.442 Oimoinioin seminaari Elise Kolola 8.4.2008 S yseemianalyysin Laboraorio Esielmä 4 Elise Kolola Oimoinioin seminaari - Kevä 2008 Esiyksen
TKK Tietoliikennelaboratorio Seppo Saastamoinen Sivu 1/5 Konvoluution laskeminen vaihe vaiheelta
 KK ieoliikennelaboraorio 7.2.27 Seppo Saasamoinen Sivu /5 Konvoluuion laskeminen vaihe vaiheela Konvoluuion avulla saadaan laskeua aika-alueessa järjeselmän lähösignaali, kun ulosignaali ja järjeselmän
KK ieoliikennelaboraorio 7.2.27 Seppo Saasamoinen Sivu /5 Konvoluuion laskeminen vaihe vaiheela Konvoluuion avulla saadaan laskeua aika-alueessa järjeselmän lähösignaali, kun ulosignaali ja järjeselmän
Käyttövarmuuden ja kunnossapidon perusteet, KSU-4310: Tentti ma
 KSU-430/Ten 4..2008/Prof. Seppo Vranen /3 Käyövarmuuden ja kunnossapdon perusee, KSU-430: Ten ma 4..2008 Huom. Vasaus van veen kysymykseen. Funko- ja/a ohjelmoavan laskmen, musnpanojen, luenomonseden ja
KSU-430/Ten 4..2008/Prof. Seppo Vranen /3 Käyövarmuuden ja kunnossapdon perusee, KSU-430: Ten ma 4..2008 Huom. Vasaus van veen kysymykseen. Funko- ja/a ohjelmoavan laskmen, musnpanojen, luenomonseden ja
Johda jakauman momenttiemäfunktio ja sen avulla jakauman odotusarvo ja varianssi.
 / Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
/ Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
JLP:n käyttämättömät mahdollisuudet. Juha Lappi
 JLP:n äyämäömä mahdollisuude Juha Lappi LP ehävä p z = a x + b z 0 Max or Min (.) 0 0 = = subjec o he following consrains: c a x + b z C, =,, q p q K r (.2) = = m n i ij K (.3) i= j= ij x xw= 0, =,, p
JLP:n äyämäömä mahdollisuude Juha Lappi LP ehävä p z = a x + b z 0 Max or Min (.) 0 0 = = subjec o he following consrains: c a x + b z C, =,, q p q K r (.2) = = m n i ij K (.3) i= j= ij x xw= 0, =,, p
8 USEAN VAPAUSASTEEN SYSTEEMIN VAIMENEMATON PAKKOVÄRÄHTELY
 Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - Molekyylibiotieteet/Bioteknologia Etunimet valintakoe Tehtävä 3 Pisteet / 30
 Helsingin yliopisto/tampereen yliopisto Henkilötunnus - hakukohde Sukunimi Molekyylibiotieteet/Bioteknologia Etunimet valintakoe 20.5.2013 Tehtävä 3 Pisteet / 30 3. Osa I: Stereokemia a) Piirrä kaikki
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - hakukohde Sukunimi Molekyylibiotieteet/Bioteknologia Etunimet valintakoe 20.5.2013 Tehtävä 3 Pisteet / 30 3. Osa I: Stereokemia a) Piirrä kaikki
MOOLIMASSA. Vedyllä on yksi atomi, joten Vedyn moolimassa M(H) = 1* g/mol = g/mol. ATOMIMASSAT TAULUKKO
 MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
Juuri 13 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. K1. A: III, B: I, C: II ja IV.
 Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
VATT-KESKUSTELUALOITTEITA VATT DISCUSSION PAPERS. JULKISEN TALOUDEN PITKÄN AIKAVÄLIN LASKENTAMALLIT Katsaus kirjallisuuteen
 VATT-KESKUSTELUALOITTEITA VATT DISCUSSION PAPERS 445 JULKISEN TALOUDEN PITKÄN AIKAVÄLIN LASKENTAMALLIT Kasaus kirjallisuueen Juho Kosiainen Valion aloudellinen ukimuskeskus Governmen Insiue for Economic
VATT-KESKUSTELUALOITTEITA VATT DISCUSSION PAPERS 445 JULKISEN TALOUDEN PITKÄN AIKAVÄLIN LASKENTAMALLIT Kasaus kirjallisuueen Juho Kosiainen Valion aloudellinen ukimuskeskus Governmen Insiue for Economic
Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin.
 1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
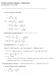 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Kaupunkikehityspalvelut. Kaupunkisuunnittelu KAAVA-ALUE 457:6:87 457:6:88 457:6:95 457:6:82 418:1: :1: :11:0 457:6:21 457:6:83 457:6:89
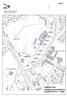 Kupunkisuunnielu Kupunkikehiysplvelu KAAVA-ALUE 8::8 8:: 8::9 8:: 8::8 8::9 8::9 8:: 8:: 8:: 8:: 8:: 8:: 8::8 8::9 8::80 8: 8::8 8::89 8::90 8::9 8:: 8::9 8: 8::0 8::0 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8::8
Kupunkisuunnielu Kupunkikehiysplvelu KAAVA-ALUE 8::8 8:: 8::9 8:: 8::8 8::9 8::9 8:: 8:: 8:: 8:: 8:: 8:: 8::8 8::9 8::80 8: 8::8 8::89 8::90 8::9 8:: 8::9 8: 8::0 8::0 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8::8
Tehtävän 1 moottorin kuormana an työkone, jonka momentti on vakio T=30 Nm. Laske
 SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
KÄYTTÖOPAS. Ilma vesilämpöpumppujärjestelmän sisäyksikkö ja lisävarusteet RECAIR OY EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1
 EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1 EKHBRD011ADY1 EKHBRD014ADY1 EKHBRD016ADY1 KÄYÖOPAS Ilma vesilämpöpumppujärjeselmän sisäyksikkö ja lisävarusee EKHBRD011ADV1+Y1 EKHBRD014ADV1+Y1 EKHBRD016ADV1+Y1
EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1 EKHBRD011ADY1 EKHBRD014ADY1 EKHBRD016ADY1 KÄYÖOPAS Ilma vesilämpöpumppujärjeselmän sisäyksikkö ja lisävarusee EKHBRD011ADV1+Y1 EKHBRD014ADV1+Y1 EKHBRD016ADV1+Y1
Tiedonhakumenetelmät Tiedonhakumenetelmät Helsingin yliopisto / TKTL. H.Laine 1. Todennäköisyyspohjainen rankkaus
 Tieonhakumeneelmä Helsingin yliopiso / TKTL.4.04 Toennäköisyyeen perusuva rankkaus Tieonhakumeneelmä Toennäköisyyspohjainen rankkaus Dokumenien haussa ongelmana on löyää käyäjän kyselynä ilmaiseman ieoarpeen
Tieonhakumeneelmä Helsingin yliopiso / TKTL.4.04 Toennäköisyyeen perusuva rankkaus Tieonhakumeneelmä Toennäköisyyspohjainen rankkaus Dokumenien haussa ongelmana on löyää käyäjän kyselynä ilmaiseman ieoarpeen
Konvoluution laskeminen vaihe vaiheelta Sivu 1/5
 S-72. Signaali ja järjeselmä Laskuharjoiukse, syksy 28 Konvoluuion laskeminen vaihe vaiheela Sivu /5 Konvoluuion laskeminen vaihe vaiheela Konvoluuion avulla saadaan laskeua aika-alueessa järjeselmän lähösignaali,
S-72. Signaali ja järjeselmä Laskuharjoiukse, syksy 28 Konvoluuion laskeminen vaihe vaiheela Sivu /5 Konvoluuion laskeminen vaihe vaiheela Konvoluuion avulla saadaan laskeua aika-alueessa järjeselmän lähösignaali,
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
CHEM-A1110 Virtaukset ja reaktorit. Laskuharjoitus 9/2016. Energiataseet
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
Rahoitusriskit ja johdannaiset Matti Estola. luento 13 Black-Scholes malli optioiden hinnoille
 Rahoiusriski ja johannaise Mai Esola lueno 3 Black-choles malli opioien hinnoille . Ion lemma Japanilainen maemaaikko Kiyoshi Iō oisi seuraavana esieävän lemman vuonna 95 arikkelissaan: On sochasic ifferenial
Rahoiusriski ja johannaise Mai Esola lueno 3 Black-choles malli opioien hinnoille . Ion lemma Japanilainen maemaaikko Kiyoshi Iō oisi seuraavana esieävän lemman vuonna 95 arikkelissaan: On sochasic ifferenial
5. Vakiokertoiminen lineaarinen normaaliryhmä
 1 MAT-145 LAAJA MATEMATIIKKA 5 Tampereen eknillinen yliopiso Riso Silvennoinen Kevä 21 5. Vakiokeroiminen lineaarinen normaaliryhmä Todeaan ensin ilman odisuksia (ulos on syvällinen) rakaisujen olemassaoloa
1 MAT-145 LAAJA MATEMATIIKKA 5 Tampereen eknillinen yliopiso Riso Silvennoinen Kevä 21 5. Vakiokeroiminen lineaarinen normaaliryhmä Todeaan ensin ilman odisuksia (ulos on syvällinen) rakaisujen olemassaoloa
KÄYTTÖOPAS. -järjestelmän sisäyksikkö HXHD125A8V1B
 KÄYÖOPAS -järjeselmän sisäyksikkö SISÄLÖ 1. Määrielmä... 1 1.1. Merkkien ja varoiusen arkoiukse... 1 1.2. Käyeyjen ermien merkiys... 1 2. Yleise varooime... 2 3. Johdano... 2 3.1. Yleisä... 2 3.2. ämän
KÄYÖOPAS -järjeselmän sisäyksikkö SISÄLÖ 1. Määrielmä... 1 1.1. Merkkien ja varoiusen arkoiukse... 1 1.2. Käyeyjen ermien merkiys... 1 2. Yleise varooime... 2 3. Johdano... 2 3.1. Yleisä... 2 3.2. ämän
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Laskelmia verotuksen painopisteen muuttamisen vaikutuksista dynaamisessa yleisen tasapainon mallissa
 Laskelmia verouksen painopiseen muuamisen vaikuuksisa dynaamisessa yleisen asapainon mallissa Juha Kilponen ja Jouko Vilmunen TTässä arikkelissa esieään laskelmia siiä, mien verouksen painopiseen siiräminen
Laskelmia verouksen painopiseen muuamisen vaikuuksisa dynaamisessa yleisen asapainon mallissa Juha Kilponen ja Jouko Vilmunen TTässä arikkelissa esieään laskelmia siiä, mien verouksen painopiseen siiräminen
Y m p ä r i s t ö k a t s a u s
 Y m p ä r i s ö k a s a u s 2007 Finavia ja ympärisö vuonna 2007 Ympärisölupia vireillä ympäri maaa Vuonna 2007 Länsi-Suomen ympärisölupaviraso anoi pääöksen ympärisönsuojelulain mukaisesa luvasa Tampere-
Y m p ä r i s ö k a s a u s 2007 Finavia ja ympärisö vuonna 2007 Ympärisölupia vireillä ympäri maaa Vuonna 2007 Länsi-Suomen ympärisölupaviraso anoi pääöksen ympärisönsuojelulain mukaisesa luvasa Tampere-
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
KOMISSION KERTOMUS. Suomi. Perussopimuksen 126 artiklan 3 kohdan nojalla laadittu kertomus
 EUROOPAN KOMISSIO Bryssel 27.2.205 COM(205) 4 final KOMISSION KERTOMUS Suomi Perussopimuksen 26 ariklan 3 kohdan nojalla laadiu keromus FI FI KOMISSION KERTOMUS Suomi Perussopimuksen 26 ariklan 3 kohdan
EUROOPAN KOMISSIO Bryssel 27.2.205 COM(205) 4 final KOMISSION KERTOMUS Suomi Perussopimuksen 26 ariklan 3 kohdan nojalla laadiu keromus FI FI KOMISSION KERTOMUS Suomi Perussopimuksen 26 ariklan 3 kohdan
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 1 SÄHKÖTKNIIKKA JA LKTONIIKKA X-2 2017, Kimmo Silvonen Osa II, 25.9.2017 1 Muuosilmiö ja differeniaaliyhälö Tässä luvussa rajoiuaan pääasiassa asajännieläheisiin liiyviin muuosilmiöihin, vaikka samanlainen
1 SÄHKÖTKNIIKKA JA LKTONIIKKA X-2 2017, Kimmo Silvonen Osa II, 25.9.2017 1 Muuosilmiö ja differeniaaliyhälö Tässä luvussa rajoiuaan pääasiassa asajännieläheisiin liiyviin muuosilmiöihin, vaikka samanlainen
KULMAMODULOITUJEN SIGNAALIEN ILMAISU DISKRIMINAATTORILLA
 1 KULMMOULOITUJEN SIGNLIEN ILMISU ISKRIMINTTORILL Millaisia keinoja on PM & FM -ilmaisuun? 51357 Tieoliikenneekniikka I Osa 17 Kai Käkkäinen Kevä 015 ISKRIMINTTORIN TOIMINTKÄYRÄ J -YHTÄLÖ FM-signaalin
1 KULMMOULOITUJEN SIGNLIEN ILMISU ISKRIMINTTORILL Millaisia keinoja on PM & FM -ilmaisuun? 51357 Tieoliikenneekniikka I Osa 17 Kai Käkkäinen Kevä 015 ISKRIMINTTORIN TOIMINTKÄYRÄ J -YHTÄLÖ FM-signaalin
YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY 1 YRITYSKOHTAISEN TEHOSTAMISPOTENTIAALIN MITTAAMINEN
 ENERGIAMARKKINAVIRASTO 1 Le 2 Säkön jakeluverkkoomnnan yryskoasen eosamsavoeen määrely YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY Asanosanen: Vaasan Säköverkko Oy Lyy pääökseen dnro 491/424/2007 Energamarkknavraso
ENERGIAMARKKINAVIRASTO 1 Le 2 Säkön jakeluverkkoomnnan yryskoasen eosamsavoeen määrely YRITYSKOHTAISEN TEHOSTAMISTAVOITTEEN MÄÄRITTELY Asanosanen: Vaasan Säköverkko Oy Lyy pääökseen dnro 491/424/2007 Energamarkknavraso
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Piennopeuslaite FMH. Lapinleimu
 Piennopeuslaie FMH Floormaser FMH on puolipyöreä uloilmalaie, joka on arkoieu käyeäväksi syrjäyävään ilmanjakoon Floormaser- järjeselmässä. KANSIO VÄLI 6 ESITE Lapinleimu.1.0 Floormaser Yleisä Floormaser
Piennopeuslaie FMH Floormaser FMH on puolipyöreä uloilmalaie, joka on arkoieu käyeäväksi syrjäyävään ilmanjakoon Floormaser- järjeselmässä. KANSIO VÄLI 6 ESITE Lapinleimu.1.0 Floormaser Yleisä Floormaser
Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Toistoleuanvedon kilpailusäännöt
 1.0 Yleisä Toisoleuanvedossa kilpailija suoriaa häjaksoisesi mahdollisimman mona leuanveoa omalla kehonpainollaan. Kilpailijalla on käössään ksi kilpailusuorius sekä asauloksen sauessa mahdollise uusinakierrokse
1.0 Yleisä Toisoleuanvedossa kilpailija suoriaa häjaksoisesi mahdollisimman mona leuanveoa omalla kehonpainollaan. Kilpailijalla on käössään ksi kilpailusuorius sekä asauloksen sauessa mahdollise uusinakierrokse
OSINKOJEN JA PÄÄOMAVOITTOJEN VEROTUKSEN VAIKUTUKSET OSAKKEEN ARVOON
 AMPN YLIOPISO Kauppaieeien laios OSINKOJN JA PÄÄOMAVOIOJN VOUKSN VAIKUUKS OSAKKN AVOON Laskenaoimi Seminaariukielma Helmikuu 2004 Ohjaaja: Ismo Vuorinen apani Höök 3 SISÄLLYS JOHDANO... 4. ukielman ausaa...4.2
AMPN YLIOPISO Kauppaieeien laios OSINKOJN JA PÄÄOMAVOIOJN VOUKSN VAIKUUKS OSAKKN AVOON Laskenaoimi Seminaariukielma Helmikuu 2004 Ohjaaja: Ismo Vuorinen apani Höök 3 SISÄLLYS JOHDANO... 4. ukielman ausaa...4.2
XII RADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA
 II ADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA Laskenaaajuus akiivisuus Määrieäessä radioakiivisen näyeen akiivisuua (A) uloksena saadaan käyeyn miausyseemin anama laskenaaajuus (). = [II.I] jossa =
II ADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA Laskenaaajuus akiivisuus Määrieäessä radioakiivisen näyeen akiivisuua (A) uloksena saadaan käyeyn miausyseemin anama laskenaaajuus (). = [II.I] jossa =
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
