HARJOITUSTYÖ Pudotusputken pinnankorkeuden ja DD-pesurin syöttövirtauksen säätö
|
|
|
- Eero Jokinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 RAPORTTI HARJOITUSTYÖ Pudotusputken pinnankorkeuden ja DD-pesurin syöttövirtauksen säätö Hans Baumgartner xxxxxxx nimi nimi
2 1 SISÄLLYSLUETTELO KÄYTETYT MERKINNÄT JA LYHENTEET JOHDANTO TUTKITTAVAN PIIRIN TOIMINTA Prosessin kuvaus Prosessin nykyinen toiminta ja säätö Nykyisen säädön ongelmat MATEMAATTINEN MALLI Lohkokaavio Systeemin mallintaminen Pudotusputken dynaaminen malli Siirtofunktiot Pudotusputki Säätöventtiilit Viiveet Simulink-malli Mallin puutteet SÄÄTÖPARAMETRIEN VALINTA Integrointiaika Näytteenottoaika Vahvistus Uudet parametrit SÄÄDÖN TESTAUS TODELLISESSA YMPÄRISTÖSSÄ YHTEENVETO... 21
3 2 KÄYTETYT MERKINNÄT JA LYHENTEET A f a f DD1 f DD2 f in f out h K q in q out t t r T I τ ρ pudotusputken pohjan pinta-ala alalaimennusvirtaus DD-pesuri 1:n tulovirtaus DD-pesuri 2:n tulovirtaus pudotusputken tulovirtaus pudotusputken lähtövirtaus pudotusputken pinnankorkeus PID-säädön vahvistus pudotusputken tuleva massavirtaus pudotusputken lähtevä massavirtaus aika nousuaika PID-säädön integrointiaika aikavakio tiheys
4 3 1. JOHDANTO Enocell Oy:n ruskean massan pesulinjastossa on havaittu säätöteknisiä ongelmia pesulinjaan kuuluvan pudotusputken ja kolmen DD-pesurin muodostamassa piirissä. Pudotusputken pinnankorkeus värähtelee voimakkaasti ja tämä värähtely näkyy myös seuraavan prosessivaiheen eli pesurin DD3 syötön epätasaisuutena. Tarkastelun tavoitteena on löytää säätötapa, jolla voidaan rauhoittaa pudotusputken pinnankorkeuden vaihtelua ja parantaa pesurin DD3 sisään tulevaa massavirtaa. Massavirran tulee olla mahdollisimman tasainen ja vakiosakeuksinen. Myös pudotusputken pinnankorkeus pyritään pitämään sallituissa rajoissa ja pinnankorkeuden värähtelyt minimoimaan. Työssä on selvitetty pudotusputken sekä ympäröivän pesulinjaston toimintaa ja tarkasteltu nykyisen säädön käyttäytymistä. Systeemistä on muodostettu matemaattinen mallin, jolla voidaan kuvata prosessin toimintaa. Mallin avulla voidaan löytää pudotusputken säädölle uudet parametrit, joilla nykyisen säädön värähtelyjä pystytään pienentämään. Mallinnuksen lisäksi uusia säätöparametreja on testattu todellisessa käyttöympäristössä ja voitu näin havaita parametrimuutosten vaikutus käytännössä.
5 4 2. TUTKITTAVAN PIIRIN TOIMINTA 2.1 Prosessin kuvaus Tutkittava kohde koostuu kolmesta DD-pesurista sekä pudotusputkesta. Kahden ensimmäisen pesurin, DD1 ja DD2, sekä pudotusputken tarkoitus on syöttää mahdollisimman tasainen virtaus mahdollisimman tasalaatuista massaa kolmannelle pesurille DD3. Kuvaan 1 on piirretty tutkittavan prosessin prosessikaavio. Kuva 1 Tutkittavan prosessin prosessikaavio Prosessissa pudotusputkeen syötetään massaa kahdelta edeltävältä pesurilta sekä vettä alalaimennusventtiilin kautta. Nämä virrat toimivat pudotusputken sisääntuloina. Pudotusputken lähtönä on MC-pumpun avulla saatu virtaus kolmannelle pesurille. 2.2 Prosessin nykyinen toiminta ja säätö Järjestelmän säätönä toimii pinnankorkeuden PI-säätö, jonka PID-parametrien lisäksi pystytään muuttamaan säädön suodatusta ja näytteenottoaikaa. Venttiileitä FV-347, FV-348 ja FV-349 säädetään pinnankorkeuden LICA342 mukaan, venttiilin LV1-342 ollessa auki ja venttiilin LV2-342 ollessa kiinni.
6 venttiilikulma [%] 5 Pudotusputken alalaimennusventtiilin avaumaa HV-341 ohjataan automaattisesti pudotusputken pinnankorkeuden LICA342 ulostulon mukaan kuvan 2 mukaisesti. 8 4 % => 1 % 5 % => % 7 % => % 9 % =>..75 % pinnankorkeus [%] Kuva 2 Alalaimennusventtiilin ohjauskulman riippuvuus pudotusputken pinnankorkeudesta Tällöin MC-pumppu sekä pesusuodospumppu ovat käynnissä. Mikäli DD-pesurin 3 syöttöpaine PIC35 tai PIC386 nousee yli piirin hälytysrajan 85 kpa, suljetaan pinnansäätöventtiiliä LV %. Venttiilin säätö palautetaan normaaliksi paineen laskettua takaisin. DD-pesuri 3 voidaan ohittaa avaamalla venttiili LV2-342 ja sulkemalla venttiili LV Venttiilit FV-347, FV-348 ja FV-349 voivat avautua vain mikäli kuormitus WIA351 < 5 knm, mikäli kuormitus ylittää arvon käynnin aikana, venttiilit sulkeutuvat ja avautuvat, kun kuormitus laskee takaisin. Massalinjojen huuhteluventtiilit HV-371 ja HV-372 voivat avautua ainoastaan mikäli vastaavat venttiilit LV1-342 ja LV2-342 ovat kiinni. Kokoojaruuvi SS pysähtyy, mikäli pudotusputken pinnan yläraja ylittää 95 %. Mikäli MCpumppu tai kokoojaruuvi pysähtyy, piiri menee manual-tilaan, jolloin säätöpiiri täytyy käynnistää käsin uudestaan. Venttiilit LV1-342 ja LV2-342 sulkeutuvat MC-pumpun pysähtyessä. MC-pumpun kaasunpoistoventtiili HS343 avautuu pudotusputken pinnankorkeuden laskettua 2 % alapuolelle. Säädön tarkoitus on siis tasoittaa DD-pesureilta 1 ja 2 tuleva massavirtaus ennen DD-pesuria 3. DD-pesuri 3:lle menevää virtausta ohjataan pudotusputken pinnankorkeuden perusteella venttiileillä FV Lisäksi systeemissä on useita hälytysrajoja sekä venttiileitä, joita ohjataan erikoistapauksissa ja estetään suurta vahinkoa aiheuttavat vikatapaukset.
7 virtaus [l/s] pinnankorkeus [%] Nykyisen säädön ongelmat Tällä hetkellä säätö pyrkii pitämään pudotusputken pinnankorkeutta LICA342 4 % tasossa. Vakio pinnankorkeus helpottaa piirin valvontaa ja on tehokas tapa estää pinnankorkeuden putoaminen liian alas tai pudotusputken ylivuotaminen. Pinnankorkeutta säädetään venttiilien FV virtausta säätämällä. Säätöpiirin tarkoituksena on tuottaa mahdollisimman tasainen virtaus, mahdollisimman tasasakeuksista massaa DD-pesurille 3. Mikäli virtaus pystytään pitämään tasaisena, myös DDpesuri 3:n rummulle muodostuva paine ja pesurin pesutulos ovat tasaisempia. Säätöpiiri täytyy siis virittää siten, että saavutetaan mahdollisimman tasainen virtaus DD-pesurille 3, jolloin pinnankorkeuden vakiona pitäminen on säädön toissijainen tehtävä. Nykyinen säätö ei kuitenkaan toimi halutulla tavalla, sillä sekä pinnankorkeus, että DD-pesuri 3:n sisääntulovirtaus värähtelevät. Kuvaan 3 on piirretty kuvaajat DD-pesuri 3:n sisääntulovirtauksesta, DD-pesurien 1 ja 2 lähtövirtaus sekä pudotusputken pinnankorkeus. Koska DD-pesurien 1 ja 2 lähtövirtausta ei mitata, on ne arvioitu DD-pesurien sisääntulovirtauksista aika [min] Kuva 3 Säätöpiirin mittausarvoja. DD 3:n sisääntulovirtaus (sininen), DD-pesurien 1 ja 2 lähtövirtaus (vihreä), pudotusputken pinnankorkeus (punainen). Kuvasta 3 havaitaan, että säätö ei toimi oikein. Pinnankorkeus ei asetu 4 %:n asetusarvoonsa, vaan värähtelee merkittävästi. Vastaavasti heilahtelu aiheuttaa DD-pesuri 3:lle menevän virtauksen vaihtelua. Kuvasta voidaan myös havaita DD 1 ja 2 lähtövirtauksen pysyvän melko tasaisena, joten pinnankorkeuden ja virtauksen huojunta ei johdu pudotusputken sisääntulovirtauksen heilahteluista.
8 7 3. MATEMAATTINEN MALLI 3.1 Lohkokaavio Järjestelmän toiminta voidaan kuvata lohkokaaviona, johon on merkitty systeemiin sisään tulevat ja systeemistä lähtevät virtaukset sekä säädön ohjeena toimivat pinnankorkeuden olo- ja asetusarvot. Säätöjärjestelmän periaatteellinen toiminta lohkokaaviona on esitetty kuvassa 4. Kuva 4 Pudotusputken pinnankorkeuden säätö 3.2 Systeemin mallintaminen Järjestelmästä voidaan muodostaa mittaustulosten ja järjestelmän kuvauksen perusteella matemaattinen malli, jota voidaan käyttää systeemin toiminnan kuvaamiseen. Mallin tarkkuus riippuu käytettävissä olevien parametrien lukumäärästä ja tarkkuudesta. Esimerkiksi malli pudotusputken pinnankorkeudelle voidaan määrittää hyvinkin tarkasti, jos tiedetään pudotusputken lähtevät- ja tulevat massavirrat. Venttiilien ja systeemin muun dynamiikan mallintaminen tarkasti on hyvin haastavaa. Erityisesti venttiilit ja pitkät putket aiheuttavat epälineaarisuutta ja viiveitä järjestelmään. Jos mainittuja muuttujia ei oteta riittävästi huomioon, ei malli kuvaa järjestelmän todellista dynamiikkaa. Esimerkiksi tyypillinen viive tutkittavassa järjestelmässä on massan kulku pudotusputkelta pesurille. Pitkä putkisto aiheuttaa massavirtaukseen viivettä, joka voi olla hyvinkin merkittävä. Kaikkia systeemin mallinnuksessa tarvittavia tietoja ei ole kuitenkaan aina saatavilla, jolloin ne on korvattava arviolla tai yrittää laskea matemaattisesti. Jos tieto ei ole kokonaisuuden kannalta merkittävä, voidaan se jättää kokonaan pois tai ajatella sen olevan vakio ja silti saada järkevä simulointitulos Pudotusputken dynaaminen malli Pudotusputken dynaaminen malli voidaan laskea massataseen avulla, kun tiedetään tulo- ja lähtövirtaukset, sekä putken mitat. Massatase kuvaa tarkasteltavaan systeemiin varastoituneen massan muutosnopeutta dm(t)/dt. Pudotusputken pinnankorkeus riippuu tulo- ja lähtövirtausten suhteesta.
9 8 dm( t) q( t) dt in dh( t) q( t) out ( t) A (1) dt Systeemissä liikkuvan massan sakeusmittaukset suoritetaan ennen DD-pesureita 1 ja 2 sekä DDpesurin 3 jälkeen, joten yksinkertaistetaan järjestelmää olettamalla tiheys vakioksi. Todellisuudessa pudotusputkessa olevan massan sakeus muuttuu mm. alalaimennuksen takia, mutta koska pudotusputkeen tulevan massan sakeutta ei mitata, täytyy sen olettaa pysyvän vakiona. Massan sakeutta muuttavan alalaimennuksen vaikutusta systeemin toimintaan tarkastellaan tarkemmin myöhemmin. Kun tiheyden tarkastelu jätetään pois, käsitellään ainoastaan järjestelmän tilavuusvirtauksia. Merkitsemällä tilavuusvirtauksia symbolilla f, saadaan yhtälö (1) muotoon dh( t) f ( t) in f ( t) out A (2) dt Yhtälöstä (2) tiedetään lähtövirtaus f out, pudotusputken pohjan pinta-ala A sekä pinnankorkeus h. Tiedetään myös, että lähtövirtausta f out säädetään pinnankorkeuden h perusteella. Säiliön sisääntulovirtaus koostuu alalaimennuksesta f a, sekä purkuruuvin syöttämästä, DD-pesureilta 1 ja 2 tulevista virtauksista f DD1 ja f DD2. Näistä virtauksista ei ole suoraa mittaustietoa, koska pesureiden jättösakeutta ei tiedetä ja pesurin suodoksien virtauksia ei mitata. Yhtälössä (3) on eritelty sisääntulovirtaukset. dh( t) f ( t) a f ( t) DD1 f ( t) DD2 f ( t) out A, (3) dt 3.3 Siirtofunktiot Pudotusputki Lähtöventtiilien avaumaa säädetään pinnankorkeuden mukaan. Säiliön pinnakorkeudelle voidaan muodostaa siirtofunktio suoraan dynaamisesta mallista (3). Siirtofunktio saadaan muuttamalla dynaaminen malli taajuustasoon Laplace-muunnoksella. Laplace-muunnos saadaan tehtyä yksinkertaisesti korvaamalla aikaderivaatta dh/dt merkinnällä h s ja ratkaisemalla yhtälöstä pinnankorkeuden suhde virtauksiin. Siirtofunktion lähtönä on siis säiliön pinnakorkeus ja tulona lähtö- ja tulovirtausten erotus. Mikäli yksikköinä käytetään metrejä ja lieriön muotoisen säiliön säde on.5 metriä, toimii säiliö integraattorin tavoin ja sen siirtofunktio on yhtälön (3) mukaan
10 virtaus [l/s] 9 f ( s) in h( s) f ( s) out 1 2 r s 1.785, (4) s missä f(s) in on tulovirtaus (f(s) a + f(s) DD1 + f(s) DD2 ) ja f(s) out lähtövirtaus Säätöventtiilit DD-pesurin 3 tulovirtauksien säätöventtiilien FV mallintaminen on huomattavasti pudotusputken mallintamista hankalampaa. Venttiilien käyttäytyminen on tavallisesti hyvin epälineaarista ja virtaus riippuu paljon venttiilin tyypistä ja järjestelmän rakenteesta. Tämän takia venttiileitä ei edes yritetä mallintaa täysin realistisesti, vaan venttiilit mallinnetaan yhtenä venttiilinä, jonka virtaus on linearisoitu tarkasteltavalle virtausalueelle. Kuvaan 5 on merkitty vihreillä pisteillä venttiilien ohjauskulman ja yhteenlasketun virtauksen mittauspisteet. Sininen suora on mallinnuksessa käytetty linearisointisuora, jonka kulmakerroin on ohjauskulma [%] Kuva 5 Venttiilien FV yhteenlaskettu virtaus ohjauskulman (%) funktiona. Viheillä pisteillä merkattu mitatut arvot, sininen suora mallinnuksessa käytetty linearisointi. Venttiileille voidaan nyt määrittää vahvistus suoran kulmakertoimen perusteella. Jos ohjauskulma on %, myös virtaus on nolla, jos ohjauskulma on 45 %, virtaus on 73 l/s eli.73 m 3 /s. Venttiilien vahvistukseksi saadaan siis df ( ) d (5)
11 virtaus [m3/s] 1 Venttiilin käyttäytymistä voidaan kuvata ensimmäisen kertaluvun siirtofunktiolla.162 s 1 (6) Yhtälön (6) τ on venttiilin aikavakio eli aika, jossa venttiilin kulma muuttuu 63 % asetusarvosta. Kyseinen aika siis kuluu venttiilikulman muutokseen 63 % askelmaisessa asetusarvon muutoksessa 1 %. Yhtälön (6) mukaan sama aika kuluu myös muutokseen % asetusarvon muutoksessa 1 2 %. Tämän takia kyseisellä siirtofunktiolla ei voida kuvata täydellisesti venttiilin koko toimialueen käyttäytymistä. Mutta koska venttiilien kulman muutokset ovat kohtalaisen pieniä, joitakin kymmeniä prosentteja, kuvaa yhtälön (6) siirtofunktio venttiilien toimintaa tarkastelualueella melko hyvin. Valmistaja ilmoittaa venttiilikulman muuttuvan - 1 % yhdessä sekunnissa. Venttiilien dynamiikkaa mitattiin myös todellisessa käyttöympäristössä askelmaisella, 2 prosentin kulman muutoksella. Testien perusteella venttiilikulma muuttuu erittäin nopeasti, joten valitaan aikavakioksi τ.5 sekuntia. Venttiilien siirtofunktioksi saadaan nyt.162.5s 1 (7) Yhtälön (7) mukaisen venttiilin lähtövirtaus muuttuu nyt askelmaisessa muutoksessa 4 6 % kuvan 6 mukaisesti aika [s] Kuva 6 Lähtöventtiilien FV virtauksen muutos venttiilikulman muutoksella 4 6 %
12 Viiveet Käytännön järjestelmissä on myös paljon viiveitä. Esimerkiksi viive, joka kuluu pudotusputken pinnankorkeuden muutoksesta venttiilikulmassa havaittavaan muutokseen tai viive pudotusputken sisääntulovirtauksen muutoksesta pinnankorkeusanturissa havaittavaan muutokseen. Viiveiden vaikutus on monesti hyvinkin merkittävä, sillä eri viiveet summautuvat yhteen. Toisaalta viiveet on yleensä melko helposti mitattavissa, joten viiveiden mallinnus on helppoa. Säätöjä ei voi virittää nopeammaksi, mitä järjestelmän viiveet ovat, sillä tällöin säätö alkaa reagoida muutoksiin, joita ei todellisuudessa ole edes mitattu ja säätö alkaa värähdellä. Helposti mallinnettavia viiveitä tutkittavassa systeemissä on esimerkiksi viive pudotusputken pinnankorkeuden muutoksen ja lähtöventtiilien virtauksen välillä. Mittausten mukaan kyseinen viive on noin kolme sekuntia Simulink-malli Tutkittavaa systeemiä voidaan kuvata mallilla, joka koostuu venttiilin, pudotusputken ja viiveen muodostamasta PID-säätöpiiristä. Kuvassa 7 on esitetty tutkittavan systeemin Simulink-malli. Kuva 7 Venttiilien ja pudotusputken muodostama säätöpiiri Kuvan 7 mallissa venttiilien lähtövirtaus ja pudotusputken pinnankorkeus on rajoitettu vastaamaan todellisuutta. Lähtöventtiilien virtaus on rajattu negatiiviseksi ja pudotusputken pinnankorkeus välille m. Pudotusputken keskellä sijaitsevan pinnankorkeusanturin lähtö on myös rajoitettu erikseen välille..3 m. Kuvan 7 mallissa on PID-säätönä käytetty valmista, diskreettiaikaista PID-säätölohkoa, jonka muutettavia parametreja ovat PID-parametrien lisäksi näytteenottoaika, derivaattoriaproksimaation aikavakio sekä lähtörajat. Säätölohkon sisäinen rakenne on esitetty kuvassa 8.
13 12 Kuva 8 Simulink-mallissa käytetyn diskreettiaikaisen PID-säätölohkon sisäinen rakenne Mallin puutteet Tutkittavan systeemin käyttäytymiseen vaikuttaa myös pudotusputken alalaimennuksen määrä. Alalaimennus koostuu suodosvedestä, joten sen tiheys on lähellä veden tiheyttä. Laimennusventtiilin virtausta ei kuitenkaan mitata, joten alalaimennuksen määrää ei suoraan tiedetä. Alalaimennuksen vaikutusta lähtövirtauksen suuruuteen ei myöskään yleisesti ottaen tunneta kovin tarkasti. Kokeellisten mittausten valossa näyttäisi siltä, että alalaimennus auttaa MCpumppua sakean massan pumppauksessa laimentamalla pumpattavaa massa. Mikäli alalaimennus katkaistaan, massa sakeutuu liikaa, jolloin MC-pumppu tukkeutuu, eikä kykene enää pumppaamaan massaa ja pudotusputken pinnankorkeus lähtee kohoamaan. Kyseinen alalaimennuksen vaikutus oli havaittavissa vain mäntykuitua ajettaessa. Alalaimennuksella oli koivukuitua ajettaessa erilainen merkitys. Alalaimennuksen katkaisemisella ei ollut näkyvää vaikutusta pudotusputken pinnankorkeuteen koivukuidulla. Alalaimennuksen katkaisu jopa rahoitti systeemin värähtelyjä hieman. Alalaimennusta ei voida siis yksiselitteisesti mallintaa. Koska alalaimennuksen vaikutus erityisesti koivukuidulla oli vähäinen, voidaan alalaimennus jättää yksinkertaisesta mallista pois. Muita systeemimallin puutteita ovat esimerkiksi järjestelmässä olevat muut viiveet, kuin mallinnettu viive pudotusputken pinnankorkeuden ja lähtöventtiilien virtauksen muutoksen välillä. Myös näiden tuntemattomien viiveiden mittaus ja mallinnus tarkentaa mallia.
14 virtaus [l/s] pinnankorkeus [%] SÄÄTÖPARAMETRIEN VALINTA Kuvan 7 järjestelmää voidaan simuloida tekemällä pudotusputken sisääntulovirtaukseen askelmainen, 2 l/s muutos. PID-säätimen parametrit ovat K =.45 ja T I =.7 s. Näytteenottoaika on 1 sekunti. Kuvassa 9 on esitetty pinnankorkeus ja lähtövirtaus ajan funktiona aika [s] aika [s] Kuva 9 Pudotusputken pinnankorkeus ja lähtövirtaus sisääntulovirtauksen muutoksella - 2 l/s. Kuvasta 9 havaitaan pudotusputken pinnankorkeuden sekä lähtövirtauksen alkavan värähtelemään käytetyillä PID-parametrien ja näytteenottoajan arvoilla. 4.1 Integrointiaika PID-parametrien valintaan on olemassa säätöteknisiä menetelmiä, joiden avulla voidaan löytää oikeansuuntaiset säätöparametrit. Systeemin vasteen muutosta parametreja muutettaessa voidaan tarkastella esimerkiksi luodun Simulink-mallin aikatason vastetta tarkastelemalla. Hyvä työkalu systeemin käyttäytymisen tarkastelemiseen on myös Bode-diagrammi, josta voidaan nähdä systeemin vahvistus- ja vaihevarat. Bode-diagrammin muodostamiseksi tarvitaan koko systeemin siirtofunktio, joka saadaan kertomalla kuvan 7 venttiilin, pudotusputken, viiveen ja yksikönmuunnoksen siirtofunktiot. Systeemin kokonaissiirtofunktioksi saadaan.162 e.5s 1 3s e s s.5s 1 s (8) Siirtofunktiosta (8) voidaan nyt muodostaa Bode-diagrammi
15 Phase (deg) Magnitude (db) 14 5 Bode Diagram Gm = 16.6 db (at.451 rad/sec), Pm = 76.2 deg (at.687 rad/sec) Frequency (rad/sec) Kuva 1 Siirtofunktion (8) Bode-diagrammi Kuvan 1 Bode-diagrammista voidaan nähdä säätämättömän, avoimen piirin vaihe- ja vahvistusvaran olevan hyvät. Koska kyseessä on kuitenkin säätämätön systeemi, toisin sanoen P- säädin vahvistuksen arvolla yksi, jää systeemiin aina jatkuvuustilan virhettä. Integroivalla säädöllä pystytään poistamaan jatkuvuustilan virhe, mutta integroiva säädin huonontaa systeemin vaihevaraa. Aikajatkuvan PID-säätimen siirtofunktio on T Is 1 T s 1 K D, (9) T s I missä K on vahvistus, T I integrointiaika ja T D derivointiaika Kertomalla PID-säätimen siirtofunktio (9) säätämättömän systeemin siirtofunktiolla (8) saadaan säädetyn systeemin siirtofunktioksi K 3s T Is e TDs 1 T s s.5s 1 I (1) Valitsemalla integrointiajaksi T I =.7 s ja vahvistukseksi K =.45 voidaan Bode-diagrammista nähdä sekä vaihe-, että vahvistusvaran olevan negatiivisia
16 Phase (deg) Phase (deg) Magnitude (db) Magnitude (db) Phase (deg) Phase (deg) Magnitude (db) Magnitude (db) Phase (deg) Magnitude (db) 15 5 Bode Diagram Gm = -Inf db (at rad/sec), Pm = deg (at.211 rad/sec) Frequency (rad/sec) Kuva 11 Säädetyn systeemin (1) Bode-diagrammi säätöparametrien arvoilla K=.45 ja T I =.7s Negatiivinen vaihe- tai vahvistusvara tekee systeemistä epästabiilin. Vaihevaraa voidaan kasvattaa integrointiaikaa suurentamalla tai vahvistusta pienentämällä. Kasvattamalla integrointiaikaa ja pitämällä vahvistus samana, voidaan Bode-diagrammista nähdä vaihevaran kasvavan. Bode Diagram Gm = -Inf db (at rad/sec), Pm = deg (at.177 rad/sec) 2 Bode Diagram Gm = 16.7 db (at.264 rad/sec), Pm = 5.84 deg (at.817 rad/sec) Frequency (rad/sec) Frequency (rad/sec) Bode Diagram Gm = 2 db (at.334 rad/sec), Pm = 12.1 deg (at.72 rad/sec) 2 Bode Diagram Gm = 21.5 db (at.376 rad/sec), Pm = 19 deg (at.61 rad/sec) Frequency (rad/sec) Frequency (rad/sec) Kuva 12 PI-säädetyn systeemin vaihe- ja vahvistusvarat eri integrointiajan arvoilla. Vahvistus K=.45, integrointiajat ylhäältä vasemmalta 1s, 5s, 7s ja 1s.
17 16 Kuvan 12 Bode-diagrammeista nähdään vaihevaran kasvavan integrointiaikaa kasvattamalla. Vaihevaraa voitaisiin edelleen kasvattaa integrointiaikaa kasvattamalla, mutta tämä hidastaa systeemin dynamiikkaa. Koska systeemissä on äärellinen säiliö, ei dynamiikka voi olla liian hidas, sillä säiliö vuotaa tällöin yli. 4.2 Näytteenottoaika Mallin perusteella näytteenottovälin pienentäminen ei merkittävästi paranna säädön käyttäytymistä ideaalisella, askelmaisella sisääntulolla. Häiriöisellä sisääntulolla ja huonosti valituilla PIDparametreilla näytteenottoajalla on kuitenkin merkittävä vaikutus. Kuvan 7 malliin voidaan ideaalisen askelherätteen sijasta tuoda myös todellisesta järjestelmästä saatua mittausdataa. Tutkittavassa järjestelmässä mitataan DD-pesurien 1 ja 2 sisääntulovirtauksia, joten näistä virtauksista voidaan tehdä jonkinlainen approksimaatio pudotusputken sisääntulovirtaukselle. Digitaalisen säädön näytteenottoajaksi suositellaan 4..1 näytettä systeemin nousuajalle. Pudotusputken siirtofunktiosta (4) saadaan pudotusputken aikavakioksi.785 sekuntia. 1. kertaluvun systeemin nousuaika on likimain t s, (11) r josta suositusten mukaiseksi näytteenottoajaksi saadaan noin.2 sekuntia. Pienennettäessä näytteenottoaikaa yhdestä sekunnista.2 sekuntiin, saadaan häiriöisen systeemin värähtelyä pienennettyä huomattavasti. Kuvassa 13 on havainnollistettu näytteenottoajan vaikutus systeemin käyttäytymiseen.
18 lähtövirtaus [l/s] lähtövirtaus [l/s] aika [s] x aika [s] x 1 4 Kuva 13 Näytteenottoajan vaikutus muodostetun mallin käyttäytymiseen. Yläkuvassa näytteenottoaika yksi sekunti, alakuvassa.2 sekuntia. Käytetyt PID-parametrit K = 1, T I = 1.5 s. Kuvan 13 mukainen huomattava näytteenottoajan vaikutus havaittiin vain tietyillä, huonosti valituilla PID-parametrien arvoilla. Koska systeemin suositelluksi integrointiajaksi saatiin useita sekunteja, on.2 sekunnin näytteenottoaika melko lyhyt. Näytteenottoaikaa pienentämällä ei kyseisessä järjestelmässä voida kuitenkaan huonontaa säädön käyttäytymistä, joten pienempi näytteenottoaika on ainakin suotavaa. 4.3 Vahvistus Vahvistuksen pienentäminen rauhoittaa systeemiä, mutta tällöin järjestelmän vaste suuremmille virtauksen muutoksille aiheuttaa enemmän värähtelyä. Toisaalta vahvistuksen kasvattaminen lyhentää värähtelyn kestoa, mutta vastaavasti kasvattaa amplitudia. Vahvistuksen valinnassa onkin mietittävä, kuinka hitaaksi säätimen vaste voidaan asettaa, jotta suuremmat virtauksen muutokset eivät aiheuttaisi ongelmia, kuten pudotusputken ylivuotamista. 4.4 Uudet parametrit Simuloimalla muodostettua mallia todellista sisääntuloa approksimoivalla mittausdatalla, voidaan huomattavasti alkuperäisiä paremmiksi säätöparametreiksi löytää K =.45 ja T I = 7. Häiriöisellä sisääntulolla myös näytteenottovälin valinnalla on mallissa merkittävä rooli, joten näytteenottovälin pienentäminen.2 sekuntiin parantaa säädön käyttäytymistä. Kuvassa 14 on esitetty lähtövirtauksen askelvaste alkuperäisillä sekä uusilla säätöparametreilla.
19 virtaus [l/s] virtaus [l/s] aika [min] aika [min] Kuva 14 Pudotusputken lähtövirtaus alkuperäisillä (yläkuva) sekä uusilla (alakuva) säätöparametreilla sisääntulovirtauksen muutoksella 2 l/s. Kuvasta 14 voidaan havaita säätöä pystyttävän parantamaan merkittävästi integrointiaikaa kasvattamalla ja näytteenottoaikaa pienentämällä. Vahvistuksen oikea valinta riippuu paljon pudotusputken sisääntulovirtauksen muutoksen suuruudesta, joten sen kasvattamisen tai pienentämisen tutkiminen kannattaa tehdä todellisessa ympäristössä.
20 virtaus [l/s] pinnankorkeus [%] SÄÄDÖN TESTAUS TODELLISESSA YMPÄRISTÖSSÄ Tutkittavaa pudotusputken ja DD-pesurien muodostamaa systeemiä testattiin todellisessa käyttöympäristössä. Testaushetkellä linjassa ajettiin koivukuitua ja venttiileitä FV ohjaavan PID-säädön parametrit olivat K=.45 ja T I =.7. Säädön näytteenottoväli oli 1 sekunti. Kuvassa 15 on esitetty pudotusputken pinnankorkeus ja venttiilin FV-347 virtaus aika [min] aika [min] Kuva 15 Pudotusputken pinnankorkeuden ja venttiilin FV-347 virtauksen kuvaajat. Kuvasta 15 voidaan havaita sekä pinnankorkeuden, että lähtövirtauksen värähtelevän merkittävästi. Erityisesti lähtövirtauksen värähtelyt häiritsevät prosessia. Kuvan 15 virtauskuvaaja on vain yhdestä venttiilistä kolmesta, joten todelliset värähtelyt ovat karkeasti kolminkertaiset. Järjestelmän yhden sekunnin näytteenottoväli selvisi vastaa tehtaan automaatiojärjestelmään tutustumisen yhteydessä. Joten näytteenottovälin vaikutusta käytännössä ei päästy kokeilemaan. PID-parametreja pystyttiin kuitenkin muuttamaan ja niiden vaikutus säädön käyttäytymiseen toteamaan. Paremmiksi parametreiksi löydettiin K =.45 ja T I = 5 s. Kuvassa 16 on esitetty uusien PID-parametrien vaikutus lähtövirtaukseen.
21 virtaus [l/s] virtaus [l/s] aika [min] aika [min] Kuva 16 Venttiilin FV-347 virtauksen kuvaajat alkuperäisillä ja uusilla PID-parametreilla Kuvasta 16 havaitaan PID-parametrien muutoksella voitavan selvästi vaikuttaa säädön käyttäytymiseen. Lisäksi säädössä oli mahdollista muuttaa suodatusparametria. Suodatuksen toiminnasta ei löytynyt dokumenttia, joten suodatusalgoritmin rakenne ei selvinnyt, mutta kokeellisesti pystyttiin toteamaan suodatuksen lisäämisen vaikuttavan myönteisesti säätöön. Virtauksen hajonta pieneni 56 % kun verrataan kuvan 16 mukaisia ajanjaksoja ennen järjestelmässä tehtyä tuotannon muutosta, joka näkyy kuvassa 395 minuutin kohdalla. Koska tarkasteltava systeemi on suhteellisen hidas, kului säätöparametrien muutoksen vaikutuksen toteamiseen paljon aikaa. Lisäksi järjestelmää tarkkaileva ohjelmisto piirsi mittaussignaaleista kuvaajan parhaimmillaan 15 minuutin viiveellä, joten parametrien arvoja ei pystytty muuttamaan kovin usein. Tästä johtuen parhaita mahdollisia säätöparametreja ei ajanpuutteen vuoksi pystytty löytämään. Simulointitulosten mukainen oikea suunta kuitenkin löydettiin. Säätö parani selvästi, kun integrointiaikaa kasvatettiin. Myös suodatuksen lisääminen vähensi säädön värähtelyjä. Mielenkiintoista olisi ollut kokeilla myös näytteenottoajan pienennyksen vaikutusta säätöön, mutta koska näytteenottoaika selvisi vasta tehtaalla, ei sen pituuteen ollut mahdollista vaikuttaa. Lisäksi simulointitulosten mukaan järjestelmän hidastaminen eli vahvistuksen pienentäminen rauhoittaa värähtelyjä, joten myös tätä vaihtoehtoa olisi hyvä kokeilla. Vahvistuksen pienentäminen liikaa tosin lisää värähtelyä suuremmissa sisääntulovirtauksen muutoksissa ja saa pahimmassa tapauksessa pudotusputken vuotamaan yli. Parhaan mahdollisen yhdistelmän löytäminen onkin haastavaa ja riippuu paljon sisääntulovirtauksen muutoksista.
22 21 6. YHTEENVETO Työn tarkoituksena oli selvittää pudotusputken ja DD-pesurien muodostaman systeemin toimintaa ja muodostaa systeemille matemaattinen simulointimalli. Mallin avulla voitiin selvittämään, miten värähtelevän systeemin säätöä pystytään parantamaan. Pudotusputken ja kolmen DD-pesurin muodostaman järjestelmän säätönä toimii perinteinen PIsäätö, jonka PID-parametrien lisäksi pystytään muuttamaan säädön suodatusta ja näytteenottoaikaa. Tutkittavasta järjestelmästä muodostettiin matemaattinen malli, jonka avulla pystytään simuloimaan säätöparametrien muutoksen vaikutusta todellisessa käyttöympäristössä. Malli muodostettiin teoreettisten laskelmien, sekä kokeellisten mittausten perusteella ja näin ollen mallista saatiin melko hyvin todellisen järjestelmän käyttäytymistä kuvaava. Muodostetun mallin avulla tutkittiin säätöparametrien vaikutusta järjestelmän käyttäytymiseen ja voitiin todeta nykyisessä säädössä olevan huomattavasti parannettavaa. Mallin avulla pystyttiin löytämään paremmiksi säätöparametreiksi K=.45, T I =5s, joita todellisessa järjestelmässä testaamalla voitiin saavuttaa jopa 6 prosentin pienennys värähtelevän virtauksen hajonnassa.
Tehtävä 1. Vaihtoehtotehtävät.
 Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
1 PID-taajuusvastesuunnittelun esimerkki
 Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank
 MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank Sonja Lindman Kandidaatintyö 10.4.2014 LUT Energia Sähkötekniikan koulutusohjelma TIIVISTELMÄ Lappeenrannan teknillinen yliopisto Teknillinen
MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank Sonja Lindman Kandidaatintyö 10.4.2014 LUT Energia Sähkötekniikan koulutusohjelma TIIVISTELMÄ Lappeenrannan teknillinen yliopisto Teknillinen
RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007
 RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007 Automaatiotekniikka Lähtöarvot: Säiliö T1: A = 500 x 600 mm, h = 500 mm Säiliö T2: Ø = 240 mm, h = 1000
RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007 Automaatiotekniikka Lähtöarvot: Säiliö T1: A = 500 x 600 mm, h = 500 mm Säiliö T2: Ø = 240 mm, h = 1000
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Systeemitekniikan laboratorio Jan 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Systeemitekniikan laboratorio Jan 2019
Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu. Vinkit 1 a
 ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
Hyvyyskriteerit. ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
Osatentti
 Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / Systeemitekniikka Jan 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / Systeemitekniikka Jan 2019
Osatentti
 Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi. Servokäyttö (0,9 op)
 LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi Servokäyttö (0,9 op) JOHDNTO Työssä tarkastellaan kestomagnetoitua tasavirtamoottoria. oneelle viritetään PI-säätäjä
LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi Servokäyttö (0,9 op) JOHDNTO Työssä tarkastellaan kestomagnetoitua tasavirtamoottoria. oneelle viritetään PI-säätäjä
Säätötekniikan perusteet. Merja Mäkelä 3.3.2003 KyAMK
 Säätötekniikan perusteet Merja Mäkelä 3.3.2003 KyAMK Johdanto Instrumentointi automaation osana teollisuusprosessien hallinnassa Mittalaitteet - säätimet - toimiyksiköt Paperikoneella 500-1000 mittaus-,
Säätötekniikan perusteet Merja Mäkelä 3.3.2003 KyAMK Johdanto Instrumentointi automaation osana teollisuusprosessien hallinnassa Mittalaitteet - säätimet - toimiyksiköt Paperikoneella 500-1000 mittaus-,
PID-sa a timen viritta minen Matlabilla ja simulinkilla
 PID-sa a timen viritta minen Matlabilla ja simulinkilla Kriittisen värähtelyn menetelmä Tehtiin kuvan 1 mukainen tasavirtamoottorin piiri PID-säätimellä. Virittämistä varten PID-säätimen ja asetettiin
PID-sa a timen viritta minen Matlabilla ja simulinkilla Kriittisen värähtelyn menetelmä Tehtiin kuvan 1 mukainen tasavirtamoottorin piiri PID-säätimellä. Virittämistä varten PID-säätimen ja asetettiin
SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS),
 SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS), 5.2.2019 Tentin arvosteluperusteita: o Kurssin alku on osin kertausta SäAn ja prosessidynamiikkakursseista, jotka oletetaan
SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS), 5.2.2019 Tentin arvosteluperusteita: o Kurssin alku on osin kertausta SäAn ja prosessidynamiikkakursseista, jotka oletetaan
Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. = K K K M. s 2 3s 2 KK P
 Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
3. kierros. 2. Lähipäivä
 3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
Y (s) = G(s)(W (s) W 0 (s)). Tarkastellaan nyt tilannetta v(t) = 0, kun t < 3 ja v(t) = 1, kun t > 3. u(t) = K p y(t) K I
 Aalto-yliopiston Perustieteiden korkeakoulu Matematiikan systeemianalyysin laitos Mat-2.429 Systeemien Identifiointi 6. harjoituksen ratkaisut. Laplace-tasossa saadaan annetulle venttiilille W (s) W (s)
Aalto-yliopiston Perustieteiden korkeakoulu Matematiikan systeemianalyysin laitos Mat-2.429 Systeemien Identifiointi 6. harjoituksen ratkaisut. Laplace-tasossa saadaan annetulle venttiilille W (s) W (s)
ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
Aikatason vaste vs. siirtofunktio Tehtävä
 Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
MATLAB harjoituksia RST-säädöstä (5h)
 Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C (s+1)(s+0.02) 50s+1
 ENSO IKONEN PYOSYS Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C. 1 P(s) = -----------------(s+1)(s+0.02) C(s) = 50s+1 --------50s Piirrä vasteet asetusarvosta. Kommentoi
ENSO IKONEN PYOSYS Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C. 1 P(s) = -----------------(s+1)(s+0.02) C(s) = 50s+1 --------50s Piirrä vasteet asetusarvosta. Kommentoi
Elektroniikka, kierros 3
 Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Lauri Karppi j82095. SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI.
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Oskari Uitto i78966 Lauri Karppi j82095 SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI Sivumäärä: 14 Jätetty tarkastettavaksi: 25.02.2008 Työn
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Oskari Uitto i78966 Lauri Karppi j82095 SATE.2010 Dynaaminen kenttäteoria DIPOLIRYHMÄANTENNI Sivumäärä: 14 Jätetty tarkastettavaksi: 25.02.2008 Työn
Kon Hydraulijärjestelmät
 Kon-41.4040 Hydraulijärjestelmät Laboratorioharjoitus 2: Sähköhydraulisen järjestelmän säätö Jyri Juhala Jyrki Kajaste (Heikki Kauranne) Hydraulijärjestelmän venttiilin ohjausmenetelmät Ohjaus Kompensointi
Kon-41.4040 Hydraulijärjestelmät Laboratorioharjoitus 2: Sähköhydraulisen järjestelmän säätö Jyri Juhala Jyrki Kajaste (Heikki Kauranne) Hydraulijärjestelmän venttiilin ohjausmenetelmät Ohjaus Kompensointi
Luento 7. LTI-järjestelmät
 Luento 7 Lineaaristen järjestelmien analyysi taajuustasossa Taajuusvaste Stabiilisuus..7 LTI-järjestelmät u(t) h(t) y(t) Tarkastellaan lineaarista aikainvarianttia järjestelmää n n m m d d d d yt () =
Luento 7 Lineaaristen järjestelmien analyysi taajuustasossa Taajuusvaste Stabiilisuus..7 LTI-järjestelmät u(t) h(t) y(t) Tarkastellaan lineaarista aikainvarianttia järjestelmää n n m m d d d d yt () =
Agenda. Johdanto Säätäjiä. Mittaaminen. P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen
 8. Luento: Laitteiston ohjaaminen Arto Salminen, arto.salminen@tut.fi Agenda Johdanto Säätäjiä P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen Mittaaminen Johdanto Tavoitteena: tunnistaa
8. Luento: Laitteiston ohjaaminen Arto Salminen, arto.salminen@tut.fi Agenda Johdanto Säätäjiä P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen Mittaaminen Johdanto Tavoitteena: tunnistaa
Luento 8. Suodattimien käyttötarkoitus
 Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
SMITH-PREDICTOR Kompensaattori PI-Säätimellä. Funktiolohko Siemens PLC. SoftControl Oy
 SMITH-PREDICTOR Kompensaattori PI-Säätimellä Funktiolohko Siemens PLC SoftControl Oy 1.0 Smith Predictor kompensaattori PI-säätimellä... 3 1.1 Yleistä...3 1.2 Sovellus...3 1.3 Kuvaus...4 1.4 Muuttujat...5
SMITH-PREDICTOR Kompensaattori PI-Säätimellä Funktiolohko Siemens PLC SoftControl Oy 1.0 Smith Predictor kompensaattori PI-säätimellä... 3 1.1 Yleistä...3 1.2 Sovellus...3 1.3 Kuvaus...4 1.4 Muuttujat...5
Laskun vaiheet ja matemaattiset mallit
 Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
Boost-hakkuri. Hakkurin tilaesitykset
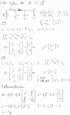 Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
Tehtävä 1. Vaihtoehtotehtävät.
 Kem-9.7 Proeiautomaation peruteet Perutehtävät Tentti 9.. Tehtävä. Vaihtoehtotehtävät. Oikea vatau,p, väärä vatau -,p ja ei vatauta p Makimi,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN
Kem-9.7 Proeiautomaation peruteet Perutehtävät Tentti 9.. Tehtävä. Vaihtoehtotehtävät. Oikea vatau,p, väärä vatau -,p ja ei vatauta p Makimi,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN
LOPPURAPORTTI 19.11.2007. Lämpötilahälytin. 0278116 Hans Baumgartner xxxxxxx nimi nimi
 LOPPURAPORTTI 19.11.2007 Lämpötilahälytin 0278116 Hans Baumgartner xxxxxxx nimi nimi KÄYTETYT MERKINNÄT JA LYHENTEET... 3 JOHDANTO... 4 1. ESISELOSTUS... 5 1.1 Diodi anturina... 5 1.2 Lämpötilan ilmaisu...
LOPPURAPORTTI 19.11.2007 Lämpötilahälytin 0278116 Hans Baumgartner xxxxxxx nimi nimi KÄYTETYT MERKINNÄT JA LYHENTEET... 3 JOHDANTO... 4 1. ESISELOSTUS... 5 1.1 Diodi anturina... 5 1.2 Lämpötilan ilmaisu...
Esimerkki: Laaduntasaussäiliö. Esimerkki: Laaduntasaussäiliö. Taajuusanalyysi. ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Laskun vaiheet ja matemaattiset mallit
 Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 28. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 28. syyskuuta 2016 1 / 22 Hieman kertausta
Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 28. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 28. syyskuuta 2016 1 / 22 Hieman kertausta
Dynaamisten systeemien teoriaa. Systeemianalyysilaboratorio II
 Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät, Systeemitekniikka
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät, Systeemitekniikka
Esimerkki: Laaduntasaussäiliö. Esimerkki: Laaduntasaussäiliö. Taajuusanalyysi. ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Säätötekniikan matematiikan verkkokurssi, Matlab tehtäviä ja vastauksia 29.7.2002
 Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
ELEC-C1230 Säätötekniikka 10. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu
 ELEC-C23 Säätötekniikka. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrait, kopensaattorien suunnittelu Quiz: Alla olevassa kuvassa on esitetty vaiheenjohtokopensaattorin siirtofunktio,
ELEC-C23 Säätötekniikka. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrait, kopensaattorien suunnittelu Quiz: Alla olevassa kuvassa on esitetty vaiheenjohtokopensaattorin siirtofunktio,
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619
 KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
SwemaAir 5 Käyttöohje
 SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
12. Stabiilisuus. Olkoon takaisinkytketyn vahvistimen vahvistus A F (s) :
 1. Stabiilisuus Olkoon takaisinkytketyn vahvistimen vahvistus A F (s) : AOL ( s) AF ( s) (13 10) 1+ T ( s) A OL :n ja T:n määrittäminen kuvattiin oppikirjan 1-7 kappaleessa. Näiden taajuus käyttäytyminen
1. Stabiilisuus Olkoon takaisinkytketyn vahvistimen vahvistus A F (s) : AOL ( s) AF ( s) (13 10) 1+ T ( s) A OL :n ja T:n määrittäminen kuvattiin oppikirjan 1-7 kappaleessa. Näiden taajuus käyttäytyminen
Van der Polin yhtälö
 Van der Polin yhtälö RLC-virtapiirissä oleva vastus vaikuttaa varsin olennaisesti piirissä esiintyviin värähtelyilmiöihin. Kuitenkin aivan uuden elementin komponenttitekniikkaan toivat aikoinaan puolijohdediodeja
Van der Polin yhtälö RLC-virtapiirissä oleva vastus vaikuttaa varsin olennaisesti piirissä esiintyviin värähtelyilmiöihin. Kuitenkin aivan uuden elementin komponenttitekniikkaan toivat aikoinaan puolijohdediodeja
Mat Systeemien identifiointi, aihepiirit 1/4
 , aihepiirit 1/4 Dynaamisten systeemien matemaattinen mallintaminen ja analyysi Matlab (System Identification Toolbox), Simulink 1. Matemaattinen mallintaminen: Mallintamisen ja mallin määritelmät Fysikaalinen
, aihepiirit 1/4 Dynaamisten systeemien matemaattinen mallintaminen ja analyysi Matlab (System Identification Toolbox), Simulink 1. Matemaattinen mallintaminen: Mallintamisen ja mallin määritelmät Fysikaalinen
Säätöjen peruskäsitteet ja periaatteet parempaan hallintaan. BAFF-seminaari 2.6.2004 Olli Jalonen EVTEK 1
 Säätöjen peruskäsitteet ja periaatteet parempaan hallintaan Olli Jalonen EVTEK 1 Esityksen luonne Esitys on lyhyt perusasioiden mieleen - palautusjakso Esityksessä käsitellään prosessia säätöjärjestelmän
Säätöjen peruskäsitteet ja periaatteet parempaan hallintaan Olli Jalonen EVTEK 1 Esityksen luonne Esitys on lyhyt perusasioiden mieleen - palautusjakso Esityksessä käsitellään prosessia säätöjärjestelmän
Matemaattisesta mallintamisesta
 Matemaattisesta mallintamisesta (Fysikaalinen mallintaminen) 1. Matemaattisen mallin konstruointi dynaamiselle reaalimaailman järjestelmälle pääpaino fysikaalisella mallintamisella samat periaatteet pätevät
Matemaattisesta mallintamisesta (Fysikaalinen mallintaminen) 1. Matemaattisen mallin konstruointi dynaamiselle reaalimaailman järjestelmälle pääpaino fysikaalisella mallintamisella samat periaatteet pätevät
Moottorin kierrosnopeus Tämän harjoituksen jälkeen:
 Moottorin kierrosnopeus Tämän harjoituksen jälkeen: osaat määrittää moottorin kierrosnopeuden pulssianturin ja Counter-sisääntulon avulla, osaat siirtää manuaalisesti mittaustiedoston LabVIEW:sta MATLABiin,
Moottorin kierrosnopeus Tämän harjoituksen jälkeen: osaat määrittää moottorin kierrosnopeuden pulssianturin ja Counter-sisääntulon avulla, osaat siirtää manuaalisesti mittaustiedoston LabVIEW:sta MATLABiin,
Harjoitus 6: Simulink - Säätöteoria. Syksy 2006. Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1
 Harjoitus 6: Simulink - Säätöteoria Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen säätötekniikkaan Takaisinkytkennän
Harjoitus 6: Simulink - Säätöteoria Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen säätötekniikkaan Takaisinkytkennän
(c) Kuinka suuri suhteellinen virhe painehäviön laskennassa tehdään, jos virtaus oletetaan laminaariksi?
 Tehtävä 1 Vettä (10 astetta) virtaa suorassa valurautaisessa (cast iron) putkessa, jonka sisähalkaisija on 100 mm ja pituus 70 m. Tilavuusvirta on 15 litraa minuutissa. (a) Osoita, että virtaus on turbulenttia.
Tehtävä 1 Vettä (10 astetta) virtaa suorassa valurautaisessa (cast iron) putkessa, jonka sisähalkaisija on 100 mm ja pituus 70 m. Tilavuusvirta on 15 litraa minuutissa. (a) Osoita, että virtaus on turbulenttia.
Luku 13. Kertausta Hydrostaattinen paine Noste
 Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Säätötekniikkaa. Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla
 Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
H(s) + + _. Ymit(s) Laplace-tason esitykseksi on saatu (katso jälleen kalvot):
 ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
Kuva 1. Virtauksen nopeus muuttuu poikkileikkauksen muuttuessa
 8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 ELEC-C123 Säätötekniikka Luku 7: Taajuusanalyysi Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
ELEC-C123 Säätötekniikka Luku 7: Taajuusanalyysi Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Mat Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ
 Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
Lämpötilan säätö. S Elektroniset mittaukset Mikko Puranen Luennon sisältö
 Lämpötilan säätö S-108.2010 Elektroniset mittaukset Mikko Puranen 20.2.2006 Luennon sisältö 1. Termodynaaminen malli 2. Jäähdytyksen suunnittelu 3. Peltier-elementit 4. Lämpötilasäätäjät PID-säädin Termodynaaminen
Lämpötilan säätö S-108.2010 Elektroniset mittaukset Mikko Puranen 20.2.2006 Luennon sisältö 1. Termodynaaminen malli 2. Jäähdytyksen suunnittelu 3. Peltier-elementit 4. Lämpötilasäätäjät PID-säädin Termodynaaminen
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
Derivoimalla kerran saadaan nopeus ja toisen kerran saadaan kiihtyvyys Ña r
 Vuka HT 4 Tehtävä. Lyhyenä alustuksena tehtävään johdetaan keskeiskiihtyvyys tasaisessa pyörimisessä. Meillä on ympyräradalla liikkuva kappale joka pyörii vakiokulmanopeudella ω dϕ säteellä r origosta.
Vuka HT 4 Tehtävä. Lyhyenä alustuksena tehtävään johdetaan keskeiskiihtyvyys tasaisessa pyörimisessä. Meillä on ympyräradalla liikkuva kappale joka pyörii vakiokulmanopeudella ω dϕ säteellä r origosta.
1 Vastaa seuraaviin. b) Taajuusvasteen
 Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Luento 10. Virtaventtiilit Vastusventtiilit Virransäätöventtiilit Virranjakoventtiilit. BK60A0100 Hydraulitekniikka
 Luento 10 Virtaventtiilit Vastusventtiilit Virransäätöventtiilit Virranjakoventtiilit BK60A0100 Hydraulitekniikka 1 Yleistä Toimilaitteen liikenopeus määräytyy sen syrjäytystilavuuden ja sille tuotavan
Luento 10 Virtaventtiilit Vastusventtiilit Virransäätöventtiilit Virranjakoventtiilit BK60A0100 Hydraulitekniikka 1 Yleistä Toimilaitteen liikenopeus määräytyy sen syrjäytystilavuuden ja sille tuotavan
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Aineopintojen laboratoriotyöt 1. Veden ominaislämpökapasiteetti
 Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei.
 5.5 Surjektio Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei. Määritelmä 5.5.1. Kuvaus f : X æ Y on surjektio, jos jokaisella
5.5 Surjektio Surjektion käsitteen avulla kuvauksia voidaan luokitella sen mukaan, kuvautuuko kaikille maalin alkioille jokin alkio vai ei. Määritelmä 5.5.1. Kuvaus f : X æ Y on surjektio, jos jokaisella
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät, Systeemitekniikka Feb 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät, Systeemitekniikka Feb 2019
Tilayhtälötekniikasta
 Tilayhtälötekniikasta Tilayhtälöesityksessä it ä useamman kertaluvun differentiaaliyhtälö esitetään ensimmäisen kertaluvun differentiaaliyhtälöryhmänä. Jokainen ensimmäisen kertaluvun differentiaaliyhtälö
Tilayhtälötekniikasta Tilayhtälöesityksessä it ä useamman kertaluvun differentiaaliyhtälö esitetään ensimmäisen kertaluvun differentiaaliyhtälöryhmänä. Jokainen ensimmäisen kertaluvun differentiaaliyhtälö
Missä mennään. systeemi. identifiointi. mallikandidaatti. validointi. malli. (fysikaalinen) mallintaminen. mallin mallin käyttötarkoitus, reunaehdot
 Missä mennään systeemi mallin mallin käyttötarkoitus, reunaehdot käyttö- (fysikaalinen) mallintaminen luonnonlait yms. yms. identifiointi kokeita kokeita + päättely päättely vertailu mallikandidaatti validointi
Missä mennään systeemi mallin mallin käyttötarkoitus, reunaehdot käyttö- (fysikaalinen) mallintaminen luonnonlait yms. yms. identifiointi kokeita kokeita + päättely päättely vertailu mallikandidaatti validointi
Kon Simuloinnin Rakentaminen Janne Ojala
 Kon 16.4011 Simuloinnin Rakentaminen Janne Ojala Simulointi käytännössä 1/3 Simulaatiomalleja helppo analysoida Ymmärretään ongelmaa paremmin - Opitaan ymmärtämään koneen toimintaa ja siihen vaikuttavia
Kon 16.4011 Simuloinnin Rakentaminen Janne Ojala Simulointi käytännössä 1/3 Simulaatiomalleja helppo analysoida Ymmärretään ongelmaa paremmin - Opitaan ymmärtämään koneen toimintaa ja siihen vaikuttavia
Van der Polin yhtälö. virtap6.nb 1
 virtap6.nb Van der Polin yhtälö RLC-virtapiirissä oleva vastus vaikuttaa varsin olennaisesti piirissä esiintyviin värähtelyilmiöihin. Kuitenkin aivan uuden elementin komponenttitekniikkaan toivat aikoinaan
virtap6.nb Van der Polin yhtälö RLC-virtapiirissä oleva vastus vaikuttaa varsin olennaisesti piirissä esiintyviin värähtelyilmiöihin. Kuitenkin aivan uuden elementin komponenttitekniikkaan toivat aikoinaan
Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6
 Lattialämmitetyn rivitalon perusparannus 2015 Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6 Maakaasukattila Lattialämmitys. Putkipituus tuntematon. Ilmanvaihto koneellinen. Ei lämmön talteenottoa.
Lattialämmitetyn rivitalon perusparannus 2015 Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6 Maakaasukattila Lattialämmitys. Putkipituus tuntematon. Ilmanvaihto koneellinen. Ei lämmön talteenottoa.
Luku 13. Kertausta Hydrostaattinen paine Noste
 Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Säätötekniikkaa. Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla
 Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t,
 AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t, v)-koordinaatistossa ruutumenetelmällä. Tehtävä 4 (~YO-K97-1). Tekniikan
AUTON LIIKETEHTÄVIÄ: KESKIKIIHTYVYYS ak JA HETKELLINEN KIIHTYVYYS a(t) (tangenttitulkinta) sekä matka fysikaalisena pinta-alana (t, v)-koordinaatistossa ruutumenetelmällä. Tehtävä 4 (~YO-K97-1). Tekniikan
Dynamiikan hallinta Lähde: Zölzer. Digital audio signal processing. Wiley & Sons, 2008. Zölzer (ed.) DAFX Digital Audio Effects. Wiley & Sons, 2002.
 Dynamiikan hallinta Lähde: Zölzer. Digital audio signal processing. Wiley & Sons, 2008. Zölzer (ed. DAFX Digital Audio Effects. Wiley & Sons, 2002. Sisältö:! Johdanto!! Ajallinen käyttäytyminen! oteutus!
Dynamiikan hallinta Lähde: Zölzer. Digital audio signal processing. Wiley & Sons, 2008. Zölzer (ed. DAFX Digital Audio Effects. Wiley & Sons, 2002. Sisältö:! Johdanto!! Ajallinen käyttäytyminen! oteutus!
Ei välttämättä, se voi olla esimerkiksi Reuleaux n kolmio:
 Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Alias-ilmiö eli taajuuden laskostuminen
 Prosessiorientoituneet mallit Todellista hybridijärjestelmää ELEC-C1230 Säätötekniikka Luku 12: Näytteenottoteoreema ja jatkuvien säätimien diskreetit approksimaatiot Prosessiorientoituneet mallit katsotaan
Prosessiorientoituneet mallit Todellista hybridijärjestelmää ELEC-C1230 Säätötekniikka Luku 12: Näytteenottoteoreema ja jatkuvien säätimien diskreetit approksimaatiot Prosessiorientoituneet mallit katsotaan
2. kierros. 2. Lähipäivä
 2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
Matlab-tietokoneharjoitus
 Matlab-tietokoneharjoitus Tämän harjoituksen tavoitteena on: Opettaa yksinkertaisia piirikaavio- ja yksikkömuunnoslaskuja. Opettaa Matlabin perustyökaluja mittausten analysoimiseen. Havainnollistaa näytteenottotaajuuden,
Matlab-tietokoneharjoitus Tämän harjoituksen tavoitteena on: Opettaa yksinkertaisia piirikaavio- ja yksikkömuunnoslaskuja. Opettaa Matlabin perustyökaluja mittausten analysoimiseen. Havainnollistaa näytteenottotaajuuden,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
y 2 h 2), (a) Näytä, että virtauksessa olevan fluidialkion tilavuus ei muutu.
 Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Kojemeteorologia (53695) Laskuharjoitus 1
 Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
Suodattimet. Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth. Suodattimet samalla asteluvulla (amplitudivaste)
 Suodattimet Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth Suodattimet samalla asteluvulla (amplitudivaste) Kuvasta nähdään että elliptinen suodatin on terävin kaikista suodattimista, mutta sisältää
Suodattimet Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth Suodattimet samalla asteluvulla (amplitudivaste) Kuvasta nähdään että elliptinen suodatin on terävin kaikista suodattimista, mutta sisältää
IIZE3010 Elektroniikan perusteet Harjoitustyö. Pasi Vähämartti, C1303, IST4SE
 IIZE3010 Elektroniikan perusteet Harjoitustyö Pasi Vähämartti, C1303, IST4SE 2 (11) Sisällysluettelo: 1. Tehtävänanto...3 2. Peruskytkentä...4 2.1. Peruskytkennän käyttäytymisanalyysi...5 3. Jäähdytyksen
IIZE3010 Elektroniikan perusteet Harjoitustyö Pasi Vähämartti, C1303, IST4SE 2 (11) Sisällysluettelo: 1. Tehtävänanto...3 2. Peruskytkentä...4 2.1. Peruskytkennän käyttäytymisanalyysi...5 3. Jäähdytyksen
Mikrofonien toimintaperiaatteet. Tampereen musiikkiakatemia Studioäänittäminen Klas Granqvist
 Mikrofonien toimintaperiaatteet Tampereen musiikkiakatemia Studioäänittäminen Klas Granqvist Mikrofonien luokittelu Sähköinen toimintaperiaate Akustinen toimintaperiaate Suuntakuvio Herkkyys Taajuusvaste
Mikrofonien toimintaperiaatteet Tampereen musiikkiakatemia Studioäänittäminen Klas Granqvist Mikrofonien luokittelu Sähköinen toimintaperiaate Akustinen toimintaperiaate Suuntakuvio Herkkyys Taajuusvaste
6.8 Erityisfunktioiden sovelluksia
 6.8 Erityisfunktioiden sovelluksia Tässä luvussa esitellään muutama esimerkki, joissa käytetään hyväksi eksponentti-, logaritmi- sekä trigonometrisia funktioita. Ensimmäinen esimerkki juontaa juurensa
6.8 Erityisfunktioiden sovelluksia Tässä luvussa esitellään muutama esimerkki, joissa käytetään hyväksi eksponentti-, logaritmi- sekä trigonometrisia funktioita. Ensimmäinen esimerkki juontaa juurensa
KESTOMAGNEETTI VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Jani Vitikka p87434 Hannu Tiitinen p87432. Dynaaminen kenttäteoria SATE2010
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jani Vitikka p87434 Hannu Tiitinen p87432 Dynaaminen kenttäteoria SATE2010 KESTOMAGNEETTI Sivumäärä: 10 Jätetty tarkastettavaksi: 16.1.2008 Työn tarkastaja
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jani Vitikka p87434 Hannu Tiitinen p87432 Dynaaminen kenttäteoria SATE2010 KESTOMAGNEETTI Sivumäärä: 10 Jätetty tarkastettavaksi: 16.1.2008 Työn tarkastaja
PROSESSISUUNNITTELUN SEMINAARI. Luento 5.3.2012 3. vaihe
 PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
SwemaMan 7 Käyttöohje
 SwemaMan 7 Käyttöohje HUOM! Ennen mittausten aloittamista, lue kohta 6. Asetukset (SET). Vakiona k2-kompensointi on päällä. 1. Esittely SwemaMan 7 on mikro manometri paine-eron, ilmanvirtauksen sekä -nopeuden
SwemaMan 7 Käyttöohje HUOM! Ennen mittausten aloittamista, lue kohta 6. Asetukset (SET). Vakiona k2-kompensointi on päällä. 1. Esittely SwemaMan 7 on mikro manometri paine-eron, ilmanvirtauksen sekä -nopeuden
AS-74.2111 Analoginen säätö. Luento 1: Johdanto, dynaamiset mallit ja rakenteet, lohkokaaviot, säädön periaatteet
 AS-74.2111 Analoginen säätö Luento 1: Johdanto, dynaamiset mallit ja rakenteet, lohkokaaviot, säädön periaatteet Mitä säätötekniikka on? Control Systems Engineering Laaja näkemys: Systeemien sekä niiden
AS-74.2111 Analoginen säätö Luento 1: Johdanto, dynaamiset mallit ja rakenteet, lohkokaaviot, säädön periaatteet Mitä säätötekniikka on? Control Systems Engineering Laaja näkemys: Systeemien sekä niiden
Differentiaali- ja integraalilaskenta
 Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
ELEC-C1230 Säätötekniikka
 Johdanto: Digitaalinen (diskreetti, diskreettiaikainen) säätöjärjestelmä ELEC-C1230 Säätötekniikka Luku 10: Digitaalinen säätö, perusteet, jatkuu A/D-muunnoksessa analoginen signaali näytteistetään (sampling);
Johdanto: Digitaalinen (diskreetti, diskreettiaikainen) säätöjärjestelmä ELEC-C1230 Säätötekniikka Luku 10: Digitaalinen säätö, perusteet, jatkuu A/D-muunnoksessa analoginen signaali näytteistetään (sampling);
1.1 Funktion määritelmä
 1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
