12. Stabiilisuus. Olkoon takaisinkytketyn vahvistimen vahvistus A F (s) :
|
|
|
- Liisa Sala
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 1. Stabiilisuus Olkoon takaisinkytketyn vahvistimen vahvistus A F (s) : AOL ( s) AF ( s) (13 10) 1+ T ( s) A OL :n ja T:n määrittäminen kuvattiin oppikirjan 1-7 kappaleessa. Näiden taajuus käyttäytyminen saadaan selville aikavakio menetelmällä (kappale 11-9). A F (s):n navat ovat 1 + T(s):n nollakohtia sekä A OL (s):n navat, jotka eivät ole yhteisiä T(s):n kanssa. Nyquistin periaatteen mukaan pisteen 1 + j0 sisältävien myötäsuuntaisten ympyröiden lukumäärä vastaa 1+T(s)F(s):n oikealla puolitasolla olevien napojen ja nollakohtien erotusta. Koska stabiiliuden vuoksi F(s):llä ei saa olla nollakohtia oikealla puolitasolla (A F (s):llä ei oikean puolen napoja), sekä takaisinkytkemättömän vahvistimen ollessa stabiili ei F(s):llä ole napoja oikealla puolitasolla. Tämän vuoksi pisteen 1 + j0 kiertoa ei saa olla stabiililla takaisinkytketyllä vahvistimella. Jos takaisinkytkemätön vahvistin on stabiili, niin A OL :n kaikki navat ovat vasemmalla puolitasolla. Tällöin takaisinkytketty vahvistin on stabiili, jos 1 + T(s):n kaikki nollakohdat ovat vasemmalla puolitasolla. Nyquistin diagrammissa T(jω) kuvataan napakoordinaatistossa. T ( jω) sekä θ ( jω) välillä < ω < + määrittelevät kuvaajan napakoordinaatistossa. Yllä olevan kuvan (illman 13-3a) mukaisessa tapauksessa ei pistettä ole kierretty, joten avoimen kytkennän ollessa stabiili, ei takaisinkytketyllä vahvistimella ole A F (s):n oikean puoleisia napoja ja se on stabiili Sitä vastoin alla olevan kuvan (illman 13-3b) diagrammissa on piste kierretty kaksi kertaa, joten 1+T (s):llä on kaksi oikeanpuoleista nollakohtaa. A F (s):llä on siten kaksi oikeanpuoleista napaa ja vahvistin on epästabiili. Kulmataajuutta, jolla yksikköympyrä ja Nygquistin diagrammi leikkaavat toisensa on ω (gain-crossover frequency). T ( jω ) > 1 kun ω < ω T ( jω ) < 1 kun ω > ω Verrattaessa kuvan 13-3 tapauksia keskenään nähdään, että stabiilin systeemin (13-3a) kulmataajuuden ω 1 kohdalla T(jω 1 ) >-180 (eli T(jω 1 < 180 ). Sitä vastoin epästabiilissa tapauksessa (kuva 13-3b) T(jω ) <-180 (eli T(jω > 180 ). Vaihevara Alla olevassa kuvassa (illman 13-4) on piirretty mukaan yksikköympyrä, joka vastaa T(jω)1 (0dB) ympyrää. ääritellään vaihevara (Pase argin) T ( jω ) (13 11) Huomaa, että T(jω ) on yleensä negatiivinen. Takaisinkytketty vahvistin on siten stabiili, jos vaihevara on positiivinen. Kulman T(jω ) on siten oltava pienempi kuin 180, jotta vaihemarginaalia jäisi riittävästi
2 Vahvistusvara Boden diagrammi Kulmataajuus ω, jossa Nyquistin diagrammi leikkaa negatiivisen reaaliakselin, vastaa kulmaa -180 T(jω ) (phase crossover angular frequency). T < 180 T > 180 kun kun ω > ω ω < ω ääritellään vahvistusvara (ain argin) 0logT ( jω ) T ( jω ) db (13 1) Usein on käytännöllisempää käyttää Boden diagrammia, koska sen uudelleen piirtäminen on helppoa, kun napojen (nollakohtien) paikkoja tai T:n keskikaistan arvoa muutetaan. Etenkin asymptoottisen Boden diagrammin käyttö kynää ja paperia käytettäessä on hyvin käyttökelpoinen. Sen jälkeen tietokone simulaatioilla voidaan komponenttien arvot sovittaa tarkasti. Katsotaan lyhyesti läpi kirjan esimerkki, jossa silmukkavahvistus T on seuraava : T( s) ( 1+ s 10 )( 1+ s 10 ) Nyquistin diagrammiksi saadaan alla olevan kuvan mukainen käyrä, joka leikkaa napakoordinaatistoon lisätyn yksikkö ympyrän kulmataajuudella ω rad/s, jossa vaihevara on n Kuvasta 13-4a nähdään,että stabiilille systeemille (T 1 (jω )<1) 1 on positiivinen, koska logaritmi ykköstä pienemmästä luvusta on negatiivinen. Sitä vastoin epästabiilille systeemille (kuva 13-4b) on negatiivinen Alla olevassa kuvassa (illman 13-6) on esitetty samalle tapaukselle Boden diagrammi, johon on merkitty vaihevara. Koska T on avoimen kytkennän vahvistuksen A OL (s):n ja β(s):n tulo, voidaan Boden diagrammia hyödyntää myös seuraavasti. Piirretään A OL (s) ja β(s) erikseen Boden diagrammiin seuraavasti: Seuraavassa on esitetty silmukkavahvistus T(jω) toisessa muodossa, missä a 10 6 ja b 10 7, josta voidaan määrittää T ja T. ω 100 ( ) ab T jω ω ω + ab a b a b jω ω ω + ab a b Koska β(s):n < 1, on se negatiivisella puolella desibeli asteikkoa. Koska kahden muuttujan tulo voidaan esittää logaritmisella asteikolla summana, saadaan T(s) 1/β(s):n ja A OL (s):n väliin jäävästä alueesta
3 1.1 Kompensointi Takaisinkytketyn vahvistimen suunnittelussa on yleensä kolme pääkohtaa: 1. Keskikaistan ominaisuuksien toteuttaminen Vahvistuskerroin DC stabiilius Särö Tulo- ja lähtöimpedanssit Ym. Oletetaan aluksi, että takaisinkytkentäelimen siirtofunktio β(s) on taajuudesta riippumaton. Tällöin taajuudesta riippuva vaihesiirto liittyy avoimen (esimerkiksi operaatiovahvistimen raakavahvistus Avo(s) ) vahvistinkytkennän vaihekäyttäytymiseen. Huonoin tilanne on silloin, kun β on lähes yksi, jolloin T(s) on suurin. Tällöin vaiheen on oltava vähemmän, kuin 180 jäljessä, jotta takaisinkytketty vahvistin olisi stabiili. Jos tämä ehto on voimassa, on vahvistin ns. unity-gain stable. Tyypillisesti operaatiovahvistimilla vaihevara on Stabiiliuden testaaminen 3. Tee siitä stabiili Kuten aiemmin todettiin, niin vahvistimen tietyt ominaisuudet lähestyivät ideaalista, kun T 0 oli suuri. Toisaalta takaisinkytketyn vahvistimen osalta sen suuri arvo johtaa helposti epästabiiliin tilanteeseen. Takaisin kytketyn vahvistimen vaste määräytyy A F (s):n navoista. T 0 :n arvoa ei voida paljon muuttaa keskikaistan ominaisuuksien säilyttämiseksi. Takaisin kytketyn vahvistimen stabiiliuden varmistamiseksi, voidaan T(s):n napoja muuttaa halutulla tavalla. Tällä tavoin stabiiliksi tehtyä vahvistinta kutsutaan kompensoiduksi. Kytkentään lisätään muutama lisä komponentti, joilla saadaan T(s):n navat haluttuun kohtaan muuttamatta T 0 :n arvoa. Tapa miten edellä mainittu ehto voidaan täyttää on muokata operaatiovahvistimen A VO (s) siten, että sen arvo on 0dB ennen, kuin vaihe-ero saavuttaa -180 (Dominantpole compensation). Keino miten se tehdään on yksinkertainen. Lisätään operaatiovahvistimen sisäiseen efektiiviseen alipäästöön lisäkapasitanssi. Tapa on esitetty yllä olevassa kuvassa, jossa on kuvattu operaatiovahvistimen (34, 358) yksinkertaistettu sisäinen rakenne. Tällä tavoin saadaan siirrettyä A VO (s):n alin napa niin alas, että avoimen kytkennän vahvistus on 0dB ennen seuraavan ylemmän navan kulmataajuutta. Edellä annetun ehdon ja oletuksen perusteella voidaan piirtää T(s):n asymptoottinen vaihekäyttäytyminen, joka on esitetty alla olevassa kuvassa (illman 13-9a). Yleisesti ottaen vastakytkentäkerroin ei ole taajuudesta riippumaton, joten kompensoinnissa järjestetään tarkoituksellisesti T(s):lle kapeampi kaista. Eli kompensoimattoman T(s):n hallitseva napa siirretään riittävän pienelle kulmataajuudelle. Olkoon silmukkavahvistus seuraava: ( ) T s T0 (13 13) ( + s ω )( 1+ s ω )( 1+ s ω ) Takaisinkytketyn vahvistimen stabiiliuden varmistamiseksi, siirretään alin kulmataajuus ω 1 riittävän lähelle origoa, jotta saamme ehdon: Oletetaan lisäksi, että 10ω 1 ω ω3 10ω 10 Ensimmäinen napa on siis siirretty kaksi dekadia alemmalle kulmataajuudelle, kuin ω. Tämän vuoksi kulmataajuuden ω /10 alapuolisella lähialueella on vaiheero vakio -90. Kun valitsemme vaihevaraksi: ääräytyy ω edellisen kuvan esittämällä tavalla. Jos halutaan, että vaihevara on vähintään 45, saadaan tulos: ω ω Tällöin kulmataajuuden ω alapuolella T(jω) putoaa 0dB dekadia kohti saavuttaen 0dB kulmataajuudella ω. 51 5
4 Koska ω tiedetään voidaan ω 1 määrittää graafisesti piirtämällä ω :n kautta suora, jonka kulmakerroin on -0dB/dekadi. T 0 :n ja piirretyn suoran leikkauskohdasta saadaan kulmataajuus ω 1. Katso alla olevaa kuvaa (illman 13-9b). Jos vastakytkentäkerroin β(s) ja vahvistimen avoimen kytkennän vahvistus A VO (s) tiedetään, kuten operaatiovahvistimilla, voidaan Boden-diagrammin avulla tarkastella kytkennän stabiilisuutta seuraavasti. Huomattakoon, että vaihekäyttäytymistä esittävässä kuvassa (13-9a) kulmakertoimella -45 /dekadi vaiheen muutos aiheutuu navasta -ω. Jos vaihevaraa pienennetään kasvavat ω 1 ja ω. Pidä vaihevara riittävän suurena (45 ), ettei komponenttien ikääntyminen saa aikaan epästabiilia tilannetta. Jos A VO (s) ja 1/β(s) leikkaavat toisensa efektiivisellä kulmakertoimella 40dB/dekadi, on kytkentä epästabiili, jos kohtauskulma on asettunut vakioksi jo dekadia ennen leikkauspistettä. Stabiilille kytkennälle kohtauskulma on 0dB/dekadi, joka tulisi asettua vakioksi noin dekadia ennen leikkauspistettä Tarkastellaan lopuksi lyhyesti alla olevan kuvan mukaista derivoivaa piiriä, jossa on otettava huomioon kytkennän stabiilius tekijät. Derivointipiirin vastakytkentäkertoimen sisältäessä kapasitanssin, on β taajuudesta riippuva. Tällöin 1/ β kasvaa 0dB/dekadi tietyn kulmataajuuden jälkeen. Tällöin se kohtaa A VO :n netto kulmakertoimella 40dB/dekadi, jolloin kytkentä on epästabiili (katso alla oleva kuva). Edellisessä kuvassa on esitetty myös vastakytkennän aikaansaama vaihesiirto. Kun lisäämme siihen A VO :n taajuusriippuvuudesta johtuvan vaihesiirron, kutistuu vaihevara nollaan saavuttaessa 40dB/dekadi kohtaamiskulmalla käyrien leikkauskohtaan. Seuraavassa alla olevassa kuvassa on kytkentään lisätty kondensaattorin kanssa sarjaan resistanssi (510Ω), joten 1/β kohtaa A VO :n -0dB/dekadi kohtauskulmassa, joka on vakio lähes dekadia ennen leikkaus kohtaa
5 Tällöin β:n osuus vaihesiirrossa on häviävän pieni, joten vaihevaraksi saadaan likimäärin : Alla olevassa kuvassa on esitetty tilanne, jossa on lisätty toinen kapasitanssi. Kapasitanssin C lisääminen pienentää kohinavahvistuksen 1/β arvoa suuremmilla taajuuksilla, joten matalataajuuksinen pieniamplitudinen signaali ei peity niin helposti kohinaan. Alla olevassa kuvassa on esitetty asymptoottinen Boden diagrammi kytkennälle eri vastakytkentä tapauksille. Piiri toimii toimii derivoivana piirinä alle f 3 taajuuksilla, sekä integroivana sitä suuremmilla taajuuksilla. Operaatiovahvistimen ottonavoissa näkyvä muutaman pikofaradin kapasitanssi C o voi aiheuttaa stabiilisuus ongelmia, jos kytkennän resistanssitaso on suuri ja halutaan käyttää mahdollisimman suurta kaistanleveyttä. Ottonapoihin liittyvien piirikortin kytkentäjohdinten kapasitanssi maatason suhteen kytkeytyessä C o :n kanssa rinnan, saadaan vastakytkentäkertoimen kulmapiste siirtymään kohtalaisen helposti pienille taajuuksille (khz) (katso seuraava kuva)
3. kierros. 2. Lähipäivä
 3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
Elektroniikka, kierros 3
 Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
4. kierros. 1. Lähipäivä
 4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. = K K K M. s 2 3s 2 KK P
 Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Osatentti
 Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
Osatentti
 Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
Esimerkki: Laaduntasaussäiliö. Esimerkki: Laaduntasaussäiliö. Taajuusanalyysi. ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Esimerkki: Laaduntasaussäiliö. Esimerkki: Laaduntasaussäiliö. Taajuusanalyysi. ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Taajuusanalyysi ELEC-C1230 Säätötekniikka Luku 7: Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu. Vinkit 1 a
 ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
Tehtävä 1. Vaihtoehtotehtävät.
 Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
Hyvyyskriteerit. ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
ELEC-C1230 Säätötekniikka. Luku 7: Taajuusanalyysi
 ELEC-C123 Säätötekniikka Luku 7: Taajuusanalyysi Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
ELEC-C123 Säätötekniikka Luku 7: Taajuusanalyysi Taajuusanalyysi Aikaisemmilla luennoilla on tarkasteltu systeemien käyttäytymistä aikatasossa (differentiaaliyhtälöt, herätteet ja vasteet) tai Laplace-tasossa
Vcc. Vee. Von. Vip. Vop. Vin
 5-87.2020 Elektroniikka II Tentti ja välikoeuusinnat 27.05.2011 1. Våitikokeen tehtiivät l-4,2. välikokeen tehtävät 5-8 ja tentin tehtävät l,2,6ja 8. Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin
5-87.2020 Elektroniikka II Tentti ja välikoeuusinnat 27.05.2011 1. Våitikokeen tehtiivät l-4,2. välikokeen tehtävät 5-8 ja tentin tehtävät l,2,6ja 8. Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin
Säätötekniikan matematiikan verkkokurssi, Matlab tehtäviä ja vastauksia 29.7.2002
 Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
R = Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen on tällöin jännitteenjako = 1
 Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
3. kierros. 1. Lähipäivä
 3. kierros 1. Lähipäivä Viikon aihe (viikko 1/2) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros 1. Lähipäivä Viikon aihe (viikko 1/2) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
Mat Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ
 Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
ELEC-C1230 Säätötekniikka 10. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu
 ELEC-C23 Säätötekniikka. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrait, kopensaattorien suunnittelu Quiz: Alla olevassa kuvassa on esitetty vaiheenjohtokopensaattorin siirtofunktio,
ELEC-C23 Säätötekniikka. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrait, kopensaattorien suunnittelu Quiz: Alla olevassa kuvassa on esitetty vaiheenjohtokopensaattorin siirtofunktio,
1 Vastaa seuraaviin. b) Taajuusvasteen
 Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Säätötekniikkaa. Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla
 Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Vastaus: Määrittelyehto on x 1 ja nollakohta x = 1.
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
Operaatiovahvistimen vahvistus voidaan säätää halutun suuruiseksi käyttämällä takaisinkytkentävastusta.
 TYÖ 11. Operaatiovahvistin Operaatiovahvistin on mikropiiri ( koostuu useista transistoreista, vastuksista ja kondensaattoreista juotettuna pienelle piipalaselle ), jota voidaan käyttää useisiin eri kytkentöihin.
TYÖ 11. Operaatiovahvistin Operaatiovahvistin on mikropiiri ( koostuu useista transistoreista, vastuksista ja kondensaattoreista juotettuna pienelle piipalaselle ), jota voidaan käyttää useisiin eri kytkentöihin.
SMG-1100: PIIRIANALYYSI I. Verkkojen taajuusriippuvuus: suo(dat)timet
 SMG-00: PIIRIANALYYSI I Verkkojen taajuusriippuvuus: suo(dat)timet alipäästösuodin ylipäästösuodin kaistanpäästösuodin kaistanestosuodin jännitevahvistus rajataajuus kaistanleveys resonanssi Suotimet:
SMG-00: PIIRIANALYYSI I Verkkojen taajuusriippuvuus: suo(dat)timet alipäästösuodin ylipäästösuodin kaistanpäästösuodin kaistanestosuodin jännitevahvistus rajataajuus kaistanleveys resonanssi Suotimet:
1 PID-taajuusvastesuunnittelun esimerkki
 Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Digitaalinen Signaalinkäsittely T0125 Luento 4-7.04.2006
 Digitaalinen Signaalinkäsittely T5 Luento 4-7.4.6 Jarkko.Vuori@evtek.fi Z-taso Z-taso on paljon käytetty graafinen esitystapa jonka avulla voidaan tarkastella signaalien taajuussisältöjä sekä järjestelmien
Digitaalinen Signaalinkäsittely T5 Luento 4-7.4.6 Jarkko.Vuori@evtek.fi Z-taso Z-taso on paljon käytetty graafinen esitystapa jonka avulla voidaan tarkastella signaalien taajuussisältöjä sekä järjestelmien
RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2)
 SÄHKÖ- JA TIETOTEKNIIKAN OSASTO Radiotekniikka I RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2) Työn tekijät Katja Vitikka 1835627 Hyväksytty / 2009 Arvosana Vitikka K. (2009) Oulun yliopisto, sähkö- ja
SÄHKÖ- JA TIETOTEKNIIKAN OSASTO Radiotekniikka I RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2) Työn tekijät Katja Vitikka 1835627 Hyväksytty / 2009 Arvosana Vitikka K. (2009) Oulun yliopisto, sähkö- ja
Dynaamisten systeemien teoriaa. Systeemianalyysilaboratorio II
 Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
MAB3 - Harjoitustehtävien ratkaisut:
 MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia
 KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
OPERAATIOVAHVISTIN. Oulun seudun ammattikorkeakoulu Tekniikan yksikkö. Elektroniikan laboratoriotyö. Työryhmä Selostuksen kirjoitti 11.11.
 Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
ENSO IKONEN PYOSYS SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
2 Raja-arvo ja jatkuvuus
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.6 Raja-arvo ja jatkuvuus. a) Kun suorakulmion kärki on kohdassa =, on suorakulmion kannan pituus. Suorakulmion korkeus on käyrän y-koordinaatti
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.6 Raja-arvo ja jatkuvuus. a) Kun suorakulmion kärki on kohdassa =, on suorakulmion kannan pituus. Suorakulmion korkeus on käyrän y-koordinaatti
Analogiapiirit III. Keskiviikko , klo , TS128. Operaatiovahvistinrakenteet
 Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 3. Keskiviikko 11.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. a) Laske kuvan 1 käännetty kaskadi (folded-cascode)
Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 3. Keskiviikko 11.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. a) Laske kuvan 1 käännetty kaskadi (folded-cascode)
Harjoitus 1. Tehtävä 1. Malliratkaisut. f(t) = e (t α) cos(ω 0 t + β) L[f(t)] = f(t)e st dt = e st t+α cos(ω 0 t + β)dt.
![Harjoitus 1. Tehtävä 1. Malliratkaisut. f(t) = e (t α) cos(ω 0 t + β) L[f(t)] = f(t)e st dt = e st t+α cos(ω 0 t + β)dt. Harjoitus 1. Tehtävä 1. Malliratkaisut. f(t) = e (t α) cos(ω 0 t + β) L[f(t)] = f(t)e st dt = e st t+α cos(ω 0 t + β)dt.](/thumbs/95/125776102.jpg) Harjoitus Malliratkaisut Tehtävä L[f(t)] ˆ f(t) e (t α) cos(ω t + β) f(t)e st dt ˆ e st t+α cos(ω t + β)dt cos(ω t + β) 2 (ej(ωt+β) + e j(ωt+β) ) L[f(t)] 2 eα 2 ˆ ˆ e st t+α (e j(ω t+β) + e j(ω t+β) )
Harjoitus Malliratkaisut Tehtävä L[f(t)] ˆ f(t) e (t α) cos(ω t + β) f(t)e st dt ˆ e st t+α cos(ω t + β)dt cos(ω t + β) 2 (ej(ωt+β) + e j(ωt+β) ) L[f(t)] 2 eα 2 ˆ ˆ e st t+α (e j(ω t+β) + e j(ω t+β) )
H(s) + + _. Ymit(s) Laplace-tason esitykseksi on saatu (katso jälleen kalvot):
 ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
VAIHTOVIRTAPIIRI. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Sähkö- ja magnetismiopin laboratoriotyöt AHTOTAP Työn tavoitteet aihtovirran ja jännitteen suunta vaihtelee ajan funktiona. Esimerkiksi Suomessa käytettävä verkkovirta
Oulun yliopisto Fysiikan opetuslaboratorio Sähkö- ja magnetismiopin laboratoriotyöt AHTOTAP Työn tavoitteet aihtovirran ja jännitteen suunta vaihtelee ajan funktiona. Esimerkiksi Suomessa käytettävä verkkovirta
Systeemin käyttäytyminen. ELEC-C1230 Säätötekniikka. Systeemin navat ja nollat. Systeemin navat ja nollat
 Systeemin käyttäytyminen ELEC-C1230 Säätötekniikka Luku 5: Navat ja nollat, systeemin nopeus, stabiilisuus ja värähtelyt, Routh-Hurwitz-kriteeri Systeemin tai järjestelmän tärkein ominaisuus on stabiilisuus.
Systeemin käyttäytyminen ELEC-C1230 Säätötekniikka Luku 5: Navat ja nollat, systeemin nopeus, stabiilisuus ja värähtelyt, Routh-Hurwitz-kriteeri Systeemin tai järjestelmän tärkein ominaisuus on stabiilisuus.
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä
 Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Luento 7. LTI-järjestelmät
 Luento 7 Lineaaristen järjestelmien analyysi taajuustasossa Taajuusvaste Stabiilisuus..7 LTI-järjestelmät u(t) h(t) y(t) Tarkastellaan lineaarista aikainvarianttia järjestelmää n n m m d d d d yt () =
Luento 7 Lineaaristen järjestelmien analyysi taajuustasossa Taajuusvaste Stabiilisuus..7 LTI-järjestelmät u(t) h(t) y(t) Tarkastellaan lineaarista aikainvarianttia järjestelmää n n m m d d d d yt () =
Kuva 1. Ohmin lain kytkentäkaavio. DC; 0 6 V.
 TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Fy06 Koe 20.5.2015 Kuopion Lyseon lukio (KK) 1/7
 Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
Tehtävä 4.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla.
 Tehtävä.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla. x = (a + b cos(θ)) cos(ψ) y = (a + b cos(θ)) sin(ψ) = b sin(θ), a > b, θ π, ψ π Figure. Toruksen hajoituskuva Oletetaan,
Tehtävä.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla. x = (a + b cos(θ)) cos(ψ) y = (a + b cos(θ)) sin(ψ) = b sin(θ), a > b, θ π, ψ π Figure. Toruksen hajoituskuva Oletetaan,
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
FYSP105 / K3 RC-SUODATTIMET
 FYSP105 / K3 R-SODATTIMET Työn tavoitteita tutustua R-suodattimien toimintaan oppia mitoittamaan tutkittava kytkentä laiterajoitusten mukaisesti kerrata oskilloskoopin käyttöä vaihtosähkömittauksissa Työssä
FYSP105 / K3 R-SODATTIMET Työn tavoitteita tutustua R-suodattimien toimintaan oppia mitoittamaan tutkittava kytkentä laiterajoitusten mukaisesti kerrata oskilloskoopin käyttöä vaihtosähkömittauksissa Työssä
Aikatason vaste vs. siirtofunktio Tehtävä
 Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
yleisessä muodossa x y ax by c 0. 6p
 MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
FYSP105/2 VAIHTOVIRTAKOMPONENTIT. 1 Johdanto
 FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteet o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteet o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
FYS206/5 Vaihtovirtakomponentit
 FYS206/5 Vaihtovirtakomponentit Tässä työssä pyritään syventämään vaihtovirtakomponentteihin liittyviä käsitteitä. Tunnetusti esimerkiksi käsitteet impedanssi, reaktanssi ja vaihesiirto ovat aina hyvin
FYS206/5 Vaihtovirtakomponentit Tässä työssä pyritään syventämään vaihtovirtakomponentteihin liittyviä käsitteitä. Tunnetusti esimerkiksi käsitteet impedanssi, reaktanssi ja vaihesiirto ovat aina hyvin
a) I f I d Eri kohinavirtakomponentit vahvistimen otossa (esim. http://www.osioptoelectronics.com/)
 a) C C p e n sn V out p d jn sh C j i n V out Käytetyt symbolit & vakiot: P = valoteho [W], λ = valodiodin ilmaisuvaste eli responsiviteetti [A/W] d = pimeävirta [A] B = kohinakaistanleveys [Hz] T = lämpötila
a) C C p e n sn V out p d jn sh C j i n V out Käytetyt symbolit & vakiot: P = valoteho [W], λ = valodiodin ilmaisuvaste eli responsiviteetti [A/W] d = pimeävirta [A] B = kohinakaistanleveys [Hz] T = lämpötila
Analogiapiirit III. Keskiviikko , klo , TS127. Jatkuva-aikaiset IC-suodattimet ja PLL-rakenteet
 Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 8. Keskiviikko 5.2.2003, klo. 12.15-14.00, TS127. Jatkuva-aikaiset IC-suodattimet ja PLL-rakenteet 1. Mitoita kuvan 1 2. asteen G m -C
Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 8. Keskiviikko 5.2.2003, klo. 12.15-14.00, TS127. Jatkuva-aikaiset IC-suodattimet ja PLL-rakenteet 1. Mitoita kuvan 1 2. asteen G m -C
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
origo III neljännes D
 Sijoita pisteet A(1,4) ja B(4,5;5) sekä C(-3,4) ja D(-4,--5) y II neljännes C A I neljännes B x origo III neljännes D IV neljännes KOTIT. Sijoita ja nimeä koordinaatistoon pisteitä niin, että pisteet yhdistettäessä
Sijoita pisteet A(1,4) ja B(4,5;5) sekä C(-3,4) ja D(-4,--5) y II neljännes C A I neljännes B x origo III neljännes D IV neljännes KOTIT. Sijoita ja nimeä koordinaatistoon pisteitä niin, että pisteet yhdistettäessä
Lukuväleistä. MB 3 Funktio. -2 < x < 5 tai ]-2,5] x < 3 tai ]-,3]
![Lukuväleistä. MB 3 Funktio. -2 < x < 5 tai ]-2,5] x < 3 tai ]-,3] Lukuväleistä. MB 3 Funktio. -2 < x < 5 tai ]-2,5] x < 3 tai ]-,3]](/thumbs/47/23676089.jpg) Lukuväleistä MB Funktio - < < tai ]-,] < tai ]-,] Yksikäsitteisyys Täytyy tuntea/arvata tyyppi T 0. (sivu ) f() = a) f () = = 9 = 4 T 0. (sivu ) T 0. (sivu ) f() = f() = b) f(k) = k c) f(t + ) = (t + )
Lukuväleistä MB Funktio - < < tai ]-,] < tai ]-,] Yksikäsitteisyys Täytyy tuntea/arvata tyyppi T 0. (sivu ) f() = a) f () = = 9 = 4 T 0. (sivu ) T 0. (sivu ) f() = f() = b) f(k) = k c) f(t + ) = (t + )
Funktio. Funktio on kahden luvun riippuvuuden ilmaiseva sääntö, joka annetaan usein laskulausekkeena.
 n ja muuttujan arvon laskeminen on kahden luvun riippuvuuden ilmaiseva sääntö, joka annetaan usein laskulausekkeena. ESIMERKKI Tarkastele funktiota f() = + 7. a) Laske funktion arvo, kun =. b) Millä muuttujan
n ja muuttujan arvon laskeminen on kahden luvun riippuvuuden ilmaiseva sääntö, joka annetaan usein laskulausekkeena. ESIMERKKI Tarkastele funktiota f() = + 7. a) Laske funktion arvo, kun =. b) Millä muuttujan
z muunnos ja sen soveltaminen LTI järjestelmien analysointiin
 z muunnos ja sen soveltaminen LTI järjestelmien analysointiin muunnoksella (eng. transform) on vastaava asema diskreettiaikaisten signaalien ja LTI järjestelmien analyysissä kuin Laplace muunnoksella jatkuvaaikaisten
z muunnos ja sen soveltaminen LTI järjestelmien analysointiin muunnoksella (eng. transform) on vastaava asema diskreettiaikaisten signaalien ja LTI järjestelmien analyysissä kuin Laplace muunnoksella jatkuvaaikaisten
Kertaus. x x x. K1. a) b) x 5 x 6 = x 5 6 = x 1 = 1 x, x 0. K2. a) a a a a, a > 0
 Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3
 51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
CC-ASTE. Kuva 1. Yksinkertainen CC-vahvistin, jossa virtavahvistus B + 1. Kuva 2. Yksinkertaisen CC-vahvistimen simulaatio
 CC-ASTE Yhteiskollektorivahvistin eli emitteriseuraaja on vahvistinkytkentä, jota käytetään jännitepuskurina. Sisääntulo on kannassa ja ulostulo emitterissä. Koska transistorin kannan ja emitterin välinen
CC-ASTE Yhteiskollektorivahvistin eli emitteriseuraaja on vahvistinkytkentä, jota käytetään jännitepuskurina. Sisääntulo on kannassa ja ulostulo emitterissä. Koska transistorin kannan ja emitterin välinen
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-1200 Signaalinkäsittelyn menetelmät, Tentti 30.1.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SG-1200 Signaalinkäsittelyn menetelmät, Tentti 30.1.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
Jos siis ohjausrajoitusta ei olisi, olisi ratkaisu triviaalisti x(s) = y(s). Hamiltonin funktio on. p(0) = p(s) = 0.
 Mat-.148 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 1 1. Olkoon maaston korkeus y(s) derivoituva funktio ja etsitään tien profiilia x(s). Päätösmuuttuja on tien jyrkkyys
Mat-.148 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 1 1. Olkoon maaston korkeus y(s) derivoituva funktio ja etsitään tien profiilia x(s). Päätösmuuttuja on tien jyrkkyys
ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen.
 ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen. X.X.2015 Tehtävä 1 Bipolaaritransistoria käytetään alla olevan kuvan mukaisessa kytkennässä, jossa V CC = 40 V ja kuormavastus
ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen. X.X.2015 Tehtävä 1 Bipolaaritransistoria käytetään alla olevan kuvan mukaisessa kytkennässä, jossa V CC = 40 V ja kuormavastus
FYSP105/2 VAIHTOVIRTAKOMPONENTIT. 1 Johdanto. 2 Teoreettista taustaa
 FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteita o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteita o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty c) sin 50 = sin ( ) = sin 130 = 0,77
 Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty.5.07 Kertaus K. a) sin 0 = 0,77 b) cos ( 0 ) = cos 0 = 0,6 c) sin 50 = sin (80 50 ) = sin 0 = 0,77 d) tan 0 = tan (0 80 ) = tan 0 =,9 e)
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty.5.07 Kertaus K. a) sin 0 = 0,77 b) cos ( 0 ) = cos 0 = 0,6 c) sin 50 = sin (80 50 ) = sin 0 = 0,77 d) tan 0 = tan (0 80 ) = tan 0 =,9 e)
2. kierros. 2. Lähipäivä
 2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
5 Rationaalifunktion kulku
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.06 5 Rationaalifunktion kulku. Funktion f määrittelyehto on. Muodostetaan symbolisen laskennan ohjelman avulla derivaattafunktio f ja
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.06 5 Rationaalifunktion kulku. Funktion f määrittelyehto on. Muodostetaan symbolisen laskennan ohjelman avulla derivaattafunktio f ja
4.1 Kaksi pistettä määrää suoran
 4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
1 Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
Ensimmäisen asteen polynomifunktio ENNAKKOTEHTÄVÄT. a) f(x) = x 4 b) Nollakohdassa funktio f saa arvon nolla eli kuvaaja kohtaa x-akselin. Kuvaajan perusteella funktion nollakohta on x,. c) Funktion f
1 db Compression point
 Spektrianalysaattori mittaukset 1. Työn tarkoitus Työssä tutustutaan vahvistimen ja mixerin perusmittauksiin ja spektrianalysaattorin toimintaan. 2. Teoriaa RF- vahvistimen ominaisuudet ja käyttäytyminen
Spektrianalysaattori mittaukset 1. Työn tarkoitus Työssä tutustutaan vahvistimen ja mixerin perusmittauksiin ja spektrianalysaattorin toimintaan. 2. Teoriaa RF- vahvistimen ominaisuudet ja käyttäytyminen
TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio. Mat Systeemien Identifiointi. 4. harjoitus
 TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Mat-2.4129 Systeemien Identifiointi 4. harjoitus 1. a) Laske valkoisen kohinan spektraalitiheys. b) Tarkastellaan ARMA-prosessia C(q 1 )y = D(q 1 )e,
TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Mat-2.4129 Systeemien Identifiointi 4. harjoitus 1. a) Laske valkoisen kohinan spektraalitiheys. b) Tarkastellaan ARMA-prosessia C(q 1 )y = D(q 1 )e,
6. Differentiaaliyhtälösysteemien laadullista teoriaa.
 1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
määrittelyjoukko. 8 piirretään tangentti pisteeseen, jossa käyrä leikkaa y-akselin. Määritä tangentin yhtälö.
 MAA8 Juuri- ja logaritmifunktiot 5.4.0 Jussi Tyni. a) Derivoi f ( ) 3e 5 Mikä on funktion f () = ln(5 ) 00 määrittelyjoukko. c) Derivoi g( t) 4ln( t t ). Käyrälle g( ) e 8 piirretään tangentti pisteeseen,
MAA8 Juuri- ja logaritmifunktiot 5.4.0 Jussi Tyni. a) Derivoi f ( ) 3e 5 Mikä on funktion f () = ln(5 ) 00 määrittelyjoukko. c) Derivoi g( t) 4ln( t t ). Käyrälle g( ) e 8 piirretään tangentti pisteeseen,
Y (s) = G(s)(W (s) W 0 (s)). Tarkastellaan nyt tilannetta v(t) = 0, kun t < 3 ja v(t) = 1, kun t > 3. u(t) = K p y(t) K I
 Aalto-yliopiston Perustieteiden korkeakoulu Matematiikan systeemianalyysin laitos Mat-2.429 Systeemien Identifiointi 6. harjoituksen ratkaisut. Laplace-tasossa saadaan annetulle venttiilille W (s) W (s)
Aalto-yliopiston Perustieteiden korkeakoulu Matematiikan systeemianalyysin laitos Mat-2.429 Systeemien Identifiointi 6. harjoituksen ratkaisut. Laplace-tasossa saadaan annetulle venttiilille W (s) W (s)
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
Boost-hakkuri. Hakkurin tilaesitykset
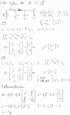 Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Differentiaalilaskenta 1.
 Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
Tekijä Pitkä matematiikka
 Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-00 Signaalinkäsittelyn menetelmät, Tentti 6.3.006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja
SG-00 Signaalinkäsittelyn menetelmät, Tentti 6.3.006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja
x = π 3 + nπ, x + 1 f (x) = 2x (x + 1) x2 1 (x + 1) 2 = 2x2 + 2x x 2 = x2 + 2x f ( 3) = ( 3)2 + 2 ( 3) ( 3) + 1 3 1 + 4 2 + 5 2 = 21 21 = 21 tosi
 Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
SMG-2100: SÄHKÖTEKNIIKKA
 Vaihtosähkö SMG-2100: SÄHKÖTEKNIIKKA Sinimuotoiset suureet Tehollisarvo Sinimuotoinen vaihtosähkö & passiiviset piirikomponentit Käydään läpi, mistä sinimuotoiset jännite ja virta ovat peräisin. Näytetään,
Vaihtosähkö SMG-2100: SÄHKÖTEKNIIKKA Sinimuotoiset suureet Tehollisarvo Sinimuotoinen vaihtosähkö & passiiviset piirikomponentit Käydään läpi, mistä sinimuotoiset jännite ja virta ovat peräisin. Näytetään,
