PID-sa a timen viritta minen Matlabilla ja simulinkilla
|
|
|
- Marja-Leena Majanlahti
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 PID-sa a timen viritta minen Matlabilla ja simulinkilla Kriittisen värähtelyn menetelmä Tehtiin kuvan 1 mukainen tasavirtamoottorin piiri PID-säätimellä. Virittämistä varten PID-säätimen ja asetettiin nollaksi ja alettiin nostaa arvoa, kunnes askelvaste oli sellainen, että se asettui värähtelemään vakioamplitudilla, eikä vaimentunut tai kasvanut ajan kuluessa. Kuva 1: DC-moottorin malli ja PID-säädin Huomattiin, että :n arvolla 96,66 (kuva 2) askelvaste oskilloi varsin tasaisella amplitudilla, kun taas arvolla 90 (kuva 3) askelvasteen värähtely vaimeni vielä selvästi. Arvon kasvattaminen 100:n (kuva 4) ei puolestaan aiheuttanut silmin nähtävää merkittävää muutosta. Huomattiin myös, että :n arvoa saattoi kasvattaa useilla dekadeilla, jolloin askelvaste pysyi toki stabiilina, mutta värähtelyn amplitudi kasvoi jonkin verran.
2 Kuva 2: vahvistus 96,66, värähtelee tasaisesti Kuva 3: vahvistus 90,värähtely vaimenee
3 Kuva 4:vahvistus 100, värähtelee edelleen tasaisesti Kuva 5: Värähtelyn jaksonajan määrittäminen Lopulliseksi arvoksi saatiin siis 96,66. Määritettiin vielä värähtelyn jaksonaika kuvan 5 osoittamalla tavalla. Kriittisen vahvistuksen ja jaksonajan perusteella voitiin laskea PID-säätimelle arvot, ja kuvan 6 taulukon mukaisesti.
4 Säädintyyppi P 4, PI 43,96 175,75 - PID 57,97 386,64 2,17 Pessen Integral Rule 67,66 563,85 3,04 vähän ylitystä 31,90 106,33 3,19 ei ylitystä 19,33 128,88 1,93 Kuva 6: kriittisen värähtelyn menetelmällä saadut säätimen arvot Kuvassa 7 on simuloitu säädettyä piiriä neljän jälkimmäisen kriteerin mukaan. Tämän kuvan 2 taulukon mukaisilla arvoilla simuloituna PI-säädin osoittautuikin epästabiiliksi ja on siksi jätetty pois tästä kuvasta. P- säätimen kuvaaja ei poikkea juurikaan. Kuva 7: Kriittisen värähtelyn menetelmällä, eri kriteerein valittuja säätimen arvoja Askelvastemenetelmä Tässä menetelmässä otettiin suljetusta piiristä, ilman säädintä yksikkövaste, jonka nousun jyrkimpään kohtaan piirrettiin tangentti ja katsottiin pisteet, joissa tangentti leikkaa aika-akselin ja amplitudiakselin (kuva 8). Leikkauspisteiden perusteella määriteltiin parametrit ja, joiden perusteella puolestaan voitiin määrittää PID-säätimen parametreille arvot kuvan 9 taulukon mukaisesti.
5 Kuva 8: suljetun piirin askelvaste ja arvojen määrittäminen Säädin P 1 = 0, PI 0,9 = 0,15 0,9 3 = 0,042 - PID 1,2 = 0,2 1,2 3 = 0,056 Kuva 9: Arvoja eri säätimille Simuloimalla taulukon arvoilla saatiin kuvan 10 mukaisia tuloksia. 1,2 2 = 0,12
6 Kuva 10: Askelvastemenetelmällä viritettyjä säädettyjä piirejä Peukalosäännöt Peukalosääntöjen avulla voidaan virittää askelvastemenetelmällä tai kriittisen värähtelyn menetelmällä viritettyä säädintä edelleen. Askelvastemenetelmällä virittämämme PID-säädin on varsin hidas, joten sitä voidaan nopeuttaa kasvattamalla D-termiä, kuten kuvasta 11 näkyy. Kuva 11: D-termin kasvattaminen
7 Huomataan, että vaikka nopeutta lisätään D-termiä kasvattamalla, vaste jää alkusekunneilla hyvin vaisuksi. Korjataan tätä ilmiötä nostamalla P-termin arvoa kuvan 12 tavalla. Kuva 12: P-termin kasvattaminen Nähdään, että vaste alkaa olla melko hyvä. Ylitystä vasteessa ei esiinny lainkaan ja päästään suhteellisen lähelle loppuarvoa melko nopeasti, joskin pientä aaltoilua on nähtävissä. Vähennetään värähtelyä vielä kasvattamalla I-termiä kuvan 13 tavalla. Huomataan, että vaste parani entisestään. Kuva 13: I-termin kasvattaminen
8 Menetelmien välinen vertailu Simuloitiin lopuksi kaikilla kolmella menetelmällä viritettyjä tavallisia PID-säätimiä sekä ilman häiriöitä (kuva 14), että häiriöiden kanssa (kuvat 15 ja 16), ja vertailtiin tuloksia. Kuva 14: Eri tavoin viritetyt säätimet Kuva 15: Eri tavoin viritetyt säätimet ja kohtuullisesti häiriötä
9 Kuva 16: Eri tavoin viritetyt säätimet ja paljon häiriötä Loppuyhteenveto Tuloksia tarkasteltaessa on syytä huomioida, että tässä simuloinnissa on käytetty askelherätteelle amplitudia 12, lähinnä kuvastamaan tilannetta, että käytetään 12 voltin tasajännitemoottoria yhden voltin moottorin sijaan ja siten haettu lähempää kosketusta reaalimaailmaan. Huomataan ainakin, että näillä tavoin viritetyt säätimet vaikuttavat moottorin käyttäytymiseen selkeästi eri tavoin. Kriittisen värähtely menetelmällä onkin tarkoitus saada aikaan säädin, joka olisi nopea, mutta kestäisi samalla hyvin myös häiriöitä. Huomaamme, että kriittisen värähtelyn menetelmällä viritetty säädin on nopeampi ja kestää häiriöitä aavistuksen paremmin kuin askelvastemenetelmällä viritetty säädin. Huomaamme myös, että askelvastemenetelmällä viritetty säädin on huomattavan paljon hitaampi, mutta toisaalta se ei aiheuta ollenkaan ylitystä, kun kriittisen värähtelyn menetelmällä viritetty säädin tuottaa melkoisen ylityksen. Suurista eroista johtuen voisi olettaa, että vastaan tullee tilanteita, joissa tarvitaan säädintä, joka toiminta on näiden kahden välistä. Sellaisen säätimen loimme peukalosäännöillä, joskin se on jokseenkin epätieteellistä ja vaatii useita simulointeja saavuttaa haluttu lopputulos. Lienee myös aiheellista pohtia, että onko jossakin kohtaa työtä tehty jokin virhe. Arveluksia ainakin aiheuttaa se, että kuvan 5 taulukon mukaisilla arvoilla PI-säädin tuottaa äärimmäisen epävakaan säädön, mutta senkin saa asettumaan kasvattamalla D-termiä hieman. Tietolähteitä säätimien virittämiseen löytyy Internetistä kohtalaisesti, mutta valitettavasti samaa virittämistapaa koskevissa tiedoissa löytyy jonkin verran eroja, mikä saattaa tuottaa virheitä tai ainakin vähemmän hyviä säädinten virityksiä. On toki syytä ymmärtää, että virheellinen viritystapakin saattaa tuottaa haluttuun tilanteeseen varsin optimaalisen säätimen. Siksi näitä viritystapoja on syytä pitää suuntaa antavina ja tapauskohtaisesti aina tarkistaa täyttääkö näillä tavoin viritetty säädin vaaditut kriteerit.
Hyvyyskriteerit. ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
Hyvyyskriteerit ELEC-C1230 Säätötekniikka Aikaisemmilla luennoilla on havainnollistettu, miten systeemien käyttäytymiseen voi vaikuttaa säätämällä niitä. Epästabiileista systeemeistä saadaan stabiileja,
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Systeemitekniikan laboratorio Jan 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Systeemitekniikan laboratorio Jan 2019
Boost-hakkuri. Hakkurin tilaesitykset
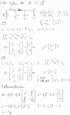 Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
1 PID-taajuusvastesuunnittelun esimerkki
 Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. = K K K M. s 2 3s 2 KK P
 Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Agenda. Johdanto Säätäjiä. Mittaaminen. P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen
 8. Luento: Laitteiston ohjaaminen Arto Salminen, [email protected] Agenda Johdanto Säätäjiä P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen Mittaaminen Johdanto Tavoitteena: tunnistaa
8. Luento: Laitteiston ohjaaminen Arto Salminen, [email protected] Agenda Johdanto Säätäjiä P-, I-,D-, PI-, PD-, ja PID-säätäjä Säätäjän valinta ja virittäminen Mittaaminen Johdanto Tavoitteena: tunnistaa
ELEC-C1230 Säätötekniikka. Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit
 ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
ELEC-C3 Säätötekniikka Luku 8: Säädetyn järjestelmän hyvyys aika- ja taajuustasossa, suunnittelu taajuustasossa, kompensaattorit Hyvyyskriteerit Aikaisemmilla luennoilla on havainnollistettu, miten systeemien
3. kierros. 2. Lähipäivä
 3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
Osatentti
 Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
Osatentti 3 1.4.016 Nimi: Opiskelijanumero: Ohjeet: Kirjoita vastaukset paperissa annettuun tilaan. Lisävastaustilaa on paperin lopussa. Käytä selvää käsialaa. Laskin EI ole sallittu. Tenttikaavasto jaetaan.
Tehtävä 1. Vaihtoehtotehtävät.
 Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
Kem-9.47 Prosessiautomaation perusteet Tentti.4. Tehtävä. Vaihtoehtotehtävät. Oikea vastaus +,5p, väärä vastaus -,5p ja ei vastausta p Maksimi +5,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA
Hakkuritehola hteet Janne Askola Jari-Matti Hannula Jonas Nordfors Joni Kurvinen Semu Mäkinen
 Hakkuritehola hteet 4.5.2012 Janne Askola Jari-Matti Hannula Jonas Nordfors Joni Kurvinen Semu Mäkinen Fysikaalinen toiminta Buck-Boost -hakkuriteholähde on DC/DC -muunnin. Se on yhdistelmä Buck- ja Boost
Hakkuritehola hteet 4.5.2012 Janne Askola Jari-Matti Hannula Jonas Nordfors Joni Kurvinen Semu Mäkinen Fysikaalinen toiminta Buck-Boost -hakkuriteholähde on DC/DC -muunnin. Se on yhdistelmä Buck- ja Boost
LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi. Servokäyttö (0,9 op)
 LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi Servokäyttö (0,9 op) JOHDNTO Työssä tarkastellaan kestomagnetoitua tasavirtamoottoria. oneelle viritetään PI-säätäjä
LTY/SÄTE Säätötekniikan laboratorio Sa2730600 Säätötekniikan ja signaalinkäsittelyn työkurssi Servokäyttö (0,9 op) JOHDNTO Työssä tarkastellaan kestomagnetoitua tasavirtamoottoria. oneelle viritetään PI-säätäjä
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
H(s) + + _. Ymit(s) Laplace-tason esitykseksi on saatu (katso jälleen kalvot):
 ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
Aikatason vaste vs. siirtofunktio Tehtävä
 Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
Aikatason vaste vs. siirtofunktio Tehtävä Millainen toisen kertaluvun siirtofunktio vastaa systeemiä jonka ylitys on 10% ja asettumisaika 4 min? Y s X s = 2 n s 2 2 2 n s n M p =e t r 1.8 n t s 4.6 n 1
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät helmikuu
Voimalaitoksen lisästabiloinnin virittämisohje. Voimalaitospäivä Scandic Park Antti Harjula
 Voimalaitoksen lisästabiloinnin virittämisohje Voimalaitospäivä Scandic Park 24.2.2016 Antti Harjula Sisältö Pohjoismainen voimajärjestelmä ja lisästabiloinnit VJV 2013, vaatimukset lisästabiloinnille
Voimalaitoksen lisästabiloinnin virittämisohje Voimalaitospäivä Scandic Park 24.2.2016 Antti Harjula Sisältö Pohjoismainen voimajärjestelmä ja lisästabiloinnit VJV 2013, vaatimukset lisästabiloinnille
Kon Hydraulijärjestelmät
 Kon-41.4040 Hydraulijärjestelmät Laboratorioharjoitus 2: Sähköhydraulisen järjestelmän säätö Jyri Juhala Jyrki Kajaste (Heikki Kauranne) Hydraulijärjestelmän venttiilin ohjausmenetelmät Ohjaus Kompensointi
Kon-41.4040 Hydraulijärjestelmät Laboratorioharjoitus 2: Sähköhydraulisen järjestelmän säätö Jyri Juhala Jyrki Kajaste (Heikki Kauranne) Hydraulijärjestelmän venttiilin ohjausmenetelmät Ohjaus Kompensointi
Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C (s+1)(s+0.02) 50s+1
 ENSO IKONEN PYOSYS Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C. 1 P(s) = -----------------(s+1)(s+0.02) C(s) = 50s+1 --------50s Piirrä vasteet asetusarvosta. Kommentoi
ENSO IKONEN PYOSYS Harjoitus (15min) Prosessia P säädetään yksikkötakaisinkytkennässä säätimellä C. 1 P(s) = -----------------(s+1)(s+0.02) C(s) = 50s+1 --------50s Piirrä vasteet asetusarvosta. Kommentoi
MATLAB harjoituksia RST-säädöstä (5h)
 Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Osatentti
 Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
Osatentti 2.8.205 Nimi: Opiskelijanumero: Ohjeet: Vastaa kysymyspaperiin ja kysymyksille varattuun tilaan. Laskin ei ole sallittu. Tenttikaavasto jaetaan. Kaavastoon EI merkintöjä. Palauta kaavasto tämän
SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS),
 SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS), 5.2.2019 Tentin arvosteluperusteita: o Kurssin alku on osin kertausta SäAn ja prosessidynamiikkakursseista, jotka oletetaan
SaSun VK1-tenttikysymyksiä 2019 Enso Ikonen, Älykkäät koneet ja järjestelmät (IMS), 5.2.2019 Tentin arvosteluperusteita: o Kurssin alku on osin kertausta SäAn ja prosessidynamiikkakursseista, jotka oletetaan
RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007
 RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007 Automaatiotekniikka Lähtöarvot: Säiliö T1: A = 500 x 600 mm, h = 500 mm Säiliö T2: Ø = 240 mm, h = 1000
RAPORTTI Eemil Tamminen Markus Virtanen Pasi Vähämartti Säätötekniikan harjoitustyö Joulukuu 2007 Automaatiotekniikka Lähtöarvot: Säiliö T1: A = 500 x 600 mm, h = 500 mm Säiliö T2: Ø = 240 mm, h = 1000
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät, Systeemitekniikka
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Teknillinen tiedekunta Älykkäät koneet ja järjestelmät, Systeemitekniikka
SMITH-PREDICTOR Kompensaattori PI-Säätimellä. Funktiolohko Siemens PLC. SoftControl Oy
 SMITH-PREDICTOR Kompensaattori PI-Säätimellä Funktiolohko Siemens PLC SoftControl Oy 1.0 Smith Predictor kompensaattori PI-säätimellä... 3 1.1 Yleistä...3 1.2 Sovellus...3 1.3 Kuvaus...4 1.4 Muuttujat...5
SMITH-PREDICTOR Kompensaattori PI-Säätimellä Funktiolohko Siemens PLC SoftControl Oy 1.0 Smith Predictor kompensaattori PI-säätimellä... 3 1.1 Yleistä...3 1.2 Sovellus...3 1.3 Kuvaus...4 1.4 Muuttujat...5
3. kierros. 1. Lähipäivä
 3. kierros 1. Lähipäivä Viikon aihe (viikko 1/2) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros 1. Lähipäivä Viikon aihe (viikko 1/2) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Säätötekniikkaa. Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla
 Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu. Vinkit 1 a
 ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / Systeemitekniikka Jan 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / Systeemitekniikka Jan 2019
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
20 Kollektorivirta kun V 1 = 15V 10. 21 Transistorin virtavahvistus 10. 22 Transistorin ominaiskayrasto 10. 23 Toimintasuora ja -piste 10
 Sisältö 1 Johda kytkennälle Theveninin ekvivalentti 2 2 Simuloinnin ja laskennan vertailu 4 3 V CE ja V BE simulointituloksista 4 4 DC Sweep kuva 4 5 R 2 arvon etsintä 5 6 Simuloitu V C arvo 5 7 Toimintapiste
Sisältö 1 Johda kytkennälle Theveninin ekvivalentti 2 2 Simuloinnin ja laskennan vertailu 4 3 V CE ja V BE simulointituloksista 4 4 DC Sweep kuva 4 5 R 2 arvon etsintä 5 6 Simuloitu V C arvo 5 7 Toimintapiste
Säätötekniikan matematiikan verkkokurssi, Matlab tehtäviä ja vastauksia 29.7.2002
 Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
Laboratorioraportti 3
 KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä
 Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: [email protected] Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: [email protected] Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank
 MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank Sonja Lindman Kandidaatintyö 10.4.2014 LUT Energia Sähkötekniikan koulutusohjelma TIIVISTELMÄ Lappeenrannan teknillinen yliopisto Teknillinen
MASSASÄILIÖN SIMULOINTI JA SÄÄTÖ Simulation and control of pulp tank Sonja Lindman Kandidaatintyö 10.4.2014 LUT Energia Sähkötekniikan koulutusohjelma TIIVISTELMÄ Lappeenrannan teknillinen yliopisto Teknillinen
Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
Säätötekniikkaa. Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla
 Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
Säätötekniikkaa Säätöongelma: Hae (mahdollisesti ulostulon avulla) ohjaus, joka saa systeemin toimimaan halutulla tavalla servo-ongelma: ulostulon seurattava referenssisignaalia mahdollisimman tarkasti,
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
S-114.3812 Laskennallinen Neurotiede
 S-114.381 Laskennallinen Neurotiede Projektityö 30.1.007 Heikki Hyyti 60451P Tehtävä 1: Virityskäyrästön laskeminen Luokitellaan neuroni ensin sen mukaan, miten se vastaa sinimuotoisiin syötteisiin. Syöte
S-114.381 Laskennallinen Neurotiede Projektityö 30.1.007 Heikki Hyyti 60451P Tehtävä 1: Virityskäyrästön laskeminen Luokitellaan neuroni ensin sen mukaan, miten se vastaa sinimuotoisiin syötteisiin. Syöte
Ratkaise tehtävä 1 ilman teknisiä apuvälineitä! 1. a) Yhdistä oikea funktio oikeaan kuvaajaan. (2p)
 Matematiikan TESTI 3, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/07 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
Matematiikan TESTI 3, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/07 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Harjoitus 6: Simulink - Säätöteoria. Syksy 2006. Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1
 Harjoitus 6: Simulink - Säätöteoria Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen säätötekniikkaan Takaisinkytkennän
Harjoitus 6: Simulink - Säätöteoria Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen säätötekniikkaan Takaisinkytkennän
Lämpötilan säätö. S Elektroniset mittaukset Mikko Puranen Luennon sisältö
 Lämpötilan säätö S-108.2010 Elektroniset mittaukset Mikko Puranen 20.2.2006 Luennon sisältö 1. Termodynaaminen malli 2. Jäähdytyksen suunnittelu 3. Peltier-elementit 4. Lämpötilasäätäjät PID-säädin Termodynaaminen
Lämpötilan säätö S-108.2010 Elektroniset mittaukset Mikko Puranen 20.2.2006 Luennon sisältö 1. Termodynaaminen malli 2. Jäähdytyksen suunnittelu 3. Peltier-elementit 4. Lämpötilasäätäjät PID-säädin Termodynaaminen
8. kierros. 2. Lähipäivä
 8. kierros 2. Lähipäivä Viikon aihe Tilaestimointi Tilasäätö Saavutettavuus, ohjattavuus Tarkkailtavuus, havaittavuus Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 tuntia Tavoitteet: tietää Saavutettavuus
8. kierros 2. Lähipäivä Viikon aihe Tilaestimointi Tilasäätö Saavutettavuus, ohjattavuus Tarkkailtavuus, havaittavuus Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 tuntia Tavoitteet: tietää Saavutettavuus
Moottorin säätö. Miikka Ihonen 67367P Sampo Salo 79543L Kalle Spoof 83912K John Boström 83962B Venla Viitanen 84514C
 Moottorin säätö Miikka Ihonen 67367P Sampo Salo 79543L Kalle Spoof 83912K John Boström 83962B Venla Viitanen 84514C Tehtävän määrittely Tehtävän aiheena on moottorin tyhjäkäynnin säätö. Tehtävässä tulee
Moottorin säätö Miikka Ihonen 67367P Sampo Salo 79543L Kalle Spoof 83912K John Boström 83962B Venla Viitanen 84514C Tehtävän määrittely Tehtävän aiheena on moottorin tyhjäkäynnin säätö. Tehtävässä tulee
Sulateliimaprosessin säätöpiirien tutkiminen, virittäminen
 Sulateliimaprosessin säätöpiirien tutkiminen, virittäminen ja ohjeistaminen Matti Puttonen Opinnäytetyö syyskuu 2016 Kone- ja tuotantotekniikka Kone- ja laiteautomaatio TIIVISTELMÄ Tampereen ammattikorkeakoulu
Sulateliimaprosessin säätöpiirien tutkiminen, virittäminen ja ohjeistaminen Matti Puttonen Opinnäytetyö syyskuu 2016 Kone- ja tuotantotekniikka Kone- ja laiteautomaatio TIIVISTELMÄ Tampereen ammattikorkeakoulu
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Vanhoja koetehtäviä. Analyyttinen geometria 2016
 Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 . Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
. Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
3 Raja-arvo ja jatkuvuus
 3 Raja-arvo ja jatkuvuus 3. Raja-arvon käsite Raja-arvo kuvaa funktion kättätmistä jonkin lähtöarvon läheisdessä. Raja-arvoa tarvitaan toisinaan siksi, että funktion arvoa ei voida laskea kseisellä lähtöarvolla
3 Raja-arvo ja jatkuvuus 3. Raja-arvon käsite Raja-arvo kuvaa funktion kättätmistä jonkin lähtöarvon läheisdessä. Raja-arvoa tarvitaan toisinaan siksi, että funktion arvoa ei voida laskea kseisellä lähtöarvolla
3.1 Väliarvolause. Funktion kasvaminen ja väheneminen
 Väliarvolause Funktion kasvaminen ja väheneminen LAUSE VÄLIARVOLAUSE Oletus: Funktio f on jatkuva suljetulla välillä I: a < x < b f on derivoituva välillä a < x < b Väite: On olemassa ainakin yksi välille
Väliarvolause Funktion kasvaminen ja väheneminen LAUSE VÄLIARVOLAUSE Oletus: Funktio f on jatkuva suljetulla välillä I: a < x < b f on derivoituva välillä a < x < b Väite: On olemassa ainakin yksi välille
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
1. a. Ratkaise yhtälö 8 x 5 4 x + 2 x+2 = 0 b. Määrää joku toisen asteen epäyhtälö, jonka ratkaisu on 2 x 1.
 ABIKertaus.. a. Ratkaise yhtälö 8 5 4 + + 0 b. Määrää joku toisen asteen epäyhtälö, jonka ratkaisu on. 4. Jaa polynomi 8 0 5 ensimmäisen asteen tekijöihin ja ratkaise tämän avulla 4 epäyhtälö 8 0 5 0.
ABIKertaus.. a. Ratkaise yhtälö 8 5 4 + + 0 b. Määrää joku toisen asteen epäyhtälö, jonka ratkaisu on. 4. Jaa polynomi 8 0 5 ensimmäisen asteen tekijöihin ja ratkaise tämän avulla 4 epäyhtälö 8 0 5 0.
Integrointialgoritmit molekyylidynamiikassa
 Integrointialgoritmit molekyylidynamiikassa Markus Ovaska 28.11.2008 Esitelmän kulku MD-simulaatiot yleisesti Integrointialgoritmit: mitä integroidaan ja miten? Esimerkkejä eri algoritmeista Hyvän algoritmin
Integrointialgoritmit molekyylidynamiikassa Markus Ovaska 28.11.2008 Esitelmän kulku MD-simulaatiot yleisesti Integrointialgoritmit: mitä integroidaan ja miten? Esimerkkejä eri algoritmeista Hyvän algoritmin
PIIRIANALYYSI. Harjoitustyö nro 7. Kipinänsammutuspiirien mitoitus. Mika Lemström
 PIIRIANAYYSI Harjoitustyö nro 7 Kipinänsammutuspiirien mitoitus Mika emström Sisältö 1 Johdanto 3 2 RC-suojauspiiri 4 3 Diodi suojauspiiri 5 4 Johtopäätos 6 sivu 2 [6] Piirianalyysi Kipinänsammutuspiirien
PIIRIANAYYSI Harjoitustyö nro 7 Kipinänsammutuspiirien mitoitus Mika emström Sisältö 1 Johdanto 3 2 RC-suojauspiiri 4 3 Diodi suojauspiiri 5 4 Johtopäätos 6 sivu 2 [6] Piirianalyysi Kipinänsammutuspiirien
TASA- JA VAIHTOVIRTAPIIRIEN LABORAATIOTYÖ 5 SUODATINPIIRIT
 TASA- JA VAIHTOVIRTAPIIRIEN LABORAATIOTYÖ 5 SUODATINPIIRIT Työselostuksen laatija: Tommi Tauriainen Luokka: TTE7SN1 Ohjaaja: Jaakko Kaski Työn tekopvm: 02.12.2008 Selostuksen luovutuspvm: 16.12.2008 Tekniikan
TASA- JA VAIHTOVIRTAPIIRIEN LABORAATIOTYÖ 5 SUODATINPIIRIT Työselostuksen laatija: Tommi Tauriainen Luokka: TTE7SN1 Ohjaaja: Jaakko Kaski Työn tekopvm: 02.12.2008 Selostuksen luovutuspvm: 16.12.2008 Tekniikan
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
Harjoitus 7: Dynaamisten systeemien säätö (Simulink)
 Harjoitus 7: Dynaamisten systeemien säätö (Simulink) MS-C2107 Sovelletun matematiikan tietokonetyöt MS-C2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Dynaamisten (=ajassakehittyvien)
Harjoitus 7: Dynaamisten systeemien säätö (Simulink) MS-C2107 Sovelletun matematiikan tietokonetyöt MS-C2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Dynaamisten (=ajassakehittyvien)
Tehtävä 8. Jännitelähteenä käytetään yksipuolista 12 voltin tasajännitelähdettä.
 Tehtävä 8 1. Suunnittele Micro-Cap-simulaatio-ohjelman avulla kaistanpäästösuodin, jonka -alarajataajuus f A = 100 Hz @-3 db -ylärajataajuus f Y = 20 khz @-3 db -jännitevahvistus A U = 2 Jännitelähteenä
Tehtävä 8 1. Suunnittele Micro-Cap-simulaatio-ohjelman avulla kaistanpäästösuodin, jonka -alarajataajuus f A = 100 Hz @-3 db -ylärajataajuus f Y = 20 khz @-3 db -jännitevahvistus A U = 2 Jännitelähteenä
Osoitin ja viittaus C++:ssa
 Osoitin ja viittaus C++:ssa Osoitin yksinkertaiseen tietotyyppiin Osoitin on muuttuja, joka sisältää jonkin toisen samantyyppisen muuttujan osoitteen. Ohessa on esimerkkiohjelma, jossa määritellään kokonaislukumuuttuja
Osoitin ja viittaus C++:ssa Osoitin yksinkertaiseen tietotyyppiin Osoitin on muuttuja, joka sisältää jonkin toisen samantyyppisen muuttujan osoitteen. Ohessa on esimerkkiohjelma, jossa määritellään kokonaislukumuuttuja
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
Tehtävä 1. Vaihtoehtotehtävät.
 Kem-9.7 Proeiautomaation peruteet Perutehtävät Tentti 9.. Tehtävä. Vaihtoehtotehtävät. Oikea vatau,p, väärä vatau -,p ja ei vatauta p Makimi,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN
Kem-9.7 Proeiautomaation peruteet Perutehtävät Tentti 9.. Tehtävä. Vaihtoehtotehtävät. Oikea vatau,p, väärä vatau -,p ja ei vatauta p Makimi,p ja minimi p TÄMÄ PAPERI TÄYTYY EHDOTTOMASTI PALAUTTAA TENTIN
4. kierros. 1. Lähipäivä
 4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
KESTOMAGNEETTI VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Jani Vitikka p87434 Hannu Tiitinen p87432. Dynaaminen kenttäteoria SATE2010
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jani Vitikka p87434 Hannu Tiitinen p87432 Dynaaminen kenttäteoria SATE2010 KESTOMAGNEETTI Sivumäärä: 10 Jätetty tarkastettavaksi: 16.1.2008 Työn tarkastaja
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jani Vitikka p87434 Hannu Tiitinen p87432 Dynaaminen kenttäteoria SATE2010 KESTOMAGNEETTI Sivumäärä: 10 Jätetty tarkastettavaksi: 16.1.2008 Työn tarkastaja
8. kierros. 1. Lähipäivä
 8. kierros 1. Lähipäivä Viikon aihe Tilaestimointi Tilasäätö Saavutettavuus, ohjattavuus Tarkkailtavuus, havaittavuus Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 tuntia Tavoitteet: tietää Saavutettavuus
8. kierros 1. Lähipäivä Viikon aihe Tilaestimointi Tilasäätö Saavutettavuus, ohjattavuus Tarkkailtavuus, havaittavuus Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 tuntia Tavoitteet: tietää Saavutettavuus
Elektroniikka, kierros 3
 Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Asennusohje Viritettävä terrestiaalipäävahvistin HMB 6. SSTL n:o 75 631 26 ULA-VHF I, VHF III, 6 x UHF ja AUX
 Asennusohje Viritettävä terrestiaalipäävahvistin SSTL n:o 75 631 26 ULA-VHF I, VHF III, 6 x UHF ja AUX I. Käyttötarkoitus Päävahvistin on valmistettu kansainvälisten laatustandardien mukaisesti ja se täyttää
Asennusohje Viritettävä terrestiaalipäävahvistin SSTL n:o 75 631 26 ULA-VHF I, VHF III, 6 x UHF ja AUX I. Käyttötarkoitus Päävahvistin on valmistettu kansainvälisten laatustandardien mukaisesti ja se täyttää
VLT 6000 HVAC vakiopaineen säädössä ja paine-erosäädössä. (MBS 3000, 0-10V)
 VLT 6000 HVAC vakiopaineen säädössä ja paine-erosäädössä. (MBS 3000, 0-10V) 1 VLT 6000 HVAC Sovellusesimerkki 1 - Vakiopaineen säätö vedenjakelujärjestelmässä Vesilaitoksen vedenkysyntä vaihtelee runsaasti
VLT 6000 HVAC vakiopaineen säädössä ja paine-erosäädössä. (MBS 3000, 0-10V) 1 VLT 6000 HVAC Sovellusesimerkki 1 - Vakiopaineen säätö vedenjakelujärjestelmässä Vesilaitoksen vedenkysyntä vaihtelee runsaasti
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Matematiikan tukikurssi: kurssikerta 10
 Matematiikan tukikurssi: kurssikerta 10 1 Newtonin menetelmä Oletetaan, että haluamme löytää funktion f(x) nollakohan. Usein tämä tehtävä on mahoton suorittaa täyellisellä tarkkuuella, koska tiettyjen
Matematiikan tukikurssi: kurssikerta 10 1 Newtonin menetelmä Oletetaan, että haluamme löytää funktion f(x) nollakohan. Usein tämä tehtävä on mahoton suorittaa täyellisellä tarkkuuella, koska tiettyjen
1 Asentaminen. 2 Yleistä ja simuloinnin aloitus 12/2006 1.1.1
 1 Asentaminen...2 2 Yleistä ja simuloinnin aloitus...2 2.1 PI-säätimet...3 2.2 Trendit...4 3 Lämpölaitoksen ohjaus...5 4 Voimalan alkuarvojen muuttaminen...6 5 Tulostus...8 6 Mahdollisia ongelmia...8 6.1
1 Asentaminen...2 2 Yleistä ja simuloinnin aloitus...2 2.1 PI-säätimet...3 2.2 Trendit...4 3 Lämpölaitoksen ohjaus...5 4 Voimalan alkuarvojen muuttaminen...6 5 Tulostus...8 6 Mahdollisia ongelmia...8 6.1
Matematiikan tukikurssi, kurssikerta 1
 Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
jakokulmassa x 4 x 8 x 3x
 Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Mat Systeemien identifiointi, aihepiirit 1/4
 , aihepiirit 1/4 Dynaamisten systeemien matemaattinen mallintaminen ja analyysi Matlab (System Identification Toolbox), Simulink 1. Matemaattinen mallintaminen: Mallintamisen ja mallin määritelmät Fysikaalinen
, aihepiirit 1/4 Dynaamisten systeemien matemaattinen mallintaminen ja analyysi Matlab (System Identification Toolbox), Simulink 1. Matemaattinen mallintaminen: Mallintamisen ja mallin määritelmät Fysikaalinen
SMG-4500 Tuulivoima. Neljännen luennon aihepiirit. Tuulivoimalan rakenne. Tuuliturbiinin toiminta TUULIVOIMALAN RAKENNE
 SMG-4500 Tuulivoima Neljännen luennon aihepiirit Tuulivoimalan rakenne Tuuliturbiinin toiminta Turbiinin teho Nostovoima ja vastusvoima Suhteellinen tuuli Pintasuhde Turbiinin tehonsäätö 1 TUULIVOIMALAN
SMG-4500 Tuulivoima Neljännen luennon aihepiirit Tuulivoimalan rakenne Tuuliturbiinin toiminta Turbiinin teho Nostovoima ja vastusvoima Suhteellinen tuuli Pintasuhde Turbiinin tehonsäätö 1 TUULIVOIMALAN
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
TYÖ 2: OPERAATIOVAHVISTIMEN PERUSKYTKENTÖJÄ
 TYÖ 2: OPERAATIOVAHVISTIMEN PERUSKYTKENTÖJÄ Työselostus xxx yyy, ZZZZZsn 25.11.20nn Automaation elektroniikka OAMK Tekniikan yksikkö SISÄLLYS SISÄLLYS 2 1 JOHDANTO 3 2 LABORATORIOTYÖN TAUSTA JA VÄLINEET
TYÖ 2: OPERAATIOVAHVISTIMEN PERUSKYTKENTÖJÄ Työselostus xxx yyy, ZZZZZsn 25.11.20nn Automaation elektroniikka OAMK Tekniikan yksikkö SISÄLLYS SISÄLLYS 2 1 JOHDANTO 3 2 LABORATORIOTYÖN TAUSTA JA VÄLINEET
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) E a 2 ds
 Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia
 KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
Luento 8. Suodattimien käyttötarkoitus
 Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
Differentiaaliyhtälöt II, kevät 2017 Harjoitus 5
 Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Luentokalvot lämpötilasäätimistä Elektroniset mittaukset-kurssiin
 TEKNILLINEN KORKEAKOULU Sähkö- ja tietoliikennetekniikan osasto MIKES TKK Mittaustekniikka Luentokalvot lämpötilasäätimistä Elektroniset mittaukset-kurssiin 1.3.2006 DI Mikko Puranen Mittaustekniikan erikoistyö
TEKNILLINEN KORKEAKOULU Sähkö- ja tietoliikennetekniikan osasto MIKES TKK Mittaustekniikka Luentokalvot lämpötilasäätimistä Elektroniset mittaukset-kurssiin 1.3.2006 DI Mikko Puranen Mittaustekniikan erikoistyö
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
ELEC-C1230 Säätötekniikka
 Johdanto: Digitaalinen (diskreetti, diskreettiaikainen) säätöjärjestelmä ELEC-C1230 Säätötekniikka Luku 10: Digitaalinen säätö, perusteet, jatkuu A/D-muunnoksessa analoginen signaali näytteistetään (sampling);
Johdanto: Digitaalinen (diskreetti, diskreettiaikainen) säätöjärjestelmä ELEC-C1230 Säätötekniikka Luku 10: Digitaalinen säätö, perusteet, jatkuu A/D-muunnoksessa analoginen signaali näytteistetään (sampling);
RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2)
 SÄHKÖ- JA TIETOTEKNIIKAN OSASTO Radiotekniikka I RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2) Työn tekijät Katja Vitikka 1835627 Hyväksytty / 2009 Arvosana Vitikka K. (2009) Oulun yliopisto, sähkö- ja
SÄHKÖ- JA TIETOTEKNIIKAN OSASTO Radiotekniikka I RADIOTEKNIIKKA 1 HARJOITUSTYÖ S-2009 (VERSIO2) Työn tekijät Katja Vitikka 1835627 Hyväksytty / 2009 Arvosana Vitikka K. (2009) Oulun yliopisto, sähkö- ja
Experiment Finnish (Finland) Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä)
 Q2-1 Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä) Lue yleisohjeet erillisestä kuoresta ennen tämän tehtävän aloittamista. Johdanto Faasimuutokset ovat tuttuja
Q2-1 Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä) Lue yleisohjeet erillisestä kuoresta ennen tämän tehtävän aloittamista. Johdanto Faasimuutokset ovat tuttuja
Harjoitus 5 -- Ratkaisut
 Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio oskilloi äärettömän tiheään nollan lähellä. PlotPoints-asetus määrää, kuinka tiheästi Plot-funktio ottaa piirrettävästä funktiosta "näytteitä"
Harjoitus -- Ratkaisut 1 Ei kommenttia. Tutkittava funktio oskilloi äärettömän tiheään nollan lähellä. PlotPoints-asetus määrää, kuinka tiheästi Plot-funktio ottaa piirrettävästä funktiosta "näytteitä"
KONETEKNIIKAN KOULUTUSOHJELMA
 KONETEKNIIKAN KOULUTUSOHJELMA Elektromekaanisen täristimen taajuussäädön suunnittelu ja toteutus Santeri Kaisanlahti KANDIDAATINTYÖ 2015 Ohjaajat: Yrjö Louhisalmi, Konsta Karioja TIIVISTELMÄ Elektromekaanisen
KONETEKNIIKAN KOULUTUSOHJELMA Elektromekaanisen täristimen taajuussäädön suunnittelu ja toteutus Santeri Kaisanlahti KANDIDAATINTYÖ 2015 Ohjaajat: Yrjö Louhisalmi, Konsta Karioja TIIVISTELMÄ Elektromekaanisen
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
 Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
2. kierros. 2. Lähipäivä
 2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
b) Määritä/Laske (ei tarvitse tehdä määritelmän kautta). (2p)
 Matematiikan TESTI, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
Matematiikan TESTI, Maa7 Trigonometriset funktiot RATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT
Tilaesityksen hallinta ja tilasäätö. ELEC-C1230 Säätötekniikka. Luku 6: Tilasäätö, tilaestimointi, saavutettavuus ja tarkkailtavuus
 Tilaesityksen hallinta ja tilasäätö ELEC-C1230 Säätötekniikka Luku 6: Tilasäätö, tilaestimointi, saavutettavuus ja tarkkailtavuus Edellisessä luvussa tarkasteltiin napoja ja nollia sekä niiden vaikutuksia
Tilaesityksen hallinta ja tilasäätö ELEC-C1230 Säätötekniikka Luku 6: Tilasäätö, tilaestimointi, saavutettavuus ja tarkkailtavuus Edellisessä luvussa tarkasteltiin napoja ja nollia sekä niiden vaikutuksia
x 5 15 x 25 10x 40 11x x y 36 y sijoitus jompaankumpaan yhtälöön : b)
 MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
BM30A0240, Fysiikka L osa 4
 BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
