Rinnakkaistietokoneet luento S

Transkriptio

1 Rinnakkaistietokoneet luento S

2 Tietokonealgoritmien rinnakkaisuuden analysointi Algoritmi on proseduuri, joka koostuu äärellisestä joukosta yksiselitteisiä sääntöjä jotka muodostavat operaatiosekvenssin, joka johtaa ongelman ratkaisuun Rinnakkaisuuden analysointi tarkoittaa algoritmin rinnakkain suoritettavien osien (=laskutoimitusten) etsimistä Analysointi perustuu datariippuvuuksien tutkimiseen: riippuvuus kahden laskennan välillä merkitsee, että niitä EI VOI suorittaa rinnakkain Kuta vähemmän riippuvuuksia, sitä enemmän rinnakkaistettavissa olevaa laskentaa Rinnakkaisuuden analysointi mahdollistaa rinnakkaisalgoritmien suunnittelun, sekventiaalisten algoritmien muuntamisen rinnakkaismuotoon, algoritmien kuvaamisen rinnakkaistietokonearkkitehtuuriin ja rinnakkaistietokoneiden suunnittelun

3 Data- ja kontrolliriippuvuudet Data- ja kontrolliriippuvuudet määrittelevät algoritmin perusrakenteen: riippuvuudet on huomioitava oikeellisen toiminnan varmistamiseksi Riippuvuuksien puuttumien kielii mahdollisuudessa rinnakkaislaskentaan Riippuvuuksia voidaan tutkia eri tasoilla: lohkotasolla (lohko sisältää joukon laskutoimituksia) esim. moniprosessorijärjestelmät: lohko voidaan suorittaa yhdessä prosessorissa lausetasolla esim. S1: a = b + c; S2: b = a + e (S1 ja S2 ovat lauseita) muuttuja tasolla esim. b:n riippuvuus a:sta bittitasolla esim. ALU: binäärilukuaritmetiikka

4 Katsotaan C-silmukkaa: for (i=0;i<n;i++) { for (j=0;j<m;j++) { for (k=0;j<k;k++) { S1(I); S2(I); S3(I); } } } missä S edustaa lausetta ja I = (i,j,k) on indeksiavaruuden piste Indeksiavaruuden pisteen voidaan ajatella järjestyneen sanakirjamaisesti, eli esim. I2 > I1, jos I2 = (4,3,1) ja I1 = (2,4,1): ensimmäinen indeksi on tärkein sitten seuraava jne. (=aakkosjärjestys)

5 Riippuvuudet ilmenevät tuotettujen (generated) ja käytettyjen (used) muuttujien välillä jos tuotettua (generoitua) muuttujaa käytetään jossain lauseessa: riippuvuus toteutuu se, että estääkö riippuvuus rinnakkaistamisen riippu riippuvuuden tyypistä Esimerkki 2.1 (kuva 2.1) S1: A = B + C S2: B = A + E S3: A = A + B Tutkitaan mitä riippuvuuksia edellisten lauseiden välillä on

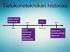
6 Datariippuvuusgraafi (data dependence graph) DDG on esitetty kuvassa 2.1 S1 tuottaa muuttujan A jota käytetään lauseessa S2 (d1) ja S3 (d2) S2 tuottaa muuttujan B jota käytetään lauseessa S3 (d3) ja S1 (d4) S1 ja S3 tuottavat molemmat muuttujan A (d5) S3 tuottaa muuttujan A jota käytetään (aikaisemmin) lauseissa S2 (d6) ja S3 (itse) (d7) Nämä riippuvuudet on otettava huomioon, kun rinnakkaisuutta analysoidaan!

7 Kuva 2.1 S1: A = B + C S2: B = A + E S3: A = A + B datavuoriippuvuus (data-flow dependence) epäriipuvuus (anti dependence) dataulostuloriippuvuus (output dependence)

8 Riippuvuudet d1, d2 ja d3 kertovat, että lauseessa tuotettua muuttujaa käytetään seuraavissa lauseissa: lauseita ei voida suorittaa tällöin rinnakkain riippuvuutta kutsutaan datavuoriippuvuudeksi Riippuvuudet d4,d6 ja d7 kertovat, että lauseessa tuotettu muuttuja on ollut aikaisemmin käytössä toisessa lauseessa tai samassa lauseessa: riippuvuudet estävät rinnakkaistamisen, koska jos niitä rikotaan on mahdollista, että ylikirjoitetaan muuttuja ennen sen käyttöä riippuvuutta kutsutaan epäriippuvuudeksi Riippuvuus d5 kertoo, että kaksi lausetta tuottaa saman muuttujan: jos lauseet suoritetaan yht aikaa ne ylikirjoittavat saman muistipaikan riippuvuutta kutsutaan ulostuloriippuvuudeksi

9 Myöhemmin esitellään kuinka epäriippuvuudet ja ulostuloriippuvuude voidaan poistaa käyttämällä ylimääräisiä muuttujia ja useampia muistipaikkoja Datariippuvuusgraafi G(V,E) on suunnattu graafi missä piste (vertex) V vastaa ohjelman lausetta ja reuna (edge) E riippuvuutta lauseiden välillä Kuvataan riippuvuudet yleisesti ohjelmille joissa on silmukoita: X(f(I)) on ulostulo muuttuja (tuotettava muuttuja) ja X(g(I)) on syötemuuttuja (käytetty muuttuja). f(i) ja g(i) ovat indeksifuntioiden f ja g arvot iteraatioavaruuden pisteessa I

10 Datavuoriippuvuus: lause S(I2) on datavuoriippuvainen lauseesta S(I1) ja lauseiden suhde kirjoitetaan S(I1) S(I2), jos: 1. I1 I2 2. f(i1) = g(i2) 3. X(f(I1)) on ulostulomuuttuja lauseessa S(I1) ja X(g(I2)) on syöte muuttuja lauseessa S(I2) Koska I1 I2 ulostulomuuttuja X(f(I1)) tuotetaan ennen, kun syötemuuttujaa käytetään ts. kirjoitus edeltää lukemista Koska f(i1) = g(i2), X(f(I1)) ja X(g(I2)) viittaavat samaan muuttujaan ts. f(i1) ja g(i2) edustavat samaa indeksiavaruuden pistettä ja X:ää voidaan ajatella taulukkona johon viitataan n-ulotteisella indeksillä (=indeksiavaruuden pisteellä) Tämä voidaan ilmaista sanoin: muuttuja X(g(I2)) on riippuvainen muuttujasta X(f(I1)) eli, S(I1): X(f(I1)) = ( ) S(I2): ( ) = (, X(g(I2)), ) lause S(I1) tuottaa arvon jota käytetään lauseessa S(I2) myöhemmällä tai samalla iteraatiolla (I1 I2). Merkinnät S(I1) ja S(I2) tarkoittavat, että lauseet on määritetty kyseisillä iteraatoilla

11 Dataepäriippuvuus: lause S(I2) on dataepäriippuvainen lauseesta S(I1) ja lauseiden suhde kirjoitetaan S(I1) S(I2), jos: 1. I1 I2 2. g(i1) = f(i2) 3. X(g(I1)) on syöte muuttuja lauseessa S(I1) ja X(f(I2)) on ulostulomuuttuja lauseessa S(I2) Koska I1 I2, syötemuuttuja X(g(I1)) luetaan ennen ulotulomuuttujan X(f(I2)) tuottamista ts. luku edeltää kirjoitusta eli, S(I1): ( ) = (, X(g(I1)), ) S(I2): X(f(I2) = ( )

12 Ulostuloriippuvuus: lause S(I2) on dataepäriippuvainen lauseesta S(I1) ja lauseiden suhde kirjoitetaan S(I1) S(I2), jos: 1. I1 I2 2. f1(i1) = f2(i2) 3. X(f1(I1)) on ulostulomuuttuja lauseessa S(I1) ja X(f2(I2)) on ulostulomuuttuja lauseessa S(I2) koska I1 I2, lauseen S(I1) muuttuja generoidaan ensin eli, S(I1): X(f1(I1)) = ( ) S(I2): X(f2(I2)) = ( )

13 Datariippuvuusvektori d määritellään: d = Ij Ii kun f(ii) = g(ij), eli d kuvaa siirtymää indeksiavaruudessa (iteraatioiden tai silmukoiden määrää), joka erottaa tuotetun ja käytetyn muuttujan toisistaan Esimerkissä 2.1 ei ole indeksejä, joten riippuvuus vektorit ovat nolla: ei riippuvuuksia eri iteraatioiden välillä, vaikka lauseiden välillä onkin riippuvuuksia samalla iteraatiolla

14 Proseduuri riippuvuusvektorien löytämiseksi: 1. Etsi kaikki tuotettu-käytetty muuttuja parit 2. Yhdistä niiden indeksifunktiot eli merkitse f(i) = g(i) ja johda vektorit d kuten aiemmin

15 Esimerkki 2.2 Tutkitaan seuraavaa ohjelmasilmukkaa (Ckieltä vapaasti soveltaen): for (i=0; i<10; i++) { S1: a(i) = x(i) 3; S2: b(i+1) = a(i) * c(i+1); S3: c(i+4) = b(i) + a(i+1); S4: d(i+2) = d(i) + d(i+1); S5: c(i+3) = x(i); }

16 Esimerkki 2.2: riippuvuusgraafi S1: a(i) = x(i) 3; S2: b(i+1) = a(i) * c(i+1); S3: c(i+4) = b(i) + a(i+1); S4: d(i+2) = d(i) + d(i+1); S5: c(i+3) = x(i);

17 Esimerkki 2.2: riippuvuusvektorit S1: a(i) = x(i) 3; S2: b(i+1) = a(i) * c(i+1); S3: c(i+4) = b(i) + a(i+1); S4: d(i+2) = d(i) + d(i+1); S5: c(i+3) = x(i);

18 d1 johtuu lauseiden S1 ja S2 järjestyksestä silmukassa: lauseiden riippuvuus saman iteraation sisällä Kaikki muut riippuvuudet ovat riippuvuuksia eri iteraatioiden välillä, eli d 0 Riippuvuusvektorit ovat tässä esimerkissa skalaariarvoja (kokonaislukuja), koska indeksiavaruus on yksiulotteinen (yksi indeksi i) Jokaisen riippuvuusvektorin arvo ilmaisee iteraatioiden määrän joka erottaa muuttujan tuottamisen sen käyttämisestä d4 kertoo, että muuttuja luetaan ennen sen tuottamista (dataepäriippuvuus), koska d4:n arvo on < 0 Ohjelmat joissa on sisäkkäisiä silmukoita iteraatioavaruus on moniulotteinen ja riippuvuudet ovat vektoreita Algoritmin riippuvuusvektorit voidaan ilmaista riippuvuusmatriisilla (dependency matrix): D = [d1,d2,,dm], jolloin jokainen riippuvuusvektori on yksi matriisin sarakevektoreista

19 Esimerkki 2.3 Tutkitaan silmukkaa: for (i=0;i<n;i++) { for (j=0;j<m;j++) { for (k=0;j<k;k++) { S1(I):a(i,j,k) = a(i-1,j,k+1) + b(i,j,k) S2(I): b(i,j,k+1) = b(i,j-1,k-1) + 3 } } } Tuotettu-käytetty muuttujaparit: d1: a(i,j,k); a(i-1,j,k+1) d2: b(i,j,k+1); b(i,j,k) d3: b(i,j,k+1); b(i,j-1,k-1) D = [ d1, d2, d3] 1 =

20 Kontrolliriippuvuus Kontrolliriippuvuus esiintyy ohjelmissa joissa on ehdollisia haarautumisia Kontrolliriippuvuus esiintyy lauseiden Si ja lauseen Sj välillä, jos lauseeseen Si liittyy ehdollinen haarautuminen ja jos haarautumislause kontrolloi lauseen Sj suorittamista: merkitään Si -- Sj

21 Esimerkki 2.4 Tutkitaan seuraavaa ohjelmaa: if (a > 1) goto S4; else if (b > 0) { d = 3; goto S4; } else goto S5 S4: e = 5 S5: b = e + d Ohjelma voidaan kirjoittaa muotoon (lause: muuttuja : boolean lause): S1: b1 : a > 1 S2: b2 : b > 0 when not b1 S3: d = 3 when not b1 and b2 S4: e = 5 when b1 or b2 S5: b = e + d

22 Kun lauseet (S1-S5) on muodostettu voidaan tehdä riippuvuusgraafi: d1: S2 on datariippuvainen S1:stä muuttujan b1 kautta d2: S3 on datariippuvainen S1:stä muuttujan b1 kautta d3: S4 on datariippuvainen S1:stä muuttujan b1 kautta d2 d1 d3 d4: S3 on datariippuvainen S2:sta muuttujan b2 kautta d5: S4 on datariippuvainen S2:sta muuttujan b2 kautta d6: S5 on datariippuvainen S3:sta muuttujan d kautta d4 d7 d5 d7: S5 on dataepäriippuvainen S2:sta muuttujan B kautta d8: S5 on datariippuvainen S4:sta muuttujan e kautta d6 d8