Gradienttimalli: Lajin esiintyminen. Eliömaantiede: kasvimaantiede. Ilmasto ja levikki. Gradienttiavaruus ja lehmus
|
|
|
- Aune Salo
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Eliömaantiede: kasvimaantiede V Gradienttimalli: Lajin esiintymisen ennustaminen Jari Oksanen Ekologia ja genetiikka SL 2016 Gradienttimalli on individualistinen: jokainen laji vastaa itsenäisesti ja muista riippumatta ympäristögradientteihin. Yhteisö on fiktio, joka muodostuu vain siksi, että lajeilla on samantapainen suhde gradientteihin. Yksittäisen lajin esiintymisen mallintaminen on gradienttianalyysin perusta. Klassinen gradienttiteoria pitää gaussilaista vastetta perusmallina, mutta nykyään käytetään useammin joustavampia malleja (ja vaihtoehtoisia malleja on paljon). Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kuorimallit Ilmasto ja levikki Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kuorimallit Gradienttiavaruus ja lehmus Veikko Hintikka uranuurtaja (1961): Kasvilajin levikki ilmastodiagrammassa, jonka akseleina heinäkuun ja tammikuun keskilämpötila Kesän ja talven olosuhteet Lämpötilaero kesän ja talven välillä Oletuksena tasapaino levikin ja ilmaston välillä Paleoekologia kertoo: ei tasapainoa Mallivirhe = todellisen ja potentiaalisen (mallitetun) levikin ero Nykyään modernit regressiotekniikat, mutta periaate sama Ilmastomuuttujat spatiaalisesti riippuvaisia: Mikä tahansa spatiaalisesti yhtenäinen kuvio voidaan selittää Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
2 Kuorimallit Gradienttiavaruus takaisin kartalle Ilmastollinen kuori Climatic Envelope Kuorimallit Hintikan mallit varhaisia esimerkkejä ilmastollisista kuorimalleista: ilmaston tai yleensä ympäristön rajat, joissa laji esiintyy muodostavat ne olosuhteet, joissa laji voi esiintyä Perustuvat vain lajin esiintymiseen: presence-only data Esimerkiksi herbaariot: tiedämme, missä laji esiintyy, muttemme tiedä, missä se ei esiinny Keruuaktiivisuus ja lajin kiinnostavuus vaikuttavat esiintymistietojen tarkkuuteen Kuorimallit yksinkertaisin vaihtoehto: nykyään maksimientropiamallit kuumia Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kuorimallit Ilmastollisen kuorimallin laatiminen Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kuorimallit Levikki: repaleinen kuva Pulsatilla vernalis January Avg. Temperature Pulsatilla vernalis, convex hull Pulsatilla vernalis, with envelope Levikki tunnetaan epätäydellisesti: reikä voi tarkoittaa, että laji puuttuu tai että sitä ei ole käyty katsomassa Havainnot usein vain esiintymistä: puuttumisista ei ole tietoa Reiät hyvin tutkituilla alueilla ovat todennäköisesti oikeita Kuvan restauroinnin ongelma: palauta osittain tuhoutunut kuva Bayesilainen lähestymistapa: ota huomioon tutkimusintensiteetti ja lähialueet arvioidessasi lajin uskottavaa esiintymistä tyhjillä alueilla July Avg. Temperature Aineistot: LTKM Kastikka-tietokanta, Ilmatieteen laitos Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
3 Bayesilaista eliömaantiedettä Kuorimallit Esiintymismallit Regressiomallit ja lajin esiintyminen Mallitetaan kasvilajin esiintymistodennäköisyys Tarvitaan tieto lajin esiintymisestä ja puuttumisesta: mallinnetaan esiintyminen Ei välttämättä esiinny kaikkialla, ja voi esiintyä myös epätodennäköisellä alueella mutta harvoin Vastemuuttuja yleensä joko 0 tai 1: binominen jakauma Bin(π, m = 1), missä π on lajin esiintymistodennäköisyys ja m on binominen nimittäjä (havaintojen kokonaismäärä) Ennustetaan esiintymistodennäköisyys π: reaaliluku välillä Selittävinä tekijänä ympäristömuuttujat, eivät maantieteelliset koordinaatit Lukuisia tekniikoita: Yleistetyt lineaariset mallit (GLM), yleistetyt additiiviset mallit (GAM), regressiopuut... Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Esiintymismallit Gaussilainen malli Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Esiintymismallit Kaksiulotteinen gaussilainen malli Incidence of Pulsatilla vernalis January Avg. Temp π i = h exp [ (x i u) 2 ] 2t 2 = exp(b 0 b 1 x i b 2 x 2 i ) Gradienttiteoriassa gaussilainen vastemalli suosituin Erittäin helppo sovittaa käyttämällä yleistettyjä lineaarisia malleja (generalized linear models, GLM) Lineaarinen prediktori (η) on selittäjien lineaarinen funktio: gaussilaisessa mallissa toisen asteen polynomi (η = b 0 b 1 x b 2 x 2 ) Linkkifunktio (g) muuntaa ennustetut arvot (µ) lineaariseksi prediktoriksi: gaussilaisessa mallissa log, jonka käänteisfunktio exp (log(µ) = η eli µ = exp(η)) Virhejakauma: gaussilaisessa binominen tai runsausaineistolle (kvasi-)poisson Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Pulsatilla vernalis P. vernalis: Gaussian JulAvg Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 JanAvg
4 Tulosten esitys Esiintymismallit Esiintymismallit Yleistetyt additiiviset mallit (GAM) Tilastollisen esiintymismallin tulosten esitys on vaikeaa: antaa todennäköisyyden, ihmiset haluavat varmuuden Frekventistinen tulkinta: esiintymistodennäköisyys ˆπ = 0.5 tarkoittaa, että laji esiintyy puolella tutkituista näyteyksiköistä Karttoja varten halutaan usein jokin raja-arvo Arvo joka vastaa runsautta pisteessä x = u ± 2t eli kahden t-yksikön päässä optimista u Arvo, joka vastaa lajin prevalenssia tutkimusalueella 0.5 P. vernalis, Gauss limit=0.04 Probability Altitude (m) Bauera rubioides (Cunoniaceae) Kuten GLM, mutta lineaarinen prediktori korvattu silottajalla (smoother) Silottaja kulkee mahdollisimman lähellä havaintopisteitä, mutta sitä rangaistaan äkillisistä mutkista Tavallisimpia silottajia splinit ja paikalliset estimaatit (loess) Linkkifunktio ja virhejakauma kuten GLM Nykyään suositumpia kuin gaussilainen malli Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Esiintymismallit Silotus Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Esiintymismallit Kaksiulotteinen GAM EPACSERP Silotuksen voimakkuutta kuvaa ikkunaleveys: ikkunan sisällä pisteet vaikuttavat käyrään Kapea ikkuna vastaa monta selittävää tekijää ja suurta määrää käytettyjä vapausasteita tavallisessa regressiossa EPACSERP JanAvg Pulsatilla vernalis P. vernalis:gam Altitude Altitude Epacris serpyllifolia (Ericaceae), Mt Field, Tasmania Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 JulAvg Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
5 Mitä vain voi selittää Esiintymismallit ovat tasapainomalleja: ne olettavat, että lajin tämänhetkinen levikki määräytyy gradienteista. Tämä ei välttämättä pidä paikkaansa. Lajien levikki on usein aika yhtenäinen ja selittävät tekijät ovat usein spatiaalisesti riippuvaisia. Esimerkiksi ilmasto muuttuu melko vähän pienellä matkalla. Vaikka lajilla ja ympäristötekijällä ei olisi mitään riippuvuutta, malli voi hyvin selittää lajin esiintymisen aineistossa. Tämän takia mallien hyvyys on aina tutkittava riippumattomassa aineistossa. Hyvä malli on ennustuskykyinen uusissa aineistoissa. Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kuinka uskottava on kangasvuokkomalli? Maantieteellisesti yhtenäisen alueen voi kuvata maantieteellisesti tasaisilla muuttujilla (kuten ilmasto) Paikallisesti hyvä malli ei välttämättä ole kausaalisesti oikea Mallin luotettavuus testattava ristivalidoinnilla: mallin rakennus ja testaus eri aineistoissa Suomeen sovitettu kangasvuokkomalli ei ennusta oikein lajin eurooppalaista levikkiä (Etelä-Norja, Puola, Alpit... ) Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Kangasvuokko ja ilmastonmuutos P. vernalis: Ilmastonmuutos Oletetaan malli oikeaksi ja kausaaliseksi: selittävät tekijät todella määräävät levikin Oletetaan tasapainomalli Oletetaan, että laji voi liikkua kyllin nopeasti FMI, 19 ennustetta Suomeen sovitetun gaussilaisen mallin ekstrapolointi raja-arvolla ˆπ 0.1 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 heinäkuu 2, tammikuu 4.5 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
6 Paleoilmaston rekonstruktio Tasapaino? Kuusi vasta leviämässä Skandinaviaan jääkauden jälkeen Levikki ei tasapainossa vaan muuttumassa? Jari Oksanen (Biologian t.o.) Biogeo: KAMA B. Huntley, J. Veg. Sci. 1, ; / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA Kuusen leviäminen / 39 Epätasapaino Tsuga ja Fagus: eurooppalaisten kolonialistien saapuessa luontainen ja alkuperäinen kasvillisuustyyppi Lajit muodostaneet yhteisön vasta hiljan Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
7 Tietokannat Intergovermental Panel on Climate Change (IPCC), Data Distribution Centre Koko maailma 0.5 verkossa Myös ilmastonmuutosskenaarioita, muuta dataa ja linkkejä muihin lähteisiin WorldClim Global Climate Data Estimoitu hyvin tarkkaan resoluutioon, jopa 30 = 1/120 Bioclim-muuttujat lajien esiintymisen mallinnukseen Myös lajien levikkitietoja, korkeusmalli PaITuli Tieteen tietotekniikan keskuksen paikkatietopalvelut Ilmatieteen laitoksen havainnot sekä 30-vuotiset yhteenvedot estimoituina km ruutuihin Myös muita valtion julkisia tietoja (SYKE, Maanmittauslaitos, GTK jne.) Kirjautuminen yliopiston käyttäjätunnuksilla, käyttöön liittyy ehtoja ja rajoituksia Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Mikä on ahomansikan levikki? Olemme puhuneet lajien levikistä ja näyttäneet levikkikarttoja ikään kuin lajin levikki voitaisiin yksiselitteisesti esittää kartalla. Lajien esiintyminen maastossa on pienipiirteistä ja sisältää huomattavan satunnaisen elementin. Lisäksi tietomme ja aineistomme lajin levikistä on puutteellista ja harhaista. Kartta on aina tulkinta eikä totuus. Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Ikkunaleveyden vaikutus levikkikuvaan Linkola VMI Hultén Retkeilykasvio Tasoitus eksponentiaalisessa ikkunassa, jonka keskileveys 1/α km Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
8 Ruutukartoitus Ruudukot I Ruutukartat nykyään suosituimpia Sopii tietokonekartoitukseen : kasvistotietokanta Kastikka Optimaalinen ruutukoko näyttää levikin pääpiirteet, mutta häivyttää tutkimusintensiteetin vaikutuksen: tapauskohtainen Kansallisessa kartoituksessa yleensä 10 km ruutu, eurooppalaisessa 50 km ruutu 50 km UTM-ruutu eurooppalaisessa kartoituksessa UTM-pohjainen Military Grid Reference System (MGRS) poikkeuksia mukavuuden vuoksi Universal Transverse Mercator -koordinaatistossa maailma jaettu 6 vyöhykkeisiin ja nämä 100 km ruutuihin: kartoitusruutu perusruudun neljännes Kotimaisissa peruskartoissa yhtenäiskoordinaatisto vuoteen 2010: poistunut käytöstä 2012 Peruskarttavyöhyke 3, kussakin oma keskimeridiaani Yhtenäiskoordinaatiston keskimeridiaani 27 E Pohjoisluku etäisyys päiväntasaajasta (m), itäluku kohtisuora etäisyys perusmeridiaanista = 3500 km poikittaisessa Mercator-projektiossa (metreinä) Itäluvun ensimmäinen numero on kaistan tunnus (yllä 3) Käytetään edelleen tietokannoissa Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Ruudukot II Vuodesta 2010 EU:n UTM-järjestelmä keskimeridiaanina 27 Keskimeridiaani sama kuin yhtenäiskoordinaateissa, mutta kartoituslieriö leikkaa maan pintaa, joten mittavirheet pienemmät: oikea leikkauspinta n. 180 km keskimeridiaanista Myös karttalehtijako muuttui Koko Suomi samassa vyöhykkeessä vaikka osia muissakin UTM-kaistoissa: kansallisen sovellutuksen nimi ETRS89 TM35FIN Koordinaattimuunnokset hankalia: otettava huomioon myös maata aproksimoivan ellipsoidin muoto ja datum Ennen sivuava poikittainen Mercator (Gauss-Krüger), nyt leikkaava (UTM) projektio, lisäksi muuttuivat ellipsoidi (Hayward GRS80 WGS84) ja datum (ED50 ETRS89) Uusi järjestelmä paremmin suoraan yhteensopiva GPS-laitteisiin koordinaatti-korkeusjarjestelmat European Petroleum Survey Group (EPSG) kehittänyt ohjelmakirjaston koordinaattimuunnoksiin (GDAL) Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Koordinaattimuunnoksia: Huone KS208 Pohjoiskoordinaatti Itäkoordinaatti EPSG GPS N E 4258 Peruskartta (< 2012) N E 4123 Yhtenäiskoordinaatit ETRS89-TM35FIN ETRS89-GK27FIN Pohjoisluku on etäisyys päiväntasaajalta (metriä) Itäkoordinaattiluku on suorakulmainen etäisyys projisoidussa kartassa perusmeridiaanista 27 ja perusmeridiaanin arvo on (metriä) Yhtenäiskoordinaatistossa itäluvun eteen lisätään kaistanumero (3) ja ETRS89-GKx-järjestelmässä keskimeridiaanin asteluku ETRS89-järjestelmässä ja GPS:ssä ellipsoidi on GRS80 (WGS84), vanhassa järjestelmässä Hayward GK ja peruskartta käyttävät sivuavaa poikittaista Mercator-projektiota (Gauss-Krüger), TM leikkaavaa (UTM) Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
9 Projekteja Spatiaalinen tasoitus Luonnontieteellisen keskusmuseon kasvistotietokanta (Kastikka): museonäytteet ja kirjallisuustiedot (nykyään) yhtenäiskoordinaatistossa Kasviatlasprojekti: tasainen, edustava, satunnaistettu verkko Vapaaehtoistyöllä kerätty uusi, itsenäinen aineisto Kartat ja muuta tietoa saatavissa nykyään verkossa ( mutta raakadata vaikeasti saatavissa Metla: Valtakunnan metsien inventointi (VMI) Systemaattinen otanta metsien seurantaan: muunkin kuin puun tuoton Ei varsinaisesti floristinen, mutta yleisten ja runsaiden metsäkasvien seuranta Uhanalaisten lajien seuranta: Syke ja ympäristökeskukset Atlas Florae Europeae Interpolointi välipisteisiin tasaisessa verkossa: Krigen tasoitus (kriging) spatiaalisen semivarianssin avulla Hippuvarianssi ( nugget ): vaihtelu 0-etäisyydellä eli havainnon varianssi Semivarianssin jyrkkyys: pisteen vaikutusalue Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Ahomansikan yleisyyden ja levikin muutos Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39 Jari Oksanen (Biologian t.o.) Biogeo: KAMA / 39
Gradienttimalli: Lajin esiintyminen. Eliömaantiede: kasvimaantiede. Ilmasto ja levikki. Gradienttiavaruus ja lehmus
 Eliömaantiede: kasvimaantiede V Gradienttimalli: Lajin esiintymisen ennustaminen Jari Oksanen Oulun yliopisto KL 2015 Gradienttimalli on individualistinen: jokainen laji vastaa itsenäisesti ja muista riippumatta
Eliömaantiede: kasvimaantiede V Gradienttimalli: Lajin esiintymisen ennustaminen Jari Oksanen Oulun yliopisto KL 2015 Gradienttimalli on individualistinen: jokainen laji vastaa itsenäisesti ja muista riippumatta
Yleistetyistä lineaarisista malleista
 Yleistetyistä lineaarisista malleista Tilastotiede käytännön tutkimuksessa -kurssi, kesä 2001 Reijo Sund Klassinen lineaarinen malli y = Xb + e eli E(Y) = m, jossa m = Xb Satunnaiskomponentti: Y:n komponentit
Yleistetyistä lineaarisista malleista Tilastotiede käytännön tutkimuksessa -kurssi, kesä 2001 Reijo Sund Klassinen lineaarinen malli y = Xb + e eli E(Y) = m, jossa m = Xb Satunnaiskomponentti: Y:n komponentit
Paikkatiedon JHS-seminaari. Paikkatietomarkkinat 2016
 Paikkatiedon JHS-seminaari Paikkatietomarkkinat 2016 Ohjelma 9:00 Tervetuloa JHS-seminaarin Katsaus Paikkatiedon JHS:iin Pekka Sarkola, paikkatiedon JHS ohjausryhmä Paikkatiedot JUHTAn toiminnassa Jari
Paikkatiedon JHS-seminaari Paikkatietomarkkinat 2016 Ohjelma 9:00 Tervetuloa JHS-seminaarin Katsaus Paikkatiedon JHS:iin Pekka Sarkola, paikkatiedon JHS ohjausryhmä Paikkatiedot JUHTAn toiminnassa Jari
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
EUREF-FIN/N2000-MUUNNOKSET HELSINGIN KAUPUNGISSA
 1 (10) EUREF-FIN/N2000-MUUNNOKSET HELSINGIN KAUPUNGISSA 5.3.2012 2 (10) Sisältö: 1 Johdanto... 3 1.1 Muunnosasetukset paikkatieto-ohjelmistoissa... 3 1.2 Lisätiedot... 3 2 Korkeusjärjestelmän muunnos NN
1 (10) EUREF-FIN/N2000-MUUNNOKSET HELSINGIN KAUPUNGISSA 5.3.2012 2 (10) Sisältö: 1 Johdanto... 3 1.1 Muunnosasetukset paikkatieto-ohjelmistoissa... 3 1.2 Lisätiedot... 3 2 Korkeusjärjestelmän muunnos NN
Diskriminanttianalyysi I
 Diskriminanttianalyysi I 12.4-12.5 Aira Hast 24.11.2010 Sisältö LDA:n kertaus LDA:n yleistäminen FDA FDA:n ja muiden menetelmien vertaaminen Estimaattien laskeminen Johdanto Lineaarinen diskriminanttianalyysi
Diskriminanttianalyysi I 12.4-12.5 Aira Hast 24.11.2010 Sisältö LDA:n kertaus LDA:n yleistäminen FDA FDA:n ja muiden menetelmien vertaaminen Estimaattien laskeminen Johdanto Lineaarinen diskriminanttianalyysi
l (φ; y) = l(θ(φ); y) Toinen derivaatta saadaan tulon derivaatan laskusäännöllä Uudelleenparametroidun mallin Fisherin informaatio on
 HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
Dynaamiset regressiomallit
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Lajien levinneisyysmuutokset ja ilmastonmuutos - Linnut ympäristömuutosten ilmentäjinä
 Lajien levinneisyysmuutokset ja ilmastonmuutos - Linnut ympäristömuutosten ilmentäjinä Aleksi Lehikoinen Luonnontieteellinen keskusmuseo, HY aleksi.lehikoinen@helsinki.fi Oma esittely Gradu 2003 HY: Merimetson
Lajien levinneisyysmuutokset ja ilmastonmuutos - Linnut ympäristömuutosten ilmentäjinä Aleksi Lehikoinen Luonnontieteellinen keskusmuseo, HY aleksi.lehikoinen@helsinki.fi Oma esittely Gradu 2003 HY: Merimetson
MAANMITTAUSLAITOKSEN ILMAISTEN KARTTOJEN TULOSTAMINEN QUANTUM GIS -OHJELMALLA
 1 (6) MAANMITTAUSLAITOKSEN ILMAISTEN KARTTOJEN TULOSTAMINEN QUANTUM GIS -OHJELMALLA TEEMU SALORIUTTA 17.6.2012 Päivitetty 28.6.2013 1. Avaa Maanmittauslaitoksen latauspalvelu osoitteesta https://tiedostopalvelu.maanmittauslaitos.fi/tp/kartta.
1 (6) MAANMITTAUSLAITOKSEN ILMAISTEN KARTTOJEN TULOSTAMINEN QUANTUM GIS -OHJELMALLA TEEMU SALORIUTTA 17.6.2012 Päivitetty 28.6.2013 1. Avaa Maanmittauslaitoksen latauspalvelu osoitteesta https://tiedostopalvelu.maanmittauslaitos.fi/tp/kartta.
JHS 154 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako
 JHS 154 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako Versio: Julkaistu: Voimassaoloaika: Toistaiseksi Sisällys 1 Johdanto... 1 2 Soveltamisala... 2 3 Viittaukset...
JHS 154 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako Versio: Julkaistu: Voimassaoloaika: Toistaiseksi Sisällys 1 Johdanto... 1 2 Soveltamisala... 2 3 Viittaukset...
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Johdatus regressioanalyysiin Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen vaihtelun avulla.
Johdatus regressioanalyysiin Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen vaihtelun avulla.
KASVIATLAS 2015: TILASTOKARTTOJA (Raino Lampinen )
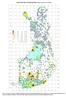 KASVIATLAS 2015: TILASTOKARTTOJA (Raino Lampinen 4.5.2016) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (23 1.1%) 30-49 (22 1.1%) 20-29 (30 1.5%) 15-19 (30 1.5%) 10-14 (119 5.9%) 5-9 (93 4.6%) 3-4 (153 7.6%) 2 (435
KASVIATLAS 2015: TILASTOKARTTOJA (Raino Lampinen 4.5.2016) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (23 1.1%) 30-49 (22 1.1%) 20-29 (30 1.5%) 15-19 (30 1.5%) 10-14 (119 5.9%) 5-9 (93 4.6%) 3-4 (153 7.6%) 2 (435
Radiotekniikan sovelluksia
 Poutanen: GPS-paikanmääritys sivut 72 90 Kai Hahtokari 11.2.2002 Konventionaalinen inertiaalijärjestelmä (CIS) Järjestelmä, jossa z - akseli osoittaa maapallon impulssimomenttivektorin suuntaan standardiepookkina
Poutanen: GPS-paikanmääritys sivut 72 90 Kai Hahtokari 11.2.2002 Konventionaalinen inertiaalijärjestelmä (CIS) Järjestelmä, jossa z - akseli osoittaa maapallon impulssimomenttivektorin suuntaan standardiepookkina
KASVIATLAS 2017: TILASTOKARTTOJA (Raino Lampinen )
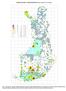 KASVIATLAS 2017: TILASTOKARTTOJA (Raino Lampinen 13.6.2018) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (23 1.1%) 30-49 (22 1.1%) 20-29 (32 1.5%) 15-19 (29 1.4%) 10-14 (118 5.6%) 5-9 (102 4.8%) 3-4 (160 7.6%) 2
KASVIATLAS 2017: TILASTOKARTTOJA (Raino Lampinen 13.6.2018) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (23 1.1%) 30-49 (22 1.1%) 20-29 (32 1.5%) 15-19 (29 1.4%) 10-14 (118 5.6%) 5-9 (102 4.8%) 3-4 (160 7.6%) 2
KASVIATLAS 2018: TILASTOKARTTOJA (Raino Lampinen )
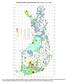 KASVIATLAS 2018: TILASTOKARTTOJA (Raino Lampinen 14.6.2019) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (24 1.1%) 30-49 (23 1.1%) 20-29 (30 1.4%) 15-19 (30 1.4%) 10-14 (118 5.6%) 5-9 (102 4.8%) 3-4 (172 8.1%) 2
KASVIATLAS 2018: TILASTOKARTTOJA (Raino Lampinen 14.6.2019) 100 (4 0.2%) 90-99 (3 0.1%) 50-89 (24 1.1%) 30-49 (23 1.1%) 20-29 (30 1.4%) 15-19 (30 1.4%) 10-14 (118 5.6%) 5-9 (102 4.8%) 3-4 (172 8.1%) 2
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä
 Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Paikkatietoon liittyvistä JHShankkeista. Pekka Sarkola Paikkatiedon JHS ohjausryhmä
 Paikkatietoon liittyvistä JHShankkeista Pekka Sarkola Paikkatiedon JHS ohjausryhmä Esityksen sisältö Paikkatiedon JHS ohjausryhmä Voimassaolevat paikkatiedon JHS:t Työryhmävaiheessa olevat hankkeet Suunnitteilla
Paikkatietoon liittyvistä JHShankkeista Pekka Sarkola Paikkatiedon JHS ohjausryhmä Esityksen sisältö Paikkatiedon JHS ohjausryhmä Voimassaolevat paikkatiedon JHS:t Työryhmävaiheessa olevat hankkeet Suunnitteilla
Regressioanalyysi. Kuusinen/Heliövaara 1
 Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
Regressioanalyysi. Vilkkumaa / Kuusinen 1
 Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
Palautekooste: JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako (korvaa JHS 154-suosituksen)
 Palautekooste: JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako (korvaa JHS 154-suosituksen) 1. Organisaatio Vastaajien määrä: 9 - Työ- ja elinkeinoministeriö
Palautekooste: JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako (korvaa JHS 154-suosituksen) 1. Organisaatio Vastaajien määrä: 9 - Työ- ja elinkeinoministeriö
EUREF-FIN/N2000 käyttöönotto Helsingissä
 EUREF-FIN/N2000 käyttöönotto Helsingissä http://www.hel.fi/hki/kv/fi/kaupunkimittausosasto/kartat+ja+paikkatiedot/koordinaatisto Muutokset Helsngissä: Korkeusjärjestelmä: Tasokoordinaatisto: Pohjoiskoordinaatti
EUREF-FIN/N2000 käyttöönotto Helsingissä http://www.hel.fi/hki/kv/fi/kaupunkimittausosasto/kartat+ja+paikkatiedot/koordinaatisto Muutokset Helsngissä: Korkeusjärjestelmä: Tasokoordinaatisto: Pohjoiskoordinaatti
JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Liite 2: Projektiokaavat
 JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Liite 2: Projektiokaavat Versio: 1.0 / 5.2.2016 Julkaistu: 5.4.2016 Voimassaoloaika: toistaiseksi Sisällys 1
JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Liite 2: Projektiokaavat Versio: 1.0 / 5.2.2016 Julkaistu: 5.4.2016 Voimassaoloaika: toistaiseksi Sisällys 1
1. Tilastollinen malli??
 1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
Logistinen regressio, separoivat hypertasot
 Logistinen regressio, separoivat hypertasot Topi Sikanen Logistinen regressio Aineisto jakautunut K luokkaan K=2 tärkeä erikoistapaus Halutaan mallintaa luokkien vedonlyöntikertoimia (odds) havaintojen
Logistinen regressio, separoivat hypertasot Topi Sikanen Logistinen regressio Aineisto jakautunut K luokkaan K=2 tärkeä erikoistapaus Halutaan mallintaa luokkien vedonlyöntikertoimia (odds) havaintojen
JHS 154 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako, Liite 1: Projektiokaavat
 LUONNOS 008-09-0 JHS 15 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako, Liite 1: Projektiokaavat Versio: Julkaistu: Voimassaoloaika: Toistaiseksi Transverse Mercator-projektiolle
LUONNOS 008-09-0 JHS 15 ETRS89-järjestelmään liittyvät karttaprojektiot, tasokoordinaatistot ja karttalehtijako, Liite 1: Projektiokaavat Versio: Julkaistu: Voimassaoloaika: Toistaiseksi Transverse Mercator-projektiolle
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio
 Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
Vastepintamenetelmä. Kuusinen/Heliövaara 1
 Vastepintamenetelmä Kuusinen/Heliövaara 1 Vastepintamenetelmä Vastepintamenetelmässä pyritään vasteen riippuvuutta siihen vaikuttavista tekijöistä approksimoimaan tekijöiden polynomimuotoisella funktiolla,
Vastepintamenetelmä Kuusinen/Heliövaara 1 Vastepintamenetelmä Vastepintamenetelmässä pyritään vasteen riippuvuutta siihen vaikuttavista tekijöistä approksimoimaan tekijöiden polynomimuotoisella funktiolla,
Ilmastonmuutos pähkinänkuoressa
 Ilmastonmuutos pähkinänkuoressa Sami Romakkaniemi Sami.Romakkaniemi@fmi.fi Itä-Suomen ilmatieteellinen tutkimuskeskus Ilmatieteen laitos Ilmasto kuvaa säämuuttujien tilastollisia ominaisuuksia Sää kuvaa
Ilmastonmuutos pähkinänkuoressa Sami Romakkaniemi Sami.Romakkaniemi@fmi.fi Itä-Suomen ilmatieteellinen tutkimuskeskus Ilmatieteen laitos Ilmasto kuvaa säämuuttujien tilastollisia ominaisuuksia Sää kuvaa
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.14 Tilastollisen analyysin perusteet, kevät 7 7. luento: Tarina yhden selittään lineaarisesta regressiomallista atkuu Kai Virtanen 1 Luennolla 6 opittua Kuvataan havainnot (y, x ) yhden selittään
Mat-.14 Tilastollisen analyysin perusteet, kevät 7 7. luento: Tarina yhden selittään lineaarisesta regressiomallista atkuu Kai Virtanen 1 Luennolla 6 opittua Kuvataan havainnot (y, x ) yhden selittään
KASVIATLAS 2012: TILASTOKARTTOJA (Raino Lampinen )
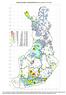 KASVIATLAS 2012: TILASTOKARTTOJA (Raino Lampinen 15.5.2013) 775 100 (2 0.1%) 90-99 (4 0.2%) 50-89 (24 1.3%) 30-50 (20 1.1%) 20-29 (31 1.7%) 15-19 (29 1.6%) 10-14 (118 6.4%) 5-9 (87 4.7%) 3-4 (119 6.4%)
KASVIATLAS 2012: TILASTOKARTTOJA (Raino Lampinen 15.5.2013) 775 100 (2 0.1%) 90-99 (4 0.2%) 50-89 (24 1.3%) 30-50 (20 1.1%) 20-29 (31 1.7%) 15-19 (29 1.6%) 10-14 (118 6.4%) 5-9 (87 4.7%) 3-4 (119 6.4%)
Tilastolliset mallit hakkuukoneen katkonnan ohjauksessa. Tapio Nummi Tampereen yliopisto
 Tilastolliset mallit hakkuukoneen katkonnan ohjauksessa Tapio Nummi Tampereen yliopisto Runkokäyrän ennustaminen Jotta runko voitaisiin katkaista optimaalisesti pitäisi koko runko mitata etukäteen. Käytännössä
Tilastolliset mallit hakkuukoneen katkonnan ohjauksessa Tapio Nummi Tampereen yliopisto Runkokäyrän ennustaminen Jotta runko voitaisiin katkaista optimaalisesti pitäisi koko runko mitata etukäteen. Käytännössä
Harjoitus 9: Excel - Tilastollinen analyysi
 Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
Johdatus regressioanalyysiin. Heliövaara 1
 Johdatus regressioanalyysiin Heliövaara 1 Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen
Johdatus regressioanalyysiin Heliövaara 1 Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen
Gradienttimalli. Eliömaantiede: kasvimaantiede. Gradienttimalli. Wisconsin: Kontinuumi-indeksi
 Eliömaantiede: kasvimaantiede IV ja gradienttianalyysi Jari Oksanen Oulun yliopisto SL 2015 Neutraaleissa malleissa ympäristöä tarkasteltiin homogeenisena tai merkityksettömänä. ssa ympäristötekijät joita
Eliömaantiede: kasvimaantiede IV ja gradienttianalyysi Jari Oksanen Oulun yliopisto SL 2015 Neutraaleissa malleissa ympäristöä tarkasteltiin homogeenisena tai merkityksettömänä. ssa ympäristötekijät joita
Johdatus geospatiaaliseen tutkimukseen
 LYY-menetelmä työpaja, 15.2.2012, Joensuu Johdatus geospatiaaliseen tutkimukseen Olli Lehtonen Historia- ja maantieteiden laitos Itä-Suomen yliopisto SISÄLLYS: Paikkatieto Spatiaalinen autokorrelaatio
LYY-menetelmä työpaja, 15.2.2012, Joensuu Johdatus geospatiaaliseen tutkimukseen Olli Lehtonen Historia- ja maantieteiden laitos Itä-Suomen yliopisto SISÄLLYS: Paikkatieto Spatiaalinen autokorrelaatio
Johdatus regressioanalyysiin
 Ilkka Mellin Tilastolliset menetelmät Osa 4: Lineaarinen regressioanalyysi Johdatus regressioanalyysiin TKK (c) Ilkka Mellin (2007) 1 Johdatus regressioanalyysiin >> Regressioanalyysin lähtökohdat ja tavoitteet
Ilkka Mellin Tilastolliset menetelmät Osa 4: Lineaarinen regressioanalyysi Johdatus regressioanalyysiin TKK (c) Ilkka Mellin (2007) 1 Johdatus regressioanalyysiin >> Regressioanalyysin lähtökohdat ja tavoitteet
Keskipisteen lisääminen 2 k -faktorikokeeseen (ks. Montgomery 9-6)
 Mat-.3 Koesuunnittelu ja tilastolliset mallit kevät Keskipisteen lisääminen k -faktorikokeeseen (ks. Montgomery 9-6) Esim (Montg. ex. 9-, 6-): Tutkitaan kemiallisen prosessin saannon Y riippuvuutta faktoreista
Mat-.3 Koesuunnittelu ja tilastolliset mallit kevät Keskipisteen lisääminen k -faktorikokeeseen (ks. Montgomery 9-6) Esim (Montg. ex. 9-, 6-): Tutkitaan kemiallisen prosessin saannon Y riippuvuutta faktoreista
Todennäköisyyden ominaisuuksia
 Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa
 Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa Jouni Räisänen Helsingin yliopiston fysiikan laitos Kimmo Ruosteenoja Ilmatieteen laitos Sisältöä ACCLIM-skenaariot
Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa Jouni Räisänen Helsingin yliopiston fysiikan laitos Kimmo Ruosteenoja Ilmatieteen laitos Sisältöä ACCLIM-skenaariot
Jokamiehen havaintopäiväkirja verkossa
 Hatikka Jokamiehen havaintopäiväkirja verkossa Hatikan kehitys alkoi 2001 Lähtökohtana kasviharrastajien havaintoaineistot Mukaan kaikki eliöryhmät Monet harrastajat havainnoivat useita eliöryhmiä Julkaistiin
Hatikka Jokamiehen havaintopäiväkirja verkossa Hatikan kehitys alkoi 2001 Lähtökohtana kasviharrastajien havaintoaineistot Mukaan kaikki eliöryhmät Monet harrastajat havainnoivat useita eliöryhmiä Julkaistiin
pitkittäisaineistoissa
 Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Paloriskin ennustaminen metsäpaloindeksin avulla
 Paloriskin ennustaminen metsäpaloindeksin avulla Ari Venäläinen, Ilari Lehtonen, Hanna Mäkelä, Andrea Understanding Vajda, Päivi Junila the ja Hilppa climate Gregow variation and change Ilmatieteen and
Paloriskin ennustaminen metsäpaloindeksin avulla Ari Venäläinen, Ilari Lehtonen, Hanna Mäkelä, Andrea Understanding Vajda, Päivi Junila the ja Hilppa climate Gregow variation and change Ilmatieteen and
Esimerkki: Tietoliikennekytkin
 Esimerkki: Tietoliikennekytkin Tämä Mathematica - notebook sisältää luennolla 2A (2..26) käsitellyn esimerkin laskut. Esimerkin kuvailu Tarkastellaan yksinkertaista mallia tietoliikennekytkimelle. Kytkimeen
Esimerkki: Tietoliikennekytkin Tämä Mathematica - notebook sisältää luennolla 2A (2..26) käsitellyn esimerkin laskut. Esimerkin kuvailu Tarkastellaan yksinkertaista mallia tietoliikennekytkimelle. Kytkimeen
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO
 Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
KASVIATLAS 2011: TILASTOKARTTOJA, Raino Lampinen
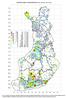 KASVIATLAS 2011: TILASTOKARTTOJA, Raino Lampinen 23.5.2012 775 100 (2 0.1%) 90-99 (4 0.2%) 50-89 (22 1.2%) 30-50 (22 1.2%) 20-29 (29 1.6%) 15-19 (29 1.6%) 10-14 (117 6.5%) 5-9 (89 5.0%) 3-4 (106 5.9%)
KASVIATLAS 2011: TILASTOKARTTOJA, Raino Lampinen 23.5.2012 775 100 (2 0.1%) 90-99 (4 0.2%) 50-89 (22 1.2%) 30-50 (22 1.2%) 20-29 (29 1.6%) 15-19 (29 1.6%) 10-14 (117 6.5%) 5-9 (89 5.0%) 3-4 (106 5.9%)
2. Uskottavuus ja informaatio
 2. Uskottavuus ja informaatio Aluksi käsittelemme uskottavuus- ja log-uskottavuusfunktioita Seuraavaksi esittelemme suurimman uskottavuuden estimointimenetelmän Ensi viikolla perehdymme aiheeseen lisääkö
2. Uskottavuus ja informaatio Aluksi käsittelemme uskottavuus- ja log-uskottavuusfunktioita Seuraavaksi esittelemme suurimman uskottavuuden estimointimenetelmän Ensi viikolla perehdymme aiheeseen lisääkö
Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä
 Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä Sisältö Riippumattomuus Jos P(A B) = P(A)P(B), niin tapahtumat A ja B ovat toisistaan riippumattomia. (Keskustelimme
Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä Sisältö Riippumattomuus Jos P(A B) = P(A)P(B), niin tapahtumat A ja B ovat toisistaan riippumattomia. (Keskustelimme
Load
 Tampereen yliopisto Tilastollinen mallintaminen Mikko Alivuotila ja Anne Puustelli Lentokoneiden rakennuksessa käytettävien metallinkiinnittimien puristuskestävyys Matematiikan, tilastotieteen ja filosofian
Tampereen yliopisto Tilastollinen mallintaminen Mikko Alivuotila ja Anne Puustelli Lentokoneiden rakennuksessa käytettävien metallinkiinnittimien puristuskestävyys Matematiikan, tilastotieteen ja filosofian
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.104 Tilastollisen analyysin perusteet, kevät 007 8. luento: Usean selittäjän lineaarinen regressiomalli Kai Virtanen 1 Usean selittäjän lineaarinen regressiomalli Selitettävän muuttujan havaittujen
Mat-.104 Tilastollisen analyysin perusteet, kevät 007 8. luento: Usean selittäjän lineaarinen regressiomalli Kai Virtanen 1 Usean selittäjän lineaarinen regressiomalli Selitettävän muuttujan havaittujen
Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos /Malmivuori MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi,
 Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos /Malmivuori MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi, kesä 2016 Laskuharjoitus 5, Kotitehtävien palautus laskuharjoitusten
Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos /Malmivuori MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi, kesä 2016 Laskuharjoitus 5, Kotitehtävien palautus laskuharjoitusten
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
Tilastollisen analyysin perusteet Luento 9: Moniulotteinen lineaarinen. regressio
 Tilastollisen analyysin perusteet Luento 9: lineaarinen lineaarinen Sisältö lineaarinen lineaarinen lineaarinen Lineaarinen Oletetaan, että meillä on n kappaletta (x 1, y 1 ), (x 2, y 2 )..., (x n, y n
Tilastollisen analyysin perusteet Luento 9: lineaarinen lineaarinen Sisältö lineaarinen lineaarinen lineaarinen Lineaarinen Oletetaan, että meillä on n kappaletta (x 1, y 1 ), (x 2, y 2 )..., (x n, y n
Niinimäki 7801/1. Tutkimustyöselostus Sanna Juurela. ALTONA MINING LTD/VULCAN KOTALAHTI OY Tutkimustyöselostus
 31.01.2013 Sanna Juurela VULCAN KOTALAHTI OY (Y-tunnus: 2300990-5) Sänkinotkonkatu 6, FIN-83500 Outokumpu, FINLAND Tel. +358 10 271 0090, E-mail. Finland@altonamining.com 1. JOHDANTO Tämä on Vulcan Kotalahti
31.01.2013 Sanna Juurela VULCAN KOTALAHTI OY (Y-tunnus: 2300990-5) Sänkinotkonkatu 6, FIN-83500 Outokumpu, FINLAND Tel. +358 10 271 0090, E-mail. Finland@altonamining.com 1. JOHDANTO Tämä on Vulcan Kotalahti
JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako
 JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Versio: 1.1 / 9.12.2016 Julkaistu: 5.4.2016 Voimassaoloaika: toistaiseksi Sisällys 1 Johdanto...2 2 Soveltamisala...3
JHS 197 EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Versio: 1.1 / 9.12.2016 Julkaistu: 5.4.2016 Voimassaoloaika: toistaiseksi Sisällys 1 Johdanto...2 2 Soveltamisala...3
Puumenetelmät. Topi Sikanen. S ysteemianalyysin. Laboratorio Aalto-yliopiston teknillinen korkeakoulu
 Puumenetelmät Topi Sikanen Puumenetelmät Periaate: Hajota ja hallitse Jaetaan havaintoavaruus alueisiin. Sovitetaan kuhunkin alueeseen yksinkertainen malli (esim. vakio) Tarkastellaan kolmea mallia Luokittelu-
Puumenetelmät Topi Sikanen Puumenetelmät Periaate: Hajota ja hallitse Jaetaan havaintoavaruus alueisiin. Sovitetaan kuhunkin alueeseen yksinkertainen malli (esim. vakio) Tarkastellaan kolmea mallia Luokittelu-
Tilastotieteen aihehakemisto
 Tilastotieteen aihehakemisto hakusana ARIMA ARMA autokorrelaatio autokovarianssi autoregressiivinen malli Bayes-verkot, alkeet TILS350 Bayes-tilastotiede 2 Bayes-verkot, kausaalitulkinta bootstrap, alkeet
Tilastotieteen aihehakemisto hakusana ARIMA ARMA autokorrelaatio autokovarianssi autoregressiivinen malli Bayes-verkot, alkeet TILS350 Bayes-tilastotiede 2 Bayes-verkot, kausaalitulkinta bootstrap, alkeet
T Luonnollisten kielten tilastollinen käsittely
 T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
(b) Vedonlyöntikertoimet syytetyn ihonvärin eri luokissa
 Oulun yliopiston matemaattisten tieteiden tutkimusyksikkö/tilastotiede 805306A JOHDATUS MONIMUUTTUJAMENETELMIIN, sl 2017 (Jari Päkkilä) Harjoitus 3, viikko 47 (19.20.11.): kotitehtävät Ratkaisuja 1. Floridan
Oulun yliopiston matemaattisten tieteiden tutkimusyksikkö/tilastotiede 805306A JOHDATUS MONIMUUTTUJAMENETELMIIN, sl 2017 (Jari Päkkilä) Harjoitus 3, viikko 47 (19.20.11.): kotitehtävät Ratkaisuja 1. Floridan
P (X B) = f X (x)dx. xf X (x)dx. g(x)f X (x)dx.
 Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
4. Anna arviosi seuraavista suositusluonnokseen liittyvistä väitteistä asteikolla 1-5 (5 = samaa mieltä, 1 = eri mieltä)
 kooste ja työryhmän vastine: JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako (korvaa JHS 154-suosituksen) 1. Organisaatio Vastaajien määrä: 9 - Työ- ja elinkeinoministeriö
kooste ja työryhmän vastine: JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako (korvaa JHS 154-suosituksen) 1. Organisaatio Vastaajien määrä: 9 - Työ- ja elinkeinoministeriö
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
T Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti , 8:30-10:00 Kollokaatiot, Versio 1.1
 T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
pitkittäisaineistoissa
 Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Numeeriset menetelmät TIEA381. Luento 6. Kirsi Valjus. Jyväskylän yliopisto. Luento 6 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 6 Kirsi Valjus Jyväskylän yliopisto Luento 6 () Numeeriset menetelmät 4.4.2013 1 / 33 Luennon 6 sisältö Interpolointi ja approksimointi Polynomi-interpolaatio: Vandermonden
Numeeriset menetelmät TIEA381 Luento 6 Kirsi Valjus Jyväskylän yliopisto Luento 6 () Numeeriset menetelmät 4.4.2013 1 / 33 Luennon 6 sisältö Interpolointi ja approksimointi Polynomi-interpolaatio: Vandermonden
Männyn laaturajojen integrointi runkokäyrän ennustamisessa. Laura Koskela Tampereen yliopisto 9.6.2003
 Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
Uusi koordinaatti- ja korkeusjärjestelmä
 Uusi koordinaatti- ja korkeusjärjestelmä Markku Poutanen Geodeettinen laitos Uusi koordinaatti- ja korkeusjärjestelmä Taustaa Uuden koordinaattijärjestelmän perusteet JHS ja käyttöönotto Uusi korkeusjärjestelmä
Uusi koordinaatti- ja korkeusjärjestelmä Markku Poutanen Geodeettinen laitos Uusi koordinaatti- ja korkeusjärjestelmä Taustaa Uuden koordinaattijärjestelmän perusteet JHS ja käyttöönotto Uusi korkeusjärjestelmä
Saarijärvi Soidinmäen tuulipuiston muinaisjäännösten täydennysinventointi 2014
 1 Saarijärvi Soidinmäen tuulipuiston muinaisjäännösten täydennysinventointi 2014 Timo Sepänmaa Tilaaja: Megatuuli Oy 2 Sisältö Perustiedot... 2 Yleiskartta... 3 Inventointi... 4 Kansikuva: Vuoden 2014
1 Saarijärvi Soidinmäen tuulipuiston muinaisjäännösten täydennysinventointi 2014 Timo Sepänmaa Tilaaja: Megatuuli Oy 2 Sisältö Perustiedot... 2 Yleiskartta... 3 Inventointi... 4 Kansikuva: Vuoden 2014
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos K:n lähimmän naapurin menetelmä (K-Nearest neighbours) Tarkastellaan aluksi pientä (n = 9) kurjenmiekka-aineistoa, joka on seuraava:
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos K:n lähimmän naapurin menetelmä (K-Nearest neighbours) Tarkastellaan aluksi pientä (n = 9) kurjenmiekka-aineistoa, joka on seuraava:
805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016)
 805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016) Tavoitteet (teoria): Hallita autokovarianssifunktion ominaisuuksien tarkastelu. Osata laskea autokovarianssifunktion spektriiheysfunktio. Tavoitteet
805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016) Tavoitteet (teoria): Hallita autokovarianssifunktion ominaisuuksien tarkastelu. Osata laskea autokovarianssifunktion spektriiheysfunktio. Tavoitteet
Maantieteellisen alueen huomioiminen vahinkovakuutustuotteiden hinnoittelussa
 Maantieteellisen alueen huomioiminen vahinkovakuutustuotteiden hinnoittelussa SHV-harjoitustyö (suppea) Teija Talvensaari Suomen Aktuaariyhdistyksen kuukausikokous 27.10.2014 Esityksen sisältö Johdanto
Maantieteellisen alueen huomioiminen vahinkovakuutustuotteiden hinnoittelussa SHV-harjoitustyö (suppea) Teija Talvensaari Suomen Aktuaariyhdistyksen kuukausikokous 27.10.2014 Esityksen sisältö Johdanto
Johdatus tilastotieteeseen Johdatus regressioanalyysiin. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Johdatus regressioanalyysiin TKK (c) Ilkka Mellin (2005) 1 Johdatus regressioanalyysiin Regressioanalyysin lähtökohdat ja tavoitteet Deterministiset mallit ja regressioanalyysi
Johdatus tilastotieteeseen Johdatus regressioanalyysiin TKK (c) Ilkka Mellin (2005) 1 Johdatus regressioanalyysiin Regressioanalyysin lähtökohdat ja tavoitteet Deterministiset mallit ja regressioanalyysi
Lineaariset luokittelumallit: regressio ja erotteluanalyysi
 Lineaariset luokittelumallit: regressio ja erotteluanalyysi Aira Hast Johdanto Tarkastellaan menetelmiä, joissa luokittelu tehdään lineaaristen menetelmien avulla. Avaruus jaetaan päätösrajojen avulla
Lineaariset luokittelumallit: regressio ja erotteluanalyysi Aira Hast Johdanto Tarkastellaan menetelmiä, joissa luokittelu tehdään lineaaristen menetelmien avulla. Avaruus jaetaan päätösrajojen avulla
Kartta-design monikanavajulkaisemisessa: Tapaustutkimus MenoMaps Nuuksion kansallispuistossa
 Kartta-design monikanavajulkaisemisessa: Tapaustutkimus MenoMaps Nuuksion kansallispuistossa Juha Oksanen FT Geoinformatiikan ja kartografian osasto Mitä on kartta-design? 1. Kartan sisällön suunnittelu
Kartta-design monikanavajulkaisemisessa: Tapaustutkimus MenoMaps Nuuksion kansallispuistossa Juha Oksanen FT Geoinformatiikan ja kartografian osasto Mitä on kartta-design? 1. Kartan sisällön suunnittelu
KUUSAMO TEOLLISUUSALUEEN OSAYLEISKAAVA ARKEOLOGINEN INVENTOINTI 2017
 Kuusamon kaupunki KUUSAMO TEOLLISUUSALUEEN OSAYLEISKAAVA ARKEOLOGINEN INVENTOINTI 2017 Laatinut FM Kalle Luoto Kuusamo Arkeologinen inventointi SISÄLLYSLUETTELO 1 Johdanto... 1 3 Perustietoa inventointialueesta...
Kuusamon kaupunki KUUSAMO TEOLLISUUSALUEEN OSAYLEISKAAVA ARKEOLOGINEN INVENTOINTI 2017 Laatinut FM Kalle Luoto Kuusamo Arkeologinen inventointi SISÄLLYSLUETTELO 1 Johdanto... 1 3 Perustietoa inventointialueesta...
Avoimet luontohavainnot
 Avoimet luontohavainnot Ekologiset yhteydet -seminaari 9.3.2012 Luonnontieteellinen keskusmuseo Miten luontohavainnot syntyvät? Tutkimuksen tuloksena Tieteellisistä kokoelmista Luontoharrastajat keräävät
Avoimet luontohavainnot Ekologiset yhteydet -seminaari 9.3.2012 Luonnontieteellinen keskusmuseo Miten luontohavainnot syntyvät? Tutkimuksen tuloksena Tieteellisistä kokoelmista Luontoharrastajat keräävät
1. Tutkitaan regressiomallia Y i = β 0 + β 1 X i + u i ja oletetaan, että tavanomaiset
 TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016
 BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016 1. Hahmottele karkeasti funktion f : R R 2 piirtämällä sen arvoja muutamilla eri muuttujan arvoilla kaksiulotteiseen koordinaatistoon
BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016 1. Hahmottele karkeasti funktion f : R R 2 piirtämällä sen arvoja muutamilla eri muuttujan arvoilla kaksiulotteiseen koordinaatistoon
Harjoitustehtävät 6: mallivastaukset
 Harjoitustehtävät 6: mallivastaukset Niku Määttänen & Timo Autio Makrotaloustiede 31C00200, talvi 2018 1. Maat X ja Y ovat muuten identtisiä joustavan valuuttakurssin avotalouksia, mutta maan X keskuspankki
Harjoitustehtävät 6: mallivastaukset Niku Määttänen & Timo Autio Makrotaloustiede 31C00200, talvi 2018 1. Maat X ja Y ovat muuten identtisiä joustavan valuuttakurssin avotalouksia, mutta maan X keskuspankki
Natura -luontotyyppien mallinnus FINMARINET -hankkeessa. Henna Rinne Åbo Akademi, Ympäristö- ja meribiologian laitos
 Natura -luontotyyppien mallinnus FINMARINET -hankkeessa Henna Rinne Åbo Akademi, Ympäristö- ja meribiologian laitos 1 Natura luontotyypit FINMARINETissa Luontodirektiivin liitteessä I mainittuja luontotyyppejä,
Natura -luontotyyppien mallinnus FINMARINET -hankkeessa Henna Rinne Åbo Akademi, Ympäristö- ja meribiologian laitos 1 Natura luontotyypit FINMARINETissa Luontodirektiivin liitteessä I mainittuja luontotyyppejä,
Climate change induced drought effects on forest growth and vulnerability - Climforisk -
 Climate change induced drought effects on forest growth and vulnerability - Climforisk - 1st Advisory group meeting 24.2.2011 Mikko Peltoniemi, Aleksi Lehtonen, Seppo Neuvonen et al. www.metla.fi/life/climforisk
Climate change induced drought effects on forest growth and vulnerability - Climforisk - 1st Advisory group meeting 24.2.2011 Mikko Peltoniemi, Aleksi Lehtonen, Seppo Neuvonen et al. www.metla.fi/life/climforisk
1. Tutkitaan tavallista kahden selittäjän regressiomallia
 TA7, Ekonometrian johdantokurssi HARJOITUS 5 RATKAISUEHDOTUKSET 232215 1 Tutkitaan tavallista kahden selittäjän regressiomallia Y i = β + β 1 X 1,i + β 2 X 2,i + u i (a) Kirjoita regressiomalli muodossa
TA7, Ekonometrian johdantokurssi HARJOITUS 5 RATKAISUEHDOTUKSET 232215 1 Tutkitaan tavallista kahden selittäjän regressiomallia Y i = β + β 1 X 1,i + β 2 X 2,i + u i (a) Kirjoita regressiomalli muodossa
Kalojen lisääntymisaluekartoitukset Tietoa kestäviin valintoihin
 Kalojen lisääntymisaluekartoitukset Antti Lappalainen Riista- ja kalatalouden tutkimuslaitos 7.12.2010 Tavoitteet: 1. Kehittää toimivia ja kustannustehokkaita menetelmiä rannikon talouskalalajien lisääntymisalueiden
Kalojen lisääntymisaluekartoitukset Antti Lappalainen Riista- ja kalatalouden tutkimuslaitos 7.12.2010 Tavoitteet: 1. Kehittää toimivia ja kustannustehokkaita menetelmiä rannikon talouskalalajien lisääntymisalueiden
Harha mallin arvioinnissa
 Esitelmä 12 Antti Toppila sivu 1/18 Optimointiopin seminaari Syksy 2010 Harha mallin arvioinnissa Antti Toppila 13.10.2010 Esitelmä 12 Antti Toppila sivu 2/18 Optimointiopin seminaari Syksy 2010 Sisältö
Esitelmä 12 Antti Toppila sivu 1/18 Optimointiopin seminaari Syksy 2010 Harha mallin arvioinnissa Antti Toppila 13.10.2010 Esitelmä 12 Antti Toppila sivu 2/18 Optimointiopin seminaari Syksy 2010 Sisältö
KARTAT JA KOORDINAATIT
 KARTAT JA KOORDINAATIT Esityksen sisältöä KARTAT JA KOORDINAATIT Yleistä kartoista ja karttapalveluista http://www.maanmittauslaitos.fi/kartat/koordinaatit/koordinaatti-korkeusjarjestelmat Peruskartan
KARTAT JA KOORDINAATIT Esityksen sisältöä KARTAT JA KOORDINAATIT Yleistä kartoista ja karttapalveluista http://www.maanmittauslaitos.fi/kartat/koordinaatit/koordinaatti-korkeusjarjestelmat Peruskartan
Harjoitukset 3 : Monimuuttujaregressio 2 (Palautus )
 31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 3 : Monimuuttujaregressio 2 (Palautus 7.2.2017) Tämän harjoituskerran tehtävät
31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 3 : Monimuuttujaregressio 2 (Palautus 7.2.2017) Tämän harjoituskerran tehtävät
Pikajohdatus bayesilaiseen tilastoanalyysiin ja monimuuttuja-analyysiin
 ja monimuuttuja-analyysiin Loppuseminaari: Terveydenhuollon uudet analyysimenetelmät (TERANA) Aki Vehtari AB HELSINKI UNIVERSITY OF TECHNOLOGY Department of Biomedical Engineering and Computational Science
ja monimuuttuja-analyysiin Loppuseminaari: Terveydenhuollon uudet analyysimenetelmät (TERANA) Aki Vehtari AB HELSINKI UNIVERSITY OF TECHNOLOGY Department of Biomedical Engineering and Computational Science
Örön putkilokasvikartoitukset 2015
 Örön putkilokasvikartoitukset 2015 Riitta Ryömä Paahde Life (LIFE13NAT/FI/000099) JOHDANTO JA MENETELMÄT Kartoitusten tavoite ja tarkoitus Kartoitusten tarkoitus oli dokumentoida erityisesti merivehnäkasvustojen
Örön putkilokasvikartoitukset 2015 Riitta Ryömä Paahde Life (LIFE13NAT/FI/000099) JOHDANTO JA MENETELMÄT Kartoitusten tavoite ja tarkoitus Kartoitusten tarkoitus oli dokumentoida erityisesti merivehnäkasvustojen
LEMPÄÄLÄ Moisio-Hakkarin asemakaavan Kiviahon pohjoisosan laajennusalueen muinaisjäännösinventointi 2015 Johanna Rahtola Timo Jussila
 1 LEMPÄÄLÄ Moisio-Hakkarin asemakaavan Kiviahon pohjoisosan laajennusalueen muinaisjäännösinventointi 2015 Johanna Rahtola Timo Jussila Tilaaja: Lempäälän kunta 2 Sisältö Kansikuva: Perustiedot... 2 Yleiskartat...
1 LEMPÄÄLÄ Moisio-Hakkarin asemakaavan Kiviahon pohjoisosan laajennusalueen muinaisjäännösinventointi 2015 Johanna Rahtola Timo Jussila Tilaaja: Lempäälän kunta 2 Sisältö Kansikuva: Perustiedot... 2 Yleiskartat...
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
Koordinaattimuunnospalvelut Reino Ruotsalainen
 Koordinaattimuunnospalvelut 11.12.2009 Reino Ruotsalainen MAANMITTAUSLAITOS TIETOA MAASTA 2009 Lisätietoja: http://www.fgi.fi/julkaisut/pdf/gltiedote30.pdf Geodeettisen laitoksen tiedote 30/2009: SUOMEN
Koordinaattimuunnospalvelut 11.12.2009 Reino Ruotsalainen MAANMITTAUSLAITOS TIETOA MAASTA 2009 Lisätietoja: http://www.fgi.fi/julkaisut/pdf/gltiedote30.pdf Geodeettisen laitoksen tiedote 30/2009: SUOMEN
JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako
 JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Versio: 27.7.2015 palautekierrosta varten Julkaistu: Voimassaoloaika: toistaiseksi Sisällys 1 Johdanto... 3 2
JHS XXX EUREF-FIN -koordinaattijärjestelmät, niihin liittyvät muunnokset ja karttalehtijako Versio: 27.7.2015 palautekierrosta varten Julkaistu: Voimassaoloaika: toistaiseksi Sisällys 1 Johdanto... 3 2
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Osa 2: Otokset, otosjakaumat ja estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
LIITO-ORAVAN LISÄÄNTYMIS- JA LEVÄHDYSPAIKAT PALJON MELUA TYHJÄSTÄ?
 LIITO-ORAVAN LISÄÄNTYMIS- JA LEVÄHDYSPAIKAT PALJON MELUA TYHJÄSTÄ? Metsätieteen päivä 12.11.2014 Maarit Jokinen (SYKE), Sanna Mäkeläinen (Helsingin yliopisto), Otso Ovaskainen (Helsingin yliopisto) Johdanto
LIITO-ORAVAN LISÄÄNTYMIS- JA LEVÄHDYSPAIKAT PALJON MELUA TYHJÄSTÄ? Metsätieteen päivä 12.11.2014 Maarit Jokinen (SYKE), Sanna Mäkeläinen (Helsingin yliopisto), Otso Ovaskainen (Helsingin yliopisto) Johdanto
MATEMATIIKKA 5 VIIKKOTUNTIA. PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009
 EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
