PHYS-C0210 Kvanttimekaniikka Exercise 2, extra challenges, week 45
|
|
|
- Juha-Pekka Salminen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 PHYS-C0210 Kvanttimekaniikka Exercise 2, extra challenges, week Dirac delta-function is an eigenstate of the position operator. I.e. you get such a wavefunction from an infinitely precise measurement of position (peak position of the Dirac delta-function is the measurement outcome). Dirac distribution can be represented in terms of a normal distribution whose width is pushed to zero (x) = lim!0 + Ce x 2 /(4 ). (1) Using the property R 11 (x)dx = 1, determine C. If wavefunction would be (x) = (x), explore if it is correctly normalized. How should we inteprete (x) 2 here? What does this have to do with the probability of finding particle at x = 0? What about planewave solution(which is an eigenstate of momentum operator) (x) = exp(ikx)/ p 2? What does (x) 2 then have to do with the probability of finding a particle in some region of space? 2. Convince yourself why time-dependent Schrödinger equation is first order in time and why there is an imaginary term in front of the time-derivative. (Liboff page 87 Ex and 3.21) Time-dependent Schödinger equation is of = Ĥ (2) where a is some constant. Assume a system with two independent parts so that H(x 1, x 2 )= H 1 (x 1 )+H 2 (x 2 ), 1 (x 1, t) and 2 (x 2, t) are states of systems 1 and 2 respectively. a) Show that the states of the combined system that have the form (x 1, x 2 )= 1 (x 1, t) 2 (x 2, t) solve the Schrödinger equation b) Show that this would not be true if Schrödinger equation would be of 2 = Ĥ. (3) c) Based on Born posulate argue that the wavefunction of the system made from independent parts must have the product form (i.e. argue for first order time-derivative in the Schrödinger equation). d) Show that the equation = Ĥ implies oskillating solutions only if a is purely imaginary. You can assume one particle so that H = H 1 (x 1 ) and explore the time-evolution of the energy eigenstates. (Note: if a is imaginary, then also the wavefunction must be complex in general)
2 3. Schrödinger equation emerges from the Hamiltonian H = T + V of classical mechanics. We enter quantum mechanics with substitutions x! ˆx, H! Ĥ = i p! ˆp = i and multiplying with the wavefunction (x, t). Let us do the same from a relativistic starting point. a) Derive the relativistic relation between energy and momentum E 2 = p 2 c 2 + m 2 c 4. b) Turn this into quantum mechanical expression. c) From the same starting point, is it possible to form two expressions, one with firstorder time derivative and another with second order time-derivative? Tip: H = E = mc 2 = m 0 c 2, where m is the particle mass, m 0 is the rest mass, and q =1/ 1 v 2 c 2 Lorentz factor. Not to be returned and these will not be graded. Intended for those aiming a bit deeper than usual in this course.
3
4
5
6 mukaan se, ettei se saa ehtiä ulos ytimestä edes liikkuessaan valonnopeudella. Tällöin hän sai epätarkkuusperiaatteesta hiukkasen energian ja pystyi suhteellisuusteorian avulla laskemaan sen massan. Vastaavan massainen hiukkanen löytyi ennenpitkää kokeellisesti, joten oliko vahva vuorovaikutus nyt selitetty? Malliratkaisu Ei välttämättä, sillä epätarkkuusperiaatehan on epäyhtälö, joka voi antaa korkeintaan ylärajan hiukkasen massalle. Voi olla myös sattumaa että menetelmällä ennustettu massa ylipäätään vastaa minkään hiukkasen massaa. Lisätietoa: tehtävä perustuu itse asiassa tositapahtumiin, ja kyseisen hiukkasen on sittemin todettu olevan jotain aivan muuta kuin vahvan vuorovaikutuksen välittäjä. Nykyisessä standardimallissa vahva vuorovaikutus selitetäänkin massattomaksi teoretisoidulla gluonilla ja lyhyelle kantamalle on keksitty aivan muita selityksiä kuin epätarkkuusperiaatteesta johtuva elinikärajoite. 3 Relativistinen kvanttimekaniikka Schrödingerin yhtälö edustaa klassisen mekaniikan lauseketta H = T + V, eli yksinkertaistettuna kokonaisenergia on liike-energian ja potentiaalienergian summa. Lausekkeesta tehdään sitten kvanttia sijoittamalla siihen x! ˆx, H! Ĥ ja p! ˆp sekä kertomalla se aaltofunktiolla (x, t). Tehdään nyt sama temppu suhteellisuusteoreettisista lähtökohdista. a) Johda relativistinen liikemäärän ja energian relaatio E 2 = p 2 c 2 + m 2 c 4. b) Tee johtamastasi relaatiosta kvanttimekaaninen lauseke. c) Onko samasta lähtökohdasta mahdollista muodostaa kaksi lauseketta, joista toinen on ensimmäistä ja toinen toista kertalukua ajan derivaatan suhteen? Vinkki: zh = E = mc 2 = m 0 c 2,missämon hiukkasen liikemassa, m 0 lepo- q massa ja = 1/ Malliratkaisu a) 1 v 2 c 2 Lorentzin kerroin. E = m 0 c 2 () 2 E 2 = 2 m 2 0c 4 E 2 = (1 v 2 /c 2 )E 2 = m 2 0c v 2 /c 2 m2 0c 4 E 2 E 2 v 2 /c 2 = m 2 0c 4 E = mc 2 E 2 m 2 v 2 c 2 = m 2 0c 4 mv = p 2 E 2 = p 2 c 2 + m 2 0c 4 b) Tarkastellaan vain 1-D ongelmaa p = p x ja tehdään tavanomaiset sijoitukset p x! ˆp ja E! Ĥ sekä kertomalla puolittain oikealta 4
7 aaltofunktiolla (x, t) (operaattoreidenhan täytyy aina operoida johonkin tai lausekkeessa ei ole järkeä!), jolloin (a) -kohdan tuloksesta 2 (x, t) = 2 c 2 (x, t)+m 0c 4 (x, t) (x, t) 2 c2 (x, t)+m 2 0c 4 (x, t) c 2 2 (x, t) 0c 2 =m2 (x, t) ~ 2 Tämä yhtälö on toista kertalukua ajan derivaatan suhteen ja tunnetaan Klein- Gordonin yhtälönä. c) Jos tarkastellaan 3-D jolloin 2 i c 2 r2 = + i mikäli A, B, C ovat matriiseja, joille pätee ja A 2 = B 2 = C 2 = I [A, B] =0, [A, C] =0, [B,C] =0. Nyt Klein-Gordonin yhtälö saadaankin muotoon mistä voidaan päätellä (x, t) = m2 0c 2 (x, ~ (x, t) = m 0c ~ (x, t). Tämä tulos tunnetaan Diracin yhtälönä, joskin tämä muoto on varsin vanhanaikainen ja useimmiten yhtälöä käsitellään relativistisille tarkasteluille tavanomaiseen tapaan tensorinotaatiolla, jolloin se yksinkertaistuu muotoon (i~ µ mc) = 0. 5
8 Lisätietoa: relativistisessa kvanttimekaniikassa on kolme Schrödingerin yhtälöä vastaavaa liikeyhtälöä: Klein-Gordon, Dirac ja Proca. Se, mitä näistä kulloinkin tulee käyttää, riippuu kyseisen hiukkasen spin-kvanttiluvusta. Aina niin mystiseltä vaikuttava spin taitaa siis liittyä jotenkin perustavanlaatuisesti hiukkasen luonteeseen, hmm... 6
The Viking Battle - Part Version: Finnish
 The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
Capacity Utilization
 Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Kvanttilaskenta - 1. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
The CCR Model and Production Correspondence
 The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
Network to Get Work. Tehtäviä opiskelijoille Assignments for students. www.laurea.fi
 Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
MRI-sovellukset. Ryhmän 6 LH:t (8.22 & 9.25)
 MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
Kvanttilaskenta - 2. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Efficiency change over time
 Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward.
 START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
Information on preparing Presentation
 Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007
 National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
Kvanttimekaniikkaa yhdessä ulottuvuudessa
 Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
anna minun kertoa let me tell you
 anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
1. Liikkuvat määreet
 1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
Choose Finland-Helsinki Valitse Finland-Helsinki
 Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Huom. tämä kulma on yhtä suuri kuin ohjauskulman muutos. lasketaan ajoneuvon keskipisteen ympyräkaaren jänteen pituus
 AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
Bounds on non-surjective cellular automata
 Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
make and make and make ThinkMath 2017
 Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Returns to Scale II. S ysteemianalyysin. Laboratorio. Esitelmä 8 Timo Salminen. Teknillinen korkeakoulu
 Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
FinFamily PostgreSQL installation ( ) FinFamily PostgreSQL
 FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
Statistical design. Tuomas Selander
 Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
Exercise 1. (session: )
 EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
T Statistical Natural Language Processing Answers 6 Collocations Version 1.0
 T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine Centre for Language and Communication Studies
 Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Information on Finnish Courses Autumn Semester 2017 Jenni Laine & Päivi Paukku Centre for Language and Communication Studies
 Information on Finnish Courses Autumn Semester 2017 Jenni Laine & Päivi Paukku 24.8.2017 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve terve!
Information on Finnish Courses Autumn Semester 2017 Jenni Laine & Päivi Paukku 24.8.2017 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve terve!
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Operatioanalyysi 2011, Harjoitus 2, viikko 38
 Operatioanalyysi 2011, Harjoitus 2, viikko 38 H2t1, Exercise 1.1. H2t2, Exercise 1.2. H2t3, Exercise 2.3. H2t4, Exercise 2.4. H2t5, Exercise 2.5. (Exercise 1.1.) 1 1.1. Model the following problem mathematically:
Operatioanalyysi 2011, Harjoitus 2, viikko 38 H2t1, Exercise 1.1. H2t2, Exercise 1.2. H2t3, Exercise 2.3. H2t4, Exercise 2.4. H2t5, Exercise 2.5. (Exercise 1.1.) 1 1.1. Model the following problem mathematically:
Alternative DEA Models
 Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Results on the new polydrug use questions in the Finnish TDI data
 Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKK LKTRONKK. välikoe 0.3.006. Saat vastata vain neljään tehtävään!. Laske jännite U. R = =Ω, R 3 =3Ω, = =4V, 3 =6V, = + R + R 3 + U 3. Konkka on varautunut jännitteeseen u C (0) =. Kytkin
S-55.00 SÄHKÖTKNKK LKTRONKK. välikoe 0.3.006. Saat vastata vain neljään tehtävään!. Laske jännite U. R = =Ω, R 3 =3Ω, = =4V, 3 =6V, = + R + R 3 + U 3. Konkka on varautunut jännitteeseen u C (0) =. Kytkin
Green Growth Sessio - Millaisilla kansainvälistymismalleilla kasvumarkkinoille?
 Green Growth Sessio - Millaisilla kansainvälistymismalleilla kasvumarkkinoille? 10.10.01 Tuomo Suortti Ohjelman päällikkö Riina Antikainen Ohjelman koordinaattori 10/11/01 Tilaisuuden teema Kansainvälistymiseen
Green Growth Sessio - Millaisilla kansainvälistymismalleilla kasvumarkkinoille? 10.10.01 Tuomo Suortti Ohjelman päällikkö Riina Antikainen Ohjelman koordinaattori 10/11/01 Tilaisuuden teema Kansainvälistymiseen
3.6 Feynman s formulation of quantum mechanics
 3.6 Feynman s formulation of quantum mechanics Course MAT-66000: Quantum mechanics and the particles of nature Ilkka Kylänpää Tampere University of Technology 14.10.2010 Sisältö Johdattelua Klassinen action
3.6 Feynman s formulation of quantum mechanics Course MAT-66000: Quantum mechanics and the particles of nature Ilkka Kylänpää Tampere University of Technology 14.10.2010 Sisältö Johdattelua Klassinen action
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto
 Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
812336A C++ -kielen perusteet, 21.8.2010
 812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
S-55.1100 SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖKNKKA A KONKKA. välikoe 2..2008. Saat vastata vain neljään tehtävään!. aske jännite U. = 4 Ω, 2 = Ω, = Ω, = 2, 2 =, = A, 2 = U 2 2 2 2. ännitelähde tuottaa hetkestä t = t < 0 alkaen kaksiportaisen
S-55.00 SÄHKÖKNKKA A KONKKA. välikoe 2..2008. Saat vastata vain neljään tehtävään!. aske jännite U. = 4 Ω, 2 = Ω, = Ω, = 2, 2 =, = A, 2 = U 2 2 2 2. ännitelähde tuottaa hetkestä t = t < 0 alkaen kaksiportaisen
16. Allocation Models
 16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
EUROOPAN PARLAMENTTI
 EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
1.3 Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 811122P (5 op.) 12.12.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 811122P (5 op.) 12.12.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition)
 Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
MEETING PEOPLE COMMUNICATIVE QUESTIONS
 Tiistilän koulu English Grades 7-9 Heikki Raevaara MEETING PEOPLE COMMUNICATIVE QUESTIONS Meeting People Hello! Hi! Good morning! Good afternoon! How do you do? Nice to meet you. / Pleased to meet you.
Tiistilän koulu English Grades 7-9 Heikki Raevaara MEETING PEOPLE COMMUNICATIVE QUESTIONS Meeting People Hello! Hi! Good morning! Good afternoon! How do you do? Nice to meet you. / Pleased to meet you.
Operatioanalyysi 2011, Harjoitus 4, viikko 40
 Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
ALOITUSKESKUSTELU / FIRST CONVERSATION
 ALOITUSKESKUSTELU / FIRST CONVERSATION Lapsen nimi / Name of the child Lapsen ikä / Age of the child yrs months HYVINKÄÄN KAUPUNKI Varhaiskasvatuspalvelut Lapsen päivähoito daycare center / esiopetusyksikkö
ALOITUSKESKUSTELU / FIRST CONVERSATION Lapsen nimi / Name of the child Lapsen ikä / Age of the child yrs months HYVINKÄÄN KAUPUNKI Varhaiskasvatuspalvelut Lapsen päivähoito daycare center / esiopetusyksikkö
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKKA JA LKTONKKA. välikoe 3.0.2006. Saat vastata vain neljään tehtävään!. Laske jännite U. = =4Ω, 3 =2Ω, = =2V, J =2A, J 2 =3A + J 2 + J 3 2. Kondensaattori on aluksi varautunut jännitteeseen
S-55.00 SÄHKÖTKNKKA JA LKTONKKA. välikoe 3.0.2006. Saat vastata vain neljään tehtävään!. Laske jännite U. = =4Ω, 3 =2Ω, = =2V, J =2A, J 2 =3A + J 2 + J 3 2. Kondensaattori on aluksi varautunut jännitteeseen
Aatofunktiot ja epätarkkuus
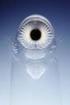 Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Other approaches to restrict multipliers
 Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Lab SBS3.FARM_Hyper-V - Navigating a SharePoint site
 Lab SBS3.FARM_Hyper-V - Navigating a SharePoint site Note! Before starting download and install a fresh version of OfficeProfessionalPlus_x64_en-us. The instructions are in the beginning of the exercise.
Lab SBS3.FARM_Hyper-V - Navigating a SharePoint site Note! Before starting download and install a fresh version of OfficeProfessionalPlus_x64_en-us. The instructions are in the beginning of the exercise.
Information on Finnish Language Courses Spring Semester 2017 Jenni Laine
 Information on Finnish Language Courses Spring Semester 2017 Jenni Laine 4.1.2017 KIELIKESKUS LANGUAGE CENTRE Puhutko suomea? Do you speak Finnish? -Hei! -Moi! -Mitä kuuluu? -Kiitos, hyvää. -Entä sinulle?
Information on Finnish Language Courses Spring Semester 2017 Jenni Laine 4.1.2017 KIELIKESKUS LANGUAGE CENTRE Puhutko suomea? Do you speak Finnish? -Hei! -Moi! -Mitä kuuluu? -Kiitos, hyvää. -Entä sinulle?
4x4cup Rastikuvien tulkinta
 4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
Travel Getting Around
 - Location Olen eksyksissä. Not knowing where you are Voisitko näyttää kartalta missä sen on? Asking for a specific location on a map Mistä täällä on? Asking for a specific...wc?...pankki / rahanvaihtopiste?...hotelli?...huoltoasema?...sairaala?...apteekki?...tavaratalo?...ruokakauppa?...bussipysäkki?
- Location Olen eksyksissä. Not knowing where you are Voisitko näyttää kartalta missä sen on? Asking for a specific location on a map Mistä täällä on? Asking for a specific...wc?...pankki / rahanvaihtopiste?...hotelli?...huoltoasema?...sairaala?...apteekki?...tavaratalo?...ruokakauppa?...bussipysäkki?
x = y x i = y i i = 1, 2; x + y = (x 1 + y 1, x 2 + y 2 ); x y = (x 1 y 1, x 2 + y 2 );
 LINEAARIALGEBRA Harjoituksia/Exercises 2017 1. Olkoon n Z +. Osoita, että (R n, +, ) on lineaariavaruus, kun vektoreiden x = (x 1,..., x n ), y = (y 1,..., y n ) identtisyys, yhteenlasku ja reaaliluvulla
LINEAARIALGEBRA Harjoituksia/Exercises 2017 1. Olkoon n Z +. Osoita, että (R n, +, ) on lineaariavaruus, kun vektoreiden x = (x 1,..., x n ), y = (y 1,..., y n ) identtisyys, yhteenlasku ja reaaliluvulla
FinFamily Installation and importing data (11.1.2016) FinFamily Asennus / Installation
 FinFamily Asennus / Installation 1 Sisällys / Contents FinFamily Asennus / Installation... 1 1. Asennus ja tietojen tuonti / Installation and importing data... 4 1.1. Asenna Java / Install Java... 4 1.2.
FinFamily Asennus / Installation 1 Sisällys / Contents FinFamily Asennus / Installation... 1 1. Asennus ja tietojen tuonti / Installation and importing data... 4 1.1. Asenna Java / Install Java... 4 1.2.
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.1100 SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe 14.12.2010. Saat vastata vain neljään tehtävään! Sallitut: Kako, (gr.) laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!] 1. Missä rajoissa
S-55.1100 SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe 14.12.2010. Saat vastata vain neljään tehtävään! Sallitut: Kako, (gr.) laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!] 1. Missä rajoissa
Kielenkäytön näkökulma oppimisvuorovaikutukseen
 Kielenkäytön näkökulma oppimisvuorovaikutukseen Tarja Nikula Soveltavan kielentutkimuksen keskus tarja.nikula@jyu.fi Kiinnostuksen kohteena Luokkahuonevuorovaikutus vieraalla kielellä englannin kielen
Kielenkäytön näkökulma oppimisvuorovaikutukseen Tarja Nikula Soveltavan kielentutkimuksen keskus tarja.nikula@jyu.fi Kiinnostuksen kohteena Luokkahuonevuorovaikutus vieraalla kielellä englannin kielen
FYSA235, Kvanttimekaniikka I, osa B, tentti Tentin yhteispistemäärä on 48 pistettä. Kaavakokoelma ja CG-taulukko paperinipun lopussa.
 FYSA5, Kvanttimekaniikka I, osa B, tentti..4 Tentin yhteispistemäärä on 48 pistettä. Kaavakokoelma ja CG-taulukko paperinipun lopussa.. Selitä lyhyesti (a) Larmorin prekessio [ pt] (b) Clebsch-Gordan kertoimet
FYSA5, Kvanttimekaniikka I, osa B, tentti..4 Tentin yhteispistemäärä on 48 pistettä. Kaavakokoelma ja CG-taulukko paperinipun lopussa.. Selitä lyhyesti (a) Larmorin prekessio [ pt] (b) Clebsch-Gordan kertoimet
AYYE 9/ HOUSING POLICY
 AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
ATLAS-kartan esittely - Peli palveluiden yhteiskehittämisen menetelmistä Päivi Pöyry-Lassila, Aalto-yliopisto
 ATLAS-kartan esittely - Peli palveluiden yhteiskehittämisen menetelmistä Päivi Pöyry-Lassila, Aalto-yliopisto Serve Research Brunch 24.10.2013 Esityksen sisältö ATLAS-hanke lyhyesti ATLAS-kartan kehittäminen:
ATLAS-kartan esittely - Peli palveluiden yhteiskehittämisen menetelmistä Päivi Pöyry-Lassila, Aalto-yliopisto Serve Research Brunch 24.10.2013 Esityksen sisältö ATLAS-hanke lyhyesti ATLAS-kartan kehittäminen:
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
1.3Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
J 2 = J 2 x + J 2 y + J 2 z.
 FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
C++11 seminaari, kevät Johannes Koskinen
 C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
LYTH-CONS CONSISTENCY TRANSMITTER
 LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
Bohr Einstein -väittelyt. Petteri Mäntymäki Timo Kärkkäinen
 Bohr Einstein -väittelyt Petteri Mäntymäki Timo Kärkkäinen Esityksen sisältö Kvanttivallankumous Epätarkkuusperiaate Väittelyt Yhteenveto 24.4.2013 2 Kvanttivallankumous Alkoi 1900-luvulla (Einstein, Planck,
Bohr Einstein -väittelyt Petteri Mäntymäki Timo Kärkkäinen Esityksen sisältö Kvanttivallankumous Epätarkkuusperiaate Väittelyt Yhteenveto 24.4.2013 2 Kvanttivallankumous Alkoi 1900-luvulla (Einstein, Planck,
Korrespondenssiperiaate. Tapio Hansson Oulun Yliopisto, Fysiikan laitos Ohjaaja: Mikko Saarela
 Korrespondenssiperiaate Tapio Hansson Oulun Yliopisto, Fysiikan laitos Ohjaaja: Mikko Saarela Sisältö 1 Johdanto 2 2 Liikeyhtälöt 2 2.1 Klassisen mekaniikan liikeyhtälöt................ 2 2.2 Poissonin
Korrespondenssiperiaate Tapio Hansson Oulun Yliopisto, Fysiikan laitos Ohjaaja: Mikko Saarela Sisältö 1 Johdanto 2 2 Liikeyhtälöt 2 2.1 Klassisen mekaniikan liikeyhtälöt................ 2 2.2 Poissonin
SIMULINK S-funktiot. SIMULINK S-funktiot
 S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
Salasanan vaihto uuteen / How to change password
 Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin. Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana
 ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
SAGA 150. Asennusohjeet. Mittaa oven korkeus. Piirrä seinään oven kiinni -päätyyn seinäkannattimen kohdalle vaakaviiva korkeudelle ovi + 75mm + 20 mm.
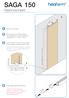 SAGA 150 Asennusohjeet 500 1 2 Mittaa oven korkeus. Piirrä seinään oven kiinni -päätyyn seinäkannattimen kohdalle vaakaviiva korkeudelle ovi + 75mm + 20 mm. 3 Piirrä vesivaa an avulla viiva myös kiskon
SAGA 150 Asennusohjeet 500 1 2 Mittaa oven korkeus. Piirrä seinään oven kiinni -päätyyn seinäkannattimen kohdalle vaakaviiva korkeudelle ovi + 75mm + 20 mm. 3 Piirrä vesivaa an avulla viiva myös kiskon
Aikariippuva Schrödingerin yhtälö
 Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Ajettavat luokat: SM: S1 (25 aika-ajon nopeinta)
 SUPERMOTO SM 2013 OULU Lisämääräys ja ohje Oulun Moottorikerho ry ja Oulun Formula K-125ry toivottaa SuperMoto kuljettajat osallistumaan SuperMoto SM 2013 Oulu osakilpailuun. Kilpailu ajetaan karting radalla
SUPERMOTO SM 2013 OULU Lisämääräys ja ohje Oulun Moottorikerho ry ja Oulun Formula K-125ry toivottaa SuperMoto kuljettajat osallistumaan SuperMoto SM 2013 Oulu osakilpailuun. Kilpailu ajetaan karting radalla
Salausmenetelmät 2015/Harjoitustehtävät
 Salausmenetelmät 2015/Harjoitustehtävät 1. Ystäväsi K lähettää sinulle Caesarin yhteenlaskumenetelmällä kirjoitetun viestin ÖHXHHTTLOHUPSSHSSH R. Avaa viesti. 2. Avaa Caesarin yhteenlaskumenetelmällä laadittu
Salausmenetelmät 2015/Harjoitustehtävät 1. Ystäväsi K lähettää sinulle Caesarin yhteenlaskumenetelmällä kirjoitetun viestin ÖHXHHTTLOHUPSSHSSH R. Avaa viesti. 2. Avaa Caesarin yhteenlaskumenetelmällä laadittu
PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL
 MAV4 MAV5 MAV6 PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL Käyttöohje Instruction manual HUOMIO! Lue käyttöohjeet huolellisesti ennen laitteen käyttöä ja noudata kaikkia annettuja ohjeita. Säilytä
MAV4 MAV5 MAV6 PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL Käyttöohje Instruction manual HUOMIO! Lue käyttöohjeet huolellisesti ennen laitteen käyttöä ja noudata kaikkia annettuja ohjeita. Säilytä
Expression of interest
 Expression of interest Avoin hakemus tohtorikoulutettavaksi käytäntö Miksi? Dear Ms. Terhi virkki-hatakka I am writing to introduce myself as a volunteer who have the eagerness to study in your university.
Expression of interest Avoin hakemus tohtorikoulutettavaksi käytäntö Miksi? Dear Ms. Terhi virkki-hatakka I am writing to introduce myself as a volunteer who have the eagerness to study in your university.
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
Teknillinen tiedekunta, matematiikan jaos Numeeriset menetelmät
 Numeeriset menetelmät 1. välikoe, 14.2.2009 1. Määrää matriisin 1 1 a 1 3 a a 4 a a 2 1 LU-hajotelma kaikille a R. Ratkaise LU-hajotelmaa käyttäen yhtälöryhmä Ax = b, missä b = [ 1 3 2a 2 a + 3] T. 2.
Numeeriset menetelmät 1. välikoe, 14.2.2009 1. Määrää matriisin 1 1 a 1 3 a a 4 a a 2 1 LU-hajotelma kaikille a R. Ratkaise LU-hajotelmaa käyttäen yhtälöryhmä Ax = b, missä b = [ 1 3 2a 2 a + 3] T. 2.
Akateemiset fraasit Tekstiosa
 - Väitteen hyväksyminen Broadly speaking, I agree with because Samaa mieltä jostakin näkökulmasta One is very much inclined to agree with because Samaa mieltä jostakin näkökulmasta Yleisesti ottaen olen
- Väitteen hyväksyminen Broadly speaking, I agree with because Samaa mieltä jostakin näkökulmasta One is very much inclined to agree with because Samaa mieltä jostakin näkökulmasta Yleisesti ottaen olen
1. (a) (2p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori
 FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
Ohjelmointikielet ja -paradigmat 5op. Markus Norrena
 Ohjelmointikielet ja -paradigmat 5op Markus Norrena Kotitehtävä 6, toteuttakaa alla olevan luokka ja attribuutit (muuttujat) Kotitehtävä 6, toteuttakaa alla olevan luokka ja attribuutit (muuttujat) Huom!
Ohjelmointikielet ja -paradigmat 5op Markus Norrena Kotitehtävä 6, toteuttakaa alla olevan luokka ja attribuutit (muuttujat) Kotitehtävä 6, toteuttakaa alla olevan luokka ja attribuutit (muuttujat) Huom!
Topologies on pseudoinnite paths
 Topologies on pseudoinnite paths Andrey Kudinov Institute for Information Transmission Problems, Moscow National Research University Higher School of Economics, Moscow Moscow Institute of Physics and Technology
Topologies on pseudoinnite paths Andrey Kudinov Institute for Information Transmission Problems, Moscow National Research University Higher School of Economics, Moscow Moscow Institute of Physics and Technology
OP1. PreDP StudyPlan
 OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
TIEKE Verkottaja Service Tools for electronic data interchange utilizers. Heikki Laaksamo
 TIEKE Verkottaja Service Tools for electronic data interchange utilizers Heikki Laaksamo TIEKE Finnish Information Society Development Centre (TIEKE Tietoyhteiskunnan kehittämiskeskus ry) TIEKE is a neutral,
TIEKE Verkottaja Service Tools for electronic data interchange utilizers Heikki Laaksamo TIEKE Finnish Information Society Development Centre (TIEKE Tietoyhteiskunnan kehittämiskeskus ry) TIEKE is a neutral,
Luento5 8. Atomifysiikka
 Atomifysiikka Luento5 8 54 Kvanttimekaniikan avulla ymmärrämme atomin rakenteen ja toiminnan. Laser on yksi esimerkki atomien ja valon kvanttimekaniikasta. Luennon tavoite: Oppia ymmärtämään atomin rakenne
Atomifysiikka Luento5 8 54 Kvanttimekaniikan avulla ymmärrämme atomin rakenteen ja toiminnan. Laser on yksi esimerkki atomien ja valon kvanttimekaniikasta. Luennon tavoite: Oppia ymmärtämään atomin rakenne
Uusia kokeellisia töitä opiskelijoiden tutkimustaitojen kehittämiseen
 The acquisition of science competencies using ICT real time experiments COMBLAB Uusia kokeellisia töitä opiskelijoiden tutkimustaitojen kehittämiseen Project N. 517587-LLP-2011-ES-COMENIUS-CMP This project
The acquisition of science competencies using ICT real time experiments COMBLAB Uusia kokeellisia töitä opiskelijoiden tutkimustaitojen kehittämiseen Project N. 517587-LLP-2011-ES-COMENIUS-CMP This project
Erityinen suhteellisuusteoria (Harris luku 2)
 Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Mitä Master Class:ssa opittiin?
 Mitä Master Class:ssa opittiin? Tutkimuskoordinaattori Kaisa Korhonen-Kurki, Helsingin yliopisto Tutkija Katriina Soini, Helsingin yliopisto Yliopistopedagogi Henna Asikainen, Helsingin yliopisto Tausta
Mitä Master Class:ssa opittiin? Tutkimuskoordinaattori Kaisa Korhonen-Kurki, Helsingin yliopisto Tutkija Katriina Soini, Helsingin yliopisto Yliopistopedagogi Henna Asikainen, Helsingin yliopisto Tausta
Vertaispalaute. Vertaispalaute, /9
 Vertaispalaute Vertaispalaute, 18.3.2014 1/9 Mistä on kyse? opiskelijat antavat palautetta toistensa töistä palaute ei vaikuta arvosanaan (palautteen antaminen voi vaikuttaa) opiskelija on työskennellyt
Vertaispalaute Vertaispalaute, 18.3.2014 1/9 Mistä on kyse? opiskelijat antavat palautetta toistensa töistä palaute ei vaikuta arvosanaan (palautteen antaminen voi vaikuttaa) opiskelija on työskennellyt
Kvanttifysiikan perusteet, harjoitus 5
 Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
Suihkukoneet 1:73 ja pienemmät. Potkurikoneet 1:72-1:49. Suihkukoneet 1:72-1:49. Potkurikoneet 1:35 ja suuremmat. Suihkukoneet 1:35 ja suuremmat
 Kilpailuluokat Ohessa kilpailuluokat NC 2016 ja IPMS Open. Ilma-alukset Potkurikoneet 1:73 ja pienemmät Suihkukoneet 1:73 ja pienemmät Potkurikoneet 1:72-1:49 Suihkukoneet 1:72-1:49 Potkurikoneet 1:48
Kilpailuluokat Ohessa kilpailuluokat NC 2016 ja IPMS Open. Ilma-alukset Potkurikoneet 1:73 ja pienemmät Suihkukoneet 1:73 ja pienemmät Potkurikoneet 1:72-1:49 Suihkukoneet 1:72-1:49 Potkurikoneet 1:48
Alueellinen yhteistoiminta
 Alueellinen yhteistoiminta Kokemuksia alueellisesta toiminnasta Tavoitteet ja hyödyt Perusterveydenhuollon yksikön näkökulmasta Matti Rekiaro Ylilääkäri Perusterveydenhuollon ja terveyden edistämisen yksikkö
Alueellinen yhteistoiminta Kokemuksia alueellisesta toiminnasta Tavoitteet ja hyödyt Perusterveydenhuollon yksikön näkökulmasta Matti Rekiaro Ylilääkäri Perusterveydenhuollon ja terveyden edistämisen yksikkö
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat
 Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi
 Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
Returns to Scale Chapters
 Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
Guidebook for Multicultural TUT Users
 1 Guidebook for Multicultural TUT Users WORKPLACE PIRKANMAA-hankkeen KESKUSTELUTILAISUUS 16.12.2010 Hyvää käytäntöä kehittämässä - vuorovaikutusopas kansainvälisille opiskelijoille TTY Teknis-taloudellinen
1 Guidebook for Multicultural TUT Users WORKPLACE PIRKANMAA-hankkeen KESKUSTELUTILAISUUS 16.12.2010 Hyvää käytäntöä kehittämässä - vuorovaikutusopas kansainvälisille opiskelijoille TTY Teknis-taloudellinen
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa. Tapio Hansson
 Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
Operatioanalyysi 2011, Harjoitus 3, viikko 39
 Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
7.4 Variability management
 7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
Security server v6 installation requirements
 CSC Security server v6 installation requirements Security server version 6.4-0-201505291153 Pekka Muhonen 8/12/2015 Date Version Description 18.12.2014 0.1 Initial version 10.02.2015 0.2 Major changes
CSC Security server v6 installation requirements Security server version 6.4-0-201505291153 Pekka Muhonen 8/12/2015 Date Version Description 18.12.2014 0.1 Initial version 10.02.2015 0.2 Major changes
VAASAN YLIOPISTO Humanististen tieteiden kandidaatin tutkinto / Filosofian maisterin tutkinto
 VAASAN YLIOPISTO Humanististen tieteiden kandidaatin tutkinto / Filosofian maisterin tutkinto Tämän viestinnän, nykysuomen ja englannin kandidaattiohjelman valintakokeen avulla Arvioidaan viestintävalmiuksia,
VAASAN YLIOPISTO Humanististen tieteiden kandidaatin tutkinto / Filosofian maisterin tutkinto Tämän viestinnän, nykysuomen ja englannin kandidaattiohjelman valintakokeen avulla Arvioidaan viestintävalmiuksia,
