Kuvat: Anju Asunta, Tuusulanjärven kamarimusiikki / Maarit Kytöharju, Järvenpään Teatteri / Timo Saarinen

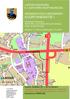
TALVIKAUDEN LINJASTOSUUNNITELMALUONNOS

1 () död 10 TIUDE -1 IJTOUUITEUOO öd J - d T g g d 09 - -d 1 %: 18 %: g J % d 09 11, d 0 % ö ö, d d, g d ö T - b ö d, d, ö T d T d d T, d ö J 11 (://f/f///), d, d -, ö d T 8, Fc 2 B, 1 T, 0-11, fx 0- @f,

TEOLOGIAN YLIOPPILAIDEN TIEDEKUNTAYHDISTYKSEN JULKAISU VUODESTA 1853 4/2012

TEOLOGIAN YLIOPPILAIDEN TIEDEKUNTAYHDISTYKSEN JULKAISU VUODESTA 1853 4/2012 P 4 V 5 P 6 L 7 A H g 10 K 12 N ö ( ) 15 T,, 16 A3 - N 20 Dg! 18 R 21 E 19 K: K R 22 R 23 L - Hd R, Sf L, I V A V K - Sf L K

SAVONLINNAN KAUPUNKI KAAVOITUSKATSAUS Tekninen toimiala

ONLINNN UUNI OITUTU T T g OITUTU Jd LITU OLET T IEILLÄ OLET T ä y - ä, ä d UUDET HNEET, EI OITUÄÄTÖTÄ NÄYTTÖOIUET UNTOITU OLLITUINEN LIITTEET:,, y, - Eä- yä yö yyd: T / O: O, ONLINN d:, Fx: - äö: ()f :wwwf

-Jotta maailma olisi parempi paikka wappuna. RAKENNUSINSINÖÖRIKILLAN VIRALLINEN KILTALEHTI JO VUODESTA 1963 2/2012

-J w. RAKENNUSINSINÖÖRIKILLAN VIRALLINEN KILTALEHTI JO VUODESTA 1963 2/2012 JOS ET NÄE LUKEA ALLAOLEVAA PIILOTETTUA TEKSTIÄ, JUO LISÄÄ SKUMPPAA, SILLÄ STEREOGRAMMIEN NÄKEMINEN ONNISTUU VAIN SILMÄT KILLISSÄ.

Rakennepoikkileikkaus 1:100

B x ( ) x h ( h) - h x x UYUO x x h x OU gd d - -gd h " -" OU U Yhd - h C - OOD -G Y g x g d B O U b Y d g ) ( G O g C x + O U C - x +- C- x +- d ) ( h h b C d h ( h h ) h» h C h C - b d UOU h b h c hh

KAAVOITUSKATSAUS VALMISTUMASSA OLEVAT KAAVAT 3 VIREILLÄ OLEVAT KAAVAT 6 UUDET KAAVAHANKKEET, EI KAAVOITUSPÄÄTÖSTÄ 18 MAAKUNTAKAAVOITUS 18

OIUU LIU OLE IEILLÄ OLE ä - ä, ä d UUDE HNEE, EI OIUÄÄÖÄ UNOIU OLLIUINEN LIIEE:,,, - d: / O: O, ONLINN d:, Fx: - äö: ()f :wwwf / / Höö, ääö B ä, - H, äö, H, N E,,, OIUU ää ä ä ää d ä ää ä, dää g äö- :

LÄNSI-LAAJASALON KÄYTTÄJÄKYSELY

FCG P Oy HELINGIN AUPUNI LÄNI-LAAJAALON ÄYTTÄJÄYELY Yv ö -D.. FCG P Oy Yv ö () Hg.. L-L yyy -D IÄLLYLUETTELO YLEITÄ... YELY.... V d.... Y d.... Ad v.... Ad yö.... Eöyy v... LIITTEET... T... FCG P Oy Yv

LAPUAN KAUPUNKI 8. LIUHTARIN KAUPUNGINOSA ASEMAKAAVAN KUMOAMINEN KUORTANEENTIE I

. G ä y, ä y-, y-.., äydy.... äyö- ö.. yäyy g xx.xx. xx yäyy g xx.xx. xx - . - D.. d.. ääyä. ä y-, - y., ö ---, ---, ---, --- (ä) - --... - g - -. y - y d ä. - -,. - .., Ä, yydä g d ää :., ä äy äää ä-.

3 *ä;r ä:e 5ä ä{ :i. c oo) S g+;!qg *r; Er ; l[$ E ;;iä F:ä ä :E ä: a bo. =. * gäf$iery g! Eä. a is äg*!=."fl: ä; E!, \ ins:" qgg ;._ EE üg.

t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >

Hysteerinen komedia meistä naisista...(ja vähän myös miehistä)! oivatuotanto.fi

H d (j v ö )! H: Kj j j: Apö : S: Tjjj: Lv: V: V-p: Ä: M: Kp: Pv: Nö: Gfi : Kv: S Sd Bjö Jbdó N Hg T P Tj V Gd Ö J Tv K K J Tv, K Kj R H, K W K W Gd Ö J H, K Ld Mj H K Kj K 1 30 j 15 v Ap : Sf Ed 3 Sg,

ALA-MALMIN ALUESUUNNITTELU KÄYTTÄJÄKYSELYN TULOKSET

ALA-ALIN ALUEUUNNITTELU ÄYTTÄJÄYELYN TULOET Hg g / - - Yh hö (7) Hg 8 A- yyy IÄLLYLUETTELO YLEITÄ YELY d Y d h Ad 9 Ad yö Eöyy Yh hö (7) Hg 8 A- yyy HELINGIN AUPUNI ALA-ALIN ÄYTTÄJÄYELY YLEITÄ YELY A-

asunnottoman äänenkannattaja vuodesta 1987 nro 2 / 2017 hinta 3

m d 1987 2 / 2017 3 2 3 KOHTI PAREMPAA www..f m.m@.f m m TOIMISTO K 2 D 3.. 00500 H m().f Tm S T 050 407 9702 Jö Vd P 050 407 9703 Am O U P 050 443 0102 m().f Aö Om Am2 - C Bd 050 443 1063 M m J L 050

MAHDOLLISUUKSIEN TASA-ARVO, SIVISTYS, KANNUSTAVUUS, SUVAITSEVAISUUS, VÄLITTÄMINEN

H V: Vr Pr: Mr V: Syrjyy yrjy Nr S K S 3 S 3 S 6 2/2012 UUSISIPOO NYA SIBBO 7500 Hy, MAHDOLLISUUKSIEN TASA-ARVO, SIVISTYS, KANNUSTAVUUS, SUVAITSEVAISUUS, VÄLITTÄMINEN rj, j d rd yö yö S Työ j yr y yd O

SAVONLINNAN KAUPUNKI KAAVOITUSKATSAUS 2018

ONLINNN UUNI OIUU g OIUU LIU OLE IEILLÄ OLE ä ä, ä d UUDE HNEE, EI OIUÄÄÖÄ UNOIU OLLIUINEN LIIEE:,,, d: / O: O, ONLINN d:, Fx: äö: ()f : wwwf / / Höö, ääö B ä, H, äö, H, N E,,, OIUU ää ä ä ää d ä ää ä,

!! "! # $ %! &# '( ) * # + " & (, & # - "./ $ &!!! " " $ 0! &# '( ) # *& - 1 # 3 ) 45$!! "! $ # " ' "! 1 5 * ! 1 *#- $5 * $ : 5 ; 1<

!"! ##"$ !! "! # $ %! &# '( ) * # + " & (, & # - "./ $ &!!! " " $ 0! &# '( ) # *& - 1 # 3 ) 45$!! "! $ # " ' "! 1 5 * - 16 5! 1 *#- $5 * 4-14 5$ 7 89 1: 5 ; 1< 5 $ =! %>

KÄPYLÄN ALUESUUNNITELMA KÄYTTÄJÄKYSELYN TULOKSET

ÄPYÄN UESUUNNITEM ÄYTTÄJÄYSEYN TUSET Hg g / - - FCG S y Y ö () Hg.. y yyy -C96 SISÄYSUETTE YEISTÄ... YSEY.... d.... Y d....3 d... 9. d yö.... Eöyy... FCG S y Y ö () Hg.. y yyy -C96 HESINGIN UPUNI ÄPYÄN

AIKAKAUSLEHDET. tammik. Suomen Suurin SiSuStuSlehti. Kevään. värikkäät astiat. Talvi 1/0. arke. herkut. retkel MAK

1 UU mmk 2006 AIKAKAUSLHDT 75 : O R V A I L m U J Am I M Kää JAS ä M A KU r 0 1 ä y ö d K h h H r Sm Sr SSSSh ärkkää RUOKA, JUOM A, KITT IÖ, M AT K A ILU, HY VIVO ITI r y, y 3 ää & r h r d 2008 öö r g

Toiminta- ja taloussuunnitelma 2010-2012 sekä talousarvio vuodelle 2010 KHALL 532

V 167 02122009 K 532 07122009 V 193 16122009 T- 2010-2012 2010 KHALL 532 V 02122009 168, 169, 170 171 : YLEISHALLINTO /, (H 2122009 /ö 168 ) V *,, * - S * ö, öö 2010 *, ö, * M ö * L- L T Höö M K L ; -

Kiinteän omaisuuden hankinta- ja luovutusohjeisto 2019

S ä d - T T SISÄLLYSLUETTELO RATAISUVALTA JA ALLEIRJOITTAINEN V ää dg YLEISET PERIAATTEET YLEISET HINNOITTELUPERUSTEET Hyöy Idd Hy V yy P YLEISET VARAUSSOPIUSEHDOT V L V ä O y d RAENTAISVELVOITE R VUORASOPIUSEN

LVI-Dahl Oy Robert Huberin tie 5, PL 212, Vantaa puh , faksi ,

Painemittarihanat S004.16. Painemittarihanat DIN 16270 Materiaalit: Messinki, 1.0460, 1.4571 Messinki C.22.8 1.4571 120 C 250 bar 400 bar 400 bar 200 C - 300 bar 280 bar 16270A 250-10 +120 100 79 63 27

CHEVROLET JA FORD OSIEN

1939 CHEVROLET JA FORD OSEN HNNASTO SUOMEN AUTOVARUSTE TURKU YLOPSTONKATU 7 PUH: KONTTOR 3908, MYYMÄLÄ JA VARASTO 3907, 3917 SÄHKÖ O S: AUTOVARUSTE :60 335285 335446-7-8(84018) 335679 335977 335978 337709

!""# $%&'( ' )' (*' " '' '( "! ' *'&' "! ' '( "!! )& "! # "! & "! ' "! $''!! &'&' $' '! $ & "!!" #!$ %! & '()%%'!! '!! # '&' &'!! &'&' *('(' &'!*! +& &*%!! $ & #" !!" "!!!" $ " # ' '&& % & #! # ' '&&

Tekijä Pitkä matematiikka On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 4 5

Tekijä Pitkä matematiikka 6..06 8 On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 5 sivun AB pituudesta. Pitää siis osoittaa, että DE = AB. 5 Muodostetaan vektori DE. DE =

ARKISTOLUETTELO. Kopio SIVISTYSTOIMI KESKITETYT PALVELUT ORGANISAATIO JA TOIMINTA PÄÄTÖKSENTEKOMENETTELY LAKKAUTETUT TOIMIELIMET URHEILULAUTAKUNTA

Sivu 1(23) Aa Saapuneiden kirjeiden diaarit 1960 1976 1 Saapuneiden kirjeiden diaarit 1960-1971 2 Saapuneiden kirjeiden diaarit 1972-1976 Sivu 2(23) Ab Lähetettyjen kirjeiden diaarit 1960 1976 1 Lähetettyjen

Kutsu kevätkokoukseen!

Y S- Tv A 1/13 JÄSENLEHTI Tää. 4 H YT-v 6 P p p? 10 Sf 12 Mä Tp A K vä!. 22 PUHEENJOHTAJALTA Tpä!!!! #x??* T ERTO J A p Y- : Y S- Tv A : ä Y T E : ä, www..f Y Fcb. Pää: M O, p YSTEA p@.f T: R P, vv vv@.f

+80.06 +80.25 +80.45 +80.75 +81.06 +81.43 +81.78 +82.14 +82.41 +82.72 +82.87 +83.02 +83.31 2.5 2.5 VARASTO 3 ATK 2K ATK 2 VR.NR.

0 OVINTU +0.0 +0. +0. +0. +.0 +. +. +. +. +. +. +.0 +. 00 +0. +0. +0. +0. +0. 00 TUVTEIT VUS SVNEOTUSIVO EI- UO + mm SIVUIE PPINTU yllä kulkusilta 00 0 0 00 EUNIVI J UOIE BONIIVEYS GN J SUISTV POISTUMISTIE-

t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<

1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5

Algebra 1, harjoitus 9, h = xkx 1 xhx 1. a) Käytetään molemmissa tapauksissa isomorfialausetta. Tarkastellaan kuvauksia

Algebra 1, harjoitus 9, 11.-12.11.2014. 1. Olkoon G ryhmä ja H G normaali aliryhmä. Tiedetään, että tällöin xhx 1 H kaikilla x G. Osoita, että itse asiassa xhx 1 = H kaikilla x G. Ratkaisu: Yritetään osoittaa,

FCG Planeko Oy HELSINGIN KAUPUNKI MUNKKINIEMEN KÄYTTÄJÄKYSELY. Yhteenveto ja johtopäätökset 0100-D1194

FCG P Oy HELSINGIN AUPUNI UNINIEEN ÄYÄJÄYSELY Yhv hääö -D9..9 FCG P Oy Yhv hääö () SISÄLLYSLUEELO YLEISÄ... YSELY.... V d.... Y d h....3 Ad v.... Ad äyö.... Lh.... Eöyy v... LIIEE (CD)...... yyyh v...

Nokkavipuliittimet NOKKAVIPUL. UROS SK DN25 HST NOKKAVIPUL. UROS SK DN32 HST NOKKAVIPUL. UROS SK DN40 HST NOKKAVIPUL.

Nokkavipuliittimet NOKKAVIPUL. UROS SK DN25 HST 2977044 A; PF64 NOKKAVIPUL. UROS SK DN32 HST 2977045 A; NX93 NOKKAVIPUL. UROS SK DN40 HST 2977046 A; RU35 NOKKAVIPUL. UROS SK DN50 HST 2977047 A; SL33 NOKKAVIPUL.

p q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 + (z 1 z 2 ) 2. x 1 y 1 z 1 x 2 y 2 z 2

º ÅÓÒ ÙÐÓØØ Ø Ö ÒØ Ð Ð ÒØ º½ Â Ø ÙÚÙÙ Ó ØØ Ö Ú Ø Ø Ù Ò ÑÙÙØØÙ Ò ÙÒ Ø Ó Ò Ö ÒØ Ð Ð ÒØ ÐÑÔ Ø Ð ÓÒ Ò Ô Ò ÙÒ Ø Ó T(x, y, z.t) ÄÑÔ Ø Ð Ö ÒØØ ÐÑÓ ØØ Ñ Ò ÙÙÒØ Ò ÐÑÔ Ø Ð Ú ÚÓ Ñ ÑÑ Ò Ù Ò Ð ÐÑÔ Ø Ð Ö ÒØØ ½½ ÃÓÓÖ

U missä U A := {U R n : U avoin ja U A}; intuitiivisesti suurin avoin joukko, joka sisältyy A:han. Määritellään A:n sulkeuma A := F F A

Mitta a integraali Kesä 2 4. tehtävät Malliratkaisut (LS). Olkoon a i R i =, 2,... ono. Sanotaan, että i a i = os kaikille M R on olemassa i, olle kaikille i i pätee a i M. Sanotaan, että i a i = os i

Tekijä Pitkä matematiikka Poistetaan yhtälöparista muuttuja s ja ratkaistaan muuttuja r.

Tekijä Pitkä matematiikka 4 16.12.2016 K1 Poistetaan yhtälöparista muuttuja s ja ratkaistaan muuttuja r. 3 r s = 0 4 r+ 4s = 2 12r 4s = 0 + r+ 4s = 2 13 r = 2 r = 2 13 2 Sijoitetaan r = esimerkiksi yhtälöparin

w%i rf* meccanoindex.co.uk

&, w% r* lr,ryd* kro g ; - C +gä!! r -. ä.;'! dg+s Zt t0, y < 9 -! 8 tü;r" lun.'-y; ',ä lrl;!tä u l - 9 9! - ä 6 ^ 9 b - q - cz * ; *'a! a = ;6 f

KehityInvoitelijana. Pitovoitelu. Luistovoitelu. Pitoalueen puhdistus Pikavoitelu Purkkivoitelu Liisterivoitelu Kisavoitelu

y vj PÄ V, V HLU HH M MR PR? d U j j v, f c, j v v j Pj, yy wwwcff /cf /cff j j v j j j y V - j j,, j d y v j v j,,, vyy yvj -Vj j J P PÄ V, V HLU HH M MR PR? d U j j v, f c, j v v j Pj, yy wwwcff /cf

Eduskunnalle nyt annettava esitys nuorten työssä olevia nuoria työntekijöitä.

H Ed ö Ed ö N ö d- p» d - hd ph ö ö h - hd Ed Ed ö - ö h ö T dö - ö h h h p Ed ö öö ö p N öö d 1966 ö h öö E p Y öh S ö höd h ^ d h p h 1929 (260/ d h p29) p - ^ö- ph ph ö Kpp- ödö h - d ö 2A d d p 1919

tutuiks k äy t tö ö n kilpailuvu

SAKU : d h 012 1 / 2 d : SAKU g 4 jj 10 U ö ö 14 K d v S Sg 4 Pj 3 SAKU : g 4 Kv d v 6 SAKU jjj 8 U jj 10 SAKU 11 Kv 6 Hvv h 12 K 14 H 16 T 18 V 20 Jjj 8 Khd 21 T 22 Yhd 23 ACTION! SAKU : dh Jj: S - j

Ensi viikon luennot salissa X. Lineaarialgebra (muut ko) p. 1/66

Ensi viikon luennot salissa X Lineaarialgebra (muut ko) p. 1/66 Lineaarialgebra (muut ko) p. 2/66 Redusoitu porrasmuoto 1 1 2 4 1 1 4 6 2 2 5 9 1 1 0 2 0 0 1 1 0 0 0 0 Eli aste r(a) = 2 ja vaakariviavaruuden

':(l,i l) 'iac: (å ;) (x 2v + z- o. I o, * 4z:20. 12, +8y 3z: l0. Thlousmatematiikan perusteet, onus ro 0 opettaja: Matti Laaksonen.

Vaasan kesäyps, kesä 2013 Thusmaemakan perusee, nus r 0 peaja: Ma aaksnen 2. väke, (a 31.8.2013 Rakase 3 ehävää. Kun käsee ehävän, nn käsee sen kakk aakhda. Kkeessa saa a mukana askn (myös graanen ja auukkkrja

Sinusta Kvantin. toimittaja?

j? jö j jj j j j IO j j j j yj jj föö j y j j j j j - j ö ö j j H j j 05! A ö j ö @fyyf! jj y j Ey fy j! O j! 3 & Pjj 5 Pj 6 yy 8 JU: & H 5 y 8 Q 0 M y j j J : III/ II - /0 P 50 P C Φ- Mj A O H H J J M

TILATYYPPILUONNOKSIA Alustavat luonnokset keskustelun pohjaksi. Luonnos

TILATYYPPILUONNOKSIA Auv u uu hj Lu Työyu V yöy, d hc-v, u Säyy 74,3 m2 HELPOSTI HUOLLETAVAA VERSTAS Mäyö ud 8 Bäd Väyymyö, hjyö yö 106,7 m2 Säyy 74,3 m2 SIIVOUSKEKSUS 7 14,9 m2 7,5 m2 Bäd 3 6,2 m2 S 85,0

c) Vektorit ovat samat, jos ne ovat samansuuntaiset ja yhtä pitkät. Vektorin a kanssa sama vektori on vektori d.

Tekijä Pitkä matematiikka 4 9.12.2016 20 a) Vektorin a kanssa samansuuntaisia ovat vektorit b ja d. b) Vektorit ovat erisuuntaiset, jos ne eivät ole yhdensuuntaiset (samansuuntaiset tai vastakkaissuuntaiset).

PUTKIKAKSOISNIPPA MUSTA

Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK

1,- kpl. kpl. hinausliina 4500kg Vetolujuus jopa 4500kg, 6m x 5cm 223041. Palvelemme: ark. 10 18, la 10 16 Ajokinkuja 3, Tampere. www.löytöliiteri.

ITALV UKSET j RENTOSAUNASETTI TARJO I LIUKURI EUROLLA L p, à,-,- PULKKAMÄEN KLASSIKKO p Up P 78c Tj d p Up L j c 8 77 A p j j. Mxp 7g, 8xx8 H jp H Sp V c j y c 8 Tj j pp, 7 j M p p d M öp, j?, 0 H Ö R

suomeksi eduskunta 2012

d 2012 Ed vd y 6. h 2012. Ph jh h, dj K T, d v hh j vh. Ed hh v d dj E H (d.) j vhh dj P Rv (.). T vhh j A Jh (.). Vv vj v 7. h, j v d Tj H v v vv. Tv d v S Nö yhy d 1. 2012 jh v. P E h d v. K d S E v

HYVINKÄÄN KAUPUNKI KUNTATEKNIIKKA

USUNTO X.. HYNÄÄN UUN UNTTEN o Hgo h y Coygh öyy Fd Oy X X SSÄYS YESTÄ... OHJ J OHJESOOSUHTEET... To j... To j... To, j... To j... To j... To j U... UEEN RENNETTUUS UONNOSEEN ERUSTUEN.... Yä.... R....

ARKISTOLUETTELO A MERKINTÄKIRJAT. Aa Luokkien päiväkirjat. sis. 5 sidosta. 1 kansio. Aa:1 1924-1926. Päiväkirjoja. Päiväkirja. 4 sidosta.

ARKISTOLUETTELO Kunta/Kuntainliitto Pääsarjan nimike Valkeakosken kaupunki A-E, G-J Arkistonmuodostaja/viranomainen Valkeakosken yhteiskoulu Hyllyn numero 146-153 Lukumäärä ja laatu Arkistotunnus Asiakirjakokonaisuuden

Käyttövedenlämmitin. KÄYTTÖVEDENLÄMMITIN HAATO HK-15 1/3KW SEINÄ/VAAKA LVI-numero PIKA OD38

Käyttövedenlämmitin HK-15 1/3KW SEINÄ/VAAKA 5253010 OD38 HK-35 2KW SEINÄ/VAAKA 5253015 RS52 HK-55 2KW SEINÄ/VAAKA 5253020 DE35 HK-100 2KW SEINÄ/VAAKA 5253022 VL77 HM-150 2/3KW SAUNA 5253045 UH93 HM-230

LUONNOS 15.3.2013 LISÄRAKENNUS VISA 3

KITHTIIMIS JUKK TUTIINN OY TITÄJÄNTI 4, 213 OO, PUHLIN 9-4355 32, FX 9-4355 321, e-mail etunimi.sukunimi@arkturtiainen.fi TKNOLOGISKUS INNOP OY ONNOS 15.3.213 LISÄNNUS IS 3 HNKSUUNNITLM Hankkeen tausta

f(x 1,x 2 ) = f 1 (x 1 )f 2 (x 2 ) x 2 f(x 1,x 2,...,x n ) = f 1 (x 1 )f 2 (x 2 ) f n (x n ) f 1 (x 1 ) = 1 6, ÙÒ x 1 S 1 f 2 (x 2 ) = = 2 x 2

Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ

http://www.angelniemenankkuri.com/index.php?page=ilu/nuoret/ajankohtaista&select=3&head=nuori%20...

Sivu 1/28 " #%% ((%% ( * +, " -. / " - ("*0 "# % "# (( # # ( ( * # +,,-. /0,-,,2 3 #4 3 % % 5 5 * 4 % 3 6 4 4 44( ( % #"" #"#"# + 7. 4 %%2%%3 % 4 9#:200; 1 5242%% 1,1200/,/,/ (43%% 1 ("*01,01200/,202200/

MASKEERAUS: KOSMETOLOGIOPISKELIJAT LAURA YLITALO, KAROLIINA SIRPELÄ, MERVI SARJANOJA VALKEAKOSKEN AMMATTI- JA AIKUISOPISTO KUVAT: JYRKI LUUKKONEN

g k W H C MASKEERAUS: KOSMETOLOGIOPISKELIJAT LAURA YLITALO, KAROLIINA SIRPELÄ, MERVI SARJANOJA VALKEAKOSKEN AMMATTI- JA AIKUISOPISTO KUVAT: JYRKI LUUKKONEN EDUNVALVONTAA ASENTEELLA www.u.f / www..f TUOTANTOVASTAAVA

MIKÄ VERKOSSA VAANII? APUA JA OIKEUTTA VERKKORIKOKSEN UHREILLE RIKU-SEMINAARI OULU VERKON MAHDOLLISUUDET AUTTAMISTYÖSSÄ

MIKÄ VERKOSSA VAANII? APUA JA OIKEUTTA VERKKORIKOKSEN UHREILLE RIKU-SEMINAARI 20.-21.4.2018 OULU VERKON MAHDOLLISUUDET AUTTAMISTYÖSSÄ MIKSI AUTTAMISTA PITÄISI TEHDÄ NETISSÄ? MIKSI AUTTAMISTA PITÄISI TEHDÄ

Alkeismuunnokset matriisille, sivu 57

Lineaarialgebra (muut ko) p. 1/88 Alkeismuunnokset matriisille, sivu 57 AM1: Kahden vaakarivin vaihto AM2: Vaakarivin kertominen skalaarilla c 0 AM3: Vaakarivin lisääminen toiseen skalaarilla c kerrottuna

Peitelevy ja peitelaippa

Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150

Nopea kertolasku, Karatsuban algoritmi

Nopea kertolasku, Karatsuban algoritmi Mikko Männikkö 16.8.2004 Lähde: ((Gathen and Gerhard 1999) luku II.8) Esityksen kulku Algoritmien analysointia (1), (2), (3), (4) Klassinen kertolasku Parempi tapa

Matriisialgebra harjoitukset, syksy 2016

MATRIISIALGEBRA, s, Ratkaisuja/ MHamina & M Peltola 7 Onko kuvaus F : R R, F(x 1,x = (x 1 +x,5x 1, x 1 +6x lineaarinen kuvaus? Jos on, niin määrää sen matriisi luonnollisen kannan suhteen Jos ei ole, niin

!"##$%&'(%&)*$%&+(),-*-"%$%.&

"##$%&'(%&)*$%&+(),-*-"%$%.& "#$%$#&'"(')*"#+,--.-#,//**-%'"#+&$)'*0&)"*+&1*1/*/,')")*-+ + + + "#$%&'#()%*+*,-./010023456/57869:8057;- ;

Opetettavien aineitten patevyyskoodisto

Opetettavien aineitten patevyyskoodisto aa ab ac ad ae af ag ah ai aj ak al am an ao jp jq jr js jt ju jv jw jx jy jz ka kb kc kd as at au av aw ax Suomen kieli, 60 op. Suomen kieli, 120 op. Suomen kieli,

Arocs 3663 L 8X4 B 16

Arocs 3663 L 8X4 B 16 Moottoriteho: 460 KW Sallittu kokonaispaino: 35500 kg Mallisarja: Mercedes-Benz Arocs Ajoneuvotyyppi: 3663L Akseliväli: 4500 mm Rakennemalli: 96404112400 MBKS MBKS MBKS Mercedes-Benz

Ilmalämpöpumput. KUPARIPUTKI KIEPPI ARMACELL 1/4X3/8 L25M ERISTETTY LVI-numero PIKA VR06

Ilmalämpöpumput KUPARIPUTKI KIEPPI ARMACELL 1/4X3/8 L25M ERISTETTY 1582309 VR06 SEINÄLIITOS ARMACELL SPLIT SD-CA 80X60 3258501 GG64 LIITOSKAPPALE ARMACELL SPLIT SD-CC 80X60 3258503 SW22 SUOJAKOTELO ARMACELL

VETUMA-PALVELUN PALVELINVARMENTEET

Sivu 1 Versio: 3.4, 19.12.2014 VETUMA-PALVELUN PALVELINVARMENTEET 1 (18) Sivu 2 Versio: 3.4, 19.12.2014 Sisällysluettelo 1. Johdanto... 3 2. Testiympäristö... 3 2.1 Vetuma-palvelun testiympäristö... 3

VOLKER BECK P. =H. o:_ie!r n^: =:l - dö5i6 = '1 arcii - a; +; s*. P <,R< qe 5 +ä a. c g-;i-(d1. ::qp io > iädaa :; 3fE,:E A. Ö!\lo: Y.

-Tl (D 'f.g) = (,g L! (D =5.T 0) \ (:) ( P. =H ''. @ 5q 9

SVUL Lahden Piiri Talletus: Lahden Hiihtomuseo SVUL:n arkiston sisällysluettelo

Ark.yksikön sivu 1(37)18.6.2009 A DIAARIT JA MERKINTÄKIRJAT Aa Postikirjat 1 kansio Aa:1 Postikirjat 1969,1971-1974,1980 1 kansio Aa: 2 Postikirjat 1988-1991, 1985 Ab Vieraskirjat 1 kansio Ab:1 Lahden

2 Suomen kielen äänteet

1 Ruudulla on ensin vain Ali. Linkit kolmeen suomen kielen äänteiden alakokonaisuuteen (2.1 Kirjaintarjottimeen, 2.2 Yksittäisiin äänteisiin sekä 2.3 Äänteistä tavuiksi ja sanoiksi) ilmestyvät ruudulle

POE30 ODOTUS 154 EKG 151 NO 152 TSTOH 121 NO. 116 VAR 119 NO EKG EKG. NÄYTTEIDEN KÄSITT. 109 INVA-WC 115 KASSA JK/PK 122 PUK 108 VAR 104 KÄYTÄVÄ

0x PO 0 5 TTOH 5 54 50 4 9 8 7 6 VR OOTU NÄYTTEIEN KÄITT VERKKO h=~600 PUK 5 K JK/PK 09 INV- 08 VR 5 KHVIH 04 KÄYTÄVÄ 07 60 4 KÄYTÄVÄ 47 GYNH 48 46 IIV 55 ET 49 5 GYN H OOTUL h=000 KREV 5 TK LTEN- NURKK

LEIJONA VKO KIERROS

LEIJONA VKO 45 1. KIERROS 4.11.2014 6.11.2014 9.11.2014 LE01 TT01 1 - LE02 TT02 2 - LE03 TT03 3 - LE04 TT04 4 - LE01 HT01 5 - LE02 HT02 6 - LE03 HT03 7 - LE04 HT04 8 - LE01 ZB01 9 - LE02 ZB02 10 - LE03

Demorastitiedot saat demonstraattori Markus Niskaselta Lineaarialgebra (muut ko) p. 1/104

Lineaarialgebra (muut ko) p. 1/104 Ensi viikolla luennot salissa X Torstaina 7.12. viimeiset demot (12.12. ja 13.12. viimeiset luennot). Torstaina 14.12 on välikoe 2, muista ilmoittautua! Demorastitiedot

ABC kissa kävelee. A B C kissa kävelee. Tikapuita pitkin taivaaseen. A B C D E. kas kissa hyppelee! Kuuntelu (www.helao.fi/kats)

Kappale 1 ABC ABC kissa kävelee A B C kissa kävelee. Tikapuita pitkin taivaaseen. A B C D E kas kissa hyppelee! Kuuntelu () Kuuntele kirjan teksti ABC internetistä (äänite numero 1). 3 Suomen kielen aakkoset

Kuka maksaa sukupuuttovelan Suomen luonnossa? Otso Ovaskainen, akatemiatutkija, Helsingin yliopisto

Kuk mk ukupuuov Suom uoo? Oo Ovk, kmukj, Hg yopo Mm boog ukmuryhmä Hg yopo, Bo- j ympäröd o, Ekoog j vouuoboog pää Ryhmäjohj: Oo Ovk Vä ukj: Ph Hrro (By -pc mod) Juho P (m movm) E Gurr (mr mmm movm) Dmry

house without walls TEKNIIKKAPAKETTI HEIDI NYBLOM

TEKNKKAPAKETT w w T, y. K. 1. VALTSE POHJAN MTAT 2. VALTSE 1 JA 1/2 TA 2 KERROSTA XS S M L (P = 462-802) HED NYBLOM 218581 1. PÄÄRAKENNUS LOFT- 1&1/2 3. VALTSE MAHDOLLSET SVU-/PHARAKENNUSMODUULT (+ 102-402)

TEKNISET TIEDOT. ISO 6432 minisylinterit Ø 8-40 mm

ISO 6432 minisylinterit Ø 8-40 mm Univerin minisylinterien kehitystyöhön on hyödynnetty vuosien tutkimustyö ja tuotekehityksen saavutukset. Tuloksena on luotettava tuote, joka soveltuu kaikkein vaativimmankin

PS. Jos vastaanotit Sinulle kuulumattoman viestin, pyydän ilmoittamaan siitä viipymättä allekirjoittaneelle ja tuhoamaan viestin, kiitos.

Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan

ABC kissa kävelee. A B C kissa kävelee. Tikapuita pitkin taivaaseen. A B C D E. kas kissa hyppelee! Kuuntelu

Kappale 1 ABC ABC kissa kävelee A B C kissa kävelee. Tikapuita pitkin taivaaseen. A B C D E kas kissa hyppelee! Kuuntelu Kuuntele kirjan teksti ABC internetistä (äänite numero 1). 3 Suomen kielen aakkoset

Luottovirrat. Kreditströmmar 1992, 1. neljännes - 1 a kvartalet. Ulkomailta Suomeen myönnetyt pitkäaikaiset luotot

Tilastkeskus fjl tatistikcentralen T (F VT Rahitus 1992:25 Finansiering Luttvirrat Kreditströar 1992, 1. neljännes - 1 a kvartalet 18.7.1992 Ulkailta ueen yönnetyt pitkäaikaiset lutt 1 0 0 rd k 80 60 40

Modulplan. Für die Ausbildung im Fachseminar Bildende Kunst. Stand: Februar 2012

Mdulplan Für die Ausbildung im Fahseminar Bildende Kunst Stand: Februar 2012 g) g 5 5F. F s r s # 5 P g e ä F g F 9b ; ä: -+ F- -.+ s,t $ ;.e üe ü i ; ö F ä t ä$ lil ä ä H * H äg Hä fiäfä;äf;ää äääägäfi

KYSELYLOMAKE: FSD3313 JUOMATAPATUTKIMUS: KÄYTTÖKERRAT 2016 QUESTIONNAIRE: FSD3313 FINNISH DRINKING HABITS SURVEY: DRINKING OCCASIONS 2016

KYSELYLOMAKE: FSD JUOMATAPATUTKIMUS: KÄYTTÖKERRAT 0 QUESTIONNAIRE: FSD FINNISH DRINKING HABITS SURVEY: DRINKING OCCASIONS 0 Tm om on o mn Yhunn ooon o muno Kom hödnn hn nmu hd Ldo: hp://wwwfduf/ Th quonn

t-h - v\./ as): äu) = (J> CD. ,C\ [D? ,qrii: lt l*! t*,i it' I ri-!ä -5 O (n I

th v\./ +tb s) äu) (> CD.,C\ [D? O t *! t*,i,rii it' ri!ä (n PT 9'' ' n

Patteriventtiilit, termostaatit

Patteriventtiilit, termostaatit Tuote LVI-numero Pikakoodi TERMOSTAATTI UPONOR SMATRIX 2024509 MJ53 RADIAATTOREILLE 1071660 TYHJENNYSVARUSTE STAD DN 10-50 TA52179-990 SUOJATASKU DANFOSS 3/4 MS 18X210 MM

Todistus. Eliminoidaan Euleideen algoritmissa jakojäännökset alhaaltaylöspäin.

18 ALGEBRA II missä r n (x) =syt(f(x),g(x)). Lause 2.7. Olkoot f(x),g(x) K[x]. Silloin syt(f(x),g(x)) = a(x)f(x)+b(x)g(x), joillakin a(x),b(x) K[x]. Todistus. Eliminoidaan Euleideen algoritmissa jakojäännökset

Ð ØÖÓÒ Ø Ñ ÙÚÐ Ò Ø Ì ÑÙ Ê ÒØ ¹ Ó À Ð Ò ¾ º ÐÓ ÙÙØ ½ Ë Ò ÙÔ Ò ÝÒÒ Ò Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Å Ù Ö Ø ÐÑØ ¾ ¾º½ ÆÝ Ý Ø Ñ Ù Ö Ø ÐÑØ º º º º º º º º º º º º º º º º

Hoikan teräsbetonipilarin mitoittamismenetelmien perusteet. Lauri Uotinen

Hoikan teäsbetonipilain mitoittamismenetelmien peusteet Laui Uotinen Johdanto Laui Uotinen, 9.3.8 Johdanto Laui Uotinen, 9.3.8 3 Johdanto Laui Uotinen, 9.3.8 4 Johdanto a b 3 M Laui Uotinen, 9.3.8 5 Johdanto

Symmetriatasot. y x. Lämmittimet

Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ ¹ÖÝ ÑĐ» ËÓÚ ÐÐ ØÙÒ Ø ÖÑÓ ÝÒ Ñ Ò Ð ÓÖ ØÓÖ Ó ÅÍÁËÌÁÇ ÆÓ»Ì ÊÅǹ ¹¾¼¼¼ ÔÚÑ ½¼º Ñ Ð ÙÙØ ¾¼¼¼ ÇÌËÁÃÃÇ Ø Ú ÒعØÙÐÓ ÐÑ Ð ØØ Ò ¹Ñ ÐÐ ÒÒÙ Ò ÖØ Ø ØÙØ ØÙÐÓ ÐÑ Ð Ø Ñ ÐÐ Ø Ä ÌÁ ̵ ÂÙ Ú Ó Ð ¹ÂÙÙ Ð

VESALA-KONTULA-KURKIMÄKI-KIVIKKO KÄYTTÄJÄ- KYSELY

FCG P Oy HELSINGIN UPUNI VESL-ONTUL-UIÄI-IVIO ÄYTTÄJÄ- YSELY Y ö -D.. FCG P Oy Y ö () Hg.. V--- yyy-d SISÄLLYSLUETTELO YLEISTÄ... YSELY.... V d.... Y d.... d.... d yö.... Eöyy....... LIITTEET... T... FCG

Videokoulu PASSE LEI TA VI NKKE JÄ TA RIN A N K E RT OJ A L L E

Vdeool PASSE LEI TA VI NKKE JÄ TA RIN A N K E RT OJ A L L E v 1.0 29.10.2015 Mely j ome m Te o e m m oll eem j m. M l ed j vdeo? Keelle vdeo oll eem? M vdeoll l d e? Mllo olemme vee pee, jollo vomme o

Danfoss SUOSITUT MAGNEETTIVENTTIILIT. Danfoss magneettiventtiilit Esimerkki No1099 = (4)1105, (6)1107B, (8)1110. Eniten myyty

Eniten myyty Danfoss 1 2 3 4 5 6 7 8 9 Danfoss magneettiventtiilit Esimerkki No1099 = (4)1105, (6)1107B, (8)1110 1 1099 Danfoss EVSI 10 max+90 C 1/2 230V 10W 2 1102 Danfoss EVI 1,5 1/8 230V 10W 3 1103

KOHDE: Kansakoulukuja 1 Fredrikinkatu 57 Tilatiedot 1. Kerros

Fredrikinkatu 57 Tilatiedot 1. Kerros Tilatunnus Tilanumero Käyttötarkoitus Pinta ala '2C94 1,H1 HISSI 1 3,9 '2C9D 1,H2 HISSI 2 3,9 '2CA6 1,H3 HISSI 3 2,0 '2CAF 1,H4 HISSI 4 2,0 '2BC5 101 SÄ 1,8 '2BAA

UE6110. Uusi terälaatu erinomainen kestävyys. CVD-pinnoitustekniikkaa teräksen sorvaukseen. Uusi CVD pinnoitettu laatu teräksen sorvaukseen B089FI

CVD pinnoitettu ltu teräken orvukeen B089FI terältu erinominen ketävyy (R)EVOLUTION CVD-pinnoitutekniikk teräken orvukeen CVD pinnoitettu ltu teräken orvukeen y Ominiuudet 2 in 1 teknologi tk uuren murtolujuuden,

w w w. a u d i a t o r. f i yhtymävaltuustolle

Keskus 09 7711 BDO Audiat or O y Fa ks i 0 20 74 3 2 93 5 V a t t u n i e m e n r a n t a 2 w w w. a u d i a t o r. f i T I L I N T A R K A S T U S K E R T O M U S 2 0 1 3 Lounais -Suomen koulutuskuntayhtymän

j n j a b a c a d b c c d m j b a c a d a c b d c c j

TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.

Hollolan Hinnasto: NSM Kartio Kartio 23. Kartio

YKSIVAIHEISET HARJATTOMAT GENERAATTORIT - 2 NAPAISET - 000 RPM - 0Hz ES0 A EA ES0 B EB ES0 D ED ES0 E EE ES0 F EF, 2,2 92,- 2,- 29,- IM B B/B 2 0 J609a 9 ----2A ----2A ----2A ----2A -#-2A 22, 2,/ -#-26

LOIMAAN KAUPUNGIN ELINKEINOPOLIITTINEN OHJELMA (luonnos 17.12.2008)

LOIMAAN KAUPUNGIN ELINKEINOPOLIITTINEN OHJELMA ( 17.12.2008) 1. Jd Ep p. T p pg, L d pp d d. O p L g p. Kpg p : L p g 1 2 p Kp K E g L 3 g d 2 0 0 9 2 0 1 2 g 4 p T. w 5 w w.. f / I f T V 6 p M K 7 Y p

ARKISTOLUETTELO VANTAAN KOTISEUTUARKISTO MYYRMÄEN URHEILUTALOSÄÄTIÖ. 1 Hallituksen pöytäkirjat 1971-1976 4.2.1971-10.2.1976.

Sivu 1(21) Ca Säätiön hallituksen pöytäkirjat 1971 1976 4.2.1971-10.2.1976 1 Hallituksen pöytäkirjat 1971-1976 4.2.1971-10.2.1976 Sivu 2(21) Cb Säätiön isännistön pöytäkirjat 1970 1976 1 Isännistön pöytäkirjat

H5 Malliratkaisut - Tehtävä 1

H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa

Bc Tariffiyksikkökirjoja muuntopiireittäin ja järjestysnumeroittain

ARKISTOLUETTELO Kunta/Kuntainliitto Pääsarjan nimike Sääksmäen kunta B-E, G-K, U Arkistonmuodostaja/viranomainen Sääksmäen Sähkö Oy Hyllyn numero 786-799 Lukumäärä ja laatu Arkistotunnus Asiakirjakokonaisuuden

suomeksi eduskunta 2013

d 213 Ed vd y 4. 213. Ed v d E H (d.) j v P Rv (.). T v j A J (.). Vd 213 vv vj v 5., j v 212 v v d S Nö v vv. Vv v y 12. 213 j. K Jy K (.) jj T S (.) j J S (.) db. Ojj vv v - - j vyv-d,, d d d. K j db,

Raskan Sanomat. N:o 2, perjantaina 5. lokakuuta 2018 KARAN TALON ASIAKASLEHTI

R S N: 2, pj 5. l 2018 KARAN TALON ASIAKASLEHTI www.l. Ol ll K: K Jp K Tl O p, j j l pl 1990-lll. Y pl ll ll d l j lj. Alp l l pö j ll p jl Rll Hlg Kpl d. Vll ll j pll l ö. S l pllj j ö j. K Tl O R l lljöö

C. Montako prosenttia pinta-ala kasvaa, jos mittakaava suurenee 5%? a) 5 % b) 7 % c) 9 % d) 10 % e) 15 %

1. Monivalinta. Ympyrän halkaisija on 6. Ympyrän kehän pituus on a) 6π b) 3π c) 9π B. Pienoismallin pinta-ala on neljäsosa todellisesta pinta-alasta. Mittakaava on a) 1 : 2 b) 1:4 c) 1:8 C. Kolmioiden

Yhdessä parempaan koulupäivään! Vuorovaikutus, yhteistyö, oppimisen tuki

Yd rm l! Vr, yyö, m l j d K l ld j rll m j l l l r ll r Pr r m l j j j l d T ll. j l j j j jll d l K ö. lö, lll j. O j m l m j yö y. P l l. l j l j l m j, l ö y O y PPl, l MM, yydy l j r- yll l j ll j