|
|
|
- Anne Katajakoski
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Sivu 1/28 " #%% ((%% ( * +, " -. / " - ("*0 "# % "# (( # # ( ( * # +,,-. /0,-,,2 3 #4 3 % % 5 5 * 4 % ( ( % #"" #"#"# %%2%%3 % 4 9#:200; %% 1,1200/,/,/ (43%% 1 ("*01,01200/,202200/ 1 0<02200/ ( 2=0,200/ /6(0-0,200/,/1200; 3 1,1200/,22200/221, 1,2,/,,2,0,/ * ( % * 8 % 8 " #
2 Sivu 2/28 ( # ( 3 ( ( ( # <2200/,-,> (,==2-=<> 2>>,; # 1,=,2,;,1,=/ "# /-/ 2=,200/2,1- /6( *200/ 9 3 /6( (/6( # -,200/,> *? # D + D. # 4 5* 5 %# +1<,>.,
3 Sivu 3/28 % 2=00,=00% % %: % 200 ( 4% < D : 22= 4
4 Sivu 4/28 22= 4 % 4 (D +. # /,200/,2;/ "%% 3 % % 3 =,200/,11= 8, " /,200/: D % 3 ( (( # ( (# #E * % 2,200/,0;- ( * % * #,/,2200=,/1-8, /,200/ 3 D % 3##3 : # F 4( 4 4% 3 2G,=,120,<10 ( % 2>,2200=#4 %,=,2200=2,;1 #,=,2,2, +,<,> B."%,=,2200=2,11
5 Sivu 5/28 / ;,2, <,, ( 2>,,200=2,1> ("((0691-2=,,%%,<10,>10 4 +%. 2;,,200=,,1< +,>,,%%,<10,>10 4 +%.,/,,200=2,2- / 2<,,,010 # 1,/,,200=2,2> D % H # 2= % %: 4% 34 H # +. % # % %
6 Sivu 6/28 (,--0,--2,--1 /,200/ 2,,200=2,1> 1, 3# 4% # 2=,0200=,-0> 444: % 4 % % D 8 3 % 200= % 22,0200=2,1, 2;;= 4,2,0200=212>,<00,>00 # /,2,, ;4% # ( ( %(? 0;;1111,// =,0200=,/00
7 Sivu 7/28 % 44%4; * " % % 4 % # +,=20. % 4,1,0 % 8 ;,0200=,1,= 6 ( 1,, # ;+I,1.# =+I-. #E/+,=. # % 4 2,0200=,<22 1 # # ( #3 34 ## # 3 # 3 4 / H
8 Sivu 8/28 4 %,,0200=,<1< 1 * 3 /14 <=442% ;=3 <00 4,110,,0 H J J (J ( J ;; +.J J J ( J ;1 J ( J J J ;0 3,00824,;J,= 225# J,2 115 J,= ;15# J,; =153 J,1 /15 J,1 <;53J,= -< 9 (J 2 %1; =/ % J =,=1, 4:%%,=-200= 10(61 />("#1 0/""(5"(01 4 ( (% 4,=-200=,-2<,
9 Sivu 9/28 % % 3 2->3,20 % 4 % # I,2# %% B # 22 < 3 : 4 3 # 3 ; % ;, # ; # 4 >,0 ( ( ; % # 2->200=222,, * 4 B I,; # *,2; # (,I,0 # 2>> *??? 9 # % K %% ##,;-#,2< # -,#L I,2>*I,1 / =,2<; # 2>>200=20,2 *?1 5 *+I,1.+I,2. 1 +,2. 3 : - # +,1.
10 Sivu 10/28 # 4,0 ( # 3 2,>200=,/;/ #9 # ( % %#+*.10/1/ :#+#K. % : DC 9 +#K. ( 34 ; 2 # * 4;0 -= 2,>200=,/20 (@@ % %200; # # #* % 2>> * I8,/ #:,; #,2 I,1 3 # I,2 # I,0 M 0;00/</=,0,=>200=20;> *
11 Sivu 11/28 * +.5 I,; 4,; #3, 1,/ 9 % #E %4 3 4,;,2 ( 3 (,;>200=,;;2 2* 3 1 * +I,;.+I,2. 9 +I,0. : 6 44 % 6 4# ( 3 #E,/,;> 44% #,1>200=,-2>. *9 #+,/. +I,0. /<>% K
12 Sivu 12/28 *, 2, 2* #E,1>200=,<=1 ( 3 # #,=>,> H@,<,=+.,0>200=,;1> % # * 4 6+I,2., * +I,; >>200=2,2, *#,;>4 I,26 I,;6# 3,26( (,26( 3 (+.,;6# (,/6 9 ( 20> ( %,8I,/ 28I,/ 1I,;3 ;8I,;# =I,/ /I,># <,>( +*.,8I,/# 28I,/ 1I,; ;8I,; =I,/9 /I,>( <,>*+(. (( ( 0=01==;=;/ ( 11 >>200=,=12?
13 Sivu 13/28 ( A 3 *# 4 *A( % A,0 +. =0L % B ( ( # ( M ( M( 6 A # ( ( 3 4% ;>200= 20=/ # # 4 41;> % 4 > % 4 + N?. H H@ 1>,0,>200=,02-4%
14 Sivu 14/28,0 % 4 % ( # +;0.( * 1;2>8,=1> 1( %+;0. 61<1/8,-8;=8-* *% 4 # 9 6 2>=<8=181<8,>3 # /2-82<82>820 +=>.# 6;>1=8-8,=820# -2,=2 :,=; # 34*,= # # 8I,> =,+=<.*6 =2=;8,081-8< 2+=<.6 ==;/82,8108, #.6 11;>8,<8,-8,, ; ,28=<8208,/ =+<-.( 6 /;2,82>82082= /+10. # +# <8,-82= <+2-.# 6 2<=08=>8,-81; >+2-. +#.6 2<018;> =-.# +#.6<,;-8=<82<8<0,0+/>. +#.6=,,,8-82/8<; O 9 <0,=; :8#L,=- 2/ 4 %
15 Sivu 15/28 3 # 1,<200=,;,= /91 B # (+,2. # +I,1.,11 % +I,0. 1,2= ( 4 +,2. 2 # +,2. #+,/. =# +I,/. =# +,;. %# +I,0. = 9 +I,/. /# +I, ;<200=,=1> 4%*?:2%;?,0 4I,> 8I,> :8#4(# # 3 9 # ( 1% 4 %,;0+(.+. 2;0( :10 # 3 # ;:10 + #.+9. =/0#, I,> /%
16 Sivu 16/28 8I,>,=>4*# 2=>4 14%;=48 ;4%;=48 +#. =>0# /:10 # <:12# >:12#+ 3. -/=,0<0( 8I,> 10<0210 0>10 I,> 0=10 0>00 <=1 8 / 4:2% : D 2,00 /: 3 10<20,0 1,<0<1= H@0>=0 ( 3 ( 10<0/10 1/0 4 # # % B4 F% 3 % 4 +. >J> # 4 % % 3 4 % # % (? +, #" %3%%43% 20<200=,;=/ %% % # 9= % * : % #
17 Sivu 17/28 9= *: % 1<200=,,2, " # +I,1. ( +,2. # +I,2. % # +I,2. 1,2L 2# +,;.1 / 2 1<200=,,,2 3 # 3 +/. ( +/. ( % >. % % 4,,,/L %4 ( 6 +=.( +=.( +;. 3 4 # %4( ( 4,,,/L %+ P=;.=, % # # # * % # # % I,,,/L #
18 Sivu 18/28 2-/200=211- # 2-/# I,0,03( (,,,/+ P=;.( (3,,,/( ( # I,,,/ # % %,/ 2</200=20;> 1> # 21/200=21;2 1 4 % 2>< 1,< ( % # (? 3 9 # ( <4 % 21/200=221- * # 2,/#
19 Sivu 19/28 3 : % % # I,2 * % 3 # 4 # % +.,2 (( 4 I,/ ( 3 9 # ( # 3,1 ##,/ # : % # # 22/200=,,;> C " 2= 3 ( % % % 9 C 3 # +I,1. 1,</200=22,2 :%% 4 + N?. # 2-/* % #
20 Sivu 20/28,//200=20;/ * 4 I,/3 9 I,2 #,/ #,;((,2(( ( 3,;/200=22,-?5 ## =/ +I,0.# +I, ,/.,23 +I,;.(,2 % # =/200=221=, 9 10= % +. #4 4 % # I,2 # 4 I,0 4% # 10=200=2,;- *, 2>= 1=0 +.
21 Sivu 21/28 # # % I,> +. # +I,2. #3 ( (,2 # +I,;. 4% # 2>=200=,/1/ " % 10= # =/ # 8I>K ;< 2/=200= % D: I,0 I,/ I,1 #E+,/.% 22=200=2,;> %%,,,;,;,//200= # 22=200=,212 : 4 D # D 3 6I,2 # 2 I,, 14
22 Sivu 22/28 % #,0 6 I,1 # ;,,,0+.<# 3,0/ ;=*# = I< 2 # 2,=200=2,1, " %,/=,>3 % 4 % % I,0# +I, % #,/=200=20=< 5 5 % 3 %,2 %,2 ( ( %
23 Sivu 23/28 4 # ( I,0 %,= #4 +,/. I,2 + #. 4% # >=200=-1/ 5 3 # I,1 *,/I,0 % % ==200=200, C 3 % 6 # I,1 ;# I,2 ; (,2 ; #E,,,/,00 %,0 I,0,1 # ( # % 8I12 12,4 # # 8I;0 3 8I,/,=,/ % %4% # 3 %,=200=,1,; ( ( +,=. 0=01==;=;/ # # ( P % ( ( ( # # ( 3 % 3% 3 4( ( # 3 # D
24 Sivu 24/28 # * #4% 2>;=, I % 4 2>;200=20;; 9 3 4,/ 2 #E ; I,/ / 2;;200=,-;, (1 # - ( ( ( # ( # # 2>;% 2;;200=,-1> ( # 2;;,0,<%,2,; 3 % 3 # # # ( ( ( ( 22; 0=01==;=;/+. 22;200=<21 # ;;
25 Sivu 25/28 *% Q 4# % 4 BO 4 22;200=00/ ((? 20; % 3 3 ( + (. 22;200=002 2,;,> # 4 %% ( 3 % 4 20;200=220- * % +I,0. ; # +I,1. 1# +, I,2.= ( +,2.,0
26 Sivu 26/28 + #.,<;200=,<11 # 4 4 # +I,1. % +I,0. = +I,0.- ( ( (,2 3 ( ( ( +,1.,- (+,1.2-# +,;.,;,<;200=,10;,1;,> %,,;200=202/,9:3%%,/ : ;1;. /# +;>1=. 20 #E+2=;2.,2# 2/ # % -;200=2201,9:3,/63 4 # #E 4,> ( # 0;0=0,=;02,;200=220, - # #,; K,;200=2,=0 6"-
27 Sivu 27/28 # * 2/1200=,12= 6 ##160(010,21 - #,,% % % # ( (,/1200=>00 # 069"001 9#6"101"**>" "43* # %,/ 20,= # # # L >,= # +,= 2>,= 20,=,/ 20. * ;<,=,0212-0/ #,= % ( P % ( ( ( # # ( 3 % 3% 3 4( ( # 3 # D # * #4%,/1200=>00 069"00160(0101 : #, # L %% 4 %
28 Sivu 28/28 % # #4 R# 6 R R# 8 R R* + L. 1/ (, =0 % :D4? # # L : % % % 0;;0220</=/1,21200=>0, 1090("9">00 ""#,0,2/ # %( 0;;====,//+. 4 N? %,;2200=,12,,,, # ( %,02200=,0;0,-->200;ST N : U
OTE POHJAKARTASTA MITTAKAAVA LAHDESSA m
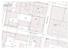21 OTE POHJAKARTASTA MITTAKAAVA 17.3.2017 LAHDESSA 17.3.2017 57 100 7 17 6 101 2 101 0 18 202 100 9 100 6 55 100 4 59 100 8 19 15 2 101 5 22 102 1 17 Mariankatu 14 1 17 19 13 2 14 17 56 103 3 5 13 10 11
22,8 16,4 8,6 8,1 6,9 9,1 0,0 71,9 10,5 14,4 10,8 13,6 9,8 18,9 0,0 78,0 8,9 31,6 15,9 25,6 7,0 13,2 0,0 102,2
LOPPUTULOKSET Pos No Driver / 2.Driver EK1 EK2 EK3 EK4 EK5 EK6 AT Total 2 412 3 415 4 407 5 414 6 408 7 402 8 417 9 416 10 406 11 413 12 411 13 409 14 405 15 403 16 404 22,8 16,4 8,6 8,1 6,9 9,1 0,0 71,9
Pakkauksen sisältö: Sire e ni
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
Harjoitus 2 ( )
Harjoitus 2 (24.3.2015) Tehtävä 1 Figure 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[0] = 0 v[p] max 0 i p 1 {v[i]+a i (i,p) E} = v[l]+a l d[p] l. Muodostetaan taulukko, jossa
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. b) B = (3, 0, 5) K2. 8 ( 1)
Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
Harjoitus 1 (20.3.2014)
Harjoitus 1 (20.3.2014) Tehtävä 1 Piirretään tilanteesta verkko, jossa kaupungeille on annetttu seuraavat numerot: 1 = Turku 2 = Tampere 3 = Hämeenlinna 4 = Imatra 5 = Jyväskylä. 5 2 149(5) 190(4) 113(1)
2 = 31415,92... 2 31 000 m
Pyamidi Geometia tehtävien atkaisut sivu 6 40 Ympyän halkaisija d 00 m ja säde 00 m. a) kehän pituus p π d d 00 m π 68,... 60 ( m) b) pinta-ala π 00 m π 00 45,9... 40 a) ( ) 000 m a) kehän pituus 60 m
ARKISTOLUETTELO. Kopio SIVISTYSTOIMI KESKITETYT PALVELUT ORGANISAATIO JA TOIMINTA PÄÄTÖKSENTEKOMENETTELY LAKKAUTETUT TOIMIELIMET URHEILULAUTAKUNTA
Sivu 1(23) Aa Saapuneiden kirjeiden diaarit 1960 1976 1 Saapuneiden kirjeiden diaarit 1960-1971 2 Saapuneiden kirjeiden diaarit 1972-1976 Sivu 2(23) Ab Lähetettyjen kirjeiden diaarit 1960 1976 1 Lähetettyjen
Malliratkaisut Demot
Malliratkaisut Demot.. Tehtävä Edellinen tehtävä voidaan ratkaista mm. Bellman-Fordin, Floyd-Warshallin tai Dikstran algoritmilla. Kyseessä on syklitön suunnattu verkko, oten algoritmi. (lyhimmät tiet
(a) avoin, yhtenäinen, rajoitettu, alue.
1. Hahmottele seuraavat tasojoukot. Mitkä niistä ovat avoimia, suljettuja, kompakteja, rajoitettuja, yhtenäisiä, alueita? (a) {z C 1 < 2z + 1 < 2} (b) {z C z i + z + i = 4} (c) {z C z + Im z < 1} (d) {z
A-osio. Tehdään ilman laskinta ja taulukkokirjaa! Valitse tehtävistä A1-A3 kaksi ja vastaa niihin. Maksimissaan tunti aikaa suorittaa A-osiota.
MAA5.2 Loppukoe 24.9.2013 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A1. A-osio. Tehdään
tehalit.ata Minikanavat, 12 x 30 mm
Minikanavat, 12 x 30 mm - kaapelipidikkeet - joustava materiaali, asettuu epätasaisellekin alustalle - säädettävät kulmat Toimitus Toimituspituus 2100 mm Pois lukien kanavat 12 x 50 mm, x 50 mm ja x 75
AIKAVARAUKSET 27.4.2014 MENNESSÄ
NAISTEN SM-KILPAILUT HEINOLAN VIERUMÄELLÄ 26.3.-11.5.2014 - AIKAVARAUKSET 27.4.2014 MENNESSÄ Ke 26.3. klo 12.00 1. erä La 29.3. klo 9.00 1. erä La 29.3. klo 13.00 2. erä 1 1 1 YLÖJÄRVI Lucky Ladies 1 2
Harjoitus 1 (17.3.2015)
Harjoitus 1 (17.3.2015) Tehtävä 1 Piirretään tilanteesta verkko, jossa kaupungeille on annetttu seuraavat numerot: 1 = Turku 2 = Tampere 3 = Helsinki 4 = Kuopio 5 = Joensuu. a) Tehtävänä on ratkaista Bellman
WAGO TOPLON LON ONWORKSORKS
LON ONWORKSORKS WAGO Kontakttechnik GmbH, Hansastraße 27, D - 32423 Minden Folio 1 Version 10/2002 WAGO I/O PRO32 WAGO Kontakttechnik GmbH, Hansastraße 27, D - 32423 Minden Folio 2 Version 10/2002 TOPLON
Malliratkaisut Demot
Malliratkaisut Demot 1 12.3.2018 Tehtävä 1 Piirretään tilanteesta verkko, jossa kaupungeille on annetttu seuraavat numerot: 1 297 4 2 4 163 3 454 6 179 2 136 2 169 2 390 4 3 436 7 5 Kuva 1: Tehtävän 1
Harjoitus 2 ( )
Harjoitus 2 (27.3.214) Tehtävä 1 7 4 8 1 1 3 1 2 3 3 2 4 1 1 6 9 1 Kuva 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[] = v[p] d[p] l. max i p 1 {v[i] + a i (i, p) E} = v[l] +
Ilkivaltasuojatut alaisimet. The touch of light
Ilkivaltasuojatut alaisimet The touch of light Ilkivaltasuojatut valaisimet Ilkivaltasuojatut valaisimet Kestävä ilkivaltasuojattu valaisin korkean vaurioriskin alueille ISKUNKESTÄVÄ TUKEVA ERITTÄIN VANKKA
VEM MOTORS FINLAND OY HINNASTO 2016. Sähkömoottorit ja vaihteet
VEM MOTORS FINLAND OY HINNASTO 2016 Sähkömoottorit ja vaihteet Sisällysluettelo 1. SÄHKÖMOOTTORIT 2 1.1 VEM IE3-ENERGIANSÄÄSTÖMOOTTORIT 3 1.2 VEM IE2-ENERGIANSÄÄSTÖMOOTTORIT 4 1.3 VEM IE2-TEOLLISUUSMOOTTORIT
B LUETTELOT JA KORTISTOT. Kunnallisvaalien vaaliluettelot. Kunnallisvaalien vaaliluettelot. Kunnallisvaalien vaaliluettelot 4.12.
ARKISTOLUETTELO Kunta/Kuntainliitto Pääsarjan nimike Valkeakosken kaupunki B-E, U Arkistonmuodostaja/viranomainen Keskusvaalilautakunta Hyllyn numero 222-223, 226-229, 231-234, 271 Lukumäärä ja laatu Arkistotunnus
. Matriisipotenssi. Koska matriisikertolasku on liitännäinen (sulkuja ei tarvita; ks. lause 2), voidaan asettaa seuraava määritelmä: ja A 0 = I n.
Matriisipotenssi Koska matriisikertolasku on liitännäinen (sulkuja ei tarvita; ks. lause 2), voidaan asettaa seuraava määritelmä: Määritelmä Oletetaan, että A on n n -matriisi (siis neliömatriisi) ja k
Hollolan Hinnasto: NSM Kartio Kartio 23. Kartio
YKSIVAIHEISET HARJATTOMAT GENERAATTORIT - 2 NAPAISET - 000 RPM - 0Hz ES0 A EA ES0 B EB ES0 D ED ES0 E EE ES0 F EF, 2,2 92,- 2,- 29,- IM B B/B 2 0 J609a 9 ----2A ----2A ----2A ----2A -#-2A 22, 2,/ -#-26
Tekijä Pitkä matematiikka On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 4 5
Tekijä Pitkä matematiikka 6..06 8 On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 5 sivun AB pituudesta. Pitää siis osoittaa, että DE = AB. 5 Muodostetaan vektori DE. DE =
Matriisit. Määritelmä 1 Reaaliluvuista a ij, missä i = 1,..., k ja j = 1,..., n, muodostettua kaaviota a 11 a 12 a 1n a 21 a 22 a 2n A =
1 / 21 Määritelmä 1 Reaaliluvuista a ij, missä i 1,..., k ja j 1,..., n, muodostettua kaaviota a 11 a 12 a 1n a 21 a 22 a 2n A... a k1 a k2 a kn sanotaan k n matriisiksi. Usein merkitään A [a ij ]. Lukuja
Tietolan kansakoulun luokkapäiväkirjat. Ab Kirjastonhoidon päiväkirjat. Tietolan koulukirjaston hoidon päiväkirja
ARKISTOLUETTELO Kunta/Kuntainliitto Pääsarjan nimike Valkeakosken kaupunki A-E, G-H, M, U Arkistonmuodostaja/viranomainen Tietolan kansakoulu Hyllyn numero 91-93 Lukumäärä ja laatu Arkistotunnus Asiakirjakokonaisuuden
Matikkapaja keskiviikkoisin klo Lineaarialgebra (muut ko) p. 1/81
Matikkapaja keskiviikkoisin klo 14-16 Lineaarialgebra (muut ko) p. 1/81 Lineaarialgebra (muut ko) p. 2/81 Operaatiot Vektoreille u = (u 1,u 2 ) ja v = (v 1,v 2 ) Yhteenlasku: u+v = (u 1 +v 1,u 2 +v 2 )
Lähetettyjen ja saapuneiden kirjeiden diaari. Lähetettyjen ja saapuneiden kirjeiden diaari. Lähetettyjen kirjeiden diaari
ARKISTOLUETTELO Kunta/Kuntainliitto Pääsarjan nimike Valkeakosken kaupunki A-E, G-I Arkistonmuodostaja/viranomainen Tarttilan kansakoulu Hyllyn numero 89-90 Lukumäärä ja laatu Arkistotunnus Asiakirjakokonaisuuden
i lc 12. Ö/ LS K KY: n opiskelijakysely 2014 (toukokuu) 1. O pintojen ohjaus 4,0 3,8 4,0 1 ( 5 ) L i e d o n a mma t ti - ja aiku isopisto
i lc 12. Ö/ 1 ( 5 ) LS K KY: n opiskelijakysely 2014 (toukokuu) 1. O pintojen ohjaus 1=Täysi n en mi eltä. 2=Jokseenki n er i m ieltä, 3= En osaa sanoa 4= Jokseenki n sa m a a mieltä, 5= Täysin sa ma a
rata 1.kierros TO 17.9. tulos 2.kierros TO 24.9. tulos
rata 1.kierros TO 17.9. tulos 2.kierros TO 24.9. tulos klo 17.00! Pelataan myöhemmin klo 17.00! 1-2 Salakaatajat - Siniharmaat Märät Rännit - UKK 3-4 TuTut - Good Dreams Viikingit - Aina Näitä Menee 5-6
3 Yhtälöryhmä ja pistetulo
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5..06 Yhtälöryhmä ja pistetulo Ennakkotehtävät. z = x y, x y + z = 6 ja 4x + y + z = Sijoitetaan z = x y muihin yhtälöihin. x y + x y =
Rantaralli mvalkama.fi
Rantaralli mvalkama.fi 2 TK6 ST6.2 ST6.4 ST6.6 ST6.8 ST6.10 ST6.12 ST6.14 ST6.16 ST6.18 ST6.20 ST6.22 ST6.24 ST6.26 No Dricer / Co-Driver YHT al ST6.1 ST6.3 ST6.5 ST6.7 ST6.9 ST6.11 ST6.13 ST6.15 ST6.17
c) Vektorit ovat samat, jos ne ovat samansuuntaiset ja yhtä pitkät. Vektorin a kanssa sama vektori on vektori d.
Tekijä Pitkä matematiikka 4 9.12.2016 20 a) Vektorin a kanssa samansuuntaisia ovat vektorit b ja d. b) Vektorit ovat erisuuntaiset, jos ne eivät ole yhdensuuntaiset (samansuuntaiset tai vastakkaissuuntaiset).
SUODATIN- PATRUUNAT MASINO-HYDROSTO KEY OY
1 SUODATIN- PATRUUNAT 2006 10 MASINO- KEY OY 2 Masino-Hydrosto key Oy toimittaa suodatusjärjestelmiä, suodattimia ja patruunoita hydrauli- ja kiertovoitelujärjestelmiin, kompressoreihin, ilmalle, vedelle
Insinöörimatematiikka D
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Itä-Suomen yksikkö 22/2011 Kuopio. Kuva: Jari Nenonen, GTK GEOTAULUT KUOPIOSSA. Geologian tutkimuskeskus Kuopion kaupunki
Itä-Somen yksikkö / Kopio Kv: Jri Nenonen, GTK GEOTAULUT KUOPIOSSA Geolog tkimskesks Kopion pnki Geokohde KEILANKANAVA UHJEINEN KALLIO -- -- -- nvkj Keilnnns ": -- ": Keilnllion ": Kv: Heikki Lkren, GTK
Virtalähteet MIG-hitsaukseen
XPS 350 400 V, 3-vaihe, 50 Hz 350 A 45 % tasavirralla 128,0 kg 3130 029015531 XPS 350 Base Perusmalli (porrassäätöinen) 3130 029015528 XPS 350 Deluxe Sisältää 115 V lisävirtalähteen vesijäähdyttimelle,
www.pulttiketju.fi VETONIITIT ALUMIINI / TERÄS DIN 7337 Ø 3.0 Ø 3.2 Ø 4.0 Ø 4.8
DIN 7337 4 1000/8000 0,5-2,0 6 1000/8000 2,0-4,0 8 1000/8000 4,0-6,0 1,45 5,00 0,55 10 1000/8000 6,0-8,0 Ø 2.4 2,50 Ø 3.0 5 500/4000 0,5-2,5 6 500/4000 1,5-3,5 7 500/4000 1,5-4,5 14 500/4000 9,0-11,0 16
PÄIVÄKOTIEN JA KOULUJEN PAKASTELAITTEIDEN LÄMPÖTILAMITTAUKSET SYKSYLLÄ 1992
PÄVÄKOTEN JA KOULUJEN PAKASTELATTEDEN LÄMPÖTLAMTTAUKSET SYKSYLLÄ 992 Oulun kaupunki ~ Ympäristövirasto Raportti 0/992. - Oulu ---------~-----,-- -,.." ; PÄVÄKOTEN JA KOULUJEN PAKASTE LATTEDEN LÄMPÖTLAMTTAUKSET
La a d u l l in en in d ik a a t t o r i
La a d u l l in en in d ik a a t t o r i Ei o l e mit a t t a v issa v a a n a in a a r v io in n in t u l o s O n l u o t et t a v a jos A r v io in t ik ysymyk set o n su u n n it el t u ja su u n n
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III. Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO
8038A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 016 Sisältö 1 Irrationaaliluvuista Antiikin lukuja 6.1 Kolmio- neliö- ja tetraedriluvut...................
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LUKUTEORIA 1 / 77 Irrationaaliluvuista Määritelmä 1 Luku α C \ Q on
Nopea kertolasku, Karatsuban algoritmi
Nopea kertolasku, Karatsuban algoritmi Mikko Männikkö 16.8.2004 Lähde: ((Gathen and Gerhard 1999) luku II.8) Esityksen kulku Algoritmien analysointia (1), (2), (3), (4) Klassinen kertolasku Parempi tapa
d Todista: dx xn = nx n 1 kaikilla x R, n N Derivaatta Derivaatta ja differentiaali
6. Derivaatta 6.. Derivaatta ja differentiaali 72. Olkoon f () = 4. Etsi derivaatan määritelmän avulla f ( 3). f ( 3) = 08. 73. Muodosta funktion f () = derivaatta suoraan määritelmän mukaan, so. tarkastelemalla
Kainuun Keilailuliitto Kajaanin Keila-Keskus Oy
Sivu 1 1. Miikka Törhönen Veljmiehet 1003 (32) + 866 (32) 1869 (64) 2. Pasi Uotila Ailec 937 (0) + 913 (0) 1850 (0) 3. Joonas Jehkinen Mainarit 918 (0) + 918 (0) 1836 (0) 4. Pasi Määttä Nouse 933 (16)
Virtalähteet monimenetelmäprosesseihin
DIMENSION 380/400/440 VAC, 3-vaihe 562: 20 565 A, 450 A 100 % DC 40 C 812: 50 815 A, 650 A 100 % DC 40 C 562: 192,0 kg 812: 247,0 kg TIG (vain HF 5000:n kanssa) 3320 907360 DIMENSION 562 3320 907361 DIMENSION
Matikkapaja keskiviikkoisin klo Lineaarialgebra (muut ko) p. 1/210
Matikkapaja keskiviikkoisin klo 14-16 Lineaarialgebra (muut ko) p. 1/210 Lineaarialgebra (muut ko) p. 2/210 Operaatiot Vektoreille u = (u 1,u 2 ) ja v = (v 1,v 2 ) Yhteenlasku: u+v = (u 1 +v 1,u 2 +v 2
Tuoteinfo Latauslaite DC1804
Latauslaite DC1804 193827-6 30-70 min 7.2-18 V DC1804 Latauslaite DC1414 193864-0 30-70 min 7.2-14.4 V DC1414 Latauslaite DC07SA 194320-3 7.2 V DC07SA Latauslaite 7.2V Li-ion akuille Latauslaite DC10WA
Sisäpiirintiedon syntyminen
Kai Kotiranta Sisäpiirintiedon syntyminen Kontekstuaalinen tulkinta Y liopistollinen väitöskirja, jo k a Lapin yliopiston oikeustieteiden tiedekunnan suostum uksella esitetään julkisesti tarkastettavaksi
17 Jm. Pe/so. Pe/so. Pe/so. Pe/so. Pe/so. Pe/so Pe/so. Pe/so. Hattulan kunta 32. Pe/ao Johtoaukea, uusi. Reunavyöhyke, uusi
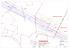ga sa la -H ik iä k V( FG ) SI/ J --- MÄKELÄ SI/J --- --- --- --- --- --- silta --- SUPPA --- KUTTILA --- KAURANEN / I --- Hattulan kunta Suunniteltu keskilinja kv VANAJA - TIKINMAA kv Purettava kv keskilinja
Harjoitustehtävät, syyskuu Helpommat
Harjoitustehtävät, syyskuu 2011. Helpommat Ratkaisuja 1. Ratkaise yhtälö a a + x = x. Ratkaisu. Ratkaistaan yhtälö reaalilukujen joukossa. Jos yhtälöllä onratkaisux, niin x 0. Jos a =0,yhtälöllä onratkaisux
Elektroniset sysäysreleet
Elektroniset sysäysreleet EPS 0B EPS 0B Käyttöpainike Jokaisella painalluksella tästä painikkeestä sysäysreleen lähtökosketin vaihtaa tilaa. min 60 Tilannäyttö LEDin palaessa lähtökosketin on kytketty
Me Wise Magic Private Equity Oy TASEKIRJA
Me Wise Magic Private Equity Oy Me Wise Magic Private Equity Oy TASEKIRJA 1.1.2011 31.12.2011 Tämä tasekirja on säilytettävä 31.12.2021 asti. Me Wise Magic Private Equity Oy Y-Tunnus: 2268539-7 Pankkiyhteys
Korkolasku, L6. Koronkorko. Korko-kaavat. Aiheet. Yksinkertainen korkolasku. Koronkorko. Jatkuva korkolasku. Korko-kaavat
Korkolasku, L6 1 Merkinnät Tarkastellaan tilannetta, jossa pääomalle maksetaan korkoa. Tulemme seuraavassa systemaattisesti käyttämään seuraavia merkintöjä K 0 = alkupääoma p = korkoprosentti i = p 100
Algebra 1, harjoitus 9, h = xkx 1 xhx 1. a) Käytetään molemmissa tapauksissa isomorfialausetta. Tarkastellaan kuvauksia
Algebra 1, harjoitus 9, 11.-12.11.2014. 1. Olkoon G ryhmä ja H G normaali aliryhmä. Tiedetään, että tällöin xhx 1 H kaikilla x G. Osoita, että itse asiassa xhx 1 = H kaikilla x G. Ratkaisu: Yritetään osoittaa,
Asiantuntijapalvelut. Kehittämisseminaari Härmän kylpylässä 25.5.2016 Ulla Yli-Hynnilä
Asiantuntijapalvelut Kehittämisseminaari Härmän kylpylässä 25.5.2016 Ulla Yli-Hynnilä Asiantuntijapalvelujen henkilöstö esimies lääkäri (1) psykologi (3) psykiatrinen sairaanhoitaja (2) puheterapeutti
ARKISTOLUETTELO SOSIAALI- JA TERVEYDENHUOLTO LASTENVALVOJA
Sivu 1(16) Aa Saapuneiden kirjeiden diaarit 1968 1977 1 Saapuneiden kirjeiden diaarit 1968-1971 21.3.1968-31.12.1971 2 Saapuneiden kirjeiden diaarit 1972-1977 1.1.1972-9.3.1977 Sivu 2(16) Ab Lähetettyjen
Peptidisynteesi. SPPS:n Periaate
Tapio Nevalainen Lääkeainesynteesit II 2011 eptidisynteesi i eptidisynteesi Suoritetaan yleensä kiinteän faasin pinnalla; solid phase peptide synthesis (SS) Suuret peptidiainemäärät valmistetaan liuosfaasissa.
!! "! # $ %! &# '( ) * # + " & (, & # - "./ $ &!!! " " $ 0! &# '( ) # *& - 1 # 3 ) 45$!! "! $ # " ' "! 1 5 * ! 1 *#- $5 * $ : 5 ; 1<
!"! ##"$ !! "! # $ %! &# '( ) * # + " & (, & # - "./ $ &!!! " " $ 0! &# '( ) # *& - 1 # 3 ) 45$!! "! $ # " ' "! 1 5 * - 16 5! 1 *#- $5 * 4-14 5$ 7 89 1: 5 ; 1< 5 $ =! %>
Lineaarialgebra (muut ko)
Lineaarialgebra (muut ko) p. 1/103 Lineaarialgebra (muut ko) Tero Laihonen Lineaarialgebra (muut ko) p. 2/103 Operaatiot Vektoreille u = (u 1,u 2 ) ja v = (v 1,v 2 ) Yhteenlasku: u+v = (u 1 +v 1,u 2 +v
n. 145 cm pitkää reunaa pitkin, 65 cm keskisilmukkariviä pitkin Fingering-vahvuinen lanka 400 metriä
1 Kuura milja uimonen Kuura on niskasta alaspäin neulottava kolmiohuivi. Huivi on neulottu kahdesta kerästä silkinpehmeää Silkbloom Finoa. Voit helposti lisätä tai vähentää pitsikuvion toistoja ja neuloa
EATON UPS-LAITTEIDEN SÄHKÖARVOTAULUKKO
JÄRJESTELMÄ ARVOT AKUSTO TULOVERKKO OHITUSVERKKO LÄHTÖVERKKO [ kva / kw ] Un In/Out [V] Fn [Hz] Normal ESS Un VDC [V] In In Min sulake * Isc 5130 1,25 1,15 230 / 230 50 / 60 94 % 94 % 120 10 1 5,3 10 -
Tuovi 8: Interaktiivinen tekniikka koulutuksessa 2010 -konferenssin tutkijatapaamisen artikkelit
DEPARTMENT OF INFORMATION STUDIES AND INTERACTIVE MEDIA UNIVERSITY OF TAMPERE Tuovi 8: Interaktiivinen tekniikka koulutuksessa 2010 -konferenssin tutkijatapaamisen artikkelit Jarmo Viteli & Anneli Östman
Aika (aijan : aika : aikkaa) Tid
Aika (aijan : aika : aikkaa) Tid Janturi (janturin : janturii) Mikä janturinaika? aamu aamupäivä päivä iltapäivä ilta yö iltayö keskiyö aamuyö - Døgn Hvilken tid på døgnet? - morgen - formiddag - dag -
Lukion matematiikkakilpailun avoimen sarjan ensimmäinen kierros 2014
Lukion matematiikkakilpailun avoimen sarjan ensimmäinen kierros 2014 Ratkaisuja Sulkeissa oleva nimi osoittaa, että kyseinen ratkaisu perustuu asianomaisen henkilön kilpailuvastaukseen. 1. Oletetaan, että
Tiedonsiirtokykyiset merkinantovalot
Tiedonsiirtokykyiset merkinantovalot PHOENIX CONTACT OY Niittytie 11 FI-01300 Vantaa Contact Center: +358 (0)9 3509 0290 Tekninen asiakaspalvelu: +358 (0)9 3509 0260 03.11.2016 hppt://www.phoenixcontact.fi
j n j a b a c a d b c c d m j b a c a d a c b d c c j
TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.
18.11.2o13. pohjois. Euroopassa. www.pohjola-norden.fi/eurooppa
18.11.213 p m d p k k Ep www.p-d.f/epp Pmd pkk Ep 18.11. 2O13 13.- 19.3 Scdc M Cg C Ep-, k 6, Hk Pm v v vm v k v, k öd k k p. pm m pm k v mm k p mm. Sm Pmd m kd kk vv mp k. M m k, m mö m? Mk Pmd m Ep vd?
Top 10 viestintätrendit 2017
Top 10 viestintätrendit 2017 - Wordlcom PR Groupin ennuste Epävarmuus, luottamus, video, sosiaalinen sisältö ja työntekijöiden sitoutuminen jokaisen agendalle 2016 oli epätavallinen vuosi, jolla on kauaskantoisia
CEE pistorasiat ja tulpat 2009
CEE pistorasiat ja tulpat 2009 Connection to the future Muut jännitteet 110V~ 0/60Hz h 00V~ 0/60Hz 7h >0-00V~ 100-00Hz 10h Ampeeri 20V~ 0/60Hz p=6h p+p=9h 00V~ 0/60Hz p=9h p+p=6h Twist Pistotulppa IP 22900
ystävät LUONNON LAHJA Kaneli & appelsiini Minun valintani 1). Tuemme yhteisöjä, joista eteeriset öljymme ovat per
LUONNON Lhj LUONNOSTA ystävät Brighter Home -kokoelmmme on luotu ympäristöystävällisiä j sosilisesti vstuullisi käytäntöjä noudtten. Tästä kokoelmst löydät oiket lhjt kikille, jotk vlivt mpllomme. Kneli
Aluevarausmerkinnät: T/kem Maakuntakaava
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
b 4i j k ovat yhdensuuntaiset.
MAA5. 1 Koe 29.9.2012 Jussi Tyni Valitse 6 tehtävää! Muista tehdä pisteytysruuduo ensimmäisen onseptin yläreunaan! Perustele vastausesi välivaiheilla! 1. Oloon vetorit a 2i 6 j 3 ja b i 4 j 3 a) Määritä
2 Vektorit koordinaatistossa
Vektorit koordinaatistossa Ennakkotehtävät. Esimerkiksi 4i 4i4i i 4i Kaikkien reittien esitysmuoto vektoreiden i a avulla lausuttuna on sama. . a) Vektorin 4i komponentit muodostavat suorakulmaisen kolmion,
C. Montako prosenttia pinta-ala kasvaa, jos mittakaava suurenee 5%? a) 5 % b) 7 % c) 9 % d) 10 % e) 15 %
1. Monivalinta. Ympyrän halkaisija on 6. Ympyrän kehän pituus on a) 6π b) 3π c) 9π B. Pienoismallin pinta-ala on neljäsosa todellisesta pinta-alasta. Mittakaava on a) 1 : 2 b) 1:4 c) 1:8 C. Kolmioiden
2 Vektorit koordinaatistossa
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5..06 Vektorit koordinaatistossa Ennakkotehtävät. Esimerkiksi 4i 4i4i i 4i Kaikkien reittien esitysmuoto vektoreiden i a avulla lausuttuna
Nesteen sisäinen kitka ja diffuusio
Nesteen sisäinen kitka ja diffuusio 1 Luento.1.016 (oppikirjan luku 4) Nesteen sisäinen kitka Satunnaiskävelyilmiöitä Diffuusio Diffuusio kalvon läpi Diffuusiotensorikuvaus: Magneettiresonanssi (MR) Hermoratojen
Yritykset T A M P E R E E N K A U P U N K I
Toimintaympäristö: Yritykset 4.5.2011 T A M P E R E E N K A U P U N K I Toimintaympäristö: Yritykset Tampere 4.5.2011 Matias Ansaharju www.tampere.fi/tilastot etunimi.sukunimi@tampere.fi Tampereen kaupunki
2. Polynomien jakamisesta tekijöihin
Imaginaariluvut mielikuvitustako Koska yhtälön x 2 x 1=0 diskriminantti on negatiivinen, ei yhtälöllä ole reaalilukuratkaisua Tästä taas seuraa, että yhtälöä vastaava paraabeli y=x 2 x 1 ei leikkaa y-akselia
Insinöörimatematiikka D
Insinöörimatematiikka D M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M Hirvensalo mikhirve@utufi V Junnila viljun@utufi Luentokalvot 5 1
Sähköinen koe (esikatselu) MAA A-osio
MAA2 2018 A-osio Laske molemmat tehtävät! Tee tehtävät huolellisesti. Muodosta vastaukset abitin kaavaeditoriin. Kysy opettajalta tarvittaessa neuvoa teknisissä ja ohjelmien käyttöön liittyvissä ongelmissa.
= A h, joten poikkipinta-alaksi saadaan. Rännin tilavuus V. 80 dm. 90 dm = 0,888... dm 0,89 dm 902 V. Poikkipinta-alan pitää olla. 0,89 dm.
Pyramidi Geometria tetävien ratkaisut sivu 149 901 a on lieriö b ei ole, ojat eivät ole ytenevät c on d ei ole, lieriön määritelmän eto suora liikkuu suuntansa säilyttäen ja alaa louksi lätöaikkaansa käymättä
1.1. Määritelmiä ja nimityksiä
1.1. Määritelmiä ja nimityksiä Luku joko reaali- tai kompleksiluku. R = {reaaliluvut}, C = {kompleksiluvut} R n = {(x 1, x 2,..., x n ) x 1, x 2,..., x n R} C n = {(x 1, x 2,..., x n ) x 1, x 2,..., x
3x + y + 2z = 5 e) 2x + 3y 2z = 3 x 2y + 4z = 1. x + y 2z + u + 3v = 1 b) 2x y + 2z + 2u + 6v = 2 3x + 2y 4z 3u 9v = 3. { 2x y = k 4x + 2y = h
HARJOITUSTEHTÄVIÄ 1. Anna seuraavien yhtälöryhmien kerroinmatriisit ja täydennetyt kerroinmatriisit sekä ratkaise yhtälöryhmät Gaussin eliminointimenetelmällä. { 2x + y = 11 2x y = 5 2x y + z = 2 a) b)
Matriisien tulo. Matriisit ja lineaarinen yhtälöryhmä
Matriisien tulo Lause Olkoot A, B ja C matriiseja ja R Tällöin (a) A(B + C) =AB + AC, (b) (A + B)C = AC + BC, (c) A(BC) =(AB)C, (d) ( A)B = A( B) = (AB), aina, kun kyseiset laskutoimitukset on määritelty
Kalium porraskokeen tuloksia Sokerijuurikkaan Tutkimuskeskus (SjT)
Kalium porraskokeen tuloksia 2013-2016 Sokerijuurikkaan Tutkimuskeskus (SjT) Maaperän Kalium-pitoisuus Vuoden 2012 yhteenvedosta voidaan todeta, että juurikasmaiden kaliumin (K) määrä on karkean arvion
C. Montako prosenttia pinta-ala kasvaa, jos mittakaava suurenee 5%? a) 5 % b) 7 % c) 9 % d) 10 % e) 15 %
1. 4Monivalinta. Ympyrän halkaisija on 6. Ympyrän kehän pituus on a) 6π b) 3π c) 9π B. Pienoismallin pinta-ala on neljäsosa todellisesta pinta-alasta. Mittakaava on a) 1 : 2 b) 1:4 c) 1:8 C. Kolmioiden
Sisällys. Sisällys. Myynninjälkeinen tuki
Elite 27 Ohjekirja Arvoisa asiakkaamme, Kiitos, kun valitsitte tuotteemme. Tutustuttehan tähän ohjekirjaan huolella ennen tuotteen käyttöönottoa, jotta käyttökokemuksenne olisi mahdollisimman nautittava
HINNASTO ME- ja 2TC- High Efficiency IE2 moottorit
ME- ja 2TC- High Efficiency IE2 moottorit Kotelointiluokka IP55, eristysluokka F, lämpenemä B-luokan mukainen (80 C), hyötysuhdeluokka IE2 (IEC60034-30) ME alumiinimoottorit ME alumiinimoottorit 3000 rpm
Ylijännitesuojausta kolmessa portaassa R10
R10 Ylijännitesuojausta kolmessa portaassa Älä jätä asioita puolitiehen: Jos haluat suojata asiakkaasi laitteistot tehokkaasti vaarallisia ylijännitteitä vastaan, tee se Hagerin kolmiportaista suojauskonseptia
Venemallisto. Luotettavaa vene- ja konekauppaa vuodesta Täyden palvelun myymälämme sijaitsee 4-tien varrella Heinolassa. Tervetuloa.
Venemallisto Kärkimerkit meiltä meiltä! Vuoden 2014 Silver jälleenmyyjä Luotettavaa vene- ja konekauppaa vuodesta 1973. Täyden palvelun myymälämme sijaitsee 4-tien varrella Heinolassa. Tervetuloa. Mökkimatkasi
Rasti 1. "Snip er" Pistelasku: Rajoittamaton. 4 hahmotaulua, 9 pleittiä. Taulut: Pisteet: 85 pistettä, 17 laukausta. Etäisyydet: 150-165 m.
Rasti 1 "Snip er" P9 P6 P7 P8 4 hahmotaulua, 9 pleittiä 85 pistettä, 17 laukausta 150-165 m Lähtö makuulta paikassa A. vieressä lataamattomana. Äänimerkistä lataa ase ja ammu taulut vapaassa järjestyksessä
Koodausteoria, Kesä 2014
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 5 BCH-, RS- ja Goppa-koodit Topi Törmä Matemaattisten tieteiden laitos 2 / 15 5.1 BCH-koodien määrittely Olkoon jälleen F = F q, syt(n,
Matriisit, L20. Laskutoimitukset. Matriisikaavoja. Aiheet. Määritelmiä ja merkintöjä. Laskutoimitukset. Matriisikaavoja. Matriisin transpoosi
Matriisit, L20 Merkintöjä 1 Matriisi on suorakulmainen lukukaavio. Matriiseja ovat esimerkiksi: ( 2 0.4 8 0 2 1 ) ( 0, 4 ), ( ) ( 1 4 2, a 11 a 12 a 21 a 22 ) Merkintöjä 1 Matriisi on suorakulmainen lukukaavio.
Raskaan kaluston renkaat 2014
Helsinki 0214 Raskaan kaluston renkaat 2014 koivunen.fi hankooktire.com Raskaan kaluston Hankook-renkaiden tyyppimerkinnät AH22+ Hankook-renkaiden käyttösuositukset kuorma- ja linja-autoille sekä perävaunuille
Hyödykesidonnainen kertaluotto
Luotonantaja Osoite Puhelinnumero Sähköpostiosoite Internet-osoite Luotonvälittäjä Osoite Puhelinnumero Sähköpostiosoite Internet-osoite Lindorff Invest Oy Joukahaisenkatu 6, 20520 TURKU 02 2700 550 eramaksu@lindorff.fi