Kvantin olemus ja massan aaltoluonne
|
|
|
- Satu Nurmi
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Millaisen kuvan todellisuudesta kvanttiekaniikan tulkinnat antavat? Luonnonfilosofian seura, Tieteiden talo Kvantin oleus ja assan aaltoluonne Tuoo Suntola Havaitsijakeskeisestä systeeikeskeiseen todellisuuteen - Havaitsijan asea systeeissä Massan aaltoluonne - Planckin ytälön viesti - Massa koleksisuureena (aaltolukuna) Massaobjekti resonaattorina - Liikeäärä assa-aaltona - Interferenssi kaksoisrakokokeessa Mitä ostulaatteja tarvitaan itä ostulaatteja ei tarvita? - Holistisessa teoriassa saat ostulaatit ätevät kaikilla osa-alueilla!
2 Millaisen kuvan todellisuudesta kvanttiekaniikan tulkinnat antavat? Luonnonfilosofian seura, Tieteiden talo Havaitsijakeskeisestä systeeikeskeiseen todellisuuteen Havaitsijakeskeinen allinnus joti antiikissa laneettojen liikkeen kuvaaiseen eisykleinä. Suteellisuusteoria kuvaa liikkeen vaikutuksen kelloiin ja etäisyyksiin aikadilaation ja ituuskontraktion avulla. Kuvaus yksinkertaistui, kun Koernikus tunnisti avaitsijan aikan ja liikkeen energiasysteeinä kuvatussa aurinkokunnassa. Kuvaus yksinkertaistuu, kun tunnistae avaitsijan aikan ja liikkeen energiasysteeinä kuvatussa avaruudessa: Mars Mercury Sun Moon Eart Juiter Venus Saturn E c E g M " GM " R Massaobjektin leoenergia on avaruuden D-laajeneisen liikeenergia = avaruuden uun assan synnyttää gravitaatioenergia. Pallosyetriasta jotuen kokonaisuuden vaikutus näkyy. ulottuvuudessa.
3 Millaisen kuvan todellisuudesta kvanttiekaniikan tulkinnat antavat? Luonnonfilosofian seura, Tieteiden talo Havaitsijakeskeisestä systeeikeskeiseen todellisuuteen Havaitsijakeskeinen allinnus joti antiikissa laneettojen liikkeen kuvaaiseen eisykleinä. Suteellisuusteoria kuvaa liikkeen vaikutuksen kelloiin ja etäisyyksiin aikadilaation ja ituuskontraktion avulla. Havaintojen allinnuksesta iliöiden allinnukseen! Kuvaus yksinkertaistui, kun Koernikus tunnisti avaitsijan aikan ja liikkeen energiasysteeinä kuvatussa aurinkokunnassa. Kuvaus yksinkertaistuu, kun tunnistae avaitsijan aikan ja liikkeen energiasysteeinä kuvatussa avaruudessa: Mars Mercury Sun Moon Eart Juiter Venus Saturn E c E g M " GM " R Massaobjektin leoenergia on avaruuden D-laajeneisen liikeenergia = avaruuden uun assan synnyttää gravitaatioenergia. Pallosyetriasta jotuen kokonaisuuden vaikutus näkyy. ulottuvuudessa.
4 Kvantin oleus ja assan aaltoluonne Tuoo Suntola Diolin yteen säteilyjaksoon eittoia energia: z 3 E N π e μc f J 3 E f 3 Ez π e μ c f E c f c c ћk c kg Massan leoenergia aallonituusekvivalentin (Coton-aallonituuden) avulla ilaistuna: E c c ћk c
5 Pelkistetty Planckin vakio ja energian ytenäinen ilasu Säteilyn yksikköjakso E c c c Aineen leoenergia Erest i c i c i c E g Aineen kokonaisenergia Etot c i c c c c Coulobin energia Kiidytys Coulobin kentässä siirtää assan c q q E c N N c c r r 1 c 1 c E g
6 Liikkeen vaikutus leoliikeäärään Karakteristiset taajuudet: f F n, l,, E l s c 1 F n, l,, l s Liikkeessä oleva atoikello käy itaain! lativistinen assan kasvu ei ole seuraus noeudesta vaan lisäassa, joka on tarvittu liikkeen aikaansaaiseen. c 1 c v v c v c Aineen kokonaisenergia Etot c i c c c c Coulobin energia Kiidytys Coulobin kentässä siirtää assan c q q E c N N c c r r 1 c 1 c
7 Coton-aallonituudesta de Broglie-aallonituuteen i Coton resonaattori c ½ c Havaittavan jäljen varjostielle synnyttää objektin luovuttaa kineettinen energia! Nettoaalto/liikeäärä avaitaan leokeyksessä c v c 1 c 1 v v 1 1 v c v c v c Doleriliö: Havainnot leokeyksessä Etuaallon liikeäärä kasvaa Taka-aallon liikeäärä ienenee ½ 1 ½ β 1 β 1 β 1 β c rˆ db c rˆ β 7
8 Elektronin erustilat vetyatoissa sonanssieto: Elektronikeän, πr, ituus on aallonituuden onikerta k φ πr n n c c πr n r n ћ Etot r Ekin ECoulob c ћkc ћ c ћkc Zα c r r Zα EZn, c 1 1 n Z n α c Kvanttitila ei ole sesifinen energiatila, vaan assa-aallon resonanssiedon täyttävän energiatilan inii. E Z,n [ev] n= n= [ev] n= r/r
9 Millaisen kuvan todellisuudesta kvanttiekaniikan tulkinnat antavat? Luonnonfilosofian seura, Tieteiden talo Vaitoedot fysikaalisen todellisuuden kuvaaisessa Jos suteellisuuseriaate ja ekvivalenssieriaate ostuloidaan, ja valon noeus ja assaobjektien leoassa oletetaan vakioiksi, koordinaatistosuureista, ajasta ja etäisyydestä tulee funktioita gravitaatiotilasta ja objektin noeudesta avaitsijaan näden. Leotilan käsite äärtyy. Massa on energian ileneisuoto. Aaltofunktio on ostuloitu koleksisuure, jonka itseisarvon neliö kuvaa iukkasen esiintyisen todennäköisyystieyttä. Jos nollaenergiaeriaate ja allosyetrisesti suljettu avaruus ostuloidaan, ja aikaa ja etäisyyttä käsitellään koordinaatistosuureina, avaruuden laajeneinen synnyttää ortogonaalikoonentin jokaiseen liikkeeseen avaruudessa. Valon noeus ääräytyy avaruuden laajeneisesta ja aikallisesta gravitaatiotilasta. Leoassa on funktio objektin liiketilasta. Massa on aaltolukuna ilaistava energian ilentäisen substanssi (koleksisuure), assaobjekti kuvataan assa-aaltojen resonanssirakenteina.
10 Te tree of te natural sciences de Broglie Max Planck Albert Einstein Isaac Newton Galileo Galilei Claudius Ptoley Eudoxus Matter wave, wave function, inderterinis Planck equation, a quantu of action Te teory of relativity, FLRW cosology Te laws of otion, te balance of forces deterinistic, linear reality Scrödinger Te laws of nature are te sae in all systes in rectilinear otion. Ptoley astronoy Motions of lanets can be described by adding eicycles to circular orbits. - Te caracteristic frequency of atoic oscillators is deterined by te energy state te state of otion and gravitation. - lativity aears as a consequence of te conservation of total energy in sace - Quantu states are energy inia of te energy states of resonant ass wave structures Planck s equation can E c f c c Ricard be derived fro diole >> te energy of a EM-wave as te Feynan eission: 3 E A π e μc f for of te rest energy of ass E f Jaes Maxwell E Feynan s great ystery rest tot gtot Sace as te 3D surface Te energy of otion is obtained of a D sere? fro te energy of gravitation Electroagnetis can be described as interlay of otential energy and te energy of otion. Te total aount of energy in te world is conserved bot locally and globally - tere is always as uc energy in a cause as in its effect. Local is a irror of te universe (onadology).... sere is te ost erfect for, needing no joint and being a colete wole,... best suited to enclose and retain all tings and arts of te universe like te sun, oon and stars E Gottfried Leibniz Everyting in sace is united. Tales Aristotle Te ost exact of te sciences are tose wic deal ost wit first rinciles. Canges are driven by enteleceia, te actualization of otentiality. Nicolaus Coernicus
11 Newton-SR&GR-QM-FLRW aika [s] etäisyys [] assa [kg] varaus [As] t r e F=a F g = GM/R i ekvivalenssieriaate g suteellisuuseriaate Dynaainen Universui aika [s] etäisyys [] assa [kg] varaus [As] E t r = ħ k e Nolla-energia tasaaino, allosyetrisesti suljettu avaruus GM " c Eg R Taivaanekaniikka E rest(total) Kosologia E g(global) E kin Suteellisuuseriaate (aikallinen) Postulaatit: - Aika-avaruus - Valon noeuden vakioisuus - Suteellisuuseriaate - Ekvivalenssieriaate - Kosologinen eriaate Säköagnetisi Kvanttiekaniikka Postulaatit: - aaltofunktio - Planckin ytälö - Scrödingerin ytälö - Klein-Gordon ytälö - Hilbertin avaruuden syetriat gravitaatio etriikan oinaisuus FLRW -kosologia Postulaatit: - GR etriikka - Vastaavuuseriaate (SR) - Planckin ytälö - Hubble flow - Pieä aine, ieä energia - Inflaatioyoteesi - Gravitaatioaallot Energian säilyinen kaikissa vuorovaikutuksissa avaruudessa E rest(local) E kinetic E el.agn. E radiation Taivaanekaniikka E g(local) Säköagnetisi assa-aalto Massaobjektien kuvaus: Massa-aaltojen resonanssin toteuttavat rakenteet
Fysiikka 8. Aine ja säteily
Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Luonnonfilosofian seura. Mitä havainnot ja mallit viestittävät todellisuudesta?
Mitä havainnot ja mallit viestittävät todellisuudesta? Ari Lehto, Heikki Sipilä ja Tuomo Suntola 1 PhysicsWeb Summaries 20.7.2007: Pimeän energian tutkimusryhmät voittivat kosmologiapalkinnon (July 17,
Kvantittuminen. E = hf f on säteilyn taajuus h on Planckin vakio h = 6, Js = 4, evs. Planckin kvanttihypoteesi
Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Kvanttifysiikan perusteet 2017
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Erityinen suhteellisuusteoria (Harris luku 2)
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Miten Machin ajatukset ovat toteutuneet tieteen kehittyessä?
Luonnonfilosofian seura, Tieteiden talo 2018-0416 Miten Machin ajatukset ovat toteutuneet tieteen kehittyessä? Tuomo Suntola Esityksessäni tarkastelen Machin luonnonfilosofiaa suhteessa tieteen kehitykseen
Osallistumislomakkeen viimeinen palautuspäivä on maanantai
Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
S Fysiikka III (EST) Tentti ja välikoeuusinta
S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
Kvanttisointi Aiheet:
Kvanttisointi Luento 5 4 Aiheet: Valosähköilmiö Einsteinin selitys Fotonit Aineaallot ja energian kvantittuminen Bohrin kvanttimalli atomille Bohrin malli vetyatomille Vedyn spektri Mitä olet oppinut?
Todennäköisyys ja epämääräisyysperiaate
Todennäköisyys ja epämääräisyysperiaate Luento 7 Hiukkas-aaltodualismi vaatii uudenlaisen kielenkäytön omaksumista kuvaamaan iukkasten liikettä ja paikkaa. Newtonin mekaniikassa iukkanen on aina jossain
53 ELEKTRONIN SUHTEELLISUUSTEOREETTINEN LIIKE- MÄÄRÄ
53 LKTRONIN SUHTLLISUUSTORTTINN LIIK- MÄÄRÄ 53. Lorentz-uunnos instein esitti. 95 erikoisen suhteellisuusteorian eruseriaatteen, jonka ukaan kaikkien luonnonlakien tulee olla saoja haainnoitsijoille, jotka
Aineaaltodynamiikka. Aikariippuva Schrödingerin yhtälö. Stationääriset tilat. Ei-stationääriset tilat
Aieaaltodyamiikka Aikariiuva Scrödigeri ytälö Aieaaltoketä aikariiuvuude määrää ytälö Aieaaltokettie riiuvuus ajasta aikariiuva Scrödigeri ytälö Statioääriset ja ei-statioääriset tilat Aaltoaketit Kvattimekaiika
Tfy Fysiikka IIB Mallivastaukset
Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Muuttuuko ajan kulkunopeus vai kellon värähtelytaajuus? Avril Styrman Luonnonfilosofian seuran te ta Suhteellisuusteoria
Muuttuuko ajan kulkunopeus vai kellon värähtelytaajuus? Avril Styrman Luonnonfilosofian seuran teemailta Suhteellisuusteoria 30.10.2018 Sisältö Vertaillaan Yleisen Suhteellisuusteorian (GR) ja Dynaamisen
ja KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
Voima ja potentiaalienergia II Energian kvantittuminen
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
3.4 Liike-energiasta ja potentiaalienergiasta
Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Shrödingerin yhtälön johto
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
INSINÖÖRIN NÄKÖKULMA FYSIIKAN TEHTÄVÄÄN. Heikki Sipilä LF-Seura
INSINÖÖRIN NÄKÖKULMA FYSIIKAN TEHTÄVÄÄN Heikki Sipilä LF-Seura 18.9.2018 Sisältö Henkilökohtaista taustaa Insinööri ja fysiikka Dimensioanalyysi insinöörin menetelmänä Esimerkki havainnon ja teorian yhdistämisestä
Ajan filosofia aika fysiikassa
Luonnonfilosofian seua Tieteiden talo, Helsinki 15.9.9 Ajan filosofia aika fysiikassa Voidaanko luonnonilmiöitä kuvata absoluuttiajassa? Tuomo Suntola Luonnonfilosofian seua Tieteiden talo, Helsinki 15.9.9
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
Osittaisdifferentiaaliyhtälöt
Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
http://www.space.com/23595-ancient-mars-oceans-nasa-video.html
http://www.space.com/23595-ancient-mars-oceans-nasa-video.html Mars-planeetan olosuhteiden kehitys Heikki Sipilä 17.02.2015 /LFS Mitä mallit kertovat asiasta Mitä voimme päätellä havainnoista Mikä mahtaa
Tähtitieteessä SI-yksiköissä ilmaistut luvut ovat usein hyvin isoja ja epähavainnollisia. Esimerkiksi
Tähtitieteen perusteet, harjoitus 2 Yleisiä huomioita: Tähtitieteessä SI-yksiköissä ilmaistut luvut ovat usein hyvin isoja ja epähavainnollisia. Esimerkiksi aurinkokunnan etäisyyksille kannattaa usein
Ekvipartitioperiaatteen mukaisesti jokaiseen efektiiviseen vapausasteeseen liittyy (1 / 2)kT energiaa molekyyliä kohden.
. Hiilidioksidiolekyyli CO tiedetään lineaariseksi a) Mitkä ovat eteneisliikkeen, pyöriisliikkeen ja värähtelyn suuriat ekvipartitioperiaatteen ukaiset läpöenergiat olekyyliä kohden, kun kaikki vapausasteet
Liikemäärä ja törmäykset
Liikeäärä a töräykset Haarto & Karhunen www.turkuak.fi Suureita Kaaleen liikeäärä: Vektorisuure Voidaan ilaista koonenttiuodossa,, x x y y z z Voian antaa iulssi: I Aiheuttaa liikeäärän uutoksen Vektorisuure
ELEC C4140 Kenttäteoria (syksy 2015)
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 11 / versio 23. marraskuuta 2015 Aaltojohdot ja resonaattorit (Ulaby 8.6 8.11) TE-, TM- ja TEM-aaltomuodot Suorakulmaisen aaltoputken perusaaltomuoto
Aikariippuva Schrödingerin yhtälö
Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Copyright 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley.
Newtonin painovoimateoria Knight Ch. 13 Saturnuksen renkaat koostuvat lukemattomista pölyhiukkasista ja jääkappaleista, suurimmat rantapallon kokoisia. Lisäksi Saturnusta kiertää ainakin 60 kuuta. Niiden
LIITE 11A: VALOSÄHKÖINEN ILMIÖ
LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
Perusvuorovaikutukset. Tapio Hansson
Perusvuorovaikutukset Tapio Hansson Perusvuorovaikutukset Vuorovaikutukset on perinteisesti jaettu neljään: Gravitaatio Sähkömagneettinen vuorovaikutus Heikko vuorovaikutus Vahva vuorovaikutus Sähköheikkoteoria
Aineaaltodynamiikkaa
Aineaaltodynamiikkaa Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit = kuinka hiukkasen fysikaaliset
FYSA242 Statistinen fysiikka, Harjoitustentti
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
S Fysiikka III (EST) (6 op) 1. välikoe
S-114.1327 Fysiikka III (EST) (6 op) 1. välikoe 1.3.21 Ilkka Tittonen 1. Vastaa seuraaviin kysymyksiin perustellusti, mutta ytimekkäästi (esim. 5-1 lausetta) (2p per kohta). a) Mikä on sidottu tila? Anna
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
S , Fysiikka III (S) I välikoe Malliratkaisut
S-4.35, Fysiikka III (S) I välikoe 9.0.000 Malliratkaisut Tehtävä Kuution uotoisessa säiliössä, jonka särän pituus on 0,0, on 3,0 0 olekyyliä happea (O) 300 K läpötilassa. a) Kuinka onta kertaa kukin olekyyli
Ydin- ja hiukkasfysiikka 2014: Harjoitus 5 Ratkaisut 1
Ydin- ja hiukkasfysiikka 04: Harjoitus 5 Ratkaisut Tehtävä a) Vapautunut energia saadaan laskemalla massan muutos reaktiossa: E = mc = [4(M( H) m e ) (M( 4 He) m e ) m e ]c = [4M( H) M( 4 He) 4m e ]c =
3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE
3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE 3.1. DE BROGLIE AALLOT 1905: Aaltojen hiukkasominaisuudet 1924: Hiukkasten aalto-ominaisuudet: de Broglien hypoteesi Liikkuvat hiukkaset käyttäytyvät aaltojen
Lataa Maailmanviiva - Jukka Maalampi. Lataa
Lataa Maailmanviiva - Jukka Maalampi Lataa Kirjailija: Jukka Maalampi ISBN: 9789525329513 Sivumäärä: 221 Formaatti: PDF Tiedoston koko: 28.94 Mb Sata vuotta sitten Albert Einstein ilmestyi kuin tyhjästä
Wien R-J /home/heikki/cele2008_2010/musta_kappale_approksimaatio Wed Mar 13 15:33:
1.2 T=12000 K 10 2 T=12000 K 1.0 Wien R-J 10 0 Wien R-J B λ (10 15 W/m 3 /sterad) 0.8 0.6 0.4 B λ (10 15 W/m 3 /sterad) 10-2 10-4 10-6 10-8 0.2 10-10 0.0 0 200 400 600 800 1000 nm 10-12 10 0 10 1 10 2
780392A/782631S Fysikaalinen kemia II, 5 op / 4 op
78392A/782631S Fysikaalinen kemia II, 5 op / 4 op Luennot: 5.9.-15.11.216 Ma klo 8-1 PR12 Ti klo 12-14 PR12 Risto Laitinen (22.2.-14.3.) Epäorgaanisen kemian tutkimusyksikkö (KE 313) PL 3 914 Oulun yliopisto
Teoreetikon kuva. maailmankaikkeudesta
Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
Aika empiirisenä käsitteenä. FT Matias Slavov Filosofian yliopistonopettaja Jyväskylän yliopisto
Aika empiirisenä käsitteenä FT Matias Slavov Filosofian yliopistonopettaja Jyväskylän yliopisto Luonnonfilosofian seuran kokous 7.3.2017 Esitelmän kysymys ja tavoite: Pääkysymys: Onko aika empiirinen käsite?
Luento 8 6.3.2015. Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit
Luento 8 6.3.2015 1 Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) 2 Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Pimeä energia. Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla
Pimeä energia Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla 27.5.2015 Friedmann- Robertson- Walker - malli homogeeninen ja isotrooppinen approksimaa>o maailmankaikkeudelle Havaintoihin sopii
Lyhyt katsaus gravitaatioaaltoihin
: Lyhyt katsaus gravitaatioaaltoihin Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Sisältö Suppea ja yleinen suhteellisuusteoria Häiriöteoria Aaltoratkaisut
Aatofunktiot ja epätarkkuus
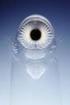Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Mekaniikan jatkokurssi Fys102
Mekaniikan jatkokurssi Fys12 Kevät 21 Jukka Maalampi LUENTO 11 Mekaaninen aaltoliike alto = avaruudessa etenevä järjestäytynyt häiriö. alto altoja on kahdenlaisia: Poikittainen aalto - poikkeamat kohtisuorassa
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
(1) (2) Normalisointiehdoksi saadaan nytkin yhtälö (2). Ratkaisemalla (2)+(3) saamme
S-446 Fysiikka IV (Sf) Tentti 3934 Oletetaan, että φ ja φ ovat ajasta riippumattoman Scrödingerin yhtälön samaan ominaisarvoon E liittyviä ominaisfunktioita Nämä funktiot ovat normitettuja, mutta eivät
PARADIGMOJEN VERTAILUPERUSTEET. Avril Styrman Luonnonfilosofian seura
PARADIGMOJEN VERTAILUPERUSTEET Avril Styrman Luonnonfilosofian seura 17.2.2015 KokonaisHede Koostuu paradigmoista Tieteen edistystä voidaan siten tarkastella prosessina missä paradigmat kehinyvät ja vaihtuvat
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Insinöörivalinnan fysiikan koe 1.6.2011, malliratkaisut
A1 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Täydennä kuhunkin kohtaan yhtälöstä puuttuva suure tai vakio alla olevasta taulukosta. Anna vastauksena kuhunkin kohtaan ainoastaan
Leptonit. - elektroni - myoni - tauhiukkanen - kolme erilaista neutriinoa. - neutriinojen varaus on 0 ja muiden leptonien varaus on -1
Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
Mekaniikan jatkokurssi Fys102
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
ψ(x) = A cos(kx) + B sin(kx). (2) k = nπ a. (3) E = n 2 π2 2 2ma 2 n2 E 0. (4)
76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
Ydin- ja hiukkasfysiikka: Harjoitus 1 Ratkaisut 1
Ydin- ja hiukkasfysiikka: Harjoitus Ratkaisut Tehtävä i) Isotoopeilla on sama määrä protoneja, eli sama järjestysluku Z, mutta eri massaluku A. Tässä isotooppeja keskenään ovat 9 30 3 0 4Be ja 4 Be, 4Si,
Valon sironta - ilmiöt ja mallinnus. Jouni Mäkitalo Fysiikan seminaari 2014
Valon sironta - ilmiöt ja mallinnus Jouni Mäkitalo Fysiikan seminaari 2014 Sisältö Johdanto Sironnan sähkömagneettinen mallinnus Analyyttinen sirontateoria Sironta ei-pallomaisista hiukkasista Johdanto
Luento 15: Mekaaniset aallot. Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot
Luento 15: Mekaaniset aallot Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot 1 / 40 Luennon sisältö Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos 1917: Einstein sovelsi yleistä suhteellisuusteoriaa koko maailmankaikkeuteen Linnunradan eli maailmankaikkeuden
Infrapunaspektroskopia
ultravioletti näkyvä valo Infrapunaspektroskopia IHMISEN JA ELINYMPÄ- RISTÖN KEMIAA, KE2 Kertausta sähkömagneettisesta säteilystä Sekä IR-spektroskopia että NMR-spektroskopia käyttävät sähkömagneettista
Mallit luonnonilmiöiden ja havaintojen kuvaajina
Mallit luonnonilmiöiden ja havaintojen kuvaajina 1. Mallien ominaisuuksista ja luokittelusta - havaintojen kuvaamisesta peruslakeihin. Energia-käsite - energian säilyminen paikallisjärjestelmissä / koko
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Ch7 Kvanttimekaniikan alkeita. Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset.
Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
J 2 = J 2 x + J 2 y + J 2 z.
FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
ELEC C4140 Kenttäteoria (syksy 2016)
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén Luentoviikko 5 / versio 7. lokakuuta 2016 Luentoviikko 5 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
Luento 10. Potentiaali jatkuu, voiman konservatiivisuus, dynamiikan ja energiaperiaatteen käyttö, reaalinen jousi
Luento 10 Potentiaali jatkuu, voiman konservatiivisuus, dynamiikan ja energiaperiaatteen käyttö, reaalinen jousi Tällä luennolla tavoitteena: Gravitaatio jatkuu Konservatiivinen voima Mitä eroa on energia-
Kuva 1: Etäisestä myrskystä tulee 100 metrisiä sekä 20 metrisiä aaltoja kohti rantaa.
Kuva : Etäisestä yrskystä tulee 00 etrisiä sekä 20 etrisiä aaltoja kohti rantaa. Myrskyn etäisyys Kuvan ukaisesti yrskystä tulee ensin pitkiä sataetrisiä aaltoja, joiden nopeus on v 00. 0 tuntia yöhein
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
Mekaniikan jatkokurssi Fys102
Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
FYSA220/K2 (FYS222/K2) Vaimeneva värähtely
FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
LUT, Sähkötekniikan osasto. 1. Ilmassa etenevällä tasoaallolla on sähkökentän voimakkuus z. d) vaihekerroin
SÄHKÖMAGNETISMI LUT, Sähkötekniikan osasto LH5/216 P.I. Ketausta: 1. Ilassa etenevällä tasoaallolla on sähkökentän voiakkuus z t E cos t z Ex,. Aallon taajuus on 2 MHz. Kuvassa 1 on esitetty tasoaallon
ELEC C4140 Kenttäteoria (syksy 2016)
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 8. marraskuuta 2016 Tasoaallot, osa 1 (Ulaby 7.1, 7.2, 7.4) Kenttäosoittimet Aikaharmoniset Maxwellin yhtälöt Tasoaaltoratkaisu Tasoaaltoyhtälöt
1.1 Vektorit. MS-A0004/A0006 Matriisilaskenta. 1.1 Vektorit. 1.1 Vektorit. Reaalinen n-ulotteinen avaruus on joukko. x 1. R n.
ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
Valosähköinen ilmiö. Kirkas valkoinen valo. Himmeä valkoinen valo. Kirkas uv-valo. Himmeä uv-valo
Valosähköinen ilmiö Vuonna 1887 saksalainen fyysikko Heinrich Hertz havaitsi sähkövarauksen purkautuvan metallikappaleen pinnalta, kun siihen kohdistui valoa. Tarkemmissa tutkimuksissa todettiin, että
Maailmankaikkeuden kriittinen tiheys
Maailmankaikkeuden kriittinen tiheys Tarkastellaan maailmankaikkeuden pientä pallomaista laajenevaa osaa, joka sisältää laajenemisliikkeessä olevia galakseja. Olkoon pallon säde R, massa M ja maailmankaikkeuden
Fysiikan perusteet. SI-järjestelmä. Antti Haarto 21.05.2012. www.turkuamk.fi
Fysiikan perusteet SI-järjestelmä Antti Haarto 21.05.2012 Fysiikka ja muut luonnontieteet Ihminen on aina pyrkinyt selittämään havaitsemansa ilmiöt Kreikkalaiset filosofit pyrkivät selvittämään ilmiöt
1. (a) (2p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori
FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
g-kentät ja voimat Haarto & Karhunen
g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Elektroni on keskeinen toimija sähkömagnetiikassa ja fysiikassa yleisestikin.
Tapio Kulmala, 10.10.2018 Puheen 11.12.18 /LFS käsikirjoitusta AALTORAKENTEISTEN HIUKKASTEN MAAILMA vs. diskreettien pistemäisten hiukkasten maailma 1. Taustaa ja motivaatiota tutkimukselle Elektroni on
ELEC C4140 Kenttäteoria (syksy 2015)
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 12 / versio 1. joulukuuta 2015 Antennit (Ulaby 9.1 9.6, 9.9) Hertzin dipoli Kaukokenttä Säteilykuvio ja suuntaavuus Antennin vahvistus ja
763105P JOHDATUS SUHTEELLISUUSTEORIAAN 1 Ratkaisut 5 Kevät 2016
7635P JOHDATUS SUHTEELLISUUSTEORIAAN Ratkaist 5 Kevät 26. Aberraatio shteellissteoriassa a) Tlkoon valo kten tehtävän kvassa (x, y)-tason x, y > neljänneksestä: x ˆx + y ŷ c cos θ ˆx c sin θ ŷ. () Lorenz
ELEC C4140 Kenttäteoria (syksy 2015)
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 6 / versio 14. lokakuuta 2015 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
n=5 n=4 M-sarja n=3 L-sarja n=2 Lisäys: K-sarjan hienorakenne K-sarja n=1
10.1 RÖNTGENSPEKTRI Kun kiihdytetyt elektronit törmäävät anodiin, syntyy jatkuvaa säteilyä sekä anodimateriaalille ominaista säteilyä (spektrin terävät piikit). Atomin uloimpien elektronien poistamiseen
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, , Ratkaisut (Sarja A)
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Braggin ehdon mukaan hilatasojen etäisyys (111)-tasoille on
763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
YLEINEN AALTOLIIKEOPPI
YLEINEN AALTOLIIKEOPPI KEVÄT 2017 1 Saana-Maija Huttula (saana.huttula@oulu.fi) Maanantai Tiistai Keskiviikko Torstai Perjantai Vk 8 Luento 1 Mekaaniset aallot 1 Luento 2 Mekaaniset aallot 2 Ääni ja kuuleminen
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä (ks. esim. http://www.kotiposti.net/ajnieminen/sutek.pdf). 1. a) Suppeamman suhteellisuusteorian perusolettamukset (Einsteinin suppeampi suhteellisuusteoria
Tekijä Pitkä matematiikka
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät y' P. α φ
76336A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät 217 1. Koordinaatiston muunnosmatriisi (a) y' P r α φ ' Tarkastellaan, mitä annettu muunnos = cos φ + y sin φ, y = sin φ + y cos φ, (1a) (1b) tekee
Fysiikan maailmankuva 2015 Luento 8. Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa?
Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
9 VALOAALTOJEN SUPERPOSITIO
09 9 VALOAALTOJEN SUPERPOSITIO Edellisissä kaaleissa olemme tutkineet valon heijastumista eileissä ja taittumista linsseissä geometrisen otiikan aroksimaation avulla Aroksimaatiossa valon aaltoluonnetta
KVANTTITELEPORTAATIO. Janne Tapiovaara. Rauman Lyseon lukio
KVANTTITELEPORTAATIO Janne Tapiovaara Rauman Lyseon lukio BEAM ME UP SCOTTY! Teleportaatio eli kaukosiirto on scifi-kirjailijoiden luoma. Star Trekin luoja Gene Roddenberry: on huomattavasti halvempaa
Kirkko ja tieteellinen maailmankuva. Arkkipiispa Tapio Luoma
Kirkko ja tieteellinen maailmankuva Arkkipiispa Tapio Luoma 15.3.2019 Maailmankuva Luontoa, ihmistä ja yhteiskuntaa koskevien oletusten tai tietojen systemaattista kokonaisuutta kutsutaan maailmankuvaksi.