Ainettarikkomaton ultraäänitarkastus Johdatus perusteisiin
|
|
|
- Pirkko Lehtilä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Ainettarikkomaton ultraäänitarkastus Johdatus perusteisiin
2 2
3 Ainettarikkomaton ultraäänitarkastus Johdatus perusteisiin Michael Berke Sisältö Johdanto 4 1. Miksi ultraääntä ainettarikkomat-tomaan tarkastukseen 4 2. Ultraäänitarkastuksen tehtävät 5 3. Epäjatkuvuuksien havaitseminen 5 4. Tarkastusmenetelmät ja laitetekniikka Ultraäänilaite Lähierotuskyky Luotain Taittuminen ja aaltomuodonmuutos Kulmaluotaimen ominaisuudet Kaksoisnormaaliluotain Epäjatkuvuuksien paikantaminen Ultraäänilaitteen säätö Säätö normaaliluotaimella Säätö kaksoisnormaaliluotaimella Säätö kulmaluotaimella Paikantaminen kulmaluotaimella Epäjatkuvuuksien arvostelu Koon määritys äänikeilan reunan avulla Pienten epäjatkuvuuksien koon arviointi: AVG-menetelmä Vaimennus Vertailukappalemenetelmä Kaikukorkeusvertailu Etäisyys-amplitudi-käyrä (DAC) Dokumentointi Näyttämien tulkinta 36 Käännös Sonar Oy 3
4 Johdanto Ultraäänitarkastusta on käytetty jo 40 vuotta. Ensimmäisistä kokeiluista löytää materiaalivikoja ultraäänen avulla on kehittynyt klassinen tarkastusmenetelmä. Nykyaikaiselta tarkastukselta vaaditaan toistettavia tuloksia. Ne on voitu saavuttaa laitetekniikan voimakkaan kehityksen ansiosta. Tämä asettaa vaatimuksia tarkastuksen rajoitusten tuntemukseen ja oikean tarkastus-tekniikan soveltamiseen. Aina eivät kuitenkaan kaikki vaikutukset ole niin merkittäviä, että ne olisi otettava huomioon. Useissa tapauksissa voidaan jokin vaikutus jättää huomioimatta ilman, että mittaustulokset vääristyisivät. Tällä tavoin tarkastus yksinkertaistuu ja tarkastusaika lyhenee. Kuitenkin vain vastuuntuntoisesti tehtävänsä suorittavilla ja itsensä uusimman tekniikan tasolla pitävillä tarkastajilla on tulevaisuus. 1. Miksi ultraääntä ainettarikkomattomaan tarkastukseen Pintatarkastukseen tarkoitettujen tunkeumanesteja magneettijauhetarkastusten lisäksi käytettiin radiografia tarkastusta sisäisten vikojen havaitsemiseksi 50 - luvun alussa. Toisen maailman-sodan jälkeen alkoi ultraäänilaitteiden valmistus. Ultraäänitarkastus perustuu kiinteiden materiaalien hyvään äänenjohtamiskykyyn. Rajapintojen lisäksi myös sisäiset viat (säröt, sulkeumat jne.) heijastavat hyvin ääntä. Materiaalin vaikutus ääneen on sitä merkittävämpi mitä pienempi aallonpituus on eli mitä korkeampi taajuus on: c = äänennopeus f = taajuus λ = aallonpituus λ = c f Jotta aallonpituus olisi mm-alueella, on ultraäänen taajuuden oltava 0,5-25 MHz. Matalammilla taajuuksilla on vikojen vaikutus ultraääniaaltoihin niin pieni, että niiden havaitseminen tulee jo kyseenalaiseksi. Ultraääni- että radiograafinen tarkastus, jotka osittain korvaavat ja täydentävät toisiaan, ovat tällä hetkellä tärkeimmät sisäisten vikojen tarkastukseen käytettävät menetelmät. Edullisella ja vaarattomalla ultraäänitarkastuksella voidaan ratkaista monia tarkastustehtäviä, kun erityistarkastuksiin käytetään kuten ennenkin radiografiaa. Suurta varmuutta vaativissa kohteissa (ydinvoimalat, lentokoneenrakennus jne.) käytetään molempia menetelmiä. 4
5 2. Ultraäänitarkastuksen tehtävät Onko ultraäänitarkastuksessa tiettyä tehtävien suoritusjärjestystä? Jos rajoitutaan pelkästään merkittäviin materiaalivikoihin, saadaan seuraava järjestys: 1. Heijastajien havaitseminen 2. Heijastajien paikantaminen 3. Heijastajien arvioiminen 4. Heijastajien arvostelu Erittäin lyhyen sähköpulssin vastaanottava pietsosähköinen muunnin lähettää ultraäänipulssin. Vastaanottaessaan äänen sama muunnin muuntaa äänen sähköiseksi pulssiksi. Luotain kytketään tarkastuskohteelle nesteen tai kytkentäaineen avulla, jotta ääni kulkisi luotaimesta kohteeseen ja takaisin. Luotainta liikutetaan kappaleen pinnalla tasaisin välein. Samanaikaisesti seurataan mahdollisista epäjatkuvuuksista saatavia kaikuja, kuva 2. Heijastajien sijasta käytetään yleisesti nimitystä epäjatkuvuus. Sillä kuvataan tarkastuskohteessa olevaa vian mahdollisesti sisältävää poikkeamaa tarkastuskohteessa. Vasta epäjatkuvuuden paikantamisen, arvioimisen ja tunnistamisen jälkeen voidaan sanoa, onko kyseessä tarkastuskohteen käyttöä haittaava vika. Sanaa epäjatkuvuus käytetään siis siihen saakka kunnes ollaan varmoja, onko kyseessä vika. 3. Epäjatkuvuuksien havaitseminen Ultraäänitarkastuksen todellinen työkalu on luotain, kuva 1a ja 1b. Kuva 2a Tasomainen vika - normaaliluotain Kuva 1 a Normaaliluotain (leikkaus) Kuva 1b Kulmaluotain (leikkaus) Kuva 2b Tasomainen vika - kulmaluotain Jokaisella luotaimella on oma vaikutusalue eli ääniaallot peittävät vain tietyn alueen tarkastuskohteesta. Tätä aluetta kutsutaan äänikeilaksi. Sen koko ja muoto ovat luotaimesta ja tarkastettavasta materiaalista riippuvaisia. Äänikeila voidaan jakaa kahteen eri alueeseen. Alueet ovat fokusoiva alue eli lähikenttä ja laajeneva alue eli kaukokenttä, kuva 3. 5
6 Kuva 4 b Tilaa ottava heijastaja - kulmaluotain Luotaimeen takaisin heijastuvan äänen määrä on riippumaton äänen tulosuunnasta. Eli on lähes samantekevää suoritetaanko tarkastus käyttäen normaali- tai kulmaluotainta ja miltä puolelta kappaletta luotaus suoritetaan, kuva 5. Kuva 3 Äänikeila Lähikentän pituus (N) ja avautumiskulma (γ) riippuvat muuntimen halkaisijasta, taajuudesta ja materiaalin äänennopeudesta. Äänikeilan keskilinjaa kutsutaan äänikeilan akseliksi. Äänikeilan muoto on tärkeää tarkastukseen sopivaa luotainta valittaessa. Tarkastuksen ratkaisun kannalta riittää usein vain keskiakselin esittäminen. Tilaa ottava epäjatkuvuus (kolo, sulkeuma jne.) heijastaa ääntä eri suuntiin, kuva 4a ja 4b: Kuva 5 Tilaa ottava heijastaja - luotaus eri suunnista Mikäli luotaimeen palaavan äänen määrä on riittävä, ei tilaa ottavan epäjatkuvuuden havaitseminen ole kriittistä, eli se voidaan havaita eri suunnilta. Tasomainen epäjatkuvuus (rajapinta, särö) heijastaa äänen tiettyyn suuntaan, kuva 6. Kuva 4 a Tilaa ottava epäjatkuvuus - normaaliluotain 6
7 Särön havaitsemis todennäköisyys on suuri sellaisissa tapauksissa, joissa voidaan hyödyntää nurkkaheijastusta, kuva 8a. Ääni heijastuu särön ja pinnan välisestä 90 o kulmasta takaisin luotaimeen, kuva 8b. Kuva 6 Heijastuminen vinosta tasomaisesta heijastajasta Jos ääni ei heijastu takaisin luotaimeen, on epäjatkuvuuden havaitseminen epävarmaa. Vain silloin kun tasomainen epäjatkuvuus kohdataan kohtisuoraan, on sen havaitsemis todennäköisyys suuri. Tämä koskee kappaleen sisäisiä epäjatkuvuuksia. Kappaleen pintaan asti kohtisuoraan avautuvia tasomaisia heijastajia, kuten pintasäröjä, ei havaita kohtisuoraan tulevan äänen avulla, koska ääni ohjautuu kappaleen sivuseinistä poispäin, kuva 7. Kuva 8a Pintasärön havaitseminen 45 o -kulmalla Kuva 8 b Nurkkaheijastus Nurkkaheijastusta voidaan hyväksikäyttää vielä silloinkin, kun särö ei ulotu aivan pintaan asti, olettaen, että säröstä saatava ääni heijastuu vielä pinnan kautta luotaimeen, kuva 9. Kuva 9 Lähellä pintaa oleva tasomainen heijastaja Kuva 7 Äänen ohjautuminen sivuseinästä Tämä ei ole useinkaan mahdollista tasomaisilla epäjatkuvuuksilla paksuseinämäisissä kohteissa. Ääni ei enää heijastu takaisin luotaimeen. Toisen luotaimen avulla voidaan vastaanottaa heijastuva ääni ja havaita epäjatkuvuus. Tällaisessa tandem-luotauksessa toinen luotain on lähetin ja toinen vastaanotin. Luotaimia liikutetaan kiinteällä etäisyydellä toisiinsa nähden kappaleen pinnalla. Luotaimien välisestä etäisyydestä 7
8 riippuen etsitään eri syvyysalueilla olevia tasomaisia heijastajia, kuva 10 a - c. Kuva 11a Epäedullinen luotauskulma Kuva 10 a Tandem luotaus: Ylempi alue Kuva 10 b Tandem luotaus: keskialue Havaitsemis todennäköisyyttä voidaan kuitenkin huomattavasti parantaa valitsemalla luotaimen kulma ja taajuus sopiviksi. Yhdellä luotaimella suoritettava tarkastus on yksinkertaisempaa kuin tandem-luotaus. Tämä pätee erityisesti alle 30 mm hitseillä. Tietysti todennäköisyys tasomaisten epäjatkuvuuksien havaitsemiseen pienenee, mutta usein tämä puute voidaan kompensoida uudella tarkastuksella eri kulmalla, kuva 11 b, tai valitsemalla matalataajuisempi luotain, kuva 11 c. Tarkastuslaajuuden määräykset löytyvät esimerkiksi hitsien tarkastusohjeista. Kuva 10 c Tandem luotaus: alempi alue Kuva 11b Oikein valittu luotauskulma Myös ohutseinämäisissä kappaleissa on mahdollista, että tasomaiset epäjatkuvuudet jäävät havaitsematta, koska niitä ei kohdata kohtisuoraan, kuva 11 a. Kuva 11 c Luotaus 2 MHz :llä: suuri avautumiskulma 8
9 4. Tarkastusmenetelmät ja laitetekniikka 4.1 Ultraäänilaite Ennen erilaisten tarkastusten ratkaisuja on käytävä tarkemmin läpi ultraäänitekniikkaa laitteineen ja luotaimineen. Epäjatkuvuuksien paikantamisen kannalta on selvää, että lähetettävien ultraääni-pulssien on oltava mahdollisimman lyhyitä, koska halutaan mitata kulkuaika luotaimesta epäjatkuvuuteen ja takaisin. Tämä on mahdollista vain silloin kun selvä aloitus- ja lopetushetki ovat olemassa. Mikäli tarkastuskohteen äänennopeus tunnetaan, voidaan yksinkertaisen kaavan avulla laskea epäjatkuvuuden etäisyys ja määrittää sen tarkka sijainti tarkastuskohteessa, kuva 12. Kuva 13 Lohkokaavio: ultraäänilaite Ajan mittaus alkaa sähköisestä lähtöpulssista, eli erittäin lyhyestä muuntimeen tulevasta sähköisestä latauksesta, joka muuttuu äänipulssiksi. Tämä ääni kulkee kappaleen läpi ja heijastuu takaisin luotaimeen epäjatkuvuudesta tai vastakkaisesta pinnasta. Luotaimessa ääni muuttuu takaisin sähköiseksi pulssiksi, johon ajan mittaus päättyy. Tällöin voidaan heijastajan etäisyys laskea. Jos kulkuaika piirretään graafisesti kuvapinnalle, ei puutu paljonkaan ultraäänilaitteesta, kuva 14. Kuva 12 Äänitie kulkuajan funktiona Äänen heijastuksia kuuluvalla alueella kutsutaan kaiuiksi. Yhtä hyvin voidaan tätä lyhyttä ja sopivaa nimeä käyttää myös ultraäänipulsseille. Tällä tavoin voidaan helposti ymmärtää eniten käytettyä pulssikaiku-menetelmää, kuva 13. Kuva 14 Ultraäänitarkastus käytännössä Kuvapinnalla näkyvien kaikujen arviointia varten on kuvapinta varustettu asteikolla, kuva 15. Asteikolle on piirretty vaaka- ja pystyrasteri. 9
10 Kuva 15 Kuvapinnan asteikko Asteikon avulla saadaan mittaustulokset. Miten tämä tapahtuu? Kuten aikaisemmin on todettu, lähettää sähköpulssin saava muunnin äänipulssin. Tämä sama lähtöpulssi tulee myös vahvistimen sisäänmenoon, joka aiheuttaa valopisteen pystyliikkeen kuvapinnan vasemmassa reunassa, kuva 16 a. Kuva 16 b 10 µs:n jälkeen Pisteen liikkumisnopeus on riippuvainen tarkastuskohteen äänennopeudesta. Pisteen siirtonopeus on säädettävissä. Valopisteen nopeus voidaan sovittaa äänennopeuteen. Oletetaan, että valopisteen nopeus on säädetty siten, että valopiste on asteikolla kohdalla 4, kun ääni on saavuttanut kappaleen vastakkaisen puolen, kuva 17a. Kuva 16 a Lähtöpulssi = aloituskohta Samanaikaisesti valopiste liikkuu kuvapinnan vasemmasta reunasta vakionopeudella peruslinjaa pitkin oikealle, kuva 16 b. 10
11 joka siirtää valopistettä ylöspäin kulkiessaan vahvistimen kautta ja näkyy takaseinäkaikuna, kuva 18. Kuva 17 a Valopiste kuvapinnalla kohdalla 4 Ääni tarvitsee saman ajan palatakseen takaisin, eli valopiste on asteikolla kohdalla 8, kuva 17 b. Kuva 18 Takaseinäkaiku kuvapinnalla kohdalla 8 Poikkeama on vain lyhytaikainen, koska erittäin lyhyt äänipulssi aiheuttaa myös lyhyen sähköpulssin. Valopiste palaa nopeasti takaisin perusviivalle ja jatkaa matkaa edelleen oikealle. Samanaikaisesti suurin osa palaavasta äänestä heijastuu kytkentäpinnasta takaisin kohteeseen. 1. Syntyneestä kuvasta saadaan kaksi mittausarvoa: Vaakasijainti: kaiun vasen reuna asteikolla kohdalla 8 2. Pystysijainti: kaiun korkeus 70% kuvapinnan korkeudesta, kuva 18 Kuva 17 b Valopiste kuvapinnalla kohdalla 8 Luotaimeen takaisin kytkentäaineen kautta palaava osa äänestä aiheuttaa sähköisen pulssin, Tämä ei kerro vielä paljon; mutta myöhemmin tulee esille, että lähes kaikki käytettävissä olevat tulokset perustuvat näihin kahteen mittausarvoon. Tarkistellaan saavutettua mittaustulosta hieman tarkemmin: Korkea lähtöpulssi alkaa vasemmalta asteikon nollakohdalta. Nousukohta vastaa sitä hetkeä, jolloin sähköpulssi tulee muuntimeen ja ääni muodostuu. Ennen tarkastuskohteen pintaan osumistaan on äänen kuljettava kuitenkin luotaimen suojapinnan (viive) läpi. Vaikka se 11
12 olisi ohut, kuluu sen läpäisyyn hetki. Tämän ajan verran on nollapiste siirrettävä kuvapinnalla vasemmalle, kuva 19 a. Kuva 20 Viasta saatava kaiku kuvapinnalla Kuva 19 a Normaaliluotain: Lähtöpulssin siirto Kulmaluotaimessa on äänen kuljettava huomattavasti pidempi matka pleksin läpi, ennen kuin se siirtyy kappaleeseen. Luotain-tyypistä riippuen voi siirto olla niin pitkä, ettei se mahdu kuvaruudulle, kuva 19 b. Tällaista kaikua kutsutaan välikaiuksi. Se, miten välikaiun sijainti muuttuu heijastajan syvyyden muuttuessa, on esitetty kuvassa 21 a ja b. Välikaiun paikka suhteessa takaseinäkaikuun muuttuu sen sijainnin mukaisesti takaseinäkaikuun nähden. Tällä tavoin voidaan vikojen paikka määrittää; tarkastajat puhuvat epäjatkuvuuksien paikantamisesta. Kuva 19 b Kulmaluotain: lähtöpulssin siirto Asteikon kohdalla 8 olevaa kaikua voidaan tarkastella tarkemmin: Se vastaa vastakkaisesta seinämästä heijastunutta ääntä eli on takaseinäkaiku. Nyt ei ole vaikeaa ymmärtää, että äänikeilassa oleva heijastaja, esimerkiksi halkeama aiheuttaa kaiun lähtöpulssin ja takaseinäkaiun välille. Ääni heijastuu osittain epäjatkuvuudesta, kuva 20. Kuva 21 a Lähellä takaseinää oleva vika 12
13 silloin kun epäjatkuvuus on tarpeeksi suuri peittämään äänikeilasta niin suuren osan, että takaseinäkaiku pienenee, kuva 23. Kuva 21 b Lähellä pintaa oleva vika 4.2 Lähierotuskyky Mitä tapahtuu, kun lähellä pintaa luotaimen alla on pieni epäjatkuvuus? Voidaanko tällainen heijastaja vielä havaita? Vastaus on ei! Välikaiku jää lähtöpulssin kohdalle ja jää sen alle. Mahdollisesti ei ole myöskään muita viitteitä siitä, että pinnan lähellä olisi epäjatkuvuus, kuva 22. Kuva 23 Takaseinäkaiun vaimeneminen lähellä pintaa olevan suuren vian johdosta Pinnan lähellä olevan epäjatkuvuuden ollessa sekä tasainen että pinnan suuntainen syntyy enemmän tai vähemmän selvä kaikujono äänen heijastuessa edestakaisin pinnan ja epäjatkuvuuden välillä, kuva 24. Etäisyyden kasvaessa pienenee kaiku-korkeus. Mitä lähempänä epäjatkuvuus on pintaa, sitä enemmän kaikuja häviää lähtöpulssiin ja sitä lähempänä kaiut ovat toisiaan. Myös tällaisissa tapauksissa on havaittavuudelle olemassa raja. Kuva 22 Lähellä pintaa oleva heijasta, ei havaittavissa Vai onko olemassa jokin toinen tapa, jolla peittoon jäänyt välikaiku (lähellä pintaa olevasta epäjatkuvuudesta) voidaan havaita? Kyllä on, Kuva 24 Kaikujono pinnan lähellä olevasta viasta 13
14 Tästä kaikesta voidaan päätellä, että lähtöpulssi ei ole tervetullut, vaikkakin teknisesti välttämätön paha: Se rajoittaa lähellä pintaa olevien epäjatkuvuuksien havaitsemista. Heijastajia, jotka sijaitsevat kuolleella alueella eli välittömästi pinnan alla tarkastamattomalla alueella, ei voida enää havaita, kuva 25. Kuollut alue on riippuvainen luotaimesta ja laitteesta. Se voidaan siten minimoida luotaimen ja laitteen oikealla valinnalla. 4.3 Luotain Ääntä kohtisuoraan pintaan nähden lähettävää ja vastaanottavaa luotainta kutsutaan normaaliluotaimeksi, kuva 1 a ja 26. Kuva 26 Normaaliluotaimet Kuva 25 Kuollut alue Useimmat normaaliluotaimet lähettävät pitkittäisaaltoa (paineaalto). Ne tunnistaa siitä, että ne etenevät kaikissa materiaaleissa tihentymien ja harventumien välityksellä, kuva 27. Aallonpituus Värähdys suunta Etenemissuunta Kuva 27 Pitkittäisaalto Normaaliluotaimia on olemassa suuri valikoima eri kokoisina ja taajuisina 0,5-25 MHz. Niiden avulla voidaan saavuttaa yli 10 m etäisyys ja näin tarkastaa suurimpiakin kappaleita. Laaja valikoima mahdollistaa luotaimen ominaisuuksien sovittamisen kaikkiin tarkastustehtäviin. Yhden joissakin tapauksissa merkittävän normaaliluotaimen rajoituksen olemme äsken oppineet tuntemaan: Lähtöpulssin leveydestä johtuva huono pintaa lähellä olevien epäjatkuvuuksien havaitsemisominaisuus. 14
15 Vinosti pintaan nähden ääntä lähettäviä ja vastaanottavia luotaimia kutsutaan kulmaluotaimiksi, kuva 1b ja Taittuminen ja aaltomuodonmuutos Kulmassa etenevät aallot syntyvät lähes poikkeuksetta siten, että ääniaallot kohtaavat luotaimen ja kappaleen välisen rajapinnan kulmassa, kuva 1 b. Helpommin tällainen saadaan liimaamalla pleksi kiila luotaimeen. Pitkittäisaallon kohdatessa tietyllä kulmalla pleksi/teräs-rajapinnan, hajoaa tuleva ääni heijastuvaan ja taittuvaan osaan, kuva 30 a: Kuva 28 Kulmaluotaimet Useimmat kulmaluotaimet lähettävät ja vastaanottavat poikittaisaaltoja tai leikkausaaltoja. Poikittaisaalloilla värähtelevät atomit (molekyylit) poikittain aallon etenemissuuntaan nähden, kuva 29. Äänen värähtely tapahtuu leikkausvoimien vaikutuksesta. Poikittaisaallot etenevät vain kiinteissä aineissa, eli ei koskaan nesteissä ja kaasuissa. Tämän lisäksi poikittaisaallot etenevät huomattavat hitaammin kuin pitkittäisaallot samassa materiaalissa. Kysymykseen, miksi kulmaluotaimet eivät lähetä pitkittäisaaltoja, ei voida antaa lyhyttä vastausta. Tähän tarvitaan laajempi selvitys. Värähdys suunta Kuva 29 Poikittaisaalto Aallonpituus Etenemissuunta Kuva 30a Heijastuminen ja taittuminen ilman poikittaisaaltoa Heijastunut ääni kuuluu heijastuslakiin (tulokulma = heijastuskulma) ja taittunut aalto käyttäytyy seuraavan kaavaan mukaan: sinα sinβ = c c α = tulokulma β = taittumiskulma c 1 = äänennopeus materiaalissa 1 c 2 = äänennopeus materiaalissa 2 Lisäksi tapahtuu jotakin muuta: Äänen kohtaamis-kohdassa muodostuu poikittaisaaltoa, kuva 30 b. Sekä heijastus- että taittumispuolella! Koska poikittaisaaltojen etenemisnopeus on vain noin puolet pitkittäisaallon etenemisnopeudesta, saadaan laskentakaavan avulla poikittaisaalloille
16 eri heijastumis- ja taittumiskulmat kuin pitkittäisaallolle. Missä epäjatkuvuus todellisuudessa sijaitsee? Tarkastaja voi olla varma asiasta vain silloin, kun käytössä on vain yksi aaltomuoto. Tämä on epäilemättä edellytys kulmaluotainten yleiselle käytölle. Tämä edellytys saadaan laskentakaavasta: Tiedetään, että pitkittäisaaltojen taittumis-kulma on noin kaksinkertainen poikittaisaaltojen taittumiskulmaan verrattuna, kuva 30 b. Suurentamalla tulokulmaa kasvaa taittumiskulma β, kunnes lopulta tulokulmalla 27,5 o (1. kriittinen kulma) pitkittäisaalto taittuu 90 o kulmalla. Se kulkee vain rajapintaa pitkin. Poikittaisaallot taittuvat edelleen kappaleeseen, kuva 32 a. Kuva 30 b Heijastuminen ja taittuminen poikittaisaalloilla Mikäli aaltomuodon muutosta ei oteta huomioon, on epäjatkuvuuksien paikantaminen ja arvostelu useimmissa tapauksissa mahdotonta. Joissakin tapauksissa jopa epäjatkuvuuksien löytäminen on kyseenalaista. Kuvapinnalle voi tulla kaiku kahdesta eri kohdasta riippuen siitä, käytetäänkö poikittais- vai pitkittäisaaltoja, kuva 31. Kuva 32a Taittuminen: 1. kriittinen kulma Tällä tavoin on vaatimus heijastajan arvosteluun täytetty: Materiaalissa on vain yksi ääniaalto joka on poikittaisaaltoa kulmassa 33,3 o (pleksi/teräs). Edelleen suurentamalla tulokulmaa voidaan poikittaisaallon taittumiskulmaa (luotauskulmaa) muuttaa, esimerkiksi tasan 45 o :ksi, kuva 32 b. Kuva 31 Paikantaminen: yksi kaiku = kaksi heijastajaa 16
17 Kuva 32 b Taittuminen; vain poikittaisaaltoa kulmassa 45 o Lopulta tulokulmalla n. 57 o (2. kriittinen kulma) muuttuu poikittaisaallon kulma 90 o ja se etenee kappaleen pinnalla muodostaen pintaaaltoa, kuva 32 c. Kuva 32 d Kokonaisheijastuminen kun α > 57 o Alueella, jolla tulokulma on 1. ja 2. kriittisen kulman välillä (27,5 o - 57 o ) saadaan teräskappaleeseen syntymään poikittaisaaltoa alueella 33,3 o - 90 o, kuva 33. Kuva 32 c Taittuminen: 2. kriittinen kulma, pinta-aalto Tämä on raja, jonka jälkeen kappaleeseen ei enää muodostu ääntä. Tästä alkaa kokonaisheijastus, kuva 32d. 17
18 4.5 Kulmaluotaimen ominaisuudet Useimmissa tapauksissa tarkastetaan terästä, joten kulmaluotain voidaan suunnitella siten, että sille saadaan järkevät luotauskulmat. Kulmaluotaimia on saatavana kulmilla 35 o, 45 o, 60 o, 70 o, 80 o ja 90 o (pinta-aalto), kuva 33. Kuva 34 a 1 mm:n syvyydellä olevan Ø 1 mm:n sivuporauksen luotaus Kuva 33 Käytettävissä oleva alue kulmaluotaimelle Tavallisimmin käytetään 45 o, 60 o ja 70 o kulmaluotainta. Kulmaluotaimien taajuusvalikoima ei ole niin suuri kuin normaaliluotaimien. Tämä johtuu siitä, että jopa seostamattomilla hienorakeisilla teräksillä poikittaisaallolla on suuri vaimennus. Äänienergia absorboituu ja siroaa kulkiessaan materiaalissa niin, että vain suhteellisen pieniä kappaleita voidaan tarkastaa riittävällä herkkyydellä. Mikäli suuremmissa kappaleissa (paksuissa) on havaittava epäjatkuvuuksia, on valittava mahdollisimman matalataajuinen ja suuri-kokoinen luotain. 2 MHz:n kulmaluotaimella voidaan havaita 700 mm päässä oleva 2 mm kokoinen heijastaja. Kulmaluotaimen lähierotus-kyky on usein parempi kuin normaaliluotaimen, koska lähtöpulssi on pitkällä vasemmalla kuvapinnalla johtuen melko pitkästä viiveestä. Lähtöpulssin laskeva oikea reuna saattaa kuitenkin peittää pinnan lähellä olevien epäjatkuvuuksien kaiut. Kuvassa 34 a ja b on esitetty, kuinka vielä 1 mm pinnan alla oleva Ø1 mm poraus voidaan havaita varmasti. Kuva 34 b Näyttö MWB70-4E kulmaluotaimella 18
19 4.6 Kaksoisnormaaliluotain Mikäli normaaliluotaimelle halutaan yhtä hyvä lähierotuskyky kuin kulmaluotaimelle, on käytettävä kaksoisnormaaliluotainta, kuva 35. Suurella vahvistuksella tai kappaleen pinnan ollessa karhea tapahtuu äänen siirtyminen suoraan lähettimestä vastaanottimeen. Kuvapinnalla tulee häiriökaiku, nimeltään kytkentäkaiku. Kytkentä-kaiku peittää juuri pinnan läheisen alueen ja vaikuttaa erityisesti pienten pinnan läheisten epäjatkuvuuksien havaitsemiseen. Tavallisesti kytkentäkaiku on niin pieni tai sitä ei edes ole olemassa, että epäjatkuvuudet ovat selvästi havaittavissa, kuva 37. Kuva 35 Kaksoisnormaaliluotain: leikkauskuva Tällaisella luotaimella käytetään kahta toisistaan akustisesti eristettyä muunninta, jotka on asennettu samaan runkoon. Lisäksi molemman muuntimen eteen on liimattu melko pitkä hieman vinossa oleva viive (pleksistä). Kaksoisluotaimen toinen muuntimista kytketään ultraäänilaitteen lähettimeen ja toinen vahvistimeen. Pitkästä viiveestä johtuen lähtöpulssi on kokonaan poissa kuvapinnalta, kuva 36. Kuva 37 Vika- ja kytkentäkaiku Kaksoisluotain sopii erinomaisesti lähellä pintaa olevien epäjatkuvuuksien etsintään ja ohuiden kohteiden paksuudenmittaukseen. Kaksoisluotain reagoi huomattavasti vähemmän kontaktin muutoksiin, erityisesti karheilla tai kaarevilla pinnoilla. Tämä selittää sen, miksi kaksoisluotaimia käytetään laajasti kemian ja energia-alan teollisuudesta: Ne ovat ideaalisia putkien ja säiliöiden tarkastukseen, korroosion havaitsemiseen ja jäljellä olevan seinämänpaksuuden mittaukseen, kuva 38. Kuva 36 Kaksoisnormaaliluotain käytössä Viiveessä syntyvät kerrannaiskaiut eivät häiritse, koska lähettimellä ei ole vastaanotintoimintoa. Vasta kun kappaleesta tulee äänipulsseja luotaimen vastaanottimeen, tulee kuvapinnalle kaikuja. Lähettimen ja vastaanottimen sähköinen eristäminen ei ole teknisistä syistä johtuen täysin mahdollista. 19
20 Kuva 38 Paksuusmittaus käytännössä 5. Epäjatkuvuuksien paikantaminen 5.1 Ultraäänilaitteen säätö Erityisillä kuumaluotaimilla voidaan mittaukset suorittaa kappaleen pintalämpötilan ollessa jopa 550 o C. Kohde voidaan mitata käytössä ollessaan. s Epäjatkuvuuden sijainti on heti pääteltävissä ultraäänilaitteen kuvapinnalta, kun se on oikein säädetty. Säätö tarkoittaa tietyn etäisyysasteikon säätämistä nollapisteestä eteenpäin lineaarisesti kuvapinnalle. Kuvapinnan asteikon kohta 0 vastaa kappaleen pintaa ja asteikon kohta 10 kuvapinnalla vastaa suurinta haluttua etäisyyttä, esimerkiksi 100 mm terästä, 10 mm alumiinia, 25 mm messinkiä jne. Mitta-alueen määritykseen liittyy aina mitattava materiaali, koska kaiun paikka eli äänitie s johdetaan äänen kulkuajasta ja materiaalin äänennopeudesta seuraavan kaavan avulla: s = Äänitie c = Äänennopeus t = Kulkuaika ct = 2 Tämä kaava ei ole merkityksetön tarkastajalle, muuta sitä ei todellisuudessa tarvita laitteen mitta-asteikon säädössä. Se tehdään yksinkertaisesti seuraavasti: Käytetään tarkastettavasta materiaalista valmistettua kappaletta, jonka mitat tunnetaan. Kytkettäessä luotain tunnetulle paksuudelle d saadaan takaseinäkaikujono, kuva 39. Kuva 39 Takaseinäkaikujono normaaliluotaimella 20
21 Kulloisetkin äänitiet vastaavat loogisesti äänen kulkemaa matkaa kappaleessa normaaliluotaimella. Ne ovat paksuuden monikertoja, eli: 1. kaiku = d, 2. kaiku = 2d, 3. kaiku = 3d jne. Mitta-alueen säätämiseksi tarvitaan vähintään kaksi kaikua, joiden paikat säädetään oikeiksi kuvapinnalla. Laite on säädetty oikein, kun lukemalla kaiun paikka asteikolla voidaan äänitie s (etäisyys) heijastajaan määrittää (heijastajien paikantaminen, paksuusmittaus) Säätö normaaliluotaimella Säätöön tarkoitettua kappaletta kutsutaan kalibrointikappaleeksi. Tarkistuskappaleeksi kutsutaan kappaletta, jonka muoto ja mitat on määritelty standardissa. Tarkistuskappaleen 1 (SFS 3288) paksuus on 25 mm ja se on valmistettu niukkaseostetusta hienorakeisesta teräksestä. Sitä voidaan käyttää lähes kaikkiin säätöihin tarkastettaessa vastaavaa terästä. Esimerkki 1: Mitta-alue 100 mm terästä. Vaaka-asteikolle säädetään mm terästä, kuva 40. Asteikon yksi jakoväli vastaa tällöin 10 mm kappaleessa. Asteikon kerroin k vastaa 10 mm /jakoväli. Kuva 40 Mitta-alue: mm terästä Luotain kytketään perusvertailukappaleelle 1, kuva 41. Kuva 41 Mitta-asteikon säätö 100 mm terästä Takaseinäkaikujono saadaan 25 mm:stä. Kaikujen paikat asteikolla T i ja äänitiet s j ovat seuraavan taulukon mukaisia: Kaiku No i Äänitie s i [mm] Asteikon kerroin k [mm/jv] Asteikon kohta T i [jv] , , , ,0 Kulloinenkin kaiun paikka asteikolla voidaan laskea seuraavan kaavan avulla: si T = i k S i = Äänitie i:n kaikuun T i = i:n kaiun paikka asteikolla k = Asteikon kerroin Tarkistuskappaleesta saatavien kaikujen tarkka säätö tapahtuu analogisella ultraäänilaitteella pulssinsiirron (tai nollapiste) ja mitta-alueen karkea- ja hienosäädön avulla. Säätö tapahtuu vuoroittain näillä säädöillä, kunnes kaiun etureunat ovat oikeilla kohdillaan. Digitaalisilla laitteilla valitaan suoraan mitta-alue ja äänennopeus säädetään 5920 m/s. Luotaimen kytkennän jälkeen tarvitsee suorittaa vain luotaimen viiveen kompensointi nollapisteen säädöllä, kuva
22 Vasta oikein tehdyn mitta-alueen säädön jälkeen on tarkka heijastajan paikannus mahdollista. Tarkastaja liikuttaa luotainta tarkastettavalla kohteella. Normaalitapauksissa, kun kappaleessa ei ole heijastajia, näkyy kuvapinnalla vain lähtöpulssi ja takaseinäkaiku. Heti kun äänikeilaan osuu epäjatkuvuus, tulee lähtöpulssin ja takaseinäkaiun välille ylimääräinen kaiku. Kuvassa 44 on esimerkiksi asteikon kohdalla 1,4 kaiku. Kun alue oli säädetty 250 mm, saadaan heijastajan paikaksi eli äänitieksi s = 1,4 x 25 = 35 mm. Kuva 42 USK7D: Luotaimen viiveen säätö Esimerkki 2: Mitta-alue 250 mm alumiinia Asteikon kohta 10 vastaa 250 mm alumiinia: k = 25 mm/jakoväli. Normaaliluotain kytketään 80 mm paksuiselle alumiiniselle tarkistuskappaleelle, eli saadaan kaikujono 80 mm välein, kuva 43. Kuva 44 USK7D: Äänitien mittaus Kuva 43 USK7D: Mitta-alueen säätö 250 mm alumiinia 80 mm:n paksuisen kappaleen avulla Säätötaulukko näyttää seuraavalta: Kaiku No i Äänitie s i [mm] Asteikon kerroin k [mm/jv] Asteikon kohta T i [jv] , , ,6 22
23 5.1.2 Säätö kaksoisnormaaliluotaimella Kaksoisluotaimen säätö on rakenteellisista syistä johtuen vain rajoitetusti mahdollista takaseinäkaikujonon avulla. Pienestä luotaimen kulmasta (kuva 35) johtuen syntyy kaksoisluotaimilla poikittaisaaltoa, joka aiheuttaa häiriökaikuja ensimmäisen takaseinäkaiun jälkeen. Toinen takaseinäkaiku ei ole enää selvästi erotettavissa. Tästä syystä säätöön käytetään porraskappaletta. Säätö suoritetaan kahden eri paksuisen kappaleen avulla (2-pisteen säätö). Esimerkki 3: Mitta-alue 10 mm terästä Porraskiilakappale VW (terästä: 1-8 mm): Mitta-alueen säätöön käytetään 3 ja 6 mm portaita. Portaat on valittava tarvittavan mittaalueen perusteella. Kaiku 3 mm portaasta säädetään asteikon kohdalle 3 ja kaiku 6 mm portaasta säädetään asteikolla kohdalle 6, kuva 45 a, b ja c. Kuva 45 c Kaiku 6 mm portaalta Säätö suoritetaan seuraavasti: a) Kaksoisluotain kytketään ensin 3 mm paksuiselle portaalle ja nollapisteen säädön avulla siirretään kaiun etureuna asteikon kohdalle 3. b) Luotain kytketään 6 mm portaalle ja mittaalueen (äänennopeuden) säädön avulla siirretään kaiun etureuna asteikon kohdalle 6. Kohtia a) ja b) toistetaan, kunnes kaikujen reunat ovat asteikon kohdilla 3 ja 6, kuva 45 b ja c. Kaksoisluotaimella voidaan havaita hyvin lähellä pintaa olevia epäjatkuvuuksia, kuva 46 a ja b. Kuva 45 a Kaksoisluotain 3 ja 6 mm portailla Kuva 46 a DA312 luotain koekappaleella, jossa pinnan lähellä olevia heijastajia Kuva 45 b Kaiku 3 mm portaalta Kuva 46 b Kaikukuvio pinnan lähellä olevasta heijastajasta 23
24 5.1.3 Säätö kulmaluotaimella Kulmaluotaimien mitta-alueen säätöön käytetään lähes yksinomaan standardisoitua tarkistuskappaletta 1, kuva 47 a ja tarkistuskappaletta 2 (EN ), kuva 47 b, koska tasomaisesta kappaleesta ei saada kulmaluotaimella kerrannaiskaikuja. Tarkistuskappaleesta 1 saadaan ensimmäinen kaiku 100 mm päästä, kun luotain on kaaren keski-pisteessä. Heijastuslain mukaisesti heijastuu kaarelta palaava ääni taaksepäin kytkentäpinnasta, kuva 49 a. Kaarelta ei saada toista kaikua, jota tarvitaan mitta-alueen säätöön. Tästä huolehtivat kuitenkin kaaren keskipisteeseen tehdyt urat: Urien ja pinnan välisessä kulmassa tapahtuu nurkkaheijastus, jolloin ääni palaa takaisin kaarelle, kuva 49 b. Kuva 49 a Äänitie tarkistuskappaleessa 1 ilman uria Kuva 47 a WB60-2E kulmaluotain tarkistuskappaleella 1 Kuva 49b Äänitie tarkistuskappaleessa 1 urilla Kuva 47 b MWB45-4E kulmaluotain tarkistuskappaleella 2 Koska kaaren säde on 100 mm, saadaan toistokaiut 100 mm, 200 mm, 300 mm jne. päästä. Mitta-alue voidaan säätää siten samalla tavoin kuin normaaliluotaimella. Kuvassa 50 on esitetty mitta-alueen säätö 250 mm perusvertailukappaleen 1 avulla. Tarkistuskappaleiden etuna on se, että niiden kaarista saadaan luotaimen kulmasta riippumatta aina kaiut samalla äänitiellä, kuva 48. Kuva 48 Luotaus eri kulmilla tarkistuskappaleessa 1 Kuva 50 Mitta-alue 250 mm WB45-2E luotaimella tarkistuskappaleen 1 avulla säädettynä 24
25 Pienoiskulmaluotaimilla käytetään mielellään huomattavasti pienempää ja ennen kaikkea kevyempää tarkistuskappaletta 2. Tässä kappaleessa on kaksi kaarta yhteisellä keskipisteellä. Tällöin ei sahauria tarvita. Tarvittava kaikujono syntyy ääniaaltojen heijastuksista kaarien välillä, kuva 51 a ja b. Kuvassa 52 on esitetty mitta-alueen säätö kulmaluotaimella 100 mm:ksi terästä käyttäen 25 mm kaarta perusvertailukappaleessa 2. Kuva 52 Mitta-alueen säätö 100 mm tarkistuskappaleen 2 avulla Kuva 51 a Äänitiet vertailukappaleessa 2 (R = 25 mm) Kuva 51 b Äänitiet vertailukappaleessa 2 (R = 50 mm) Riippuen siitä onko luotain kytketty 25 tai 50 mm kaarelle, saadaan erilainen kaikujono. Väärästä suunnasta keskikohtaan tulevat ääniaallot eivät aiheuta kaikua kuvapinnalla. Ne vaimennetaan luotaimen vaimennuskappaleessa. 25
26 5.1.4 Paikantaminen kulmaluotaimella Epäjatkuvuudesta kuvapinnalle tuleva kaiku ei kerro suoraan heijastajan sijaintia kappaleessa. Ainoa tieto heijastajan paikantamiseksi on kaiun sijainti kuvapinnalla eli äänitie s, siis etäisyys äänen sisääntulokohdasta epäjatkuvuuteen, kuva 53. Kuva 54 b Lyhennetty projektioetäisyys ja indeksi Digitaalisissa ultraäänilaitteissa suorittaa laite itse nämä laskelmat ja näyttää tuloksen välittömästi, joten tarkastajan ei tarvitse enää suorittaa laskelmia, kuva 55. Kuva 53 Heijastajan paikantaminen kulmaluotaimella Trigonometrian avulla voidaan kuitenkin ratkaista helposti ultraäänitarkastuksen kannalta tärkeät heijastajan projektioetäisyys ja syvyys, kuva 54 a. Kuva 55 USN50: Luotaus MWB60-4E kulmaluotaimella Kuva 54 a Vian paikantamiskolmio Tällä tavoin on mahdollista välittömästi merkitä heijastajan paikka kappaleen pinnalla ja ilmoittaa sen syvyyssijainti. Käytännön syistä voidaan käyttää myös lyhennettyä projektioetäisyyttä, joka mitataan luotaimen etureunasta. Lyhennetyn projektioetäisyyden ja projektioetäisyyden välinen ero on luotaimen indeksi, eli äänen ulostulokohdan ja luotaimen etureunan välinen etäisyys, kuva 54 b. Erityisesti hitsien tarkastuksessa tästä on suuri apu, koska siinä on otettava huomioon, onko ääni heijastunut jo kerran vastakkaiselta puolelta. Kolmion laskentakaavaa käyttäen saadaan heijastajalle näennäinen syvyys, joka on suurempi kuin kappaleen paksuus, kuva 56 a. Kuva 56 a Näennäinen syvyyssijainti Tarkastajan on pääteltävä, onko ääni heijastunut kerran kappaleen vastakkaiselta puolelta ja ottaa 26
27 se huomioon laskiessaan heijastajan syvyyssijaintia, kuva 56 b. Kuva 56 b Heijastajan todellinen syvyyssijainti 6. Epäjatkuvuuksien arvostelu Epäjatkuvuus voidaan parhaimmin arvostella vasta sitten kun sen koko (laajuus) tunnetaan tarkasti. Siksi heijastajan todellisen koon mahdollisimman tarkka tunteminen on ymmärrettävästi tarkastajan toive. Juuri tätä tulosta odotetaan ainettarikkomattomalta tarkastukselta, kuten ultraääni-tarkastukselta. Koska ultraäänilaitteen kuvapinnalla on vain yksi kaiku, jota voidaan tulkita, on usein erittäin vaikeaa tai jopa mahdotonta antaa varmaa tietoa heijastajan koosta. Kaikilla arvostelumenetelmillä on kaiun korkeudella suuri merkitys. 6.1 Koon määritys äänikeilan reunan avulla Heijastajan koon määrityksessä päästään melko hyviin tuloksiin heijastajan ollessa äänikeilaa suurempi. Heijastaja heijastaa nimittäin kaiken äänen takaisin luotaimeen, kuva 57. Kuva 57 Suuri heijastaja äänikeilassa 27
28 Kartoittamalla heijastajan reunat, saadaan hyvä kuva sen laajuudesta. Tarkastuksen aikana seurataan heijastajan kaiun korkeutta. Se kohta, jolla kaiun korkeus on tasan puolet maksimistaan, ilmaisee sen, että vain puolet keilasta osuu heijastajaan, kuva 58 a. Kuva 58 a Normaaliluotain heijastajan reunalla Äänikeilan akseli on sillä hetkellä epäjatkuvuuden reunalla. Luotaimen paikka merkitään ja etsitään muut rajakohdat, kunnes merkit yhdistämällä epäjatkuvuuden koko on määritelty, kuva 58 b. Kuva 58 b Heijastajan koon määritys reunojen avulla Reunojen mittaus on sitä tarkempaa mitä pienempi äänikeilan halkaisija on epäjatkuvuuden kohdalla. Jos heijastajan laajuus on mitattava tarkasti, on valittava sellainen luotain, jonka lähikenttä on epäjatkuvuuden kohdalla. Erityisen sopivia tähän ovat kaksoisluotaimet, joiden äänikeila on kapea (1-3 mm). 28
29 6.2 Pienten epäjatkuvuuksien koon arviointi: AVG-menetelmä Kokonaan äänikeilan sisään jäävää heijastajaa kutsutaan pieneksi heijastajaksi. Jos tällaisella heijastajalla yritetään mitata heijastajan koko äänikeilan reunojen avulla, on tuloksena heijastajan koon sijasta suunnilleen äänikeilan koko. Rajojen mittauksessa ei ole tällaisessa tapauksessa mitään järkeä. Jo aiemmin on selvinnyt, että kaiun korkeus on sitä suurempi mitä suuremman alueen heijastaja peittää äänikeilasta. Tätä ominaisuutta voidaan käyttää hyväksi pienien heijastajien arvostelussa: Kaikukorkeus kasvaa heijastajan koon suurentuessa, kuva 59. Optimiolosuhteissa, esimerkiksi samalla syvyydellä sijaitsevilla tasomaisilla porauksilla voidaan sanoa: Kaikukorkeus on suhteessa heijastajan pintaalaan, tai: Kaikukorkeus on suhteessa heijastajan halkaisijan neliöön. Esimerkki: Ø 2 mm porauksesta saadaan 4 kertaa korkeampi kaiku kuin Ø 1 mm porauksesta, koska sen pinta-ala on neljä kertaa suurempi. Kuva 59 Erikokoisten heijastajien kaiut 29
30 Jos verrataan kahden eri etäisyyksillä olevan porauksen kaikua, saadaan lisäksi kaikukorkeuden etäisyyslaki selville, kuva 60. Kuva 61 2 mm tasapohjareiän kaikukorkeuskäyrä Piirrettäessä tällaisia käyriä kuvapinnalle voidaan verrata todellisten vikojen kaikuja tunnettuihin tasapohjareikiin. Kuvassa 62 heijastaa epäjatkuvuus ääntä yhtä hyvin kuin 4 mm tasapohjareikä. Kuva 60 Eri etäisyydellä olevien heijastajien kaiut Eri etäisyyksillä olevien tasapohjaisten porausten avulla voidaan löytää ainakin kaukokentässä pätevä riippuvuus: Kaikukorkeus pienenee kääntäen heijastajan etäisyyden neliöön. Lähikentässä tämä ei enää päde! Kaikukorkeus on suurin äänikeilan fokuksessa ja pienenee etäisyyden tästä lyhentyessä, kuva 61. Kuva 62 Heijastajan (V) koon arviointi vertailukäyrillä Koska vain epäjatkuvuuden heijastamaa ääntä arvostellaan, ei voida suoraan sanoa, että todellinen heijastajan koko on 4 mm. Siksi sitä sanotaan vertailuvikakooksi. Vain ideaalitapauksissa vastaa vertailuvikakoko heijastajan todellista kokoa. Tämä pätee vain silloin, kun heijastaja on tasomainen ja pyöreä ja on aivan kohtisuorassa äänikeilassa. Koska näin tuskin koskaan tapahtuu käytännössä, on epäjatkuvuuden todellinen koko aina suurempi kuin vertailuvikakoko. Lainalaisuutta ei vahinko kyllä voida tässä tapauksessa johtaa. Kaikukorkeus on suuresti riippuvainen epäjatkuvuuden ominaisuuksista, kuten sen muodosta, sen suunnasta äänikeilaan nähden ja sen pinnan laadusta. 30
31 Esimerkiksi 2 mm huokonen (pallomainen heijastaja) heijastaa vain 1 mm vertailuvikaa vastaten. Vastaavasti vinossa oleva 5 mm tasomaisesta viasta saadaan vertailuvika-kooksi 0 mm (ei havaittavissa) - 2 mm riippuen sen suunnasta. Tätä koon määrityksen epätarkkuutta voidaan parantaa käyttämällä muita ultraäänitarkastuksen menetelmiä jo löydetyn epäjatkuvuuden tarkempaa arvostelua varten. Kokenut tarkastaja pystyy arvostelemaan epäjatkuvuudet melko tarkkaan. Hyvään tulokseen päästään luotaamalla eri suunnilta, seuraamalla kaiun muotoa ja sen muuttumista (kaikudynamiikka) luotainta siirrettäessä. Huolimatta vikakoon määrityksessä vielä olevista epätarkkuuksista on ylläkuvattu vikakoon määritys käytössä laajalti, koska menetelmä perustuu äänikeilan todistettuihin lainalaisuuksiin. Se on siksi toistettavissa eli arvostelutulokset ovat tarkastuslaitteistosta ja tarkastajasta riippumattomia. AVG-asteikkoja on saatavana erilaisille luotaimille ja mitta-alueille. AVG on lyhenne sanoista Etäisyys (Abstand), Vahvistus (Verstärkung) ja Koko (Grösse). Uusimmissa asteikoissa on otettu huomioon nykyiset tarkastusohjeet: Jos kappaleelle, jonka käyttö ja siten rasitukset tunnetaan, on suoritettava ultraäänitarkastus, on ensin määriteltävä minkä kokoisia vikoja sallitaan. Tämä voidaan tehdä esimerkiksi murtumismekaniikan avulla. Vikojen sijainnilla ja niiden esiintymistiheydellä on tietysti merkitystä. Jos sallittu vikakoko on määritelty, kerrotaan tämä arvo vielä varmuuskertoimella ultraäänitarkastuksen arvostelun epävarmuuden huomioimiseksi. Ultraäänitarkastuksessa on merkitystä vain tätä vikakokoa vastaavalla vertailukäyrällä. Tarkastusta suoritettaessa tarvitsee rekisteröidä vain ne näyttämät, jotka ylittävät tämän rekisteröintikäyrän, kuva 63. Kuva 63 B4S-E luotaimen AVG-asteikko Tästä syystä arvosteluun tarvitaan vain yksi käyrä. Koska eri tarkastuksiin käytetään erilaisia rekisteröintikäyriä, on oltava mahdollista muuttaa tämä käyrä eri kokoisille vertailuvioille. Asteikon oikeassa ylänurkassa olevaa ruudukkoa käytetään tähän: Lähtötilanteena on laitteen perusvahvistus, johon lisätään haluttuun rekisteröintikokoon kuuluva lisävahvistus taulukosta. Oikean mittaasteikon kanssa voidaan tarkastus aloittaa. Jos kappaleesta saadaan rekisteröintikäyrän ylittävä kaiku, on tämä kirjattava ja arvosteltava. Tarkastusohjeissa on normaalisti annettu eri vaihtoehtoja: hylkäys, korjaus tai tarkempi tutkimus epäjatkuvuuden määrittämiseksi. Kuvassa 64 on esitetty taekappaleen tarkastus. Rekisteröintikäyrä vastaa 3 mm vertailuvikakokoa. Havaittu epäjatkuvuus 110 mm syvyydellä ylittää rekisteröintikäyrän, eli siitä on tehtävä merkintä tarkastusraporttiin kaikkine mittaustuloksineen. Kuva 64 Vikakoon arviointi AVG-asteikon avulla 31
32 6.3 Vaimennus Äänikeilassa olevien tasapohjaisen heijastajan lainalaisuuksien (etäisyys ja suuruus) lisäksi on huomioitava myös eräs ominaisuus: äänen vaimennus. Äänen vaimennus johtuu materiaalin ominaisuuksista, ja on voimakkaasti riippuvainen taajuudesta ja käytetystä aaltoliikkeestä. Vasta kun vaimennus on tarkasti tiedossa, voidaan se ottaa huomioon vian koon arvioinnissa. Joka tapauksessa arvostelu tulee vaikeammaksi, aikaa vievemmäksi ja epävarmemmaksi, niin että AVG-menetelmän käytössä voi olla suuret toleranssit. 6.4 Vertailukappalemenetelmä Tämän menetelmän avulla voidaan arvostelun epätarkkuuksia pienentää, kun käytössä on vertailukappale. Se on valmistettu samasta materiaalista kuin tarkastuskohde ja siihen on tehty vertailuheijastajia, joiden kaikuja voidaan verrata suoraan kappaleessa saataviin kaikuihin. Vertailu-kappalemenetelmää käytetään kahdella eri tavalla: Kuva 66 Vertailukappale: Vertailukaiun korkeus 30 % Vertailuarvo on nyt se vahvistuksen ero, joka on epäjatkuvuuden ja vertailuvian välillä, kun niiden korkeus on sama, kuva Kaikukorkeusvertailu Tarkastus tapahtuu suurella vahvistuksella, jolloin pienimmätkin epäjatkuvuudet tulevat havaituiksi. Havaitun kaiun maksimi etsitään ja kaiun korkeus säädetään tietylle korkeudelle esim. 80 % kuva-pinnan korkeudesta (vertailukorkeus) vahvistimen avulla, kuva 65. Kuva 67 Vertailukappale: Vertailukaiku vertailukorkeudella Tulos: Epäjatkuvuudesta saatava kaiku on 8 db suurempi kuin vertailukaiku, koska vahvistusta oli lisättävä 8 db (42 db - 34 db), jotta kaiut olisivat yhtä korkeita kuvapinnalla. Normaalisti rekisteröintitaso on sama kuin vertailuheijastajan koko, joka on määriteltävä jo ennen tarkastuksen aloitusta, samoin kuin AVGmenetelmässäkin. Kuva 65 Vikakaiku: Korkeus 80 % kuvapinnan korkeudesta (vertailukorkeus) Samalla vahvistuksen arvolla etsitään vertailukappaleesta mahdollisimman lähellä samaa etäisyyttä oleva heijastaja, kuva
33 6.4.2 Etäisyys-amplitudi-käyrä (DAC) Kaikki heijastajat luodataan ennen tarkastuksen aloittamista ja saatujen kaikujen maksimit merkitään kuvapinnalle ja yhdistetään käyräksi, kuva 68. Tallennettaessa DAC-käyrä tarkastuskohdetta vastaavassa materiaalissa otetaan jo huomioon kaikki vaikutukset (etäisyyslaki, vaimennus ja siir-tohäviöt). Korjauksia ei tarvitse tehdä. Vian koon arvioinnissa on kuitenkin otettava huomioon samat asiat kuin AVG-menetelmässä eli heijastajan ominaisuudet (muoto, suuntaisuus ja pinnan-laatu). Tästä syystä vertailukappale menetelmällä suoritettuun tarkastukseen sisältyvät samat epätarkkuudet kuin AVGmenetelmään. Jommankumman menetelmän suosiminen on subjektiivista. Yleensä kansallisissa ohjeissa on määritelty vian koon mittausmenetelmä, jolloin tarkastaja ei itse voi tehdä päätöksiä menetelmän käytöstä. Jos ohjeita ei ole olemassa, on arvioitava kumpi menetelmä on tarkoituksenmukaisin: Kuva 68 Vertailukappaleen poraukset ja niiden kaiut Tätä käyrää kutsutaan DAC-käyräksi (Distance- Amplitude-Curve). Kun tarkastuskohteesta saadaan kaiku epäjatkuvuudesta, havaitaan välittömästi, ylittääkö se DAC-käyrän vai ei. Vahvistuksen muutoksen avulla voidaan mitata montako db:tä kaiku ylittää DAC-käyrän. Tämä rekisteröintitason ylitys on toistettava mittaustulos epäjatkuvuuden arvostelua ja raportointia varten. DAC-käyrän etuna on: 1. Tarkastuksen aikana ei tarvitse verrata epäjatkuvuudesta saatavan kaiun korkeutta vertailu-kappaleessa olevan heijastajan kaikuun. Arvostelu suoritetaan suoraan DACkäyrään. 2. Usein painavia ja suuria vertailukappaleita ei tarvitse siirtää tarkastuspaikalle. 3. DAC-käyrän teko irrotettavalle asteikolle tai ultraäänilaitteen muistiin on tarpeellista vain kerran tiettyä tarkastusta varten. Ensimmäiseksi on selvitettävä, onko sopivia vertailukappaleita saatavilla. Jos niitä on jo olemassa, on luonnollinen valinta vertailukappalemenetelmä. Jos kappaleita ei ole, voidaan käyttää AVG-menetelmää, tai vertailukappaleet on valmistettava. Useimmissa tapauksissa on AVG-menetelmän käyttö yhtä helposti sovellettavissa vähän seostetusta teräksestä valmistetuille kohteille, jotka ovat yksinkertaisia muodoltaan ja joiden vaimennus on pieni ja pinnan laatu on hyvä. Tarkastus on suoritettava kapeakaistaisella luotaimella, jonka taajuus on 1-6 MHz ja josta on saatavana AVG-käyrä tai AVG-asteikko. Uusimmissa laitteissa on ohjelmoitava DAC-käyrän rekisteröinti. Lisäksi niissä voi olla etäisyydestä riippuva vahvistuksen korjaus, jota kutsutaan amplitudin etäisyyskorjaukseksi (TCG tai DAC-korjaus), kuva
34 Kuva 70b Rekisteröitävä kaiku Kuva 69 DAC vertailukaiut (yllä) ja amplitudin etäisyyskorjaus (TCG, alla) Rekisteröintikäyrä muuttuu vaakalinjaksi. Tällöin voidaan monitorin porttia käyttää valo- tai ääni hälytyksen antamiseen (vikahälytys), kuva 70 a - c. Lisäksi saadaan mittaustulokset epäjatkuvuuksien paikantamiseksi sekä amplitudiero db:nä (dbr arvo kuvassa). Kuva 70 c Kaiku, jota ei tarvitse rekisteröidä DAC käyrä ja säädöt voidaan tallentaa ultraäänilaitteen muistiin. Tällä tavoin varmistutaan siitä, että seuraavat tarkastukset suoritetaan täysin samoilla säädöillä. Tallennettaessa epäjatkuvuuden A-kuva ja senhetkiset laitteen säädöt on tarkastajalla käytettävissä kaikki mahdollinen tieto myöhemmin valmisteltavaa tarkastusraporttia varten. Kuva 70 a Hitsin tarkastus USD10 ultraäänilaitteella 34
35 7. Dokumentointi Mitä suurempi tarkastuskohteen arvo on tai mitä tärkeämpi kohde on turvallisuuden kannalta, sitä tärkeämpänä pidetään ultraäänitarkastuksen dokumentointia. Dokumentin olisi ensinnäkin ilmaistava, että tarkastus on tehty kokonaan ja että se on oikein suoritettu. Lisäksi sen on mahdollistettava uusintatarkastuksen suorittaminen samoilla säädöillä (tarkastuksen toistettavuus). Ultraäänitarkastuksen dokumentti eli tarkastusraportti kostuu karkeasti kolmesta osasta: a) Tiedot tarkastuskohteesta ja tarkastusmenetelmästä. Kuva 71 Tarkastusraportin pohja ultraäänilaitteessa b) Tiedot tarkastuslaitteistosta c) Tarkastuksen tulos: Normaalisti taulukon muodossa kaikki havaitut ja arvostellut epäjatkuvuudet. Mahdollisesti myös tarkastuskohteesta piirros, johon vikojen paikat on merkitty. Tiedot on kerättävä jo tarkastuksen aikana, erityisesti tiedot havaituista epäjatkuvuuksista. Lopullisen tarkastusraportin valmistelu voi tapahtua jossakin muualla, esim. toimistossa. Tarkastus-raporttiin kuuluviin piirroksiin liittyvät laskelmat on tarkastajan tehtävä raporttia valmistelleessaan. Tarkastusraportin valmisteluun kuluu yleensä yhtä paljon aikaa kuin itse tarkastuksen suoritukseen ja se on otettava huomioon tarkastuksen laajuutta suunniteltaessa. Erityisesti suurilla tietomäärillä on jo siirto- tai laskuvirheiden mahdollisuus olemassa. Tarkastajan työn helpottamiseksi uusimissa ultraäänilaitteissa ovat säätöarvojen ja tarkastuksen aikana tallennettavien tulosten tallennus- ja tiedonsiirtomahdollisuudet niin paljon paremmat, että tarkastaja voi keskittyä todelliseen tarkastustehtävään. Tallentamalla epäjatkuvuuden tiedot ultraäänilaitteen muistiin voidaan siirtovirheet välttää. Kirjattaessa epäjatkuvuuden sijainnit laitteen muistiin sisältyvät ne A-kuvan kanssa tieto-sarjaan. Tarvittaessa tarkastusraportti voidaan tulostaa kirjoittimen avulla, kuva 71. Tiettyyn tarkastustehtävään soveltuva tarkastusraportti voidaan tehdä PC:n avulla. Mittaustietojen käsittely on yhtä monipuolista kuin ne ohjelmat, joita on saatavana. Mahdollisimman monipuolisen tiedonsiirron varmistamiseksi käytetään digitaalisten ultraäänilaitteiden kanssa utility - ohjelmia. Ne ovat helppokäyttöisiä ohjelmia, joiden avulla varmistetaan PC:n ja ultraäänilaitteen välinen tiedonsiirto. Kaikki ultraäänilaitteen säädöt (tietosarjat), siihen kuuluvat säätöarvot (toimintoarvot) ja näyttämät (A-kuvat) voidaan tallentaa levykkeelle tai kovalevylle. Tekstitiedot voidaan tallentaa ASCII-muodossa ja A-kuvat grafiikkamuodossa (PCX, IMG). Tietosarja vastaa laitteen kaikkia säätöjä ja se tallennetaan heksadesimaalimuodossa. Tällä tavoin varmistutaan, että tietojen takaisin lähettäminen laitteelle on varmaa ja arvot ovat täysin samat. Teksti- ja grafiikkatiedot ovat käyttäjän käytettävissä. Niitä voidaan sopivan tekstinkäsittely- tai grafiikkaohjelman avulla käyttää tarkastusraportteihin. Oheinen raportti on esimerkki ohjelman avulla tehdystä hitsin tarkastuksesta. Tarkastus on tehty digitaalisesti ultraäänilaitteella ja havaitut viat on tallennettu laitteelle ja siirretty sen jälkeen PC:lle. Sopivan ohjelman avulla on tietoja käsitelty ja tulostettu lopulta tarkastusraportti. 35
36 Tarkastuspöytäkirja (esimerkki) 8. Näyttämien tulkinta Edellä käsiteltyjen tarkastajan tehtävien vastakohtana ei näyttämien arviointi perustu pelkästään mittaustuloksiin. Lisätoimena on kaikujen merkityksen arviointi. Tämän merkityksen ymmärtäminen vaatii monivuotista käytännön tarkastuskokemusta ja myös ultraäänitarkastuksen tulosten vertaamista muilla menetelmillä saatuihin tuloksiin erilaisissa kohteissa. Näytön analysointiin käytettävät laitteet ja menetelmät, kuten signaalianalysaattorit eivät kuulu tämän johdatus ultraäänitarkastukseen -kirjasen piiriin. Tätä varten on olemassa suuri määrä muita kirjoja ja julkaisuja ammattilehdissä, joihin kannattaa tutustua. 36
37 Lähteet: M. Berke, U. Hoppenkamps: Einführung in die Ultraschallprüfung Krautkrämer Schulungssystem Teil 1 / Level 1 3. Aufgabe (1990) M. Berke, U. Hoppenkamps: Bewertung von Ungänzen Krautkrämer Schulungssystem Teil 2 3. Aufgabe (1991) M. Berke, U. Hoppenkamps: Praktikum mit digitalen Ultraschallgeräten Krautkrämer Schulungssystem Teil 4 3. Aufgabe (1992) M. Berke: Wanddickenmessung mit Ultraschall Krautkrämer Schulungssystem Teil 5 2. Aufgabe (1992) H.-W. Corsepius: Einführung in die Grundlagen Sonderdruck 218, (1990) Krautkrämer GmbH & Co. Alkuperäisteos: M. Berke: Zerstörungsfreie Werkstoffprüfung mit Ultraschall Einführung in die Grundlagen Sonderdruck 218, (1993) Krautkrämer GmbH & Co. 37
38 38
KUUMAVALSSATUT TERÄSLEVYT JA -KELAT Ultraäänitarkastus
 KUUMAVALSSATUT TERÄSLEVYT JA -KELAT Ultraäänitarkastus www.ruukki.fi Ruukki toimittaa kuumavalssattuja levyjä ultraäänitarkastettuina tai muiden, erikseen sovittavien vaatimusten mukaisesti. Ultraäänitarkastuksesta
KUUMAVALSSATUT TERÄSLEVYT JA -KELAT Ultraäänitarkastus www.ruukki.fi Ruukki toimittaa kuumavalssattuja levyjä ultraäänitarkastettuina tai muiden, erikseen sovittavien vaatimusten mukaisesti. Ultraäänitarkastuksesta
Monipuolinen ja helppokäyttöinen PhaseArray ja TOFD tarkastuslaite
 Monipuolinen ja helppokäyttöinen PhaseArray ja TOFD tarkastuslaite SyncScan on uusi, vuonna 2015 julkaistu SIUI:n valmistama ultraäänitarkastuslaite. SyncScan laitteessa yhdistyvät suorituskykyinen Vaiheistettu
Monipuolinen ja helppokäyttöinen PhaseArray ja TOFD tarkastuslaite SyncScan on uusi, vuonna 2015 julkaistu SIUI:n valmistama ultraäänitarkastuslaite. SyncScan laitteessa yhdistyvät suorituskykyinen Vaiheistettu
Ultraäänen kuvausartefaktat. UÄ-kuvantamisen perusoletukset. Outi Pelkonen OYS, Radiologian Klinikka 29.4.2005
 Ultraäänen kuvausartefaktat Outi Pelkonen OYS, Radiologian Klinikka 29.4.2005 kaikissa radiologisissa kuvissa on artefaktoja UÄ:ssä artefaktat ovat kaikuja, jotka näkyvät kuvassa, mutta eivät vastaa sijainniltaan
Ultraäänen kuvausartefaktat Outi Pelkonen OYS, Radiologian Klinikka 29.4.2005 kaikissa radiologisissa kuvissa on artefaktoja UÄ:ssä artefaktat ovat kaikuja, jotka näkyvät kuvassa, mutta eivät vastaa sijainniltaan
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) E a 2 ds
 Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Kuten aaltoliikkeen heijastuminen, niin myös taittuminen voidaan selittää Huygensin periaatteen avulla.
 FYS 103 / K3 SNELLIN LAKI Työssä tutkitaan monokromaattisen valon taittumista ja todennetaan Snellin laki. Lisäksi määritetään kokonaisheijastuksen rajakulmia ja aineiden taitekertoimia. 1. Teoriaa Huygensin
FYS 103 / K3 SNELLIN LAKI Työssä tutkitaan monokromaattisen valon taittumista ja todennetaan Snellin laki. Lisäksi määritetään kokonaisheijastuksen rajakulmia ja aineiden taitekertoimia. 1. Teoriaa Huygensin
Työ 21 Valon käyttäytyminen rajapinnoilla. Työvuoro 40 pari 1
 Työ 21 Valon käyttäytyminen rajapinnoilla Työvuoro 40 pari 1 Tero Marttila Joel Pirttimaa TLT 78949E EST 78997S Selostuksen laati Tero Marttila Mittaukset suoritettu 12.11.2012 Selostus palautettu 19.11.2012
Työ 21 Valon käyttäytyminen rajapinnoilla Työvuoro 40 pari 1 Tero Marttila Joel Pirttimaa TLT 78949E EST 78997S Selostuksen laati Tero Marttila Mittaukset suoritettu 12.11.2012 Selostus palautettu 19.11.2012
Aaltoliike ajan suhteen:
 Aaltoliike Aaltoliike on etenevää värähtelyä Värähdysliikkeen jaksonaika T on yhteen värähdykseen kuluva aika Värähtelyn taajuus on sekunnissa tapahtuvien värähdysten lukumäärä Taajuuden ƒ yksikkö Hz (hertsi,
Aaltoliike Aaltoliike on etenevää värähtelyä Värähdysliikkeen jaksonaika T on yhteen värähdykseen kuluva aika Värähtelyn taajuus on sekunnissa tapahtuvien värähdysten lukumäärä Taajuuden ƒ yksikkö Hz (hertsi,
SEISOVA AALTOLIIKE 1. TEORIAA
 1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
23 VALON POLARISAATIO 23.1 Johdanto. 23.2 Valon polarisointi ja polarisaation havaitseminen
 3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
FYS03: Aaltoliike. kurssin muistiinpanot. Rami Nuotio
 FYS03: Aaltoliike kurssin muistiinpanot Rami Nuotio päivitetty 24.1.2010 Sisältö 1. Mekaaninen aaltoliike 2 1.1. Harmoninen voima 2 1.2. Harmoninen värähdysliike 2 1.3. Mekaaninen aalto 3 1.4. Mekaanisen
FYS03: Aaltoliike kurssin muistiinpanot Rami Nuotio päivitetty 24.1.2010 Sisältö 1. Mekaaninen aaltoliike 2 1.1. Harmoninen voima 2 1.2. Harmoninen värähdysliike 2 1.3. Mekaaninen aalto 3 1.4. Mekaanisen
Pasi Puronhaara VUOTOMITTAUKSET JA MATERIAALIN TUTKIMINEN ULTRAÄÄNELLÄ
 Pasi Puronhaara VUOTOMITTAUKSET JA MATERIAALIN TUTKIMINEN ULTRAÄÄNELLÄ Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Kone- ja tuotantotekniikan koulutusohjelma Kesäkuu 2010 TIIVISTELMÄ OPINNÄYTETYÖSTÄ
Pasi Puronhaara VUOTOMITTAUKSET JA MATERIAALIN TUTKIMINEN ULTRAÄÄNELLÄ Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Kone- ja tuotantotekniikan koulutusohjelma Kesäkuu 2010 TIIVISTELMÄ OPINNÄYTETYÖSTÄ
Aaltojen heijastuminen ja taittuminen
 Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
Satelliittipaikannus
 Kolme maailmalaajuista järjestelmää 1. GPS (USAn puolustusministeriö) Täydessä laajuudessaan toiminnassa v. 1994. http://www.navcen.uscg.gov/gps/default.htm 2. GLONASS (Venäjän hallitus) Ilmeisesti 11
Kolme maailmalaajuista järjestelmää 1. GPS (USAn puolustusministeriö) Täydessä laajuudessaan toiminnassa v. 1994. http://www.navcen.uscg.gov/gps/default.htm 2. GLONASS (Venäjän hallitus) Ilmeisesti 11
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619
 KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
Aaltojen heijastuminen ja taittuminen
 Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
d sinα Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila
 Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618. Koesuunnitelma
 KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618 Koesuunnitelma Sisällysluettelo Sisällysluettelo 1 1 Tutkimusongelma ja tutkimuksen tavoit e 2 2 Tutkimusmenetelmät 3 5 2.1 Käytännön
KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618 Koesuunnitelma Sisällysluettelo Sisällysluettelo 1 1 Tutkimusongelma ja tutkimuksen tavoit e 2 2 Tutkimusmenetelmät 3 5 2.1 Käytännön
Lego Mindstorms NXT. OPH oppimisympäristöjen kehittämishanke 2011-2013. (C) 2012 Oppimiskeskus Innokas! All Rights Reserved 1
 Lego Mindstorms NXT OPH oppimisympäristöjen kehittämishanke 2011-2013 (C) 2012 Oppimiskeskus Innokas! All Rights Reserved 1 Anturi- ja moottoriportit A B C 1 2 3 4 (C) 2012 Oppimiskeskus Innokas! All Rights
Lego Mindstorms NXT OPH oppimisympäristöjen kehittämishanke 2011-2013 (C) 2012 Oppimiskeskus Innokas! All Rights Reserved 1 Anturi- ja moottoriportit A B C 1 2 3 4 (C) 2012 Oppimiskeskus Innokas! All Rights
Dynatel 2210E kaapelinhakulaite
 Dynatel 2210E kaapelinhakulaite Syyskuu 2001 KÄYTTÖOHJE Yleistä 3M Dynatel 2210E kaapelinhakulaite koostuu lähettimestä, vastaanottimesta ja tarvittavista johdoista. Laitteella voidaan paikantaa kaapeleita
Dynatel 2210E kaapelinhakulaite Syyskuu 2001 KÄYTTÖOHJE Yleistä 3M Dynatel 2210E kaapelinhakulaite koostuu lähettimestä, vastaanottimesta ja tarvittavista johdoista. Laitteella voidaan paikantaa kaapeleita
Valon havaitseminen. Näkövirheet ja silmän sairaudet. Silmä Näkö ja optiikka. Taittuminen. Valo. Heijastuminen
 Näkö Valon havaitseminen Silmä Näkö ja optiikka Näkövirheet ja silmän sairaudet Valo Taittuminen Heijastuminen Silmä Mitä silmän osia tunnistat? Värikalvo? Pupilli? Sarveiskalvo? Kovakalvo? Suonikalvo?
Näkö Valon havaitseminen Silmä Näkö ja optiikka Näkövirheet ja silmän sairaudet Valo Taittuminen Heijastuminen Silmä Mitä silmän osia tunnistat? Värikalvo? Pupilli? Sarveiskalvo? Kovakalvo? Suonikalvo?
Äänen eteneminen ja heijastuminen
 Äänen ominaisuuksia Ääni on ilmamolekyylien tihentymiä ja harventumia. Aaltoliikettä ja värähtelyä. Värähtelevä kappale synnyttää ääntä. Pistemäinen äänilähde säteilee pallomaisesti ilman esteitä. Käytännössä
Äänen ominaisuuksia Ääni on ilmamolekyylien tihentymiä ja harventumia. Aaltoliikettä ja värähtelyä. Värähtelevä kappale synnyttää ääntä. Pistemäinen äänilähde säteilee pallomaisesti ilman esteitä. Käytännössä
Elektroniikka, kierros 3
 Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
kartiopinta kartio. kartion pohja, suora ympyräkartio vino pyramidiksi
 5.3 Kartio Kun suora liikkuu avaruudessa niin, että yksi sen piste pysyy paikoillaan ja suoran jokin toinen piste kiertää jossakin tasossa jonkin suljetun käyrän palaten lähtöpaikkaansa, syntyy kaksiosainen
5.3 Kartio Kun suora liikkuu avaruudessa niin, että yksi sen piste pysyy paikoillaan ja suoran jokin toinen piste kiertää jossakin tasossa jonkin suljetun käyrän palaten lähtöpaikkaansa, syntyy kaksiosainen
Luento 15: Ääniaallot, osa 2
 Luento 15: Ääniaallot, osa 2 Aaltojen interferenssi Doppler Laskettuja esimerkkejä Luennon sisältö Aaltojen interferenssi Doppler Laskettuja esimerkkejä Aaltojen interferenssi Samassa pisteessä vaikuttaa
Luento 15: Ääniaallot, osa 2 Aaltojen interferenssi Doppler Laskettuja esimerkkejä Luennon sisältö Aaltojen interferenssi Doppler Laskettuja esimerkkejä Aaltojen interferenssi Samassa pisteessä vaikuttaa
Eristysvastuksen mittaus
 Eristysvastuksen mittaus Miksi eristyvastusmittauksia tehdään? Eristysvastuksen kunnon tarkastamista suositellaan vahvasti sähköiskujen ennaltaehkäisemiseksi. Mittausten suorittaminen lisää käyttöturvallisuutta
Eristysvastuksen mittaus Miksi eristyvastusmittauksia tehdään? Eristysvastuksen kunnon tarkastamista suositellaan vahvasti sähköiskujen ennaltaehkäisemiseksi. Mittausten suorittaminen lisää käyttöturvallisuutta
RAIDETESTERIN KÄYTTÖOHJE
 RAIDETESTERIN KÄYTTÖOHJE Yleiskuvaus Mittalaite tutkiin virtapiirin johtavuutta ja ilmaisee virtapiirissä olevan puhtaasti resistiivisen vastuksen. Mittalaitteen toiminnallisuus on parhaimmillaan, kun
RAIDETESTERIN KÄYTTÖOHJE Yleiskuvaus Mittalaite tutkiin virtapiirin johtavuutta ja ilmaisee virtapiirissä olevan puhtaasti resistiivisen vastuksen. Mittalaitteen toiminnallisuus on parhaimmillaan, kun
ERITTÄIN JOUSTAVAA MUKAVUUTTA AKUSTOINTIIN
 ERITTÄIN JOUSTAVAA MUKAVUUTTA AKUSTOINTIIN Suunniteltu erityisesti vähentämään hulevesi- ja viemäriputkien melua Loistava suorituskyky jo ohuella akustisella kerroksella Helppo levittää ja ylläpitää 107
ERITTÄIN JOUSTAVAA MUKAVUUTTA AKUSTOINTIIN Suunniteltu erityisesti vähentämään hulevesi- ja viemäriputkien melua Loistava suorituskyky jo ohuella akustisella kerroksella Helppo levittää ja ylläpitää 107
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
3. Optiikka. 1. Geometrinen optiikka. 2. Aalto-optiikka. 3. Stokesin parametrit. 4. Perussuureita. 5. Kuvausvirheet. 6. Optiikan suunnittelu
 3. Optiikka 1. Geometrinen optiikka 2. Aalto-optiikka 3. Stokesin parametrit 4. Perussuureita 5. Kuvausvirheet 6. Optiikan suunnittelu 3.1 Geometrinen optiikka! klassinen optiikka! Valoa kuvaa suoraan
3. Optiikka 1. Geometrinen optiikka 2. Aalto-optiikka 3. Stokesin parametrit 4. Perussuureita 5. Kuvausvirheet 6. Optiikan suunnittelu 3.1 Geometrinen optiikka! klassinen optiikka! Valoa kuvaa suoraan
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
S-114.2720 Havaitseminen ja toiminta
 S-114.2720 Havaitseminen ja toiminta Heikki Hyyti 60451P Harjoitustyö 2 visuaalinen prosessointi Treismanin FIT Kuva 1. Kuvassa on Treismanin kokeen ensimmäinen osio, jossa piti etsiä vihreätä T kirjainta.
S-114.2720 Havaitseminen ja toiminta Heikki Hyyti 60451P Harjoitustyö 2 visuaalinen prosessointi Treismanin FIT Kuva 1. Kuvassa on Treismanin kokeen ensimmäinen osio, jossa piti etsiä vihreätä T kirjainta.
2 Raja-arvo ja jatkuvuus
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.6 Raja-arvo ja jatkuvuus. a) Kun suorakulmion kärki on kohdassa =, on suorakulmion kannan pituus. Suorakulmion korkeus on käyrän y-koordinaatti
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.6 Raja-arvo ja jatkuvuus. a) Kun suorakulmion kärki on kohdassa =, on suorakulmion kannan pituus. Suorakulmion korkeus on käyrän y-koordinaatti
Valon luonne ja eteneminen. Valo on sähkömagneettista aaltoliikettä, ei tarvitse väliainetta edetäkseen
 Valon luonne ja eteneminen Valo on sähkömagneettista aaltoliikettä, ei tarvitse väliainetta edetäkseen 1 Valonlähteitä Perimmiltään valon lähteenä toimii kiihtyvässä liikkeessä olevat sähkövaraukset Kaikki
Valon luonne ja eteneminen Valo on sähkömagneettista aaltoliikettä, ei tarvitse väliainetta edetäkseen 1 Valonlähteitä Perimmiltään valon lähteenä toimii kiihtyvässä liikkeessä olevat sähkövaraukset Kaikki
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Nimi: Muiden ryhmäläisten nimet:
 Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Connexx 6 Siemens-kuulokojeiden sovitusohjelma. www.kuulotekniikka.com
 Connexx 6 Siemens-kuulokojeiden sovitusohjelma. www.kuulotekniikka.com Connexx6 sovitusohjelma Connexx6 on viimeisin Siemens-kuulokojeiden sovitusohjelma. Connexx6 sovitusohjelma on täysin NOAH yhteensopiva
Connexx 6 Siemens-kuulokojeiden sovitusohjelma. www.kuulotekniikka.com Connexx6 sovitusohjelma Connexx6 on viimeisin Siemens-kuulokojeiden sovitusohjelma. Connexx6 sovitusohjelma on täysin NOAH yhteensopiva
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
A. SMD-kytkennän kokoaminen ja mittaaminen
 A. SMD-kytkennän kokoaminen ja mittaaminen Avaa tarvikepussi ja tarkista komponenttien lukumäärä sekä nimellisarvot pakkauksessa olevan osaluettelon avulla. Ilmoita mahdollisista puutteista tai virheistä
A. SMD-kytkennän kokoaminen ja mittaaminen Avaa tarvikepussi ja tarkista komponenttien lukumäärä sekä nimellisarvot pakkauksessa olevan osaluettelon avulla. Ilmoita mahdollisista puutteista tai virheistä
Suomen ydinvoimateollisuudessa sovellettava rikkomattomien määräaikaistarkastusten
 1 (5) Suomen ydinvoimateollisuudessa sovellettava rikkomattomien määräaikaistarkastusten pätevöintijärjestelmä Teknisen perustelun laatiminen 1 Tarkoitus... 2 2 Henkilöstö, vastuut... 2 3 Alustavan teknisen
1 (5) Suomen ydinvoimateollisuudessa sovellettava rikkomattomien määräaikaistarkastusten pätevöintijärjestelmä Teknisen perustelun laatiminen 1 Tarkoitus... 2 2 Henkilöstö, vastuut... 2 3 Alustavan teknisen
Eye Pal Solo. Käyttöohje
 Eye Pal Solo Käyttöohje 1 Eye Pal Solon käyttöönotto Eye Pal Solon pakkauksessa tulee kolme osaa: 1. Peruslaite, joka toimii varsinaisena lukijana ja jonka etureunassa on laitteen ohjainpainikkeet. 2.
Eye Pal Solo Käyttöohje 1 Eye Pal Solon käyttöönotto Eye Pal Solon pakkauksessa tulee kolme osaa: 1. Peruslaite, joka toimii varsinaisena lukijana ja jonka etureunassa on laitteen ohjainpainikkeet. 2.
MAATUTKALUOTAUSTUTKIMUSRAPORTTI MÅRTENSBY VANTAA
 1 MAATUTKALUOTAUSTUTKIMUSRAPORTTI MÅRTENSBY VANTAA LKK25/9.6.2011 2 1. SISÄLLYSLUETTELO 2 2. MAATUTKALUOTAUS MÅRTENSY VANTAA 3 2.1 Tehtävä 3 2.2 Maastotyöt 3 2.2.1 Mittauskalusto 3 2.3 Tulostus 3 2.4 Yleistä
1 MAATUTKALUOTAUSTUTKIMUSRAPORTTI MÅRTENSBY VANTAA LKK25/9.6.2011 2 1. SISÄLLYSLUETTELO 2 2. MAATUTKALUOTAUS MÅRTENSY VANTAA 3 2.1 Tehtävä 3 2.2 Maastotyöt 3 2.2.1 Mittauskalusto 3 2.3 Tulostus 3 2.4 Yleistä
Työn tavoitteita. 1 Teoriaa
 FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
1 Määrittele seuraavat langattoman tiedonsiirron käsitteet.
 1 1 Määrittele seuraavat langattoman tiedonsiirron käsitteet. Radiosignaalin häipyminen. Adaptiivinen antenni. Piilossa oleva pääte. Radiosignaali voi edetä lähettäjältä vastanottajalle (jotka molemmat
1 1 Määrittele seuraavat langattoman tiedonsiirron käsitteet. Radiosignaalin häipyminen. Adaptiivinen antenni. Piilossa oleva pääte. Radiosignaali voi edetä lähettäjältä vastanottajalle (jotka molemmat
Metso Lokomo Steels Oy
 Metso Lokomo Steels Oy The biggest steel foundry in Nordic countries Net sales EUR 40 million Personnel approx. 250 Production 12 15000 tn/a Approx. 50 % Vaculok steels Net weight of steel castings from
Metso Lokomo Steels Oy The biggest steel foundry in Nordic countries Net sales EUR 40 million Personnel approx. 250 Production 12 15000 tn/a Approx. 50 % Vaculok steels Net weight of steel castings from
25 INTERFEROMETRI 25.1 Johdanto
 5 INTERFEROMETRI 5.1 Johdanto Interferometrin toiminta perustuu valon interferenssiin. Interferenssillä tarkoitetaan kahden tai useamman aallon yhdistymistä yhdeksi resultanttiaalloksi. Kuvassa 1 tarkastellaan
5 INTERFEROMETRI 5.1 Johdanto Interferometrin toiminta perustuu valon interferenssiin. Interferenssillä tarkoitetaan kahden tai useamman aallon yhdistymistä yhdeksi resultanttiaalloksi. Kuvassa 1 tarkastellaan
S-108-2110 OPTIIKKA 1/10 Laboratoriotyö: Polarisaatio POLARISAATIO. Laboratoriotyö
 S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
Sähköinen vuodontarkkailu. Suomen ympäristökeskus , Perttu Juntunen
 1 Suomen ympäristökeskus 11.10.2016 Kaitos Oy Perttu Juntunen 2 Miksi sähköistä vuodontarkkailua tarvitaan 3 3 Mikään laadunvalvontajärjestelmä ei voi täysin eliminoida kalvorakenteeseen syntyviä vaurioita.
1 Suomen ympäristökeskus 11.10.2016 Kaitos Oy Perttu Juntunen 2 Miksi sähköistä vuodontarkkailua tarvitaan 3 3 Mikään laadunvalvontajärjestelmä ei voi täysin eliminoida kalvorakenteeseen syntyviä vaurioita.
AKK-MOTORSPORT ry Katsastuksen käsikirja ISKUTILAVUUDEN MITTAAMINEN. 1. Tarkastuksen käyttö
 ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen)
 58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen) 1. Avaimet 1, 2, 3 ja 4 mahtuvat samaan lehtisolmuun. Tässä tapauksessa puussa on vain yksi solmu, joka on samaan aikaan juurisolmu
58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen) 1. Avaimet 1, 2, 3 ja 4 mahtuvat samaan lehtisolmuun. Tässä tapauksessa puussa on vain yksi solmu, joka on samaan aikaan juurisolmu
Keskeiset aihepiirit
 TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
PANK PANK-4122 ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ 1. MENETELMÄN TARKOITUS
 PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
Esimerkki - Näkymätön kuu
 Inversio-ongelmat Inversio = käänteinen, päinvastainen Inversio-ongelmilla tarkoitetaan (suoran) ongelman ratkaisua takaperin. Arkipäiväisiä inversio-ongelmia ovat mm. lääketieteellinen röntgentomografia
Inversio-ongelmat Inversio = käänteinen, päinvastainen Inversio-ongelmilla tarkoitetaan (suoran) ongelman ratkaisua takaperin. Arkipäiväisiä inversio-ongelmia ovat mm. lääketieteellinen röntgentomografia
Työ 2324B 4h. VALON KULKU AINEESSA
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/5 Työ 2324B 4h. VALON KULKU AINEESSA TYÖN TAVOITE Työssä perehdytään optisiin ilmiöihin tutkimalla valon kulkua linssisysteemeissä ja prismassa. Tavoitteena on saada
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/5 Työ 2324B 4h. VALON KULKU AINEESSA TYÖN TAVOITE Työssä perehdytään optisiin ilmiöihin tutkimalla valon kulkua linssisysteemeissä ja prismassa. Tavoitteena on saada
Laseranturit E3C-LDA-SARJA. s ä ä d e t t ä v ä p i t k ä n m a t k a n l a s e r a n t u r i. Advanced Industrial Automation
 Laseranturit E3C-LDA-SARJA s ä ä d e t t ä v ä p i t k ä n m a t k a n l a s e r a n t u r i Advanced Industrial Automation Omronin E3C-LDA-sarjan laseranturit on tarkoitettu tarkkaan kohteiden tunnistukseen
Laseranturit E3C-LDA-SARJA s ä ä d e t t ä v ä p i t k ä n m a t k a n l a s e r a n t u r i Advanced Industrial Automation Omronin E3C-LDA-sarjan laseranturit on tarkoitettu tarkkaan kohteiden tunnistukseen
Palautuslaite Boomerang ZHR
 Boomerang palautuslaitteen avulla yksi mies voi käyttää listoituskoneita ja/tai muita koneita ja laitteita puuntyöstössä. Ominaisuudet Arvot Työkappaleen mitat ilman kääntöyks. (mm) Pituus min. 300 max.
Boomerang palautuslaitteen avulla yksi mies voi käyttää listoituskoneita ja/tai muita koneita ja laitteita puuntyöstössä. Ominaisuudet Arvot Työkappaleen mitat ilman kääntöyks. (mm) Pituus min. 300 max.
Braggin ehdon mukaan hilatasojen etäisyys (111)-tasoille on
 763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
Vaihtoehtoiset tarkastusmenetelmät nostolaitteiden perusteellisissa määräaikaistarkastuksissa Juha Seppänen Inspecta Tarkastus Oy
 Vaihtoehtoiset tarkastusmenetelmät nostolaitteiden perusteellisissa määräaikaistarkastuksissa Juha Seppänen Inspecta Tarkastus Oy 1 Sisältö Lainsäädäntö Tavoite, periaatteet ja tarkastuslaajuus Tarkastusmenetelmät
Vaihtoehtoiset tarkastusmenetelmät nostolaitteiden perusteellisissa määräaikaistarkastuksissa Juha Seppänen Inspecta Tarkastus Oy 1 Sisältö Lainsäädäntö Tavoite, periaatteet ja tarkastuslaajuus Tarkastusmenetelmät
MITTALAITTEIDEN OMINAISUUKSIA ja RAJOITUKSIA
 KAJAANIN AMMATTIKORKEAKOL Tekniikan ja liikenteen ala TYÖ 21 ELEKTRONIIKAN LABORAATIOT H.Honkanen MITTALAITTEIDEN OMINAISKSIA ja RAJOITKSIA TYÖN TAVOITE: Tässä laboratoriotyössä tutustumme mittalaitteiden
KAJAANIN AMMATTIKORKEAKOL Tekniikan ja liikenteen ala TYÖ 21 ELEKTRONIIKAN LABORAATIOT H.Honkanen MITTALAITTEIDEN OMINAISKSIA ja RAJOITKSIA TYÖN TAVOITE: Tässä laboratoriotyössä tutustumme mittalaitteiden
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia
 KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
KAJAANIN AMMATTIKORKEAKOULU Tekniikan ja liikenteen ala TYÖ 11 ELEKTRONIIKAN LABORAATIOT H.Honkanen OPERAATIOVAHVISTIMET 2. Operaatiovahvistimen ominaisuuksia TYÖN TAVOITE Tutustua operaatiovahvistinkytkentään
RG-58U 4,5 db/30m. Spektrianalysaattori. 0,5m. 60m
 1. Johtuvia häiiöitä mitataan LISN:n avulla EN55022-standadin mukaisessa johtuvan häiiön mittauksessa. a. 20 MHz taajuudella laite tuottaa 1.5 mv suuuista häiiösignaalia. Läpäiseekö laite standadin B-luokan
1. Johtuvia häiiöitä mitataan LISN:n avulla EN55022-standadin mukaisessa johtuvan häiiön mittauksessa. a. 20 MHz taajuudella laite tuottaa 1.5 mv suuuista häiiösignaalia. Läpäiseekö laite standadin B-luokan
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.
![Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot. Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.](/thumbs/61/46046056.jpg) 7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
on hidastuvaa. Hidastuvuus eli negatiivinen kiihtyvyys saadaan laskevan suoran kulmakertoimesta, joka on siis
 Fys1, moniste 2 Vastauksia Tehtävä 1 N ewtonin ensimmäisen lain mukaan pallo jatkaa suoraviivaista liikettä kun kourun siihen kohdistama tukivoima (tässä tapauksessa ympyräradalla pitävä voima) lakkaa
Fys1, moniste 2 Vastauksia Tehtävä 1 N ewtonin ensimmäisen lain mukaan pallo jatkaa suoraviivaista liikettä kun kourun siihen kohdistama tukivoima (tässä tapauksessa ympyräradalla pitävä voima) lakkaa
2.3 Voiman jakaminen komponentteihin
 Seuraavissa kappaleissa tarvitaan aina silloin tällöin taitoa jakaa voima komponentteihin sekä myös taitoa suorittaa sille vastakkainen operaatio eli voimien resultantin eli kokonaisvoiman laskeminen.
Seuraavissa kappaleissa tarvitaan aina silloin tällöin taitoa jakaa voima komponentteihin sekä myös taitoa suorittaa sille vastakkainen operaatio eli voimien resultantin eli kokonaisvoiman laskeminen.
Kenttäteoria. Viikko 10: Tasoaallon heijastuminen ja taittuminen
 Kenttäteoria Viikko 10: Tasoaallon heijastuminen ja taittuminen Tämän viikon sisältöä Todellinen aalto vai tasoaalto Desibelit Esitehtävä Kohtisuora heijastus metalliseinästä Kohtisuora heijastus ja läpäisy
Kenttäteoria Viikko 10: Tasoaallon heijastuminen ja taittuminen Tämän viikon sisältöä Todellinen aalto vai tasoaalto Desibelit Esitehtävä Kohtisuora heijastus metalliseinästä Kohtisuora heijastus ja läpäisy
83950 Tietoliikennetekniikan työkurssi Monitorointivastaanottimen perusmittaukset
 TAMPEREEN TEKNILLINEN KORKEAKOULU 83950 Tietoliikennetekniikan työkurssi Monitorointivastaanottimen perusmittaukset email: ari.asp@tut.fi Huone: TG 212 puh 3115 3811 1. ESISELOSTUS Vastaanottimen yleisiä
TAMPEREEN TEKNILLINEN KORKEAKOULU 83950 Tietoliikennetekniikan työkurssi Monitorointivastaanottimen perusmittaukset email: ari.asp@tut.fi Huone: TG 212 puh 3115 3811 1. ESISELOSTUS Vastaanottimen yleisiä
TIEHÖYLÄN TERÄN KALTEVUUDEN SÄÄTÖJÄRJESTELMÄ GRADER WATCHMAN. Käyttöohjeet
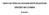 TIEHÖYLÄN TERÄN KALTEVUUDEN SÄÄTÖJÄRJESTELMÄ GRADER WATCHMAN Käyttöohjeet 2 Sisällysluettelo sivu 1. Käyttötarkoitus 3 2. Terän kaltevuuden säätöjärjestelmän rakenne 4 3. Tekniset tiedot 4 4 Tiehöylän
TIEHÖYLÄN TERÄN KALTEVUUDEN SÄÄTÖJÄRJESTELMÄ GRADER WATCHMAN Käyttöohjeet 2 Sisällysluettelo sivu 1. Käyttötarkoitus 3 2. Terän kaltevuuden säätöjärjestelmän rakenne 4 3. Tekniset tiedot 4 4 Tiehöylän
x 5 15 x 25 10x 40 11x x y 36 y sijoitus jompaankumpaan yhtälöön : b)
 MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
TUTKIMUSRAPORTTI NO. MAT12-15050-004 ULTRAÄÄNILAITTEIDEN SOVELTUVUUS LASIKUITUVENEIDEN NDT-VAURIOANALYYSIIN
 ULTRAÄÄNILAITTEIDEN SOVELTUVUUS LASIKUITUVENEIDEN NDT-VAURIOANALYYSIIN Veikko Äikäs Antti Ylhäinen Energia ja ympäristötekniikan laitos Mikkelin ammattikorkeakoulu Oy Sisältö 1. Tutkimuksen tausta... 2
ULTRAÄÄNILAITTEIDEN SOVELTUVUUS LASIKUITUVENEIDEN NDT-VAURIOANALYYSIIN Veikko Äikäs Antti Ylhäinen Energia ja ympäristötekniikan laitos Mikkelin ammattikorkeakoulu Oy Sisältö 1. Tutkimuksen tausta... 2
Mikroskooppisten kohteiden
 Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
ELEC-A4130 Sähkö ja magnetismi (5 op)
 ELEC-A4130 Sähkö ja magnetismi (5 op) Jari J. Hänninen 2015 16/IV V Luentoviikko 9 Tavoitteet Valon luonne ja eteneminen Dispersio Lähde: https: //www.flickr.com/photos/fastlizard4/5427856900/in/set-72157626537669172,
ELEC-A4130 Sähkö ja magnetismi (5 op) Jari J. Hänninen 2015 16/IV V Luentoviikko 9 Tavoitteet Valon luonne ja eteneminen Dispersio Lähde: https: //www.flickr.com/photos/fastlizard4/5427856900/in/set-72157626537669172,
Pelaajat siirtävät nappuloitaan vastakkaisiin suuntiin pelilaudalla. Peli alkaa näin. Tuplauskuutio asetetaan yhtä kauas kummastakin pelaajasta.
 DVD Backgammon Pelin tavoite Pelin tavoitteena on siirtää kaikki omat pelinappulat omalle sisäkentälle ja sieltä pois laudalta. Se pelaaja, joka ensimmäisenä on poistanut kaikki pelinappulansa pelilaudalta,
DVD Backgammon Pelin tavoite Pelin tavoitteena on siirtää kaikki omat pelinappulat omalle sisäkentälle ja sieltä pois laudalta. Se pelaaja, joka ensimmäisenä on poistanut kaikki pelinappulansa pelilaudalta,
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Tämä on PicoLog Windows ohjelman suomenkielinen pikaohje.
 Tämä on PicoLog Windows ohjelman suomenkielinen pikaohje. Asennus: HUOM. Tarkemmat ohjeet ADC-16 englanninkielisessä User Manual issa. Oletetaan että muuntimen kaikki johdot on kytketty anturiin, käyttöjännite
Tämä on PicoLog Windows ohjelman suomenkielinen pikaohje. Asennus: HUOM. Tarkemmat ohjeet ADC-16 englanninkielisessä User Manual issa. Oletetaan että muuntimen kaikki johdot on kytketty anturiin, käyttöjännite
1. Olkoot vektorit a, b ja c seuraavasti määritelty: a) Määritä vektori. sekä laske sen pituus.
 Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Ympyrä 1/6 Sisältö ESITIEDOT: käyrä, kulma, piste, suora
 Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus
 Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa
 SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
SwemaAir 5 Käyttöohje
 SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
S-72.3310 Tietoliikenteen siirtomediat
 S-72.3310 Tietoliikenteen siirtomediat Laboratoriotyö A: Johtotutkatyö Esiselostus Päiväys: Ryhmän nro: Nimet: 1. 2. 3. Tutustu huolellisesti Lauri Halmeen kirjan Johtotransmissio ja sähkömagneettinen
S-72.3310 Tietoliikenteen siirtomediat Laboratoriotyö A: Johtotutkatyö Esiselostus Päiväys: Ryhmän nro: Nimet: 1. 2. 3. Tutustu huolellisesti Lauri Halmeen kirjan Johtotransmissio ja sähkömagneettinen
Kuuloaisti. Korva ja ääni. Melu
 Kuuloaisti Ääni aaltoliikkeenä Tasapainoaisti Korva ja ääni Äänen kulku Korvan sairaudet Melu Kuuloaisti Ääni syntyy värähtelyistä. Taajuus mitataan värähtelyt/sekunti ja ilmaistaan hertseinä (Hz) Ihmisen
Kuuloaisti Ääni aaltoliikkeenä Tasapainoaisti Korva ja ääni Äänen kulku Korvan sairaudet Melu Kuuloaisti Ääni syntyy värähtelyistä. Taajuus mitataan värähtelyt/sekunti ja ilmaistaan hertseinä (Hz) Ihmisen
PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS
 1 PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen osat Lämpötilan
1 PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen osat Lämpötilan
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Kojemeteorologia, 3 op 9 luentoa, 3 laskuharjoitukset ja vierailu mittausasemalle Tentti Oppikirjana Rinne & Haapanala:
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Kojemeteorologia, 3 op 9 luentoa, 3 laskuharjoitukset ja vierailu mittausasemalle Tentti Oppikirjana Rinne & Haapanala:
Tekijä Pitkä matematiikka Pisteen (x, y) etäisyys pisteestä (0, 2) on ( x 0) Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y.
 Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
