AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE
|
|
|
- Kirsi-Kaisa Nurmi
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 TEHTÄVÄOSA AMMATTKORKEAKOULUJEN TEKNKAN JA LKENTEEN VALNTAKOE YLESOHJETA Tehtävien suoritusaika on h 45 min. Osio (Tekstin ymmärtäminen) Osiossa on valintatehtävää. Tämän osion maksimipistemäärä on 8. Osio (Matematiikka + looginen päättely + fysiikka/kemia) Osiossa on 9 tehtävää. Jokaisen tehtävän maksimipistemäärä on 3. Laskemista edellyttävien tehtävien ratkaisuksi ei riitä pelkkä lopputulos, vaan ratkaisun oleelliset laskutoimitukset on kirjoitettava näkyviin vastausosaan tehtävälle osoitettuun tilaan. Kunkin tehtävän lopullinen vastaus on kirjoitettava merkitylle kohdalle. Tehtävissä 7 9 on kaksi vaihtoehtoa (fysiikka ja kemia). Näistä vaihtoehdoista saa ratkaista vain jommankumman. ÄLÄ KÄÄNNÄ SVUA ENNEN KUN VALVOJA ANTAA LUVAN!
2 Osion tehtävät ovat vastausosassa. Aloita vastaamalla niihin. Osion tehtävät:. a) Sievennä lauseke x (3 y x) ( x+ y) b) Sievennä lauseke c) Laske lausekkeen a ab a 4b x x( y ) y x arvo, kun x = ja y = 3.. a) Ratkaise x yhtälöstä b) Ratkaise x yhtälöstä x = 3x+ = 5 x + c) Ratkaise m yhtälöstä m v = ( m + m ) v 3. Matti osti Mobiili Oy:n osakkeita. Niistä hän lahjoitti 96 osaketta tyttärelleen ja myi loput osakkeet sen jälkeen, kun osakkeiden kurssi oli noussut 5,0 %. Kurssinousun ansiosta Matti sai myymistään osakkeista saman verran rahaa kuin kaikkien osakkeiden osto oli maksanut. Kuinka monta osaketta hän oli ostanut? 4. Ullakkohuoneen takaseinää vasten on samankorkuisia kaappeja koko seinän leveydeltä. Seinä on 58 cm kaappeja korkeampi, ja kaappien syvyys on 63 cm. Ullakkohuoneen katon kaltevuus on :3. Kuinka korkea voi kuvan laatikko enintään olla, jotta sen voisi laittaa kaapiston päälle?
3 5. Myllykylän lukiossa on neljä matemaattisten aineiden opettajaa. Heistä kolme opettaa matematiikkaa, kolme fysiikkaa ja kaksi kemiaa. Jokainen opettaa kahta mainituista aineista. Lisäksi tiedetään seuraavat tosiasiat: Opettaja Laakso ei opeta fysiikkaa eikä opettaja Niemi kemiaa. Toisen kemian opettajan sukunimi on Koski ja toisen etunimi on Pekka. Opettaja Takala ja opettaja, jonka etunimi on Liisa, opettavat matematiikkaa. Matti ei opeta kemiaa mutta Anna opettaa. Selvitä näiden neljän opettajan nimet (etunimi ja sukunimi) ja opetusaineet Tehtävässä on kolme osaa (, ja ): Matilla on poika ja kaksi tytärtä. Minkä ikäisiä Matin lapset ovat, kun Annan ja Liisan ikien summa on 6, Annan ja Pekan ikien summa on 0 ja Liisan ja Pekan ikien summa on 30? Matin sisarella Ullalla on kolme tytärtä, jotka kaikki ovat syntyneet ennen vuotta 003. Tyttärien ikien tulo on 84 ja ikien summa on parillinen luku. Minkä ikäisiä Ullan tyttäret ovat? Matilla on kummipoika Kai. Kun Kain ikään lisätään kaksi vuotta ja näin saatu luku kerrotaan itsellään, saadaan niin suuri luku, että jos siitä vähennetään Kain ikä neljällä kerrottuna, tulokseksi tulee 40. Kuinka vanha Kai on? Tehtävissä 7, 8 ja 9 on kussakin vaihtoehtoisesti ratkaistava joko kohta A tai kohta B. Jos lasket molemmat kohdat, otetaan huomioon se, joka antaa vähemmän pisteitä. 7 A. Hissi, jonka massa kuormineen on 770 kg, lähtee pohjakerroksesta nousemaan ylöspäin. Hissin nopeus ajan funktiona on oheisen kuvaajan mukainen. a) Kuinka suuri on hissin kiihtyvyys sen lähtiessä liikkeelle? b) Kuinka suurella voimalla hissiä kannattava vaijeri nostaa hissiä sen lähtiessä liikkeelle? c) Kuinka paljon hissi on noussut, kun lähdöstä on kulunut 5,0 sekuntia? (Putoamiskiihtyvyys g = 9,8 m/s ) 5 4 Nopeus (m/s) Aika (s)
4 4 7 B. Rikkidioksidi voidaan pelkistää rikiksi esimerkiksi divetysulfidilla, jolloin reaktioyhtälö on SO + H S 3 S + H O Oletetaan, että rikkidioksidia on käytettävissä 5 moolia. Määritä a) reaktiossa tarvittavan divetysulfidin ainemäärä, b) reaktiossa tarvittavan divetysulfidin tilavuus NTP-olosuhteissa, c) reaktiossa muodostuvan rikin massa. Kaasujen moolitilavuus (NTP) on,4 dm 3 /mol. Alkuaineiden jaksollinen järjestelmä on viimeisellä sivulla. 8 A. Tehtävässä on kolme osaa (, ja ). Merkitse oikean vaihtoehdon (iso) kirjain vastausarkille osatehtävälle varattuun tilaan. Kaksi kiveä päästetään perätysten putoamaan korkeasta tornista, toinen kivi puoli sekuntia ensimmäisen jälkeen. Tämän jälkeen kivien etäisyys toisistaan putoamisen aikana A) kasvaa, B) lyhenee, C) pysyy vakiona. Pikku Liisa liukuu liukkaassa, ympyrän kaaren muotoisessa liukumäessä. Mikä piirroksista A, B, C ja D esittää Liisaan liu'un loppupuolella vaikuttavien voimien suunnat ja keskinäiset suuruudet oikein, ts. siten, että Liisan liiketilan muuttuminen selittyy voimilla? Vastus, jonka resistanssi on Ω, yhdistetään sähkölähteeseen, jonka sisäinen resistanssi on,6 Ω. Tällöin vastuksen kautta kulkee,5 A virta. Sähkölähteen lähdejännite on A) 4,8 V, B) 5,4 V, C) 30 V, D) 34 V. 8 B. Tehtävässä on kolme osaa (,, ). Merkitse oikean vaihtoehdon (iso) kirjain vastausarkille osatehtävälle varattuun tilaan. Kalsium ja kloori muodostavat kemiallisen yhdisteen, jonka moolimassa on A) g/mol, B) 76 g/mol, C) 6 g/mol, D) 75 g/mol. Raudan mineraaleista magnetiitti (Fe 3 O 4 ), hematiitti (Fe O 3 ), rautasälpä (FeCO 3 ) ja rikkikiisu (FeS ) pienin rautapitoisuus on A) magnetiitilla, B) hematiitilla, C) rautasälvällä, D) rikkikiisulla. Huoneen lämpötilassa on kiinteässä olomuodossa A) O, B) Hg, C) H O, D) Na O. Alkuaineiden jaksollinen järjestelmä on viimeisellä sivulla.
5 9 A. Nolla-asteista vettä ja nolla-asteisia jääpaloja laitettiin vedenkeittimeen, jonka teho oli 0,97 kw. Virran kytkemisen jälkeen veden lämpötila pysyi nollassa,0 minuutin ajan ja alkoi sen jälkeen nousta tasaisesti. Lämpötila saavutti arvon 40 o C, kun 5,0 minuuttia oli kulunut virran kytkemisestä. Kuinka paljon jäätä ja kuinka paljon vettä vedenkeittimessä oli alussa? Veden ominaislämpökapasiteetti on 4,9 kj/(kg o C), ja jään ominaissulamislämpö on 333 kj/kg. (Vedenkeittimen lämpökapasiteetti on hyvin pieni ja lämmönvaihto ympäristön kanssa vähäinen.) 5 9 B. Neutraloitaessa natriumhydroksidiliuosta rikkihapolla tapahtuu reaktio NaOH + H SO 4 Na SO 4 + H O Rikkihappoliuosta tarvittiin 30 millilitraa, kun sillä neutraloitiin 40 millilitraa natriumhydroksidiliuosta. Määritä neutralointiin käytetyn rikkihappoliuoksen konsentraatio, kun natriumhydroksidiliuoksen konsentraatio oli 0,0 mol/l. Alkuaineiden jaksollinen järjestelmä on viimeisellä sivulla.
6 Alkuaineiden jaksollinen järjestelmä H,008 He 4,003 3 Li 6,94 4 Be 9,0 5 B 0,8 6 C,0 7 N 4,0 8 O 6,00 9 F 9,00 0 Ne 0,8 Na,99 Mg 4,3 3 Al 6,98 4 Si 8,09 5 P 30,97 6 S 3,07 7 Cl 35,45 8 Ar 39,95 9 K 39,0 0 Ca 40,08 Sc 44,96 Ti 47,87 3 V 50,94 4 Cr 5,00 5 Mn 54,94 6 Fe 55,85 7 Co 58,93 8 Ni 58,69 9 Cu 63,55 30 Zn 65,4 3 Ga 69,7 3 Ge 7,64 33 As 74,9 34 Se 78,96 35 Br 79,90 36 Kr 83,80 37 Rb 85,47 38 Sr 87,6 39 Y 88,9 40 Zr 9, 4 Nb 9,9 4 Mo 95,94 43 Tc (99) 44 Ru 0, 45 Rh 0,9 46 Pd 06,4 47 Ag 07,9 48 Cd,4 49 n 4,8 50 Sn 8,7 5 Sb,8 5 Te 7,6 53 6,9 54 Xe 3,3 55 Cs 3,9 56 Ba 37, L 7 Hf 78,5 73 Ta 80,9 74 W 83,8 75 Re 86, 76 Os 90, 77 r 9, 78 Pt 95, 79 Au 97,0 80 Hg 00,6 8 Tl 04,4 8 Pb 07, 83 Bi 09,0 84 Po (09) 85 At (0) 86 Rn () 87 Fr (3) 88 Ra (6) A 04 Rf (6) 05 Db (6) L = lantanidit (alkuaineet 57 7) A = aktinidit (alkuaineet 89 03)
B sivu 1(6) AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE
 B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
Määräys STUK SY/1/ (34)
 Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta
 1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
1 (33) LUONNOS 2 -MÄÄRÄYS STUK SY/1/2017 Säteilyturvakeskuksen määräys turvallisuusluvasta ja valvonnasta vapauttamisesta Säteilyturvakeskuksen päätöksen mukaisesti määrätään säteilylain ( / ) 49 :n 3
AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE
 TEHTÄVÄOSA 6.6.2005 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän osan maksimipistemäärä
TEHTÄVÄOSA 6.6.2005 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän osan maksimipistemäärä
Jaksollinen järjestelmä ja sidokset
 Booriryhmä Hiiliryhmä Typpiryhmä Happiryhmä Halogeenit Jalokaasut Jaksollinen järjestelmä ja sidokset 13 Jaksollinen järjestelmä on tärkeä kemian työkalu. Sen avulla saadaan tietoa alkuaineiden rakenteista
Booriryhmä Hiiliryhmä Typpiryhmä Happiryhmä Halogeenit Jalokaasut Jaksollinen järjestelmä ja sidokset 13 Jaksollinen järjestelmä on tärkeä kemian työkalu. Sen avulla saadaan tietoa alkuaineiden rakenteista
JAKSOLLINEN JÄRJESTELMÄ
 JASOLLINEN JÄRJESTELMÄ Oppitunnin tavoite: Oppitunnin tavoitteena on opettaa jaksollinen järjestelmä sekä sen historiaa alkuainepelin avulla. Tunnin tavoitteena on, että oppilaat oppivat tieteellisen tutkimuksen
JASOLLINEN JÄRJESTELMÄ Oppitunnin tavoite: Oppitunnin tavoitteena on opettaa jaksollinen järjestelmä sekä sen historiaa alkuainepelin avulla. Tunnin tavoitteena on, että oppilaat oppivat tieteellisen tutkimuksen
Liitetaulukko 1/11. Tutkittujen materiaalien kokonaispitoisuudet KOTIMAINEN MB-JÄTE <1MM SAKSAN MB- JÄTE <1MM POHJAKUONA <10MM
 Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
Alikuoret eli orbitaalit
 Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE. Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia)
 B sivu 1(5) TOIMINTAOHJE 6.6.2003 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia) Laskemista sisältävien tehtävien ratkaisuksi ei riitä
B sivu 1(5) TOIMINTAOHJE 6.6.2003 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia) Laskemista sisältävien tehtävien ratkaisuksi ei riitä
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Tekstikoe ja Ongelmanratkaisu HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Tekstikoe ja Ongelmanratkaisu HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan
 Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Syntymäaika: 2. Kirjoita nimesi ja syntymäaikasi kaikkiin sivuille 1 ja 3-11 merkittyihin kohtiin.
 1 Helsingin, Jyväskylän ja Oulun yliopistojen kemian valintakoe Keskiviikkona 15.6. 2011 klo 9-12 Nimi: Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-12. 2. Kirjoita nimesi
1 Helsingin, Jyväskylän ja Oulun yliopistojen kemian valintakoe Keskiviikkona 15.6. 2011 klo 9-12 Nimi: Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-12. 2. Kirjoita nimesi
Pellettien pienpolton haasteet TUOTEPÄÄLLIKKÖ HEIKKI ORAVAINEN VTT EXPERT SERVICES OY
 Pellettien pienpolton haasteet TUOTEPÄÄLLIKKÖ HEIKKI ORAVAINEN VTT EXPERT SERVICES OY Esityksen sisältö Ekopellettien ja puupellettien vertailua polttotekniikan kannalta Koetuloksia ekopellettien poltosta
Pellettien pienpolton haasteet TUOTEPÄÄLLIKKÖ HEIKKI ORAVAINEN VTT EXPERT SERVICES OY Esityksen sisältö Ekopellettien ja puupellettien vertailua polttotekniikan kannalta Koetuloksia ekopellettien poltosta
Lukion kemia 3, Reaktiot ja energia. Leena Piiroinen Luento 2 2015
 Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
17VV VV 01021
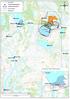 Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE. Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia)
 B sivu 1(7) TOIMINTAOHJE 7.6.2002 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE Tehtävien suoritusaika on 2 h 45 min. Osio 1 (Tekstin ymmärtäminen) Osiossa on kaksi osaa A Valintatehtävä (4
B sivu 1(7) TOIMINTAOHJE 7.6.2002 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE Tehtävien suoritusaika on 2 h 45 min. Osio 1 (Tekstin ymmärtäminen) Osiossa on kaksi osaa A Valintatehtävä (4
17VV VV Veden lämpötila 14,2 12,7 14,2 13,9 C Esikäsittely, suodatus (0,45 µm) ok ok ok ok L. ph 7,1 6,9 7,1 7,1 RA2000¹ L
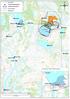 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
Sarake 1 Sarake 2 Sarake 3 Sarake 4. Vahvistumisen jälkeen tavaran hinta on 70. Uusi tilavuus on
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE 1/5 TEHTÄVÄOSA / Ongelmanratkaisu 1.6. 2017 TEHTÄVÄOSA ONGELMANRATKAISU Vastaa kullekin tehtävälle varatulle ratkaisusivulle. Vastauksista tulee selvitä tehtävien
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE 1/5 TEHTÄVÄOSA / Ongelmanratkaisu 1.6. 2017 TEHTÄVÄOSA ONGELMANRATKAISU Vastaa kullekin tehtävälle varatulle ratkaisusivulle. Vastauksista tulee selvitä tehtävien
Helsingin, Jyväskylän ja Oulun yliopistojen kemian valintakoe Keskiviikkona 11.6. 2014 klo 10-13
 1 Helsingin, Jyväskylän ja Oulun yliopistojen kemian valintakoe Keskiviikkona 11.6. 2014 klo 10-13 Yleiset ohjeet 1. Tarkasta, että tehtäväpaperinipussa ovat kaikki sivut 1-11 2. Kirjoita nimesi ja syntymäaikasi
1 Helsingin, Jyväskylän ja Oulun yliopistojen kemian valintakoe Keskiviikkona 11.6. 2014 klo 10-13 Yleiset ohjeet 1. Tarkasta, että tehtäväpaperinipussa ovat kaikki sivut 1-11 2. Kirjoita nimesi ja syntymäaikasi
5 LIUOKSEN PITOISUUS Lisätehtävät
 LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
Päähaku, kemian kandiohjelma Valintakoe klo
 Päähaku, kemian kandiohjelma Valintakoe 10.5.2019 klo 10.00 13.00 Kirjoita henkilö- ja yhteystietosi tekstaamalla. Kirjoita nimesi latinalaisilla kirjaimilla (abcd...), älä esimerkiksi kyrillisillä kirjaimilla
Päähaku, kemian kandiohjelma Valintakoe 10.5.2019 klo 10.00 13.00 Kirjoita henkilö- ja yhteystietosi tekstaamalla. Kirjoita nimesi latinalaisilla kirjaimilla (abcd...), älä esimerkiksi kyrillisillä kirjaimilla
ÄLÄ KÄÄNNÄ SIVUA ENNEN KUIN VALVOJA ANTAA LUVAN!
 B 1 (6) AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE 28.5.2015 OSION 2 TEHTÄVÄT Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia) LUE VASTAUSOHJEET C-OSAN (VASTAUSLOMAKKEEN) KANNESTA
B 1 (6) AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE 28.5.2015 OSION 2 TEHTÄVÄT Osio 2 (Matematiikka + looginen päättely + fysiikka/kemia) LUE VASTAUSOHJEET C-OSAN (VASTAUSLOMAKKEEN) KANNESTA
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
Seoksen pitoisuuslaskuja
 Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet
 www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
Malmi Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb
 11.2 Malmi % % % ppm ppm % ppm ppm ppm ppm ppm ppm ppm Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb Konttijärvi Kattopuoli 0,20 0,14 0,07 48,97 376,76 4,33
11.2 Malmi % % % ppm ppm % ppm ppm ppm ppm ppm ppm ppm Orig_ENGLISH Avolouhos Kivilajien kerrosjärjestys S Cu Ni Co Cr Fe Pb Cd Zn As Mn Mo Sb Konttijärvi Kattopuoli 0,20 0,14 0,07 48,97 376,76 4,33
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
TUTKIMUSSELOSTE. Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: Tarkkailukierros: vko 2. Tutkimuksen lopetus pvm
 TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 2 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 2 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä.
 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
TKK, TTY, LTY, OY, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 31.5.2006
 TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
AKKU- JA PARISTOTEKNIIKAT
 AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
NIMI: Luokka: c) Atomin varaukseton hiukkanen on nimeltään i) protoni ii) neutroni iii) elektroni
 Peruskoulun kemian valtakunnallinen koe 2010-2011 NIMI: Luokka: 1. Ympyröi oikea vaihtoehto. a) Ruokasuolan kemiallinen kaava on i) CaOH ii) NaCl iii) KCl b) Natriumhydroksidi on i) emäksinen aine, jonka
Peruskoulun kemian valtakunnallinen koe 2010-2011 NIMI: Luokka: 1. Ympyröi oikea vaihtoehto. a) Ruokasuolan kemiallinen kaava on i) CaOH ii) NaCl iii) KCl b) Natriumhydroksidi on i) emäksinen aine, jonka
2. Koska f(5) > 8 ja yhdeksän pisteen varaan voidaan virittää kupera viisikulmio, niin f(5) = 9.
 Dimension 1/2018 pulmasivu Ratkaisuja 1. Viiden pisteen joukosta voidaan aina valita neljä, jotka ovat kuperan monikulmion kärkipisteitä, mutta neljästä pisteestä ei muodostu aina kuperaa monikulmiota.
Dimension 1/2018 pulmasivu Ratkaisuja 1. Viiden pisteen joukosta voidaan aina valita neljä, jotka ovat kuperan monikulmion kärkipisteitä, mutta neljästä pisteestä ei muodostu aina kuperaa monikulmiota.
SÄTEILYN KÄYTÖN VAPAUTTAMINEN TURVALLISUUSLUVASTA
 OHJE ST 1.5 / 12.9.2013 SÄTEILYN KÄYTÖN VAPAUTTAMINEN TURVALLISUUSLUVASTA 1 Yleistä 3 2 Säteilyturvakeskuksen päätöksellä vapautettu säteilyn käyttö 3 2.1 Yleiset vaatimukset 3 2.2 Turvallisuusluvasta
OHJE ST 1.5 / 12.9.2013 SÄTEILYN KÄYTÖN VAPAUTTAMINEN TURVALLISUUSLUVASTA 1 Yleistä 3 2 Säteilyturvakeskuksen päätöksellä vapautettu säteilyn käyttö 3 2.1 Yleiset vaatimukset 3 2.2 Turvallisuusluvasta
2. Reaktioyhtälö 3) CH 3 CH 2 COCH 3 + O 2 CO 2 + H 2 O
 2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
A Lausekkeen 1,1 3 arvo on 1,13 3,3 1,331 B Tilavuus 0,5 m 3 on sama kuin 50 l 500 l l C Luvuista 2 3, 6 7
 1 Tuotteen hinta nousee ensin 10 % ja laskee sitten 10 %, joten lopullinen hinta on... alkuperäisestä hinnasta. alkuperäisestä hinnasta. YLIOPPILASTUTKINTO- LAUTAKUNTA 23.3.2016 MATEMATIIKAN KOE PITKÄ
1 Tuotteen hinta nousee ensin 10 % ja laskee sitten 10 %, joten lopullinen hinta on... alkuperäisestä hinnasta. alkuperäisestä hinnasta. YLIOPPILASTUTKINTO- LAUTAKUNTA 23.3.2016 MATEMATIIKAN KOE PITKÄ
luku 1.notebook Luku 1 Mooli, ainemäärä ja konsentraatio
 Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Oppikirjan tehtävien ratkaisut
 Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
B. 2 E. en tiedä C. 6. 2 ovat luonnollisia lukuja?
 Nimi Koulutus Ryhmä Jokaisessa tehtävässä on vain yksi vastausvaihtoehto oikein. Laske tehtävät ilman laskinta.. Missä pisteessä suora y = 3x 6 leikkaa x-akselin? A. 3 D. B. E. en tiedä C. 6. Mitkä luvuista,,,
Nimi Koulutus Ryhmä Jokaisessa tehtävässä on vain yksi vastausvaihtoehto oikein. Laske tehtävät ilman laskinta.. Missä pisteessä suora y = 3x 6 leikkaa x-akselin? A. 3 D. B. E. en tiedä C. 6. Mitkä luvuista,,,
Kemia 3 op. Kirjallisuus: MaoL:n taulukot: kemian sivut. Kurssin sisältö
 Kemia 3 op Kirjallisuus: MaoL:n taulukot: kemian sivut Kurssin sisältö 1. Peruskäsitteet ja atomin rakenne 2. Jaksollinen järjestelmä,oktettisääntö 3. Yhdisteiden nimeäminen 4. Sidostyypit 5. Kemiallinen
Kemia 3 op Kirjallisuus: MaoL:n taulukot: kemian sivut Kurssin sisältö 1. Peruskäsitteet ja atomin rakenne 2. Jaksollinen järjestelmä,oktettisääntö 3. Yhdisteiden nimeäminen 4. Sidostyypit 5. Kemiallinen
Fysiikan, kemian ja matematiikan kilpailu lukiolaisille
 Fysiikan, kemian ja matematiikan kilpailu lukiolaisille 28.1.2016 Kemian tehtävät Kirjoita nimesi, luokkasi ja lukiosi tähän tehtäväpaperiin. Kirjoita vastauksesi selkeällä käsialalla tehtäväpaperiin vastauksille
Fysiikan, kemian ja matematiikan kilpailu lukiolaisille 28.1.2016 Kemian tehtävät Kirjoita nimesi, luokkasi ja lukiosi tähän tehtäväpaperiin. Kirjoita vastauksesi selkeällä käsialalla tehtäväpaperiin vastauksille
c) 22a 21b x + a 2 3a x 1 = a,
 Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2 1/2 p = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 014 Insinöörivalinnan kemian koe 8.5.014 MALLIRATKAISUT ja PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 014 Insinöörivalinnan kemian koe 8.5.014 MALLIRATKAISUT ja PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
27. 10. joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja.
 ÄÙ ÓÒÑ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒÔ ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Hiiri juoksee tasaisella
ÄÙ ÓÒÑ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒÔ ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Hiiri juoksee tasaisella
Helsingin, Jyväskylän, Oulun ja Turun yliopistojen kemian valintakoe tiistaina 26.5.2009 klo 9-12
 1 Helsingin, Jyväskylän, ulun ja Turun yliopistojen kemian valintakoe tiistaina 26.5.2009 klo 9-12 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa on kaikki sivut 1-11. 2. Kirjoita nimesi ja syntymäaikasi
1 Helsingin, Jyväskylän, ulun ja Turun yliopistojen kemian valintakoe tiistaina 26.5.2009 klo 9-12 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa on kaikki sivut 1-11. 2. Kirjoita nimesi ja syntymäaikasi
MOOLIMASSA. Vedyllä on yksi atomi, joten Vedyn moolimassa M(H) = 1* g/mol = g/mol. ATOMIMASSAT TAULUKKO
 MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka. Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU
 MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
a) Piirrä hahmotelma varjostimelle muodostuvan diffraktiokuvion maksimeista 1, 2 ja 3.
 Ohjeita: Tee jokainen tehtävä siististi omalle sivulleen/sivuilleen. Merkitse jos tehtävä jatkuu seuraavalle konseptille. Kirjoita ratkaisuihin näkyviin tarvittavat välivaiheet ja perustele lyhyesti käyttämästi
Ohjeita: Tee jokainen tehtävä siististi omalle sivulleen/sivuilleen. Merkitse jos tehtävä jatkuu seuraavalle konseptille. Kirjoita ratkaisuihin näkyviin tarvittavat välivaiheet ja perustele lyhyesti käyttämästi
3 TOISEN ASTEEN POLYNOMIFUNKTIO
 3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
0, niin vektorit eivät ole kohtisuorassa toisiaan vastaan.
 Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Kevät 2010 Jukka Maalampi LUENTO 2-3 Vääntömomentti Oletus: Voimat tasossa, joka on kohtisuorassa pyörimisakselia vastaan. Oven kääntämiseen tarvitaan eri suuruinen voima
Mekaniikan jatkokurssi Fys102 Kevät 2010 Jukka Maalampi LUENTO 2-3 Vääntömomentti Oletus: Voimat tasossa, joka on kohtisuorassa pyörimisakselia vastaan. Oven kääntämiseen tarvitaan eri suuruinen voima
ARKI, 1`t_'+i APU IALk GEO Väli-Suomen aluetoimisto M19/2431/2000/1/10 ALAVIESKA Juku Jarmo Nikander SKUS KULTATUTKIMUKSET ALAVIESKASSA KART
 ARKI, 1`t_'+i APU IALk GEO Väli-Suomen aluetoimisto M19/2431/2000/1/10 ALAVIESKA Juku 28.1.2000 Jarmo Nikander SKUS KULTATUTKIMUKSET ALAVIESKASSA KARTTALEHDELLÄ 243108, KOHTEESSA JUKU, VUONNA 1998. 1 TUTKIMUSKOHTEEN
ARKI, 1`t_'+i APU IALk GEO Väli-Suomen aluetoimisto M19/2431/2000/1/10 ALAVIESKA Juku 28.1.2000 Jarmo Nikander SKUS KULTATUTKIMUKSET ALAVIESKASSA KARTTALEHDELLÄ 243108, KOHTEESSA JUKU, VUONNA 1998. 1 TUTKIMUSKOHTEEN
joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja.
 ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
Helsingin, Jyväskylän, Oulun ja Turun yliopistojen kemian valintakoe Tiistaina 25.5. 2010 klo 9-12
 1 Helsingin, Jyväskylän, Oulun ja Turun yliopistojen kemian valintakoe Tiistaina 25.5. 2010 klo 9-12 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-13. 2. Kirjoita nimesi ja
1 Helsingin, Jyväskylän, Oulun ja Turun yliopistojen kemian valintakoe Tiistaina 25.5. 2010 klo 9-12 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-13. 2. Kirjoita nimesi ja
Vedetään kiekkoa erisuuruisilla voimilla! havaitaan kiekon saaman kiihtyvyyden olevan suoraan verrannollinen käytetyn voiman suuruuteen
 4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
LAHDEN AMMATTIKORKEAKOULU TEKNIIKAN ALA MATEMATIIKAN PREPPAUSTEHTÄVIÄ Kesä 2015
 PREPPAUSTA 05.nb LAHDEN AMMATTIKORKEAKOULU TEKNIIKAN ALA MATEMATIIKAN PREPPAUSTEHTÄVIÄ Kesä 05 MURTOLUVUT. Laske murtolukujen 3 ja 5 6 summa, tulo ja osamäärä. Summa 3 5 6 4 3 5 6 8 6 5 6 3 6 6. Laske
PREPPAUSTA 05.nb LAHDEN AMMATTIKORKEAKOULU TEKNIIKAN ALA MATEMATIIKAN PREPPAUSTEHTÄVIÄ Kesä 05 MURTOLUVUT. Laske murtolukujen 3 ja 5 6 summa, tulo ja osamäärä. Summa 3 5 6 4 3 5 6 8 6 5 6 3 6 6. Laske
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Tehtävä 2. Selvitä, ovatko seuraavat kovalenttiset sidokset poolisia vai poolittomia. Jos sidos on poolinen, merkitse osittaisvaraukset näkyviin.
 KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
1. a) Laske lukujen 1, 1 ja keskiarvo. arvo. b) Laske lausekkeen. c) Laske integraalin ( x xdx ) arvo. MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta.
 Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
Lisätehtäviä. Rationaalifunktio. x 2. a b ab. 6u x x x. kx x
 MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
Joensuun yliopisto Kemian valintakoe/3.6.2009
 Joesuu yliopisto Kemia valitakoe/.6.009 Mallivastaukset 1. Selitä lyhyesti (korkeitaa kolme riviä), a) elektroegatiivisuus b) elektroiaffiiteetti c) amfolyytti d) diffuusio e) Le Chatelieri periaate. a)
Joesuu yliopisto Kemia valitakoe/.6.009 Mallivastaukset 1. Selitä lyhyesti (korkeitaa kolme riviä), a) elektroegatiivisuus b) elektroiaffiiteetti c) amfolyytti d) diffuusio e) Le Chatelieri periaate. a)
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Insinöörivalinnan fysiikan koe 1.6.2011, malliratkaisut
 A1 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Täydennä kuhunkin kohtaan yhtälöstä puuttuva suure tai vakio alla olevasta taulukosta. Anna vastauksena kuhunkin kohtaan ainoastaan
A1 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Täydennä kuhunkin kohtaan yhtälöstä puuttuva suure tai vakio alla olevasta taulukosta. Anna vastauksena kuhunkin kohtaan ainoastaan
Luvuilla laskeminen. 1. Laske. a) 2 5 b) 6 11 c) 4 + ( 4) d) 1 ( 7) Ratkaisu. a) 2 5 = 7 b) 6 11 = 5 c) 4 + ( 4) = 4 4 = 0 d) 1 ( 7) = = 6
 Luvuilla laskeminen. Laske. 6 4 + ( 4) d) ( 7) = 7 6 = 4 + ( 4) = 4 4 = 0 d) ( 7) = + 7 = 6. Laske. ( 9) 7 ( 8) 8 : ( ) d) 4 : 6 ( 9) = 7 7 ( 8) = 6 8 : ( ) = 9 d) 4 : 6 = 7. Muunna 8 sekaluvuksi 6 sekaluvuksi
Luvuilla laskeminen. Laske. 6 4 + ( 4) d) ( 7) = 7 6 = 4 + ( 4) = 4 4 = 0 d) ( 7) = + 7 = 6. Laske. ( 9) 7 ( 8) 8 : ( ) d) 4 : 6 ( 9) = 7 7 ( 8) = 6 8 : ( ) = 9 d) 4 : 6 = 7. Muunna 8 sekaluvuksi 6 sekaluvuksi
c) Tasapainota seuraava happamassa liuoksessa tapahtuva hapetus-pelkistysreaktio:
 HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
= 6, Nm 2 /kg kg 71kg (1, m) N. = 6, Nm 2 /kg 2 7, kg 71kg (3, m) N
 t. 1 Auringon ja kuun kohdistamat painovoimat voidaan saada hyvin tarkasti laksettua Newtonin painovoimalailla, koska ne ovat pallon muotoisia. Junalle sillä saadaan selville suuruusluokka, joka riittää
t. 1 Auringon ja kuun kohdistamat painovoimat voidaan saada hyvin tarkasti laksettua Newtonin painovoimalailla, koska ne ovat pallon muotoisia. Junalle sillä saadaan selville suuruusluokka, joka riittää
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
MATEMATIIKKA. Matematiikkaa pintakäsittelijöille. Ongelmanratkaisu. Isto Jokinen 2017
 MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
ICP-OES JA ICP-MS TEKNIIKAT PIENTEN METALLIPITOISUUKSIEN MÄÄRITYKSESSÄ. Matti Niemelä, Oulun yliopisto, kemian laitos
 ICP-OES JA ICP-MS TEKNIIKAT PIENTEN METALLIPITOISUUKSIEN MÄÄRITYKSESSÄ Matti Niemelä, Oulun yliopisto, kemian laitos Oulun yliopisto - Kemian laitos Laitoksen tiedealat Epäorgaaninen kemia Fysikaalinen
ICP-OES JA ICP-MS TEKNIIKAT PIENTEN METALLIPITOISUUKSIEN MÄÄRITYKSESSÄ Matti Niemelä, Oulun yliopisto, kemian laitos Oulun yliopisto - Kemian laitos Laitoksen tiedealat Epäorgaaninen kemia Fysikaalinen
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
 Raportti Sivu 1 (7) K1301600 2BQWOKQ8N98 Vahanen Oy Projekti TT 1099 Kyösti Nieminen Tilausnumero Sisäänkirjattu 2013-11-13 Linnoitustie 5 Raportoitu 2013-11-21 02600 ESPOO Materiaalin analysointi Asiakkaan
Raportti Sivu 1 (7) K1301600 2BQWOKQ8N98 Vahanen Oy Projekti TT 1099 Kyösti Nieminen Tilausnumero Sisäänkirjattu 2013-11-13 Linnoitustie 5 Raportoitu 2013-11-21 02600 ESPOO Materiaalin analysointi Asiakkaan
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /6 TEHTÄVÄOSA/ Ongelmanratkaisu 9.5.09 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /6 TEHTÄVÄOSA/ Ongelmanratkaisu 9.5.09 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
FYSIIKAN HARJOITUSKOE I Mekaniikka, 8. luokka
 FYSIIKAN HARJOITUSKOE I Mekaniikka, 8. luokka Oppilaan nimi: Pisteet: / 77 p. Päiväys: Koealue: kpl 13-18, s. 91-130 1. SUUREET. Täydennä taulukon tiedot. suure suureen tunnus suureen yksikkö matka aika
FYSIIKAN HARJOITUSKOE I Mekaniikka, 8. luokka Oppilaan nimi: Pisteet: / 77 p. Päiväys: Koealue: kpl 13-18, s. 91-130 1. SUUREET. Täydennä taulukon tiedot. suure suureen tunnus suureen yksikkö matka aika
HEVOSENLANNAN PIENPOLTTOHANKKEEN TULOKSIA. Erikoistutkija Tuula Pellikka
 HEVOSENLANNAN PIENPOLTTOHANKKEEN TULOKSIA Erikoistutkija Tuula Pellikka TUTKIMUKSEN TAUSTA Tavoitteena oli tutkia käytännön kenttäkokeiden avulla hevosenlannan ja kuivikkeen seoksen polton ilmaan vapautuvia
HEVOSENLANNAN PIENPOLTTOHANKKEEN TULOKSIA Erikoistutkija Tuula Pellikka TUTKIMUKSEN TAUSTA Tavoitteena oli tutkia käytännön kenttäkokeiden avulla hevosenlannan ja kuivikkeen seoksen polton ilmaan vapautuvia
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
TUTKIMUSSELOSTE. Tutkimuksen lopetus pvm. Näkösyv. m
 TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 3 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
TUTKIMUSSELOSTE Tarkkailu: Talvivaaran prosessin ylijäämävedet 2012 Jakelu: pirkko.virta@poyry.com Tarkkailukierros: vko 3 hanna.kurtti@poyry.com Tilaaja: Pöyry Finland Oy Havaintopaikka Tunnus Näytenumero
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
Sovelletun fysiikan pääsykoe
 Sovelletun fysiikan pääsykoe 7.6.016 Kokeessa on neljä (4) tehtävää. Vastaa kaikkiin tehtäviin. Muista kirjoittaa myös laskujesi välivaiheet näkyviin. Huom! Kirjoita tehtävien 1- vastaukset yhdelle konseptille
Sovelletun fysiikan pääsykoe 7.6.016 Kokeessa on neljä (4) tehtävää. Vastaa kaikkiin tehtäviin. Muista kirjoittaa myös laskujesi välivaiheet näkyviin. Huom! Kirjoita tehtävien 1- vastaukset yhdelle konseptille
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.3.06 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 3.3.06 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
PRELIMINÄÄRIKOE. Lyhyt Matematiikka 3.2.2015
 PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
Ideaalikaasut. 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista?
 Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
A-osio. Tehdään ilman laskinta ja taulukkokirjaa! Valitse tehtävistä A1-A3 kaksi ja vastaa niihin. Maksimissaan tunti aikaa suorittaa A-osiota.
 MAA5.2 Loppukoe 24.9.2013 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A1. A-osio. Tehdään
MAA5.2 Loppukoe 24.9.2013 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A1. A-osio. Tehdään
Tehtävä 1 2 3 4 5 6 7 8 Pisteet yhteensä Pisteet
 1 Helsingin, Jyväskylän ja ulun yliopistojen kemian valintakoe Keskiviikkona 13.6. 2012 klo 10-13 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-10. 2. Kirjoita nimesi ja syntymäaikasi
1 Helsingin, Jyväskylän ja ulun yliopistojen kemian valintakoe Keskiviikkona 13.6. 2012 klo 10-13 Yleiset ohjeet 1. Tarkista, että tehtäväpaperinipussa ovat kaikki sivut 1-10. 2. Kirjoita nimesi ja syntymäaikasi
Liike ja voima. Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä
 Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Sähkövirran määrittelylausekkeesta
 VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-6. Taulukkokirjaa saa käyttää apuna, laskinta ei.
 PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
Tärkeitä tasapainopisteitä
 Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /5 TEHTÄVÄOSA/ Ongelmanratkaisu..08 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /5 TEHTÄVÄOSA/ Ongelmanratkaisu..08 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
Pietarsaaren lukio Vesa Maanselkä
 Fys 9 / Mekaniikan osio Liike ja sen kuvaaminen koordinaatistossa Newtonin lait Voimavektorit ja vapaakappalekuvat Työ, teho,työ-energiaperiaate ja energian säilymislaki Liikemäärä ja sen säilymislaki,
Fys 9 / Mekaniikan osio Liike ja sen kuvaaminen koordinaatistossa Newtonin lait Voimavektorit ja vapaakappalekuvat Työ, teho,työ-energiaperiaate ja energian säilymislaki Liikemäärä ja sen säilymislaki,
