Maailmankaikkeuden kriittinen tiheys
|
|
|
- Hannes Sariola
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Maailmankaikkeuden kriittinen tiheys Tarkastellaan maailmankaikkeuden pientä pallomaista laajenevaa osaa, joka sisältää laajenemisliikkeessä olevia galakseja. Olkoon pallon säde R, massa M ja maailmankaikkeuden keskitiheys ρ. Pallon sisällä oleva massa on. m M Olkoon pallon pinnalla kappale (galaksi), jonka massa on m. Kappaleen m gravitaatioenergia M-massaisen ja R-säteisen pallon pinnalla on G = gravitaatiovakio (= γ, f). Kappaleen m (galaksi) liike-energia mv2. Kappaleen nopeus v saadaan Hubblen laista; v = Hr, joka sijoitetaan liike-energian lausekkeeseen. liike-energiaksi saadaan näin mv2 =.. Kappaleen eli massasysteemin m mekaaninen kokonaisenergia Kappaleen mekaaninen kokonaisenergia säilyy eli E on vakio. Mikäli E 0, niin kappale m voi edetä äärettömän kauas. Jos taas E < 0, niin kappale m putoaa takaisin. Rajatapausta E = 0 vastaa maailmankaikkeuden kriittinen tiheys ρc, joka saadaan kokonaisenergian E lausekkeesta (*), kun E = = 0 :
2 . Maailmankaikkeuden keskimääräinen kriittinen tiheys on. G = gravitaatiovakio (= γ, f). Kun kriittisen tiheyden ρc lausekkeeseen sijoitetaan Hubblen vakio; H = 72 km s -1 Mpc -1 eli = , =2, ja gravitaatiovakio G = 6, , saadaan maailmankaikkeuden keskimääräiseksi kriittiseksi tiheydeksi 8 = 2, , , (~10 vetyatomia/cm ) Aleksander Friedmann ja Georges Lemaitre tutkivat 1920-luvulla Einsteinin kenttäyhtälöiden + = ( ratkaisuja, kun kosmologinen vakio Λ = 0. Tällöin ovat mahdollisia vain laajenevat tai supistuvat maailman mallit. Seuraavassa on yhteenveto maailmankaikkeuden malleista. Friedmannin maailmankaikkeuden mallit Malli Tilavuus Tiheys Geometria Kehitys suljettu malli äärellinen ρ > ρ c elliptinen laajeneminen maksimikokoon, supistuminen Einstein-de Sitter ääretön ρ = ρ c euklidinen ikuisesti laajeneva avoin malli ääretön ρ < ρ c hyperbolinen ikuisesti laajeneva Tapaus, jossa mekaaninen kokonaisenergia E = 0, vastaa ikuisesti laajenevaa euklidista Friedmannin mallia eli Einsteinin de Sitterin mallia. Mikäli tiheys on suurempi kuin kriittinen tiheys, ρ > ρc, kappaleen nopeus hidastuu lopulta nollaksi ja se putoaa takaisin ja koko pallo kutistuu kokoon. Kyseessä on Friedmannin äärellinen, suljettu malli. Jos maailmankaikkeuden tiheys on pienempi kuin kriittinen tiheys, ρ < ρc, niin maailmankaikkeus on ikuisesti laajeneva hyperbolinen avaruus. (ks. Tähtitieteen perusteet, 6. painos 2016, s ).
3 Maailmankaikkeuden geometria ja tulevaisuus Maailmankaikkeuden koko ρ < ρ c ρ = ρ c ρ > ρ c Aika Maailmankaikkeuden geometria. Einsteinin yleisen suhteellisuusteorian ( mukaan avaruus on neliulotteinen, jossa on kolme paikkakoordinaattia ja neljäntenä ulottuvuutena on aika: (x, y, z, t). Massa ja energia saa Einsteinin suhteellisuusteorian mukaan avaruuden kaareutumaan ja ajan hidastumaan. Myös suurilla nopeuksilla ajan kulku hidastuu. Maailmankaikkeuden geometria ja tulevaisuus riippuu maailmankaikkeuden keskitiheydestä. Jos maailmankaikkeuden keskitiheys on kriittistä tiheyttä suurempi, avaruus on positiivisesti kaareva. Tällaisen avaruuden kaksiulotteinen vastine on pallopinta, jolloin avaruuden tilavuus on äärellinen. Jos taas maailmankaikkeuden keskimääräinen tiheys on yhtä suuri kuin kriittinen tiheys, avaruus on laakea. Laakeaa avaruutta vastaa kaksiulotteisessa mallissa tasopinta. Avaruus on ääretön. Jos maailmankaikkeuden tiheys on pienempi kuin kriittinen tiheys, avaruus on negatiivisesti kaareva. Kaksiulotteisessa mallissa tätä vastaa satulapinta, jolloin avaruus on ääretön. Kuva. Maailman kaikkeuden geometriset mallit; pallopinta, taso ja satulapinta Tähänastisten havaintojen perusteella maailmankaikkeuden keskimääräinen tiheys on kriittisen tiheyden suuruusluokkaa, joten maailmankaikkeus olisi näin ääretön. Galaksien ja galaksijoukkojen liikkeitä tutkimalla on kuitenkin havaittu, että suuri osa aineesta (25 %) on ns. pimeää ainetta, joka ei lähetä valoa. Näkyvää ainetta on vain noin 5 % ja loput 70 % on ns. pimeää energiaa. Pimeän aineen olemassaolo voidaan havaita ainoastaan sen aiheuttaman gravitaatiovuorovaikutuksen johdosta galaksien liikkeissä. Pimeä energia puolestaan ilmenee tuntemattomana energiana, joka todennäköisesti saa aikaan maailmankaikkeuden kiihtyvän laajenemisen.
4 Maailmankaikkeutta on mallinnettu myös ns. säieteorioilla ( joissa alkeishiukkasia tarkastellaan värähtelevinä säikeinä. Säieteorioissa avaruuden ulottuvuuksia voi olla 9-11 tai jopa enemmän. Toinen maailmankaikkeutta hahmottava teoria on ns. braaniteoria ( Maailmankaikeuden synty (ks. Maailmankaikkeus on nykykäsityksen mukaan syntynyt tyhjästä tai lähes tyhjästä äärettömän tiheästä ja kuumasta tilasta, singulariteetista, kvanttifluktuaationa eli tyhjiöenergiana ( 1,7 miljardia vuotta sitten. Tässä räjähdyksessä syntyi sekä avaruus, materia ja aika sekä jatkuvasti laajeneva maailmankaikkeus. Maailmankaikkeuden tulevaisuus Maailmankaikkeuden oma gravitaatiovoima pyrkii hidastamaan avaruuden laajenemista. Maailmankaikkeuden kriittisestä tiheydestä riippuu universumin tuleva kohtalo. Jos maailmankaikkeuden keskimääräinen tiheys on suurempi kuin kriittinen tiheys (ρ > ρc), maailmankaikkeuden gravitaatiovoima riittää pysäyttämään laajenemisen ja lopulta kääntämään sen supistumiseksi. Onko avaruudessa tarpeeksi massaa, jotta gravitaatiovuorovaikutus voisi pysäyttää laajenemisen? Miljardien ja taas miljardien vuosien kuluttua maailmankaikkeuden laajeneminen voisi viimein pysähtyä ja alkaisi avaruuden kutistuminen, joka johtaisi suureen loppurysäykseen. Kaikki avaruuden aine päätyisi lopulta tiheään alkutilaansa, singulariteettiin. Mitä sitten tämän jälkeen tapahtuisi? Tapahtuisiko kenties uusi alkuräjähdys, laajeneminen ja jälleen supistuminen ( sykkivä universumi )? Onko maailmankaikkeuttamme kenties edeltänyt toinen maailmankaikkeus, joka olisi romahtanut kasaan? Supistuuko ja laajeneeko maailmankaikkeus vuorotellen? Tämä käsitys ei nykykosmologiassa saa juurikaan kannatusta, koska kokeelliset tosiasiat eivät tue tätä mallia. Jos maailmankaikkeuden keskimääräinen tiheys on pienempi tai yhtä suuri kuin kriittinen tiheys (ρ ρc), laajeneminen ikuisesti. Lopulta tähdet käyttävät kaikki ydinpolttoaineensa loppuun, sammuvat ja hiipuvat valkoisiksi ja viimein mustiksi kääpiöiksi. Jäljellä on vain kuolleita tähtiä, neutronitähtiä ja mustia aukkoja. Lopulta suunnattomien ajanjaksojen kuluttua kuolleet tähdetkin muuttuvat säteilyksi. Galaksien keskustoihin syntyy kasvavia mustia aukkoja, jotka yhdistyvät. Näin kaikki materia päätyy mustiin aukkoihin. Mustat aukotkaan eivät ole ikuisia. Ne höyrystyvät säteilyksi ns. Hawkingin prosessilla suunnattomien ajanjaksojen kuluessa. Jäljelle jää vain säteilyä, jonka lämpötila laskee lähelle absoluuttista nollapistettä (0 K = -27 o C). Maailmankaikkeus on viimein äärettömän laaja, pimeä, kylmä ja eloton universumi. Ajankäsite menettää merkityksensä. Viimeisimmät havainnot ja teoreettiset laskelmat tukevat maailmankaikkeuden jatkuvan laajenemisen mallia. Vuonna 200 pystyttiin Wmap-satelliitin taustasäteilymittausten perusteella varsin tarkasti määrittämään aineen keskitiheys universumissa. Vuonna 2009 laukaistu Plancksatelliitti mittaa taustasäteilyn vaihteluita entistä tarkemmin. Wmapin taustasäteilykartoista nähdään, että maailmankaikkeuden tiheys on täsmälleen ns. kriittinen tiheys. Tämä vastaa euklidista, laakeaa avaruutta. Elämme siis (kaksiulotteisen mallin mukaan) tasomaisessa maailmassa, jonka laajeneminen jatkuu ikuisesti. Avaruus ei kuitenkaan ole Friedmannin laakean mallin mukainen, koska Friedmannin malleissa kosmologinen vakio oletettiin mollaksi. Viimeaikaiset havainnot osoittavat, että kosmologinen vakio Λ on nollasta poikkeava. Kosmologinen vakio toimii vastakkaiseen suuntaan kuin gravitaation vetovoima. Einstein otti kosmologisen vakion käyttöön siksi, että muuten hänen kenttäyhtälöistänsä olisi seurannut vain supistuvia tai alati laajenevia maailmankaikkeuden malleja, joita hän piti mahdottomina.
5 Siksi Einstein lisäsi kenttäyhtälöihinsä kosmologisen vakion, joka kumosi gravitaation aiheuttaman vetovoiman vaikutuksen, niin että avaruus ei laajentunut, vaan oli vakaa (staattinen). Myöhemmin Einstein piti tätä vakion lisäystä harmillisena virheenä. Nykyään tiedetään, että avaruus laajenee ja laajeneminen tapahtuu vieläpä kiihtyvällä nopeudella. Kosmologinen vakio Λ on tehnyt paluun suhteellisuusteorian kenttäyhtälöihin. Sillä selitetään nykyään maailmankaikkeuden kiihtyvä laajeneminen. Nyt nollasta poikkeava kosmologinen vakio edustaa poistovoimaa, joka gravitaation aiheuttamasta vetovoimasta huolimatta työntää galakseja kauemmaksi. Kosmologinen vakio on varsin pieni, joten maailmankaikkeuden kiihtyvä laajeneminen tulee esiin vasta suurilla etäisyyksillä. Kosmologinen vakio selittää suuren osan myös ns. pimeän aineen ja energian ongelmasta. Wmap-satelliitin tuloksista (2006) havaitaan, että maailmankaikkeuden kokonaisenergiasta noin 70 % ilmenee kosmologisen vakion poistovoimana ja vain noin 0 % aineena. Aineesta noin 5 % on tavanomaista tähtiainetta, kaasua ja pölyä. Tuntematonta, pimeää ainetta on noin 25 %, jonka olomuotoa ei edelleenkään tiedetä. Joitakin arveluja pimeän aineen olomuodosta on tehty. (ks. (Maailmankaikkeuden synty, kehitys ja tulevaisuus; ks. Tieteen menetelmä on objektiivinen, julkinen ja itseään korjaava. Uudet havainnot ja teoreettiset tulokset tuovat jatkuvasti lisätietoa maailmankaikkeuden rakenteeseen, syntyyn ja kehitykseen. Kosmologia on jatkuvasti kehittyvä tieteen ala, jonka uusia tuloksia jäämme mielenkiinnolla Kirjallisuutta: - Asko Palviainen Heikki Oja: Maailmankaikkeus, Tähtitieteen vuosikirja , Otava Heikki Oja: Polaris, Koulun tähtitieto, Otava Karttunen-Donner-Kröger-Oja-Poutanen: Tähtitieteen perusteet, 6. laitos, 2016 Tähtitieteellinen yhdistys Ursa ry, Gummerus Hannu Karttunen: Tähdet ja maailmankaikkeus, Otava Heikki Lehto Markus Hotakainen Henrik Kahanpää: Tähtitiede, Kiehtova avaruus, Kirjayhtymä, 1. painos Jukka Maalampi - Tapani Perko: Lyhyt modernin fysiikan johdatus, Limes ry, Helsinki, 4. korjattu painos
Aine ja maailmankaikkeus. Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos
 Aine ja maailmankaikkeus Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos Lahden yliopistokeskus 29.9.2011 1900-luku tiedon uskomaton vuosisata -mikä on aineen olemus -miksi on erilaisia aineita
Aine ja maailmankaikkeus Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos Lahden yliopistokeskus 29.9.2011 1900-luku tiedon uskomaton vuosisata -mikä on aineen olemus -miksi on erilaisia aineita
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos
 PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos 1917: Einstein sovelsi yleistä suhteellisuusteoriaa koko maailmankaikkeuteen Linnunradan eli maailmankaikkeuden
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos 1917: Einstein sovelsi yleistä suhteellisuusteoriaa koko maailmankaikkeuteen Linnunradan eli maailmankaikkeuden
Pimeän energian metsästys satelliittihavainnoin
 Pimeän energian metsästys satelliittihavainnoin Avaruusrekka, Kumpulan pysäkki 04.10.2012 Peter Johansson Matemaattis-luonnontieteellinen tiedekunta / Peter Johansson/ Avaruusrekka 04.10.2012 13/08/14
Pimeän energian metsästys satelliittihavainnoin Avaruusrekka, Kumpulan pysäkki 04.10.2012 Peter Johansson Matemaattis-luonnontieteellinen tiedekunta / Peter Johansson/ Avaruusrekka 04.10.2012 13/08/14
Kosmologia: Miten maailmankaikkeudesta tuli tällainen? Tapio Hansson
 Kosmologia: Miten maailmankaikkeudesta tuli tällainen? Tapio Hansson Kosmologia Kosmologiaa tutkii maailmankaikkeuden rakennetta ja historiaa Yhdistää havaitsevaa tähtitiedettä ja fysiikkaa Tämän hetken
Kosmologia: Miten maailmankaikkeudesta tuli tällainen? Tapio Hansson Kosmologia Kosmologiaa tutkii maailmankaikkeuden rakennetta ja historiaa Yhdistää havaitsevaa tähtitiedettä ja fysiikkaa Tämän hetken
MAAILMANKAIKKEUDEN SYNTY
 MAAILMANKAIKKEUDEN SYNTY Maailmankaikkeuden synty selitetään nykyään ns. alkuräjähdysteorian ( Big Bang ) avulla. Alkuräjähdysteorian mukaan maailmankaikkeus syntyi tyhjästä tai lähes tyhjästä äärettömän
MAAILMANKAIKKEUDEN SYNTY Maailmankaikkeuden synty selitetään nykyään ns. alkuräjähdysteorian ( Big Bang ) avulla. Alkuräjähdysteorian mukaan maailmankaikkeus syntyi tyhjästä tai lähes tyhjästä äärettömän
Friedmannin yhtälöt. Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G 3. yleisin mahdollinen metriikka. Friedmannin yhtälö
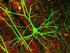 Friedmannin yhtälöt Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G G [ R( t)] T [ aine, energia, R( t)] 3 yleisin mahdollinen metriikka d sin d dr ds c dt R( t) ( r d ) 1 kr Friedmannin
Friedmannin yhtälöt Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G G [ R( t)] T [ aine, energia, R( t)] 3 yleisin mahdollinen metriikka d sin d dr ds c dt R( t) ( r d ) 1 kr Friedmannin
Kosmologian yleiskatsaus. Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos
 Kosmologian yleiskatsaus Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Päämääriä Kosmologia tutkii maailmankaikkeutta kokonaisuutena. Kehitys,
Kosmologian yleiskatsaus Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Päämääriä Kosmologia tutkii maailmankaikkeutta kokonaisuutena. Kehitys,
Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä.
 Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
Lataa Maailmanviiva - Jukka Maalampi. Lataa
 Lataa Maailmanviiva - Jukka Maalampi Lataa Kirjailija: Jukka Maalampi ISBN: 9789525329513 Sivumäärä: 221 Formaatti: PDF Tiedoston koko: 28.94 Mb Sata vuotta sitten Albert Einstein ilmestyi kuin tyhjästä
Lataa Maailmanviiva - Jukka Maalampi Lataa Kirjailija: Jukka Maalampi ISBN: 9789525329513 Sivumäärä: 221 Formaatti: PDF Tiedoston koko: 28.94 Mb Sata vuotta sitten Albert Einstein ilmestyi kuin tyhjästä
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
KOSMOLOGISIA HAVAINTOJA
 KOSMOLOGISIA HAVAINTOJA 1) Olbersin paradksi Miksi taivas n öisin musta? Js tähdet lisivat jakautuneet keskimäärin tasaisesti äärettömään ja muuttumattmaan avaruuteen, tulisi taivaan listaa yhtä kirkkaana
KOSMOLOGISIA HAVAINTOJA 1) Olbersin paradksi Miksi taivas n öisin musta? Js tähdet lisivat jakautuneet keskimäärin tasaisesti äärettömään ja muuttumattmaan avaruuteen, tulisi taivaan listaa yhtä kirkkaana
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä
 S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä (ks. esim. http://www.kotiposti.net/ajnieminen/sutek.pdf). 1. a) Suppeamman suhteellisuusteorian perusolettamukset (Einsteinin suppeampi suhteellisuusteoria
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä (ks. esim. http://www.kotiposti.net/ajnieminen/sutek.pdf). 1. a) Suppeamman suhteellisuusteorian perusolettamukset (Einsteinin suppeampi suhteellisuusteoria
Maailmankaikkeuden syntynäkemys (nykykäsitys 2016)
 Maailmankaikkeuden syntynäkemys (nykykäsitys 2016) Kvanttimeri - Kvanttimaailma väreilee (= kvanttifluktuaatiot eli kvanttiheilahtelut) sattumalta suuri energia (tyhjiöenergia)
Maailmankaikkeuden syntynäkemys (nykykäsitys 2016) Kvanttimeri - Kvanttimaailma väreilee (= kvanttifluktuaatiot eli kvanttiheilahtelut) sattumalta suuri energia (tyhjiöenergia)
Kosmologia ja alkuaineiden synty. Tapio Hansson
 Kosmologia ja alkuaineiden synty Tapio Hansson Alkuräjähdys n. 13,7 mrd vuotta sitten Alussa maailma oli pistemäinen Räjähdyksen omainen laajeneminen Alkuolosuhteet ovat hankalia selittää Inflaatioteorian
Kosmologia ja alkuaineiden synty Tapio Hansson Alkuräjähdys n. 13,7 mrd vuotta sitten Alussa maailma oli pistemäinen Räjähdyksen omainen laajeneminen Alkuolosuhteet ovat hankalia selittää Inflaatioteorian
Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN
 Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN Oppilaiden ennakkokäsityksiä avaruuteen liittyen Aurinko kiertää Maata Vuodenaikojen vaihtelu johtuu siitä,
Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN Oppilaiden ennakkokäsityksiä avaruuteen liittyen Aurinko kiertää Maata Vuodenaikojen vaihtelu johtuu siitä,
FYSA220/K2 (FYS222/K2) Vaimeneva värähtely
 FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
Pimeä energia. Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla
 Pimeä energia Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla 27.5.2015 Friedmann- Robertson- Walker - malli homogeeninen ja isotrooppinen approksimaa>o maailmankaikkeudelle Havaintoihin sopii
Pimeä energia Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla 27.5.2015 Friedmann- Robertson- Walker - malli homogeeninen ja isotrooppinen approksimaa>o maailmankaikkeudelle Havaintoihin sopii
http://www.space.com/23595-ancient-mars-oceans-nasa-video.html
 http://www.space.com/23595-ancient-mars-oceans-nasa-video.html Mars-planeetan olosuhteiden kehitys Heikki Sipilä 17.02.2015 /LFS Mitä mallit kertovat asiasta Mitä voimme päätellä havainnoista Mikä mahtaa
http://www.space.com/23595-ancient-mars-oceans-nasa-video.html Mars-planeetan olosuhteiden kehitys Heikki Sipilä 17.02.2015 /LFS Mitä mallit kertovat asiasta Mitä voimme päätellä havainnoista Mikä mahtaa
Kosmologia. Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä.
 Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
PARADIGMOJEN VERTAILUPERUSTEET. Avril Styrman Luonnonfilosofian seura
 PARADIGMOJEN VERTAILUPERUSTEET Avril Styrman Luonnonfilosofian seura 17.2.2015 KokonaisHede Koostuu paradigmoista Tieteen edistystä voidaan siten tarkastella prosessina missä paradigmat kehinyvät ja vaihtuvat
PARADIGMOJEN VERTAILUPERUSTEET Avril Styrman Luonnonfilosofian seura 17.2.2015 KokonaisHede Koostuu paradigmoista Tieteen edistystä voidaan siten tarkastella prosessina missä paradigmat kehinyvät ja vaihtuvat
perushiukkasista Perushiukkasia ovat nykykäsityksen mukaan kvarkit ja leptonit alkeishiukkasiksi
 8. Hiukkasfysiikka Hiukkasfysiikka kuvaa luonnon toimintaa sen perimmäisellä tasolla. Hiukkasfysiikan avulla selvitetään maailmankaikkeuden syntyä ja kehitystä. Tutkimuskohteena ovat atomin ydintä pienemmät
8. Hiukkasfysiikka Hiukkasfysiikka kuvaa luonnon toimintaa sen perimmäisellä tasolla. Hiukkasfysiikan avulla selvitetään maailmankaikkeuden syntyä ja kehitystä. Tutkimuskohteena ovat atomin ydintä pienemmät
MAAILMANKAIKKEUDEN SYNTY
 MAAILMANKAIKKEUDEN SYNTY Maailmankaikkeuden synty selitetään nykyään kosmisen inflaation ja alkuräjähdysteorian ( Big Bang ) avulla. Maailmankaikkeus syntyi nykytietämyksen mukaan (2016) tyhjiöenergiasta
MAAILMANKAIKKEUDEN SYNTY Maailmankaikkeuden synty selitetään nykyään kosmisen inflaation ja alkuräjähdysteorian ( Big Bang ) avulla. Maailmankaikkeus syntyi nykytietämyksen mukaan (2016) tyhjiöenergiasta
Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9
 : Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9 Horisonttiongelma Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Valtteri Lindholm
: Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9 Horisonttiongelma Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Valtteri Lindholm
Erityinen suhteellisuusteoria (Harris luku 2)
 Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Lataa Maailmankaikkeus pähkinänkuoressa - Stephen Hawking. Lataa
 Lataa Maailmankaikkeus pähkinänkuoressa - Stephen Hawking Lataa Kirjailija: Stephen Hawking ISBN: 9789510284001 Sivumäärä: 215 Formaatti: PDF Tiedoston koko: 16.67 Mb Stephen Hawkingin menestysteos Ajan
Lataa Maailmankaikkeus pähkinänkuoressa - Stephen Hawking Lataa Kirjailija: Stephen Hawking ISBN: 9789510284001 Sivumäärä: 215 Formaatti: PDF Tiedoston koko: 16.67 Mb Stephen Hawkingin menestysteos Ajan
Teoreetikon kuva. maailmankaikkeudesta
 Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Suhteellisuusteorian perusteet, harjoitus 6
 Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
Fysiikkaa runoilijoille Osa 6: kosmologia
 Fysiikkaa runoilijoille Osa 6: kosmologia Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Kaikkeuden tutkimista Kosmologia tutkii maailmankaikkeutta
Fysiikkaa runoilijoille Osa 6: kosmologia Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Kaikkeuden tutkimista Kosmologia tutkii maailmankaikkeutta
Kosmos = maailmankaikkeus
 Kosmos = maailmankaikkeus Synty: Big Bang, alkuräjähdys 13 820 000 000 v sitten Koostumus: - Pimeä energia 3/4 - Pimeä aine ¼ - Näkyvä aine 1/20: - vetyä ¾, heliumia ¼, pari prosenttia muita alkuaineita
Kosmos = maailmankaikkeus Synty: Big Bang, alkuräjähdys 13 820 000 000 v sitten Koostumus: - Pimeä energia 3/4 - Pimeä aine ¼ - Näkyvä aine 1/20: - vetyä ¾, heliumia ¼, pari prosenttia muita alkuaineita
Perusvuorovaikutukset. Tapio Hansson
 Perusvuorovaikutukset Tapio Hansson Perusvuorovaikutukset Vuorovaikutukset on perinteisesti jaettu neljään: Gravitaatio Sähkömagneettinen vuorovaikutus Heikko vuorovaikutus Vahva vuorovaikutus Sähköheikkoteoria
Perusvuorovaikutukset Tapio Hansson Perusvuorovaikutukset Vuorovaikutukset on perinteisesti jaettu neljään: Gravitaatio Sähkömagneettinen vuorovaikutus Heikko vuorovaikutus Vahva vuorovaikutus Sähköheikkoteoria
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Aineen olemuksesta. Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto
 Aineen olemuksesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Miten käsitys aineen perimmäisestä rakenteesta on kehittynyt aikojen kuluessa? Mitä ajattelemme siitä nyt? Atomistit Loogisen päättelyn
Aineen olemuksesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Miten käsitys aineen perimmäisestä rakenteesta on kehittynyt aikojen kuluessa? Mitä ajattelemme siitä nyt? Atomistit Loogisen päättelyn
Crafoord palkinto 1991. nopeus-etäisyys etäisyys
 Allan Sandage ja maailmankaikkeuden laajeneminen P. Teerikorpi Tuorlanobservatorio Turunyliopisto Allan Sandage (1924 2010) Mt. Palomar Observatory Crafoord palkinto 1991 hyvin tärkeistä tutkimuksista,
Allan Sandage ja maailmankaikkeuden laajeneminen P. Teerikorpi Tuorlanobservatorio Turunyliopisto Allan Sandage (1924 2010) Mt. Palomar Observatory Crafoord palkinto 1991 hyvin tärkeistä tutkimuksista,
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
Vuorovaikutuksien mittamallit
 Vuorovaikutuksien mittamallit Hiukkasten vuorovaikutuksien teoreettinen mallintaminen perustuu ns. mittakenttäteorioihin. Kenttä viittaa siihen, että hiukkanen kuvataan paikasta ja ajasta riippuvalla funktiolla
Vuorovaikutuksien mittamallit Hiukkasten vuorovaikutuksien teoreettinen mallintaminen perustuu ns. mittakenttäteorioihin. Kenttä viittaa siihen, että hiukkanen kuvataan paikasta ja ajasta riippuvalla funktiolla
Euclid. Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla
 Euclid Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla 27.5.2015 Mikä aiheu.aa kiihtyvän laajenemisen Kaksi vaihtoehtoa Pimeä energia (dark energy) Painovoima käyaäytyy eri lailla hyvin suurilla
Euclid Hannu Kurki- Suonio Kosmologian kesäkoulu 2015 Solvalla 27.5.2015 Mikä aiheu.aa kiihtyvän laajenemisen Kaksi vaihtoehtoa Pimeä energia (dark energy) Painovoima käyaäytyy eri lailla hyvin suurilla
LHC -riskianalyysi. Emmi Ruokokoski
 LHC -riskianalyysi Emmi Ruokokoski 30.3.2009 Johdanto Mikä LHC on? Perustietoa ja taustaa Mahdolliset riskit: mikroskooppiset mustat aukot outokaiset magneettiset monopolit tyhjiökuplat Emmi Ruokokoski
LHC -riskianalyysi Emmi Ruokokoski 30.3.2009 Johdanto Mikä LHC on? Perustietoa ja taustaa Mahdolliset riskit: mikroskooppiset mustat aukot outokaiset magneettiset monopolit tyhjiökuplat Emmi Ruokokoski
Teoreettinen hiukkasfysiikka ja kosmologia Oulun yliopistossa. Kari Rummukainen
 Teoreettinen hiukkasfysiikka ja kosmologia Oulun yliopistossa Kari Rummukainen Mitä hiukkasfysiikka tutkii? Mitä Oulussa tutkitaan? Opiskelu ja sijoittuminen työelämässä Teoreettinen fysiikka: työkaluja
Teoreettinen hiukkasfysiikka ja kosmologia Oulun yliopistossa Kari Rummukainen Mitä hiukkasfysiikka tutkii? Mitä Oulussa tutkitaan? Opiskelu ja sijoittuminen työelämässä Teoreettinen fysiikka: työkaluja
Muunnokset ja mittayksiköt
 Muunnokset ja mittayksiköt 1 a Mitä kymmenen potenssia tarkoittavat etuliitteet m, G ja n? b Mikä on massan (mass) mittayksikkö SI-järjestelmässäa? c Mikä on painon (weight) mittayksikkö SI-järjestelmässä?
Muunnokset ja mittayksiköt 1 a Mitä kymmenen potenssia tarkoittavat etuliitteet m, G ja n? b Mikä on massan (mass) mittayksikkö SI-järjestelmässäa? c Mikä on painon (weight) mittayksikkö SI-järjestelmässä?
UrSalo. Laajaa paikallista yhteistyötä
 UrSalo Laajaa paikallista yhteistyötä Ursalon ja Turun Ursan yhteistyö Tähtipäivät 2011 ja Cygnus 2012 Kevolan observatorio Tähtitieteen kurssit Yhteistyössä Salon kansalaisopiston ja Tuorlan tutkijoiden
UrSalo Laajaa paikallista yhteistyötä Ursalon ja Turun Ursan yhteistyö Tähtipäivät 2011 ja Cygnus 2012 Kevolan observatorio Tähtitieteen kurssit Yhteistyössä Salon kansalaisopiston ja Tuorlan tutkijoiden
Kosmologia. Kosmologia tutkii maailmankaikkeutta kokonaisuutena:
 Kosmologia Kosmologia tutkii maailmankaikkeutta kokonaisuutena: -laajeneminen -ainesisältö -alkuhetket -kohtalo Kosmologia käsittelee avaruuden aikakehitystä: yleisen suhteellisuusteorian sovellus suurimpaan
Kosmologia Kosmologia tutkii maailmankaikkeutta kokonaisuutena: -laajeneminen -ainesisältö -alkuhetket -kohtalo Kosmologia käsittelee avaruuden aikakehitystä: yleisen suhteellisuusteorian sovellus suurimpaan
Tähtitiede Tutkimusta maailmankaikkeuden laidoilta Aurinkokuntaan
 Tähtitiede Tutkimusta maailmankaikkeuden laidoilta Aurinkokuntaan Jyri Näränen Paikkatietokeskus, MML jyri.naranen@nls.fi http://personal.inet.fi/tiede/naranen/ Oheislukemista Palviainen, Asko ja Oja,
Tähtitiede Tutkimusta maailmankaikkeuden laidoilta Aurinkokuntaan Jyri Näränen Paikkatietokeskus, MML jyri.naranen@nls.fi http://personal.inet.fi/tiede/naranen/ Oheislukemista Palviainen, Asko ja Oja,
SUHTEELLISUUSTEORIAN TEOREETTISIA KUMMAJAISIA
 MUSTAT AUKOT FAQ Kuinka gravitaatio pääsee ulos tapahtumahorisontista? Schwarzschildin ratkaisu on staattinen. Tähti on kaareuttanut avaruuden jo ennen romahtamistaan mustaksi aukoksi. Ulkopuolinen havaitsija
MUSTAT AUKOT FAQ Kuinka gravitaatio pääsee ulos tapahtumahorisontista? Schwarzschildin ratkaisu on staattinen. Tähti on kaareuttanut avaruuden jo ennen romahtamistaan mustaksi aukoksi. Ulkopuolinen havaitsija
Luonnonfilosofian seura. Mitä havainnot ja mallit viestittävät todellisuudesta?
 Mitä havainnot ja mallit viestittävät todellisuudesta? Ari Lehto, Heikki Sipilä ja Tuomo Suntola 1 PhysicsWeb Summaries 20.7.2007: Pimeän energian tutkimusryhmät voittivat kosmologiapalkinnon (July 17,
Mitä havainnot ja mallit viestittävät todellisuudesta? Ari Lehto, Heikki Sipilä ja Tuomo Suntola 1 PhysicsWeb Summaries 20.7.2007: Pimeän energian tutkimusryhmät voittivat kosmologiapalkinnon (July 17,
Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen
 Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen Helsingin Yliopisto 14.9.2015 kello 12:50:45 Suomen aikaa: pulssi gravitaatioaaltoja läpäisi maan. LIGO: Ensimmäinen havainto gravitaatioaalloista. Syntyi
Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen Helsingin Yliopisto 14.9.2015 kello 12:50:45 Suomen aikaa: pulssi gravitaatioaaltoja läpäisi maan. LIGO: Ensimmäinen havainto gravitaatioaalloista. Syntyi
Mustien aukkojen astrofysiikka
 Mustien aukkojen astrofysiikka Peter Johansson Fysiikan laitos, Helsingin yliopisto Kumpula nyt Helsinki 19.2.2016 1. Tähtienmassaiset mustat aukot: Kuinka isoja?: noin 3-100 kertaa Auringon massa, tapahtumahorisontin
Mustien aukkojen astrofysiikka Peter Johansson Fysiikan laitos, Helsingin yliopisto Kumpula nyt Helsinki 19.2.2016 1. Tähtienmassaiset mustat aukot: Kuinka isoja?: noin 3-100 kertaa Auringon massa, tapahtumahorisontin
Sisällysluettelo. Alkusanat 11. A lbert E insteinin kirjoituksia
 Sisällysluettelo Alkusanat 11 A lbert E insteinin kirjoituksia Erityisestä ja yleisestä su hteellisuusteoriasta Alkusanat 21 I Erityisestä suhteellisuusteoriasta 23 1 Geometristen lauseiden fysikaalinen
Sisällysluettelo Alkusanat 11 A lbert E insteinin kirjoituksia Erityisestä ja yleisestä su hteellisuusteoriasta Alkusanat 21 I Erityisestä suhteellisuusteoriasta 23 1 Geometristen lauseiden fysikaalinen
Lataa Galaksit - Heikki Oja. Lataa
 Lataa Galaksit - Heikki Oja Lataa Kirjailija: Heikki Oja ISBN: 9789525985450 Sivumäärä: 239 Formaatti: PDF Tiedoston koko: 17.95 Mb Galaksit eivät ole itsenäisiä avaruuden saaria, kuten aiemmin ajateltiin,
Lataa Galaksit - Heikki Oja Lataa Kirjailija: Heikki Oja ISBN: 9789525985450 Sivumäärä: 239 Formaatti: PDF Tiedoston koko: 17.95 Mb Galaksit eivät ole itsenäisiä avaruuden saaria, kuten aiemmin ajateltiin,
Fysiikan kurssit. MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka
 Fysiikan kurssit MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka Valtakunnalliset kurssit 1. Fysiikka luonnontieteenä 2. Lämpö 3. Sähkö 4. Voima ja liike 5. Jaksollinen liike ja aallot 6. Sähkömagnetismi
Fysiikan kurssit MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka Valtakunnalliset kurssit 1. Fysiikka luonnontieteenä 2. Lämpö 3. Sähkö 4. Voima ja liike 5. Jaksollinen liike ja aallot 6. Sähkömagnetismi
yyyyyyyyyyyyyyyyy Tehtävä 1. PAINOSI AVARUUDESSA Testaa, paljonko painat eri taivaankappaleilla! Kuu kg Maa kg Planeetta yyy yyyyyyy yyyyyy kg Tiesitk
 I LUOKKAHUONEESSA ENNEN TIETOMAA- VIERAILUA POHDITTAVIA TEHTÄVIÄ Nimi Luokka Koulu yyyyyyyyyy Tehtävä 1. ETSI TIETOA PAINOVOIMASTA JA TÄYDENNÄ. TIETOA LÖYDÄT MM. PAINOVOIMA- NÄYTTELYN VERKKOSIVUILTA. Painovoima
I LUOKKAHUONEESSA ENNEN TIETOMAA- VIERAILUA POHDITTAVIA TEHTÄVIÄ Nimi Luokka Koulu yyyyyyyyyy Tehtävä 1. ETSI TIETOA PAINOVOIMASTA JA TÄYDENNÄ. TIETOA LÖYDÄT MM. PAINOVOIMA- NÄYTTELYN VERKKOSIVUILTA. Painovoima
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
L a = L l. rv a = Rv l v l = r R v a = v a 1, 5
 Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Fysiikan Nobel 2008: Uusia tosiasioita aineen perimmäisistä rakenneosasista
 Fysiikan Nobel 2008: Uusia tosiasioita aineen perimmäisistä rakenneosasista K. Kajantie keijo.kajantie@helsinki.fi Tampere, 14.12.2008 Fysiikan (teoreettisen) professori, Helsingin yliopisto, 1970-2008
Fysiikan Nobel 2008: Uusia tosiasioita aineen perimmäisistä rakenneosasista K. Kajantie keijo.kajantie@helsinki.fi Tampere, 14.12.2008 Fysiikan (teoreettisen) professori, Helsingin yliopisto, 1970-2008
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
3.4 Liike-energiasta ja potentiaalienergiasta
 Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Mitä energia on? Risto Orava Helsingin yliopisto Fysiikan tutkimuslaitos CERN
 Mitä energia on? Risto Orava Helsingin yliopisto Fysiikan tutkimuslaitos CERN 17. helmikuuta 2011 ENERGIA JA HYVINVOINTI TANNER-LUENTO 2011 1 Mistä energiaa saadaan? Perusenergia sähkö heikko paino vahva
Mitä energia on? Risto Orava Helsingin yliopisto Fysiikan tutkimuslaitos CERN 17. helmikuuta 2011 ENERGIA JA HYVINVOINTI TANNER-LUENTO 2011 1 Mistä energiaa saadaan? Perusenergia sähkö heikko paino vahva
on radan suuntaiseen komponentti eli tangenttikomponentti ja on radan kaarevuuskeskipisteeseen osoittavaan komponentti. (ks. kuva 1).
 H E I L U R I T 1) Matemaattinen heiluri = painottoman langan päässä heilahteleva massapiste (ks. kuva1) kuva 1. - heilurin pituus l - tasapainoasema O - ääriasemat A ja B - heilahduskulma - heilahdusaika
H E I L U R I T 1) Matemaattinen heiluri = painottoman langan päässä heilahteleva massapiste (ks. kuva1) kuva 1. - heilurin pituus l - tasapainoasema O - ääriasemat A ja B - heilahduskulma - heilahdusaika
Planck-satelliitti ja kaiken alku
 Planck-satelliitti ja kaiken alku Hannu Kurki-Suonio i Helsingin yliopiston fysiikan laitos 13.10.2009 Hubble Ultra Deep Field (NASA, ESA, S. Beckwith (StScI) and the HUDF Team) Aine on kerääntynyt galakseiksi
Planck-satelliitti ja kaiken alku Hannu Kurki-Suonio i Helsingin yliopiston fysiikan laitos 13.10.2009 Hubble Ultra Deep Field (NASA, ESA, S. Beckwith (StScI) and the HUDF Team) Aine on kerääntynyt galakseiksi
Leptonit. - elektroni - myoni - tauhiukkanen - kolme erilaista neutriinoa. - neutriinojen varaus on 0 ja muiden leptonien varaus on -1
 Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
2r s b VALON TAIPUMINEN. 1 r. osittaisdifferentiaaliyhtälö. = 2 suppea suht.teoria. valo putoaa tähteen + avaruus kaareutunut.
 MUSTAT AUKOT FAQ Miten gravitaatio pääsee ulos tapahtumahorisontista? massa ei sylje gravitaatiota kuin tennispalloja. Tähti on käyristänyt avaruuden jo ennen romahtamistaan mustaksi aukoksi, eikä tätä
MUSTAT AUKOT FAQ Miten gravitaatio pääsee ulos tapahtumahorisontista? massa ei sylje gravitaatiota kuin tennispalloja. Tähti on käyristänyt avaruuden jo ennen romahtamistaan mustaksi aukoksi, eikä tätä
Suhteellisuusteorian vajavuudesta
 Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
5 Kentät ja energia (fields and energy)
 5 Kentät ja energia (fields and energy) Mansfield and O Sullivan: Understanding Physics, kappaleen 5 alkuosa 5.1 Newtonin gravitaatiolaki Newton: vetovoima kahden kappaleen välillä on tai tarkemmin F m
5 Kentät ja energia (fields and energy) Mansfield and O Sullivan: Understanding Physics, kappaleen 5 alkuosa 5.1 Newtonin gravitaatiolaki Newton: vetovoima kahden kappaleen välillä on tai tarkemmin F m
CERN-matka
 CERN-matka 2016-2017 UUTTA FYSIIKKAA Janne Tapiovaara Rauman Lyseon lukio http://imglulz.com/wp-content/uploads/2015/02/keep-calm-and-let-it-go.jpg FYSIIKKA ON KOKEELLINEN LUONNONTIEDE, JOKA PYRKII SELITTÄMÄÄN
CERN-matka 2016-2017 UUTTA FYSIIKKAA Janne Tapiovaara Rauman Lyseon lukio http://imglulz.com/wp-content/uploads/2015/02/keep-calm-and-let-it-go.jpg FYSIIKKA ON KOKEELLINEN LUONNONTIEDE, JOKA PYRKII SELITTÄMÄÄN
Lataa Mustat aukot - BBC:n Reith-luennot - Stephen Hawking. Lataa
 Lataa Mustat aukot - BBC:n Reith-luennot - Stephen Hawking Lataa Kirjailija: Stephen Hawking ISBN: 9789510424148 Sivumäärä: 100 sivua Formaatti: PDF Tiedoston koko: 35.10 Mb Mustat aukot ovat avain maailmankaikkeuden
Lataa Mustat aukot - BBC:n Reith-luennot - Stephen Hawking Lataa Kirjailija: Stephen Hawking ISBN: 9789510424148 Sivumäärä: 100 sivua Formaatti: PDF Tiedoston koko: 35.10 Mb Mustat aukot ovat avain maailmankaikkeuden
Lyhyt katsaus gravitaatioaaltoihin
 : Lyhyt katsaus gravitaatioaaltoihin Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Sisältö Suppea ja yleinen suhteellisuusteoria Häiriöteoria Aaltoratkaisut
: Lyhyt katsaus gravitaatioaaltoihin Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Sisältö Suppea ja yleinen suhteellisuusteoria Häiriöteoria Aaltoratkaisut
INSINÖÖRIN NÄKÖKULMA FYSIIKAN TEHTÄVÄÄN. Heikki Sipilä LF-Seura
 INSINÖÖRIN NÄKÖKULMA FYSIIKAN TEHTÄVÄÄN Heikki Sipilä LF-Seura 18.9.2018 Sisältö Henkilökohtaista taustaa Insinööri ja fysiikka Dimensioanalyysi insinöörin menetelmänä Esimerkki havainnon ja teorian yhdistämisestä
INSINÖÖRIN NÄKÖKULMA FYSIIKAN TEHTÄVÄÄN Heikki Sipilä LF-Seura 18.9.2018 Sisältö Henkilökohtaista taustaa Insinööri ja fysiikka Dimensioanalyysi insinöörin menetelmänä Esimerkki havainnon ja teorian yhdistämisestä
Aikamatkustus. Emma Beckingham ja Enni Pakarinen
 Aikamatkustus Emma Beckingham ja Enni Pakarinen Aikamatkustuksen teoria Aikamatkustus on useita vuosisatoja kiinnostanut ihmiskuntaa. Nykyihminen useimmiten pitää aikamatkustusta vain kuvitteellisena konseptina,
Aikamatkustus Emma Beckingham ja Enni Pakarinen Aikamatkustuksen teoria Aikamatkustus on useita vuosisatoja kiinnostanut ihmiskuntaa. Nykyihminen useimmiten pitää aikamatkustusta vain kuvitteellisena konseptina,
LUENTO Kyösti Ryynänen
 LUENTO 13.12.2016 Kyösti Ryynänen ELÄMÄÄ MIKROKOSMOKSEN JA MAKROKOSMOKSEN VÄLISSÄ 1 ELÄMÄN PERUSTA ALKEISHIUKKASET PERUSVOIMAT ITSEORGANISOITUMINEN NYT HAVAITTAVISSA OLEVA UNIVERSUMI HAVAINTOJEN JA TEORIOIDEN
LUENTO 13.12.2016 Kyösti Ryynänen ELÄMÄÄ MIKROKOSMOKSEN JA MAKROKOSMOKSEN VÄLISSÄ 1 ELÄMÄN PERUSTA ALKEISHIUKKASET PERUSVOIMAT ITSEORGANISOITUMINEN NYT HAVAITTAVISSA OLEVA UNIVERSUMI HAVAINTOJEN JA TEORIOIDEN
Suhteellisuusteoria. Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos
 Suhteellisuusteoria Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos Ketkä pohjustivat modernin fysiikan? Rømer 1676 Ampere Fizeau 1849 Young 1800 Faraday Michelson 1878 Maxwell 1873 Hertz
Suhteellisuusteoria Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos Ketkä pohjustivat modernin fysiikan? Rømer 1676 Ampere Fizeau 1849 Young 1800 Faraday Michelson 1878 Maxwell 1873 Hertz
Arttu Haapiainen ja Timo Kamppinen. Standardimalli & Supersymmetria
 Standardimalli & Supersymmetria Standardimalli Hiukkasfysiikan Standardimalli on teoria, joka kuvaa hiukkaset ja voimat, jotka vaikuttavat luonnossa. Ympärillämme näkyvä maailma koostuu ylös- ja alas-kvarkeista
Standardimalli & Supersymmetria Standardimalli Hiukkasfysiikan Standardimalli on teoria, joka kuvaa hiukkaset ja voimat, jotka vaikuttavat luonnossa. Ympärillämme näkyvä maailma koostuu ylös- ja alas-kvarkeista
Planck ja kosminen mikroaaltotausta
 Planck ja kosminen mikroaaltotausta Elina Keihänen Helsingin yliopisto Fysikaalisten tieteiden laitos Fysiikan täydennyskoulutuskurssi 8.6.2007 Kiitokset materiaalista Hannu Kurki Suoniolle Planck satelliitti
Planck ja kosminen mikroaaltotausta Elina Keihänen Helsingin yliopisto Fysikaalisten tieteiden laitos Fysiikan täydennyskoulutuskurssi 8.6.2007 Kiitokset materiaalista Hannu Kurki Suoniolle Planck satelliitti
Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2
 Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2 1. (a) W on laatikon paino, F laatikkoon kohdistuva vetävä voima, F N on pinnan tukivoima ja F s lepokitka. Kuva 1: Laatikkoon kohdistuvat voimat,
Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2 1. (a) W on laatikon paino, F laatikkoon kohdistuva vetävä voima, F N on pinnan tukivoima ja F s lepokitka. Kuva 1: Laatikkoon kohdistuvat voimat,
FUNKTIONAALIANALYYSIN PERUSKURSSI 1. 0. Johdanto
 FUNKTIONAALIANALYYSIN PERUSKURSSI 1. Johdanto Funktionaalianalyysissa tutkitaan muun muassa ääretönulotteisten vektoriavaruuksien, ja erityisesti täydellisten normiavaruuksien eli Banach avaruuksien ominaisuuksia.
FUNKTIONAALIANALYYSIN PERUSKURSSI 1. Johdanto Funktionaalianalyysissa tutkitaan muun muassa ääretönulotteisten vektoriavaruuksien, ja erityisesti täydellisten normiavaruuksien eli Banach avaruuksien ominaisuuksia.
YLEINEN SUHTEELLISUUSTEORIA
 YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
Työ 5: Putoamiskiihtyvyys
 Työ 5: Putoamiskiihtyvyys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä määritetään putoamiskiihtyvyys kolmella eri tavalla. Ennakko-oletuksena mietitään, pitäisikö jollain tavoista
Työ 5: Putoamiskiihtyvyys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä määritetään putoamiskiihtyvyys kolmella eri tavalla. Ennakko-oletuksena mietitään, pitäisikö jollain tavoista
YLEINEN SUHTEELLISUUSTEORIA
 YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
SUPER- SYMMETRIA. Robert Wilsonin Broken Symmetry (rikkoutunut symmetria) Fermilabissa USA:ssa
 SUPER- SYMMETRIA Robert Wilsonin Broken Symmetry (rikkoutunut symmetria) Fermilabissa USA:ssa Teemu Löyttinen & Joni Väisänen Ristiinan lukio 2008 1. Sisällysluettelo 2. Aineen rakenteen standardimalli
SUPER- SYMMETRIA Robert Wilsonin Broken Symmetry (rikkoutunut symmetria) Fermilabissa USA:ssa Teemu Löyttinen & Joni Väisänen Ristiinan lukio 2008 1. Sisällysluettelo 2. Aineen rakenteen standardimalli
g-kentät ja voimat Haarto & Karhunen
 g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
Copyright 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley.
 Newtonin painovoimateoria Knight Ch. 13 Saturnuksen renkaat koostuvat lukemattomista pölyhiukkasista ja jääkappaleista, suurimmat rantapallon kokoisia. Lisäksi Saturnusta kiertää ainakin 60 kuuta. Niiden
Newtonin painovoimateoria Knight Ch. 13 Saturnuksen renkaat koostuvat lukemattomista pölyhiukkasista ja jääkappaleista, suurimmat rantapallon kokoisia. Lisäksi Saturnusta kiertää ainakin 60 kuuta. Niiden
Havaitsevan tähtitieteen peruskurssi I
 Havaintokohteita 9. Polarimetria Lauri Jetsu Fysiikan laitos Helsingin yliopisto Havaintokohteita Polarimetria Havaintokohteita (kuvat: @phys.org/news, @annesastronomynews.com) Yleiskuvaus: Polarisaatio
Havaintokohteita 9. Polarimetria Lauri Jetsu Fysiikan laitos Helsingin yliopisto Havaintokohteita Polarimetria Havaintokohteita (kuvat: @phys.org/news, @annesastronomynews.com) Yleiskuvaus: Polarisaatio
Gravitaatio ja heittoliike. Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike
 Gravitaatio ja heittoliike Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike KERTAUS Newtonin lait Newtonin I laki Kappale, johon ei vaikuta voimia/voimien summa on nolla, ei muuta liiketilaansa
Gravitaatio ja heittoliike Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike KERTAUS Newtonin lait Newtonin I laki Kappale, johon ei vaikuta voimia/voimien summa on nolla, ei muuta liiketilaansa
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Fysiikka 8. Aine ja säteily
 Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
LIITE 11A: VALOSÄHKÖINEN ILMIÖ
 LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
9.11 a Fysiikka. Espoon kaupungin opetussuunnitelmalinjaukset. Nöykkiön koulu Opetussuunnitelma Fysiikka
 9.11 a Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien ( = AK) käsittely seuraavin lyhentein: AK 1 = Ihmisenä kasvaminen AK 2 = Kulttuuri-identiteetti
9.11 a Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien ( = AK) käsittely seuraavin lyhentein: AK 1 = Ihmisenä kasvaminen AK 2 = Kulttuuri-identiteetti
Kahden lausekkeen merkittyä yhtäsuuruutta sanotaan yhtälöksi.
 10.1 Yleistä Kahden lausekkeen merkittyä yhtäsuuruutta sanotaan yhtälöksi. Esimerkkejä: 2x 8 = 12 A = πr 2 5 + 7 = 12 Yhtälöissä voi olla yksi tai useampi muuttuja Tuntematonta muuttujaa merkitään usein
10.1 Yleistä Kahden lausekkeen merkittyä yhtäsuuruutta sanotaan yhtälöksi. Esimerkkejä: 2x 8 = 12 A = πr 2 5 + 7 = 12 Yhtälöissä voi olla yksi tai useampi muuttuja Tuntematonta muuttujaa merkitään usein
Maan ja avaruuden välillä ei ole selkeää rajaa
 Avaruus Mikä avaruus on? Pääosin tyhjiön muodostama osa maailmankaikkeutta Maan ilmakehän ulkopuolella. Avaruuden massa on pääosin pimeässä aineessa, tähdissä ja planeetoissa. Avaruus alkaa Kármánin rajasta
Avaruus Mikä avaruus on? Pääosin tyhjiön muodostama osa maailmankaikkeutta Maan ilmakehän ulkopuolella. Avaruuden massa on pääosin pimeässä aineessa, tähdissä ja planeetoissa. Avaruus alkaa Kármánin rajasta
Fysiikan maailmankuva 2015 Luento 8. Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa?
 Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Klassisssa mekaniikassa määritellään liikemäärä p kl näin:
 Relativistinen liikemäärä Luento 3 Klassisssa mekaniikassa määritellään liikemäärä p kl näin: pkl = mv. Mekaniikan ilmiöissä on todettu olevan voimassa liikemäärän säilymisen laki: eristetyn systeemin
Relativistinen liikemäärä Luento 3 Klassisssa mekaniikassa määritellään liikemäärä p kl näin: pkl = mv. Mekaniikan ilmiöissä on todettu olevan voimassa liikemäärän säilymisen laki: eristetyn systeemin
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa. Tapio Hansson
 Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
Lataa Kosmisen kiehtova avaruuskirja - Carole Stott. Lataa
 Lataa Kosmisen kiehtova avaruuskirja - Carole Stott Lataa Kirjailija: Carole Stott ISBN: 9789510364550 Sivumäärä: 61 Formaatti: PDF Tiedoston koko: 39.28 Mb Onko muualla maailmankaikkeudessa elämää? Miksi
Lataa Kosmisen kiehtova avaruuskirja - Carole Stott Lataa Kirjailija: Carole Stott ISBN: 9789510364550 Sivumäärä: 61 Formaatti: PDF Tiedoston koko: 39.28 Mb Onko muualla maailmankaikkeudessa elämää? Miksi
Moderni fysiikka kevät 2011
 Moderni fysiikka kevät 2011 Luennot maanantaisin ja tiistaisin 12-14, D101 Syksy Räsänen: C326 Laskuharjoitukset (25% arvosanasta) Timo Rüppell ja Olli Taanila (A323) Neljä ryhmää: 14-16 & 16-18 (E205),
Moderni fysiikka kevät 2011 Luennot maanantaisin ja tiistaisin 12-14, D101 Syksy Räsänen: C326 Laskuharjoitukset (25% arvosanasta) Timo Rüppell ja Olli Taanila (A323) Neljä ryhmää: 14-16 & 16-18 (E205),
Ensimmäisessä fysiikan jaksossa käsitellään maailmankaikkeutta, aineen rakennetta ja ydinenergiaa. Oppikirja s. 7 12 ja 291 322.
 Fysiikka 1, 7. lk RUOKOLAHDEN KIRKONKYLÄN KOULU Ensimmäisessä fysiikan jaksossa käsitellään maailmankaikkeutta, aineen rakennetta ja ydinenergiaa. Oppikirja s. 7 12 ja 291 322. Tämä dokumentin versio on
Fysiikka 1, 7. lk RUOKOLAHDEN KIRKONKYLÄN KOULU Ensimmäisessä fysiikan jaksossa käsitellään maailmankaikkeutta, aineen rakennetta ja ydinenergiaa. Oppikirja s. 7 12 ja 291 322. Tämä dokumentin versio on
Lataa. Tähtitiede - Maailmankaikkeus - Aurinkokunta - Avaruuslennot. Kuinka paljon tähtiä on? Mikä on musta aukko? Miten pitkä on Jupiterin vuosi?
 Lataa Avaruus Lataa ISBN: 9783625010852 Sivumäärä: 128 Formaatti: PDF Tiedoston koko: 14.78 Mb Tähtitiede - Maailmankaikkeus - Aurinkokunta - Avaruuslennot Kuinka paljon tähtiä on? Mikä on musta aukko?
Lataa Avaruus Lataa ISBN: 9783625010852 Sivumäärä: 128 Formaatti: PDF Tiedoston koko: 14.78 Mb Tähtitiede - Maailmankaikkeus - Aurinkokunta - Avaruuslennot Kuinka paljon tähtiä on? Mikä on musta aukko?
Tampere 14.12.2013. Higgsin bosoni. Hiukkasen kiinnostavaa? Kimmo Tuominen! Helsingin Yliopisto
 Tampere 14.12.2013 Higgsin bosoni Hiukkasen kiinnostavaa? Kimmo Tuominen! Helsingin Yliopisto Perustutkimuksen tavoitteena on löytää vastauksia! yksinkertaisiin peruskysymyksiin. Esimerkiksi: Mitä on massa?
Tampere 14.12.2013 Higgsin bosoni Hiukkasen kiinnostavaa? Kimmo Tuominen! Helsingin Yliopisto Perustutkimuksen tavoitteena on löytää vastauksia! yksinkertaisiin peruskysymyksiin. Esimerkiksi: Mitä on massa?
13.3 Supernovat. Maailmankaikkeuden suurienergisimpiä ilmiöitä: L max 10 9 L. Raskaiden alkuaineiden synteesi (useimmat > Fe )
 13.3 Supernovat Maailmankaikkeuden suurienergisimpiä ilmiöitä: L max 10 9 L nähdään suurilta etäisyyksiltä tärkeitä etäisyysmittareita Raskaiden alkuaineiden synteesi (useimmat > Fe ) Kirkkausmaksimi:
13.3 Supernovat Maailmankaikkeuden suurienergisimpiä ilmiöitä: L max 10 9 L nähdään suurilta etäisyyksiltä tärkeitä etäisyysmittareita Raskaiden alkuaineiden synteesi (useimmat > Fe ) Kirkkausmaksimi:
Lataa Polaris - Heikki Oja. Lataa
 Lataa Polaris - Heikki Oja Lataa Kirjailija: Heikki Oja ISBN: 9789525329759 Sivumäärä: 159 Formaatti: PDF Tiedoston koko: 19.55 Mb Tule mukaan jännittävälle retkelle läpi tähtitaivaan maailmojen. Opi tuntemaan
Lataa Polaris - Heikki Oja Lataa Kirjailija: Heikki Oja ISBN: 9789525329759 Sivumäärä: 159 Formaatti: PDF Tiedoston koko: 19.55 Mb Tule mukaan jännittävälle retkelle läpi tähtitaivaan maailmojen. Opi tuntemaan
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
Luvun 8 laskuesimerkit
 Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
