P.a.s. gaunami skaitiniu algoritmu pagalba. Bendriausias p.a.s. gavimo algoritmas turi form :
|
|
|
- Riitta Karoliina Toivonen
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 PSEUDOATSITIKTINIU SKAIƒIU GENERAVIMAS P.a.s. gaunami skaitiniu algoritmu pagalba. Bendriausias p.a.s. gavimo algoritmas turi form : x n+1 = f(x 1, x 2,..., x n ). Naudojant toki algoritm, atmintyje reiketu laikyti visus generuotus skai ius, pradedant pirmuoju. Tokia proced ura uºimtu per daug kompiuterio atminties. 1
2 Praktinems reikmems paprastai uºtenka paprastesniu algoritmu. Dauguma ju turi toki form : (1) x n+1 = f(x n ). Funkcija f turi b uti labai atidºiai parinkta. Funkcija, pavaizduota 4 pav., ai²kiai bloga. Ta²kai, kuriu koordinates yra gretimi skai iai (x 1, x 2 ), (x 3, x 4 ), (x 5, x 6 ),..., yra kreives ta²kai, ir ai²ku nera tolygiai pasiskirst vienetiniame kvadrate {(x, y) 0 x, y < 1}. (1) funkcijos grakas turi padengti vienetini kvadrat kiek galima tolygiau (ºr. 5 pav.). Tegul (2) y = {gx}; ia g yra didelis skai ius, o skai iaus z trupmenine dalis yra ºymima {z}. I² 5 pav. matyti, kad (2) funkcijos, kai g = 19, grakas vienetini kvadrat padengia tolygiai. 2
3 KVADRATO VIDURIO METODAS Kvadrato vidurio metodas tai Noimano pasi u- lytas ir pirmas pla iai naudotas algoritminis metodas p.a.s. generuoti. Metodo ideja tokia. n-asis p.a.s. yra gaunamas paemus vidurinius (n 1)-ojo p.a.s. kvadrato skaitmenis. ši urekite 6 pav. Kvadrato vidurio metodas nera geras. Yra skai iu, kurie uºsiciklina. Forsaitas (G.E.Forsythe) patikrino 16 keturºenkliu skai iu. 12 i² ju baigesi ciklu 6100, 2100, 4100, 8100, 6100,... Dvi sekos tapo nulinemis. ši urekite 7 pav. Metropolis (N.Metropolis), tyrinedamas ²i metod, eme dvejetainius 20 ºenklu skai ius. Jis parode, kad egzistuoja 13 ciklu. Didºiausio i² ju periodas 142. Tyrinedamas 38 ºenklu dvejetainius skai ius, surado periodo sek. 3
4 γ 0 = γ 2 0 = γ 1 = γ 2 1 = γ 2 = γ 2 2 = γ 3 = γ 2 3 = γ 4 = γ 2 4 = γ 5 = γ 2 5 = γ 6 = γ 2 6 = γ 7 = γ 2 7 = γ 8 = γ 2 8 = γ 9 = γ 2 9 = pav. Noimano kvadrato vidurio metodas 4
5 pav. Bloga kvadrato vidurio metodu gauta seka 5
6 Uºksavus tokiu skai iu ciklu pabaig, galima proces pradeti i² naujo. Floidas (R.Floyd) sugalvojo metod, kaip tai padaryti. is metodas reikalauja nedaug ma²inos atminties ir triskart daugiau laiko a.s. generuoti. Taigi Noimano metodas nera geras. Pirma, jis labai nepatogus statistinei analizei atlikti. Antra, sekos link uºsiciklinti; seka labai priklauso nuo pirmojo skai iaus parinkimo; jei sekoje pasitaiko nuliai, seka baigiasi. Tre ia, skai iai generuojami ne pakankamai greitai. Atsiradus geresniems generatoriams, o ypa pradejus naudoti tiesini kongruentini metod, kvadrato vidurio metodas nebenaudojamas. Jis liko istorijoje kaip pirmas algoritminis p.a.s. generatorius. 6
7 TIESINIS KONGRUENTINIS METODAS iandien p.a.s. daºniausiai gaunami taikant Lemerio (D.H.Lehmer) 1948 m. pasi ulytos schemos dalinius atvejus. Metodas vadinamas tiesiniu kongruentiniu metodu. iame skyrelyje ji ir panagrinesime. P.a.s. seka apibreºiama lyginiu: (3) ƒia skai iai: X n+1 (ax n + c) mod m, n 0. X 0 pradine reik²me, X 0 0, a daugiklis, a 0, c prieauglis, c 0, m modulis, m > X 0, m > a, m > c, (4) yra parenkami. 7
8 Tarkime, X 0 = a = c = 7, m = 10. Gausime sek 7, 6, 9, 0, 7, 6, 9, 0,.... Gauta seka nera gera. Toliau panagrinesime principus, kaip gauti kuo ilgesnio ciklo (geras) atsitiktines sekas priklausomai nuo pradiniu parametru. Pasikartojanti p.a.s. sekos dalis vadinama jos periodu. Tislas gauti kuo ilgesnio periodo sekas. Kai c = 0, tiesines sekos gavimo metodas vadinamas multiplikatyviuoju. Multiplikatyviuoju atveju p.a.s. generavimo procesas vyksta grei- iau. Apribojimas c = 0 sumaºina sekos periodo ilgi, bet ir ²iuo atveju galima gauti gana ilgo periodo sekas. Taip pat ºymesime b = a 1 (bus patogiau). Atveju, kai a = 0 ir a = 1, nenagrinesime, nes sekos gaunasi labai skurdºios ir, ai²ku, maºai atsitiktines. Taigi turesime galvoje, kad a 2, b 1. 8
9 I² (3) lyginio turime, kad X n+k ax n+k 1 + c a(ax n+k 2 + c) + c = a 2 X n+k 2 +c(a+1) a 2 (ax n+k 3 +c)+c(a+1) arba = a 3 X n+k 3 + c(a 2 + a + 1)... a k X n + c(a k 1 + a k ) = a k X n + c(ak 1) a 1 X n+k a k X n + c(ak 1) b Paem n = lk, gausime X (l+1)k a k X lk + c(ak 1) b mod m mod m, k 0, n 0. mod m, l 0. (5) Taigi seka X 0, X k, X 2k,... tai nauja tiesine kongruentine seka su daugikliu a k ir prieaugliu c(a k 1)/b. 9
10 MODULIO PARINKIMAS Kadangi periodas negali b uti didesnis uº m, tai m reiketu imti gana didelius. Netgi jei mums reikia atsitiktines sekos i² nuliuku ir vienetuku, nereikia imti m = 2, nes ²iuo atveju daugiausiai gausime..., 0, 1, 0, 1,... arba blogiau, tik vienetukus arba tik nuliukus. Kitas faktorius, nulemiantis m parinkim, tai sekos elementu paskai iavimo greitis. Skai iuojant kompiuteriu, patogu imti m, lygu ºodºio ilgiui (vienetu daugiau negu kompiuterio ºodyje telpantis didºiausias sveikas skai ius). Tegul w toks maksimalus sveikas skai ius. iuo atveju labai paprasta atlikti operacijas moduliu w, nes rezultatas gaunamas paskutinese ºodºio skiltyse ir kas netelpa tiesiog galima i²stumti kairen. 10
11 Bet ²itas metodas galima taikyti ne visuomet. Jis nera labai geras. Ir ²tai kodel. Paskutiniai skai iaus X n skaitmenys yra daug maºiau atsitiktiniai negu pirmieji. Sakykime, d w ir Y n X n mod d. Tada Y n yra paskutinieji skai iaus X n skaitmenys. Kadangi tai X n+1 ax n + c mod m 1 d, Y n+1 X n+1 ax n + c ay n + c mod d. Vadinasi paskutiniuju skaitmenu periodas neilgesnis kaip d. Pavyzdºiui, jeigu w = 2 l, tai paskutiniojo X n skaitmens periodas lygus tik 2 (jeigu kodas dvejetainis). Taigi periodi²kai kei iasi 0 su 1, arba tik 0, arba tik 1. Paskutiniuju dvieju skaitmenu periodas b utu 2 2 = 4, paskutiniu triju 2 3 = 8 ir t.t. 11
12 Situacija visai kita, kai vietoje m pasirenkame didºiausi pirmini skai iu, maºesni uº w. ƒia problemos i²kyla (tiesa, jos nedideles, nugalimos) su to pirminio skai iaus suradimu ir su sekos elementu greitu paskai iavimu. Kuo tas pirminis skai ius artimesnis w, tuo greitesni skai iavimai. Pakanka imti m = w ± 1, ir situacija taip pat ºymiai pagereja. Paprastai laikoma c = 0. Kaip gaunamas algoritmas? Sakykime, m = w + 1. Visuomet galima uºra²yti: ax = qw + r, 0 q, r < w. 12
13 Paprastai dauginant a i² X, liekana r uºims vien ºodi, o q kit ºodi. Bet ax = q(w + 1) + r q. Taigi { r q mod (w + 1), jei r q 0, ax r q + w + 1 mod (w + 1), jei r q < 0. Uºra²ytas proced uras atlikti su kompiuteriu labai paprasta. Kai ax = w, nesunku numatyti programoje ir i²mesti toki reik²m. iuo atveju gauname perpildym (skai ius w netelpa viename ºodyje). Taigi ai²ku, kaip skai iuoti sek X n+1 ax n mod (w + 1). 13
14 DAUGIKLIO PARINKIMAS iame skyrelyje parodysime kaip parinkti a, kad gautume maksimalaus periodo p.a.s. Didelis periodas tai tik vienas i² b utinu atsitiktinumo elementu. Pavyzdºiui, kai a = c = 1, turesime maksimalaus ilgio visi²kai neatsitiktin sek X n+1 X n + 1 mod m. Kadangi seka gali igyti tik m skirtingu reik²miu, tai maksimalaus periodo ilgis yra, ai²ku, nedidesnis kaip m. Kad tokio ilgio gali b uti, rodo k tik pateiktas pavyzdys. Pastaba. Kai periodo ilgis maksimalus (= m), kiekvienas skai ius nuo 0 iki m 1 periode sutinkamas vien kart. Po to periodas pasikartoja. Todel visi²kai nesvarbu koki X 0 bepasirinksime. Pateiksime reikalingus faktus i² skai iu teorijos. 14
15 1 lema Tegul p P, l N, p l > 2. Jeigu tai x 1 mod p l, x 1 mod p l+1, x p 1 mod p l+1, x p 1 mod p l+2. 15
16 Irodymas. Turime I² ia x = qp l + 1, (q, p) = 1. x p = q p p pl + C 1 p qp 1 p (p 1)l C p 1 p qp l + 1. Niutono binomo koecientas C k p = p(p 1)... (p k + 1) k! yra nat uralusis skai ius. Kadangi k < p, tai po suprastinimo b utinai liks pirminis daugiklis p. Vadinasi p C k p, ir todel x p = 1 + qp l+1( p Cp 2 p qp l + 1 p Cp 3 p q 2 p 2l p C1 p qp 2 p (p 2)l + 1 p qp 1 p (p 1)l). Rei²kinio skliaustuose kiekvienas demuo, i²skyrus pirm ji, yra p kartotinis. Paskutinis demuo dalijasi i² p, nes p l > 2 ir todel (p 1)l > 1. Taigi x p = 1 + q p l+1, (q, p) = 1. Lema irodyta. 16
17 2 lema Tegul m = p l p l t t. Tiesines kongruentines sekos (X 0, a, c, m) periodas λ yra lygus seku (X 0 mod p l j j, a mod p l j j, c mod p l j j, p l j j ), 1 j t, periodu λ j maºiausiam bendram kartotiniui. 17
18 Irodymas. Pakanka irodyti lem, kai (r, s) = 1, λ sekos (X 0, a, c, rs) periodas, λ 1, λ 2 seku (X 0 mod r, a mod r, c mod r, r), (X 0 mod s, a mod s, c mod s, s) periodai. Pasinaudojus indukcija, i² to jau i²plauktu lema. Paºymekime minetu seku elementus atitinkamai X n, Y n, Z n. Kadangi Y 0 X 0 mod r, tai Y 1 ay 0 + c ax 0 + c X 1 mod r. Pasinaudoj indukcija, gautume, kad Y n X n mod r. Analogi²kas lyginys teisingas ir sekai Z n. Taigi (6)Y n X n mod r, Z n X n mod s, n. Irodysime, kad (7) X n = X k Y n = Y k ir Z n = Z k. I² tikruju, tegul X n = X k, tada i² (6) gausime, kad Y n = Y k ir Z n = Z k. 18
19 Tegul dabar Y n = Y k ir Z n = Z k. I² (6) turesime, kad X n = X k + ru = X k + sv, ru = sv, ir kadangi (r, s) = 1, tai u = su 1, o v = rv 1. Taigi X n = X k + rsu 1. Kadangi visuomet imame mod rs, tai i² ia i²plaukia, kad X n = X k. (7) irodyta. Tegul λ = MBK(λ 1, λ 2 ). Kai n pakankamai didelis, n µ, turime X n = X n+λ, o i² (7) Y n = Y n+λ ir Z n = Z n+λ. Taigi λ yra λ 1 ir λ 2 kartotinis. Vadinasi λ λ. I² kitos puses Y n = Y n+λ ir Z n = Z n+λ visiems pakankamai dideliems n. I² (7) i²plaukia, kad X n = X n+λ visiems pakankamai dideliems n. Taigi λ λ. Gavome, kad λ = λ. Lema irodyta. 19
20 3 lema (Maºoji Ferma teorema, 1640) Tegul p P. Tuomet a p a mod p. Irodymas. Jeigu a 0 mod p, tai lemos tvirtinimas akivaizdus. Tegul a 0 mod p. Tuomet (a, p) = 1 ir ax, x = 0, 1,..., p 1, perbega visas likiniu klases mod p. I² tikruju, jei ax 1 ir ax 2 priklauso tai pa iai likiniu klasei, tai ax 1 = k 1 p + l, ax 2 = k 2 p + l = a(x 1 x 2 ) = (k 1 k 2 )p = x 1 x 2 = kp = x 1 = x 2. Taigi seka 0 mod p, a mod p,..., (p 1)a mod p sudaryta i² skirtingu skai iu: 0, 1,..., p 1. Todel a 2a... (p 1)a (p 1) mod p. Pastar ji lygini padaugin i² a, gausime arba Lema irodyta. a p ((p 1)!) a((p 1)!) mod p, a p a mod p. 20
21 4 lema Tegul p P. Tuomet a pl a mod p. Irodymas. I² 3 lemos i²plaukia, kad a p = a + pt. Todel a p2 = (a p ) p = a p +Cp 1 ap 1 pt+...+cp p 1 a(pt) p 1 +(pt) p a p a mod p. Panaudoj indukcij gausime lemos irodym. 21
22 5 lema Tegul 1 < a < p l, p P, o λ maºiausias nat uralusis skai ius, kuriam Tuomet λ = p l a λ 1 a 1 0 mod pl. { a 1 mod p, kai p > 2, a 1 mod 4, kai p = 2. 22
23 Irodymas. B utinumas. Tegul λ = p l. Jeigu a 1 mod p, tai a n 1 a 1 0 mod pl a n 1 0 mod p l. Jeigu tai ir a pl 1 mod p l, a pl 1 mod p. I² 4 lemos turesime a pl a mod p. O i² paskutiniuju dvieju lyginiu gausime a 1 mod p. Gauta prie²tara irodo, kad a 1 mod p. Jeigu p = 2 ir a 3 mod 4, tai (8) Be to a 1 = 2(2n 1). a 2 = (4n + 3) 2 = 16n n mod 8. 23
24 Kadangi tai x 1 mod 2 l = x 2 = (n2 l +1) 2 = n 2 2 2l +n2 l mod 2 l+1, a 4 1 mod 16, a 8 1 mod 32,..., a 2l 1 1 mod 2 l+1 ; a 2l mod 2 l+1, a 2l mod 2 l. I² (8) turime, kad 2 (a 1) ir 4 (a 1). Todel a 2l 1 1 a 1 0 mod 2 l. Gavome prie²tar λ apibreºimui. Taigi, kai λ = p l, turesime, kad a = 1 + qp t, p t > 2, (q, p) = 1. 24
25 Pakankamumas. Tegul (9) I² 1 lemos turesime a = 1 + qp t, p t > 2. a p 1 mod p t+1, a p 1 mod p t+2 ; a p2 1 mod p t+2, a p2 1 mod p t+3 ; a ps 1 mod p t+s, a ps 1 mod p t+s+1. I² pastaruju lyginiu ir (9) gausime a ps 1 0 mod p t+s, a 1 0 mod p t. Dabar ai²ku, kad a ps 1 a 1 0 mod ps, Vietoje s istatome l. Tuomet a ps 1 a 1 0 mod ps+1. a pl 1 a 1 0 mod pl, a pl 1 a 1 0 mod pl+1. 25
26 Imkime tiesin kongruentin sek (0, a, 1, p l ). I² (5) formules, paem l = 0 ir k = n, gausime, kad X n an 1 a 1 mod pl. Pagal λ apibreºim, ²ios sekos periodo ilgis lygus λ, t.y. maºiausiam skai iui, kuriam a λ 1 a 1 0 mod pl, nes tik ²iuo atveju vel pasikartos X 0. Jei λ periodas, tai jis turi dalyti p l, nes ir p l periodas. Taigi λ = p s. Jeigu s < l, tai bet a ps 1 a 1 0 mod pl, a ps 1 a 1 0 mod ps+1, o l s + 1. i prie²tara irodo, kad Lema irodyta. λ = p l. 26
27 1 teorema Tiesines kongruentines sekos periodo ilgis lygus m (c, m) = 1, p m p (a 1), 4 m 4 (a 1). 27
28 Irodymas. I² 2 lemos i²plaukia, kad teorem pakanka irodyti, kai m = p l. Kai a = 1, teoremos irodymas akivaizdus. iuo atveju X 1 X 0 +c mod m, X 2 X 0 +2c mod m,..., X m X 0 + mc X 0 mod m. Kadangi (c, m) = 1, tai sandaugos ct, t = 0,..., m 1, perbega vis likiniu klas mod m. Todel gausime skirtingus mod m skai ius. I² viso ju yra m. 28
29 Sakykime, a > 1. Periodo ilgis lygus m kai kiekvienas skai ius x, 0 x < m, sutinkamas periodo ilgio sekos dalyje lygiai vien kart. Vadinasi periodas lygus m kai sekos, su X 0 = 0, periodo ilgis lygus m. Paem l = 0, k = n, i² (5) lyginio turesime X n an 1 a 1 c mod m. Kai (c, m) 1 X n 1 (skai ius 1 periodo ilgio sekos dalyje nebus sutinkamas). Del to s lyga (c, m) = 1 b utina. Periodas lygus m kai maºiausias teigiamas skai ius n, kuriam X n = X 0 = 0, yra lygus m. Dabar, kadangi (c, m) = 1, teoremos irodymas i²plaukia i² 5 lemos. 29
30 1 pavyzdys Pateiksime tiesines kongruentines sekos su maksimaliai galimu periodu, lygiu 48, pavyzdi. Kadangi m = 48 = 2 4 3, tai i² 1 teoremos i²plaukia, kad a ir c gali b uti parinkti taip: a = 13, c = 23. Tegul X 0 = 0. Visa atsitiktine seka atrodo taip: 0, 23, 34, 33, 20, 43, 6, 5, 40, 15, 26, 25, 12, 35, 46, 45, (10) 32, 7, 18, 17, 4, 27, 38, 37, 24, 47, 10, 9, 44, 19, 30, 29, 16, 39, 2, 1, 36, 11, 22, 21, 8, 31, 42, 41, 28, 3, 14,
31 Pateiktas pavyzdys nera geras. Maºas atsitiktinumo laipsnis. Kai kurie sekos desningumai lengvai pastebimi. Galima meginti parinkti kitokius a ir c, bet desningumai vis tiek b utu akivaizd us. Parinkti ger atsitiktin sek nera paprasta. O ir parinkus reikia naudoti ivairius testus, ir isitikinti, kad seka tikrai gera ir tinka modeliavimui. I² generuotos atsitiktines nat uraliuju skai iu sekos lengvai galima sudaryti tolygiai intervale [0, 1] pasiskirs iusi pseudoatsitiktin sek. Tai galima padaryti, pavyzdºiui, su formules (11) U n = X n m pagalba. Tolygiai pasiskirs iusios intervale [0, 1] sekos naudojamos kitaip pasiskirs iusioms sekoms sudaryti. Apie tai kalbesime kituose skyriuose. 31
32 2 pavyzdys I² nat uraliuju atsitiktiniu skai iu sekos (10) sukonstruokime atsitiktiniu skai iu, tolygiai pasiskirs iusiu intervale [0, 1], sek. Naudodami (11) formul (10) sekai, gausime toki tolygiai intervale [0, 1] pasiskirs iusi sek (apvaliname iki 4 vietu po kablelio tikslumu): 0 0,4792 0,7083 0,6877 0,4167 0,8958 0,125 0,1042 0,8333 0,3125 0,5417 0,5208 0,25 0,7292 0,9583 0,9375 0,6667 0,1458 0,375 0,3542 0,0833 0,5625 0,7917 0,7708 0,5 0,9792 0,2083 0,1875 0,9167 0,3958 0,625 0,6042 0,3333 0,8125 0,0417 0,0208 0,75 0,2292 0,4583 0,4375 0,1667 0,6458 0,875 0,8542 0,5833 0,0625 0,2917 0,2708 ios sekos statistines savybes kaip ir (10) nat uraliuju skai iu sekos nera geros. Per maºas atsitiktinumo laipsnis. 32
33 MULTIPLIKATYVUSIS KONGRUENTINIS METODAS Tiesine kongruentine seka, kai c = 0, vadinama multiplikatyvi ja kongruentine seka. I² 1 teoremos i²plaukia, kad ²iuo atveju maksimalaus periodo ilgio negausime. Bet sekos generavimas yra greitesnis. Pirma irodysime pagalbini rezultat, o veliau i²samiau panagrinesime multiplikatyvi sias kongruentines sekas. Tegul φ(n) Eulerio funkcija, lygi skai iui skai iu 0, 1, 2,..., n 1, kurie yra tarpusavyje pirminiai su n: φ(n) = #{i (i, n) = 1, i {0, 1,..., n 1}}. 33
34 6 lema (Eulerio teorema) Jei (a, m) = 1, tai a φ(m) mod m = 1. Irodymas. Jeigu (a 1, m) = 1 ir (a 2, m) = 1, tai (a 1 a 2 mod m, m) = 1. Tegul 0 x 1,..., x φ(m) < m skirtingi tarpusavy pirminiai su m skaičiai. Tada ax 1 mod m,..., ax φ(m) mod m tie patys skaičiai, išdėstyti, gal būt, kita tvarka. Taigi ax 1 mod m... ax φ(m) mod m = x 1... x φ(m), arba a φ(m) mod m = 1. Lema irodyta. 34
35 Jei d m ir d X n, tai d X n+j, j = 1, 2,... Todel, kai c = 0, b utu gerai, kad (X n, m) = 1, n = 1, 2,... Tai, ºinoma, taip pat riboja periodo ilgi. Turedami omenyje 2 lem, nemaºindami bendrumo galime nagrineti atveji X n a n X 0 mod p l. Jeigu p a, tai periodo ilgis nedidesnis uº l. Todel tegul (a, p) = 1. Periodas lygus maºiausiam sveikam λ, kuriam (12) X 0 a λ X 0 mod p l. Sakykime, (X 0, p l ) = p s, tuomet (12) ekvivalentu a λ 1 mod p l s. I² Eulerio teoremos (6 lema) turime, kad Taigi a φ(pl s) 1 mod p l s. λ φ(p l s ) = p l s p l s 1 = p l s 1 (p 1). 35
36 Dabar pateiksime kelet skai iu teorijos apibreºimu. Tegul (a, m) = 1. Maºiausias nat uralusis λ, kuriam a λ 1 mod m, vadinamas rodikliu mod m. Skai ius a, kuri atitinka maksimaliai galimas rodiklis mod m, vadinamas primityviuoju elementu mod m. Tegul λ(m) primityvaus elemento rodiklis, t.y. maksimaliai galimas rodiklis mod m. Tuomet λ(p l ) p l 1 (p 1), kai (X 0, p) = 1. Primityvaus elemento nereikia painioti su primityvi ja ²aknimi. Primityvios ²aknys egzistuoja ne visiems m. 36
37 Galima tiksliai paskai iuoti, kad (13) ir (14) λ(2) = 1, λ(4) = 2, λ(2 l ) = 2 l 2, kai l 3, λ(p l ) = p l 1 (p 1), kai p > 2, λ(p l p l t t ) = = MBK(λ(p l 1 1 ),..., λ(p l t t )). 37
38 Dabar galime suformuluoti Karmaiklo teorem. 2 teorema (Karmaiklo teorema) Multiplikatyviosios kongruen ios sekos maksimalus periodas yra lygus λ(m), apibreºtam (13) ir (14) formulemis. Toks periodas gaunamas, kai (X 0, m) = 1, a primityvusis elementas mod m. Pastebekime, jei m pirminis skai ius, tai galima gauti periodo ilgi lygu m 1. R.D.Carmichael, Bull. Amer. Math. Soc., 16, 1910,
39 Kaip rasti primityviuosius elementus mod m? Teisinga tokia teorema. 3 teorema Skai ius a yra primityvusis elementas mod p l p l = 2, a nelyginis skai ius; p l = 4, a mod 4 = 3; p l = 8, a mod 8 = 3, 5, 7; p = 2, l 4, a mod 8 = 3, 5; p > 2, l = 1, a 0 mod p, a (p 1)/q 1 mod p q P, q (p 1); p > 2, l > 1, a tenkina ankstesn s lyg ir a p 1 1 mod p 2. Jeigu modulis yra 2, arba 2 2, arba p l (p > 2), tai primityvieji elementai bus ir primityviosiomis ²aknimis. 39
40 Jeigu reikia rasti primityvuji element a mod m, m = p l p l t t, tai, pasirodo, egzistuoja vienintelis toks a, kad a a j mod p l j j, j = 1,..., t. ƒia a j primityvusis elementas mod p l j Kai m = 2 l, l 4, tai a = 3, 5 mod 8. iuo atveju ketvirtoji dalis visu galimu daugikliu duoda maksimalu period. j. 40
41 Antras svarbus atvejis, kai m = 10 l. atveju teisinga tokia teorema. iuo 4 teorema Tegul m = 10 l, l 5, (X 0, 10) = 1. Multiplikatyviosios kongruentines sekos periodas lygus 5 l 1 2 l 2 = 5 10 l 2 a mod 200 yra lygus vienam i² 32 skai iu: 3, 11, 13, 19, 21, 27, 29, 37, 53, 59, 61, 67, 69, 77, 83, 91, 109, 117, 123, 131, 133, 139, 141, 147, 163, 171, 173, 179, 181, 187, 189,
42 Tiesines kongruentines sekos galingumas Jau ºinome, kad maksimalus tiesines kongruentines sekos periodas gaunamas, kai b = a 1 yra visu pirminiu m dalikliu kartotinis ir 4 kartotinis, jei m dalijasi i² 4 (ºr. 1 teorem ). Tegul m = z l. Tada daugiklis a tenkina minetus reikalavimus, pavyzdºiui, kai (15) a = z k + 1, 2 k < l. I² 1 teoremos i²plaukia, kad galime paimti c = 1. Tuomet X n+1 (z k + 1)X n + 1 mod z l. i formule patogi skai iavimuose, nes galima i²vengti daugybos (kai ºodºio ilgis lygus z l ), pakei iant j post umiu ir sudetimi. Ir vis tik (15) tipo daugikliu reikia vengti. Gautos sekos nera labai atsitiktines. Kodel? 42
43 Tiesines kongruentines sekos su maksimaliu periodu galingumu vadinsime maºiausi nat uraluji skai iu s, kuriam b s 0 mod m. Toks s visuomet egzistuoja, kai a tenkina 1 teoremos reikalavimus. Nemaºindami bendrumo galime paimti X 0 = 0. Tuomet i² (5) turesime X n (an 1)c b mod m. I²skleid a n 1 = (1 + b) n 1 pagal Niutono binomo formul, (kai n pakankamai dideli, n > s) gausime X n c(n + C 2 n b Cs n bs 1 ) mod m. Narius su b s, b s+1 ir t.t. praleidºiame, nes jie yra m kartotiniai. 43
44 Jeigu a = 1, galingumas s = 1, X n cn mod m. Seka, ai²ku, neatsitiktine. Tegul s = 2. Tuomet X n cn + cbc 2 n mod m. Ir ²iuo atveju seka maºai atsitiktine: X n+1 X n c + cbn mod m. Jeigu s = 3, seka, atrodo, labiau atsitiktine, bet X n, X n+1, X n+2 dar vis stipriai susij. Priimtini rezultatai gaunami, kai s = 4, bet dar gin ytini. Reikia siekti, kad s 5. Pateikti samprotavimai ir paai²kina sekos galingumo prasm. Galingumas yra tik vienas i² kriteriju parenkant daugikli. Pabaigai pateiksime kelet pavyzdºiu. 44
45 Paimkime m = 2 35 ir a = 2 k + 1 b = 2 k. Kai k 18, b 2 = 2 2k yra m kartotinis s = 2. Kai k = 17,..., 12 s = 3. Kai k = 11, 10, 9 s = 4. Taigi reiketu imti k 8. Tada a 257. Bet ²iuo atveju daugiklis a nedidelis. Vel gaunamos sekos, kuriu reikia vengti (irodyta, kad sekos labiau atsitiktines, kai a dideli). Kai m = w ± 1 (w ºodºio ilgis), tai, bendrai imant, m nei²siskaido i auk²to laipsnio pirminius daugiklius ir s nedidelis. Todel ²iais atvejais nereiketu naudotis maksimalaus periodo metodu, o imti c = 0. Veliau nagrinesime spektrini test. Su jo pagalba bus galima isitikinti, kad daugiklis , kai m = 2 35, gana geras. Narys 2 23 padaro daugikli gana dideli, 2 2 uºtikrina dideli galingum, 2 14 naudojamas, kad daugiklis neb utu labai jau paprastas, o seka b utu pakankamai atsitiktine. 45
46 Tiesinis rekurentinis metodas Tiesine rekurentine seka vadinama dvejetaine seka X n, gaunama algoritmo X n c 1 X n 1 + c 2 X n 2 + (16)... + c p X n p mod 2 pagalba. Kad algoritmas galetu veikti, turi b uti parinkti pirmieji sekos nariai: X 1, X 2,..., X p {0, 1} ir konstantos c 1, c 2,..., c p {0, 1}. Kai konstantu seka c 1,..., c p yra ksuota, X n priklauso tik nuo p paskutiniuju sekos nariu X n 1,..., X n p. Todel tiesines rekurentines sekos periodo ilgis yra maºiausias skai ius (sekos nario indeksas), kai rinkinys X n 1,..., X n p pasikartoja. Jei rinkini i² eiles einan iu p nariu sudaro nuliukai, tai visi sekantys nariai irgi bus nuliai. Todel sekos periodas negali b uti didesnis uº 2 p 1. 46
47 5 teorema Tiesines rekurentines sekos (16) periodas yra maksimalus (lygus 2 p 1) daugianaris f(x) = 1 + c 1 x + c 2 x c p x p yra primityvusis polinomas vir² baigtinio polinomu, su koecientais 0 arba 1, k uno (vir² Galua k uno GF (2)). 3 pavyzdys Imdami primityvuji polinom f(x) = 1 + x 3 + x 5, sukonstruokime tiesin rekurentin sek. Atitinkama tiesine rekurentine seka yra X n = X n 3 + X n 5 mod 2. Paimkime pradin sek : X 1 = 1, X 2 = 1, X 3 = 0, X 4 = 1, X 5 = 0. Tuomet generuota seka atrodys taip: (17) Toliau seka vel kartosis. Sekos periodas yra lygus =
48 Yra daug b udu i² dvejetaines sekos gauti nat u- raliuju skai iu sekas. Tarkime, b i, i = 1, 2,..., yra dvejetaine seka. Sekos (18) X i = (b ik b ik+1... b ik+l ) 2, (19) Y i = (b i b i l... b i lt ) 2, su pasirinktais k, L, l, t, yra nat uraliuju skai iu sekos. Seka Y i gauta naudojant metod su velavimais. 48
49 4 pavyzdys Dvejetain sek (17) paverskime nat uraliuju skai iu sekomis pagal (18) ir (19) formules. Pasirinkime k = 5, L = 4. I² (18) formules turesime X 1 = (b 5 b 6 b 7 b 8 b 9 ) 2 = = 8, X 2 = (b 10 b 11 b 12 b 13 b 14 ) 2 = = 9, X 7 = (b 35 b 36 b 37 b 38 b 39 ) 2 = (b 4 b 5 b 6 b 7 b 8 ) 2 = = 20, X 31 = (b 31 5 b b b b ) 2 = (b 31 b 1 b 2 b 3 b 4 ) 2 = =
50 Visa seka atrodo taip: 8, 9, 12, 31, 3, 28, 20, 8, 22, 15, 17, 23, 10, 2, 11, 7, 24, 27, 21, 1, 5, 19, 28, 13, 26, 16, 18, 25, 30, 6, 29. Parink l = 6, t = 4, i² (19) formules gausime Y i = (b i b i 6 b i 12 b i 18 b i 24 ) 2. Paskai iav, turesime Y 1 = (b 1 b 5 b 11 b 17 b 23 ) 2 = (b 1 b 26 b 20 b 14 b 8 ) 2 = = 22, Y 2 = (b 2 b 27 b 21 b 15 b 9 ) 2 = = 20 ir t.t. Visa seka atrodo taip: 22, 20, 14, 31, 8, 24, 11, 10, 7, 15, 18, 12, 5, 21, 3, 23, 25, 6, 2, 26, 17, 27, 28, 19, 1, 13, 8, 29, 30, 9,
51 I² atsitiktines binarines sekos lengva padaryti atsitiktin sek i² intervalo [0, 1]. Jei binarine seka atsitiktine, tai gauta seka intervale [0, 1] turetu b uti jame tolygiai pasiskirs iusi. Yra daug b udu. Pavyzdºiui, tolygiai pasiskirs iusi seka galetu b uti gauta naudojant formul : (20) U i = (0, b ik b ik+1... b ik+l ) 2, su pasirinktais k ir L. 5 pavyzdys I² dvejetaines sekos (17) gaukime tolygiai intervale [0, 1] pasiskirs iusi sek. Naudodami (17) sek, (20) formuleje parink k = 5, L = 4, gautume U 1 = (0, b 5 b 6 b 7 b 8 b 9 ) 2 = 0, = 0, 25, U 2 = (0, b 10 b 11 b 12 b 13 b 14 ) 2 = 0, = 0, 28125, U 31 = (0, b 31 b 1 b 2 b 3 b 4 ) 2 = 0, =
52 Visa atsitiktine seka i² intervalo [0, 1] atrodytu taip: 0,25 0, ,375 0, , ,875 0,625 0,25 0,6875 0, , , ,3125 0,0625 0, , ,75 0, , , , , ,875 0, ,8125 0,5 0,5625 0, ,9375 0,1875 0,
53 Tiesinio rekurentinio metodo, lyginant ji su tiesiniu kongruentiniu, privalumai yra tokie. Pirma, tiesine rekurentine seka yra labai greitai generuojama. ƒia nereikia atlikti jokios daugybos tik sudeti mod 2 ir post umi, rekurenti²kai skai iuojant. Atminties irgi nereikia daug. Antra, periodo ilgis nera susij s su kompiuterio ºodºio ilgiu. Galima generuoti labai ilgo periodo sekas (pavyzdºiui, tokio ilgio > ar dar ilgesnes). io metodo tr u- kumas, lyginant ji su tiesiniu kongruentiniu metodu, yra tai, kad jis gerokai maºiau i²tirtas. Del ²ios prieºasties kongruentinis metodas patikimesnis ir pla iau taikomas. 53
54 Kiti metodai Yra daug p.a.s. generavimo metodu. Bet tiesinis kongruentinis metodas geras tuo, kad ºinoma teorija ir galima garantuoti atsitiktinum. Pavyzdºiui, tegul X n+1 (ax n mod (m + 1) + c) mod m. Atrodo, kad seka labiau sujaukta negu tiesinio kongruentinio metodo. Atsakymas toks: ma- ºiau atsitiktine. Apskritai, jeigu generuojame X n+1 = f(x n ), tai funkcija f turi b uti tiksliai apibreºta ir ne ypa sudetinga, kad galetume kurti teorij. Yra daug tiesinio kongruentinio metodo apibendrinimu. A) X n+1 dx 2 n + ax n + c mod m metodas geras, yra ir 1 teoremos apibendrinimas, nusakantis kada gauname maksimalu period lygu m; sunkiau realizuojamas kompiuteryje; reikia daugiau laiko generavimui. 54
55 B) X n+1 X n (X n + 1) mod 2 l, X 0 2 mod 4, geras. Pasinaudojus ²ia seka galima gauti sek, kurios gavimas sutampa, jei j skai iuotume kvadrato vidurio metodu. Imant X n+1 = f(x n, X n 1 ) mod m, periodo ilgis gali b uti m 2. C) X n+1 X n + X n 1 mod m Fibona i seka; nepakankamai atsitiktine; periodas ²iek tiek > m. D) X n+1 X n + X n k mod m kai k 15, seka nera pakankamai atsitiktine; kai k = 16, atrodo, viskas gerai. Periodas gali b uti > m. Kitas privalumas greitis; nera daugybos, tik sudetis. 55
56 E) X n a 1 X n a k X n k mod p tai ir tiesinio kongruentinio ir tiesinio rekurentinio metodu apibendrinimas. Didºiausias periodo ilgis p k 1. Kai k = 1, gauname jau nagrinet multiplikatyvi j kongruentin sek. Atveju p = 2, gauname jau nagrinet tiesin rekurentin sek. Konstantu a 1,..., a k parinkimas tik tuomet duoda laukiam rezultat, kai polinomas f(x) = x k a 1 x k 1... a k yra primityvusis daugianaris mod p. Yra sukurta teorija kaip konstantas a 1,..., a k atskirais atvejais parinkti, bet tai gana sudetingas reikalas. F ) Z n X n + Y n mod m gaunami geri razultatai, tik reikia, kad seku X n ir Y n periodai b utu tarpusavyje pirminiai. Galimi ir kitokie dvieju tiesiniu kongruentiniu seku X n ir Y n sumai²ymo variantai. 56
tytti solantaus dailininkė: antonia ringbom
 tytti solantaus dailininkė: antonia ringbom TURINYS į ž a n g a... k a s y r a p s i c h i k o s s v e i k at o s p r o b l e m o s?... Sutrikę jausmai Sutrikusi veikla Sutrikęs mąstymas k o d ė l ž m
tytti solantaus dailininkė: antonia ringbom TURINYS į ž a n g a... k a s y r a p s i c h i k o s s v e i k at o s p r o b l e m o s?... Sutrikę jausmai Sutrikusi veikla Sutrikęs mąstymas k o d ė l ž m
Europos Audito Rūmų etikos gairės
 ЕВРОПЕЙСКА СМЕТНА ПАЛАТА TRIBUNAL DE CUENTAS EUROPEO EVROPSKÝ ÚČETNÍ DVŮR DEN EUROPÆISKE REVISIONSRET EUROPÄISCHER RECHNUNGSHOF EUROOPA KONTROLLIKODA ΕΥΡΩΠΑΪΚΟ ΕΛΕΓΚΤΙΚΟ ΣΥΝΕΔΡΙO EUROPEAN COURT OF AUDITORS
ЕВРОПЕЙСКА СМЕТНА ПАЛАТА TRIBUNAL DE CUENTAS EUROPEO EVROPSKÝ ÚČETNÍ DVŮR DEN EUROPÆISKE REVISIONSRET EUROPÄISCHER RECHNUNGSHOF EUROOPA KONTROLLIKODA ΕΥΡΩΠΑΪΚΟ ΕΛΕΓΚΤΙΚΟ ΣΥΝΕΔΡΙO EUROPEAN COURT OF AUDITORS
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
 YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
2 Keminmaa 3 4 5 6. Haaparanta TORNIO. > 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db. Vt 4 Kemi
 LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
GYPROC SISTEMOS PERTVARŲ IŠ GYPROC/RIGIPS GIPSO KARTONO PLOKŠČIŲ IR METALINIŲ PROFILIUOČIŲ MONTAVIMO DARBAI
 GYPROC SISTEMOS PERTVARŲ IŠ GYPROC/RIGIPS GIPSO KARTONO PLOKŠČIŲ IR METALINIŲ PROFILIUOČIŲ MONTAVIMO DARBAI Kontaktai: DARBŲ APIBRĖŽIMAS GYPROC yra tarptautinio Saint-Gobain koncerno gipso gaminių padalinys.
GYPROC SISTEMOS PERTVARŲ IŠ GYPROC/RIGIPS GIPSO KARTONO PLOKŠČIŲ IR METALINIŲ PROFILIUOČIŲ MONTAVIMO DARBAI Kontaktai: DARBŲ APIBRĖŽIMAS GYPROC yra tarptautinio Saint-Gobain koncerno gipso gaminių padalinys.
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
Shorin algoritmin matematiikkaa Edvard Fagerholm
 Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
PUTKIKAKSOISNIPPA MUSTA
 Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
Suosituimmat kohdemaat
 Suosituimmat kohdemaat Maakuntanro Maakunta Kohdemaa Maakoodi sum_lah_opisk 21 Ahvenanmaa - Kreikka GR 3 Åland Italia IT 3 Turkki TR 2 Saksa DE 1 09 Etelä-Karjala Venäjä RU 328 Britannia GB 65 Ranska FR
Suosituimmat kohdemaat Maakuntanro Maakunta Kohdemaa Maakoodi sum_lah_opisk 21 Ahvenanmaa - Kreikka GR 3 Åland Italia IT 3 Turkki TR 2 Saksa DE 1 09 Etelä-Karjala Venäjä RU 328 Britannia GB 65 Ranska FR
Klientai mus vertina NORMALIAI. Ką dabar daryti?
 Klientai mus vertina NORMALIAI. Ką dabar daryti? Doc. dr. V. Dikčius Praktinis seminaras Vartotojų pasitenkinimo viešosiomis paslaugomis tyrimai. 2010 m. vasario 12 d. Vilnius Customer Satisfaction Index
Klientai mus vertina NORMALIAI. Ką dabar daryti? Doc. dr. V. Dikčius Praktinis seminaras Vartotojų pasitenkinimo viešosiomis paslaugomis tyrimai. 2010 m. vasario 12 d. Vilnius Customer Satisfaction Index
KIERTOKIRJEKOKO ELMA
 POSTI- JA LENNÄTINHALLITUKSEN KIERTOKIRJEKOKO ELMA 1976 N :o 126-130 N:o 126 postitoim ipaikkojen perustam isesta T a m m ik u u n 1 p ä iv ä s tä 1 9 7 7 perustetaan h aaraosa stot I I m a tra 1 2 Imatran
POSTI- JA LENNÄTINHALLITUKSEN KIERTOKIRJEKOKO ELMA 1976 N :o 126-130 N:o 126 postitoim ipaikkojen perustam isesta T a m m ik u u n 1 p ä iv ä s tä 1 9 7 7 perustetaan h aaraosa stot I I m a tra 1 2 Imatran
1. Kaikki kaatuu, sortuu August Forsman (Koskimies)
 olo q» date reliioso olo 7 K (2003) KE2a7 1. Kaikki kaatuu, sortuu uust Forsma (Koskimies) olo 14 olo 21 3 3 3 3 3 3 3 3 Ÿ ~~~~~~~~~~~ π K (2003) KE2a7 uhlakataatti (kuoro) - 2 - Kuula: - 3 - uhlakataatti
olo q» date reliioso olo 7 K (2003) KE2a7 1. Kaikki kaatuu, sortuu uust Forsma (Koskimies) olo 14 olo 21 3 3 3 3 3 3 3 3 Ÿ ~~~~~~~~~~~ π K (2003) KE2a7 uhlakataatti (kuoro) - 2 - Kuula: - 3 - uhlakataatti
& # # w. œ œ œ œ # œ œ œ œ œ # œ w. # w nœ. # œ œ œ œ œ # œ w œ # œ œ œ Œ. œ œ œ œ œ œ œ œ # œ w. œ # œ œ œ w œ œ w w w w. W # w
 Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
PS. Jos vastaanotit Sinulle kuulumattoman viestin, pyydän ilmoittamaan siitä viipymättä allekirjoittaneelle ja tuhoamaan viestin, kiitos.
 Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Kristuksen syntymän kalanda kreikaksi
 Krstuks syntymän klnd krekk 1 F G7 7 G7 K ln es pe Hrs tu n th Hrsts j n U r n rn, n r hn des, j n n rn gl ln de n n he, p, V, r, n ne rs n p strhn Vthem he r ks ms k p ss, ss. l, 9 7. 8. F G7 7 G7 En
Krstuks syntymän klnd krekk 1 F G7 7 G7 K ln es pe Hrs tu n th Hrsts j n U r n rn, n r hn des, j n n rn gl ln de n n he, p, V, r, n ne rs n p strhn Vthem he r ks ms k p ss, ss. l, 9 7. 8. F G7 7 G7 En
 KA RT TA A KARTT A T T KARTTA A KARTT R A K Kuuson kuunki Indeksikrtt LUONNOS 7..0..0 RU : 8 0 87 8 7: kv oottorikelkkilureitti 9 Mk 9:0 9,7 Alikulku + ysäkit kevyen liikenteen väylä 90 kevyen liikenteen
KA RT TA A KARTT A T T KARTTA A KARTT R A K Kuuson kuunki Indeksikrtt LUONNOS 7..0..0 RU : 8 0 87 8 7: kv oottorikelkkilureitti 9 Mk 9:0 9,7 Alikulku + ysäkit kevyen liikenteen väylä 90 kevyen liikenteen
S-ZSOTOOP DZDATA !SWIA 0 \ S-ISOTOOPPIDATA GTL-78 S AVZA. M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä
 M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
Sovellettava lainkohta: Kuntalaki 136.
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 39, 40, 41, 42, 44, 45, 46, 48, 49, 50, 55, 56, 59, 60 ja 62 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 39, 40, 41, 42, 44, 45, 46, 48, 49, 50, 55, 56, 59, 60 ja 62 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava
Pakkauksen sisältö: Sire e ni
 S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
METSÄN KYLVÖ JA ISTUTUS
 Suomen Metsänhoitoyhdistys Tapion Käsikirjasia N:o 15. METSÄN KYLVÖ JA ISTUTUS ESITTÄNYT ARVID BORG. TAPIO Metsänomistaja, jolla ei ole TAPIO-lehteä, on ajastaan aivan takapajulla. Jos haluat tietoja metsäsi
Suomen Metsänhoitoyhdistys Tapion Käsikirjasia N:o 15. METSÄN KYLVÖ JA ISTUTUS ESITTÄNYT ARVID BORG. TAPIO Metsänomistaja, jolla ei ole TAPIO-lehteä, on ajastaan aivan takapajulla. Jos haluat tietoja metsäsi
Forssan kaupunki Osavuosikatsaus YHDYSKUNTAPALVELUT. Arviointik r iteeri tr mittarit ja tavoitetaso ja t a v o i t e t a s o
 Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
NEN PAINOVOIMAMITTAUS N:o OU 10/7b
 I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
Lukuteorian kertausta
 Lukuteorian kertausta Jakoalgoritmi Jos a, b Z ja b 0, niin on olemassa sellaiset yksikäsitteiset kokonaisluvut q ja r, että a = qb+r, missä 0 r < b. Esimerkki 1: Jos a = 60 ja b = 11, niin 60 = 5 11 +
Lukuteorian kertausta Jakoalgoritmi Jos a, b Z ja b 0, niin on olemassa sellaiset yksikäsitteiset kokonaisluvut q ja r, että a = qb+r, missä 0 r < b. Esimerkki 1: Jos a = 60 ja b = 11, niin 60 = 5 11 +
Sovellettava lainkohta: Kuntalaki 91 (365/1995).
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 146, 147, 148, 150, 151, 152, 153, 155, 156, 160, 162, 163 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 146, 147, 148, 150, 151, 152, 153, 155, 156, 160, 162, 163 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava
Sisäpiirintiedon syntyminen
 Kai Kotiranta Sisäpiirintiedon syntyminen Kontekstuaalinen tulkinta Y liopistollinen väitöskirja, jo k a Lapin yliopiston oikeustieteiden tiedekunnan suostum uksella esitetään julkisesti tarkastettavaksi
Kai Kotiranta Sisäpiirintiedon syntyminen Kontekstuaalinen tulkinta Y liopistollinen väitöskirja, jo k a Lapin yliopiston oikeustieteiden tiedekunnan suostum uksella esitetään julkisesti tarkastettavaksi
Primitiiviset juuret: teoriaa ja sovelluksia
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Outi Sutinen Primitiiviset juuret: teoriaa ja sovelluksia Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Huhtikuu 2006 Tampereen yliopisto Matematiikan,
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Outi Sutinen Primitiiviset juuret: teoriaa ja sovelluksia Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Huhtikuu 2006 Tampereen yliopisto Matematiikan,
Arvio metsdmaan arvosta
 Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
OL3 tilannekatsaus. ATS:n Syysseminaari Helsinki 23.11.2005. Herkko Plit Ydinturvallisuuspäällikkö Teollisuuden Voima Oy TVO
 OL3 tilannekatsaus ATS:n Syysseminaari Helsinki 23..2005 Ydinturvallisuuspäällikkö Teollisuuden Voima Oy 23..2005 OL3 yleistilanne marraskuu 2005 Työt etenevät kaikilla osa-alueilla Laitostoimittajan (CFS)
OL3 tilannekatsaus ATS:n Syysseminaari Helsinki 23..2005 Ydinturvallisuuspäällikkö Teollisuuden Voima Oy 23..2005 OL3 yleistilanne marraskuu 2005 Työt etenevät kaikilla osa-alueilla Laitostoimittajan (CFS)
ääexgäl*ääääe ääg I ä*fre3 I äee iäa ää-äälgü il leääö ää; i ääs äei:ä ä+ i* äfä g u ;; + EF'Hi: 2 ä ; s i r E:;g 8ää-i iää: Ffärg',
 !P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
!P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
3 *ä;r ä:e 5ä ä{ :i. c oo) S g+;!qg *r; Er ; l[$ E ;;iä F:ä ä :E ä: a bo. =. * gäf$iery g! Eä. a is äg*!=."fl: ä; E!, \ ins:" qgg ;._ EE üg.
 t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
(1.1) Ae j = a k,j e k.
 Lineaarikuvauksen determinantti ja jälki 1. Lineaarikuvauksen matriisi. Palautetaan mieleen, mikä lineaarikuvauksen matriisi annetun kannan suhteen on. Olkoot V äärellisulotteinen vektoriavaruus, n = dim
Lineaarikuvauksen determinantti ja jälki 1. Lineaarikuvauksen matriisi. Palautetaan mieleen, mikä lineaarikuvauksen matriisi annetun kannan suhteen on. Olkoot V äärellisulotteinen vektoriavaruus, n = dim
1 Pöytäkirja Avaa haku
 D yn as t y t i et o pa l ve l u Sivu 1 / 9 Poistuminen ( Toimielimet 1 Jätelautakunta 1 Pöytäkirja 17.12.2013 Avaa haku 1 Jätelautakunta Pöytäkirja 17.12.2013 Pykälä 15 Edellinen asia 1Seuraava asia M
D yn as t y t i et o pa l ve l u Sivu 1 / 9 Poistuminen ( Toimielimet 1 Jätelautakunta 1 Pöytäkirja 17.12.2013 Avaa haku 1 Jätelautakunta Pöytäkirja 17.12.2013 Pykälä 15 Edellinen asia 1Seuraava asia M
Montavimo sistemos. Tvirtinimo sistemos. Hilti. Produktyvu. Patikima Montavimo sistemos
 Tvirtinimo sistemos Hilti. Produktyvu. Patikima. 00 0 Montavimo sistemos Tvirtinimo profilis MM-C Moderni tvirtinimo profilių sistema lengvoms ir vidutinio svorio vamzdynų sistemoms Pritaikymo sritys n
Tvirtinimo sistemos Hilti. Produktyvu. Patikima. 00 0 Montavimo sistemos Tvirtinimo profilis MM-C Moderni tvirtinimo profilių sistema lengvoms ir vidutinio svorio vamzdynų sistemoms Pritaikymo sritys n
Naantalin kaupungin äänestysaluejako
 Kaupunginhallitus 144 18.04.2017 Kaupunginvaltuusto 38 24.04.2017 Naantalin kaupungin äänestysaluejako 187/00.00.00/2016 Kaupunginhallitus 18.04.2017 144 Kaupunginlakimies Turo Järvinen: Naantalin kaupungin
Kaupunginhallitus 144 18.04.2017 Kaupunginvaltuusto 38 24.04.2017 Naantalin kaupungin äänestysaluejako 187/00.00.00/2016 Kaupunginhallitus 18.04.2017 144 Kaupunginlakimies Turo Järvinen: Naantalin kaupungin
sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639
 DLL sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639 *************************** ISO 639 *************************** () ab aa af sq am ar hy as ay az ba eu bn dz bh bi br bg my be 299 ( ) ( ) () () km ca zh
DLL sim.exe DLL DLL ISO 639 sim.exe DLL ISO 639 *************************** ISO 639 *************************** () ab aa af sq am ar hy as ay az ba eu bn dz bh bi br bg my be 299 ( ) ( ) () () km ca zh
Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5
 Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5 1. Näytä, että X t := Bt 3 3tB t on martingaali Brownin liikkeen B historian suhteen. Ratkaisuehdotus:
Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5 1. Näytä, että X t := Bt 3 3tB t on martingaali Brownin liikkeen B historian suhteen. Ratkaisuehdotus:
Tie- ja vesirakennushallitus. Kayttöosaston liikennetoimisto /kruunukart
 Tie- ja vesirakennushallitus Kayttöosaston liikennetoimisto 7552-76/kruunukart Y LEI 5EN FI FN JA AU'1A' 11N fauij - TEYKSISSÄ VUOSINA 1975-77 TAA11 Hi- N1EI' 0 \j NF Ii)j'I 1 JI j 1;'! le ts inki 21 2.
Tie- ja vesirakennushallitus Kayttöosaston liikennetoimisto 7552-76/kruunukart Y LEI 5EN FI FN JA AU'1A' 11N fauij - TEYKSISSÄ VUOSINA 1975-77 TAA11 Hi- N1EI' 0 \j NF Ii)j'I 1 JI j 1;'! le ts inki 21 2.
Kirjainkiemurat - mallisivu (c)
 Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
-lllii;i i Eiää: Iiiii:; ä;äiäeiäi
 I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
2017 Nr. 8 (2060) RUGPJŪTIS. Šiuolaikiniai konfliktai: kaip netapti antrąja Gruzija ar Ukraina? 3. Vilkai toliau juda pirmyn! 10
 2017 Nr. 8 (2060) RUGPJŪTIS Žurnalas KARYS įsteigtas Lietuvoje 1919 m. Nepriklausomybės kovų metais. Atgaivintas Jungtinėse Amerikos Valstijose 1950 m. Atkurtas Lietuvoje 1991 m. Šiame numeryje: Šiuolaikiniai
2017 Nr. 8 (2060) RUGPJŪTIS Žurnalas KARYS įsteigtas Lietuvoje 1919 m. Nepriklausomybės kovų metais. Atgaivintas Jungtinėse Amerikos Valstijose 1950 m. Atkurtas Lietuvoje 1991 m. Šiame numeryje: Šiuolaikiniai
VALITUSOSOITUS (Poikkeamisluvat 36)
 VALITUSOSOITUS (Poikkeamisluvat 36) Valitusaika Ympäristöteknisen lautakunnan lupajaoston päätökseen saa hakea muu tos ta va littamalla Pohjois-Suomen hallinto-oikeuteen kirjallisella va li tuk sel la.
VALITUSOSOITUS (Poikkeamisluvat 36) Valitusaika Ympäristöteknisen lautakunnan lupajaoston päätökseen saa hakea muu tos ta va littamalla Pohjois-Suomen hallinto-oikeuteen kirjallisella va li tuk sel la.
PIRTIS BUTE. [ Mediena suteikia jaukumo]
![PIRTIS BUTE. [ Mediena suteikia jaukumo] PIRTIS BUTE. [ Mediena suteikia jaukumo]](/thumbs/48/23878809.jpg) PIRTIS BUTE [ Mediena suteikia jaukumo] BENDROJI INFORMACIJA Prieš nutardami namuose įsirengti pirtį išsiaiškinkite, ar: garinės patalpai užteks vietos (minimalus dydis - apie 1,6x1,6 m); garinės patalpos
PIRTIS BUTE [ Mediena suteikia jaukumo] BENDROJI INFORMACIJA Prieš nutardami namuose įsirengti pirtį išsiaiškinkite, ar: garinės patalpai užteks vietos (minimalus dydis - apie 1,6x1,6 m); garinės patalpos
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Liisa Ilonen. Primitiiviset juuret
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Liisa Ilonen Primitiiviset juuret Matematiikan ja tilastotieteen laitos Matematiikka Joulukuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen laitos ILONEN,
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Liisa Ilonen Primitiiviset juuret Matematiikan ja tilastotieteen laitos Matematiikka Joulukuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen laitos ILONEN,
Maanantai Tiistai Keskiviikko Torstai Perjantai
 Työjärjestys ALS Liukko-Sipi Ari StarSoft Kurre 7.20b syksy 11.08. - 21.12.2015 Viikkotuntimäärä: 4 LIV8.1.1 Lii LIV8-9.1 Lii LIV8.1.1 LIV8-9.1 Lii 9A/B Lii LIV8-9.1 LIV8-9.1 9A/B Lii Lii Työjärjestys
Työjärjestys ALS Liukko-Sipi Ari StarSoft Kurre 7.20b syksy 11.08. - 21.12.2015 Viikkotuntimäärä: 4 LIV8.1.1 Lii LIV8-9.1 Lii LIV8.1.1 LIV8-9.1 Lii 9A/B Lii LIV8-9.1 LIV8-9.1 9A/B Lii Lii Työjärjestys
P S. Va r äi n. m m2 2. e a / puistossa säilyvät puut. korko muuttuu, kansi uusitaan SVK asv.
 TI E f as 8 5 5 pu ke lu pi ip iv - le / te AP 1 4 KI +8 8 +8 9 O le lem ht a ip ss uu a st ol oa ev aa rk ki ip met A L 31 6 L AP P LE IK S E T ei l y tu pu r u va liu m k u at m to äk i in u hl M 22
TI E f as 8 5 5 pu ke lu pi ip iv - le / te AP 1 4 KI +8 8 +8 9 O le lem ht a ip ss uu a st ol oa ev aa rk ki ip met A L 31 6 L AP P LE IK S E T ei l y tu pu r u va liu m k u at m to äk i in u hl M 22
Tampereen yliopisto Informaatiotieteiden yksikkö
 Tampereen yliopisto Informaatiotieteiden yksikkö Kevät 017 Luennot: Kerkko Luosto Muistiinpanot: Jesse Railo (013) ja Jussi Klemetti (017) 6 Kartioleikkaukset Vanhan ajan geometrian merkittävimpiä tuloksia
Tampereen yliopisto Informaatiotieteiden yksikkö Kevät 017 Luennot: Kerkko Luosto Muistiinpanot: Jesse Railo (013) ja Jussi Klemetti (017) 6 Kartioleikkaukset Vanhan ajan geometrian merkittävimpiä tuloksia
Europos Sąjungos Taryba Briuselis, 2015 m. gruodžio 21 d. (OR. en)
 Europos Sąjungos Taryba Briuselis, 2015 m. gruodžio 21 d. (OR. en) 15515/15 UD 263 DELACT 178 PRIDEDAMAS PRANEŠIMAS nuo: Europos Komisijos generalinio sekretoriaus, kurio vardu pasirašo direktorius Jordi
Europos Sąjungos Taryba Briuselis, 2015 m. gruodžio 21 d. (OR. en) 15515/15 UD 263 DELACT 178 PRIDEDAMAS PRANEŠIMAS nuo: Europos Komisijos generalinio sekretoriaus, kurio vardu pasirašo direktorius Jordi
MASKEERAUS: KOSMETOLOGIOPISKELIJAT LAURA YLITALO, KAROLIINA SIRPELÄ, MERVI SARJANOJA VALKEAKOSKEN AMMATTI- JA AIKUISOPISTO KUVAT: JYRKI LUUKKONEN
 g k W H C MASKEERAUS: KOSMETOLOGIOPISKELIJAT LAURA YLITALO, KAROLIINA SIRPELÄ, MERVI SARJANOJA VALKEAKOSKEN AMMATTI- JA AIKUISOPISTO KUVAT: JYRKI LUUKKONEN EDUNVALVONTAA ASENTEELLA www.u.f / www..f TUOTANTOVASTAAVA
g k W H C MASKEERAUS: KOSMETOLOGIOPISKELIJAT LAURA YLITALO, KAROLIINA SIRPELÄ, MERVI SARJANOJA VALKEAKOSKEN AMMATTI- JA AIKUISOPISTO KUVAT: JYRKI LUUKKONEN EDUNVALVONTAA ASENTEELLA www.u.f / www..f TUOTANTOVASTAAVA
Arvio metsd maa n a rvosta
 Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
Näkymät suhdanteissa ja rahoitusmarkkinoilla 26.5.2010 Lauri Uotila Pääekonomisti, Sampo Pankki 15.9.2008 12.10.2008
 Näkymät suhdanteissa ja rahoitusmarkkinoilla 26..21 Lauri Uotila Pääekonomisti, Sampo Pankki 1.9.28 12.1.28 16 12 Bruttokansantuotteen kasvu %,vuosikasvu neljänneksittäin Kiina 16 12 8 8 Euroalue Iso-Britannia
Näkymät suhdanteissa ja rahoitusmarkkinoilla 26..21 Lauri Uotila Pääekonomisti, Sampo Pankki 1.9.28 12.1.28 16 12 Bruttokansantuotteen kasvu %,vuosikasvu neljänneksittäin Kiina 16 12 8 8 Euroalue Iso-Britannia
AK 376 ASEMAPIIRROS 1: K100. var k 36 I I 145. ar k I I I I 18.6 VII kr ma rs 1 58 I I. ar k. ar k.
 6 0 rs tr.6 0. 6 P.. 6.0..6 EKK 6 Kotkankatu 0 Kotkankatu Kotkankatu Kotkankatu Kotkankatu. 6 6 iiker 66 0 V. 0de 0 00 V at k Porvoonkatu V V le maa K00 6 kr ma rs... ar K 6 V 6 ilm leksis Kiven katu.0
6 0 rs tr.6 0. 6 P.. 6.0..6 EKK 6 Kotkankatu 0 Kotkankatu Kotkankatu Kotkankatu Kotkankatu. 6 6 iiker 66 0 V. 0de 0 00 V at k Porvoonkatu V V le maa K00 6 kr ma rs... ar K 6 V 6 ilm leksis Kiven katu.0
N I K E A N U S K O N T U N N U S T U S
 100 H a n n u P o h a n n o r o N I K E A N U S K O N T U N N U S T U S lauluäänelle, kitaralle sekä viola da gamballe tai sellolle or voices, guitar, viola da gamba / violoncello - ' 00 Teosto Suomalaisen
100 H a n n u P o h a n n o r o N I K E A N U S K O N T U N N U S T U S lauluäänelle, kitaralle sekä viola da gamballe tai sellolle or voices, guitar, viola da gamba / violoncello - ' 00 Teosto Suomalaisen
Ei asemakaavaa. E3 Söörmarkun eritasoliittymä
 X= Värn slyks Suunnllu : Y = Tään suunnlan ukaan Y = raknnaa a parannaa X= Mudn suunnln ukaan raknnaa E asakaaaa Tdn hallnnllsssa järjslyssä apahdu uusa Y E Söörarkun raslyä Y Y M a s a Va Y P r R R Va
X= Värn slyks Suunnllu : Y = Tään suunnlan ukaan Y = raknnaa a parannaa X= Mudn suunnln ukaan raknnaa E asakaaaa Tdn hallnnllsssa järjslyssä apahdu uusa Y E Söörarkun raslyä Y Y M a s a Va Y P r R R Va
Fermat n pieni lause. Heikki Pitkänen. Matematiikan kandidaatintutkielma
 Fermat n pieni lause Heikki Pitkänen Matematiikan kandidaatintutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2009 Sisältö Johdanto 3 1. Fermat n pieni lause 3 2. Pseudoalkuluvut
Fermat n pieni lause Heikki Pitkänen Matematiikan kandidaatintutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2009 Sisältö Johdanto 3 1. Fermat n pieni lause 3 2. Pseudoalkuluvut
Mat Dynaaminen optimointi, mallivastaukset, kierros Johdetaan ensiksi välttämättömät ehdot diskreettiaikaiselle optimisäätötehtävälle.
 Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 9 1. Johdetaan ensiksi välttämättömät ehdot diskreettiaikaiselle optimisäätötehtävälle. Tilayhtälö on x k+1 = f k (x k, u k ), k = 1,..., N 1 alkuehdolla
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 9 1. Johdetaan ensiksi välttämättömät ehdot diskreettiaikaiselle optimisäätötehtävälle. Tilayhtälö on x k+1 = f k (x k, u k ), k = 1,..., N 1 alkuehdolla
Määräys STUK SY/1/ (34)
 Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
1, MITÄ TARKOITETAAN SEURAAVILLA TERMEILLÄ:
 KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
Pöytäkirjan 1, 2, 3, 6, 7 ja 8 :t. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 1, 2, 3, 6, 7 ja 8 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 1, 2, 3, 6, 7 ja 8 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
Sotela 158 Valmistelija: talouspäällikkö Paavo Posti, puh. 03-849 4215, etunimi.sukunimi@heinola.fi
 Sosiaali- ja terveyslautakunta 158 17.11.2015 Kaupunginhallitus 315 07.12.2015 Etevan kuntayhtymän perussopimuksen muutokset 1764/00.04.01/2012 Sotela 158 Valmistelija: talouspäällikkö Paavo Posti, puh.
Sosiaali- ja terveyslautakunta 158 17.11.2015 Kaupunginhallitus 315 07.12.2015 Etevan kuntayhtymän perussopimuksen muutokset 1764/00.04.01/2012 Sotela 158 Valmistelija: talouspäällikkö Paavo Posti, puh.
2. TUTUSTUN KIRKKOONI
 2. TUTUSTUN KIRKKOONI Ikonit kuuluvat ortodoksiseen kirkkoon ja kotiin 1. Laita rasti niiden kuvien viereen, joihin sinusta ikoni voisi kuulua. Väritä kuvat. 2. Kirjoita kir-jain-kor-teil-la-si sana IKONI.
2. TUTUSTUN KIRKKOONI Ikonit kuuluvat ortodoksiseen kirkkoon ja kotiin 1. Laita rasti niiden kuvien viereen, joihin sinusta ikoni voisi kuulua. Väritä kuvat. 2. Kirjoita kir-jain-kor-teil-la-si sana IKONI.
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
Sovellettava lainkohta: Kuntalaki 136.
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO :t 39, 40, 41, 43, 44, 45, 47, 48, 49 Valmistelua ja täytäntöönpanoa koskevaan päätöksen ei saa hakea muutos ta. Sovellettava lainkohta: Kuntalaki 136. OIKAISUVAATIMUSOHJE
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO :t 39, 40, 41, 43, 44, 45, 47, 48, 49 Valmistelua ja täytäntöönpanoa koskevaan päätöksen ei saa hakea muutos ta. Sovellettava lainkohta: Kuntalaki 136. OIKAISUVAATIMUSOHJE
KAIDE KAIDE LUMON HYÖKKÄYSTIE PALOKUNNAN PPP LUMON AUKKO SP KUNTOILUTILA LUMON KATON RAJASSA AUKKO MONITOIMITILA LUMON PPP KATON RAJASSA AUKKO
 5 5 685 5 8 6 33 585 MUITI 95 OU RAUTO OY 585 77 4 3 4 98 85 345 5 6 4 4 6 4 6 6 6 4 IVL-/45 4 757 4 757 95 585 4 476 3 39 IVL-/45 IVL-/45 IVL-/45 IVL-/45 68 4 643 769 55 8 84 96 8 79 8 käyntiovi uunnittelutoimiston
5 5 685 5 8 6 33 585 MUITI 95 OU RAUTO OY 585 77 4 3 4 98 85 345 5 6 4 4 6 4 6 6 6 4 IVL-/45 4 757 4 757 95 585 4 476 3 39 IVL-/45 IVL-/45 IVL-/45 IVL-/45 68 4 643 769 55 8 84 96 8 79 8 käyntiovi uunnittelutoimiston
Ko onnut. pianon my ö tstilyks eli e A - A - B O K J E N X T J S. S S A v II. E. /Johnin kus/mumksella. s o li / 11 a n // / o M M S I!
 \ o - i ^ / S s s / S i s i Ko onnut A - A - B O K J E N X T J S pianon my ö tstilyks eli e s o li / 11 a n // / o M M S I! M i v i h k o S S A v. 1880. II. E. /Johnin kus/mumksella. m i 11 Lev. 2 81 Lji.
\ o - i ^ / S s s / S i s i Ko onnut A - A - B O K J E N X T J S pianon my ö tstilyks eli e s o li / 11 a n // / o M M S I! M i v i h k o S S A v. 1880. II. E. /Johnin kus/mumksella. m i 11 Lev. 2 81 Lji.
Rekisteriseloste. 1. Rekisterinpitäjä. 3. Rekisterin nimi
 Rekisteriseloste 1. Rekisterinpitäjä N im i: Res p o ndeo Oy Y -t u nnus : 2 6 2 2 6 8 4-1 O s oit e: Ität u ulenkuja 11, 02100 E s p oo 2. Yhteyshenkilö rekisteriä koskevissa asioissa E lisa Tiilimäki
Rekisteriseloste 1. Rekisterinpitäjä N im i: Res p o ndeo Oy Y -t u nnus : 2 6 2 2 6 8 4-1 O s oit e: Ität u ulenkuja 11, 02100 E s p oo 2. Yhteyshenkilö rekisteriä koskevissa asioissa E lisa Tiilimäki
Käyttövedenlämmitin. KÄYTTÖVEDENLÄMMITIN HAATO HK-15 1/3KW SEINÄ/VAAKA LVI-numero PIKA OD38
 Käyttövedenlämmitin HK-15 1/3KW SEINÄ/VAAKA 5253010 OD38 HK-35 2KW SEINÄ/VAAKA 5253015 RS52 HK-55 2KW SEINÄ/VAAKA 5253020 DE35 HK-100 2KW SEINÄ/VAAKA 5253022 VL77 HM-150 2/3KW SAUNA 5253045 UH93 HM-230
Käyttövedenlämmitin HK-15 1/3KW SEINÄ/VAAKA 5253010 OD38 HK-35 2KW SEINÄ/VAAKA 5253015 RS52 HK-55 2KW SEINÄ/VAAKA 5253020 DE35 HK-100 2KW SEINÄ/VAAKA 5253022 VL77 HM-150 2/3KW SAUNA 5253045 UH93 HM-230
Osittaisdifferentiaaliyhtälöt
 Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
1 tema. Intelektin s nuosavyb s samprata
 1 tema Intelektin s nuosavyb s samprata Intelektin s nuosavyb s samprata (1) Intelektin s nuosavyb s rezultatai ir teis s į juos civilin s teis s objektai (CK 1.111-1.112 str.) Intelektin s nuosavyb s
1 tema Intelektin s nuosavyb s samprata Intelektin s nuosavyb s samprata (1) Intelektin s nuosavyb s rezultatai ir teis s į juos civilin s teis s objektai (CK 1.111-1.112 str.) Intelektin s nuosavyb s
HP Color LaserJet CP1510 serija Spausdintuvas Vartotojo vadovas
 HP Color LaserJet CP1510 serija Spausdintuvas Vartotojo vadovas Autorių teisės ir licencija 2007 Copyright Hewlett-Packard Development Company, L.P. Atkurti, pritaikyti ar versti produkto dokumentaciją
HP Color LaserJet CP1510 serija Spausdintuvas Vartotojo vadovas Autorių teisės ir licencija 2007 Copyright Hewlett-Packard Development Company, L.P. Atkurti, pritaikyti ar versti produkto dokumentaciją
1.1. Määritelmiä ja nimityksiä
 1.1. Määritelmiä ja nimityksiä Luku joko reaali- tai kompleksiluku. R = {reaaliluvut}, C = {kompleksiluvut} R n = {(x 1, x 2,..., x n ) x 1, x 2,..., x n R} C n = {(x 1, x 2,..., x n ) x 1, x 2,..., x
1.1. Määritelmiä ja nimityksiä Luku joko reaali- tai kompleksiluku. R = {reaaliluvut}, C = {kompleksiluvut} R n = {(x 1, x 2,..., x n ) x 1, x 2,..., x n R} C n = {(x 1, x 2,..., x n ) x 1, x 2,..., x
IAN FI LT IAN RACLETTE GRILL SRG 1200 B2 RACLETTE-GRILL RACLETTEGRILL RAKLETO KEPTUVAS RACLETTE-GRILLI FI SE LT DE. Bedienungsanleitung
 RACLETTE GRILL SRG 1200 B2 HOYER Handel GmbH Tasköprüstraße 3 DE-22761 Hamburg DEUTSCHLAND FI RACLETTE-GRILLI Käyttöohje SE RACLETTEGRILL Bruksanvisning Tiedot päivitetty Informationsstatus Informacijos
RACLETTE GRILL SRG 1200 B2 HOYER Handel GmbH Tasköprüstraße 3 DE-22761 Hamburg DEUTSCHLAND FI RACLETTE-GRILLI Käyttöohje SE RACLETTEGRILL Bruksanvisning Tiedot päivitetty Informationsstatus Informacijos
17 Jm. Pe/so. Pe/so. Pe/so. Pe/so. Pe/so. Pe/so Pe/so. Pe/so. Hattulan kunta 32. Pe/ao Johtoaukea, uusi. Reunavyöhyke, uusi
 ga sa la -H ik iä k V( FG ) SI/ J --- MÄKELÄ SI/J --- --- --- --- --- --- silta --- SUPPA --- KUTTILA --- KAURANEN / I --- Hattulan kunta Suunniteltu keskilinja kv VANAJA - TIKINMAA kv Purettava kv keskilinja
ga sa la -H ik iä k V( FG ) SI/ J --- MÄKELÄ SI/J --- --- --- --- --- --- silta --- SUPPA --- KUTTILA --- KAURANEN / I --- Hattulan kunta Suunniteltu keskilinja kv VANAJA - TIKINMAA kv Purettava kv keskilinja
Pöytäkirjan 32, 33, 36, 40 ja 43 :t. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 32, 33, 36, 40 ja 43 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 32, 33, 36, 40 ja 43 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muu tos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
Usko, toivo ja rakkaus
 Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census
 Suomen virallinen tilasto Finlands officiella Statistik Official Statistics of Finland VI C:106 Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census 1980 Osa XV Del XV Volume
Suomen virallinen tilasto Finlands officiella Statistik Official Statistics of Finland VI C:106 Väestö- ja asuntolaskenta Folk- och bostadsräkningen Population and Housing Census 1980 Osa XV Del XV Volume
LEIVOTAAN YHDESSÄ. Kuvat: Jutta Valtonen
 LEIVOTAAN YHDESSÄ Susanna Koistinen Miia Laho Kuvat: Jutta Valtonen SI-SÄL-LYS E-SI-VAL-MIS-TE-LUT... 2 PE-RUS-RE-SEP-TIT KAU-RA-KEK-SIT... 5 SUK-LAA-KEK-SIT... 7 MAR-JA-PII-RAK-KA... 9 MUF-FIN-IT...
LEIVOTAAN YHDESSÄ Susanna Koistinen Miia Laho Kuvat: Jutta Valtonen SI-SÄL-LYS E-SI-VAL-MIS-TE-LUT... 2 PE-RUS-RE-SEP-TIT KAU-RA-KEK-SIT... 5 SUK-LAA-KEK-SIT... 7 MAR-JA-PII-RAK-KA... 9 MUF-FIN-IT...
Jakotukit / tarvikkeet
 Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
Matriisiteoria Harjoitus 1, kevät Olkoon. cos α sin α A(α) = . sin α cos α. Osoita, että A(α + β) = A(α)A(β). Mikä matriisi A(α)A( α) on?
 Harjoitus 1, kevät 007 1. Olkoon [ ] cos α sin α A(α) =. sin α cos α Osoita, että A(α + β) = A(α)A(β). Mikä matriisi A(α)A( α) on?. Olkoon a x y A = 0 b z, 0 0 c missä a, b, c 0. Määrää käänteismatriisi
Harjoitus 1, kevät 007 1. Olkoon [ ] cos α sin α A(α) =. sin α cos α Osoita, että A(α + β) = A(α)A(β). Mikä matriisi A(α)A( α) on?. Olkoon a x y A = 0 b z, 0 0 c missä a, b, c 0. Määrää käänteismatriisi
problem computational non computational problem problem unsolvable solvable problem problem efficient solution partially solvable
 ? BA F S R ] ] UbM R H ] ] ] d ] ] M S R H 678 G ED B A> UKV ST NOKPQ K IJKLM H \ US ST NOKPQ K IJKLM h US bje bokpq T UKV ST NOKPQ K IJKLM d i mn op k v qr kst { i 0 i i i probem ompttion probem non
? BA F S R ] ] UbM R H ] ] ] d ] ] M S R H 678 G ED B A> UKV ST NOKPQ K IJKLM H \ US ST NOKPQ K IJKLM h US bje bokpq T UKV ST NOKPQ K IJKLM d i mn op k v qr kst { i 0 i i i probem ompttion probem non
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
Pöytäkirjan 1, 2, 3, 6, 8, 10, 13, 14 :t. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 1, 2, 3, 6, 8, 10, 13, 14 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muutos Sovellettava lainkohta: Kuntalaki 91 (365/1995).
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 1, 2, 3, 6, 8, 10, 13, 14 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muutos Sovellettava lainkohta: Kuntalaki 91 (365/1995).
Kęstutis PUKELIS LEARNING/STUDY MOKYMOSI/STUDIJŲ THEORETICAL DIMENSION SANTRAUKA
 12 MOKYMOSI/STUDIJŲ LEARNING/STUDY THEORETICAL DIMENSION SANTRAUKA Šiame straipsnyje aptariami vieningos Europos aukštojo mokslo (Bolonijos deklaracija, 1999) ir Europos profesinio mokymo bei rengimo (Kopenhagos
12 MOKYMOSI/STUDIJŲ LEARNING/STUDY THEORETICAL DIMENSION SANTRAUKA Šiame straipsnyje aptariami vieningos Europos aukštojo mokslo (Bolonijos deklaracija, 1999) ir Europos profesinio mokymo bei rengimo (Kopenhagos
HILBERTIN AVARUUDET 802652S MIKAEL LINDSTRÖM KEVÄÄN 2010 ANALYYSI 3 -LUENTOJEN PERUSTEELLA TOIMITTANEET TOMI ALASTE JA LAURI BERKOVITS
 HILBRTIN AVARUUDT 802652S MIKAL LINDSTRÖM KVÄÄN 2010 ANALYYSI 3 -LUNTOJN PRUSTLLA TOIMITTANT TOMI ALAST JA LAURI BRKOVITS Sisältö 1 Hilbertin Avaruudet 3 1.1 Normi- ja L p -avaruudet........................
HILBRTIN AVARUUDT 802652S MIKAL LINDSTRÖM KVÄÄN 2010 ANALYYSI 3 -LUNTOJN PRUSTLLA TOIMITTANT TOMI ALAST JA LAURI BRKOVITS Sisältö 1 Hilbertin Avaruudet 3 1.1 Normi- ja L p -avaruudet........................
DECLARATION OF PERFORMANCE
 EN DECLARATION OF PERFORMANCE According to Construction Product Regulation (EU) No 305/2011 (CPR) DoP No. 1109 CPR 0014 EN 1. Unique identification code of the product type: Sormat Chemical Capsule KEM
EN DECLARATION OF PERFORMANCE According to Construction Product Regulation (EU) No 305/2011 (CPR) DoP No. 1109 CPR 0014 EN 1. Unique identification code of the product type: Sormat Chemical Capsule KEM
4 AVililco. c- 1c o o i i n ix t. vonf. S g h a n ^t z. moni - ääni siksi "" s avittanut ( Toin en p a i n o s. HELSINGISSÄ,
 jy t / 5r/ 4 AVililco c- 1c o o i i n ix t vonf. S g h a n ^t z M a n a i a n u k a * s o i a ia a l i e moni - ääni siksi "" s avittanut ( Toin en p a i n o s. HELSINGISSÄ, 1871. G.W.Edlundin k u stan
jy t / 5r/ 4 AVililco c- 1c o o i i n ix t vonf. S g h a n ^t z M a n a i a n u k a * s o i a ia a l i e moni - ääni siksi "" s avittanut ( Toin en p a i n o s. HELSINGISSÄ, 1871. G.W.Edlundin k u stan
Ennakkotehtävän ratkaisu
 Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
TEHTÄVÄKORI Monisteita matikkaan. Riikka Mononen
 ---------------------------------------- TEHTÄVÄKORI Monisteita matikkaan Riikka Mononen ---------------------------------------- Tehtäväkori 2016 TEHTÄVÄKORI Monisteita matikkaan -materiaali on kokoelma
---------------------------------------- TEHTÄVÄKORI Monisteita matikkaan Riikka Mononen ---------------------------------------- Tehtäväkori 2016 TEHTÄVÄKORI Monisteita matikkaan -materiaali on kokoelma
Multiplikatiivisista funktioista
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Marita Riihiranta Multiplikatiivisista funktioista Matematiikan ja tilastotieteen laitos Matematiikka Toukokuu 2008 Tampereen yliopisto Matematiikan ja tilastotieteen
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Marita Riihiranta Multiplikatiivisista funktioista Matematiikan ja tilastotieteen laitos Matematiikka Toukokuu 2008 Tampereen yliopisto Matematiikan ja tilastotieteen
NIKKILÄN SYDÄMEN LAAJENTAMINEN VAIHE 2 MAANTASOKERROS 1/ / ARK - house
 tk, J e, hu p rr, Ä, 9,,, Ä Ä Ä 9,, 9 h vut tk k D uk, C lut, kpk C tr, rv tr C9, y e yv tt t rv lkr tl lut e pll t-k-hu kek u v pt + C C tr C9 tr lut C, C C, yp + phu te kt kpl bet uur rv gr ttpe t +
tk, J e, hu p rr, Ä, 9,,, Ä Ä Ä 9,, 9 h vut tk k D uk, C lut, kpk C tr, rv tr C9, y e yv tt t rv lkr tl lut e pll t-k-hu kek u v pt + C C tr C9 tr lut C, C C, yp + phu te kt kpl bet uur rv gr ttpe t +
SAMMONKATU SAMMONKATU JAAKON- SARVI- KATU SARVIJAAKONKATU 1: Kalevanrinteen katujen yleissuunnitelma, Liite 3 Asemapiirros 1/4
 KTOS L:\PROJEKTT_2012\1510001046 KLEVRTEE KTUJE YS\14_TULOKSET\3.KTUJE YLESSUUTELM\DWG\KLEVRE YS.DWG Tulostettu: 26.6.2013 n- JO KELLR- SR- JKO- KTU SMMOKTU PYSÄKÖT KORTTEL 4 +100,60 KSPHT 1/2 BUS (varaus)
KTOS L:\PROJEKTT_2012\1510001046 KLEVRTEE KTUJE YS\14_TULOKSET\3.KTUJE YLESSUUTELM\DWG\KLEVRE YS.DWG Tulostettu: 26.6.2013 n- JO KELLR- SR- JKO- KTU SMMOKTU PYSÄKÖT KORTTEL 4 +100,60 KSPHT 1/2 BUS (varaus)
Composition of binary quadratic forms Lause. On voimassa (a) ab 0 a 0 b (bb 0 + Dnn 0 )= 0 mod μ: (b) Jos m = m 0 =1, niin aa 0 0 mod μ : Todistus. Ko
 ARNDT.TEX Composition of binary quadratic forms by Veikko Ennola Tarkastellaan neliömuotojen kompositiota F. Arndtin esittämässä muodossa ([Ar59] ja [Ma61], p. 149 157) mutatis mutandis. Oletetaan, että
ARNDT.TEX Composition of binary quadratic forms by Veikko Ennola Tarkastellaan neliömuotojen kompositiota F. Arndtin esittämässä muodossa ([Ar59] ja [Ma61], p. 149 157) mutatis mutandis. Oletetaan, että
Pöytäkirjan 51-53, 58, :t. Sovellettava lainkohta: Kuntalaki 91 (365/1995).
 MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 51-53, 58, 60-64 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muutos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995). OIKAISUVAATIMUSOHJE
MUUTOKSENHAKUOHJEET MUUTOKSENHAKUKIELTO Pöytäkirjan 51-53, 58, 60-64 :t. Valmistelua ja täytäntöönpanoa koskevaan päätökseen ei saa hakea muutos ta. Sovellettava lainkohta: Kuntalaki 91 (365/1995). OIKAISUVAATIMUSOHJE
LUKUTEORIA A. Harjoitustehtäviä, kevät 2013. (c) Osoita, että jos. niin. a c ja b c ja a b, niin. niin. (e) Osoita, että
 LUKUTEORIA A Harjoitustehtäviä, kevät 2013 1. Olkoot a, b, c Z, p P ja k, n Z +. (a) Osoita, että jos niin Osoita, että jos niin (c) Osoita, että jos niin (d) Osoita, että (e) Osoita, että a bc ja a c,
LUKUTEORIA A Harjoitustehtäviä, kevät 2013 1. Olkoot a, b, c Z, p P ja k, n Z +. (a) Osoita, että jos niin Osoita, että jos niin (c) Osoita, että jos niin (d) Osoita, että (e) Osoita, että a bc ja a c,
Kattoläpiviennit KATTOLÄPIVIENTISARJA VILPE. Tuote LVI-numero Pikakoodi SOLAR TIILI MUSTA TM85 SOLAR TIILI RUSKEA AD58
 Kattoläpiviennit Tuote LVI-numero Pikakoodi 5289200 WF99 SOLAR TIILI MUSTA 75602 SOLAR TIILI RUSKEA 75604 SOLAR TIILI HARMAA 75607 SOLAR TIILI TIILENPUN. 75609 SOLAR PELTIMUSTA 75612 SOLAR CLASSIC MUSTA
Kattoläpiviennit Tuote LVI-numero Pikakoodi 5289200 WF99 SOLAR TIILI MUSTA 75602 SOLAR TIILI RUSKEA 75604 SOLAR TIILI HARMAA 75607 SOLAR TIILI TIILENPUN. 75609 SOLAR PELTIMUSTA 75612 SOLAR CLASSIC MUSTA
V a a liv o itto. H a a s ta tte lu Suomen S o sia lid e m o k ra a tissa 18/
 V a a liv o itto. H a a s ta tte lu Suomen S o sia lid e m o k ra a tissa 18/7 1933. PUOLUE Et'. MI VAALIVOITTO YLITTI ROHKEE i MATKIN ODOTUKSET. Jos v a a lit o l i s i to im ite ttu vuosi s i t t e n,
V a a liv o itto. H a a s ta tte lu Suomen S o sia lid e m o k ra a tissa 18/7 1933. PUOLUE Et'. MI VAALIVOITTO YLITTI ROHKEE i MATKIN ODOTUKSET. Jos v a a lit o l i s i to im ite ttu vuosi s i t t e n,
RIIHIMÄEN MELUSELVITYS 2008
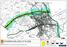 S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh
S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh

