K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraalit
|
|
|
- Eeva-Kaarina Halonen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraalit Pro gradu-tutkielma, Tekijä: Antti Kasslin Ohjaaja: Jouni Suhonen
2 2
3 3 Tiivistelmä Kasslin, Antti K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraalit Pro Gradu-tutkielma Fysiikan laitos, Jyväskylän yliopisto, 217, 53 sivua Tässä tutkimuksessa perehdytään K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraaleihin. K-kertaisesti kielletyt uniikit β-siirtymät ovat β-hajoamisten alaryhmä, ja faasiavaruusintegraalit kuvaavat hajoamisreaktion jälkeisiä lopputiloja ja antavat muun muassa tärkeää tietoa siirtymän hajoamisvakiosta. Tutkimuksessa laskettiin numeerisesti faasiavaruusintegraalit useille tunnetuille β-siirtymille, jotka voivat olla kaksi- tai useampikertaisesti kiellettyjä. Saatua laskentadataa analysoitiin eri näkökulmista. Tärkein näkökulma on kielletyn uniikin β-siirtymän ja samaa β-hajoamista kuvaavan perus- eli sallitun siirtymän välinen suhde, koska tämä näkökulma antaa parhaiten tietoa K:n vaikutuksesta faasiavaruusintegraaliin. Tulokset viittaavat siihen, että siirtymillä, joiden hajoamisenergia on pieni, sallitut ovat dominoivia. Mutta hajoamisenergiaa kasvatettaessa kiellettyjen siirtymien faasiavaruusintegraalit kasvavat suuremmiksi, ja sitä voimakkaammin, mitä suurempi K on. Seuraavaksi tarkasteltiin kielletyn siirtymän faasiavaruusintegraalin suhdetta siirtymän hajoamisenergiaan, mikä antaa tietoa lopputilojen keskimääräisestä lukumäärästä. Nämä tulokset olivat hyvin samankaltaisia kuin edellisessä näkökulmassa. Hajoamisenergian kasvaessa suhdelukukin kasvaa, ja kasvu on sitä nopeampaa, mitä suurempi K on. Kolmas näkökulma oli vertailla β + -siirtymien ja elektronisieppausten faasiavaruusintegraalien välisiä suhteita. Koska nämä kaksi β-siirtymän lajia voivat tapahtua yhtäaikaa, niiden faasiavaruusintegraalit lasketaan aina yhteen. Aikaisemmin on tiedetty, että hajoamisenergia ja atomin järjestysluku vaikuttavat näiden kahden lajin väliseen suhteeseen. Tämän tutkimuksen perusteella kuitenkin myös kiellettyyden asteella näyttäisi olevan vaikutusta. Korkeampi K vaikuttaisi suosivan elektronisieppauksia. Lopuksi vertailtiin faasiavaruusintegraaleja, joissa on otettu huomioon ytimen elektronipilven aiheuttama varjostus niihin faasiavaruusintegraaleihin, joissa sitä ei ole huomioitu. Tulokset eivät eronneet toisistaan merkittävästi, eikä kiellettyyden aste näyttäisi vaikuttavan niihin mitenkään. Avainsanat: β-hajoaminen, siirtymä, kiellettyys, uniikki, tilatiheys
4 4
5 5 Abstract Kasslin, Antti Phase space integrals of the K th forbidden unique β-translations Pro Gradu thesis Department of Physics, University of Jyväskylä, 217, 53 pages. A topic of this thesis was phase space integrals of K th forbidden unique β-transitions. K th forbidden unique β-transitions are a subgroup of the β-decays and phase space integrals depict the final states after a decay and for example give important knowledge about a decay constant of a transition. The phase space integrals for many known β-decays having a two or more times forbidden unique transition was calculated numerically in this thesis. The calculation data was then analyzed through various ways. The most important point of view is a ratio of the phase space integrals between a forbidden transition and an allowed transition of the same decay. That ratio gives most information about how the degree of K affects the phase space integral. According to the results in the transitions with small decay energy the allowed ones were dominating. But when the energy grows the phase space integrals of the forbidden transitions become larger and the increase is the faster the bigger the K is. The next point of view is the ratio between the phase space integral of the forbidden β-decay and the decay energy which gives information about the average number of the final states in transition. These results were similar to the previous point of view. When the decay energy increases the ratio increases too and the bigger is K the faster is the increasing. The third point of view was to compare the ratio between the phase space integrals of β + -decays and electron captures. Because these two types of β-decays can occur simultaneously theirs phase space integrals always sum up. It s already known that decay energy and the atomic number of the nuclear influence the ratio between these two types. According to this thesis, however, also the degree of the forbiddenness seems to have an influence. Higher degree of K seems to prefer electron captures. Finally phase space integrals without taking into account the screening effect of the electron cloud was compared to those with taking into account. The results didn t have a significant difference nor the degree of K would seem to have any influence to that. Keywords: β-decay, transition, forbiddenness, unique, state density
6 6
7 7 Sisältö Tiivistelmä 3 Abstract 5 1 Johdanto 9 2 Teoreettinen tausta β-siirtymät β-hajoaminen Sallitut ja kielletyt siirtymät Uniikit siirtymät Faasiavaruusintegraalit Fermin kultainen sääntö Liikemääräavaruus Muotofunktiot Thomas-Fermi-varjostus Menetelmät ja aineisto Numeerinen laskenta Analysoitavat siirtymät Tulokset Kiellettyjen ja sallittujen siirtymien väliset suhteet Tilatiheyksien keskiarvo β + :n ja EC:n väliset osuudet Varjostus-efekti Päätäntö 35 Lähteet 37 A K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraalit 39 B Sallittujen β-siirtymien faasiavaruusintegraalit 45 C Korjauskertoimet varjostus-arvoille 51
8 8
9 9 1 Johdanto n atomin ytimessä tapahtuu nukleonin vaihdoksia, eli protoni muuttuu neutroniksi tai toisinpäin, ja ytimen massaluku ei muutu, ydin käy läpi β-siirtymän. Samalla ytimestä vapautuu leptoneja. Vapautuvien leptonien liikemäärällä voi olla lukemattomia eri vaihtoehtoja, eli tiloja faasiavaruudessa. Näiden tilojen yhteinen summa antaa ominaisuuden, jota kutsutaan faasiavaruusintegraaliksi. Yhdessä siirtymän todennäköisyyden kanssa se on määräävä tekijä siirtymän hajoamisvakiossa. n leptonit vievät ratapyörimismäärää mukanaan ytimestä, puhutaan kielletystä β-siirtymästä, joka ei sananmukaisesti tarkoita että siirtymä olisi kielletty, vaan epätodennäköisempi kuin vastaava siirtymä, jossa ratapyörimismäärää ei siirry leptoneille eli sallittu siirtymä. Ytimen pyörimismäärän muutos on kvantittunut suure. Toisin sanoen se voi tapahtua vain asteittain, jolloin asteluku K = 1, 2, 3,... kertoo, kuinka monesti kielletty β-siirtymä on. Mitä suurempi K on, sitä vähemmän todennäköinen siirtymä on. Faasiavaruusintegraalien laskeminen on monimutkaisempaa kielletyille siirtymille. Yksinkertaisuuden vuoksi tässä tutkielmassa keskitytään kiellettyjen β-siirtymien alaryhmään, uniikkeihin β-siirtymiin, joilla pyörimismäärän muutos on K:sta riippuen suurin mahdollinen ja myös helpoimmin määritettävä. Uniikkien β-siirtymien faasiavaruusintegraaleja ei ole ennen tutkittu systemaattisesti siirtymillä, joiden kiellettyyden aste on suurempi kuin 1. Tutkielmassa keskitytäänkin eritoten siihen, kuinka kiellettyyden aste vaikuttaa faasiavaruusintegraaleihin. Tutkimusmateriaalia varten faasiavaruusintegraalit on laskettu numeerisesti. Tutkielmassa syvennytään muun muassa siihen, miten uniikin kielletyn β-siirtymän faasiavaruusintegraali käyttäytyy suhteessa vastaavaan sallitun siirtymän faasiavaruusintegraaliin ja hajoamisenergiaan.
10
11 11 2 Teoreettinen tausta 2.1 β-siirtymät β-hajoaminen Puhuttaessa β-hajoamisista tarkoitetaan kaikkia ydinreaktioita, joihin liittyy heikko vuorovaikutus. Kyseinen vuorovaikutus mahdollistaa alkeishiukkasen muuttumisen toiseksi. β-hajoamisten tapauksessa tämä tarkoittaa sitä, että heikon vuorovaikutuksen takia ylös-kvarkki muuttuu alas-kvarkiksi poistaen W + -mittabosonin, joka heti hajoaa leptoniluvun säilyttäen positroniksi ja elektronin neutriinoksi tai päinvastoin, eli alas-kvarkki muuttuu ylös-kvarkiksi, jolloin vapautuva W -mittabosoni hajoaa elektroniksi ja elektronin antineutriinoksi. On myös mahdollista, että ylöskvarkin ja elektronin vaihtaessa keskenään mittabosonin, reaktiotuotteena syntyy alas-kvarkki ja neutriino. Kvarkit ovat aina sidottuja nukleoneihin, joten protoniin sidotun alas-kvarkin muuttuminen ylös-kvarkiksi muuttaa neutronin protoniksi ja alas-kvarkin muuttuessa ylös-kvarkiksi taas päinvastoin. β-hajoamisia kirjoitettaessa jätetään usein pois välivaihe, joka sisältää mittabosonin. Näin ollen kaikki mahdolliset β-hajoamiset voidaan kirjoittaa seuraavasti: p n + e + + ν (1) n p + e + ν (2) p + e n + ν. (3) Reaktioita 1 ja 2 kutsutaan lopputilan leptonin sähkövarauksen mukaan β + - ja β - hajoamisiksi. Reaktiossa 3 atomin ytimeen sidottu protoni nappaa elektronin atomin elektronipilvestä, mistä syystä tätä reaktiota kutsutaan elektronisieppaukseksi (engl. electron capture, EC). β-hajoamisten hajoamisenergiat,q, lasketaan samalla tavalla, kuin muissakin ydinreaktioissa: alku- ja lopputilojen hiukkasten välinen massaero kerrottuna valonnopeuden neliöllä [1], eli Q = (m i m f )c 2. (4) Näitä massaeroja ei kuitenkaan yleensä lasketa reaktioista 1, 2 ja 3, sillä ne kuvaavat vapaita hiukkasia. Nukleonit ovat lähes aina sidottuja atomeihin, ja siksi
12 12 β-hajoamisia kuvataankin yleensä seuraavasti: X(Z, N) X(Z 1, N + 1) + e + + ν (5) X(Z, N) X(Z + 1, N 1) + e + ν (6) X(Z, N) + e X(Z 1, N + 1) + ν, (7) missä X kuvaa atomien ydintä sekä Z ja N järjestys- että neutronilukuja. Sidonnaisuus ytimiin mahdollistaa myös β + - ja EC-hajoamiset, koska vapaiden hiukkasten tapauksissa Q olisi tällöin negatiivinen, eivätkä reaktiot olisi näin ollen spontaaneja [1]. Jos siis lasketaan hajoamisenergiat reaktioista 5 ja 7 siten, että m X on emoytimen ja m X on tytärytimen massa sekä E = (m X m X )c 2 niin yhtälön 4 mukaan Q β + = (m X (m X + m e + m }{{} ν ))c 2 = E m e c 2, ν Q β = (m X (m X + m e + m }{{} ν ))c 2 = E m e c 2 ν Q EC = ((m X + m e ) (m X + m }{{} ν ))c 2 = E + m e c 2. ν β + -hajoamisessa ja elektronisieppauksessa ytimen alku- ja lopputilat ovat identtiset. Näin ollen E on sama molemmissa reaktioissa. Tällöin Q EC Q β + = (E + m e c 2 ) (E m e c 2 ) = 2m e c 2 Q EC = Q β + + 2m e c 2, joten identtisille ytimille elektronisieppauksen Q on aina 2 elektronin lepoenergiaa eli 22 kiloelektronivolttia suurempi kuin vastaavalla β + -siirtymällä. ja Sallitut ja kielletyt siirtymät lmaliikemäärä,j, on säilyvä ominaisuus hiukkasilla [2]. Sitä ei voi hävitä tai ilmestyä tyhjästä. Näin ollen reaktioon osallistuvien hiukkasten yhteinen kulmaliikemäärä on oltava yhtä suuri, kuin reaktiotuotteiden yhteinen kulmaliikemäärä. β (+/ ) -hajoamisten tapauksessa tämä tarkoittaa sitä, että emoytimen kokonaiskulmaliikemäärän on oltava yhtä suuri kuin tytärytimen ja kahden leptonin yhteinen kulmaliikemäärä. Elektronisieppauksessa vastaavasti elektronin ja emoytimen kulmaliikemäärän summan on oltava samansuuruinen tytärytimen ja neutriinon vastaavien kanssa. Kvanttimekaniikassa kulmaliikemäärä käsittää sekä orbitaalisen,l, että spinkulmaliikemäärän, S [1], eli J = L + S. (8)
13 13 Leptoneiden spinillä on aina kaksi tilaa: 1 /2 tai 1 /2 [3]. Täten kahden leptonin kytketty tila on joko 1 /2 + ( 1 /2) = 1, 1 /2 + 1 /2 = tai 1 /2 + 1 /2 = 1. β- hajoamisissa spinin muutos on siis aina tai 1. Jos S =, eli β-hajoamiseen osallistuvien elektronin (tai positronin) ja antineutriinon (tai neutriinon) spinit ovat vastakkaiset, kyseessä on Fermi-siirtymä. Jos taas S = 1, eli kyseisten leptonien spinit ovat samansuuntaiset, puhutaan Gamow-Teller-siirtymästä [1]. Ratakulmaliikemäärän muutos taas voi olla mikä tahansa kokonaisluku nollasta ylöspäin. Todennäköisin siirtymä on sellainen, jossa orbitaalinen kulmaliikemäärä ei muutu, eli L =. Tällaista siirtymää nimitetään sallituksi β-siirtymäksi. β- siirtymiä, joissa = 1, 2, 3,... kutsutaan vastaavasti kielletyiksi siirtymiksi. Nimitys on harhaanjohtava, sillä kielletyt β-siirtymät ovat mahdollisia, joskin huomattavasti epätodennäköisempiä [4]. Kielletyt siirtymät on lajiteltu L:n mukaan. Jos β-hajoamiseen osallistuvien leptonien L tot = 1, kyseessä on 1. kielletty siirtymä. Jos taas L tot = 2, kyseessä on 2. kielletty siirtymä. Orbitaalisen kulmaliikemäärän muutos siis kertoo, montako kertaa kielletty β-siirtymä on kyseessä. k-kertaisesti kielletty siirtymä on yleensä sitä epätodennäköisempi, mitä suurempi k:n arvo on Uniikit siirtymät k:n aste ei suoraan kerro, mikä β-hajoavan ytimen J on. ten edellä mainittiin, k merkitsee orbitaalisen kulmaliikemäärän muutosta. Mutta kuten aiemmin tuli ilmi, myös spinin muutos vaikuttaa J:hin (yhtälö (8)). Tällöin leptonien kytkennän huomioonottaen k 1 J(X X ) = k. k + 1 Kaikilla k-kertaisesti kielletyillä β-siirtymillä on tärkeä aliryhmä. Siinä ryhmässä tietyllä k:n arvolla hajoavan ytimen kulmaliikemäärän muutos on suurin mahdollinen. Tämä tarkoittaa sitä, että J(X X ) = k + 1. Tämän aliryhmän siirtymiä kutsutaan uniikeiksi siirtymiksi [4]. Kiellettyjen siirtymien rajaaminen uniikkeihin siirtymiin on usein perusteltua. Se helpottaa näiden siirtymien useiden ominaisuuksien tarkastelua, sillä kun β-siirtymät yleensä ovat sekoitus Fermi- ja Gamow-Teller-siirtymiä, uniikit siirtymät ovat aina puhtaasti Gamow-Teller-siirtymiä [5]. Tästä syystä uniikkien siirtymien elektronispektri voidaan määrittää tarkasti. Tähän palataan tarkemmin luvussa
14 Faasiavaruusintegraalit β-siirtymän luonteeseen vaikuttaa siihen osallistuvien leptonien kinematiikka. β - siirtymän e ja ν, β + -siirtymän e + ja ν sekä elektronisieppauksen neutriino eivät ole ytimeen sidottuja hiukkasia, vaan niillä on reaktion jälkeen tietty liikemäärä ja -energia. β-hajoavan ytimen massa on suuri vapautuviin leptoneihin verrattuna, joten sen voidaan olettaa pysyvän liikkumatta hajoamisreaktion jälkeenkin. Mutta leptonit puolestaan saavat osuutensa β-siirtymän hajoamisenergiasta. Leptonien tilat hajoamisen jälkeen vaikuttavat reaktion hajoamisvakioon ja tätä kautta reaktion nopeuteen, joten ne on tärkeää osata määrittää. Tähän tarvitaan faasiavaruusintegraaleja Fermin kultainen sääntö Hajoamisvakio (λ) on suure, joka kertoo reaktionopeuden ja reaktioon osallistuvien hiukkasten lukumäärän välisen suhteen. Hajoamisvakiosta määritetään myös reaktion puoliintumisaika. Lähtökohtana hajoamisvakion määrityksessä on Fermin kultainen sääntö [1]. Sen mukaan λ = 2π h f H i 2 dn f de f, (9) missä f H i 2 kuvaa alku- ja lopputilan välisen siirtymän todennäköisyyttä ja dn f de f puolestaan mahdollisten lopputilojen lukumäärää tietyllä hajoamisenergialla [1]. Jos siis halutaan määrittää β-hajoamisreaktioiden faasiavaruusintegraalit, on tutkittava lähemmin jälkimmäistä termiä Liikemääräavaruus Puhuttaessa hiukkasen tilasta voidaan ymmärtää, että puhutaan sen sijainnista. 3- ulotteisessa avaruudessa ollessamme sen määrittelyyn riittää kolme koordinaattia, joita yleensä merkitään samoin kuin Euklidisia avaruuksia: (x, y, z). Hiukkasen sijoittuminen spatiaaliseen avaruuteen on kuitenkin vain yksi tapa kuvata sen tilaa. Liikemäärä (p) on vektorisuure ja kolmiulotteisessa avaruudessa sekin saa kolme koordinaattia, joita merkitään usein p x, p y ja p z. Vaikka nämä suureet ovat jatkuvasti muuttuvia, niitä voidaan mikroskooppisella tasolla mallintaa diskreetisti. Tällöin esimerkiksi yhden diskreetin askeleen ollessa liikemääräavaruudessa x-akselin suuntaisesti dp x, liikemäärän x-komponentin muutos tällä akselilla voi olla p x + ndp x, missä n =, ±1, ±2,... [6]. Kolmiulotteisessa avaruudessa nämä diskreetit askeleet muodostavat mielivaltaisen pieniä soluja, joihin sijainti- ja liikemäärävektorit ovat jakaantuneet. Hiukkanen
15 15 sijaitsee aina solussa, jonka kulmapisteet spatiaalisessa avaruudessa ovat x, y, z, x + dx, y + dy ja z + dz. Liikemääräavaruudessa kulmapisteiden koordinaatit menevät vastaavasti. Sekä spatiaalisen että liikemääräavaruuden solut muodostavat faasiavaruuden, ja tutkittava hiukkanen sijaitsee aina jossakin tämän avaruuden laatikossa [6]. Hiukkasella on aina olemassa aaltofunktio ψ, joka kertoo sen todennäköisyyden sijaita jossain tietyssä kvanttitilassa. Jos hiukkanen sijaitsee jossain tietyssä faasiavaruuden solussa, jonka tilavuus on V = L x L y L z (L x, L y ja L z ovat solun sivujen pituudet), sen aaltofunktion on oltava nolla solun ulkopuolella. Tällöin aaltofunktion on oltava seisova aalto ja muotoa ψ(x, y, z) = A sin( n 1πx L x ) sin( n 2πy ) sin( n 3πz ), () L y L z missä n 1, n 2 ja n 3 ovat positiivisia kokonaislukuja. Tästä johtuen hiukkasen aaltofunktion aaltoluvun komponentit k i = n iπ L i ovat kvantittuneet [6]. Hiukkasen tilaa voidaan siis kuvata aaltolukuvektorilla k = (k x, k y, k z ), joka osoittaa sijainnin k-avaruudessa. Koska n i -arvot ovat positiivisia, k-vektorin komponentit saavat vain positiivisia arvoja. Tästä syystä k-avaruus käsittää vain kahdeksasosan k-säteisestä pallosta. Pallokoordinaateissa ilmaistuna k-vektorin kierto- ja atsimuuttikulmat voivat saada k-avaruudessa arvon väliltä [, π/2]. Lisäksi, koska yhden yksikkösolun tilavuus k-avaruudessa on π π π L x L y L z = π3 L xl yl z, k-tilojen tiheys on tämän ominaistilavuuden käänteisluku, eli LxLyLz. Yhden tilavuuselementin koko pallokoordinaateissa esitettynä on k 2 dk sin(θ)dθdφ, missä k on k:n pituus, φ on π 3 atsimuuttikulma ja θ on kiertokulma. Siispä tilojen lukumäärä tietynsuuruisessa tilavuuselementissä on dn = k 2 dk sin(θ)dθdφ. ten aikaisemmin tuli mainittua, k-avaruudessa θ ja φ voivat saada arvoja vain :n ja π/2:n väliltä. Tällöin k-vektorin ollessa magnitudiltaan välillä [k, k + dk], tilojen mahdollinen lukumäärä on dn = V π/2 π/2 π 3 k2 dk sin(θ)dθ dφ = V 2π 2 k2 dk. (11) Aaltohiukkasdualismiin sisältyy teoria,jonka mukaan hiukkasella, jolla on liikemäärä p, on olemassa myös niin kutsuttu de Broglien aallonpituus [6] λ = h, missä h p on Planckin vakio. Aallonpituus vastaa myös aaltofunktion aallonpituutta λ = 2π. k Näin ollen hiukkasen tarkastelu voidaan siirtää k-avaruudesta liikemääräavaruuteen ottaen huomioon muunnokset k = 2π = 2πp dp = ja dk =. Tiheysfunktio yhtälöstä 11 on liikemääräavaruudessa λ h p h h tällöin dn = V dp ( )2 2π2 p h h = V p2 dp 2π 2 h 3 (2π) 3 = 4πV h 3 p2 dp. (12)
16 16 Hiukkasen mahdollisten tilojen lukumäärästä saatiin nyt liikemäärästä riippuvainen funktio. β +/ -siirtymien lopputilojen tiheyttä määritettäessä on huomioitava, että lopputilojen kahdella leptonilla on erilliset faasiavaruudet. Lopputilojen lukumäärä on tällöin kummankin leptonin lopputilojen tulo. Näin ollen dn f = dn e dn ν. (13) Jos merkitään, että elektronin (tai positronin) liikemäärä on p ja (anti)neutriinon liikemäärä on q, lausekkeet 12 ja 13 yhdistettäessä saadaan β +/ -hajoamisten mahdollisten lopputilojen tiheydeksi dn f = 16π2 V 2 p 2 q 2 dpdq h 6. (14) Muotofunktiot ten Fermin kultainen sääntö (yhtälö 9) osoitti, reaktion jälkeisten lopputilojen funktio on hajoamisenergiasta riippuvainen funktio. Lauseke 14 esittää dn f :n liikemäärien funktiona, mutta se voidaan muuntaa elektronin (tai positronin) liikeenergiasta riippuvaiseksi funktioksi. Ensinnäkin lauseke 14 kuvaa leptoneita tilavuudessa V. Ytimestä emittoituvien leptonien ajatellaan kuitenkin olevan vapaita hiukkasia. Vapaiden hiukkasten aaltofunktiot φ ovat normalisoituja tilavuuden V neliöjuurella [1], jolloin φ e ( r) = 1 e i p r/ h V φ ν ( r) = 1 V e i q r/ h. Aaltofunktion normalisointi johtaa lopulta liikemäärien normalisointiin, sillä eksponentiaaliset aaltofunktiot voidaan esittää muodossa [1] e i p r/ h = 1 + i p r h e i q r/ h i q r = h Tämä johtaa normalisointiin, jossa p p V ja q q V, jolloin lausekkeesta 14 V 2 supistuu pois. Hajoamisenergia E f = Q jakaantuu β-hajoamisessa aina leptonien kesken, sillä luvun 2.2 alussa oletettiin tytärytimen rekyylin jäävän olemattomaksi. Lisäksi oletetaan, että (anti)neutriino on massaton. Tällöin Q = T e + qc, missä T e on elektronin liike-energia ja c on valonnopeus. Täten q = Q Te ja dq = 1. n c dq c nämä sijoitetaan normalisoituun yhtälöön 14, saadaan dn f dq = 16π2 h 6 c 3 (Q T e) 2 p 2 dp, (15)
17 17 joka esittää lopputilojen jakaumaa elektronin saaman energian funktiona [1]. Koska T e voi saada minkä tahansa arvon väliltä [, Q], integrointi kaikkien mahdollisten energiaintervallien de yli antaa kaikkien mahdollisten lopputilojen lukumäärän tietylle Q:n arvolle. Tätä integraalia muotofunktion yli kutsutaan faasiavaruusintegraaliksi. Analyyttisessä ratkaisussa siirtymän faasiavaruusintegraali lasketaan yleensä siten, että muuttujana on ɛ = Ee m ec eli elektronin saama kokonaisenergia E 2 2 e = (m e c 2 ) 2 + (T e ) 2 suhteutettuna elektronin massaan. Hajoamisenergiaa suhteutettuna elektronin massaan merkitään E = Q m ec, jolloin integrointiväliksi tulee [1, E 2 ]. Muotofunktion korkeuteen vaikuttaa osaltaan myös ytimen ja sähkövarauksellisen leptonin välinen Coulombin voima. β -hajoamisessa tytärytimen ja elektronin (β + -hajoamisessa tytärytimen ja positronin) välinen vuorovaikutus muuttaa leptonien liikemäärää vaikuttaen näin niiden tilatiheyteen. Coulombin vuorovaikutus tietyllä ytimen järjestysluvulla, Z, ja tietyllä energialla huomioidaan lisäämällä muotofunktioon erityinen Fermin funktio, F (±Z f, ɛ). Tällöin faasiavaruusintegraalin lauseke β + - ja β - lausekkeille voidaan määrittää seuraavasti: missä p = ɛ 1 [4]. f ( ) = E 1 F (±Z f, ɛ)pɛ(e ɛ) 2 dɛ, (16) Muista β-siirtymistä poiketen elektronisieppauksessa on lopputilassa vain yksi leptoni eli neutriino. Tällöin kaikki hajoamisenergia muuntuu neutriinon liike-energiaksi ja neutriinolla on lopputilassa tietty liikemäärä. Tämä johtaa siihen, että elektronisieppauksessa faasiavaruuksilla ei ole jatkuva vaan diskreetti energiajakauma. Lisäksi elektronisieppauksessa ei ole varauksellinen leptoni loppu- vaan alkutilassa, kuten kappaleessa tuli ilmi. Täten elektronisieppauksessa Fermin funktioon vaikuttaa emoytimen järjestysluku. Faasiavaruustekijä elektronisieppaukselle on siis f (EC) = 2π(αZ i ) 3 (ɛ + E ) 2, (17) missä α 1 on hienorakennevakio ja ɛ 137 = mec2 B m ec, missä B on elektronin sidosenergia emoytimen ensimmäisellä elektronikuorella 2 [4]. Jos β-siirtymä on kuitenkin kielletty, leptonien eivät ole enää perustilassa. Tällöin muotofunktioiden määrittäminen vaatii useita matriisielementtejä. Maksimissaan niitä voi olla jopa 6. Mutta kun kyse on uniikista kielletystä β-siirtymästä, matriisielementtejä tarvitaan vain yksi. Siksi niiden analyyttinen määrittely on mahdollista, toisin kuin muilla kielletyillä β-siirtymillä. Silti analyyttisestä määrityksestä tulee työlästä. K-kertaisesti kielletylle uniikille β (+/ -siirtymälle faasiavaruusintegraali on missä f ( ) = ( 3 4 S (Z f, ɛ) F (±Z f, ɛ)pɛ(e ɛ) 2 ) K (2K)!! E S (2K + 1)!! (Z f, ɛ)dɛ, (18) 1 k e+k ν=k+2 (ɛ 2 1) ke 1 (E ɛ) 2(k ν 1). (2k e 1)!(2k ν 1)!
18 r/r TH 6 8 V(r) Varjostus Ei varjostusta vio 1. Ytimen Coulombin potentiaali huomioituna varjostuksella sekä sitä ilman Vastaavalle elektronisieppaukselle faasiavaruusintegraali on puolestaan f (EC) = 2(2K)!! (2K)!!(2K + 1)! π(αz i) 3 (ɛ + E ) 2(K+1). (19) ten luvussa todettiin, β + -hajoaminen ja elektronisieppaus kuvastavat molemmat samaa siirtymää X(Z, N) X(Z 1, N + 1). Viitaten Fermin kultaiseen sääntöön 9, f H i 2 on molemmissa hajoamisissa samat, mutta dn f de f ei ole. Faasiavaruusintegraali siirtymälle, joka voi tapahtua sekä β + -hajoamisen että elektronisieppauksen kautta on siis f (+/EC) = f (+) + f (EC). (2) Sama sääntö pätee, vaikka kyseessä ei olisi uniikki siirtymä tai kiellettyvyyden aste olisi mikä tahansa. 2.3 Thomas-Fermi-varjostus Faasiavaruusintegraaleihin vaikuttaa lisäksi elektronipilven varjostus (engl. screening). Elektronin kokema Coulombin voima on otettu huomioon Fermin funktion kautta, kuten luvussa todettiin. Fermin funktio ei kuitenkaan ota huomioon elektronipilven aiheuttamaa vuorovaikutusta β-hajoamiseen osallistuviin leptoneihin. Se otetaan erikseen huomioon Thomas-Fermi-mallin approksimaatiolla. Kaikkien elektronipilven elektronien vuorovaikutusta β-hiukkaseen on hankala määrittää erikseen. Thomas-Fermi-approksimaatio onkin tilastollinen menetelmä, jossa atomille määritetään efektiivinen potentiaali. Se antaa korjaustermin ytimen
19 19 protonien muodostamalle sähkökentälle, ja korjaustermi riippuu elektronien tiheydestä [7]. Ilman varjostusefektiä potentiaalienergia V on riippuvainen etäisyydestä atomin ytimeen seuraavasti: V (r) 1. Mutta varjostuksen huomioiden V (r) r e r/r T F, missä r r T F on elektronien tiheydestä riippuvainen Thomas-Fermi-varjostuspituus (engl. Thomas-Fermi screening length) [8]. Täten jokaisen r T F :n jälkeen potentiaalien välinen ero putoaa e 1 -osaan eli noin 37 prosenttiin. Potentiaalien välinen ero näkyy kuvassa 1. Muutos potentiaalienergiassa vaikuttaa β + -hajoamisen ja elektronisieppauksen hiukkasten lopullisiin liikemääriin. β -hajoamisessa varjostus ei vaikuta.
20 2
21 21 3 Menetelmät ja aineisto 3.1 Numeerinen laskenta Tässä työssä faasiavaruusintegraaleja ei laskettu analyyttisesti vaan numeerisesti Fortran-kielisellä tietokoneohjelmalla. stakin β-siirtymästä annetaan ohjelmalle tarvittavat parametrit, joita tarvitaan faasiavaruusintegraalien laskemiseen. Ensimmäinen parametri on kiellettyyden aste. Toinen parametri kertoo, mikä β-hajoamisen laji on kyseessä siten, että jos on kyseessä β + /EC-siirtymä, parametri on +1 tai jos taas β -siirtymä, parametri on -1. Kolmas parametri on 1, jos varjostus-efekti otetaan huomioon ja, jos ei oteta. Neljäs parametri on β-hajoavan ytimen massaluku ja viides parametri sen alkutilan järjestysluku. udes ja viimeinen parametri on β- siirtymän hajoamisenergia kiloelektronivoltteina. β + /EC-siirtymän tapauksessa annetaan vain elektronisieppauksen Q. β + -siirtymän Q on aina 22 kev pienempi, kuten luvussa todettiin, ja ohjelma osaa ottaa tämän huomioon β + -siirtymien faasiavaruusintegraaleja laskettaessa. Hajoamisenergiat on otettu National Nuclear Data Center Brookhavenin (NNDC) www-sivujen Q-laskurista [9]. Tietokoneohjelma laskee luvussa esitettyjen periaatteiden mukaisesti faasiavaruusintegraalit parametrien mukaiselle K-kertaisesti kielletylle uniikille sekä sitä vastaavalle sallitulle siirtymälle. Tässä tutkielmassa laskettujen kiellettyjen siirtymien faasiavaruusintegraalit ovat liitteessä A ja vastaavasti sallittujen siirtymien faasiavaruusintegraalit liitteessä B. Useimmat faasiavaruusintegraalit on annettu logaritmimuodossa. Ohjelma antaa ulos myös β + - ja EC-siirtymien osuudet kokonaisarvosta. 3.2 Analysoitavat siirtymät Tässä työssä laskettiin käytössä olevalle ohjelmalla faasiavaruusintegraalit noin 14 uniikille β-siirtymälle []. Siirtymät koskevat sekä β - ja β + -hajoamisia, että elektronisieppauksia. Siirtymien kiellettyvyyden aste vaihteli 2:sta 7:ään. Järjestysluvut vaihtelivat 21:stä 86:een ja hajoamisenergia oli maksimissaan yli 8 kev. Yhteistä kaikille siirtymille oli siis, että ne olivat uniikkeja. Tässä työssä tietokoneohjelmalla saatua laskentadataa analysoitiin useista eri näkökulmista. Pääpaino työssä on, kuinka K:n arvo vaikuttaa faasiavaruusintegraaleihin. β/ec-siirtymille on myös laskettu erikseen faasiavaruusintegraalit tapauksille, joissa varjostus on otettu huomioon ja niille, joissa ei ole. Tulosten analysoinneissa on nyt käytetty arvoja, joissa varjostus ei ole otettu huomioon. Tämä on perusteltua,
22 22 sillä kävi ilmi, että varjostuksen huomioonottaminen ei muuta arvoja merkittävästi. Varjostuksen vähäisistä vaikutuksista kerrotaan enemmän luvussa 4.4.
23 23 (f / f) 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 1e- 1e-11 1e-12 1e-13 5 betabeta+ 15 k=2 k=3 k=4 k=5 k=6 k=7 2 1e+6 1e+5 1e+4 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 1e- 1e-11 1e-12 1e-13 1e-14 1e-15 1e-16 1e-17 1e-18 1e-19 1e-2 1e-21 1e-22 1e-23 1e-24 1e-25 5 EC 15 k=2 k=3 k=4 k=5 k=6 k=7 2 1e+4 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 k=2 1e- k=3 k=4 1e-11 k=5 k=6 1e-12 k= E E E vio 2. f f eriteltynä kiellettyyden mukaan eri β-siirtymän lajeille. 4 Tulokset 4.1 Kiellettyjen ja sallittujen siirtymien väliset suhteet Yksi näkökulma, mistä lähdin erittelemään laskenta-analyysiä, oli kuinka kiellettyjen siirtymien faasiavaruusintegraalit eroavat vastaaviin sallittuihin faasiavaruusintegraaleihin. Tietokoneohjelma laskee jokaisen siirtymän K-kertaisesti kielletyn siirtymän faasiavaruusintegraalin, f ja sitä vastaavan sallitun siirtymän faasiavaruusintegraalin arvon, f. Kiellettyyden aste on ainoa ero näiden kahden arvon välillä, joten niiden välinen suhde f f on mielestäni tärkein näkökulma tutkimuksessani. Analysoin saadut suhdeluvut katsomalla, miten ne muuttuvat hajoamisenergian suhteen. f :t on otettu liitteestä A ja niitä vastaavat f :t liitteestä B. Tulokset on yhdistetty kuvassa 2. vassa tulokset ovat logaritmisella asteikolla, koska se on helpompi tapa näyttää suhdelukujen käytös sekä suurilla että pienillä energian arvoilla yhtäaikaa. vasta huomataan, että suhdelukujen käytös on samanlaista niin β (+/ ) -siirtymille, että elektronisieppauksille. Alhaisissa energioissa siis suhdeluku
24 24 (f/f) (1/2K) 3 beta+ 5 EC 2.5 beta k=2 k=3 k=4 k=5 k=6 k=7 2 1 k=2 k=3 k=4 k=5 k=6 k= k=2 k=3 k=4 k=5 k=6 k= E E E vio 3. f f :n linearisointi eriteltynä kiellettyyden mukaan eri β-siirtymän lajeille. on sitä pienempi, mitä suurempi kiellettyys on, tarkoittaen että f on f :aan verrattuna sitä pienempi, mitä suurempi K:n arvo on. Energian kasvaessa tilanne kääntyykin toisinpäin. Kaikilla siirtymillä f alkaa kasvaa f :aa voimakkaammin, kun hajoamisenergia kasvaa, mutta f :n kasvu on sitä voimakkaampaa, mitä suurempi K on. Suhdeluvun käyttäytyminen viittasi siihen, että se on verrannollinen johonkin potenssiin energian suhteen. Analysoin suhdelukuja ottamalla sopivat juuret niistä riippuen, mitä K on. Lopulta sain kuvan 2 laskentadatasta lineaariset esitykset, jotka on esitelty kuvassa 3. Sain käyrät linearisoitua ottamalla jokaisesta suhdeluvusta f f 2K.:nen juuren. Täten f f E 2K. Odotin, että lineaaristen esitysten kulmakertoimetkin olisivat olleet K:sta riippuvaisia, mutta näin ei ole, kuten kuvasta 3 käy ilmi. β - ja β + -siirtymien tapauksessa ne kuitenkin käyvät hyvin yhteen Primakoff-Rosen-approksimaatioista johdettujen faasiavaruusintegraalien kanssa. Niissä f ( ) = 1 3 (E5 E E 6)F P R (±Z f ), missä
25 25 Taulukko I. Suhdelukujen linearisointien kulmakertoimet K Approksimaatiot vaajat(β ) vaajat(β + ) vaajat(ec) 2,177474,1829±,14,1779±,7,2581±,6 3,18538,154±,2,1528±,,2128±,6 4, ,134±,1,132±,11,184±,7 5, ,1167±,4,1161±,9,1573±,8 6 (,12775±),81±,,1537±,8 7,1335±,2357,13±,11,1997±,2 F P R (Z f ) = 2παZ f 1 e 2παZ f on itse Primakoff-Rosen-approksimaatio Fermin funktiolle. [4] Myös f :ille on olemassa approksimaatiot. Esimerkiksi f 2u:a ± voidaan esittää muodossa ( 3 E E E E E4 54 E E2 E ) F P R (±Z f ) 1134 Jokaiselle 2 K 5 on olemassa myös omat yksilölliset approksimaatiot, joissa polynomin kertoimet vaihtelevat, mutta aste on aina 2K + 5 [4]. Suhdeluvun f f likiarvo voidaan laskea siis myös approksimaatioista. Yksinkertaisuuden vuoksi huomioidaan vain korkeinta astetta olevat termit. Näin ollen esimerkiksi tapauksessa K = 2 ( 3 E 9 ) f 2u 972 F P R 1 = 9 f 3 (E5 )F P R 972 E4. n tämä suhdeluku linearisoidaan, eli siitä otetaan (2 K):s eli neljäs juuri, saadaan: ( f2u f ) 1 4, E. n K = 2, linearisoinnin kulmakertoimeksi saadaan täten, Vertasin tätä laskentadatasta saatuun vastaavaan arvoon, joka on β :lle, ±, 14 ja β + :lle, 1779 ±, 7. Approksimaatiosta johdettu suhdeluvun linearisoinnin kulmakerroin on sama sekä β - että β + -siirtymälle, mutta mittausdatan arvoista β + :n arvot ovat lähimpänä approksimaatioiden vastaavia arvoja. Muillekin K-kertaisille β ± -siirtymille voidaan johtaa approksimaatioista samalla tavalla vastaavat kulmakertoimet. Tiedossani on approksimaatiot 5-kertaisiin asti oleville uniikeille β - ja β + -siirtymille [4]. Elektronisieppauksille ei ole vastaavia approksimaatioita ainakaan minun tietääkseni. Tulokset on koottu taulukkoon I. β -siirtymien 6. kielletyt siirtymät on laitettu sulkuun johtuen siitä, ettei tulos ole täysin luotettava. Kyseisiä siirtymiä on tiedossa vain 2 eikä niille voida määrittää kunnollista suoran sovitusta.
26 26 vio 4. Keskiarvo tilatiheyksille energiajakaumassa. 4.2 Tilatiheyksien keskiarvo Seuraavaksi tarkastelin, kuinka K:n aste vaikuttaa keskimääräiseen tilatiheyteen β- siirtymässä. ten lauseke 15 osoitti, siirtymän lopputilojen tiheys on energiasta riippuva funktio, joka nousee nollasta huippuarvoonsa ja laskee takaisin nollaan päätepiste-energiassa, joka on hajoamisenergia. Tilatiheyksille β-siirtymässä saadaan siis keskiarvo jakamalla faasiavaruusintegraali siirtymän hajoamisenergialla. va 4 havainnollistaa tilannetta. Laskin kaikille liitteen A β-siirtymille keskiarvon f, mukaanlukien elektronisieppaukset. ten luvussa kerrotaan, EC-siirtymissä ei muodostu tasaista ener- Q giajakaumaa vaan diskreetti piikki. Mutta faasiavaruusintegraali on kuitenkin Q:sta riippuva EC-siirtymissä, joten laskin keskiarvon samalla tavalla niissäkin. Tulokset on yhdistetty kuvaajaan 5, kuvaajaan 6 ja kuvaajaan 7. Tulosten analysointi on keskiarvoilla vaikeampaa kuin suhdeluvuilla f f luvussa 4.1, koska tuloksissa tapahtuu selvää sahausta, etenkin elektronisieppauksilla. Tämä johtuu ytimen järjestysluvun, Z, muutoksesta laskentadatassa. Suhdeluvuissa se ei vaikuttanut samalla tavalla, sillä jaettaessa f vastaavalla f :lla Z näiden välillä ei muutu. vaajia tarkasteltaessa huomataan kuitenkin, että keskiarvojen käytös on jokseenkin samanlaista kuin suhdeluvuilla. Pienillä hajoamisenergian arvoilla ne ovat sitä suurempia, mitä pienempi kiellettyys on, mutta energian kasvaessa korkeamman K:n siirtymillä keskiarvot ovat suurempia. Tulokset viittaisivat siihen, että suurienergisissä siirtymissä tilatiheydet ovat sitä korkeampia, mitä suurempi K on.
27 27 1e+5 f_{uk}:n suhde Q:hun(beta-) 1e+4 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 log(f_{uk}/q) 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 1e- 1e-11 1e-12 1e-13 1e-14 1e Q-arvo 6 8 k=2 k=3 k=4 k=5 k=6 k=7 vio 5. Keskiarvo tilatiheyksille β -siirtymissä (logaritminen asteikko). log(f_{uk}/q) 1e+4 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 1e- 1e-11 1e-12 1e-13 1e-14 1e-15 1e-16 1e-17 1e-18 1e-19 2 f_{uk}:n suhde Q:hun(beta+) 4 Q-arvo 6 k=2 k=3 k=4 k=5 k=6 k=7 8 vio 6. Keskiarvo tilatiheyksille β + -siirtymissä (logaritminen asteikko).
28 28 log(f_{uk}/q) 1e+3 1e+2 1e+1 1e+ 1e-1 1e-2 1e-3 1e-4 1e-5 1e-6 1e-7 1e-8 1e-9 1e- 1e-11 1e-12 1e-13 1e-14 1e-15 1e-16 1e-17 1e-18 1e-19 1e-2 1e-21 1e-22 1e-23 1e-24 1e-25 1e-26 1e-27 1e-28 1e-29 2 f_{uk}:n suhde Q:hun(EC) 4 6 Q-arvo 8 k=2 k=3 k=4 k=5 k=6 k=7 vio 7. Keskiarvo tilatiheyksille elektronisieppauksissa (logaritminen asteikko) f :n suhde Q:hun(k=2) uk 5 15 beta+ beta- EC f uk :n suhde Q:hun(k=3) 5 15 beta+ beta- EC 2 E E vio 8. Keskiarvo tilatiheyksille 2- ja 3-kert. kielletyissä siirtymissä (logaritminen asteikko).
29 f :n suhde Q:hun(k=4) uk 5 15 beta+ beta- EC f uk :n suhde Q:hun(k=5) 5 15 beta+ beta- EC 2 E E vio 9. Keskiarvo tilatiheyksille 4- ja 5-kert. kielletyissä siirtymissä (logaritminen asteikko). f uk :n suhde Q:hun(k=6) f uk :n suhde Q:hun(k=7) beta+ beta- EC beta+ beta- EC E E vio. Keskiarvo tilatiheyksille 5- ja 6-kert. kielletyissä siirtymissä (logaritminen asteikko).
30 3 f (+) :n osuus (f (+) + f (EC) ):stä (%) K = 2 (%) K = 3 (%) K = E (EC) E (EC) E (EC) (%) K = 5 (%) K = 6 (%) K = E (EC) E (EC) E (EC) vio 11. β + :n osuudet β + /EC-siirtymissä. n tarkastellaan kuvaajia 8, 9 ja, huomataan että sahausefekti on jonkin verran voimakkaampaa elektronisieppauksessa kuin muissa β-hajoamisen lajeissa, varsinkin β + -siirtymissä. Kaikissa kuvissa elektronisieppauksilla on 2m e c 2 suurempi hajoamisenergia, kuin β + -siirtymillä, mutta muuten ne kuvaavat samoja siirtymiä. Näin ollen Z:n muutos on sama molemmissa lajeissa. Mutta siitä huolimatta näyttää siltä, että se vaikuttaa enemmän elektronisieppausten keskiarvoon. Syy saattaa piillä siinä, että Fermin funktio vaikuttaa enemmän diskreettiin jakaumaan. Toinen asia, minkä kuvaajista 8, 9 ja voidaan huomata, on se, että β -siirtymissä f :t ovat keskimääräisesti suurimpia, olivatpa K: ja Q:n arvot mitä hyvänsä. Tämä on kuitenkin odotettua, sillä Fermin funktio nostaa β -siirtymän tilajakaumaa kaikilla E :n arvoilla.
31 β + :n ja EC:n väliset osuudet Kolmas näkökohta, josta ryhdyin mittausdataa tarkastelemaan, on kuinka β + - ja EC-siirtymien välinen suhde käyttäytyy eri kiellettyvyyden arvoilla. ten luvussa mainittiin, tytärytimen tilat ovat molemmissa siirtymissä identtiset, jos emoytimenkin tilat ovat. Ja yhtälö 2 kertoo, että siirtymän faasiavaruusintegraali on näiden molempien mahdollisten siirtymien summa. Tässä luvussa on analysointia siitä, miten tämä summa käyttäytyy eri parametrien, varsinkin K:n, mukaan. Tietokoneohjelma antaa β + /EC-siirtymissä ulos myös näiden väliset osuudet, joten sijoitin ne kuvaajiin, jotka näkyvät kuvassa 11. vassa on β + :n osuudet siirtymistä prosenttiosuuksina elektronisieppauksen hajoamisenergian suhteen. Jos käyttäisin β + -siirtymien hajoamisenergioita, kaikki siirtymät joilla E < 2 kuvaajissa, olisivat negatiivisia, sillä, kuten luvun lopussa todettiin, elektronisieppauksessa hajoamisenergia on kaksi elektronin lepoenergiaa suurempi kuin β + -hajoamisessa. f =, kun E, joten tiedetään, että kuvaajissa kaikkilla siirtymillä, joiden E 2, elektronisieppauksen osuus on % ja β + :n osuus %, ja kun E kasvaa, myös β + :n osuus kasvaa. Tässäkin näkökulmassa suurin kiinnostuksen aihe on, kuinka K vaikuttaa näihin osuuksiin. Järjestysluvun muuttuminen aiheuttaa tässäkin tapauksessa sahausefektiä. Yleisesti E :n kasvaessa f (+) f (+/EC) kasvaa myös, mutta Z:n kasvu saa toisaalta EC:n osuuden kasvamaan. Erityisesti tämä näkyy siirtymissä, joissa K = 4. Valitettavasti Z:n pitäminen vakiona ei tule kysymykseenkään, sillä silloin laskentadatassa olisi siirtymiä, jotka eivät olisi todellisia ytimissä tapahtuvia siirtymiä. Mutta joitakin havaintoja tuloksista voidaan tehdä. Siirtymissä, joissa K = 7, järjestysluku vaihtelee vain välillä 49 55, β + : osuus pysyy alle puolessa prosentissa, vaikka E kasvaa melkein arvoon. Energialtaan suurimman siirtymän, jonka K = 7, E 9, 26 ja Z = 51, β + :n osuus on vain,259 %. Laskentadatasta löytyy vastaavanlainen siirtymä, jonka E ja Z ovat samat, mutta K = 2. Tässä tapauksessa β + :n osuus on jopa 5,285 % eli yli puolet. Suuremmilla K:n arvoilla EC pyrkii selvästikin vielä dominoimaan kynnysenergiaa suuremmillakin energioilla. Tarkastelin myös matalia E :n arvoja, joilla EC-siirtymät ovat yleisesti vallitsevia. ten aiemmin tässä luvussa todettiin, kaikilla E (EC) 2 β + /EC-siirtymät ovat puhtaasti EC-siirtymiä ja vähän sitä korkeammilla energioillakin β + :n osuus on olemattoman pieni. Tarkastellessani siis arvoja joilla EC:n osuus on %, huomasin että korkeammilla K:n arvoilla tämä sadan prosentin raja on hieman ylemmällä energialla. Toki Z:n suuruus edesauttaa sitä, mutta otetaan laskentadatasta esimerkiksi tapauksien K = 4 ja K = 5 suurienergisimmät siirtymät, joilla EC:n osuus on %. n K = 4, kyseisen siirtymän Q = 14.56keV eli E 2, 748 ja Z = 84. n taas K = 5 niin Z = 72(eli pienempi ja siten β + :aa suosiva) mutta Q = 176.8keV E 3, 341. Tämä huomio vahvistaa sitä havaintoa, että EC pyrkii dominoimaan β + /EC-siirtymiä, kun K:ta kasvatetaan.
32 32 (scr) (ei-scr)/f f (scr) (ei-scr)/f f (scr) (ei-scr)/f f k=2 E (EC) k=4 E (EC) k=6 E (EC) tot beta+ EC tot beta+ EC tot beta+ EC (scr) (ei-scr)/f f (scr) (ei-scr)/f f (ei-scr)/f (scr) f k=3 E (EC) E k=5 8 (EC) k=7 4 6 E (EC) 15 tot beta+ EC tot beta+ EC 8 12 tot beta+ EC 2 14 vio 12. f :n varjostamattomien ja varjostettujen arvojen väliset suhteet 4.4 Varjostus-efekti Edellisten kappaleiden tuloksissa on käytetty laskentadataa, jossa ei ole huomioitu luvussa 2.3 esiteltyä Thomas-Fermi-varjostusta. Varjostus muuttaa hieman β + - ja EC-siirtymiä. Olen kuitenkin laskenut myös f :t ja f :t, joissa on otettu varjostus huomioon. Sitten olen vain verrannut tuloksia toisiinsa. Uniikkien faasiavaruusintegraalien, joissa varjostusta ei ole otettu huomioon, suhteet vastaaviin arvoihin, joissa se on otettu huomioon f ei scr f scr sallituille β + - ja EC-siirtymille. Suhdeluvut f ei scr f scr on yhdistetty kuvaan 12. Sama operaatio on tehty myös on yhdistetty kuvaan 13. Näissä tuloksissa on huomioitava, että vaikka ne on eroteltu kiellettyyden mukaan, K:lla ei ole mitään tekemistä f :n arvojen kanssa. Luokittelu K:n mukaan on vain, jotta niitä voidaan verrata vastaaviin K-kertaisesti kiellettyihin uniikkeihin siirtymiin. ten kuvista 12 ja 13 nähdään, suhdeluku pysyy aika lähellä yhtä molemmissa tapauksissa, eli varjostus ei vaikuta faasiavaruusintegraaliehin merkittävästi. Tästä syystä on perusteltua pitää edellisissä luvuissa esitetyt tulokset ennallaan. Varjostusefekti näyttäisi olevan merkityksellinen lähinnä matalaenergisillä β + -siirtymillä. Niillä varjostus kasvattaa faasiavaruusintegraalien arvoa hyvinkin suureksi. Äärita-
33 33 f (ei-scr)/f (scr) f (ei-scr)/f (scr) f (ei-scr)/f (scr) k=2 E (EC) k=4 E (EC) k=6 E (EC) tot beta+ EC tot beta+ EC tot beta+ EC (scr) (ei-scr)/f f (scr) (ei-scr)/f f (scr) (ei-scr)/f f k=3 E (EC) E k=5 8 (EC) k=7 4 6 E (EC) 15 tot beta+ EC tot beta+ EC 8 12 tot beta+ EC 2 14 vio 13. f :n varjostamattomien ja varjostettujen arvojen väliset suhteet (K:n arvo kertoo vain vastaavuuden siirtymiin F :n tapauksessa)
34 34 pauksena 3. kielletty β + -siirtymä, jossa iridium-192 muuttuu osmium-192:ksi. Siirtymän Q = 24.6 kev. Tässä siirtymässä varjostus kasvattaa f :n melkein 45- kertaiseksi. Syy tähän tietysti on se, että varjostuksen matalilla energioilla aiheuttama häiriö vaikuttaa suhteessa enemmän pienen Q:n siirtymissä. Jonkin verran myös ytimen järjestysluku vaikuttaa eroon, mutta ei niin paljon kuin Q. Saadakseni kuitenkin tarkemmin selville, kuinka varjostus vaikuttaa edellisissä luvuissa esitettyihin tuloksiin, eli kiellettyjen ja sallittujen siirtymien välisiin suhteisiin, tilatiheyksien keskiarvoihin sekä β + :n ja EC:n välisiin osuuksiin, laskin miten nämä tulokset eroavat toisistaan tilanteissa, joissa varjostus on huomioitu ja tilanteissa, joissa ei ole. Itse katsoin parhaaksi määrittää näitä arvoja erottavat kertoimet. Esimerkiksi, suhdeluvulle f f saadaan relaatio seuraavasti: f (EI SCR) f (SCR) Kaikki f (EI SCR) f (SCR) f (SCR) f (SCR) = f (SCR) f (EI SCR) f (EI SCR) f (SCR) f (EI SCR) f (EI SCR) SCRRAT IO on siis suhdeluku, jota kuvassa 12 näkyvät arvot esittävät. SCRRAT IOf on puolestaan listattu kuvaan 13. Täten f (SCR) f (SCR) = SCRRAT IOf SCRRAT IO f (EI SCR) f (EI SCR) Tilatiheyksien keskiarvoille vastaava relaatio on puolestaan.. f (SCR) Q = f (EI SCR) Q f (SCR) f (EI SCR) = 1 SCRRAT IO f (EI SCR). Q β + - ja EC-siirtymien välisiä suhteita varten taas f (SCR) (β + ) f (SCR) (tot) = f (SCR) (β + ) f (EI SCR) (β + ) f (EI SCR) f (SCR) (tot) (tot) f (EI SCR) (β + ) f (EI SCR) (tot) SCRRAT IO(tot) f (EI SCR) (β + ) = SCRRAT IO(β + ) f (EI SCR) (tot). Relaatiot kaikille tapauksille on yhdistetty liitteeseen C. Relaatioissa ei kuitenkaan esiinny mitään uutta. Ne pysyvät 1:n lähettyvillä eniten ne heittelevät alhaisilla energioilla ja varsinkin β + -siirtymillä. Kiellettyyden arvolla ei näytä olevan mitään merkitystä varjostuksessa. Eniten vaikuttaa hajoamisenergian suuruus ja onko kyseessä β + - vai EC-siirtymä. Ytimen järjestysluvulla on myös vähän merkitystä.
35 35 5 Päätäntö Kaiken kaikkiaan voidaan sanoa, että K-kertaisesti kielletyt uniikit β-siirtymät ilmenevät vasta, kun siirtymän hajoamisenergia on tarpeeksi suuri. Faasiavaruusintegraalin suuruus korreloi hajoamisvakion kanssa, joka puolestaan on kääntäen verrannollinen siirtymän puoliintumisaikaan. Luvussa 4.1 esitetty suhdeluku f /f kertookin, milloin uniikkien β-siirtymien tilatiheys ohittaa vastaavan sallitun siirtymän tilatiheyden. Yleisesti voidaan todeta, että kaikissa β-siirtymän lajeissa kielletty uniikki siirtymä ohittaa tilatiheydessä sallitun siirtymän, kun hajoamisenergia, Q, on noin 2 95 kiloelektronivoltin välillä (kuva 2) riippuen ytimen järjestysluvusta sekä K:n suuruudesta. Eli β-siirtymissä, joilla Q > 95 kev, ytimen tila muuttuu nopeammin kielletyn siirtymän kautta. n kyseessä on siirtymä, jonka Kiellettyyden aste määrää myös suhdeluvun kasvun. Uniikkien siirtymien tilatiheys kasvaa sitä nopeammin hajoamisenergian kasvaessa, mitä suurempi K on. ten luvussa 4.2 tuli ilmi, β-siirtymän lopputilojen tiheys on keskimäärin isompi suurienergisemmissä siirtymissä. Myös kiellettyyden aste vaikuttaa keskimääräiseen tilatiheyteen. Matalilla energioilla tapahtuu enemmän niitä uniikkeja β-siirtymiä, joilla K on pienempi. Energiaa kasvatettaessa tilanne muuttuu lopulta päinvastaiseksi, ja korkeamman K:n siirtymät ohittavat esiitymistiheydessä alemman K:n siirtymät. Tämäkin havainto tukee sitä asiaa, että jos halutaan tutkia β-siirtymiä, joissa leptonit kuljettavat mahdollisimman paljon ratapyörimismäärää mukanaan, on syytä tutkia β-hajoamisia, joilla on mahdollisimman suuri hajoamisenergia. Mitä tulee siirtymiin, jotka voivat tapahtua sekä β + -hajoamisen että elektronisieppauksen kautta, suuremmalla kiellettyyden asteella EC:n osuus näyttäisi olevan isompi. Tiedetään jo ennalta, että matala hajoamisenergia ja korkea ytimen järjestysluku suosivat elektronisieppausta enemmän kuin β + -hajoamista. Nämä ovat tärkeitä huomioita, kun halutaan kontrolloida sitä, kumman siirtymän kautta ytimen tilaa halutaan muuttaa. Thomas-Fermi-varjostusefektin vaikutus faasiavaruusintegraaleihin on vähäistä. Ja K:n vaikutus varjostukseen on merkityksetöntä. Varjostuksen vaikutus näkyy lähinnä matalaenergisillä β-siirtymillä. Koska tutkimuksen pääpaino oli tutkia kiellettyyden asteen vaikutusta, luvun 4.4 tuloksia ei eritellä tässä luvussa sen tarkemmin. Tässä tutkimuksessa esitetyt tulokset ovat kuitenkin vain pintaraapaisu aiheeseen K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraaleihin. Laskentadatasta, joka on lisätty liitteisiin, riittää varmasti tutkittavaa tulevaisuudessakin. Tässä tutkielmassa on tarkasteltu lähemmin vain muutamaa näkökulmaa aiheeseen,
36 36 ja koska aiheesta on ollut tähän mennessä hyvin vähän tutkimuksia, uusia merkittäviä havaintoja voi odottaa vielä löytymistään.
37 37 Lähteet [1] Kenneth S. Krane. Introductory Nuclear Physics. John Wiley and Sons, [2] Francis Halzen and Alan D. Martin. Quarks and Leptons: An Introductory Course in Modern Particle Physics. John Wiley and Sons, [3] B.R. Martin and G. Shaw. Particle Physics. John Wiley and Sons, [4] Jouni Suhonen. From Nucleons to Nucleus. Springer, 27. [5] Bernard L. Cohen. Concepts of Nuclear Physics. Tata McGraw-Hill, [6] Roger Bowley and Mariana Sánchez. Introductory Statistical Mechanics. Oxford:Clarendon Press, 2 edition, [7] Matti Manninen and Risto Nieminen. Pintafysiikka. Suomen Fyysikkoseura, [8] Harald Ibach and Hans Lüth. Solid-State Physics. Springer, 4 edition, 29. [9] B. Pritychenko and A. Sonzogni. Q-value calculator (qcalc). [] Joel Kostensalo and Jouni Suhonen. Spin-multipole nuclear matrix elements in the pnqrpa - implications for β and ββ half-lives. Technical report, Jyväskylän yliopisto, 216. [11] John R. Taylor. An Introduction to Error Analysis. University Science Books, 2 edition, 1996.
38 38
39 39 A K-kertaisesti kiellettyjen uniikkien β-siirtymien faasiavaruusintegraalit Virherajat: Hajoamisenergiat epävarmuuksineen on otettu NNDC:n Q-laskurista [9] Epävarmuudet kaikille faasiavaruusintegraaleille on laskettu seuraavasti: f = f (Q) f,max = f (Q + dq) f,min = f (Q dq) d(f ) = max(f,max f, f f,min ) f (tot) = f (+) + f (EC), joten virheen yleisen etenemislain [11] mukaan ( d(f (tot)) = f (tot) d(f f (+) (+)) ) 2 ( + f (tot) d(f f (EC) (EC)) ) 2 = (d(f (+))) 2 + (d(f (EC))) 2 Kaikki d(f ):t on pyöristetty 15 yksikön säännön mukaisesti [11] Sheet1 2. kiellettyjä uniikkeja beetasiirtymiä Siirtymä Q (kev) dq (kev) f_ (-) d(f_ (-)) f_ (+) d(f_ (+)) f_ (EC) d(f_ (EC)) f_ (tot) d(f_ (tot)) Tm-168 Yb ,9 1,91 7,14E-4,3 Sn-126 Sb ,9E-3,13 Mn-54 Fe ,34 1,1 3,86E-2,5 Nb-94 Zr-94 91,69 2,18, ,6 3,49E-2,6 La-138 Ce ,8,2 2, ,2 Mn-54 Cr ,17 1,1 6,9E-5 1,4E-6, ,5 9,12E-2,6 W-174 Ta ,7 39,5 1,92E-4,15 7, , Te-116 Sb ,7 28,4 5,46E-4,3 2, ,3 2,2729,4 Cr-56 Mn ,6 1,92 16,276852,15 Tm-168 Er ,36 1,89 1,8E-3 4,E-5, ,11,927,12 La-138 Ba ,96 3,43 4,5E-3,2 6, ,9 6,442,1 Ti-52 V ,77 7,13 65, Nb-94 Mo ,64 1,81 16, ,1 Sn-8 In ,84 7,65E-2,6, ,4,875,5 Ce-13 La ,5 38,1, ,6 29, ,842 5 Te-114 Sb ,1 35,5 2,698897,4 54, ,241 7
Ydin- ja hiukkasfysiikka 2014: Harjoitus 5 Ratkaisut 1
 Ydin- ja hiukkasfysiikka 04: Harjoitus 5 Ratkaisut Tehtävä a) Vapautunut energia saadaan laskemalla massan muutos reaktiossa: E = mc = [4(M( H) m e ) (M( 4 He) m e ) m e ]c = [4M( H) M( 4 He) 4m e ]c =
Ydin- ja hiukkasfysiikka 04: Harjoitus 5 Ratkaisut Tehtävä a) Vapautunut energia saadaan laskemalla massan muutos reaktiossa: E = mc = [4(M( H) m e ) (M( 4 He) m e ) m e ]c = [4M( H) M( 4 He) 4m e ]c =
FYSN300 Nuclear Physics I. Välikoe
 Välikoe Vastaa neljään viidestä kysymyksestä 1. a) Hahmottele stabiilien ytimien sidosenergiakäyrä (sidosenergia nukleonia kohti B/A massaluvun A funktiona). Kuvaajan kvantitatiivisen tulkinnan tulee olla
Välikoe Vastaa neljään viidestä kysymyksestä 1. a) Hahmottele stabiilien ytimien sidosenergiakäyrä (sidosenergia nukleonia kohti B/A massaluvun A funktiona). Kuvaajan kvantitatiivisen tulkinnan tulee olla
766334A Ydin- ja hiukkasfysiikka
 1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
Atomin ydin. Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N
 Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
766334A Ydin- ja hiukkasfysiikka
 1 76633A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 3 5-3 Kuorimalli Juhani Lounila Oulun yliopisto, Fysiikan laitos, 011 Kuva 7-13 esittää, miten parillis-parillisten ydinten ensimmäisen
1 76633A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 3 5-3 Kuorimalli Juhani Lounila Oulun yliopisto, Fysiikan laitos, 011 Kuva 7-13 esittää, miten parillis-parillisten ydinten ensimmäisen
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
ψ(x) = A cos(kx) + B sin(kx). (2) k = nπ a. (3) E = n 2 π2 2 2ma 2 n2 E 0. (4)
 76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
J 2 = J 2 x + J 2 y + J 2 z.
 FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
 Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 /
 MS-A3x Differentiaali- ja integraalilaskenta 3, IV/6 Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 / 9..-.3. Avaruusintegraalit ja muuttujanvaihdot Tehtävä 3: Laske sopivalla muunnoksella
MS-A3x Differentiaali- ja integraalilaskenta 3, IV/6 Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitukseen 3 / 9..-.3. Avaruusintegraalit ja muuttujanvaihdot Tehtävä 3: Laske sopivalla muunnoksella
Ydinfysiikkaa. Tapio Hansson
 3.36pt Ydinfysiikkaa Tapio Hansson Ydin Ydin on atomin mittakaavassa äärimmäisen pieni. Sen koko on muutaman femtometrin luokkaa (10 15 m), kun taas koko atomin halkaisija on ångströmin luokkaa (10 10
3.36pt Ydinfysiikkaa Tapio Hansson Ydin Ydin on atomin mittakaavassa äärimmäisen pieni. Sen koko on muutaman femtometrin luokkaa (10 15 m), kun taas koko atomin halkaisija on ångströmin luokkaa (10 10
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Keät 207. Rekyyli Luentomonisteessa on käsitelty tilanne, jossa hiukkanen (massa M) hajoaa kahdeksi hiukkaseksi (massat m ja m 2 ). Tässä käytetään
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Keät 207. Rekyyli Luentomonisteessa on käsitelty tilanne, jossa hiukkanen (massa M) hajoaa kahdeksi hiukkaseksi (massat m ja m 2 ). Tässä käytetään
MAB3 - Harjoitustehtävien ratkaisut:
 MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
1. (a) (2p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori
 FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
1240eV nm. 410nm. Kun kappaleet saatetaan kontaktiin jännite-ero on yhtä suuri kuin työfunktioiden erotus ΔV =
 S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
Hiukkasfysiikan luento 21.3.2012 Pentti Korpi. Lapuan matemaattisluonnontieteellinen seura
 Hiukkasfysiikan luento 21.3.2012 Pentti Korpi Lapuan matemaattisluonnontieteellinen seura Atomi Aine koostuu molekyyleistä Atomissa on ydin ja fotonien ytimeen liittämiä elektroneja Ytimet muodostuvat
Hiukkasfysiikan luento 21.3.2012 Pentti Korpi Lapuan matemaattisluonnontieteellinen seura Atomi Aine koostuu molekyyleistä Atomissa on ydin ja fotonien ytimeen liittämiä elektroneja Ytimet muodostuvat
Kvantittuminen. E = hf f on säteilyn taajuus h on Planckin vakio h = 6, Js = 4, evs. Planckin kvanttihypoteesi
 Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
H7 Malliratkaisut - Tehtävä 1
 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
Hajoamiskaaviot ja niiden tulkinta (PHYS-C0360)
 Hajoamiskaaviot ja niiden tulkinta (PHYS-C0360) Jarmo Ala-Heikkilä, VIII/2017 Useissa tämän kurssin laskutehtävissä täytyy ensin muodostaa tilannekuva: minkälaista säteilyä lähteestä tulee, mihin se kohdistuu,
Hajoamiskaaviot ja niiden tulkinta (PHYS-C0360) Jarmo Ala-Heikkilä, VIII/2017 Useissa tämän kurssin laskutehtävissä täytyy ensin muodostaa tilannekuva: minkälaista säteilyä lähteestä tulee, mihin se kohdistuu,
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
TEHTÄVIEN RATKAISUT. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 712 p m 105 kg
 TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia: Mitä opimme?
 TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
Osallistumislomakkeen viimeinen palautuspäivä on maanantai
 Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
S Fysiikka III (EST) Tentti ja välikoeuusinta
 S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
Numeeriset menetelmät TIEA381. Luento 5. Kirsi Valjus. Jyväskylän yliopisto. Luento 5 () Numeeriset menetelmät / 28
 Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Ydin- ja hiukkasfysiikka: Harjoitus 1 Ratkaisut 1
 Ydin- ja hiukkasfysiikka: Harjoitus Ratkaisut Tehtävä i) Isotoopeilla on sama määrä protoneja, eli sama järjestysluku Z, mutta eri massaluku A. Tässä isotooppeja keskenään ovat 9 30 3 0 4Be ja 4 Be, 4Si,
Ydin- ja hiukkasfysiikka: Harjoitus Ratkaisut Tehtävä i) Isotoopeilla on sama määrä protoneja, eli sama järjestysluku Z, mutta eri massaluku A. Tässä isotooppeja keskenään ovat 9 30 3 0 4Be ja 4 Be, 4Si,
Neutriinokuljetus koherentissa kvasihiukkasapproksimaatiossa
 Neutriinokuljetus koherentissa kvasihiukkasapproksimaatiossa Graduseminaari Joonas Ilmavirta Jyväskylän yliopisto 15.6.2012 Joonas Ilmavirta (JYU) Neutriinot ja cqpa 15.6.2012 1 / 14 Osa 1: Neutriinot
Neutriinokuljetus koherentissa kvasihiukkasapproksimaatiossa Graduseminaari Joonas Ilmavirta Jyväskylän yliopisto 15.6.2012 Joonas Ilmavirta (JYU) Neutriinot ja cqpa 15.6.2012 1 / 14 Osa 1: Neutriinot
4 LUKUJONOT JA SUMMAT
 Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 10: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali.
 MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ch7 Kvanttimekaniikan alkeita. Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset.
 Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Nyt n = 1. Tästä ratkaistaan kuopan leveys L ja saadaan sijoittamalla elektronin massa ja vakiot
 S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
f (28) L(28) = f (27) + f (27)(28 27) = = (28 27) 2 = 1 2 f (x) = x 2
 BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
Kertaus. x x x. K1. a) b) x 5 x 6 = x 5 6 = x 1 = 1 x, x 0. K2. a) a a a a, a > 0
 Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
jakokulmassa x 4 x 8 x 3x
 Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Juuri 12 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Juuri Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 7.5.08 Kertaus K. a) Polynomi P() = + 8 on jaollinen polynomilla Q() =, jos = on polynomin P nollakohta, eli P() = 0. P() = + 8 = 54 08 +
Juuri Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 7.5.08 Kertaus K. a) Polynomi P() = + 8 on jaollinen polynomilla Q() =, jos = on polynomin P nollakohta, eli P() = 0. P() = + 8 = 54 08 +
Oppikirja (kertauksen vuoksi)
 Oppikirja (kertauksen vuoksi) Luento seuraa suoraan oppikirjaa: Malcolm H. Levitt: Spin Dynamics Basics of Nuclear Magnetic Resonance Wiley 2008 Oppikirja on välttämätön sillä verkkoluento sisältää vain
Oppikirja (kertauksen vuoksi) Luento seuraa suoraan oppikirjaa: Malcolm H. Levitt: Spin Dynamics Basics of Nuclear Magnetic Resonance Wiley 2008 Oppikirja on välttämätön sillä verkkoluento sisältää vain
, on säännöllinen 2-ulotteinen pinta. Määrää T x0 pisteessä x 0 = (0, 1, 1).
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
Shrödingerin yhtälön johto
 Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
y x1 σ t 1 = c y x 1 σ t 1 = y x 2 σ t 2 y x 2 x 1 y = σ(t 2 t 1 ) x 2 x 1 y t 2 t 1
 1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 varuusintegraali iemmin laskimme yksiulotteisia integraaleja b a f (x)dx, jossa integrointialue on x-akselin väli [a, b]. Lisäksi laskimme kaksiulotteisia integraaleja
Matematiikan tukikurssi Kurssikerta 6 varuusintegraali iemmin laskimme yksiulotteisia integraaleja b a f (x)dx, jossa integrointialue on x-akselin väli [a, b]. Lisäksi laskimme kaksiulotteisia integraaleja
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
Mapu 1. Laskuharjoitus 3, Tehtävä 1
 Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
a) Sievennä lauseke 1+x , kun x 0jax 1. b) Aseta luvut 2, 5 suuruusjärjestykseen ja perustele vastauksesi. 3 3 ja
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Leptonit. - elektroni - myoni - tauhiukkanen - kolme erilaista neutriinoa. - neutriinojen varaus on 0 ja muiden leptonien varaus on -1
 Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
Kvanttimekaniikkaa yhdessä ulottuvuudessa
 Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
k=0 saanto jokaisen kolmannen asteen polynomin. Tukipisteet on talloin valittu
 LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Voima ja potentiaalienergia II Energian kvantittuminen
 Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
Hiukkasfysiikkaa. Tapio Hansson
 Hiukkasfysiikkaa Tapio Hansson Aineen Rakenne Thomson onnistui irrottamaan elektronin atomista. Rutherfordin kokeessa löytyi atomin ydin. Niels Bohrin pohdintojen tuloksena elektronit laitettiin kiertämään
Hiukkasfysiikkaa Tapio Hansson Aineen Rakenne Thomson onnistui irrottamaan elektronin atomista. Rutherfordin kokeessa löytyi atomin ydin. Niels Bohrin pohdintojen tuloksena elektronit laitettiin kiertämään
Neutriino-oskillaatiot
 Neutriino-oskillaatiot Seminaariesitys Joonas Ilmavirta Jyväskylän yliopisto 29.11.2011 Joonas Ilmavirta (JYU) Neutriino-oskillaatiot 29.11.2011 1 / 16 Jotain vikaa β-hajoamisessa Ytimen β-hajoamisessa
Neutriino-oskillaatiot Seminaariesitys Joonas Ilmavirta Jyväskylän yliopisto 29.11.2011 Joonas Ilmavirta (JYU) Neutriino-oskillaatiot 29.11.2011 1 / 16 Jotain vikaa β-hajoamisessa Ytimen β-hajoamisessa
A = (a 2x) 2. f (x) = 12x 2 8ax + a 2 = 0 x = 8a ± 64a 2 48a x = a 6 tai x = a 2.
 MATP53 Approbatur B Harjoitus 7 Maanantai..5. (Teht. s. 9.) Neliön muotoisesta pahviarkista, jonka sivun pituus on a, taitellaan kanneton laatikko niin, että pahviarkin nurkista leikataan neliön muotoiset
MATP53 Approbatur B Harjoitus 7 Maanantai..5. (Teht. s. 9.) Neliön muotoisesta pahviarkista, jonka sivun pituus on a, taitellaan kanneton laatikko niin, että pahviarkin nurkista leikataan neliön muotoiset
1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria
 Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Kvanttifysiikan perusteet, harjoitus 5
 Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
Kvanttifysiikan perusteet, harjoitus 5 February 4, 07 Tehtävä Oletetaan energian ominaisfunktiot φ n ortonormitetuiksi, dxφ nφ m = δ nm, jossa δ nm on Kroneckerin delta. Määritetään ensin superpositiotilan
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Mat. tukikurssi 27.3.
 Mat. tukikurssi 7.. Tänään oli paljon vaikeita aiheita: - suunnattu derivaatta - kokonaisdierentiaali - dierentiaalikehitelmä - implisiittinen derivointi Nämä kaikki liittvät aika läheisesti toisiinsa.
Mat. tukikurssi 7.. Tänään oli paljon vaikeita aiheita: - suunnattu derivaatta - kokonaisdierentiaali - dierentiaalikehitelmä - implisiittinen derivointi Nämä kaikki liittvät aika läheisesti toisiinsa.
Määritelmä Olkoon T i L (V i, W i ), 1 i m. Yksikäsitteisen lineaarikuvauksen h L (V 1 V 2 V m, W 1 W 2 W m )
 Määritelmä 519 Olkoon T i L V i, W i, 1 i m Yksikäsitteisen lineaarikuvauksen h L V 1 V 2 V m, W 1 W 2 W m h v 1 v 2 v m T 1 v 1 T 2 v 2 T m v m 514 sanotaan olevan kuvausten T 1,, T m indusoima ja sitä
Määritelmä 519 Olkoon T i L V i, W i, 1 i m Yksikäsitteisen lineaarikuvauksen h L V 1 V 2 V m, W 1 W 2 W m h v 1 v 2 v m T 1 v 1 T 2 v 2 T m v m 514 sanotaan olevan kuvausten T 1,, T m indusoima ja sitä
1 + b t (i, j). Olkoon b t (i, j) todennäköisyys, että B t (i, j) = 1. Siis operaation access(j) odotusarvoinen kustannus ajanhetkellä t olisi.
 Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Atomimallit. Tapio Hansson
 Atomimallit Tapio Hansson Atomin käsite Atomin käsite on peräisin antiikin Kreikasta. Filosofi Demokritos päätteli (n. 400 eaa.), että äärellisen maailman tulee koostua äärellisistä, jakamattomista hiukkasista
Atomimallit Tapio Hansson Atomin käsite Atomin käsite on peräisin antiikin Kreikasta. Filosofi Demokritos päätteli (n. 400 eaa.), että äärellisen maailman tulee koostua äärellisistä, jakamattomista hiukkasista
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa
 MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ
 YLIOPPILSTUTKINTO- LUTKUNT..7 MTEMTIIKN KOE PITKÄ OPPIMÄÄRÄ -osa Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän alla olevaan ruudukkoon.
YLIOPPILSTUTKINTO- LUTKUNT..7 MTEMTIIKN KOE PITKÄ OPPIMÄÄRÄ -osa Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän alla olevaan ruudukkoon.
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
TILASTOLLISEN KVANTTIMEKANIIKAN PERUSTEITA (AH 5.1-5.3) Mikrotilat (kertausta Kvanttimekaniikan kurssilta)
 TILASTOLLISEN KVANTTIMEKANIIKAN PERUSTEITA (AH 5.1-5.3) Mikrotilat (kertausta Kvanttimekaniikan kurssilta) Kvanttimekaniikassa yhden hiukkasen systeemin täydellisen kuvauksen antaa tilavektori, joka on
TILASTOLLISEN KVANTTIMEKANIIKAN PERUSTEITA (AH 5.1-5.3) Mikrotilat (kertausta Kvanttimekaniikan kurssilta) Kvanttimekaniikassa yhden hiukkasen systeemin täydellisen kuvauksen antaa tilavektori, joka on
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
Markov-ketjut pitkällä aikavälillä
 2A Markov-ketjut pitkällä aikavälillä Tämän harjoituksen tavoitteena on oppia lukemaan siirtymämatriisista tai siirtymäkaaviosta, milloin Markov-ketju on yhtenäinen ja jaksoton; oppia tunnistamaan, milloin
2A Markov-ketjut pitkällä aikavälillä Tämän harjoituksen tavoitteena on oppia lukemaan siirtymämatriisista tai siirtymäkaaviosta, milloin Markov-ketju on yhtenäinen ja jaksoton; oppia tunnistamaan, milloin
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
Tfy Fysiikka IIB Mallivastaukset
 Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
Aatofunktiot ja epätarkkuus
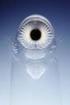 Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
