Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2010 Arkkitehtivalinnan matematiikan koe, klo Sarja A-FI
|
|
|
- Eeva-Kaarina Heidi Saarinen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 010 Arkkitehtivalinnan matematiikan koe, klo Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu usealle konseptille. Laadi ratkaisut selkeästi välivaiheineen, tarvittaessa kirjoita ratkaisu uudelleen puhtaaksi. Merkitse hylkäämäsi ratkaisu tai hylkäämäsi ratkaisun osa yliviivaamalla se sillä saman tehtävän useista ratkaisuista huonoin otetaan mukaan arvosteluun. Huomaa, että kukin tehtävä arvostellaan kokonaisuutena, eivätkä alakohdat välttämättä ole pisteytyksessä samanarvoisia. Apuvälineet: Kirjoitusvälineet ja funktiolaskin. Liite: Kaavakokoelma. A1 Pariskunta ottaa asuntolainaa e. He sopivat maksavansa pankille e kunkin täyden vuoden kuluttua lainan nostamishetkestä. Lainapääomaa lyhennetään vuosittain osalla, joka mainitusta summasta jää korkojen maksun jälkeen. Ensimmäisenä kahtena vuotena korko on,5 %. Miten suuri korkoprosentti oli kolmantena vuonna, kun laina tuolloin lyheni vain 478,85 eurolla? Anna vastaus kahden desimaalin tarkkuudella. A Harjakattoinen navetta on pohjaltaan suorakulmaisen L-kirjaimen muotoinen. Katon harja on 8 m ja räystäät 5 m korkeudella maanpinnasta. Katon leveys räystäästä räystääseen on 1 m kummassakin siivessä. Katon harja sijaitsee symmetrisesti katon keskellä ja harjan kokonaispituus on 40 m. Navetan katto maalataan. Kuinka monta,7 litran astiaa maalia on ostettava, kun maalilitra peittää 6 m? A3 Kakku on muodoltaan suora ympyräkartio, jonka korkeus on 15 cm. Kakku halutaan leikata pohjan suuntaisilla tasoilla kolmeen tilavudeltaan yhtä suureen osaan. Kuinka korkeita paloista tulee? Anna vastaukset millimetrin tarkkuudella. A4 Olet tallettanut puhelimeesi sveitsiläisen pankkikorttisi tunnusluvun ( ) viisi numeroa satunnaisessa järjestyksessä, mutta unohtanut numeroiden oikean järjestyksen. Millä todennäköisyydellä osut oikeaan jollakin kolmesta eri yrityksestä, (a) kun talletettu luku on 8756, (b) kun talletettu luku on 8755? A5 Liukumäen profiili noudattaa muotoa, y = ax (3b x), 0 x b. Tässä x ja y on ilmaistu metreinä ja a, b > 0 ovat suunnitteluparametreja. Kuinka lyhyt liukumäki voi olla (siis kuinka pieni parametri b voi olla), jos sen kaltevuus (kuvassa α) ei missään pisteessä saa ylittää 30 ja liukumäen korkeuseron pitää olla kaksi metriä? Anna vastaus yhden senttimetrin tarkkuudella. A6 Egyptologi Bryggmann näkee laskevassa auringossa, tasaisella aavikolla pyramidin. Pyramidin huippu sijaitsee kompassisuunnassa 31,0, pyramidin huipun varjo kompassisuunnassa 5,0, aurinko kompassisuunnassa 60,0. (Kompassisuunnat mitataan asteina myötäpäivään pohjoisesta.) Kartasta egyptologi mittaa pyramidin etäisyydeksi (pohjan pisteeseen suoraan huipun alla) 345 m. Edelleen hän mittaa varjonsa pituudeksi kolme kertaa pituutensa. Näillä tiedoilla hän laskee pyramidin korkeuden. Mikä korkeus on? Anna vastauksesi metrin tarkkuudella. c 010, Dia-valinta, c/o Aalto-yliopisto, opintotoimisto
2 Diplomingenjörs- och arkitektutbildningens gemensamma dia-antagning 010 Arkitekturantagningens prov i matematik, kl Serie A-SV Anvisningar. Placera varje uppgift på en egen sida. Markera om svaret fortsätter på flera koncept. Ge klart utarbetade lösningar inklusive mellanstadier, renskriv lösningen vid behov. Förkastade lösningar och förkastade delar av en lösning skall överstrykas. Om icke-överstrukna lösningar föreligger, bedöms den sämsta av dessa. Notera, att varje fråga bedöms som en helhet och att delfrågorna inte nödvändigtvis har samma vikt i bedömningen. Hjälpmedel: Skrivredskap och funktionsräknare. Bilaga: Formelsamling. A1 Ett par tar ett bostadslån på e. De kommer överens att betala banken e i slutet av varje helt år efter att lånet lyftes. Lånet avkortas årligen med den delen av den nämda summan, som blir över efter att räntan betalats. Under de första två åren är räntan,5 %. Hur hög var ränteprocenten tredje året, om lånet avkortades med bara 478,85 euro då? Ge svaret med två decimalers noggrannhet. A En lada med sadeltak har bottenprofilen i form av bokstaven L med en rät vinkel. Takåsen år 8 m och takfoten 5 m ovanför marken. Takets bredd från takfot till takfot är 1 m i bägge vingarna. Takåsen finns mitt på taket och dess sammanlagda längd är 40 m. Ladans tak målas. Hur många burker med,7 liter färg måste man köpa, om en liter täcker 6 m? A3 En kaka har formen av en rät cirkulär kon med höjden 15 cm. Man vill skära kakan i tre delar, alla med lika stor volym, med hjälp av plana snitt parallella med kakans botten. Hur höga kommer bitarna att vara? Ge svaren med en millimeters noggrannhet. A4 Du har lagrat de fem siffrorna till nummerkoden ( ) till ditt schweiziska bankkort i en slumpmässig ordning i din telefon, med glömt siffrornas rätta ordning. Med vilken sannolikhet hittar du rätt på något av tre olika försök, (a) om det lagrade talet är 8756, (b) om det lagrade talet är 8755? A5 Profilen hos en rutschbana har formen y = ax (3b x), 0 x b. Här är x och y givna i meter och a, b > 0 är planeringsparameter. Hur kort kan rutschbanan vara (dvs. hur liten kan parametern b vara), om dess lutning (α i figuren) inte får överskrida 30 och om höjdskillnaden hos rutchbanan skall vara två meter. Ge svaret med en centimeters noggranhet. A6 Egytologen Bryggmann ser en pyramid i den nedgående solens ljus på den plana öknen. Pyramidens topp är i kompassriktningen 31,0, skuggan av pyramidens topp i kompassriktningen 5,0 och solen i kompassriktningen 60,0. (Kompassriktningarna är mätta i grader medsols från norr.) Från kartan mäter egytologen avståndet till pyramiden 345 m (till punkten på bottnet direkt under toppen). Vidare uppmäter han längden hos sin skugga till att vara tre gånger sin längd. Med denna information beräknar han pyramidens höjd. Vilket var höjden? Ge svaret med en meters noggrannhet. c 010, Dia-antagningen, c/o Aalto-universitetet, studiebyrån
3 Common University Admission in Engineering and Architecture (dia-admission) 010 Mathematics examination for Architecture admission, at Series A-EN Instructions. Reserve a separate page for each problem. Indicate if the answer continues on a separate sheet. Give your solutions in a clear form including intermediate steps. Rewrite a clean copy of the solution if needed. Cross out discarded solutions and any discarded parts of the solutions. In the case of several solutions for the same problem, only the weakest one will be credited. Note that subsections of a question are not necessarily equally weighted. Allowed instruments: Writing instruments, non programmable calculators, non electronic general-language dictionaries to/from English. Attachment: Table of formulae. A1 A couple takes a e loan to finance an appartment. They agree to pay the bank e at end of every full year from the day taking the loan. Each year the capital will be payed off by the amount remaining after payment of the interest. During the first two years the interest rate is.5 %. What is the rate on the third year knowing that the capital that year was paid off by euro only? Give the answers rounded to the accuracy of two decimals. A A barn has a gable roof and a L-shaped plan with right angle. The roof peak is 8 m long and the eaves at the height of 5 m from the ground. The roof is 1 m wide from eave to eave in both wings. The peak of the roof is located symmetrically in the middle of the roof and peaks total length is 40 m. The roof is to be painted. How many.7 litre paint containers one needs to buy, when a litre paint covers 6 m? A3 An cake has the shape of a right cone with the height of 15 cm. Using planes parallel to the cake bottom the cake is cut into three pieces with the equal volume. What are the heights of the pieces? Give the answers rounded to the nearest millimeter. A4 You have stored in your phone the five digits in the pin code ( ) of your Swiss credit card. The digits are in a random order and you have forgotten the correct combination. On what propability do you find the correct combination at one of three different tries, (a) when the number written down is 8756, (b) when the number written down is 8755? A5 The side profile of a slide has the shape of the curve y = ax (3b x), 0 x b. Here x and y are given in meters and a, b > 0 are free parameters. How short can the slide be made (i.e. how small can the parameter b be), when the slope (α in the figure) cannot exceed 30 and the height difference shall be two meters. Give the answers rounded to the nearest centimeter. A6 Egyptogist Bryggmann sees, in a sunset, a pyramid on flat desert. The peak of the pyramid is seen in the compass direction 31.0, the shadow of the peak in the compass direction 5.0, the Sun in the compass direction (The compass directions are measured clockwise from the North.) From the map the egyptologist measures the distance to the pyramid (to the point on its bottom directly under its peak) 345 m. Furthermore, he measures the length of his shadow to be three times his length. Using this information he calculates the height of the pyramid. What is the height? Give the answers rounded to the nearest meter. c 010, Dia-admission, c/o Aalto University, Student Affairs
4 Tehtävä 1 c 0 = 00000, a = 1000, r 1 = r =,5%. lyhennys d i = a c i 1 r i ja uusi pääoma c i = c i 1 d i. c 1 = , c = 18585, Kolmantena vuonna siis r 3 = (a d 3 )/c = 6.0%. Arvostelu: Ratkaisun ensimmäinen vuosi (+1p), toinen vuosi (+p), kolmas vuosi (+3p). Muotovirheistä, kuten muodosta korko on 0, 06 tai 6, % vähennetään piste. Tehtävä Merkitään harjan osien pituuksia a, b. Tiedämme, että s = a + b = 40. Katon lape harjasta räystääseen on d = (8 5) + (1/) = 3 5 pitkä. Katon neljä lapetta ovat puolisuunnikkaita: A = a + (a + d) d + a + (a d) d + b + (b + d) = d(a + b) = d + b + (b + d) neliömetriä. Astian riittävyys on q = (, 7 6) l/m, joten maalin menekki on A/q 33, 1 ja tarvitaan 34 astiaa. d Arvostelu: Mallivastauksessa erottelu puolisuunnikkaiksi (+p), lausekkeen oikein laskettu (+3p), muunnos astioiksi (+1p). Tehtävässä ratkaisussa on oleellista, että siinä huomioidaan tehtävän kolmiuloitteinen luonne. Mikäli tarkastellaan vain projektiota on epäselvää, miten päättely on tehty. Kuten ratkaisusta näkyy, katon pinta-ala vastaa s pitkää ja d leveää suorakaidetta. Monessa vastauksessa on pyritty näyttämään ensi tämä ja laskettu näin pinta-ala suoraan lausekkeen ds. Tämä on täysin perusteltua, mutta perustelu on hyväksytty, vain mikäli siitä on käynyt ilmi, että tarkastelu on suoritettu huomioiden tehtävän kolmiulotteinen luonne: mikäli perustelussa on vedottu vain suoraan ylhäältä nähtyy projektioon, tehtävästä on annettu vain 3p, koska projektiossa osien mitata eivät skaalaudu samassa suhteessa (samansuuntaisetkin eri mittaiset viivat voivat olla eripituisia). Tehtävän rajoittaminen ilman huolellisia perusteluja tietyyn erityistapaukseenvalitsemalla a:lle ja b:lle arvo, kuten a = b = 0, arvostellaan 4p arvoiseksi tehtävästä.
5 Tehtävä 3 Merkitään palojen korkeutta ylhäältä laskien h 1, h, h 3. Korkeuksille pätee h 1 + h + h 3 = h. Ylimmälle kappaleelle saamme yhdenmuotoisten kappaleiden tilavuuksia suhteen perusteella h 3 1 : h 3 = 1 : 3, h 1 = h 1 = (1/3) 1/3 h. Tarkastellaan nyt kappaletta, jonka muodostavat kaksi ylintä palaa yhdessä. Merkitään sen korkeutta k. k 3 : h 3 = : 3, k = h 1 + h = (/3) 1/3 h, Tästä edelleen ( h = k h 1 = (/3) 1/3 (1/3) 1/3) h ( h 3 = h k = 1 (/3) 1/3) h Vastaus, kun h = 150 mm: h 1 = mm, h = mm, h 3 = mm. Arvostelu: Tehtävän arvostelu perustuu kahteen osaan: ylimmän palan korkeuden laskeminen (3p) ja kahden muun palan korkeus (3p). Mikäli tehtävässä tehtävä on ratkaistu vain jossakin erityistapauksessa pisteet ovat korkeintaan 4p. Tehtävä 4 Kohdassa (a) mahdollisia kombinaatioita on n = 5! = 10, joten todennäköisyys epäonnistua (n 1) (n ) (n 3) 1 p = n (n 1) (n ) = n 3 = 1 3 n n eli onnistumiselle p = 3 n = 1 40 = 0.05 Kohdassa (b) mahdollisia kombinaatioita on n = 5!/! = 60, joten todennäköisyys onnistua on edellisen perusteella nyt p = 3 n = 1 0 = 0.05 Vaihtoehtoisesti kummassakin kohdassa voidaan tarkastella tapausta, jossa kombinaatioiden (n kpl) joukosta on valittu m = 3 kombinaatiota. Todennäköisyys sille, että pankkikortin oikea kombinaatio on valittujen joukossa, on selvästi p = m/n. Arvostelu: Tehtävässä osakysymyksistä annetaan lähtökohtaisesti kummastakin 3p. Kummassakin alitehtävässä erikseen kombinaatioiden määrästä (n) hyvitetään 1p. Alitehtävän todennäköisyyden laskeminen antaan loput pisteistä. Pääsääntöisesti väärä kombinaatioiden määrä estää hyvittämästä alitehtävän lopusta riippumatta sen suorituksesta. Perustelun puuttumisesta vastausta on sakotettu lähtökohtaisesti 1p. Mikäli tarkastellaan kolmea nostoa, ne eivät muodosta kolmea riippumatonta alkeistapausta: esimerkkinä väärästä väitteestä on: tapahtuma/nostot ovat riippumattomia, joten kysytty todennäköisyys p = 1/n + 1/n + 1/n.
6 Tehtävä 5 y = ax (3b x) = a(3bx x 3 ) (1) k := tan α = y = a(6bx 6x ) = 6a(bx x ) () Koska y 0 koko liukumäen matkalla (0 x b) on vastaavasti liukumäen korkeuserolle = y(b) y(0) = ab (3b b) = ab 3. (3) Lyhyin liukumäki saavutetaan, kun jyrkkyys on maksimissaan: a = /b 3. (4) k = (y ) = y = 6a(b x) = 0 x = x 0 := b/ [0, b]. (5) Koska kyseessä on alapäin aukeava parabeli, jyrkin kohta sijaitsee k:n derivaatan nollakohdassa. Niinpä Tehtävä 6 Merkitään pyramidin pohjan keskipisteen, egyptologin ja varjon kärjen paikkoja P, E, V. Etäisyys EP = 345. Kolmion P EV kulma V = (60 180) 5 = 8, ja E = 5 31 = 1, joten sinilausetta käyttämällä saamme EP sin V = P V sin E, P V = 345 sin(1 ) sin(8 ) Pyramidin korkeus kolmasosa varjonsa pituudesta, eli 87, m. Arvostelu: Tehtävässä kulmien V ja E löytäminen antaa (+p), P V ratkaiseminen (+3p) ja korkeuden lausuminen oikein (+1p). tan α = tan(30 ) = 1/ 3 k = y (x = x 0 ) = 6a(b / (b/) ) = 3 ab (6) Yhdistetään tämä ehtoon (4) ab 3 3 (7) joten alarajaksi saadaan: b 50 cm. b 3 3 = (8) Arvostelu: Mäen korkeusvaatimuksen pukeminen yhteydeksi +1p, jyrkimmän pisteen selvittämien perusteluineen (5) +p, jyrkkyyden rajan käsitteleminen (7) +p, vastaus oikeassa muodossa +1p. Pelkästä y:n ensimmäisen derivaatan mekaanisesta laskemisesta ei ole hyvitetty. Kaltevuuden maksimin lausekkeesta hyvittäminen sisältää perustelun ääriarvon olemassaolosta (tarkastelu päissä tms). c 010, Dia-valinta, c/o Aalto-yliopisto, opintotoimisto
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2007 Insinöörivalinnan matematiikankoe, 29.5.2007 klo 14-17
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 007 Insinöörivalinnan matematiikankoe, 9.5.007 klo 14-17 Sarja A Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 007 Insinöörivalinnan matematiikankoe, 9.5.007 klo 14-17 Sarja A Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2015 Insinöörivalinnan matematiikan koe, 26.5.2015 klo 14-17 Sarja A-FI. A3 Ratkaise yhtälöt:
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 015 Insinöörivalinnan matematiikan koe, 6.5.015 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 015 Insinöörivalinnan matematiikan koe, 6.5.015 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
DIA-valinta 2009 ArkMat +sv. 18.5.2009 nippukoko 10+10=20 (1/1)
 DIA-valinta 2009 ArkMat +sv sarja A 18.5.2009 nippukoko 10+10=20 (1/1) Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Arkkitehtivalinnan matematiikan koe, 18.5.2009 Sarja A-FI Ohjeita. Sijoita
DIA-valinta 2009 ArkMat +sv sarja A 18.5.2009 nippukoko 10+10=20 (1/1) Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Arkkitehtivalinnan matematiikan koe, 18.5.2009 Sarja A-FI Ohjeita. Sijoita
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2011 Insinöörivalinnan matematiikan koe, 31.5.2010 klo 14-17. Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 0 Insinöörivalinnan matematiikan koe, 3..00 klo -7. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu usealle
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 0 Insinöörivalinnan matematiikan koe, 3..00 klo -7. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu usealle
HTKK, TTKK, OY/Arkkitehtiosastot Valintakuulustelujen matematiikan koe 17.5.2002. arvoilla leikkauspisteen molemmat koordinaatit ovat positiiviset?
 HTKK, TTKK, OY/Arkkitehtiosastot Valintakuulustelujen matematiikan koe 17..00 Sarja A A1. Määritä suorien ax + y ja x y 3 leikkauspiste. Millä vakion a arvoilla leikkauspisteen molemmat koordinaatit ovat
HTKK, TTKK, OY/Arkkitehtiosastot Valintakuulustelujen matematiikan koe 17..00 Sarja A A1. Määritä suorien ax + y ja x y 3 leikkauspiste. Millä vakion a arvoilla leikkauspisteen molemmat koordinaatit ovat
A5 Yhtälössä ax 2 + bx + c = 0 esiintyvät kertoimet a, b, c saavat arvoja joukosta
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 22 Insinöörivalinnan matematiikan koe, 3.5.22 klo 4-7. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 22 Insinöörivalinnan matematiikan koe, 3.5.22 klo 4-7. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2013 Arkkitehtivalinnan matematiikan koe, 20.5.2013 klo 13-16. Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 013 Arkkitehtivalinnan matematiikan koe, 0.5.013 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 013 Arkkitehtivalinnan matematiikan koe, 0.5.013 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2015 Insinöörivalinnan matematiikan koe, 26.5.2015 klo 14-17 Sarja A-FI. A3 Ratkaise yhtälöt:
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2015 Insinöörivalinnan matematiikan koe, 26.5.2015 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2015 Insinöörivalinnan matematiikan koe, 26.5.2015 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
anna minun kertoa let me tell you
 anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2013 Insinöörivalinnan matematiikan koe, 28.5.2013 klo 14-17. Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 013 Insinöörivalinnan matematiikan koe, 8.5.013 klo 14-17. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 013 Insinöörivalinnan matematiikan koe, 8.5.013 klo 14-17. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2012 Arkkitehtivalinnan matematiikan koe, 21.5.2012 klo 13-16. Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2012 Arkkitehtivalinnan matematiikan koe, 21.5.2012 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2012 Arkkitehtivalinnan matematiikan koe, 21.5.2012 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2014 Arkkitehtivalinnan matematiikan koe, 19.5.2014 klo 13-16 Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 014 Arkkitehtivalinnan matematiikan koe, 19.5.014 klo 1-16 Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 014 Arkkitehtivalinnan matematiikan koe, 19.5.014 klo 1-16 Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä jatkuu
Other approaches to restrict multipliers
 Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
2.1 Yhdenmuotoiset suorakulmaiset kolmiot
 2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
2.1 Yhdenmuotoiset suorakulmaiset kolmiot 2.2 Kulman tangentti 2.3 Sivun pituus tangentin avulla 2.4 Kulman sini ja kosini 2.5 Trigonometristen funktioiden käyttöä 2.7 Avaruuskappaleita 2.8 Lieriö 2.9
A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-6. Taulukkokirjaa saa käyttää apuna, laskinta ei.
 PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
PITKÄ MATEMATIIKKA PRELIMINÄÄRIKOE 7..07 NIMI: A-osa. Ratkaise kaikki tämän osan tehtävät. Tehtävät arvostellaan pistein 0-. Taulukkokirjaa saa käyttää apuna, laskinta ei.. Valitse oikea vaihtoehto ja
make and make and make ThinkMath 2017
 Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2010 Insinöörivalinnan matematiikan koe, 1.6.2010 klo 14-17... Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2010 Insinöörivalinnan matematiikan koe, 1.6.2010 klo 14-17... Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2010 Insinöörivalinnan matematiikan koe, 1.6.2010 klo 14-17... Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Efficiency change over time
 Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Choose Finland-Helsinki Valitse Finland-Helsinki
 Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
The Viking Battle - Part Version: Finnish
 The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
Fraktaalit. Fractals. Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto. 1 / 8 R. Kangaslampi Fraktaalit
 Fraktaalit Fractals Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.-7.10.2012 1 / 8 R. Kangaslampi Fraktaalit Bottomless wonders spring from simple rules, which are repeated
Fraktaalit Fractals Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.-7.10.2012 1 / 8 R. Kangaslampi Fraktaalit Bottomless wonders spring from simple rules, which are repeated
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
d h Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2011 Arkkitehtivalinnan matematiikan koe, 23.5.2011 klo 13-16.
 Diplomi-insinöörien ja arkkitehtien ia-yhteisvalinta 2011 Arkkitehtivalinnan matematiikan koe, 23.5.2011 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Diplomi-insinöörien ja arkkitehtien ia-yhteisvalinta 2011 Arkkitehtivalinnan matematiikan koe, 23.5.2011 klo 13-16. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
812336A C++ -kielen perusteet, 21.8.2010
 812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward.
 START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
Kysymys 5 Compared to the workload, the number of credits awarded was (1 credits equals 27 working hours): (4)
 Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Arkkitehtivalinnan matematiikan koe, 18.5.2009 Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 009 Arkkitehtivalinnan matematiikan koe 18.5.009 Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse jos tehtävä jatkuu usealle
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 009 Arkkitehtivalinnan matematiikan koe 18.5.009 Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse jos tehtävä jatkuu usealle
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Metsälamminkankaan tuulivoimapuiston osayleiskaava
 VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
1.3 Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 811122P (5 op.) 12.12.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 811122P (5 op.) 12.12.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Insinöörivalinnan matematiikan koe, 26.5.2009 klo 14-17 Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Insinöörivalinnan matematiikan koe, 2652009 klo 14-17 Sarja A-FI Ohjeita Sijoita jokainen tehtävä omalle sivulleen Merkitse, jos tehtävä jatkuu
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2009 Insinöörivalinnan matematiikan koe, 2652009 klo 14-17 Sarja A-FI Ohjeita Sijoita jokainen tehtävä omalle sivulleen Merkitse, jos tehtävä jatkuu
Capacity Utilization
 Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Preliminäärikoe Tehtävät Pitkä matematiikka 4.2.2014 1 / 3
 Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Salasanan vaihto uuteen / How to change password
 Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
( ( OX2 Perkkiö. Rakennuskanta. Varjostus. 9 x N131 x HH145
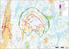 OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
c) Millä todennäköisyydellä virtapiiri 2 on osittain toimiva?
 TKK, TTY, LTY, OY, Å / Insinööriosastot Valintakuulustelujen matematiikan koe 7.5.003 Sarja Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Laadi ratkaisut selkeästi välivaiheineen, tarvittaessa kirjoita
TKK, TTY, LTY, OY, Å / Insinööriosastot Valintakuulustelujen matematiikan koe 7.5.003 Sarja Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Laadi ratkaisut selkeästi välivaiheineen, tarvittaessa kirjoita
Lataa ilmaiseksi mafyvalmennus.fi/mafynetti. Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla!
 Miten opit parhaiten? Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla! n Harjoittelu tehdään aktiivisesti tehtäviä ratkomalla. Tehtävät kattavat kaikki yo-kokeessa
Miten opit parhaiten? Valmistaudu pitkän- tai lyhyen matematiikan kirjoituksiin ilmaiseksi Mafynetti-ohjelmalla! n Harjoittelu tehdään aktiivisesti tehtäviä ratkomalla. Tehtävät kattavat kaikki yo-kokeessa
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2018 Insinöörivalinnan matematiikan koe, 2952018, Ratkaisut (Sarja A) 1 Anna kaikissa kohdissa vastaukset tarkkoina arvoina Kohdassa d), anna kulmat
Tynnyrivaara, OX2 Tuulivoimahanke. ( Layout 9 x N131 x HH145. Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a
 , Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
, Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
Huom. tämä kulma on yhtä suuri kuin ohjauskulman muutos. lasketaan ajoneuvon keskipisteen ympyräkaaren jänteen pituus
 AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Juuri 3 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. A III, B II, C ei mikään, D I. a) Kolmion kulmien summa on 80. Kolmannen kulman suuruus on 80 85 0 85. Kolmiossa on kaksi 85 :n kulmaa, joten se on tasakylkinen.
Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. A III, B II, C ei mikään, D I. a) Kolmion kulmien summa on 80. Kolmannen kulman suuruus on 80 85 0 85. Kolmiossa on kaksi 85 :n kulmaa, joten se on tasakylkinen.
TM ETRS-TM35FIN-ETRS89 WTG
 VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
Anna jokaisen kohdan vastaus kolmen merkitsevän numeron tarkkuudella muodossa
 Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Preliminäärikoe Tehtävät Pitkä matematiikka / Kokeessa saa vastata enintään kymmeneen tehtävään Tähdellä (* merkittyjen tehtävien maksimipistemäärä on 9, muiden tehtävien maksimipistemäärä on 6 Jos tehtävässä
Travel Getting Around
 - Location Olen eksyksissä. Not knowing where you are Voisitko näyttää kartalta missä sen on? Asking for a specific location on a map Mistä täällä on? Asking for a specific...wc?...pankki / rahanvaihtopiste?...hotelli?...huoltoasema?...sairaala?...apteekki?...tavaratalo?...ruokakauppa?...bussipysäkki?
- Location Olen eksyksissä. Not knowing where you are Voisitko näyttää kartalta missä sen on? Asking for a specific location on a map Mistä täällä on? Asking for a specific...wc?...pankki / rahanvaihtopiste?...hotelli?...huoltoasema?...sairaala?...apteekki?...tavaratalo?...ruokakauppa?...bussipysäkki?
16. Allocation Models
 16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
Fonte 16045SAVA 16045VAVA 16045SAVA 16045VAVA ASENNUSOHJE MONTERINGSANVISNING ASSEMBLY INSTRUCTIONS K16045VAK2 K16045SAK1 K16045K3 K16045K3
 Fonte 16045SAVA 16045VAVA ASENNUSOHJE MONTERINGSANVISNING ASSEMBLY INSTRUCTIONS 16045SAVA K16045SAK1 K16045VAK2 K16045K3 16045VAVA K16045VAK1 K16045VAK2 K16045K3 1 2 900167 LE22SWL003 LE22VWL003 LE18VWL001
Fonte 16045SAVA 16045VAVA ASENNUSOHJE MONTERINGSANVISNING ASSEMBLY INSTRUCTIONS 16045SAVA K16045SAK1 K16045VAK2 K16045K3 16045VAVA K16045VAK1 K16045VAK2 K16045K3 1 2 900167 LE22SWL003 LE22VWL003 LE18VWL001
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Juuri 3 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Juuri Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 17.10.016 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ 1. A III, B II, C ei mikään, D I. a) Kolmion kulmien summa on 180. Kolmannen kulman
Juuri Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 17.10.016 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ 1. A III, B II, C ei mikään, D I. a) Kolmion kulmien summa on 180. Kolmannen kulman
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
WindPRO version joulu 2012 Printed/Page :47 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Kenguru 2019 Student lukio
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
Arkeologian valintakoe 2015
 Sukunimi Kaikki etunimet Henkilötunnus Puhelinnumero Valintatoimiston merkintöjä KAR A (C) Sähköpostiosoite Helsingin yliopisto Humanistinen tiedekunta Arkeologian valintakoe 2015 Tarkista sivunumeroiden
Sukunimi Kaikki etunimet Henkilötunnus Puhelinnumero Valintatoimiston merkintöjä KAR A (C) Sähköpostiosoite Helsingin yliopisto Humanistinen tiedekunta Arkeologian valintakoe 2015 Tarkista sivunumeroiden
WindPRO version joulu 2012 Printed/Page :42 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2014 Insinöörivalinnan matematiikan koe, klo Sarja A-FI.
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2014 Insinöörivalinnan matematiikan koe, 27.5.2014 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2014 Insinöörivalinnan matematiikan koe, 27.5.2014 klo 14-17 Sarja A-FI Ohjeita. Laita mielellään useamman tehtävän ratkaisu samalle konseptiarkille,
Kvanttilaskenta - 1. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2011 Insinöörivalinnan matematiikan koe, klo Sarja A-FI
 Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2011 Insinöörivalinnan matematiikan koe, 31.5.2010 klo 14-17. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
Diplomi-insinöörien ja arkkitehtien dia-yhteisvalinta 2011 Insinöörivalinnan matematiikan koe, 31.5.2010 klo 14-17. Sarja A-FI Ohjeita. Sijoita jokainen tehtävä omalle sivulleen. Merkitse, jos tehtävä
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
OFFICE 365 OPISKELIJOILLE
 OFFICE 365 OPISKELIJOILLE Table of Contents Articles... 3 Ohjeet Office 365 käyttöönottoon... 4 One Driveen tallennetun videon palauttaminen oppimisympäristön palautuskansioon... 5 Changing default language
OFFICE 365 OPISKELIJOILLE Table of Contents Articles... 3 Ohjeet Office 365 käyttöönottoon... 4 One Driveen tallennetun videon palauttaminen oppimisympäristön palautuskansioon... 5 Changing default language
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 6.3.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 6.3.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
TKK, TTY, LTY, OY, ÅA, VY, TY / Insinööriosastot Valintakuulustelujen matematiikan koe 31.5.2005
 TKK, TTY, LTY, OY, ÅA, VY, TY / Isiööriosastot Valitakuulusteluje matematiika koe.5.005 sarja A Ohjeita. Sijoita jokaie tehtävä omalle sivullee. Laadi ratkaisut selkeästi välivaiheiee, tarvittaessa kirjoita
TKK, TTY, LTY, OY, ÅA, VY, TY / Isiööriosastot Valitakuulusteluje matematiika koe.5.005 sarja A Ohjeita. Sijoita jokaie tehtävä omalle sivullee. Laadi ratkaisut selkeästi välivaiheiee, tarvittaessa kirjoita
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ.0.08 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ.0.08 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL
 MAV4 MAV5 MAV6 PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL Käyttöohje Instruction manual HUOMIO! Lue käyttöohjeet huolellisesti ennen laitteen käyttöä ja noudata kaikkia annettuja ohjeita. Säilytä
MAV4 MAV5 MAV6 PAINEILMALETKUKELA-AUTOMAATTI AUTOMATIC AIR HOSE REEL Käyttöohje Instruction manual HUOMIO! Lue käyttöohjeet huolellisesti ennen laitteen käyttöä ja noudata kaikkia annettuja ohjeita. Säilytä
( ,5 1 1,5 2 km
 Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
Suihkunurkka Shower enclosure / Duschhörna
 Suihkunurkka Shower enclosure / Duschhörna Opal suhkunurkissa on kaksi karkaistua 6 mm kirkkaasta turvalasista valmistettua kaarevaa lasiovea jotka avautuvat sisään- ja ulospäin. Ovet kiinnittyvät toisiinsa
Suihkunurkka Shower enclosure / Duschhörna Opal suhkunurkissa on kaksi karkaistua 6 mm kirkkaasta turvalasista valmistettua kaarevaa lasiovea jotka avautuvat sisään- ja ulospäin. Ovet kiinnittyvät toisiinsa
Alternative DEA Models
 Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
x 5 15 x 25 10x 40 11x x y 36 y sijoitus jompaankumpaan yhtälöön : b)
 MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
KMTK lentoestetyöpaja - Osa 2
 KMTK lentoestetyöpaja - Osa 2 Veijo Pätynen 18.10.2016 Pasila YHTEISTYÖSSÄ: Ilmailun paikkatiedon hallintamalli Ilmailun paikkatiedon hallintamalli (v0.9 4.3.2016) 4.4 Maanmittauslaitoksen rooli ja vastuut...
KMTK lentoestetyöpaja - Osa 2 Veijo Pätynen 18.10.2016 Pasila YHTEISTYÖSSÄ: Ilmailun paikkatiedon hallintamalli Ilmailun paikkatiedon hallintamalli (v0.9 4.3.2016) 4.4 Maanmittauslaitoksen rooli ja vastuut...
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
Mark Summary Form Taitaja-Mästare 2009
 Form 6 Summary Form Page 1 of 1 11-03-2011 16:07:10 Skill No 105 Skill Metsäkoneen käyttö Criterion Criterion Description s Day 1 Day 2 Day 3 Day 4 Total Award A B C D E Uppgörande av apteringsfil / Apteeraustiedoston
Form 6 Summary Form Page 1 of 1 11-03-2011 16:07:10 Skill No 105 Skill Metsäkoneen käyttö Criterion Criterion Description s Day 1 Day 2 Day 3 Day 4 Total Award A B C D E Uppgörande av apteringsfil / Apteeraustiedoston
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
,0 Yes ,0 120, ,8
 SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
Juuri 3 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K1. a) Ratkaistaan suorakulmaisen kolmion kateetin pituus x tangentin avulla. tan9 x,5,5 x,5 tan 9 x 2,8... x» 2,8 (cm) Kateetin pituus x on 2,8 cm. b) Ratkaistaan vinokulmaisen kolmion sivun pituus
Kertaus K1. a) Ratkaistaan suorakulmaisen kolmion kateetin pituus x tangentin avulla. tan9 x,5,5 x,5 tan 9 x 2,8... x» 2,8 (cm) Kateetin pituus x on 2,8 cm. b) Ratkaistaan vinokulmaisen kolmion sivun pituus
RATKAISUT a + b 2c = a + b 2 ab = ( a ) 2 2 ab + ( b ) 2 = ( a b ) 2 > 0, koska a b oletuksen perusteella. Väite on todistettu.
 RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
Kolmiot, L1. Radiaani. Kolmiolauseet. Aiheet. Kulmayksiköt, aste. Radiaani. Suorakulmainen kolmio. Kolmiolauseet
 Kolmiot, L1 Kulmayksiköt 1 Aste, 1 (engl. degree) Kun kellon viisari kiertyy yhden kierroksen, sanomme, että se kääntyy 360 (360 astetta). Ajatus täyden kierroksen jakamisesta 360 asteeseen, juontaa kaldealaiseen
Kolmiot, L1 Kulmayksiköt 1 Aste, 1 (engl. degree) Kun kellon viisari kiertyy yhden kierroksen, sanomme, että se kääntyy 360 (360 astetta). Ajatus täyden kierroksen jakamisesta 360 asteeseen, juontaa kaldealaiseen
Network to Get Work. Tehtäviä opiskelijoille Assignments for students. www.laurea.fi
 Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto
 Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
Expression of interest
 Expression of interest Avoin hakemus tohtorikoulutettavaksi käytäntö Miksi? Dear Ms. Terhi virkki-hatakka I am writing to introduce myself as a volunteer who have the eagerness to study in your university.
Expression of interest Avoin hakemus tohtorikoulutettavaksi käytäntö Miksi? Dear Ms. Terhi virkki-hatakka I am writing to introduce myself as a volunteer who have the eagerness to study in your university.
RINNAKKAINEN OHJELMOINTI A,
 RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous
 Tuula Sutela toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous äidinkieli ja kirjallisuus, modersmål och litteratur, kemia, maantiede, matematiikka, englanti käsikirjoitukset vuoden
Tuula Sutela toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous äidinkieli ja kirjallisuus, modersmål och litteratur, kemia, maantiede, matematiikka, englanti käsikirjoitukset vuoden
Kuvaile tai piirrä, millainen on sinun kotiovesi. Beskriv eller rita dörren till ditt hem.
 Yllättävät ympäristökysymykset Överraskande frågor om omgivningen Miltä ympäristösi tuntuu, kuulostaa tai näyttää? Missä viihdyt, mitä jää mieleesi? Tulosta, leikkaa suikaleiksi, valitse parhaat ja pyydä
Yllättävät ympäristökysymykset Överraskande frågor om omgivningen Miltä ympäristösi tuntuu, kuulostaa tai näyttää? Missä viihdyt, mitä jää mieleesi? Tulosta, leikkaa suikaleiksi, valitse parhaat ja pyydä
1.3Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
FIS IMATRAN KYLPYLÄHIIHDOT Team captains meeting
 FIS IMATRAN KYLPYLÄHIIHDOT 8.-9.12.2018 Team captains meeting 8.12.2018 Agenda 1 Opening of the meeting 2 Presence 3 Organizer s personell 4 Jury 5 Weather forecast 6 Composition of competitors startlists
FIS IMATRAN KYLPYLÄHIIHDOT 8.-9.12.2018 Team captains meeting 8.12.2018 Agenda 1 Opening of the meeting 2 Presence 3 Organizer s personell 4 Jury 5 Weather forecast 6 Composition of competitors startlists
1. Liikkuvat määreet
 1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
yleisessä muodossa x y ax by c 0. 6p
 MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
MAA..0 Muista kirjoittaa jokaiseen paperiin nimesi! Tee vastauspaperin yläreunaan pisteytysruudukko! Valitse kuusi tehtävää! Perustele vastauksesi välivaiheilla! Jussi Tyni Ratkaise: a) x x b) xy x 6y
Operatioanalyysi 2011, Harjoitus 4, viikko 40
 Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
c) Määritä paraabelin yhtälö, kun tiedetään, että sen huippu on y-akselilla korkeudella 6 ja sen nollakohdat ovat x-akselin kohdissa x=-2 ja x=2.
 MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
MAA4 Koe 5.5.01 Jussi Tyni Kaikkiin tehtäviin ratkaisujen välivaiheet näkyviin! Ota kokeesta poistuessasi tämä paperi mukaasi! Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Valitse
1 2 x2 + 1 dx. (2p) x + 2dx. Kummankin integraalin laskeminen oikein (vastaukset 12 ja 20 ) antaa erikseen (2p) (integraalifunktiot
 Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014
 MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014 KOE 2: Ympäristöekonomia KANSANTALOUSTIEDE JA MATEMATIIKKA Sekä A- että B-osasta tulee saada vähintään 10 pistettä. Mikäli A-osan pistemäärä on vähemmän
MAATALOUS-METSÄTIETEELLISEN TIEDEKUNNAN VALINTAKOE 2014 KOE 2: Ympäristöekonomia KANSANTALOUSTIEDE JA MATEMATIIKKA Sekä A- että B-osasta tulee saada vähintään 10 pistettä. Mikäli A-osan pistemäärä on vähemmän
Hankkeen toiminnot työsuunnitelman laatiminen
 Hankkeen toiminnot työsuunnitelman laatiminen Hanketyöpaja LLP-ohjelman keskitettyjä hankkeita (Leonardo & Poikittaisohjelma) valmisteleville11.11.2011 Työsuunnitelma Vastaa kysymykseen mitä projektissa
Hankkeen toiminnot työsuunnitelman laatiminen Hanketyöpaja LLP-ohjelman keskitettyjä hankkeita (Leonardo & Poikittaisohjelma) valmisteleville11.11.2011 Työsuunnitelma Vastaa kysymykseen mitä projektissa
