T Hahmontunnistuksen perusteet

Transkriptio

1 T Hahmontunnistuksen perusteet Harjoitustyö Käsin kirjoitettujen numeroiden tunnistus LVQ menetelmällä Heikki Hyyti 60451P

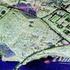
2 Yleistä Harjoitustyössä piti tehdä käsinkirjoitettujen numeroiden tunnistusjärjestelmä Learning Vector Quantization (LVQ) algoritmin avulla. LVQ algoritmissa valitaan halutun monta mallivektoria, joita harjoitetaan niin, että mallivektori muuttuu opetusdatassa vastaavia numeroita kohti ja poispäin eri numeroista. Tällöin esimerkiksi malli, joka on indeksoitu vastaamaan käsin kirjoitettua numeroa 1 alkaa muistuttaa eniten numeroa 1 ja mahdollisimman vähän muita numeroita. LVQ algoritmi toimii niin, että järjestänsä jokaista mittauspistettä kohden lasketaan lähin mallivektori. Jos mallivektori on samaa tyyppiä kuin opetusnäyte, niin mallia siirretään hieman opetusnäytteen suuntaan. Toisaalta, jos mallivektori ja opetusnäyte ovat eri numeroita, siirretään opetusvektoria hieman poispäin mallista. Mittausdata ja sen esikäsittely Esikäsittelijällä muokattiin alkuperäinen mittausdata siihen muotoon, että sitä voitiin käyttää tunnistusalgoritmissa. Mittausdatassa on neljän eri kirjoittajan käsin kirjoittamia numeroita. Numerot on piirretty yhdellä tai kahdella viivalla ja näytteet on lajiteltu viivan määrän mukaan. Viivan piirroista on otettu näytepisteitä vakioväliajoin. Ensin esikäsittelijä vähensi pisteitä niin, että yhden vedon numeroista jäi vain joka 3. piste ja kahden vedon numeroista vain joka 6. piste. Tämä tehtiin laskentanopeuden lisäämiseksi. Sitten esikäsittelijä normalisoi kaikki numerot niin, että jokaisen keskipisteeksi tuli origo ja niin, että jokaisen numeron koko tuli samaksi. Kuvassa 1 on nähtävillä esikäsiteltynä kansikuvan numero neljä. Vielä viimeiseksi esikäsittelijä jakoi datan satunnaisesti puoliksi kahteen osaan, opetus ja testausnäytteisiin. Esikäsittelyyn tarvittu Matlab koodi on liitteessä 1. Kuva 1. Kuvassa on esikäsiteltynä käsin piirretty numero neljä.

3 Algoritmi Toteutuksessa oletin, että yhden ja kahden viivan numeroiden tunnistus voidaan tehdä erillisesti, niin että ennalta tiedetään kuinka monella vedolla tunnistettava numero piirretään. Näin voidaan vähentää mahdollisten vaihtoehtojen määrää ja edelleen laskentamäärää. Lisäksi oikean tunnistuksen todennäköisyys kasvaa. Tunnistusalgoritmi siis käsittelee täysin erillisesti yhden vedon numerot ja kahden vedon numerot. Tässä onkin tehty kaksi erillistä tunnistusjärjestelmää täysin samoin periaattein. Yhden vedon numeroissa mahdollisia numeroiden vaihtoehtoja oli 8: 0,1,2,3,4,6,8 ja 9. Valittiin opetettavien mallivektorien määräksi 16 niin, että jokaiselle luokalle oli kaksi erilaista prototyyppiä. Prototyyppivektorien alkuarvoiksi valittiin satunnainen oikean luokan opetusmallinäyte. Tällä tavoin voitiin säästää todella paljon laskenta aikaa, kun ei tarvinnut aloittaa satunnaisesti jakautuneista pistejoukoista, joista algoritmi olisi hiljalleen hakeutunut kohti oikeita numeroita. Lisäksi näin päästiin paljon parempaan tunnistustodennäköisyyteen. Havaitsin tämän, kun kokeilin ensin laskea satunnaisista alkuarvoista. Yhden vedon opetetut mallivektorit ovat kuvassa 2, josta voidaankin havaita, että saman numeron kaksi eri vaihtoehtoa voivat olla hyvin erilaiset. Näin ollen olisi saatu huomattavasti epätarkempi tunnistustulos, jos mallivektoreita olisi ollut vain yksi jokaista luokkaa kohti. Kuva 2. Kuvassa on yhdellä vedolla piirrettyjen numeroiden 16 mallivektoria.

4 Kahdella vedolla piirrettyjen numeroiden tunnistus tehtiin täysin samalla tavalla kuin yhden viivan vedolla piirrettyjenkin numeroiden tunnistus. Tässä tapauksessa oikeita numeroarvoja oli vain 4: 1, 4, 5 ja 7. Taas valittiin kaksi mallivektoria jokaisesta luokasta, siis yhteensä 8 mallivektoria. Samalla tavalla kuin edellisessäkin kohdassa saatiin tulokseksi kuvassa 3 nähtävät mallivektorit. Kuva 3. Kuvassa on kahdella vedolla piirrettyjen numeroiden 8 mallivektoria. Laskennassa ja kuvien piirrossa tarvittiin monimutkaisia algoritmeja ja funktioita. Ne ovat liitteessä 2. Testaus ja johtopäätökset Toinen satunnaisesti jaettu puolikas piirrettyjen numeroiden joukosta tarvittiin järjestelmän testaamiseen. Järjestelmän tunnistusalgoritmi toteutettiin pitkälti samalla periaatteella kuin opetusalgoritmikin. Jokaiselle tunnistettavalle näytteelle haettiin lähin prototyyppi. Tunnistettu arvo oli prototyypille ennen opetusta annettu arvo. Testijärjestelmäni merkitsi ne numerot jotka tunnistuivat, ja ne jotka eivät tunnistuneet. Yhden vedon numeroista tunnistettiin 200 kpl 204 testinäytteestä. Saavutettiin siis % tunnistustodennäköisyys. Kahden vedon numerot tunnistettiin kaikki eli saavutettiin 100 % tunnistustodennäköisyys. Kahden vedon numeroita oli kuitenkin vähemmän ja testijoukkoon kuului vain 92 näytettä, joten tuloksen virhearvio on hieman epätarkempi kuin yhden vedon numeroiden tunnistuksessa, joita oli testijoukossa 204. Kuitenkin kahden vedon numeroiden tunnistuksessa mahdollisia luokkia oli vain neljä, joten tämä 100 % tunnistustodennäköisyys on mahdollinen. Todellisuudessa tässäkin tunnistuksessa tulisi virheitä, mutta testausdatan joukossa niitä ei tullut. Testauksen Matlab koodi on liitteessä 3. Lopuksi voi sanoa, että hyvin toimi ja numerot tunnistuivat hienosti. Jos tästä haluaisi tehdä jotenkin monimutkaisemman version, niin voisi jättää pois oletuksen, jossa yhden ja kahden vedon numeroiden välillä tiedettiin ero jo etukäteen. Tällöin järjestelmälle tulisi hieman enemmän haastetta.

5 Liitteet Liite 1: esikasittelija.m %% Harjoitustyön esikäsittelijä % Heikki Hyyti 60451P hhyyti@cc.hut.fi % Käytetään characters4.mat dataa, jossa on 4 ihmisen kirjoittamia % numeroita. Ladataan kuvat ja selvitetään datatiedostoston muuttujat load('/p/edu/tik /Data/characters4.mat'); whos file /p/edu/tik /Data/characters4.mat %% Plotataan yksi kuva malliksi: figure(1); plot(chars1stroke(1,1,1), Chars1Stroke(1,2,1), 'kd') hold on; for i = 2:50 x = Chars1Stroke(1,1,i); y = Chars1Stroke(1,2,i); plot(x, y, 'kd'); hold off; axis equal; title('ensimmäinen mittausdatan näyte'); xlabel('x = Chars1Stroke(1,1,i), i=1...50'); ylabel('y = Chars1Stroke(1,2,i), i=1...50'); %% kuvassa näyttäisi olevan niin paljon mittauspisteitä, että % tunnistustarkkuutta paljoa heikentämättä voidaan poistaa suurin osa % pisteistä. Seuraavaksi poistetaan 2/3 pisteistä ja näin jätetään vain % joka kolmas mittauspiste. Sen pitäisi riittää vielä sujuvaan % tunnistukseen. % [StrokeTable_new] = Decimate(StrokeTable,N,d) % N = vetojen lukumäärä, d = monesko jätetään [Chars1Stroke_new] = Decimate(Chars1Stroke,1,3); %% Piirretään uudelleen kuva, jotta tiedetään vähenikö mittauspisteiden % lukumäärä liikaa. figure(2); n = 1; plot(chars1stroke_new(n,1,1), Chars1Stroke_new(n,2,1), 'kd') hold on; koko = length(chars1stroke_new(n,1,:)); for i = 2:koko x = Chars1Stroke_new(n,1,i); y = Chars1Stroke_new(n,2,i); plot(x, y, 'kd'); hold off; axis equal;

6 title('ensimmäinen mittausdatan näyte datasta, josta on vähennetty mittauspisteitä'); xlabel(['x = Chars1Stroke new(1,1,i), i=1...' int2str(koko)]); ylabel(['y = Chars1Stroke new(1,2,i), i=1...' int2str(koko)]); % nähdään että numero on edelleen tunnistettavissa, joten mittausdataa ei % karsittu liikaa. %% seuraavaksi keskitetään mittauspisteet ja normalisoidaan koko koko = length(chars1stroke_new(:,1,1)); Chars1Stroke_new2 = zeros(size(chars1stroke_new)); for i = 1:koko clear X; X(:,1) = Chars1Stroke_new(i,1,:); X(:,2) = Chars1Stroke_new(i,2,:); % keskitetään X = Centralize(X); % normalisoidaan X = NormalizeSize(X); Chars1Stroke_new2(i,1,:) = X(:,1); Chars1Stroke_new2(i,2,:) = X(:,2); %% Piirretään taas jotta nähdään toimiko lopputulos figure(3); n = 1; plot(chars1stroke_new2(n,1,1), Chars1Stroke_new2(n,2,1), 'kd') hold on; koko = length(chars1stroke_new2(n,1,:)); for i = 2:koko x = Chars1Stroke_new2(n,1,i); y = Chars1Stroke_new2(n,2,i); plot(x, y, 'kd'); hold off; axis([ 1100,1100, 1100,1100]); title('ensimmäinen mittausdatan näyte datasta, josta on vähennetty mittauspisteitä'); xlabel(['x = Chars1Stroke new2(1,1,i), i=1...' int2str(koko)]); ylabel(['y = Chars1Stroke new2(1,2,i), i=1...' int2str(koko)]); % kuten kuvasta 3 nähdään, keskitys ja skaalaus toimivat oikein. %% tehdään samat operaatiot 2vedon numeroille % vähennetään kahden vedon numeroista tuplasti enemmän mitauspisteitä, niin % saadaan yhteensä kaikille numeroille yhtä monta mittauspistettä. Näin % numeroita on paljon helpompi verrata keskenään. % [StrokeTable_new] = Decimate(StrokeTable,N,d) % N = vetojen lukumäärä, d = monesko jätetään [Chars2Stroke_new] = Decimate(Chars2Stroke,1,6);

7 koko = length(chars2stroke_new(:,1,1)); Chars2Stroke_new2 = zeros(size(chars2stroke_new)); for i = 1:koko clear X; X(:,1) = Chars2Stroke_new(i,1,:); X(:,2) = Chars2Stroke_new(i,2,:); % keskitetään X = Centralize(X); % normalisoidaan X = NormalizeSize(X); Chars2Stroke_new2(i,1,:) = X(:,1); Chars2Stroke_new2(i,2,:) = X(:,2); %% Piirretään taas jotta nähdään toimiko lopputulos figure(4); n = 1; plot(chars2stroke_new2(n,1,1), Chars2Stroke_new2(n,2,1), 'kd') hold on; koko = length(chars2stroke_new2(n,1,:)); for i = 2:koko x = Chars2Stroke_new2(n,1,i); y = Chars2Stroke_new2(n,2,i); plot(x, y, 'kd'); hold off; axis([ 1100,1100, 1100,1100]); title('ensimmäinen mittausdatan näyte datasta, josta on vähennetty mittauspisteitä'); xlabel(['x = Chars2Stroke new2(1,1,i), i=1...' int2str(koko)]); ylabel(['y = Chars2Stroke new2(1,2,i), i=1...' int2str(koko)]); %% Erotetaan kaksi luokkaa, testaus ja opetus puoliksi [S1A,S1B,S2A,S2B,L1A,L1B,L2A,L2B] =... DivideSetsLottery(Chars1Stroke_new2,Chars2Stroke_new2,Labels1StrokeChars,... Labels2StrokeChars,30); % S1A sisältää nyt satunnaisesti arvotuista 1 vedon numeroista puolet ja % S1B loput. S2A ja B samoin 2 vedon numeroista. L1(A/B) ja L2(A/B) samoin % oikeat numeroarvot. Esikäsittelijä tiedoston lisäksi käytettiin kaikkia tarjottuja, valmiita Matlab tiedostoja, jotka olivat löydettävissä kurssin kotisivuilta. Näitä tiedostoja olivat: Decimate.m, Centralize.m, NormalizeSize.m, DivideSetsLottery.m, DtwDistance.m.

8 Liite 2: algoritmi.m: %% LVQ tunnistusalgoritmi. % Heikki Hyyti 60451P hhyyti@cc.hut.fi % opetukseen tarkoitetut tiedot: % 1 vedon numerot: S1A, oikea numero L1A % 2 vedon numerot: S2A, oikea numero L2A % tässä tapauksessa tiedetään, että 1 vedon numeroita voi olla vain: % 0, 1, 2, 3, 4, 6, 8, 9 % 8 eri vaihtoehtoa % samoin 2 vedon numeroita voi olla vain % 1, 4, 5, 7 % 4 eri vaihtoehtoa %otetaan huomioon eri luokkien erilainen määrä ja valitaan 1 vedon %numeroiden tunnistamiseen 2x8 mallivektoria ja 2 vedon numeroiden %tunnistukseen 2x4 mallivektoria. Näin jokaiselle halutulle luokalle jää 2 %mallivektoria. %% Data vektorin uudelleenmuodostus niin että sillä laskeminen on % tehokkaampaa clear X; X = zeros(length(s1a(1,1,:)),2,length(s1a(:,1,1))); for i = 1: length(s1a(:,1,1)) X(:,1,i) = S1A(i,1,:); X(:,2,i) = S1A(i,2,:); %% 1 vedon numeroiden opetus % määritetään mallivektorien oikeat arvot, kun mallivektori voi saada % arvoja: 0, 1, 2, 3, 4, 6, 8, 9. M_num = [0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 6, 6, 8, 8, 9, 9]; % M on 17,2,16 kokoinen vektori jossa on 16 eri m vektoria, jotka ovat 17,2 % kokoisia. Arvotaan mallivektorien matriisille M alkuarvot niin, että % jokainen M_i on jokin oikea näyte X_i, näin nopeutetaan laskentaa M = zeros(length(s1a(1,1,:)),2,16); for i = 1:length(M_num); loop = 0; while loop == 0 index = ceil(rand*length(x(1,1,:))); if L1A(index) == M_num(i) M(:,:,i) = X(:,:,index); loop = 1; % Satunnainen vaihtoehto, (hidas löytämään numeroita)

9 % M = rand(length(s1a(1,1,:)),2,16) * *ones(length(S1A(1,1,:)),2,16); %% varsinainen laskenta d_max = ; % alpha on opetuskerroin alpha = 0.05; for k = 1:20 for i = 1:length(X(1,1,:)); d = zeros(1,16); D = zeros(length(s1a(1,1,:)),2,16); for j = 1:length(M(1,1,:)) [d(j),d(:,:,j)] = DtwDistance(M(:,:,j),X(:,:,i),d_max); % haetaan pienin indeksi, I_min [C,I_min] = min(d); % Päivitetään I_min numeroista m vektoria matriisista M, koska % käsitelty X oli sitä lähimpänä if L1A(i) == M_num(I_min) kerroin = alpha; else kerroin = alpha; % päivityssääntö M(:,:,I_min) = M(:,:,I_min) + kerroin.*d(:,:,i_min); alpha = alpha 0.002; %% Plotataan mallivektorit m matriisista M, niin nähdään näyttävätkö ne % samalta kuin niitä vastaava numero. Jos näyttää, niin järjestelmä on % oppinut tunnistamaan numeron. figure(5); for j = 1:16; subplot(4,4,j); plot(m(1,1,j), M(1,2,j), 'kd') hold on; koko = length(m(:,1,j)); for i = 2:koko x = M(i,1,j); y = M(i,2,j); plot(x, y, 'kd'); hold off; axis([ 1100,1100, 1100,1100]);

10 set(gca,'xtick',[],'ytick', []) xlabel(int2str(m_num(j))); %% tallennetaan mallivektorien matriisi M save('s1a_m.mat', 'M'); %% 2 vedon numeroiden tunnistus %% Data vektorin uudelleenmuodostus niin että sillä laskeminen on % tehokkaampaa clear X; X = zeros(length(s2a(1,1,:)),2,length(s2a(:,1,1))); for i = 1: length(s2a(:,1,1)) X(:,1,i) = S2A(i,1,:); X(:,2,i) = S2A(i,2,:); %% 2 vedon numeroiden opetus % määritetään mallivektorien oikeat arvot, kun mallivektori voi saada % arvoja: 1, 4, 5, 7 % 4 eri vaihtoehtoa, otetaan taas kaksi mallivektoria jokaista numeroa % kohden M2_num = [1, 1, 4, 4, 5, 5, 7, 7]; % M2 on 17,2,8 kokoinen vektori jossa on 8 eri m vektoria, jotka ovat 17,2 % kokoisia. Arvotaan mallivektorien matriisille M2 alkuarvot niin, että % jokainen M2_i on jokin oikea näyte X_i, näin nopeutetaan laskentaa M2 = zeros(length(s2a(1,1,:)),2,8); for i = 1:length(M2_num); loop = 0; while loop == 0 index = ceil(rand*length(x(1,1,:))); if L2A(index) == M2_num(i) M2(:,:,i) = X(:,:,index); loop = 1; %% varsinainen laskenta d_max = ; % alpha on opetuskerroin alpha = 0.05; for k = 1:20 for i = 1:length(X(1,1,:)); d = zeros(1,8); D = zeros(length(s2a(1,1,:)),2,8); for j = 1:length(M2(1,1,:)) [d(j),d(:,:,j)] = DtwDistance(M2(:,:,j),X(:,:,i),d_max);

11 % haetaan pienin indeksi, I_min [C,I_min] = min(d); % Päivitetään I_min numeroista m vektoria matriisista M, koska % käsitelty X oli sitä lähimpänä if L2A(i) == M2_num(I_min) kerroin = alpha; else kerroin = alpha; % päivityssääntö M2(:,:,I_min) = M2(:,:,I_min) + kerroin.*d(:,:,i_min); alpha = alpha 0.002; %% Plotataan mallivektorit m matriisista M2, niin nähdään näyttävätkö ne % samalta kuin niitä vastaava numero. Jos näyttää, niin järjestelmä on % oppinut tunnistamaan numeron. figure(6); for j = 1:8; subplot(2,4,j); plot(m2(1,1,j), M2(1,2,j), 'kd') hold on; koko = length(m2(:,1,j)); for i = 2:koko x = M2(i,1,j); y = M2(i,2,j); plot(x, y, 'kd'); hold off; axis([ 1100,1100, 1100,1100]); set(gca,'xtick',[],'ytick', []) xlabel(int2str(m2_num(j))); %% tallennetaan mallivektorien matriisi M2 save('s1a_m2.mat', 'M2');

12 Liite 3: testaus.m: %% testaus % Heikki Hyyti 60451P hhyyti@cc.hut.fi % testaukseen tarkoitetut tiedot: % 1 vedon numerot: S1B, oikea numero L1B % 2 vedon numerot: S2B, oikea numero L2B %% 1 vedon numeroiden tunnistuksen testaus % määritetään mallivektorien oikeat arvot, kun mallivektori voi saada % arvoja: 0, 1, 2, 3, 4, 6, 8, 9. M_num = [0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 6, 6, 8, 8, 9, 9]; % Data vektorin uudelleenmuodostus niin, että sillä laskeminen on % tehokkaampaa ja helpompaa clear X; X = zeros(length(s1b(1,1,:)),2,length(s1b(:,1,1))); for i = 1: length(s1b(:,1,1)) X(:,1,i) = S1B(i,1,:); X(:,2,i) = S1B(i,2,:); % testausvektori, johon merkitään nollan tilalle 1 jos testaus onnistuu. tulos = zeros(1,length(x(1,1,:))); for i = 1:length(X(1,1,:)); d = zeros(1,16); D = zeros(length(s1b(1,1,:)),2,16); for j = 1:length(M(1,1,:)) [d(j),d] = DtwDistance(M(:,:,j),X(:,:,i),d_max); % haetaan pienimmän etäisyyden indeksi, I_min [C,I_min] = min(d); if L1B(i) == M_num(I_min) tulos(i) = 1; %% tuloksen ilmoitus tunnistui = sum(tulos); naytteita = length(tulos); ['1 vedon tulostus. '... 'Algoritmi tunnisti oikein ' int2str(tunnistui) ' näytettä ' int2str(naytteita)... ' näytteestä (' num2str(100.00*tunnistui/naytteita, '%.2f') '%)'] %% 2 vedon numeroiden tunnistuksen testaus

13 % määritetään mallivektorien oikeat arvot, kun mallivektori voi saada % arvoja: 1, 4, 5, 7 M2_num = [1, 1, 4, 4, 5, 5, 7, 7]; % Data vektorin uudelleenmuodostus niin, että sillä laskeminen on % tehokkaampaa ja helpompaa clear X; X = zeros(length(s2b(1,1,:)),2,length(s2b(:,1,1))); for i = 1: length(s2b(:,1,1)) X(:,1,i) = S2B(i,1,:); X(:,2,i) = S2B(i,2,:); % testausvektori, johon merkitään nollan tilalle 1 jos testaus onnistuu. tulos = zeros(1,length(x(1,1,:))); for i = 1:length(X(1,1,:)); d = zeros(1,8); D = zeros(length(s2b(1,1,:)),2,8); for j = 1:length(M2(1,1,:)) [d(j),d] = DtwDistance(M2(:,:,j),X(:,:,i),d_max); % haetaan pienimmän etäisyyden indeksi, I_min [C,I_min] = min(d); if L2B(i) == M2_num(I_min) tulos(i) = 1; %% tuloksen ilmoitus tunnistui = sum(tulos); naytteita = length(tulos); ['2 vedon tulostus. '... 'Algoritmi tunnisti oikein ' int2str(tunnistui) ' näytettä ' int2str(naytteita)... ' näytteestä (' num2str(100.00*tunnistui/naytteita, '%.2f') '%)']