Mitä on konvoluutio? Tutustu kuvankäsittelyyn

Transkriptio

1 Mitä on konvoluutio? Tutustu kuvankäsittelyyn Tieteenpäivät 2015, Työohje Sami Varjo

2 Johdanto Digitaalinen signaalienkäsittely on tullut osaksi arkipäiväämme niin, ettemme yleensä edes huomaa sen olemassa oloa. Puhummepa sitten puhelimella tai otamme kuvia, niin käsittelemme laitteillamme ympäristöstämme kerättyjä signaaleja. Syitä signaalien käsittelyyn ovat esimerkiksi taustahäiriöiden poistaminen, eli signaalin laadun parantaminen, datan valmistelu tiedonsiirtoa varten tai datan vastaanottaminen ja sisällön purkaminen. Sovellukset vaihtelevat siis aina telekommunikaatiosta ja kuvankäsittelystä puheentunnistukseen, robottinäköön ja koneoppimiseen. Suodattaminen on yksi signaalin käsittelyn perusoperaatioista. Suodattamalla signaalista voidaan poistaa häiriöitä, kuten kohinaa, arvioida puuttuvia signaalin termejä (interpoloida), tai vaikkapa etsiä tiettyjä muotoja. Konvoluutio on yksi paljon käytetty suodattimien toteutustapa. Matemaattisesti konvoluutio on kahden funktion f ja g välinen operaatio *, joka tuottaa uuden funktion (f*g). Diskreeteille yksiulotteisille funktioille konvoluutio määritellään summasarjana: (1) Eli (f*g) saa pisteessä (n) arvokseen summan kaikista tuloista funktion pisteiden f(k) ja g(n-k) välillä. Funktion g pituus on n, eli tulo muodostetaan syötteen suhteen peilatulla funktiolla g. Funktio g periaatteessa liu utetaan koko syötteen f yli tuloksen laskemiseksi jokaisessa pisteessä n. Harjoitusohjelma havainnollistaa tätä. Yleensä konvoluution kohdetta kutsutaan syötteeksi tai näytesignaaliksi ja tunnettua signaalia suodattimeksi tai kerneliksi. Esimerkiksi otettua kuvaa tai nauhoitettua ääntä kutsutaan syötteeksi f ja kohinaa poistavaa funktiota g suodattimeksi. Tämän harjoituksen tarkoituksena on saada ymmärtämys siitä mitä konvoluutio käytännössä tarkoittaa ja kuinka se voidaan laskea kuvasta. Alla kaavaa (1) vastaava esitys kuvalla havainnollistettuna: Kuva 1: Konvoluutio yhdelle pisteelle 3x3 ympäristössä, sekä koko kuvalle suoritettuna. 2

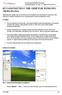
3 1. Matlab ohjelma ja konvoluutio demo Harjoitus suoritetaan Matlab-ympäristössä (omana ohjelmanaan), joka on tieteellisen laskennan tarpeisiin kehitetty ohjelmointi ja testausympäristö. Työ aloitetaan kirjoittamalla Matlab komentoikkunaan ( Command Window ) käskyt: >> cd konvoluutio_demo (siirrytään kansioon jossa konvoluutiodemo.m tiedosto sijaitsee) >> konvoluutiodemo (käynnistetään ohjelma), tai käynnistämällä erillisohjelma (KonvoluutioDemo.exe). Käyttöliittymä on esitetty kuvassa 2. Syötekuva voidaan valita annetusta valikosta (1.), tai avata oma haluttu kuva painonapista (2.). Vastaavasti erilaisia suodattimia on luotu valmiiksi harjoituksen avuksi (3.). Suodatin näytetään sekä kuvana (4.), että suodattimen sisältäminä kertoimina g(n) (5.). Tuloskuva näyttää valitun suodattimen tuottamaa tulosta (6.). Suodattimen arvoja voi muuttaa suoraan taulukkoon, sekä suodattimen kokoa liukupalkkien avulla (7.). Tuloskuvan alapuolella olevasta valitsimesta kuvan skaalaus voidaan vaihtaa eksponentiaaliseksi sekä asettaa eksponentin arvo liukusäätimellä (8.). Skaalauksen toimintaa tarkennetaan myöhemmin. Askel-painikkeella (9.) syötekuva voidaan ajaa suodattimen läpi pieni pala kerrallaan, jolloin syötteen alla näytetään syötteen sisältöä (10.) (värikuville vain punaisen värikanavan sisältö) sekä kaavan (1) mukaisen laskennan tuottama yhtälö sekä sen tulos (11.). Suoritettavien askelten lukumäärää voi muuttaa (12.). Askeleen syöte paikka korostuu kullakin askeleella syötekuvaan sinisenä laatikkona ja laskettavan tulospikselin paikka keltaisella (13.). Kuva 2: Harjoitusohjelman käyttöliittymä. 3

4 2. Tutustuminen ohjelmaan Kokeile vaihtaa syötekuvaa sekä suodatinta. Mitä eri suodattimet tekevät kuville? Exponentiaalinen skaalaus painottaa tuloskuvan arvoja tehden suodattimien vasteet helpommin ymmärrettäviksi. Kokeile toimintoa esimerkiksi reunasuodattimien kanssa. 3. Suodattimen toiminta: Ykkönen -suodatin sisältää ainoastaan yhden kertoimen yksi -. a) Mitä suodatin tekee? Valitse jokin pieni kuva (esim dots.png tai ruutu.png) ja yritä ajaa suodatinta askel kerrallaan kuvan läpi. b) Mitä tapahtuu jos kertoimen etumerkki muutetaan (etumerkin voi vaihtaa taulukkoon kohdasta 5.)? Kokeile! c) Muuttele suodattimen arvoja vapaasti. Yritä ymmärtää kuinka keltaisen tulospikselin arvo muodostuu kullekin syötteelle. 4. Reunojen löytäminen kuvasta Ohjelmassa on valmiina vaaka- ja pystyreunasuodatin. Kokeile niitä erilaisilla syötekuvilla. a) Mitä havaitset niiden toiminnasta? b) Löytyvätkö kaikki reunat? Tässä voi käyttää eksponentiaalista skaalausta korostamaan tulosvastetta. c) Mikäli kaikki reunat eivät löydy pystytkö selittämään miksi? Voisiko suodattimia muuttaa jotenkin että toiset reunat löytyvät? d) Voiko kaikki reunat löytää yhdellä suodattimella? e) Osaatko suunnitella suodattimen joka löytäisi vinot viivat (kokeile 2x2 tai 3x3 suodattimella ja vino.png syötekuvalla)? 4

5 5. Kohinan poisto Tutki syöte kuvaa kids.tif. Huomaat pieniä yksittäisiä pisteitä, kohinaa, siellä täällä kuvassa. Kokeile sumennussuodattimia ja tarkastele mitä kohinalle tapahtuu. Onko toimenpiteellä jotakin haittavaikutuksia? 6. Kolikoiden löytäminen kuvasta Ohjelmalla on mahdollista valita suodatin myös kuvasta. Valitse coins.png syötekuvaksi ja valitse suodatin syötekuvasta (painike- Valitse syötekuvasta ) piirtämällä neliö jonkin kolikon päälle. Muuta eksponentiaalinen skaalausarvo melko isoksi (esim 6-10). a) Mitä voit sanoa tuloksesta? b) Vertaa tuolosta valmiisiin suodattimiin tuottaako näistä jokin vastaavaa tulosta? c) Voisiko tällaisesta suodattimesta olla jossakin hyötyä...? 7. Yhteenveto Kerro omin sanoin mitä suodattaminen ja konvoluutio tarkoittavat. 5