Aki Taanila AIKASARJAENNUSTAMINEN
|
|
|
- Eeva-Kaarina Korpela
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Aki Taanila AIKASARJAENNUSTAMINEN
2 SISÄLLYS JOHDANTO AIKASARJA ILMAN SYSTEMAATTISTA VAIHTELUA Liukuvan keskiarvon menetelmä Eksponentiaalinen tasoitus AIKASARJASSA ON TRENDI AIKASARJASSA ON TRENDI JA KAUSIVAIHTELU Lasketaan kausivaihtelusta puhdistettu aikasarja Lasketaan trendi Lasketaan kausivaihtelun suuruus Korjataan trendiä kausivaihtelun verran ENNUSTEVIRHE AIKASARJAENNUSTEISSA HUOMIOITAVAA... 9
3 JOHDANTO Aikasarjaennustaminen Tässä monisteessa käsitellään aikasarjaennustamista. Mukana ovat tarvittavat Excelohjeet. Viimeisin versio tästä monisteesta ja siihen liittyvästä materiaalista löytyy osoitteesta Yllä mainitusta osoitteesta löytyvät myös tähän monisteeseen liittyvät Excel-esimerkit. Aikasarjaennustamisessa oletetaan, että toteutuneiden havaintojen muodostama aikasarja sisältää informaatiota, joka auttaa tulevien havaintojen ennustamisessa. Käytettävä ennustusmenetelmä riippuu siitä, minkälaista systemaattista vaihtelua aikasarjassa havaitaan. Seuraavassa tarkasteltavat tapaukset ovat: aikasarja ilman systemaattista vaihtelua aikasarja, jossa on trendi (pitkän aikavälin kehityssuunta) aikasarja, jossa on trendi ja kausivaihtelu (yleensä vuodenaikoihin liittyvä). Olipa käytetty menetelmä mikä tahansa, niin ennusteet poikkeavat enemmän tai vähemmän toteutuvasta. Ennustusmenetelmän valinnassa pyritään siihen, että ennusteiden keskimääräinen virhe saadaan mahdollisimman pieneksi. Virhe voidaan yksinkertaisimmin laskea ennusteen ja toteutuneen erotuksena. Tällöin keskimääräinen virhe saadaan virheiden itseisarvojen keskiarvona. Vaihtoehtoisten ennustusmenetelmien vertailu voidaan toteuttaa seuraavasti: 1. lasketaan menetelmän mukaisia ennusteita jo toteutuneita havaintoja vastaaville periodeille 2. lasketaan kuhunkin periodiin liittyvä virhe 3. lasketaan keskimääräinen virhe 4. valitaan ennustusmenetelmäksi se, joka tuottaa pienimmän keskimääräisen virheen. Tutustu myös muihin oppimateriaaleihini ~ 1 ~
4 1 AIKASARJA ILMAN SYSTEMAATTISTA VAIHTELUA Yksinkertaisin menetelmä on käyttää ennusteena viimeisintä toteutunutta kysyntää. Jos tuotteen kysynnän satunnainen vaihtelu on vähäistä, niin yksinkertaisuudestaan huolimatta menetelmä on varteenotettava. Jos tuotteen kysyntä vaihtelee satunnaisesti, niin viimeisin toteutunut kysyntä ei ole yleensä paras mahdollinen ennuste seuraavan periodin kysynnälle. Viimeisin toteutunut kysyntähän voi sattumalta poiketa paljonkin kysynnän keskimääräisestä tasosta. Parempi ennuste saadaan laskemalla keskiarvo useamman periodin kysynnästä. Menetelmää kutsutaan liukuvan keskiarvon menetelmäksi. 1.1 Liukuvan keskiarvon menetelmä Jos ennuste lasketaan toteutuneiden havaintojen keskiarvona, niin laskijan on valittava, kuinka monen havainnon keskiarvoa käytetään. Mitä useamman havainnon keskiarvoa lasketaan sitä enemmän aikasarjassa esiintyvää satunnaista vaihtelua tasoitetaan. Valinta tehdään yleensä siten että keskimääräinen ennustevirhe saadaan mahdollisimman pieneksi. Seuraavassa taulukossa on käytetty viiden viikon keskiarvoja. Solussa C10 on kaava =AVERAGE(B5:B9) (KESKIARVO) Solussa D10 on kaava =ABS(C10-B10) (ITSEISARVO) Solussa D21 on kaava =AVERAGE(D10:D19) (KESKIAR- VO) Kaaviosta nähdään, miten keskiarvojen käyttö tasoittaa aikasarjassa esiintyvää epäsäännöllistä vaihtelua. ~ 2 ~
5 Kysyntä Toteutunut kysyntä Liukuva keskiarvo (5) Viikko Kuvio 1. Ennuste 5 viikon liukuvia keskiarvoja käyttäen Jos vanhempia havaintoja halutaan painottaa vähemmän kuin tuoreimpia havaintoja, niin keskiarvo voidaan laskea painotettuna keskiarvona. Vaihtoehtoisesti voidaan käyttää seuraavassa kuvattavaa eksponentiaalista tasoitusta, jossa havainnon painoarvo ennusteessa on sitä pienempi, mitä vanhemmasta havainnosta on kyse. 1.2 Eksponentiaalinen tasoitus Eksponentiaalisessa tasoituksessa ennuste lasketaan kaavalla alfa*edellinen havainto + (1 - alfa)*edellinen ennuste Ennuste saadaan siis viimeisimmän tunnetun havainnon ja siihen liittyneen ennusteen painotettuna summana. Painokerroin alfa on välillä 0-1 oleva luku, joka ilmaisee, kuinka suurella painolla edellistä havaintoa painotetaan ennustetta laskettaessa. Jos alfa on 0, niin ennuste on sama kuin edellinen ennuste. Jos alfa on 1, niin ennuste on sama kuin edellinen toteutunut havainto. Suuret alfan arvot antavat ennusteita, jotka reagoivat herkästi aikasarjassa esiintyvään vaihteluun, koska viimeisimmillä havainnoilla on suurempi paino. Pienet alfan arvot tasoittavat voimakkaasti aikasarjan vaihtelua. Alfan arvo valitaan yleensä siten että keskimääräinen ennustevirhe saadaan mahdollisimman pieneksi. Ennusteen kaava voidaan kirjoittaa myös toiseen muotoon edellinen ennuste + alfa*(edellinen havainto edellinen ennuste) = edellinen ennuste + alfa*virhe Ennustetta siis korjataan jokaisen toteutuneen havainnon jälkeen korjaustermillä alfa*virhe. Seuraavan taulukon ensimmäinen ennuste (viikko 1) on laskettu keskiarvona viikkojen 1-15 toteutuneista kysynnöistä. Solussa C5 on siis kaava =AVERAGE(B5:B19) (KES- KIARVO). Solussa C6 on kaava =$F$4*B5+(1-$F$4)*C5. ~ 3 ~
6 Kysyntä Sopiva alfan arvo, joka tuottaa pienimmän keskimääräisen ennustevirheen, löydetään helposti kokeilemalla Viikko Toteutunut kysyntä Kuvio 2. Ennuste eksponentiaalista tasoitusta käyttäen, alfa = 0,24 ~ 4 ~
7 Kysyntä 2 AIKASARJASSA ON TRENDI Jos aikasarjassa on trendi (pitkän aikavälin kehityssuunta), niin ennusteita voidaan laskea tapaukseen sopivaa regressiomallia käyttäen. Jos trendi on lineaarinen, niin ennusteena käytetään lineaarisen regressiomallin antamalta suoralta laskettuja pisteitä Toteutunut kysyntä Trendi Viikko Kuvio 3. Trendiennuste Excelissä on helppo laskea regressiosuoran pisteitä funktiolla =FORECAST(x; tunnetut x;tunnetut y) (ENNUSTE) Funktion ensimmäinen lähtötieto x tarkoittaa sen periodin järjestysnumeroa, jolle lasketaan ennuste. Funktion toinen lähtötieto tunnetut x tarkoittaa niiden periodien järjestysnumeroita, joista on käytettävissä havainnot. Funktion kolmas lähtötieto tunnetut y tarkoittaa käytettävissä olevia havaintoja. Mallin laskennan yksityiskohdat selviävät Excel-esimerkistä. Jos trendissä esiintyy ajan myötä vaihtelua, niin trendiä on syytä korjata jokaisen uuden havainnon perusteella. Tämä voidaan tehdä yhdistämällä eksponentiaaliseen tasoitukseen trendi, jota korjataan jokaisen toteutuneen havainnon jälkeen. Mallia kutsutaan kehittäjänsä mukaan Holtin malliksi. Excel-esimerkeistä löytyy laskettu esimerkki Holtin mallista. ~ 5 ~
8 3 AIKASARJASSA ON TRENDI JA KAUSIVAIHTELU Trendin ja kausivaihtelun huomiointi voidaan toteuttaa seuraavassa kuvattavien vaiheiden kautta. 3.1 Lasketaan kausivaihtelusta puhdistettu aikasarja Lasketaan kausivaihtelusta puhdistettu aikasarja liukuvia keskiarvoja käyttäen. Jos havainnot ovat vuosineljänneksittäin, niin kausivaihtelu puhdistuu neljän vuosineljänneksen keskiarvoilla (vastaavasti kuukausittaisista havainnoista puhdistetaan kausivaihtelu 12 kuukauden keskiarvoilla). Seuraavassa solun D7 liukuva keskiarvo on laskettu kaavalla =AVERAGE(C5:C8) (KESKIARVO) ja solun D8 liukuva keskiarvo kaavalla =AVERAGE(C6:C9) (KESKIARVO) Koska soluun D7 sijoitettu keskiarvo on neljännesten 1-4 keskiarvo, niin sen oikea paikka olisi neljännesten 2 ja 3 puolivälissä. Koska soluun D8 sijoitettu keskiarvo on neljännesten 2-5 keskiarvo, niin sen oikea paikka olisi neljännesten 3 ja 4 puolivälissä. Jotta keskiarvot voidaan sijoittaa taulukkoon asianmukaisesti, lasketaan vielä kahden liukuvan keskiarvon keskiarvot (keskistetyt liukuvat keskiarvot). Solujen D7 ja D8 keskiarvon oikea paikka on neljänneksen 3 kohdalla. Näin ollen soluun E7 on laskettu keskistetty liukuva keskiarvo kaavalla =AVERAGE(D7:D8) (KESKIARVO) Keskistettyjen liukuvien keskiarvojen muodostamaa aikasarjaa voidaan pitää kausivaihtelusta puhdistettuna aikasarjana. 3.2 Lasketaan trendi Trendi lasketaan kausivaihtelusta puhdistetun aikasarjan avulla. Esimerkissämme periodiin 1 liittyvä trendiennuste saadaan Excelissä kaavalla =FORECAST(B5;$B$7:$B$14;$E$7:$E$14) (ENNUSTE) Kaavaa alaspäin kopioimalla saadaan muihin periodeihin liittyvät trendiennusteet. ~ 6 ~
9 3.3 Lasketaan kausivaihtelun suuruus Kausivaihtelun suuruuden laskemisessa voidaan soveltaa summamallia tai tulomallia. Summamalli soveltuu hyvin tilanteisiin, joissa kausivaihtelun absoluuttinen suuruus on ennustettavan muuttujan arvoista riippumaton. Tulomalli taas soveltuu tilanteisiin, joissa kausivaihtelun absoluuttinen suuruus on sitä suurempi, mitä suurempi on ennustettavan muuttujan arvo. Seuraavista kuvista vasemmanpuoleiseen sopii summamalli, kun taas oikeanpuoleiseen tulomalli on sopivampi. Kuvio 4. Vasemmanpuoleiseen sopii summamalli, oikeanpuoleiseen tulomalli Summamallissa lasketaan kutakin havaintoa vastaava kausivaihtelu toteutuneen havainnon ja trendin erotuksena. Tulomallissa lasketaan kausivaihtelu toteutuneen havainnon ja trendin osamääränä. Seuraavassa taulukossa solun G5 kausivaihtelu on laskettu kaavalla =C5/F5 (tulomalli). Jos samasta periodista on käytettävissä useampia arvoja, niin lopullinen kausivaihtelu saadaan keskiarvona. Seuraavassa taulukossa solun K5 ensimmäisen neljänneksen kausivaihtelu on laskettu kaavalla =AVERAGE(G5;G9;G13) (KESKIARVO). 3.4 Korjataan trendiä kausivaihtelun verran Lopulliset ennusteet saadaan korjaamalla trendiä kausivaihtelun verran. Summamallissa trendiin lisätään kyseessä olevan periodin kausivaihtelu. Tulomallissa trendi kerrotaan kyseessä olevan periodin kausivaihtelulla. Seuraavassa taulukossa solun H17 ennuste on laskettu kaavalla =F17*K5 (tulomalli). ~ 7 ~
10 Kysyntä Jos trendissä ja kausivaihtelun laajuudessa esiintyy ajan mukana vaihtelua, niin trendiä ja kausivaihtelua on syytä korjata jokaisen uuden havainnon perusteella. Tämä voidaan tehdä laajentamalla Holtin malli Holt-Winterin malliksi, jossa myös kausivaihtelua korjataan uusien havaintojen myötä. Excel-esimerkeistä löytyy laskettu esimerkki Holt- Winterin mallista. 4 ENNUSTEVIRHE Ennustusmenetelmä valitaan siten, että ennusteiden keskimääräinen virhe on mahdollisimman pieni. Jos ennustusmenetelmä on hyvin valittu, niin systemaattinen vaihtelu saadaan ennustettua. Ennustevirhe kuvastaa tällöin satunnaisvaihtelun osuutta. Ennusteen virhe voidaan jälkikäteen laskea vähentämällä ennusteesta toteutunut kysyntä. Useamman periodin perusteella voidaan laskea keskimääräinen virhe. Usein käytettyjä virheen mittareita ovat MAD = virheiden itseisarvojen keskiarvo (Mean Absolute Deviation) MSE = virheiden neliöiden keskiarvo (Mean Squared Error) Keskimääräinen ennustevirhe antaa kuvan siitä kuinka suuriin virheisiin täytyy keskimäärin varautua. Jos keskimääräinen ennustevirhe alkaa kasvaa, niin tällöin on syytä tarkistaa ennustusmenetelmän toimivuus. Kannattaa myös seurata antaako ennustusmenetelmä järjestelmällisesti liian suuria tai liian pieniä ennusteita. Tämän selvittämiseksi voidaan käyttää seuraavaa mittaria TS = virheiden summa/mad (Tracking Signal) Jos TS on välin [-6, +6] ulkopuolella, niin ennustusmenetelmä antaa liian pieniä (TS < -6) tai liian suuria (TS > +6) ennusteita. Tällöin on syytä kokeilla toisenlaista ennustusmenetelmää. Ennusteiden tarkkuutta kannattaa aina arvioida myös kaavion avulla. Seuraava kaavio kuvaa aiemmin esitettyyn esimerkkilaskelmaan liittyviä ennusteita Neljännes Toteutunut kysyntä Trendi Kuvio 5. Ennusteen tarkkuuden arviointi kaavion avulla ~ 8 ~
11 Kaavion mukaan ennusteet näyttävät seuraavan hyvin toteutunutta kysyntää ja näin ollen voidaan odottaa ennusteiden toteutuvan hyvin myös jatkossa (olettaen, että toimintaympäristössä ei tapahdu olennaisia muutoksia). 5 AIKASARJAENNUSTEISSA HUOMIOITAVAA Edellä kuvatuilla menetelmillä lasketut ennusteet ovat usein vasta lähtökohta lopulliselle ennusteelle. Ennustetta voidaan korjata esimerkiksi Valmisohjelmat ennustettavaan ilmiöön liittyvän kokemustiedon pohjalta tutkimuslaitoksilta saatavien suhdanne-ennusteiden pohjalta suunniteltujen kampanjoiden tai hinnanmuutosten johdosta. Ennustamiseen on olemassa valmiita tietokoneohjelmia. Esimerkiksi moniin toiminnanohjausjärjestelmiin liittyy ennustamismoduuli. Ohjelmat suorittavat tarvittavat laskutoimitukset ja joissain tapauksissa valitsevat jopa käytettävän menetelmän. Ennusteiden järkevyyden ja käyttökelpoisuuden arviointi sekä ennusteisiin mahdollisesti tehtävät korjaukset jäävät kuitenkin aina ihmisen tehtäväksi. ~ 9 ~
Aki Taanila TOIMITUSKETJUN HALLINNAN TYÖKALUJA
 Aki Taanila TOIMITUSKETJUN HALLINNAN TYÖKALUJA 10.9.2015 SISÄLLYS JOHDANTO... 1 1 TILASTOLLINEN LAADUNVALVONTA... 2 1.1 Prosessin kyvykkyys... 2 1.2 Prosessin valvonta... 4 1.2.1 Kontrollikaavio keskiarvolle...
Aki Taanila TOIMITUSKETJUN HALLINNAN TYÖKALUJA 10.9.2015 SISÄLLYS JOHDANTO... 1 1 TILASTOLLINEN LAADUNVALVONTA... 2 1.1 Prosessin kyvykkyys... 2 1.2 Prosessin valvonta... 4 1.2.1 Kontrollikaavio keskiarvolle...
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO
 Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Aki Taanila MATEMAATTISIA MALLEJA
 Aki Taanila MATEMAATTISIA MALLEJA 7.2.2010 SISÄLLYS 1 ORIENTAATIO... 1 1.1 Matemaattiset mallit... 1 1.2 Kriittinen ajattelu... 2 2 YHDEN SELITTÄJÄN REGRESSIO... 3 2.1 Lineaarinen malli... 3 2.2 Selityskerroin...
Aki Taanila MATEMAATTISIA MALLEJA 7.2.2010 SISÄLLYS 1 ORIENTAATIO... 1 1.1 Matemaattiset mallit... 1 1.2 Kriittinen ajattelu... 2 2 YHDEN SELITTÄJÄN REGRESSIO... 3 2.1 Lineaarinen malli... 3 2.2 Selityskerroin...
Aki Taanila AIKASARJOJEN ESITTÄMINEN
 Aki Taanila AIKASARJOJEN ESITTÄMINEN 4.12.2012 Viivakaavio Excelissä voit toteuttaa viivakaavion kaaviolajilla Line (Viiva). Viivakaavio onnistuu varmimmin, jos taulukon ensimmäisessä sarakkeessa ovat
Aki Taanila AIKASARJOJEN ESITTÄMINEN 4.12.2012 Viivakaavio Excelissä voit toteuttaa viivakaavion kaaviolajilla Line (Viiva). Viivakaavio onnistuu varmimmin, jos taulukon ensimmäisessä sarakkeessa ovat
Kysynnän ennustaminen muuttuvassa maailmassa
 make connections share ideas be inspired Kysynnän ennustaminen muuttuvassa maailmassa Nina Survo ja Antti Leskinen SAS Institute Mitä on kysynnän ennustaminen? Ennakoiva lähestymistapa, jolla pyritään
make connections share ideas be inspired Kysynnän ennustaminen muuttuvassa maailmassa Nina Survo ja Antti Leskinen SAS Institute Mitä on kysynnän ennustaminen? Ennakoiva lähestymistapa, jolla pyritään
LASKENTATOIMEN OSAAMINEN vs. LIIKETALOUDELLINEN ENNUSTETARKKUUS
 LASKENTATOIMEN OSAAMINEN vs. LIIKETALOUDELLINEN ENNUSTETARKKUUS Helsinki 26..200 4 2 5 Seminaari 26..200 Mikko Hakola Laskentatoimen osaaminen Testatut tahot Selvittäjiä Yrittäjiä KLT-kirjanpitäjiä Virallisen
LASKENTATOIMEN OSAAMINEN vs. LIIKETALOUDELLINEN ENNUSTETARKKUUS Helsinki 26..200 4 2 5 Seminaari 26..200 Mikko Hakola Laskentatoimen osaaminen Testatut tahot Selvittäjiä Yrittäjiä KLT-kirjanpitäjiä Virallisen
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.14 Tilastollisen analyysin perusteet, kevät 7 7. luento: Tarina yhden selittään lineaarisesta regressiomallista atkuu Kai Virtanen 1 Luennolla 6 opittua Kuvataan havainnot (y, x ) yhden selittään
Mat-.14 Tilastollisen analyysin perusteet, kevät 7 7. luento: Tarina yhden selittään lineaarisesta regressiomallista atkuu Kai Virtanen 1 Luennolla 6 opittua Kuvataan havainnot (y, x ) yhden selittään
Oma nimesi Tehtävä (5)
 Oma nimesi Tehtävä 3.1 1 (5) Taulukot ja niiden laatiminen Tilastotaulukko on perinteinen ja monikäyttöisin tapa järjestää numeerinen havaintoaineisto tiiviiseen ja helposti omaksuttavaan muotoon. Tilastoissa
Oma nimesi Tehtävä 3.1 1 (5) Taulukot ja niiden laatiminen Tilastotaulukko on perinteinen ja monikäyttöisin tapa järjestää numeerinen havaintoaineisto tiiviiseen ja helposti omaksuttavaan muotoon. Tilastoissa
Aki Taanila LINEAARINEN OPTIMOINTI
 Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Aki Taanila LINEAARINEN OPTIMOINTI 26.4.2011 JOHDANTO Tässä monisteessa esitetään lineaarisen optimoinnin alkeet. Moniste sisältää tarvittavat Excel ohjeet. Viimeisin versio tästä monisteesta ja siihen
Harjoitus 9: Excel - Tilastollinen analyysi
 Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
Ennustaminen ARMA malleilla ja Kalmanin suodin
 Ennustaminen ARMA malleilla ja Kalmanin suodin MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017
Ennustaminen ARMA malleilla ja Kalmanin suodin MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017
Dynaamiset regressiomallit
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
LABORAATIOSELOSTUSTEN OHJE H. Honkanen
 LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Ennustaminen. Ennusteet ovat operaatioiden pohjana. Luennon sisältö. Ennusteet ovat operaatioiden pohjana - case EuroDisney ja yliarvioitu kysyntä -
 L u e n t o Ennusteet ovat operaatioiden pohjana Ennustaminen Luennon sisältö Ennusteiden merkitys Ennustemenetelmät Ennusteiden tekeminen käytännössä Ennusteet suunnittelun, päätöksenteon ja resurssien
L u e n t o Ennusteet ovat operaatioiden pohjana Ennustaminen Luennon sisältö Ennusteiden merkitys Ennustemenetelmät Ennusteiden tekeminen käytännössä Ennusteet suunnittelun, päätöksenteon ja resurssien
Ennustaminen. Yritykset ennustavat monia asioita. Luennon sisältö. Ennusteet ovat operaatioiden pohjana - case EuroDisney ja yliarvioitu kysyntä -
 L u e n t o Ennustaminen Luennon sisältö Ennusteiden merkitys Ennustemenetelmät Ennusteiden tekeminen käytännössä Yritys Toimiala Yhteiskunta Yritykset ennustavat monia asioita Poliittiset tapahtumat Arvojen
L u e n t o Ennustaminen Luennon sisältö Ennusteiden merkitys Ennustemenetelmät Ennusteiden tekeminen käytännössä Yritys Toimiala Yhteiskunta Yritykset ennustavat monia asioita Poliittiset tapahtumat Arvojen
Regressioanalyysi. Kuusinen/Heliövaara 1
 Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
TTY Mittausten koekenttä. Käyttö. Sijainti
 TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Matkailun tulo- ja työllisyysselvitys v. 2017
 Matkailun tulo- ja työllisyysselvitys v. 2017 Rakennetiedot Jämsän matkailukeskus Laskettavan muuttujan vuositaso (YTR) Yritykset YTR:n mukaan Toimipaikat YTR:n mukaan Henkilöstömäärä (2015) 322 69 77
Matkailun tulo- ja työllisyysselvitys v. 2017 Rakennetiedot Jämsän matkailukeskus Laskettavan muuttujan vuositaso (YTR) Yritykset YTR:n mukaan Toimipaikat YTR:n mukaan Henkilöstömäärä (2015) 322 69 77
ASIAKASKOHTAINEN SUHDANNEPALVELU. Lappeenranta 1.10.2008. - Nopeat alueelliset ja toimialoittaiset suhdannetiedot
 ASIAKASKOHTAINEN SUHDANNEPALVELU - Nopeat alueelliset ja toimialoittaiset suhdannetiedot Tiina Karppanen (09) 1734 2656 palvelut.suhdanne@tilastokeskus.fi Lappeenranta 1.10.2008 1.10.2008 A 1 Mihin suhdannetietoja
ASIAKASKOHTAINEN SUHDANNEPALVELU - Nopeat alueelliset ja toimialoittaiset suhdannetiedot Tiina Karppanen (09) 1734 2656 palvelut.suhdanne@tilastokeskus.fi Lappeenranta 1.10.2008 1.10.2008 A 1 Mihin suhdannetietoja
Virhearviointi. Fysiikassa on tärkeää tietää tulosten tarkkuus.
 Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
T Luonnollisten kielten tilastollinen käsittely
 T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama.
 Aikasarjat Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama. Aikasarja on laajassa mielessä stationäärinen (wide sense stationary, WSS), jos odotusarvo
Aikasarjat Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama. Aikasarja on laajassa mielessä stationäärinen (wide sense stationary, WSS), jos odotusarvo
1. Keskimääräisen nimellistuottoprosentin laskenta
 1 3.10.2011/TELA/Tuotonlaskentaryhmä/R.Vanne Yli vuoden mittaisen aikavälin tuoton raportointi 1. Keskimääräisen nimellistuottoprosentin laskenta FIVAn määräykset yksityisalojen työeläkevakuuttajille sisältävät
1 3.10.2011/TELA/Tuotonlaskentaryhmä/R.Vanne Yli vuoden mittaisen aikavälin tuoton raportointi 1. Keskimääräisen nimellistuottoprosentin laskenta FIVAn määräykset yksityisalojen työeläkevakuuttajille sisältävät
Taulukko 2. Ennustevirheet ennustajittain vuosina ; virheiden itseisarvojen keskiarvo / virheiden keskiarvo, %-yksikköä
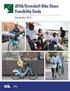 Taulukko 1. Ennustevirheet ennustajittain vuosina 1997-2000; virheiden itseisarvojen keskiarvo / virheiden keskiarvo, -yksikköä (pl. vaihtotase mrd.mk.) BKT Inflaatio Työttömyys Vaihtotase ETLA 1,67 /-1,67
Taulukko 1. Ennustevirheet ennustajittain vuosina 1997-2000; virheiden itseisarvojen keskiarvo / virheiden keskiarvo, -yksikköä (pl. vaihtotase mrd.mk.) BKT Inflaatio Työttömyys Vaihtotase ETLA 1,67 /-1,67
TAVOITERIITON MÄÄRITTÄMINEN
 TAVOITERIITON MÄÄRITTÄMINEN Ammattikorkeakoulun opinnäytetyö Logistiikan koulutusohjelma Forssa, kevät 2014 Ilari Korpela Ilari Korpela TIIVISTELMÄ FORSSA Logistiikan koulutusohjelma Tekijä Ilari Korpela
TAVOITERIITON MÄÄRITTÄMINEN Ammattikorkeakoulun opinnäytetyö Logistiikan koulutusohjelma Forssa, kevät 2014 Ilari Korpela Ilari Korpela TIIVISTELMÄ FORSSA Logistiikan koulutusohjelma Tekijä Ilari Korpela
SAIMAANNORPPA Kannan koon arvioinnista Tero Sipilä & Tuomo Kokkonen Metsähallitus, Etelä-Suomen Luontopalvelut Akselinkatu 8, 57130, Savonlinna
 Saimaannorppa, ilmastonmuutos ja kalastus seminaari. Rantasalmi 28.5.21 SAIMAANNORPPA Kannan koon arvioinnista Tero Sipilä & Tuomo Kokkonen Metsähallitus, Etelä-Suomen Luontopalvelut Akselinkatu 8, 5713,
Saimaannorppa, ilmastonmuutos ja kalastus seminaari. Rantasalmi 28.5.21 SAIMAANNORPPA Kannan koon arvioinnista Tero Sipilä & Tuomo Kokkonen Metsähallitus, Etelä-Suomen Luontopalvelut Akselinkatu 8, 5713,
Regressioanalyysi. Vilkkumaa / Kuusinen 1
 Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
Kemometriasta. Matti Hotokka Fysikaalisen kemian laitos Åbo Akademi Http://www.abo.fi/~mhotokka
 Kemometriasta Matti Hotokka Fysikaalisen kemian laitos Åbo Akademi Http://www.abo.fi/~mhotokka Mistä puhutaan? Määritelmiä Määritys, rinnakkaismääritys Mittaustuloksen luotettavuus Kalibrointi Mittausten
Kemometriasta Matti Hotokka Fysikaalisen kemian laitos Åbo Akademi Http://www.abo.fi/~mhotokka Mistä puhutaan? Määritelmiä Määritys, rinnakkaismääritys Mittaustuloksen luotettavuus Kalibrointi Mittausten
pitkittäisaineistoissa
 Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
T Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti , 8:30-10:00 Kollokaatiot, Versio 1.1
 T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
Näistä standardoiduista arvoista laskettu keskiarvo on nolla ja varianssi 1, näin on standardoidulle muuttujalle aina.
 [MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, kevät 2019 https://coursepages.uta.fi/mtttp1/kevat-2019/ HARJOITUS 3 Joitain ratkaisuja 1. x =(8+9+6+7+10)/5 = 8, s 2 = ((8 8) 2 + (9 8) 2 +(6 8) 2 + (7 8) 2 ) +
[MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, kevät 2019 https://coursepages.uta.fi/mtttp1/kevat-2019/ HARJOITUS 3 Joitain ratkaisuja 1. x =(8+9+6+7+10)/5 = 8, s 2 = ((8 8) 2 + (9 8) 2 +(6 8) 2 + (7 8) 2 ) +
n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa.
 MAA 12 kertaus Funktion kuvaaja n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa. Funktion nollakohta on piste, jossa f () = 0, eli kuvaaja leikkaa -akselin. Kuvaajan avulla
MAA 12 kertaus Funktion kuvaaja n. asteen polynomilla on enintään n nollakohtaa ja enintään n - 1 ääriarvokohtaa. Funktion nollakohta on piste, jossa f () = 0, eli kuvaaja leikkaa -akselin. Kuvaajan avulla
Kompleksiluvut., 15. kesäkuuta /57
 Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
Metsämuuronen: Tilastollisen kuvauksen perusteet ESIPUHE... 4 SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 2. AINEISTO...
 Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA...9 1.2 AIHEESEEN PEREHTYMINEN...9 1.3
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... SISÄLLYSLUETTELO... 6 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 8 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA...9 1.2 AIHEESEEN PEREHTYMINEN...9 1.3
pitkittäisaineistoissa
 Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
1 MATEMAATTISIA VÄLINEITÄ TALOUSELÄMÄN ONGELMIIN Algebran perusteita 8 Potenssit Juuret 15 Tuntematon ja muuttuja 20 Lausekkeen käsittely 24
 SISÄLTÖ 1 MATEMAATTISIA VÄLINEITÄ TALOUSELÄMÄN ONGELMIIN 7 1.1 Algebran perusteita 8 Potenssit Juuret 15 Tuntematon ja muuttuja 20 Lausekkeen käsittely 24 1.2 Yhtälöitä 29 Epäyhtälö 30 Yhtälöpari 32 Toisen
SISÄLTÖ 1 MATEMAATTISIA VÄLINEITÄ TALOUSELÄMÄN ONGELMIIN 7 1.1 Algebran perusteita 8 Potenssit Juuret 15 Tuntematon ja muuttuja 20 Lausekkeen käsittely 24 1.2 Yhtälöitä 29 Epäyhtälö 30 Yhtälöpari 32 Toisen
Näistä standardoiduista arvoista laskettu keskiarvo on nolla ja varianssi 1, näin on standardoidulle muuttujalle aina.
 [MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, Syksy 2017 http://www.uta.fi/sis/mtt/mtttp1/syksy_2017.html HARJOITUS 3 viikko 40 Joitain ratkaisuja 1. Suoritetaan standardointi. Standardoidut arvot ovat z 1 =
[MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, Syksy 2017 http://www.uta.fi/sis/mtt/mtttp1/syksy_2017.html HARJOITUS 3 viikko 40 Joitain ratkaisuja 1. Suoritetaan standardointi. Standardoidut arvot ovat z 1 =
Seurantalaskimen simulointi- ja suorituskykymallien vertailu (valmiin työn esittely) Joona Karjalainen
 Seurantalaskimen simulointi- ja suorituskykymallien vertailu (valmiin työn esittely) Joona Karjalainen 08.09.2014 Ohjaaja: DI Mikko Harju Valvoja: Prof. Kai Virtanen Työn saa tallentaa ja julkistaa Aalto-yliopiston
Seurantalaskimen simulointi- ja suorituskykymallien vertailu (valmiin työn esittely) Joona Karjalainen 08.09.2014 Ohjaaja: DI Mikko Harju Valvoja: Prof. Kai Virtanen Työn saa tallentaa ja julkistaa Aalto-yliopiston
Virheen arviointia
 16.4.014 Vireen arviointia NUMEERISIA JA ALGEBRAL- LISIA MENETELMIÄ, MAA1 Virettä, tai oikeammin vireen suuruutta, voidaan arvioida seuraavilla tavoilla: 1. Maksimi-minimikeino (-menettely), nopea ja yksinkertainen,
16.4.014 Vireen arviointia NUMEERISIA JA ALGEBRAL- LISIA MENETELMIÄ, MAA1 Virettä, tai oikeammin vireen suuruutta, voidaan arvioida seuraavilla tavoilla: 1. Maksimi-minimikeino (-menettely), nopea ja yksinkertainen,
Estimointi. Estimointi. Estimointi: Mitä opimme? 2/4. Estimointi: Mitä opimme? 1/4. Estimointi: Mitä opimme? 3/4. Estimointi: Mitä opimme?
 TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
Mittaustekniikka (3 op)
 530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
4 LUKUJONOT JA SUMMAT
 Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Määrällisen aineiston esittämistapoja. Aki Taanila
 Määrällisen aineiston esittämistapoja Aki Taanila 24.4.2017 1 Kategoriset muuttujat Lukumääriä Prosentteja (muista n-arvot) Pylväitä 2 Yhteenvetotaulukko (frekvenssitaulukko) TAULUKKO 1. Asunnon tyyppi
Määrällisen aineiston esittämistapoja Aki Taanila 24.4.2017 1 Kategoriset muuttujat Lukumääriä Prosentteja (muista n-arvot) Pylväitä 2 Yhteenvetotaulukko (frekvenssitaulukko) TAULUKKO 1. Asunnon tyyppi
Korvausvastuun ennustejakauma bootstrap-menetelmän avulla
 Korvausvastuun ennustejakauma bootstrap-menetelmän avulla Sari Ropponen 13.5.2009 1 Agenda Korvausvastuu vahinkovakuutuksessa Korvausvastuun arviointi Ennustevirhe Ennustejakauma Bootstrap-/simulointimenetelmä
Korvausvastuun ennustejakauma bootstrap-menetelmän avulla Sari Ropponen 13.5.2009 1 Agenda Korvausvastuu vahinkovakuutuksessa Korvausvastuun arviointi Ennustevirhe Ennustejakauma Bootstrap-/simulointimenetelmä
Demo 1: Simplex-menetelmä
 MS-C2105 Optimoinnin perusteet Malliratkaisut 3 Ehtamo Demo 1: Simplex-menetelmä Muodosta lineaarisen tehtävän standardimuoto ja ratkaise tehtävä taulukkomuotoisella Simplex-algoritmilla. max 5x 1 + 4x
MS-C2105 Optimoinnin perusteet Malliratkaisut 3 Ehtamo Demo 1: Simplex-menetelmä Muodosta lineaarisen tehtävän standardimuoto ja ratkaise tehtävä taulukkomuotoisella Simplex-algoritmilla. max 5x 1 + 4x
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Osa 2: Otokset, otosjakaumat ja estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
MTTTP5, luento Otossuureita ja niiden jakaumia (jatkuu)
 21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Rakennusalan tarjouskilpailujen toteutus tasapuoliseksi: kokonaistaloudellisuuden arviointi hinta-laatu -menetelmällä.
 ARKKITEHTITOIMISTOJEN LIITTO ATL RY Rakennusalan tarjouskilpailujen toteutus tasapuoliseksi: kokonaistaloudellisuuden arviointi hinta-laatu -menetelmällä. Julkisten hankintojen tarjousten valintakriteerinä
ARKKITEHTITOIMISTOJEN LIITTO ATL RY Rakennusalan tarjouskilpailujen toteutus tasapuoliseksi: kokonaistaloudellisuuden arviointi hinta-laatu -menetelmällä. Julkisten hankintojen tarjousten valintakriteerinä
58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut
 58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut 1. Palautetaan vielä mieleen O-notaation määritelmä. Olkoon f ja g funktioita luonnollisilta luvuilta positiivisille
58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut 1. Palautetaan vielä mieleen O-notaation määritelmä. Olkoon f ja g funktioita luonnollisilta luvuilta positiivisille
Koska ovat negatiiviset. Keskihajontoja ei pystytä laskemaan mutta pätee ¾.
 24.11.2006 1. Oletetaan, että kaksiulotteinen satunnaismuuttuja µ noudattaa kaksiulotteista normaalijakaumaa. Oletetaan lisäksi, että satunnaismuuttujan regressiofunktio satunnaismuuttujan suhteen on ݵ
24.11.2006 1. Oletetaan, että kaksiulotteinen satunnaismuuttuja µ noudattaa kaksiulotteista normaalijakaumaa. Oletetaan lisäksi, että satunnaismuuttujan regressiofunktio satunnaismuuttujan suhteen on ݵ
Johdatus tilastotieteeseen Estimointi. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
n! k!(n k)! n = Binomikerroin voidaan laskea pelkästään yhteenlaskun avulla käyttäen allaolevia ns. palautuskaavoja.
 IsoInt Tietokoneiden muisti koostuu yksittäisistä muistisanoista, jotka nykyaikaisissa koneissa ovat 64 bitin pituisia. Muistisanan koko asettaa teknisen rajoituksen sille, kuinka suuria lukuja tietokone
IsoInt Tietokoneiden muisti koostuu yksittäisistä muistisanoista, jotka nykyaikaisissa koneissa ovat 64 bitin pituisia. Muistisanan koko asettaa teknisen rajoituksen sille, kuinka suuria lukuja tietokone
Kysynnän ennustaminen
 t-2.108 Sovelletun matematiikan erikoistyöt ura Salmi 41917D Kysynnän ennustaminen Sisällys 1 1. Johdanto... 2 2. Kysyntä... 3 3. Ennustamismenetelmät... 4 3.1 Kvalitatiiviset menetelmät... 4 3.2 Kvantitatiiviset
t-2.108 Sovelletun matematiikan erikoistyöt ura Salmi 41917D Kysynnän ennustaminen Sisällys 1 1. Johdanto... 2 2. Kysyntä... 3 3. Ennustamismenetelmät... 4 3.1 Kvalitatiiviset menetelmät... 4 3.2 Kvantitatiiviset
Aki Taanila TAVOITTEEN HAKU JA VAIHTOEHTOLASKELMIA
 Aki Taanila TAVOITTEEN HAKU JA VAIHTOEHTOLASKELMIA 4.12.2012 Johdanto Tässä monisteessa käsittelen Excelin tavoitteen haku -toimintoa ja erilaisia tapoja vaihtoehtolaskelmien laatimiseen. Monisteessa esiintyy
Aki Taanila TAVOITTEEN HAKU JA VAIHTOEHTOLASKELMIA 4.12.2012 Johdanto Tässä monisteessa käsittelen Excelin tavoitteen haku -toimintoa ja erilaisia tapoja vaihtoehtolaskelmien laatimiseen. Monisteessa esiintyy
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Seuraavassa taulukossa on annettu mittojen määritelmät ja sijoitettu luvut. = 40% = 67% 6 = 0.06% = 99.92% 6+2 = 0.
 T-6.28 Luonnollisen kielen tilastollinen käsittely Vastaukset, ti 7.2.200, 8:30-0:00 Tiedon haku, Versio.0. Muutetaan tehtävässä annettu taulukko sellaiseen muotoon, joka paremmin sopii ensimmäisten mittojen
T-6.28 Luonnollisen kielen tilastollinen käsittely Vastaukset, ti 7.2.200, 8:30-0:00 Tiedon haku, Versio.0. Muutetaan tehtävässä annettu taulukko sellaiseen muotoon, joka paremmin sopii ensimmäisten mittojen
Excel-harjoitus 1. Tietojen syöttö työkirjaan. Taulukon muotoilu
 Excel-harjoitus 1 Tietojen syöttö työkirjaan Kuvitteellinen yritys käyttää Excel-ohjelmaa kirjanpidon laskentaan. He merkitsevät taulukkoon päivittäiset ostot, kunnostuskulut, tilapäistilojen vuokramenot,
Excel-harjoitus 1 Tietojen syöttö työkirjaan Kuvitteellinen yritys käyttää Excel-ohjelmaa kirjanpidon laskentaan. He merkitsevät taulukkoon päivittäiset ostot, kunnostuskulut, tilapäistilojen vuokramenot,
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio
 Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016)
 805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016) Tavoitteet (teoria): Hahmottaa aikasarjan klassiset komponentit ideaalisessa tilanteessa. Ymmärtää viivekuvauksen vaikutus trendiin. ARCH-prosessin
805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016) Tavoitteet (teoria): Hahmottaa aikasarjan klassiset komponentit ideaalisessa tilanteessa. Ymmärtää viivekuvauksen vaikutus trendiin. ARCH-prosessin
VALTION MAATALOUSKONEIDEN TUTKIMUSLAITOS
 VAKOLA Zial Helsinki Rukkila Helsinki 43 41 61 Pitäjänmai VALTION MAATALOUSKONEIDEN TUTKIMUSLAITOS Finnish Research Institute of Agricultural Engineering 1965 Koetusselostus 578 Test report Eii va 1. Presto-viljankost
VAKOLA Zial Helsinki Rukkila Helsinki 43 41 61 Pitäjänmai VALTION MAATALOUSKONEIDEN TUTKIMUSLAITOS Finnish Research Institute of Agricultural Engineering 1965 Koetusselostus 578 Test report Eii va 1. Presto-viljankost
VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ
 56 VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ Hyvällä havaitsijalla keskimääräinen virhe tähdenlennon kirkkauden arvioimisessa on noin 0.4 magnitudia silloin, kun meteori näkyy havaitsijan näkökentän keskellä.
56 VIII LISÄTIETOA 8.1. HAVAINTOVIRHEISTÄ Hyvällä havaitsijalla keskimääräinen virhe tähdenlennon kirkkauden arvioimisessa on noin 0.4 magnitudia silloin, kun meteori näkyy havaitsijan näkökentän keskellä.
VMI kasvututkimuksen haasteita
 VMI kasvututkimuksen haasteita Annika Kangas & Helena Henttonen 18.8.2016 1 Teppo Tutkija VMIn aikasarjat mahdollistavat kasvutrendien tutkimuksen 2 Korhonen & Kangas Missä määrin kasvu voidaan ennustaa?
VMI kasvututkimuksen haasteita Annika Kangas & Helena Henttonen 18.8.2016 1 Teppo Tutkija VMIn aikasarjat mahdollistavat kasvutrendien tutkimuksen 2 Korhonen & Kangas Missä määrin kasvu voidaan ennustaa?
Seuratiedote 2/09 LIITE 4
 CSA-järjestelmä Johdantoa USGAn Course Rating -järjestelmässä todetaan: USGAn Course Ratingin ja Slope Ratingin määritysten tulee vastata olosuhteita kauden aikana, jolloin suurin osa kierroksista pelataan.
CSA-järjestelmä Johdantoa USGAn Course Rating -järjestelmässä todetaan: USGAn Course Ratingin ja Slope Ratingin määritysten tulee vastata olosuhteita kauden aikana, jolloin suurin osa kierroksista pelataan.
Muutoksen arviointi differentiaalin avulla
 Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
Lukujonon raja-arvo 1/7 Sisältö ESITIEDOT: lukujonot
 Lukujonon raja-arvo 1/7 Sisältö Esimerkki lukujonon raja-arvosta Lukujonossa a 1,a 2,a 3,... (jossa on äärettömän monta termiä) voivat luvut lähestyä jotakin arvoa, kun jonossa edetään yhä pidemmälle.
Lukujonon raja-arvo 1/7 Sisältö Esimerkki lukujonon raja-arvosta Lukujonossa a 1,a 2,a 3,... (jossa on äärettömän monta termiä) voivat luvut lähestyä jotakin arvoa, kun jonossa edetään yhä pidemmälle.
MONISTE 2 Kirjoittanut Elina Katainen
 MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
MONISTE 2 Kirjoittanut Elina Katainen TILASTOLLISTEN MUUTTUJIEN TYYPIT 1 Mitta-asteikot Tilastolliset muuttujat voidaan jakaa kahteen päätyyppiin: kategorisiin ja numeerisiin muuttujiin. Tämän lisäksi
Martingaalit ja informaatioprosessit
 4A Martingaalit ja informaatioprosessit Tämän harjoituksen tavoitteena on tutustua satunnaisvektorin informaation suhteen lasketun ehdollisen odotusarvon käsitteeseen sekä oppia tunnistamaan, milloin annettu
4A Martingaalit ja informaatioprosessit Tämän harjoituksen tavoitteena on tutustua satunnaisvektorin informaation suhteen lasketun ehdollisen odotusarvon käsitteeseen sekä oppia tunnistamaan, milloin annettu
J. Virtamo Jonoteoria / Prioriteettijonot 1
 J. Virtamo 38.3143 Jonoteoria / Prioriteettijonot 1 Prioriteettijonot Tarkastellaan M/G/1-jonojärjestelmää, jossa asiakkaat on jaettu K:hon prioriteettiluokkaan, k = 1,..., K: - luokalla 1 on korkein prioriteetti
J. Virtamo 38.3143 Jonoteoria / Prioriteettijonot 1 Prioriteettijonot Tarkastellaan M/G/1-jonojärjestelmää, jossa asiakkaat on jaettu K:hon prioriteettiluokkaan, k = 1,..., K: - luokalla 1 on korkein prioriteetti
SELVITTÄJÄN KOMPETENSSISTA
 OTM, KTM, Mikko Hakola, Vaasan yliopisto, Laskentatoimen ja rahoituksen laitos Helsinki 20.11.200, Helsingin kauppakorkeakoulu Projekti: Yrityksen maksukyky ja strateginen johtaminen SELVITTÄJÄN KOMPETENSSISTA
OTM, KTM, Mikko Hakola, Vaasan yliopisto, Laskentatoimen ja rahoituksen laitos Helsinki 20.11.200, Helsingin kauppakorkeakoulu Projekti: Yrityksen maksukyky ja strateginen johtaminen SELVITTÄJÄN KOMPETENSSISTA
Teema 3: Tilastollisia kuvia ja tunnuslukuja
 Teema 3: Tilastollisia kuvia ja tunnuslukuja Tilastoaineiston peruselementit: havainnot ja muuttujat havainto: yhtä havaintoyksikköä koskevat tiedot esim. henkilön vastaukset kyselylomakkeen kysymyksiin
Teema 3: Tilastollisia kuvia ja tunnuslukuja Tilastoaineiston peruselementit: havainnot ja muuttujat havainto: yhtä havaintoyksikköä koskevat tiedot esim. henkilön vastaukset kyselylomakkeen kysymyksiin
3. Tietokoneharjoitukset
 3. Tietokoneharjoitukset Aikasarjan logaritmointi Aikasarjoja analysoidaan usein logaritmisessa muodossa. Asialooginen perustelu logaritmoinnille: Muuttujan arvojen suhteelliset muutokset ovat usein tärkeämpiä
3. Tietokoneharjoitukset Aikasarjan logaritmointi Aikasarjoja analysoidaan usein logaritmisessa muodossa. Asialooginen perustelu logaritmoinnille: Muuttujan arvojen suhteelliset muutokset ovat usein tärkeämpiä
Huippu 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 KERTAUS KERTAUSTEHTÄVIÄ K1. a) Kun suoran s pisteen -koordinaatti kasvaa yhdellä, pisteen y- koordinaatti kasvaa kahdella. Suoran s kulmakerroin on siis. Kun suoran t pisteen -koordinaatti kasvaa kahdella,
KERTAUS KERTAUSTEHTÄVIÄ K1. a) Kun suoran s pisteen -koordinaatti kasvaa yhdellä, pisteen y- koordinaatti kasvaa kahdella. Suoran s kulmakerroin on siis. Kun suoran t pisteen -koordinaatti kasvaa kahdella,
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN-
 Q 16.1/21/73/1 Seppo Elo 1973-11-16 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Painovoimapisteiden korkeuden mittauksesta statoskoopeilla VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN- MÄARITYKSESTA
Q 16.1/21/73/1 Seppo Elo 1973-11-16 GEOLOGINEN TUTKIMUSLAITOS Geofysiikan osasto Painovoimapisteiden korkeuden mittauksesta statoskoopeilla VAISALAN STATOSKOOPPIEN KÄYTTÖÖN PERUSTUVASTA KORKEUDEN- MÄARITYKSESTA
k=0 saanto jokaisen kolmannen asteen polynomin. Tukipisteet on talloin valittu
 LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
Matkailun tulo- ja työllisyysselvitys v. 2016
 Matkailun tulo- ja työllisyysselvitys v. 2016 Rakennetiedot Jämsän matkailukeskus Laskettavan muuttujan vuositaso (YTR) Yritykset YTR:n mukaan Toimipaikat YTR:n mukaan Henkilöstömäärä (2015) 322 69 77
Matkailun tulo- ja työllisyysselvitys v. 2016 Rakennetiedot Jämsän matkailukeskus Laskettavan muuttujan vuositaso (YTR) Yritykset YTR:n mukaan Toimipaikat YTR:n mukaan Henkilöstömäärä (2015) 322 69 77
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä
 Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Johdatus regressioanalyysiin. Heliövaara 1
 Johdatus regressioanalyysiin Heliövaara 1 Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen
Johdatus regressioanalyysiin Heliövaara 1 Regressioanalyysin idea Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun selittävien muuttujien havaittujen arvojen
Mitä kalibrointitodistus kertoo?
 Mitä kalibrointitodistus kertoo? Luotettavuutta päästökauppaan liittyviin mittauksiin MIKES 21.9.2006 Martti Heinonen Tavoite Laitteen kalibroinnista hyödytään vain jos sen tuloksia käytetään hyväksi.
Mitä kalibrointitodistus kertoo? Luotettavuutta päästökauppaan liittyviin mittauksiin MIKES 21.9.2006 Martti Heinonen Tavoite Laitteen kalibroinnista hyödytään vain jos sen tuloksia käytetään hyväksi.
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016
1 KAUPALLISIA SOVELLUKSIA 7. 1.1 Tulovero 8
 SISÄLTÖ 1 KAUPALLISIA SOVELLUKSIA 7 1.1 Tulovero 8 1.2 Hintaan vaikuttavia tekijöitä 13 - Arvonlisävero 13 - Myyntipalkkio ja myyntikate 15 - Alennus ja hävikki 17 1.3 Indeksit 22 - Indeksin käsite 22
SISÄLTÖ 1 KAUPALLISIA SOVELLUKSIA 7 1.1 Tulovero 8 1.2 Hintaan vaikuttavia tekijöitä 13 - Arvonlisävero 13 - Myyntipalkkio ja myyntikate 15 - Alennus ja hävikki 17 1.3 Indeksit 22 - Indeksin käsite 22
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Männyn laaturajojen integrointi runkokäyrän ennustamisessa. Laura Koskela Tampereen yliopisto 9.6.2003
 Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
4. Funktion arvioimisesta eli approksimoimisesta
 4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
Näihin harjoitustehtäviin liittyvä teoria löytyy Adamsista: Ad6, Ad5, 4: 12.8, ; Ad3: 13.8,
 TKK, Matematiikan laitos Gripenberg/Harhanen Mat-1.432 Matematiikan peruskurssi K2 Harjoitus 4, (A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä ) 12 16.2.2007, viikko
TKK, Matematiikan laitos Gripenberg/Harhanen Mat-1.432 Matematiikan peruskurssi K2 Harjoitus 4, (A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä ) 12 16.2.2007, viikko
Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4
 18.9.2018/1 MTTTP1, luento 18.9.2018 KERTAUSTA Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4 pyöristetyt todelliset luokka- frekvenssi luokkarajat luokkarajat keskus 42 52 41,5
18.9.2018/1 MTTTP1, luento 18.9.2018 KERTAUSTA Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4 pyöristetyt todelliset luokka- frekvenssi luokkarajat luokkarajat keskus 42 52 41,5
6. laskuharjoitusten vastaukset (viikot 10 11)
 6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
Ellipsoidimenetelmä. Samuli Leppänen Kokonaislukuoptimointi. S ysteemianalyysin Laboratorio
 Ellipsoidimenetelmä Kokonaislukuoptimointi Sovelletun matematiikan lisensiaattiseminaari Kevät 2008 / 1 Sisällys Ellipsoidimenetelmän geometrinen perusta ja menetelmän idea Formaali ellipsoidimenetelmä
Ellipsoidimenetelmä Kokonaislukuoptimointi Sovelletun matematiikan lisensiaattiseminaari Kevät 2008 / 1 Sisällys Ellipsoidimenetelmän geometrinen perusta ja menetelmän idea Formaali ellipsoidimenetelmä
Aikasarjamallit. Pekka Hjelt
 Pekka Hjelt Aikasarjamallit Aikasarja koostuu järjestyksessä olevista havainnoista, ja yleensä se on tasavälinen ja diskreetti eli havaintopisteet ovat erillisiä. Lisäksi aikasarjassa on yleensä autokorrelaatiota
Pekka Hjelt Aikasarjamallit Aikasarja koostuu järjestyksessä olevista havainnoista, ja yleensä se on tasavälinen ja diskreetti eli havaintopisteet ovat erillisiä. Lisäksi aikasarjassa on yleensä autokorrelaatiota
5.6.3 Matematiikan lyhyt oppimäärä
 5.6.3 Matematiikan lyhyt oppimäärä Matematiikan lyhyen oppimäärän opetuksen tehtävänä on tarjota valmiuksia hankkia, käsitellä ja ymmärtää matemaattista tietoa ja käyttää matematiikkaa elämän eri tilanteissa
5.6.3 Matematiikan lyhyt oppimäärä Matematiikan lyhyen oppimäärän opetuksen tehtävänä on tarjota valmiuksia hankkia, käsitellä ja ymmärtää matemaattista tietoa ja käyttää matematiikkaa elämän eri tilanteissa
