Korkealämpötilakemia
|
|
|
- Anita Lattu
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Korkealämpötilakemia Gibbsin faasisääntö, kuvaajien laadinta sekä1-komponenttipiirrokset To klo 8-10 SÄ114 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen laadintaan ja siten oppia arvioimaan faasipiirrostarkastelujen mahdollisuuksia ja rajoituksia Oppia Gibbsin faasisääntö ja miten se näkyy faasipiirroksissa Oppia tulkitsemaan ja lukemaan 1- komponenttipiirroksia 1
2 Sisältö Mihin tasapainopiirroksia käytetään? laadinta - Kokeellisesti - Dynaamiset ja tasapainomenetelmät - Gibbsin faasisääntö - Laskennallisesti Yksikomponenttisysteemien tasapainopiirrokset Invariantti, univariantti ja bivariantti tasapaino Mihin tasapainopiirroksia käytetään korkealämpötilatarkasteluissa? Olosuhteiden määrittäminen tietyn faasirakenteen/koostumuksen aikaansaamiseksi Tietyissä olosuhteissa esiintyvien faasien sekä niiden koostumusten ja osuuksien määrittäminen Monikomponenttisysteemien sulamisen ja jähmettymisen tarkastelu Usein tukena esim. kokeellista tutkimusta suunniteltaessa tai tuloksia tulkittaessa Käyttökelpoinen työkalu, koska: - Korkeissa lämpötiloissa tasapaino saavutetaan usein nopeasti pelkkä tasapainokuvaaja kertoo jo paljon - Nopea tarkastelu (verrattuna esim. laskentaan) 2
3 Tasapainopiirrokset Selkeää kuvaajaa on aina miellyttävämpää tarkastella kuin selkeää differentiaaliyhtälöä, minkä lisäksi kuvaajien tarjoama tieto on helpommin insinöörien sovellettavissa. Matemaatikot voivat aina lohduttautua ajattelemalla, että kuvaajat ovat käytännössä differentiaaliyhtälöiden graafisia esityksiä. - P. Perrot (vapaasti suomennettu) laadinta Kokeellisesti - Olosuhteet hallittava tarkasti - Riittävän pitkät koeajat tasapainon saavuttamiseksi - Luotettava analysointi - Tulosten noudatettava Gibbsin faasisääntöä - Dynaamiset ja tasapainomenetelmät Laskennallisesti - Tunnettava Gibbsin vapaaenergian pitoisuusriippuvuus vakiopaineessa - Jokaisella mahdollisella kiderakenteella ja olomuodololla on tietyissä olosuhteissa tietty vapaaenergian arvo - Stabiilin olomuodon vapaaenergia on alhaisin - Käytännössä laskentaohjelmistoja hyödyntäen - Ns. nollaosuuskäyrien (a = 1, n = 0) määritys Faasirajat 3
4 laadinta kokeellisesti Dynaaminen määritys - Kuumennus- ja/tai jäähdytyssyklin aikana tapahtuvien entalpian (ja massan) muutosten rekisteröinti - ThermoGravimetric Analysis (TGA) Termovaa at - Differential Thermal Analysis (DTA) - Differential Scanning Calorimetry (DSC) (+ Ulostulokaasun koostumuksen analysointi) - Etuina nopeus ja suhteellisen helppo toteutus - Haittana mahdottomuus arvioida, onko tasapainotilaa todella saavutettu - Dynaamisuuden aiheuttamia ongelmia voidaan yrittää korjata suorittamalla kokeiden kuumennus-/jäähdytyssyklit eri nopeuksilla - Tulosten ekstrapolointi nollakuumennusnopeuteen - Esimerkkinä spodumeenin - -faasitranformaatiolämpötilan määritys eri kuumennusnopeuksilla Kuva: Tanskanen, Heikkinen, Karjalainen, Seppelin & Lassi. Proceedings of Eco-mates Osaka, Japan. pp laadinta kokeellisesti Dynaaminen määritys Esimerkki - Sulaminen Endotermisyys, ei massanmuutosta - Höyrystyiminen Endotermisyys + massanmuutos 4
5 Lämpötila laadinta kokeellisesti Dynaaminen määritys Esimerkki - H 2 O:n poistuminen vaiheittain - Näkyy massanmuutoksessa, entalpiakäyrässä ja ulostulokaasun koostumuksessa laadinta kokeellisesti Tasapainomenetelmät - Tutkittavan näytteen tasapainottaminen hallituissa ja tunnetuissa olosuhteissa jonkin toisen (tunnetun) faasin kanssa - Nopea sammutus - Faasien ja niiden koostumuksen analysointi - Etuna kyky kontrolloida tasapainotilaa - Haittana hitaus - Yhden olosuhdepisteen määritys kerrallaan - Tasapainotilan varmistaminen - Kokeiden suoritus eri mittaisina Minkä jälkeen mitattavissa suureissa ei enää tapahdu muutoksia? - Mikäli tulokset eivät vastaa Gibbsin faasisääntöä, ei systeemi ole ollut tasapainotilassa A = 0 % B = 100 % Pitoisuus A = 100 % B = 0 % Vasen kuva: Seo, Han, Kim & Pak: ISIJ Int. 43(2003)2, Oikea kuva: Jahanshahi & Wright: ISIJ Int. 33(1993)1,
6 Gibbsin faasisääntö Ehto, joka määrittää kuinka monta faasia (f) voi olla keskenään tasapainossa systeemissä, jonka komponenttien lukumäärä (K) ja vapausasteiden lukumäärä (F) tunnetaan F = K f Ei aseta mitään ehtoja systeemille eikä siihen kuuluvien komponenttien ja faasien ominaisuuksille Useat tasapainopiirrokset ovat isobaarisia - Tarvitaan yksi vapausaste paineen kiinnittämiseksi - Yleensä p kok = 1 atm - F = 1 f = K ts. toistensa kanssa tasapainossa olevien faasien lukumäärä voi olla korkeintaan yhden enemmän kuin systeemin komponenttien lukumäärä - Tällöin vapausteiden määrä on nolla laadinta laskennallisesti Tasapainopiirroksissa esitetään eri faasien stabiilisuusalueita olosuhteiden (yleensä lämpötila, paine ja koostumus) funktiona Laskennallisessa määrityksessä lasketaan eri faasien Gibbsin vapaaenergiat haluttujen olosuhteiden funktiona - Alhaisimman Gibbsin energian omaava faasi on stabiilein - Määritetään faasirajat, joissa useampi faasi on tasapainossa keskenään Käytännössä tarkastellaan aina useamman kuin yhden komponentin systeemejä - Kuvaajien yksinkertaistamiseksi paine vakioidaan - Paineen muutokset teollisissa prosesseissa vähäisiä - Paineen vaikutus kondensoitujen faasien stabiilisuuksiin vähäinen - Eli tunnettava Gibbsin vapaaenergian lämpötila- ja koostumusriippuvuudet - Laskentaohjelmistoissa määritetään ns. nollaosuuskäyrät 6
7 laadinta laskennallisesti Gibbsin vapaaenergia koostumuksen funktiona - Tarkastellaan kahdessa osassa: G = H 0 TS m - H 0 kuvaa systeemin atomien lämpösisältöä - S m on sekoittumisentropia - Vapaaenergian pitoisuusriippuvuuden muoto riippuu seoksen komponenttien välisistä vuorovaikutuksista - Sekoittumisentropia ja lämpötila ovat aina positiivisia - TS m termi on aina alaspäin kaareutuva käyrä/pinta - Komponenttien (esim. binäärisysteemin A ja B) väliset vuorovaikutusenergiat (merkitään V AA, V BB ja V AB ) vaihtelevat - H 0 -käyrä voi kaartua ylös- tai alaspäin - Vapaaenergiakäyrän tai pinnan muoto saadaan näiden kahden termin summana laadinta laskennallisesti G = H - TS Entalpian lämpötilariippuvuus H = C P dt Lämpökapasiteetti lämpötilan funktiona esim. Kelleyn yhtälö C P = a + bt + ct 2 + dt -2 Entropian lämpötilariippuvuus S = C P /T dt Gibbsin vapaaenergia koostumuksen funktiona - Tarkastellaan kahdessa osassa: G = H 0 TS m - H 0 kuvaa systeemin atomien lämpösisältöä - S m on sekoittumisentropia - Vapaaenergian pitoisuusriippuvuuden muoto riippuu seoksen komponenttien välisistä vuorovaikutuksista - Sekoittumisentropia ja lämpötila ovat aina positiivisia - TS m termi on aina alaspäin kaareutuva käyrä/pinta - Komponenttien (esim. binäärisysteemin A ja B) väliset vuorovaikutusenergiat (merkitään V AA, V BB ja V AB ) vaihtelevat - H 0 -käyrä voi kaartua ylös- tai alaspäin - Vapaaenergiakäyrän tai pinnan muoto saadaan näiden kahden termin summana Gibbsin vapaaenergia lämpötilan funktiona - Koostumusriippuvuutta on luonnollisesti tarkasteltava eri lämpötiloissa - Gibbsin vapaaenergian lämpötilariippuvuuden mallinnus palautuu vapaaenergian määritelmän kautta entalpian ja entropian lämpötilariippuvuuksiin ja edelleen C P -funktioon 7
8 laadinta laskennallisesti Vapaaenergian pitoisuusriippuvuuden muoto voi olla erilainen eri lämpötiloissa - Heijastuu lopulliseen tasapainopiirrokseen - To be continued... laadinta laskennallisesti Faasien nollaosuuskäyrät (engl. Zero Phase Fraction, ZPF-lines) - Kuvaavat faasien stabiilisuusalueiden rajoja - Raja, jossa tietyn faasin a = 1 ja n = 0 - Rajan toisella puolella ao. faasi on stabiili, toisella puolen ei - Alkavat ja loppuvat akseleilta tai muodostavat silmukan - Hyödyksi paitsi kuvaajien laskennallisessa laadinnassa, myös avuksi monikomponenttisysteemeistä tehtyjen leikkausten hahmottamisessa - esimerkkinä Fe-Cr-V-C-systeemi - Isoterminen, isobaarinen systeemi - Vakio hiilipitoisuus - Stabiilit faasit V- ja Cr-pitoisuuksien funktiona 8
9 Koostumus jo määritelmän mukaan vakio - Muuttujina yleensä lämpötila ja paine Faasisääntö yksikomponenttisysteemissä - F = 1 f + 2 F = 3 f - Vapausasteiden ja keskenään tasapainossa olevien faasien lukumäärät ovat sidottu toisiinsa Yksikomponenttisysteemit Yksikomponenttisysteemit Koostumus jo määritelmän mukaan vakio - Muuttujina yleensä lämpötila ja paine Faasisääntö yksikomponenttisysteemissä - F = 1 f + 2 F = 3 f - Vapausasteiden ja keskenään tasapainossa olevien faasien lukumäärät ovat sidottu toisiinsa Tarkastellaan tilannetta, jossa ei ole vapausasteita (F = 0) - 0 = 1 f + 2 f = 3 - Kolme eri faasia ovat tasapainossa keskenään - Koska vapausasteita ei ole, muuttuu ainakin yksi faaseista epästabiiliksi, mikäli olosuhteita (T, p) muutetaan Invariantti tasapaino vallitsee pisteessä 0 - Tilannetta, jossa vapausasteiden lukumäärä on nolla, kutsutaan INVARIANTIKSI tasapainoksi - Myös muissa kuin yksikomponenttisysteemeissä 9
10 Koostumus jo määritelmän mukaan vakio - Muuttujina yleensä lämpötila ja paine Faasisääntö yksikomponenttisysteemissä - F = 1 f + 2 F = 3 f - Vapausasteiden ja keskenään tasapainossa olevien faasien lukumäärät ovat sidottu toisiinsa Tarkastellaan tilannetta, jossa on yksi vapausaste (F = 1) - 1 = 1 f + 2 f = 2 - Kaksi eri faasia ovat tasapainossa keskenään - Koska vapausasteita on yksi, voidaan yksi olosuhdemuuttuja valita vapaasti, mutta toinen on siitä riippuvainen Univariantti tasapaino vallitsee käyrillä A0, B0 ja C0 - Tilannetta, jossa vapausasteiden lukumäärä on yksi, kutsutaan UNIVARIANTIKSI tasapainoksi - Myös muissa kuin yksikomponenttisysteemeissä Yksikomponenttisysteemit Yksikomponenttisysteemit Koostumus jo määritelmän mukaan vakio - Muuttujina yleensä lämpötila ja paine Faasisääntö yksikomponenttisysteemissä - F = 1 f + 2 F = 3 f - Vapausasteiden ja keskenään tasapainossa olevien faasien lukumäärät ovat sidottu toisiinsa Tarkastellaan tilannetta, jossa on kaksi vapausastetta (F = 2) - 2 = 1 f + 2 f = 1 - Yksi faasi on stabiili - Koska vapausasteita on kaksi, voidaan kahta olosuhdemuuttujaa muuttaa toisistaan riippumatta Bivariantti tasapaino vallitsee käyrien A0, B0 ja C0 väleihin jäävillä alueilla - Tilannetta, jossa vapausasteiden lukumäärä on kaksi, kutsutaan BIVARIANTIKSI tasapainoksi - Myös muissa kuin yksikomponenttisysteemeissä 10
11 Tehtävä Onko seuraavissa systeemeissä voimassa invariantti, bivariantti vai univariantti tasapaino? - Jää tasapainossa vesihöyryn kanssa? Univariantti (F = K f + 2 = = 1) - Monokliinisen kiderakenteen omaava ZrO 2 huoneenlämpötilassa? Univariantti (yksi vapausaste kiinnitetty T:aan) - Monokliinisen kiderakenteen omaava ZrO 2 huoneenlämpötilassa ja normaalissa ilmanpaineessa? Invariantti (kaksi vapausastetta kiinnitetty T:aan ja p:een) - -kvartsi tasapainossa -kvartsin kanssa faasimuutoslämpötilassa? Invariantti (jos faasimuutoslämpötila tulkitaan yhdeksi lämpötilaksi) tai univariantti (jos faasimuutoslämpötila tulkitaan paineen funktioksi) Periklaasi Protoenstatiitti Forsteriitti Toinen tehtävä Kristobaliitti SiO 2 Kordieriitti Safiriini Mulliitti Korundi MgO Spinelli Al 2 O 3 Määritettäessä monikomponenttisysteemin tasapainopiirrosta kokeellisesti havaittiin, että seuraavat faasit esiintyivät samassa näytteessä vakiolämpötilassa ja paineessa: - Kordieriitti (2MgO 2Al 2 O 3 5SiO 2 ) - Mulliitti (3Al 2 O 3 2SiO 2 ) - Forsteriitti (2MgO SiO 2 ) - Periklaasi (MgO) Mitkä ovat systeemin komponentit? Voivatko kaikki em. faasit esiintyä tasapainotilassa yhtäaikaa? Komponentit valitaan siten, että niitä on pienin mahdollinen lukumäärä, jolla kaikki systeemin yhdisteet voidaan yksiselitteisesti kuvata: MgO, Al 2 O 3 ja SiO 2 Neljä faasia ei voi esiintyä tasapainossa keskenään, koska Gibbsin faasisäännön mukaan: F = K - f + 2 = = 1, joka ei riitä, kun lämpötilan ja paineen kiinnittämiseksi tarvitaan kaksi vapausastetta. 11
12 Periklaasi Protoenstatiitti Forsteriitti Toinen tehtävä Kristobaliitti SiO 2 Kordieriitti Safiriini Mulliitti Korundi MgO Spinelli Al 2 O 3 Määritettäessä monikomponenttisysteemin tasapainopiirrosta kokeellisesti havaittiin, että seuraavat faasit esiintyivät samassa näytteessä vakiolämpötilassa ja paineessa: - Kordieriitti (2MgO 2Al 2 O 3 5SiO 2 ) - Mulliitti (3Al 2 O 3 2SiO 2 ) - Forsteriitti (2MgO SiO 2 ) - Periklaasi (MgO) Mitkä ovat systeemin komponentit? Voivatko kaikki em. faasit esiintyä tasapainotilassa yhtäaikaa? Neljä Komponentit ilmoitettua valitaan faasia siten, eivät että sijoitu niitä pitoisuuskolmioon on pienin mahdollinen siten, että lukumäärä, niistä edes jolla kolme kaikki (miten systeemin tahansa yhdisteet valittuna) voidaan voisivat esiintyä yksiselitteisesti tasapainossa kuvata: samanaikaisesti, MgO, Al 2 O 3 ja SiO koska 2 kuvaajaan ei muodostu niille yhteistä pitoisuusaluetta/-kolmiota. Neljä faasia ei voi esiintyä tasapainossa keskenään, koska Gibbsin Mahdollisia faasisäännön yhdisteitä voisivat mukaan: olla esim. periklaasiforsteriitti-spinelli, = K - f + 2 = 3-4 forsteriitti-protoenstatiitti-kordieriitti + 2 = 1, joka ei riitä, kun lämpötilan tai ja F paineen kordieriitti-mulliitti-safiriini. kiinnittämiseksi tarvitaan kaksi vapausastetta. yksinkertaistaminen vakio-oletuksilla Vakioidaan paine, lämpötila tai jokin pitoisuusmuuttuja - Tuloksena helpommin luettava kuvaajat 12
13 Yhteenveto hyödyntäminen - Faasikoostumuksen määritys tietyissä olosuhteissa - Olosuhteiden määritys tietylle faasikoostumukselle laadinta - Kokeellisesti joko dynaamisia tai tasapainomenetelmiä hyödyntäen - Laskennallisesti Gibbsin vapaaenergiaa hyödyntäen Yksikomponenttisysteemit - Olomuodot/faasit lämpötilan ja paineen funktiona Invariantti, univariantti ja bivariantti tasapaino Kuva: FactSage Versio
Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta
 Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 3 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen
Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 3 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen
Korkealämpötilakemia
 Korkealämpötilakemia Binääriset tasapainopiirrokset To 30.10.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan binäärisiä tasapainopiirroksia 1 Sisältö Hieman kertausta - Gibbsin vapaaenergian
Korkealämpötilakemia Binääriset tasapainopiirrokset To 30.10.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan binäärisiä tasapainopiirroksia 1 Sisältö Hieman kertausta - Gibbsin vapaaenergian
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta
 Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
Korkealämpötilakemia
 Korkealämpötilakemia Useamman komponentin tasapainopiirrokset To 7.12.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan ternäärisiä tasapainopiirroksia 1 Sisältö Ternääriset tasapainopiirrokset
Korkealämpötilakemia Useamman komponentin tasapainopiirrokset To 7.12.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan ternäärisiä tasapainopiirroksia 1 Sisältö Ternääriset tasapainopiirrokset
Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta
 Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 5 Tavoite Oppia tulkitsemaan 3-komponenttisysteemien faasipiirroksia
Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 5 Tavoite Oppia tulkitsemaan 3-komponenttisysteemien faasipiirroksia
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Korkealämpötilakemia
 Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Korkealämpötilakemia
 1.11.217 Korkealämpötilakemia Standarditilat Ti 1.11.217 klo 8-1 SÄ11 Tavoite Tutustua standarditiloihin liuosten termodynaamisessa mallinnuksessa Miksi? Millaisia? Miten huomioidaan tasapainotarkasteluissa?
1.11.217 Korkealämpötilakemia Standarditilat Ti 1.11.217 klo 8-1 SÄ11 Tavoite Tutustua standarditiloihin liuosten termodynaamisessa mallinnuksessa Miksi? Millaisia? Miten huomioidaan tasapainotarkasteluissa?
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Chem-C2400 Luento 3: Faasidiagrammit Ville Jokinen
 Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Sulamisen ja jähmettymisen tarkastelu faasipiirroksia hyödyntäen
 Sulamisen ja jähmettymisen tarkastelu faasipiirroksia hyödyntäen Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 6 Tavoite Oppia muutamien esimerkkien avulla tarkastelemaan monikomponenttisysteemien
Sulamisen ja jähmettymisen tarkastelu faasipiirroksia hyödyntäen Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 6 Tavoite Oppia muutamien esimerkkien avulla tarkastelemaan monikomponenttisysteemien
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Ratkaisu. Tarkastellaan aluksi Fe 3+ - ja Fe 2+ -ionien välistä tasapainoa: Nernstin yhtälö tälle reaktiolle on:
 Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Ellinghamin diagrammit
 Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1
 Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1 A B B Piirroksen alue 1: Sularajan yläpuolella on seos aina täysin sula => yksifaasialue (L). Alueet 2 ja 5: Nämä ovat
Faasialueiden nimeäminen/tunnistaminen (eutek1sessa) tasapainopiirroksessa yleises1 A B B Piirroksen alue 1: Sularajan yläpuolella on seos aina täysin sula => yksifaasialue (L). Alueet 2 ja 5: Nämä ovat
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Korkealämpötilakemia
 Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 1
 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy 6 Teema - Luento Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy 6 Teema - Luento Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
Tärkeitä tasapainopisteitä
 Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Dislokaatiot - pikauusinta
 Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2012 Teema 1 - Luento 1
 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Standarditilat. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 2 - Luento 2. Tutustua standarditiloihin
 Standarditilat Ilmiömallinnus prosessimetallurgiassa Syksy 216 Teema 2 - Luento 2 Tavoite Tutustua standarditiloihin Miksi käytössä? Millaisia käytössä? Miten huomioitava tasapainotarkasteluissa? 1 Miten
Standarditilat Ilmiömallinnus prosessimetallurgiassa Syksy 216 Teema 2 - Luento 2 Tavoite Tutustua standarditiloihin Miksi käytössä? Millaisia käytössä? Miten huomioitava tasapainotarkasteluissa? 1 Miten
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä.
 FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin
 Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 27.10.2016 klo 14-16 Luennon tavoite Tutustua eri tapoihin määrittää termodyn. tasapaino laskennallisesti Tutustua termodynaamisten
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 27.10.2016 klo 14-16 Luennon tavoite Tutustua eri tapoihin määrittää termodyn. tasapaino laskennallisesti Tutustua termodynaamisten
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
 6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
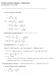 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
8 Aineen olomuodot. 8-1 Olomuodon muutokset
 96 8 Aineen olomuodot 8-1 Olomuodon muutokset Vesi voi esiintyä eri lämpötiloissa hyvin erilaisissa tiloissa jäänä, nestemäisenä vetenä ja höyrynä. Tällaisia tiloja sanotaan aineen olomuodoiksi (engl.
96 8 Aineen olomuodot 8-1 Olomuodon muutokset Vesi voi esiintyä eri lämpötiloissa hyvin erilaisissa tiloissa jäänä, nestemäisenä vetenä ja höyrynä. Tällaisia tiloja sanotaan aineen olomuodoiksi (engl.
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen [email protected] 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen [email protected] 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
(l) B. A(l) + B(l) (s) B. B(s)
 FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 LIUKOISUUDEN IIPPUVUUS LÄMPÖTILASTA 6. 11. 1998 (HJ) A(l) + B(l) µ (l) B == B(s) µ (s) B FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 1. TEOIAA Kyllästetty liuos LIUKOISUUDEN
FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 LIUKOISUUDEN IIPPUVUUS LÄMPÖTILASTA 6. 11. 1998 (HJ) A(l) + B(l) µ (l) B == B(s) µ (s) B FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 1. TEOIAA Kyllästetty liuos LIUKOISUUDEN
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 1: Lämpötila ja Boltzmannin jakauma Ke 24.2.2016 1 YLEISTÄ KURSSISTA Esitietovaatimuksena
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 1: Lämpötila ja Boltzmannin jakauma Ke 24.2.2016 1 YLEISTÄ KURSSISTA Esitietovaatimuksena
Sähkökemialliset tarkastelut HSC:llä
 Sähkökemialliset tarkastelut HSC:llä Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 5 Tavoite Oppia hyödyntämään HSC-ohjelmistoa sähkökemiallisissa tarkasteluissa 1 Sisältö Sähkökemiallisiin
Sähkökemialliset tarkastelut HSC:llä Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 5 Tavoite Oppia hyödyntämään HSC-ohjelmistoa sähkökemiallisissa tarkasteluissa 1 Sisältö Sähkökemiallisiin
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
W el = W = 1 2 kx2 1
 7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
LUKU 16 KEMIALLINEN JA FAASITASAPAINO
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin
 Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 7.9.2017 klo 8-10 Prosessimetallurgian tutkimusyksikkö Eetu-Pekka Heikkinen, 2017 Luennon tavoite Tutustua eri tapoihin määrittää
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 7.9.2017 klo 8-10 Prosessimetallurgian tutkimusyksikkö Eetu-Pekka Heikkinen, 2017 Luennon tavoite Tutustua eri tapoihin määrittää
Kertaus. x x x. K1. a) b) x 5 x 6 = x 5 6 = x 1 = 1 x, x 0. K2. a) a a a a, a > 0
 Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
1 Di erentiaaliyhtälöt
 Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
MAA2.3 Koontitehtävät 2/2, ratkaisut
 MAA.3 Koontitehtävät /, ratkaisut. (a) 3x 5x 4 = 0 x = ( 5) ± ( 5) 4 3 ( 4) 6 (b) (x 4) = (x 4)(x + 4) (x 4)(x 4) = (x 4)(x + 4) x 8x + 6 = x 6 x 6 8x = 3 : 8 x = 4 = 5 ± 73 6 (c) 4 x + x + = 0 4 x + 4x
MAA.3 Koontitehtävät /, ratkaisut. (a) 3x 5x 4 = 0 x = ( 5) ± ( 5) 4 3 ( 4) 6 (b) (x 4) = (x 4)(x + 4) (x 4)(x 4) = (x 4)(x + 4) x 8x + 6 = x 6 x 6 8x = 3 : 8 x = 4 = 5 ± 73 6 (c) 4 x + x + = 0 4 x + 4x
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
E p1 = 1 e 2. e 2. E p2 = 1. Vuorovaikutusenergian kolme ensimmäistä termiä on siis
 763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
LASKENNALLISEN TIETEEN OHJELMATYÖ: Diffuusion Monte Carlo -simulointi yksiulotteisessa systeemissä
 LASKENNALLISEN TIETEEN OHJELMATYÖ: Diffuusion Monte Carlo -simulointi yksiulotteisessa systeemissä. Diffuusio yksiulotteisessa epäjärjestäytyneessä hilassa E J ii, J ii, + 0 E b, i E i i i i+ x Kuva.:
LASKENNALLISEN TIETEEN OHJELMATYÖ: Diffuusion Monte Carlo -simulointi yksiulotteisessa systeemissä. Diffuusio yksiulotteisessa epäjärjestäytyneessä hilassa E J ii, J ii, + 0 E b, i E i i i i+ x Kuva.:
1 Johdanto. 2 Lähtökohdat
 FYSP106/K4 VIRITYSTILAN ELINAIKA 1 Johdanto Työssä tutustutaan hajoamislakiin ja määritetään 137 Ba:n viritystilan 661.7 kev keskimääräinen elinaika ja puoliintumisaika. 2 Lähtökohdat 2.1 Radioaktiivinen
FYSP106/K4 VIRITYSTILAN ELINAIKA 1 Johdanto Työssä tutustutaan hajoamislakiin ja määritetään 137 Ba:n viritystilan 661.7 kev keskimääräinen elinaika ja puoliintumisaika. 2 Lähtökohdat 2.1 Radioaktiivinen
Esim: Mikä on tarvittava sylinterin halkaisija, jolla voidaan kannattaa 10 KN kuorma (F), kun käytettävissä on 100 bar paine (p).
 3. Peruslait 3. PERUSLAIT Hydrauliikan peruslait voidaan jakaa hydrostaattiseen ja hydrodynaamiseen osaan. Hydrostatiikka käsittelee levossa olevia nesteitä ja hydrodynamiikka virtaavia nesteitä. Hydrauliikassa
3. Peruslait 3. PERUSLAIT Hydrauliikan peruslait voidaan jakaa hydrostaattiseen ja hydrodynaamiseen osaan. Hydrostatiikka käsittelee levossa olevia nesteitä ja hydrodynamiikka virtaavia nesteitä. Hydrauliikassa
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla [email protected] tai [email protected] vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla [email protected] tai [email protected] vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
Integrointialgoritmit molekyylidynamiikassa
 Integrointialgoritmit molekyylidynamiikassa Markus Ovaska 28.11.2008 Esitelmän kulku MD-simulaatiot yleisesti Integrointialgoritmit: mitä integroidaan ja miten? Esimerkkejä eri algoritmeista Hyvän algoritmin
Integrointialgoritmit molekyylidynamiikassa Markus Ovaska 28.11.2008 Esitelmän kulku MD-simulaatiot yleisesti Integrointialgoritmit: mitä integroidaan ja miten? Esimerkkejä eri algoritmeista Hyvän algoritmin
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Mikroskooppisten kohteiden
 Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
Mikroskooppisten kohteiden lämpötilamittaukset itt t Maksim Shpak Planckin laki I BB ( λ T ) = 2hc λ, 5 2 1 hc λ e λkt 11 I ( λ, T ) = ε ( λ, T ) I ( λ T ) m BB, 0 < ε
6. Differentiaaliyhtälösysteemien laadullista teoriaa.
 1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Faasimuutokset ja lämpökäsittelyt
 Faasimuutokset ja lämpökäsittelyt Yksinkertaiset lämpökäsittelyt Pehmeäksihehkutus Nostetaan lämpötilaa Diffuusio voi tapahtua Dislokaatiot palautuvat Materiaali pehmenee Rekristallisaatio Ei ylitetä faasirajoja
Faasimuutokset ja lämpökäsittelyt Yksinkertaiset lämpökäsittelyt Pehmeäksihehkutus Nostetaan lämpötilaa Diffuusio voi tapahtua Dislokaatiot palautuvat Materiaali pehmenee Rekristallisaatio Ei ylitetä faasirajoja
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola [email protected] Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola [email protected] Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt
 Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt Digress: vakio- vs. muuttuva kiihtyvyys käytännössä Kinematiikkaa yhdessä dimensiossa taustatietoa Matlab-esittelyä 1 / 20 Luennon sisältö Digress: vakio-
Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt Digress: vakio- vs. muuttuva kiihtyvyys käytännössä Kinematiikkaa yhdessä dimensiossa taustatietoa Matlab-esittelyä 1 / 20 Luennon sisältö Digress: vakio-
Puhtaat aineet ja seokset
 Puhtaat aineet ja seokset KEMIAA KAIKKIALLA, KE1 Määritelmä: Puhdas aine sisältää vain yhtä alkuainetta tai yhdistettä. Esimerkiksi rautatanko sisältää vain Fe-atomeita ja ruokasuola vain NaCl-ioniyhdistettä
Puhtaat aineet ja seokset KEMIAA KAIKKIALLA, KE1 Määritelmä: Puhdas aine sisältää vain yhtä alkuainetta tai yhdistettä. Esimerkiksi rautatanko sisältää vain Fe-atomeita ja ruokasuola vain NaCl-ioniyhdistettä
CHEM-A1110 Virtaukset ja reaktorit. Laskuharjoitus 9/2016. Energiataseet
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla [email protected] tai [email protected] vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla [email protected] tai [email protected] vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
782630S Pintakemia I, 3 op
 782630S Pintakemia I, 3 op Ulla Lassi Puh. 0400-294090 Sposti: [email protected] Tavattavissa: KE335 (ma ja ke ennen luentoja; Kokkolassa huone 444 ti, to ja pe) Prof. Ulla Lassi Opintojakson toteutus
782630S Pintakemia I, 3 op Ulla Lassi Puh. 0400-294090 Sposti: [email protected] Tavattavissa: KE335 (ma ja ke ennen luentoja; Kokkolassa huone 444 ti, to ja pe) Prof. Ulla Lassi Opintojakson toteutus
derivaatta pisteessä (YOS11) a) Näytä, että a n+1 > a n, kun n = 1, 2, 3,.
 Matematiikka, MAA9. a) Ratkaise yhtälö tan (YOS) Kulma on välillä [, 6]. Ratkaise asteen tarkkuudella seuraavat yhtälöt: b) sin c) cos (YOs). Kulmalle [9,6 ] on voimassa sin = 8 7. Määritä cos ja tan..
Matematiikka, MAA9. a) Ratkaise yhtälö tan (YOS) Kulma on välillä [, 6]. Ratkaise asteen tarkkuudella seuraavat yhtälöt: b) sin c) cos (YOs). Kulmalle [9,6 ] on voimassa sin = 8 7. Määritä cos ja tan..
Esimerkiksi ammoniakin valmistus typestä ja vedystä on tyypillinen teollinen tasapainoreaktio.
 REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
x = π 3 + nπ, x + 1 f (x) = 2x (x + 1) x2 1 (x + 1) 2 = 2x2 + 2x x 2 = x2 + 2x f ( 3) = ( 3)2 + 2 ( 3) ( 3) + 1 3 1 + 4 2 + 5 2 = 21 21 = 21 tosi
 Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
Mallivastaukset - Harjoituskoe F F1 a) (a + b) 2 (a b) 2 a 2 + 2ab + b 2 (a 2 2ab + b 2 ) a 2 + 2ab + b 2 a 2 + 2ab b 2 4ab b) tan x 3 x π 3 + nπ, n Z c) f(x) x2 x + 1 f (x) 2x (x + 1) x2 1 (x + 1) 2 2x2
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Fysikaaliset ominaisuudet
 Fysikaaliset ominaisuudet Ominaisuuksien alkuperä Mistä materiaalien ominaisuudet syntyvät? Minkälainen on materiaalin rakenne? Onko rakenteellisesti samankaltaisilla materiaaleilla samankaltaiset ominaisuudet?
Fysikaaliset ominaisuudet Ominaisuuksien alkuperä Mistä materiaalien ominaisuudet syntyvät? Minkälainen on materiaalin rakenne? Onko rakenteellisesti samankaltaisilla materiaaleilla samankaltaiset ominaisuudet?
