Taide opetuksessa. Käytännönläheisiä taidekasvatusmenetelmiä peruskoulun opetussuunnitelmien tueksi. Kulttuuriaitta klnwp
|
|
|
- Hanna Laakso
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Tie opetuksess Käytäöäheisiä tieksvtusmeetemiä peuskouu opetussuuitemie tueksi Kuttuuiitt 2010 kwp
2 me s e 2 Tie opetuksess Tie o uooie os eämää se vikutt kikki. Kuttuuiit Tie opetuksess -kokoisuuess kehitetää titeeisi toimitmuoto ivom iitä kouuopetuksee. Peuskouu oppiieet tuevt uue tv tutuiksi, ku fysiik imiöihi tutustut tssie ti mutouku opiske ue. o b f m Kuttuuiit Tie opetuksess -kokoisuutee kuuuu eä p os-uett: Kuttuuioiskeit-kouutus, kuttuuiopetussuuitemyhteistyö, Titeii too -työpoe voi mi Tie opetuksess -meetemä työpt. Tässä oppss esiteää Tie opetuksess -meetemä eiisi muoto. Tie opetuksess -meetemässä mmeet ieoit peuskouu opetussuuitemist tuo uutt äkökum tuttue ieie opiskeuu. Tvoittee o, että oppiie seekyys ei oppiieit koht mtuu käytäöäheiste Tie opetuksess -hoituste vu. Kuttuuiitss o kehitetty Tie opetuksess -meetemää yä- kouuu vuoest 2007 ähtie, meetemää kehitetää eet koko. Tie opetuksess -kokoisuus: Kuttuuioiskeit-kouutus f Täyeyskouutuksiss ohkist opetti tttum titeeisii työväieisii omksum e osksi om työtää. h k Kuttuuiopetussuuitemyhteistyö Kuttuuiitt o muk kehittämässä kuttuuiopetussuuitemi toimit-uees kouuihi päiväkoteihi tuottmss iihi sisätöä. Titeii too -työpoe voi mi Titeiit opett ti stethopett suuitteevt yhessä työpkokoisuue, ok tukee kouu ti päivähoio opetust. p b Tie opetuksess -meetemä s Tässä oppss esiteää käytäöäheisiä Tie opetuksess -meetemiä. Kokoisuuksi voi käyttää kouutyössä seisi, ti poimi iistä vikkeä viikkeitä oppitueie. 2 ih p s tef
3 h 14 Tie opetuksess f m p s tef h b Tssii fysiik kss Piopiste, tspio, tukipit Pyöimistä Liike kitk Neueikävokuvus Neueikäimiö Kmeoie ketmie kuvmie Kuvie kehittämie Rytmikästä äikkää mtikk Hvioistmie Nuottie väätämie skteupuoksest Nimiytmit Rytmittpei 3 k19 Sisäys: 24 Dmttist kemi Aistie mimt Teksteä tioit Symboiikk Toimit Kemi v Kuvt somuss Kuv kuvt Tik Kuvist tioiksi 1 Kuvist tioiksi 2 3
4 me s e 4 Tssii fysiik kss o b f m Fysiik imiöt piopisteestä kitk tuevt tutuksi tssi p fysiikk yhistävässä kuusitutisess pkokoisuuess. Meetemä o suuttu uokkisie, mutt sitä voi sovete hyöytää myös yäkouu fysiik opetuksess. Meetemä o kittu muistii fysiikopett-m- tssipeoi Hu Moise suuitteem toteuttm työpkokoisuue poht. Otteit vtkuisist peusopetukse opetussuuitem peusteist FYSIIKKA / 5. 7.k h k M vetovoim kitk sekä voimist iheutuvi iike- tspioimiöitä. f Tuvie iikkumie tptumie p b ehkäisemie. Vuoovikutukset iistä sytyvät voimt sekä iistä iheutu- vt iike- tspioimiöt sekä iie esiitymie ympäistössä. s Liike: tsise tsisesti kiihtyvä iikkee mit. 4 ih p s tef
5 Piopiste Työp kesto: 2 oppituti Piopiste, tspio tukipit (Beke feezet, beti beskit) Tssi peustuu vto tspio hit. Tssi muuteee hitusti piopisteesä pikk suhteess tukipits iikkeeseesä. h f m p s tef h b Piopisteeksi ei msskeskipisteeksi kutsut pistettä, oho kppee piovoim yhteisvikutukse te kohistuv. Mikä ths kppee piopiste voi peitteess sevittää kokeeisesti etsimää piste, ost tuettu kppe pysyy tspioss. Koe 1: Tspio voi etsiä kokeiem. Esimekiksi phvievy s pysymää tspioss kyä käeä, ku etsii tukipistee, oho kyä käe sett. Tätä pistettä kutsut evy piopisteeksi. Etsi eimuotoiste kppeie piopisteitä. Mite voisi sevittää ihmise msskeskipistee? Koe 2: Piopiste voi öytää ipustm evy tspioo yhestä pisteestä ke, piitämää kuki ipustuspistee kutt uotisuo. Kikki äi sut suot eikkvt toises piopisteessä. 5 X Tukipit Suuittee sopiv koeäestey määitä kppee piopiste. Piopiste o kppee pio tetu vikutuspiste. Ku ktse kuvi tssioist, huomt, että moet heis- k tä ovt mitä kummisimmiss tspioseoiss. Esimekiksi beikk stt o yhe käe vss tspiosemss bettitssi vvstossue käkios vss. Miksi he eivät ku? Kppee tukipit o kppee ust koskettvie uommiste osie m ue. Kppe ktuu, ku se piopisteestä veetty uotisuo yittää tukipi. Kppe o sitä vkmpi, mitä suuempi tukipit siä o mitä mtmm se piopiopiste siitsee: vet bei sumok. Koe 3: Sevitä tukipito: miie o pöyä ti tuoi tukipit? Etä ihmise tukipit khe yheä seistessä, vpi seistessä, pyyää oess ti yheä käeä seistessä? m Mikä o yhe vpi seisov tssi tukipit? Kokoisuutee voi iittää myös muoviutyöp vokuvustyöp: Muoviutyöp: Tehää muoviuvhst ti muust mssst sekä tuitikuist beikki ti tssi, ok o tspiosemss. Vokuvustyöp: Kuvt eueikäkmeoi oppiit eiisiss tspiosemiss. 5
6 me s e 6 Mitä kuemp piot ovt pyöimiskseist, sitä suuempi o kppee hitusmometti. Kppee Kppee ktumie pyöimisopeutt sot fysiikss o b f m Koe 4: No seiää site, että sekäsi o suo ktpäät kiii seiässä. Sioit koikko oi 30 m etäisyyee keä pkäis- tä. Nost h mst site, että povesi ovt koko suo. kumopeueksi. Kumopeue hitusmometi tuo kutsut pyöimismäääksi se o vkio: ku toie ksv ii toie väheee. Hitusmometti muutteem voi muutt pyöimisopeutt. Bettitssit, uisteit, beikkit, k- Miksi h poimimie oistuu ti epäois tuu? Mite peekeät muuttisivt tiett? obtit uimhyppääät käyttävät tätä fysiik ki hyväksee. Ku Koe 5: esimekiksi uistei vetää kätesä No vsemm kyeäsi seiää site, että sekäsi o suo. Piä okpää kiii seiässä ost oike ksi pieeee, ooi kumopeus ks- ähemmäksi itseää, hitusmometti yöspäi. v uistei pyöii opemmi. Kuik kokee voi ost? Miksi hoht heposti oikee? h k p b 6 ih p s tef
7 f m p Työp kesto: 2 oppituti Pyöimistä h s tef h b Tssiss pyöimisiikkeet kute piuetit spiit ovt äyttäviä po käytettyä. Pyöimisee iittyvät kä- sitteet pyöimisksei, kumopeus pyöivä kppee hitusmometti. Pyöimisessä yhistyvät myös tspioimiöt: hyä ei pysy pystyssä, mikäi se piopisteestä piietty uotik yittää se tukipi. Pyöimiskseiksi sot kuvitetu uotisuo, ok o pyöimisiikkee keskipiste. Yeesä pyöimisksei osuu piopistee kohe. 7 Etsitää pyöimisksei ei kppeist, esimekiksi hyästä ihmisestä. Koe 2: Koe 1: k Mite pioe isäämie hyää vikutt se pyöimisopeu- tee? z Ktsot vieo bekest pohit beikkie pyöimistä pääää, isk, seäää e. Mite pyöimisee s vuhti? Koe 3: Pää pyöäe Istut tuoi käet t suoiksi oeettui. Tuoi pyöitetää se pyöimisopeutt tkki sm ku istu vetää käet t mhoisimm ähee vto. v Mitä hvit? Mikä mht o syyä imiöö? Toistet koe piot käsissä. Oko eo eeisee titeesee vettu? Miksi? Toistet koe ii, että isäpuukset o kiiitetty myös ikkoihi. Kokei hoite iikutsiss yksiketisi piuette spieä. Oppit kokeievt, mikä keho-osie vss o mhoist pyöiä mikä o kuoiki tukipit. Tkoitukse o hvioist käytäössä, mite hitusmometi muutos siitä seuv kumopeue muutos s ik. 7
8 s e 8 Työp kesto: 2 oppituti Liike kitk Aiemmi o tutustuttu tssi tspiosemii pyöimisiikkeisii. Tssii kuuuu oeise os myös iike eteemie tiss. b f m Fysiikss puhut usei kppeie iikkeistä. Esimekiksi Liikkee p tssi o pekistetysti tetu iikettä kppee ei tssi toise kppee ei mpo väisessä vuoovikutuksess, tästä vuoovikutuksest iheutuvi muutoksi iikkeissä. tkuvuus Koe 3: Liu ut tiss visukt oiss, tvisi suki pi Liikkeitä o tkoituksemukist uokite yhmii. Tssi iikettä voi kuvt eiisi omiisuuksi: ope his, t- vpi. sie muuttuv, suoviivie käyäviivie. Kppeie iikkeiä o tkuvuusomiisuus, ok tkoitt pykimystä säiyttää iike smise. Ku iukuu ti uoksee Koe 1: visukt ss ii huom, kuik vike o tehä opeit kääöksiä. Tämä ohtuu siitä, että kppe pykii tkm Kokei ei iikkumistpo: opesti hitsti, tsisesti muuttuvsti, suoviivisesti käyäviivisesti. iikettää sm suut. Vstvsti pikoi oev kppe pykii säiyttämää iikkumttomuutes. Jtkuvuue ei Liikettä tkste i iikkuv kppee suhteess toisee kppeesee. Esimekiksi tssi iikkuu suhteess piviivisesti tsise ei muuttumttom opeue ti pysyy Newtoi I i muk vp kppe tk iikettää suok oev Mh. Liike o suhteeist: kppee iike evoss. tphtuu i suhteess toisee kppeesee. h k Liikettä voi kuvt eteevä iikkee isäksi myös pyöimisiikkeeksi väähysiikkeeksi. Kppe, kute tssi, voi Liikkee muutos voi o : eetä, pyöiä ti heiu. Esimekiksi keiuu ti heiuikeo iikettä kutsut väähysiikkeeksi. Myös ihmie voi pyö- Liikkeee ähtemistä ti pysähtymistä u iteä heiute o vto heiuimisesti. Nopeue muuttumist p b Koe 2: Liikkee suu muuttumist Kokei musiiki thtii tiss eteevää pyöimisiikettä eiisi heihusiikkeitä. Voiko ihmie uo väähysiikkee? o 8 ih p s tef
9 Vuoovikutus muutt iikettä h f m p s tef h b Kitk ei ksomisesti pito o täkeä omiisuus tssiss. Ku iukuu tiss visukt oiss, pito o huoo ei kitk piei. Liikkeee ähtemie, pysähtymie käätymie o vikemp kui pi vpi iikuttess. Kitk tssiss: H T I L Mitä hyötyä hitt kitkst o bekess ti pyöimisessä? Mite beikissä kitk pyitää vähetämää? Etä betiss? Voisiko tssi ik, os kitk ei oisi? Mite kitk otet huomioo tssittioiss? Etä tssikeissä? Kitkimiössä o i kksi ospuot, toisi hkvt kppe ust. Täisist imiöitä käytetää fysiikss yeisemmi imitystä vuoovikutus. Tssikeä poh tssitti väie kitk o esimekki koskemisvuoovikutuksess, ooi kosketus tphtuu hkm. 9 Newtoi II i muk vi vuoovikutus toise kppee kss voi muutt kppee iikettä. Mikäi kitk ei oisi, tssi ei pääsisi iikkeee oek toist pysähtymie oisi mhotot. Suui kitk hitt pääsä vss pyöivää beikki. Kitk suuuutee vikuttvt pitoe tu, hkvie pitoe, kppee mss kppee opeus. kkosk äää o eittäi piei kitk, äätssit voivt pyöiä Lopputssi pitkiä piuettiso iuku äyttävästi. Jää piei kitk seitettii pitkää siä, että uistime teä ää su kov piee vikutuksest, ohut vesikvo pieetää kitk. Tkemmt tutkimukset ovt osoitteet, että vesikvo sytyyki kitk iheuttmst ämpeemisestä. p s Suuite pieyhmissä piei tssikoeofi, ok sisätää 2 tspioseto, 2 pyöimisiikettä 2 eteemisiikettä tiss. Liikkeie vu tuee voi viht pikk. Vmiit tssit esitetää muie esitykset vieoi. 9
g c MENETELMÄOPAS sanataidetta ja musiikkia yhdistävä taidekasvatusmenetelmä 1.-4.-luokkalaisille nt värin äänin akulttuuriaitta 2010
q s f t värin ääi p ef MENETELMÄOPAS Kuttuuiitt 2010 m stiett musiii yistävä tiesvtusmeetemä 1.-4.-uoisie 1 1 me s e 2 o f p m Oo puie ue väi? Tuoo etie i mieee ioisi tusi? Etä os vieä oisii suu väi? Meitä
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
1.3 Toispuoleiset ja epäoleelliset raja-arvot
. Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Sähkömagneettinen induktio
ähkömgneettinen inuktio Kun johinsilmukn läpi menevä mgneettikentän vuo muuttuu, silmukkn inusoituu jännite j silmukss lk kulke sähkövit. Mgneettikentässä liikkuvn johtimeen syntyy myös jännite. Näitä
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
Vastaa tehtäviin 1-4 ja valitse toinen tehtävistä 5 ja 6. Vastaat siis enintään viiteen tehtävään.
S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
Polynomien laskutoimitukset
Polyomie lskutoimitukset Polyomi o summluseke, joss jokie yhteelskettv (termi) sisältää vi vkio j muuttuj välisiä kertolskuj. Esimerkki 0. Mm., 6 j ovt polyomej. Polyomist, joss o vi yksi termi, käytetää
Kertausosa. Kertausosa. 3. Merkitään. Vastaus: 2. a) b) 600 g. 4. a)
Kertusos Kertusos ). ) : j 7 0 7 ) 0 :( ) c) :( ). Merkitää merirosvorht (kg) sukltrffelit (kg) ) 7, 0 hit: /kg hit: 7 /kg ) 00 g 0,kg 7 0,,0,,0, 0, (kg) :. ) Vstus: ) 7, 0 ( ) ) 00 g. ) 0 7 9 7 0 0 Kertusos
Neliömatriisin A determinantti on luku, jota merkitään det(a) tai A. Se lasketaan seuraavasti: determinantti on
4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
Usko, toivo ja rakkaus
Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Pakkauksen sisältö: Sire e ni
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
****************************************************************** MÄÄRITELMÄ 4:
. Murtopotessi MÄÄRITELMÄ : O Olkoo prillie, positiivie kokoisluku. Ei egtiivise luvu :s juuri trkoitt sellist ei-egtiivist luku b, jok :s potessi o. Merkitää b. Kute eliöjuureki tpuksess, luku b täyttää
Tuen rakenteiden toteuttaminen Pispalan koulussa. Rehtorin näkökulma arjen työhön Rehtori Satu Sepänniitty- Valkama
Tuen rkenteiden toteuttminen Pispln kouluss Rehtorin näkökulm ren työhön Rehtori Stu Sepänniitty- Vlkm Pispln koulu Khdess toimipisteessä Pispl vl 1.-6. oppilit 232 Hyhky vl 1.-6. oppilit 164 yht. 396
1. Asiakaslähtöisyys
. Aiklähtöiyy,,,,,,,,,,,, Vtute k.. Vtuki yht. kpl. - - vtuki - vtuki - - vtuki Plvelut vtv t ikki de trpeit Toimi huomioi d ikk etu Aikk toiveet otet huomioo Kotiplv elut kotiir hoido mie vikutu ikk m
Jäykän kappaleen tasokinetiikka harjoitustehtäviä
ynmiikk 1 Liite lukuun 6. Jäykän kppleen tskinetiikk - hrjitustehtäviä 6.1 vlvpkettiutn mss n 1500 kg. ut lähtee levst liikkeelle 10 % ylämäkeen j svutt vkikiihtyvyydellä npeuden 50 km / h 1 10 60 m mtkll.
TEHTÄVÄKORI Monisteita matikkaan. Riikka Mononen
---------------------------------------- TEHTÄVÄKORI Monisteita matikkaan Riikka Mononen ---------------------------------------- Tehtäväkori 2016 TEHTÄVÄKORI Monisteita matikkaan -materiaali on kokoelma
1. Kaikki kaatuu, sortuu August Forsman (Koskimies)
olo q» date reliioso olo 7 K (2003) KE2a7 1. Kaikki kaatuu, sortuu uust Forsma (Koskimies) olo 14 olo 21 3 3 3 3 3 3 3 3 Ÿ ~~~~~~~~~~~ π K (2003) KE2a7 uhlakataatti (kuoro) - 2 - Kuula: - 3 - uhlakataatti
P S. Va r äi n. m m2 2. e a / puistossa säilyvät puut. korko muuttuu, kansi uusitaan SVK asv.
TI E f as 8 5 5 pu ke lu pi ip iv - le / te AP 1 4 KI +8 8 +8 9 O le lem ht a ip ss uu a st ol oa ev aa rk ki ip met A L 31 6 L AP P LE IK S E T ei l y tu pu r u va liu m k u at m to äk i in u hl M 22
i lc 12. Ö/ LS K KY: n opiskelijakysely 2014 (toukokuu) 1. O pintojen ohjaus 4,0 3,8 4,0 1 ( 5 ) L i e d o n a mma t ti - ja aiku isopisto
i lc 12. Ö/ 1 ( 5 ) LS K KY: n opiskelijakysely 2014 (toukokuu) 1. O pintojen ohjaus 1=Täysi n en mi eltä. 2=Jokseenki n er i m ieltä, 3= En osaa sanoa 4= Jokseenki n sa m a a mieltä, 5= Täysin sa ma a
+80.06 +80.25 +80.45 +80.75 +81.06 +81.43 +81.78 +82.14 +82.41 +82.72 +82.87 +83.02 +83.31 2.5 2.5 VARASTO 3 ATK 2K ATK 2 VR.NR.
0 OVINTU +0.0 +0. +0. +0. +.0 +. +. +. +. +. +. +.0 +. 00 +0. +0. +0. +0. +0. 00 TUVTEIT VUS SVNEOTUSIVO EI- UO + mm SIVUIE PPINTU yllä kulkusilta 00 0 0 00 EUNIVI J UOIE BONIIVEYS GN J SUISTV POISTUMISTIE-
Näytä tai jätä tarkistettavaksi tämän jakson tehtävät viimeistään tiistaina 18.6. ylimääräisessä tapaamisessa.
Jkso 12. Sähkömgneettinen induktio Tässä jksoss käsitellään sähkömgneettist induktiot, jok on tärkeimpiä sioit sähkömgnetismiss. Tätä tphtuu koko jn rkisess ympäristössämme, vikk emme sitä välttämättä
& # # w. œ œ œ œ # œ œ œ œ œ # œ w. # w nœ. # œ œ œ œ œ # œ w œ # œ œ œ Œ. œ œ œ œ œ œ œ œ # œ w. œ # œ œ œ w œ œ w w w w. W # w
Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
16-300mm 50 EURON CASHBACK! Ehdot PARAS KOLMESTA MAAILMASTA. www.tamron.fi. F/3.5-6.3 Di II VC PZD Macro
Ehdot 3. Mksu suoritet se m vluutss, mistä objektiivi o ostettu. Mksu suoritet 4 viiko kuluess cshbck-dokumettie spumisest. 4. Objektiivi tulee oll Focus Nordici mhtuom j se tulee oll ostettu virllise
N I K E A N U S K O N T U N N U S T U S
100 H a n n u P o h a n n o r o N I K E A N U S K O N T U N N U S T U S lauluäänelle, kitaralle sekä viola da gamballe tai sellolle or voices, guitar, viola da gamba / violoncello - ' 00 Teosto Suomalaisen
Syksyn 2015 Pitkän matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
ystävät LUONNON LAHJA Kaneli & appelsiini Minun valintani 1). Tuemme yhteisöjä, joista eteeriset öljymme ovat per
LUONNON Lhj LUONNOSTA ystävät Brighter Home -kokoelmmme on luotu ympäristöystävällisiä j sosilisesti vstuullisi käytäntöjä noudtten. Tästä kokoelmst löydät oiket lhjt kikille, jotk vlivt mpllomme. Kneli
Laskut kirjoitetaan vasempaan reunaan, vastaukset tulevat oikeaan reunaan.
2. Peruslsket 2.1 Yhtee- j väheyslsku Lske: 23 14 9 MENU. Vlitse Mi Syötä lskuluseke. Pi EXE. Lskut kirjoitet vsemp reu, vstukset tulevt oike reu. 2.2 Näytö tyhjeys Vlitse Edit j pi Cler All. Pi OK. Huom!
JARRUDYNAMOMETRIN LASKENTAOHJELIITE
LIITE JARRUDYNAMOMETRIN LASKENTAOHJELIITE Jrruje surtuskyvy määrtys jrrudymmetrllä Määräksktsstuksess rsk kurm-ut j erävuu jrrujärjestelmä surtuskyky määrtetää jrrudymmetrmttuksll. Jrrujärjestelmä mttussuurede
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
Geometrinen lukujono. Ratkaisu. a2 = 50 4 = 200 a3 = = 800 a4 = = 3 200
Geometrie lukujoo 7. Geometrise lukujoo esimmäie jäse o = 0 j peräkkäiste jäsete suhde =. Määritä lukujoo kolme seurv jäsetä. = 0 = 00 = 0 = 800 = 0 = 00 8. Geometrie lukujoo lk seurvsti: ), 0, 0, b) 000,
Kirkkonummen kunta Yhdyskuntatekniikan toimiala Pöyry Finland Oy / Veikko Urmas 13.5.2015
rkkoumm kut dyskuttkk tom öyry Fd y / kko rms M - D M yrkv j oktty strbyt, strbykr, oktyt, oktytörmä, oktyoku jk-t, ysäkötut tuuokk strbyt o v mt, jok muuttuu kduks o yrkv j okty kv-u ääktu j v myös joukkokttä
VÄRÄHTELYMEKANIIKKA SESSIO 16: Yhden vapausasteen vaimeneva pakkovärähtely, yleinen jaksollinen kuormitus
6/ VÄRÄHTELYMEKANIIKKA SESSIO 6: Yhde vpussee vimeev poväähely, yleie jsollie uomius YLEINEN JAKSOLLINEN KUORMITUS Hmois heäeä vsv pysyvä poväähely lusee löyyy helposi oeilemll. Hmoise heäee eoi void hyödyää
c SKAPAT JULKINEN HANKINTA Sivu 1/3
c SKAPAT JULKINEN HANKINTA Sivu 1/3 e n o n c, i n 28.10.2014 S Ä H K Ö N H A N K IN T A L O U N A IS -S U O M E N K O U L U T U S K U N T A Y H T Y M Ä Mukana ovat Lounais -Suomen Koulutuskuntayhtymän
LIITE 1 LEHTONIEMI JA PEIKKOMETSÄN ALUE, VUOROPYSÄKÖINTIKYSELY TULOKSET V.2014
LIITE 1 LEHTONIEMI JA PEIKKOMETSÄN ALUE, VUOROPYSÄKÖINTIKYSELY TULOKSET V.2014 Liite 1: Vuoropysäköintikysey 2014 Lehtoniemen aueeta tueiden asukaspaautteiden pohjata on Kanavaharjunkadua sekä Järvihemenkadua
Kasvatus- ja opetuslautakunta Perusopetuksen koulun hyvinvointiprofiili
Kasvatus- ja opetuslautakunta 53 11.08.2014 Perusopetuksen koulun hyvinvointiprofiili KOLA 53 Valmistelija / lisätiedot: Perusopetusjohtaja Mari Routti, puh. 040 837 2646 etunimi.sukunimi@lappeenranta.fi
Paraabelikin on sellainen pistejoukko, joka määritellään urakäsitteen avulla. Paraabelin jokainen piste toteuttaa erään etäisyysehdon.
5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
Kirjainkiemurat - mallisivu (c)
Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Pinta-alan laskeminen
Pint-ln lskeminen Esimerkki Välillä, jtkuvn, einegtiivisen funktion f määrätt integrli nt suorn pint-ln, eli f = A. INTEGRAALILASKENTA, MAA9 A = f Toislt, jos f on välillä,, eipositiivinen, eli f R, niin
LIITE 1 Jaksoarviointi, Syntymäpäivätaivas Opettaja
LIITE 1 Jaksoarviointi, Syntymäpäivätaivas Opettaja SYNTYMÄPÄIVÄTAIVAS (aapinen s. 114 125): JAKSOARVIOINTI, opettajan ohjeet Jaksoarvioinnin kolme ensimmäistä tehtävää ovat sanelutehtäviä ja ne tehdään
lim + 3 = lim = lim (1p.) (3p.) b) Lausekkeen täytyy supistua (x-2):lla, joten osoittajan nollakohta on 2.
Mtemtiikk III 0600 Kurssi / Differetili- j itegrlilske jtkokurssi Tee 7 tehtävää ) Määritä lim ( ) ) + b) Määritä vkio site, että luseke ( ) + + ( )( ) ( + + ) + + + + + lim + lim lim (p) o jtkuv myös
P ER I.JS KI.J NTOARVIOil PÄMTYS. As Oy Saariselänkuja 1 $aariselänkuja I 00970 HELSINKT. Laadifiu: 3.9.20'13
t, P R I.S KI. TARVIil PÄMTYS As y Siselänkuj 1 iselänkuj I 00970 HSIKT difiu: 3.9.20'13 Y}ITVT Rkennustekniikk Asunt y Siselänkuj 1 n Helsinin Mellunmäess sijitsev kuuden suinkestln nudstm yhti. Rkennusvusi
2.4. Juurifunktio ja -yhtälöt
.. Juurifuktio j -yhtälöt.. Juurifuktio j -yhtälöt Juurifuktio lähtökoht void pitää potessifuktiot: f (x) x, missä o luoollie luku;,,,, j yhdistety potessifuktio määrittelee puolest yhtälö f (x) [g(x)],,,,,...
Taidetta pitkin ja poikin. MENETELMÄOPAS Monitaiteista taidekasvatusta alakouluihin
Titt pitki piki MENETELMÄOPAS Mititist tiksvtust kuuihi Kuttuuiitt 2010 m s 2 b f p m Rytmikästä miikiä si, kuvi tssi! Pii histuksi käsi, ääi sittä! Kupuki väis vsi kt ti- t s, kivt uksivt kukist sttuihi
Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu
MTEMTIIKN KOE mmatiisen kouutuksen kaikkien aojen yhteinen matematiikan vamiuksien kipaiu Nimi: Oppiaitos:.. Kouutusaa:... Luokka:.. Sarjat: LIT MERKKI OMN SRJSI. Tekniikka ja iikenne:... Matkaiu-,ravitsemus-
METSÄN KYLVÖ JA ISTUTUS
Suomen Metsänhoitoyhdistys Tapion Käsikirjasia N:o 15. METSÄN KYLVÖ JA ISTUTUS ESITTÄNYT ARVID BORG. TAPIO Metsänomistaja, jolla ei ole TAPIO-lehteä, on ajastaan aivan takapajulla. Jos haluat tietoja metsäsi
omakotitontit omakotitontit Saaristokaupungin Pirttiniemessä
KUOPON KAUPUNK Maaoaisuuden hallintapalvelut Tarjousten Tarjousten perusteella perusteella yytävät yytävät oakotitontit oakotitontit Saaristokaupungin Pirttinieessä Tarjousten Tarjousten jättöaika jättöaika
Ko onnut. pianon my ö tstilyks eli e A - A - B O K J E N X T J S. S S A v II. E. /Johnin kus/mumksella. s o li / 11 a n // / o M M S I!
\ o - i ^ / S s s / S i s i Ko onnut A - A - B O K J E N X T J S pianon my ö tstilyks eli e s o li / 11 a n // / o M M S I! M i v i h k o S S A v. 1880. II. E. /Johnin kus/mumksella. m i 11 Lev. 2 81 Lji.
Kertaustehtävien ratkaisut
Rtkisuist Nämä Trigoometriset fuktiot j lukujoot kurssi kertustehtävie j -srjoje rtkisut perustuvt oppikirj tietoihi j meetelmii. Kustki tehtävästä o yleesä vi yksi rtkisu, mikä ei kuitek trkoit sitä,
1.1. Laske taskulaskimella seuraavan lausekkeen arvo ja anna tulos kolmen numeron tarkkuudella: tan 60,0 = 2,950... 2,95
9..008 (9). Lskime käyttö.. Lske tskulskimell seurv lusekkee rvo j tulos kolme umero trkkuudell: 4 + 7 t 60,0 + Rtkisu: 4 + 7 =,950...,95 t 60,0 + Huom: Lskimiss o yleesä kolme eri kulmyksikköjärjestelmää:
3.7. Rekursiivisista lukujonoista
.7 Rekursiivisist lukujooist.7. Rekursiivisist lukujooist Kerrt vielä, että lukujoo void määritellä khdell eri tvll, joko käyttämällä lyyttistä säätöä ti rekursiivist säätöä. Joo määrittelemie rekursiivisesti
PS. Jos vastaanotit Sinulle kuulumattoman viestin, pyydän ilmoittamaan siitä viipymättä allekirjoittaneelle ja tuhoamaan viestin, kiitos.
Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Menetelmiä formuloinnin parantamiseen
Meetelmiä formuloii prtmisee Mikko Korpel Dimitris Bertsims & Robert Weismtel, 2005, Optimiztio over Itegers, ch 2.-2.5 S ysteemilyysi Lbortorio Tekillie korkekoulu Mikko Korpel Sovelletu mtemtiik tutkisemiri-
l n Neulanreikävalokuvaus Neulanreikäkuvaamiseen liittyvät myös:
s e 10 Neuaeikävaokuvaus o b fa p m Neuaeikäkuvaus o ikivaha tapa ottaa vaokuvia. Neuaeikäkamea toimitaiea o sama kui ihmise simässä: vao taittuu piee eiä kautta pimeää tiaa a heiastaa vastakkaisee seiäe
Kristuksen syntymän kalanda kreikaksi
Krstuks syntymän klnd krekk 1 F G7 7 G7 K ln es pe Hrs tu n th Hrsts j n U r n rn, n r hn des, j n n rn gl ln de n n he, p, V, r, n ne rs n p strhn Vthem he r ks ms k p ss, ss. l, 9 7. 8. F G7 7 G7 En
Käydään läpi: ääriarvo tarkastelua, L Hospital, integraalia ja sarjoja.
DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
Suorakaidekanavat. lindab suorakaidekanavat
Suorkideknvt lind suorkideknvt lind suorkideknvt Sisällysluettelo Suorkideknvt Knv LKR... Liitosost Liitoslist LS... Liitoslist LS-... Kulmyhde LBR... Liitoslist LS... S-mutk LBXR... LBSR... Liitoslist
KUN RANGAISTUS TULEE KOTIIN: LASTENSUOJELUN ROOLI VALVONTARANGAISTUKSESSA
KUN RANGAISTUS TULEE KOTIIN: LASTENSUOJELUN ROOLI VALVONTARANGAISTUKSESSA Sosiaaityöntekijä Kirsi Koivistoinen Lapsiperhepaveut/poiisin sosiaaityö LASTENSUOJELU JA VALVONTARANGAISTUS Taustaa 9/2013 ähtien
Koulutoimen henkilöstörakenne
Koulutoimen henkilöstörakenne 11.11.2016 Virka/toimi Toimen/viran nimike Toimisto V 1 koulutusjohtaja T 2 toimistosihteeri T 3 toimistosihteeri V0033 4 koulukuraattori T 5 koulupsykologi Yhtenäiskoulu,
Marina Kostik. Joulu. Naiskuorolle
32 758 Marina Kostik Joulu Naiskuorolle 2017 Copyright by the Composer All Rights Reserved No part of this publication may be copied or reproduced in any form or by any means without the prior permission
BK80A2500 Dynamiikka II (5 ECTC), tentti (2) Professori Jussi Sopanen, Konetekniikka / LUT School of Energy Systems
BK8A5 Dyaiikka II (5 ECC), tetti 3.11.15 1 () Pofessoi Jussi Sopae, Koetekiikka / LU School of Eegy Systes etissä ei saa olla ukaa oheisateiaalia! Laskiie käyttö sallittu (yös ohjeloitavat laskiet). 1.
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
ARK 01-01. Asiakirjaluettelo. Jyrki Ala-Mäkelä, per. Koy:n lukuun Pinotie 33470 YLÖJÄRVI ENECON OY. Laksontie 11 60420 SEINÄJOKI
ENECON OY Lksoti SEINÄJOKI 9 timo.mtil@co.fi Uudisrkus, Jyrki Al-Mäklä, pr. Koy lukuu, Pioti, Ylöjärvi Piirustusluttlo.. Vstuuhkilö Timo Mtil, RI Asikirj Sisältö Mittkv Luttlot - Asikirjluttlo.. Pääpiirustukst
2 Keminmaa 3 4 5 6. Haaparanta TORNIO. > 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db. Vt 4 Kemi
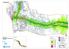LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
Meditaatioita Kristuksen kärsimyksen salaisuudesta
Meditaatioita Kristuksen kärsimyksen salaisuudesta Kirkkokuorolle, baritonisolistille ja uruille Tämä virren 64, kahden Piae Cantiones-laulun ja kolmen evankeliumikatkelman pohjalle rakentuva pieni passiomusiikki
Kvanttimekaniikan perusteet
Kvttimekiik perusteet Aieltokettä j todeäköisyystieys Scrödigeri ytälö Sirot potetiliskeleest lektroitilt potetilikuopss Hrmoie oskillttori Tiltieys lisää sirotilmiöistä Altofuktio o yleisesti kompleksie
SAMMONKATU SAMMONKATU JAAKON- SARVI- KATU SARVIJAAKONKATU 1: Kalevanrinteen katujen yleissuunnitelma, Liite 3 Asemapiirros 1/4
KTOS L:\PROJEKTT_2012\1510001046 KLEVRTEE KTUJE YS\14_TULOKSET\3.KTUJE YLESSUUTELM\DWG\KLEVRE YS.DWG Tulostettu: 26.6.2013 n- JO KELLR- SR- JKO- KTU SMMOKTU PYSÄKÖT KORTTEL 4 +100,60 KSPHT 1/2 BUS (varaus)
MATP153 Approbatur 1B Harjoitus 1, ratkaisut Maanantai
MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
Riemannin integraalista
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Perusturvalautakunta Perusturvalautakunta
Perusturvalautakunta 6 30.08.2016 Perusturvalautakunta 4 25.09.2018 Pohjanmaan maakuntien sosiaalialan osaamiskeskus SONet BOTNIAn kuntasopimusten uusiminen ja kuntarhoitus vuosille 2017-2018 / kuntarahoitus
LEIVOTAAN YHDESSÄ. Kuvat: Jutta Valtonen
LEIVOTAAN YHDESSÄ Susanna Koistinen Miia Laho Kuvat: Jutta Valtonen SI-SÄL-LYS E-SI-VAL-MIS-TE-LUT... 2 PE-RUS-RE-SEP-TIT KAU-RA-KEK-SIT... 5 SUK-LAA-KEK-SIT... 7 MAR-JA-PII-RAK-KA... 9 MUF-FIN-IT...
Lyhyt kuvaus harjoitukse sta. Kommentit harjoitukse n toimivuude sta
Tui yleistavoite:tutustumie toisii (oppilas-opetta), oppilaide tasoo. Kokeilemie eri tassiliikeita. Ee tutia oppilailla oli veryttely, lihasvoima, veyttely tuti. Harjoituks e tavoite Lyhyt kuvaus sta Kommetit
ENNAKOINTIKAMARIFOORUMI Jonna Heliskoski CEO, PhD candidate
ENNAKOINTIKAMARIFOORUMI 27.9.2018 Jonna Heliskoski CEO, PhD candidate Kuva: unplash.com VAIKUTTAVUUSAJATTELUN VIITEKEHYS Vaikutusketju (The iooi method by Bertelsmann Stiftung) Vaikuttavuus (impact) (input)
SATE2140 Dynaaminen kenttäteoria syksy / 6 Laskuharjoitus 0: Siirrosvirta ja indusoitunut sähkömotorinen voima
ATE14 Dynminen kenttäteori syksy 1 1 / skuhrjoitus : iirrosvirt j inusoitunut sähkömotorinen voim Tehtävä 1. All olevss kuvss esitetyssä pitkässä virtlngss kulkee virt i 1 (t) j sen vieressä on kuvn mukinen
Perusturvalautakunta 60 11.06.2013 Kaupunginhallitus 280 17.06.2013 Tarkastuslautakunta 2013-2016 40 28.08.2013
Perusturvalautakunta 60 11.06.2013 Kaupunginhallitus 280 17.06.2013 Tarkastuslautakunta 2013-2016 40 28.08.2013 Sosiaaliasiamiehen selvitys vuodelta 2012 PERLTK 60 Sosiaalityön johtaja Marketta Tiihala
F e. R kertaa ioniparien lukumäärä N. Kun laskemme tämän yhteen Coulombin attraktioenergian kanssa saamme kiteen kokonaisenergiaksi.
S-436, FYSIIKKA IV (EST) Kevät 5, LH Rtisut LH- Lse liui Ferieergi olettll että joie toi luovutt yhde eletroi johtovyöhö Johtvuuseletroit uodostvt vp vuoroviutttto eletroisu Kliui tiheys o 8,5 g / c 3
E-ka-luok-ki-en. O-ma ni-mi : ... Luok-ka : ...
E-ka-luok-ki-en lu-ku-dip-lo-mi-vih-ko Lu-ku-dip-lo-miin vii-si lu-e-taan yh-teen-sä kir-jaa: kir-jaa las-ten 3 ker-to-makir-jal-li-suu-des-ta (ta-vu-te-tut ja help-po-lu-kui-set, muut) ku-va-kir-ja tie-to-kir-ja
LASKENTA laskentakaavat
LASKENA lketkvt Kvkokoelm älle ivulle o koottu yleiiät j ueiite trvitut lketkvt. Näitä käytetää hihleveyde j keliväli lket. Liäki o koottu muutmi muuokvoj. Hhih mitoittmie käy helpoti Heomitoituohjelmll.
Lujuusopin jatkokurssi III.1 III. LAATTARAKENTEET
Lujuusopi jtkokussi III. III. LAATTARAKENTEET Lttketeet tti Lähteemäki Lujuusopi jtkokussi III. JOHDANTO Tsopitketee kuomitus void jk keskipi suutisee j sitä vst kohtisuo kuomituksee eli lev- j lttkuomituksee.
3.3 KIELIOPPIEN JÄSENNYSONGELMA Ratkaistava tehtävä: Annettu yhteydetön kielioppi G ja merkkijono x. Onko
3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
ellipsirata II LAKI eli PINTA-ALALAKI: Planeetan liikkuessa sitä Aurinkoon yhdistävä jana pyyhkii yhtä pitkissä ajoissa yhtä suuret pinta-alat.
KEPLERIN LAI: (Ks. Physic 5, s. 5) Johnnes Keple (57-60) yhtyi yko Bhen (546-60) hintoineiston pohjlt etsimään tinmekniikn linlisuuksi. Keple tiiisti tutkimustyönsä kolmeen lkiins (Keplein lit). I LAKI
Millainen olo sinulle tulee saunassa?
Millainen olo sinulle tulee saunassa? hyvä rauhallinen rento nälkäinen lämmin virkeä huono kiireinen kireä janoinen viluinen väsynyt CC Kirsi Alastalo 2016 Sauna-tekstiin liittyviä kysymyksiä Jos keskustelua
LINSSI- JA PEILITYÖ TEORIAA. I Geometrisen optiikan perusaksioomat
(0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
TIIVISTELMÄRAPORTTI (SUMMARY REPORT)
2012/MAT814 ISSN 1797-3457 (vekkojulkaisu) ISBN (PDF) 978-951-25-2408-2 TIIVISTELMÄRAPORTTI (SUMMARY REPORT) Vaiheistettu heijastipita valemaalia Joha Ste, Päivi Koivisto, Ato Hujae, Tommi Dufva, VTT,
Yhteistoimintamenettelyn päättäminen / sosiaali- ja terveyspalveluiden liikkeenluovutus
Kunnanhallitus 59 23.03.2016 Kunnanhallitus 94 23.05.2016 Yhteistoimintamenettelyn päättäminen / sosiaali- ja terveyspalveluiden liikkeenluovutus 1.1.2017 107/010/013/2015 KHALL 59 Selostus: Kunnanvaltuusto
Aluevarausmerkinnät: T/kem Maakuntakaava
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
1 Pöytäkirja Avaa haku
D yn as t y t i et o pa l ve l u Sivu 1 / 9 Poistuminen ( Toimielimet 1 Jätelautakunta 1 Pöytäkirja 17.12.2013 Avaa haku 1 Jätelautakunta Pöytäkirja 17.12.2013 Pykälä 15 Edellinen asia 1Seuraava asia M
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
Kieli, merkitys ja logiikka, kevät 2011 HY, Kognitiotiede. Vastaukset 2.
Kieli, merkitys j logiikk, kevät 2011 HY, Kognitiotiede stukset 2. ** Kikiss utomteiss lkutil on. 1.. nn äärelliset utomtit luseille (1-c), jokiselle omns. (1).. c. q3 q4 q3 q4 q5 q6. Muodost äärellinen
TEHTÄVIEN RATKAISUT. Luku a) Jonon neljä ensimmäistä jäsentä saadaan sijoittamalla n= 1, n= 2, n= 3 ja n = 4 lausekkeeseen
TEHTÄVIEN RATKAIUT Luku 5. 0. ) Joo eljä esimmäistä jäsetä sd sijoittmll,, j lusekkeesee +. + + 5 + + 7 + 6+ 9 + 8 + b) ijoitet,, j lusekkeesee + ( ). + ( ) + ( ) + + ( ) + ( ) + Vstus: ) 5, 7, 9, b),,,
Integraalilaskentaa. 1. Mihin integraalilaskentaa tarvitaan? MÄNTÄN LUKIO
Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. b) B = (3, 0, 5) K2. 8 ( 1)
Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
KIERTOKIRJEKOKO ELMA
POSTI- JA LENNÄTINHALLITUKSEN KIERTOKIRJEKOKO ELMA 1976 N :o 126-130 N:o 126 postitoim ipaikkojen perustam isesta T a m m ik u u n 1 p ä iv ä s tä 1 9 7 7 perustetaan h aaraosa stot I I m a tra 1 2 Imatran
Kertausosa. Kertausosa. Verrattuna lähtöarvoon kurssi oli laskenut. Kalliimman tukkuhinta 1,2 480 = 576 Kalliimman myyntihinta 1,3
Kertusos. ) Edullisemm hit 480, = 64 Klliimm tukkuhit, 480 = 576 Klliimm myytihit, 576 = 748,80 b) 748,80 64 = 0,666... = 6,66% 7% 748,80. Liittymä puhelimell mks khde vuode ik 4 8,50 = 684. Liittymä ilm
V a a liv o itto. H a a s ta tte lu Suomen S o sia lid e m o k ra a tissa 18/
V a a liv o itto. H a a s ta tte lu Suomen S o sia lid e m o k ra a tissa 18/7 1933. PUOLUE Et'. MI VAALIVOITTO YLITTI ROHKEE i MATKIN ODOTUKSET. Jos v a a lit o l i s i to im ite ttu vuosi s i t t e n,