Juoksumatkoista ja maantiereittien mitoista pjh , v1.0: Ensimmäinen julkaistu versio. Tekstin selkeys kaipaa hiomista.
|
|
|
- Outi Härkönen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Juoksumatkoista ja maantiereittien mitoista pjh , v1.0: Ensimmäinen julkaistu versio. Tekstin selkeys kaipaa hiomista. Osa 1: Juoksijan kulkema matka Johdanto "Paljonko juoksit?" on yksi tyypillinen kysymys lenkiltä palaavalle juoksijalle. Kysymykseen odotetaan siis vastaukseksi lenkin pituutta. Useimmat juoksua harrastavat antavat kysymykseen luontevasti jonkun vastauksen, mutta mitä se juoksun mitta oikeastaan tarkoittaa? Tässä kirjoitussarjassa käsitellään juoksureittien ja juoksujen mittoihin ja mittaukseen liittyvä kysymyksiä. Maantiejuoksuissa ja varsinkin maastossa tai epämääräisillä alustoilla juoksureittien mitat eivät ole lainkaan yksiselitteisiä ja mitään absoluuttisia totuuksia ei edes ole olemassa. Kirjoitussarjan ensimmäisessä osassa pohditaan sitä kuinka voitaisiin määritellä mitä tarkoitetaan juoksijan lenkin aikana kulkemalla matkalla. Tulevissa muissa osissa tarkastellaan ainakin maantiereittien määrittelyä ja mittauksen tarkkuuteen liittyviä kysymyksiä. Juoksureitin pituus vs. juoksijan kulkeman matkan pituus Juoksukilpailuissa yleensä määritellään reitti, joka juoksijan on kilpailun aikana kuljettava. Kilpareitillä on joku mitta x km, joka on mahdollisesti virallisesti mitattu tai muilla keinoin arvioitu. Kun juoksija on kilpasuorituksensa tehnyt, niin hän on siis juossut x km. Sama periaate toimii omilla lenkeilläkin, kun juoksee jonkun tunnetun vakioreitin. Kun käyn kotoa kiertämässä Iidesjärven, niin tiedän lenkin pituudeksi 8.0 km ja merkitsen exceliini harjoituksen pituudeksi 8.0 km. Juoksijan kulkeman matkan arviointi tunnetun juoksureitin pituuden perusteella lienee yleisin tapa tehdä juostun matkan määrittely. Vaikka unohdettaisiin tuohon tunnetun reitin pituuteen liittyvät epävarmuudet, niin todellisuudessahan kaksi eri juoksua samalla reitillä eivät kuitenkaan ole täsmälleen yhtä pitkiä minkään järkevän tarkemman määrittelyn mukaisesti. Ei ole realistista, että juoksija kulkisi reitin kaksi kertaa täsmälleen samalla tavalla. Kun ratakisoissa juostaan vaikkapa 1500m kilpailua, niin selostaja usein kommentoi toisella tai kolmannella radalla juoksevan kilpailijan joutuvan kiertämään ylimääräisiä metrejä ja se vaikeuttaa hänen asemaansa. On katsojallekin itsestään selvää, että ulkoratoja kiertävä juoksija juoksee kilpailun aikana pitemmän matkan kuin 1500m. GPS-mittarien yleistyttyä harrastelijat usein maratonin jälkeen keskustelufoorumeilla pohtivat paljonko tuli juostua ylimääräistä. On yleisesti tiedossa, että maratonreitit mitataan ns. lyhintä mahdollista reittiä ja jos juoksija ei huolellisesti optimoi omia juoksulinjojaan, niin hän oletettavasti juoksee kisan aikana enemmän kuin metriä (jälleen siis ottamatta huomioon itse kisareitin mittaan liittyviä kysymyksiä).
2 Toivottavasti yllä olevat esimerkit tekevät selväksi mitä yhtäällä tarkoitan juoksureitin pituudella ja toisaalta juoksijan kulkeman matkan pituudella. Juoksureittien huolellinen määrittely ja mittaus on jo monimutkaista ja siitä on omat sääntönsä, mutta juoksijan kulkeman matkan määrittäminen, saati sitten tarkka mittaus, on vielä kertaluokkaa vaikeampaa (tai jopa mahdotonta). Onneksi juoksukilpailujen kannalta juoksijan kulkemalla matkalla ei ole yleensä mitään merkitystä vaan kilpailut perustuvat puhtaasti juoksureittien pituuksiin. Tämän takia juoksukilpailujen säännöissä ei ole ollut tarvetta määritellä muuta. Ja usein kilpailussa juoksureitin pituudellakaan ei ole merkitystä, kunhan se on periaatteessa sama kaikille kilpailijoille. Juoksijan kulkeman matkan pituudella on tietysti merkitystä myös siinä yleisessä tapauksessa, että harjoituslenkki tehdään jossain muualla kuin tunnetun mittaisella juoksureitillä. Yleinen tapa mitata juostu matka tällöin on kuljettaa mukana GPS-vastaanotinta, joka mittaa laitteen kulkemaa matkaa jollakin tavalla. Juoksijan kulkeman matkan määrittelystä ja mittaustarkkuudesta On selvää, että tunnetun juoksureitin pituuden tai GPS-mittarin antaman lukeman käyttö estimoimaan juoksijan kulkemaa matkaa on käytännössä täysin kelvollinen menetelmä useimpiin tarkoituksiin. Minulla ei itselläni ole mitään ongelmia käyttää noita lukemia harjoituspäväkirjassa juoksulenkkien pituutena ja ne täyttävät tuon tarpeen täydellisesti. On kuitenkin epätyydyttävää ja jopa erikoista, että kuljetulle matkalle ei ole mitään tarkkaa määritelmää. En ole itse ikinä nähnyt yritystä määritellä kuljettua matkaa siten, että se vastaisi yleistä käsitystä juostun matkan pituudesta ja olisi matemaattisesti tarkka. Itse asiassa on melko erikoista puhua edes mittauksen tarkkuudesta, jos mitattavaa asiaa ei ole määritelty! Ongelma syntyy siitä, että juoksu ei tuota mitään yksiselitteistä jälkeä, jonka mittaamalla voisi päätyä juostuun matkaan. Raajat liikkuvat sinne tänne ja jalat osuvat maahan eri paikoissa ja ylävartalo saattaa vielä heilua. Välillä hypätään ojan yli ja välillä astutaan kuoppaan tai kompastutaan kantoon. Ei todellakaan ole selvää mikä tarkalleen on kuljettu matka. Maantiereittien mittauksen säännöissä sanotaan, että mittaus tulee tehdä lyhintä mahdollista reittiä siten, että juoksija ei voi juosta mittausta lyhyempää matkaa. Kuitenkaan säännöissä ei sanota mitään siitä miten tuo juoksijan kulkema matka mitattaisiin tai mitä sillä tarkoitetaan. Sitä pidetään jotenkin itsestäänselvänä. Juoksun harrastajien kuulee usein lenkin jälkeen toteavan GPS-mittaristaan jotain tyyliin Onpa tämä mittari tarkka! Se näyttää 10.04km!. Tämäkin toteamus sisältää oletuksen, että on olemassa joku oikea luku, josta 10.04km on tarkka mittatulos. Mutta eihän tuolla juoksijalla ole oikeasti mitään perustetta sanoa, että 10.04km on tarkka mittatulos jostain, mitä ei ole edes määritelty ja jota juoksija ei ainakaan tiedä! Ilmeisesti juoksija tarkoittaa tarkkuudella vain sitä, että mittari ei ole niin epätarkka, että näyttäisi jotain ilmeisen väärää, kuten vaikkapa 15km, kun on kierretty noin 10km pituinen juoksureitti. Siitä tuskin kannattaa mittarin tarkkuutta kuitenkaan hurrata. Tämän kirjoituksen tarkoituksena on etsiä universaalisti kelvollista määritelmää juoksijan kulkemalle matkalle maastosta ja tyylistä riippumatta. Maantiereittien mittaukseen liittyen on todettava, että ehkä tuo juoksijan kulkeman matkan pitäminen itsestäänselvänä ei ole kuitenkaan niin erikoista. Kun juoksualusta oletetaan melko tasaiseksi ja sileäksi asfalttitieksi, niin juoksijan massakeskipisteen
3 projektio juoksualustaan jättää mitattavan jäljen, jota tuossa käytännössä tarkoitetaan juoksijan kulkeman matkan mittana vaikka sitä ei missään sanotakaan. Se ei kuitenkaan kelpaa yleiseksi määritelmäksi ja siinä voi olla ongelmansa myös maantiereiteillä, kuten tässä kirjoituksessa tullaan osoittamaan. Massakeskipisteen liikkeen käyttö kuljetun matkan määrittelemiseen Alkeellisin mahdollinen tapa mitata kuljettu matka voisi olla määritellä ensin juoksulle alkupiste ja loppupiste (vaikkapa ensimmäisen ja viimeisen askeleen jalkaterän jättämää pistettä käyttäen), ja sitten mitata näiden pisteiden välinen etäisyys. Tämä juostun matkan määrittely ei varmaankaan tyydyttäisi useimpia harrastajia, ja varsinkaan niitä, jotka aloittavat ja lopettavat lenkkinsä kotipihasta. On siis melko selvää, että kelvollisen määritelmän tulee sisältää tapa seurata kehon liikkeitä koko lenkin ajan. Luonnollinen yritys määritellä juoksijan kulkema matka olisi käyttää juoksijan massakeskipisteen (käytännössä sama kuin juoksijan painopiste) kulkemaa matkaa lenkin aikana. Tässä määritelmässä on kuitenkin yksi merkittävä ongelma ja toinen vähäisempi ongelma. Merkittävä ongelma on se, että juoksussa juoksijan keho liikkuu myös vertikaalisesti ylös-alas-suunnassa ponnistuksen viedessä massakeskipistettä ylös ja painovoiman tuodessa sen taas alas. Tuo vertikaalinen liike tulisi laskettua mukaan juoksumatkaan, jos matka määriteltäisiin massakeskipisteen liikkeenä. Vertikaalisen edestakaisen liikkeen ottaminen mukaan laskuun ei kuitenkaan vastaa yleistä käsitystä kuljetun matkan pituudesta. Jos esim. juoksija juoksee 25 kierrosta radalla hienosti sisärataa pitkin, niin oikea vastaus kuljetuksi matkaksi on ilmiselvästi noin 10000m. Kuitenkin massakeskipiste on liikkunut tuona aikana selvästi pitemmän matkan ja ero voi olla varsin merkittävä. Tämän takia massakeskipisteen liike ei ole hyvä määritelmä kuljetulle matkalle. Massakeskipisteen kulkemalla matkalla on toki selvä fyysinen merkitys ja sen kulkema matka on jossain suhteessa juoksussa tehtyyn työhön. Onkin mielenkiintoista tutkia kuinka paljon juoksun askellus vaikuttaa massakeskipisteen kulkemaan matkaan. Juoksu voidaan yo kuvan mukaisesti mallintaa massakeskipisteen liikkeen osalta sarjaksi paraabeleita, jossa askelpituus on d ja askeleen korkeus (=massakeskipisteen vertikaalinen liike) on h. Arvelisin useimpien juoksijoiden askelpituuden lenkillä osuvan välille 0,8-2,0 metriä. Askelkorkeus vaihdellee välillä 5-15 cm. Nykyisin monet ranteessa kuljetettavat juoksutietokoneet mittaavat myös askelpituutta ja askelkorkeutta ja niiden avulla voi itse kukin saada jonkinlaisen arvion omasta askeleestaan eri vauhdeilla. Esim. kun minä juoksin Hampurissa maratonin 2014 (aika 3.05), niin askelpituuteni oli noin 1,29 metriä ja askelkorkeuteni noin 10,3 cm. Näillä arvoilla laskettuna kuljetin massakeskipistettäni maratonin aikana noin 650 ylimääräistä metriä verrattuna siihen, että en olisi pomppinut ylös-alassuunnassa lainkaan.
4 Askeleella on yllättävän suuri merkitys tuohon ylimääräiseen matkaan. Hidas aloitteleva juoksija minimaalisella 80 cm askelpituudella ja pomppivalla 15cm korkealla askeleella liikuttaa massakeskipistettään maratonilla melkein 3700 ylimääräistä metriä, kun taas kenialainen huippujuoksija 5cm korkealla 2m pitkällä askeleella kulkee ylimääräistä matkaa vain noin 70 metriä! Oheinen taulukko kuvaa metreinä massakeskipisteen kulkeman ylimääräisen matkan maratonin aikana askeleen pituuden ja korkeuden funktiona. Askelkorkeus / Askelpituus Toinen vähäisempi ongelma massakeskipisteen liikkeen käytössä juoksumatkan mittarina on se, että massakeskipistettä voi siirtää paikallaan seisten vaikkapa käsiään liikuttamalla. Kuitenkaan mielestäni järkevän juoksumatkan mittarin ei voi hyväksyä tuottavan liikettä paikallaan seistessä. Massakeskipisteen liikkeen käyttö juoksumatkan mittarina olisi erittäin houkutteleva vaihtoehto, jos ylös-alas-liikkeen ja muun väärän liikkeen voisi eliminoida, mutta sitä ei voi tehdä tekemättä liian rajoittavia oletuksia juoksijan hyväksyttävästä liikkeestä ja sitä kautta juoksualustasta. Liikkuuhan massakeskipiste vertikaalisuunnassa myös maaston muotojen takia ja tuo liike on laskettava juoksun matkaan. On todettava, että ratajuoksussa voitaisiin hyvin käyttää juoksumatkan mittarina massakeskipisteen projektiota ratatasoon ja se antaisi järkevän mittarin (lukuunottamatta siis tuota pienempää ongelmaa liikkeestä paikallaan seisten). Tämän mahdollistaa se, että ratajuoksussa juoksualusta voidaan olettaa matemaattiseksi vaakasuoraksi tasoksi. Pienin lisärajoituksin massakeskipisteen projektiosta juoksualustaan saataisiin kelvollinen mittari myös hyväkuntoisella asfaltilla tapahtuviin katujuoksuihin, jos oletetaan asfaltin pinta sileäksi ja hyvin käyttäytyväksi paikan funktioksi ilman kuoppia tai muita epäjatkuvuuksia. Ratajuoksu ja erinomaisella teoreettisella asfaltilla tapahtuva juoksu ovat kuitenkin erikoistapauksia ja etsin määritelmää, joka on täysin juoksualustasta riippumaton ja toimisi vaikkapa suunnistuksessa metsässä.
5 GPS-mittarin käyttö kuljetun matkan mittaamisessa Kehon massakeskipisteen vertikaalisen liikkeen ongelma pätee tietysti kaikkiin muihinkin kehon osiin, joten minkään kehon osan liikkeen käyttö suoraan matkan mittaamiseen ei tuota teoreettisesti tyydyttävää tulosta. Ongelma vielä korostuu raajojen osalta, koska niiden liike sisältää muitakin kehon kokonaisliikkeen kannalta epäoleellisia komponentteja. GPS-mittari on yleisin juoksijan kulkeman matkan mittaamiseen käytetty laite ja sitä useimmiten kuljetetaan ranteessa. Periaatteessa voisi kuvitella, että mittari pyrkii mittaamaan oman liikkeensä juoksun aikana, eli käytännössä siis juoksijan ranteen liikkeen. Teroreettisesti tuskin kukaan on sitä mieltä, että ranteen juoksun aikana tekemä liikerata olisi matemaattisesti tyydyttävä määritelmä kuljetusta matkasta. Asian tekee vielä mielenkiintoisemmaksi se, että todellisuudessa GPS-mittarit eivät edes pyri mittaamaan omaa liikettään tarkasti, vaan ne mittaavat jotain muuta. Mutta mitä ne mittaavat? Minkään mittarin käyttöohjeissa tai teknisissä tiedoissa en ole nähnyt tietoa siitä, että mitä se mittarin matkamittari pyrkii mittaamaan. On selvää, että joku ajatus mittarien suunnittelijoilla mitattavasta suureesta täytyy olla, mutta sitä ei ole ainakaan näkyvästi julkistettu. Erilaisia tietoja on saatavilla käytetyistä algoritmeista matkan laskemiseen, mutta ei mitään kovin selkeää ja algoritmit lienevätkin liikesalaisuuksia. Lisäksi algoritmit vastaavat vain kysymyksiin kuinka mittaus tehdään, mutta eivät siihen mitä yritetään mitata. Jälkimmäisen voi toki yrittää algoritmeista itse päätellä. Tietenkin mittarivalmistajat sanovat, että mittari mittaa juostua matkaa, mutta kuten tässä on jo todettu, niin se ei tarkoita mitään kovin yksiselitteistä. Miksi sanon, että GPS-mittari ei yritä mitata omaa liikettään tarkasti? No juuri sen takia, että tuo liike ei kenenkään mielestä edusta kovin hyvää mallia kuljetusta matkasta. Itse kukin voi tehdä kokeen, jossa seisoo paikallaan ulkona tunnin ajan GPS-mittari ranteessa ja heiluttaa kättään laajassa kaaressa edestakaisin (sitä kättä, jossa mittari on ranteessa). Mittarin saa helposti liikkumaan useita kilometrejä tunnin aikana, mutta mittatulos ei todellakaan vastaa tuota totuutta. Syy ei ole mittaustarkkuudessa vaan siinä, että mittari ei laske edestakaista liikettä kunnolliseksi juoksijan kulkemaksi matkaksi. Kuitenkin järkevän kuljetun matkan mittarin pitää mielestäni hyväksyä myös metrin radalla edestakaisin juostu matka. Muistammehan kaikki legendaarisen suorituksen, jossa eräs juoksija lähti suorittamaan 50km kotirataultraa juoksemalla keittiön pöydän ympäri toistuvasti. Vaikka yritys muistaakseni keskeytyi vammautumiseen noin 30km kohdalla, niin ilmiselvästi juostuksi matkaksi tuli se noin 30km ja GPSmittari ei tätä olisi mitannut vaikka kattoa ei olisikaan ollut signaalia häiritsemässä. Näillä esimerkeillä pyrin vain sanomaan, että GPS-mittarien valmistajat eivät ole määritelleet julkisesti mitä he tarkoittavat juoksijan kulkemalla matkalla ja mitä he yrittävät mittareillaan mitata. Käytännössä mittarivalmistajat ovat olettaneet tietyn mallin juoksulle ja sovittavat mittatuloksia tuohon malliin. Tämä menettely ei voi johtaa teoreettisesti hyväksyttävään malliin juoksumatkan määrittelylle. Koska kuitenkin mittarien tarkkuus on melko huono, niin käytännön merkitystä tällä asialla mittatulokseen tuskin on. Vaikka mittarivalmistajat eivät kerrokaan mitä he yrittävät mitata, niin mittatulos on vielä aina sen verran epätarkka, että se on yhtä huono oli tavoite sitten mikä tahansa. Ehkä tämän takia mittarivalmistajat eivät ole nähneet tarpeelliseksi kertoa mitä he mittaavat. Todetaan vielä lopuksi yksi sellainen mahdollinen määrittely kuljetulle matkalle, joka varmasti on myös GPS-mittarivalmistajien mielessä vaikka sitä ei erikseen olekaan sanottu. Kuljettu matka voitaisiin
6 määritellä jonkin kehon osan (kuten massakeskipisteen tai ranteen) liikkeenä mitattuna tietyin aikavälein. Eli esim. 1s välein mitataan ranteen (tai GPS-laitteen) paikka ja mitataan näin syntyneiden pisteiden muodostaman murtoviivan pituus. Valitsemalla riittävän pitkä mittaväli voidaan vähentää eitoivottujen liikkeiden, kuten käden heilumisen tai vertikaalisen liikkeen, vaikutusta mittatulokseen. Näin saadaan matemaattisesti toimiva määritelmä juoksumatkalle ja se normaalisti vastaisi hyvin myös käytännön kokemusta, mutta teoreettisesti tämä ei kuitenkaan ole kelvollinen määritelmä. Mitä lyhyempi valittu aikaväli on, niin sen enemmän väärät liikkeet siellä kuitenkin vaikuttavat, ja mitä pitempi väli on, niin sitä enemmän juoksijan oletettuja liikkeita rajoitetaan. Vaikka tästä teemasta kehitettäisiin minkälaisia variaatioita, niin raajojen heiluminen ja vertikaalinen liike eivät ole erotettavissa keittiön pöydän kiertämisestä ja maaston epätasaisuuksista. Askelten käyttö kuljetun matkan määrittelyssä Juoksija jättää normaalisti juostessaan ainakin virtuaalisen jäljen, eli askeleet osuvat maahan. Eikö tuota jälkeä voisi suoraan käyttää kuljetun matkan määrittelyyn? Tämä yksinkertainen ajatus on itse asiassa varsin toimiva vaikka se ei kaikkea ratkaisekaan. Jalanjälkiin perustuva mittaus eliminoi ongelmat juoksun vertikaalisen liikkeen suhteen ja tuo laskuihin mukaan juoksualustan muodot oikealla tavalla. Jäljelle jää kuitenkin kaksi ongelmaa: 1. Kaksi jalkaa jättää jälkiä juoksusuuntaan nähden vasemmalle ja oikealle. Mittaamalla peräkkäisten askelten etäisyyksiä saadaan länkisääriselle pitempi matka kuin oikeaoppisesti lähelle samaa linjaa askeleensa asettavalle vaikka juostaisiin suoraan eteenpäin. Tämä ei ole hyväksyttävissä. 2. Jälkien toisena ongelmana on juoksualustan mahdollinen epätasaisuus, jolloin jalan alla maasto voi vaihdella paljonkin. Ääritapauksena voisi olla juoksija, joka juoksee Grand Canyonin yllä harvaa riippusiltaa pitkin siten, että osa jalkapohjasta on sillalla ja osa tyhjän päällä. Eli itse jäljen määrittely voi olla vaikeaa. Seuraavassa kuvassa oleva esimerkki osoittaa askelten käytön tärkeyden juoksijan kulkeman matkan määrityksessä. Kuvassa kolme erikokoista juoksijaa lähestyy kuoppaista maastoa. Heistä pitkäjalkaisin juoksee kuoppien yli niiden mitenkään häneen vaikuttamatta. Keskikokoinen juoksija juoksee isompien kuoppien pohjan kautta, mutta astuu pienempien kuoppien yli. Pienin juoksija joutuu juoksemaan kaikkien kuoppien pohjalta.
7 Järkevän kuljetun matkan mittarin pitää mielestäni heijastaa näitä eroja askelluksessa, eli pienin juoksija juoksee pisimmän matkan ja isoin juoksija lyhimmän matkan. Mittarissa ei käytännössä ole mielekästä kuitenkaan käyttää juoksijan kokoa tai askeleen pituutta parametrina, joten mittarissa on jotenkin käytettävä askeleen maakosketusta hyväksi. Voihan samankokoisistakin juoksijoista toinen astua kuoppaan ja toinen ei. Kuinka juostaan 2h-maraton? Edellisissä kappaleissa on esitetty joitakin näkökohtia juoksijan kulkemasta matkasta. Yksi hyvä tapa korostaa sitä, että reitin mitta ja juoksijan juoksema matka todella ovat käytännössäkin eri asioita, on spekuloida kuinka voitaisiin juosta sääntöjen mukainen 2h-alitus maratonilla jo nykyisten juoksijoiden toimesta. Virallisen alle 2h ME:n juoksemiseen maratonilla vaaditaan seuraavaa: - Yksi kenialainen 2.04-tason maratoonari, jonka luonnollinen askelpituus maratonvauhdissa on 180 cm. (Huom: joku muukin askelpituus kelpaa, mutta ratkaisun muutkin parametrit sitten vaihtuvat askelpituuden mukaan. Tässä esimerkissä käytän askelpituutta 180cm.) - Mielellään pari osaavaa jänistä, joilla on sama 180cm askelpituus kuin sankarillamme. - Yksi asfalttitien tekemiseen tarvittava laitteisto ja osaava miehistö sen käyttöön. - Yksi tasainen metriä pitkä täysin tasainen suora maratonreittiä varten - Yksi hyvä doping-asiantuntija (esim. Oregon-projektista lainattuna) - Kaksi A-tason maantiereittien mittaajaa - Järjestävä SUL:n jäsenseura, joka osaa täyttää kaikki ME:n ratifioimiseen tarvittavat lomakkeet ja hoitaa muunkin byrokratian (esim. Wihan kilometrit ry) Näin varustettuna voidaan aloittaa projekti. Kaiken avaimena on reittisuunnittelu. Maraton juostaan edestakaisena reittinä lähtö- ja maaliviivan ollessa samassa paikassa. Reitin pohjaksi luodaan metriä pitkä suora, joka muokataan loiville painanteille kuvan mukaisesti. Yksi painanne on 19cm syvä ja ympyrän kaaren osan muotoinen (ympyrän säde noin 157,5 cm). Painanteen pituus suoraan mitattuna
8 on 150cm. Painanteita erottaa toisistaan 30 cm mittainen tasainen osuus. Tämä painanteiden ja tasaisten osuuksien sarja toistuu reitillä 180 cm:n välein kuvan mukaisesti. Reitin metrin mittaiselle suoralle tulee painannetta. Lopuksi painanteinen tie asfaltoidaan, jotta se olisi IAAF:n sääntöjen mukaisesti päällystetty. Yksittäisinä tapauksina tuollaiset painanteet voivat hyvinkin esiintyä hieman huonoon kuntoon päässeillä asfalttiteillä (ainakin Suomessa). On tietysti poikkeuksellista löytää tien pätkä, jossa näitä painanteita on säännöllisesti, mutta ei mikään sääntö niitä erityisesti kiellä ja olisikin vaikeaa määritellä päällystetylle tielle reitin tasaisuuden kelpoisuusindeksi. Ajoväylällä tuollaiset painanteet vastaavat jollain lailla hidastekumpareita ja useat isotkin maratonreitit kulkevat erilaisten korokkeiden tai hidasteiden yli. Kun reitti on valmisteltu, niin Wihan kilometrit järjestää virallisen kisan kaikkien taiteen sääntöjen mukaan. Reitti mittautetaan A-tason reitinmittaajalla, joka toteaa edestakaisen reitin mitaksi metriä. Reittihän on täysin mitattavissa pyörällä ja siinä ei ole mittauksen kannalta mitään erikoista. Kukin painanne tuo reitille mittaa lisää hieman yli 6cm verrattuna suoraan vedetyllä teräsmitalla tehtyyn mittaukseen. Niinpä painannetta edestakaisin juostuna tuottaa lisämatkaa 1418 metriä. Seuraavaksi doping-asiantuntijan kanssa varmistetaan etukäteen, että mahdollinen kenialaisemme kiellettyjen aineiden käyttö ei enää kisan aikana näy testeissä. Kisa onkin sitten helppo. Jänisten avustamana kenialainen sankarimme juoksee koko matkan tasaista 2:56/km-vauhtia (eli aikaan 2:04 tähtäävää maratonvauhtia) välttäen painanteita ja astuen 180cm välein reitillä oleville 30cm levyisille tasaisille alueille. Tämä on hänen luonnollinen askelrytminsä ja juoksijan kannalta painanteet eivät vaikuta juoksuun millään lailla. Maaliviiva ylittyy ajassa 1:59:50 ja kansa juhlii. Doping-testit tehdään ja Wihan kilometrit täyttää tarvittavat lomakkeet ME:n ratifioimiseksi. Reitti vielä tarkistusmitataan ja toinenkin A-luokan mittaaja toteaa sen oikean mittaiseksi ja sääntöjen mukaiseksi. IAAF toki kokoontuu tämän jälkeen hätäkokoukseen ja muuttaa katujuoksujen rettien sääntöjä estämään tämän tyyppiset reitit jatkossa. Estäminen tehdään vaatimalla reittien olevan tasaisia ja tasaisuuden tulkinta jätetään IAAF:n pomojen tehtäväksi. Odotuksia kuljetun matkan pituuden määritelmälle Ennen kuin teen ehdotukseni juoksussa kuljetun matkan määrittelemiseksi esitän tässä vielä yhteenvetona joukon vaatimuksia hyvälle määrittelylle. - Kuljetun matkan mitan on oltava järkevässä suhteessa kehon liikkeeseen juoksun aikana. Jos keho etenee pitkän matkan (vaikkapa juoksurataa kiertäen), niin tuloksena on oltava pitkä matka. - Jos jalat eivät liiku, niin kuljettu matka on 0. Paikallaan juoksu ei tuota kuljettua matkaa.
9 - Kaikki edestakainenkin todellinen liike tuottaa kuljettua matkaa vaikka edestakainen liike olisi kuinka lyhyttä. - Askeleen korkeus ja juoksijan maastosta riippumaton ylös-alas-liike eivät vaikuta kuljetun matkan mittaan. - Askeleen pituus ei suoraan vaikuta kuljetun matkan mittaan, mutta voi vaikuttaa maaston muotojen kautta. - Askeleen leveys (=jalkojen etäisyys toisistaan suoraan juostessa) ei vaikuta kuljetun matkan mittaan, mutta todelliset sivulle otetut askeleet vaikuttavat. - Maaston muodot vaikuttavat suoraan kuljettuun matkaan, eli maastosta johtuva korkeussuuntainen liike lasketaan mukaan matkaan kaikissa tapauksissa vaikka se tapahtuisi joka askeleella. - Maaston muotojen seuraamisen takia myös upottavassa maastossa (kuten suolla) juoksu pidentää matkaa verrattuna kovalla alustalla juoksuun, kunhan askelten vajoaminen alustalla vaihtelee askeleesta toiseen. Ehdotus juostun matkan pituuden määritelmäksi Juostun matkan yksinkertaisessa määrittelyssä on siis ratkaisematon ristiriita: Juoksijan jonkin kehon osan liikkuman matkan käyttö määritelmänä ei onnistu, koska juoksijan ylös-alas-liikettä tai kehon osien "turhaa" liikettä ei pysty tyydyttävästi eliminoimaan. Toisaalta juoksualustan pinnan muotojen epämääräisyydet estävät määrittelyn pelkästään juoksureitin perusteella. Näin ollen määritelmän on oltava jonkinlainen yhdistelmä alustan ja juoksijan kehon liikkeen suhteen. Olen vakuuttunut siitä, että hyvä määritelmä perustuu askelten maakosketusten käyttämiseen määritelmän pohjana. Ehdotan, että kansainväliset stardardointijärjestöt hyväksyvät viralliseksi juoksijan juokseman matkan mitaksi seuraavan määritelmän: Määritellään ensin ns. kosketuspiste k siten, että se on juoksijan askeleen alin piste (=lähinnä maapallon keskipistettä oleva piste), jossa juoksijan jalka (tai yleisemmin keho) käy maakosketuksen aikana. Maakosketukseksi lasketaan vain todellinen askel, jossa painoa varataan maakosketuksessa olevalle jalalle (tai muulle kehon osalle). Näin siis heilahdusvuorossa olevan jalan mahdollisia painottomia maakosketuksia ei oteta huomioon. Juoksukengät ja kaikki juoksijan mukana kulkema varustus tulkitaan tässä määritelmässä olevan osa juoksijaa. Näin määriteltynä jokainen juoksijan askel tuottaa yhden yksiselitteisen kosketuspisteen ja koko lenkki tuottaa sarjan kosketuspisteitä k1, k 2, k 3,..., k N. Kosketuspisteen lisäksi määritellään kosketushetki, joka on se ajan hetki t, jolloin kosketuspiste syntyy. Juostu lenkki siis tuottaa myös sarjan kosketushetkiä t 1, t 2,..., t N. Juoksumatkalle tarvitaan mitan määrittelyä varten tietysti alku- ja loppupiste. Juoksun aloittaminen ja lopettaminen ovat juoksijan itsensä mielivaltaisesti valitsemia tapahtumia, kuten esimerkiksi ajanoton aloittaminen ja lopettaminen lenkillä. Juoksu alkaa juoksijan oman valinnan mukaan ensimmäisestä kosketuspisteestä k 1 ja päättyy viimeiseen kosketuspisteeseen k N. Kisassa juoksumatkan alkupisteeksi määrittyy viimeisin kosketushetki k 1 ennen kisan starttia ja loppupisteeksi määrittyy ensimmäinen kosketuspiste k N kisan maaliviivan ylityksen tai muun kisan päättymistavan jälkeen. Seuraavaksi määritellään kosketushetken juoksusuunta, joka on juoksijan massakeskipisteen hetkellinen nopeus s n kosketushetkellä t n. Ja määritellään vielä juoksijan paikka p n juoksijan massakeskipisteen paikaksi kosketushetkellä t n.
10 Näin juoksussa kutakin askelta numero n kohti syntyy kolme täsmällisesti määriteltyä arvoa: kosketuspiste k n, juoksijan paikka p n ja juoksunopeus s n. Seuraavaksi määritellään taso A n joka kulkee maapallon keskipisteen ja juoksijan paikan p n kautta ja on saman suuntainen kuin juoksusuunta s n. Kullekin kosketuspisteelle tulee siis näin määriteltyä oma tasonsa. Seuraavaksi kosketuspisteet k n projisoidaan kohtisuoraan määriteltyyn tasoon A n. Kukin kosketuspiste siis projisoidaan omaan tasoonsa. Näin juoksulenkki tuottaa yksikäsitteisen sarjan projisoituja kosketuspisteitä k n. Juoksumatkan pituudeksi määritellään näin syntyvien projisoitujen kosketuspisteiden kautta piirretyn murtoviivan pituus k 1, k 2,..., k N. Näin määritelty juoksumatka on matemaattisesti täysin tarkka ja täyttää kaikki asettamani ehdot ja tuottaa "järkevän" tuloksen. Määritelmä on käyttökelpoinen kaikille jalan tapahtuville etenemismuodoille (juoksu, kävely, hyppely yhdellä jalalla, hyppely tasajalkaa jne). Koska tämä pohdinta on tehty nimenomaan juoksua varten, niin normaalissa tapauksessa kosketuspisteen tuottaa aina jalka askelkosketuksessa ja näin määritelmä on myös helppo ymmärtää. Määritelmä on silti täysin toimiva myös vaikka käsilläkävelyyn tai konttaamiseen, kun kosketuspisteeksi lasketaan aina minkä tahansa kehon osan painollinen varaaminen maahan. Juoksussakin mahdolliset kaatumiset tuottavat kosketuspisteitä muista kehon osista kuin jaloista. Yllä esitetty määritelmä on kuvattu perustapauksessa, jossa juoksu tapahtuu maapallon suhteen levossa olevassa koordinaatistossa. Tämän käsittelyn kannalta voidaan myös olettaa maapallon koordinaatiston olevan käytännössä intertiaalikoordinaatisto. Määritelmää voidaan hyvin soveltaa kaikissa muissakin maapallolla olevissa intertiaalikoordinaatistoissa. Oletetaan, että juostaan juoksumatolla tai muussa tasaisessa liikkeessä olevassa kulkuneuvossa (laiva, juna jne), jonka nopeus maapallon intertiaalikoordinaatistoon verrattuna on v. Ennen juoksumatkan määritelmän soveltamista tuossa liikkuvassa koordinaatistossa on siinä määriteltyjen kosketuspisteiden K n, juoksijan paikkojen P n ja juoksusuuntien S n arvot muunnettava Galilein muunnoksella maapallon inertiaalikoordinaatistoon: k n = K n v t n p n = P n v t n s n = S n v Muunnosta varten on luonnollisestikin määriteltävä ajanhetki t 0, jolloin molempien kordinaatistojen origot linjataan yhteneviksi. Muunnoksen jälkeen voidaan määritellä projisointitasot A n ja projisoidut kosketuspisteet k n ja laskea juoksumatkan pituus kuten perustapauksessa on esitetty. Näin määritelmä tuottaa järkevän tuloksen myös matolla ja tasaisesti liikkuvissa kulkuneuvoissa. Järkevä juoksumatkan määrittely muissa kuin intertiaalikoordinaatistoissa on joko mahdotonta tai ainakin erittäin vaikeaa. Yksinkertaisinta olisi kansainvälisissä laeissa kieltää juoksuharrastus muissa kuin intertiaalikoordinaatistoissa, koska exceliin ei saa kirjattua ymmärrettävää juoksun mittaa. Sen verran voidaan kuitenkin joustaa, että juoksumaton vauhdin vaihtelu (tai maltillisesti vaihteleva vauhti liikkuvissa kulkuneuvoissa) hyväksytään ja matkaksi määritellään approksimaatio, jossa vaihtuvavauhtinen lenkki jaetaan useaan lähes tasavauhtiseen osaan ja kullekin lenkin osalle lasketaan
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
4. Funktion arvioimisesta eli approksimoimisesta
 4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
Ratamestarin analyysiä muutamista avainväleistä eri radoilta
 Ratamestarin analyysiä muutamista avainväleistä eri radoilta Kaikki ykköset 3, 5, 7 ja 10km radoilla oli lyhyemmät ykköset (56 ja 53). 9, 12 ja 15km radoilla pidemmät (62 ja 67). Lyhyillä ykkösillä oli
Ratamestarin analyysiä muutamista avainväleistä eri radoilta Kaikki ykköset 3, 5, 7 ja 10km radoilla oli lyhyemmät ykköset (56 ja 53). 9, 12 ja 15km radoilla pidemmät (62 ja 67). Lyhyillä ykkösillä oli
MITTAUSPÖYTÄKIRJA Pyynikin näkötornilenkki, Tampere 18.5.2011, v 1.0
 MITTAUSPÖYTÄKIRJA Pyynikin näkötornilenkki, Tampere 18.5.2011, v 1.0 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Pyynikin näkötornilenkki, Tampere 18.5.2011, v 1.0 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
LIIKUNTALUOKAN SOVELTUVUUSTESTIT 2017
 LIIKUNTALUOKAN SOVELTUVUUSTESTIT 2017 A. FYSIIKKA 1. Voima (etunojapunnerrus rintakehä nyrkkiä koskettaen) Suoritusohjeet: Oikeaa suoritustekniikkaa saa kokeilla kaksi toistoa. Lähtöasento on etunoja,
LIIKUNTALUOKAN SOVELTUVUUSTESTIT 2017 A. FYSIIKKA 1. Voima (etunojapunnerrus rintakehä nyrkkiä koskettaen) Suoritusohjeet: Oikeaa suoritustekniikkaa saa kokeilla kaksi toistoa. Lähtöasento on etunoja,
3 Suorat ja tasot. 3.1 Suora. Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta.
 3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
Tekijä Pitkä matematiikka Pisteen (x, y) etäisyys pisteestä (0, 2) on ( x 0) Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y.
 Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
Tekijä Pitkä matematiikka 5 7..017 37 Pisteen (x, y) etäisyys pisteestä (0, ) on ( x 0) + ( y ). Pisteen (x, y) etäisyys x-akselista, eli suorasta y = 0 on y. Merkitään etäisyydet yhtä suuriksi ja ratkaistaan
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
- 8 viikon ohjelma puolimaratonille - (kolme erilaista ohjelmaa) www.fitlandia.fi
 - 8 viikon ohjelma puolimaratonille - (kolme erilaista ohjelmaa) ENNEN OHJELMIEN ALOITTAMISTA Haluamme, että harjoittelusi ja ohjelmasi etenee mahdollisimman sujuvasti alusta lähtien. Jotta saat parhaan
- 8 viikon ohjelma puolimaratonille - (kolme erilaista ohjelmaa) ENNEN OHJELMIEN ALOITTAMISTA Haluamme, että harjoittelusi ja ohjelmasi etenee mahdollisimman sujuvasti alusta lähtien. Jotta saat parhaan
PLUS PÄIVÄ 1 PÄIVÄ 3 PÄIVÄ 4 PÄIVÄ 5 PÄIVÄ 6. Pidä 1 min tauko intervallien. Askelkyykky kävellen: 12 toistoa x 3 sarjaa
 3 naista nipisti ajoistaan minuutteja näin se onnistui! Omaa ennätysaikaa voi parantaa vain 30 päivässä KUNTO -juoksuohjelmaa noudattamalla. Ohjelma sopii kaikille, sillä sen lähtökohtana on juoksijan
3 naista nipisti ajoistaan minuutteja näin se onnistui! Omaa ennätysaikaa voi parantaa vain 30 päivässä KUNTO -juoksuohjelmaa noudattamalla. Ohjelma sopii kaikille, sillä sen lähtökohtana on juoksijan
MITTAUSPÖYTÄKIRJA Wihan kilometrit 2015 18.10.2015, v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä)
 MITTAUSPÖYTÄKIRJA Wihan kilometrit 2015 18.10.2015, v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Wihan kilometrit 2015 18.10.2015, v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
OMATOIMIKAUDEN HARJOITUSOHJELMA HARJOITUS 1. OHJEITA OMATOIMIKAUDELLE:
 OMATOIMIKAUDEN HARJOITUSOHJELMA OHJEITA OMATOIMIKAUDELLE: Harjoittele omatoimikauden aikana omia kehityskohteitasi tavoitteesi mukaisesti ja tee joukkueen omatoimiharjoitukset. Suunnittele viikon harjoittelu
OMATOIMIKAUDEN HARJOITUSOHJELMA OHJEITA OMATOIMIKAUDELLE: Harjoittele omatoimikauden aikana omia kehityskohteitasi tavoitteesi mukaisesti ja tee joukkueen omatoimiharjoitukset. Suunnittele viikon harjoittelu
KAARINAN SYYSMARATON
 KAARINAN SYYSMARATON 22.10.2016 Mittausraportti Mittauspäivä: 20.10.2016, klo 18:00 19:30 Olosuhteet: Mittaaja: Avustajat: +5 C, pilvistä Jari Tomppo Janne Klasila, Tuomo Sibakov, Jaakko Uotila Kaarinan
KAARINAN SYYSMARATON 22.10.2016 Mittausraportti Mittauspäivä: 20.10.2016, klo 18:00 19:30 Olosuhteet: Mittaaja: Avustajat: +5 C, pilvistä Jari Tomppo Janne Klasila, Tuomo Sibakov, Jaakko Uotila Kaarinan
Suomen Urheiluliitto Kilpailuvaliokunta. Kalevan kisat. SM-kisojen tulosrajat ulkoratakaudella 2015. Vahvistettu SUL:n kilpailuvaliokunnassa 25.2.
 Suomen Urheiluliitto Kilpailuvaliokunta SM-kisojen tulosrajat ulkoratakaudella 2015 Vahvistettu SUL:n kilpailuvaliokunnassa 25.2.2015 Tulosrajakauden alku on 1.5.2014 Kalevan kisat SUL Kalevan kisojen
Suomen Urheiluliitto Kilpailuvaliokunta SM-kisojen tulosrajat ulkoratakaudella 2015 Vahvistettu SUL:n kilpailuvaliokunnassa 25.2.2015 Tulosrajakauden alku on 1.5.2014 Kalevan kisat SUL Kalevan kisojen
Luento 5: Käyräviivainen liike. Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike
 Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset
 4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
4.1 Urakäsite. Ympyräviiva. Ympyrään liittyvät nimitykset MÄÄRITELMÄ 6 URA Joukko pisteitä, joista jokainen täyttää määrätyn ehdon, on ura. Urakäsite sisältää siten kaksi asiaa. Pistejoukon jokainen piste
Erityinen suhteellisuusteoria (Harris luku 2)
 Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Tärkeimmät Sääntömuutokset. Voimassa 1.11.2013 (kansallisesti 1.1.2014)
 Tärkeimmät Sääntömuutokset Voimassa 1.11.2013 (kansallisesti 1.1.2014) Vammaisurheilijan osallistuminen Lajinjohtaja voi tarvittaessa soveltaa sääntöjä mahdollistaakseen urheilijan osallistumisen, kuitenkin
Tärkeimmät Sääntömuutokset Voimassa 1.11.2013 (kansallisesti 1.1.2014) Vammaisurheilijan osallistuminen Lajinjohtaja voi tarvittaessa soveltaa sääntöjä mahdollistaakseen urheilijan osallistumisen, kuitenkin
OITTAA-MARATON REITINMITTAUS
 OITTAA-MARATON REITINMITTAUS TAPAHTUMA Tapahtuma: Oittaa-maraton Kilpailunjohtaja: Toni Valido Paikka: Oittaa, Espoo Web: https://oittaamaraton.wordpress.com/ Mittausajankohta: 1.8.2016 klo 9.30 12.30
OITTAA-MARATON REITINMITTAUS TAPAHTUMA Tapahtuma: Oittaa-maraton Kilpailunjohtaja: Toni Valido Paikka: Oittaa, Espoo Web: https://oittaamaraton.wordpress.com/ Mittausajankohta: 1.8.2016 klo 9.30 12.30
Valmistelut: Aseta kartiot numerojärjestykseen pienimmästä suurimpaan (alkeisopiskelu) tai sekalaiseen järjestykseen (pidemmälle edenneet oppilaat).
 Laske kymmeneen Tavoite: Oppilaat osaavat laskea yhdestä kymmeneen ja kymmenestä yhteen. Osallistujamäärä: Vähintään 10 oppilasta kartioita, joissa on numerot yhdestä kymmeneen. (Käytä 0-numeroidun kartion
Laske kymmeneen Tavoite: Oppilaat osaavat laskea yhdestä kymmeneen ja kymmenestä yhteen. Osallistujamäärä: Vähintään 10 oppilasta kartioita, joissa on numerot yhdestä kymmeneen. (Käytä 0-numeroidun kartion
Firmaliiga Högbacka
 Firmaliiga 16.5.2017 Högbacka Analyysi reittihärvelipiirrosten pohjalta A-rata 3-4: Pitkä väli, jossa oli useita eri reitinvalintavaihtoehtoja. Haasteita oli rastilta lähdössä ja toteutuksen sujuvuudessa.
Firmaliiga 16.5.2017 Högbacka Analyysi reittihärvelipiirrosten pohjalta A-rata 3-4: Pitkä väli, jossa oli useita eri reitinvalintavaihtoehtoja. Haasteita oli rastilta lähdössä ja toteutuksen sujuvuudessa.
Opetusmateriaali. Fermat'n periaatteen esittely
 Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Vektorien pistetulo on aina reaaliluku. Esimerkiksi vektorien v = (3, 2, 0) ja w = (1, 2, 3) pistetulo on
 13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
 MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
JUOKSUTEKNIIKAN HARJOITUKSET
 1 JUOKSUTEKNIIKAN HARJOITUKSET Eri lähteistä koonnut ja suunnitellut Ari Hakahuhta JäPS P96 Näitä harjoituksia kootessani olen käyttänyt mm. JäPSin valmentajakerhon antia (kiitos Mikko Eskelinen, Jaakko
1 JUOKSUTEKNIIKAN HARJOITUKSET Eri lähteistä koonnut ja suunnitellut Ari Hakahuhta JäPS P96 Näitä harjoituksia kootessani olen käyttänyt mm. JäPSin valmentajakerhon antia (kiitos Mikko Eskelinen, Jaakko
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
MITTAUSPÖYTÄKIRJA Teivo Cup -testijuoksu 21.7.2011, v 1.1
 MITTAUSPÖYTÄKIRJA Teivo Cup -testijuoksu 21.7.2011, v 1.1 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Teivo Cup -testijuoksu 21.7.2011, v 1.1 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA HämSY aluemestaruus 2016, pitkät kävelyt , v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä)
 MITTAUSPÖYTÄKIRJA HämSY aluemestaruus 2016, pitkät kävelyt 3.9.2016, v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen maantiereittien virallisten mittaussääntöjen
MITTAUSPÖYTÄKIRJA HämSY aluemestaruus 2016, pitkät kävelyt 3.9.2016, v 1.0 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen maantiereittien virallisten mittaussääntöjen
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
SUUNNISTUKSEN HARJOITTELU
 SUUNNISTUKSEN HARJOITTELU Taitoharjoittelu Suunnistustaito SUUNNISTAJAN TAVOITTEENA on löytää kullekin rastivälille paras mahdollinen reitti ja toteuttaa se nopeasti ja virheettömästi. Suunnistustaito
SUUNNISTUKSEN HARJOITTELU Taitoharjoittelu Suunnistustaito SUUNNISTAJAN TAVOITTEENA on löytää kullekin rastivälille paras mahdollinen reitti ja toteuttaa se nopeasti ja virheettömästi. Suunnistustaito
MITTAUSPÖYTÄKIRJA Wihan kilometrit 2014 31.8.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä)
 MITTAUSPÖYTÄKIRJA Wihan kilometrit 2014 31.8.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Wihan kilometrit 2014 31.8.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Västilän maraton ja puolimaraton 2.10.2010, v 1.0
 MITTAUSPÖYTÄKIRJA Västilän maraton ja puolimaraton 2.10.2010, v 1.0 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA Västilän maraton ja puolimaraton 2.10.2010, v 1.0 Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aims-association.org/measurement/measurementofroadracecourses.pdf)
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
Tietotekniikan valintakoe
 Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
 Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Tilastoja yleisurheillen
 Tilastoja yleisurheillen Millainen mehupurkki on halvin valmistaa? Voisiko kaupan mehupurkki olla muodoltaan pallo? Entä lieriö? Opettaja jakaa luokan oppilaat noin kolmen henkilön ryhmiin. Työohjeet:
Tilastoja yleisurheillen Millainen mehupurkki on halvin valmistaa? Voisiko kaupan mehupurkki olla muodoltaan pallo? Entä lieriö? Opettaja jakaa luokan oppilaat noin kolmen henkilön ryhmiin. Työohjeet:
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
5.3 Ensimmäisen asteen polynomifunktio
 Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Maanmittauspäivät 2014 Seinäjoki
 Maanmittauspäivät 2014 Seinäjoki Parempaa tarkkuutta satelliittimittauksille EUREF/N2000 - järjestelmissä Ympäristösi parhaat tekijät 2 EUREF koordinaattijärjestelmän käyttöön otto on Suomessa sujunut
Maanmittauspäivät 2014 Seinäjoki Parempaa tarkkuutta satelliittimittauksille EUREF/N2000 - järjestelmissä Ympäristösi parhaat tekijät 2 EUREF koordinaattijärjestelmän käyttöön otto on Suomessa sujunut
Lähtötaso: Et ole harrastanut juoksemista, mutta olet harrastanut liikuntaa muutaman kerran viikossa.
 HARJOITUSOHJELMA 1 Et ole harrastanut juoksemista, mutta olet harrastanut liikuntaa muutaman kerran viikossa. Harjoitteet ovat kestoltaan hyvin samanpituisia siihen saakka kunnes pohjakunto on luotu vahvemmaksi
HARJOITUSOHJELMA 1 Et ole harrastanut juoksemista, mutta olet harrastanut liikuntaa muutaman kerran viikossa. Harjoitteet ovat kestoltaan hyvin samanpituisia siihen saakka kunnes pohjakunto on luotu vahvemmaksi
VIISIPALLO PELI JOKA KEHITTÄÄ YHTENÄISYYTTÄ YHTEISTYÖTÄ YHTEISÖÄ
 VIISIPALLO PELI JOKA KEHITTÄÄ YHTENÄISYYTTÄ YHTEISTYÖTÄ YHTEISÖÄ LYHYESTI VIISIPALLOSTA Viisipallo muistuttaa pohjimmiltaan paljon polttopalloa: Siinä on sisäjoukkue ja ulkojoukkue. Sisäjoukkue lyö pallon
VIISIPALLO PELI JOKA KEHITTÄÄ YHTENÄISYYTTÄ YHTEISTYÖTÄ YHTEISÖÄ LYHYESTI VIISIPALLOSTA Viisipallo muistuttaa pohjimmiltaan paljon polttopalloa: Siinä on sisäjoukkue ja ulkojoukkue. Sisäjoukkue lyö pallon
SPRINTTISUUNNISTUS. Kuinka kehittyä sujuvaksi rintteriksi
 SPRINTTISUUNNISTUS Kuinka kehittyä sujuvaksi rintteriksi SPRINTTISUUNNISTUKSEN MÄÄRITELMÄ Suunnistusmatka, joka kilpaillaan rakennetussa ympäristössä kulkukelpoisuudeltaan hyvällä ja reitinvalintoja mahdollistavalla
SPRINTTISUUNNISTUS Kuinka kehittyä sujuvaksi rintteriksi SPRINTTISUUNNISTUKSEN MÄÄRITELMÄ Suunnistusmatka, joka kilpaillaan rakennetussa ympäristössä kulkukelpoisuudeltaan hyvällä ja reitinvalintoja mahdollistavalla
Aritmeettinen summa Laske. a) b) 23 + ( 24) + ( 25) + ( 26) + ( 27) + ( 28) Ratkaisu.
 Aritmeettinen summa 403. Laske. a) 101 + 103 + 105 + 107 + 109 + 111 b) 3 + ( 4) + ( 5) + ( 6) + ( 7) + ( 8) a) 636 b) 153 404. ijoita ensimmäinen yhteenlaskettava a1, viimeinen yhteenlaskettava an sekä
Aritmeettinen summa 403. Laske. a) 101 + 103 + 105 + 107 + 109 + 111 b) 3 + ( 4) + ( 5) + ( 6) + ( 7) + ( 8) a) 636 b) 153 404. ijoita ensimmäinen yhteenlaskettava a1, viimeinen yhteenlaskettava an sekä
AKK-MOTORSPORT ry Katsastuksen käsikirja ISKUTILAVUUDEN MITTAAMINEN. 1. Tarkastuksen käyttö
 ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
Syötteen ensimmäisellä rivillä on kokonaisluku n, testien määrä (1 n 10). Tämän jälkeen jokaisella seuraavalla rivillä on kokonaisluku x (0 x 1000).
 A Summat Tehtäväsi on selvittää, monellako tavalla luvun n voi esittää summana a 2 + b 2 + c 2 + d 2. Kaikki luvut ovat ei-negatiivisia kokonaislukuja. Esimerkiksi jos n = 21, yksi tapa muodostaa summa
A Summat Tehtäväsi on selvittää, monellako tavalla luvun n voi esittää summana a 2 + b 2 + c 2 + d 2. Kaikki luvut ovat ei-negatiivisia kokonaislukuja. Esimerkiksi jos n = 21, yksi tapa muodostaa summa
MasKi P03 Siniset. Taitokisan suunnitelma, syyskuu 2009. Yleiset järjestelyt: kunkin lajin kolme parasta saa mitalit
 MasKi P03 Siniset Taitokisan suunnitelma, syyskuu 2009 Yleiset järjestelyt: kunkin lajin kolme parasta saa mitalit kaikille jaetaan diplomit osallistumisesta taitokisaan. kaikilla osallistujilla on "MM-kisapassit",
MasKi P03 Siniset Taitokisan suunnitelma, syyskuu 2009 Yleiset järjestelyt: kunkin lajin kolme parasta saa mitalit kaikille jaetaan diplomit osallistumisesta taitokisaan. kaikilla osallistujilla on "MM-kisapassit",
Kolmioitten harjoituksia. Säännöllisten monikulmioitten harjoituksia. Pythagoraan lauseeseen liittyviä harjoituksia
 Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Kolmioitten harjoituksia Piirrä kolmio, jonka sivujen pituudet ovat 4cm, 5 cm ja 10 cm. Minkä yleisen kolmion sivujen pituuksia ja niitten eroja koskevan johtopäätöksen vedät? Määritä huippukulman α suuruus,
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Injektio (1/3) Funktio f on injektio, joss. f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f )
 Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Espoon Urheilijat ry Judojaos. Fyysisen harjoittelun opas
 Espoon Urheilijat ry Judojaos Fyysisen harjoittelun opas 1 Sisällysluettelo 1 KUNNON HARJOITTAMINEN... 3 2 KESTÄVYYSHARJOITTELU... 4 2.1 PERUSKESTÄVYYS... 4 2.2 VAUHTIKESTÄVYYS... 4 2.3 MAKSIMIKESTÄVYYS...
Espoon Urheilijat ry Judojaos Fyysisen harjoittelun opas 1 Sisällysluettelo 1 KUNNON HARJOITTAMINEN... 3 2 KESTÄVYYSHARJOITTELU... 4 2.1 PERUSKESTÄVYYS... 4 2.2 VAUHTIKESTÄVYYS... 4 2.3 MAKSIMIKESTÄVYYS...
1. Alkulämmittely kuntopyörällä 15min, josta viimeinen 5min aerobisen kynnyksen. 2. Keskivartalojumppa 15min jumppa kiertävänä, 30 työtä/ 1 palautus
 Pyöräilyvoimaa Lihaskunto- ohjelma pyöräilijälle Harjoituksilla on tarkoitus parantaa liikkuvuutta, nostaa jalkojen voimatasoa, harjoittaa tukilihaksia sekä parantaa keskivartalon lihaskestävyyttä. Keskity
Pyöräilyvoimaa Lihaskunto- ohjelma pyöräilijälle Harjoituksilla on tarkoitus parantaa liikkuvuutta, nostaa jalkojen voimatasoa, harjoittaa tukilihaksia sekä parantaa keskivartalon lihaskestävyyttä. Keskity
MITTAUSPÖYTÄKIRJA SAUL:n SM-maantie 2014 12.9.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä)
 MITTAUSPÖYTÄKIRJA SAUL:n SM-maantie 2014 12.9.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aimsassociation.org/measurement/measurementofroadracecourses.pdf)
MITTAUSPÖYTÄKIRJA SAUL:n SM-maantie 2014 12.9.2014, v 1.1 (Uusin versio tästä dokumentista löytyy tästä linkistä) Tämä dokumentti sisältää selvityksen IAAF:n maantiereittien mittaussääntöjen (http://www.aimsassociation.org/measurement/measurementofroadracecourses.pdf)
1) Maan muodon selvittäminen. 2) Leveys- ja pituuspiirit. 3) Mittaaminen
 1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.
![Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot. Matematiikan taito 9, RATKAISUT. , jolloin. . Vast. ]0,2] arvot.](/thumbs/61/46046056.jpg) 7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
7 Sovelluksia 90 a) Koska sin saa kaikki välillä [,] olevat arvot, niin funktion f ( ) = sin pienin arvo on = ja suurin arvo on ( ) = b) Koska sin saa kaikki välillä [0,] olevat arvot, niin funktion f
Tässä dokumentissa esiintyvä materiaali on tekijänoikeuslain alaista. Materiaalia ei saa levittää, myydä tai luovuttaa eteenpäin missään muodossa
 Tässä dokumentissa esiintyvä materiaali on tekijänoikeuslain alaista. Materiaalia ei saa levittää, myydä tai luovuttaa eteenpäin missään muodossa ilman Media Clever Oy:n kirjallista lupaa. 1 Tämän kyselyn
Tässä dokumentissa esiintyvä materiaali on tekijänoikeuslain alaista. Materiaalia ei saa levittää, myydä tai luovuttaa eteenpäin missään muodossa ilman Media Clever Oy:n kirjallista lupaa. 1 Tämän kyselyn
Tilastoja yleisurheillen
 Koostanut Elina Viro Opettajalle Tilastoja yleisurheillen Kohderyhmä: Luokat 7-9 Esitiedot: Prosenttilaskenta Taustalla oleva matematiikka: Frekvenssi, suhteellinen frekvenssi, moodi, mediaani, keskiarvo,
Koostanut Elina Viro Opettajalle Tilastoja yleisurheillen Kohderyhmä: Luokat 7-9 Esitiedot: Prosenttilaskenta Taustalla oleva matematiikka: Frekvenssi, suhteellinen frekvenssi, moodi, mediaani, keskiarvo,
Liiketaitotestit ja tuloskortti
 Liiketaitotestit ja tuloskortti 1 taso Perus liiketaidot Syväkyykky 1 - integroitu liikkuvuus käsivarret vaakatasossa edessä - suorita kyykkyliike niin alas kuin sujuvasti liike on mahdollista - lantiotason
Liiketaitotestit ja tuloskortti 1 taso Perus liiketaidot Syväkyykky 1 - integroitu liikkuvuus käsivarret vaakatasossa edessä - suorita kyykkyliike niin alas kuin sujuvasti liike on mahdollista - lantiotason
Tämä luku nojaa vahvasti esimerkkeihin. Aloitetaan palauttamalla mieleen, mitä koordinaatistolla tarkoitetaan.
 MAB: Koordinaatisto geometrian apuna Aluksi Geometriassa tulee silloin tällöin eteen tilanne, jossa piirroksen tekeminen koordinaatistoon yksinkertaistaa laskuja. Toisinaan taas tilanne on muuten vaan
MAB: Koordinaatisto geometrian apuna Aluksi Geometriassa tulee silloin tällöin eteen tilanne, jossa piirroksen tekeminen koordinaatistoon yksinkertaistaa laskuja. Toisinaan taas tilanne on muuten vaan
metsämatikkaa Sata käpyä Lukuja metsästä Laskutarina Mittaaminen punaisella narulla Päin mäntyä (metsän yleisin puu)
 metsämatikkaa Sata käpyä Lukuja metsästä Laskutarina Mittaaminen punaisella narulla Päin mäntyä (metsän yleisin puu) Vinkki! MAPPAsta www.mappa.fi löytyy haulla matematiikkaa ulkona valmiita tuntisuunnitelmia
metsämatikkaa Sata käpyä Lukuja metsästä Laskutarina Mittaaminen punaisella narulla Päin mäntyä (metsän yleisin puu) Vinkki! MAPPAsta www.mappa.fi löytyy haulla matematiikkaa ulkona valmiita tuntisuunnitelmia
PISTEMÄÄRÄ ISTUMAANNOUSU, ETUNOJAPUNNERRUS (kpl) 5 45 > 4 40 44 3 35 39 2 30 34 1 25-29 0 < 24
 Rukan Alppikoulun valintakokeiden fysiikkatestit: Testataan hakijan fyysistä kuntoa lajin vaatimin edellytyksin ja testein. Testit pisteytetään 0-5 pistettä per testi. Testejä ovat seuraavat: - Istumaannousu
Rukan Alppikoulun valintakokeiden fysiikkatestit: Testataan hakijan fyysistä kuntoa lajin vaatimin edellytyksin ja testein. Testit pisteytetään 0-5 pistettä per testi. Testejä ovat seuraavat: - Istumaannousu
B-luokka 20.12.2013. Yleistä. Hyppy. Hyppy. Hypyn arvostelu juoksu. Hypyn arvostelu. mattokasa
 Yleistä B-luokka Kilpailuihin voi osallistua aikaisintaan sen vuoden syksynä, kun voimistelija täyttää 7 vuotta (lisenssikausi syksy 2013 - kevät 2014 / 2006 syntynyt) B-luokkaan voi siirtyä kilpailemaan,
Yleistä B-luokka Kilpailuihin voi osallistua aikaisintaan sen vuoden syksynä, kun voimistelija täyttää 7 vuotta (lisenssikausi syksy 2013 - kevät 2014 / 2006 syntynyt) B-luokkaan voi siirtyä kilpailemaan,
Luento 3: Käyräviivainen liike
 Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat,! ja Yhdistetty liike 2015-09-14 13:50:32 1/40 luentokalvot_03_combined.pdf (#36) Luennon
Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat,! ja Yhdistetty liike 2015-09-14 13:50:32 1/40 luentokalvot_03_combined.pdf (#36) Luennon
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
WSC7 analysointia. 24.2.2013 Vanha-Ulvila
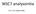 WSC7 analysointia 24.2.2013 Vanha-Ulvila Rastiväli 1 Lyhin valinta on sininen Sininen vai Punainen: sininen voi olla pari sekuntia nopeampi. Kesällä keltainen oikaistaisiin katkoviivalla merkittyä reittiä
WSC7 analysointia 24.2.2013 Vanha-Ulvila Rastiväli 1 Lyhin valinta on sininen Sininen vai Punainen: sininen voi olla pari sekuntia nopeampi. Kesällä keltainen oikaistaisiin katkoviivalla merkittyä reittiä
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Juoksun ja pituushypyn matemaattinen mallintaminen
 Koostanut: Juho Salminen, Elina Viro, Essi Rasimus Opettajalle Juoksun ja pituushypyn matemaattinen mallintaminen Kohderyhmä: Luokat 8-9 Esitiedot: Vertailuprosentti Taustalla oleva matematiikka: Suoran
Koostanut: Juho Salminen, Elina Viro, Essi Rasimus Opettajalle Juoksun ja pituushypyn matemaattinen mallintaminen Kohderyhmä: Luokat 8-9 Esitiedot: Vertailuprosentti Taustalla oleva matematiikka: Suoran
1 Laske ympyrän kehän pituus, kun
 Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
LENTOPALLON PERUSTEKNIIKOITA
 LENTOPALLON PERUSTEKNIIKOITA Sormilyönti (passi) o liike nopeasti pallon alle, lantio pallon alle o juoksuvauhdin pysäytys, tasapainoinen asento, toinen (oikea) jalka hiukan eteen: pienellä askeleella
LENTOPALLON PERUSTEKNIIKOITA Sormilyönti (passi) o liike nopeasti pallon alle, lantio pallon alle o juoksuvauhdin pysäytys, tasapainoinen asento, toinen (oikea) jalka hiukan eteen: pienellä askeleella
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Injektio. Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim.
 Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
NÄIN JUOSTAAN OIKEIN. Virheitä korjaamalla kohti parempaa juoksutekniikkaa
 NÄIN JUOSTAAN OIKEIN Virheitä korjaamalla kohti parempaa juoksutekniikkaa NÄIN JUOSTAAN OIKEIN Virheitä korjaamalla kohti parempaa juoksutekniikkaa Juoksutekniikan suhteen urheilija toimii kuin kone: vahvasta
NÄIN JUOSTAAN OIKEIN Virheitä korjaamalla kohti parempaa juoksutekniikkaa NÄIN JUOSTAAN OIKEIN Virheitä korjaamalla kohti parempaa juoksutekniikkaa Juoksutekniikan suhteen urheilija toimii kuin kone: vahvasta
2.3 Voiman jakaminen komponentteihin
 Seuraavissa kappaleissa tarvitaan aina silloin tällöin taitoa jakaa voima komponentteihin sekä myös taitoa suorittaa sille vastakkainen operaatio eli voimien resultantin eli kokonaisvoiman laskeminen.
Seuraavissa kappaleissa tarvitaan aina silloin tällöin taitoa jakaa voima komponentteihin sekä myös taitoa suorittaa sille vastakkainen operaatio eli voimien resultantin eli kokonaisvoiman laskeminen.
LIPPUPALLODEMO 90min 1
 LIPPUPALLODEMO 90min 1 1.TUTUSTUMINEN PALLOON pareittain heittoharjoittelua kahdessa rivissä huomioi turvallisuusseikat - rauhallisia, tarkkoja heittoja 2 2.OPETUSKESKUSTELU a) OTE PALLOSTA HEITOSSA etusormi
LIPPUPALLODEMO 90min 1 1.TUTUSTUMINEN PALLOON pareittain heittoharjoittelua kahdessa rivissä huomioi turvallisuusseikat - rauhallisia, tarkkoja heittoja 2 2.OPETUSKESKUSTELU a) OTE PALLOSTA HEITOSSA etusormi
v 8 v 9 v 5 C v 3 v 4
 Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
1.3 Kappaleen tasaisesta liikkeestä
 Arkikielen sana vauhti (speed) tarkoittaa fysiikassa nopeuden (velocity) suuruutta (magnitude of velocity). Kun nopeus on fysiikassa vektorisuure, niin vauhti taas on vain luku skalaari johon liittyy yksikkö.
Arkikielen sana vauhti (speed) tarkoittaa fysiikassa nopeuden (velocity) suuruutta (magnitude of velocity). Kun nopeus on fysiikassa vektorisuure, niin vauhti taas on vain luku skalaari johon liittyy yksikkö.
Tässä ei ole tarkoitus kirjata kaikkia yksittäisiä virheitä vaan yleisiä usein kilpailuissa nähtyjä virhesuorituksia.
 Poomse virhekanta Tänne kerätään tietoa, mistä suorituksista virhepisteitä annetaan. Virheitä voidaan vähentää joko Accuracy tai osuuksista. Accuracy osuuden maksimipistemäärä on 4.0 ja osuuden maksimipistemäärä
Poomse virhekanta Tänne kerätään tietoa, mistä suorituksista virhepisteitä annetaan. Virheitä voidaan vähentää joko Accuracy tai osuuksista. Accuracy osuuden maksimipistemäärä on 4.0 ja osuuden maksimipistemäärä
Ukkohallan opit vs kuinka suunnistan Paljakassa?
 Ukkohallan opit vs kuinka suunnistan Paljakassa? Paljakassa kilpaillaan Kainuun Rastiviikon ohessa MM-katsastukset 7.7 keskimatkalla sekä 9.7 pitkällä matkalla. Tämän maastoanalyysin myötä luon katsauksen
Ukkohallan opit vs kuinka suunnistan Paljakassa? Paljakassa kilpaillaan Kainuun Rastiviikon ohessa MM-katsastukset 7.7 keskimatkalla sekä 9.7 pitkällä matkalla. Tämän maastoanalyysin myötä luon katsauksen
CTIF 100 metrin estejuoksu
 CTIF 100 metrin estejuoksu Säännöt (6. painos 2004, keskeisimmät kohdat Suomessa järjestettävää kilpailua varten) Kilpailusarjat (1.2) Kilpailussa on erikseen sarjat vapaaehtoisille palokunnille ja ammattipalokunnille.
CTIF 100 metrin estejuoksu Säännöt (6. painos 2004, keskeisimmät kohdat Suomessa järjestettävää kilpailua varten) Kilpailusarjat (1.2) Kilpailussa on erikseen sarjat vapaaehtoisille palokunnille ja ammattipalokunnille.
Loimaan Korikonkarit Valmentajakerho Petri Kajander 13.4.2010
 Loimaan Korikonkarit Valmentajakerho Petri Kajander 13.4.2010 Aihe: Puolustus / joukkuepuolustus (pelaajavartiointi) Mikään puolustusmuoto ei toimi, jollei pelaaja osaa puolustuksen perustaitoja. Joukkuepuolustus
Loimaan Korikonkarit Valmentajakerho Petri Kajander 13.4.2010 Aihe: Puolustus / joukkuepuolustus (pelaajavartiointi) Mikään puolustusmuoto ei toimi, jollei pelaaja osaa puolustuksen perustaitoja. Joukkuepuolustus
KTK ohjeet ja kuvat TASAPAINOILU TAAKSEPÄIN
 KTK ohjeet ja kuvat TASAPAINOILU TAAKSEPÄIN Valmistautuminen Ohjaaja asettaa valmiiksi kolme palkkia (leveys 6 cm, 4,5 cm, 3 cm). Ensin tehtävässä käytettävän 6 cm leveän palkin päätyyn kiinnitetään tehtävän
KTK ohjeet ja kuvat TASAPAINOILU TAAKSEPÄIN Valmistautuminen Ohjaaja asettaa valmiiksi kolme palkkia (leveys 6 cm, 4,5 cm, 3 cm). Ensin tehtävässä käytettävän 6 cm leveän palkin päätyyn kiinnitetään tehtävän
Opinnäytetyö Fysioterapiaopiskelijat Mari Kopra Eija Saarinen. Opinnäytetyö: Mari Kopra ja Eija Saarinen
 Opinnäytetyö Fysioterapiaopiskelijat Mari Kopra TASAPAINOHARJOITUKSIA VERTAISOHJAAJIEN KÄYTTÖÖN Tasapainoharjoitukset on suunniteltu vertaisohjaajien työkaluiksi, he voivat hyödyntää näitä kortteja omissa
Opinnäytetyö Fysioterapiaopiskelijat Mari Kopra TASAPAINOHARJOITUKSIA VERTAISOHJAAJIEN KÄYTTÖÖN Tasapainoharjoitukset on suunniteltu vertaisohjaajien työkaluiksi, he voivat hyödyntää näitä kortteja omissa
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Agility Games Gamblers
 Agility Games Gamblers Games-lajeista ehkä hieman helpommin sisäistettävä on Gamblers, jota on helppo mennä kokeilemaan melkein ilman sääntöjä lukematta. Rata koostuu kahdesta osuudesta: 1. Alkuosa, jossa
Agility Games Gamblers Games-lajeista ehkä hieman helpommin sisäistettävä on Gamblers, jota on helppo mennä kokeilemaan melkein ilman sääntöjä lukematta. Rata koostuu kahdesta osuudesta: 1. Alkuosa, jossa
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
FITLANDIA-TREENIOPAS. - Juoksijan lihaskunto-
 FITLANDIA-TREENIOPAS - Juoksijan lihaskunto- ASIANTUNTIJA Sanna Malinen Sanna Malinen on 27-vuotias viittä vaille valmis lääkäri. Sanna on harrastanut liikuntaa pikkutytöstä lähtien, ja urheilulajeista
FITLANDIA-TREENIOPAS - Juoksijan lihaskunto- ASIANTUNTIJA Sanna Malinen Sanna Malinen on 27-vuotias viittä vaille valmis lääkäri. Sanna on harrastanut liikuntaa pikkutytöstä lähtien, ja urheilulajeista
LIPPUPALLODEMO 1,5 H 1
 LIPPUPALLODEMO 1,5 H 1 1.TUTUSTUMINEN PALLOON pareittain heittoharjoittelua kahdessa rivissä huomioi turvallisuusseikat - rauhallisia, tarkkoja heittoja 2 2. OPETUSKESKUSTELU: OTE PALLOSTA HEITOSSA etusormi
LIPPUPALLODEMO 1,5 H 1 1.TUTUSTUMINEN PALLOON pareittain heittoharjoittelua kahdessa rivissä huomioi turvallisuusseikat - rauhallisia, tarkkoja heittoja 2 2. OPETUSKESKUSTELU: OTE PALLOSTA HEITOSSA etusormi
Ota tämä paperi mukaan, merkkaa siihen omat vastauksesi ja tarkista oikeat vastaukset klo 11:30 jälkeen osoitteesta
 MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
2. a- ja b-kohdat selviä, kunhan kutakuinkin tarkka, niin a-kohta 1 p b-kohta 1 p
 LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
Algoritmit 2. Luento 11 Ti Timo Männikkö
 Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
LUMILAJIKOULU SISÄKERRAN OHJELMA (V4) Laatinut Antton Lämsä
 LUMILAJIKOULU SISÄKERRAN OHJELMA (V4) 08.04.2019-29.04.2019 Laatinut Antton Lämsä Aika & Paikka Maanantai klo 18:30-19:30 Liikuntahallin yleisurheilutila Pääohjaaja Antton Lämsä 040 148 5527 Apuohjaajat
LUMILAJIKOULU SISÄKERRAN OHJELMA (V4) 08.04.2019-29.04.2019 Laatinut Antton Lämsä Aika & Paikka Maanantai klo 18:30-19:30 Liikuntahallin yleisurheilutila Pääohjaaja Antton Lämsä 040 148 5527 Apuohjaajat
