S Laskennallinen systeemibiologia
|
|
|
- Minna Mäkinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 S Laskennallinen systeemibiologia 3. Harjoitus 1. Koska tilanne on Hardy-Weinbergin tasapainossa luonnonvalintaa lukuunottamatta, saadaan alleeleista muodostuvien eri tsygoottien genotyyppifrekvenssit helposti: Freq(AA) = p 2 Freq(Aa) = 2 pq Freq(aa) = q 2 Luonnonvalinta vaikuttaa siihen, kuinka moni yksilö selviää aikuiseksi asti lisääntymään. Tämä vaikutus tuodaan mukaan kelpoisuustermillä. Keskimääräinen kelpoisuus lasketaan painottamalla suhteellisia kelpoisuuksia genotyyppifrekvensseillä: = AA p 2 + Aa 2pq + aa q 2. Kun kelpoisuus otetaan huomioon, lisääntyvien eläinten genotyyppifrekvensseiksi saadaan Freq(AA) = AA p 2 Freq(Aa) = Aa2pq Freq(aa) = aaq 2 Tällä tapaa jakautuneet genotyypit omistavat eläimet tuottavat sukusoluja, joiden alleelifrekvenssit saadaan laskettua helposti: Freq(A) = p = Freq(AA) Freq(Aa) Freq(a) = q = Freq(aa) + 1 Freq(Aa) = 1 p 2 (Kaikki AA:n tuottamat gameetit ovat tyyppiä A ja vastaavasti aa:n tuottamat gameetit tyyppiä a. Puolet Aa:n tuottamista gameeteista on a-tyyppiä ja puolet A:ta) 1
2 Nyt ollaan uuden sukupolven alussa. Edellä esitetyllä tavalla voidaan edetä sukupolvi kerrallaan ottaen aina huomioon kelpoisuuden vaikutukset. Lasketaan seuraavaksi tilanne annetuilla arvoilla. 1. sukupolvi Alussa p = 0.2 ja q = 0.8. Lasketaan tsygoottien genotyyppifrekvenssit Freq(AA) = p 2 = 0.04 Freq(Aa) = 2 pq = 0.32 Freq(aa) = q 2 = 0.64 Lasketaan kelpoisuus ja sen perusteella kypsään ikään elävien eläinten genotyyppifrekvenssit. = AA p 2 + Aa 2pq + aa q 2 = = sukupolvi Freq(AA) = AA p 2 = Freq(Aa) = Aa2pq = Freq(aa) = aaq 2 = Lasketaan nyt 1. sukupolven tuottamien sukusolujen alleelifrekvenssit p = Freq(AA) + Freq(Aa)/2 = q = Freq(aa) + Freq(Aa)/2 = Edetään samalla tavalla kuin 1. sukupolvella, ja lasketaan tsygoottien genotyyppifrekvenssit Freq(AA) = p 2 = Freq(Aa) = 2p q = Freq(aa) = q 2 =
3 Lasketaan kelpoisuus ja sen perusteella kypsään ikään elävien eläinten genotyyppifrekvenssit. = AA p 2 + Aa 2p q + aa q 2 = Freq(AA) = AA p 2 = Freq(Aa) = Aa2p q = Freq(aa) = aaq 2 = sukupolvi Kysyttiin ainoastaan alleelifrekvenssejä: p = Freq(AA) + Freq(Aa)/2 = q = Freq(aa) + Freq(Aa)/2 = Nähdään että kahden sukupolven jälkeen alleelifrekvenssit ovat jo melkein tasoittuneet. 2. Jos tilannetta tarkasteltaisiin formaalisti, pitäisi sukupuulle laskea likelihood annetulla sairausmallilla, jotta erilaisia vaihtoehtoja voitaisiin vertailla. Nyt ei tehdä niin, vaan tarkastellaan tilannetta ainoastaan ylimalkaisesti. Tutkitaan eri vaihtoehdot: Autosomaali kromosomi, resessiivi Autosomaalissa kromosomissa sijaitseva resessiivinen alleeli on mahdollinen. Tätä tilannetta esittää kuva 1. Autosomaali kromosomi, dominantti Geeni ei voi olla dominantti ja sijaita autosomaalikromosomissa. Jos näin olisi, jokaisen sairastuneen yksilön vanhemman pitäisi myös olla sairastunut. Näin ei selvästikään ole tutkittavassa tapauksessa. (Lisäksi tällaisessa tapauksessa keskimäärin puolet sairastuneen yksilön lapsista pitäisi olla myös sairastuneita. Tässä tapauksessa puu on niin pieni, ettei päättelyä lasten määristä voida suorittaa. Ensimmäinen ehto on kuitenkin riittävä toteamaan, ettei tämä vaihtoehto voi selittää tilannetta.) 3
4 Kuva 1: Tehtävän 2. sukupuu, autosomaali resessiivinen Kuva 2: Tehtävän 2. sukupuu, X-kromosomi resessiivinen X-kromosomi, resessiivi X-kromosomissa sijaitseva resessiivinen alleeli on mahdollinen. Kuva 2 esittää tätä tilannetta. Jos sairausgeeni sijaitsee X-kromosomissa, voi tehtävänannossa kuvattu sukupuu syntyä siten, että tarvitaan ainoastaan yksi naispuolinen kantaja (ensimmäiseen sukupolveen). Sen sijaan aiemmassa vaihtoehdossa (autosomaalinen kromosomi, resessiivinen) tarvitaan samanlaisen sukupuun aikaansaamiseksi kolme toisistaan riippumatonta taudinkantajaa. Näistä kahdesta vaihtoehdosta X-kromosomi on siis todennäköisempi. Tarkkoja todennäköisyyksiä ei tässä tehtävässä nyt tarvitse laskea. Y-kromosomi Vaikka kaikki sairaat yksilöt ovatkin miehiä, ei Y-kromosomi ole mahdollinen selitys. Esimerkiksi toisen sukupolven miehillä on sama isältä peritty Y-kromosomi, mutta ainoastaan toinen on sairas. Kaiken lisäksi isä on terve. Y-kromosomi voidaan sulkea pois selitysvaihtoehtona. Mitokondrio Geeni ei voi sijaita mitokondriossa. Mitokondrioiden DNA periytyy äidiltä lapsille, joten jos sairauden aiheuttava geeni sijaitsisi mitokondriossa, periytyisi sairaus äidiltä kaikille lapsille. Tutkittavassa tapauksessa on kuitenkin tilanteita, joissa osa lapsista on sairaita ja osa terveitä. 4
5 Lisäksi molemmissa tapauksissa lasten äidit ovat terveitä. Mitokondrio-vaihtoehto voidaan siis sulkea pois. Näillä vaihtoehdoilla ja tällä datalla voidaan siis arvioida, että todennäköisimmin geeni on resessiivinen ja se sijaitsee X-kromosomissa. Huom! Tilanne on usein todellisuudessa huomattavasti monimutkaisempi. Tässä tehtävässä käsiteltiin ainoastaan osa vaihtoehdoista, esimerkiksi geenien penetransseista ei puhuttu mitään. 3. Markkerin informatiivisuus on melko epämääräinen käsite, jota voidaan kuvata matemaattisesti esimerkiksi juuri PIC-kaavan avulla. Otetaan esimerkkitilanne, jossa tietyllä markkerilla on kolme alleelia. Eräs alleeli esiintyy paljon useammin kuin toiset kaksi, sen todennäköisyys populaatiossa on 99%. Muiden alleelien todennäköisyydet ovat 0.5% ja 0.5%. Tällaisessa tilanteessa lähes jokaisella tutkittavalla kohteella kyseisessä populaatiossa on alleeli 1 tästä markkerista. Tällöin tämä markkeri ei sisällä juurikaan informaatiota; tieto tästä markkerista ei esimerkiksi pysty erottamaan yksilöitä toisistaan, jos lähes kaikilla on sama alleeli. Tilanne, jossa alleelifrekvenssit ovat tasajakautuneet, on puolestaan samalla päättelyllä intuitiivisesti informatiivisin. Tällöin tutkittava populaatio jakautuu mahdollisimman useaan yhtä suureen ryhmään. Saman intuitiivisen päättelyn mukaan mitä enemmän näitä ryhmiä on, sitä suuremman informaation kyseinen markkeri sisältää. Jos alleelifrekvenssit ovat tasajakautuneet, on yhden alleelin todennäköisyys tietenkin p i = 1/n, kun alleeleita on n kappaletta. Sijoitetaan tämä annettuun kaavaan, jolloin voidaan kirjoittaa PIC-kriteeri muodossa: P I C = 1 = 1 = 1 pi 2 ( 1 n )2 j=i+1 j=i+1 ( 1 n ) 2 2 j=i+1 2p 2 i p2 j (1) 2( 1 n )2 ( 1 n )2 (2) ( 1 n ) (3) 4 = 1 1 n 2 (n i) 1 (4) n 4 = 1 1 n 2 n i n 4 (5) Tutkitaan seuraavaksi miten PIC-kriteerin arvo riippuu tasajakautuneiden alleelien lukumäärästä n. Tulokset on esitetty seuraavassa: 5
6 n PIC Esitetään sama tulos vielä graafisesti (laajemmalla alleelimäärällä): Kuva 3: PIC-kriteeri n:n funktiona Kuvasta nähdään, että noin kymmenen alleelin jälkeen kriteerin kasvu on melko hidasta. Selvästi nähdään myös, että pienillä alleelimäärillä yhdenkin alleelin lisäys vaikuttaa hyvin voimakkaasti markkerin informatiivisuuteen. Näiden tulosten perusteella PIC-kriteeri onnistuu siis tavoittamaan markkerin informatiivisuuden kannalta tärkeitä seikkoja. 4. TDT-testin idea on seuraava. Otokseen valitaan sairaita lapsia, joilla tiedetään olevan riskialleeli. Riskialleeli on periytynyt luonnollisesti lasten vanhemmilta. Jos riskialleeliin on assosioitunut jokin markkerialleeli, myös tämä on periytynyt vanhemmilta. Testissä etsitään siis markkerialleeleita, joita sairailla lapsilla on useammin kuin mendelistisesti pitäisi olla. 6
7 Testissä tarkastellaan ainoastaan vanhempia, joista vähintään toinen on heterotsygootti. Merkitään taulukkoon kuin moni vanhemmista on heterotsygootti, ja merkitään millä tavalla eri alleelit heterotsygoottivanhemmilta siirtyvät. Homotsygoottivanhemmista ei tehdä merkintöjä, hehän siirtävät joka kerta saman alleelityypin. 7
8 Perhe Isä Äiti Lapsi Vanhemmat alleeli 1 alleeli 2 heterotsygootteja siirtynyt siirtynyt 1 1,2 1,1 1, ,2 1,2 1, ,2 1,2 1, ,2 1,1 1, ,2 1,2 1, ,1 1,2 1, ,2 1,2 2, ,1 1,2 1, ,2 1,1 1, ,2 1,1 1, ,1 1,2 1, ,2 1,1 1, ,1 1,2 1, ,1 1,1 1, ,2 1,2 1, ,2 1,2 1, ,1 1,2 1, ,2 1,2 1, ,1 1,1 1, ,2 1,1 1,2 1 1 Yhteensä heterotsygoottivanhempia on siis 23 kpl. Näiltä vanhemmilta alleeli 1 siirtyi 17 kertaa ja alleeli 2 siirtyi 6 kertaa. Mendelistisesti pitäisi kummankin alleelin siirtyä keskimäärin yhtä usein. Tehdään 1 vapausasteen χ 2 -testi käyttäen testisuuretta S = (6 17) = , joka kuvaa perimän epätasapainoa. Testin p-arvoksi saadaan p = 0.02, joten voidaan sanoa, ettei nollahypoteesi, eli mendelistinen perimä, pidä paikkaansa. Toisin sanoen markkerialleeli ja riskialleeli ovat assosioituneet toisiinsa. Edellä on esitetty alkuperäinen versio TDT-testissä, jossa siis käytetään χ 2 -approksimaatiota. Tarkka tarkastelu tehdään käyttämällä binomijakaumaa; tässä tapauksessa tarkasteltaisiin siis tapauksia p 0 = P(X 17) ja p 1 = P(Y 4), jolloin p-arvo olisi p = p 0 + p 1. Binomijakauman symmetrisyydestä kuitenkin seuraa, että p-arvo voidaan laskea helpomminkin; p = 2p 0. Tällä kertaa tulos on käytännössä yhteneväinen χ 2 -approksimaation kanssa, joten se on riittävä tapa laskea tulos. 8
VASTAUS 2a: Ruusukaijasten väri
 VASTAUS 2a: Ruusukaijasten väri Merkitään: ZK= Vihreän värin aiheuttava dominoiva alleeli Zk= keltaisen värin aiheuttava resessiivinen alleeli W= W-kromosomi Keltaisen koiraan perimä ZkZk, vihreän naaraan
VASTAUS 2a: Ruusukaijasten väri Merkitään: ZK= Vihreän värin aiheuttava dominoiva alleeli Zk= keltaisen värin aiheuttava resessiivinen alleeli W= W-kromosomi Keltaisen koiraan perimä ZkZk, vihreän naaraan
Geenikartoitusmenetelmät. Kytkentäanalyysin teoriaa. Suurimman uskottavuuden menetelmä ML (maximum likelihood) Uskottavuusfunktio: koko aineisto
 Kytkentäanalyysin teoriaa Pyritään selvittämään tiettyyn ominaisuuteen vaikuttavien eenien paikka enomissa Perustavoite: löytää markkerilokus jonka alleelit ja tutkittava ominaisuus (esim. sairaus) periytyvät
Kytkentäanalyysin teoriaa Pyritään selvittämään tiettyyn ominaisuuteen vaikuttavien eenien paikka enomissa Perustavoite: löytää markkerilokus jonka alleelit ja tutkittava ominaisuus (esim. sairaus) periytyvät
Miten geenit elelevät populaatioissa, vieläpä pitkiä aikoja?
 Miten geenit elelevät populaatioissa, vieläpä pitkiä aikoja? Populaatio on lisääntymisyhteisö ja lisääntymisjatkumo Yksilöt ovat geenien tilapäisiä yhteenliittymiä, mutta populaatiossa geenit elelevät
Miten geenit elelevät populaatioissa, vieläpä pitkiä aikoja? Populaatio on lisääntymisyhteisö ja lisääntymisjatkumo Yksilöt ovat geenien tilapäisiä yhteenliittymiä, mutta populaatiossa geenit elelevät
III Perinnöllisyystieteen perusteita
 Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 15. Populaatiogenetiikka ja evoluutio 1. Avainsanat 2. Evoluutio muuttaa geenipoolia 3. Mihin valinta kohdistuu? 4. Yksilön muuntelua
Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 15. Populaatiogenetiikka ja evoluutio 1. Avainsanat 2. Evoluutio muuttaa geenipoolia 3. Mihin valinta kohdistuu? 4. Yksilön muuntelua
a. Mustan ja lyhytkarvaisen yksilön? b. Valkean ja pitkäkarvaisen yksilön? Perustele risteytyskaavion avulla.
 1. Banaanikärpänen dihybridiristeytys. Banaanikärpäsillä silmät voivat olla valkoiset (resessiivinen ominaisuus, alleeli v) tai punaiset (alleeli V). Toisessa kromosomissa oleva geeni määrittää siipien
1. Banaanikärpänen dihybridiristeytys. Banaanikärpäsillä silmät voivat olla valkoiset (resessiivinen ominaisuus, alleeli v) tai punaiset (alleeli V). Toisessa kromosomissa oleva geeni määrittää siipien
Symbioosi 2 VASTAUKSET
 Luku 13 Symbioosi 2 VASTAUKSET 1. Termit Vastaus: a= sukusolut b= genotyyppi c= F2-polvi d= F1-polvi e= P-polvi 2. Termien erot a. Fenotyyppi ja genotyyppi Vastaus: fenotyyppi on yksilön ilmiasu, genotyyppi
Luku 13 Symbioosi 2 VASTAUKSET 1. Termit Vastaus: a= sukusolut b= genotyyppi c= F2-polvi d= F1-polvi e= P-polvi 2. Termien erot a. Fenotyyppi ja genotyyppi Vastaus: fenotyyppi on yksilön ilmiasu, genotyyppi
alleelipareja dominoiva dominoiva resessiivinen
 11 RISTEYTYKSET Merkintätapoja Mendelin säännöt Yhden alleeliparin periytyminen Monohybridiristeytys Multippelit alleelit Letaalitekijät Yhteisvallitseva periytyminen Välimuotoinen periytyminen Testiristeytys
11 RISTEYTYKSET Merkintätapoja Mendelin säännöt Yhden alleeliparin periytyminen Monohybridiristeytys Multippelit alleelit Letaalitekijät Yhteisvallitseva periytyminen Välimuotoinen periytyminen Testiristeytys
Perinnöllisyys harvinaisten lihastautien aiheuttajana. Helena Kääriäinen Terveyden ja hyvinvoinnin laitos Tampere
 Perinnöllisyys harvinaisten lihastautien aiheuttajana Helena Kääriäinen Terveyden ja hyvinvoinnin laitos Tampere 17.11.2011 Mistä lihastauti aiheutuu? Suurin osa on perinnöllisiä Osassa perimä altistaa
Perinnöllisyys harvinaisten lihastautien aiheuttajana Helena Kääriäinen Terveyden ja hyvinvoinnin laitos Tampere 17.11.2011 Mistä lihastauti aiheutuu? Suurin osa on perinnöllisiä Osassa perimä altistaa
Perinnöllisyyden perusteita
 Perinnöllisyyden perusteita Perinnöllisyystieteen isä on augustinolaismunkki Gregor Johann Mendel (1822-1884). Mendel kasvatti herneitä Brnon (nykyisessä Tsekissä) luostarin pihalla. 1866 julkaisu tuloksista
Perinnöllisyyden perusteita Perinnöllisyystieteen isä on augustinolaismunkki Gregor Johann Mendel (1822-1884). Mendel kasvatti herneitä Brnon (nykyisessä Tsekissä) luostarin pihalla. 1866 julkaisu tuloksista
Perinnöllisyys. Enni Kaltiainen
 Perinnöllisyys Enni Kaltiainen Tällä tunnilla: - Lyhyt kertaus genetiikasta - Meioosi - Perinnöllisyyden perusteet - Risteytystehtävät h"p://files.ko-sivukone.com/refluksi.ko-sivukone.com/j0284919.jpg Kertausta
Perinnöllisyys Enni Kaltiainen Tällä tunnilla: - Lyhyt kertaus genetiikasta - Meioosi - Perinnöllisyyden perusteet - Risteytystehtävät h"p://files.ko-sivukone.com/refluksi.ko-sivukone.com/j0284919.jpg Kertausta
Tilastollinen testaaminen tai Tilastollinen päättely. Geneettinen analyysi
 Tilastollinen testaaminen tai Tilastollinen päättely Geneettinen analyysi Tilastollisen testaamisen tarkoitus Tilastollisten testien avulla voidaan tutkia otantapopulaatiota (perusjoukkoa) koskevien väittämien
Tilastollinen testaaminen tai Tilastollinen päättely Geneettinen analyysi Tilastollisen testaamisen tarkoitus Tilastollisten testien avulla voidaan tutkia otantapopulaatiota (perusjoukkoa) koskevien väittämien
DNA sukututkimuksen tukena
 Järvenpää 12,2,2019 Teuvo Ikonen teuvo.ikonen@welho.com DNA sukututkimuksen tukena DNA sukututkimuksessa (Peter Sjölund: Släktforska med DNA) tiesitkö, että olet kävelevä sukukirja? on kuin lukisit kirjaa
Järvenpää 12,2,2019 Teuvo Ikonen teuvo.ikonen@welho.com DNA sukututkimuksen tukena DNA sukututkimuksessa (Peter Sjölund: Släktforska med DNA) tiesitkö, että olet kävelevä sukukirja? on kuin lukisit kirjaa
Populaatiosimulaattori. Petteri Hintsanen HIIT perustutkimusyksikkö Helsingin yliopisto
 Populaatiosimulaattori Petteri Hintsanen HIIT perustutkimusyksikkö Helsingin yliopisto Kromosomit Ihmisen perimä (genomi) on jakaantunut 23 kromosomipariin Jokaisen parin toinen kromosomi on peritty isältä
Populaatiosimulaattori Petteri Hintsanen HIIT perustutkimusyksikkö Helsingin yliopisto Kromosomit Ihmisen perimä (genomi) on jakaantunut 23 kromosomipariin Jokaisen parin toinen kromosomi on peritty isältä
52746 Geneettinen analyysi
 52746 Geneettinen analyysi Kaikille yhteiset luennot (3 kpl) Maanantai 3.2. Klo 10.15-12 Biokeskus 2 auditorio 1041 Todennäköisyyslaskennan kertaus, merkitys perinnöllisyystieteessä! Keskiviikko 5.2. Tilastotiede
52746 Geneettinen analyysi Kaikille yhteiset luennot (3 kpl) Maanantai 3.2. Klo 10.15-12 Biokeskus 2 auditorio 1041 Todennäköisyyslaskennan kertaus, merkitys perinnöllisyystieteessä! Keskiviikko 5.2. Tilastotiede
Jos nyt on saatu havaintoarvot Ü ½ Ü Ò niin suurimman uskottavuuden
 1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
III Perinnöllisyystieteen perusteita
 Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 12. Ominaisuuksien periytymistä tutkitaan risteytyksillä 1. Avainsanat 2. Geenit ja alleelit 3. Mendelin herneet 4. Monohybridiristeytys
Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 12. Ominaisuuksien periytymistä tutkitaan risteytyksillä 1. Avainsanat 2. Geenit ja alleelit 3. Mendelin herneet 4. Monohybridiristeytys
Symbioosi 2 VASTAUKSET. b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl
 Luku 14 Symbioosi 2 VASTAUKSET 1. Banaanikärpänen dihybridiristeytys a. Mikä on vanhempien genotyyppi? Vastaus: VvLl b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl c.
Luku 14 Symbioosi 2 VASTAUKSET 1. Banaanikärpänen dihybridiristeytys a. Mikä on vanhempien genotyyppi? Vastaus: VvLl b. Millaisia sukusoluja vanhemmat tuottavat (4 erilaista)? Vastaus: VL, vl, Vl, vl c.
Jos nollahypoteesi pitää paikkansa on F-testisuuren jakautunut Fisherin F-jakauman mukaan
 17.11.2006 1. Kahdesta kohteesta (A ja K) kerättiin maanäytteitä ja näistä mitattiin SiO -pitoisuus. Tulokset (otoskoot ja otosten tunnusluvut): A K 10 16 Ü 64.94 57.06 9.0 7.29 Oletetaan mittaustulosten
17.11.2006 1. Kahdesta kohteesta (A ja K) kerättiin maanäytteitä ja näistä mitattiin SiO -pitoisuus. Tulokset (otoskoot ja otosten tunnusluvut): A K 10 16 Ü 64.94 57.06 9.0 7.29 Oletetaan mittaustulosten
Perinnöllisyyden perusteita
 Perinnöllisyyden perusteita Eero Lukkari Tämä artikkeli kertoo perinnöllisyyden perusmekanismeista johdantona muille jalostus- ja terveysaiheisille artikkeleille. Koirien, kuten muidenkin eliöiden, perimä
Perinnöllisyyden perusteita Eero Lukkari Tämä artikkeli kertoo perinnöllisyyden perusmekanismeista johdantona muille jalostus- ja terveysaiheisille artikkeleille. Koirien, kuten muidenkin eliöiden, perimä
Perinnöllisyys 2. Enni Kaltiainen
 Perinnöllisyys 2 Enni Kaltiainen Tunnin sisältö: Kytkeytyneiden geenien periytyminen Ihmisen perinnöllisyys Sukupuu Mutaatiot Kytkeytyneet geenit Jokainen kromosomi sisältää kymmeniä geenejä (= kytkeytyneet)
Perinnöllisyys 2 Enni Kaltiainen Tunnin sisältö: Kytkeytyneiden geenien periytyminen Ihmisen perinnöllisyys Sukupuu Mutaatiot Kytkeytyneet geenit Jokainen kromosomi sisältää kymmeniä geenejä (= kytkeytyneet)
6. laskuharjoitusten vastaukset (viikot 10 11)
 6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
T Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti , 8:30-10:00 Kollokaatiot, Versio 1.1
 T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisen kielen tilastollinen käsittely Vastaukset 3, ti 10.2.2004, 8:30-10:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
Evoluutio. BI Elämä ja evoluutio Leena Kangas-Järviluoma
 Evoluutio BI Elämä ja evoluutio Leena Kangas-Järviluoma 1 Evoluutio lajinkehitystä, jossa eliölajit muuttuvat ja niistä voi kehittyä uusia lajeja on jatkunut elämän synnystä saakka, sillä ei ole päämäärää
Evoluutio BI Elämä ja evoluutio Leena Kangas-Järviluoma 1 Evoluutio lajinkehitystä, jossa eliölajit muuttuvat ja niistä voi kehittyä uusia lajeja on jatkunut elämän synnystä saakka, sillä ei ole päämäärää
DNA-testit. sukututkimuksessa Keravan kirjasto Paula Päivinen
 DNA-testit sukututkimuksessa 28.11.2017 Keravan kirjasto Paula Päivinen Solu tuma kromosomit 23 paria DNA Tumassa olevat kromosomit periytyvät jälkeläisille puoliksi isältä ja äidiltä Y-kromosomi periytyy
DNA-testit sukututkimuksessa 28.11.2017 Keravan kirjasto Paula Päivinen Solu tuma kromosomit 23 paria DNA Tumassa olevat kromosomit periytyvät jälkeläisille puoliksi isältä ja äidiltä Y-kromosomi periytyy
T Luonnollisten kielten tilastollinen käsittely
 T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
T-61.281 Luonnollisten kielten tilastollinen käsittely Vastaukset 3, ti 11.2.2003, 16:15-18:00 Kollokaatiot, Versio 1.1 1. Lasketaan ensin tulokset sanaparille valkoinen, talo käsin: Frekvenssimenetelmä:
11. laskuharjoituskierros, vko 15, ratkaisut
 11. laskuharjoituskierros vko 15 ratkaisut D1. Geiger-mittari laskee radioaktiivisen aineen emissioiden lukumääriä. Emissioiden lukumäärä on lyhyellä aikavälillä satunnaismuuttuja jonka voidaan olettaa
11. laskuharjoituskierros vko 15 ratkaisut D1. Geiger-mittari laskee radioaktiivisen aineen emissioiden lukumääriä. Emissioiden lukumäärä on lyhyellä aikavälillä satunnaismuuttuja jonka voidaan olettaa
Genetiikan perusteet 2009
 Genetiikan perusteet 2009 Malli selittää, mutta myös ennustaa ja ennusteen voi testata kokeella. Mendel testasi F 2 -mallinsa tuottamalla itsepölytyksellä F 3 -polven Seuraava sukupolvi tai toinen, riippumaton
Genetiikan perusteet 2009 Malli selittää, mutta myös ennustaa ja ennusteen voi testata kokeella. Mendel testasi F 2 -mallinsa tuottamalla itsepölytyksellä F 3 -polven Seuraava sukupolvi tai toinen, riippumaton
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE Ratkaisut ja arvostelu < X 170
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
c) A = pariton, B = ainakin 4. Nyt = silmäluku on5 Koska esim. P( P(A) P(B) =, eivät tapahtumat A ja B ole riippumattomia.
 Tehtävien ratkaisuja 4. Palloja yhteensä 60 kpl. a) P(molemmat vihreitä) = P((1. pallo vihreä) ja (. pallo vihreä)) = P(1. pallo vihreä) P(. pallo vihreä 1. pallo vihreä) = 0.05 (yleinen kertolaskusääntö)
Tehtävien ratkaisuja 4. Palloja yhteensä 60 kpl. a) P(molemmat vihreitä) = P((1. pallo vihreä) ja (. pallo vihreä)) = P(1. pallo vihreä) P(. pallo vihreä 1. pallo vihreä) = 0.05 (yleinen kertolaskusääntö)
Darwin nuorena. Darwinin syntymästä on 201 vuotta ja "Lajien synnystä" 151 vuotta.
 Darwin nuorena Darwinin syntymästä on 201 vuotta ja "Lajien synnystä" 151 vuotta. Evoluutio on dynaaminen prosessi, joka pohjautuu populaatiogenetiikkaan Darwinin suurin ansio oli luonnonvalinta adaptaation
Darwin nuorena Darwinin syntymästä on 201 vuotta ja "Lajien synnystä" 151 vuotta. Evoluutio on dynaaminen prosessi, joka pohjautuu populaatiogenetiikkaan Darwinin suurin ansio oli luonnonvalinta adaptaation
806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy (1 α) = 99 1 α = 0.
 806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy 2012 1. Olkoon (X 1,X 2,...,X 25 ) satunnaisotos normaalijakaumasta N(µ,3 2 ) eli µ
806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy 2012 1. Olkoon (X 1,X 2,...,X 25 ) satunnaisotos normaalijakaumasta N(µ,3 2 ) eli µ
Tilastollinen testaus. Vilkkumaa / Kuusinen 1
 Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Geenikartoituksen käsitteet ja lähestymistavat
 Geenikartoituksen käsitteet ja lähestymistavat Luentomateriaalin pohjana Vesa Ollikainen, CSC Geenikartoituskurssin kalvot Geenikartoitus ongelmana Tavoitteena on löytää tilastollisia yhteyksiä yksilöillä
Geenikartoituksen käsitteet ja lähestymistavat Luentomateriaalin pohjana Vesa Ollikainen, CSC Geenikartoituskurssin kalvot Geenikartoitus ongelmana Tavoitteena on löytää tilastollisia yhteyksiä yksilöillä
Peittyvä periytyminen. Potilasopas. Kuvat: Rebecca J Kent www.rebeccajkent.com rebecca@rebeccajkent.com
 12 Peittyvä periytyminen Muokattu allamainittujen instanssien julkaisemista vihkosista, heidän laatustandardiensa mukaan: Guy's and St Thomas' Hospital, London, United Kingdom; and the London IDEAS Genetic
12 Peittyvä periytyminen Muokattu allamainittujen instanssien julkaisemista vihkosista, heidän laatustandardiensa mukaan: Guy's and St Thomas' Hospital, London, United Kingdom; and the London IDEAS Genetic
KEESHONDIEN MONIMUOTOISUUSKARTOITUS
 KEESHONDIEN MONIMUOTOISUUSKARTOITUS 2 3. 0 1. 2 0 1 1 K A A R I N A Marjut Ritala DNA-diagnostiikkapalveluja kotieläimille ja lemmikeille Polveutumismääritykset Geenitestit Serologiset testit Kissat, koirat,
KEESHONDIEN MONIMUOTOISUUSKARTOITUS 2 3. 0 1. 2 0 1 1 K A A R I N A Marjut Ritala DNA-diagnostiikkapalveluja kotieläimille ja lemmikeille Polveutumismääritykset Geenitestit Serologiset testit Kissat, koirat,
Symbioosi 2 TEHTÄVÄT
 Luku 13 Symbioosi 2 TEHTÄVÄT 1. Yhdistä kaavioon oikealle paikalle a. P-polvi b. F 1 -polvi c. F 2 -polvi d. sukusolut e. genotyyppi 2. Miten seuraavat käsitteet eroavat toisistaan? a. Fenotyyppi ja genotyyppi
Luku 13 Symbioosi 2 TEHTÄVÄT 1. Yhdistä kaavioon oikealle paikalle a. P-polvi b. F 1 -polvi c. F 2 -polvi d. sukusolut e. genotyyppi 2. Miten seuraavat käsitteet eroavat toisistaan? a. Fenotyyppi ja genotyyppi
Väliestimointi (jatkoa) Heliövaara 1
 Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
Epigeneettinen säätely ja genomin leimautuminen. Tiina Immonen Medicum, Biokemia ja kehitysbiologia
 Epigeneettinen säätely ja genomin leimautuminen Tiina Immonen Medicum, Biokemia ja kehitysbiologia 12.12.2017 Epigenetic inheritance: A heritable alteration in a cell s or organism s phenotype that does
Epigeneettinen säätely ja genomin leimautuminen Tiina Immonen Medicum, Biokemia ja kehitysbiologia 12.12.2017 Epigenetic inheritance: A heritable alteration in a cell s or organism s phenotype that does
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Tilastollisen merkitsevyyden testaus Osa II Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Tilastollisen merkitsevyyden testaus Osa II Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
Bayesin pelit. Kalle Siukola. MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly
 Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Kynä-paperi -harjoitukset. Taina Lehtinen Taina I Lehtinen Helsingin yliopisto
 Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
Geenitekniikan perusmenetelmät
 Loppukurssikoe To klo 14-16 2 osiota: monivalintatehtäväosio ja kirjallinen osio, jossa vastataan kahteen kysymykseen viidestä. Koe on auki klo 14.05-16. Voit tehdä sen oppitunnilla, jolloin saat tarvittaessa
Loppukurssikoe To klo 14-16 2 osiota: monivalintatehtäväosio ja kirjallinen osio, jossa vastataan kahteen kysymykseen viidestä. Koe on auki klo 14.05-16. Voit tehdä sen oppitunnilla, jolloin saat tarvittaessa
Miten letaalialleeleita käsitellään Drosophilalla? Välttämätön taito esimerkiksi alkionkehityksen alkuvaiheiden selvittämisessä
 Miten letaalialleeleita käsitellään Drosophilalla? Välttämätön taito esimerkiksi alkionkehityksen alkuvaiheiden selvittämisessä Balansoitu kanta Koejärjestely perustuu ns. balansoidun kannan käyttöön.
Miten letaalialleeleita käsitellään Drosophilalla? Välttämätön taito esimerkiksi alkionkehityksen alkuvaiheiden selvittämisessä Balansoitu kanta Koejärjestely perustuu ns. balansoidun kannan käyttöön.
Valitaan testisuure, jonka jakauma tunnetaan H 0 :n ollessa tosi.
 9.10.2018/1 MTTTP1, luento 9.10.2018 KERTAUSTA TESTAUKSESTA, p-arvo Asetetaan H 0 H 1 Valitaan testisuure, jonka jakauma tunnetaan H 0 :n ollessa tosi. Lasketaan otoksesta testisuureelle arvo. 9.10.2018/2
9.10.2018/1 MTTTP1, luento 9.10.2018 KERTAUSTA TESTAUKSESTA, p-arvo Asetetaan H 0 H 1 Valitaan testisuure, jonka jakauma tunnetaan H 0 :n ollessa tosi. Lasketaan otoksesta testisuureelle arvo. 9.10.2018/2
Jokaisesta sairausgeenistä saa lisätietoa klikkaamalla kyseisen sairauden kohtaa ohjelmassa.
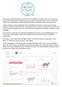 Genoscoopper julkaisi MyCatDNA-testin 13.06.2018. MyCatDNA-testi voidaan ottaa niin rodullisesta kuin roduttomasta kissasta ja kaiken ikäisistä kissoista. Testi tarkistaa jokaisesta kissasta yli 40 eri
Genoscoopper julkaisi MyCatDNA-testin 13.06.2018. MyCatDNA-testi voidaan ottaa niin rodullisesta kuin roduttomasta kissasta ja kaiken ikäisistä kissoista. Testi tarkistaa jokaisesta kissasta yli 40 eri
a) dominoivaan: esiintyy joka sukupolvessa, sairaille vanhemmille voi syntyä terveitä lapsia
 1. Sukupuut Seuraavat ihmisen sukupuut edustavat periytymistä, jossa ominaisuuden määrää yksi alleeli. Päättele sukupuista A-F, mitä periytymistapaa kukin niistä voi edustaa. Vastaa taulukkoon kirjaimin
1. Sukupuut Seuraavat ihmisen sukupuut edustavat periytymistä, jossa ominaisuuden määrää yksi alleeli. Päättele sukupuista A-F, mitä periytymistapaa kukin niistä voi edustaa. Vastaa taulukkoon kirjaimin
Periytyvyys ja sen matematiikka
 Periytyvyys ja sen matematiikka 30.7.2001 Katariina Mäki MMM,tutkija Helsingin yliopisto, Kotieläintieteen laitos / kotieläinten jalostustiede katariina.maki@animal.helsinki.fi Jalostuksen tavoitteena
Periytyvyys ja sen matematiikka 30.7.2001 Katariina Mäki MMM,tutkija Helsingin yliopisto, Kotieläintieteen laitos / kotieläinten jalostustiede katariina.maki@animal.helsinki.fi Jalostuksen tavoitteena
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
Genetiikan perusteet. Tafel V Baur E. (1911) Einführung in die experimentelle Vererbungslehre. Verlag von Gebrüder Borntraeger, Berlin.
 Genetiikan perusteet Tafel V Baur E. (1911) Einführung in die experimentelle Vererbungslehre. Verlag von Gebrüder Borntraeger, Berlin. Transmissiogenetiikka l. mendelistinen genetiikka Historia Yksinkertaiset
Genetiikan perusteet Tafel V Baur E. (1911) Einführung in die experimentelle Vererbungslehre. Verlag von Gebrüder Borntraeger, Berlin. Transmissiogenetiikka l. mendelistinen genetiikka Historia Yksinkertaiset
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
DNA testit sukututkimuksessa
 DNA testit sukututkimuksessa Pakkasten sukuseura ry:n 20 v juhlakokous 19.9.2015 Jyväskylä Raimo Pakkanen, sukuneuvoston pj A,T,G,C. Ihmisen genetiikan lyhyt oppimäärä mtdna diploidinen kromosomisto =
DNA testit sukututkimuksessa Pakkasten sukuseura ry:n 20 v juhlakokous 19.9.2015 Jyväskylä Raimo Pakkanen, sukuneuvoston pj A,T,G,C. Ihmisen genetiikan lyhyt oppimäärä mtdna diploidinen kromosomisto =
χ = Mat Sovellettu todennäköisyyslasku 11. harjoitukset/ratkaisut
 Mat-2.091 Sovellettu todennäköisyyslasku /Ratkaisut Aiheet: Yhteensopivuuden testaaminen Homogeenisuuden testaaminen Riippumattomuuden testaaminen Avainsanat: Estimointi, Havaittu frekvenssi, Homogeenisuus,
Mat-2.091 Sovellettu todennäköisyyslasku /Ratkaisut Aiheet: Yhteensopivuuden testaaminen Homogeenisuuden testaaminen Riippumattomuuden testaaminen Avainsanat: Estimointi, Havaittu frekvenssi, Homogeenisuus,
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa. Luentokuulustelujen esimerkkivastauksia. Pertti Palo. 30.
 FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa Luentokuulustelujen esimerkkivastauksia Pertti Palo 30. marraskuuta 2012 Saatteeksi Näiden vastausten ei ole tarkoitus olla malleja vaan esimerkkejä.
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa Luentokuulustelujen esimerkkivastauksia Pertti Palo 30. marraskuuta 2012 Saatteeksi Näiden vastausten ei ole tarkoitus olla malleja vaan esimerkkejä.
¼ ¼ joten tulokset ovat muuttuneet ja nimenomaan huontontuneet eivätkä tulleet paremmiksi.
 10.11.2006 1. Pituushyppääjä on edellisenä vuonna hypännyt keskimäärin tuloksen. Valmentaja poimii tämän vuoden harjoitusten yhteydessä tehdyistä muistiinpanoista satunnaisesti kymmenen harjoitushypyn
10.11.2006 1. Pituushyppääjä on edellisenä vuonna hypännyt keskimäärin tuloksen. Valmentaja poimii tämän vuoden harjoitusten yhteydessä tehdyistä muistiinpanoista satunnaisesti kymmenen harjoitushypyn
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
Järvitesti Ympäristöteknologia T571SA 7.5.2013
 Hans Laihia Mika Tuukkanen 1 LASKENNALLISET JA TILASTOLLISET MENETELMÄT Järvitesti Ympäristöteknologia T571SA 7.5.2013 Sarkola Eino JÄRVITESTI Johdanto Järvien kuntoa tutkitaan monenlaisilla eri menetelmillä.
Hans Laihia Mika Tuukkanen 1 LASKENNALLISET JA TILASTOLLISET MENETELMÄT Järvitesti Ympäristöteknologia T571SA 7.5.2013 Sarkola Eino JÄRVITESTI Johdanto Järvien kuntoa tutkitaan monenlaisilla eri menetelmillä.
52746 Geneettinen analyysi
 52746 Geneettinen analyysi Päivi Onkamo Sampo Sammalisto Jack Leo Pekka Uimari Perinnöllisyystieteen oppiaine, Biotieteiden laitos, Helsingin yliopisto 2011 Sisällysluettelo Johdanto... 3 Luennot... 4
52746 Geneettinen analyysi Päivi Onkamo Sampo Sammalisto Jack Leo Pekka Uimari Perinnöllisyystieteen oppiaine, Biotieteiden laitos, Helsingin yliopisto 2011 Sisällysluettelo Johdanto... 3 Luennot... 4
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Geneettinen analyysi. Tilastotieteen kertausta
 Kertaus: Luento 1 Todennäköisyyksien perusperiaatteita Testille suotuisten tapauksien joukko Toisensa poissulkevat tapaukset Leikkaus Yhdiste Komplementti Riippumattomat tapahtumat, niiden kertolasku Ehdollinen
Kertaus: Luento 1 Todennäköisyyksien perusperiaatteita Testille suotuisten tapauksien joukko Toisensa poissulkevat tapaukset Leikkaus Yhdiste Komplementti Riippumattomat tapahtumat, niiden kertolasku Ehdollinen
Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita
 Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 14. Useamman ominaisuusparin periytyminen 1. Avainsanat 2. Mendelin lait 3. Dihybridiristeytys 4. Mendelin tulosten taustaa 5. Tekijäinvaihdunta
Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 14. Useamman ominaisuusparin periytyminen 1. Avainsanat 2. Mendelin lait 3. Dihybridiristeytys 4. Mendelin tulosten taustaa 5. Tekijäinvaihdunta
Vallitseva periytyminen. Potilasopas. Kuvat: Rebecca J Kent www.rebeccajkent.com rebecca@rebeccajkent.com
 12 Vallitseva periytyminen Muokattu allamainittujen instanssien julkaisemista vihkosista, heidän laatustandardiensa mukaan: Guy's and St Thomas' Hospital, London, United Kingdom; and the London IDEAS Genetic
12 Vallitseva periytyminen Muokattu allamainittujen instanssien julkaisemista vihkosista, heidän laatustandardiensa mukaan: Guy's and St Thomas' Hospital, London, United Kingdom; and the London IDEAS Genetic
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
X-kromosominen periytyminen. Potilasopas. TYKS Perinnöllisyyspoliklinikka PL 52, 20521 Turku puh (02) 3131 390 faksi (02) 3131 395
 12 X-kromosominen periytyminen TYKS Perinnöllisyyspoliklinikka PL 52, 20521 Turku puh (02) 3131 390 faksi (02) 3131 395 FOLKHÄLSANS GENETISKA KLINIK PB 211, (Topeliusgatan 20) 00251 Helsingfors tel (09)
12 X-kromosominen periytyminen TYKS Perinnöllisyyspoliklinikka PL 52, 20521 Turku puh (02) 3131 390 faksi (02) 3131 395 FOLKHÄLSANS GENETISKA KLINIK PB 211, (Topeliusgatan 20) 00251 Helsingfors tel (09)
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
Luento 2. Yksiparametrisia malleja. Binomi-malli. Posteriorijakauman esittämisestä. Informatiivisista priorijakaumista. Konjugaattipriori.
 Luento 2 Binomi-malli Posteriorijakauman esittämisestä Informatiivisista priorijakaumista Konjugaattipriori Slide 1 Yksiparametrisia malleja Binomi Jacob Bernoulli (1654-1705), Bayes (1702-1761) Normaali
Luento 2 Binomi-malli Posteriorijakauman esittämisestä Informatiivisista priorijakaumista Konjugaattipriori Slide 1 Yksiparametrisia malleja Binomi Jacob Bernoulli (1654-1705), Bayes (1702-1761) Normaali
Matemaatikot ja tilastotieteilijät
 Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
P(X = x T (X ) = t, θ) = p(x = x T (X ) = t) ei riipu tuntemattomasta θ:sta. Silloin uskottavuusfunktio faktorisoituu
 1. Tyhjentävä tunnusluku (sucient statistics ) Olkoon (P(X = x θ) : θ Θ) todennäköisyysmalli havainnolle X. Datan funktio T (X ) on Tyhjentävä tunnusluku jos ehdollinen todennäköisyys (ehdollinen tiheysfunktio)
1. Tyhjentävä tunnusluku (sucient statistics ) Olkoon (P(X = x θ) : θ Θ) todennäköisyysmalli havainnolle X. Datan funktio T (X ) on Tyhjentävä tunnusluku jos ehdollinen todennäköisyys (ehdollinen tiheysfunktio)
Tiedonjyväsiä cavalierien geenitestauksista imuroituna maailmalta
 Tiedonjyväsiä cavalierien geenitestauksista imuroituna maailmalta Genetiikan tutkijat Englannin Kennel Clubin ja AHT:n kanssa yhteistyössä ovat laatineet seuraavanlaisen artikkelin Episodic Fallingista
Tiedonjyväsiä cavalierien geenitestauksista imuroituna maailmalta Genetiikan tutkijat Englannin Kennel Clubin ja AHT:n kanssa yhteistyössä ovat laatineet seuraavanlaisen artikkelin Episodic Fallingista
Odotusarvoparien vertailu. Vilkkumaa / Kuusinen 1
 Odotusarvoparien vertailu Vilkkumaa / Kuusinen 1 Motivointi Viime luennolta: yksisuuntaisella varianssianalyysilla testataan nollahypoteesia H 0 : μ 1 = μ 2 = = μ k = μ Jos H 0 hylätään, tiedetään, että
Odotusarvoparien vertailu Vilkkumaa / Kuusinen 1 Motivointi Viime luennolta: yksisuuntaisella varianssianalyysilla testataan nollahypoteesia H 0 : μ 1 = μ 2 = = μ k = μ Jos H 0 hylätään, tiedetään, että
pitkittäisaineistoissa
 Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Sukusiitoksesta sukulaistumiseen - jalostustietojärjestelmä työkaluna. Rovaniemi Susanna Back, Suomen Hippos ry
 Sukusiitoksesta sukulaistumiseen - jalostustietojärjestelmä työkaluna Rovaniemi 22.3.2018 Susanna Back, Suomen Hippos ry Sukulaisuussuhde Kahden yksilön yhteisten geenien todennäköinen osuus Riippuu eläinten
Sukusiitoksesta sukulaistumiseen - jalostustietojärjestelmä työkaluna Rovaniemi 22.3.2018 Susanna Back, Suomen Hippos ry Sukulaisuussuhde Kahden yksilön yhteisten geenien todennäköinen osuus Riippuu eläinten
MTTTP5, luento Kahden jakauman sijainnin vertailu (jatkoa) Tutkimustilanteita y = neliöhinta x = sijainti (2 aluetta)
 MTTTP5, luento 7.12.2017 7.12.2017/1 6.1.3 Kahden jakauman sijainnin vertailu (jatkoa) Tutkimustilanteita y = neliöhinta x = sijainti (2 aluetta) y = lepopulssi x = sukupuoli y = musikaalisuus x = sukupuoli
MTTTP5, luento 7.12.2017 7.12.2017/1 6.1.3 Kahden jakauman sijainnin vertailu (jatkoa) Tutkimustilanteita y = neliöhinta x = sijainti (2 aluetta) y = lepopulssi x = sukupuoli y = musikaalisuus x = sukupuoli
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
f (28) L(28) = f (27) + f (27)(28 27) = = (28 27) 2 = 1 2 f (x) = x 2
 BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
Tilastollinen aineisto Luottamusväli
 Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
ax + y + 2z = 0 2x + y + az = b 2. Kuvassa alla on esitetty nesteen virtaus eräässä putkistossa.
 BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 7, Syksy 206 Tutkitaan yhtälöryhmää x + y + z 0 2x + y + az b ax + y + 2z 0 (a) Jos a 0 ja b 0 niin mikä on yhtälöryhmän ratkaisu? Tulkitse ratkaisu
BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 7, Syksy 206 Tutkitaan yhtälöryhmää x + y + z 0 2x + y + az b ax + y + 2z 0 (a) Jos a 0 ja b 0 niin mikä on yhtälöryhmän ratkaisu? Tulkitse ratkaisu
Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria.
 5.10.2017/1 MTTTP1, luento 5.10.2017 KERTAUSTA Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla todennäköisyydellä,
5.10.2017/1 MTTTP1, luento 5.10.2017 KERTAUSTA Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla todennäköisyydellä,
Testit järjestysasteikollisille muuttujille
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testit järjestysasteikollisille muuttujille TKK (c) Ilkka Mellin (2007) 1 Testit järjestysasteikollisille muuttujille >> Järjestysasteikollisten
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testit järjestysasteikollisille muuttujille TKK (c) Ilkka Mellin (2007) 1 Testit järjestysasteikollisille muuttujille >> Järjestysasteikollisten
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I
 HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Tehtävä 1 on klassikko. 1. Tässä tehtävässä tapahtumat A ja B eivät välttämättä
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Tehtävä 1 on klassikko. 1. Tässä tehtävässä tapahtumat A ja B eivät välttämättä
1 Kannat ja kannanvaihto
 1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
HAVAITUT JA ODOTETUT FREKVENSSIT
 HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
Demonstraatiot Luento 7 D7/1 D7/2 D7/3
 TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-8.45 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 7 7.2.2008 D7/ Tarkastellaan piirikytkentäisen järjestelmän n-kanavaista
TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-8.45 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 7 7.2.2008 D7/ Tarkastellaan piirikytkentäisen järjestelmän n-kanavaista
Mallin arviointi ja valinta. Ennustevirhe otoksen sisällä, parametrimäärän valinta, AIC, BIC ja MDL
 Mallin arviointi ja valinta Ennustevirhe otoksen sisällä, parametrimäärän valinta, AIC, BIC ja MDL Sisältö Otoksen ennustevirheen estimointi AIC - Akaiken informaatiokriteeri mallin valintaan Parametrimäärän
Mallin arviointi ja valinta Ennustevirhe otoksen sisällä, parametrimäärän valinta, AIC, BIC ja MDL Sisältö Otoksen ennustevirheen estimointi AIC - Akaiken informaatiokriteeri mallin valintaan Parametrimäärän
Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit
 Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit Sisältö Tilastollisia testejä tehdään jatkuvasti lukemattomilla aloilla. Meitä saattaa kiinnostaa esimerkiksi se, että onko miesten ja
Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit Sisältö Tilastollisia testejä tehdään jatkuvasti lukemattomilla aloilla. Meitä saattaa kiinnostaa esimerkiksi se, että onko miesten ja
Geneettinen analyysi 2014, laskuharjoitukset
 Geneettinen analyysi 2014, laskuharjoitukset 1. Mendelistinen genetiikka 1.1 Oletetaan, että ihmisellä nipukattomat korvat on resessiivinen ominaisuus nipukallisiin nähden. Naisella ja tämän miehellä on
Geneettinen analyysi 2014, laskuharjoitukset 1. Mendelistinen genetiikka 1.1 Oletetaan, että ihmisellä nipukattomat korvat on resessiivinen ominaisuus nipukallisiin nähden. Naisella ja tämän miehellä on
Monogeeniset sairaudet. Monogeeninen periytyminen. Perinnöllisten tautien prevalenssi. Monitekijäiset sairaudet. Dominantti vs.
 Monogeeniset sairaudet Monogeeninen Pirkka-Pekka Laurila, LL Lääketieteellisen genetiikan osasto, HY Finnish Institute for Molecular Medicine, FIMM Mutaatio yhdessä geenissä riittävä aiheuttamaan sairauden
Monogeeniset sairaudet Monogeeninen Pirkka-Pekka Laurila, LL Lääketieteellisen genetiikan osasto, HY Finnish Institute for Molecular Medicine, FIMM Mutaatio yhdessä geenissä riittävä aiheuttamaan sairauden
6.1.2 Yhdessä populaatiossa tietyn tyyppisten alkioiden prosentuaalista osuutta koskeva päättely
 3.12.2018/1 MTTTP5, luento 3.12.2018 6.1.2 Yhdessä populaatiossa tietyn tyyppisten alkioiden prosentuaalista osuutta koskeva päättely H 0 : = 0 Oletetaan, että populaatiossa viallisia %. Olkoon X 1, X
3.12.2018/1 MTTTP5, luento 3.12.2018 6.1.2 Yhdessä populaatiossa tietyn tyyppisten alkioiden prosentuaalista osuutta koskeva päättely H 0 : = 0 Oletetaan, että populaatiossa viallisia %. Olkoon X 1, X
TAPAUS-VERROKKITUTKIMUS
 TAPAUS-VERROKKI TUTKIMUKSEN TYYPIT JA TULOSTEN ANALYYSI Simo Näyhä Jari Jokelainen Kansanterveystieteen ja yleislääketieteen laitoksen jatkokoulutusmeeting.3.4.2007 TAPAUS-VERROKKITUTKIMUS Idea Tutkimusryhmät
TAPAUS-VERROKKI TUTKIMUKSEN TYYPIT JA TULOSTEN ANALYYSI Simo Näyhä Jari Jokelainen Kansanterveystieteen ja yleislääketieteen laitoksen jatkokoulutusmeeting.3.4.2007 TAPAUS-VERROKKITUTKIMUS Idea Tutkimusryhmät
l (φ; y) = l(θ(φ); y) Toinen derivaatta saadaan tulon derivaatan laskusäännöllä Uudelleenparametroidun mallin Fisherin informaatio on
 HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
1. Tutkitaan regressiomallia Y i = β 0 + β 1 X i + u i ja oletetaan, että tavanomaiset
 TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
mendelististä genetiikkaa joukoissa: Hardyn ja Weinbergin "laki" Selektio, sattuma
 Populaatiogenetiikka = mendelististä genetiikkaa joukoissa: Hardyn ja Weinbergin "laki" Selektio, sattuma Monisteen sivu 53 Kurssilla on yksi ainoa populaatiogenetiikkaa sivuava empiirinen työ: Oman veriryhmän
Populaatiogenetiikka = mendelististä genetiikkaa joukoissa: Hardyn ja Weinbergin "laki" Selektio, sattuma Monisteen sivu 53 Kurssilla on yksi ainoa populaatiogenetiikkaa sivuava empiirinen työ: Oman veriryhmän
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-200 Todennäköisyyslaskenta Tentti 29.04.20 / Kimmo Vattulainen Funktiolaskin sallittu.. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi kuutosen. A aloittaa
MAT-200 Todennäköisyyslaskenta Tentti 29.04.20 / Kimmo Vattulainen Funktiolaskin sallittu.. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi kuutosen. A aloittaa
Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle
 Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle - Sisältö - - - Varianssianalyysi Varianssianalyysissä (ANOVA) testataan oletusta normaalijakautuneiden otosten odotusarvojen
Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle - Sisältö - - - Varianssianalyysi Varianssianalyysissä (ANOVA) testataan oletusta normaalijakautuneiden otosten odotusarvojen
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.04 Tilastollisen analyysin perusteet, kevät 007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen Jakaumaoletuksien testaamiseen soveltuvat testit χ -yhteensopivuustesti yksi otos otoksen vertaaminen
Mat-.04 Tilastollisen analyysin perusteet, kevät 007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen Jakaumaoletuksien testaamiseen soveltuvat testit χ -yhteensopivuustesti yksi otos otoksen vertaaminen
