TEKNILLINEN KORKEAKOULU Tietoliikenneohjelmistojen ja Multimedian Laboratorio T Tietokonegrafiikan seminaari L.
|
|
|
- Reijo Ilmari Saarinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 TEKNILLINEN KORKEAKOULU Tietoliikenneohjelmistojen ja Multimedian Laboratorio T Tietokonegrafiikan seminaari L Billboard Clouds Jon Franzas, TKK jfranzas@cc.hut.fi 52365B
2 Billboard Clouds Jon Franzas TKK, Tietoliikenneohjelmistojen ja Multimedian Laboratorio Abstrakti Artikkelissa esitetään uusi tekniikka nimeltään Billboard Clouds (lyhennetty jatkossa BC) joka mahdollistaa monimutkaisten staattisten kolmiulotteisten mallien renderöimisen oleellisesti nopeammin nykyisiin tapoihin verrattuna. Huomattavasti suurempi nopeus saavutetaan approksimoimalla mallit oleellisesti pienemmällä polygonimäärällä ja käyttämällä tekstuureja ja niiden läpinäkyvyyksiä hyväkseen. Tämä geometrian huomattava yksinkertaistaminen ei juuri huononna mallin visuaalista laatua. 1 JOHDANTO Osiossa käydään lyhyesti läpi mitä reaaliaikaisella tietokonegrafiikalla tarkoitetaan, kerrotaan lyhyesti taustaa, sekä käydään läpi BC:n idea lyhyesti. 1.1 Reaaliaikainen tietokonegrafiikka Reaaliaikaisessa tietokonegrafiikassa on tärkeää käyttää mahdollisimman yksinkertaisia malleja visuaalista laatua unohtamatta. Jotta syntyisi vaikutelma liikkeestä, eikä katsoja erottaisi kuvia toisistaan, koneen pitää pystyä laskemaan vähintään 30 ruutua sekunnissa. Reaaliaikaisen grafiikan tunnetuimpia ja käytetyimpiä sovelluskohteita ovat konsoli- ja tietokonepelit. Koska tietokoneilla on rajoitettu laskenta- ja piirtonopeus, pitää mallien olla mahdollisimman yksinkertaisia jottei nopeus kärsisi liikaa. Nykyään tietokoneet ovat kuitenkin erittäin nopeita ja mahdollistavat yhä monimutkaisimpien ja realistisempien maailmojen renderöimisen. Tehoa ei kuitenkaan koskaan ole liikaa ja peliohjelmoijat löytävät aina käyttöä ylimääräiselle teholle. Tästä johtuen pyritään luomaan pienemmästä polygonimäärästä koostuvia malleja, kuitenkin niin että visuaalinen laatu samalla paranisi. Reaaliaikaisen tietokonegrafiikan mallit koostuvat polygoneista jotka ovat kaksiulotteisia pintoja. Näitä pintoja yhdistelemällä voidaan rakentaa niin monimutkaisia malleja kuin halutaan. Yksinkertaisin polygoni on kolmio. Kolmiot on myös erityisasemassa siksi että lähes kaikki grafiikkakiihdyttimet piirtävät ainoastaan niitä. Käytännössä monimutkaisempi pinta jaetaan aina kolmioihin ennen sen piirtämistä. 1
3 1.2 Mallien yksinkertaistaminen Meshien desimaatio, ja tekniikka nimeltään Edge collapse (Heckbert & Garland 1997, Puppo & Scopigno 1997, Luebke 2001) ovat tehokkaita tapoja vähentää polygonien määrää mallissa. Nämä eivät kuitenkaan toimi yksinkertaistuksissa, joissa tavoitteena on saada suuria muutoksia polygonien määrään, ja vaativat yleensä mallien yhtenäisyyttä. Puu on esimerkki epäyhtenäisestä monimutkaisesta objektista jota on vaikea yksinkertaistaa meshien desimaation avulla. Peleissä puut ovat usein esitetty kahden billboardin ristinä, joiden avulla saadaan aikaiseksi illuusio monimutkaisemmasta geometriasta. Tämä tekniikka ei kuitenkaan ole hyvä kun puuta tarkastellaan lähietäisyydeltä. Billboardien käyttäminen puiden yhteydessä on esimerkki kuvapohjaisesta yksinkertaistamismenetelmästä. Muita monimutkaisempia menetelmiä on olemassa, ja BC on juuri tällainen kuvapohjainen yksinkertaistamismenetelmä. BC:n innoittajana voitaisiin mainita esim. Superfaces (Kalvin & Taylor 1996), joka yhdistää lähes samassa tasossa olevat polygonit yhdeksi polygoniksi. Yksi tapa esittää kaukana olevat monimutkaiset mallit perustuvat niistä otettuihin valokuvanomaisiin, Impostorseihin (Maciel & Shirley 1995). Ne valitaan aina sen mukaan missä suunnassa katsoja on. 1.3 Tekstuureilla approksimointi BC:n avulla BC:n ideana on vähentää polygonien määrää huomattavasti ja tekstuureja hyväksikäyttämällä luoda illuusio monimutkaisemmasta geometriasta. Mallille pyritään löytämään ympäröiviä tasoja, niin että ne parhaiten kaappaisivat mallin geometrian, joihin sitten luodaan sopivat tekstuurit. Kun tasot on luotu, projisoidaan polygonit jotka tason pitää esittää niihin. Tämä vastaa tekstuurien ja niiden läpinäkyvyyskomponenttien generoimista. Jos normaalit vielä lasketaan, voidaan BC valaista reaaliaikaisesti käyttäen hyväkseen Bump-mapping ja Pixel shader tekniikoita. Yksinkertaiset varjot voidaan myös helposti laskea projisoimalla BC:n tasot esim. lattiatasoon. BC luodaan etukäteen eikä sitä voi tehdä reaaliajassa. Sen suurimpiin hyötyihin kuuluu se ettei mitään topologista informaatiota itse mallin lisäksi tarvita. Mallin skaalaaminen suuremmaksi tai pienemmäksi on yksinkertaista, mutta muut transformaatiot ovat sitten hankalampia. Jos BC:tä halutaan esim. venyttää hajoavat approksimoidut tekstuuripinnat, eikä malli enää näytä yhtenäiseltä. 2 MENETELMÄN KUVAUS Osiossa kerrotaan ensin lyhyesti BC:n yleiskuvaus, jonka jälkeen siirrytään tasojen valitsemisprosessin tarkempaan tarkasteluun. Lopuksi kerrotaan tekstuurien generoimisprosessista. 2
4 2.1 Yleiskuvaus Décoret et al. (2003) julkaisemassa artikkelissa johon tekstini perustuu, käytetään BC:n luomiseen, iteratiivista ja diskreettiä (muuten tasojen iteroiminen olisi äärettömän pitkä operaatio) menetelmää jossa on kaksi funktiota, virhe- ja hintafunktio, jotka määräävät miten ympäröivät pinnat valitaan. Ensin valitaan suurin hyväksyttävä virhe E, jonka jälkeen tavoitteena on luoda ympäröivät pinnat mahdollisimman pienellä hinnalla. Kun pinnat on löydetty generoidaan niihin sopivat tekstuurit. Hintafunktion minimoiminen johtaa mahdollisimman pieneen määrään tasoja, sekä kompakteihin tekstuureihin. Virhefunktio taas kertoo kuinka kaukana yksittäinen verteksi saa olla sen esittämästä tasosta jotta se voidaan siihen tasoon hyväksyä. Virheen pienentäminen vaikuttaa suoraan lopputuloksen visuaaliseen laatuun, tasojen määrän kustannuksella. Menetelmän idea on löytää mahdollisimman pieni määrä pintoja, kuitenkin niin että jokainen mallin polygoni saadaan projisoitua vähintään yhdelle pinnalle (2.2.1 Kelpoisuus). Tärkeää on myös projisoida polygonit pinnalle joka on korkeintaan valitun virheen päässä polygoneista (tai sen jokaisesta verteksistä). Suuret polygonit jotka projisoituvat suuremmalle pinnalle ovat tärkeämpiä kuin pienet polygonit (2.2.2 Peittävyys). Pinnat jotka eivät onnistu esittämään niitä lähellä olevia polygoneja karsitaan myös pois (2.2.3 Sakotus), muuten polygoni saattaa saada huonomman esityksen kauemmalle pinnalle projisoituessaan. Systeemistä rakennetaan tasoavaruus (2.2.4 Diskreetti tasoavaruus) jossa jokaisen diskreetin pisteen läpi kulkee diskreettejä pintoja, joilla on yllämainitut tiedot. Tasot valitaan lopuksi niin että hintafunktio minimoituu. Kun tasot on valittu generoidaan niihin tekstuurit katsomalla mallia tasojen läpi ja renderöimällä siihen tasoon kuuluvat polygonit. Tässä esitetään yksi tapa joka hoitaa tämän prosessin. Kyseessä on kaksivaiheinen prosessi, ensin lasketaan tiheys tasoavaruudessa, jonka jälkeen suoritetaan ahne optimointi, joka löytää tasot ja generoi niihin tekstuurit. 2.2 Tiheys tasoavaruudessa Jotta parhaat tasot saadaan selvitettyä lasketaan niiden ns. tiheydet tasoavaruudessa. Tiheys koostuu kolmesta tärkeästä tekijästä: kelpoisuudesta, peittävyydestä ja sakosta. Kelpoisuus kertoo onko taso validi yksinkertaistus polygonista (tässä aina kolmioita). Peittävyys ottaa huomioon polygonin koon, tai tarkemmin ilmaistuna sen tasolle projisoidun pinta-alan koon. Isoja polygoneja suositaan. Sakko taas kertoo kuinka paljon epäkelpoisia polygoneja pinnan läheisyydessä on. Tasoja joilla on paljon sakkopolygoneja pyritään välttämään. Tason P tiheys d(p) määritellään kaavalla: d(p) = C(P) P(P) (1) jossa C(P) on tason peittävyys (kuinka paljon ja kuinka isoja polygoneja se voi esittää) ja P(P) tason sakko (kuinka paljon ja kuinka isoja polygoneja on sen lähellä jotka ovat epävalideja). 3
5 2.2.1 Kelpoisuus Taso on validi polygonille jos polygonin kaikki verteksit ovat korkeintaan etäisyydellä E tasosta. Jokainen polygoni pitää projisoida vähintään yhdelle tasolle, ja kun kaikki verteksit käydään läpi saadaan avaruudessa alue joka rajaa jo melko tarkkaan mihin tasot tulee sijoittaa. Jokaisen verteksin ympärille muodostuu pallo jonka läpi tason pitää mennä jotta se on validi verteksille (kuva 1c.) Taso pitää kuitenkin valita niin että se on validi polygonin kaikille vertekseille. (kuva 1d.) Jokaiselle tasolle määritellään validi joukko joka kertoo kuinka monta polygonia se voi esittää Peittävyys Jokaista validia polygonia painotetaan vielä sen tasolle projisoidulla pinta-alalla. Näin taso joka on validi suurelle määrälle pieniä polygoneja ei ole tärkeämpi kuin taso joka pystyy esittämään pienemmän määrän suuria polygoneja. Tämä suosii myös polygoneja jotka ovat samansuuntaisia tason kanssa. Tämä on erittäin tärkeätä koska suuret polygonit ovat kuitenkin ratkaisevassa asemassa koko mallin visuaalisuuden kannalta Sakotus Tärkeänä parametrinä on myös sakko joka estää sellaisten tasojen valitsemisen joiden läheisyydessä on polygoneja joita taso ei voi esittää. Tämä sen takia että jos yhden valitun tason lähellä on polygoneja joita taso ei voi esittää joutuu joku toinen taso, todennäköisesti huonommasta kohtaa, esittämään ne Diskreetti tasoavaruus Tiheyttä estimoidaan diskreetissä tasoavaruudessa (kuva 1e.). Avaruus jaetaan bineihin, pieniin neliönmuotoisiin laatikoihin, ja jokaiselle binille lasketaan tiheys. Binin tiheys lasketaan summaamalla jokaisen sen sisällä olevan tason tiheysarvot. Bineihin tallennetaan ainoastaan tieto siitä kuinka monta polygonia sen sisällä olevat tasot yhteensä pystyvät esittämään. Tätä diskreettiä tasoavaruutta käytetään suuntaan antavana tasojen valinnan yhteydessä. Jos binissä on suuri määrä valideja polygoneja on sen sisällä tai sen naapureissa yleensä taso joka on validi myös suurelle määrällä näistä polygoneista. 4
6 Kuva 1: Tiheys tasoavaruudessa. (a) Malli josta yhden polygonin verteksit korostettu. (b) Tasot jotka kulkevat verteksien läpi. Tätä tietoa ei käytännössä käytetä mihinkään, c-kohdan kuva on oleellisempi. Jos maksimivirheeksi laitetaan 0 (mitä ei kuitenkaan käytännössä koskaan tehdä) olisi kuva c tämän näköinen. (c) Kelpoisuusalue jokaiselle verteksille (maksimivirheen rajat mukana). Tasot jotka pystyvät esittämään polygonin löytyvät näiden alueiden leikkauspisteistä. (d) Diskreetti kelpoisuusalue koko polygonille. Polygonin kaikki verteksit on oltava korkeintaan maksimivirheen päässä tasosta jotta se kelpaisi. (e) Koko talon peittävyysalue. Lähde: Décoret et al. (2003) 2.3 Ahne optimointi Kun tasoavaruuden tiheys on laskettu, voidaan aloittaa tasojen valitsemisprosessi. Valitaan aina suurimman tiheyden omaava bini ja etsitään sille taso joka pystyy esittämään polygonit jotka ovat valideja kyseiselle binille. Tämä saattaa vaatia adaptiivista korjausta joka selitetään alla. Kun taso löytyy, päivitetään tasoavaruuden tiheyttä poistamalla polygonit jotka olivat valideja juuri valitulle tasolle. Valitaan seuraavaksi taas tihein bini. Kun jokainen polygoni on poistettu ollaan valmiita siirtymään tekstuurigenerointivaiheeseen Adaptiivinen korjaus tasoavaruudessa Jokaisesta binistä on muistissa ainoastaan validien polygonien määrä, ei niiden laatu (tasolle projisoitu pinta-ala). Kun uusi bini valitaan, lasketaan sille validit polygonit ainoastaan niistä jotka ovat jäljellä (niitä poistetaan aina kun binille on lödetty taso). Uusia tasoja valitessa informaation määrä pienenee jokaisella kierroksella. Koska bineissä on ainoastaan tieto validien polygonien määrästä, ei binin jokainen taso välttämättä ole validi binin jokaiselle validille polygonille. Tämän takia joudutaan tarkastelemaan biniä ja sen naapureita tarkemmin jotta tihein taso löytyisi. Biniä jaetaan pienempiin osiin niin kauan että löytyy jaettu bini jonka keskellä oleva taso on validi jaetun binin jokaiselle validille polygonille. Koska bineissä on ainoastaan tieto validien polygonien määrästä, ei tihein taso välttämättä ole kyseisen binin sisällä. Sen takia tarkistetaan kyseinen bini ja sen 26 naapuria. Kun tihein taso löytyy päivitetään binien tiedot (eli poistetaan tasolle valitut polygonit, tai siis niiden vaikutus tasoavaruustiheyteen). 5
7 2.3.2 Tekstuurien laskeminen Jokaiselle tasolle tallennetaan sen valitsemisen yhteydessä tieto polygoneista jotka sen pitää esittää. Tieto ei ole täydellinen koska polygoneja poistetaan aina jokaisen tason valitsemisen yhteydessä. Ensin etsitään pienin nelikulmio jolle kaikki vuorossa olevan tason polygonit saadaan projisoitua, jonka jälkeen tekstuuri generoidaan renderöimällä nämä polygonit tasosta katsottuna ortografista projektiota käyttäen. Normaalit lasketaan myös jokaiselle tekselille (tekstuurin pikseli) jos tarvitaan mahdollisuutta uudelleenvalaistukseen. Polygonit voivat tottakai näkyä monesta tasosta katsottuna, joten looginen ratkaisu on renderöidä ne jokaiseen tasoon johon ne kuuluvat. Tämä estää pahimmat epämääräisyydet tasojen välissä, ja tekee sen että tasot sopivat paremmin yhteen. Tasojen välinen epämääräisyys, jota tällä tekniikalla kuitenkin aina tulee, nähdään kuvasta Tekstuurien optimointi Koska tasoihin projisoidut polygonit voivat tulla aivan eri paikoista, syntyy usein tekstuureja jotka ovat suurimmaksi osaksi tyhjiä. Tämän takia tarvitaan kohta joka rajoittaa projisoituja polygoneja kompaktiksi joukoksi. Kun taso on valittu ja tekstuuri generoitu, käydään tasoa läpi neljään eri suuntaan (45 välein). Kun löytyy väli jossa on paljon tyhjiä pikseleitä, jaetaan taso kahtia, valitaan niistä suurempi ja tehdään rekursiivisesti sama operaatio uudelle tasolle. Kun löytyy taso jossa ei enää ole paljon tyhjiä kohtia valitaan se. Huomioitavaa on että taso ei enää esitä kaikkia polygoneja, ja jonkun muun tason on esitettävä nämä poistuneet polygonit. 3 MENETELMÄN JA IMPLEMENTAATION ARVIOINTI Osiossa käydään läpi menetelmän heikkoudet ja vahvuudet. Ensin tarkastellaan itse BC:n generoimista, jonka jälkeen paneudumme sen renderöimiseen reaaliajassa. Viimeiseksi tarkastelemme vielä tekniikan tulevaisuudennäkymiä. 3.1 Esilaskenta Menetelmässä on panostettu visuaaliseen latuun eikä resurssien optimointia olla harjoitettu. Laskenta-ajat ovat melko lyhyitä (taulukko 1., suuruusluokkaa kymmeniä sekunteja), mutta eivät missään nimessä sovellu reaaliaikaiseen laskentaan. Mielenkiintoinen ominaisuus on myös se ettei alkuperäisen mallin polygonimäärä paljonkaan vaikuta billboardien määrään. Menetelmän tehokkuus on O(kn) missä n on mallin koko ja k billboardien lukumäärä. Tiheyden laskeminen on tehokkuusluokkaa O(n). Tiheyden laskemistehokkuutta voidaan parantaa käyttämällä ainoastaan satunnaista pientä joukkoa polygoneista. Tämä ei välttämättä kovinkaan paljon huononna lopputuloksen laatua koska tiheyttä käytetään ainoastaan suuntaa-antavana tasojen valinnan yhteydessä. Kuvassa 2. esitetään miten maksimivirheen valinta vaikuttaa lopputuloksen tasojen määrään. Logaritmisessa asteikossa olevasta kuvaajasta voidaan todeta että tasojen määrä on suurin piirtein 1/E, jossa E vastaa maksimivirhettä. Kuvissa 3 ja 4 verrataan alkuperäisiä malleja niiden BC:hen. 6
8 Ainoan implementaation (Gregory P. Roth: Billboard Clouds), jonka verkosta löysin, tekijä suhtautuu hieman kriittisemmin tähän menetelmään. Rothin implementaatio kuitenkin eroaa hieman Décoret et al. (2003) artikkelin implementaatiosta. Hänen ohjelmassaan parhaisiin tuloksiin päästiin useasta tuhannesta polygonista koostuvien puiden yhteydessä. Tasojen määräksi Roth sai 24 kappaletta, ja hän piti visuaalista laatua hyvänä. Kaarevat pinnat ovat hänen ohjelmassaan ongelmallisia. Normaalin pallon malli joka koostuu 255 polygonista näyttää epämuodostuneelta joistakin suunnista katsottuna, vaikka tasot sijoittuvatkin symmetrisesti pallon ympärille. Hänen mukaansa ongelma johtuu siitä että menetelmä on riippumaton katsojan suunnasta. Kuva 2: Hinta/Virhe käyrät linnalle, dinosaurukselle ja puulle. X akselilla virheen suuruus (prosenttia BC:tä ympäröivän laatikon koosta) ja y-akselilla tasojen lukumäärä. Vasen käyrä käyttää lineaarista asteikkoa ja oikeanpuoleinen logaritmista. Lähde: Décoret et al. (2003). Taulukko 1: Esilaskenta-ajat kuvien 3 ja 4 tapauksista. Koneena on toiminut 2 GHz Pentium IV jossa NVidian GeForce 4 Ti MB. Lähde: Décoret et al. (2003). 7
9 3.2 Renderöiminen reaaliajassa Koska hyvinkin monimutkaiset mallit saadaan esitettyä pienellä määrällä BC tasoja, voidaan monimutkaisiakin malleja renderöidä reaaliajassa BC:n avulla. Tekniikka soveltuu hyvin kuitenkin ainoastaan kaukaa katsottuihin malleihin. Jos malleja tarkastellaan lähietäisyydeltä, huomataan selkeästi halkeamia tasojen välissä. Tämän voi huomata tarkastelemalla kuvaa 6. Lähietäisyydellä olevat mallit kannattaa edelleen renderöidä muita keinoja käyttäen. Taulukossa 2. esitetään renderöintinopeuksia eri kokoisille BC:ille. Ajat ovat monen renderöintikerran keskiarvoja. Display listoja käytettiin ja tekstuuri kutsuttiin aktiiviseksi ennen jokaisen instanssin piirtoa. Mallin projisoitu leveys oli noin 128 pikseliä. Décoret et al. (2003) artikkelissa todetaan vielä että vapaamuotoiset laskennat näyttävät että 60 tason BC:n renderöiminen, vastaa noin 250 polygonin yksinkertaistetun meshin renderöimistä. Näiden kahden eri asian renderöiminen vaatii kuitenkin erilaisia resursseja. BC:n renderöimistä rajoittaa eniten Fill rate ja Context switching, eikä suurempi määrä tasoja juurikaan huononna nopeutta. Kun käyttää suurta määrää malleja samaan aikaan vähenee yhden mallin renderöintiaika huomattavasti, koska Context switchejä ei tarvita niin paljon. Jos normaalikartta on laskettu voidaan BC valaista reaaliajassa. Yksinkertaisten varjojenkin tekeminen on nopeaa, projisoimalla BC:n tasot esim. lattiatasoon. Tästä on esimerkki kuvassa 5. Tiheän ja sulavasti pyörivän metsän tekeminen tällä tekniikalla on hyvä esimerkki BC:n tehokkuudesta (Gregory P. Roth: Billboard Clouds). Mitä enemmän malleja on, sitä enemmän hyödytään. Esimerkiksi missään tämänhetkisessä tietokonepelissä en ole nähnyt tarpeeksi tiheitä metsiä. Tämän tekniikan avulla voidaan ehkä saada muutos aikaiseksi. Taulukko 2: Renderöintiaikoja eri kokoisille BC:ille. Lähde: Décoret et al. (2003). Kuva 3: Ylempi rivi: Polygonimalli. Alempi rivi: BC. Lähde: Décoret et al. (2003). 8
10 Kuva 4: Vasen: polygonimalli. Oikea: BC. Lähde: Décoret et al. (2003). Kuva 5: Uudelleenvalaistus ja varjot. Lähde: Décoret et al. (2003). Kuva 6: Lähikuva. Vasen: polygonimalli. Oikea: BC. Lähde: Décoret et al. (2003). 9
11 3.3 Tulevaisuus Tulevaisuuden näkymät ovat BC:lle mielestäni kohtalaiset. Peleihin halutaan metsiä joissa on paljon puita, taistelutantereita joissa on tuhansia ajoneuvoja ja kymmeniätuhansia sotilaita. Tekniikka voisi soveltua hyvin esim. ylhäältäpäin kuvattuun peliin jossa malleja ei koskaan tarkastella läheltä. Kun kyseessä on pelaajan silmistä kuvattu peli, voidaan BC:tä käyttää esittämään kaukana olevat monimutkaiset mallit. Ongelmana kuitenkin on, ettei BC:n animointi suju kätevästi. Artikkelin kirjoittajat mainitsevat kuvakulmariippuvaiset BC:t jotka vielä entisestään tulevat yksinkertaistamaan malleja. Tämä tekniikka sopisi mainiosti juuri mainitsemaani ylhäältäpäin kuvattuun massiiviseen sotapeliin. Muita tulevaisuuden tutkimuksen aiheita ovat törmäystarkistus ja pehmeät varjot. 4 YHTEENVETO Tutustuimme BC tekniikkaan, joka pienentää monimutkaisen mallin geometriaa huomattavalla tavalla. Totesimme että tekniikka soveltuu mainiosti staattisten kolmiulotteisten mallien yksinkertaistamiseen, kunhan mallia ei tarkastella lähietäisyydeltä. Huomasimme myös ettei se välttämättä sovellu minkä tahansa mallin esittämiseen, vaan parhaiten se toimii epäyhtenäisten monimutkaisten mallien yhteydessä. Parhaiten tämä tekniikka soveltuisi mielestäni tiheän metsän tekemiseen, tai ylhäältäpäin kuvattuun sotapeliin. 10
12 5 LÄHDELUETTELO Teksti perustuu artikkeliin: Xavier Décoret, Frédo Durand, François X. Sillion, Julie Dorsey: Billboard Clouds for Extreme Model Simplification, ACM Transactions on Graphics 22 (3), 2003, pp Muita lähteitä: 1. Heckbert P, Garland M 1997: Survey of polygonal surface simplification algorithms. Tech. rep. Carnegie Mellon University. 2. Puppo E, Scopigno R 1997: Simplification, lod and multiresolution principles and applications. 3. Luebke D 2001: A developer s survey of polygonal simplification algorithms. IEEE CG&A 21, 3, Kalvin A, Taylor R 1996: Superfaces: Polygonal mesh simplification with bounded error. IEEE CG&A 16, 3, Maciel P, Shirley P 1995: Visual navigation of large environments using textured clusters. In ACM Symp. Interactive 3D graphics. 6. Gregory P. Roth: Billboard Clouds. Saatavissa: 11
Visualisoinnin perusteet
 1 / 12 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Visualisoinnin perusteet Mitä on renderöinti? 2 / 12 3D-mallista voidaan generoida näkymiä tietokoneen avulla. Yleensä perspektiivikuva Valon
1 / 12 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Visualisoinnin perusteet Mitä on renderöinti? 2 / 12 3D-mallista voidaan generoida näkymiä tietokoneen avulla. Yleensä perspektiivikuva Valon
Videon tallentaminen Virtual Mapista
 Videon tallentaminen Virtual Mapista Kamera-ajon tekeminen Karkean kamera ajon teko onnistuu nopeammin Katseluohjelmassa (Navigointi > Näkymät > Tallenna polku). Liikeradan ja nopeuden tarkka hallinta
Videon tallentaminen Virtual Mapista Kamera-ajon tekeminen Karkean kamera ajon teko onnistuu nopeammin Katseluohjelmassa (Navigointi > Näkymät > Tallenna polku). Liikeradan ja nopeuden tarkka hallinta
Luku 6: Grafiikka. 2D-grafiikka 3D-liukuhihna Epäsuora valaistus Laskostuminen Mobiililaitteet Sisätilat Ulkotilat
 2D-grafiikka 3D-liukuhihna Epäsuora valaistus Laskostuminen Mobiililaitteet Sisätilat Ulkotilat 2D-piirto 2-ulotteisen grafiikan piirto perustuu yleensä valmiiden kuvien kopioimiseen näyttömuistiin (blitting)
2D-grafiikka 3D-liukuhihna Epäsuora valaistus Laskostuminen Mobiililaitteet Sisätilat Ulkotilat 2D-piirto 2-ulotteisen grafiikan piirto perustuu yleensä valmiiden kuvien kopioimiseen näyttömuistiin (blitting)
Tampereen yliopisto Tietokonegrafiikka 2013 Tietojenkäsittelytiede Harjoitus
 Tampereen yliopisto Tietokonegrafiikka 201 Tietojenkäsittelytiede Harjoitus 6 1..201 1. Tarkastellaan Gouraudin sävytysmallia. Olkoon annettuna kolmio ABC, missä A = (0,0,0), B = (2,0,0) ja C = (1,2,0)
Tampereen yliopisto Tietokonegrafiikka 201 Tietojenkäsittelytiede Harjoitus 6 1..201 1. Tarkastellaan Gouraudin sävytysmallia. Olkoon annettuna kolmio ABC, missä A = (0,0,0), B = (2,0,0) ja C = (1,2,0)
Yksinkertaistaminen normaalitekstuureiksi
 TEKNILLINEN KORKEAKOULU 30.4.2003 Tietoliikenneohjelmistojen ja multimedian laboratorio Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003: Reaaliaikainen 3D grafiikka Yksinkertaistaminen normaalitekstuureiksi
TEKNILLINEN KORKEAKOULU 30.4.2003 Tietoliikenneohjelmistojen ja multimedian laboratorio Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003: Reaaliaikainen 3D grafiikka Yksinkertaistaminen normaalitekstuureiksi
10. Esitys ja kuvaus
 10. Esitys ja kuvaus Kun kuva on ensin segmentoitu alueisiin edellisen luvun menetelmin, segmentoidut pikselit kootaan esittämään ja kuvaamaan kohteita muodossa, joka sopii hyvin jatkokäsittelyä varten.
10. Esitys ja kuvaus Kun kuva on ensin segmentoitu alueisiin edellisen luvun menetelmin, segmentoidut pikselit kootaan esittämään ja kuvaamaan kohteita muodossa, joka sopii hyvin jatkokäsittelyä varten.
Geometrian yksinkertaistaminen Quadric error metrics -menetelmällä
 TEKNILLINEN KORKEAKOULU 5.5.003 Tietoliikenneohelmistoen a multimedian laboratorio T-.500 Tietokonegrafiikan seminaari Kevät 003: Reaaliaikainen 3d-grafiikka, visualisoinnin tehokkuuden lisääminen Geometrian
TEKNILLINEN KORKEAKOULU 5.5.003 Tietoliikenneohelmistoen a multimedian laboratorio T-.500 Tietokonegrafiikan seminaari Kevät 003: Reaaliaikainen 3d-grafiikka, visualisoinnin tehokkuuden lisääminen Geometrian
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Tampereen yliopisto Tietokonegrafiikka 2013 Tietojenkäsittelytiede Harjoitus
 Tampereen yliopisto Tietokonegrafiikka 2013 Tietojenkäsittelytiede Harjoitus 2 7.2.2013 1. Matematiikan lukiokurssissa on esitetty, että ylöspäin aukeavan paraabelin f(x) = ax 2 +bx+c,a > 0,minimikohtasaadaan,kunf
Tampereen yliopisto Tietokonegrafiikka 2013 Tietojenkäsittelytiede Harjoitus 2 7.2.2013 1. Matematiikan lukiokurssissa on esitetty, että ylöspäin aukeavan paraabelin f(x) = ax 2 +bx+c,a > 0,minimikohtasaadaan,kunf
T-111.4310 Vuorovaikutteinen tietokonegrafiikka Tentti 14.12.2011
 T-111.4310 Vuorovaikutteinen tietokonegrafiikka Tentti 14.12.2011 Vastaa kolmeen tehtävistä 1-4 ja tehtävään 5. 1. Selitä lyhyesti mitä seuraavat termit tarkoittavat tai minkä ongelman algoritmi ratkaisee
T-111.4310 Vuorovaikutteinen tietokonegrafiikka Tentti 14.12.2011 Vastaa kolmeen tehtävistä 1-4 ja tehtävään 5. 1. Selitä lyhyesti mitä seuraavat termit tarkoittavat tai minkä ongelman algoritmi ratkaisee
4. Funktion arvioimisesta eli approksimoimisesta
 4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
4. Funktion arvioimisesta eli approksimoimisesta Vaikka nykyaikaiset laskimet osaavatkin melkein kaiken muun välttämättömän paitsi kahvinkeiton, niin joskus, milloin mistäkin syystä, löytää itsensä tilanteessa,
Digitaalisen arkkitehtuurin alkeet
 1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Digitaalisen arkkitehtuurin alkeet Miten tehdä mallin loppuosat? 2 / 18 Patch on helppo tehdä sisäosille, mutta alueen rajan ja korkeuskäyrien
1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Digitaalisen arkkitehtuurin alkeet Miten tehdä mallin loppuosat? 2 / 18 Patch on helppo tehdä sisäosille, mutta alueen rajan ja korkeuskäyrien
7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen
 1 / 11 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen Kertauslista yleisimmistä komennoista 2 / 11 Kuvan tuominen: PictureFrame Siirtäminen:
1 / 11 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen Kertauslista yleisimmistä komennoista 2 / 11 Kuvan tuominen: PictureFrame Siirtäminen:
Luento 3: 3D katselu. Sisältö
 Tietokonegrafiikan perusteet T-.43 3 op Luento 3: 3D katselu Lauri Savioja Janne Kontkanen /27 3D katselu / Sisältö Kertaus: koordinaattimuunnokset ja homogeeniset koordinaatit Näkymänmuodostus Kameran
Tietokonegrafiikan perusteet T-.43 3 op Luento 3: 3D katselu Lauri Savioja Janne Kontkanen /27 3D katselu / Sisältö Kertaus: koordinaattimuunnokset ja homogeeniset koordinaatit Näkymänmuodostus Kameran
Stabiloivat synkronoijat ja nimeäminen
 Stabiloivat synkronoijat ja nimeäminen Mikko Ajoviita 2.11.2007 Synkronoija Synkronoija on algoritmi, joka muuntaa synkronoidun algoritmin siten, että se voidaan suorittaa synkronoimattomassa järjestelmässä.
Stabiloivat synkronoijat ja nimeäminen Mikko Ajoviita 2.11.2007 Synkronoija Synkronoija on algoritmi, joka muuntaa synkronoidun algoritmin siten, että se voidaan suorittaa synkronoimattomassa järjestelmässä.
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
10.2. Säteenjäljitys ja radiositeettialgoritmi. Säteenjäljitys
 10.2. Säteenjäljitys ja radiositeettialgoritmi Säteenjäljitys Säteenjäljityksessä (T. Whitted 1980) valonsäteiden kulkema reitti etsitään käänteisessä järjestyksessä katsojan silmästä takaisin kuvaan valolähteeseen
10.2. Säteenjäljitys ja radiositeettialgoritmi Säteenjäljitys Säteenjäljityksessä (T. Whitted 1980) valonsäteiden kulkema reitti etsitään käänteisessä järjestyksessä katsojan silmästä takaisin kuvaan valolähteeseen
Algoritmi I kuvioiden ja niille johtavien ajourien erottelu. Metsätehon tuloskalvosarja 7a/2018 LIITE 1 Timo Melkas Kirsi Riekki Metsäteho Oy
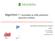 Algoritmi I kuvioiden ja niille johtavien ajourien erottelu Metsätehon tuloskalvosarja 7a/2018 LIITE 1 Timo Melkas Kirsi Riekki Metsäteho Oy Algoritmi I kuvioiden ja niille johtavien ajourien erottelu
Algoritmi I kuvioiden ja niille johtavien ajourien erottelu Metsätehon tuloskalvosarja 7a/2018 LIITE 1 Timo Melkas Kirsi Riekki Metsäteho Oy Algoritmi I kuvioiden ja niille johtavien ajourien erottelu
Luento 6: Geometrinen mallinnus
 Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Geometrinen mallinnus Lauri Savioja, Janne Kontkanen 11/2007 Geometrinen mallinnus / 1 Sisältö Mitä on geometrinen mallinnus tietokonegrafiikassa
Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Geometrinen mallinnus Lauri Savioja, Janne Kontkanen 11/2007 Geometrinen mallinnus / 1 Sisältö Mitä on geometrinen mallinnus tietokonegrafiikassa
Opetusmateriaali. Fermat'n periaatteen esittely
 Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Paretoratkaisujen visualisointi. Optimointiopin seminaari / Kevät 2000 Esitelmä 11 Petteri Kekäläinen 45305L
 Paretoratkaisujen visualisointi Optimointiopin seminaari / Kevät 2000 Esitelmä 11 Petteri Kekäläinen 45305L 1. Johdanto Monitavoiteoptimointitehtävät ovat usein laajuutensa takia vaikeasti hahmotettavia
Paretoratkaisujen visualisointi Optimointiopin seminaari / Kevät 2000 Esitelmä 11 Petteri Kekäläinen 45305L 1. Johdanto Monitavoiteoptimointitehtävät ovat usein laajuutensa takia vaikeasti hahmotettavia
Lauseen erikoistapaus on ollut kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa seuraavassa muodossa:
 Simo K. Kivelä, 13.7.004 Frégier'n lause Toisen asteen käyrillä ellipseillä, paraabeleilla, hyperbeleillä ja niiden erikoistapauksilla on melkoinen määrä yksinkertaisia säännöllisyysominaisuuksia. Eräs
Simo K. Kivelä, 13.7.004 Frégier'n lause Toisen asteen käyrillä ellipseillä, paraabeleilla, hyperbeleillä ja niiden erikoistapauksilla on melkoinen määrä yksinkertaisia säännöllisyysominaisuuksia. Eräs
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
Nspire CAS - koulutus Ohjelmiston käytön alkeet Pekka Vienonen
 Nspire CAS - koulutus Ohjelmiston käytön alkeet 3.12.2014 Pekka Vienonen Ohjelman käynnistys ja käyttöympäristö Käynnistyksen yhteydessä Tervetuloa-ikkunassa on mahdollisuus valita suoraan uudessa asiakirjassa
Nspire CAS - koulutus Ohjelmiston käytön alkeet 3.12.2014 Pekka Vienonen Ohjelman käynnistys ja käyttöympäristö Käynnistyksen yhteydessä Tervetuloa-ikkunassa on mahdollisuus valita suoraan uudessa asiakirjassa
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Laskuharjoitus 9, tehtävä 6
 Aalto-yliopiston perustieteiden korkeakoulu Jouni Pousi Systeemianalyysin laboratorio Mat-2.4129 Systeemien identifiointi Laskuharjoitus 9, tehtävä 6 Tämä ohje sisältää vaihtoehtoisen tavan laskuharjoituksen
Aalto-yliopiston perustieteiden korkeakoulu Jouni Pousi Systeemianalyysin laboratorio Mat-2.4129 Systeemien identifiointi Laskuharjoitus 9, tehtävä 6 Tämä ohje sisältää vaihtoehtoisen tavan laskuharjoituksen
Peilatun kuvion ominaisuudet
 Peilatun kuvion ominaisuudet Piirretään GeoGebralla koordinaatistoon kuvan mukainen nelikulmio Peilataan kuvio x-akselin suhteen origon suhteen. miten pisteiden koordinaatit muuttuvat, kun piste peilataan
Peilatun kuvion ominaisuudet Piirretään GeoGebralla koordinaatistoon kuvan mukainen nelikulmio Peilataan kuvio x-akselin suhteen origon suhteen. miten pisteiden koordinaatit muuttuvat, kun piste peilataan
Satunnaisalgoritmit. Topi Paavilainen. Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
Lineaarinen yhtälöryhmä
 Lineaarinen yhtälöryhmä 1 / 39 Lineaarinen yhtälö Määritelmä 1 Lineaarinen yhtälö on muotoa a 1 x 1 + a 2 x 2 + + a n x n = b, missä a i, b R, i = 1,..., n ovat tunnettuja ja x i R, i = 1,..., n ovat tuntemattomia.
Lineaarinen yhtälöryhmä 1 / 39 Lineaarinen yhtälö Määritelmä 1 Lineaarinen yhtälö on muotoa a 1 x 1 + a 2 x 2 + + a n x n = b, missä a i, b R, i = 1,..., n ovat tunnettuja ja x i R, i = 1,..., n ovat tuntemattomia.
Cloud rendering. Juho Karppinen 49480E
 HELSINKI UNIVERSITY OF TECHNOLOGY 12.5.2003 Telecommunications Software and Multimedia Laboratory Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003 Cloud rendering Juho Karppinen 49480E Cloud rendering
HELSINKI UNIVERSITY OF TECHNOLOGY 12.5.2003 Telecommunications Software and Multimedia Laboratory Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003 Cloud rendering Juho Karppinen 49480E Cloud rendering
3D-mallinnus ja teksturointi tietokonepeleissä
 3D-mallinnus ja teksturointi tietokonepeleissä Markus Palviainen Johdantoa aiheeseen Graafikko sekoitus taiteilijaa ja teknistä tuntijaa Graafikolla oltava visuaalista näkemystä asioihin ja hänen pitäisi
3D-mallinnus ja teksturointi tietokonepeleissä Markus Palviainen Johdantoa aiheeseen Graafikko sekoitus taiteilijaa ja teknistä tuntijaa Graafikolla oltava visuaalista näkemystä asioihin ja hänen pitäisi
MAB3 - Harjoitustehtävien ratkaisut:
 MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
Harjoitus Bones ja Skin
 LIITE 3 1(6) Harjoitus Bones ja Skin Harjoituksessa käsiteltävät asiat: Yksinkertaisen jalan luominen sylinteristä Luurangon luominen ja sen tekeminen toimivaksi raajaksi Luurangon yhdistäminen jalka-objektiin
LIITE 3 1(6) Harjoitus Bones ja Skin Harjoituksessa käsiteltävät asiat: Yksinkertaisen jalan luominen sylinteristä Luurangon luominen ja sen tekeminen toimivaksi raajaksi Luurangon yhdistäminen jalka-objektiin
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Vastaus: Määrittelyehto on x 1 ja nollakohta x = 1.
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
Pintamallintaminen ja maastomallinnus
 1 / 25 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Pintamallintaminen ja maastomallinnus Muistilista uuden ohjelman opetteluun 2 / 25 1. Aloita käyttöliittymään tutustumisesta: Mitä hiiren näppäintä
1 / 25 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Pintamallintaminen ja maastomallinnus Muistilista uuden ohjelman opetteluun 2 / 25 1. Aloita käyttöliittymään tutustumisesta: Mitä hiiren näppäintä
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Topologia Syksy 2010 Harjoitus 4. (1) Keksi funktio f ja suljetut välit A i R 1, i = 1, 2,... siten, että f : R 1 R 1, f Ai on jatkuva jokaisella i N,
 Topologia Syksy 2010 Harjoitus 4 (1) Keksi funktio f ja suljetut välit A i R 1, i = 1, 2,... siten, että f : R 1 R 1, f Ai on jatkuva jokaisella i N, i=1 A i = R 1, ja f : R 1 R 1 ei ole jatkuva. Lause
Topologia Syksy 2010 Harjoitus 4 (1) Keksi funktio f ja suljetut välit A i R 1, i = 1, 2,... siten, että f : R 1 R 1, f Ai on jatkuva jokaisella i N, i=1 A i = R 1, ja f : R 1 R 1 ei ole jatkuva. Lause
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet )
 T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
Tieteellinen laskenta 2 Törmäykset
 Tieteellinen laskenta 2 Törmäykset Aki Kutvonen Op.nmr 013185860 Sisällysluettelo Ohjelman tekninen dokumentti...3 Yleiskuvaus...3 Kääntöohje...3 Ohjelman yleinen rakenne...4 Esimerkkiajo ja käyttöohje...5
Tieteellinen laskenta 2 Törmäykset Aki Kutvonen Op.nmr 013185860 Sisällysluettelo Ohjelman tekninen dokumentti...3 Yleiskuvaus...3 Kääntöohje...3 Ohjelman yleinen rakenne...4 Esimerkkiajo ja käyttöohje...5
Johdatus verkkoteoriaan 4. luento
 Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Kombinatorinen optimointi
 Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Algoritmit 1. Luento 3 Ti Timo Männikkö
 Algoritmit 1 Luento 3 Ti 17.1.2017 Timo Männikkö Luento 3 Algoritmin analysointi Rekursio Lomituslajittelu Aikavaativuus Tietorakenteet Pino Algoritmit 1 Kevät 2017 Luento 3 Ti 17.1.2017 2/27 Algoritmien
Algoritmit 1 Luento 3 Ti 17.1.2017 Timo Männikkö Luento 3 Algoritmin analysointi Rekursio Lomituslajittelu Aikavaativuus Tietorakenteet Pino Algoritmit 1 Kevät 2017 Luento 3 Ti 17.1.2017 2/27 Algoritmien
ARVO - verkkomateriaalien arviointiin
 ARVO - verkkomateriaalien arviointiin Arvioitava kohde: Jenni Rikala: Aloittavan yrityksen suunnittelu, Arvioija: Heli Viinikainen, Arviointipäivämäärä: 12.3.2010 Osa-alue 1/8: Informaation esitystapa
ARVO - verkkomateriaalien arviointiin Arvioitava kohde: Jenni Rikala: Aloittavan yrityksen suunnittelu, Arvioija: Heli Viinikainen, Arviointipäivämäärä: 12.3.2010 Osa-alue 1/8: Informaation esitystapa
811312A Tietorakenteet ja algoritmit, , Harjoitus 3, Ratkaisu
 811312A Tietorakenteet ja algoritmit, 2018-2019, Harjoitus 3, Ratkaisu Harjoituksessa käsitellään algoritmien aikakompleksisuutta. Tehtävä 3.1 Kuvitteelliset algoritmit A ja B lajittelevat syötteenään
811312A Tietorakenteet ja algoritmit, 2018-2019, Harjoitus 3, Ratkaisu Harjoituksessa käsitellään algoritmien aikakompleksisuutta. Tehtävä 3.1 Kuvitteelliset algoritmit A ja B lajittelevat syötteenään
Sami Hirvonen. Ulkoasut Media Works sivustolle
 Metropolia ammattikorkeakoulu Mediatekniikan koulutusohjelma VBP07S Sami Hirvonen Ulkoasut Media Works sivustolle Loppuraportti 14.10.2010 Visuaalinen suunnittelu 2 Sisällys 1 Johdanto 3 2 Oppimisteknologiat
Metropolia ammattikorkeakoulu Mediatekniikan koulutusohjelma VBP07S Sami Hirvonen Ulkoasut Media Works sivustolle Loppuraportti 14.10.2010 Visuaalinen suunnittelu 2 Sisällys 1 Johdanto 3 2 Oppimisteknologiat
58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen)
 58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen) 1. Avaimet 1, 2, 3 ja 4 mahtuvat samaan lehtisolmuun. Tässä tapauksessa puussa on vain yksi solmu, joka on samaan aikaan juurisolmu
58131 Tietorakenteet (kevät 2009) Harjoitus 6, ratkaisuja (Antti Laaksonen) 1. Avaimet 1, 2, 3 ja 4 mahtuvat samaan lehtisolmuun. Tässä tapauksessa puussa on vain yksi solmu, joka on samaan aikaan juurisolmu
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Numeeriset menetelmät Pekka Vienonen
 Numeeriset menetelmät Pekka Vienonen 1. Funktion nollakohta Newtonin menetelmällä 2. Määrätty integraali puolisuunnikassäännöllä 3. Määrätty integraali Simpsonin menetelmällä Newtonin menetelmä Newtonin
Numeeriset menetelmät Pekka Vienonen 1. Funktion nollakohta Newtonin menetelmällä 2. Määrätty integraali puolisuunnikassäännöllä 3. Määrätty integraali Simpsonin menetelmällä Newtonin menetelmä Newtonin
STL:n luonti IronCADillä
 STL:n luonti IronCADillä STL-tiedoston luonti IronCADilla etenee seuraavasti: 1. Avataan haluttu kappale IronCADilla. 2. Kappaletta napsautetaan hiiren oikealla näppäimellä ja valitse pudotusvalikosta
STL:n luonti IronCADillä STL-tiedoston luonti IronCADilla etenee seuraavasti: 1. Avataan haluttu kappale IronCADilla. 2. Kappaletta napsautetaan hiiren oikealla näppäimellä ja valitse pudotusvalikosta
Geometrian yksinkertaistaminen: Progressive Meshes
 TEKNILLINEN KORKEAKOULU, HELSINKI 29.4.2003 Tietoliikenneohjelmistojen ja multimedian laboratorio Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003: Reaaliaikaisen 3D grafiikan laadun ja nopeuden parantaminen
TEKNILLINEN KORKEAKOULU, HELSINKI 29.4.2003 Tietoliikenneohjelmistojen ja multimedian laboratorio Tik-111.500 Tietokonegrafiikan seminaari Kevät 2003: Reaaliaikaisen 3D grafiikan laadun ja nopeuden parantaminen
Matematiikan tukikurssi: kurssikerta 10
 Matematiikan tukikurssi: kurssikerta 10 1 Newtonin menetelmä Oletetaan, että haluamme löytää funktion f(x) nollakohan. Usein tämä tehtävä on mahoton suorittaa täyellisellä tarkkuuella, koska tiettyjen
Matematiikan tukikurssi: kurssikerta 10 1 Newtonin menetelmä Oletetaan, että haluamme löytää funktion f(x) nollakohan. Usein tämä tehtävä on mahoton suorittaa täyellisellä tarkkuuella, koska tiettyjen
ja λ 2 = 2x 1r 0 x 2 + 2x 1r 0 x 2
 Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
Videon tallentaminen Virtual Mapista
 Videon tallentaminen Virtual Mapista Kamera-ajon tekeminen Karkean kamera ajon teko onnistuu nopeimmin Katseluohjelmassa (Navigointi > Näkymät > Tallenna polku). Liikeradan ja nopeuden tarkka hallinta
Videon tallentaminen Virtual Mapista Kamera-ajon tekeminen Karkean kamera ajon teko onnistuu nopeimmin Katseluohjelmassa (Navigointi > Näkymät > Tallenna polku). Liikeradan ja nopeuden tarkka hallinta
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Teoriatausta. Mallinnuksen vaiheet. CAD työkalut harjoituksessa. Uppokipinätyöstön elektrodi
 Uppokipinätyöstön elektrodi Tuula Höök, Tampereen teknillinen yliopisto Teoriatausta Muotin perusrakenne Uppokipinätyöstö Kipinätyöstön elektrodit Muottipesän valmistettavuus CAD työkalut harjoituksessa
Uppokipinätyöstön elektrodi Tuula Höök, Tampereen teknillinen yliopisto Teoriatausta Muotin perusrakenne Uppokipinätyöstö Kipinätyöstön elektrodit Muottipesän valmistettavuus CAD työkalut harjoituksessa
jakokulmassa x 4 x 8 x 3x
 Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
1. Lineaarinen optimointi
 0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
2.2. Kohteiden konstruktiivinen avaruusgeometrinen esitys
 .. Kohteiden konstruktiivinen avaruusgeometrinen esitys Avaruusgeometrinen esitys on käyttäjäriippuvainen ja vaati erikoismenetelmiä tai lopuksi konversion monikulmiomalliksi. Se on korkean tason esitys
.. Kohteiden konstruktiivinen avaruusgeometrinen esitys Avaruusgeometrinen esitys on käyttäjäriippuvainen ja vaati erikoismenetelmiä tai lopuksi konversion monikulmiomalliksi. Se on korkean tason esitys
Luento 10: Näkyvyystarkastelut ja varjot. Sisältö
 Tietokonegrafiikka / perusteet T-111.300/301 4 ov / 2 ov Luento 10: Näkyvyystarkastelut ja varjot Marko Myllymaa / Lauri Savioja 10/04 Näkyvyystarkastelut ja varjot / 1 Näkyvyystarkastelu Solurenderöinti
Tietokonegrafiikka / perusteet T-111.300/301 4 ov / 2 ov Luento 10: Näkyvyystarkastelut ja varjot Marko Myllymaa / Lauri Savioja 10/04 Näkyvyystarkastelut ja varjot / 1 Näkyvyystarkastelu Solurenderöinti
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 30.4.2019 Timo Männikkö Luento 13 Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Ositus ja rekursio Rekursion toteutus Algoritmit 2 Kevät 2019 Luento 13 Ti 30.4.2019
Algoritmit 2 Luento 13 Ti 30.4.2019 Timo Männikkö Luento 13 Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Ositus ja rekursio Rekursion toteutus Algoritmit 2 Kevät 2019 Luento 13 Ti 30.4.2019
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 varuusintegraali iemmin laskimme yksiulotteisia integraaleja b a f (x)dx, jossa integrointialue on x-akselin väli [a, b]. Lisäksi laskimme kaksiulotteisia integraaleja
Matematiikan tukikurssi Kurssikerta 6 varuusintegraali iemmin laskimme yksiulotteisia integraaleja b a f (x)dx, jossa integrointialue on x-akselin väli [a, b]. Lisäksi laskimme kaksiulotteisia integraaleja
x 5 15 x 25 10x 40 11x x y 36 y sijoitus jompaankumpaan yhtälöön : b)
 MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
MAA4 ratkaisut. 5 a) Itseisarvon vastauksen pitää olla aina positiivinen, joten määritelty kun 5 0 5 5 tai ( ) 5 5 5 5 0 5 5 5 5 0 5 5 0 0 9 5 9 40 5 5 5 5 0 40 5 Jälkimmäinen vastaus ei toimi määrittelyjoukon
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
Algoritmit 2. Luento 6 To Timo Männikkö
 Algoritmit 2 Luento 6 To 28.3.2019 Timo Männikkö Luento 6 B-puun operaatiot Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2019 Luento 6 To 28.3.2019 2/30 B-puu 40 60 80 130 90 100
Algoritmit 2 Luento 6 To 28.3.2019 Timo Männikkö Luento 6 B-puun operaatiot Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2019 Luento 6 To 28.3.2019 2/30 B-puu 40 60 80 130 90 100
Määrittelydokumentti
 Määrittelydokumentti Aineopintojen harjoitustyö: Tietorakenteet ja algoritmit (alkukesä) Sami Korhonen 014021868 sami.korhonen@helsinki. Tietojenkäsittelytieteen laitos Helsingin yliopisto 23. kesäkuuta
Määrittelydokumentti Aineopintojen harjoitustyö: Tietorakenteet ja algoritmit (alkukesä) Sami Korhonen 014021868 sami.korhonen@helsinki. Tietojenkäsittelytieteen laitos Helsingin yliopisto 23. kesäkuuta
Algoritmit 2. Luento 7 Ti Timo Männikkö
 Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
1 Funktiot, suurin (max), pienin (min) ja keskiarvo
 1 Funktiot, suurin (max), pienin (min) ja keskiarvo 1. Avaa uusi työkirja 2. Tallenna työkirja nimellä perusfunktiot. 3. Kirjoita seuraava taulukko 4. Muista taulukon kirjoitusjärjestys - Ensin kirjoitetaan
1 Funktiot, suurin (max), pienin (min) ja keskiarvo 1. Avaa uusi työkirja 2. Tallenna työkirja nimellä perusfunktiot. 3. Kirjoita seuraava taulukko 4. Muista taulukon kirjoitusjärjestys - Ensin kirjoitetaan
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
GEOMETRIA MAA3 Geometrian perusobjekteja ja suureita
 GEOMETRI M3 Geometrian perusobjekteja ja suureita Piste ja suora: Piste, suora ja taso ovat geometrian peruskäsitteitä, joita ei määritellä. Voidaan ajatella, että kaikki geometriset kuviot koostuvat pisteistä.
GEOMETRI M3 Geometrian perusobjekteja ja suureita Piste ja suora: Piste, suora ja taso ovat geometrian peruskäsitteitä, joita ei määritellä. Voidaan ajatella, että kaikki geometriset kuviot koostuvat pisteistä.
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
Mb8 Koe Kuopion Lyseon lukio (KK) sivu 1/2
 Mb8 Koe 0.11.015 Kuopion Lyseon lukio (KK) sivu 1/ Kokeessa on kaksi osaa. Osa A ratkaistaan tehtäväpaperille ja osa B ratkaistaan konseptipaperille. Osa A: saat käyttää taulukkokirjaa mutta et laskinta.
Mb8 Koe 0.11.015 Kuopion Lyseon lukio (KK) sivu 1/ Kokeessa on kaksi osaa. Osa A ratkaistaan tehtäväpaperille ja osa B ratkaistaan konseptipaperille. Osa A: saat käyttää taulukkokirjaa mutta et laskinta.
Viimeistely Ajourien huomiointi puutiedoissa ja lopullinen kuviointi. Metsätehon tuloskalvosarja 5/2018 LIITE 4 Timo Melkas Kirsi Riekki Metsäteho Oy
 Viimeistely Ajourien huomiointi puutiedoissa ja lopullinen kuviointi Metsätehon tuloskalvosarja 5/2018 LIITE 4 Timo Melkas Kirsi Riekki Metsäteho Oy Viimeistely ajourien huomiointi ja lopullinen kuviointi
Viimeistely Ajourien huomiointi puutiedoissa ja lopullinen kuviointi Metsätehon tuloskalvosarja 5/2018 LIITE 4 Timo Melkas Kirsi Riekki Metsäteho Oy Viimeistely ajourien huomiointi ja lopullinen kuviointi
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
TIES592 Monitavoiteoptimointi ja teollisten prosessien hallinta. Yliassistentti Jussi Hakanen syksy 2010
 TIES592 Monitavoiteoptimointi ja teollisten prosessien hallinta Yliassistentti Jussi Hakanen jussi.hakanen@jyu.fi syksy 2010 Optimaalisuus: objektiavaruus f 2 min Z = f(s) Parhaat arvot alhaalla ja vasemmalla
TIES592 Monitavoiteoptimointi ja teollisten prosessien hallinta Yliassistentti Jussi Hakanen jussi.hakanen@jyu.fi syksy 2010 Optimaalisuus: objektiavaruus f 2 min Z = f(s) Parhaat arvot alhaalla ja vasemmalla
Numeeriset menetelmät
 Numeeriset menetelmät Luento 11 Ti 11.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 11 Ti 11.10.2011 p. 1/34 p. 1/34 Automaattiset integrointialgoritmit Numeerisen integroinnin tarkkuuteen
Numeeriset menetelmät Luento 11 Ti 11.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 11 Ti 11.10.2011 p. 1/34 p. 1/34 Automaattiset integrointialgoritmit Numeerisen integroinnin tarkkuuteen
Kanta ja Kannan-vaihto
 ja Kannan-vaihto 1 Olkoon L vektoriavaruus. Äärellinen joukko L:n vektoreita V = { v 1, v 2,..., v n } on kanta, jos (1) Jokainen L:n vektori voidaan lausua v-vektoreiden lineaarikombinaationa. (Ts. Span(V
ja Kannan-vaihto 1 Olkoon L vektoriavaruus. Äärellinen joukko L:n vektoreita V = { v 1, v 2,..., v n } on kanta, jos (1) Jokainen L:n vektori voidaan lausua v-vektoreiden lineaarikombinaationa. (Ts. Span(V
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
GeoGebran 3D paketti
 GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
Algoritmit 1. Luento 10 Ke Timo Männikkö
 Algoritmit 1 Luento 10 Ke 14.2.2018 Timo Männikkö Luento 10 Algoritminen ongelmanratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Lisäyslajittelu Valintalajittelu Permutaatiot
Algoritmit 1 Luento 10 Ke 14.2.2018 Timo Männikkö Luento 10 Algoritminen ongelmanratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Lisäyslajittelu Valintalajittelu Permutaatiot
Kuva maailmasta Pakettiverkot (Luento 1)
 M.Sc.(Tech.) Marko Luoma (1/20) M.Sc.(Tech.) Marko Luoma (2/20) Kuva maailmasta Pakettiverkot (Luento 1) WAN Marko Luoma TKK Teletekniikan laboratorio LAN M.Sc.(Tech.) Marko Luoma (3/20) M.Sc.(Tech.) Marko
M.Sc.(Tech.) Marko Luoma (1/20) M.Sc.(Tech.) Marko Luoma (2/20) Kuva maailmasta Pakettiverkot (Luento 1) WAN Marko Luoma TKK Teletekniikan laboratorio LAN M.Sc.(Tech.) Marko Luoma (3/20) M.Sc.(Tech.) Marko
Trafficars - Ruuhkaara
 760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
Tilanhallintatekniikat
 Tilanhallintatekniikat 3D grafiikkamoottoreissa Moottori on projektin osa joka vastaa tiettyjen toiminnallisuuksien hallinnasta hallitsee kaikki vastuualueen datat suorittaa kaikki tehtäväalueen toiminnot
Tilanhallintatekniikat 3D grafiikkamoottoreissa Moottori on projektin osa joka vastaa tiettyjen toiminnallisuuksien hallinnasta hallitsee kaikki vastuualueen datat suorittaa kaikki tehtäväalueen toiminnot
Verkon värittämistä hajautetuilla algoritmeilla
 Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Luento 6: Tulostusprimitiivien toteutus
 Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Tulostusprimitiivien toteutus Lauri Savioja 11/07 Primitiivien toteutus / 1 ntialiasointi Fill-algoritmit Point-in-polygon Sisältö Primitiivien toteutus
Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Tulostusprimitiivien toteutus Lauri Savioja 11/07 Primitiivien toteutus / 1 ntialiasointi Fill-algoritmit Point-in-polygon Sisältö Primitiivien toteutus
TEEMU ROOS (KALVOT MUOKATTU PATRIK HOYERIN LUENTOMATERIAALISTA)
 JOHDATUS TEKOÄLYYN TEEMU ROOS (KALVOT MUOKATTU PATRIK HOYERIN LUENTOMATERIAALISTA) KONEOPPIMISEN LAJIT OHJATTU OPPIMINEN: - ESIMERKIT OVAT PAREJA (X, Y), TAVOITTEENA ON OPPIA ENNUSTAMAAN Y ANNETTUNA X.
JOHDATUS TEKOÄLYYN TEEMU ROOS (KALVOT MUOKATTU PATRIK HOYERIN LUENTOMATERIAALISTA) KONEOPPIMISEN LAJIT OHJATTU OPPIMINEN: - ESIMERKIT OVAT PAREJA (X, Y), TAVOITTEENA ON OPPIA ENNUSTAMAAN Y ANNETTUNA X.
Demo 1: Simplex-menetelmä
 MS-C2105 Optimoinnin perusteet Malliratkaisut 3 Ehtamo Demo 1: Simplex-menetelmä Muodosta lineaarisen tehtävän standardimuoto ja ratkaise tehtävä taulukkomuotoisella Simplex-algoritmilla. max 5x 1 + 4x
MS-C2105 Optimoinnin perusteet Malliratkaisut 3 Ehtamo Demo 1: Simplex-menetelmä Muodosta lineaarisen tehtävän standardimuoto ja ratkaise tehtävä taulukkomuotoisella Simplex-algoritmilla. max 5x 1 + 4x
Luento 6: Piilopinnat ja Näkyvyys
 Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Piilopinnat ja Näkyvyys Janne Kontkanen Geometrinen mallinnus / 1 Johdanto Piilopintojen poisto-ongelma Syntyy kuvattaessa 3-ulotteista maailmaa 2-ulotteisella
Tietokonegrafiikan perusteet T-111.4300 3 op Luento 6: Piilopinnat ja Näkyvyys Janne Kontkanen Geometrinen mallinnus / 1 Johdanto Piilopintojen poisto-ongelma Syntyy kuvattaessa 3-ulotteista maailmaa 2-ulotteisella
PRELIMINÄÄRIKOE. Lyhyt Matematiikka 3.2.2015
 PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
PRELIMINÄÄRIKOE Lyhyt Matematiikka..015 Vastaa enintään kymmeneen tehtävään. Kaikki tehtävät arvostellaan asteikolla 0-6 pistettä. 1. a) Sievennä x( x ) ( x x). b) Ratkaise yhtälö 5( x 4) 5 ( x 4). 1 c)
4 Tehokkuus ja algoritmien suunnittelu
 TIE-20100 Tietorakenteet ja algoritmit 52 4 Tehokkuus ja algoritmien suunnittelu Tässä luvussa pohditaan tehokkuuden käsitettä ja esitellään kurssilla käytetty kertaluokkanotaatio, jolla kuvataan algoritmin
TIE-20100 Tietorakenteet ja algoritmit 52 4 Tehokkuus ja algoritmien suunnittelu Tässä luvussa pohditaan tehokkuuden käsitettä ja esitellään kurssilla käytetty kertaluokkanotaatio, jolla kuvataan algoritmin
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Hannu Mäkiö. kertolasku * jakolasku / potenssiin korotus ^ Syöte Geogebran vastaus
 Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
Perusohjeita, symbolista laskentaa Geogebralla Kielen vaihtaminen. Jos Geogebrasi kieli on vielä englanti, niin muuta se Options välilehdestä kohdasta Language suomeksi (finnish). Esittelen tässä muutaman
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
Tehtävä 3 ja 4. 3. aikakausilehden kansi pastissi 4. runokirjan kansi
 Tehtävä 3 ja 4 3. aikakausilehden kansi pastissi 4. runokirjan kansi 3. Valitse esim. Opettaja-lehti ja tee sille uusi kansi lehden tyyliin samoilla fonteilla ym. (ohje sille), NYT-liite, tms. käy myös
Tehtävä 3 ja 4 3. aikakausilehden kansi pastissi 4. runokirjan kansi 3. Valitse esim. Opettaja-lehti ja tee sille uusi kansi lehden tyyliin samoilla fonteilla ym. (ohje sille), NYT-liite, tms. käy myös
