Kohti yleistä suhteellisuusteoriaa
|
|
|
- Jalmari Sipilä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Kohti yleistä suhteellisuusteoriaa Miksi vakionopeudella liikkuvat koordinaatistot ovat erityisasemassa (eli miksi Lorentz-muunnos tehdään samalla tavalla joka paikassa aika-avaruudessa)? Newtonin gravitaatiolaki ei ole Lorentz-kovariantti. Miten se pitäisi yleistää? 1
2 Yleinen suhteellisuusteoria Suppea suhteellisuusteoria on rakennettu siten, että se on yhteensopiva klassisen sähkömagnetismin lakien (Maxwellin yhtälöiden ja sähkömagneettisen voiman) kanssa. Klassisen fysiikan toinen perustavanlaatuinen vuorovaikutus on gravitaatio. Miten se sopii yhteen suppean suhteellisuusteorian kanssa? Osoittautuu, että vastaus tähän kysymykseen selvittää myös sen, miksi suppean suhteellisuusteorian avaruus on homogeeninen (eli Lorentz-muunnoksen kertoimet ovat samat kaikkialla). Yleinen suhteellisuusteoria on suppean suhteellisuusteorian ja gravitaation yhdistävä teoria. (Yleinen suhteellisuusteoria kuvaa aika-avaruuden yleistä rakennetta, ja silloin kun gravitaatio jätetään huomiotta, se surkastuu suppeaksi suhteellisuusteoriaksi.) 2
3 Newtonin gravitaatiolaki Newtonin gravitaatiolaki ei ole yhteensopiva suppean suhteellisuusteorian kanssa. Se on Galilei-kovariantti, ei Lorentzkovariantti. F 12 =!G N m 1 m 2 x 1! x 2 x 1! x 2 3 Mikä olisi sen yleistys suppeaan suhteellisuusteoriaan? Pitäisikö löytää sopiva nelivektori, joka kuvaa gravitaatiota? Newtonin gravitaatiovoiman (toisin kuin Maxwellin sähkömagnetismin) kohdalla informaatio välittyy äärettömällä nopeudella. Vastaavasti gravitaatioaaltoja ei Newtonin teoriassa ole olemassa. Mikä välittää gravitaatiota? Kuvataan gravitaatiota kentällä, sähkömagnetismin tapaan. 3
4 Klassinen gravitaatiokenttä Otetaan käyttöön gravitaatiopotentiaali φ. Tarkastellaan paikassa x 2 sijaitsevan kappaleen, jonka massa on M, aiheuttamaa voimaa kappaleeseen, joka on paikassa x ja jonka massa on m G. Myös Newtonin 2. laissa esiintyy massa, merkitään sitä symbolilla m I (inertiaalimassa eli hitausmassa). Gravitaatiomassalla m G ja hitausmassalla m I ei tarvitsisi olla mitään tekemistä toistensa kanssa. Ne kuitenkin ovat samat suurella tarkkuudella. G m G =!"!! =!G N M 1 x! x 2 #% G =!m G "! $ &% F = m I!!x '!!x =! m G m I "! 4
5 Massojen yhteneväisyys F = mia hitausmassa, inertiaalinen massa F =! G NM G m G r 2 e r painava massa TESTS OF THE WEAK EQUIVALENCE PRINCIPLE Havaintojen mukaan Eötvös Renner Free-fall m G! m I m I << Princeton Moscow Boulder Eöt-Wash LLR Fifth-force searches Eöt-Wash = a 1 -a 2 (a 1 +a 2 )/ YEAR OF EXPERIMENT 5
6 Kaikki putoaa yhtä lailla Gravitaatiomassan ja hitausmassan yhtäsuuruudesta seuraa se, että kaikki kappaleet putoavat samalla tavalla gravitaatiokentässä. (Vrt. kappaleet eivät liiku samalla tavalla sähkökentässä, liike riippuu sähkövarauksesta.) Joskus tätä nimitetään ekvivalenssiperiaatteeksi tai heikoksi ekvivalenssiperiaatteeksi. (Selitys termille tulee myöhemmin.) #% G =!m G "! $ &% F = m I!!x '!!x =! m G m I "! 6
7 Poissonin yhtälö Newtonin gravitaatiolain voi kirjoittaa yhtälönä gravitaatiopotentiaalin ja massatiheyden välillä. Tämä yhtälö on nimeltään Poissonin yhtälö.! 2! = 4"G N # m # m = dm dv Poissonin yhtälö ei ole Lorentz-kovariantti. Miten sen voisi yleistää Lorentz-kovariantiksi? 7
8 Nordströmin gravitaatioteoria Ensimmäinen yritys yhdistää gravitaatiota ja suppeaa suhteellisuusteoria oli suomalaisen Gunnar Nordströmin käsialaa. Nordström esitti vuonna 1912 seuraavan yleistyksen Poissonin yhtälölle:! 2! " 1 c 2 # 2! #t 2 = 4"G N# m (Lisäksi pitää yleistää gravitaatiovoiman määritelmä.) Tämä yhtälö ei kuitenkaan ole Lorentz-kovariantti, koska tiheys ei ole invariantti Lorentz-muunnoksessa (tilavuus kutistuu). Nordström kehitti uuden teorian vuonna 1913, mutta se ei osoittautunut oikeaksi. 8
9 Gravitaatio aika-avaruuden kaarevuutena Einstein esitti vuonna 1915 yleisen suhteellisuusteorian. Se on käsitteellisesti hyvin erilainen kuin Nordströmin teoria. Gravitaation kuvaamiseksi ei oteta mukaan uutta voimaa aika-avaruudessa, vaan muutetaan aika-avaruuden rakennetta. Suppea suhteellisuusteoria yhdisti ajan ja avaruuden, yleinen suhteellisuusteoria tekee aika-avaruudesta dynaamisen. Yleisen suhteellisuusteorian mukaan: Aika ja avaruus eivät ole muuttumattomia, vaan muodostavat dynaamisen kokonaisuuden, jonka paikallinen muoto (kaareutuminen) määräytyy ainesisällöstä. Aineen ominaisuudet määräävät, miten aika-avaruus kaartuu. Aika-avaruus määrää, miten aine liikkuu. 9
10 SUPPEA SUHTEELLISUUSTEORIA ds 2 =! "# dx " dx # = c 2 dt 2! dx 2! dy 2! dz 2 Muuttumaton, tasainen aika-avaruus (Minkowskin avaruus) YLEINEN SUHTEELLISUUSTEORIA 3 ds 2 =! g!" (t, x) dx! dx " " g!" dx! dx "!,"=0 = g 00 dx 0 dx 0 + g 01 dx 0 dx g 33 dx 3 dx 3 Dynaaminen, kaareva aika-avaruus g ( t, x) αβ Metriikka on tensori eli 4 4 matriisi. Tuntematon suure, joka pitää ratkaista liikeyhtälöistä. g ( t, x) g ( t, x) metriikka on symmetrinen αβ = βα 10 tuntematonta funktiota 10
11 MITEN NIIN KAAREVA? 2D analogia s = t 2,x 2! ds =! g!" dx! dx " t 1,x 1 t 2,x 2 t 1,x 1 t 1,x 1 t 2,x 2 Neliulotteisen aika-avaruuden aika- ja avaruusvälit riippuvat paikasta ja ajasta, koska avaruus on kaareva. Kaarevuus määräytyy ainesisällöstä. Ei ole ylimääräistä ulottuvuutta, jossa kaareutuminen tapahtuisi. 11
12 Suoraviivainen liike kaarevassa avaruudessa näyttää käyrältä suoraviivaisissa koordinaateissa. suora viiva Paikallisesti Minkowski suppea suhteellisuusteoria voimassa paikallisesti 12
13 MITKÄ OVAT HYVÄKSYTTÄVIÄ KOORDINAATISTOJA? kaikki! YLEINEN SUHTEELLISUUSPERIAATE: Kaikki matemaattisesti säännölliset koordinaatistot ovat yhdenvertaisia. Suppea suhteellisuusteoria: fysiikka sama kaikissa inertiaalikoordinaatistoissa x α x α = L α β (v) xβ Lorentz-muunnos Yleinen suhteellisuusteoria: fysiikka sama kaikissa koordinaatistoissa x α x α = M α β (xγ ) x β yleinen koordinaattimuunnos 13
14 MIKÄ MÄÄRÄÄ METRIIKAN? liikeyhtälöt = Einsteinin yhtälö on muotoa GEOMETRIA [g!" ] = AINE [E, p, ] MITEN LÖYDETÄÄN TÄMÄ YHTÄLÖ? 14
15 ! " g!" # 2! " G!" # m " T!" Einsteinin tensori metriikan ja sen kahden ensimmäisen derivaatan funktio energia-impulssitensori riippuu aineen ominaisuuksista G!" = 8#G N c 4 T!" Einsteinin yhtälö: 2. kertaluvun differentiaaliyhtälö metriikan komponenteille g αβ tunnetaan kun aine tunnetaan 10 yhtälöä ratkaistaan metriikka g αβ (t,x) kun aine T αβ (t,x) on annettu AINE MÄÄRÄÄ AIKA-AVARUUDEN GEOMETRIAN 15
16 Heikko kenttä ja hidas liike Yleisen suhteellisuusteorian approksimaationa saadaan Newtonin gravitaatioteoria kun gravitaatiokenttä on heikko ja liikkeet ovat hitaita. Aika-avaruus on silloin Minkowskin avaruus plus pieni häiriö. ds 2 = ( 1+ 2! )c 2 dt 2! (! ij! 2"! ij! h ij )dx i dy j = (! "# + 2$% "# + h "# )dx " dx # (h 00 = h 0i = 0, " h ii = 0) 3 i=1 " T!" = diag $ #,! P c,! P 2 c,! P # 2 c 2 % ' ( diag # m, 0, 0, 0 & ( ) (v << c) 16
17 ! 2! = 4"G N c 2 # m $! 2 " 1 # 2 ' & )h % c 2 #t 2 ij = 0 (! " =!c 2 Newtonin gravitaatio Gravitaatioaallot Saadaan Newtonin laki plus aaltoyhtälö: Newtonin gravitaatiopotentiaali vastaa pientä häiriötä aika-avaruuden etäisyyksissä. Yleisessä suhteellisuusteoriassa on lisäksi gravitaatioaaltoja, joiden nopeus on valonnopeus. 17
18 Korjauksia planeettojen ratoihin Merkuriuksen radan perihelin prekessio Perihelin kiertymä poikkeaa vuodessa klassisen mekaniikan ennusteesta, kun kaikkien planeettojen vaikutus on huomioitu. Etäisyyden muutos on 29 km 46 miljoonasta kilometristä. Määrä (kaarisekuntia/100 v) Syy maapallon koordinaatiston kiertyminen toisten planeettojen vaikutus Auringon litteys ±0.04 yleisen suhteellisuusteorian korjaus yhteensä havaittu 18
19 Pioneer-anomalia: ei ongelma suhteellisuusteorialle Luotaimet Pioneer 10 ja 11 Laukaistu 1972 ja 1973 tutkimaan Jupiteria ja Saturnusta. Siistein mittaus liikkeistä aurinkokunnassa. Luotaimilla ylimääräinen kiihtyvyys (8.74 ± 1.33)x10-10 m/s 2 kohti Aurinkoa etäisyyksillä au. Selittyy luotaimien lämpösäteilyllä. 19
20 Valon suora kulku aika-avaruudessa Valo matkaa aika-avaruudessa suoraa viivaa (eli geodeettia) joka on valonkaltainen, eli etäisyys aika-avaruudessa on nolla. Minkowskin avaruus: ds 2 =! "# dx " dx # = c 2 dt 2! dx 2! dy 2! dz 2 = 0 " x = ±ct Yleinen aika-avaruus: ds 2 = g!" dx! dx " = 0 Suoraviivaisuus tarkoittaa suoraa liikettä kaarevassa avaruudessa. On tärkeää tuntea valon kulku, sillä lähes kaikki havainnot maapallon ulkopuolisesta maailmankaikkeudesta tehdään valon (sähkömagneettisen säteilyn) avulla. 20
21 Valon taipuminen avaruudessa δ Ennuste valon taipumiskulmalle: havaittu paikka ds 2 = ( 1+ 2! )c 2 dt 2! ( 1! 2! )! ij dx i dy j = 0 törmäysparametri b M! = 4G N M bc 2! 2r s b = 2 Newtonin teorian ennuste 21
22 AURINGONPIMENNYS 1919 Sobral, Brasilia Principe (Afrikka), Arthur Eddington Einsteinin ennuste Nordströmin ennuste Newtonin ennuste! =1.75"! = 0"! = 0.87" pilvistä! 16 kuvaa, 2 onnistui, 5 tähteä näkyvissä (kalibraatio: vaaditaan 7) Sobral δ δ keskim 8 hyvää huonoa Principe δ δ keskim 2 huonoa Eddington: valo taipuu! 22
23 Nykyaika: THE PARAMETER (1+ )/ Optical Radio DEFLECTION OF LIGHT VLBI 2X (1+ )/ SHAPIRO TIME DELAY Hipparcos PSR Voyager yleinen suhteellisuusteoria Viking Cassini (1X10-5 ) YEAR OF EXPERIMENT 23
24 GRAVITAATIOLINSSI Einsteinin rengas 24
25 Vahva gravitaatiolinssi: useita kuvia 25
26 26
27 Heikko gravitaatiolinssi: kuvan muutos (E. Grocutt, IfA, Edinburgh) 27
28 Hubble Ultra Deep Field 28
29 Euclid ESA 2020 ESA hyväksyi Euclid-satelliitin lokakuussa 2011 ja lopullisesti valitsi kesäkuussa 2012 Kartoittaa 40% taivaasta. Fysiikan laitos mukana. 29
30 Gravitaatioaallot Pallosymmetrinen tilanne ei synnytä gravitaatiosäteilyä. Gravitaatio heikko: tarvitaan nopeita aineen muutoksia: neutronitähtien ja mustien aukkojen törmäykset, supernovaräjähdykset, varhainen maailmankaikkeus valonsäde ohimenevä metristen ominaisuuksien muutos: kellojen käynti, pituusvälit gravitaatioaalto avaruusaika paikallisesti Minkowski (esim. maapallolla sijaitsevan mittalaitteen ympäristössä) voidaan periaatteessa havaita maapallolla 30
31 Gravitaatioaallot staattinen tai pallosymmetrinen tähti staattinen avaruusaika pallosymmetrian rikkova liike väreitä avaruusaikaan kaksoistähti 31
32 Gravitaatioaaltojen suora havaitseminen Gravitaatio on heikko pieni efekti Kahden mustan aukon törmäys (massa kymmenen Auringon massaa) gravitaatioaaltoja, jotka muuttavat etäisyyksiä tekijällä Miten mitata? Esimerkki: peili gravitaatioaalto Interferenssikuvio muuttuu koska valonsäteen kulkuaika muuttuu. (vrt. Michelsonin ja Morleyn koe) 32
33 LIGO Laser Interferometer Gravitational wave Observatory, USA Advanced LIGO km 33
34 Virgo Italia
35 Gravitaatioaaltojen epäsuora havaitseminen Kaksoispulsari PSR (Hulse & Taylor; löytö 1974, Nobel-palkinto 1993) Systeemi menettää energiaa gravitaatioaaltoihin. 35
36 Yleisen suhteellisuusteorian ennuste pätee tarkasti 3 MASS OF COMPANION (solar masses) d /dt ( %) ' (0.02%) dp b /dt (0.2 %) 2 a MASS OF PULSAR (solar masses) 36
37 Planck ESA Planck pystyy näkemään vain primordiaalisia gravitaatioaaltoja, kun taas LIGO/Virgo näkevät vain astrofysikaalisten lähteiden aaltoja. Fysiikan laitos mukana. 37
38 LISA NGO, elisa Laser Interferometer Space Antenna Next Gravitational Wave Observatory ESA LISA Pathfinder laukaistaan 2015 elisa 2020-luvulla? Erittäin haastava. 3 satelliittia lentää muodostelmassa, etäisyys 5 miljoonaa km 38
SUHTEELLISUUSTEORIAN TEOREETTISIA KUMMAJAISIA
 MUSTAT AUKOT FAQ Kuinka gravitaatio pääsee ulos tapahtumahorisontista? Schwarzschildin ratkaisu on staattinen. Tähti on kaareuttanut avaruuden jo ennen romahtamistaan mustaksi aukoksi. Ulkopuolinen havaitsija
MUSTAT AUKOT FAQ Kuinka gravitaatio pääsee ulos tapahtumahorisontista? Schwarzschildin ratkaisu on staattinen. Tähti on kaareuttanut avaruuden jo ennen romahtamistaan mustaksi aukoksi. Ulkopuolinen havaitsija
YLEINEN SUHTEELLISUUSTEORIA
 YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
YLEINEN SUHTEELLISUUSTEORIA
 YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
YLEINEN SUHTEELLISUUSTEORIA suppean suhteellisuusteorian yleistys mielivaltaisiin, ei-inertiaalisiin koordinaatistoihin teoria painovoimasta lähtökohta: periaatteessa kahdenlaisia massoja F mia hidas,
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä
 S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä (ks. esim. http://www.kotiposti.net/ajnieminen/sutek.pdf). 1. a) Suppeamman suhteellisuusteorian perusolettamukset (Einsteinin suppeampi suhteellisuusteoria
S U H T E E L L I S U U S T E O R I AN P Ä Ä P I I R T E I T Ä (ks. esim. http://www.kotiposti.net/ajnieminen/sutek.pdf). 1. a) Suppeamman suhteellisuusteorian perusolettamukset (Einsteinin suppeampi suhteellisuusteoria
Lyhyt katsaus gravitaatioaaltoihin
 : Lyhyt katsaus gravitaatioaaltoihin Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Sisältö Suppea ja yleinen suhteellisuusteoria Häiriöteoria Aaltoratkaisut
: Lyhyt katsaus gravitaatioaaltoihin Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Sisältö Suppea ja yleinen suhteellisuusteoria Häiriöteoria Aaltoratkaisut
2r s b VALON TAIPUMINEN. 1 r. osittaisdifferentiaaliyhtälö. = 2 suppea suht.teoria. valo putoaa tähteen + avaruus kaareutunut.
 MUSTAT AUKOT FAQ Miten gravitaatio pääsee ulos tapahtumahorisontista? massa ei sylje gravitaatiota kuin tennispalloja. Tähti on käyristänyt avaruuden jo ennen romahtamistaan mustaksi aukoksi, eikä tätä
MUSTAT AUKOT FAQ Miten gravitaatio pääsee ulos tapahtumahorisontista? massa ei sylje gravitaatiota kuin tennispalloja. Tähti on käyristänyt avaruuden jo ennen romahtamistaan mustaksi aukoksi, eikä tätä
Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen
 Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen Helsingin Yliopisto 14.9.2015 kello 12:50:45 Suomen aikaa: pulssi gravitaatioaaltoja läpäisi maan. LIGO: Ensimmäinen havainto gravitaatioaalloista. Syntyi
Gravitaatioaallot - uusi ikkuna maailmankaikkeuteen Helsingin Yliopisto 14.9.2015 kello 12:50:45 Suomen aikaa: pulssi gravitaatioaaltoja läpäisi maan. LIGO: Ensimmäinen havainto gravitaatioaalloista. Syntyi
Suhteellisuusteorian perusteet 2017
 Suhteellisuusteorian perusteet 017 Harjoitus 5 esitetään laskuharjoituksissa viikolla 17 1. Tarkastellaan avaruusaikaa, jossa on vain yksi avaruusulottuvuus x. Nollasta poikkeavat metriikan komponentit
Suhteellisuusteorian perusteet 017 Harjoitus 5 esitetään laskuharjoituksissa viikolla 17 1. Tarkastellaan avaruusaikaa, jossa on vain yksi avaruusulottuvuus x. Nollasta poikkeavat metriikan komponentit
Sisällysluettelo. Alkusanat 11. A lbert E insteinin kirjoituksia
 Sisällysluettelo Alkusanat 11 A lbert E insteinin kirjoituksia Erityisestä ja yleisestä su hteellisuusteoriasta Alkusanat 21 I Erityisestä suhteellisuusteoriasta 23 1 Geometristen lauseiden fysikaalinen
Sisällysluettelo Alkusanat 11 A lbert E insteinin kirjoituksia Erityisestä ja yleisestä su hteellisuusteoriasta Alkusanat 21 I Erityisestä suhteellisuusteoriasta 23 1 Geometristen lauseiden fysikaalinen
Erityinen suhteellisuusteoria (Harris luku 2)
 Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Suhteellisuusteoria. Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos
 Suhteellisuusteoria Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos Ketkä pohjustivat modernin fysiikan? Rømer 1676 Ampere Fizeau 1849 Young 1800 Faraday Michelson 1878 Maxwell 1873 Hertz
Suhteellisuusteoria Jouko Nieminen Tampereen Teknillinen Yliopisto Fysiikan laitos Ketkä pohjustivat modernin fysiikan? Rømer 1676 Ampere Fizeau 1849 Young 1800 Faraday Michelson 1878 Maxwell 1873 Hertz
Moderni fysiikka. Syyslukukausi 2008 Jukka Maalampi
 Moderni fysiikka Syyslukukausi 008 Jukka Maalampi 1 1. Suhteellisuus Galilein suhteellisuuus Fysiikan lakien suhteellisuus Suppea suhteellisuusteoria Samanaikaisuuden suhteellisuus Ajan dilaatio Pituuden
Moderni fysiikka Syyslukukausi 008 Jukka Maalampi 1 1. Suhteellisuus Galilein suhteellisuuus Fysiikan lakien suhteellisuus Suppea suhteellisuusteoria Samanaikaisuuden suhteellisuus Ajan dilaatio Pituuden
Suhteellinen nopeus. Matkustaja P kävelee nopeudella 1.0 m/s pitkin 3.0 m/s nopeudella etenevän junan B käytävää
 3.5 Suhteellinen nopeus Matkustaja P kävelee nopeudella 1.0 m/s pitkin 3.0 m/s nopeudella etenevän junan B käytävää P:n nopeus junassa istuvan toisen matkustajan suhteen on v P/B-x = 1.0 m/s Intuitio :
3.5 Suhteellinen nopeus Matkustaja P kävelee nopeudella 1.0 m/s pitkin 3.0 m/s nopeudella etenevän junan B käytävää P:n nopeus junassa istuvan toisen matkustajan suhteen on v P/B-x = 1.0 m/s Intuitio :
Fysiikkaa runoilijoille Osa 2: suppea suhteellisuusteoria
 Fysiikkaa runoilijoille Osa 2: suppea suhteellisuusteoria Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Hiukkaset ja kentät Klassisessa mekaniikassa
Fysiikkaa runoilijoille Osa 2: suppea suhteellisuusteoria Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Hiukkaset ja kentät Klassisessa mekaniikassa
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
Tähtitieteessä SI-yksiköissä ilmaistut luvut ovat usein hyvin isoja ja epähavainnollisia. Esimerkiksi
 Tähtitieteen perusteet, harjoitus 2 Yleisiä huomioita: Tähtitieteessä SI-yksiköissä ilmaistut luvut ovat usein hyvin isoja ja epähavainnollisia. Esimerkiksi aurinkokunnan etäisyyksille kannattaa usein
Tähtitieteen perusteet, harjoitus 2 Yleisiä huomioita: Tähtitieteessä SI-yksiköissä ilmaistut luvut ovat usein hyvin isoja ja epähavainnollisia. Esimerkiksi aurinkokunnan etäisyyksille kannattaa usein
Pimeän energian metsästys satelliittihavainnoin
 Pimeän energian metsästys satelliittihavainnoin Avaruusrekka, Kumpulan pysäkki 04.10.2012 Peter Johansson Matemaattis-luonnontieteellinen tiedekunta / Peter Johansson/ Avaruusrekka 04.10.2012 13/08/14
Pimeän energian metsästys satelliittihavainnoin Avaruusrekka, Kumpulan pysäkki 04.10.2012 Peter Johansson Matemaattis-luonnontieteellinen tiedekunta / Peter Johansson/ Avaruusrekka 04.10.2012 13/08/14
Kosmologian yleiskatsaus. Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos
 Kosmologian yleiskatsaus Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Päämääriä Kosmologia tutkii maailmankaikkeutta kokonaisuutena. Kehitys,
Kosmologian yleiskatsaus Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Päämääriä Kosmologia tutkii maailmankaikkeutta kokonaisuutena. Kehitys,
Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä.
 Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
Kosmologia Kosmologia on yleisen suhteellisuusteorian sovellus suurimpaan mahdolliseen systeemiin: tutkitaan koko avaruuden aikakehitystä. Kosmologia tutkii maailmankaikkeutta kokonaisuutena. (Vrt. astrofysiikka,
Perusvuorovaikutukset. Tapio Hansson
 Perusvuorovaikutukset Tapio Hansson Perusvuorovaikutukset Vuorovaikutukset on perinteisesti jaettu neljään: Gravitaatio Sähkömagneettinen vuorovaikutus Heikko vuorovaikutus Vahva vuorovaikutus Sähköheikkoteoria
Perusvuorovaikutukset Tapio Hansson Perusvuorovaikutukset Vuorovaikutukset on perinteisesti jaettu neljään: Gravitaatio Sähkömagneettinen vuorovaikutus Heikko vuorovaikutus Vahva vuorovaikutus Sähköheikkoteoria
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Leptonit. - elektroni - myoni - tauhiukkanen - kolme erilaista neutriinoa. - neutriinojen varaus on 0 ja muiden leptonien varaus on -1
 Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
Mistä aine koostuu? - kaikki aine koostuu atomeista - atomit koostuvat elektroneista, protoneista ja neutroneista - neutronit ja protonit koostuvat pienistä hiukkasista, kvarkeista Alkeishiukkaset - hiukkasten
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN
 Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN Oppilaiden ennakkokäsityksiä avaruuteen liittyen Aurinko kiertää Maata Vuodenaikojen vaihtelu johtuu siitä,
Tarinaa tähtitieteen tiimoilta FYSIIKAN JA KEMIAN PERUSTEET JA PEDAGOGIIKKA 2014 KARI SORMUNEN Oppilaiden ennakkokäsityksiä avaruuteen liittyen Aurinko kiertää Maata Vuodenaikojen vaihtelu johtuu siitä,
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
Maailmankaikkeuden kriittinen tiheys
 Maailmankaikkeuden kriittinen tiheys Tarkastellaan maailmankaikkeuden pientä pallomaista laajenevaa osaa, joka sisältää laajenemisliikkeessä olevia galakseja. Olkoon pallon säde R, massa M ja maailmankaikkeuden
Maailmankaikkeuden kriittinen tiheys Tarkastellaan maailmankaikkeuden pientä pallomaista laajenevaa osaa, joka sisältää laajenemisliikkeessä olevia galakseja. Olkoon pallon säde R, massa M ja maailmankaikkeuden
ELEC-A3110 Mekaniikka (5 op)
 ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Mikro- ja nanotekniikan laitos Syksy 2016 1 / 21 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Mikro- ja nanotekniikan laitos Syksy 2016 1 / 21 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
Shrödingerin yhtälön johto
 Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Copyright 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley.
 Newtonin painovoimateoria Knight Ch. 13 Saturnuksen renkaat koostuvat lukemattomista pölyhiukkasista ja jääkappaleista, suurimmat rantapallon kokoisia. Lisäksi Saturnusta kiertää ainakin 60 kuuta. Niiden
Newtonin painovoimateoria Knight Ch. 13 Saturnuksen renkaat koostuvat lukemattomista pölyhiukkasista ja jääkappaleista, suurimmat rantapallon kokoisia. Lisäksi Saturnusta kiertää ainakin 60 kuuta. Niiden
Fysiikkaa runoilijoille Osa 7: kohti kaiken teoriaa
 Fysiikkaa runoilijoille Osa 7: kohti kaiken teoriaa Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Modernin fysiikan sukupuu Klassinen mekaniikka
Fysiikkaa runoilijoille Osa 7: kohti kaiken teoriaa Syksy Räsänen Helsingin yliopisto, fysiikan laitos ja fysiikan tutkimuslaitos www.helsinki.fi/yliopisto 1 Modernin fysiikan sukupuu Klassinen mekaniikka
LORENTZIN MUUNNOSTEN FYSIKAALISIA SEURAAMUKSIA
 LORENTZIN MUUNNOSTEN FYSIKAALISIA SEURAAMUKSIA Lorentzin kontraktio: liikkuva sauva kutistuu Aikadilataatio: liikkuva kello jätättää Nämä fysikaaliset efektit johtavat arkijärjen kannalta vaikeasti ymmärrettäviin
LORENTZIN MUUNNOSTEN FYSIKAALISIA SEURAAMUKSIA Lorentzin kontraktio: liikkuva sauva kutistuu Aikadilataatio: liikkuva kello jätättää Nämä fysikaaliset efektit johtavat arkijärjen kannalta vaikeasti ymmärrettäviin
Yleisen suhteellisuusteorian kokeelliset tes/t. Hannu Kurki- Suonio Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos
 Yleisen suhteellisuusteorian kokeelliset tes/t Hannu Kurki- Suonio Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos 25.11.2015 Yleisen suhteellisuusteorian klassiset tes/t Einstein 1916:
Yleisen suhteellisuusteorian kokeelliset tes/t Hannu Kurki- Suonio Helsingin yliopisto, fysiikan laitos ja Fysiikan tutkimuslaitos 25.11.2015 Yleisen suhteellisuusteorian klassiset tes/t Einstein 1916:
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Mustien aukkojen astrofysiikka
 Mustien aukkojen astrofysiikka Peter Johansson Fysiikan laitos, Helsingin yliopisto Kumpula nyt Helsinki 19.2.2016 1. Tähtienmassaiset mustat aukot: Kuinka isoja?: noin 3-100 kertaa Auringon massa, tapahtumahorisontin
Mustien aukkojen astrofysiikka Peter Johansson Fysiikan laitos, Helsingin yliopisto Kumpula nyt Helsinki 19.2.2016 1. Tähtienmassaiset mustat aukot: Kuinka isoja?: noin 3-100 kertaa Auringon massa, tapahtumahorisontin
53714 Klassinen mekaniikka syyslukukausi 2010
 53714 Klassinen mekaniikka syyslukukausi 2010 Luennot: Luennoitsija: Kurssin kotisivu: ma & to 10-12 (E204) Rami Vainio, [email protected] http://theory.physics.helsinki.fi/~klmek/ Harjoitukset:
53714 Klassinen mekaniikka syyslukukausi 2010 Luennot: Luennoitsija: Kurssin kotisivu: ma & to 10-12 (E204) Rami Vainio, [email protected] http://theory.physics.helsinki.fi/~klmek/ Harjoitukset:
3.1 Lineaarikuvaukset. MS-A0004/A0006 Matriisilaskenta. 3.1 Lineaarikuvaukset. 3.1 Lineaarikuvaukset
 31 MS-A0004/A0006 Matriisilaskenta 3 Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2292015 Lineaariset yhtälöt ovat vektoreille luonnollisia yhtälöitä, joita
31 MS-A0004/A0006 Matriisilaskenta 3 Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2292015 Lineaariset yhtälöt ovat vektoreille luonnollisia yhtälöitä, joita
Suhteellisuusteorian vajavuudesta
 Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
9 Maxwellin yhtälöt. 9.5 Aaltoyhtälö ja kenttien lähteet Aaltoyhtälö tyhjössä Potentiaaliesitys Viivästyneet potentiaalit
 9 Maxwellin yhtälöt 9.5 Aaltoyhtälö ja kenttien lähteet 9.5.1 Aaltoyhtälö tyhjössä 9.5.2 Potentiaaliesitys 9.5.3 Viivästyneet potentiaalit 9.5.4 Aaltoyhtälön Greenin funktio 9.6 Mittainvarianssi Typeset
9 Maxwellin yhtälöt 9.5 Aaltoyhtälö ja kenttien lähteet 9.5.1 Aaltoyhtälö tyhjössä 9.5.2 Potentiaaliesitys 9.5.3 Viivästyneet potentiaalit 9.5.4 Aaltoyhtälön Greenin funktio 9.6 Mittainvarianssi Typeset
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
Teoreetikon kuva. maailmankaikkeudesta
 Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Luento 12: Keskeisvoimat ja gravitaatio
 Luento 12: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä Ajankohtaista Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja
Luento 12: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä Ajankohtaista Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja
Aikariippuva Schrödingerin yhtälö
 Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Suhteellisuusteoria. Valo on sähkömagneettisia aaltoja
 Suhteellisuusteoria Suhteellisuusteoriaa on mahdoton edes yrittää ymmärtää, ellei ota ensin selkoa valon ominaisuuksista. Valon äärellinen nopeus oli tunnettu jo 1600-luvulta asti, kun Ole Roemer huomasi
Suhteellisuusteoria Suhteellisuusteoriaa on mahdoton edes yrittää ymmärtää, ellei ota ensin selkoa valon ominaisuuksista. Valon äärellinen nopeus oli tunnettu jo 1600-luvulta asti, kun Ole Roemer huomasi
Gravitaatio ja heittoliike. Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike
 Gravitaatio ja heittoliike Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike KERTAUS Newtonin lait Newtonin I laki Kappale, johon ei vaikuta voimia/voimien summa on nolla, ei muuta liiketilaansa
Gravitaatio ja heittoliike Gravitaatiovoima Numeerisen ratkaisun perusteet Heittoliike KERTAUS Newtonin lait Newtonin I laki Kappale, johon ei vaikuta voimia/voimien summa on nolla, ei muuta liiketilaansa
Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia
 Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia extraa 1 / 31 Luennon sisältö Suhteellinen translaatioliike
Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia extraa 1 / 31 Luennon sisältö Suhteellinen translaatioliike
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
Dynaamiset regressiomallit
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Viikko 6: 1 Kalmanin suodatin Aiemmin käsitellyt
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Viikko 6: 1 Kalmanin suodatin Aiemmin käsitellyt
JOHDATUS SUHTEELLISUUSTEORIAAN 763102P
 JHDATUS SUHTEELLISUUSTERIAAN 763102P Petri Mutka Fysikaalisten tieteiden laitos ulun yliopisto 2005 1. Johdanto Suhteellisuusteoria, joka koostuu kahdesta erillisestä teoriasta, on toinen modernin fysiikan
JHDATUS SUHTEELLISUUSTERIAAN 763102P Petri Mutka Fysikaalisten tieteiden laitos ulun yliopisto 2005 1. Johdanto Suhteellisuusteoria, joka koostuu kahdesta erillisestä teoriasta, on toinen modernin fysiikan
Etäisyyden yksiköt tähtitieteessä:
 Tähtitiedettä Etäisyyden yksiköt tähtitieteessä: Astronominen yksikkö AU = 149 597 870 kilometriä. Tämä vastaa sellaisen Aurinkoa kiertävän kuvitellun kappaleen etäisyyttä, jonka kiertoaika on sama kuin
Tähtitiedettä Etäisyyden yksiköt tähtitieteessä: Astronominen yksikkö AU = 149 597 870 kilometriä. Tämä vastaa sellaisen Aurinkoa kiertävän kuvitellun kappaleen etäisyyttä, jonka kiertoaika on sama kuin
Luento 8: Liikemäärä ja impulssi. Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste Muuttuva massa Harjoituksia ja esimerkkejä
 Luento 8: Liikemäärä ja impulssi Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste Muuttuva massa Harjoituksia ja esimerkkejä 1 / 46 Luennon sisältö Liikemäärä ja impulssi Liikemäärän säilyminen
Luento 8: Liikemäärä ja impulssi Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste Muuttuva massa Harjoituksia ja esimerkkejä 1 / 46 Luennon sisältö Liikemäärä ja impulssi Liikemäärän säilyminen
Ei-inertiaaliset koordinaatistot
 orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
2 Keskeisvoimakenttä. 2.1 Newtonin gravitaatiolaki
 2 Keskeisvoimakenttä 2.1 Newtonin gravitaatiolaki Newton oletti, että kappale, jolla on massa m 1, vaikuttaa etäisyydellä r 12 olevaan toiseen kappaleeseen, jonka massa on m 2, gravitaatiovoimalla, joka
2 Keskeisvoimakenttä 2.1 Newtonin gravitaatiolaki Newton oletti, että kappale, jolla on massa m 1, vaikuttaa etäisyydellä r 12 olevaan toiseen kappaleeseen, jonka massa on m 2, gravitaatiovoimalla, joka
Luento 12: Keskeisvoimat ja gravitaatio. Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä
 Luento 12: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä 1 / 46 Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja
Luento 12: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä 1 / 46 Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
Luento 5: Käyräviivainen liike. Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike
 Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
Liike pyörivällä maapallolla
 Liike pyörivällä maapallolla Voidaan olettaa: Maan pyöriminen tasaista Maan rataliikkeen näennäisvoimat tasapainossa Auringon vetovoiman kanssa Riittää tarkastella Maan tasaisesta pyörimisestä akselinsa
Liike pyörivällä maapallolla Voidaan olettaa: Maan pyöriminen tasaista Maan rataliikkeen näennäisvoimat tasapainossa Auringon vetovoiman kanssa Riittää tarkastella Maan tasaisesta pyörimisestä akselinsa
Luento 3: Käyräviivainen liike
 Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike Luennon sisältö Kertausta viime viikolta Käyräviivainen liike
Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike Luennon sisältö Kertausta viime viikolta Käyräviivainen liike
Luento 10: Keskeisvoimat ja gravitaatio
 Luento 10: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä
Luento 10: Keskeisvoimat ja gravitaatio Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä Luennon sisältö Gravitaatio Liike keskeisvoimakentässä Keplerin lait Laskettuja esimerkkejä
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 31.3.2016 Susanna Hurme Dynamiikan välikoe 4.4.2016 Ajankohta ma 4.4.2016 klo 16:30 19:30 Salijako Aalto-Sali: A-P (sukunimen alkukirjaimen mukaan) Ilmoittautuminen
KJR-C1001 Statiikka ja dynamiikka Luento 31.3.2016 Susanna Hurme Dynamiikan välikoe 4.4.2016 Ajankohta ma 4.4.2016 klo 16:30 19:30 Salijako Aalto-Sali: A-P (sukunimen alkukirjaimen mukaan) Ilmoittautuminen
6. TAIVAANMEKANIIKKA. Antiikki: planeetat = vaeltavia tähtiä jotka liikkuvat kiintotähtien suhteen
 6. TAIVAANMEKANIIKKA Antiikki: planeetat = vaeltavia tähtiä jotka liikkuvat kiintotähtien suhteen Näennäinen liike voi olla hyvinkin monimutkaista: esim. ulkoplaneetan suunta retrograadinen opposition
6. TAIVAANMEKANIIKKA Antiikki: planeetat = vaeltavia tähtiä jotka liikkuvat kiintotähtien suhteen Näennäinen liike voi olla hyvinkin monimutkaista: esim. ulkoplaneetan suunta retrograadinen opposition
Friedmannin yhtälöt. Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G 3. yleisin mahdollinen metriikka. Friedmannin yhtälö
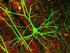 Friedmannin yhtälöt Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G G [ R( t)] T [ aine, energia, R( t)] 3 yleisin mahdollinen metriikka d sin d dr ds c dt R( t) ( r d ) 1 kr Friedmannin
Friedmannin yhtälöt Einsteinin yhtälöt isotrooppisessa, homogeenisessa FRW-universumissa 8 G G [ R( t)] T [ aine, energia, R( t)] 3 yleisin mahdollinen metriikka d sin d dr ds c dt R( t) ( r d ) 1 kr Friedmannin
yyyyyyyyyyyyyyyyy Tehtävä 1. PAINOSI AVARUUDESSA Testaa, paljonko painat eri taivaankappaleilla! Kuu kg Maa kg Planeetta yyy yyyyyyy yyyyyy kg Tiesitk
 I LUOKKAHUONEESSA ENNEN TIETOMAA- VIERAILUA POHDITTAVIA TEHTÄVIÄ Nimi Luokka Koulu yyyyyyyyyy Tehtävä 1. ETSI TIETOA PAINOVOIMASTA JA TÄYDENNÄ. TIETOA LÖYDÄT MM. PAINOVOIMA- NÄYTTELYN VERKKOSIVUILTA. Painovoima
I LUOKKAHUONEESSA ENNEN TIETOMAA- VIERAILUA POHDITTAVIA TEHTÄVIÄ Nimi Luokka Koulu yyyyyyyyyy Tehtävä 1. ETSI TIETOA PAINOVOIMASTA JA TÄYDENNÄ. TIETOA LÖYDÄT MM. PAINOVOIMA- NÄYTTELYN VERKKOSIVUILTA. Painovoima
Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9
 : Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9 Horisonttiongelma Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Valtteri Lindholm
: Valtteri Lindholm (Helsingin Yliopisto) Horisonttiongelma 21.11.2013 1 / 9 Horisonttiongelma Valtteri Lindholm Helsingin Yliopisto Teoreettisen fysiikan syventävien opintojen seminaari Valtteri Lindholm
Luento 6: Liikemäärä ja impulssi
 Luento 6: Liikemäärä ja impulssi Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste Muuttuva massa Laskettuja esimerkkejä Luennon sisältö Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste
Luento 6: Liikemäärä ja impulssi Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste Muuttuva massa Laskettuja esimerkkejä Luennon sisältö Liikemäärä ja impulssi Liikemäärän säilyminen Massakeskipiste
Normaaliryhmä. Toisen kertaluvun normaaliryhmä on yleistä muotoa
 Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
g-kentät ja voimat Haarto & Karhunen
 g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
g-kentät ja voimat Haarto & Karhunen Voima Vuorovaikutusta kahden kappaleen välillä tai kappaleen ja sen ympäristön välillä (Kenttävoimat) Yksikkö: newton, N = kgm/s Vektorisuure Aiheuttaa kappaleelle
Luento 10: Työ, energia ja teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
Suhteellisuusteorian perusteet, harjoitus 6
 Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
Suhteellisuusteorian perusteet, harjoitus 6 May 5, 7 Tehtävä a) Valo kulkee nollageodeettia pitkin eli valolle pätee ds. Lisäksi oletetaan valon kulkevan radiaalisesti, jolloin dω. Näin ollen, kun K, saadaan
4. Käyrän lokaaleja ominaisuuksia
 23 VEKTORIANALYYSI Luento 3 4 Käyrän lokaaleja ominaisuuksia Käyrän tangentti Tarkastellaan parametrisoitua käyrää r( t ) Parametrilla t ei tarvitse olla mitään fysikaalista merkitystä, mutta seuraavassa
23 VEKTORIANALYYSI Luento 3 4 Käyrän lokaaleja ominaisuuksia Käyrän tangentti Tarkastellaan parametrisoitua käyrää r( t ) Parametrilla t ei tarvitse olla mitään fysikaalista merkitystä, mutta seuraavassa
Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia
 Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Pyörimisliikkeestä Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia Luennon sisältö Suhteellinen translaatioliike
Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Pyörimisliikkeestä Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia Luennon sisältö Suhteellinen translaatioliike
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos
 PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos 1917: Einstein sovelsi yleistä suhteellisuusteoriaa koko maailmankaikkeuteen Linnunradan eli maailmankaikkeuden
PIMEÄ ENERGIA mysteeri vai kangastus? Kari Enqvist Helsingin yliopisto ja Fysiikan tutkimuslaitos 1917: Einstein sovelsi yleistä suhteellisuusteoriaa koko maailmankaikkeuteen Linnunradan eli maailmankaikkeuden
PARADIGMOJEN VERTAILUPERUSTEET. Avril Styrman Luonnonfilosofian seura
 PARADIGMOJEN VERTAILUPERUSTEET Avril Styrman Luonnonfilosofian seura 17.2.2015 KokonaisHede Koostuu paradigmoista Tieteen edistystä voidaan siten tarkastella prosessina missä paradigmat kehinyvät ja vaihtuvat
PARADIGMOJEN VERTAILUPERUSTEET Avril Styrman Luonnonfilosofian seura 17.2.2015 KokonaisHede Koostuu paradigmoista Tieteen edistystä voidaan siten tarkastella prosessina missä paradigmat kehinyvät ja vaihtuvat
Luento 3: Käyräviivainen liike
 Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat,! ja Yhdistetty liike 2015-09-14 13:50:32 1/40 luentokalvot_03_combined.pdf (#36) Luennon
Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat,! ja Yhdistetty liike 2015-09-14 13:50:32 1/40 luentokalvot_03_combined.pdf (#36) Luennon
ja KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 1: Parametrisoidut käyrät ja kaarenpituus
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 1: Parametrisoidut käyrät ja kaarenpituus Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 1: Parametrisoidut käyrät ja kaarenpituus Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
Energia, energian säilyminen ja energiaperiaate
 E = γmc 2 Energia, energian säilyminen ja energiaperiaate Luennon tavoitteet Lepoenergian, liike-energian, potentiaalienergian käsitteet haltuun Työ ja työn merkki* Systeemivalintojen miettimistä Jousivoiman
E = γmc 2 Energia, energian säilyminen ja energiaperiaate Luennon tavoitteet Lepoenergian, liike-energian, potentiaalienergian käsitteet haltuun Työ ja työn merkki* Systeemivalintojen miettimistä Jousivoiman
Fysiikan olympiavalmennus, avoin sarja Palautus mennessä
 Fysiikan olympiavalmennus, avoin sarja Kirje 1 Palautus 31.1.2012 mennessä Olet menestynyt hyvin MAOL:n fysiikkakilpailussa, ja sinut on valittu mukaan fysiikan olympiavalmennukseen. Valmennuksen ensimmäinen
Fysiikan olympiavalmennus, avoin sarja Kirje 1 Palautus 31.1.2012 mennessä Olet menestynyt hyvin MAOL:n fysiikkakilpailussa, ja sinut on valittu mukaan fysiikan olympiavalmennukseen. Valmennuksen ensimmäinen
Perustutkimus ei elä. Gravitaatioaaltojen ensimmäiset sata vuotta. Suppeasta yleiseen suhteellisuusteoriaan
 Kari Enqvist Gravitaatioaaltojen ensimmäiset sata vuotta Perustutkimus ei elä kvartaalitaloudessa. Aika-avaruuden väreilyn eli gravitaatioaaltojen ennustamisen ja niiden suoran havaitsemisen välissä ehti
Kari Enqvist Gravitaatioaaltojen ensimmäiset sata vuotta Perustutkimus ei elä kvartaalitaloudessa. Aika-avaruuden väreilyn eli gravitaatioaaltojen ennustamisen ja niiden suoran havaitsemisen välissä ehti
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN. Fysiikan ja kemian perusteet ja pedagogiikka, luento Kari Sormunen
 VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian perusteet ja pedagogiikka, 1.-2. luento Kari Sormunen Mitä yhteistä? Kirja pöydällä Opiskelijapari Teräskuulan liike magneetin lähellä
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian perusteet ja pedagogiikka, 1.-2. luento Kari Sormunen Mitä yhteistä? Kirja pöydällä Opiskelijapari Teräskuulan liike magneetin lähellä
Matematiikka ja teknologia, kevät 2011
 Matematiikka ja teknologia, kevät 2011 Peter Hästö 13. tammikuuta 2011 Matemaattisten tieteiden laitos Tarkoitus Kurssin tarkoituksena on tutustuttaa ja käydä läpi eräisiin teknologisiin sovelluksiin liittyvää
Matematiikka ja teknologia, kevät 2011 Peter Hästö 13. tammikuuta 2011 Matemaattisten tieteiden laitos Tarkoitus Kurssin tarkoituksena on tutustuttaa ja käydä läpi eräisiin teknologisiin sovelluksiin liittyvää
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
Lataa Maailmanviiva - Jukka Maalampi. Lataa
 Lataa Maailmanviiva - Jukka Maalampi Lataa Kirjailija: Jukka Maalampi ISBN: 9789525329513 Sivumäärä: 221 Formaatti: PDF Tiedoston koko: 28.94 Mb Sata vuotta sitten Albert Einstein ilmestyi kuin tyhjästä
Lataa Maailmanviiva - Jukka Maalampi Lataa Kirjailija: Jukka Maalampi ISBN: 9789525329513 Sivumäärä: 221 Formaatti: PDF Tiedoston koko: 28.94 Mb Sata vuotta sitten Albert Einstein ilmestyi kuin tyhjästä
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit
 MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
5.9 Voiman momentti (moment of force, torque)
 5.9 Voiman momentti (moment of force, torque) Voiman momentti määritellään ristitulona M = r F missä r on voiman F vaikutuspisteen paikkavektori tarkasteltavan pisteen suhteen Usean voiman tapauksessa
5.9 Voiman momentti (moment of force, torque) Voiman momentti määritellään ristitulona M = r F missä r on voiman F vaikutuspisteen paikkavektori tarkasteltavan pisteen suhteen Usean voiman tapauksessa
TAIVAANMEKANIIKKA IHMISEN PERSPEKTIIVISTÄ
 TAIVAANMEKANIIKKA IHMISEN PERSPEKTIIVISTÄ ARKIPÄIVÄISTEN ASIOIDEN TÄHTITIETEELLISET AIHEUTTAJAT, FT Metsähovin Radio-observatorio, Aalto-yliopisto KOPERNIKUKSESTA KEPLERIIN JA NEWTONIIN Nikolaus Kopernikus
TAIVAANMEKANIIKKA IHMISEN PERSPEKTIIVISTÄ ARKIPÄIVÄISTEN ASIOIDEN TÄHTITIETEELLISET AIHEUTTAJAT, FT Metsähovin Radio-observatorio, Aalto-yliopisto KOPERNIKUKSESTA KEPLERIIN JA NEWTONIIN Nikolaus Kopernikus
Kvarkeista kvanttipainovoimaan ja takaisin
 1/31 Kvarkeista kvanttipainovoimaan ja takaisin Niko Jokela Hiukkasfysiikan kesäkoulu Helsinki 18. toukokuuta 2017 2/31 Säieteorian perusidea Hieman historiaa 1 Säieteorian perusidea Hieman historiaa 2
1/31 Kvarkeista kvanttipainovoimaan ja takaisin Niko Jokela Hiukkasfysiikan kesäkoulu Helsinki 18. toukokuuta 2017 2/31 Säieteorian perusidea Hieman historiaa 1 Säieteorian perusidea Hieman historiaa 2
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
Luento 11: Potentiaalienergia. Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia
 Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
Kompleksiluvun logaritmi: Jos nyt z = re iθ = re iθ e in2π, missä n Z, niin saadaan. ja siihen vaikuttava
 Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Wien R-J /home/heikki/cele2008_2010/musta_kappale_approksimaatio Wed Mar 13 15:33:
 1.2 T=12000 K 10 2 T=12000 K 1.0 Wien R-J 10 0 Wien R-J B λ (10 15 W/m 3 /sterad) 0.8 0.6 0.4 B λ (10 15 W/m 3 /sterad) 10-2 10-4 10-6 10-8 0.2 10-10 0.0 0 200 400 600 800 1000 nm 10-12 10 0 10 1 10 2
1.2 T=12000 K 10 2 T=12000 K 1.0 Wien R-J 10 0 Wien R-J B λ (10 15 W/m 3 /sterad) 0.8 0.6 0.4 B λ (10 15 W/m 3 /sterad) 10-2 10-4 10-6 10-8 0.2 10-10 0.0 0 200 400 600 800 1000 nm 10-12 10 0 10 1 10 2
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 26. syyskuuta 2016 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali Dipolin potentiaali
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 26. syyskuuta 2016 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali Dipolin potentiaali
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN. Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen
 VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen Vuorovaikutus on yksi keskeisimmistä fysiikan peruskäsitteistä
VUOROVAIKUTUKSESTA VOIMAAN JA EDELLEEN LIIKKEESEEN Fysiikan ja kemian pedagogiikan perusteet (mat/fys/kem suunt.), luento 1 Kari Sormunen Vuorovaikutus on yksi keskeisimmistä fysiikan peruskäsitteistä
ELEC-A3110 Mekaniikka (5 op)
 ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Elektroniikan ja nanotekniikan laitos (ELE) Syksy 2017 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
ELEC-A3110 Mekaniikka (5 op) Yliopistonlehtori, tkt Sami Kujala Elektroniikan ja nanotekniikan laitos (ELE) Syksy 2017 Luento 2: Kertausta ja johdantoa Suoraviivainen liike Jumppaa Harjoituksia ja oivalluksia
