VII LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ
|
|
|
- Sanna Tuominen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ Kaasun tekemä laajenemistyö Laajenemistyön erityistapauksia Työ isobaarisessa tilanmuutoksessa Työ isotermisessä tilanmuutoksessa Lämpöopin ensimmäinen pääsääntö Määritelmä Ensimmäinen pääsääntö ja pt -systeemin tilanmuutokset Adiabaattinen prosessi Isokoorinen prosessi Ideaalikaasun isoterminen prosessi Kiertoprosessi Muita konfiguraatiotöitä pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti Ominaislämmön määritelmä pt-systeemin ominaislämpö ja ensimmäinen pääsääntö Ideaalikaasun ominaislämmöt Ominaislämpöjen c p ja c erotus reaalikaasuille Ideaalikaasun adiabaattinen prosessi Paineen ja tilavuuden yhteys adiabaattisessa prosessissa Makroskooppinen tilanmuutos Työ ja sisäenergia adiabaattisessa muutoksessa Ideaalikaasun polytrooppinen prosessi Polytrooppisen prosessin ominaislämpö Työ polytrooppisessa prosessissa Polytrooppivakion ja vastaavan ominaislämmön suhde... 93
2 70 II Lämpöopin ensimmäinen pääsääntö II Lämpöopin ensimmäinen pääsääntö 7. Lämpö ja työ Systeemin sisäenergia muuttua kahdella eri tavalla: () siten, että systeemi tekee työtä (W) tai (2) siten, että se saa energiaa lämpönä (Q). Systeemin tekemä työ voi sisältää myös kitkatyötä, jossa tehty työ muuttuu lämmöksi. Kun systeemi saa energiaa lämmön muodossa, systeemin mikroskooppiset osat vuorovaikuttavat ympäristön kanssa ilman, että systeemiä rajoittavat makroskooppiset osat (esimerkiksi kaasusäiliön seinämät) liikkuvat. Yleisenä tapana on valita lämmön etumerkin siten, että lämmön virratessa ympäristöstä systeemiin Q > 0. astaavasti W > 0 silloin, kun systeemin tekemä työ on positiivinen. Kokeellisesti on havaittu, että jos kahden systeemin välillä on lämmön vaihtoa, niin lämpö virtaa aina korkeammassa lämpötilassa olevasta systeemistä alhaisemmassa lämpötilassa olevaan systeemiin. Jos kaksi systeemiä on tarkalleen samassa lämpötilassa, niillä ei voi olla lämmön vaihtoa, mutta jos niiden välillä on ideaalinen lämmönjohde, äärettömän pieni lämpötilaero riittää ylläpitämään lämmön siirtymistä systeemien välillä. Jälkimmäisessä tapauksessa lämmön siirtyminen tapahtuu reversiibelisti - äärettömän Kuva 7- Kaasun sisäenergia pienenee kaasun tehdessä työtä ja kasvaa kaasun saadessa lämpöä. pieni lämpötilan muutos riittää Lämpöenergian siirtyminen kaasuun tapahtuu kääntämään lämpövuon suunnan. satunnaisissa mikroskooppisissa vuorovaikutuksissa. Systeemin tekemällä työllä (kirjallisuudessa usein konfiguraa-
3 7.2 Kaasun tekemä laajenemistyö 7 tiotyö) tarkoitetaan mikroskooppisten osasten liikkeestä aiheutuvan keskimääräisen voiman tekemää työtä systeemiä rajoittavien makroskooppisten ympäristön osien liikkuessa. Kitkatyössä osa systeemin tekemästä työstä muuttuu lämmöksi. Se, miten kitkalämpö jakautuu systeemin ja ympäristön välillä on tapauskohtaista. Seuraavassa tarkastelussa oletamme, että tilanmuutoksiin ei liity kitkatyön kaltaisia häviöitä. Lämpöeristetylle systeemille sisäenergian muutos on tällöin yhtä suuri kuin systeemin tekemä työ: U = W. (7.) Ympäristön tekemä työ on systeemin tekemän työn vastaluku U = Wext = W. Myös lämpöön voidaan ajatella liittyvän mikroskooppista työtä, jota esim. kaasusäiliön seinämän yksittäiset atomit tekevät vuorovaikuttaessaan kaasumolekyylien kanssa. Symbolia W käytämme kuitenkin vain makroskooppiselle eli mekaaniselle työlle. 7.2 Kaasun tekemä laajenemistyö Molekyylien satunnaisista törmäyksistä aiheutuu liikkuvaan seinämään paine, jota vastaava voima on F = pa (7.2) Oletetaan, että x-akseliin nähden kohtisuorassa oleva säiliön seinämä voi liikkua ja tarkastellaan differentiaalista siirtymää dx. Klassisen meka- Kuva 7-2 Kaasun laajenemiseen liittyvän differentiaalisen työn laskeminen.
4 72 II Lämpöopin ensimmäinen pääsääntö niikan mukaan vastaava työ on dw = Fdx = padx = pd. (7.3) Siirtymän ollessa äärellinen paine ei välttämättä ole vakio, joten kokonaistyö saadaan integroimalla paine alkutilavuudesta lopputilavuuteen 2 2 W = pd. (7.4) Yhtälöissä oletettiin, että kaasun laajeneminen tapahtuu kvasistaattisesti. Kaasun sisäenergian muutos voidaan esittää systeemin saaman lämpömäärän ja systeemin tekemän työn summana silloinkin, kun tilanmuutos ei ole kvasistaattinen. Tällöin ei kuitenkaan työtä voida esittää paineen ja tilavuuden differentiaalin tulona, kuten yhtälössä 7.3. Kuva 7.3. esittää kaasun laajenemiseen liittyvää tilanmuutosta p-tasossa. Kuva 7.3a. esittää integraalin 7.4 geometristä tulkintaa; kaasun tekemä työ Kuva 7-3 Kuva a) esittää työn geometrista tulkintaa paineen kuvaajan avulla. arjostettu alue on differentiaaliseen tilavuudenmuutokseen liittyvä työ suuruudeltaan pd. Kuva b) esittää työn riippuvuutta siitä reitistä, jota myöten tilanmuutos pisteestä () pisteeseen (2) tapahtuu. on yhtä suuri kuin paineen kuvaajan ja tilavuusakselin väliin jäävän alueen pinta-ala. Kuva 7.3b. osoittaa, että kaasun tekemä työ siirryttäessä tilasta () tilaan (2) riippuu paineen käyttäytymisestä tilavuuden funktiona tämän siirtymän aikana.
5 7.3 Laajenemistyön erityistapauksia 73 Lämpövoimasovellutuksissa on erityisasemassa ns. kiertoprosessi. Tällä tarkoitetaan tilanmuutosten sarjaa (vähintään 2 osaprosessia), joiden tuloksena systeemi päätyy alkutilaansa. Kaasun laajetessa työ on positiivinen ja sitä edustaa kuvaajan () ja tilavuusakselin väliin jäävä alue. Kaasua puristettaessa kaasun tekemä työ on negatiivinen ja sen itseisarvoa edustaa kuvaajan (2) ja tilavuusakselin väliin jäävä alue. Yhteenlaskettu kokonaistyö kiertoprosessin aikana on näiden erotus eli kuvan varjostettu alue. Jos tilanmuutokset olisi tehty kuvassa vastapäivään, olisi yhtä jaksoa kohti työ ollut negatiivinen. Tämä on tilanne esimerkiksi lämpöpumpun tai jäähdytyskoneen kohdalla. Kuva 7-4 Kaasun kiertoprosessissa p tasossa. 7.3 Laajenemistyön erityistapauksia 7.3. Työ isobaarisessa tilanmuutoksessa Yksinkertaisin laajenemistyön erityistapaus on isobaarinen tilanmuutos, jossa paine pysyy vakiona. Työn lausekkeesta saadaan tällöin 2 2 W = pd = p d = p( 2 ). (7.5) Yhtälö 7.5 on yleinen ja pätee mille tahansa isobaariselle laajenemistyölle kaikissa pt-systeemeissä. Ideaalikaasulle isobaarisessa prosessissa tehdyn työn lauseke voidaan tilanyhtälön avulla kirjoittaa myös muodossa ν W = kn( T2 T) = R(T 2 T). (7.6)
6 74 II Lämpöopin ensimmäinen pääsääntö Työ isotermisessä tilanmuutoksessa Ideaalikaasun tilanyhtälöstä saadaan p = ( knt / ). Sijoittamalla tämä työn lausekkeeseen saadaan 2 2 W = pd = knt josta integroimalla d, (7.7) W knt RT 2 2 = ln = ν ln. (7.8) Kuva 7-5 Kaasun tekemä työ isobaarisessa (a) ja isotermisessä (b) prosessissa. 7.4 Lämpöopin ensimmäinen pääsääntö 7.4. Määritelmä Lämpöopin ensimmäinen pääsääntö on lyhyesti sanottuna energian säilymislaki sovellettuna termodynamiikkaan. Ensimmäisen pääsäännön mukaan kaasun sisäenergian muutos tilanmuutoksessa 2 on yhtä suuri kuin kaasun saama lämpömäärä vähennettynä kaasun tekemällä työllä. Differentiaalisen pienelle tilanmuutokselle saamme du = δq δw = δq + δw ext. (7.9)
7 7.4 Lämpöopin ensimmäinen pääsääntö 75 Jos tilanmuutos on äärellinen, voidaan yhtälö 7.9 integroida alkupisteestä loppupisteeseen: U (7.0) U du = δq δw du = δq δw U U = Q W Ensimmäisen pääsäännön kuvaamaa energian säilymislakia on havainnollistettu kuvassa 7.6. aikka suureiden etumerkit ja keskinäiset suuruudet vaikuttavat yksinkertaisilta asioilta, niiden muistamista on helpotettu vielä yhteenvedolla taulukossa 7.2. Yllä olemme merkinneet energian differentiaalia du, kun taas differentiaalisia lämpömääriä ja töitä on merkitty δ Q ja δ W vastaavasti. Olemme käyttäneet eri merkintää korostaaksemme, että lämpömäärä ja työ eivät ole tilanfunktioita ts. niiden differentiaaleja ei Kuva 7-6 Energiavirtojen suunta ensimmäisessä pääsäännössä (a) esitettynä systeemin tekemän työn avulla ja (b) ympäristön tekemän työn avulla. voida ymmärtää usean muuttujan funktion kokonaisdifferentiaaleiksi. Tilanmuutoksessa ( p, T, ) ( p + dp, T + dt, + d ) sisäenergian muutos riippuu Taulukko 7.2 Sisäenergian, työn ja lämpömäärän etumerkit tärkeimmissä perustapauksissa. Positiivinen Negatiivinen Q systeemi saa lämpöä systeemi luovuttaa lämpöä W systeemi tekee työtä ympäristö tekee työtä W ext ympäristö tekee työtä systeemi tekee työtä U sisäenergia kasvaa sisäenergia pienenee
8 76 II Lämpöopin ensimmäinen pääsääntö vain alku- ja loppupisteistä du = U ( p + dp, T + dt, + d ) U ( p, T, ). sen sijaan suureet δqjaδ W riippuvat myös siitä, miten (mitä reittiä pitkin p-tasossa) tilanmuutos tapahtuu. 7.5 Ensimmäinen pääsääntö ja pt -systeemin tilanmuutokset Tarkastelemme seuraavassa lyhyesti I pääsäännön soveltamista tärkeimpiin tilanmuutoksiin Adiabaattinen prosessi Systeemi on lämpöeristetty tilanmuutoksen aikana, joten systeemin saama lämpömäärä δ Q = 0. Adiabaattista prosessia käsitellään lähemmin myöhemmin tässä luvussa. Ensimmäisestä pääsäännöstä saadaan U = W. (7.) Isokoorinen prosessi Tilavuus on vakio, joten kaasun tekemä työ δ W = pd = 0 ja ensimmäisestä pääsäännöstä saadaan U = δq. (7.2) Ideaalikaasun isoterminen prosessi Ideaalikaasulle U T, joten jos T = vakio, niin U = δq δw = 0 δq = δw. (7.3) Ideaalikaasun saama lämpömäärä isotermisessä prosessissa on siis sama kuin sen tekemä työ. Äärellisessä tilanmuutoksessa 2 saadaan lämpömääräksi ( ) Q = kntln /. (7.4) 2 2
9 7.6 Muita konfiguraatiotöitä Kiertoprosessi Kiertoprosessissa systeemi palaa alkuperäiseen tilaansa, joten U = 0. Tästä seuraa: U = Q W = 0 Q = W. (7.5) Kiertoprosessin aikana systeemin tekemä työ on siis yhtä suuri kuin systeemin saama lämpömäärä. Esimerkki 7.. Ideaalikaasu suorittaa kuvan kiertoprosessin 00 kertaa minuutissa. Laske kaasun tekemän työn teho. Lasketaan systeemin tekemä työ yhtä kiertoprosessia kohden W = W + W = pd + pd = AB BC 20 bar 6 0 bar 6 = 6 0 J Tästä saadaan teho eli työ/aika: B A C B 3 Kuva 7-7 Kiertoprosessissa tehty työ on paineen kuvaajan rajoittaman alueen pinta-ala. W 00 6 kj P = = = 0 kw. t 60 s 7.6 Muita konfiguraatiotöitä Olemme aiemmin osoittaneet, että kiinteästä aineesta valmistetun palkin tekemä työ sen pituuden muuttuessa differentiaalisen määrän on dw = FdL, missä F on palkissa vaikuttava voima (venyttävä voima positiivinen). Yleisesti voidaan osoittaa, että systeemin tekemä työ voidaan aina esittää intensiivisen muuttujan Y ja ekstensiivisen muuttujan dx tulona: dw = YdX. (7.6)
10 78 II Lämpöopin ensimmäinen pääsääntö Tällaisesta työstä käytetään nimitystä konfiguraatiotyö. Kaasun laajenemistyö on myös esimerkki konfiguraatiotyöstä. Tarkastelemme vielä esimerkkinä magnetoitumistyötä, joka on myös yhtälön 7.6 esittämää muotoa eli konfiguraatiotyötä. Esimerkki 7.2. Magnetoitumistyö Kuten luvussa 5.7 olemme osoittaneet, isotrooppisessa paramagneettisessa väliaineessa magnetoituma on Curien lain pätemisalueella suoraan verrannollinen magneettikentän voimakkuuteen ja kääntäen verrannollinen lämpötilaan: M = CCH/ T = χmh, missä χ m on magneettinen suskeptiivisuus. Magneettikentän energiatiheys väliaineessa voidaan esittää muodossa w = H B, (7.7) 2 (ks. I. Lindell ja A. Sihvola: Sähkömagneettinen kenttäteoria I, Staattiset kentät, luku 6). Magneettivuon tiheyttä B, magneettikentän voimakkuutta H ja magnetoitumaa M sitoo toisiinsa yhtälö B = µ 0 ( H + M ). (7.8) Sijoittamalla tämä yhtälöön 7.7 ja muodostamalla energiatiheyden differentiaali saamme dw = d = 0d + 0d ( H B) µ ( H H) µ ( H M ). (7.9) Yhtälön 7.9 ensimmäisestä termistä saadaan µ 0H dh. (7.20) Tämä energia liittyy kentän voimakkuuden kasvattamiseen eikä riipu väliaineesta. Yhtälön 7.9 toisesta termistä saadaan µ 0d µ 0χ md µ 0 d 2 2 ( H M) = ( H H) = H M. (7.2) Yhtälön 7.2 antama energiatiheyden lisäys on magnetoitumiseen liittyvä työ tilavuusyksikköä kohden. Jos määrittelemme polarisaatiomomentin yhtälöllä TOT = µ 0 P M, (7.22)
11 7.7 pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti 79 voimme esittää systeemin tekemän magnetoitumistyön muodossa dwm = H dp TOT. (7.23) Tämä on muodoltaan yhtälön 7.6 mukainen konfiguraatiotyö. 7.7 pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti Nestettä ja kaasua kutsutaan usein yhteiseltä nimeltään fluidiksi. Nesteen ja kaasun termodynaaminen tila määräytyy paineen, lämpötilan ja tilavuuden perusteella edellyttäen, että gravitaation ja muiden ulkoisten kenttien vaikutus systeemin tilaan on merkityksetön. Ominaislämpö on käsitteenä tullut aiemmin tutuksi tilastollisen mekaniikan osassa, mutta seuraavassa pyrimme määrittelemään sen täsmällisemmin käyttämällä esimerkkinä pt-systeemiä Ominaislämmön määritelmä Kokeellisesti on havaittu, että kaasun tai nesteen lämpötila kasvaa, kun systeemiin virtaa lämpöä. Tarkastellaan lähemmin systeemin tilan pientä muutosta, kun systeemiin tuodaan pieni lämpömäärä δ Q. Lämpötilan muutoksen tunteminen ei riitä fluidin termodynaamisen tilan muutoksen määräämiseen, sillä lämpötilan lisäksi fluidilla on aina toinen riippumaton tilanmuuttuja. Tiettyä systeemiin tuotua lämpömäärää δ Q kohti tapahtuva lämpötilan nousu riippuu tämän toisen tilanmuuttujan muutoksesta sinä aikana, kun δ Q tuodaan systeemiin. Olkoon δ Q se lämpömäärä, joka systeemiin on tuotava, jotta sen lämpötila nousee määrällä dt. Systeemin lämpökapasiteetti moolia kohden on tällöin δ Q c. (7.24) ν dt Systeemiin tuotu lämpö äärellisessä tilanmuutoksessa 2 saadaan kertomalla yhtälö 7.24 puolittain differentiaalilla dt ja integroimalla
12 80 II Lämpöopin ensimmäinen pääsääntö T2 Q= ν cdt. (7.25) T Tarvittava lämpömäärä δ Q riippuu prosessista eli toisen riippumattoman tilanmuuttujan muutoksesta. Tästä syystä on tapana merkitä ominaislämmölle alaindeksi, joka kertoo, minkälaisen tilanmuutoksen yhteydessä lämpömäärä δ Q tuodaan systeemiin. Erityisesti, jos jokin tilanmuuttuja x on tässä prosessissa vakio, merkitään: x = δ Q c ν dt. (7.26) x Esimerkiksi, jos lämpömäärä δ Q tuodaan systeemiin pitämällä tilavuutta vakiona, sijoitetaan x =, jolloin saadaan c δ Q = ν dt. (7.27) Yhtälön 7.27 määrittelemää ominaislämpöä kutsutaan ominaislämmöksi vakiotilavuudessa. Ominaislämmön vakiopaineessa määrittelee vastaavasti yhtälö δ Q cp = ν dt p. (7.28) Ominaislämpö voidaan määritellä periaatteessa mille tahansa tilanmuutokselle. Myöhemmin tarkastelemme yleiseen kaasun kvasistaattiseen prosessiin liittyvää ominaislämpöä. Systeemin kokonaislämpökapasiteetti (tai usein lyhyesti lämpökapasiteetti) on moolinen ominaislämpö kerrottuna ainemäärällä. CTOT, x = ν cx. Ominaislämpö riippuu yleensä tilanmuuttujista. Olemme jo tilastollisen mekaniikan osuudessa todenneet, että ominaislämpö riippuu kaasumolekyylien aktiivisten vapausasteiden määrästä. Koska esimerkiksi värähtelyvapausasteiden mukaantulo tapahtuu laajan lämpötilavälin alueella, omi-
13 7.7 pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti 8 naislämpö kasvaa hitaasti lämpötilan funktiona. Myös molekyylien välinen vuorovaikutus aiheuttaa ominaislämmön riippuvuuden tilanmuuttujista. Jos ominaislämpö c on vakio, voidaan tilanmuutokseen 2 liittyvä lämpömäärä esittää muodossa Q = ν cx ( T2 T ). (7.29) pt-systeemin ominaislämpö ja ensimmäinen pääsääntö Johdamme seuraavaksi ensimmäisen pääsäännön avulla eräitä keskeisiä pt-systeemin ominaislämmölle päteviä tuloksia. Ominaislämmön määritelmän perusteella δq cx = δqx = νcxdt, (7.30) ν dt x missä alaindeksi on merkkinä siitä, että muutokset on laskettava tietylle indeksin x määräämälle tilanmuutokselle. Sisäenergian U = U( T, ) kokonaisdifferentiaali taas voidaan ensimmäisen pääsäännön perusteella kirjoittaa du = δq δw. (7.3) Kvasistaattisessa isokoorisessa prosessissa d = 0, joten δw = pd = 0 du = = δq. (7.32) Sijoittamalla tämä yhtälöön 7.30 saadaan isokooriselle prosessille: du = ν cdt. (7.33) Merkitsimme sisäenergian differentiaalille alaindeksin osoittamaan, että differentiaali on muodostettu tietylle tilanmuutokselle. Tarkasteltaessa systeemin saamaa lämpömäärää isobaarisessa prosessissa on edullista käyttää apuvälineenä entalpiaa. Entalpia määritellään yhtälöllä H U + p dh = du + pd + dp. (7.34)
14 82 II Lämpöopin ensimmäinen pääsääntö Entalpia on siis tilanfunktio, kuten sisäenergiakin. pt-systeemin entalpian differentiaalille saadaan du = δq pd dh = δq+ dp. (7.35) akiopaineessa dp = 0, joten entalpian muutos on tällöin yhtä suuri kuin systeemin saama lämpömäärä: dh p = δ Q. (7.36) Yhtälön 7.30 perusteella δ ν Qp = cpdt. (7.37) Sijoittamalla tämä yhtälöön 7.36 saadaan ν dh p = cpdt. (7.38) Yhtälöt 7.33 ja 7.38 voidaan kirjoittaa äärelliselle tilanmuutokselle muodossa T2 U2 U = ν c dt (vakiotilavuudessa) (7.39) T ja T2 H2 H = ν cpdt (vakiopaineessa) (7.40) T vastaavasti Ideaalikaasun ominaislämmöt Ideaalikaasun molekyyleillä ei ole keskinäistä vuorovaikutusta, joten sisäenergia on molekyylien kineettisen energian ja rotaatio- ja värähtelyenergioiden summa. Yleisesti U = U( T) = (/2) fν RT, (7.4)
15 7.7 pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti 83 missä f on efektiivisten vapausasteiden lukumäärä lämpötilassa T (f = aktiivisten vapausasteiden kokonaismäärä laskettuna siten, että aktiivisten värähtelyvapausasteiden lukumäärä kerrotaan kahdella, kertaa luku 2.6) ja ν ainemäärä mooleina. Yhtälöstä 7.33 saadaan du = νc dt = ν frdt. (7.42) 2 Jakamalla yhtälö 7.42 differentiaalilla dt saadaan ominaislämpö vakiotilavuudessa: c U du = = ν T ν dt = 2 fr. (7.43) Huomaa, että osittaisdifferentiaali voitiin korvata kokonaisdifferentiaalilla. Myös ideaalikaasun entalpia riippuu vain lämpötilasta. Käyttämällä ideaalikaasun tilanyhtälöä saadaan H = U + p = U + νrt = ( f + 2) νrt, (7.44) 2 joten dh = ( f + 2) ν RdT. (7.45) 2 Entalpian kokonaisdifferentiaali voidaan esittää yhtälön 7.45 avulla muodossa H H dh ( T, p) = dt + dp T p p H = dt = νcpdt = ( f + 2) νrdt. T 2 p T (7.46) Jakamalla yhtälö 7.46 lämpötilan differentiaalilla dt saadaan dh cp = ( f 2) R ν dt = 2 +. (7.47)
16 84 II Lämpöopin ensimmäinen pääsääntö Ominaislämpö vakiopaineessa on suurempi kuin ominaislämpö vakiotilavuudessa, sillä nostettaessa systeemin lämpötilaa vakiopaineessa, on systeemin saatava laajentua, jolloin systeemi tekee työtä. Tähän työhön kuluva energia on tuotava kaasuun lämpönä. astaavaa energiahäviötä ei esiinny lämmitettäessä kaasua vakiotilavuudessa. Yhtälöt du = ν c dt ja dh = ν cpdt ovat voimassa ideaalikaasun tilanmuutokselle prosessin tyypistä riippumatta. Tämä johtuu siitä, että ideaalikaasun sisäenergia ja entalpia riippuvat vain lämpötilasta. Ideaalikaasun ominaislämpöjen erotukselle ja suhteelle saadaan: ominaislämpöjen erotus: cp c = R (7.48) cp ( f + 2) R 2 ominaislämpöjen suhde: γ = = = + (7.49) c fr f Suuretta γ kutsutaan myös adiabaattivakioksi syystä, johon palaamme seuraavassa luvussa. Esimerkiksi kaksiatomiselle ideaalikaasulle, jossa rotaatiovapausasteet ovat virittyneet, mutta värähtely ei, f = 5 ja adiabaattivakioksi saadaan 2 7 γ = + = =, Yksiatomiselle kaasulle f = 3, joten 2 γ = +, Ominaislämpöjen c p ja c erotus reaalikaasuille Ensimmäisen pääsäännön perusteella voimme kirjoittaa δ Q = du + pd. (7.50) Sijoittamalla tähän sisäenergian differentiaali yhtälöstä 7.3 saadaan
17 7.7 pt-systeemin (kaasu, neste) ominaislämpö ja lämpökapasiteetti 85 δ U U Q = dt + + p d. (7.5) T T Sijoittamalla tähän ominaislämmön vakiotilavuudessa yhtälöstä 7.34 saamme δ U Q = νc dt + + p d T. (7.52) Laskemme nyt suureen 7.52 arvon tilanmuutokselle, joka tapahtuu vakiopaineessa. Tällöin yhtälön vasen puoli antaa δ Qp = cpdt. Laskemalla myös yhtälön oikea puoli vakiopaineessa saadaan: ( p ) U c dt = ν c p dt + + p d T Jakamalla puolittain differentiaalilla dt ja siirtämällä ominaislämmöt vasemmalle puolelle saadaan p. U Um m cp c = + p = + p ν T T p m T, (7.53) T p missä viimeinen esitysmuoto on kirjoitettu moolisen tilavuuden ja sisäenergian avulla. Ideaalikaasulle huomataan helposti, että yhtälön 7.52 oikea puoli antaa tulokseksi kaasuvakion R. Seuraavassa laskemme ominaislämpöjen erotuksen van der Waalsin kaasulle. Esimerkki 7.3. van der Waalsin kaasun sisäenergia moolia kohden voidaan a kirjoittaa muodossa Um = frt + vakio. Johda ominaislämpöjen erotus 2 m van der Waalsin kaasulle. Sisäenergian derivaataksi tilavuuden suhteen vakiolämpötilassa saadaan Um a = 2 m T m. (7.54) Lisäksi tarvitaan tilavuuden derivaatta lämpötilan suhteen vakiopaineessa. Kirjoittamalla tilanyhtälö moolisen tilavuuden avulla ja derivoimalla puolittain saadaan
18 86 II Lämpöopin ensimmäinen pääsääntö 2a a ( ) 3 m b + p+ d 2 m = RdT m m (vakiopaineessa). (7.55) Jakamalla lämpötilan differentiaalilla voimme kirjoittaa yhtälön 7.55 muodossa m 2a a = R 3( m b ) + p+ T 2 p m m Sijoittamalla 7.54 ja 7.56 yhtälöön 7.7 saadaan. (7.56) R 2a a cp c = RT 3( m b ) + p+ 2 m b m m. (7.57) Etsimällä yhteiset tekijät ja käyttämällä tilanyhtälöä 2 ( ) ( / ) m b = RT p+ a m saadaan lopputulokseksi R cp c = 2 a b / RT 2 3 ( m ) ( m). (7.58) Tarkastellaan lopuksi ominaislämpöjen erotusta hiilidioksidille normaaliolosuhteissa, jolloin van der Waalsin kaasu on lähellä ideaalikaasua. Koska jakajan toinen termi on pieni korjaus, voimme käyttää binomiapproksimaatiota /( x) + x ja lisäksi approksimoida korjaustermissä ilman suurta virhettä m b m ja pm = RT, jolloin 2ap cp c R R T Hiilidioksidin van der Waalsin vakio a = Jm mol, joten 300 K 2 2 lämpötilassa ja,9 baarin paineessa 2 a /( RT) 0. Ominaislämpöjen erotus on van der Waalsin kaasulle cp c R yhden prosentin tarkkuudella. 7.8 Ideaalikaasun adiabaattinen prosessi Tilanmuutosta, joka on () kvasistaattinen ja (2) jonka aikana systeemi on lämpöeristetty (jolloin Q = 0 ), sanotaan adiabaattiseksi. Seuraavassa käsittelemme lähemmin ideaalikaasun adiabaattista prosessia.
19 7.8 Ideaalikaasun adiabaattinen prosessi Paineen ja tilavuuden yhteys adiabaattisessa prosessissa Johdamme aluksi adiabaattiselle prosessille paineen ja tilavuuden välisen yhteyden ideaalikaasun tilanyhtälön avulla. Adiabaattisen prosessin tilanyhtälö on johdettu jo aiemmin kineettisen teorian avulla luvussa 2.4. Sisäenergian differentiaalille saadaan adiabaattisessa prosessissa du = δq δw = ν frdt = pd, (7.59) 2 sillä oletuksen perusteella δ Q = 0. Ideaalikaasun tilanyhtälöstä ν RT = p saamme derivoimalla ν RdT = pd + dp. (7.60) Kertomalla yhtälö 7.60 puolittain tekijällä (/2) f ja sijoittamalla saatu tulos yhtälöön 7.59 saadaan 2 ( ) f pd + vdp = pd, (7.6) josta uudelleen järjestelyllä dp f + 2 d d = = γ. (7.62) p f Yhtälössä 7.62 käytettiin lopuksi adiabaattivakion määritelmää Makroskooppinen tilanmuutos Integroidaan differentiaaliyhtälö 7.62 mielivaltaiselle äärelliselle tilanmuutokselle p T p2t22 p2 2 2 dp d d p2 ln ln 2 ln = p γ γ = γ = γ. (7.63) p p 2 Ottamalla puolittain eksponenttifunktion saamme γ γ p = p22.
20 88 II Lämpöopin ensimmäinen pääsääntö Koska pisteet ja 2 valittiin mielivaltaisesti, voidaan adiabaattiselle tilanmuutokselle kirjoittaa yleisesti p γ = vakio. (7.64) Yhtälöä 7.63 voidaan pitää myös ideaalikaasun adiabaattisen prosessin vaihtoehtoisena määritelmänä Työ ja sisäenergia adiabaattisessa muutoksessa Yhtälön 7.64 perusteella (merkitään yhtälön 7.64 vakiota kirjaimella a) saadaan työn lausekkeeksi 2 2 γ γ ( 2 ) γ a W = pd = a d = γ (7.65) Sijoittamalla yhtälöstä 7.65 a = p2 γ 2 (ensimmäinen termi) ja a = p γ (toinen termi) saadaan ν R W = ( p22 p ) ( T2 T) =, (7.66) γ γ missä käytettiin lopuksi tilanyhtälöä. Sijoittamalla adiabaattivakion määritelmästä 2/ f γ = + saadaan W = fν R( T T2) = U U2. (7.67) 2 Adiabaattisessa prosessissa systeemin tekemä työ on systeemiin sisäisen energian lisäyksen vastaluku. Tämä seuraan myös ensimmäisestä pääsäännöstä, sillä adiabaattisessa prosessissa Q = 0, joten U2 U = Q W = W. Kuva 7.8 esittää paineen ja tilavuuden suhdetta isotermisessä ja adiabaattisessa laajentumisessa pa, A, TA pb, B, TB. Huomaa, että adiabaattisen prosessin paineen kuvaaja on aina isotermisen prosessin paineen alapuolella. Adiabaattisessa prosessissa lämpötila laskee laajenemisen aikana ja tämä nopeuttaa paineen alenemista. Paineen kuvaaja isotermisessä muutoksessa on
21 7.8 Ideaalikaasun adiabaattinen prosessi 89. A = ν A = A p RT p Adiabaattiselle prosessille saamme vastaavasti paine-tilavuus suhteesta p γ = vakio ja täten p γ p A = A. Adiabaattivakion määritelmän perusteella γ >, joten paine laskee nopeammin adiabaattisessa kuin isotermisessä tilanmuutoksessa. Kuva 7-8 Paineen käyttäytyminen ideaalikaasun isotermisessä ja adiabattisessa tilanmuutoksessa. Esimerkki 7.4. Kaasunäytteen annetaan laajeta adiabaattisesti, jolloin sen paine alenee 20 kpa:sta 00 kpa:iin samalla kun lämpötila laskee 300 K:stä 280 K:iin. Onko kaasu yksiatomista vai kaksiatomista? Ko. lämpötilassa mahdolliset rotaatio-vapausasteet ovat virittyneet. γ γ Adiabaattiselle prosessille pätee p = p22. Sijoittamalla νrt νrt 2 = ja 2 =, p p2 saadaan / γ / γ / γ p T p 2 2 T2 = p T = p2 T. Ottamalla tästä puolittain logaritmi saadaan ln( T2/ T) γ.6 γ = ln( p/ p2) = =. Kaksiatomiselle kaasulle (viisi vapausastetta) γ =, 40 ja yksiatomiselle kaasulle (kolme vapausastetta) γ =, 67, mistä päätellään, että kaasu on yksiatomista. Esimerkki 7.5. Pitkittäisten aaltojen nopeus kaasussa on
22 90 II Lämpöopin ensimmäinen pääsääntö dp c =, (7.68) d ρ missä p on kaasun paine ja ρ kaasun tiheys. Johda ideaalikaasulle äänen nopeus olosuhteissa, joissa kaasun tilanmuutokset ovat a) adiabaattisia ja b) isotermisiä. Huomaa, että entropian määritelmän ds = δ Q / T mukaan, entropia on vakio adiabaattisessa tilanmuutoksessa. Taustaa: Koska kaasussa etenevän aallon nopeus on yleensä tapana esittää hieman eri muodossa kuin tässä tehtävässä, palautamme aluksi mieliin sähkö- ja aaltoliikeopin yhteydessä johdetun kaasussa etenevän ääniaallon nopeuden lausekkeen c = / κρ, (7.69) missä κ = P S (7.70) on adiabaattinen kokoonpuristuvuus. Huomattakoon, että ρ on tässä kaasun massatiheys tilavuusyksikköä kohden, eli ρ ( N/ ) m ( ν / ) m on yhden molekyylin massa ja M moolimassa. = = M, missä Äänen nopeus adiabaattisissa värähtelyissä (yhtälöiden 7.69 ja 7.70 perusteella) Adiabaattisen kokoonpuristuvuuden käyttö on perusteltua, kun ääniaallon värähtelyt tapahtuvat niin nopeasti, ettei kaasussa ehdi tapahtua lämmön siirtymistä kaasun eri osien välillä (aallonpituuden mittakaavassa). Kaasun laajeneminen ja supistuminen tapahtuu siis adiabaattisesti. Adiabaattisen prosessin yhtälöstä saamme / γ γ a p = a =. / γ p Derivoimalla paineen suhteen (entropia on vakio) saadaan / γ a = = p / γ + p S p γ γ. (7.7) kokoonpuristuvuudeksi ( ) Sijoittamalla yhtälö (7.7) yhtälöön 7.70 saamme adiabaattiseksi κ = γ p. Kaasun tiheydelle pätee ρ = νm /, joten äänen nopeudeksi saadaan yhtälöstä 7.69
23 7.9 Ideaalikaasun polytrooppinen prosessi 9 ν M c = /. γ p Käyttämällä vielä tilanyhtälöä p = ν RT saadaan äänen nopeudeksi /2 γ RT c =. M Isoterminen aaltoliike Tarkastelemme nyt lähemmin isotermistä aaltoliikettä ideaalikaasulle. Ideaalikaasun tilanyhtälöstä saadaan ν p = RT = ρrt/ M. Sijoittamalla tehtävän määritelmään (7.68) saamme ρ p = T RT M. Isotermiseksi nopeudeksi saadaan dp RT c = dρ = M. Johdamme lopuksi adiabaattisen ääniaallon nopeuden lähtien yhtälöstä (7.68). Käyttämällä yllä johdettuja tuloksia saadaan p p γ p γ p ν M γ pν M = = = = ρ 2 2 S S ρ ρ ρ ρ. Sijoittamalla lopuksi ρ = νm / saamme kuin yllä yhtälön 7.69 perusteella. /2 γ RT c = M eli saman tuloksen 7.9 Ideaalikaasun polytrooppinen prosessi 7.9. Polytrooppisen prosessin ominaislämpö Polytrooppinen tilanmuutos on adiabaattisen prosessin yleistys, jossa suure p τ on vakio tilanmuutoksen aikana. Tässä τ on niin sanottu polotrooppivakio. Yleisesti τ γ, mutta adiabaattinen prosessi on tietenkin polytrooppisen prosessin erikoistapaus. Oletetaan aluksi, että polytrooppi-
24 92 II Lämpöopin ensimmäinen pääsääntö sen prosessin ominaislämpö on lämpötilasta riippumaton vakio. Määritellään ominaislämpö yhtälöllä δq = νcτ dt (7.72) ja johdetaan yhteys polytrooppivakion τ ja ominaislämmön välille. Yhtälön 7.72 lisäksi käytämme kaikille ideaalikaasun tilanmuutoksille prosessista riippumatta päteviä yhtälöitä δq = du + pd = ν frdt + pd = νc dt + pd, (7.73) 2 ja δq = νc dt dp. (7.74) p Jälkimmäinen seuraa edellisestä käyttämällä ominaislämpöjen erotusta c c = R ja yhtälöä p Sovelletaan nyt yhtälöitä ( ) polytrooppiseen prosessiin. Merkitään yhtälöissä ( ), yhtälöiden vasemmat puolet δq = νcτ dt. Ratkaistaan (7.73) p :n ja (7.74) dp :n suhteen. Jakamalla yhtälöt puolittain saadaan dp cτ cp d = p cτ c. (7.75) Polytrooppisen prosessin määritelmän mukaan p τ = vakio. Ottamalla τ τ tästä kokonaisdifferentiaali saamme ( τ ) uudelleenjärjestelyllä dp + p d = 0, josta edelleen dp d = τ. (7.76) p Yhtälö 7.76 vastaa adiabaattisen prosessin tarkastelun yhtälöä Yhtälöt 7.75 ja 7.76 ovat yhtä aikaa voimassa vain, jos
25 7.9 Ideaalikaasun polytrooppinen prosessi 93 τ c c τ p = cτ c. (7.77) Työ polytrooppisessa prosessissa Kaasun tekemä työ polytrooppisessa prosessissa lasketaan samaan tapaan kuin adiabaattisen prosessin työ: ( 2 ) 2 2 τ a τ τ W = pd = a d = τ. Sijoittamalla a = p 2 τ 2 (ensimmäinen termi) ja a = p τ (toinen termi) saadaan R W = ν ( p22 p ) ( T2 T) τ = τ. (7.78) Huomaa, että mielivaltaisella τ :n arvolla ν R W = ( T T ) U U τ 2 2, (7.79) sillä δ Q = 0 on voimassa vain silloin, kun τ = γ eli kun prosessi on adiabaattinen Polytrooppivakion ja vastaavan ominaislämmön suhde Määritelmän 7.26 mukaan (oletetaan, että c τ ei riipu lämpötilasta ) T2 τ τ τ( 2 ). (7.80) T δq = νc dt Q = ν c dt = νc T T Ensimmäisen pääsäännön ja yhtälön 7.79 perusteella ν R Q = U U + W = U U T T τ ( ) (7.8) Sijoittamalla tähän ideaalikaasun sisäenergia U = (/2) ν frt saadaan
26 94 II Lämpöopin ensimmäinen pääsääntö νr νr Q2 = fνr ( T2 T) = νc ( T2 T). (7.82) 2 τ τ Yhtälön 7.8 mukaan yhtälön oikea puoli on ν cτ ( T2 T), joten ominaislämmöksi saadaan R R cτ = c = c + τ τ. (7.83) Taulukko 7.4 Polytrooppisen prosessin erikoistapauksia τ = 0 cτ = cp isobaarinen prosessi τ =± c τ = c Isokoorinen " τ = c τ =± isoterminen " τ = γ c τ = 0 adiabaattinen " Polytrooppinen prosessi on aiemmin käsiteltyjen kvasistaattisten tilanmuutosten yleistys, ja useimmat kaasun tilanmuutokset voidaan esittää polytrooppisen prosessin erikoistapauksina. Oheisessa taulukossa on yhteenveto eri kvasistaattisiin tilanmuutoksiin liittyvistä polytrooppivakioista ja ominaislämmöistä. Kuva 7-9 Paine tilavuuden funktiona polytrooppisen prosessin erityistapauksissa.
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Luku6 Tilanyhtälö. Ideaalikaasun N V. Yleinen aineen. paine vakio. tilavuus vakio
 Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
VI TILANYHTÄLÖ
 VI TILANYHTÄLÖ... 150 6.1 Ideaalikaasun tilanyhtälö...150 6. Van der Waalsin tilanyhtälö...151 6..1 Semiempiirinen lähestymistapa...151 6.. Van der Waalsin kaasun ominaisuuksia:...154 6..3 Van der Waalsin
VI TILANYHTÄLÖ... 150 6.1 Ideaalikaasun tilanyhtälö...150 6. Van der Waalsin tilanyhtälö...151 6..1 Semiempiirinen lähestymistapa...151 6.. Van der Waalsin kaasun ominaisuuksia:...154 6..3 Van der Waalsin
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
3Työ. 3.1 Yleinen määritelmä
 3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
X JOULEN JA THOMSONIN ILMIÖ...226
 X JOULEN JA HOMSONIN ILMIÖ...6 10.1 Ideaalikaasun tilanyhtälö ja sisäenergia... 6 10. van der Waals in kaasun sisäenergia... 7 10..1 Reaalikaasun energiayhtälö... 7 10.. van der Waalsin kaasun entroia...
X JOULEN JA HOMSONIN ILMIÖ...6 10.1 Ideaalikaasun tilanyhtälö ja sisäenergia... 6 10. van der Waals in kaasun sisäenergia... 7 10..1 Reaalikaasun energiayhtälö... 7 10.. van der Waalsin kaasun entroia...
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
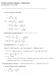 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi [email protected] Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi [email protected] Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Termofysiikan perusteet
 Termofysiikan perusteet Ismo Napari ja Hanna Vehkamäki T 2 Q 2 C W Q 1 T 1 (< T 2 ) Helsingin yliopisto, 2013 (Päivitetty 18. joulukuuta 2013) Sisältö 1 Johdanto 1 1.1 Termofysiikan osa-alueet.......................
Termofysiikan perusteet Ismo Napari ja Hanna Vehkamäki T 2 Q 2 C W Q 1 T 1 (< T 2 ) Helsingin yliopisto, 2013 (Päivitetty 18. joulukuuta 2013) Sisältö 1 Johdanto 1 1.1 Termofysiikan osa-alueet.......................
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja [email protected] Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja [email protected] Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
Ensimmäinen pääsääntö
 4 Ensimmäinen ääsääntö Luvuissa 2 ja 3 käsiteltiin eri taoja siirtää energiaa termodynaamisten systeemien välillä joko lämmön tai työn kautta. 1840-luvulla erityisesti Robert Julius von Mayern ja James
4 Ensimmäinen ääsääntö Luvuissa 2 ja 3 käsiteltiin eri taoja siirtää energiaa termodynaamisten systeemien välillä joko lämmön tai työn kautta. 1840-luvulla erityisesti Robert Julius von Mayern ja James
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
7 Termodynaamiset potentiaalit
 82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit
 19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 [email protected] 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 [email protected] 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
DEE Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen 2 ratkaisuiksi
 DEE-4000 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen ratkaisuiksi Yleistä asiaa lämmönjohtumisen yleiseen osittaisdifferentiaaliyhtälöön liittyen Lämmönjohtumisen yleinen osittaisdifferentiaaliyhtälön
DEE-4000 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen ratkaisuiksi Yleistä asiaa lämmönjohtumisen yleiseen osittaisdifferentiaaliyhtälöön liittyen Lämmönjohtumisen yleinen osittaisdifferentiaaliyhtälön
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
